Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Mar 1.
Published in final edited form as: Ceram Int. 2016 Dec 1;43(4):3670–3678. doi: 10.1016/j.ceramint.2016.11.209

THERMAL RESIDUAL STRESSES IN BILAYERED, TRILAYERED AND GRADED DENTAL CERAMICS

Douglas Fabris a, Júlio CM Souza b,c, Filipe S Silva b, Márcio Fredel a, Joana Mesquita-Guimarães a, Yu Zhang d, Bruno Henriques a,c,*
PMCID: PMC5289668  NIHMSID: NIHMS842990  PMID: 28163345

Abstract

Layered ceramic systems are usually hit by residual thermal stresses created during cooling from high processing temperature. The purpose of this study was to determine the thermal residual stresses at different ceramic multi-layered systems and evaluate their influence on the bending stress distribution. Finite elements method was used to evaluate the residual stresses in zirconia-porcelain and alumina-porcelain multi-layered discs and to simulate the ‘piston-on-ring’ test. Temperature-dependent material properties were used. Three different multi-layered designs were simulated: a conventional bilayered design; a trilayered design, with an intermediate composite layer with constant composition; and a graded design, with an intermediate layer with gradation of properties. Parameters such as the interlayer thickness and composition profiles were varied in the study. Alumina-porcelain discs present smaller residual stress than the zirconia-porcelain discs, regardless of the type of design. The homogeneous interlayer can yield a reduction of ~40% in thermal stress relative to bilayered systems. Thinner interlayers favoured the formation of lower thermal stresses. The graded discs showed the lowest thermal stresses for a gradation profile given by power law function with p=2. The bending stresses were significantly affected by the thermal stresses in the discs. The risk of failure for all-ceramic dental restorative systems can be significantly reduced by using trilayered systems (homogenous or graded interlayer) with the proper design.

Keywords: Thermal residual stresses, functionally graded ceramic, zirconia, alumina, feldspar-based porcelain, multilayer

1. Introduction

All ceramic systems are nowadays the aesthetic standard for dental restorations. Dental restorations are made usually by a strong framework, responsible for withstanding masticatory stresses, and a veneer layer responsible for aesthetics. Zirconia and alumina have been used as framework materials due to their excellent mechanical properties, good aesthetic and biocompability [1–3]. Porcelain is the material chosen as veneer for both all-ceramic and metal-ceramic restorations, due to its colour that matches the remaining teeth. In the processing of all-ceramic restorations, porcelain is fired onto the framework at high temperatures, creating thermal residual stresses upon cooling to room temperature that arise mainly at their interfaces due to differences in the CTEs (Coefficients of Thermal Expansion) between the framework and the veneering porcelain [4,5]. In addition, the mismatch between the Young’s moduli creates stress fields upon the mastication that can lead to crack formation [5,6]. Tensile residual stresses formed in multimaterial prostheses have been pointed one of the major causes of catastrophic failure [5–11]. Failure types typically reported for alumina-based restorations are the core and the veneering ceramics fracture, while for the zirconia-based restorations is the chipping of the veneering ceramics [12–15]. Alumina crowns tend to present a catastrophic fracture with the cracks propagating through the core [15,16]. In zirconia crowns, chipping in the veneer layer prevails over other failure types, with cracks growing parallel to the interface [17,18]. Changes in design (layer thicknesses) and fabrication variables (cooling rates) have been shown to play a critical role in crack initiation and propagation in bilayered ceramic structures, with fast cooling leading to thermal fracture [19].

A solution to overcome this problem is using a composite interlayer with intermediate properties between the framework and the overlay that will reduce the mismatches in materials properties. An intermediate layer can account for a significant decrease of thermal and mechanical stresses arising from the mismatch between properties of the two materials. Studies have shown that gradation of properties across the two materials present excellent results related to residual stresses for dental restorations [20–26]. While several studies have demonstrated that graded prosthetic systems exhibit superior load-bearing capacity, improved damage resistance [23,24] and enhanced bond strength resistance [27], to the author’s best knowledge, little work has been reported on modeling thermal stresses in functionally graded restorations [22,25,28]. Functionally Graded Materials (FGMs) consist in a gradual change in the volume fraction between two phases [29]. Its design allows a smooth transition in thermal expansion coefficients, decreasing their mismatch and minimizing residual thermal stresses [30]. FGMs building parameters, such as the thickness and the transition configuration of the graded layer, can have great influence in the stress field and magnitude, thus it is important to optimize such parameters and minimise stresses in critical locations.

The standard methods to evaluate flexural strength of dental materials are the biaxial tests, such as piston-on-three balls and piston-on-ring tests. Biaxial tests generated a multiaxial stress state near the centre of the specimen, eliminating edge failures that occurs in uniaxial tests, resulting in a more accurate estimate of strength [31]. Besides, restorations are usually subjected to multiaxial loading due to the occlusal force, thus the biaxial test data are more meaningful for material design [32]. In biaxial tests, the sample, usually a disc, is supported on its lower surface and a load is applied on its upper surface. The load can be applied through either a ball, a ring or a piston, while the support usually is a ring or rigid balls.

The aim of this study was to determine the thermal residual stresses at different ceramic multi-layered discs and evaluate their influence on the bending stress distribution. Three different multilayered disc configurations were studied: a conventional bilayered design; a trilayered design, with an intermediate composite layer with constant composition; and a graded design, which has an intermediate layer with gradation of properties. Functionally graded materials can have different geometries or material distributions. The study of these parameters is important to optimize the residual stress state considering the component properties and its application. In this work, finite elements method was used to simulate the cooling of discs with different material distribution configuration and simulate a piston-on-ring test. The simulations were performed for discs made by both porcelain and zirconia, and porcelain and alumina. Different layer thicknesses and compositions were evaluated to minimize the residual tensile stresses. The results were compared to evaluate the influence of these parameters (thickness and composition of the interlayer) on the thermal and mechanical stresses.

2. Materials and methods

2.1. Material properties

In this study, zirconia (Y-TZP) and alumina were used as framework materials while feldspar-based porcelain was used as veneering material. In order to increase the accuracy of simulation, the temperature dependent properties of these homogeneous and isotropic materials where adopted from literature [19].

The properties of the composite materials (zirconia-porcelain and alumina-porcelain) used in the composite interlayers and graded interlayers, as presented ahead in the text, were estimated by Voigt’s rule of mixtures. Voigt’s rule of mixtures is given by:

Pi=PfVf+PvVv (1)

where Pi is the calculated property value of the intermediate layer, Pf and Pv are the property values of the framework and veneer materials, and Vf and Vv are the volume fraction of the materials in the composite.

2.2. Models and finite method analysis

2.2.1. Thermal residual stresses

The geometry chosen for the FEM analysis was a 2.7 mm layered disc with a radius of 4 mm, modelled with two or three layers, which mimics the three components of a dental restoration: the framework, the veneer and the interlayer with intermediate properties. The disc is subjected to a cooling simulating manufacturing process of dental restorations. The disc is cooled from 500°C to 20°C during 950 seconds. Three different situations were simulated (Figure 2): a classic sharp interface between zirconia/alumina and porcelain, a disc with an intermediate layer with constant composition between the two materials and an intermediate layer with a gradient of composition. The discs with residual stress are then subjected to a piston-on-ring biaxial test.

Figure 2.

Figure 2

Open in a new tab

Three different situations simulated: sharp disc, a disc with an interlayer, and a disc with gradation of composition

The bilayered discs (sharp transition) were made from a 2 mm thick top layer of feldspar-based porcelain and a 0.7 mm thick bottom layer of alumina (or zirconia (Y-TZP)).

The trilayered discs consist in a bottom layer of pure alumina (or zirconia) with 0.7 mm of thickness, a interlayer with varying thickness and a top felsdspar-based layer. Interlayers with 0.25 mm, 0.5 mm, 0.75 mm and 1 mm were simulated, decreasing the porcelain layer thickness with the increasing of interlayer thickness. Aditionally, five different interlayer compositions were simulated, consisting of different porcelain contents (10%, 30%, 50%, 70% and 90%, vol.%) in the zirconia-porcelain (or alumina-porcelain) composites.

The graded discs also have three layers; however, the intermediate layer has a gradient of composition between the alumina/zirconia and the porcelain layers. In this study, the gradient was considered as continuous. The gradient profiles studied were based on a power-law function (Eq. 3) and on a sigmoid function (Eq. 4).

fporc=(zt)p (3)
fporc=1001+e−z−zmeank (4)

where fporc is the volume fraction of porcelain, z is the distance from the bottom layer, zmean is half of the interlayer thickness and t is the thickness of the graded region. p and k are the parameters that change the function shape, meaning that different values of p and k lead to different material distribution. In this study, k was considered as one tenth of the thickness of the graded region, and p was considered as 0.5, 1 and 2. Figure 3 shows the change in composition according with these functions for a 1 mm graded layer.

Figure 3.

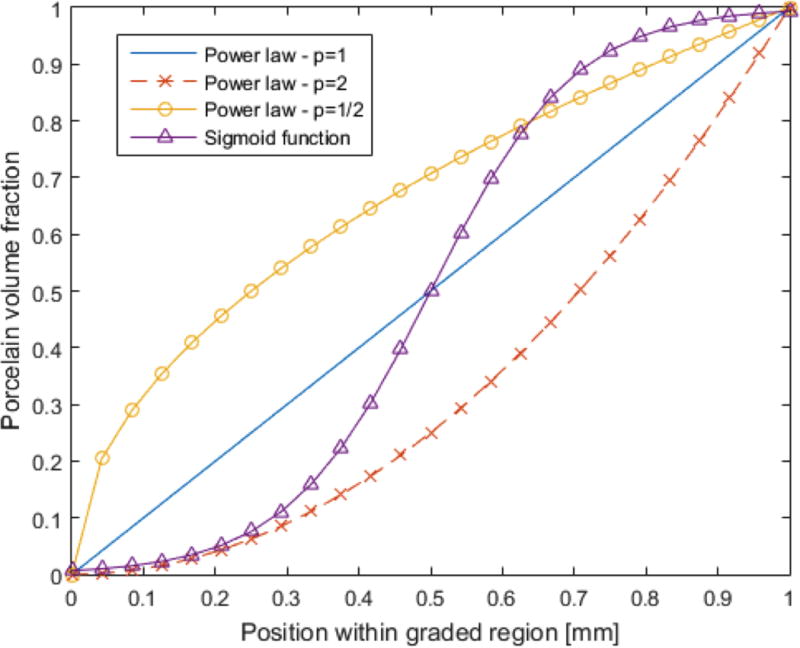
Figure 3

Open in a new tab

Change in porcelain volume fraction throughout the graded region for the power law and sigmoid functions.

Figure 4 and Figure 5 shows the evolution of CTE and Young’s modulus across discs with the different configurations used in this paper.

Figure 4.

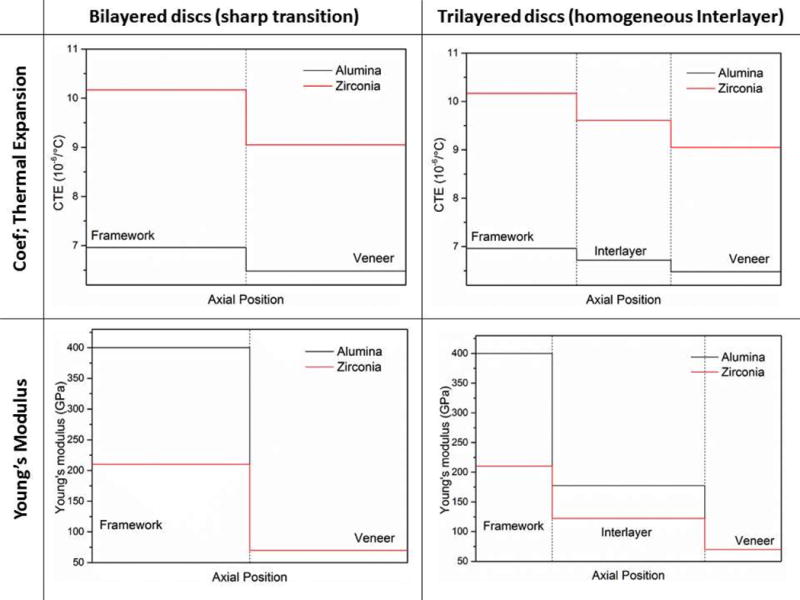
Figure 4

Open in a new tab

Evolution of the coefficient of thermal expansion (CTE) and Young’s modulus for the alumina/porcelain and zirconia/porcelain discs with sharp transition and an intermediate composite layer at 298 K.

Figure 5.

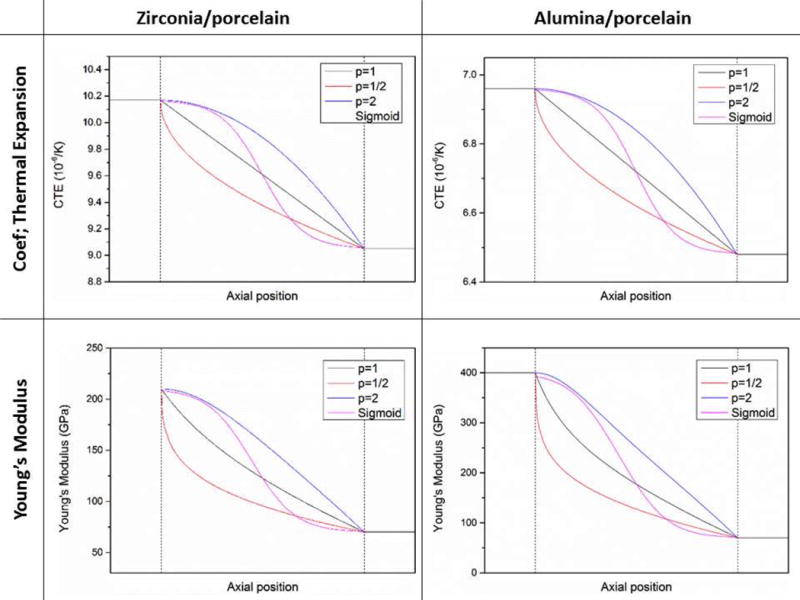
Figure 5

Open in a new tab

Evolution of the CTE and Young’s modulus for graded alumina/porcelain and zirconia/porcelain discs at 298 K.

2.2.2. Bending stress distribution considering thermal stresses

The influence of the thermal residual stresses in the bending stress distribution was determined for the classic bilayered and trilayered (with a homogeneous or graded interlayer) discs. The simulation procedure is described as follows.

Finite elements method was used to simulate the conditions of cooling and calculate the residual stress on the discs and use these results in the simulation of the piston-on-ring test. A two dimensional axisymmetric model was used to simplify and speed up the calculations. At the beginning of the simulation, the entire disc is considered to be at 773.15 K (500°C). The temperature on the disc walls then decreases from the initial temperature to 273.15 K (20°C) in 950 seconds. The generated stress state is then inserted as initial condition for the biaxial test simulation. In this test, the ring is considered fully constraint, supporting the disc, and the force is applied directly on the disc surface. The layers were considered fully bonded during the simulation. A fine free-triangular element size mesh was used, ensuring the accuracy of the simulation. The maximum size of each element was 0.148 mm in the superior and inferior layers and 0.08 mm in the intermediate layer. A finer mesh was used in the interlayer to increase the accuracy of composition gradient in the graded discs. The convergence analysis was performed in order to examine the sensitivity of the results to the size of the mesh. Differences in maximum principle stresses were found to be lower than 3% for consecutive mesh refinements. The FEA was conducted using the commercial finite element software COMSOL Multiphysics (Comsol Inc, Los Angeles, USA).

The piston-on-ring test consists of a disc supported by a rigid ring on its bottom surface, while a piston applies a perpendicular force at the centre of the disc top surface. The applied force generates a biaxial moment throughout the disc thickness, creating higher stresses at the centre of the disc. A schematic drawing of the piston-on-ring test is shown in Figure 6. In this work, the radius of the disc R is 4 mm, the radius c is 0.5 mm, the distance between the ring and the disc centre (a) is 3.4 mm and the applied force P is 500N.

Figure 6.

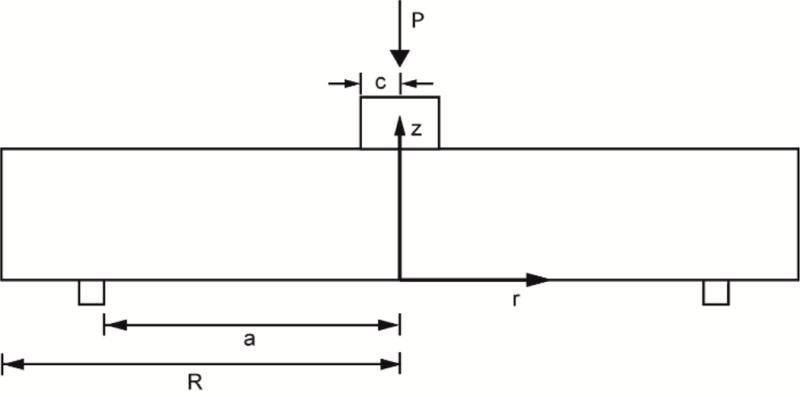
Figure 6

Open in a new tab

Schematic of a piston-on-ring biaxial test. P is the applied force.

3. Results

3.1. Bilayered discs

The three principal stresses were simulated on the disc. For the sharp transition, the maximum and minimum stresses for the zirconia-porcelain and alumina-porcelain discs are shown on Table 1. The maximum tensile stress is the first principal stress, which will be used as reference in the following studies involving trilayered discs. The maximum first principal stress is located at the centre of the disc, in the interface between layers.

Table 1.

Maximum and minimum principal stresses on the discs with sharp transition

First principal stress (zirconia/alumina) Second principal stress (zirconia/alumina) Third principal stress (zirconia/alumina)
Maximum 72.4/35 MPa 62.1/31 MPa 8/4 MPa
Minimum −5/−1.7 MPa −39/−17 MPa −63/−35 MPa
Open in a new tab

3.2. Trilayered discs with homogeneous interlayer

The resulting maximum principal stress is shown in Figure 7 for the interlayer with 0.25 mm (a), 0.5 mm (b), 0.75 mm (c) and 1 mm (d) thicknesses.

Figure 7.

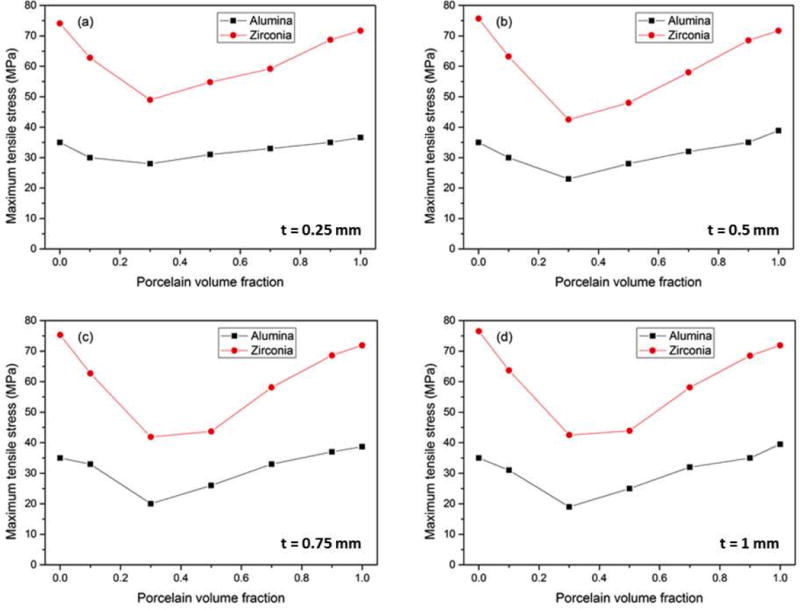
Figure 7

Open in a new tab

Simulated maximum tensiles stress for an interlayer thickness of (a) 0.25 mm, (b) 0.5 mm, (c) 0.75 mm and (d) 1 mm.

The alumina-porcelain discs present much smaller residual stress than the zirconia-porcelain discs. The stresses are minimized when the volume fraction of porcelain is 0.3 (30%, vol.%). A reduction in stress magnitude by 40% was observed on the results modifying the interlayer composition for both zirconia and alumina discs. The maximum stress is located at the framework layer, at the interface with the interlayer, except for the discs with 10% of porcelain in the composite layer, which presented maximum stress in the interface between the interlayer and the veneer. This creates a great mismatch in the thermal residual stress, with one layer presenting high tensile stress and the other presenting compressive stress. Figure 8 shows the maximum tensile stress as function of the interlayer thickness for the porcelain volumetric fraction of 0.3 (30 vol.%). The stresses decrease with increasing layer thicknesses, however they tend to stabilise for thicknesses greater than 0.75 mm. Further calculations for thickness of 1.1 mm and 1.25 mm were also performed to confirm this tendency.

Figure 8.

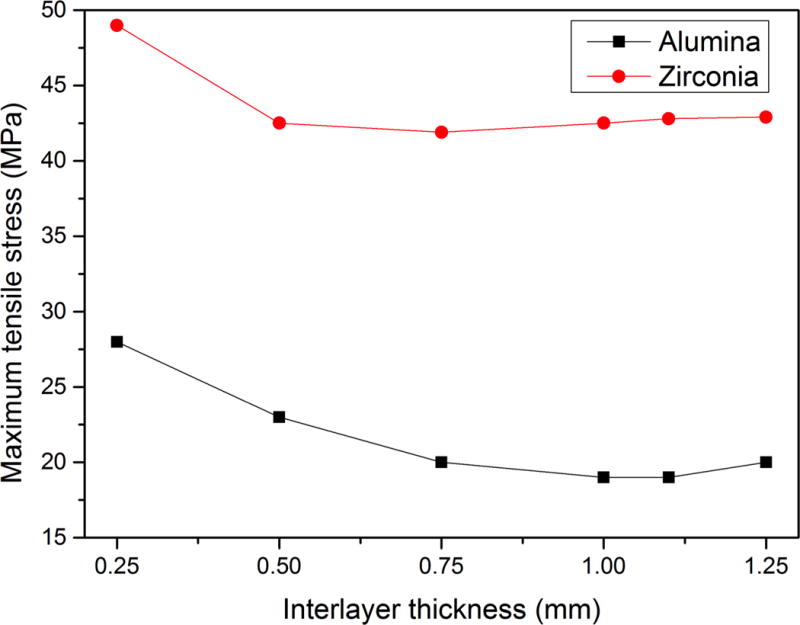
Figure 8

Open in a new tab

Influence of layer thickness on the maximum residual stresses for the interlayer composition of 30 vol.% of porcelain for the zirconia and alumina discs.

3.3. Trilayered discs with graded interlayer

Results for the power law function for different p values are shown in Figure 9 for interlayers with the following thicnesses: 0.25 mm (a), 0.5 mm (b), 0.75 mm (c) and 1 mm (d).

Figure 9.

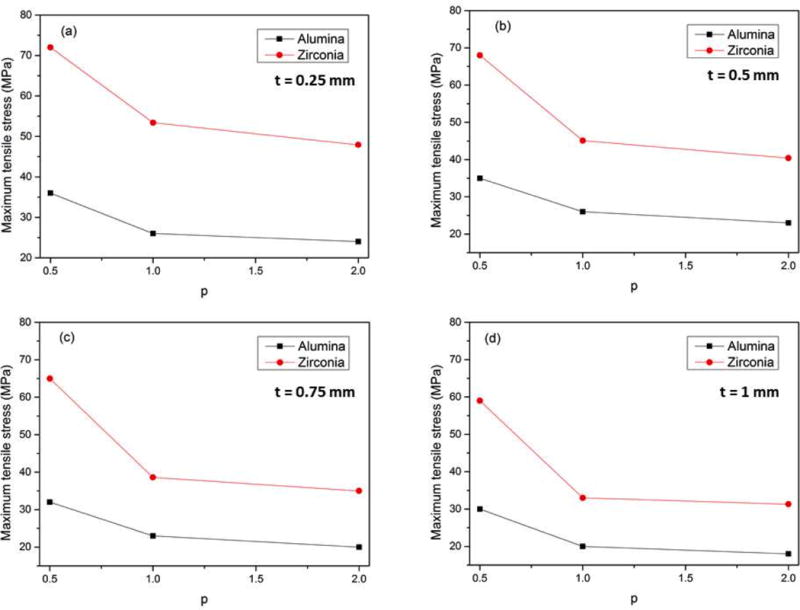
Figure 9

Open in a new tab

Maximum tensile stress for the graded disc, with the graded layer thickness of (a) 0.25 mm, (b) 0.5 mm, (c) 0.75 mm and (d) 1 mm.

The best situation is when the exponential parameter p is equal to 2, which is slightly better than a linear transition (p=1). For graded discs, increasing the graded interlayer thickness results in a reduction of maximum stresses. The interlayer with composition distribution based on the sigmoid function was also simulated. The lowest stresses found were 18 MPa (alumina disc) and 31.3 MPa (zirconia disc) for 1 mm thick graded interlayer and p=2, which is smaller than the best results seen before for discs with homogeneous interlayers (19.5 MPa and 41.9 MPa, respectively). The sigmoid function showed a slightly higher maximum stress than the power law function. However it shows the same tendency, decreasing the maximum stress as the graded layer thickness increases. While in the latter situation (discs with homogeneous interlayer) the maximum stress was localized at the interface between layers, in graded discs, the maximum stress region is located in a larger area, which involves the inferior region of the graded layer and the superior region of the framework layer. The results, comparing the power law function when p=2 and the sigmoid function and showing the maximum tensile stress as function of interlayer thickness, are shown on Figure 10.

Figure 10.

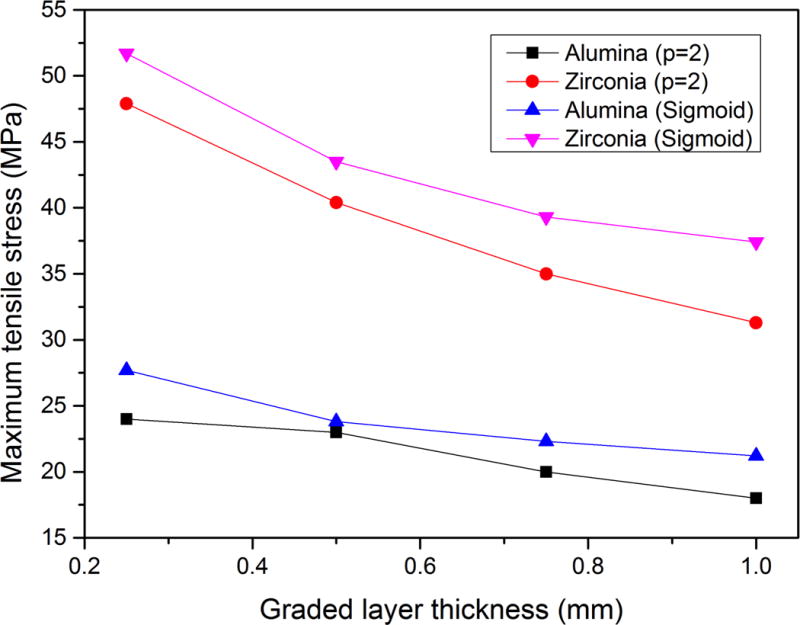
Figure 10

Open in a new tab

Influence of the graded layer thickness in the maximum stress for the power law function when p=2 and the sigmoid function for the alumina and zirconia discs.

3.4. Piston on ring test with and without considering thermal stresses on discs

The piston-on-ring test was simulated using disc with the design corresponding to best result for each condition previously reported (i.e the test was simulated with a disc with sharp transition, a disc with 0.75 mm interlayer with 30% of porcelain content, and a disc with 0.75 mm thick graded layer (p=2)) and incorporating the thermal residual stresses as initial stress condition. Figure 11 shows the first principal stress distribution at the centre of the disc, comparing zirconia and alumina discs for all situations, including a thermal stress free condition for comparison purposes. The upper 0.5 mm had been omitted from the results for presenting high compressive stresses due to the contact between the disc and the applied force, which are not of interest in this case. The results showed the benefits of using the interlayer, either homogeneous or graded, in the reduction of maximum stresses in the discs. The maximum stresses seen in the tensile surface (bottom surface) of the trilayered discs were lower than bilayered ones, with the graded disc displaying the lowest stress values. Aditionally, as expected, the bending stress distribution were different in discs where the thermal stresses were considered from those seen in the thermal stress free discs. The stress mismatch at the intefaces of bilayered and trilayered (homogeneous interlayer) discs were lower when the thermal stresses were considered. On the other hand, the maximum stresses at the tensile surface (bottom surface) were decreased up to 20% in trilayered discs, when thermal stresses were considered in the calculation of bending stresses. No significant differences was observed in this case for bilayered discs.

Figure 11.

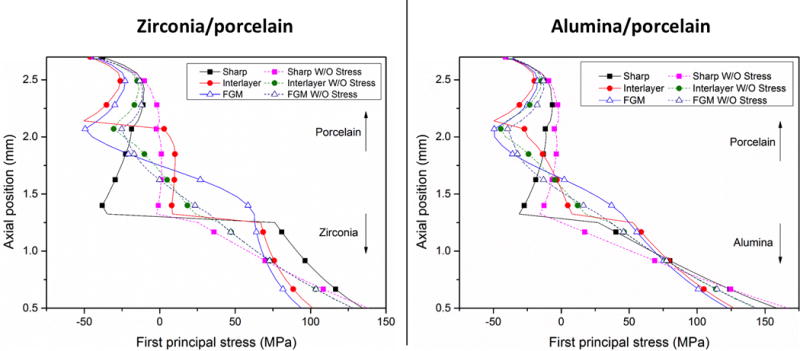
Figure 11

Open in a new tab

Stress distribution in a piston-on-ring test for zirconia/porcelain (left) and alumina/porcelain (right) discs for the different disc configurations studied in this paper, and considering and not considering (W/O) thermal residual stresses.

4. Discussion

Catastrophic fracture and porcelain chipping have been reported as the most common failures of multilayered ceramic restorations [33–35]. This has been attributed to materials’ thermal and mechanical mismatch and occurrences goes from laboratorial fabrication to in-mouth incidents. Recently developed graded structures have been proposed to address thermal and mechanical coupling in dental restorations with significant improvements in load-bearing capacity, adhesion, wear resistance and aesthetics [23,24,27,36,37]. However, to the authors’ best knowledge, no studies are available on the residual thermal stresses in graded dental ceramic systems. Henriques et al. [22,28] has addressed that topic for metal-ceramic restorations. Therefore, with this study we intend to analyze the influence of the constructive parameters such as type of framework material, interlayer composition, interlayer thickness and type of gradation profile on the thermal residual stresses formed in multilayered dental ceramic systems. The influence of thermal stresses on the bending stress distribution in multilayered discs was also investigated.

The thermal stress analysis in bilayered discs revealed higher stresses being formed in zirconia based systems than in alumina based systems, which is accordance to literature [18,38]. Due to the higher flexural strength of zirconia relative to alumina (about twice as strong as alumina), it has been shown to be more adequate, from the reliability and aesthetic point of view for using as framework in dental restorations [3,39].

The highest thermal stresses were reported to occur at the interface of the bilayered discs, which according to literature, is the critical site where cracks are nucleated and propagated [18,40]. Zhang et al. [18] reported that crack consistently initiated and ran tangentially to the porcelain–zirconia interface within the porcelain and in some samples, propagated completely through the porcelain layer and caused chipping.

The presence of an intermediate layer of constant composition showed great influence on the maximum tensile stress in zirconia-porcelain and alumina-porcelain discs. A stress reduction in the magnitude of 40% was observed when the interlayer was 0.75 mm thick and had constant composition of 30% of porcelain. This substantial decrease can account for a reduction in the probability of crack nucleation and growth due to thermal stress and, therefore, increase the restoration lifetime. High stresses at the interfaces could also cause delamination if layers are not properly bonded in the manufacturing process. When the volume fraction of porcelain is 0.1 (10 vol.%), the maximum stress region moves from the bottom alumina or zirconia disc to the interlayer, which is more brittle, and therefore this situation must be avoided. The maximum stress must be localized in the framework, which is designed to withstand higher tensile stresses.

The variation of the interlayer thickness resulted in a significant resduction in maximum thermal stresses in trilayered discs (with homogeneous and graded interlayer composition). A decrease up to 30% could be seen in thermal stresses when thicker interlayers were used. The stress reduction seen with increasing interlayer thickness tended to stabilise for thickness greater than 0.75mm for the alumina-porcelain discs and 0.5 mm for the zirconia-porcelain discs.

Regarding the graded discs, a slight reduction of thermal stress was seen relative to the trilayered discs with an interlayer of constant composition. The lower thermal stresses was seen for discs with a composition profile of the graded interlayer given by p=2 in the power law function, i.e., the disc with higher alumina/zirconia phase content within the graded interlayer. The discs exibiting a sigmoidal transition between framework and venner presented a great thermal stress reduction relative to bilayered discs, but they were slightly higher than those seen in discs featuring a power law function. Sigmoidal gradient shapes are typical profiles resulting from the interdiffusion of two materials [41]. A continuous change in composition was adopted in this study, however this structure is fairly complex to manufacture, thus stepwise transition using several layers has been often adopted in the production of graded materials. Ravichandran [42] showed that a stepwise approach having several layers (typically at least 11) presents similar results regarding thermal stress to that of continuously graded structure.

Residual thermal stresses are inevitable in multilayered systems due to high temperature processing routes used in their manufacturing, with significant impacts on the component performance and life time. Therefore, processing thermal residual stresses must be taken in account when designing new multimaterial components processed at high temperatures. We have shown that bending stresses in multilayered ceramic discs can be underestimated when thermal stresses are not considered in the study. In bilayered discs, the underestimation of the stress mismatch at the interface can result in unexpected crack and delamination occurences of the veneering porcelain. On the other hand, maximum tensile stresses at the bottom surface of the framework were overestimated by not considering thermal stresses in the calculation of bending stresses. This fact can inflence on the design of dental restorations, allowing a reduction in the thichness of the ceramic framework.

It must be pointed out that graded systems have showed a smoother transition when subjected to the biaxial test, showing almost a linear change in the maximum stress across layers when the residual stresses are disregarded. Even considering the thermal stresses, the disc with graded layer presented a mild transition compared with the abrupt change in stress that the other discs showed.

The model used in this study incorporates some simplifications that may be considered as limitations. First, it was assumed a symmetric cooling pattern, which may contrast to eventual asymmetric thermal gradients occurring in real discs cooling. Additionally, a perfect coupling between layers was also assumed, which might be distinct from a real scenario. Finally, currect model did not take into account the viscoelastic behavior of porcelain at the temperature above its Tg. Therefore, the true stress profiles might not be captured accurately. Despite the limitations, this study provides general insights as regard to the influence of multilayers design in the formation of thermal stresses in graded dental ceramic systems.

5. Conclusion

In this work, thermal residual stress in multilayered discs were succesfully calculated using finite elements method. From the results, the following conclusions can be drawn:

  • The presence of an interlayer with intermediate properties between two materials can markedly reduce residual thermal stresses. Reductions in the thermal stress magnitude could go up to 40%.

  • The composition and the thickness of the interlayer (constant or graded composition) have a significant influence on the residual stresses in trilayered ceramic discs. For the constant composition interlayer, the residual stress is minimized when the porcelain content of the interlayer is 30%. The thermal stress start increasing for interlayer thicknesses bellow 0.75 mm.

  • The graded interlayer showed to reduce the maximum thermal stress by 50% relative to bilayered discs. The stress reduction is maximized for a graded profile with a power function p=2 and for thicker interlayers.

  • The bending stress distribution is greatly influenced by the presence of thermal residual stresses in multilayered discs. Without accounting for them, can underestimate the stress mismatch at the interface in bilayered discs and overestimate the maximum stresses at the tensile surface of trilayered discs.

Figure 1.

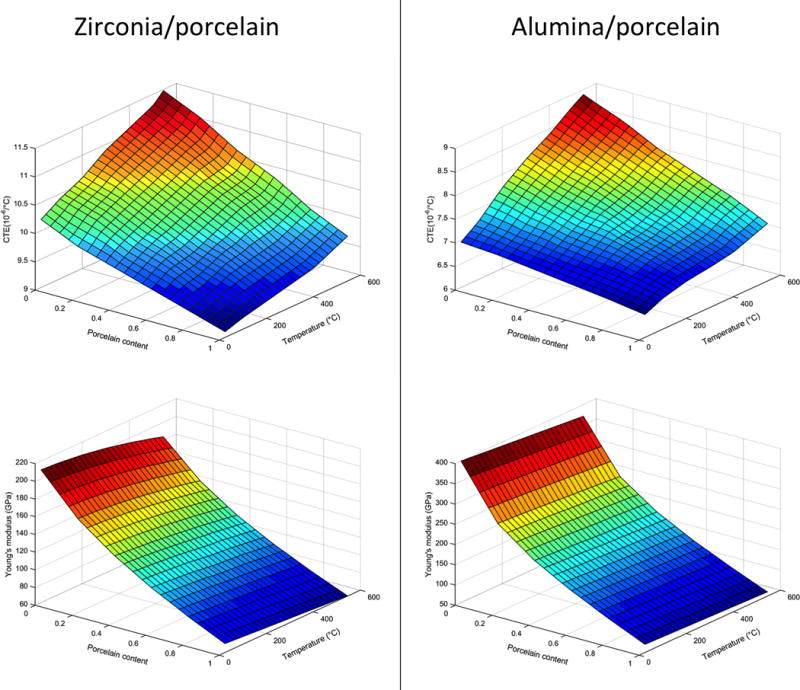
Figure 1

Open in a new tab

CTE and Young’s modulus of the zirconia/porcelain and alumina/porcelain composites plotted as function of temperature and porcelain content in the mixture.

Acknowledgments

This study was supported by FCT-Portugal (EXCL/EMS-TEC/0460/2012; UID/EEA/04436/2013; NORTE-01-0145-FEDER-000018 - HAMaBICo), CNPq-Brazil and the US National Institute of Dental and Craniofacial Research Grant 2R01 DE017925.

References

  • 1.Zarone F, Russo S, Sorrentino R. From porcelain-fused-to-metal to zirconia: clinical and experimental considerations. Dent Mater. 2011;27:83–96. doi: 10.1016/j.dental.2010.10.024. [DOI] [PubMed] [Google Scholar]
  • 2.Willmann G. Medical-grade alumina during the past Two decades. Bioceramics. 1994;7:359–364. [Google Scholar]
  • 3.Conrad HJ, Seong WJ, Pesun IJ. Current ceramic materials and systems with clinical recommendations: a systematic review. J Prosthet Dent. 2007;98:389–404. doi: 10.1016/S0022-3913(07)60124-3. [DOI] [PubMed] [Google Scholar]
  • 4.Baldassarri M, Zhang Y, Thompson VP, Rekow ED, Stappert CFJ. Reliability and failure modes of implant-supported zirconium-oxide fixed dental prostheses related to veneering techniques. J Dent. 2011;39:489–98. doi: 10.1016/j.jdent.2011.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Choi JE, Waddell JN, Swain MV. Pressed ceramics onto zirconia. Part 2: Indentation fracture and influence of cooling rate on residual stresses. Dent Mater. 2011;27:1111–1118. doi: 10.1016/j.dental.2011.08.003. [DOI] [PubMed] [Google Scholar]
  • 6.Swain MV. Unstable cracking (chipping) of veneering porcelain on all-ceramic dental crowns and fixed partial dentures. Acta Biomater. 2009;5:1668–1677. doi: 10.1016/j.actbio.2008.12.016. [DOI] [PubMed] [Google Scholar]
  • 7.Isgrò G, Wang H, Kleverlaan CJ, Feilzer AJ. The effects of thermal mismatch and fabrication procedures on the deflection of layered all-ceramic discs. Dent Mater. 2005;21:649–655. doi: 10.1016/j.dental.2004.09.001. [DOI] [PubMed] [Google Scholar]
  • 8.DeHoff PH, Anusavice KJ. Viscoelastic finite element stress analysis of the thermal compatibility of dental bilayer ceramic systems. Int J Prosthodont. 2009;22:56–61. [PubMed] [Google Scholar]
  • 9.DeHoff PH, Anusavice KJ, Götzen N. Viscoelastic finite element analysis of an all-ceramic fixed partial denture. J Biomech. 2006;39:40–48. doi: 10.1016/j.jbiomech.2004.11.007. [DOI] [PubMed] [Google Scholar]
  • 10.Benetti P, Della Bona A, Kelly JR. Evaluation of thermal compatibility between core and veneer dental ceramics using shear bond strength test and contact angle measurement. Dent Mater. 2010;26:743–750. doi: 10.1016/j.dental.2010.03.019. [DOI] [PubMed] [Google Scholar]
  • 11.Baldassarri M, Stappert CFJ, Wolff MS, Thompson VP, Zhang Y. Residual stresses in porcelain-veneered zirconia prostheses. Dent Mater. 2012;28:873–879. doi: 10.1016/j.dental.2012.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Heintze SD, Rousson V. Survival of zirconia- and metal-supported fixed dental prostheses: a systematic review. Int J Prosthodont. 2010;23:493–502. doi: 10.1038/sj.bdj.2011.263. [DOI] [PubMed] [Google Scholar]
  • 13.Pjetursson BE, Sailer I, Makarov NA, Zwahlen M, Thoma DS. All-ceramic or metal-ceramic tooth-supported fixed dental prostheses (FDPs)? A systematic review of the survival and complication rates. Part II: Multiple-unit FDPs. Dent Mater. 2015:624–639. doi: 10.1016/j.dental.2015.02.013. [DOI] [PubMed] [Google Scholar]
  • 14.Schley JS, Heussen N, Reich S, Fischer J, Haselhuhn K, Wolfart S. Survival probability of zirconia-based fixed dental prostheses up to 5 yr: A systematic review of the literature. Eur J Oral Sci. 2010;118:443–450. doi: 10.1111/j.1600-0722.2010.00767.x. [DOI] [PubMed] [Google Scholar]
  • 15.Odman P, Andersson B. Procera AllCeram crowns followed for 5 to 10.5 years: a prospective clinical study. Int J Prosthodont. 2001;14:504–9. [PubMed] [Google Scholar]
  • 16.Stappert CFJ, Baldassarri M, Zhang Y, Hänssler F, Rekow ED, Thompson VP. Reliability and fatigue failure modes of implant-supported aluminum-oxide fixed dental prostheses. Clin Oral Implants Res. 2012;23:1173–1180. doi: 10.1111/j.1600-0501.2011.02281.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Sailer I, Fehér A, Filser F, Gauckler LJ, Lüthy H, Hämmerle CHF. Five-year clinical results of zirconia frameworks for posterior fixed partial dentures. Int J Prosthodont. 2007;20:383–8. [PubMed] [Google Scholar]
  • 18.Zhang Z, Guazzato M, Sornsuwan T, Scherrer SS, Rungsiyakull C, Li W, et al. Thermally induced fracture for core-veneered dental ceramic structures. Acta Biomater. 2013;9:8394–8402. doi: 10.1016/j.actbio.2013.05.009. [DOI] [PubMed] [Google Scholar]
  • 19.Zhang Z, Zhou S, Li Q, Li W, Swain MV. Sensitivity analysis of bi-layered ceramic dental restorations. Dent Mater. 2012;28 doi: 10.1016/j.dental.2011.11.012. [DOI] [PubMed] [Google Scholar]
  • 20.Henriques B, Gasik M, Soares D, Silva FS. Experimental evaluation of the bond strength between a CoCrMo dental alloy and porcelain through a composite metal-ceramic graded transition interlayer. J Mech Behav Biomed Mater. 2012;13:206–14. doi: 10.1016/j.jmbbm.2012.04.019. [DOI] [PubMed] [Google Scholar]
  • 21.Henriques B, Gonçalves S, Soares D, Silva FS. Shear bond strength comparison between conventional porcelain fused to metal and new functionally graded dental restorations after thermal-mechanical cycling. J Mech Behav Biomed Mater. 2012;13:194–205. doi: 10.1016/j.jmbbm.2012.06.002. [DOI] [PubMed] [Google Scholar]
  • 22.Henriques B, Miranda G, Gasik M, Souza JCM, Nascimento RM, Silva FS. Finite element analysis of the residual thermal stresses on functionally gradated dental restorations. J Mech Behav Biomed Mater. 2015;50:123–130. doi: 10.1016/j.jmbbm.2015.06.003. [DOI] [PubMed] [Google Scholar]
  • 23.Zhang Y, Kim JW. Graded structures for damage resistant and aesthetic all-ceramic restorations. Dent Mater. 2009;25:781–90. doi: 10.1016/j.dental.2009.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Zhang Y, Sun MJ, Zhang D. Designing functionally graded materials with superior load-bearing properties. Acta Biomater. 2012;8:1101–8. doi: 10.1016/j.actbio.2011.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Tsukada G, Sueyoshi H, Kamibayashi H, Tokuda M, Torii M. Bending strength of zirconia/porcelain functionally graded materials prepared using spark plasma sintering. J Dent. 2014;42:1569–76. doi: 10.1016/j.jdent.2014.09.012. [DOI] [PubMed] [Google Scholar]
  • 26.Fabris D, Souza JCM, Silva FS, Fredel M, Mesquita-Guimarães J, Zhang Y, et al. The bending stress distribution in bilayered and graded zirconia-based dental ceramics. Ceram Int. 2016 doi: 10.1016/j.ceramint.2016.03.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Chai H, Lee JJW, Mieleszko AJ, Chu SJ, Zhang Y. On the interfacial fracture of porcelain/zirconia and graded zirconia dental structures. Acta Biomater. 2014;10:3756–3761. doi: 10.1016/j.actbio.2014.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Henriques B, Gasik M, Miranda G, Souza JCM, Nascimento RM, Silva FS. Improving the functional design of dental restorations by adding a composite interlayer in the multilayer system: Multi-aspect analysis. Cienc E Tecnol Dos Mater. 2015;27:36–40. doi: 10.1016/j.ctmat.2015.06.002. [DOI] [Google Scholar]
  • 29.Kawasaki A, Watanabe R. Concept and P/M fabrication of functionally gradient materials. Ceram Int. 1997;23:73–83. doi: 10.1016/0272-8842(95)00143-3. [DOI] [Google Scholar]
  • 30.Lee CS, Ahn SH, DeJonghe LC, Thomas G. Effect of functionally graded material (FGM) layers on the residual stress of polytypoidally joined Si3N4-Al2O3. Mater Sci Eng A. 2006;434:160–165. doi: 10.1016/j.msea.2006.06.139. [DOI] [Google Scholar]
  • 31.Thompson GA. Determining the slow crack growth parameter and weibull two-parameter estimates of bilaminate disks by constant displacement-rate flexural testing. Dent Mater. 2004;20:51–62. doi: 10.1016/S0109-5641(03)00068-X. [DOI] [PubMed] [Google Scholar]
  • 32.Hsueh CH, Luttrell CR, Becher PF. Modelling of bonded multilayered disks subjected to biaxial flexure tests. Int J Solids Struct. 2006;43:6014–6025. doi: 10.1016/j.ijsolstr.2005.07.020. [DOI] [Google Scholar]
  • 33.Benetti P, Pelogia F, Valandro LF, Bottino MA, Della Bona A. The effect of porcelain thickness and surface liner application on the fracture behavior of a ceramic system. Dent Mater. 2011;27:948–953. doi: 10.1016/j.dental.2011.05.009. [DOI] [PubMed] [Google Scholar]
  • 34.Christensen RP, Ploeger BJ. A clinical comparison of zirconia, metal and alumina fixed-prosthesis frameworks veneered with layered or pressed ceramic: a three-year report. J Am Dent Assoc. 2010;141:1317–29. doi: 10.14219/jada.archive.2010.0076. [DOI] [PubMed] [Google Scholar]
  • 35.Pang Z, Chughtai A, Sailer I, Zhang Y. A fractographic study of clinically retrieved zirconia-ceramic and metal-ceramic fixed dental prostheses. Dent Mater. 2015;31:1198–1206. doi: 10.1016/j.dental.2015.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Liu R, Sun T, Zhang Y, Zhang Y, Jiang D, Shao L. The effect of graded glass-zirconia structure on the bond between core and veneer in layered zirconia restorations. J Mech Behav Biomed Mater. 2015;46:197–204. doi: 10.1016/j.jmbbm.2015.02.017. [DOI] [PubMed] [Google Scholar]
  • 37.Zhang Y, Ma L. Optimization of ceramic strength using elastic gradients. Acta Mater. 2009;57:2721–2729. doi: 10.1016/j.actamat.2009.02.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Zhang ZP, Zhou SW, Li Q, Li W, Swain M. Residual Stresses in Fabrication of Core-Veneered Ceramic Prostheses. Adv Mater Res. 2010;97–101:2241–2244. doi: 10.4028/www.scientific.net/AMR.97-101.2241. [DOI] [Google Scholar]
  • 39.Teixeira EC, Piascik JR, Stoner BR, Thompson JY. Dynamic fatigue and strength characterization of three ceramic materials. J Mater Sci Mater Med. 2007;18:1219–1224. doi: 10.1007/s10856-007-0131-4. [DOI] [PubMed] [Google Scholar]
  • 40.DeHoff PH, Barrett AA, Lee RB, Anusavice KJ. Thermal compatibility of dental ceramic systems using cylindrical and spherical geometries. Dent Mater. 2008;24:744–752. doi: 10.1016/j.dental.2007.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Becker TL, Cannon RM, Ritchie RO. An approximate method for residual stress calculation in functionally graded materials. Mech Mater. 2000;32:85–97. doi: 10.1016/S0167-6636(99)00042-3. [DOI] [Google Scholar]
  • 42.Ravichandran KS. Thermal residual stresses in a functionally graded material system. Mater Sci Eng A. 1995;201:269–276. doi: 10.1016/0921-5093(95)09773-2. [DOI] [Google Scholar]

RESOURCES