Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2016 Dec 1;205(2):503–516. doi: 10.1534/genetics.116.195578

Genetic Contributors to Intergenerational CAG Repeat Instability in Huntington’s Disease Knock-In Mice

João Luís Neto *,†,‡, Jong-Min Lee *,§, Ali Afridi *, Tammy Gillis *, Jolene R Guide *, Stephani Dempsey **, Brenda Lager ††, Isabel Alonso †,‡‡, Vanessa C Wheeler *,§,1, Ricardo Mouro Pinto *,§,1
PMCID: PMC5289832  PMID: 27913616

Abstract

Huntington’s disease (HD) is a neurodegenerative disorder caused by the expansion of a CAG trinucleotide repeat in exon 1 of the HTT gene. Longer repeat sizes are associated with increased disease penetrance and earlier ages of onset. Intergenerationally unstable transmissions are common in HD families, partly underlying the genetic anticipation seen in this disorder. HD CAG knock-in mouse models also exhibit a propensity for intergenerational repeat size changes. In this work, we examine intergenerational instability of the CAG repeat in over 20,000 transmissions in the largest HD knock-in mouse model breeding datasets reported to date. We confirmed previous observations that parental sex drives the relative ratio of expansions and contractions. The large datasets further allowed us to distinguish effects of paternal CAG repeat length on the magnitude and frequency of expansions and contractions, as well as the identification of large repeat size jumps in the knock-in models. Distinct degrees of intergenerational instability were observed between knock-in mice of six background strains, indicating the occurrence of trans-acting genetic modifiers. We also found that lines harboring a neomycin resistance cassette upstream of Htt showed reduced expansion frequency, indicative of a contributing role for sequences in cis, with the expanded repeat as modifiers of intergenerational instability. These results provide a basis for further understanding of the mechanisms underlying intergenerational repeat instability.

Keywords: Huntington’s disease, intergenerational CAG repeat instability, HD knock-in mouse models, genetic background

HUNTINGTON’S disease (HD) is a progressive, degenerative, autosomal dominant disorder caused by the expansion of a CAG repeat located in exon 1 of the HTT gene (4p16.3), producing an extended polyglutamine tract in the huntingtin protein (The Huntington’s Disease Collaborative Research Group 1993). Alleles over 35 repeats are associated with disease, with 36–39 CAGs showing reduced penetrance, and 40 or more repeats being fully penetrant (The Huntington’s Disease Collaborative Research Group 1993; McNeil et al. 1997). The length of the expanded repeat is also a major modifier of the age of disease onset (Andrew et al. 1993; Duyao et al. 1993; Telenius et al. 1993; Trottier et al. 1994; Ranen et al. 1995; Lee et al. 2012a). Underlying the variation in inherited CAG repeat length between individuals are high rates (∼70–80%) of intergenerationally unstable transmissions (Duyao et al. 1993; Zühlke et al. 1993; Telenius et al. 1994; Kremer et al. 1995; Wheeler et al. 2007). Intergenerational instability of the HTT CAG repeat accounts for genetic anticipation seen in HD families (Kremer et al. 1995; Ranen et al. 1995), as well as for changes from high normal alleles (27–35 CAGs) to disease alleles (i.e., de novo mutations) and transitions from alleles associated with incomplete penetrance to those causing completely penetrant disease (Myers et al. 1993; Hendricks et al. 2009; Sequeiros et al. 2010).

Mechanisms underlying intergenerational instability are unclear, but important to understand in order to refine variable estimates of new mutation rates for genetic counseling (Brocklebank et al. 2009; Hendricks et al. 2009; Sequeiros et al. 2010), and for the potential to suppress expansions and/or induce contractions. Studies of intergenerational instability in HD families have shown that the HTT CAG repeat is strongly biased toward expansions in transmission from fathers, while transmissions from mothers have a higher tendency to be stable or contract (Duyao et al. 1993; Telenius et al. 1993; Zühlke et al. 1993; Trottier et al. 1994; Kremer et al. 1995; Ranen et al. 1995; Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012). In addition to parent sex, CAG repeat length strongly influences intergenerational repeat instability, with longer repeats being more susceptible to larger changes (Duyao et al. 1993; Kremer et al. 1995; Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012). Minor effects of offspring sex, size of the normal CAG repeat, and parental age have also been documented in some but not all HD cohorts examined (Kremer et al. 1995; Leeflang et al. 1999; Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012).

Clustering of transmitted repeat length changes among HD families implicates genetic modifiers of intergenerational instability (Wheeler et al. 2007; Ramos et al. 2012). Familial segregation of instability in a large HD Venezuelan pedigree that shares a 4p16.3 (HTT) haplotype provides evidence for other genes that can modify instability (trans-acting) (Wheeler et al. 2007). A 4p16.3 predisposing haplotype (cis-modifier) has been proposed to underlie the expansion of high normal length HTT CAG repeats into the disease range (Warby et al. 2009). However, this haplotype was not associated with the length of the expanded CAG repeat (Lee et al. 2012b), or with its intergenerational instability (Ramos et al. 2015).

Transgenic and knock-in mouse models of HD recapitulate many aspects of intergenerational CAG repeat instability seen in patients (Mangiarini et al. 1997; Shelbourne et al. 1999; Wheeler et al. 1999; Kovtun et al. 2000; Lloret et al. 2006), notably: CAG repeat length-dependent instability at similar high frequency (>65%) for long alleles (>∼100 CAGs) (Wheeler et al. 1999), as well as paternal expansion and maternal contraction biases (Shelbourne et al. 1999; Wheeler et al. 1999; Kovtun et al. 2000). Offspring sex was also found to contribute to instability in HTT exon 1 (R6/1) transgenic mice (Kovtun et al. 2000). No obvious role of parental age was discernible in knock-in models (Wheeler et al. 1999). Cis-modifiers of intergenerational instability were suggested based on differential instability in HTT exon 1 transgenic (R/6) models, with similar CAG repeat sizes, but distinct transgene insertion sites (Mangiarini et al. 1997). DNA repair genes Msh2, Msh3, Msh6, and Neil1 have been identified as trans-acting modifiers of intergenerational repeat instability (Wheeler et al. 2003; Lloret et al. 2006; Møllersen et al. 2010), and a comparison of HttQ111 knock-in lines on different genetic backgrounds indicated the presence of trans-factors that drive strain-specific intergenerational instability (Lloret et al. 2006).

Here, we have taken advantage of two large breeding datasets comprising thousands of transmissions from allelic series of Htt CAG knock-in mice that differ in CAG length, genetic background, and the presence of a cis-element—a neomycin resistance cassette (neo)—upstream of the CAG repeat, to perform a comprehensive assessment of the factors that drive intergenerational instability of expanded CAG repeat at the mouse Htt locus. These analyses confirm major modifiers of instability, distinguish more subtle effects, and provide novel insight into potential trans and cis-mediated effects.

Materials and Methods

Mouse lines

Breeding data were obtained from The Jackson Laboratory (JAX) for the following lines of Htt (formerly Hdh) CAG knock-in mice on a C57BL6/J (B6J) background: HttQ20, HttQ50, HttQ80, HttQ92, HttQ111, HttQ140, and HttQ175. The HttQ20, HttQ50, HttQ80, HttQ92, and HttQ111 lines were originally derived in the MacDonald laboratory (White et al. 1997; Wheeler et al. 1999), with HttQ80 being a derivative of the original HttQ92 line obtained by selective breeding to smaller CAG repeats. The HttQ140 line was originally derived in the Zeitlin laboratory (Menalled et al. 2003), with HttQ175 being a derivative of HttQ140, obtained by selective breeding to obtain longer CAG repeats (Menalled et al. 2012). HttQ20, HttQ50, HttQ80, HttQ92, and HttQ111 lines represented in the JAX dataset do not contain the upstream neo cassette used in targeting these alleles; however, the HttQ140 and HttQ175 lines retain a neo cassette (Supplemental Material, Figure S1). Together, these lines form part of an “allelic series” of Htt CAG knock-in mice for analyses of repeat length-dependent phenotypes (Alexandrov et al. 2016; Langfelder et al. 2016). Subsequent excision of the neo cassette using Cre-mediated recombination resulted in a new line of B6J HttQ175neo− mice (B6.129S1-Htt < tm1.1Mfc>/190ChdiJ). Here, for simplicity, we refer to the HttQ175neo+ mice that form part of the allelic series simply as HttQ175, unless we specifically need to distinguish them from their neo− counterpart, in which case we refer to the lines as HttQ175neo+ and HttQ175neo−.

Separately, in-house [Center for Human Genetic Research (CHGR)] breeding data were obtained for the HttQ111 line on six background strains: CD1, B6J, C57BL/6NCrl (B6N), 129S2/SvPasCrlf (129), FVB/NCrl (FVB) and DBA/2J (DBA); as well as for HttQ80 and HttQ92 on CD1 and B6J backgrounds (Wheeler et al. 1999; Lloret et al. 2006; Pinto et al. 2013). Data from CD1 or B6J lines (HttQ80, HttQ92, and HttQ111) were combined to provide a broad CAG repeat range for each of these background strains. None of the lines used for comparisons of instability across different genetic backgrounds had a neo cassette. We also analyzed breeding data from CD1.HttQ111 mice that included an upstream neo cassette (Auerbach et al. 2001), which we compared against the set of CD1 mice that were missing the neo cassette. In this comparison, we refer to these mice as CD1neo+ and CD1neo−, respectively.

Mouse breeding, husbandry, and genotyping

This study was carried out in strict accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals, National Research Council (2011). All animal procedures were carried out to minimize pain and discomfort, under approved IACUC protocols of the Massachusetts General Hospital, or The Jackson Laboratory.

Data collected from JAX-maintained Htt CAG knock-in lines followed breeding and husbandry conditions described in Langfelder et al. (2016), with genotyping and CAG length determination performed in tail DNA at weaning by Laragen Inc. CHGR breeding was performed as described in previous work (Dragileva et al. 2009; Pinto et al. 2013), and genotyping and CAG length determination were performed in tail DNA at weaning as previously described (Mangiarini et al. 1997; Dragileva et al. 2009).

Intergenerational transmission data

Both JAX and CHGR breeding data records were quality controlled to eliminate entries with obvious and systematic errors (e.g., typographical), or from crosses with inconclusive assignment of parental CAG repeat length (e.g., crosses between two heterozygous parents and harem breedings). In CHGR’s strain-specific data, only mice that were at least sixth-generation backcross progeny (F6, >98% congenic) were included, except for B6J.HttQ111, where speed congenics were utilized to generate the line (Lee et al. 2011) and generations F4 (∼95% congenic), and after, were included.

Following quality control, the JAX dataset comprised 44,324 pups from crosses between a heterozygous knock-in and a wild-type parent. Of these, 22,063 pups carried a mutant allele, allowing us to determine CAG repeat length change upon transmission. In the JAX dataset, accurate parental age at which the pups were born could not be determined. After quality control, the CHGR dataset comprised 1829 pups carrying a mutant allele from crosses between heterozygous knock-in sires and wild-type dams. In these data, we were able to assign parental age at the time of birth of the pups unambiguously.

Repeat length change was determined by subtracting the CAG repeat length in the heterozygous knock-in progeny from the CAG repeat length in the respective heterozygous knock-in parent. It should be noted that, for both the JAX and CHGR data, breeding records were accumulated over periods of months/years, and that parent and progeny genotyping were performed at separate times. While standardized CAG repeat genotyping assays are used in both cases, there may be some small degree of error in the determination of repeat length change; however, this is likely to have a negligible impact given the large size of the datasets used in this study.

Frequency modeling

To control for possible confounding effects of parental CAG size in the frequency of unstable transmissions between different strains/lines, we implemented a modeling methodology that allowed a pairwise comparison of the rates of expansions, contractions, and unchanged transmissions between test strains and a reference strain.

This modeling procedure is represented in File S1. In essence, (1) weighted linear regressions for relative frequencies of expansions, contractions, and unchanged transmissions vs. parental CAG size were determined for the reference strain using PASW Statistics 18; (2) a modeled dataset was generated through random number generation, and allocation as expansion, contraction, or stable transmission based on the frequency intervals of these events (per paternal CAG size) established from the weighted linear regression lines; (3) this was repeated 1000 times, the modeled datasets were averaged, and a dataset based on the average values was used for comparative and statistical analyses. To validate this methodology, we randomly divided the CHGR B6J set into two subsets with comparable number of transmissions: reference and test subsets (n = 354 and n = 353, respectively). Based on the reference dataset, we modeled the frequencies for the test subset, and, after comparison against the observed values, we confirmed that the expected frequencies of the test dataset could be predicted with this process (Figure S2). We then applied this methodology to compare transmission frequencies: (1) in CD1, B6N, 129, DBA, and FVB strains against B6J (reference strain); and (2) in neo+ vs. neo− mice, where either CD1neo− or Q175neo+ were the reference strains (File S1).

Statistical analyses

Frequency analyses were performed using Microsoft Excel 2007 and PASW Statistics 18 (IBM). χ2 tests of independence, unpaired Student’s t-test for mean comparison, Pearson correlation analyses, and z-tests for column proportions were carried out using PASW Statistics 18 (IBM)—actual z-scores and P-values were determined using Microsoft Excel 2007, or the online Z-Score calculator for two population proportions (http://www.socscistatistics.com/tests/ztest/Default2.aspx). To determine the effect of strain background on the magnitude of repeat length changes mixed effect model analyses were performed using “nlme” packages in R program (v3.2.2). Briefly, CAG repeat size changes (expansions or contractions) were modeled as a function of paternal CAG and mouse strain as main effects, with random intercepts for sire. Kruskal-Wallis one-way analysis of variance and Dunn’s post-test were performed with GraphPad Prism 6. Bonferroni correction was applied when multiple testing was performed (P-value thresholds stated in text/figure legends). Weighted regression lines for number of transmissions per CAG size were calculated with PASW Statistics 18.

Data availability

Datasets can be provided by the authors upon request. The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Results

To gain insight into factors that influence the intergenerational instability of the Htt CAG repeat, we first analyzed a very large breeding dataset from JAX comprising >44,000 offspring from heterozygous parents of an allelic series of HD knock-in mice – HttQ20, HttQ50, HttQ80, HttQ92, HttQ111, HttQ140, and HttQ175, on a B6J genetic background (Table 1). The vast majority of transmissions were from heterozygous knock-in sires, with the HttQ80 and HttQ92 lines also harboring transmissions from mutant dams.

Table 1. Heterozygous and wild-type progeny from Htt knock-in lines in the JAX dataset.

Line Paternal Transmissions Maternal Transmissions
Total Heterozygous Progeny Wild-Type Progeny Total Heterozygous Progeny Wild-Type Progeny
N N (%) N (%) N N (%) N (%)
HttQ20 7189 3595 (50.0) 3594 (50.0) — — —
HttQ50 1025 511 (49.9) 514 (50.1) — — —
HttQ80 4989 2465 (49.4) 2524 (50.6) 263 129 (49.0) 134 (51.0)
HttQ92 5970 2883 (48.3) 3087 (51.7) 412 200 (48.5) 212 (51.5)
HttQ111 3079 1550 (50.3) 1529 (49.7) — — —
HttQ140 3109 1558 (50.1) 1551 (49.9) — — —
HttQ175 18288 9172 (50.2) 9116 (49.8) — — —
Open in a new tab

N, number of transmissions. HttQ20, HttQ50, HttQ80, HttQ92, HttQ111: neo−. HttQ140, HttQ175: neo+.

Segregation of Htt CAG knock-in alleles studied follows Mendelian ratios and is independent of CAG length

A 1:1 Mendelian ratio of heterozygous vs. wild-type progeny was broadly observed among the lines, with the exception of paternal transmissions in HttQ92, where a significant difference (two-proportion z-test, P < 0.001) of fairly small effect (1.7% lower than expected frequency of heterozygotes) was observed. As this effect was unique to this line and not seen in lines with larger repeat sizes, overall, these results indicate the lack of an obvious effect of the CAG mutation on the transmission of the Htt allele over a large range of repeat lengths among a very high number of transmissions.

Parental sex influences the direction of repeat length changes but does not have a major impact on magnitude

In human HTT mutation carriers, parental sex is a major determinant of intergenerational repeat instability (Duyao et al. 1993; Telenius et al. 1993; Trottier et al. 1994; Kremer et al. 1995; Ranen et al. 1995; Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012). We therefore compared frequencies of stable and unstable transmissions (expansions and contractions), as well as the magnitude of these alterations between paternal and maternal transmissions of the HttQ80 and HttQ92 alleles (Table 2 and Table 3).

Table 2. Paternal CAG size and transmission information for the different lines in the JAX breeding data.

Paternal Transmissions
Parent CAG Total Stable Contractions Expansions
Line Min. Max. Mean N N (%) N (%) Max. Mean N (%) Max. Mean
HttQ20 18 18 18.0 3595 3591 (99.89) 1 (0.03) 1 1.0 3 (0.08) 1 1.0
HttQ50 46 48 46.6 511 460 (90.0) 29 (5.7) 2 1.1 22 (4.3) 1 1.0
HttQ80 80 86 83.1 2465 921 (37.4) 330 (13.4) 15 1.2 1214 (49.2) 29 1.7
HttQ92 91 98 95.8 2883 1010 (35.0) 268 (9.3) 12 1.3 1605 (55.7) 50 1.9
HttQ111 106 121 113.9 1550 300 (19.5) 248 (16.0) 28 2.1 983 (64.5) 14 2.3
HttQ140 130 150 137.4 1558 232 (14.9) 172 (11.0) 18 2.2 1154 (74.1) 65 3.2
HttQ175 178 199 188.9 9172 592 (6.5) 927 (10.1) 128 5.1 7653 (83.4) 153 5.2
Open in a new tab

N, number. HttQ20, HttQ50, HttQ80, HttQ92, HttQ111: neo−. HttQ140, HttQ175: neo+.

Table 3. Maternal CAG size and transmission information for the different lines in JAX’s breeding data.

Maternal Transmissions
Parent CAG Total Stable Contractions Expansions
Line Min. Max. Mean N N (%) N (%) Max. Mean N (%) Max. Mean
HttQ80 83 84 83.2 129 59 (45.7) 59 (45.7) 5 1.4 11 (8.5) 3 1.3
HttQ92 94 98 96.8 200 70 (35.0) 82 (41.0) 5 1.6 48 (24.0) 20 2.2
Open in a new tab

N, number. HttQ80, HttQ92: neo−.

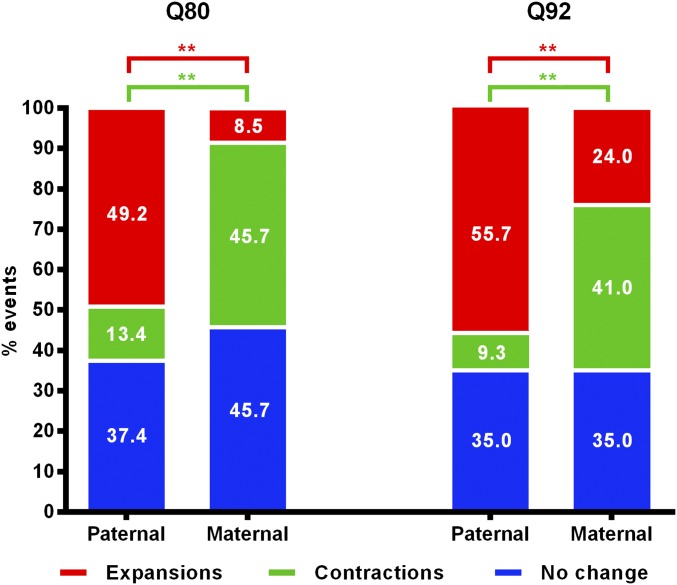
For both lines, parent-of-origin determined the frequency distribution of repeat length changes (HttQ80: χ2 = 130.86, 2 df, P < 0.001; HttQ92: χ2 = 200.58, 2 df, P < 0.001), with paternal transmissions showing a higher occurrence of expansions, and maternal transmissions showing a higher occurrence of contractions (two-proportion z-test, P < 0.01) but no significant differences in the frequencies of stable transmissions (Figure 1).

Figure 1.

Figure 1

Open in a new tab

Frequency of stable transmissions, contractions, and expansions in paternal and maternal transmissions of the HttQ80 and HttQ92 alleles in the JAX transmission data. **P < 0.01.

Larger maximum expansions and contractions were observed in paternal transmissions compared to maternal transmissions, probably partly driven by the greater total number of paternal transmissions (Table 2 and Table 3). However, parental sex did not significantly alter the mean magnitude of the changes in HttQ80 mice (contractions: unpaired t-test, P = 0.235; expansions: unpaired t-test, P = 0.312), or the mean magnitude of expansions in HttQ92 mice (unpaired t-test, P = 0.467), though the mean magnitude of contractions was significantly increased in maternal transmissions of the HttQ92 line (unpaired t-test, mean difference = 0.348 CAGs, P = 0.003; Figure S3; Table 2 and Table 3). The significance of this is unclear in the absence of additional maternal transmission data from longer alleles, but may indicate a differential sensitivity to repeat length of the mechanisms that mediate contractions in the male and female germline.

Overall, in Htt CAG knock-in mice, parent-of-origin mainly influences the relative frequencies of expansions and contractions, with a minor impact on the magnitude of repeat contractions.

Offspring sex does not influence intergenerational instability in Htt CAG knock-in mice

Previously, effects of offspring sex on intergenerational CAG repeat instability were identified in human HTT mutation carriers, and R6/1 mouse models of the disorder (Kovtun et al. 2000; Wheeler et al. 2007). We took advantage of this large breeding dataset to determine whether this effect might be recapitulated in transmissions from Htt CAG knock-in mice. We examined the frequency and magnitude of repeat length changes inherited by male and female progeny in the expanded Htt CAG knock-in lines with available data, analyzing paternal and maternal transmissions separately (Table S1).

For all lines, in both paternal and maternal transmissions, offspring sex did not significantly influence either the relative frequencies of contractions, expansions or stable alleles (χ2, Figure S4 and Table S2), or the magnitude of expansions or contractions (unpaired t-tests, P > 0.05, Figure S5). Thus, offspring sex is not a major determinant of intergenerational instability in this allelic series of HD knock-in mouse models.

Distinct effects of paternal CAG repeat length on the frequency and magnitude of changes

Intergenerational repeat instability is strongly determined by parental CAG repeat length in HTT mutation carriers (Kremer et al. 1995; Wheeler et al. 2007; Semaka et al. 2010; Aziz et al. 2011; Ramos et al. 2012). The wide range of CAG repeat lengths afforded by the Htt knock-in allelic series allowed us to perform a comprehensive analysis of the effect of parental CAG repeat length on various measures of intergenerational repeat instability.

Given the parent-of-origin effects described above, the influence of parental CAG size on repeat transmissions was assessed in paternal transmissions only—which constitute the majority of the breeding data available, and encompass the widest range of allele sizes (Table 2). The HttQ20 line showed ∼99.9% stable transmissions. The high stability of this normal CAG length allele is to be expected, with the very rare repeat length changes consistent with occasional unstable normal alleles in humans (Ramos et al. 2015). Note that HttQ20 was not included in subsequent analyses due to the extremely low number of unstable events.

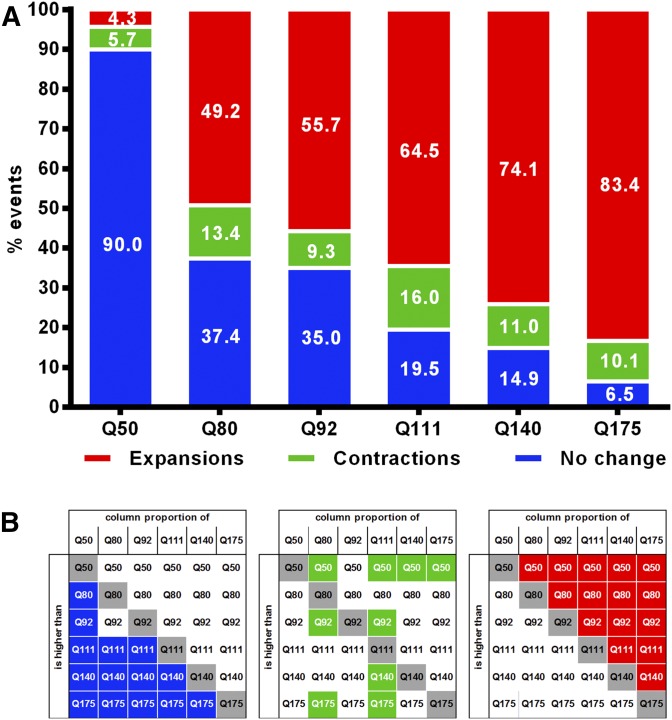
Frequency distributions of expansions, contractions, and unchanged alleles for the expanded Htt CAG alleles are shown in Figure 2. In HttQ50 repeat length was unchanged in the vast majority of transmissions (90%), while the longer Htt alleles showed considerable levels of instability. Mouse line significantly predicted the frequency distribution of repeat length change (χ2 = 3774.23, 10 df, P < 0.001) and proportion comparisons revealed that longer repeat lines had significantly higher expansion frequencies, and significantly lower frequencies of unchanged alleles when compared to lines of shorter repeat length (two-proportion z-tests, P < 0.003 – Bonferroni corrected; Figure 2B). For contractions, significant differences between some of the lines were observed, but they did not follow any continuous CAG length dependence. To better understand these trends, we determined frequencies of expansions, contractions, and unchanged alleles among the more unstable HttQ80, HttQ92, HttQ111, HttQ140, and HttQ175 lines, taking parental CAG size as a continuous variable, and weighting trend lines by the number of transmissions for each CAG length (Figure S6). This confirmed that expansion frequency is positively correlated with CAG repeat length (slope = 0.298; R2 = 0.728), that the frequency of unchanged alleles is negatively correlated with CAG repeat length (slope = −0.280; R2 = 0.809), and highlights a clearer picture of a fairly constant (∼10–12%) contraction frequency throughout the broad CAG range being studied (slope = −0.018; R2 = 0.029).

Figure 2.

Figure 2

Open in a new tab

Relative frequency and significant differences of stable and unstable paternal transmissions in JAX’s dataset. (A) Breakdown of transmission frequency by expansions, contractions, and stable transmissions. (B) Significant differences (P < 0.003 threshold after Bonferroni correction) between proportions of the different lines are highlighted for expansions (right), contractions (center) and stable transmissions (left).

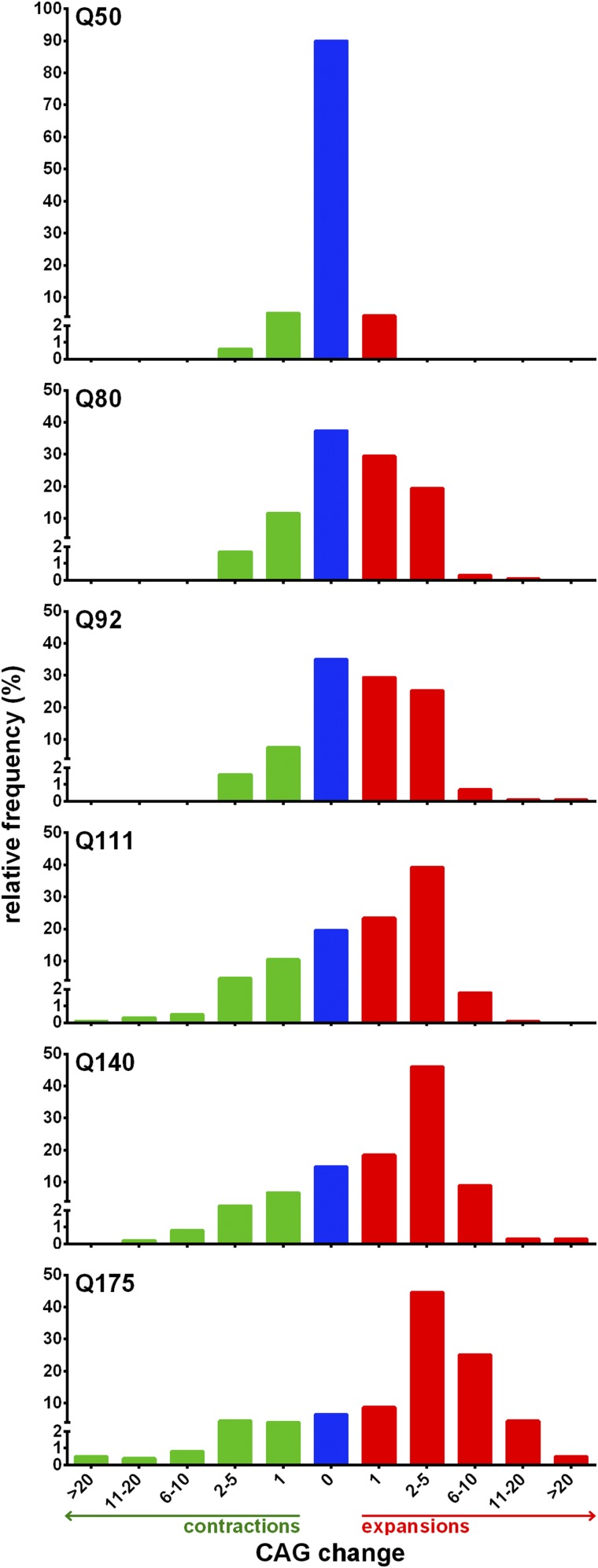
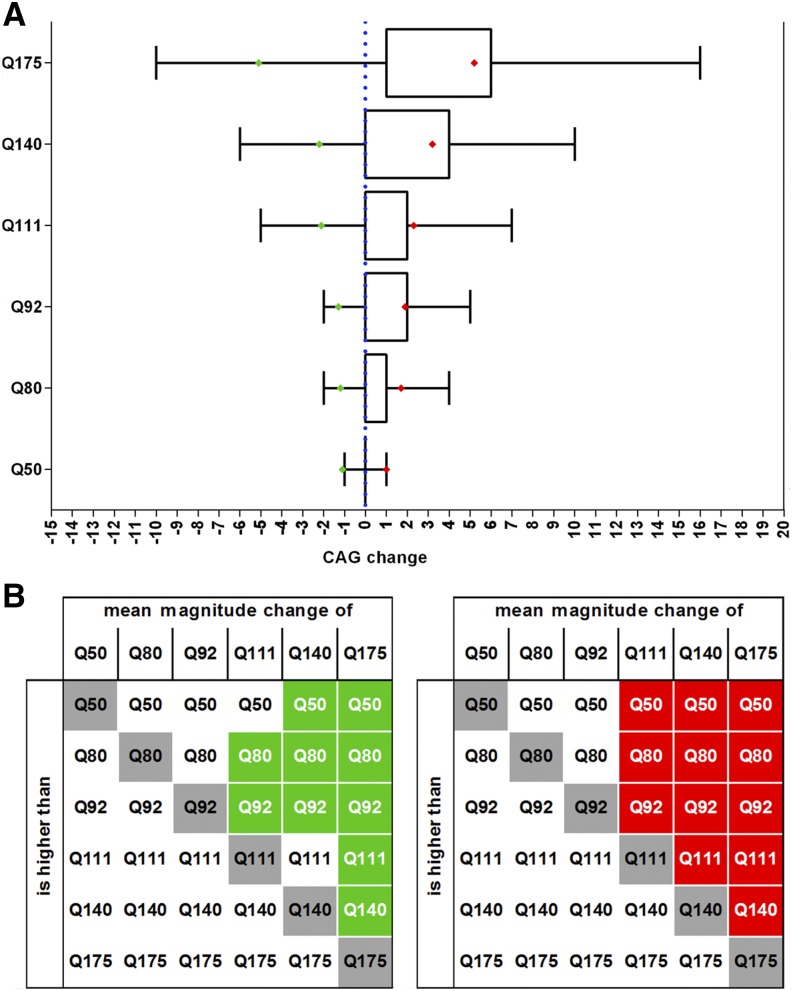
We also analyzed the effect of CAG repeat length on the magnitude of expansions and contractions. The large number of transmissions available for analysis allowed us to capture a wide distribution of CAG changes across the different lines (Figure 3, Figure 4, and Table 2), undetected in previous analyses of intergenerational instability in mouse models (Wheeler et al. 1999; Lloret et al. 2006). For most lines, very large changes (>20 CAGs) were observed, albeit at low frequencies, with the largest repeat size change being an expansion of 153 CAGs in HttQ175 (Figure S5). Mouse line was found to significantly predict the magnitude of both expansions and contractions (Kruskal-Wallis test, P < 0.0001). Dunn’s multiple comparisons test showed significantly higher mean expansions and contractions for most lines when compared to others with lower repeat lengths [P < 0.05, multiplicity adjusted (Wright 1992); Figure 4B]. Expansions appeared more sensitive to CAG repeat length, with expansions up to 20 CAGs apparent by ∼80 CAGs (HttQ80, Figure S5), and contractions of the same magnitude only apparent by ∼106 CAGs (HttQ111, Figure S5). Notably, in HttQ50 transmissions, repeat length changes varied only from −2 to +1 CAGs, demonstrating the relatively high stability of this repeat size in these mice.

Figure 3.

Figure 3

Open in a new tab

Relative frequency of CAG size changes within specific ranges across all lines. Stable transmissions (blue), contractions (green), and expansions (red).

Figure 4.

Figure 4

Open in a new tab

Magnitude of change and significant differences in mean expansion and contraction among paternal transmissions in the JAX transmission data. (A) Boxplot representation of CAG change in paternal transmissions for each line (boxes, interquartile range of transmissions; whiskers, 1–99 percentile of transmissions; red diamonds, average expansion size; green diamonds, average contraction size). Although substantially larger CAG changes were observed, these were relatively rare (<2%), and are summarized in Table 2 and Figure S5. (B) Significant differences in mean contractions (left, in green), and mean expansions (right, in red) between the six lines (P < 0.05, multiplicity adjusted).

Overall, while CAG repeat length in transmitting fathers is a major driver of intergenerational CAG instability, our analyses have distinguished CAG length-dependent effects on the frequency and magnitude of expansion and contraction events. Thus, while longer CAG lengths are associated with larger expansions and contractions, they do not impact the likelihood of contraction events, but only increase the frequency of expansions at the expense of unchanged alleles.

Paternal age has a minor impact on the magnitude of CAG repeat expansions

In an effort to probe for additional factors that might contribute to intergenerational CAG instability, we analyzed a second dataset of intergenerational repeat length transmissions generated from CHGR’s breeding of Htt CAG knock-in mice. This dataset is composed of ∼1800 paternal transmissions of heterozygous Htt knock-in alleles, on six different genetic backgrounds—129, CD1, FVB, DBA, B6N, and B6J—spanning a range of 81–153 CAGs (Figure S7B and Table 4).

Table 4. Paternal age at offspring birth, CAG size and transmission information for the different lines in CHGR’s breeding data.

BG Parent Transmissions
N Age at Offspring Birth (Weeks) CAG N Stable Contractions Expansions
Min. Max. Mean Min. Max. Mean N (%) N (%) Max. Mean N (%) Max. Mean
129 32 9 40 21.4 105 114 109.7 213 72 (33.8) 63 (29.6) 8 1.6 78 (36.6) 9 1.7
CD1 59 7 42 18.6 81 139 105.7 439 116 (26.4) 51 (11.6) 8 1.7 272 (62.0) 12 1.8
FVB 24 9 41 18.9 111 147 132.0 180 32 (17.8) 25 (13.9) 5 2.2 123 (68.3) 9 2.7
DBA 12 9 38 17.3 115 129 123.0 64 8 (12.5) 8 (12.5) 4 2.8 48 (75.0) 6 2.4
B6N 38 9 74 26.1 109 138 119.2 226 40 (17.7) 51 (22.6) 11 1.8 135 (59.7) 6 2.3
B6J 55 8 62 28.0 83 153 128.3 707 73 (10.3) 74 (10.5) 19 2.9 560 (79.2) 21 3.5
Open in a new tab

BG, background; N, number. All strains: neo−.

This dataset included paternal age at offspring birth, therefore allowing us to evaluate its potential contribution to intergenerational instability. Given that the B6J strain had both the largest number of transmissions, and a broad paternal age range, we analyzed the effect of paternal age on a subset of B6J transmissions (parental age: 8–62 weeks; HttQ111, CAG range: 113–153; N = 690). In this dataset and select repeat length range, there was no relationship between paternal age at offspring birth and paternal CAG (Figure S8). Therefore, we used this dataset to determine whether paternal age influenced intergenerational instability.

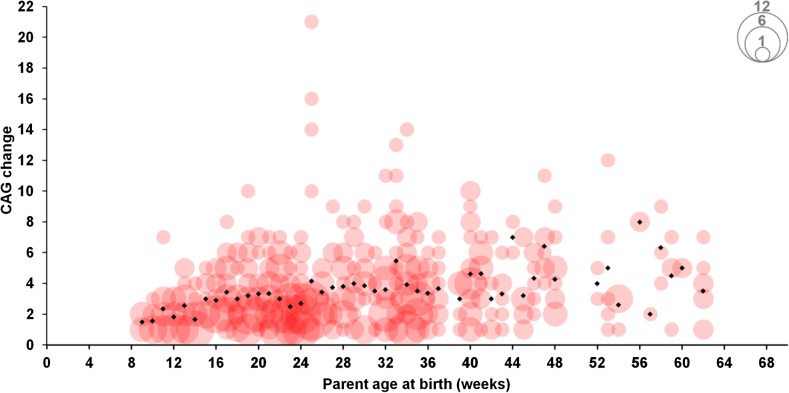
Paternal age did not significantly alter the frequency of expansions, contractions, or unchanged alleles (Figure S9), showed no correlation with the magnitude of repeat contractions (Pearson correlation = 0.031, P = 0.8), but showed a modest though statistically significant correlation with the magnitude of the expansions (Pearson correlation = 0.253, P < 0.001; Figure 5).

Figure 5.

Figure 5

Open in a new tab

CAG expansions by paternal age at offspring birth (weeks) in CHGR’s B6J.HttQ111. Bubble size is proportional to the total number of observed events (expansions). Black diamonds, average expansion per discrete age (N = 690).

Multiple background strains alter intergenerational CAG repeat instability

We previously analyzed, using a much smaller transmission dataset, strain-specific differences in paternal intergenerational instability of the CAG repeat in Htt CAG knock-in mice using three inbred mouse strains (B6N, FVB, 129) and found a significantly greater frequency of intergenerational changes in repeat length (combined expansions and contractions) in B6N mice compared to 129 mice (Lloret et al. 2006). Here, afforded by a greatly increased number of transmissions, and an expanded set of mouse strains, we aimed to investigate further potential effects of genetic background on intergenerational instability upon paternal CAG repeat transmission.

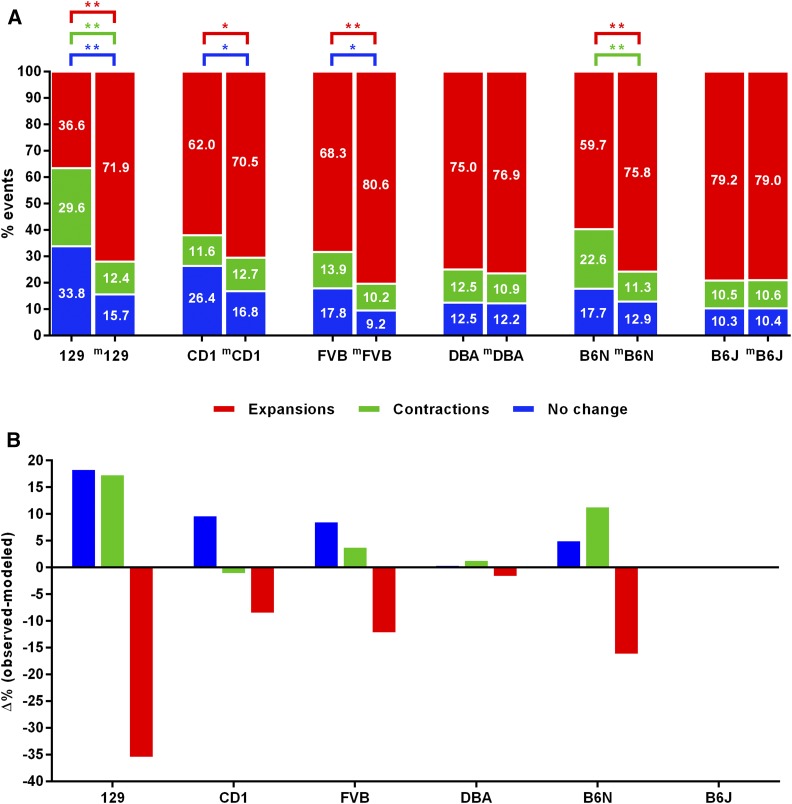
A comparison of the frequencies of expansions, contractions, and stable transmissions across the six strains revealed clear differences in instability (Table 4, Figure S7A); however, the different paternal CAG repeat length distributions for each of the different strains suggest that CAG repeat length (Table 4, Figure S7B) may, in part, contribute to the differences in instability between the strains. To control for this, we modeled the frequencies of expansions, contractions, and unchanged alleles as a function of CAG repeat length in the B6J strain that has the broadest range of parental CAGs as well as the most transmissions. We then compared the actual transmission frequencies observed in each of the other five strains to transmission frequencies predicted from the B6J model (File S1 and Materials and Methods). These results are represented in Figure 6 as pairwise comparisons between the observed (e.g., 129), and the expected, transmission distributions determined by B6J modeling (e.g., m129).

Figure 6.

Figure 6

Open in a new tab

Comparison of expansions, contractions, and stable transmissions frequencies in various strain backgrounds with B6J-modeled distributions. (A) Observed and expected (m) frequencies for each strain. (B) Percent difference between observed and expected frequencies for expansions, contractions, and unchanged transmissions. **P < 0.01, *P < 0.05.

The data show that frequencies of expansions, contractions, and unchanged alleles in the DBA strain do not differ significantly from those in B6J. In contrast, 129 is the most dissimilar to B6J, with 35% fewer expansions (two-proportion z-test, P < 0.01) and 17–18% more contractions and stable transmissions (two-proportion z-tests, P < 0.01). CD1 and FVB both show significantly reduced frequencies of expansions (two-proportion z-test; CD1, P < 0.05; FVB, P < 0.01), and significantly increased frequencies of unchanged alleles (two-proportion z-test, P < 0.05) compared to B6J. Interestingly, despite being the most highly related to B6J, B6N exhibited a 16.1% decrease in expansion frequency (two-proportion z-test, P < 0.01), and an 11.2% increase in the frequency of contractions (two-proportion z-test, P < 0.01).

It is notable that the results obtained based on modeling in B6J as a means to overcome paternal repeat length differences are mostly consistent with the initially observed differences in instability across the strains (Figure S7A), suggesting that, at least within the range of CAG repeats encompassed by these strains, genetic background, rather than CAG repeat length, is the more significant determinant of repeat instability, with distinct strains differentially modifying the frequencies of expansions, contractions, and stable alleles.

The effect of background strain on the magnitude of repeat length change was also assessed using B6J as a reference, and controlling for CAG size effects through mixed model analyses. Strain background did not influence the size of the contractions (data not shown). However, analysis of the strain effect on magnitude of expansions revealed significantly smaller changes compared to B6J in all strains except DBA, with 129 and CD1 being the most dissimilar to B6J, and having the greatest “protective” effect (Table 5).

Table 5. Effect of background strain on the magnitude of CAG expansions.

Strain Intercept P-Value
B6J 1.09 NA
B6N 0.27 0.001
129 −0.17 <0.001
CD1 −0.09 <0.0001
DBA 0.33 0.054
FVB 0.31 0.005
Open in a new tab

CAG changes in offspring were modeled, as a function of paternal CAG repeat length and strain background, in a mixed effect model context with random intercept. Paternal CAG repeat significantly explained variance in size of CAG expansions, with an estimated effect size of 0.017 increase in expansion magnitude per paternal CAG repeat unit increment (P = 0.0182). P-values represent significance when compared to the reference strain B6J.

The presence of a neo cassette upstream of Htt reduces the CAG expansion frequency

Previous data have indicated a role for cis-acting modifiers of CAG repeat instability in HD transgenic mice (Mangiarini et al. 1997; Goula et al. 2012). To explore the role of cis elements that might influence CAG repeat instability at the Htt locus, we have taken advantage of Htt knock-in lines that differ by the presence or absence of an upstream neomycin (neo) resistance cassette (Figure S1 and Table S3). We compared intergenerational instability in paternal transmissions from the CD1 Htt CAG knock-in mice described above, which do not contain a neo cassette (CD1neo−), with intergenerational instability in paternal transmissions from CD1 Htt CAG knock-in mice harboring an upstream neo cassette (CD1neo+) (White et al. 1997) (Table S3).

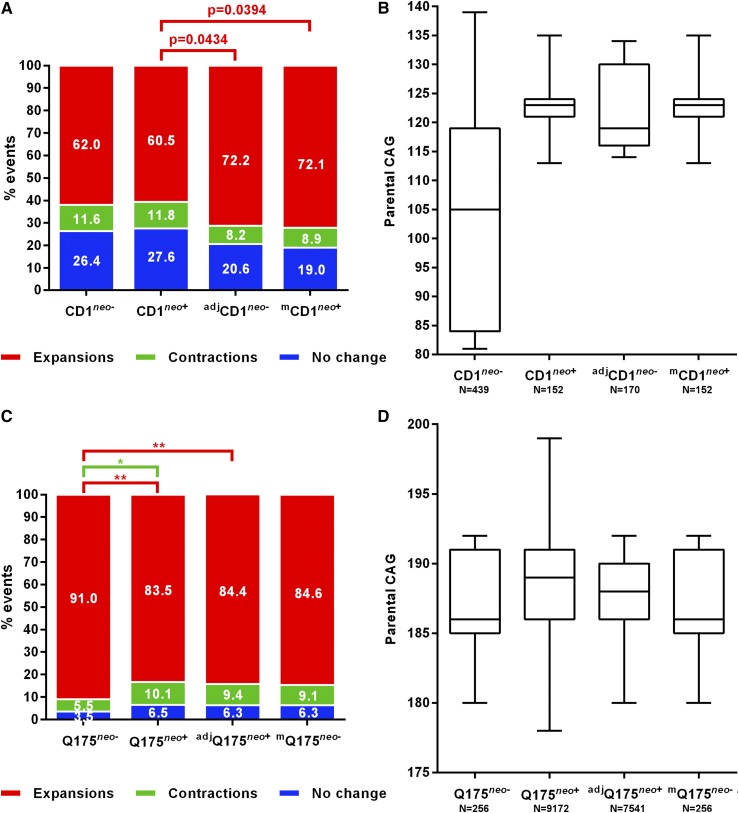
Direct comparison between these two strains indicated the absence of any significant differences in frequencies of expansions, contractions, or stable alleles (Figure 7A, two leftmost bars). However, the significantly higher mean paternal CAG size (unpaired t-test, P < 0.001), and range of CAG repeats in the CD1neo+ mice (Figure 7B, two leftmost bars) suggested that we may be underestimating instability in the CD1neo− mice relative to that in the CD1neo+ mice due to repeat size effects. We dealt with the CAG size discrepancies using two approaches (Figure 7, A and B): (1) adjusting the CD1neo− dataset to only include transmissions from a paternal CAG range equivalent to the CD1neo+ set (adjCD1neo−); and (2) modeling frequencies of events in the CD1neo+ mice based on data from the CD1neo− mice (mCD1neo+)—as previously performed for the strain background analyses; see Materials and Methods and File S1 for details. When controlling for paternal CAG size by either of these two approaches, we find that CD1neo+ sires are ∼10% less prone to expansions, with nominal significance (two-proportion z-tests, P < 0.05) that did not withstand multiple test correction (Bonferroni significance threshold set at P = 0.0167), with minor and not statistically significant differences in frequencies of contractions or stable transmissions (Figure 7A).

Figure 7.

Figure 7

Open in a new tab

Effect of an upstream neo cassette on the frequency of stable and unstable transmissions. (A) Frequency of changes in CD1 background lines either containing a neo cassette upstream of the Htt gene (neo+), or not (neo−), as well as adjusted and modeled corrections for parental CAG size effects (see Table S3). (B) Parental CAG range for the different CD1 lines, as well as adjusted and modeled subsets. (C) Frequency of changes in HttQ175 B6J background lines containing (neo+) or not (neo−) a neo cassette upstream of the repeat, as well as adjusted and modeled corrections for parental CAG size effects (see Table S3). (D) Parental CAG range for the different HttQ175 (B6J) lines, as well as adjusted and modeled subsets. **P < 0.01, *P < 0.0167 (Bonferroni corrected).

Differences in the magnitude of changes were evaluated by comparing mean changes between the CD1neo+ and the adjCD1neo− set. No significant differences were observed in either mean expansion size (CD1neo+: 2.1 CAGs; adjCD1neo−: 2.1 CAGs; unpaired t-test, P = 0.961) or contraction size (CD1neo+: 1.6 CAGs; adjCD1neo−: 1.4 CAGs; unpaired t-test, P = 0.610).

As these results indicated cis effects on the frequency of unstable transmissions, we also investigated a distinct breeding set from the JAX that comprised transmissions from HttQ175neo− parents on a B6J background (Table S3). We compared the instability in paternal transmissions of this allele with those from the HttQ175neo+ allele (B6J), which formed part of the allelic series described above.

Direct comparison between the two lines revealed significantly lower expansion frequency in HttQ175neo+ mice (two-proportion z-test, P < 0.01; Figure 7C), despite a higher mean paternal CAG repeat size (unpaired t-test, P < 0.001; Figure 7D), as well as a significantly increased contraction frequency (two-proportion z-test, P < 0.0167), and a small nonsignificant increase in the frequency of stable transmissions (two-proportion z-test, P = 0.057; significance threshold set at P = 0.0167).

To control for CAG repeat length, we employed the two approaches described above: (1) using a subset of the HttQ175neo+ mice with parental CAGs in the same range as those in the HttQ175neo− mice (adjHttQ175neo+; Table 2 and Table S3), and (2) modeling frequencies of events in the HttQ175neo− line based on data from the HttQ175neo+ mice (mHttQ175neo−; see Materials and Methods and File S1). When controlling for CAG size using the adjustment method, we found a significantly reduced expansion frequency in HttQ175neo+ (two-proportion z-test, P < 0.01), while the effect was only nominally significant when adjusting through the modeling methodology (two-proportion z-test, P = 0.03; Bonferroni corrected significance threshold P = 0.0167), likely due to the reduced sample size enforced by this methodology (Figure 7D and Table S3). We did not find any significant differences in the mean magnitude of expansions (HttQ175neo−: 5.7 CAGs, adjHttQ175neo+: 5.2 CAGs; unpaired t-test, P = 0.565), or contractions (HttQ175neo−: 9.07 CAGs, adjHttQ175neo+: 5.42 CAGs; unpaired t-test, P = 0.112), in a comparison between HttQ175neo− and the paternal CAG-adjusted HttQ175neo− mice.

Taken together, these analyses indicate that the existence of a neo cassette upstream of the repeat seems to be a protective factor, reducing the frequency of expansions (by ∼6.5–11.5%), in two different HD knock-in mouse models, but having no discernible effects on the magnitude of the repeat length changes.

Discussion

The length of the expanded CAG repeat plays a critical role in HD, influencing both penetrance and age of onset (Andrew et al. 1993; Duyao et al. 1993; Telenius et al. 1993; The Huntington’s Disease Collaborative Research Group 1993; Ranen et al. 1995; McNeil et al. 1997; Lee et al. 2012a). Underlying the variation in inherited CAG repeat length between individuals are high rates (∼70–80%) of intergenerational instability (Duyao et al. 1993; Zühlke et al. 1993; Telenius et al. 1994; Kremer et al. 1995; Wheeler et al. 2007). Here, we have analyzed thousands of intergenerational transmissions across multiple lines of Htt CAG knock-in mice, in order to gain further insight into factors that may influence instability.

The availability of an allelic series of mice differing by CAG repeat tract length provided the opportunity to investigate CAG-dependent aspects of repeat transmissions. We first determined whether there was any evidence for segregation distortion of the Htt allele. This has previously been suggested for a number of CAG/CTG repeat diseases, although the data in support of this phenomenon are conflicting (Carey et al. 1994; Ikeuchi et al. 1996; Leeflang et al. 1996; Takiyama et al. 1997). The majority of the allelic series lines showed the expected 1:1 Mendelian ratio of heterozygous and wild-type mice in transmissions from heterozygous parents. The only exception occurred in HttQ92 paternal transmissions, which showed a relatively small decrease in the number of heterozygous progeny (∼1.7% less than expected). Given that this was not seen in lines with shorter or longer repeat lengths, this minor deviation from the expected 1:1 ratio is likely a stochastic effect, clearly not driven by CAG repeat length. Overall, our transmission analyses of a broad range of expanded CAG repeats provide evidence for no segregation distortion of the mutant Htt allele in mouse, supporting data derived from single sperm genotyping in HD individuals (Leeflang et al. 1995), and suggesting that locus-specific effects rather than repeat length, primarily drive any potential segregation distortion seen in other diseases (Carey et al. 1994; Ikeuchi et al. 1996; Leeflang et al. 1996; Takiyama et al. 1997).

For the lines with both paternal and maternal transmissions (HttQ80 and HttQ92, B6J background), we confirmed previous results in HD patients, and in knock-in mice on a different (CD1) genetic background (Wheeler et al. 1999), showing a strong expansion bias in male transmissions. We also confirmed a contraction bias in maternal transmissions observed previously in CD1 knock-in mice (Wheeler et al. 1999), differing somewhat from maternal transmissions in HD patients that show approximately equal expansion and contraction frequencies (Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012). Limited studies carried out to date indicate that repeat expansions in the male germline can occur at multiple stages during spermatogenesis (Kovtun and McMurray 2001; Yoon et al. 2003). Though the male expansion bias may be related to the large number of mitotic cell divisions of premeiotic spermatogonia, in the present study, and in line with previous data in HD patients (Wheeler et al. 2007), we found only a minor effect of paternal age in determining the magnitude of CAG expansions, despite our analyses of a large number of transmissions over a broad age range. As increasing paternal age is expected to correlate with increased accumulation of repeat expansions in continually replicating spermatogonia, the mouse and human data overall do not strongly support spermatogonial cell divisions as the major source of CAG expansions, consistent with the lack of positive correlation of cell division rate with repeat instability (Gomes-Pereira et al. 2001; Lee et al. 2010). Further understanding of the sex- and cell-type-specific processes that drive the generation of repeat expansions and contractions would be of considerable interest.

A small effect of offspring sex on intergenerational instability has been previously observed in a large Venezuelan HD pedigree, implying a role for postzygotic factors that influence instability (Wheeler et al. 2007). Embryo sex also influenced instability in the R6/1 transgenic mouse model (Kovtun et al. 2000). Here, analyzing large numbers of transmissions, we observed no significant effects of offspring sex on the frequency or magnitude of repeat length changes in either paternal or maternal transmissions in any of the lines studied. Even though a minor effect of offspring sex may be present in humans and transgenic mouse models, it is not observable in the knock-in.

Parental CAG repeat length has been proposed as a major contributor to intergenerational repeat instability in patients (Kremer et al. 1995; Wheeler et al. 2007; Aziz et al. 2011; Ramos et al. 2012). Here, we have examined paternally transmitted CAG repeats over a large range of repeat lengths (18–∼200), and found that CAG repeat length determines the magnitude of both expansions and contractions. With the number of transmissions analyzed in this study, we were able to detect large (>10–20 CAGs) repeat length changes that are found, typically in paternal transmissions in HD patients that push the repeat into the range associated with juvenile-onset disease. Notably, however, such repeat length changes are rare in the mouse, and were not detected in HttQ50 mice harboring CAG repeat lengths typical of adult-onset HD in patients. What underlies the apparent stability of the Htt CAG repeat in the mouse compared to that in humans is unclear. This may simply be related to the distinct time-spans of gametogenesis in the two species, or, alternatively, may reflect underlying differences in the mechanisms that drive repeat length changes. However, the high frequency of small repeat length changes and the detection of larger changes, albeit at low frequency, in mice harboring longer CAG repeats would suggest that the mechanisms that generate such changes are conserved in the mouse.

We also found that longer CAG repeat lengths were associated with a higher frequency of repeat expansions. Interestingly, this was mirrored by a decrease in the frequency of unchanged alleles, with no effect on the frequency of contractions, despite the association of repeat length with the magnitude of the contractions. This may reflect different mechanisms underlying expansions and contractions. In this scenario, mechanism(s) driving expansions are engaged in a repeat length-dependent manner; in contrast, mechanism(s) driving contractions are engaged regardless of repeat length, but once engaged, longer CAG lengths are more likely to drive larger contractions. Previous observations in which paternal transmissions of HttQ111 Msh2 knockout mice exclusively exhibited contractions, in contrast to the predominant expansions in HttQ111 mice wild-type for Msh2 (Wheeler et al. 2003), support separate expansion and contraction mechanisms that are, respectively, dependent on, and independent of, Msh2. Different mechanisms of intergenerational expansion and contraction of CAG/CTG repeats are supported by several additional studies (Foiry et al. 2006; Dragileva et al. 2009; Tomé et al. 2011; Slean et al. 2016).

Expanding on previous work (Lloret et al. 2006), we analyzed intergenerational changes across six genetic backgrounds — 129, CD1, FVB, DBA, B6N, and B6J — and in expanded datasets that afford the power to distinguish strain-specific effects on both the frequency and magnitude of changes, as well as on expansions and contractions.

Overall, B6J and DBA were the most unstable strains, possessing similar frequencies and magnitudes of repeat length changes, while 129 was the most stable strain, with the low frequency and magnitude of changes in this strain consistent with previous data (Lloret et al. 2006). More specifically, we observed that different strains variably altered the relative frequencies of expansions, contractions, and stable transmissions (Figure 6). Strain background also modified the magnitude of the expansions, but not the magnitude of the contractions, though this may be, in part, due to the lower number of contraction events. As all of these strains were derived from an initial HttQ111 line, generated by targeting in 129 embryonic stem cells (Wheeler et al. 1999), all the Htt knock-in alleles are on a local 129 haplotype, and any differences in instability can likely be attributed to trans-effects, mediated by variation in other genes.

Previous analyses point to Mlh1 genetic variation underlying differences in Htt CAG somatic instability between 129 and B6N strains (Pinto et al. 2013). Given overlapping roles of mismatch repair (MMR) genes in somatic and intergenerational instability in HD (Wheeler et al. 2003; Dragileva et al. 2009), and other repeat disorders (Foiry et al. 2006; Ezzatizadeh et al. 2014), it seems likely that Mlh1 genetic variation underlies the 129 vs. B6 (B6N and B6J) differences in intergenerational instability. Interestingly, the reduced frequency of expansions in the 129 strain was accompanied by an increased contraction frequency, reminiscent of the impact of loss of Msh2 (Wheeler et al. 2003), and further suggesting that genetic variation in 129 might impact the same pathway(s). Additional, unbiased genetic analyses would be needed to uncover the modifier(s) responsible for the reduced intergenerational instability in 129 mice, as well as in other strains. Interestingly, although B6J and B6N are closely related strains, B6N showed an increase in the frequency of contractions and a decrease in frequency and magnitude of expansions relative to B6J. While these strains do not have any coding or obvious regulatory region SNPs in MMR genes (data not shown), the limited genetic variation between the two strains may provide an opportunity to uncover new modifiers that shift the balance of repeat length changes from expansions toward contractions.

In addition to genetic background strain effects attributable to trans-acting modifiers, we also examined potential cis-effects by comparing intergenerational instability in strains with and without a neo cassette upstream of the knock-in repeat. The presence of the neo cassette was associated with reduced expansion frequency in paternal transmissions, without having an effect on the magnitude. We observed this effect independently of paternal CAG size effects, in two different background strains (CD1 and B6J) in the context of two knock-in lines (HttQ111 and HttQ175) with different sites of neo insertion (Figure S1).

Considerable data support a role for cis-acting modifiers of trinucleotide repeat instability (Libby et al. 2008; Nestor and Monckton 2011; Goula et al. 2012). At the human HTT locus itself, an instability-promoting haplogroup has been proposed to drive expansion from the high normal range (Warby et al. 2009); however, HTT haplotype does not modify the intergenerational instability of expanded CAG repeats (Lee et al. 2012b). Regardless, cis-modifiers of HTT CAG instability in model systems may provide insight into underlying mechanisms. Reduced instability in the presence of the neo insertions may be a consequence of chromatin structural changes, and/or alteration of Htt transcription levels during germ cell generation. Interestingly, the orientation of the neo cassette, in relation to the Htt knock-in allele, is different between the HttQ111 and HttQ175 lines (sense and antisense, respectively), and, although the neo insertion in the HttQ111 allele dramatically reduces its transcription resulting in a “hypomorphic” allele (Auerbach et al. 2001), the neo insertion in the HttQ175 allele does not have the same impact on Htt expression (Alexandrov et al. 2016). This suggests that altered transcription may not be the major contributor to reduced instability in the neo+ mice, but rather that local sequence structure/chromatin configuration may impact CAG instability via other mechanisms.

While this study was not specifically geared toward providing a comprehensive understanding of the molecular mechanisms underlying CAG repeat instability, our results provide some general insights that may help to direct future research in this area. Our observation that age is not a major determinant of intergenerational instability implies a major role for DNA repair processes that are not directly linked to DNA replication. We suggest that a minor component of intergenerational instability is driven by processes directly linked to DNA replication, where MMR proteins may act at the level of post-replicative MMR, or may play a direct role at the replication fork (Slean et al. 2016; Viterbo et al. 2016). We also provide further evidence that mechanisms of intergenerational expansion and contraction can be distinguished, perhaps in part reflecting different cell-types in which these events may predominate. Thus, further efforts to understand mechanisms underlying repeat contraction are warranted to provide opportunities for therapeutic strategies aimed at reducing repeat length.

In summary, our comprehensive analyses of intergenerational transmissions of Htt CAG repeats in HD knock-in mice confirms parent-of-origin and CAG repeat length as the major modifiers of intergenerational instability, as in HD patients. The large datasets have also allowed us, for the first time, to discern more subtle effects on instability, e.g., distinguishing CAG-dependent effects on frequency and magnitude of expansions and contractions, and to identify large repeat size jumps seen in HD patients, the latter suggesting that fundamental mechanisms of CAG instability are shared between human and mouse. Evidence for both cis- and trans-modifiers of instability provides a starting point to uncover the underlying modifying factors in the mouse, which will provide further insight into intergenerational instability in patients.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.116.195578/-/DC1.

Click here for additional data file. (200.8KB, tif)
Click here for additional data file. (29KB, tif)
Click here for additional data file. (65.8KB, tif)
Click here for additional data file. (258.4KB, tif)
Click here for additional data file. (272.2KB, tif)
Click here for additional data file. (196.7KB, tif)
Click here for additional data file. (151.7KB, tif)
Click here for additional data file. (132.8KB, tif)
Click here for additional data file. (138.4KB, tif)
Click here for additional data file. (691.3KB, pdf)
Click here for additional data file. (1.5MB, pdf)
Click here for additional data file. (20.6KB, pdf)
Click here for additional data file. (21KB, pdf)
Click here for additional data file. (12.3KB, pdf)

Acknowledgments

J.L.N. is a recipient of a Fundação para a Ciência e a Tecnologia (FCT) fellowship (SFRH/BD/51705/2011; www.fct.pt). This work was supported by the National Institutes of Health [NS049206] grant attributed to V.C.W.

Footnotes

Communicating editor: J. R. Lupski

Literature Cited

  1. Alexandrov V., Brunner D., Menalled L. B., Kudwa A., Watson-Johnson J., et al. , 2016.  Large-scale phenome analysis defines a behavioral signature for Huntington’s disease genotype in mice. Nat. Biotechnol. 34: 838–844. [DOI] [PubMed] [Google Scholar]
  2. Andrew S. E., Goldberg Y. P., Kremer B., Telenius H., Theilmann J., et al. , 1993.  The relationship between trinucleotide (CAG) repeat length and clinical features of Huntington’s disease. Nat. Genet. 4: 398–403. [DOI] [PubMed] [Google Scholar]
  3. Auerbach W., Hurlbert M. S., Hilditch-Maguire P., Wadghiri Y. Z., Wheeler V. C., et al. , 2001.  The HD mutation causes progressive lethal neurological disease in mice expressing reduced levels of huntingtin. Hum. Mol. Genet. 10: 2515–2523. [DOI] [PubMed] [Google Scholar]
  4. Aziz N. A., Van Belzen M. J., Coops I. D., Belfroid R. D. M., Roos R. A. C., 2011.  Parent-of-origin differences of mutant HTT CAG repeat instability in Huntington’s disease. Eur. J. Med. Genet. 54: e413–e418. [DOI] [PubMed] [Google Scholar]
  5. Brocklebank D., Gayán J., Andresen J. M., Roberts S. A., Young A. B., et al. , 2009.  Repeat instability in the 27–39 CAG range of the HD gene in the venezuelan kindreds: counseling implications. Am. J. Med. Genet. B Neuropsychiatr. Genet. 150B: 425–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Carey N., Johnson K., Nokelainen P., Peltonen L., Savontaus M.-L., et al. , 1994.  Meiotic drive at the myotonic dystrophy locus? Nature 6: 117–118. [DOI] [PubMed] [Google Scholar]
  7. Dragileva E., Hendricks A., Teed A., Gillis T., Lopez E. T., et al. , 2009.  Intergenerational and striatal CAG repeat instability in Huntington’s disease knock-in mice involve different DNA repair genes. Neurobiol. Dis. 33: 37–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Duyao M., Ambrose C., Myers R., Novelletto A., Persichetti F., et al. , 1993.  Trinucleotide repeat length instability and age of onset in Huntington’s disease. Nat. Genet. 4: 387–392. [DOI] [PubMed] [Google Scholar]
  9. Ezzatizadeh V., Sandi C., Sandi M., Anjomani-Virmouni S., Al-Mahdawi S., et al. , 2014.  MutLα heterodimers modify the molecular phenotype of Friedreich ataxia. PLoS One 9: e100523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Foiry L., Dong L., Savouret C., Hubert L., te Riele H., et al. , 2006.  Msh3 is a limiting factor in the formation of intergenerational CTG expansions in DM1 transgenic mice. Hum. Genet. 119: 520–526. [DOI] [PubMed] [Google Scholar]
  11. Gomes-Pereira M., Fortune M. T., Monckton D. G., 2001.  Mouse tissue culture models of unstable triplet repeats: in vitro selection for larger alleles, mutational expansion bias and tissue specificity, but no association with cell division rates. Hum. Mol. Genet. 10: 845–854. [DOI] [PubMed] [Google Scholar]
  12. Goula A. V., Stys A., Chan J. P. K., Trottier Y., Festenstein R., et al. , 2012.  Transcription elongation and tissue-specific somatic CAG instability. PLoS Genet. 8: e1003051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hendricks A. E., Latourelle J. C., Lunetta K. L., Cupples L. A., Wheeler V., et al. , 2009.  Estimating the probability of de novo HD cases from transmissions of expanded penetrant CAG alleles in the Huntington disease gene from male carriers of high normal alleles (27–35 CAG). Am. J. Med. Genet. A. 149: 1375–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ikeuchi T., Igarashi S., Takiyama Y., Onodera O., Oyake M., et al. , 1996.  Non-Mendelian transmission in dentatorubral-pallidoluysian atrophy and Machado-Joseph disease: the mutant allele is preferentially transmitted in male meiosis. Am. J. Hum. Genet. 58: 730–733. [PMC free article] [PubMed] [Google Scholar]
  15. Kovtun I. V., McMurray C. T., 2001.  Trinucleotide expansion in haploid germ cells by gap repair. Nat. Genet. 27: 407–411. [DOI] [PubMed] [Google Scholar]
  16. Kovtun I. V., Therneau T. M., McMurray C. T., 2000.  Gender of the embryo contributes to CAG instability in transgenic mice containing a Huntington’s disease gene. Hum. Mol. Genet. 9: 2767–2775. [DOI] [PubMed] [Google Scholar]
  17. Kremer B., Almqvist E., Theilmann J., Spence N., Telenius H., et al. , 1995.  Sex-dependent mechanisms for expansions and contractions of the CAG repeat on affected Huntington disease chromosomes. Am. J. Hum. Genet. 57: 343–350. [PMC free article] [PubMed] [Google Scholar]
  18. Langfelder P., Cantle J. P., Chatzopoulou D., Wang N., Gao F., et al. , 2016.  Integrated genomics and proteomics define huntingtin CAG length–dependent networks in mice. Nat. Neurosci. 19: 623–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lee J.-M., Zhang J., Su A. I., Walker J. R., Wiltshire T., et al. , 2010.  A novel approach to investigate tissue-specific trinucleotide repeat instability. BMC Syst. Biol. 4: 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lee J. M., Pinto R. M., Gillis T., St. Claire J. C., Wheeler V. C., 2011.  Quantification of age-dependent somatic CAG repeat instability in Hdh CAG knock-in mice reveals different expansion dynamics in striatum and liver. PLoS One 6: 6–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lee J. M., Ramos E. M., Lee J. H., Gillis T., Mysore J. S., et al. , 2012a CAG repeat expansion in Huntington disease determines age at onset in a fully dominant fashion. Neurology 78: 690–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lee J. M., Gillis T., Mysore J. S., Ramos E. M., Myers R. H., et al. , 2012b Common SNP-based haplotype analysis of the 4p16.3 Huntington disease gene region. Am. J. Hum. Genet. 90: 434–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Leeflang E. P., Zhang L., Tavare S., Hubert R., Srinidhi J., et al. , 1995.  Single sperm analysis of the trinucleotide repeats in the Huntingtons-disease gene—quantification of the mutation frequency-spectrum. Hum. Mol. Genet. 4: 1519–1526. [DOI] [PubMed] [Google Scholar]
  24. Leeflang E. P., McPeek M. S., Arnheim N., 1996.  Analysis of meiotic segregation, using single-sperm typing: meiotic drive at the myotonic dystrophy locus. Am. J. Hum. Genet. 59: 896–904. [PMC free article] [PubMed] [Google Scholar]
  25. Leeflang E. P., Tavaré S., Marjoram P., Neal C. O. S., Srinidhi J., et al. , 1999.  Analysis of germline mutation spectra at the Huntington’s disease locus supports a mitotic mutation mechanism. Hum. Mol. Genet. 8: 173–183. [DOI] [PubMed] [Google Scholar]
  26. Libby R. T., Hagerman K. A., Pineda V. V., Lau R., Cho D. H., et al. , 2008.  CTCF cis-regulates trinucleotide repeat instability in an epigenetic manner: a novel basis for mutational hot spot determination. PLoS Genet. 4: e1000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Lloret A., Dragileva E., Teed A., Espinola J., Fossale E., et al. , 2006.  Genetic background modifies nuclear mutant huntingtin accumulation and HD CAG repeat instability in Huntington’s disease knock-in mice. Hum. Mol. Genet. 15: 2015–2024. [DOI] [PubMed] [Google Scholar]
  28. Mangiarini L., Sathasivam K., Mahal A., Mott R., Seller M., et al. , 1997.  Instability of highly expanded CAG repeats in mice transgenic for the Huntington’s disease mutation. Nat. Genet. 15: 197–200. [DOI] [PubMed] [Google Scholar]
  29. McNeil S. M., Novelletto A., Srinidhi J., Barnes G., Kornbluth I., et al. , 1997.  Reduced penetrance of the Huntington’s disease mutation. Hum. Mol. Genet. 6: 775–779. [DOI] [PubMed] [Google Scholar]
  30. Menalled L. B., Sison J. D., Dragatsis I., Zeitlin S., Chesselet M. F., 2003.  Time course of early motor and neuropathological anomalies in a knock-in mouse model of Huntington’s disease with 140 CAG repeats. J. Comp. Neurol. 465: 11–26. [DOI] [PubMed] [Google Scholar]
  31. Menalled L. B., Kudwa A. E., Miller S., Fitzpatrick J., Watson-Johnson J., et al. , 2012.  Comprehensive behavioral and molecular characterization of a new knock-in mouse model of Huntington’s disease: ZQ175. PLoS One 7: e49838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Møllersen L., Rowe A. D., Larsen E., Rognes T., Klungland A., 2010.  Continuous and periodic expansion of CAG repeats in Huntington’s disease R6/1 mice. PLoS Genet. 6: 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Myers R. H., MacDonald M. E., Koroshetz W. J., Duyao M. P., Ambrose C. M., et al. , 1993.  De novo expansion of a (CAG)n repeat in sporadic Huntington’s disease. Nat. Genet. 5: 168–173. [DOI] [PubMed] [Google Scholar]
  34. National Research Council , 2011.  Guide for the Care and Use of Laboratory Animals, Ed. 8 The National Academies Press, Washington, DC. [Google Scholar]
  35. Nestor C. E., Monckton D. G., 2011.  Correlation of inter-locus polyglutamine toxicity with CAG•CTG triplet repeat expandability and flanking genomic DNA GC content. PLoS One 6: e28260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pinto R. M., Dragileva E., Kirby A., Lloret A., Lopez E., et al. , 2013.  Mismatch repair genes Mlh1 and Mlh3 modify CAG instability in Huntington’s disease mice: genome-wide and candidate approaches. PLoS Genet. 9: e1003930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ramos E. M., Cerqueira J., Lemos C., Pinto-Basto J., Alonso I., et al. , 2012.  Intergenerational instability in huntington disease: extreme repeat changes among 134 transmissions. Mov. Disord. 27: 580–581. [DOI] [PubMed] [Google Scholar]
  38. Ramos E. M., Gillis T., Mysore J. S., Lee J. M., Gögele M., et al. , 2015.  Haplotype analysis of the 4p16.3 region in Portuguese families with Huntington’s disease. Am. J. Med. Genet. B Neuropsychiatr. Genet. 168: 135–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ranen N. G., Stine O. C., Abbott M. H., Sherr M., Codori A. M., et al. , 1995.  Anticipation and instability of IT-15 (CAG)n repeats in parent-offspring pairs with Huntington disease. Am. J. Hum. Genet. 57: 593–602. [PMC free article] [PubMed] [Google Scholar]
  40. Semaka A., Collins J. A., Hayden M. R., 2010.  Unstable familial transmissions of Huntington disease alleles with 27–35 CAG repeats (intermediate alleles). Am. J. Med. Genet. Neuropsychiatr. Genet. 153: 314–320. [DOI] [PubMed] [Google Scholar]
  41. Sequeiros J., Ramos E. M., Cerqueira J., Costa M. C., Sousa A., et al. , 2010.  Large normal and reduced penetrance alleles in Huntington disease: instability in families and frequency at the laboratory, at the clinic and in the population. Clin. Genet. 78: 381–387. [DOI] [PubMed] [Google Scholar]
  42. Shelbourne P. F., Killeen N., Hevner R. F., Johnston H. M., Tecott L., et al. , 1999.  A Huntington’s disease CAG expansion at the murine Hdh locus is unstable and associated with behavioural abnormalities in mice. Hum. Mol. Genet. 8: 763–774. [DOI] [PubMed] [Google Scholar]
  43. Slean M. M., Panigrahi G. B., Castel A. L., Pearson A. B., Tomkinson A. E., et al. , 2016.  Absence of MutSβ leads to the formation of slipped-DNA for CTG/CAG contractions at primate replication forks. DNA Repair (Amst.) 42: 107–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Takiyama Y., Sakoe K., Soutome M., Namekawa M., Ogawa T., et al. , 1997.  Single sperm analysis of the CAG repeats in the gene for Machado-Joseph disease (MJD1): evidence for non-Mendelian transmission of the MJD1 gene and for the effect of the intragenic CGG/GGG polymorphism on the intergenerational instability. Hum. Mol. Genet. 6: 1063–1068. [DOI] [PubMed] [Google Scholar]
  45. Telenius H., Kremer H. P., Theilmann J., Andrew S. E., Almqvist E., et al. , 1993.  Molecular analysis of juvenile Huntington disease: the major influence on (CAG)n repeat length is the sex of the affected parent. Hum. Mol. Genet. 2: 1535–1540. [DOI] [PubMed] [Google Scholar]
  46. Telenius H., Kremer B., Goldberg Y., 1994.  Somatic and gonadal mosaicism of the Huntington disease gene CAG repeat in brain and sperm. Nat. Genet. 6: 409–414. [DOI] [PubMed] [Google Scholar]
  47. The Huntington’s Disease Collaborative Research Group , 1993.  A novel gene containing a trinucleotide repeat that is expanded and unstable on Huntington’s disease chromosomes. Cell 72: 971–983. [DOI] [PubMed] [Google Scholar]
  48. Tomé S., Panigrahi G. B., Castel A. L., Foiry L., Melton D. W., et al. , 2011.  Maternal germline-specific effect of DNA ligase I on CTG/CAG instability. Hum. Mol. Genet. 20: 2131–2143. [DOI] [PubMed] [Google Scholar]
  49. Trottier Y., Biancalana V., Mandel J. L., 1994.  Instability of CAG repeats in Huntington’s disease: relation to parental transmission and age of onset. J. Med. Genet. 31: 377–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Viterbo D., Michoud G., Mosbach V., Dujon B., Richard G. F., 2016.  Replication stalling and heteroduplex formation within CAG/CTG trinucleotide repeats by mismatch repair. DNA Repair (Amst.) 42: 94–106. [DOI] [PubMed] [Google Scholar]
  51. Warby S. C., Montpetit A., Hayden A. R., Carroll J. B., Butland S. L., et al. , 2009.  CAG expansion in the Huntington disease gene is associated with a specific and targetable predisposing haplogroup. Am. J. Hum. Genet. 84: 351–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Wheeler V. C., Auerbach W., White J. K., Srinidhi J., Auerbach A., et al. , 1999.  Length-dependent gametic CAG repeat instability in the Huntington’s disease knock-in mouse. Hum. Mol. Genet. 8: 115–122. [DOI] [PubMed] [Google Scholar]
  53. Wheeler V. C., Lebel L. A., Vrbanac V., Teed A., te Riele H. T., et al. , 2003.  Mismatch repair gene Msh2 modifies the timing of early disease in HdhQ111 striatum. Hum. Mol. Genet. 12: 273–281. [DOI] [PubMed] [Google Scholar]
  54. Wheeler V. C., Persichetti F., McNeil S. M., Mysore J. S., Mysore S. S., et al. , 2007.  Factors associated with HD CAG repeat instability in Huntington disease. J. Med. Genet. 44: 695–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. White J. K., Auerbach W., Duyao M. P., Vonsattel J. P., Gusella J. F., et al. , 1997.  Huntingtin is required for neurogenesis and is not impaired by the Huntington’s disease CAG expansion. Nat. Genet. 17: 404–410. [DOI] [PubMed] [Google Scholar]
  56. Wright S. P., 1992.  Adjusted P-values for simultaneous inference. Biometrics 48: 1005. [Google Scholar]
  57. Yoon S.-R., Dubeau L., de Young M., Wexler N. S., Arnheim N., 2003.  Huntington disease expansion mutations in humans can occur before meiosis is completed. Proc. Natl. Acad. Sci. USA 100: 8834–8838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zühlke C., Riess O., Bockel B., Lange H., Thies U., 1993.  Mitotic stability and meiotic variability of the (CAG)n repeat in the Huntington disease gene. Hum. Mol. Genet. 2: 2063–2067. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (200.8KB, tif)
Click here for additional data file. (29KB, tif)
Click here for additional data file. (65.8KB, tif)
Click here for additional data file. (258.4KB, tif)
Click here for additional data file. (272.2KB, tif)
Click here for additional data file. (196.7KB, tif)
Click here for additional data file. (151.7KB, tif)
Click here for additional data file. (132.8KB, tif)
Click here for additional data file. (138.4KB, tif)
Click here for additional data file. (691.3KB, pdf)
Click here for additional data file. (1.5MB, pdf)
Click here for additional data file. (20.6KB, pdf)
Click here for additional data file. (21KB, pdf)
Click here for additional data file. (12.3KB, pdf)

Data Availability Statement

Datasets can be provided by the authors upon request. The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article.

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES