A virtual sizing tool for mitral valve annuloplasty

SUMMARY

Functional mitral regurgitation, a backward leakage of the mitral valve, is a result of left ventricular growth and mitral annular dilatation. Its gold standard treatment is mitral annuloplasty, the surgical reduction in mitral annular area through the implantation of annuloplasty rings. Recurrent regurgitation rates may, however, be as high as 30% and more. While the degree of annular downsizing has been linked to improved long-term outcomes, too aggressive downsizing increases the risk of ring dehiscences and significantly impairs repair durability. Here we prototype a virtual sizing tool to quantify changes in annular dimensions, surgically-induced tissue strains, mitral annular stretches, and suture forces in response to mitral annuloplasty. We create a computational model of dilated cardiomyopathy onto which we virtually implant annuloplasty rings of different sizes. Our simulations confirm the common intuition that smaller rings are more invasive to the surrounding tissue, induce higher strains, and require larger suture forces than larger rings: The total suture force was 2.2N for a 24mm ring, 1.9N for a 28mm ring, and 0.8N for a 32mm ring. Our model predicts the highest risk of dehiscence in the septal and postero-lateral annulus where suture forces are maximal. These regions co-localize with regional peaks in myocardial strain and annular stretch. Our study illustrates the potential of realistic predictive simulations in cardiac surgery to identify areas at risk for dehiscence, guide the selection of ring size and shape, rationalize the design of smart annuloplasty rings and, ultimately, improve long-term outcomes after surgical mitral annuloplasty.

1. MOTIVATION

Functional mitral regurgitation is a backward leakage of the mitral valve in the absence of any disease to the valve itself [26, 34, 42]. A major cause of functional mitral regurgitation is dilated cardiomyopathy, in which pathologic remodeling of the myocardium results in increased chamber size [11]. During the course of dilated cardiomyopathy, the growing ventricle dilates the mitral annulus and increases tension on the chordae tendineae [24]. These pathological forces on annulus and chordae eventually render the mitral valve unable to seal against systolic blood pressure, resulting in retrograde blood flow, further reduction in ejection fraction, arrhythmic disorder, and increased risk for myocardial infarction [32].

Mitral valve annuloplasty, as illustrated in Figure 1, remains the number one surgical treatment for functional mitral regurgitation [27, 33, 45]. Correcting the distorted mitral annulus through the implantation of undersized annuloplasty prostheses has been shown to temporarily improve symptoms of functional mitral regurgitation. However, to date, there is no accepted standard for the optimal ring choice or degree of downsizing [7, 41]. Recent studies have shown that a large population of patients treated with undersized annuloplasty show recurrent mitral regurgitation and require re-operation [33, 46]. Continued ventricular remodeling might be responsible for the return of mitral regurgitation and for the suboptimal long-term results of undersized annuloplasty [29]. We propose that successful mitral annuloplasty is a compromise between fixing the leaking valve and minimizing the insult to the surrounding tissue [41]. The heart, both in a physiological and pathological setting, responds to mechanical stimuli to maintain a homeostatic equilibrium state [20, 49]. In dilated cardiomyopathy, the ventricular myocardium dilates in response to myocardial infarction or other insults to the myocardial tissue to establish a new state of mechanical equilibrium [13,42]. The implantation of an undersized annuloplasty ring, initially aimed at surgically reversing the effects of ventricular remodeling, induces additional non-homeostatic deformations and forces in the surrounding tissue [4, 5]. Long-term, these alterations trigger changes in flow conditions and continued ventricular remodeling [30], which can ultimately render the original intervention suboptimal. Quantifying surgically-induced forces is an important first step towards an improved understanding of the effects of undersized annuloplasty on the mitral valve and the surrounding myocardium. To date, there is neither a model to quantify surgical strains and forces, nor a tool to optimize ring choice and the degree of undersizing.

Figure 1.

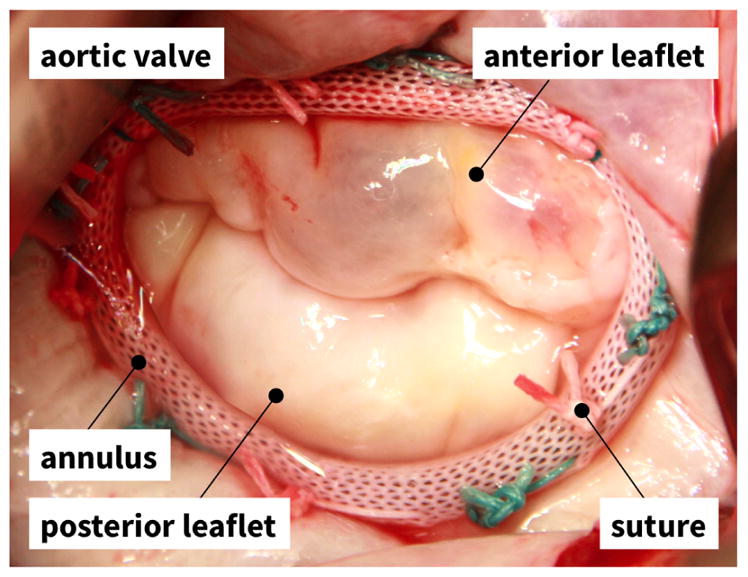
Mitral annuloplasty. Intraoperative photograph of mitral valve complex with anterior and posterior leaflets and annuloplasty ring with eleven sutures.

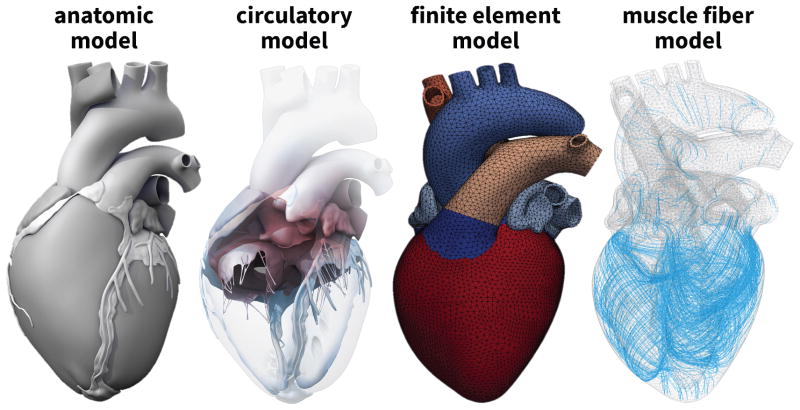
Simulating the human heart–with all four chambers and valves–is increasingly recognized as a critical step towards quantifying myocardial strain and stress [4]. Until recently, whole heart simulations were virtually impossible because of insufficient medical image resolution and a lack of computational power. Recent advances in non-invasive imaging and computer simulation now allows us to create three-dimensional models of the entire human heart [50]. Figure 2 illustrates the Living Heart model, a high-fidelity multiphysics model of a healthy, four-chamber adult human heart and its proximal vasculature [3]. Created from computer tomography and magnetic resonance images, the Living Heart model consist of 47,323 nodes, 141,969 degrees of freedom, and 208,561 linear tetrahedral elements with individual fiber and sheet directions [48]. Combined with algorithms of growth and remodeling [40], it allows us to reliably predict alterations in cardiac form and function during dilated cardiomyopathy [13]. Here we use the dilated Living Heart model as a starting point to quantify surgically-induced strains and forces in response to mitral annuloplasty.

Figure 2.

The Living Heart model. Anatomic model created from computer tomography and magnetic resonance images (left) [50]. Circulatory model with the two atria, the two ventricles, the four valves, and the major vessels (center, left) [50]. Finite element model with 208,561 linear tetrahedral elements and 47,323 nodes (center, right) [3]. Muscle fiber model with 208,561 discrete fiber and sheet directions interpolated from geometric image reconstruction (right) [48].

The objective of this manuscript is two-fold: First, we quantify the geometric size reduction, mitral annular stretches, and mitral valvular strains in response to different degrees of downsizing using the dilated Living Heart model; second, we quantify the suture forces associated with annular downsizing to characterize the trade-off between maximizing the degree of repair and minimizing the insult to the surrounding tissue. Our overall goal is to prototype a virtual surgical tool for the optimal design and selection of cardiovascular devices using predictive computational simulation.

2. METHODS

2.1. Cardiac Growth Model

To create the geometry of dilated cardiomyopathy, we multiplicatively decompose the deformation gradient F, the spatial gradient of the deformation map φ, into an elastic part F^e and a growth part F^g [44],

$$\mathit{F}={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}}\text{with}\mathit{F}={\nabla }_{\mathit{X}}\mathit{\phi }.$$ (1)

To account for quasi-incompressibility of the elastic tissue response, we further decompose the elastic tensor F^e into volumetric and isochoric parts,

$${\mathit{F}}^{\mathrm{e}}={\mathit{F}}_{\text{vol}}^{\mathrm{e}}·{\overline{\mathit{F}}}^{\mathrm{e}}\text{with}{\mathit{F}}_{\text{vol}}^{\mathrm{e}}={(J^{\mathrm{e}})}^{1/3}\mathit{I}\text{and}{\overline{\mathit{F}}}^{\mathrm{e}}={(J^{\mathrm{e}})}^{-1/3}{\mathit{F}}^{\mathrm{e}}.$$ (2)

Here I denotes the second-order unit tensor, $J^{\mathrm{e}}=det({\mathit{F}}^{\mathrm{e}})=J_{\text{vol}}^{\mathrm{e}}$ is the elastic Jacobian and J̄^e = det(F̄^e) = 1 is the isochoric Jacobian [19]. We can now characterize the elastic deformation in terms of the elastic Jacobian J^e and the isochoric elastic Green-Lagrange strain tensor Ē^e,

$$J^{\mathrm{e}}=det({\mathit{F}}^{\mathrm{e}})\text{and}{\overline{\mathit{E}}}^{\mathrm{e}}=\frac{1}{2}[{(J^{\mathrm{e}})}^{-2/3}{({\mathit{F}}^{\mathrm{e}})}^{\mathrm{t}}·{\mathit{F}}^{\mathrm{e}}-\mathit{I}].$$ (3)

The underlying principle of the theory of finite growth is that only elastic deformations generate stress. We thus introduce the following strain energy function ψ(J^e,E^e),

$$\psi (J^{\mathrm{e}},{\overline{\mathit{E}}}^{\mathrm{e}})=U(J^{\mathrm{e}})+\overline{\psi }({\overline{\mathit{E}}}^{\mathrm{e}}),$$ (4)

which we decompose additively into a volumetric part U(J^e) and an isochoric part ψ̄(Ē^e),

$$U(J^{\mathrm{e}})=\frac{1}{2}{K}_0[{(J^{\mathrm{e}})}^2-2ln(J^{\mathrm{e}})]\text{and}\overline{\psi }({\overline{\mathit{E}}}^{\mathrm{e}})=\frac{1}{2}{C}_0[exp({\overline{\mathit{E}}}^{\mathrm{e}}:{\mathit{B}}_0:{\overline{\mathit{E}}}^{\mathrm{e}})-1].$$ (5)

Here K₀ and C₀ are the volumetric and isochoric elastic stiffnesses, and the fourth-order tensor B₀ contains the weighting factors of the orthotropic Fung-type model for myocardial tissue [18]. In Voigt notation, B₀ takes a diagonal representation, $\widehat{{\mathit{B}}_0}=\text{diag}\{B_{\text{ff}},B_{\text{ss}},B_{\text{nn}},2B_{\text{fs}},2B_{\text{fn}},2B_{\text{sn}}\}$, where the individual entries are the weights of the normal and shear strains in the fiber, sheet, and normal directions. According to the standard arguments of thermodynamics, the Piola-Kirchhoff stress S follows as thermodynamically conjugate to the Green-Langrage strain $\mathit{E}=\frac{1}{2}[{\mathit{F}}^{\mathrm{t}}·\mathit{F}-\mathit{I}]$,

$$\mathit{S}=\frac{\partial \psi }{\partial \mathit{E}}=\frac{\partial \psi }{\partial {\mathit{E}}^{\mathrm{e}}}:\frac{\partial {\mathit{E}}^{\mathrm{e}}}{\partial \mathit{E}}={({\mathit{F}}^{\mathrm{g}})}^{-1}·{\mathit{S}}^{\mathrm{e}}·{({\mathit{F}}^{\mathrm{g}})}^{-\mathrm{t}}.$$ (6)

The above relation suggests to interpret the Piola Kirchhoff stress S as the pull back of the elastic Piola Kirchhoff stress S^e, which is thermodynamically conjugate to the elastic Green-Langrage strain, ${\mathit{E}}^{\mathrm{e}}=\frac{1}{2}[{({\mathit{F}}^{\mathrm{e}})}^{\mathrm{t}}·{\mathit{F}}^{\mathrm{e}}-\mathit{I}]$,

$${\mathit{S}}^{\mathrm{e}}=\frac{\partial \psi }{\partial {\mathit{E}}^{\mathrm{e}}}={\mathit{S}}_{\text{vol}}^{\mathrm{e}}+{\mathit{S}}_{\text{iso}}^{\mathrm{e}}=\frac{\partial U}{\partial {\mathit{E}}^{\mathrm{e}}}+\frac{\partial \overline{\psi }}{\partial {\mathit{E}}^{\mathrm{e}}}.$$ (7)

To model cardiac dilation through chronic cardiomyocyte lengthening, we introduce a scalar-valued growth multiplier ϑ that reflects the serial deposition of sarcomeres along the fiber direction f₀ [14]. The growth tensor F^g and the elastic tensor F^e then take a simple rank-one update structure,

$${\mathit{F}}^{\mathrm{g}}=\mathit{I}+[\vartheta -1]{\mathit{f}}_0\otimes {\mathit{f}}_0\text{and}{\mathit{F}}^{\mathrm{e}}=\mathit{F}+\frac{1-\vartheta }{\vartheta }\mathit{f}\otimes {\mathit{f}}_0,$$ (8)

where f = F · f₀. This implies that the growth multiplier ϑ = det(F^g) = J^g not only characterizes the local muscle cell lengthening but also the local volume change J^g. We assume that chronic cardiomyocyte lengthening is induced by mechanical overstretch [23],

$$\stackrel{.}{\vartheta }=\frac{1}{T}\langle \lambda -{\lambda }^{\text{crit}}\rangle \text{with}\lambda ={[{\mathit{f}}_0·{\mathit{F}}^{\mathrm{t}}·\mathit{F}·{\mathit{f}}_0]}^{1/2},$$ (9)

where the term in the Macaulay brackets ensures that growth is activated only if the current fiber stretch λ exceeds the physiological stretch limit λ^crit. We calculate λ^crit as a regionally varying baseline stretch under physiological conditions. The parameter τ characterizes the timeline of dilated cardiomyopathy.

We implement the cardiac growth model as a user defined subroutine into the non-linear finite element program Abaqus/Standard version 6.13 [1]. We represent the growth multiplier ϑ as an internal variable and store the current growth state locally on the integration point level. For a given deformation state F, we evolve the growth multiplier in time using a finite difference approximation of the first order time derivative, ϑ̇ = [ϑ − ϑ_n]/Δt, where ϑ_n denotes the growth multiplier of the previous time step and Δt = t − t_n is the current time increment. We update the growth multiplier of the current time step according to the evolution equation (9) as ϑ = ϑ_n + 〈 λ − λ^crit 〉 Δt/τ. From the updated growth state, we successively calculate the elastic tensor F^e using equation (8.2), the elastic Jacobian J^e and the isochoric elastic Green-Lagrange strain tensor Ē^e using equations (3.1) and (3.2), and the Piola Kirchhoff stress S using equation (6). Rather than working with the Piola Kirchhoff stress S, Abaqus/Standard uses the Cauchy stress σ = F · S · F^t/J where J = det(F). To ensure optimal quadratic convergence of the Newton-Raphson procedure during the global equilibrium iteration, Abaqus/Standard requires the Jaumann rate of the Kirchhoff stress τ = J σ [13].

2.2. Living Heart Model

Figure 2, left, illustrates the Living Heart model, an anatomically accurate four-chamber model of the healthy human heart that provides the basis for our simulation [3]. The underlying anatomic model was created from magnetic resonance images of a healthy, 21-year old, 50th percentile U.S. male. Images were reconstructed from 0.75mm thick slices using a medium soft-tissue kernel with retrospective electrocardiogram gating [51]. The initial DICOM images were exported as JPEG files, segmented using Amira, post-processed using Maya, and converted into NURBS surfaces, from which the final solid model was created. Figure 2, center left, illustrates the resulting geometric model of the heart with all four chambers, the left and right atria and the left and right ventricles, connected by the four valves [50]. Figure 2, center right, illustrates the finite element model of the Living Heart discretized with 208,561 linear tetrahedral elements and 47,323 nodes. This discretization introduces 141,969 degrees of freedom for the vector-valued deformation φ and 208,561 internal variables for the growth multiplier ϑ. The Living Heart model exists in different discretization levels, coarse, medium, and fine. For this particular problem, convergence studies have shown that the coarse version of the model, which we use here, yields sufficiently accurate results [3, 13]. Figure 2, right, shows the muscle fiber model with 208,561 discrete fiber vectors f₀ wrapping helically around the heart and 208,561 discrete sheet vectors s₀ pointing transmurally outward [48]. To fix the heart in space, we apply homogeneous Dirichlet boundary conditions at the geometric centers of the in- or outlets of all blood vessels. To prescribe different pressure values in each chamber, we model all valves in a fully closed state and allow no volume exchange between the individual chambers.

2.3. Dilated Cardiomyopathy Model

To calibrate the model at its healthy baseline state, we adopt the averaged patient-specific parameter values from an in vivo inverse finite element analysis of five healthy human hearts, three male and two female, age 36±11 years [12]. Specifically, we select the volumetric stiffness in (5.1) to K₀ = 1, 000 kPa and use a transversely isotropic version of the isochoric model (5.2), which we further reduce to two independent parameters, the isochoric stiffness C₀ and the nonlinearity parameter B₀. We scale the fiber stiffness to B_ff = B₀, the transverse stiffnesses to B_ss = B_nn = 0.4B₀, and the shear stiffnesses to B_sn = 0.2B₀ and B_fs = B_fn = 0.35B₀ [12]. Using the five subject-specific sets of magnetic resonance images, we identify the two isochoric parameters to C₀ = 0.115 ± 0.008 kPa and B₀ = 14.4 ± 3.2 such that B_ff = 14.4, B_ss = B_nn = 5.76, B_sn = 2.88, and B_fs = B_fn = 5.04. To identify the growth threshold λ^crit in equation (9), we train the model with its baseline conditions. We simulate the physiological end-diastolic state by applying a left ventricular and atrial pressure of 5mmHg and a right ventricular and atrial pressure of 2mmHg [15]. For each integration point, we record the physiological fiber stretch λ = [f₀ · F^t · F · f₀ ]^1/2 and store it locally as the growth threshold λ^crit. To model overload-induced cardiac dilation, we double the left ventricular and atrial pressures towards an end-diastolic pressure of 10 mmHg, while keeping the right ventricular and arterial pressures at their baseline value of 2mmHg [38]. We gradually increase the pressure, then keep it at its maximum value to allow the ventricles to grow until they have reached their new homeostatic equilibrium state, and finally unload the heart. Since we are only interested in this converged state of growth, the simulation is independent of the parameter τ and the time step size Δt. We only consider growth in the ventricles, not in the atria and main blood vessels.

2.4. Mitral Annuloplasty Model

We use the dilated, unloaded heart to simulate the effects of mitral annuloplasty and quantify mitral annular changes after implantation of rings in three different sizes. We select the commonly used Carpentier-Edwards Physio ring as a typical example of a semi-rigid, closed annuloplasty ring and virtually implant rings with 24 mm, 28 mm, and 32mm diameter onto the dilated annulus [6, 8].

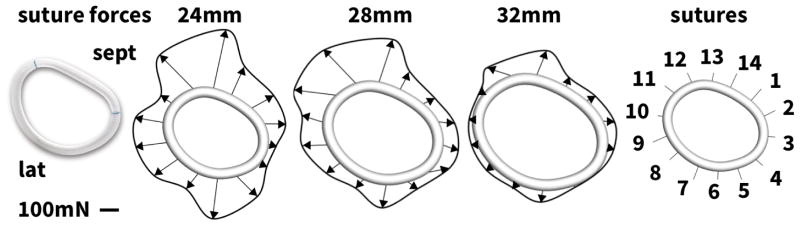
Figure 3 illustrates the Carpentier-Edwards Physio ring, its reconstructed geometries with 24 mm, 28 mm, and 32mm diameter, and its fourteen sutures for virtual ring implantation. The mechanical design goal of the Physio ring is to remodel the mitral annulus while maintaining coaptation and valve integrity in systole and permitting good hemodynamics in diastole [41]. Throughout this study, we assume that the ring stiffness is much larger than the stiffness of the dilated ventricular wall and model the ring as a rigid body. We position the ring into the dilated mitral annulus and represent its sutures using fourteen one-dimensional, rigid connector elements [1]. We record the suture forces as we reduce the length of the connector elements to zero. Throughout this procedure, we do not allow the heart to undergo further growth.

Figure 3.

Using the Living Heart model as virtual sizing tool for mitral annuloplasty. The Carpentier- Edwards Physio ring (left), its reconstructed geometry with 24 mm, 28 mm, and 32mm diameter (center), and its fourteen sutures for virtual ring implantation with sutures 10–13 marking the anterior, 13-2 the septal, 2–6 the posterior, and 6–10 the lateral annulus (right).

To visualize the annulus, we identify the annular nodes as the nodes separating the ventricle and the mitral leaflet, which is not included explicitly in this simulation. To calculate the stretch λ along the annulus, we fit cubic splines through these annular nodes and determine the ratio between the lengths of the local tangent vectors in the current configuration and in the reference configuration [41].

3. RESULTS

3.1. Dilated Cardiomyopathy

Before we employ the Living Heart model to elucidate the effects of undersized annuloplasty, we create the geometry of a dilated human heart using the theory of finite growth.

3.1.1. Ventricular Remodeling

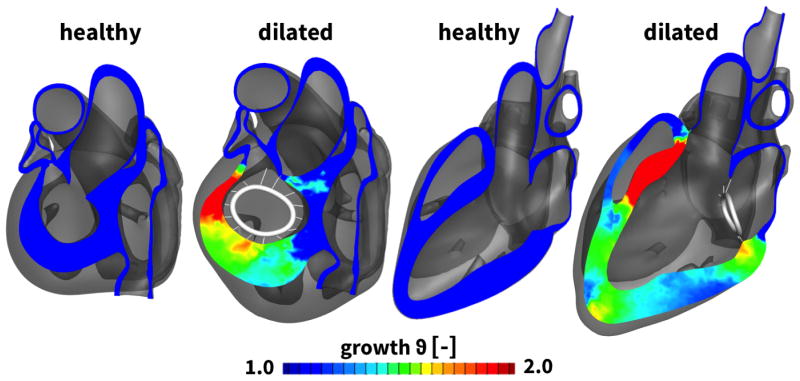
Figure 4 illustrates the two chamber and four chamber views of the heart before and after ventricular remodeling in response to diastolic overload. The color code indicates the growth multiplier ϑ, which varies from the baseline state with ϑ = 1.0, shown in blue, to the dilated state with up to ϑ = 2.0, shown in red. Stretch-induced overload of the left ventricle results in significant ventricular dilation driven largely by changes in the antero-septal region. Specifically, the basal portion of the left ventricle, close to the mitral valve, displays the largest degree of dilation.

Figure 4.

Two chamber and four chamber views of the heart before and after ventricular remodeling in response to diastolic overload. Ventricular remodeling is modeled using the continuum theory of finite growth. The growth multiplier ϑ characterizes chronic cardiomyocyte lengthening from the baseline state ϑ = 1.0, shown in blue, to the elongated state up to ϑ = 2.0, shown in red. Cardiomyocyte lengthening displays regional variations with maximum values at the apex and the base of the left ventricle, specifically in the anterior and septal portions. For illustration purposes, a representative annuloplasty ring is included in the figure. However, its sutures have not been tensioned yet.

3.1.2. Annular Dilation

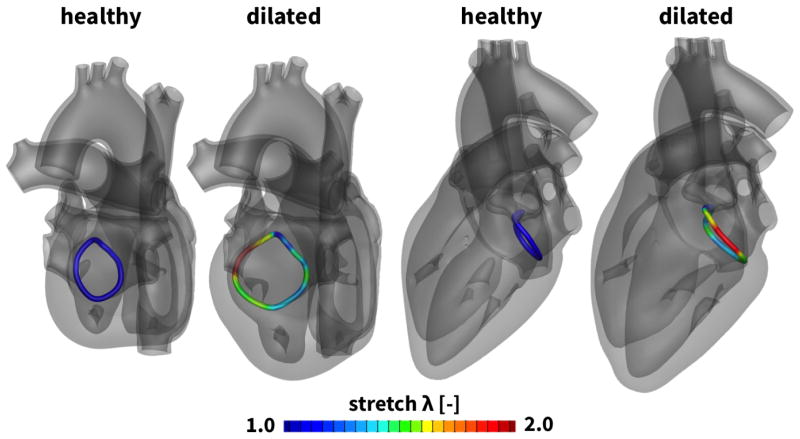
Figure 5 highlights the geometry of the mitral annulus before and after ventricular remodeling in response to diastolic overload. Overload-induced remodeling in the myocardial tissue directly affected the size and geometry of the mitral annulus. The annular stretch λ characterizes chronic annular dilation from the healthy, ungrown state with λ = 1.0, shown in blue, to the dilated state up to λ = 2.0, shown in red [41]. Annular dilation is largest in the anterior region, while the posterior region displays the least growth. Naturally, mitral annular dilation is co-localized with growth-induced deformations of the surrounding myocardial tissue highlighted in Figure 4.

Figure 5.

Two chamber and four chamber views of the heart before and after annular dilation in response to diastolic overload. Annular dilation is a consequence of ventricular remodeling. The annular stretch λ characterizes chronic annular dilation from the baseline state λ = 1.0, shown in blue, to the dilated state up to λ = 2.0, shown in red. Annular dilation displays regional variations with maximum values in the anterior region.

Table I summarizes the mitral annular area, mitral annular perimeter, septal-lateral distance, and commissure-commissure distance for the healthy and dilated hearts. Specifically, the mitral annular area increases from 581.05 mm² to 988.01 mm², a degree of dilation that has previously been reported to result in severe mitral regurgitation. Changes in the septal-lateral and commissure-commissure distances from 27.47mm and 23.72mm to 36.14mm and 36.66mm indicate a significant circularization of the mitral annulus.

Table I.

Annular dimensions of healthy and dilated annulus. Changes in mitral annular area, mitral annular perimeter, septal-lateral distance, and commissure-commissure distance.

	mitral annular area [mm2]	mitral annular perimeter [mm]	septal-lateral distance [mm]	comm-comm distance [mm]
healthy	581.05	88.07	27.47	23.72
dilated	988.01	116.50	36.14	36.66

3.2. Mitral Annuloplasty

We now use the dilated Living Heart model to explore the effects of mitral annuloplasty on annular geometry, annular dilation, and the mechanics of the peri-annular tissues. To highlight the potential of the Living Heart model as a virtual sizing tool, we implant three common rings of standard sizes 24, 28, and 32mm diameter. This virtual surgery takes approximately three hours on eight CPUs.

3.2.1. Ventricular Effects

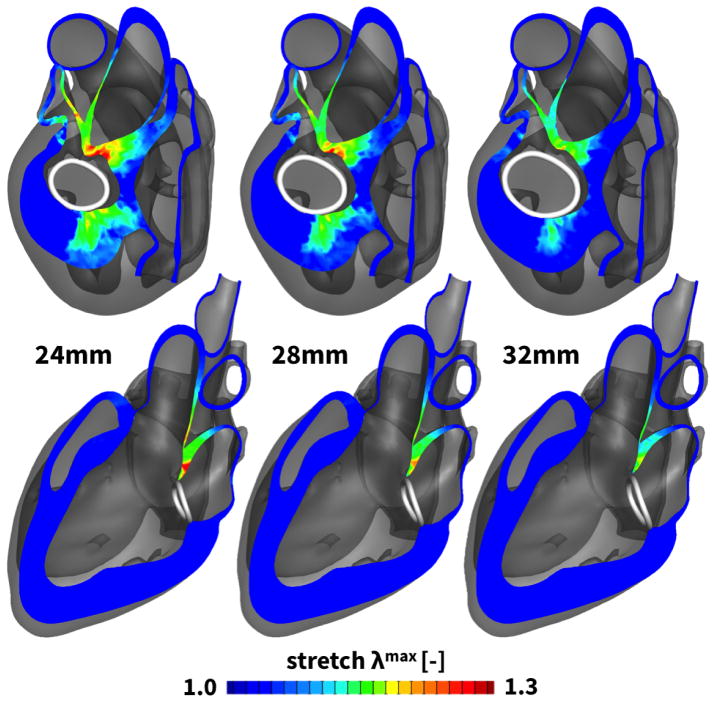
Figure 6 illustrates the two chamber and four chamber views after the implantation of all three rings. The color code indicates the surgically induced maximum principal stretch λ^max, which varies from the baseline state λ^max = 1.0, shown in blue, to a maximum stretch state of λ^max = 1.3, shown in red. From a mechanical perspective, ring implantation induces the largest stretches septally toward the aorto-mitral junction and in the postero-lateral region. Surgically induced maximum stretches were λ^max = 1.30 for the 24 mm-diameter ring, λ^max = 1.24 for the 28 mm-diameter ring, λ^max = 1.18 for the 32 mm-diameter ring. Maximum principal stretches increase with decreasing rings size, while the overall stretch pattern remain invariant to the degree of downsizing.

Figure 6.

Two chamber and four chamber views of the heart after virtual ring implantation. Three Physio© rings of 24, 28, and 32mm diameter were virtually implanted around the dilated mitral annulus. The maximum principal stretch λ^max characterizes the surgically induced insult to the tissue from the baseline state of λ^max = 1.0, shown in blue, to the maximum stretch state of λ^max = 1.3, shown in red. Tissue stretch displays regional variations with maximum values septally near the aorto-mitral junction and in the postero-lateral region.

3.2.2. Annular Effects

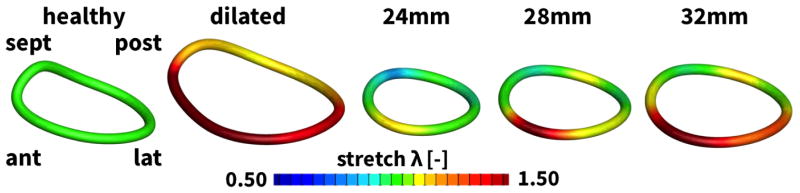
Figure 7 highlights the effects of mitral annuloplasty on mitral dimensions. Figure 7, left, displays the initial healthy annulus and the dilated annulus in response to ventricular remodeling. Figure 7, right, depicts the stretch introduced through annuloplasty with rings of 24, 28, and 32mm diameter. For all three cases, compressive stretches of λ < 1.0 indicate a reduction in annular dimensions in response to surgical downsizing. Downsizing is largest in the septal and postero-lateral regions and smallest in the anterior and posterior regions. The magnitude of compressive stretch is inversely proportional to the ring size; the 24mm ring introduces the largest compressive stretch and the 32mm ring the smallest. Specifically, mean compressive stretches were 0.75, 0.85, and 0.92 for the 24, 28, and 32mm rings. Interestingly, peak compressive stretches were rather invariant to ring size with 0.51, 0.46, and 0.54, respectively. Notably, the saddle-height, a measure for the out-of-plane topology of the mitral annulus, is markedly reduced with all three rings.

Figure 7.

Annular stretch in the healthy and dilated annulus, and after ring-implantation. The annular stretch λ characterizes the local annular dilation with respect to the baseline state of λ = 1.0, shown in green, with a maximum stretch of λ = 1.5 and more in the dilated annulus, shown in red, and a minimum stretch of λ = 0.5 and less upon ring implantation, shown in blue. Annuloplasty downsizing is largest in the septal and postero-lateral regions and smallest in the anterior and posterior regions.

Table II summarizes the mitral annular area, mitral annular perimeter, septal-lateral distance, and commissure-commissure distance after the implantation of the three rings. As expected, the three rings significantly reduce all four metrics. The most significant size reduction results from implanting the 24mm diameter ring, which essentially re-establishes the ungrown mitral valve dimensions with septal-lateral and commissure-commissure distances of 27.86mm and 23.49mm in comparison to the healthy baseline state with 27.47mm and 23.72 mm.

Table II.

Annular dimensions with 24 mm, 28 mm, and 32mm diameter Physio rings implanted. Changes in mitral annular area, mitral annular perimeter, septal-lateral distance, and commissure-commissure distance.

ring size [mm]	mitral annular area [mm2]	mitral annular perimeter [mm]	septal-lateral distance [mm]	comm-comm distance [mm]
24	480.20	81.94	23.49	27.86
28	612.76	92.77	26.66	30.90
32	772.05	104.06	29.87	35.17

3.2.3. Suture Forces

Figure 8 and Table III summarize the suture forces upon ring implantation. In agreement with the stretch distributions in Figure 7, suture forces increase with the degree of downsizing. The total force to implant the 24mm diameter ring is 2.2 N; for the 28mm and 32mm diameter rings, the total force decreases to 1.9N and 0.8 N, respectively. The individual suture forces are distributed heterogeneously around the perimeter of the annuloplasty ring. Generally, suture forces are highest in the antero-septal region, on sutures #12 and #13, and in the postero-lateral region, on sutures #5 and #6, which coincide with the regions of largest myocardial strains in Figure 6 and largest annular downsizing in Figure 7.

Figure 8.

Suture forces upon ring implantation. Suture forces are largest for the 24mm ring and smallest for the 32mm ring. Suture forces are largest in the antero-septal regions, sutures #12 and #13, and in the postero-lateral regions, sutures #5 and #6, see Table III.

Table III.

Suture forces upon ring implantation. Suture forces are largest in the antero-septal regions, sutures #12 and #13, and in the postero-lateral regions, sutures #5 and #6, see Figure 8.

size [mm]	#1 [mN]	#2 [mN]	#3 [mN]	#4 [mN]	#5 [mN]	#6 [mN]	#7 [mN]
24	119.0	142.8	42.7	39.8	163.5	235.2	111.3
28	70.8	94.7	92.0	119.7	65.5	134.5	65.9
32	51.5	66.7	32.7	34.6	7.6	61.3	29.5
size [mm]	#8 [mN]	#9 [mN]	#10 [mN]	#11 [mN]	#12 [mN]	#13 [mN]	#14 [mN]
24	166.6	179.1	161.0	71.2	275.6	349.8	182.6
28	96.4	144.7	122.9	244.0	217.8	260.6	116.4
32	36.5	29.8	16.3	53.0	143.5	151.1	53.6

4. DISCUSSION

The objective of this manuscript was to explore the Living Heart model as a virtual surgical tool for the optimal design, selection, and sizing of cardiovascular devices. Here we have focused specifically on characterizing and quantifying the effects of undersized annuloplasty in the context of dilated cardiomyopathy.

4.1. Dilated Cardiomyopathy

To create a model of dilated cardiomyopathy, we used the Living Heart model in combination with the theory of finite growth [14]. Specifically, we focused on the effects of overstretch-induced growth on ventricular remodeling and mitral annular dilation. Understanding remodeling-induced alterations in mitral valve geometry is critical to tailor mitral valve repair to a specific remodeling pattern [36]. Our simulations in Figure 4 predict a significant dilation of the left ventricle, particularly in the anterior and septal regions of the mitral annulus. In addition to annular stretch as a mechanical measure of annular deformation in Figure 5, we quantify standard clinical metrics of annular dimension in Table I. Both mechanical and clinical data are in good agreement with literature reports: Our model predicts an increase of mitral annular area by a factor of 1.7 and an increase in septal-lateral distance of 1.3, values, which are in agreement with three-dimensional ultrasound measurements in patients with dilated cardiomyopathy [26]. Our model also predicts a marked circularization of the mitral annulus with a healthy and diseased ellipticity of 1.16 and 0.99, characteristic of patients with dilated cardiomyopathy [26]. Both mechanical and clinical changes observed during ventricular growth are also in good agreement with experimental measurements in an ovine model of ischemic dilated cardiomyopathy [42].

4.2. Mitral Annuloplasty

To explore the effects of device selection on the myocardial tissue surrounding the mitral valve, we virtually implanted three annuloplasty rings into the dilated Living Heart model and quantified myocardial strains and mitral annular downsizing using both mechanical and clinical metrics. Our results suggest that more severe downsizing, as quantified in Table II, introduces larger tissue deformation both in the myocardium and the mitral annulus itself. Surgically-induced deformations in the ventricular myocardium in Figure 6 and in the mitral annulus in Figure 7 are co-localized. While these observations agree with our common intuition, our simulations also predict the regional variation of surgically-induced deformations with peak values in the septal and postero-lateral regions of the myocardium and the mitral annulus.

Regional variations in myocardial strain, stretch, and stress are virtually impossible to quantify in the beating heart, but critically important to optimize surgical procedures and device design. For example, our model predicts large stretches in response to undersized annuloplasty in the posterolateral region of the mitral valve. This region is also largely affected in patients with ischemic cardiomyopathy following infarction of the posterior wall [17]. Disease-specific rings have been developed for this patient population to minimize stress on the posterior wall segment by use of a postero-lateral dip [9]. In addition, the Edwards IMR ETLogix ring provides an increased sewing margin to accommodate double row sutures that may prevent potential ring dehiscence in this particular pathology. In the present case, the Edwards IMR ETLogix ring would have provided an advantage over the standard Physio ring. While our findings may, in part, be specific to the particular anatomy of the Living Heart model, they generally highlight the potential of a virtual surgical test environment for optimizing ring selection.

The junction between the mitral and aortic valves is another region of elevated annular strain as predicted by our simulation. From a structural point of view, this region is thin and non-muscular and provides little resistance to the laterally oriented suture forces. Our results suggest that, because of the proximity of the mitral valve to the aortic valve complex, undersized annuloplasty may indirectly affect the performance of an otherwise fully functional aortic valve [10]. A decreased proximity between the mitral and aortic valves, as seen in patients with hypertrophic cardiomyopathy, may further increase the risk of systolic anterior motion of the anterior mitral valve leaflet [28]. Predictive simulations of surgical procedures provide informed criteria to balance the benefits of undersized annuloplasty and the increased risk of disrupting cardiac physiology.

Our current study focuses exclusively on the acute response of the heart to the implantation of annuloplasty devices. It would be interesting to explore the chronic effects of annuloplasty rings on cardiac form and function. Future studies will focus on simulating growth and remodeling after ring implantation to predict the long-term behavior of the heart in response to different annuloplasty devices.

4.3. Suture Forces

Without doubt, the Living Heart model ranks among the most detailed human heart simulators to date. Such complexity, however, comes at the cost of many potential sources of uncertainty. So far, we have discussed primarily strains that can been validated using invasive and non-invasive imaging modalities including implanted marker techniques in animals [2, 16, 39, 47] and tissue doppler imaging in patients [37]. In addition to strains, we also report suture forces. Mechanical loading along the suture lines has been closely associated with repair durability [35]. In Abaqus/Standard, one-dimensional connector elements allow us to gradually decrease the distance between selected points to simulate sutures and postprocess the required suture forces [1]. These forces are strongly dependent on the material model and its associated parameters [31, 43]. For example, increasing the myocardial stiffness would increase the suture forces, and both would be almost linearly related. However, this would only have a minor effect on the regional variation of the simulated suture forces. Overall, our results from Table III are in good agreement with in vivo measurements of suture forces during annular downsizing in a porcine model [21, 22]. Our simulations predict a total force of 2.2 N, which lies well within the range of the reported total suture force for maximum downsizing of 3.5N [22].

The quantification of suture forces is not only interesting from a validation point of view, it is also of practical importance to the cardiac surgeon. Suture bites represent focal stress points both in the fabric of the annuloplasty ring and in the myocardial tissue. High suture forces indicate risk of tissue damage and ring dehiscence [25]. Our simulations not only provide insight into the long-term failure of undersized annuloplasty by predicting regions of continued ventricular remodeling, but also help prevent short-term failure by identifying potential sites of ring dehiscence.

4.4. Conclusion

We have, for the first time, used a human heart simulator to model the surgical procedure of mitral valve repair. Our simulations utilize the Living Heart model, a highly accurate, anatomic representation of a healthy adult human heart with all four chambers and valves. Starting with a healthy heart, we simulated the progression of dilated cardiomyopathy, its impact on the mitral valve complex, and its repair using annuloplasty rings. While it is virtually impossible to characterize the entire mechanical environment of the mitral valve complex in vivo, our simulations allow us to precisely quantify tissue strains, annular stretch, mitral valve kinematics, and suture forces and identify local regions of maximum stretch or force. Taken together, our simulations suggests that during undersized valvular annuloplasty, the highest suture forces co-localize with regional peaks in myocardial strain and annular stretch. Our model predicts the highest risk of dehiscence in the septal and postero-lateral regions. In agreement with our intuition, our simulations demonstrate that a more drastic downsizing results in higher suture forces. However, our simulations precisely quantify the individual suture forces and show that in our case, implanting a 24mm ring requires three times larger forces than implanting the same ring with 32mm diameter. Realistic predictive simulations of surgical intervention have the potential to optimize surgical procedures, improve device design, and guide treatment planning on an individual, personalized basis.