Abstract
Tubuloglomerular feedback and the myogenic response are widely appreciated as important regulators of renal blood flow, but the role of the sympathetic nervous system in physiological renal blood flow control remains controversial. Where classic studies using static measures of renal blood flow failed, dynamic approaches have succeeded in demonstrating sympathetic control of renal blood flow under normal physiological conditions. This review focuses on transfer function analysis of renal pressure-flow, which leverages the physical relationship between blood pressure and flow to assess the underlying vascular control mechanisms. Studies using this approach indicate that the renal nerves are important in the rapid regulation of the renal vasculature. Animals with intact renal innervation show a sympathetic signature in the frequency range associated with sympathetic vasomotion that is eliminated by renal denervation. In conscious rabbits, this sympathetic signature exerts vasoconstrictive, baroreflex control of renal vascular conductance, matching well with the rhythmic, baroreflex-influenced control of renal sympathetic nerve activity and complementing findings from other studies employing dynamic approaches to study renal sympathetic vascular control. In this light, classic studies reporting that nerve stimulation and renal denervation do not affect static measures of renal blood flow provide evidence for the strength of renal autoregulation rather than evidence against physiological renal sympathetic control of renal blood flow. Thus, alongside tubuloglomerular feedback and the myogenic response, renal sympathetic outflow should be considered an important physiological regulator of renal blood flow. Clinically, renal sympathetic vasomotion may be important for solving the problems facing the field of therapeutic renal denervation.
MeSH Keywords: Renal Circulation, Sympathetic Nervous System, Baroreflex, Homeostasis, Kidney/Blood supply, Vasoconstriction, Renal Artery
INTRODUCTION
The maintenance of renal blood flow (RBF) is crucial for renal function. The kidney is accordingly endowed with two powerful autoregulatory mechanisms, tubuloglomerular feedback (TGF) and the myogenic response (MR), which are widely appreciated as important controllers of RBF(Carlström et al., 2015). Tubuloglomerular feedback is a mechanism that is unique to the kidney whereby changes in RBF-dependent NaCl flux in the distal thick ascending limb are sensed by macula densa cells and transduced to modulate the diameter of the anatomically juxtaposed afferent arteriole. The MR is observed in other vascular beds but is particularly strong in the kidney where it senses changes in transmural pressure and responds by adjusting afferent arteriolar diameter to preserve a near constant RBF. Together these mechanisms maintain RBF and glomerular filtration over a wide range of perfusion pressures by modulating renal vascular conductance (RVC).
Conversely, the classic dogma maintains that the renal nerves are quiescent in the control of RBF in a normal, healthy state, causing vasoconstriction and a reduction in RBF only in response to experimental stimuli or in the setting of disease, where renal sympathetic nerve activity (RSNA) exceeds physiological levels(DiBona and Kopp, 1997). This dogma, based mainly on steady-state measurements of mean RBF over minutes, has eroded as more dynamic approaches have revealed the involvement of the renal nerves in the beat-to-beat dynamic regulation of RBF. This review focuses on studies which have used pressure-flow transfer function analysis, leveraging the physical relationship between blood pressure and blood flow to yield insights into the physiological role of the sympathetic nervous system in RBF control.
Dynamic Approaches for a Dynamic Phenomenon
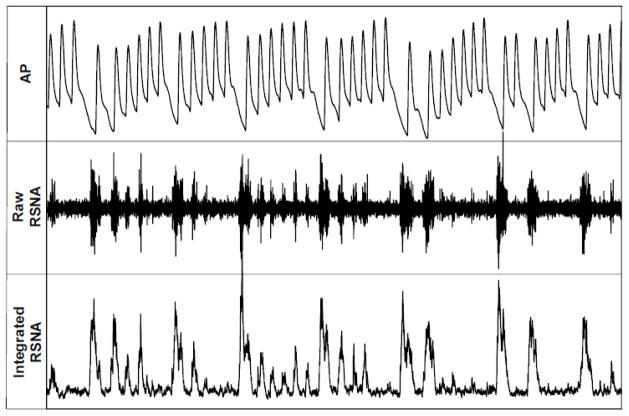
Following the proliferation of techniques allowing for chronic, conscious recordings of renal sympathetic nerve activity, the dynamic nature of RSNA became obvious. Figure 1 shows a 14-second sample of a recording from a conscious rabbit instrumented with RSNA electrodes that demonstrates rhythmicity, beat-to-beat variability, and baroreflex control of RSNA, with lower diastolic pressures followed by large RSNA bursts. The inarguably dynamic nature of RSNA necessitates the use of dynamic approaches to study the neural control of renal function.
Figure 1. RSNA is Dynamically Controlled.
14-second recording of AP, raw RSNA, and integrated RSNA in a healthy, calmly resting rabbit one-week after RSNA electrode implantation. Note the dynamic nature of RSNA and the strong baroreflex control of RSNA, with the amplitude and incidence of RSNA bursts strongly corresponding to DBP.
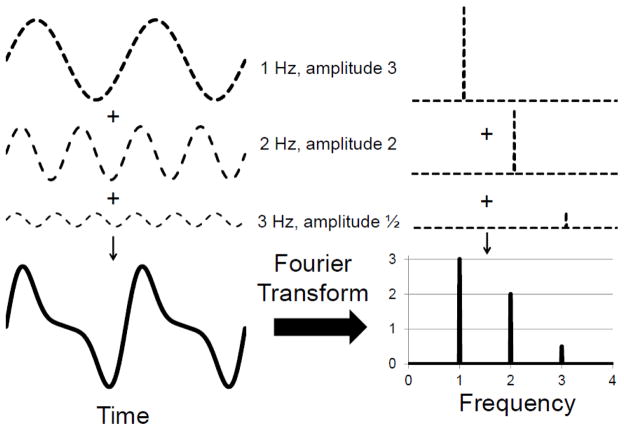
One common dynamic method of analysis for studying rhythmic physiological time series data is frequency analysis. This decomposes a physiologic signal occurring in time into its multiple frequencies, allowing quantification of the power of each rhythm. Figure 2A shows how a seemingly complex signal occurring in time can arise from a few simple rhythms and how frequency analysis facilitates the identification and quantification of these rhythms. Frequency analysis is a powerful tool for studying the control of physiological parameters as different physiological control mechanisms operate at different frequencies. By separating physiological mechanisms based on their operating frequencies, frequency analysis allows for their individual assessment as they operate in vivo. This is in contrast with classic, steady-state measures such as heart rate or RVC which have no ability to assess the contributions of individual physiological mechanisms working together to regulate the parameter of interest. For example, if heart rate increases, one does not know if this is due to vagal withdrawal or cardiac sympatho-excitation or both; if RVC decreases, one does not know if this is mediated by sympathetic vasoconstriction, MR, or TGF. Frequency analysis offers a window into the participation of individual physiological control mechanisms – although it is not without limitations.
Figure 2. Frequency Analysis.
A rhythmic signal which appears complex when viewed in time can be better understood after its transformation to the frequency domain. The composite waveform on the left is the simple addition of three other oscillations of different frequencies and amplitudes. When viewed in the frequency domain, the amplitude spectrum (right) reveals very clearly the frequencies of the underlying rhythms and their relative contributions (amplitudes). The phase spectrum (not shown) gives information about when each oscillation occurs (i.e. is at 0°).
One of these limitations is that the operating frequencies of different physiological mechanisms may overlap. Such is the case with heart rate: both parasympathetic and sympathetic input to the sinoatrial node contribute to low-frequency (LF) oscillations in heart rate variability. Fortunately, in the rabbit, rat, and mouse, the important dynamic controllers of the renal vasculature operate at distinct frequencies. The important autoregulatory mechanism of TGF operates between 0.02–0.08 Hz while MR operates between 0.08–0.20 Hz(Carlström et al., 2015). In the rabbit, LF sympathetic vasomotion occurs between 0.20 Hz to 0.46 Hz, and HF respiratory modulation occurs between 0.76 to 1.5 Hz(Malpas, 2002). If some aspects of this terminology are confusing (e.g., the fact that the so-called LF range is the second-highest frequency range), this is because we have united terminology from two different fields, renal autoregulation and autonomic neurophysiology. The frequency ranges for TGF and MR come both from dynamic autoregulation and autoregulatory modeling studies (Holstein-Rathlou et al., 1991; Sgouralis et al., 2016), constituting what autonomic researchers (particularly in the field of heart rate variability) call the very-low frequency range(Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology, 1996). The frequency ranges where LF sympathetic vasomotion and HF respiratory modulation occur come from autonomic studies and are frequently ignored or combined in studies of renal autoregulation.
Poiseuille’s Law tells us that the steady-state flow through a rigid tube is equal to the perfusion pressure divided by the resistance of the tube. Thus, while the dynamic controllers of RVC are important, so, too, is renal perfusion pressure. In healthy animals, the venous pressure is negligible, and thus arterial pressure (AP) can be used as a surrogate for perfusion pressure. This powerful physical relationship between AP and RBF allows for the study of the dynamic control of the renal vasculature.
Transfer Function Analysis of Renal Pressure-Flow
One way that the physical relationship between blood pressure and flow can be leveraged is by using a classic system identification approach called transfer function analysis. Transfer function analysis allows for the quantification of a dynamic input-output relationship, that is, an input-output relationship as a function of frequency. This review focuses on studies in which transfer function analysis was used to identify the input-output relationship between AP and RBF for innervated and denervated kidneys. Multiple approaches exist for transfer function analysis, but the most common method, and the one employed in all the studies reviewed here, is based on the Welch method of frequency analysis. The basics of this method are important to understanding the results and avoiding the pitfalls of this approach. The original AP and RBF signals are divided into several, overlapping time windows. Each time window is multiplied by a window function, which reduces spurious edge effects caused by this division. The Fast Fourier Transform (FFT) of each contemporaneous AP and RBF time window is computed, converting the signals from the time domain to the frequency domain, where they are referred to as spectra and have both real and imaginary components. The RBF spectrum and the complex conjugate of the AP spectrum are multiplied to yield the cross-spectrum, which is then normalized by the AP power spectrum (i.e. magnitude squared of the FFT). This is averaged across all time windows to yield the final transfer function. Gain is calculated as the magnitude of the transfer function as a function of frequency. Phase shift is calculated as the inverse tangent of the real and imaginary components of the transfer function for every frequency. Coherence is calculated by squaring the magnitude of the transfer function and normalizing by the RBF power spectrum.
The Welch method of transfer function analysis is widely employed for several reasons. First, averaging over multiple time windows greatly improves the signal-to-noise ratio; however, there is an important tradeoff between signal-to-noise and frequency resolution. Increasing the number of time windows accordingly decreases the length of each time window (e.g., deciding to chop a 600-second recording into 6 non-overlapped 100-second windows instead of 3 non-overlapped 200-second windows). This sacrifices frequency resolution as the frequency resolution of the Welch method equals the reciprocal of the time window length (e.g., 0.01 Hz for a 100-second window, 0.005 Hz for a 200-second window). As we show below, this tradeoff is important in resolving physiological mechanisms. Second, calculating the transfer function over multiple time windows allows one to assess the consistency of the linear input-output relationship over time, which is quantified as coherence. Methods that do not use multiple time windows cannot compute this physiologically significant measure.
When calculated carefully, the gain, phase shift, and coherence of the renal pressure-flow relationship have distinct physiological meanings and show a clear role for the renal nerves in the physiological control of RBF. However, it is important to understand that a one-size-fits-all approach to the Welch method is inappropriate; the parameters of the analysis must be chosen thoughtfully based on the physiological question at hand. We discuss herein the physiological meanings of gain, phase shift, and coherence in the context of the renal pressure-flow relationship and what the contribution of the renal nerves to these three transfer function parameters tells us about their role in the normal physiological control of RBF. At the same time, we touch on some signal processing issues which may explain discrepancies in the literature.
The data presented in Figures 3–5 come from rabbits that underwent either bilateral renal denervation (DDNx) or a sham procedure (INV)(Schiller et al., 2016). These rabbits were chronically instrumented with an AP telemeter and a RBF probe on the left renal artery. After a two-week recovery and acclimation to the procedure room, AP and RBF were recorded, and AP-RBF transfer function analysis was performed. We observed a clear sympathetic signature in the LF range where sympathetic vasomotion is prominent. The specific gain, phase shift, and coherence of this LF signature demonstrate how the renal nerves contribute to the physiological control of RBF.
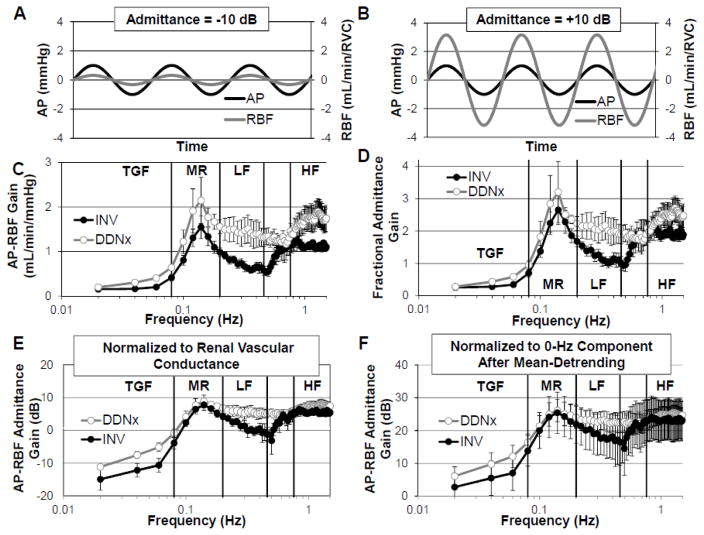
Figure 3. Renal Pressure-Flow Gain.
Representative AP and RBF oscillations depicting (A) buffering of AP oscillations by active renal vascular control mechanisms resulting in negative admittance gain and (B) amplification of AP oscillations by passive renal arterial elastance resulting in positive admittance gain. INV kidneys show lower LF gain whether quantified as (C) raw gain, (D) fractional admittance gain, or (E) admittance gain. (F) Erroneous normalization abolishes the ability of transfer function analysis to demonstrate physiology, be it autoregulation or the contribution of the renal nerves. Data adapted from (Schiller et al., 2016).
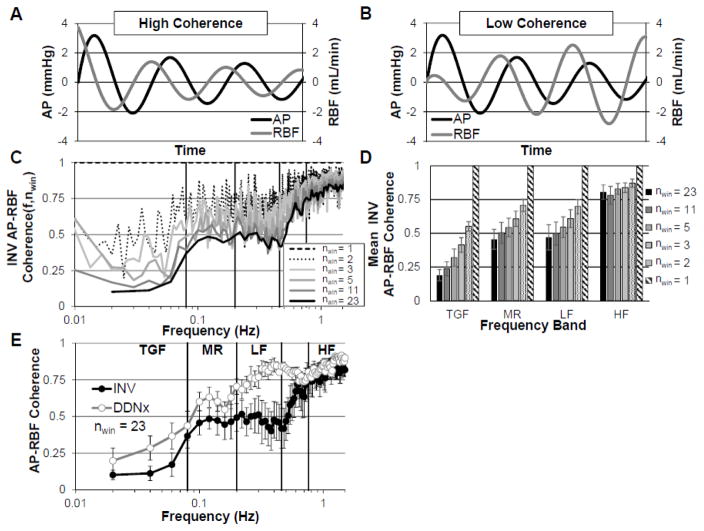
Figure 5. Renal Pressure-Flow Coherence.
Representative depictions of (A) a RBF oscillation with high coherence to the AP oscillation and (B) a RBF oscillation with low coherence to the AP oscillation. (C) Coherence depends on signal processing parameters and decreases with increasing number of windows. (D) Mean coherence over frequency bands for TGF, MR, LF, and HF, demonstrating the sensitivity of coherence to signal processing parameters. (E) Renal denervation selectively increases AP-RBF coherence in the LF range.
nwin, number of 50% overlapping windows used for Welch method. Data adapted from (Schiller et al., 2016).
Renal Pressure-Flow Gain
Transfer function gain quantifies how much an AP oscillation at a given frequency affects RBF. This is often normalized to the RVC, in which case it is called admittance gain and expressed as a unitless quantity (often specified as fractional gain) or in decibels (dB). The idea of this normalization is that it accounts for the passive differences in the renal vasculature, thereby emphasizing the dynamic contributions of the physiological control mechanisms. Admittance gains less than 0 dB indicate that renal vascular control mechanisms are buffering the AP oscillations relative to what would be expected from Poiseuille’s Law. Admittance gains greater than 0 dB, indicative of amplified transduction of pressure into flow, are believed to result due to the elastic nature of the renal artery or from intrinsic oscillations from vascular control mechanisms(Cupples and Braam, 2007; Holstein-Rathlou and Marsh, 1994).
From Figures 3C and 3D, one can appreciate that transfer function gain shows the strong dynamic autoregulatory capacity of the kidney. Renal autoregulation results in low gain below the operating frequencies of the autoregulatory mechanisms, highlighting the ability of these mechanisms to effectively buffer slow AP oscillations. Measures of AP-RBF gain reveal that the renal nerves buffer the transduction of LF AP oscillations into RBF, whether calculated as raw gain, fractional admittance gain, or admittance gain in decibels (Figure 3C, 3D, and 3E). Other studies in the chronically denervated, conscious rabbit and acutely denervated, anesthetized rat have similarly shown that renal denervation increases raw gain and admittance gain, respectively, beyond the autoregulatory frequency range(Abu-Amarah et al., 1998; Malpas et al., 1998). Thus, in both rats and rabbits, sympathetic control of RVC attenuates the effect of LF AP oscillations on RBF, consistent with the presence of a dynamic vasoconstrictive influence.
One notable study, however, failed to find an increase in admittance gain after acute renal denervation of healthy, anesthetized rats(DiBona and Sawin, 2004). This may be due to how the admittance gain was normalized in this study. The authors performed mean subtraction, which eliminates the 0-Hz component, and then normalized the transfer function gain for all frequencies by the calculated transfer function gain at 0 Hz. This is analogous to dividing by zero. Figure 2F shows the effect of such a procedure on our data. This alternate normalization yields physiologically implausible data (e.g., admittance gain > 0 dB for all frequencies), and the effect of renal denervation on gain is completely abolished. This demonstrates how important signal processing methods are in obtaining accurate descriptions of physiology.
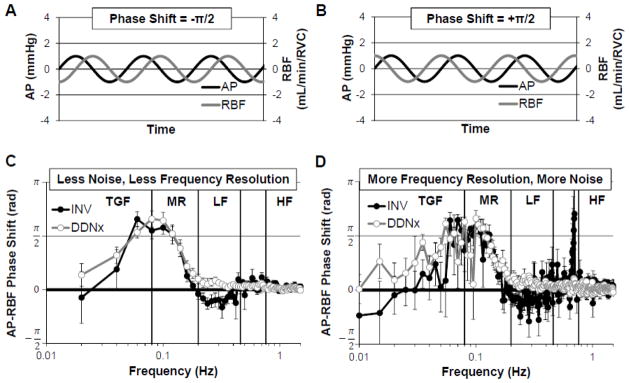
Renal Pressure-Flow Phase Shift
The AP-RBF transfer function phase shift quantifies when RBF oscillations occur relative to AP oscillations. If an AP oscillation occurs before a RBF oscillation, the phase shift is negative (Figure 4A). If an AP oscillation occurs after a RBF oscillation, the phase shift is positive (Figure 4B). Phase shift may be expressed as radians, in which case it is bounded between −π and +π, or degrees, in which case it is bounded between −180 and 180, as one cannot distinguish between oscillations leading or lagging by more than one half-phase. The time lag between AP and RBF oscillations can be calculated as the product of the phase shift and the period of the oscillation of interest. If AP and RBF are synchronized (as depicted in Figure 3A and 3B), the phase shift is zero; this is the case for passive pressure-flow. When non-zero, phase shift also conveys important information about causality in a Granger sense (i.e. the cause occurs before the effect). Thus, when AP-RBF phase shift is positive, RBF oscillations precede AP oscillations, indicating the presence of an active control system which modulates RVC in response to RBF oscillations. Conversely, when AP-RBF phase shift is negative, AP oscillations precede RBF oscillations, indicating the presence of an active control system which modulates RVC in response to AP oscillations. While a zero phase shift is characteristic of passive, Poiseuille flow, it can also arise from an AP-independent active control system (e.g., RSNA not under baroreflex control) which will contribute phase asynchrony, decreasing AP-RBF coherence despite the zero phase shift.
Figure 4. Renal Pressure-Flow Phase Shift.
Representative depictions of (A) AP oscillations leading RBF oscillations as would be expected for an active control system sensing AP and modulating RVC (e.g., baroreflex) and (B) RBF oscillations leading AP oscillations as would be expected for an active control system sensing RBF and modulating RVC (e.g., autoregulation). (C) INV kidneys show a negative phase shift in the LF range which is abolished by renal denervation. (D) This difference is masked when longer time windows, which result in greater frequency resolution but poorer signal-to-noise, are used. Data adapted from (Schiller et al., 2016).
The contribution of sympathetic control to the renal pressure-flow phase shift can be appreciated in Figure 4C. INV rabbits show a negative phase shift in the LF range, characteristic of baroreflex control of RVC. Renal denervation abolishes this negative phase shift, indicating that renal sympathetic control of RBF matches well with the previous observation that resting RSNA is under strong baroreflex control (Figure 1). Interestingly, while our study was the first to report this effect as statistically significant, a clear trend for renal denervation to increase LF phase shift can be seen in studies in the conscious rabbit and acutely denervated anesthetized rat(Abu-Amarah et al., 1998; Malpas et al., 1998). This may be due to the signal processing parameters used in these studies, which were targeted at resolving autoregulatory frequency ranges. When we use similar parameters, increasing window length to 200 seconds and thereby decreasing the number of time windows, the noise in the LF range increases greatly and the effect of renal denervation is masked (Figure 4D).
Of course, variations in underlying RSNA are also undoubtedly important as RSNA which is not under baroreflex control may contribute to phase asynchrony instead of a negative phase shift. Further emphasizing this idea are reports that a negative AP-RBF phase shift is frequently observed but only in a subset of recordings (~1 in 7) from INV rats(Lessard et al., 1999). Because of the importance of the murine model, it is worth noting that a negative phase shift is also seen in the LF range of conscious, INV mice(Iliescu et al., 2008). The fact that the renal vasculature is under sympathetic baroreflex control indicates that the renal nerves modulate RVC as part of a concerted systemic mechanism for modulating total peripheral resistance to maintain AP, not as a local reflex which autoregulates RBF.
Renal Pressure-Flow Coherence
Strictly speaking, coherence measures the proportion of the variance in AP oscillations that is explained by a linear relationship with AP oscillations for all the time windows in the recording. Thus, coherence is a measure of the strength of the linear, time-invariant relationship between AP and RBF at a given frequency. Put more plainly, coherence is a quantification of how consistently linear the pressure-flow relationship is over time; it’s the transfer function analog of the correlation coefficient and similarly ranges from zero to one. Figure 5A depicts an example of high coherence; the RBF oscillation follows the AP oscillation perfectly, amplifying the AP oscillation by 20% and lagging by a quarter phase. Figure 5B depicts low coherence; in this case, the RBF oscillation is a time-varying, nonlinear function of the AP oscillation.
Frequently, coherence is used as a quality control method, with a cut-off of 0.5 applied to determine whether the physiological control mechanism (e.g., TGF, MR) is effectively characterized by the estimated transfer function. Unfortunately, this is not an appropriate interpretation of coherence as the calculated coherence is not a characteristic, invariant quantity of the AP-RBF system or even of the individual recording; instead, it depends highly on the parameters used for the Welch method. To illustrate this point, we have calculated coherence for AP and RBF from INV rabbits, varying only the parameters of the Welch method. Specifically, 50%-overlapping windows of 50, 100, 200, 300, 400, and 600 seconds were used to yield 23, 11, 5, 3, 2, and 1 window(s) for analysis. As one can see in Figure 5C and 5D, as the number of windows decreases, the coherence in the presence of active control mechanisms (i.e. in TGF, MR, and LF range) increases greatly. Obviously, the underlying physiological system has not changed, nor has the quality of the data, and, in a statistical sense, the lower coherence values with greater window number are offset by the increase in the degrees of freedom. It should be noted that although coherence can be calculated using less than three independent (i.e. non-overlapping) windows, calculations of coherence performed in this way are invalid.
Despite this misunderstanding, coherence provides immensely important insight into the renal-pressure flow relationship. In the absence of active modulation of RVC, the conditions for Poiseuille flow are well-met below the cardiac frequency, ensuring a linear pressure-flow relationship. Thus, any departures from the linear relationship between pressure and flow are indicative of active modulation of RVC. In other words, pressure-flow coherence is low in the presence of active control mechanisms (i.e. where pressure is not the only determinant of flow) and high where a passive pressure-flow relationship predominates. Accordingly, we urge the reader to consider AP-RBF coherence as accurate only when the calculated coherence is low in the autoregulatory frequency range and high in the high frequency (respiratory) range. In the absence of interventions which inhibit autoregulation, high coherence in the autoregulatory frequencies is highly indicative of incorrectly calculated coherence; low coherence in the respiratory frequency range may indicate poor data quality. The literature is unfortunately full of such examples.
With this understanding of coherence, the fact that the renal nerves contribute to the active control of RBF can be appreciated from Figure 5E. In INV kidneys, AP-RBF coherence is low for the TGF, MR, and LF ranges, increasing rapidly to a passive maximum in the HF range. Renal denervation eliminates this LF active controller, and the coherence instead increases to the passive maximum over the LF range. This indicates that the renal nerves mediate active control of renal pressure-flow in the LF range where sympathetic vasomotion is prominent. The other study which reports AP-RBF coherence similarly found that renal denervation increases coherence beyond the autoregulatory frequencies, again emphasizing that the renal nerves are an important contributor to the rapid control of RBF(Malpas et al., 1998).
Summary of the Sympathetic Regulation of Renal Pressure-Flow
In summary, renal sympathetic control buffers the transduction of LF AP oscillations to RBF, exerts LF baroreflex control over RVC, and decreases LF renal-pressure flow coherence. The integration of these three findings is important to fully understand renal sympathetic vascular control.
It may seem counterintuitive that a baroreflex controller of pressure-flow would decrease pressure-flow gain; indeed, some have stated that a baroreflex controller would increase pressure-flow gain although all experimental evidence has shown the opposite to be true(Abu-Amarah et al., 1998). Consider the case where AP rises above the set point, initiating a baroreflex-mediated decrease in total vascular conductance. A decrease in RVC in response to increased AP would result in amplification of AP oscillations and thus high AP-RBF gain.
In reality, this is not what happens because the sympathetic nervous system relies predominantly on α1-adrenergic-mediated vasoconstriction to modulate total peripheral conductance and RVC. Thus, to be able to respond to both increases and decreases in AP, the sympathetic nervous system must provide some basal level of systemic vasoconstriction. This rhythmic sympathetic vasoconstriction gives rise to the LF AP oscillations known as the Mayer waves, which are minor and variable in an unstressed, healthy animal but increase manifold when strong hemodynamic stimuli like hemorrhage and hypoxia drive global LF sympathetic synchronization(Malpas and Leonard, 2000). It is this rhythmic vasoconstriction which explains the decreased AP-RBF LF gain in INV kidneys. In response to an increase in pressure, this rhythmic vasoconstriction is withdrawn, contributing to the baroreflex-mediated increase in total vascular conductance and resulting in a relative elevation in AP-RBF gain. In the case that the nerves are completely silenced by the increase in AP, the AP-RBF gain in the LF range will reach the passive AP-RBF gain.
This same variability in the underlying RSNA explains the decreased LF coherence observed in INV rabbits that is restored by renal denervation. The sympathetic rhythms generating renal sympathetic vasomotion, sometimes participating in the generation of LF AP oscillations and other times responding to them, sometimes exerting strong vasoconstriction in response to decreased AP and other times going quiescent in response to increased AP, decrease the consistency of the AP-RBF relationship. Moreover, the fact that RSNA can be entrained by other reflexes including the central/peripheral chemoreceptor reflexes, cardiopulmonary baroreflex, and the cardiac sympathetic afferent reflex, further contributes to the variability in the AP-RBF relationship(Dick et al., 2014; Marcus et al., 2014; Wang et al., 2014; Zucker, 2006).
OTHER DYNAMIC STUDIES
Studies performing dynamic electrical stimulation of the renal sympathetic nerves, either by sine wave or pseudorandom binary sequences, are particularly relevant to the discussion of the relationship between the underlying renal sympathetic nerve activity and the resultant renal vasomotion(DiBona and Sawin, 2003; Guild et al., 2001; Malpas et al., 1999). These studies indicate that the renal vasculature works as a low-pass filter, effectively eliminating sympathetic rhythms in the HF range while passing LF sympathetic rhythms to renal vasomotion. This explains why RSNA power at the respiratory and cardiac cycle frequencies does not affect the AP-RBF relationship while LF RSNA oscillations significantly affect the renal pressure-flow relationship.
Other convincing studies show how the renal nerves play a role in RBF control during normal activities. Chronically instrumented rats while grooming or sleeping show simultaneous increases in RSNA and decreases in RBF(Yoshimoto et al., 2004). During brief, episodic activity, unilaterally denervated rabbits instrumented with bilateral renal flow probes showed increased variability in the episode-averaged RBF and the AP-RBF relationship(Barrett et al., 2001). These studies clearly show that rapid, physiological changes in sympathetic outflow influence RBF.
Still other studies have used dynamic approaches to examine the response to experimental stimuli like hypoxia and hemorrhage(Janssen et al., 1997; Malpas et al., 1998). These studies have shown an important role for the renal nerves in the generation of LF RBF oscillations in these sympatho-excitatory conditions and are reviewed more comprehensively elsewhere(Malpas and Leonard, 2000).
STEADY-STATE STUDIES
The dogma that the renal nerves do not play a role in the physiological regulation of RBF developed over many decades(Berne, 1952; DiBona and Kopp, 1997; Kopp et al., 1981, 1980; Suleiman et al., 1997; With et al., 1939). These studies made important contributions to our understanding of sympathetic neural control of renal function, but erred in assuming that steady-state (i.e. static or mean) measures of RBF could capture what we know today to be a dynamic process. To be fair, many of these studies preceded modern technologies for the assessment of renal blood flow and relied on a much less complete understanding of renal autoregulation, and they should be viewed in this context. Today, the dogma rests primarily on findings from two sets of studies.
We will briefly present the main findings of these studies and show how this fits with the dynamic role that we have demonstrated for the renal nerves in RBF control.
One set of studies involves electrical stimulation of the renal nerves, which shows that low stimulation frequencies are sufficient to cause renin release, intermediate stimulation frequencies stimulate sodium reabsorption, and high stimulation frequencies are necessary to decrease RBF (DiBona and Kopp, 1997). This data was interpreted to mean that the renal nerves play a role in basal renin release and sodium reabsorption, but not RBF control. We raise two problems with this interpretation. The first problem is that steady-state electrical stimulation of the renal nerves does not reflect physiological control of RSNA in any way. Thus, such a paradigm, while powerful for addressing whether or not a parameter can be affected by RSNA, is ill-suited for addressing how the parameter is normally regulated by physiological sympathetic outflow. The second problem is that all of these studies looked at mean RBF averaged over minutes. As described previously, renal perfusion is also controlled by powerful autoregulatory mechanisms which are very effective in buffering changes in RBF over such a time span. Indeed, one study cited in support of this dogma reported that renal nerve stimulation results in an immediate drop in RBF, presumably the rapid effect of renal sympathetic vasoconstriction, which then recovers to pre-stimulation levels, presumably due to the engagement of slower autoregulatory mechanisms(Coote et al., 1972). Thus, these stimulation intensities do not correspond to the minimum threshold required to initiate renal vasoconstriction; instead, they are the threshold at which the autoregulatory mechanisms fail.
The second set of studies supporting this dogma comes from select studies in chronically denervated dogs and rabbits that failed to detect a statistically significant difference between innervated and denervated kidneys (Barrett et al., 2001; Berne, 1952; Sadowski et al., 1979a). We again raise two issues. The first is statistical; the second is physiological.
It is a fundamental aspect of statistical hypothesis testing to understand that the result obtained from an unpowered inference test is of little value. In the case that the null hypothesis is rejected, one does not know if no difference exists or if the test was underpowered, and it is wrong to simply assume the former. As such, does removal of the renal nerves truly not affect RBF or have previous tests been underpowered? We propose that, because of the high variability in RBF between kidneys, the latter is the case. A previous study of interest showed that conscious dogs have a mean para-aminohippuric acid clearance, a surrogate for renal plasma flow, of 187 mL/min with a standard deviation of 28 mL/min (n = 6)(Sadowski et al., 1979a) while a decent-sized (n = 10) study showed that INV conscious rabbits have a resting RBF with a mean of 50 mL/min and standard deviation of 15.8 mL/min(Brown and Venuto, 1989). If one considers a physiological difference in RBF to be a difference of 15% (i.e. the renal nerves decrease RVC by 15%), then one would need to perform a study with 64 dogs or 71 rabbits per group in order to have the statistical power to detect a 15% change in mean RBF by two-tailed t-test with α = 0.05 given the high degree of variability in basal RBF. No study this large has ever been attempted, and the vast majority are not even within one order of magnitude of the requisite sample sizes. It is also worth noting that the finding that renal denervation does not affect mean RBF is not consistent. Many studies have found significantly increased RBF in conscious animals after chronic renal denervation (Janssen et al., 1997; Malpas et al., 1998; Sadowski et al., 1979b), including the same groups that have also published studies where the RBF difference between intact and denervated kidneys was not statistically significant. This does little to resolve any controversy, however, as underpowered studies are also prone to Type I (false positive) errors as well as Type II (false negative) errors.
The physiological argument is that, again, mean RBF is autoregulated, so the effect of removing the renal nerves does not reflect the sympathetic contribution to mean RBF as the powerful autoregulatory mechanisms exist to buffer such disturbances. Such an interpretation neglects not only the role of the renal nerves but the strength of autoregulatory mechanisms as well. Since the autoregulatory mechanisms can modulate RVC over two-fold (Carlström et al., 2015), even a large sympathetic contribution to basal RVC could be completely masked by compensation by TGF and MR. Indeed, we regard findings from both electrical stimulation and chronic denervation studies as a testament to the power of renal autoregulation, rather than as evidence of the absence of physiological renal sympathetic control of RBF.
CLINICAL SIGNIFICANCE
Because of recent clinical trials of catheter-based renal denervation as a therapy for hypertension, the clinical significance of physiological sympathetic renal vascular control is worthy of discussion. First, this underappreciated physiological role for the renal nerves raises questions about the depth of our understanding of the function of the renal nerves both in health and disease, especially given the recent high-profile efficacy shortcomings of therapeutic renal denervation (Bhatt et al., 2014; Desch et al., 2015). Mirroring how the dogma that the renal nerves do not physiologically affect RBF prevails despite a very mixed and nuanced literature on the topic, surgical renal denervation is frequently presented as universally anti-hypertensive (DiBona and Kopp, 1997; Esler, 2014) despite a rich history of mixed results (McBryde et al., 2007; Page and Heuer, 1935; Stella and Zanchetti, 1991). Second, this indicates that clinical renal denervation may have hemodynamic effects beyond the intended therapeutic decrease in mean AP. Due to the high level of renal perfusion – the kidneys receive approximately 22% of resting cardiac output despite constituting only 0.4% of total body mass – it is possible that the loss of renal sympathetic vascular control will affect baroreflex buffering of AP and dynamic control of RVC during exercise and postural changes on a subclinical scale. Finally, and perhaps most interesting, the fact that the renal nerves exert a dynamic influence on RBF raises the possibility for using dynamic measures of RBF as a biomarker in the context of therapeutic renal denervation. As RBF can be assessed non-invasively with transabdominal ultrasound, it is possible that dynamic measures of RBF could serve as a prognostic marker for patient selection, an intraprocedural marker of renal denervation efficacy, or a marker of reinnervation months to years post-procedure. This review emphasizes that the renal nerves are an important physiological component of the renal vascular control system, and the capacity of this untapped physiological substrate to form the basis for clinical markers of therapeutic renal denervation awaits further investigation.
SUMMARY
In summary, current data refute the classic belief that renal sympathetic nerves do not contribute to physiological RBF control. The evidence for this dogma derives from historical interpretations which overlook both the role of the renal nerves and the strength of renal autoregulation. Careful dynamic analysis of the intact and denervated renal pressure-flow system reveals a clear role for the renal nerves as physiological regulators of RBF, operating on a beat-to-beat basis to recruit the renal vasculature according to underlying sympathetic rhythms.
Highlights.
The renal sympathetic nerves are underappreciated controllers of renal blood flow
Unlike static measures, dynamic measures show sympathetic control of renal blood flow
The dynamic renal-pressure flow relationship exhibits a clear sympathetic signature
This signature shows that the renal nerves cause fast, vasoconstrictive vasomotion
Renal sympathetic vasomotion could be a biomarker for therapeutic renal denervation
Acknowledgments
GRANTS
This work was supported by National Institutes of Health National Heart, Lung, and Blood Institute (NIH NHLBI) grant P01 HL62222. P.R. Pellegrino was partially supported by NIH NHLBI grant F30 HL118974. A.M. Schiller was partially supported by AHA award 13PRE14700045.
Footnotes
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abu-Amarah I, Ajikobi DO, Bachelard H, Cupples WA, Salevsky FC. Responses of mesenteric and renal blood flow dynamics to acute denervation in anesthetized rats. Am J Physiol. 1998;275:R1543–52. doi: 10.1152/ajpregu.1998.275.5.R1543. [DOI] [PubMed] [Google Scholar]
- Barrett CJ, Navakatikyan MA, Malpas SC, Carolyn J. Long-term control of renal blood flow: what is the role of the renal nerves ? Am J Physiol Regul Integr Comp Physiol. 2001:1534–1545. doi: 10.1152/ajpregu.2001.280.5.R1534. [DOI] [PubMed] [Google Scholar]
- Berne R. Hemodynamics and sodium excretion of denervated kidney in anesthetized and unanesthetized dog. Am J Physiol. 1952;171:148–58. doi: 10.1152/ajplegacy.1952.171.1.148. [DOI] [PubMed] [Google Scholar]
- Bhatt DL, Kandzari DE, O’Neill WW, D’Agostino R, Flack JM, Katzen BT, Leon MB, Liu M, Mauri L, Negoita M, Cohen SA, Oparil S, Rocha-Singh K, Townsend RR, Bakris GL. A controlled trial of renal denervation for resistant hypertension. N Engl J Med. 2014;370:1393–401. doi: 10.1056/NEJMoa1402670. [DOI] [PubMed] [Google Scholar]
- Brown G, Venuto R. Measurement of Renal Blood-Flow of Conscious Rabbits Utilizing Ultrasonic Flowprobes - The Effect of Cyclooxygenase Inhibition. Clinical Research. 1989:A950–A950. [Google Scholar]
- Carlström M, Wilcox CS, Arendshorst WJ. Renal Autoregulation in Health and Disease. Physiol Rev. 2015;95:405–511. doi: 10.1152/physrev.00042.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coote JH, Johns EJ, Macleod VH, Singer B. Effect of renal nerve stimulation, renal blood flow and adrenergic blockade on plasma renin activity in the cat. J Physiol. 1972;226:15–36. doi: 10.1113/jphysiol.1972.sp009971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cupples WA, Braam B. Assessment of renal autoregulation. Am J Physiol Renal Physiol. 2007;292:F1105–23. doi: 10.1152/ajprenal.00194.2006. [DOI] [PubMed] [Google Scholar]
- Desch S, Okon T, Heinemann D, Kulle K, Röhnert K, Sonnabend M, Petzold M, Müller U, Schuler G, Eitel I, Thiele H, Lurz P. Randomized sham-controlled trial of renal sympathetic denervation in mild resistant hypertension. Hypertension. 2015;65:1202–8. doi: 10.1161/HYPERTENSIONAHA.115.05283. [DOI] [PubMed] [Google Scholar]
- DiBona GF, Kopp UC. Neural control of renal function. Physiol Rev. 1997;77:75–197. doi: 10.1152/physrev.1997.77.1.75. [DOI] [PubMed] [Google Scholar]
- DiBona GF, Sawin LL. Effect of renal denervation on dynamic autoregulation of renal blood flow. Am J Physiol Renal Physiol. 2004;286:F1209–18. doi: 10.1152/ajprenal.00010.2004. [DOI] [PubMed] [Google Scholar]
- DiBona GF, Sawin LL. Frequency response of the renal vasculature in congestive heart failure. Circulation. 2003;107:2159–64. doi: 10.1161/01.CIR.0000062647.30366.98. [DOI] [PubMed] [Google Scholar]
- Dick TE, Hsieh YH, Dhingra RR, Baekey DM, Galán RF, Wehrwein E, Morris KF. Cardiorespiratory coupling: Common rhythms in cardiac, sympathetic, and respiratory activities. Prog Brain Res. 2014;209:191–205. doi: 10.1016/B978-0-444-63274-6.00010-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esler M. Illusions of truths in the Symplicity HTN-3 trial: generic design strengths but neuroscience failings. J Am Soc Hypertens. 2014;8:593–8. doi: 10.1016/j.jash.2014.06.001. [DOI] [PubMed] [Google Scholar]
- Guild SJ, Austin PC, Navakatikyan M, Ringwood JV, Malpas SC. Dynamic relationship between sympathetic nerve activity and renal blood flow: a frequency domain approach. Am J Physiol Regul Integr Comp Physiol. 2001;281:R206–12. doi: 10.1152/ajpregu.2001.281.1.R206. [DOI] [PubMed] [Google Scholar]
- Holstein-Rathlou NH, Marsh DJ. Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol Rev. 1994;74:637–81. doi: 10.1152/physrev.1994.74.3.637. [DOI] [PubMed] [Google Scholar]
- Holstein-Rathlou NH, Wagner AJ, Marsh DJ. Tubuloglomerular feedback dynamics and renal blood flow autoregulation in rats. Am J Physiol. 1991;260:F53–68. doi: 10.1152/ajprenal.1991.260.1.F53. [DOI] [PubMed] [Google Scholar]
- Iliescu R, Cazan R, McLemore GR, Venegas-Pont M, Ryan MJ. Renal blood flow and dynamic autoregulation in conscious mice. Am J Physiol Renal Physiol. 2008;295:F734–F740. doi: 10.1152/ajprenal.00115.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssen BJ, Malpas SC, Burke SL, Head GA. Frequency-dependent modulation of renal blood flow by renal nerve activity in conscious rabbits. Am J Physiol. 1997;273:R597–608. doi: 10.1152/ajpregu.1997.273.2.R597. [DOI] [PubMed] [Google Scholar]
- Kopp U, Aurell M, Nilsson IM, Ablad B. The role of beta-1-adrenoceptors in the renin release response to graded renal sympathetic nerve stimulation. Pflügers Arch Eur J Physiol. 1980;387:107–13. doi: 10.1007/BF00584260. [DOI] [PubMed] [Google Scholar]
- Kopp U, Aurell M, Sjölander M, Ablad B. The role of prostaglandins in the alpha- and beta-adrenoceptor mediated renin release response to graded renal nerve stimulation. Pflügers Arch Eur J Physiol. 1981;391:1–8. doi: 10.1007/BF00580685. [DOI] [PubMed] [Google Scholar]
- Lessard A, Salevsky FC, Bachelard H, Cupples WA. Incommensurate frequencies of major vascular regulatory mechanisms. Can J Physiol Pharmacol. 1999;77:293–9. [PubMed] [Google Scholar]
- Malpas SC. Neural influences on cardiovascular variability: possibilities and pitfalls. Am J Physiol Hear Circ Physiol. 2002;282:H6–20. doi: 10.1152/ajpheart.2002.282.1.H6. [DOI] [PubMed] [Google Scholar]
- Malpas SC, Evans RG, Head GA, Lukoshkova EV. Contribution of renal nerves to renal blood flow variability during hemorrhage. Am J Physiol. 1998;274:R1283–94. doi: 10.1152/ajpregu.1998.274.5.R1283. [DOI] [PubMed] [Google Scholar]
- Malpas SC, Hore TA, Navakatikyan M, Lukoshkova EV, Nguang SK, Austin PC. Resonance in the renal vasculature evoked by activation of the sympathetic nerves. Am J Physiol. 1999;276:R1311–9. doi: 10.1152/ajpregu.1999.276.5.R1311. [DOI] [PubMed] [Google Scholar]
- Malpas SC, Leonard BL. Neural Regulation Of Renal Blood Flow: A Re-Examination. Clin Exp Pharmacol Physiol. 2000;27:956–964. doi: 10.1046/j.1440-1681.2000.03386.x. [DOI] [PubMed] [Google Scholar]
- Marcus NJ, Del Rio R, Schultz EP, Xia XH, Schultz HD. Carotid body denervation improves autonomic and cardiac function and attenuates disordered breathing in congestive heart failure. J Physiol. 2014;592:391–408. doi: 10.1113/jphysiol.2013.266221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McBryde FD, Guild SJ, Barrett CJ, Osborn JW, Malpas SC. Angiotensin II-based hypertension and the sympathetic nervous system: the role of dose and increased dietary salt in rabbits. Exp Physiol. 2007;92:831–840. doi: 10.1113/expphysiol.2007.037473. [DOI] [PubMed] [Google Scholar]
- Page IH, Heuer GJ. The Effect of Renal Denervation on Patients Suffering from Nephritis. J Clin Invest. 1935;14:27–30. doi: 10.1172/JCI100652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadowski J, Kurkus J, Gellert R. Denervated and intact kidney responses to saline load in awake and anesthetized dogs. Am J Physiol. 1979a;237:F262–7. doi: 10.1152/ajprenal.1979.237.4.F262. [DOI] [PubMed] [Google Scholar]
- Sadowski J, Kurkus J, Gellert R. Reinvestigation of denervation diuresis and natriuresis in conscious dogs. Arch Int Physiol Biochim. 1979b;87:663–72. doi: 10.3109/13813457909070527. [DOI] [PubMed] [Google Scholar]
- Schiller AM, Pellegrino PR, Zucker IH. Renal nerves dynamically regulate renal blood flow in conscious, healthy rabbits. Am J Physiol Regul Integr Comp Physiol. 2016;310:R156–66. doi: 10.1152/ajpregu.00147.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sgouralis I, Maroulas V, Layton AT. Transfer Function Analysis of Dynamic Blood Flow Control in the Rat Kidney. Bull Math Biol. 2016;78:923–960. doi: 10.1007/s11538-016-0168-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stella A, Zanchetti A. Functional role of renal afferents. Physiol Rev. 1991;71:659–82. doi: 10.1152/physrev.1991.71.3.659. [DOI] [PubMed] [Google Scholar]
- Suleiman MY, Passannante aN, Onder RL, Greene-Helms WF, Perretta SG. Alteration of renal blood flow during epidural anesthesia in normal subjects. Anesth Analg. 1997;84:1076–1080. doi: 10.1097/00000539-199705000-00022. [DOI] [PubMed] [Google Scholar]
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability: standards of measurement, physiological interpretation and clinical use. Circulation. 1996;93:1043–65. [PubMed] [Google Scholar]
- Wang HJ, Wang W, Cornish KG, Rozanski GJ, Zucker IH. Cardiac sympathetic afferent denervation attenuates cardiac remodeling and improves cardiovascular dysfunction in rats with heart failure. Hypertension. 2014;64:745–55. doi: 10.1161/HYPERTENSIONAHA.114.03699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- With, M.A.N., Autonomy, T.H.E., The, O.F., Those, E. the Effects of Spinal Anesthesia on the Circulation. 1939:319–341. [Google Scholar]
- Yoshimoto M, Sakagami T, Nagura S, Miki K. Relationship between renal sympathetic nerve activity and renal blood flow during natural behavior in rats. Am J Physiol Regul Integr Comp Physiol. 2004;286:R881–7. doi: 10.1152/ajpregu.00105.2002. [DOI] [PubMed] [Google Scholar]
- Zucker IH. Novel Mechanisms of Sympathetic Regulation in Chronic Heart Failure. Hypertension. 2006;48:1005–1011. doi: 10.1161/01.HYP.0000246614.47231.25. [DOI] [PubMed] [Google Scholar]