Using cell deformation and motion to predict forces and collective behavior in morphogenesis

Abstract

In multi-cellular organisms, morphogenesis translates processes at the cellular scale into tissue deformation at the scale of organs and organisms. To understand how biochemical signaling regulates tissue form and function, we must understand the mechanical forces that shape cells and tissues. Recent progress in developing mechanical models for tissues has led to quantitative predictions for how cell shape changes and polarized cell motility generate forces and collective behavior on the tissue scale. In particular, much insight has been gained by thinking about biological tissues as physical materials composed of cells. Here we review these advances and discuss how they might help shape future experiments in developmental biology.

1. Introduction

Morphogenesis is a fundamental example of a biological process that must involve both biochemical signaling processes and mechanical forces. This convergence makes morphogenesis an exciting and fruitful research area that requires close and interactive collaborations between mechanical modelers and developmental and cell biologists.

One of the goals of morphogenesis research is to understand how forces alter cell and tissue shape to generate functional organs and body plans. Similar questions are studied in the physical sciences and engineering, where researchers have developed rules that characterize how forces affect the shape of an object. Depending on the field, these are called “constitutive” or “rheological” equations.

These rules are different for different types of materials. For example, the force required to push on a fluid is proportional to how fast you push, while the force required to push on a solid is proportional to how far you push. More interesting materials like silly putty or mayonnaise exhibit aspects of both solid-like and fluid-like behavior, and a significant fraction of current research in materials science is devoted to organizing and quantifying rules for these types of materials.

Importantly, all modeling of morphogenetic processes must involve some assumptions about the underlying constitutive law for the material properties of cells and/or tissues [1]. Of course, in biological tissues these laws are much more interesting because they are under the direct control of signaling molecules (e.g. morphogens) that can alter mechanical properties during a developmental process. In addition, there are complex feedback mechanisms such as mechanosensitive signaling pathways that allow cells to change their behavior depending on their local microenvironment. Furthermore, cells can grow, divide, extrude, and die, allowing a much greater range of behavior than could possibly be found in non-biological materials.

Because of these novel features specific to biology, one might despair of ever developing a correct constitutive law for cells and tissues. It is true that new techniques are needed to handle new twists on how a material composed of cells behaves in response to forces. However, there are some remarkably simple ways of categorizing the material properties of tissues, and we will show in this review that simple mechanical models can make quantitative predictions about tissue behavior.

For example, one important question is whether cells inside a tissue intercalate or exchange neighbors. Neighbor exchange is a primary hallmark of a fluid, and the number of neighbor exchanges can be used to determine a diffusion constant that quantifies how likely an individual cell is to move through a dense tissue. In developmental processes associated with large-scale flow or deformation (such as convergent extension in Drosophila or the shield stage involving mesendoderm/ectoderm sorting in zebrafish) cells diffuse over large distances and the tissue behaves as a fluid. In contrast, when cells do not exchange neighbors the tissue often behaves more like a solid, supporting stresses and buckling or folding to form functional shapes. Of course, there are some unique features of biological tissues that can alter this simple picture. For example, cell divisions may fluidize [2] or solidify [3] a tissue.

So far, we have discussed constitutive laws for cells and tissues somewhat interchangeably. However, the type of constitutive law that is most useful depends on the scale at which one images and quantifies the system. For example, very large scale structures such as spinal cords or limbs have been successfully modeled using continuum or finite element models that approximate the structure using a single, simple equation, such as that for an elastic solid [4, 5]. At the much smaller intracellular scale, the dynamics of the actomyosin cytoskeleton during processes such as blebbing and cell division have been remarkably well-described by active gel models that exhibit both fluid-like and solid-like properties [6–8]. In this review, we focus on constitutive models at the intermediate scale of cellular morphogenesis that predict how cell-level shape changes, movements, and rearrangements give rise to tissue-scale behavior.

It is important to note that the constitutive law for a material (such as a tissue) can be very different from the constitutive laws for the underlying constituents (such as cells), depending on how those constituents interact with one another. For example, an individual grain of sand behaves as an elastic solid, but a pile of sand can flow like a fluid or anchor a sand castle depending on the magnitude of water-based adhesion between the grains.

Another insight is that complex, large-scale patterns in groups of cells or tissues do not necessarily require complex, large-scale control mechanisms. Specifically, local rules, such as alignment interactions between the migration direction of pairs of cells, can give rise to collective migration patterns where large groups of hundreds of cells move in the same direction. One can also find other patterns such as hexagonal lattices [9] or spiral waves [10]. Taken together, these observations suggest that minimal models may be able to capture some of the complicated features seen in developmental biology.

There are many excellent models that try to explain and predict features of tissues at a wide variety of scales, and this review cannot be comprehensive. Instead, we will focus on reviewing a class of recent techniques that model features at the cellular (but not intracellular) scale and then make prediction for collective, more global properties of tissues. Although some results are explicitly from embryonic model organisms, we will also review discoveries made in non-developmental tissues and discuss how they might be used to generate new hypotheses about morphogenesis. Importantly, recent advances in imaging, force measurement, and mutant analysis have made it possible to test these quantitative theories.

In the remainder of this review article, we focus on three recent advances that we believe are directly relevant for cellular morphogenesis: Section 2 focuses on establishing how small-scale cell deformation generates large-scale tissue deformation, Section 3 discusses new predictions about how forces are related to cell deformation by casting the problem in terms of a fluid-to-solid transition, and Section 4 focuses on how polarized cell motility leads to collective motion in groups of cells.

2. Connecting cellular deformation processes to global tissue deformation

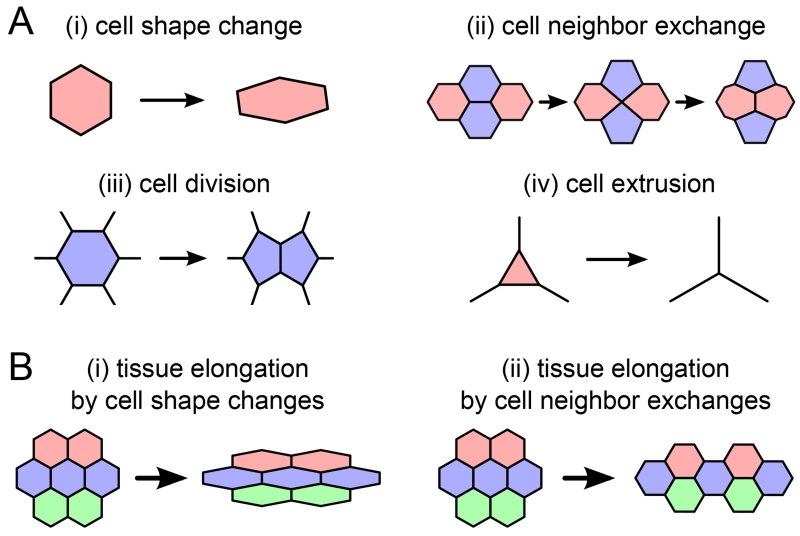
Before studying the cellular forces that drive morphogenesis, much can already be learned by quantifying the cellular processes that underlie tissue deformation. Such cellular processes could be cell shape changes, cell neighbor exchanges, cell divisions, and cell extrusions (Figure 1A). For instance, the elongation of a piece of tissue could equally be accounted for by cell shape changes or by oriented cell neighbor exchanges (Figure 1B).

Figure 1.

(A) Cellular processes underlying large-scale tissue deformation. (B) Large-scale elongation of a piece of tissue could be accounted for by (i) cell shape changes or (ii) cell neighbor exchanges.

To identify the cellular processes at work in a deforming piece of tissue, time-lapse imaging of fluorescently labeled cell membranes has turned out to be a useful tool. Recent techniques allow imaging of developing organs or even entire embryos in vivo, as well as automated tracking of the motion and deformation of each individual cell [11–17]. From such data, tissue deformation can be quantified in a straightforward manner using particle image velocimetry [13, 18]. However, if one is interested in systematically characterizing the cellular processes that underlie this large-scale tissue deformation, segmentation of the image data is required, including tracking of cell identities across subsequent images [13, 15, 19–24]. Moreover, just counting how often a cellular process occurs is in general not enough to know how much it actually contributes to tissue deformation. For instance many randomly oriented T1 transitions will not contribute to overall tissue deformation.

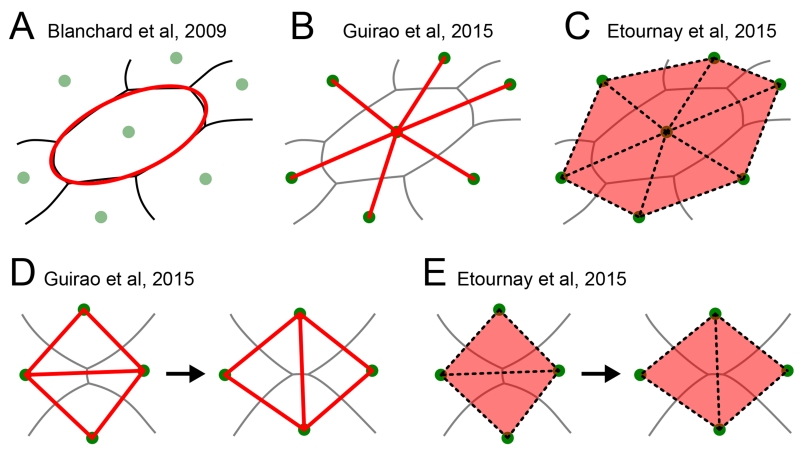
To precisely quantify the contribution of each cellular event to the overall deformation based on segmented image data, two classes of methods have been developed [11, 15, 17, 25–31]. The first class focuses on the shape of cell outlines and their deformation [11, 12, 25, 27, 28]. For example, Blanchard et al. define cell shape by fitting an ellipse to the cell outline (Figure 2A) [11]. Cellular shape change is thus measured by a change of aspect ratio and angle of this ellipse, and cell neighbor exchange is characterized by a continuous sliding of cells past one another. Based on theoretical arguments, the authors quantify such a cellular sliding as the difference between local tissue deformation and cell shape change.

Figure 2.

Different methods to quantify cellular contributions to large-scale tissue deformation use different ways to measure cell shape. (A) Blanchard et al. fit the cell outline to an ellipse (red). Aspect ratio and angle of the ellipse are then used to characterize cell shape. (B) Guirao et al. define cell shape based on the connection lines (red) between neighboring cell centers (green dots). (C) Etournay et al. characterize cell shape based on triangles (red) whose corners are three neighboring cell centers (green dots). (D,E) Guirao et al. and Etournay et al. account for cell neighbor exchanges by addition and removal of either cell center connection lines or triangles, respectively. In all panels, gray lines represent cell-cell interfaces, green dots are cell centers, and the structures used to quantify cell shape are shown in red, respectively.

The second class of methods focuses on the relative position of neighboring cell centers, where cell neighbor relations are extracted from tissue segmentation [15, 17, 26, 29–31]. One approach by Guirao et al. uses the lines connecting neighboring cell centers to represent cell shape, captured by a so-called texture tensor (Figure 2B) [17, 26]. In contrast to the approach by Blanchard et al, cell neighbor exchanges are not represented by a continuous process but instead are regarded as instantaneous. When two cells lose or gain a common cell-cell interface, the respective connection line is removed or added (Figure 2D). By keeping track of all the connection lines, overall tissue deformation can be decomposed into a contribution from cell shape changes and one from cell neighbor changes.

A recent triangle method [15, 29–31] follows a similar approach, but instead of using connection lines it represents cellular processes using triangles formed by neighboring cell centers (Figure 2C). By tracking all triangles and their deformation, one can precisely quantify four cellular contributions to overall tissue deformation: i) cell shape change induces triangle shape change, ii) neighbor exchange induces the addition and removal of triangles (Figure 2E), iii) cell divisions add triangles and iv) cell extrusions remove triangles.

Although one might think that those four processes are sufficient to describe tissue deformation, the triangle method reveals that there are also collective effects that contribute to the overall tissue deformation. These collective effects arise when cell shapes vary across the tissue in their aspect ratios and/or axes, and these variations are correlated with local rotation and/or local area growth. Such correlations can arise for instance when rows of cells slide with respect to each other [15]. In the triangle method, the collective effect contribution to tissue deformation is directly computed from correlations between shape, rotations, and area growth of the individual triangles.

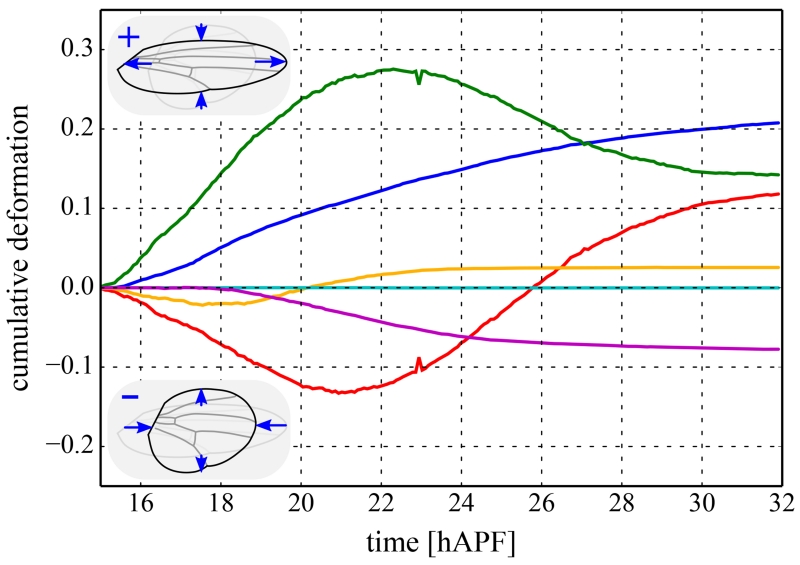
As an example, Figure 3 shows the cellular contributions to a continuous convergence extension-like deformation of the pupal Drosophila wing along its long axis [15].

Figure 3.

Cellular contributions to the convergence-extension-like deformation of the Drosophila melanogaster wing between the developmental times of 15 and 32 hours after puparium formation (hAPF) [15]. All curves shown were quantified using the triangle method and are cumulated over time. The overall deformation of the wing is shown as a blue solid curve. Positive and negative deformation correspond to shape changes in the fly wing shown in the upper and lower inset, respectively. This overall deformation is the precise sum of the following cellular contributions: cell shape changes (green), cell neighbor exchanges (red), cell divisions (orange), cell extrusions (cyan), and collective effects (magenta).

These approaches have different strengths. The approach by Blanchard et al. has the advantage of representing cell shapes directly. However, this approach does not distinguish deformations induced by cell neighbor exchanges, cell divisions, and cell extrusions. This is different for the second class of methods, which includes the work of Guirao et al. and the triangle method. In these methods, the deformation induced by all of these cellular processes can be properly distinguished. In principle, even processes like multicellular rosette formation and resolution [32, 33] can be accounted for by these methods. In addition, the triangle method accounts for collective effects, which were not characterized by previous methods but can account for a significant fraction of the deformation (as evidenced by the magenta line in Fig. 3).

Looking ahead, straightforward extensions of these approaches could include additional cellular processes such as cell fusion or intrusion. And although these methods have so far been applied to flat monolayers, the approach by Guirao et al. can be readily applied to three dimensions, and with only few modifications the same is likely to be true for the method of Blanchard et al. [11] and the triangle method.

3. Connecting cell-level forces and mechanics to tissue-level forces and mechanics

The previous section focuses on an important step: understanding how cellular-scale deformation gives rise to tissue-scale deformation. But to make predictions and formulate new hypotheses, we additionally need to know how deformation relates to forces, stresses, and the mechanical response of a tissue.

The goal of one class of recent theoretical work is to infer cellular forces within epithelia based on images of flourescently labeled membranes [17, 34–40]. These methods attempt to infer tensions along cell-cell interfaces and pressures within cells by observing the angles at which cell-cell interfaces intersect.

Most of these methods make two assumptions: (i) the mechanics of an epithelium is dominated by the cell-cell interfacial tensions and pressure differences between adjacent cells, and (ii) all forces that appear must balance one another. A third assumption must be made to infer tensions, and and three different strategies have been proposed for doing so. First, one can make additional assumptions about the biological system, for instance that cell pressure differences do not play a large role [37, 40]. Second, additional measurements can be taken into account, for instance the curvature of cell-cell interfaces [39]. Third, Ishihara et al. [36, 38] make use of the “Bayesian statistical inference method”, a method that makes probabilistic statements about target quantities when measurements provide insufficient information.

These force inference methods have been validated using artificial data from vertex model simulations [36, 38, 39], and experimental data such as intensities of labeled myosin along interfaces and retraction rates in laser ablation experiments [34, 36]. While promising, all of these methods are subject to the restriction that forces can only be determined up to a single unknown prefactor. In other words, only the ratios between forces can be measured unless one combines these methods with a direct force measurement. In addition, several of these methods are very sensitive to small errors in measuring cell shapes. Nevertheless, they represent a very useful step forward in quantifying forces and stresses in developmental systems.

Even with new tools for quantifying forces, we still need to quantify how cells and tissues respond to forces. Empirically, researchers often observe a close relationship between cellular-scale processes and the mechanical properties of the tissue. If cells change their shapes but not their neighbors, the tissue typically responds in a solid-like manner to applied forces, at least on short timescales [41, 42]. In contrast, if the cells change their neighbors, the tissue typically responds like a fluid [43]. Although this is similar to what is seen in non-biological materials such as foams and polymers, biological tissues are more interesting and complex because individual cells can generate their own forces.

This is particularly evident in the case of the fruit fly wing. Etournay et al use laser ablation to infer forces and then explain those forces using a model where cell shape changes give rise to solid-like elastic forces, while cell rearrangements relax those stresses, much like in a fluid [15]. They find that in some time windows during morphogenesis, cells actively rearrange in a direction that is opposite of that expected for a passive material and that cell rearrangements in response to stresses are delayed compared to what one would expect for a passive material like a foam. These deviations suggest that cells are actively changing the mechanical properties of the tissue by exerting local forces.

In the fly wing, a specific and carefully calibrated model demonstrates that a robustly orchestrated combination of cell shape changes and cell rearrangements governs tissue deformation. We would like to understand if there is a general framework for quantifying how forces are generated from interactions between cells in many different tissue types.

To answer this question, modelers have developed three classes of models: particle-based models, cellular potts models, and vertex models. All share a few common ideas. First, they assume that cells carefully regulate their volume, so that at a given time a cell can be characterized by its typical size or average radius. Second, they assume the cytoskeleton and especially the cortical actomyosin network provide structural integrity to the cell. This explains why most cells tend to round up into a sphere in suspension, and also why two cells cannot share the same space. Third, they assume cells can adhere to one another and the substrate via adhesion molecules. Cell-cell adhesion is assumed to increase the amount of surface area cells share with other cells, and cell-substrate adhesion can either facilitate or hinder cell motility. However, these assumptions are implemented in different ways in different models.

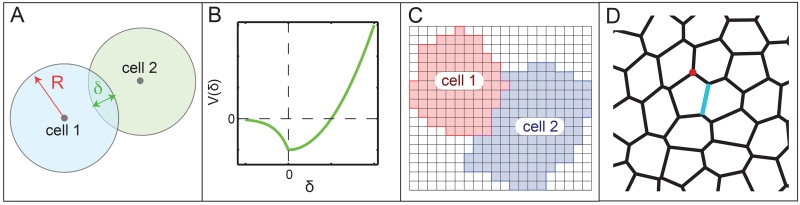
In particle-based models [2, 44–48] (Fig 4 A), each cell is represented by its center and a few parameters describing its shape, such as the radius, for circular or spherical particles. Two particles interact via an “interaction potential” V (δ), where δ is the distance between the edges of the circles representing the cells. δ is positive when the circles overlap and negative if there is empty space between the circles. A typical example of such a potential is shown in Fig 4 B; the potential is positive and the particles repel if the overlap is large, mimicking cortical tension and cytoskeletal rigidity, and V (δ) is negative and particles attract if overlap or spacing between cells is small, mimicking cell-cell adhesion.

Figure 4.

(A) Schematic diagram for a particle model of cells, where cells are circles with radius R and the distance between the edges of the cells is the overlap δ. δ is defined to be positive when cells overlap and negative when they are not touching. (B) Interaction potential V (δ) for a typical particle model. V (δ) is positive and the particles repel when δ is large and positive and the particles overlap significantly. The particles attract in the region where V (δ) is negative. Cells do not change shape, but their interaction changes as the cell centers move. (C) Schematic diagram of a cellular potts model for cells, where each cell is composed of a group of squares on a grid. Cells change shape when squares switch identity between cells. (D) Schematic diagram of a vertex model for cells, where each cell is composed of a series of vertices (such as the point labeled in red) connected by edges (such as the one labeled in blue). Cells change shape when vertices move or edges are added or removed.

Both cellular potts models [49–56] and vertex models [57–65] assume that an energy functional describes the mechanical work required for cells to change their shapes. A typical example of such an energy functional for single cell within an epithelial monolayer is [59]:

$$E_{\text{cell}}=K_A(A-A_0{)}^2+K_p(P-P_0{)}^2,$$ (1)

where E_cell is the mechanical energy associated with that cell, A and P are the actual cross-sectional area and perimeter of each cell in the monolayer, respectively, A₀ and P₀ are a cell’s “preferred” or “target” area and perimeter, and K_A and K_P are two model parameters describing the effective stiffness of the cell body and cell cortex. This equation implies that cells can independently regulate their cross-sectional area (by regulating their volume and height in the monolayer) and their cross-sectional perimeter (by regulating their cortical tension and adhesion). It is important to note that there are other variations on these types of energy functionals: 3D versions [57, 63, 65–68], ones where the area is fixed [60], where there is no P² term [58], and where edges are viscoelastic [69, 70].

Although they use similar energy functionals, cellular potts models and vertex models differ in how they represent individual cells and how they explore the energy states. In cellular potts models, each cell is composed of a group of grid points, illustrated schematically in Fig 4 C. A so-called “monte carlo” algorithm is typically used to find the pattern of cell shapes that minimizes the sum of all the cellular energies, each given by Eq 1. Roughly, the algorithm monitors the mechanical energy as a “trial move” switches a square in the grid from being grouped with one cell to being grouped with a neighboring cell, and keeps trial moves with lower energies. After many such moves, the cells in the model have shapes that require the least possible amount of mechanical energy.

In contrast, vertex models represent cells in a tissue as a network of vertices connected by edges (and faces, in three dimensions), as shown in Fig 4 D. Because the model is a bit simpler, one can calculate directly how to move each vertex so that the system moves “downhill” in the energy [71]. Once a minimum energy state is identified, both vertex and cellular potts models can be used to make predictions about the statistics of cell shapes in a tissue [59, 60], emergence of order in cellular patterns [9, 62], cell proliferation [52, 58], cell sorting and compartmentalization [50–52, 72], and/or rounding of three-dimensional cell aggregates [57].

Which model works best is highly system- and context-dependent. Particle models are easy to simulate and have very few model parameters, which makes them ideal for large scale simulations over long times. However, it is difficult for the particles to change shape, and the interaction potential becomes unrealistic when the tissue is at very high densities – i.e. when the tissue is confluent and there are no or very small empty spaces between cells. Potts model and vertex models require more computational time, but they do a better job of representing changes to cell shapes, especially at higher densities. While vertex models are slightly simpler and therefore potentially more amenable to the discovery of universal features, they are restricted to confluent tissues. Potts models can handle both confluent and non-confluent tissues, and are often more amenable to adding additional internal dynamics within cells such as diffusion of morphogen signals or chemotaxis. While all of these models can be independently useful in specific situations, until recently there were few unifying or organizing ideas to characterize how these cellular-scale mechanical models generically give rise to tissue-scale mechanical properties.

A recent series of experiments (both in developmental model systems and in other tissues) has shed light on a new paradigm that could change that. Specifically, researchers in many fields of biology are finding evidence that dense tissues are near a so-called “glass” or “jamming” transition [48, 73–77]. “Glass” and “Jamming” are physics/engineering terms that refer to a transition where a material changes from being fluid-like to being solid-like while remaining disordered. Unlike the familiar fluid-to-solid transition of liquid water into ordered, crystalline ice, disordered jamming transitions have specific universal signatures, including characteristic collective or “swirly” motion and a slowing down or “caging” of the motion of individual cells. These precise signatures have been found in cultured epithelial layers [3, 73, 78], cultured cancer cell lines [75, 79] and zebrafish embryonic explants [48].

Obviously, an important open question is whether various cell-level models can recapitulate this jamming behavior, and whether the jamming paradigm might provide a quantitative universal framework for predicting tissue level forces and mechanical response from single-cell properties. Importantly, jamming transitions have been identified both in particle models [47, 80, 81] and in vertex models [82–84]. There is also implicit evidence for them in potts models [56], and we expect them because of the similarities between potts and vertex models, although they have yet to be explicitly studied there.

In particle-based models, appropriate for systems where cells are not confluent, jamming transitions look similar to those in passive non-biological materials [47, 80]. In these models, a tissue solidifies when the cells become more dense or “crowded”. These particle-based pictures were recently proposed as a unifying way to describe tissue mechanics in terms of single-cell mechanical properties [76].

However, in many developmental processes, such as convergent extension in Drosophila or differentiation and cell sorting into ectoderm and mesendoderm layers in the zebrafish shield stage, the cells are confluent or nearly confluent and so they cannot become more crowded. Yet, they appear to change their behavior from fluid-like to solid like or vice versa. Therefore, the discovery of a jamming transition in the vertex model [83] provides an explanation for this phenomena. In this transition, the entire tissue can solidify if cells decrease their preferred perimeter relative to their preferred area, potentially by downregulating cell-cell adhesion or upregulating cortical tension. In addition, the model predicts that the transition takes place when the observed cell shapes in a monolayer take on a specific, universal value: if the tissue is a solid, the ratio between the observed perimeter and the square root of the observed area is preceisely 3.81 (which is the perimeter-to-area ratio of a perfect pentagon), while the ratio should rise above 3.81 as the tissue becomes more and more fluid-like. This stringent a priori prediction is precisely realized in epithelial monolayers cultured from the lungs of human patients, with implications for asthma pathobiology [77].

These results could have important consequences for developmental biology. First, it suggests that in confluent epithelial layers in developing embryos, biologists can predict the mechanical properties of a tissue (whether it is fluid-like or solid-like) simply by imaging cell shapes in the monolayer and calculating the perimeter-to-area ratio. If a tissue is solid-like, we expect that tissue-level morphogenesis will proceed via buckling, folding, and other mechanisms that preserve cell neighbors. In contrast, if the tissue is fluid-like, we expect intercalation, convergent extension, or other large-scale flows of cells will occur. Second, it suggests that the important control parameter for epithelial mechanics is how the cell regulates its perimeter in contact with other cells (or surface area in three-dimensional tissue structures) relative to its area (volume in 3D). Cells could regulate this perimeter in many ways, for example, by downregulating cadherin expression or decreasing their perimeters along certain directions via myosin contractility. It is possible that many different signaling pathways could be grouped according to how they alter this property, providing a theoretical framework for mutant analysis.

4. Cell motility and coordination

In the previous section, we highlighted results from cell-level models that predict that cell crowding or individual cell shape changes can drastically change the global mechanical behavior of a tissue. In this section, we describe how including active cell motility in cell-level models modifies and extends those predictions.

In many developmental systems, cells move by exerting active forces on an underlying substrate or on surrounding cells. In cell-level models, there are two main methods for incorporating these forces. In cellular potts or vertex models, the tension along a specific cell-cell interface can be increased or decreased, causing the interface to shrink or grow and potentially initiating a neighbor exchange or cellular rearrangement [85, 86]. This approach has been very successful in modeling convergent extension [85, 87] and cell shape remodeling processes [88] in several developmental systems.

Alternatively, in all three types of models an additional polarized “motile force” can be added to the center of mass of each cell. The direction of the polarization is intended as a minimal representation of the front/rear asymmetry of force-generating cytoskeletal machinery in a motile cell [55, 89]. While the precise mechanisms for polarization in cell motility are still under investigation, this is often modeled by adding a “motile force” that causes the cell to move at a constant speed v₀ in a direction θ. The direction θ is typically assumed to rotate a little bit at each time step, with the magnitude of rotation given by a parameter D_r. If v₀ is very large compared to D_r, a cell is very persistent and moves in a nearly straight line (Fig 5 A), while if v₀ is very small compared to D_r, the cell executes a jerky random walk [90] (Fig 5 B).

Figure 5.

(A) Single cell trajectory from a model where the velocity v₀ = 10 is much larger than the rotational noise D_r = 1. (B) Trajectory from a model where the rotational noise D_r = 10 is much greater than the velocity v₀ = 1. (C) Snapshot of motility-induced phase separation in a particle simulation with repulsive-only interactions and periodic boundaries, when v₀ = 50 and D_r = 1. (D,E) Cell polarization directions in simulations of a model (D) in a parameter regime where there is no collective motion or flocking and cell polarization directions are random, and (E) in a flocking regime where all cell polarization directions are strongly correlated.

Although this is a minimal representation of polarized cell motility, researchers have been surprised by complex collective behaviors that emerge in systems that obey these simple rules. A recent comprehensive review of these active matter models has been published for an audience of physicists and engineers [91]; here we will focus on a select group of phenomena that may be particularly relevant for developmental biology.

A first surprise is that polarized, motile agents can spontaneously self-organize into dense clusters of cells co-existing with sparse regions with few cells in between [92], as shown in Fig 5 C, and that the ratio v₀/D_r controls that process. The same principles will spontaneously give rise to segregation of motile cells [81], even in the absence of adhesion. This is interesting, because it suggests that cell clustering, sorting, and compartmentalization could arise as a purely dynamical process, without any need for differential adhesion [93], contraction [94] or interfacial tension [95].

A second interesting result is that active polarized motion can significantly alter the fluid-to-solid jamming transition in tissues. In both particle and vertex models, increasing the motile speed v₀ of individual cells makes the entire tissue more fluid-like. While this is not surprising, the models are able to make specific, testable predictions about how the fluid-solid transition shifts as a function of v₀ [80, 84]. More surprising is the prediction that cell rearrangements occur more often in tissues where the cell motion is more persistent. In other words, tissues become more fluid-like as the rotational noise D_r decreases. For developmental systems, this suggests that cells can move or migrate more quickly through a dense tissue simply by becoming more persistently polarized, even if that direction of polarization is not coordinated with other cells.

However, in many biological and developmental systems there are mechanisms that help coordinate the direction that cells move. Several models include coordination using an explicit “alignment” rule, which says that a cell’s direction θ will tend to align with those of its nearest neighbors as a function of time [46, 96]. Other models use a more subtle rule, which assumes that the polarity of a cell is given by the past motion of the cell during a time window τ [47, 55, 56, 89, 97]. Since the past motion of the cell is affected by the neighboring cells, such a rule can indirectly induce polarity alignment of neighboring cells.

In systems with alignment interactions a new type of “flocking” transition can occur [96, 98]. At low densities, weak alignment, or large τ, the cells tend to move in random directions (Fig 5 D). However, at high densities, strong alignment, or small τ, the cells will all begin to move in the same direction, or “flock” (Fig 5 E). It is important to note that the flocking transition can be independent from the jamming transition: in a fluid-like tissue cells change neighbors, while in a flocking tissue cells do not necessarily change neighbors even though the cells are moving quickly.

Importantly, alignment interactions between cells can also enhance collective motion even in systems that do not exhibit a full-fledged flocking transition. For example, for sufficiently large motile force, cellular potts models with a subtle alignment interaction exhibit so-called cell streaming behavior [55, 56], which was previously found in experiments [55]. Cell streaming refers to a coordinated cellular motion where individual cell velocities tend to correlate with the overall direction of motion. In other words, a cell tends to move in the same direction as the cell in front of it. Alignment can also alter the jamming transition in a confined particle-based model [47].

5. Discussion and Conclusions

In this review we focused on three recent advances in modeling tissues at the cellular scale: relating cell shapes and patterns to tissue deformation, relating cell shapes and structures to forces within tissues, and relating individual cell motility and polarization to tissue deformation and forces in tissues. These models have been validated in developmental model organisms (including Drosophila and zebrafish) as well as epithelial cell cultures.

One over-arching theme is that many tissue types are close to a transition point. In other words, small changes to cellular parameters can lead to very large changes in large-scale tissue behavior. For example, a small increase in the effective adhesion between cells in an epithelial layer can cause the tissue to abruptly change from a solid that buckles to a fluid that flows. Similarly, a small increase in the persistence of single-cell motility can cause cells to switch from moving randomly to moving together in a “flock”.

The fact that we observe living tissues close to these transitions motivates speculations about possible functional roles in developmental biology. For example, a morphogenetic deformation could potentially be arrested at a precisely controlled time by tuning cellular parameters to achieve tissue jamming. Alternatively, a continuous morphogen gradient could lead to an abrupt change in tissue behavior at a programmed location along the gradient.

Although we understand some aspects of these transitions, many biologically relevant questions remain. For example, tissue fluid-to-solid transitions have been identified in models where either cells change shape or cells proliferate, but the effect of simultaneous shape change and proliferation on the jamming transition has not yet been carefully studied.

Additionally, most of the models discussed here are explicitly two-dimensional. While some flat epithelial layers are effectively two-dimensional, most tissues in development are curved epithelial layers or fully three-dimensional. Some progress has been made in imaging and segmentation [16, 19–24, 99] as well as modeling [63, 65–67, 100–103] epithelial sheets that form curved structures, and several groups are currently working to extend existing models to fully three-dimensional shapes.

Finally, many of these models have so far been tested in a single model organism, and then only on one tissue type at a single stage of development. It would be useful to attempt to validate these models in different tissues and organisms, because they will almost certainly fail in interesting ways. This will not only help us improve and generalize our models, but it might also potentially lead to new discoveries about how developing embryos use mechanics to regulate form and function.

Taken together, the work discussed here demonstrates that mechanics plays an important role in the regulation of morphogenesis, and that the transduction and patterning of mechanical signals often occurs at the cellular scale [104–106]. In hindsight, it is not surprising that many important discoveries involve collaborations between theoretical modelers and experimental biologists or biophysicists. Quite often, theorists attempt to extract universal features that are independent of the precise details at the molecular scale, that hopefully provide a framework for understanding similarities between diverse developmental processes. Of course, the richness of biological systems often leads to new types of unexpected phenomena, which provide motivation for theorists to revise their models. This rapid back-and-forth makes it an exciting time to be studying model-based predictions for cellular morphogenesis.

• -The mechanical properties of biological tissues are important for their function
• -Models predict Constitutive laws explaining how tissues deform in response to forces
• -Cellular contributions to overall tissue deformation can be precisely quantified
• -Cell shape may indicate whether a tissue behaves as a solid or a fluid
• -Cell motility can induce unexpected collective behavior on the tissue scale