Abstract
RNA recognition motif (RRM) proteins represent an abundant class of proteins playing key roles in RNA biology. We present a joint atomistic molecular dynamics (MD) and experimental study of two RRM-containing proteins bound with their single-stranded target RNAs, namely the Fox-1 and SRSF1 complexes. The simulations are used in conjunction with NMR spectroscopy to interpret and expand the available structural data. We accumulate more than 50 μs of simulations and show that the MD method is robust enough to reliably describe the structural dynamics of the RRM–RNA complexes. The simulations predict unanticipated specific participation of Arg142 at the protein–RNA interface of the SRFS1 complex, which is subsequently confirmed by NMR and ITC measurements. Several segments of the protein–RNA interface may involve competition between dynamical local substates rather than firmly formed interactions, which is indirectly consistent with the primary NMR data. We demonstrate that the simulations can be used to interpret the NMR atomistic models and can provide qualified predictions. Finally, we propose a protocol for ‘MD-adapted structure ensemble’ as a way to integrate the simulation predictions and expand upon the deposited NMR structures. Unbiased μs-scale atomistic MD could become a technique routinely complementing the NMR measurements of protein–RNA complexes.
INTRODUCTION
The RNA recognition motif (RRM) is the most common RNA-binding protein motif in eukaryotes, including humans (1). The RRM-containing proteins have been observed at all levels of post-transcriptional genetic expression, including RNA splicing, export and stability (2). Structurally, the RRM is composed of about 90 amino-acids that form a four-stranded β-sheet packed against two α-helices. It has a consensual secondary structure of β1α1β2β3α2β4 (3). Although RRM/protein (4,5) recognition has been reported, this domain binds primarily RNA molecules. Despite high similarity between individual RRMs, the motif is able to bind a wide-range of RNAs (6,7). These can differ both in sequence and in length (8,9). The RRM typically binds a short, single stranded or stem-looped RNA molecule in a highly specific manner. The ability to bind different RNA molecules is mainly due to diverse modes of the protein/RNA recognition. Typically, the β-sheet surface of the domain is used to interact with RNA (10). This canonical mode of binding involves stacking interactions with conserved aromatic residues and hydrogen-bond formation with additional side chains and main chains of the protein. However, interactions with the α-helices (11,12), protein loops (13,14), and the N- and C-terminal extensions (15–18) have been described in the literature. The RNA binding proteins often contain multiple RRM domains, each associating with the RNA in distinct way. The versatility of the RRM motif and its binding modes make it a centerpiece of the structural studies of protein/RNA complexes. The X-ray crystallography and the NMR solution spectroscopy are the leading methods in the structural determination of RRM domains and their complexes (2).
The molecular dynamics (MD) simulations in explicit solvent are an important tool for study of biomolecular systems (19). They allow us to examine the development of the entire molecular structure on atomistic level with ps-scale time resolution and can supply information unavailable to most experimental techniques. However, the simulations are limited by the affordable sampling (the length of the simulation) and the quality of the force field (the theoretical model used to represent the biomolecule). Due to computational demands and force field limitations, most past MD studies dealt with isolated protein or nucleic acid molecules. With the exception of series of studies of the U1A protein/RNA complex (20–25), there are only few studies describing the simulations of RRM/RNA complexes in contemporary literature (26–29). In a recent μs-scale simulation benchmark study of six diverse protein/RNA complexes, we highlighted the basic accuracy limits of the MD method and demonstrated that it can be successfully applied to many protein/RNA complexes (25). In this work, we report extensive MD simulations on two RRM/RNA complexes. We reveal structural-dynamics features that are not apparent from the experimental data, evaluate limits of the simulation methodology and propose an updated simulation protocol aimed at improving the agreement between theory and experiments.
The MD simulations and NMR spectroscopy have a synergic relationship. In the past, the NMR data has often been used as a reference for the quality of MD simulations (30–36). The new versions of the force field are frequently assessed by comparing the experimental NMR parameters with those obtained from the simulation trajectories (37–39). The NMR structural data can also be used to create biasing potentials to improve the simulation stability (38,40). The performance of MD simulations is also a notable concern for the NMR spectroscopy as part of the NMR structure refinement process involves the use of the empirical force fields (41). Targeted use of MD was shown to improve the quality of the resulting atomistic models (42).
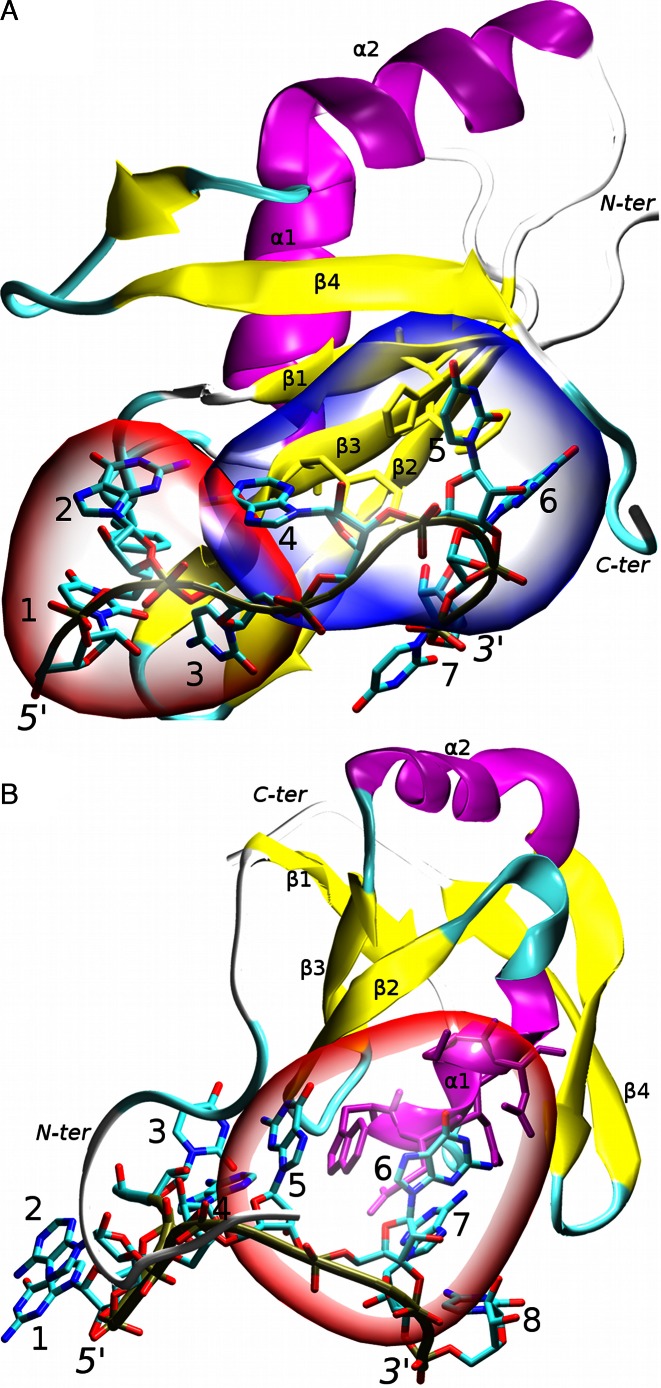
In this work, we examine high-precision NMR solution structures of two RRMs bound to RNA. Both of them exhibit atypical modes of RNA recognition (11,43). The first complex is the human Fox-1 protein interacting with UGCAUGU RNA (43). The Fox-1 protein regulates alternative splicing of several tissue-specific exons by recognizing a UGCAUG sequence of the RNA (44). It was originally identified as sex determining element in Caenorhabditis elegans (45). Since then, its homologs have been observed in other organisms, including humans. Different forms of the protein are found in specific tissues (46,47). Structurally, the Fox-1 protein exhibits a mixed mode of RNA recognition. Specifically, the AUG element is bound in a canonical way by the aromatic residues of the β-sheet surface while the UGC nucleotides are recognized non-canonically by the loop residues (43). The first three nucleotides are wrapped around a single phenylalanine aromatic ring, forming a hydrophobic pocket. Additionally, nucleotides G2 and A4 form an intramolecular mismatch base pair (Figure 1). The two binding modes are structurally separated (43).
Figure 1.
The studied RRM protein/RNA complexes: (A) Fox-1 complex. The non-canonical (hydrophobic pocket) and canonical parts of the protein/RNA interface are highlighted in red and blue respectively; (B) SRSF1 complex. The protein/RNA interface is highlighted in red. Other parts of the RNA molecule do not form specific interactions with the protein; the secondary structure of the proteins is labeled and highlighted in purple (α-helices), yellow (β-sheets) and cyan/white (loops). The RNA backbone is traced in brown. The nucleotides are numbered and the chain termini labeled. For additional structural details see Supplementary Figures S1 and S2.
The second complex is a human SRSF1 pseudo-RRM domain (RRM2) bound to UGAAGGAC RNA (11). Unlike canonical RRM, the pseudo-RRM has a distinct sequence of seven invariantly conserved amino-acids in the α1 helix which participate in its unusual mode of RNA recognition (48). Its β-sheet surface lacks the aromatic residues that are canonically involved in the RNA binding. The seven conserved residues of the SRSF1 α1 helix recognize the GGA triplet (nucleotides 5–7) of the RNA. The other nucleotides do not participate in the protein/RNA interface (Figure 1). This makes the mode of recognition very different from the Fox-1 protein and the other RRMs (11). The SRSF1 protein is a well-studied molecule belonging to the serine/arginine (SR) family of proteins. The SR proteins are important in the gene expression by regulating splicing, transport and the translation of mRNA molecules (49). They are a potential therapeutic target in several diseases (50) and malfunction of the SRSF1 activity was shown to be lethal in developing cells (51,52).
MATERIALS AND METHODS
Structure building and force field selection
We used the first frames of the NMR ensembles (PDB codes: 2err and 2m8d) (11,43) as starting structures. The 2err system contains nucleotides 1–7 and a.a. 109–196. The 2m8d system contains nucleotides 1–8 and a.a. 106–196. The same residue numbering is used in this article. The topology and coordinate files for the simulations were prepared using the tleap module of Amber 14 (53). We have used the ff99bsc0χOL3 force field (54–58) for RNA, which is default for RNA since Amber 11. It combines the original Cornell et al. parametrization (54), and three subsequent reparametrizations. Specifically, the sugar pucker (55), α/γ backbone dihedrals (56), and χ dihedrals (57,58). For proteins, we have used the ff14SB, ff12SB and ff99SB (abbreviated as 14, 12 or 99 in the Table 1) force fields. The ff99SB force field combines the original Cornell et al. parametrization (54) corrected by two reparametrizations of φ/ψ protein backbone dihedrals (ff99 (55) and SB (59)). Recently, the ff99SB side-chain dihedral parameters were reparametrized, resulting in ff12SB and ff14SB protein force fields (60). Ff12SB is a predecessor of ff14SB released ca. two years earlier and containing already majority of the ff14SB refinements.
Table 1. List of simulations.
| Simulation namea,b | NMR restraints initially applied | Length (ns) |
|---|---|---|
| Fox-1 structure | ||
| 2err_14_1 | No | 1000 |
| 2err_14_2 | No | 1000 |
| 2err_14_rst1 | Yes | 1000 |
| 2err_14_rst2 | Yes | 1000 |
| 2err_14_rst3 | Yes | 1000 |
| 2err_12_1 | No | 1000 |
| 2err_12_2 | No | 1000 |
| 2err_12_rst1 | Yes | 1000 |
| 2err_12_rst2 | Yes | 1000 |
| 2err_12_rst3 | Yes | 1000 |
| 2err_12_rst4 | Yes | 1000 |
| 2err_99_1 | No | 1000 |
| 2err_99_2 | No | 1000 |
| 2err_99_rst1 | Yes | 1000 |
| 2err_99_rst2 | Yes | 1000 |
| 2err_99_rst3 | Yes | 1000 |
| 2err_99_rst4 | Yes | 1000 |
| SRSF1 structure | ||
| 2m8d_14_1 | No | 1000 |
| 2m8d_14_2 | No | 1000 |
| 2m8d_14_rst1 | Yes | 1000 |
| 2m8d_14_rst2 | Yes | 1000 |
| 2m8d_14_rst3 | Yes | 1000 |
| 2m8d_14_rst4 | Yes | 1000 |
| 2m8d_12_1 | No | 1000 |
| 2m8d_12_2 | No | 1000 |
| 2m8d_12_rst1 | Yes | 1000 |
| 2m8d_12_rst2 | Yes | 1000 |
| 2m8d_12_rst3 | Yes | 1000 |
| 2m8d_12_rst4 | Yes | 1000 |
| 2m8d_12_rst5 | Yes | 1000 |
| 2m8d_99_1 | No | 700 |
| 2m8d_99_2 | No | 600 |
| 2m8d_99_rst1 | Yes | 1000 |
| 2m8d_99_rst2 | Yes | 1000 |
| 2m8d_99_rst3 | Yes | 1000 |
| 2m8d_99_rst4 | Yes | 1000 |
| 2m8d_99_rst5 | Yes | 1000 |
| 2m8d_14_short1c | Yes | 1000 |
| 2m8d_14_short2c | Yes | 1000 |
| 2m8d_12_short1c | Yes | 1000 |
| 2m8d_12_short2c | Yes | 1000 |
| 2m8d_99_short1c | Yes | 2000 |
| 2m8d_99_short2c | Yes | 1000 |
| 2m8d_14_R142Ad | No | 1000 |
| 2m8d_12_R142Ad | No | 4000 |
| 2m8d_12_R142A_2d | No | 2000 |
| 2m8d_12_R142A_TI_1e | No | 54 × 50 |
| 2m8d_12_R142A_TI_2e | No | 54 × 200 |
aAfter 120 ns of the simulation (unrestrained part, see Materials and Methods section), all of the initially restrained trajectories (marked as ‘_rst’) are fully independent simulation runs. However, up to 120 ns, some of them share a common restrained part of the trajectory. Full explanation is in the Supplementary Scheme S1.
bThe ‘14’, ‘12’ and ‘99’ numerals in the simulation name indicate ff14SB, ff12SB and ff99SB protein force field versions, respectively. For the RNA, the ff99bsc0χOL3 force field was used in all simulations.
cThe nucleotides 1–3 and amino-acids 106–114 were removed.
dThe R142A mutation was introduced into the system by molecular modeling, with the final structure of the 2m8d_12_rst1 simulation used as the starting configuration.
eBoth TI calculations consist of 54 independent simulations, each lasting either 50 (first simulation run) or 200 ns (second simulation run).
System solvation
The protein/RNA complexes were solvated in an octahedral box of SPC/E (61) waters with minimal distance of 10 Å between the solute and the box border. The systems were solvated with KCl (62) salt, achieving ∼150 mM excess salt condition. Extensive discussion of differences between the experimental and simulation buffer compositions is given in the Supporting Information.
Simulation protocol
The systems were minimized and equilibrated using standard equilibration protocols (25). The production simulations were run with either the pmemd.MPI (CPU based, simulations using NMR restraints) or pmemd.cuda (63,64) (GPU based, unrestrained simulations) modules of Amber 14. The Particle mesh Ewald method (65,66) was used for calculations of the electrostatic interactions. Periodic boundary conditions were used to prevent the system border bias. The cut off distance for the non-bonded Lennard-Jones interactions was 9 Å. The SHAKE algorithm (67) was used to constrain the covalent bonds involving hydrogen, allowing a 2 fs integration step to be used. We have used the Berendsen weak-coupling (68) thermostat and barostat to maintain the systems at a temperature of 300 K and pressure of 1 bar, respectively. We note that the weak-coupling algorithms such as Berendsen thermostat do not exactly produce the canonical ensemble. This may cause errors in, e.g. temperature replica-exchange MD simulations. However, the use Berendsen thermostat is deemed appropriate in standard MD simulations of extended systems (69). The associated errors are assumed to be rather negligible compared to other sources of the errors in the simulations. To prevent the ‘flying ice cube’ phenomenon (70), the systems translational center of mass motion was removed every 10 ps.
Use of NMR restraints in the initial phases of simulations
Our recent studies of protein/RNA complexes (25,71,72) indicate that the standard equilibration protocols are sometimes unable to produce structures from which stable production simulations can be started. The experimental structures are, for a variety of reasons, high in force-field potential energy. While the equilibration relaxes the simplest high-energy features such as unoptimal bond lengths and angles, the equilibrated structure may still contain more complex unnatural high-energy structural features due to the overall ruggedness of the potential energy surface. Their presence may afterwards disturb the production simulations and cause excessive departures from the experimental geometry. Thus, in majority of our simulations, we used the first part of production simulations to stabilize the structures using NMR restraints, to give the system more time to relax and adapt to the primary experimental data. Specifically, after the initial standard equilibration (see above), the systems were simulated in the following way: 0–100 ns—all available NMR hydrogen restraints (both inter- and intramolecular ones) were utilized, 100–120 ns—only protein–RNA (intermolecular) NMR hydrogen restraints were utilized and after 120 ns—entirely unrestrained simulations followed. Only the primary NMR data (NOE hydrogen distance restraints) were used, using the flat-well potentials (53). For control, some simulations were done without the NMR restraints.
Simulation analyses
The simulation trajectories were analyzed in ptraj and cpptraj modules (73) of Amber 14. The VMD program (74) was used for visualization. We have used gnuplot and Raster3D (75) to produce graphs and figures, respectively.
The complex stability and the agreement with the primary experimental data were assessed by computing distance violations of experimental intermolecular NOE (Nuclear Overhauser effect) distances. We have computed the (r−6)(−1/6) weighted average of the NOE distances in the simulation ensemble. This value was straightforwardly compared with the experimental upper-bound values of the intermolecular NOE data. Note that we discuss only NOE violations larger than 1 Å although smaller violations were still monitored. A complete list of the simulation intermolecular NOE violations is available in Supporting Information.
The protein/RNA H-bond interactions were analyzed by monitoring the distances and angles between relevant heavy atoms. We report the simulation time developments of all H-bonds with over 90% presence in the NMR ensemble. The H-bond is considered to be present when the distance between the two heavy atoms is below 3.5 Å. The H bonds with smaller occurrence in the NMR ensemble are reported only when interesting for some specific reasons. In addition, we report several non-native H-bonds that were absent in the NMR ensemble but were consistently formed during the simulations. Stacking interactions in the MD simulations were analyzed visually using VMD. The differentiation between stacked and unstacked structures was very clear and no quantitative criteria were needed. The occupancies of the stacking interactions in the NMR structures were obtained by visual inspection of the NMR ensemble frames.
To produce the MD-adapted structure ensembles (see below), the K-means clustering algorithm was used to cluster the simulation trajectories based on the complex RMS deviation.
Thermodynamics integration (TI) calculations
We have used a mixed single/double topology approach as implemented in Amber 14 to set up the TI calculations (53). The mutated residue was represented by dual topology model while the rest of the complex and the solvent were described by single topology. We used the soft core vdW potentials (76) to handle the appearing and disappearing atoms in the dual topology region. The traditional three-step method of discharging–transforming–recharging the mutated atoms (53) was used to handle the electrostatic component. The pmemd.MPI (CPU based) module of Amber 14 was used to collect the free energy derivation statistics (δV/δλ) at every integration step. The simulations were carried out for nine lambda windows in parallel runs. The standard simulation protocol (see above) was fully applied except that the Langevin thermostat was used to regulate the temperature. We used the nine-point Gaussian quadrature to numerically estimate the final free energy integral. The statistical error of the calculations was evaluated using the block averaging method with block sizes of two million δV/δλ values (77,78).
The TI computations were carried out for both the protein/RNA complex system and the isolated protein. At the end, the final free energy difference of the mutated and WT protein/RNA complex stability (ΔΔG) was computed according to the thermodynamics cycle equation ΔΔG = ΔGco – ΔGs = ΔGWT – ΔGmut. The ΔGco and ΔGs represent the results of our TI calculation in the mutated protein/RNA complex and in the lone protein, respectively. The ΔGWT and ΔGmut are the dissociation energies of the wild-type and the mutated complex, respectively, as commonly measured in the experimental setting. According to the thermodynamics cycle, both approaches obtain physically equivalent result (ΔΔG).
TI is one of the most robust and most straightforward methods to calculate free energy differences in biomolecular systems (http://www.alchemistry.org). It implicitly includes both the enthalpic and entropic components of the free energy change and when its basic methodological limitations are properly respected, it is often considered of semi-quantitative accuracy and is ideally suited for the calculations executed in this study. The method is suitable for evaluation of free energy impacts of single-residue substitutions in molecular complexes, especially in cases where the substitution is not associated with large changes of the molecular topology and large rearrangements of the structures. In our particular case, we have performed an arginine → alanine alchemical mutation, which should satisfy the general criteria of applicability of the TI procedure. For further details, see the Supporting Information.
Preparation of RNA and protein samples
The SRSF1 RRM2 ORF corresponding to amino acids 107–203 was cloned in the pET24 expression vector. A GB1 tag was fused at the N-terminal extremity of the protein to increase its solubility and stability (11). The protein was overexpressed at 37°C in Escherichia coli BL21 (DE3) codon plus cells in minimal M9 medium containing 1 g/l 15NH4Cl and 4 g/l glucose. The protein was purified by two successive nickel affinity chromatography (QIAGEN) steps using an N-terminal 6x His tag, dialysed against NMR buffer (20 mM phosphate buffer at pH 5.5, 50 mM l-Glu, 50 mM l-Arg, 0.05% β-mercaptoethanol) and concentrated to 0.4 mM with a 10-kDa molecular mass cutoff Centricon device (Vivascience). The GB1 tag was kept for all NMR and ITC titrations performed in the presence of SRSF1 RRM2, as it was previously reported that its presence does not influence the protein interaction with RNA (11). The RNA oligonucleotide was purchased from Dharmacon, deprotected according to the manufacturer's instructions, lyophilised and resuspended in NMR buffer. The NMR titrations were performed in the NMR buffer at 40°C.
Isothermal titration calorimetry
ITC experiments were performed on a VP-ITC instrument (Microcal) calibrated according to the manufacturer's instructions. Protein and RNA samples were dialyzed against the NMR buffer. Concentrations of proteins and RNA were determined using optical-density absorbance at 280 and 260 nm, respectively. 20 μM of RNA was titrated with 400 μM of recombinant proteins by 40 injections of 6 μl every 5 min at 40°C. Raw data were integrated, normalized for the molar concentration and analyzed using Origin 7.0 software according to a 1:1 RNA:protein ratio binding model.
RESULTS
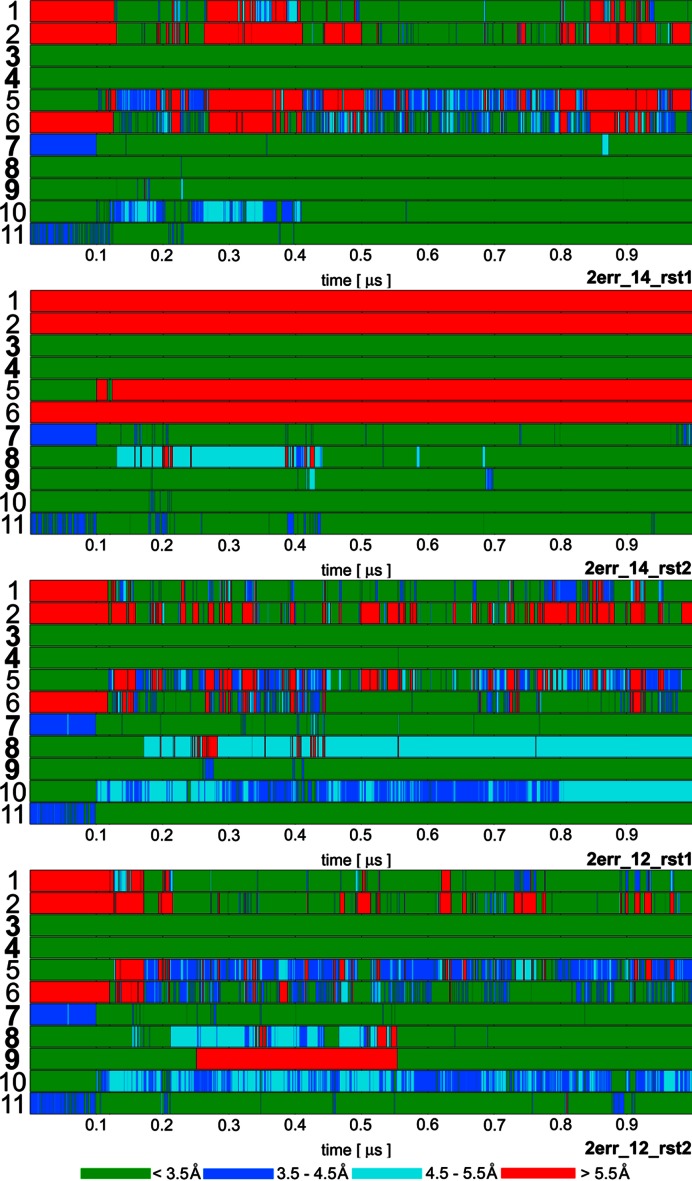
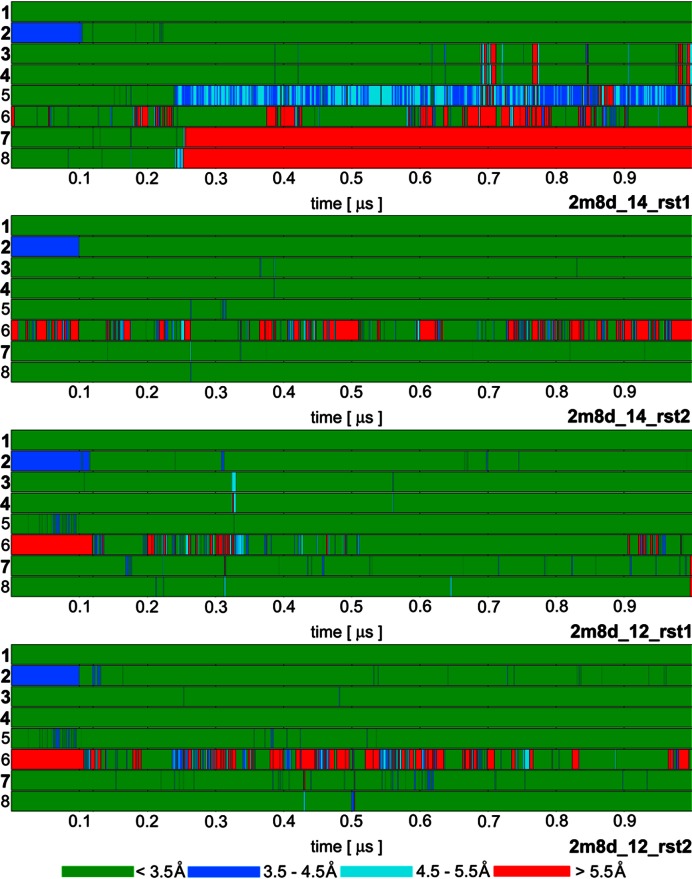
We have computed over 50 μs of MD simulations of the Fox-1 and SRSF1 protein/RNA complexes (Table 1). Multiple μs-scale trajectories were used to verify reproducibility of the results (25). Three different protein force fields were tested. Tables 2 and 3 compare the average intermolecular NOE violations in simulation ensembles with the experimental NMR ensemble of Fox-1 and SRSF1 complexes, respectively. Figures 2 and 3 summarize development of key protein–RNA hydrogen-bonds in four selected simulations of Fox-1 and SRSF1 complexes, respectively. Additional structural features (such as stacking) are commented in the text.
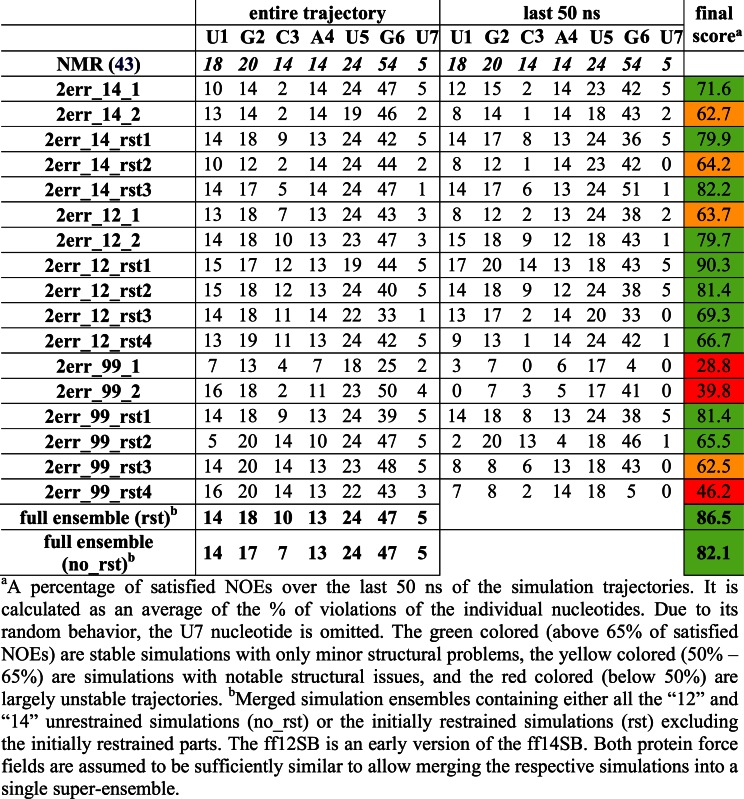
Table 2. Number of protein–RNA NOE distances that are satisfied in the simulations of the Fox-1 complex for the individual nucleotides (the number of the observed NOEs is given on the first line). Averaged values of weighted NOE distances (see Materials and Methods) calculated over the entire simulation trajectories and over the last 50 ns are used. Please see Supplementary Figures S5 and S6 for structure visualization of the NOE violations.
|
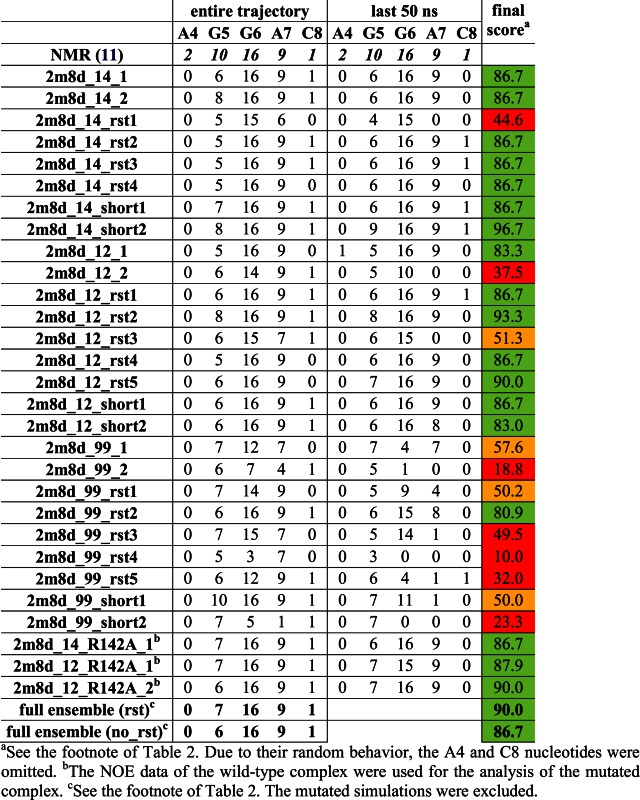
Table 3. Number of protein–RNA NOE distances that are satisfied in the simulations of the SRSF1 complex for the individual nucleotides (the number of the observed NOEs is given on the first line). Averaged values of weighted NOE distances (see Materials and Methods) calculated over the entire simulation trajectories and over the last 50 ns are used. Please see Supplementary Figure S7 for structure visualization of the NOE violations.
|
Figure 2.
Time development of heavy atom distances of specific intermolecular H-bond interactions in selected Fox-1 protein / RNA complex (PDB: 2err) simulations: 1. U1(N3)/Ser155(O); 2. U1(O2)/Asn151(ND2); 3. G2(N1)/Ile124(O); 4. G2(N2)/Ile124(O); 5. C3(N3)/Asn151(ND2); 6. C3(N4)/Ser155(O); 7. U5(N3)/Asn190(O); 8. U5(O2)/Thr192(N); 9. G6(N1)/Thr192(O); 10.G6(O6)/Arg118(sc); 11. G6(N7)/Arg118(sc). The H-bonds written in bold are present in the experimental NMR ensemble structures with over 90% occurrence. The H-bonds ‘1’ and ‘2’ are absent in the NMR ensemble but are often formed during the simulations. The ‘sc’ abbreviation for Arginine indicates any of the three side-chain nitrogen atoms potentially acting as donors in an H-bond. The bond angles were monitored to verify that short interatomic distances correspond to H-bonding but are not shown for space reasons. The remaining simulations are summarized in Supplementary Figure S4.
Figure 3.
Time development of heavy atom distances of specific intermolecular H-bond interactions in selected SRSF1 protein / RNA complex (PDB: 2m8d) simulations: 1. G5(N1)/Ala150(O); 2. G5(O6)/Ala150(N); 3. G6(N1)/Asp139(OD); 4. G6(N2)/Asp139(OD); 5. G6(O4')/Gln135(NE2); 6. G6(O6)/Arg142(sc); 7. A7(N6)/Asp136(OD); 8. A7(N1)/Ser133(OG). The H-bonds written in bold are present in the experimental NMR ensemble structures with over 90% occurrence. The H-bond ‘6’ is present in just one structure of the NMR ensemble but it is frequently observed in our simulations. The remaining simulations are summarized in Supplementary Figure S3.
Initial restraining stabilizes the subsequent unrestrained trajectories
Although visible structural deformations occurred in some of our individual trajectories, using multiple simulations we were capable to obtain sufficient data to characterize structural dynamics of the studied complexes (25). The simulations that were restrained during their initial 120 ns (see Materials and Methods) typically achieved better agreement with the experimental data in the subsequent unrestrained time portions (after 120 ns) than simulations using just the standard equilibration protocol (25). Several of the later simulations (Table 1) resulted in quick loss of key H-bonds and stacking interactions at the complex interface. When using only the standard equilibration protocol, 66% and 50% of the simulations of Fox-1 and SRSF1 complex, respectively, showed notable structural distortions of the protein/RNA interface. With the initial use of the NMR restraints, this failure rate was reduced down to 27% for Fox-1 and 40% for SRSF1 (Tables 2 and 3). The influence of initial restraints was more obvious in simulations of the Fox-1 structure (149 NOEs) than of the SRSF1 structure (38 NOEs). With fewer intermolecular NMR restraints, unrelated simulation factors (e.g. random sampling, force field errors) had greater influence on the simulation, somewhat obscuring the benefit of the initial restraining.
Comparison of the protein force fields
The ff14SB and ff12SB variants show visibly improved simulation behavior compared to the ff99SB. For the SRSF1 complex, this was evident from the NOE violations (Table 3) and the time development of two H-bonds (G6(N1)/Asp139(OD) and G6(N2)/Asp139(OD)—see Supplementary Figure S3, simulations 2m8d_99_rst1—2m8d_99_rst5). Also, the ff99SB has inferior description of phenylalanine and tyrosine side-chain dihedrals (25). It resulted in visible disruption of stacking interactions in both SRSF1 and Fox-1 systems (see below and Supporting Information). Curiously, the number of NOE violations was initially lower in some ff99SB simulations of the Fox-1 system. However, the number of violations was increasing as the ff99SB simulations progressed while the newer force field versions were much steadier over the time (Table 2).
Subsequent paragraphs describe the ff14SB and ff12SB simulation data. Both force fields are very similar (60) and are considered to have equivalent validity within the sampling achieved in our study. For each nucleotide, we first describe the protein/RNA interactions observed in the NMR ensemble and their simulation behavior. Afterwards, new interactions suggested by the MD simulations are discussed. The ff99SB data is given in the Supporting Information.
Fox-1 protein/RNA complex
The following paragraphs analyze interactions of the individual nucleotides of the Fox-1/RNA complex interface based on the initially restrained simulations of the system (see Table 1). However, a quite consistent picture would emerge also from the unrestrained simulations (Supporting Information). When comparing the computed and experimental structures, it is also important to consider the difference between the primary NMR data and the geometries of the ensemble of the refined NMR structures. None of the NMR ensemble models fully satisfy every NMR restraint (11,43).
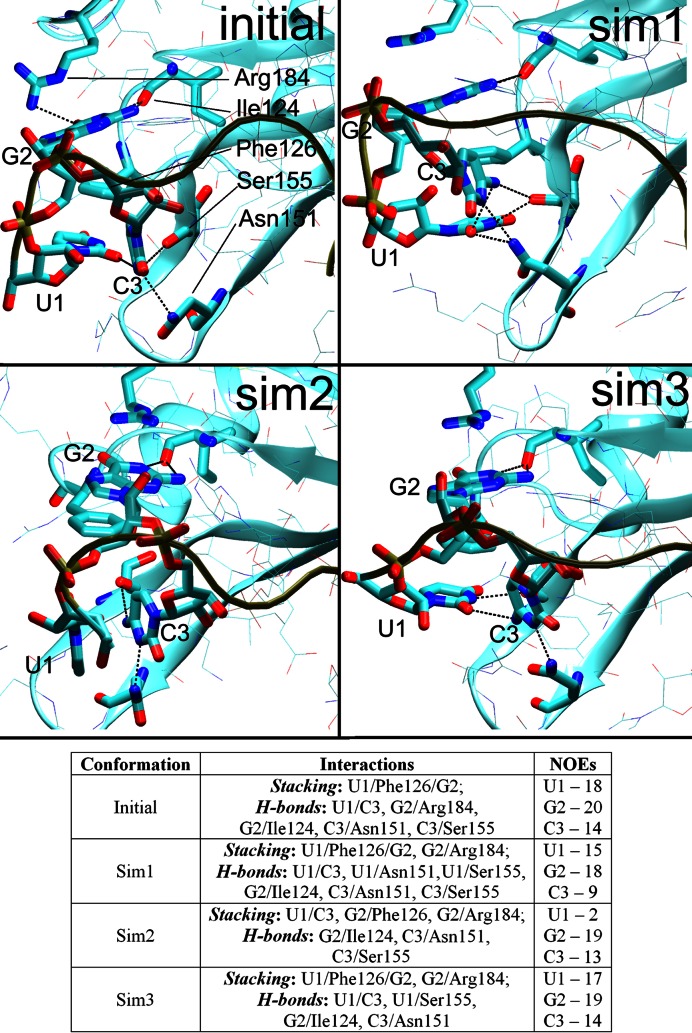
Rapidly shifting substates in the U1, G2, C3 and Phe126 hydrophobic pocket
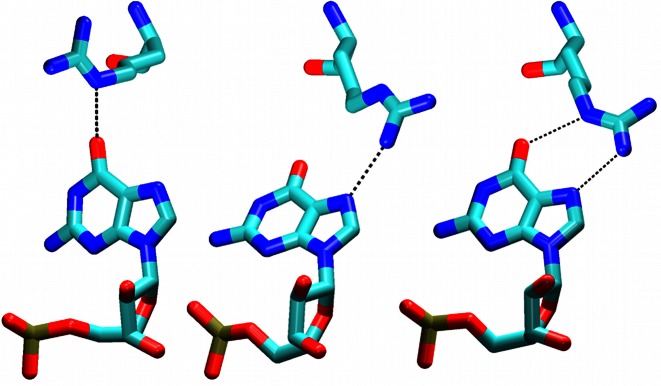
The listed aromatic residua form a hydrophobic pocket composed of U1/Phe126 (43% presence in the NMR ensemble) and G2/Phe126 (100% in NMR) stacks and C3/Phe126 overlap interaction (100% in NMR) (see Introduction and Figure 4). The pocket was well maintained in the simulations with some exceptions that are detailed below.
Figure 4.
The initial arrangement (the first NMR frame, top left) of the U1/G2/C3/Phe126 hydrophobic pocket and the three alternative conformations seen in the simulations during time periods where the C3 nucleotide was stably bound. The Sim1 conformation was the most common while the others were less frequent. The H-bonds are indicated by dotted lines between heavy atoms. The Table summarizes the stacking interactions, H-bonds, and the number of satisfied protein–RNA intermolecular NOE distances in the specific conformations. PDB files of representative structures can be found in Supporting Information.
MD predicts that the U1/G2/C3/Phe126 hydrophobic pocket exists as a rapidly shifting population of several substates. In addition to the ‘full’ U1/G2/C3/Phe126 substate (captured by NMR), there may also be significant substates G2/C3/Phe126 and U1/G2/Phe126 where either the U1 or C3 nucleotides are unbound (i.e. not interacting with the hydrophobic pocket). Distinguishing these substates in NMR would be technically difficult due to signal averaging and the lack of measurable NOE signals for the unbound states. Therefore, the MD prediction is not contradicting the experimental data and the observed simulation behavior may represent a real molecular motion of the hydrophobic pocket on a microsecond timescale. Still, the force field limitations must also be considered. In the simulations, the G2/Phe126 stack is stable while the U1 and C3 nucleotides seem to be dynamically competing for the binding site on a submicrosecond timescale. If so, the balance (relative populations) of distinct substates would be difficult to be accurately described with the simulations as even a small force field inaccuracy could result in biased population of the substates having free energy difference ∼0. Thus, we have not attempted to interpret the relative populations in quantitative sense.
The U1/Phe126 stack was essentially stable, except of few reversible disruptions. In many simulations, the U1 nucleotide formed two additional H-bonds that are not present in the NMR ensemble—U1(N3)/Ser155(O) and U1(O2)/Asn151(ND2) (H-bonds #1 and 2 in Figure 2, Supplementary Figure S8). These interactions cannot be ruled out by the primary NMR data. The NOE violations of U1 nucleotide occurred mostly as a result of the temporary flipping of its base away from the rest of the structure (namely, a.a. Phe126 and Arg153). The simulations predict the U1 nucleotide to be very flexible, which is in agreement with the NMR data (43).
The G2/Phe126 stack was fully stable with all force fields. It was further stabilized by permanent formation of G2/Arg184 stacking interaction in the simulations. In the NMR ensemble, this stack was present only in 33% of the structures, while 47% revealed a G2(O6)/Arg184 H-bond interaction instead (Supplementary Figure S9). Even though our simulations started from a frame with the H-bonding structure, the G2(O6)/Arg184 H-bond was entirely absent in both restrained and unrestrained simulation time portions. The simulations predicted larger degree of stacking in this area than the NMR ensemble. In good agreement with the involvement of the Arg184 side chain in a stacking interaction, our experimental data show that the chemical shift of the HE proton is shifted upfield to 6 ppm upon RNA binding due to the ring current of the guanine base. The G2(N1)/Ile124(O) and G2(N2)/Ile124(O) H-bonds (100% in NMR) were fully stable in simulations, as was the tSW (trans sugar edge/Watson–Crick) (79) G2/A4 intramolecular base pair.
The C3/Phe126 interaction was somewhat unstable in the simulations and the C3 nucleotide assumed diverse orientations towards the hydrophobic pocket, many of which resulted in NOE violations and loss of H-bonds. Still, in some simulations, (e.g. the 2err_12_rst2, 2err_14_rst1) it was stably positioned and the C3 native H-bond interactions were able to coexist with the above-noted additional U1 H-bonds (Figure 2) by forming a network of bifurcated H-bonds (Figure 4, top right). Strikingly, the C3 native H-bonds and position were fully maintained in one simulation (2err_99_rst2; Figure 4, bottom left), albeit at the cost of a permanent loss of the U1/Phe126 stack.
The simulations reveal a strain associated with the initial position of the C3 nucleotide and a difficulty to keep it in place. Nevertheless, we identified substantial trajectory portions where the C3 nucleotide was stably positioned in well-defined conformations (Figure 4, for overall population, see Supplementary Table S1). Conformation Sim1 was observed most frequently while Sim2 was seen in 2err_99_rst2 simulation and as a minor substate in the others. The Sim1 and Sim2 conformations had NOE violations for the C3 or U1 nucleotide, respectively, indicating that the simulations had trouble simultaneously balancing the interactions of these two nucleotides. Still, the simulations also showed a capability to temporarily return to an arrangement (Sim3) with almost no NOE violations for either nucleotide, indicating a reasonable conformational sampling.
The remaining Fox-1 complex nucleotides
A4
In the NMR ensemble, this nucleotide forms a G2/A4 intramolecular base pair but does not form any direct H-bonds with the protein. In simulations, the position of A4 was well maintained with minimal intermolecular NOE violations.
U5
This nucleotide is very well defined in the NMR ensemble by 24 intermolecular NOE restraints. Its base is stacked with the His120 side-chain ring (100% in the NMR) and there are two H-bonds—U5(N3)/Asn190(O) (100%) and U5(O2)/Thr192(N) (97%). The U5/His120 stacking interaction was fully stable in all simulations. The U5(O2)/Thr192(N) H-bond was usually stable, though it became temporarily or permanently water-mediated in some simulations. Curiously, the U5(N3)/Asn190(O) H-bond was somewhat unstable (with the heavy atom distance 3.5–4.0 Å) in the fully restrained parts (0–100 ns) of the simulations but it became perfectly stable after the intramolecular restraints were removed (Figure 2).
The Asn190 and Thr192 are both located at the C-end of the protein and are naturally quite dynamical in the simulations. The majority of NOE violations of U5 were related to its interactions with this flexible segment of the protein. In simulations, the unstructured C-terminus chain often reversibly changed its internal conformation and some of those conformations were violating the NOE distances to the RNA.
G6
With 54 intermolecular NOE restraints, the G6 nucleotide is the best determined region of the protein–RNA interface and forms many interactions with the protein. In the NMR ensemble, there is a stacking interaction between Phe160 (100%) and the aliphatic part of the Arg194 side-chain (100%). This is supplemented by G6(N1)/Thr192(O) (100%) and G6(O6,N7)/Arg118 H-bond interactions. The later interaction is variable in the NMR ensemble. Specifically, a double H-bond state using Arg118(NH2)/G6(N7) and Arg118(NE)/G6(O6) atoms occurs 10-times, single Arg118(NH1)/G6(N7) H-bond once, and single Arg118(NE)/G6(O6) H-bond 14 times. Five structures lack any H-bond interaction.
The G6/Phe160 stack was fully stable in all simulations. The G6(N1)/Thr192(O) H-bond interaction was mostly stable, albeit it was occasionally lost due to the random dynamics of the protein C-terminus (Thr192 is a fifth residue from the end). In most simulations, the loss was only temporary and the H-bond was eventually restored. The prime source of NOE violations in simulations for G6 was again the naturally flexible C-terminus of the protein (residues 190–196) that, however, contributed to many signals in the NMR data. A second source of NOE violations were the G6 signals to the Phe158 and Ile149 side-chains.
A complicated simulation development occurred with the Arg118/G6 interaction which shows multiple binding options in the NMR ensemble (see above). In the restrained part of the simulations, we always evidenced the Arg118(NE)/G6(O6) single H-bond arrangement (by additional simulation tests we verified that this was not influenced by the starting structure). After the restraints were released, there was either a single Arg118(NH1)/G6(N7) H-bond or simultaneous Arg118(NH2)/G6(N7) and Arg118(NE)/G6(O6) H-bonds (Figure 5). Both arrangements could be seen within a single trajectory. All of the arrangements observed in our simulations were also found in the NMR ensemble.
Figure 5.
Fox-1 complex. The Arg118 side chain is forming H-bonds with the G6 base as either Arg118(NE)/G6(O6) (left), the Arg118(NH1)/G6(N7) (middle), or the Arg118(NH2)/G6(N7) and Arg118(NE)/G6(O6) interactions (right). The first arrangement is populated only in restrained parts of the simulations while the other two are populated in the unrestrained parts.
The simulations predicted that the Arg118–G6 interaction may consist of several dynamical competing micro-arrangements separated by a low energy barrier. Still, such dynamical interactions could contribute to stability of the protein/RNA complexes.
U7
The terminal nucleotide has merely five intermolecular NOEs in the NMR data and does not form sequence-specific interactions with the protein. In simulations, it was largely exposed to the solvent and randomly fluctuating.
SRSF1 protein/RNA complex
The overall behavior
The protein/RNA interface of SRSF1 complex is composed of only three nucleotides—G5, G6, and A7. Consequently, the 38 protein/RNA NOE upper bound distances were determined exclusively for these nucleotides, with the exception of two NOEs for A4 and one for U8. No intermolecular NOE could be detected for the rest of the RNA molecule (nucleotides 1–3) and the N-terminus of the protein (a.a. 106–115), which is positioned close to the RNA due to intra protein-protein contacts. The simulation behavior of these flexible segments is summarized in the Supporting Information. The protein–RNA interface was very stable in ff12SB and ff14SB simulations. The ff99SB simulations almost always led to a complete loss of the protein–RNA complex (Table 3). This was caused by an ff99SB-specific reorientation of the Asp139 side-chains which led to a gradual destabilization of the entire system. Subsequently, at the end of the ff99SB simulations, the native protein–RNA H-bond interactions were nearly always lost (Supplementary Figure S3) and NOE violations large (Table 3). The full description of the ff99SB simulations is in the Supporting Information.
The protein–RNA interface
G5
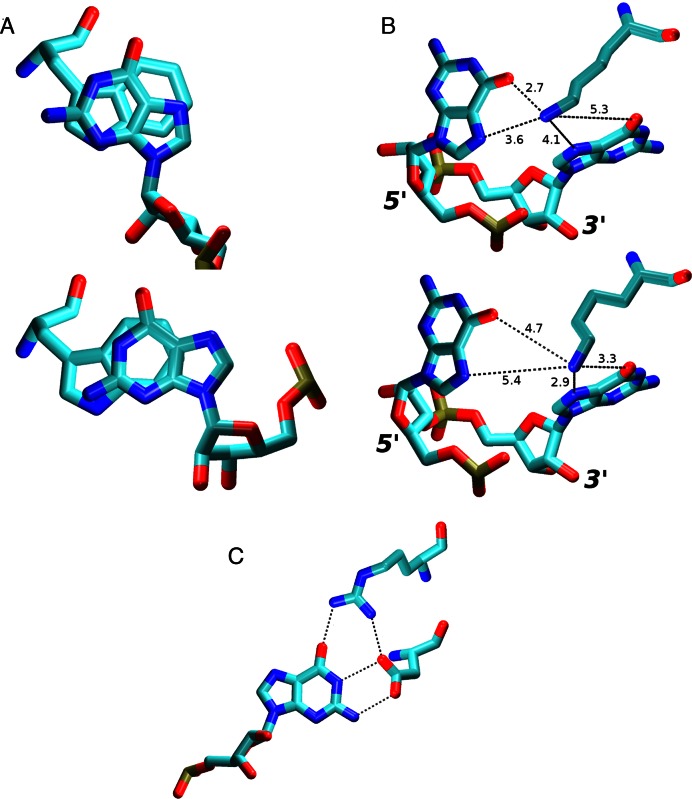
In the NMR ensemble, this nucleotide always forms H-bonds G5(N1)/Ala150(O) and G5(O6)/Ala150(N) and a base stacking interaction with the ring of Trp134. In simulations, the G5 interactions formed the most stable part of the entire protein–RNA interface. They were often maintained even in simulations where the rest of the protein–RNA interface was lost. The G5(N1)/Ala150(O) H-bond interaction was fully stable. The G5(O6)/Ala150(N) H-bond interaction was initially perturbed in the restrained parts of the simulations but then it was stable (Figure 3). Thus, both H-bonds were perfectly reproduced by the simulations. Despite the overall stability of this region, the G5 nucleotide still caused the largest number of NOE violations in the simulations. Specifically, all simulations revealed violations with Ser116. Being part of the flexible linker chain at the N-terminus of the protein, Ser116 is the first residue in the protein chain with intermolecular NOEs. However, in simulations, it permanently moved away from the G5 as a consequence of the linker chain dynamics explained in the Supporting Information. This behavior was avoided in only one of the simulations (2m8d_99_short1, see Table 3) with a truncated linker. Another source of NOE violations in the simulations was a slight alteration of the G5/Trp134 stacking conformation. Specifically, the overlap of the base and tryptophan side-chain aromatic rings changed compared to the NMR ensemble (Figure 6A).
Figure 6.
(A) Overlap of G5 and Trp134 aromatic rings in the NMR (top) and in the simulations (bottom). This change, while minor, usually resulted into at least one G5/Trp134 NOE distance violation greater than 1 Å. (B) In simulations of the SRSF1 complex, the Lys138 side chain fluctuated between G5 (top) and G6 (bottom) Hoogsteen base edges. The typical heavy atom distances are shown (in Å). (C) The Arg142 side chain was often simultaneously interacting with G6 and Asp139 residues in the SRSF1 simulations, effectively increasing the protein's specificity for the guanine in this position by simultaneously recognizing the entire Watson-Crick edge of the base in a highly specific way.
G6
The G6 nucleotide has the largest number of intermolecular NOE upper bound distances. The NMR ensemble reveals G6(N1)/Asp139(OD), G6(N2)/Asp139(OD), and G6(O4')/Gln135(NE2) H-bond interactions. The G6 base is also stacked with the Gln135 side-chain carbon atoms and the edge of the Trp134 aromatic ring. All of these interactions were fully stable in simulations.
Interaction between Arg117 and G5/G6 bases
In the NMR ensemble, the Arg117 side-chain is forming an H-bond interaction with G6 (8 frames), G5 (2 frames), or is unbound (6 frames). There is not a direct evidence for this interaction based on the primary NMR data. Rather, its presence is being inferred from the existence of nearby Arg118/Tyr149 interaction (confirmed by NOE signals). These two arginine side-chains were previously shown to be important for SRSF1 interaction with RNA (12). The G5/Arg117 interaction was stable only in the fully restrained parts of our simulations. It was lost once the intramolecular restraints were removed, even in simulations where the Arg118/Tyr149 interaction was fully stable. It should be noted that the Arg117 amino acid is a part of the flexible protein linker chain (see above and Supporting Information), a region which is subjected to a considerable sampling uncertainty and potential force field bias. Still, the simulations with truncated linker chain (Table 1) showed identical behavior.
Interaction between Lys138 and G5/G6 bases
In the NMR ensemble, the Lys138 side-chain is H-bonded with G6(O6) atom (14 frames), G6(N7) atom (1 frame) or is unbound (1 frame). It interacted with the G6(N7) atom during the restrained parts of our simulations. Afterwards, in addition to the G6(N7) atom, it was also sampling the G6(O6), G5(N7) and G5(O6) atoms (not shown in Figure 3). The Lys138 was capable to rapidly switch its interaction between the G5 and G6 bases on a nanosecond timescale scale (Figure 6B). Typically, there was a direct H-bond interaction between Lys138 and one of the bases while the interaction with the second base was water-mediated. Thus, the protein can simultaneously discriminate for guanine as both fifth and sixth base of the RNA using a single amino acid residue.
Interaction between G6 base and Arg142
A formation of new G6(O6)/Arg142(sc) H-bond interaction between the G6 base and Arg142 side-chain was universally observed in the simulations (Figure 3). This interaction is present in only a single frame of the NMR ensemble. In all others, the Arg142 side-chain is exposed to the solvent, being far away from the RNA. There is no conclusive NMR data about this residue. In our simulations, it showed cooperation with the nearby Asp139 side-chain by establishing a partial Asp139/Arg142 salt bridge (Figure 6C). Stability of the G6(O6)/Arg142(sc) interaction correlated with the presence of the Asp139 and, thus, the stability of the G6/Asp139 interaction. While the formation of this interaction might be a simulation artifact, it is also noteworthy that the Arg142 residue is evolutionary conserved (11), suggesting a potential specific role of its side chain. To further clarify the role of this residue, we have conducted both experimental and simulation measurements of the R142A mutant complex (see below).
A7
In the NMR ensemble, the A7 nucleotide is always forming an A7(N6)/Asp136(OD) H-bond interaction and a base stacking with the Gln135 side-chain. Additionally, one third of the NMR ensemble suggests an A7(N1)/Ser133(OG) H-bond. In simulations, the interactions and position of the A7 were usually fully stable with minimal intermolecular NOE violations. However, in several trajectories, the entire nucleotide suddenly bulged away into solvent, temporarily breaking all of its native protein/RNA interactions. In most cases, it then moved back on a nanosecond timescale and restored its interactions. However, the process was irreversible in several simulations—namely with the ff99SB force field, but also to certain extent with the other force fields (see Figure 3 and Supplementary Figure S3, 2m8d_14_rst1 and 2m8d_12_rst3 simulations). In these simulations, the A7 nucleotide fluctuated in the solvent or stacked with G6.
Experiments and simulations with mutated Arg142 residue of SRFS1
The NMR allows highly accurate determination of RRM–RNA structures, but certain structural elements cannot be observed. For example, the MD simulations predict formation of the Arg142/G6 interaction which is missing from the NMR ensemble and can be neither proved nor disproved based on the NMR data. To examine the possible role of the Arg142 side chain in the recognition of the G6 nucleotide (Figure 6C), we have prepared SRSF1 protein containing the R142A mutation and measured the change of its affinity to the RNA by NMR and ITC experiments. We also conducted MD simulations and TI free energy calculations of the mutated system. For details of the experimental and computational techniques used, see the Methods.
R142A mutation in SRSF1
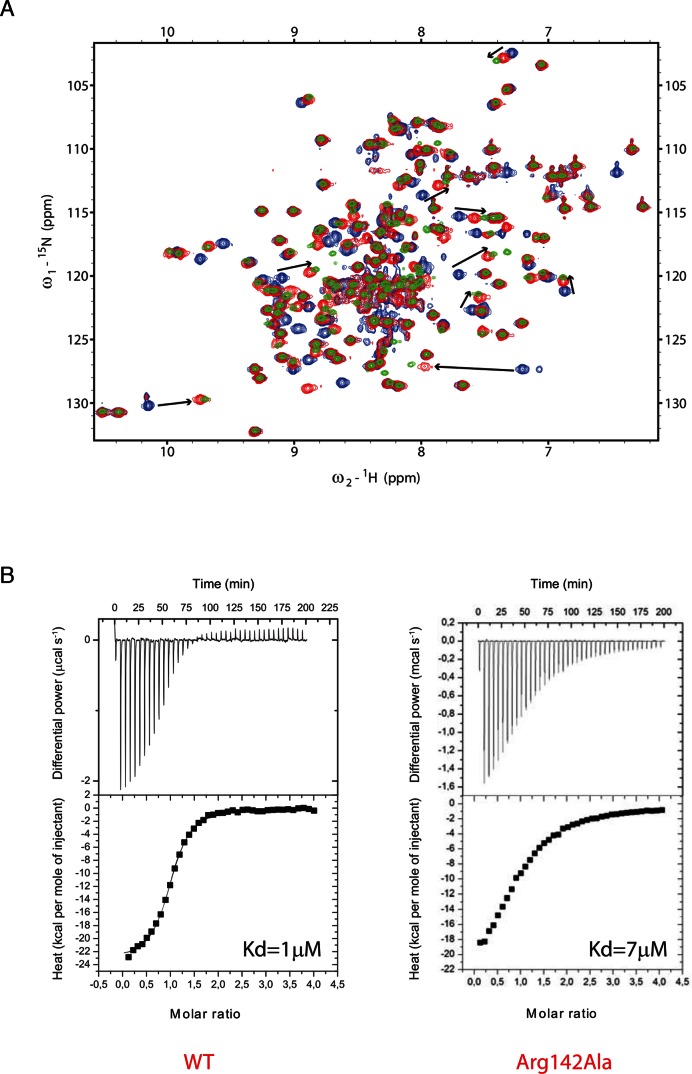
Simulation – By interacting with the G6(O6) atom, the Arg142 could be increasing the specificity of the RNA recognition by the SRSF1 protein. To test the effect of its absence on the simulation stability of the complex, we have replaced it with alanine. Despite extensive simulations (7 μs on aggregate), we have observed no structural effects in the complex structure that would be attributable to this mutation. There was no increase in NOE violations in the simulations (Table 3). There were just few temporary disruptions of the G6/Asp139 H-bond interactions (Supplementary Figure S10) and slightly increased dynamics of the G6 base. Therefore, the simulations suggested that the system was able to structurally tolerate this mutation without altering its RNA binding mode. However, the crucial G6/Asp139 interaction may still be weakened in absence of the Arg142 in the thermodynamics sense. We have thus performed thermodynamics integration (76,80) (TI) free energy calculation (see the Methods) to compute the free energy penalty of the R142A mutation on the complex stability. Our initial calculation set was 50 ns long for each λ window (Table 1) and predicted 1.1 ± 0.6 kcal/mol free energy penalization of the protein/RNA complex stability due to the R142A substitution (Supplementary Figure S11). To verify reproducibility and convergence of this result, we have conducted another set of simulations with 200 ns long λ windows. This second set of calculations predicted a very similar value of 1.1 ± 0.5 kcal/mol. Thus, we suggest that the result of our calculations is in fact quite well converged. The consistency of the two computations with different windows is a primary indicator of the convergence and it appears that a sufficient conformational sampling describing the change was achieved.
Experiment – The Arg142/G6 interaction could not be observed experimentally by NMR because the distance between the two closest observable hydrogens (G6(H1) and Arg142(HE)) is longer than 6 Å. To investigate whether the Arg142 side chain is indeed involved in this interaction, we mutated the residue to an alanine (R142A) and used NMR and ITC to investigate the effect on SRSF1 RRM2 interaction with RNA. We used the 5′-AGGAC-3′ sequence, which contains the GGA motif recognized by SRSF1 RRM2 (G6 corresponds to the third position of the studied sequence). Upon NMR titration, we could observe large chemical shift perturbations in the presence of the SRSF1 RRM2 R142A mutant, very similar to those observed with the WT protein, although a bit shorter (Figure 7A). This result shows a decrease in affinity of the R142A protein variant for RNA. To quantify this difference in affinity, we performed ITC titrations of SRSF1 RRM2 WT and R142A proteins in the presence of the same RNA molecule. As shown in the Figure 7B, a Kd value of 7 μM was determined in the presence of the mutated protein while 1 μM was measured with the WT protein. This corresponds to a significant decrease in affinity (by a factor 7, i.e. ∼1.2 kcal/mol). This effect could be explained by the interaction of SRSF1 RRM2 Arg142 side chain with the guanine G6 and/or the stabilization of Asp139 side chain, which is also involved in the RNA binding (Figure 6C).
Figure 7.
(A) NMR titrations of the 15N-labeled GB1-SRSF1 RRM2 WT and R142A proteins with the unlabeled 5′-AGGAC-3′ RNA. The peaks corresponding to the free WT protein are colored blue. The 1:1 RNA-bound proteins (with WT or mutant protein) are colored green and red, respectively. The differences in chemical shift perturbations observed upon RNA binding are indicated by black arrows. (B) ITC data recorded with SRSF1 RRM2 WT and R142A proteins in the presence of the 5′-AGGAC-3′ RNA. The estimated Kd values are shown.
DISCUSSION
We have carried out over 50 μs of standard MD simulations of the Fox-1 RRM and SRSF1 RRM2 protein/RNA complexes, followed by one thermodynamics integration calculation (over 13 μs on aggregate) and two NMR and ITC measurements. We show that MD simulations can be efficiently used to supplement the data obtained by NMR spectroscopy. Although NMR allows the determination of high-precision RRM–RNA structures, some structural elements cannot be observed. These include involvement of protein side chains with hydrogens located at more than 6Å from the RNA molecule and many highly dynamical interactions. Interactions that are dynamical in solution would be difficult to capture even by X-ray crystallography, which probably would reveal a static structure selecting one of the possible conformations. Thus, explicit solvent atomistic MD simulations can bring additional information and help to refine the picture obtained by the NMR experiments.
The RRM complex simulations are sufficiently stable
Both the Fox-1 and SRSF1 complexes were largely stable in the simulations, which is not always happening in simulations of protein–RNA complexes (25). This reflects the excellent quality of the experimental structures and a reasonable performance of the latest force fields (58,60) for this type of protein/RNA interface. Still, it is fair to say that perfect agreement between the simulation and the experiment cannot and should not be realistically expected. The current generation of force fields uses major approximations such as fixed-point charges, van der Waals spheres, harmonic potentials, etc. The basic force field approximations are well visualized by sizable disagreements with benchmark quantum-chemical computations (81). The simulations can be affected also by other approximations such as periodic boundary conditions and rather small simulation boxes (78,82,83). However, the experimental methods also have their genuine error margins. Thus, when disregarding few unstable trajectories, we conclude that the present RRM–RNA complexes are very well described by the simulation technique and MD is a viable tool to complement the experiments.
Initial use of NMR restraints helps to stabilize the simulations
We show that the use of experimental NMR NOEs-based restraints in the early stages of the simulations (first 120 ns in our case) leads to more stable simulations. Note that when experimental structures are used as start for MD simulation, there can be many ‘high-energy hotspots’ in the initial system. These hotspots arise due to combined errors of the experimental method and the inaccuracies of the simulation force field (25). The use of NMR restraints in the beginning of the simulation appears to smoothly handle high-energy hotspots of the initial system, i.e., it allows to sufficiently relax the structures without excessively departing from the NMR ensemble. In essence, it allows us to seamlessly bridge the world of NMR into the world of explicit solvent MD simulations. The subsequent unbiased simulations are then less affected by random unphysical simulation events at the beginning of the simulations. If available, we highly recommend the initial utilization of experimental NMR restraints in all protein/RNA simulations in explicit solvent. Even in cases where they ultimately would not lead to better stabilization of the complex, the fully restrained simulations could still provide interesting information about the complex, and about the NMR and computational methodologies. When the simulation struggle to simultaneously satisfy all the restraints and observed interactions, it may be indication of either presence of dynamically competing substates or force field imbalances. The benefit of initial use of the NMR restraints may depend on the number of such intermolecular restraints and complexity of the protein/RNA interface. For example, the Fox-1 complex which had a large protein/RNA interface, was more stabilized by the initial restraining than the SRSF1 complex which had a smaller interface with only 38 intermolecular restraints (Table 2 and 3). Using the restraints in the initial part of the simulations does not add any bias to the subsequent, unrestrained parts of the simulations. The temporary use of the restraints merely settles the initial simulation behavior and reduces likelihood of disruptive events due to structural conflicts not eliminated by the standard equilibration. The bias of the restraints fades away once they are switched off. However, note that all MD simulations are inherently biased by the choice of the starting structure and this bias is not reduced by the initial use of the NOE restraints (25).
Multiple μs-scale simulations are required
Our results illustrate large influence of random sampling (stochasticity) of the simulations, as equivalent trajectories often produce visibly different results. This confirms that multiple μs-scale trajectories are an imperative minimal requirement in simulation studies of protein–RNA complexes (25). The use of either series of shorter simulations or of only one long simulation could easily produce false results, as explicitly demonstrated here. We are obviously far from claiming that our present results are quantitatively converged, but they are sufficient to identify a typical simulation behavior of both studied complexes. We obviously do not rule out that some other protein–RNA complexes may require even more expanded sampling.
Aggregate trajectories show reduction of NOE violations
As suggested long time ago by others (84), when using aggregate trajectories created by merging unrestrained parts of all initially restrained ff12SB and ff14SB trajectories (6.2 μs and 7.9 μs for Fox-1 and SRSF1 systems, respectively), the NOE violations were reduced compared to most of the individual trajectories (cf. the last lines of Tables 2 and 3). This indirectly suggests that the RRM–RNA complexes are intrinsically dynamical, utilize dynamical interactions for the recognition and cannot be fully represented by single static structures. This may also be the reason why some interactions are perturbed in the fully restrained parts of our simulations but are re-established once the restraints are lifted.
The sampling is the main limitation for direct comparison of NMR with MD
While the core of the protein–RNA interfaces was described very well in the simulations, we have noted that a greater number of simulation NOE violations occurred for the peripheral regions of the protein–RNA interface. For example, nucleotide 7 in Fox-1 system and nucleotides 4 and 8 in SRSF1 system showed entirely random behavior and NOE violations (Tables 2 and 3). Similar issue was seen with the flexible C-terminal part of Fox-1 RRM. For these flexible regions, we obtained broad spectrum of behaviors ranging from completely stable to largely unstable (in terms of NOE violations) regardless of the protein force field selection. While this can be interpreted as a poor simulation performance, it is important to consider the fundamental timescale differences when interpreting the NMR data in context of the MD simulations. Namely, the spectroscopy signal is often collected over many hours, with the final values representing an ensemble average computed over time and all the biomolecules in the sample tube. On the other hand, the simulations work with comparatively shorter timescales and with a single molecule. We suggest that the simulation dynamics of the flexible segments is qualitatively consistent with the experimental findings but that the sampling is not complete. This leads to simulation NOE violations because some conformational states present in the experiment are missing from the simulation ensemble or because the sizes of their populations are not identical. At the same time, we can see structural details in the simulation with a time resolution inaccessible for the experimental methods.
In the simulations of the Fox-1 and SRSF1 complexes, this issue was not too serious as most of their protein/RNA interface involved segments with clearly defined conformation. However, there are many known RRM systems where the protein/RNA interaction is largely facilitated by flexible chain ends (2). Classical MD simulations of such systems may be exceptionally challenging from the point of view of the sampling of the conformational space. Selective use of NMR restraints or enhanced-sampling methods may be necessary to successfully study these systems, although such approaches have their own sets of limitations (19). A partial solution is to merge the individual simulations into a single super-trajectory prior to the NOE violation analysis (see above). The NOE distance averaging then reduces the random NOE violations caused by insufficient sampling of individual simulations while still displaying systematic violations caused by potential force field errors.
The ff14/12SB protein force fields are superior to ff99SB
The simulations showed universally better performance when using the ff14SB or ff12SB force fields for the protein (60). The simulations using the older ff99SB force field, while not terribly bad, were always less stable. In particular, the tyrosine and phenylalanine side-chains are known to be poorly described with the ff99SB (25). The stacking interactions involving these residues were often disrupted in the ff99SB simulations of both systems. We also observed ff99SB-specific aspartate side-chain flip that sometimes led to complete loss of the protein/RNA interface in the SRSF1 complex.
Curiously, the ff99SB gave somewhat better performance for the Fox-1 system in the initial stages of the simulation but the system would usually degrade later on. We suggest that this observation can be explained in the following way. The intricate protein–RNA interface is rather challenging for the force field description and none of the existing force fields is perfect (19). There are many contributions that need to be balanced simultaneously and their not fully perfect description then results in a mutual struggle between various forces. In the ff99SB simulations of the Fox-1 system, the ff99SB performance could initially appear better simply because this protein force field has simpler dihedral parametrization compared to the new versions. This initially allows the system to more easily (kinetically) resolve the conflicting interactions at the protein–RNA interface, however, the ff99SB weaknesses are becoming visible later on, leading to progressive distortions of the simulated systems. The later parametrizations (60) need more time to settle down the basic equilibration but allow then more reliable simulations. This behavior again illustrates the necessity for long simulation timescales as shorter trajectories would give a misleading picture of the protein force field performance.
Regarding the protein–RNA interface, the ff12SB and ff14SB protein force fields appear to produce equivalent results. We did observe different behavior of the flexible protein chain ends, however, we suggest that their variable behavior (and different amounts of NOE violations) in the individual simulations rather reflects the non-converged sampling. The RNA part of the system was described by the current default AMBER ff99bsc0χOL3 (54–58) RNA force field which appears to give satisfactory results for the present systems.
Protein–RNA interfaces may include intrinsically dynamical interactions that are difficult to be captured by experiments but are identified by MD simulations
We have noted several instances where parts of the protein/RNA interface do not appear as single defined structures in the simulations. Instead, they consist of series of distinct micro-arrangements that compete with each other on a submicrosecond timescale while still remaining in good agreement with the primary experimental data. Such interactions could be challenging for many experimental methods, namely X-ray crystallography, which would have to represent the binding either by a single structure, or by a disordered binding. For example, in the Fox-1 complex simulations, the interaction between Arg118 and G6 was represented by three distinct conformations, all seen within a single simulation. The U1 and C3 nucleotides in the Fox-1 hydrophobic pocket were rapidly competing for binding with the Phe126 side-chain. The Lys138 side chain was alternately interacting with G5 or G6 base. Time-averaged or ensemble-averaged structure determination experiments can give an incomplete description of such recognition patterns, so their occurrence and significance in biomolecular complexes may be in general underestimated. With theoretically infinite time resolution, the simulation technique is an effective tool for uncovering the structure averaging and decomposing it into the actual real-time conformers. We obviously do not claim that the force fields are always accurate enough to reliably capture such dynamical recognition patterns and the exact population of the competing micro-arrangements. However, the simulations can give a strong indication of existence of such binding modes, which are essentially inaccessible to the experimental methods.
The MD simulations predicted an important role of Arg142 at the interface of the SRSF1 complex, which was then confirmed by experiments
The simulations provided a prediction that we tried to verify experimentally. Namely, we predicted an unanticipated involvement of Arg142 side-chain in the protein/RNA interface of the SRSF1 system where it recognized the G6 nucleotide in cooperation with Asp139. Changes in the stability of Fox-1 and SRSF1 protein/RNA complexes (in terms of Gibbs free energy differences of complex formation) as a result of various residue specific mutations are well documented in experimental works (11,43). However, the R142A mutation in the SRSF1 protein was never studied before. The simulation prediction was then confirmed experimentally, as the ITC measured 1.2 kcal/mol free energy loss upon complex formation of the R142A mutant, in excellent agreement with our TI free energy prediction of 1.1 kcal/mol.
MD-adapted structure ensemble
MD simulations give an alternative representation of the studied protein/RNA complexes. Therefore, we propose a protocol for an ‘MD-adapted structure ensemble’ that would combine the NMR and simulation data. We use the aggregate simulation trajectories (cf. the last lines of Tables 2 and 3) and from each select 10% of frames with fewest NOE violations. This group of frames is then divided into 20 clusters based on the RMSd of the complex (see Methods) and a representative structure of each cluster is computed. In this way, we obtain sets of atomic coordinates (deposited as PDB files in the Supporting Information) that capture the flexibility (Supplementary Figure S12) and the various new interactions and alternative conformers suggested by MD simulations while still retaining the highest possible level of agreement with the primary NMR data (Supplementary Table S2). For example, the Fox-1 MD-adapted structure ensemble shows the U1/C3 competitive binding to the hydrophobic pocket and the different binding modes between Arg118 side chain and the G6 nucleotide. The SRSF1 MD-adapted structure ensemble captures the previously unknown G6/Arg142 interaction and the Lys138 flexible recognition mode of the G5 and G6 nucleotides. Despite high quality of the experimental structures, these structural details are not readily available in the original NMR ensembles due to technical reasons such as NOE signal averaging or lack of observable hydrogens.
CONCLUSION
MD simulations of RRM complexes can complement and expand the experimental studies and vice-versa. With strict consideration of all the limits of the method, it is possible to achieve a very good agreement with the experiment and identify features that are not apparent from the experiment. The MD simulations are especially useful when dealing with protein–RNA complexes that cannot be fully represented by single static structures. We suggest that the studied RRM–RNA complexes are examples of such interaction patterns that in addition can be common in the astonishingly variable world of protein/RNA complexes. We consider the prediction of dynamical but yet specific interactions at the protein–RNA interface as the most important message of our work. Dynamical interactions at the protein/RNA interfaces offer an interesting type of sequence-dependent molecular recognition, allowing to read multiple residues in fairly simple recognition patterns and fine-tuning of the specificity. Due to the limitations of experimental techniques, MD simulations represent a viable tool to identify such interactions.
Supplementary Material
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Czech Science Foundation [P305/12/G034]; Project CEITEC 2020 [LQ1601] with financial support from the Ministry of Education, Youth and Sports of the Czech Republic under the National Sustainability Programme II; Praemium Academiae (to J.S.); Access to storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the programme ‘Projects of Large Infrastructure for Research, Development, and Innovations’ [LM2010005]; The simulations were done exclusively using equipment funded by the CEITEC project; NCCR RNA and Disease funded by the Swiss National Science Foundation; Fondation Suisse de Recherche sur les Maladies Musculaires (to F.A. and A.C.). Funding for open access charge: The open access publication charge for this paper has been waived by Oxford University Press - NAR Editorial Board members are entitled to one free paper per year in recognition of their work on behalf of the journal.
Conflict of interest statement. None declared.
REFERENCES
- 1.Venter J.C., Adams M.D., Myers E.W., Li P.W., Mural R.J., Sutton G.G., Smith H.O., Yandell M., Evans C.A., Holt R.A., et al. The sequence of the human genome. Science. 2001;291:1304–1351. doi: 10.1126/science.1058040. [DOI] [PubMed] [Google Scholar]
- 2.Daubner G.M., Cléry A., Allain F.H.T. RRM–RNA recognition: NMR or crystallography…and new findings. Curr. Opin. Struct. Biol. 2013;23:100–108. doi: 10.1016/j.sbi.2012.11.006. [DOI] [PubMed] [Google Scholar]
- 3.Muto Y., Yokoyama S. Structural insight into RNA recognition motifs: versatile molecular lego building blocks for biological systems. Wiley Interdiscip. Rev.: RNA. 2012;3:229–246. doi: 10.1002/wrna.1107. [DOI] [PubMed] [Google Scholar]
- 4.Kielkopf C.L., Lücke S., Green M.R. U2AF homology motifs: protein recognition in the RRM world. Genes Dev. 2004;18:1513–1526. doi: 10.1101/gad.1206204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cléry A., Blatter M., Allain F.H.T. RNA recognition motifs: boring? Not quite. Curr. Opin. Struct. Biol. 2008;18:290–298. doi: 10.1016/j.sbi.2008.04.002. [DOI] [PubMed] [Google Scholar]
- 6.Burd C.G., Dreyfuss G. Conserved structures and diversity of functions of RNA-binding proteins. Science. 1994;265:615–621. doi: 10.1126/science.8036511. [DOI] [PubMed] [Google Scholar]
- 7.Afroz T., Cienikova Z., Cléry A., Allain F.H.T. One, two, three, four! How multiple RRMs read the genome sequence. In: Woodson SA, Allain FHT, editors. Methods Enzymol. Vol. 558. Academic Press; 2015. pp. 235–278. [DOI] [PubMed] [Google Scholar]
- 8.Mazza C., Segref A., Mattaj I.W., Cusack S. Large-scale induced fit recognition of an m(7)GpppG cap analogue by the human nuclear cap-binding complex. EMBO J. 2002;21:5548–5557. doi: 10.1093/emboj/cdf538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Johansson C., Finger L.D., Trantirek L., Mueller T.D., Kim S., Laird-Offringa I.A., Feigon J. Solution structure of the complex formed by the two N-terminal RNA-binding domains of nucleolin and a pre-rRNA target. J. Mol. Biol. 2004;337:799–816. doi: 10.1016/j.jmb.2004.01.056. [DOI] [PubMed] [Google Scholar]
- 10.Allain F.H.T., Bouvet P., Dieckmann T., Feigon J. Molecular basis of sequence-specific recognition of pre-ribosomal RNA by nucleolin. EMBO J. 2000;19:6870–6881. doi: 10.1093/emboj/19.24.6870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cléry A., Sinha R., Anczuków O., Corrionero A., Moursy A., Daubner G.M., Valcárcel J., Krainer A.R., Allain F.H.-T. Isolated pseudo–RNA-recognition motifs of SR proteins can regulate splicing using a noncanonical mode of RNA recognition. Proc. Natl. Acad. Sci. U.S.A. 2013;110:E2802–E2811. doi: 10.1073/pnas.1303445110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tintaru A.M., Hautbergue G.M., Hounslow A.M., Hung M.-L., Lian L.-Y., Craven C.J., Wilson S.A. Structural and functional analysis of RNA and TAP binding to SF2/ASF. EMBO Rep. 2007;8:756–762. doi: 10.1038/sj.embor.7401031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dominguez C., Fisette J.F., Chabot B., Allain F.H.T. Structural basis of G-tract recognition and encaging by hnRNP F quasi-RRMs. Nat. Struct. Mol. Biol. 2010;17:853–861. doi: 10.1038/nsmb.1814. [DOI] [PubMed] [Google Scholar]
- 14.Nagata T., Suzuki S., Endo R., Shirouzu M., Terada T., Inoue M., Kigawa T., Kobayashi N., Güntert P., Tanaka A., et al. The RRM domain of poly(A)-specific ribonuclease has a noncanonical binding site for mRNA cap analog recognition. Nucleic Acids Res. 2008;36:4754–4767. doi: 10.1093/nar/gkn458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Oubridge C., Ito N., Evans P.R., Teo C.H., Nagai K. Crystal-structure at 1.92 angstrom resolution of the RNA-binding domain of the U1A spliceosomal protein complexed with an RNA Hhirpin. Nature. 1994;372:432–438. doi: 10.1038/372432a0. [DOI] [PubMed] [Google Scholar]
- 16.Oberstrass F.C., Auweter S.D., Erat M., Hargous Y., Henning A., Wenter P., Reymond L., Amir-Ahmady B., Pitsch S., Black D.L., et al. Structure of PTB bound to RNA: specific binding and implications for splicing regulation. Science. 2005;309:2054–2057. doi: 10.1126/science.1114066. [DOI] [PubMed] [Google Scholar]
- 17.Tsuda K., Kuwasako K., Takahashi M., Someya T., Inoue M., Terada T., Kobayashi N., Shirouzu M., Kigawa T., Tanaka A., et al. Structural basis for the sequence-specific RNA-recognition mechanism of human CUG-BP1 RRM3. Nucleic Acids Res. 2009;37:5151–5166. doi: 10.1093/nar/gkp546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cléry A., Jayne S., Benderska N., Dominguez C., Stamm S., Allain F.H.T. Molecular basis of purine-rich RNA recognition by the human SR-like protein Tra2-β1. Nat. Struct. Mol. Biol. 2011;18:443–450. doi: 10.1038/nsmb.2001. [DOI] [PubMed] [Google Scholar]
- 19.Šponer J., Banáš P., Jurečka P., Zgarbová M., Kührová P., Havrila M., Krepl M., Stadlbauer P., Otyepka M. Molecular dynamics simulations of nucleic acids. From tetranucleotides to the ribosome. J. Phys. Chem. Lett. 2014;5:1771–1782. doi: 10.1021/jz500557y. [DOI] [PubMed] [Google Scholar]
- 20.Reyes C.M., Kollman P.A. Structure and thermodynamics of RNA-protein binding: using molecular dynamics and free energy analyses to calculate the free energies of binding and conformational change. J. Mol. Biol. 2000;297:1145–1158. doi: 10.1006/jmbi.2000.3629. [DOI] [PubMed] [Google Scholar]
- 21.Blakaj D.M., McConnell K.J., Beveridge D.L., Baranger A.M. Molecular dynamics and thermodynamics of protein–RNA interactions: mutation of a conserved aromatic residue modifies stacking interactions and structural adaptation in the U1A-stem Loop 2 RNA complex. J. Am. Chem. Soc. 2001;123:2548–2551. doi: 10.1021/ja005538j. [DOI] [PubMed] [Google Scholar]
- 22.Law M.J., Linde M.E., Chambers E.J., Oubridge C., Katsamba P.S., Nilsson L., Haworth I.S., Laird-Offringa I.A. The role of positively charged amino acids and electrostatic interactions in the complex of U1A protein and U1 hairpin II RNA. Nucleic Acids Res. 2006;34:275–285. doi: 10.1093/nar/gkj436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kormos B.L., Pieniazek S.N., Beveridge D.L., Baranger A.M. U1A protein-stem loop 2 RNA recognition: prediction of structural differences from protein mutations. Biopolymers. 2011;95:591–606. doi: 10.1002/bip.21616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kurisaki I., Takayanagi M., Nagaoka M. Combined mechanism of conformational selection and induced fit in U1A–RNA molecular recognition. Biochemistry. 2014;53:3646–3657. doi: 10.1021/bi401708q. [DOI] [PubMed] [Google Scholar]
- 25.Krepl M., Havrila M., Stadlbauer P., Banas P., Otyepka M., Pasulka J., Stefl R., Sponer J. Can we execute stable microsecond-scale atomistic simulations of protein–RNA complexes? J. Chem. Theory Comput. 2015;11:1220–1243. doi: 10.1021/ct5008108. [DOI] [PubMed] [Google Scholar]
- 26.Guo J.X., Gmeiner W.H. Molecular dynamics simulation of the human U2B '' protein complex with U2 snRNA hairpin IV in aqueous solution. Biophys. J. 2001;81:630–642. doi: 10.1016/s0006-3495(01)75728-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schmid N., Zagrovic B., van Gunsteren W.F. Mechanism and thermodynamics of binding of the polypyrimidine tract binding protein to RNA. Biochemistry. 2007;46:6500–6512. doi: 10.1021/bi6026133. [DOI] [PubMed] [Google Scholar]
- 28.Clingman C.C., Deveau L.M., Hay S.A., Genga R.M., Shandilya S.M.D., Massi F., Ryder S.P. Allosteric inhibition of a stem cell RNA-binding protein by an intermediary metabolite. Elife. 2014;3:e02848. doi: 10.7554/eLife.02848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Schmid N., Eichenberger A.P., Choutko A., Riniker S., Winger M., Mark A.E., van Gunsteren W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. Biophys. Lett. 2011;40:843–856. doi: 10.1007/s00249-011-0700-9. [DOI] [PubMed] [Google Scholar]
- 30.Palazzesi F., Prakash M.K., Bonomi M., Barducci A. Accuracy of current all-atom force-fields in modeling protein disordered states. J. Chem. Theory Comput. 2015;11:2–7. doi: 10.1021/ct500718s. [DOI] [PubMed] [Google Scholar]
- 31.Beauchamp K.A., Lin Y.-S., Das R., Pande V.S. Are protein force fields getting better? A systematic benchmark on 524 diverse NMR measurements. J. Chem. Theory Comput. 2012;8:1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Georgoulia P.S., Glykos N.M. Using J-coupling constants for force field validation: application to hepta-alanine. J. Phys. Chem. B. 2011;115:15221–15227. doi: 10.1021/jp209597e. [DOI] [PubMed] [Google Scholar]
- 33.Aliev A.E., Courtier-Murias D. Experimental verification of force fields for molecular dynamics simulations using Gly-Pro-Gly-Gly. J. Phys. Chem. B. 2010;114:12358–12375. doi: 10.1021/jp101581h. [DOI] [PubMed] [Google Scholar]
- 34.Condon D.E., Kennedy S.D., Mort B.C., Kierzek R., Yildirim I., Turner D.H. Stacking in RNA: NMR of four tetramers benchmark molecular dynamics. J. Chem. Theory Comput. 2015;11:2729–2742. doi: 10.1021/ct501025q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bergonzo C., Henriksen N.M., Roe D.R., Swails J.M., Roitberg A.E., Cheatham T.E. Multidimensional replica exchange molecular dynamics yields a converged ensemble of an RNA tetranucleotide. J. Chem. Theory Comput. 2014;10:492–499. doi: 10.1021/ct400862k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Giambaşu G.M., York D.M., Case D.A. Structural fidelity and NMR relaxation analysis in a prototype RNA hairpin. RNA. 2015;21:963–974. doi: 10.1261/rna.047357.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Huang J., MacKerell A.D. CHARMM36 all-atom additive protein force field: validation vased on comparison to NMR data. J. Comput. Chem. 2013;34:2135–2145. doi: 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Li D.-W., Brüschweiler R. Protocol to make protein NMR structures amenable to stable long time scale molecular dynamics simulations. J. Chem. Theory Comput. 2014;10:1781–1787. doi: 10.1021/ct4010646. [DOI] [PubMed] [Google Scholar]
- 39.Lindorff-Larsen K., Piana S., Palmo K., Maragakis P., Klepeis J.L., Dror R.O., Shaw D.E. Improved side-chain torsion potentials for the amber ff99SB protein force field. Proteins: Struct., Funct., Bioinf. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hansen N., Heller F., Schmid N., van Gunsteren W. Time-averaged order parameter restraints in molecular dynamics simulations. J. Biomol. NMR. 2014;60:169–187. doi: 10.1007/s10858-014-9866-7. [DOI] [PubMed] [Google Scholar]
- 41.Allison J.R., Hertig S., Missimer J.H., Smith L.J., Steinmetz M.O., Dolenc J. Probing the structure and dynamics of proteins by combining molecular dynamics simulations and experimental NMR data. J. Chem. Theory Comput. 2012;8:3430–3444. doi: 10.1021/ct300393b. [DOI] [PubMed] [Google Scholar]
- 42.Henriksen N., Davis D., Cheatham Iii T. Molecular dynamics re-refinement of two different small RNA loop structures using the original NMR data suggest a common structure. J. Biomol. NMR. 2012;53:321–339. doi: 10.1007/s10858-012-9642-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Auweter S.D., Fasan R., Reymond L., Underwood J.G., Black D.L., Pitsch S., Allain F.H.T. Molecular basis of RNA recognition by the human alternative splicing factor Fox-1. EMBO J. 2006;25:163–173. doi: 10.1038/sj.emboj.7600918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Brudno M., Gelfand M.S., Spengler S., Zorn M., Dubchak I., Conboy J.G. Computational analysis of candidate intron regulatory elements for tissue-specific alternative pre-mRNA splicing. Nucleic Acids Res. 2001;29:2338–2348. doi: 10.1093/nar/29.11.2338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hodgkin J., Zellan J.D., Albertson D.G. Identification of a candidate primary sex determination locus, Fox-1, on the X-chromosome of Caenorhabditis elegans. Development. 1994;120:3681–3689. doi: 10.1242/dev.120.12.3681. [DOI] [PubMed] [Google Scholar]
- 46.Nakahata S., Kawamoto S. Tissue-dependent isoforms of mammalian Fox-1 homologs are associated with tissue-specific splicing activities. Nucleic Acids Res. 2005;33:2078–2089. doi: 10.1093/nar/gki338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Underwood J.G., Boutz P.L., Dougherty J.D., Stoilov P., Black D.L. Homologues of the Caenorhabditis elegans Fox-1 protein are neuronal splicing regulators in mammals. Mol. Cell. Biol. 2005;25:10005–10016. doi: 10.1128/MCB.25.22.10005-10016.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Birney E., Kumar S., Krainer A.R. Analysis of the RNA-recognition motif and RS and RGG domains: conservation in metazoan pre-mRNA splicing factors. Nucleic Acids Res. 1993;21:5803–5816. doi: 10.1093/nar/21.25.5803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Long J.C., Caceres J.F. The SR protein family of splicing factors: master regulators of gene expression. Biochem. J. 2009;417:15–27. doi: 10.1042/BJ20081501. [DOI] [PubMed] [Google Scholar]
- 50.Soret J., Gabut M., Tazi J. SR proteins as potential targets for therapy. In: Jeanteur P, editor. Alternative Splicing and Disease. Vol. 44. Berlin, Heidelberg: Springer; 2006. pp. 65–87. [DOI] [PubMed] [Google Scholar]
- 51.Wang J., Takagaki Y., Manley J.L. Targeted disruption of an essential vertebrate gene: ASF/SF2 is required for cell viability. Genes Dev. 1996;10:2588–2599. doi: 10.1101/gad.10.20.2588. [DOI] [PubMed] [Google Scholar]
- 52.Longman D., Johnstone I.L., Cáceres J.F. Functional characterization of SR and SR-related genes in Caenorhabditis elegans. EMBO J. 2000;19:1625–1637. doi: 10.1093/emboj/19.7.1625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Case D.A.V.B., Berryman J.T., Betz R.M., Cai Q., Cerutti D.S., Cheatham T.E. III, Darden T.A., Duke R.E., Gohlke H., Goetz A.W., et al. San Francisco: University of California; 2014. [Google Scholar]
- 54.Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A 2nd generation force-field for the simulation of proteins, nucleic-acids, and organic-molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 55.Wang J.M., Cieplak P., Kollman P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000;21:1049–1074. [Google Scholar]
- 56.Perez A., Marchan I., Svozil D., Sponer J., Cheatham T.E., Laughton C.A., Orozco M. Refinenement of the AMBER force field for nucleic acids: improving the description of alpha/Gamma Conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Banas P., Hollas D., Zgarbova M., Jurecka P., Orozco M., Cheatham T.E., Sponer J., Otyepka M. Performance of molecular mechanics force fields for RNA simulations: stability of UUCG and GNRA hairpins. J. Chem. Theory Comput. 2010;6:3836–3849. doi: 10.1021/ct100481h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zgarbova M., Otyepka M., Sponer J., Mladek A., Banas P., Cheatham T.E., Jurecka P. Refinement of the Cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput. 2011;7:2886–2902. doi: 10.1021/ct200162x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hornak V., Abel R., Okur A., Strockbine B., Roitberg A., Simmerling C. Comparison of multiple amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Maier J.A., Martinez C., Kasavajhala K., Wickstrom L., Hauser K., Simmerling C. ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015;11:3696–3713. doi: 10.1021/acs.jctc.5b00255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Berendsen H.J.C., Grigera J.R., Straatsma T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987;91:6269–6271. [Google Scholar]
- 62.Joung I.S., Cheatham T.E. Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Salomon-Ferrer R., Götz A.W., Poole D., Le Grand S., Walker R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh Ewald. J. Chem. Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
- 64.Le Grand S., Götz A.W., Walker R.C. SPFP: speed without compromise—a mixed precision model for GPU accelerated molecular dynamics simulations. Comput. Phys. Commun. 2013;184:374–380. [Google Scholar]
- 65.Darden T., York D., Pedersen L. Particle mesh Ewald – an n.log(n) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 66.Essmann U., Perera L., Berkowitz M.L., Darden T., Lee H., Pedersen L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 67.Ryckaert J.P., Ciccotti G., Berendsen H.J.C. Numerical-integration of Cartesian equations of motion of a system with constraints – molecular-dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 68.Berendsen H.J.C., Postma J.P.M., Vangunsteren W.F., Dinola A., Haak J.R. Molecular-dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 69.Rosta E., Buchete N.-V., Hummer G. Thermostat artifacts in replica exchange molecular dynamics simulations. J. Chem. Theory Comput. 2009;5:1393–1399. doi: 10.1021/ct800557h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Harvey S.C., Tan R.K.Z., Cheatham T.E. The flying ice cube: velocity rescaling in molecular dynamics leads to violation of energy equipartition. J. Comput. Chem. 1998;19:726–740. [Google Scholar]
- 71.Krepl M., Reblova K., Koca J., Sponer J. Bioinformatics and molecular dynamics simulation study of L1 stalk non-canonical rRNA elements: kink-turns, loops, and tetraloops. J. Phys. Chem. B. 2013;117:5540–5555. doi: 10.1021/jp401482m. [DOI] [PubMed] [Google Scholar]
- 72.Estarellas C., Otyepka M., Koca J., Banas P., Krepl M., Sponer J. Molecular dynamic simulations of protein/RNA complexes: CRISPR/Csy4 endoribonuclease. Biochim. Biophys. Acta, Gen. Subj. 2015;1850:1072–1090. doi: 10.1016/j.bbagen.2014.10.021. [DOI] [PubMed] [Google Scholar]
- 73.Roe D.R., Cheatham T.E. PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013;9:3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 74.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 75.Merritt E.A., Bacon D.J. Raster3D: photorealistic molecular graphics. In: Carter CW, Sweet RM, editors. Macromolecular Crystallography, Pt B. Vol. 277. San Diego: Elsevier Academic Press Inc; 1997. pp. 505–524. [DOI] [PubMed] [Google Scholar]
- 76.Steinbrecher T., Mobley D.L., Case D.A. Nonlinear scaling schemes for Lennard-Jones interactions in free energy calculations. J. Chem. Phys. 2007;127:214108. doi: 10.1063/1.2799191. [DOI] [PubMed] [Google Scholar]
- 77.Lawrenz M., Baron R., McCammon J.A. Independent-trajectories thermodynamic-integration free-energy changes for biomolecular systems: determinants of H5N1 avian influenza virus neuraminidase inhibition by Peramivir. J. Chem. Theory Comput. 2009;5:1106–1116. doi: 10.1021/ct800559d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Krepl M., Otyepka M., Banas P., Sponer J. Effect of guanine to inosine substitution on stability of canonical DNA and RNA duplexes: molecular dynamics thermodynamics integration study. J. Phys. Chem. B. 2013;117:1872–1879. doi: 10.1021/jp311180u. [DOI] [PubMed] [Google Scholar]
- 79.Leontis N.B., Stombaugh J., Westhof E. The non-Watson-Crick base pairs and their associated isostericity matrices. Nucleic Acids Res. 2002;30:3497–3531. doi: 10.1093/nar/gkf481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Steinbrecher T., Joung I., Case D.A. Soft-core potentials in thermodynamic integration: comparing one- and two-step transformations. J. Comput. Chem. 2011;32:3253–3263. doi: 10.1002/jcc.21909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Sponer J., Mladek A., Sponer J.E., Svozil D., Zgarbova M., Banas P., Jurecka P., Otyepka M. The DNA and RNA sugar-phosphate backbone emerges as the key player. An overview of quantum-chemical, structural biology and simulation studies. Phys. Chem. Chem. Phys. 2012;14:15257–15277. doi: 10.1039/c2cp41987d. [DOI] [PubMed] [Google Scholar]
- 82.Sponer J., Cang X.H., Cheatham T.E. Molecular dynamics simulations of G-DNA and perspectives on the simulation of nucleic acid structures. Methods. 2012;57:25–39. doi: 10.1016/j.ymeth.2012.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Rocklin G.J., Mobley D.L., Dill K.A., Hünenberger P.H. Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: an accurate correction scheme for electrostatic finite-size effects. J. Chem. Phys. 2013;139:184103. doi: 10.1063/1.4826261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Caves L.S.D., Evanseck J.D., Karplus M. Locally accessible conformations of proteins: multiple molecular dynamics simulations of crambin. Protein Sci. 1998;7:649–666. doi: 10.1002/pro.5560070314. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.