Statistical-thermodynamic model for light scattering from eye lens protein mixtures

Abstract

We model light-scattering cross sections of concentrated aqueous mixtures of the bovine eye lens proteins γB- and α-crystallin by adapting a statistical-thermodynamic model of mixtures of spheres with short-range attractions. The model reproduces measured static light scattering cross sections, or Rayleigh ratios, of γB-α mixtures from dilute concentrations where light scattering intensity depends on molecular weights and virial coefficients, to realistically high concentration protein mixtures like those of the lens. The model relates γB-γB and γB-α attraction strengths and the γB-α size ratio to the free energy curvatures that set light scattering efficiency in tandem with protein refractive index increments. The model includes (i) hard-sphere α-α interactions, which create short-range order and transparency at high protein concentrations, (ii) short-range attractive plus hard-core γ-γ interactions, which produce intense light scattering and liquid-liquid phase separation in aqueous γ-crystallin solutions, and (iii) short-range attractive plus hard-core γ-α interactions, which strongly influence highly non-additive light scattering and phase separation in concentrated γ-α mixtures. The model reveals a new lens transparency mechanism, that prominent equilibrium composition fluctuations can be perpendicular to the refractive index gradient. The model reproduces the concave-up dependence of the Rayleigh ratio on α/γ composition at high concentrations, its concave-down nature at intermediate concentrations, non-monotonic dependence of light scattering on γ-α attraction strength, and more intricate, temperature-dependent features. We analytically compute the mixed virial series for light scattering efficiency through third order for the sticky-sphere mixture, and find that the full model represents the available light scattering data at concentrations several times those where the second and third mixed virial contributions fail. The model indicates that increased γ-γ attraction can raise γ-α mixture light scattering far more than it does for solutions of γ-crystallin alone, and can produce marked turbidity tens of degrees celsius above liquid-liquid separation.

I. INTRODUCTION

Mammalian eye lens cytoplasm contains concentrated aqueous mixtures of three principal globular proteins, the α-, β-, and α-crystallins, which differ substantially in size and interactions. Eye lens transparency is sensitive to changes in attractive or repulsive crystallin interactions. Excluded-volume interactions between α-crystallins lead to short-range order that is fundamental to lens transparency.^1–3 Short-range γ-crystallin attractions cause intense light scattering and phase separation.^4–10 Interactions between different γ-crystallin subtypes produce non-monotonic dependence of phase boundaries on subtype composition.⁸ γ-α mixtures have phase separation characteristics that are not simple combinations of those of the individual α- and γ-crystallins,¹¹ and γ-α size disparity as well as short-range γ-α attractions play roles in this behavior.^12,13 In particular, γ-α mixture phase boundaries depend non-monotonically on $\gamma$-$\alpha$ interaction strength.^12–14 Interactions between γ- and β-crystallins set their ternary liquid-liquid phase boundaries, tie lines, and light scattering.¹⁵ Interactions of crystallins with many other lens proteins and with cell membranes, and many post-translational modifications and mutations can also sensitively affect transparency.^16–18

The sensitivity of transparency to crystallin interactions is illustrated by the fact that single mutations of γ-crystallin can dramatically change phase boundaries and cause cataract,¹⁹ and by findings that either a reduction or an increase of just (1/2)k_BT in attractive interactions between α- and γ-crystallins can lead to phase separation and opacification.^12,13 An increase in γ-α attraction has been found to result from a single-point, cataractogenic mutation of human γD-crystallin, and is implicated in the molecular origins of that cataract.²⁰

The variety of lens protein interactions, the exquisite sensitivity of transparency to molecular properties, and the multicomponent, concentrated nature of the lens cytoplasm are challenges for understanding the degree to which given molecular changes affect the scattering of light. Taken together, present findings about the influence of altered crystallin interactions on lens transparency suggest that congenital cataracts will eventually be identified that arise from mutations that alter any of the six pairwise interactions between α-, β-, and γ-crystallins. Furthermore, typical lens cytoplasm protein concentrations are several times those at which single-particle properties such as molecular weight, or even two- and three-particle properties such as second and third virial coefficients, are adequate to quantitatively model light scattering, as we show below. In view of these complexities, building useful statistical-mechanical models of the underlying lens protein mixture light scattering, liquid structure, and thermodynamics is essential for understanding the molecular origins of lens transparency.

In this work we build a model of the liquid structure and thermodynamic susceptibilities of mixtures of two types of eye lens proteins that can have short-range attractions. For simplicity, we represent the proteins by spheres that have different diameters and pairwise, infinitely short-range, “sticky” attractions. The sticky-sphere mixture model we use was originally developed with use of the Percus-Yevick closure of the Ornstein-Zernike relations of liquid-state theory²¹ by Baxter, Barboy, Perram, Smith, and Tenne.^22–25 Further developments, use of other closures, and related molecular simulations have been studied since by many researchers.^26–39 A model like the one we detail below, that used the Percus-Yevick closure, has previously been successfully used to represent turbidity data of colloid mixtures.⁴⁰

Here we apply the formulation of Barboy and Tenne^23,25 to model light scattering efficiency data from concentrated aqueous mixtures of the bovine eye lens proteins γB-crystallin and α-crystallin.¹¹ Model parameters are chosen to be consistent with data on γ- and α-crystallin structure and interactions, and include hard-sphere α-α interactions, hard-sphere plus short-range attractive γ-γ interactions that lead to liquid-liquid phase separation, and hard-sphere plus short-range, attractive γ-α interactions. The present model complements the neutron scattering, molecular dynamics, and perturbation theory work previously applied to this system.^12–14

Use of a sticky-sphere mixture light scattering model for γ-α mixtures was suggested by previous findings: (i) A single-component sticky-sphere model successfully represents static light scattering data from concentrated γB-crystallin solutions;⁹ (ii) the sticky-sphere model closely represents low-angle neutron scattering⁴¹ from concentrated γB-crystallin solutions; (iii) when sticky interactions are turned off, the sticky-sphere mixture model reproduces the analytic Percus-Yevick results for hard-sphere mixtures,^22,42,43 which is relevant because a Percus-Yevick hard-sphere liquid structure model can fit light scattering, small-angle X-ray scattering, and neutron scattering from α-crystallin solutions;⁴⁴ (iv) sticky spheres provide a convenient representation of the tuned short-range attraction between α- and γ-crystallins that is needed for stability at high concentrations;^12–14 and (v) the sticky-sphere model can potentially incorporate all 6 types of effective short-range interactions between protein molecule pairs in quaternary mixtures of an aqueous buffer with α-, β-, and γ-crystallins, albeit with the restriction to spherical models of molecular shapes.

We have used the sticky sphere model to provide a useful quantitative representation of the observed Rayleigh ratio data while recognizing that sticky spheres of equal diameter, in this model, have been shown to have a thermodynamic instability.²⁶ In Ref. 26, the potential roles of both orientation-dependent interactions and size polydispersity in possibly ameliorating the consequences of this instability are discussed. While the present formulation of the model is that of a strictly bidisperse system, in this connection it may be relevant that the α-crystallin studied here is inherently polydisperse (e.g., Refs. ⁴⁴ and ⁴⁵), and that the γ-crystallins exhibit orientation-dependent interactions (e.g., Ref. 46).

We also do not expect that the Percus-Yevick closure version of the model used here will extend to give a robust representation of the underlying liquid-liquid phase boundaries¹¹ found in γB- and α-crystallin mixtures. This expectation arises because the Percus-Yevick single-component version of the sticky-sphere model shows quite different predictions for the critical volume fraction for phase separation, depending on whether the compressibility, pressure, or energy routes to the equation of state are used;⁴⁷ similar considerations apply to the mixture version.²⁵ In this context, the light scattering model here is studied for conditions that range from at least several degrees C to many tens of degrees away from phase separation.¹¹

The paper is organized as follows. In Section II A we review the relationship between the free energy and the efficiency of light scattering from an isotropic liquid mixture, and illustrate the principal features of this relationship geometrically. In Section II B we summarize relevant parts of the Barboy-Tenne version of the sticky-sphere mixture model, and introduce a compact algebraic formulation. In Section II C we describe the analysis and numerical methods we have used for finding the needed spatial correlation function parameters (the “λs”) from stickiness parameters (the “τs”). In Section II D we find an expression for the excess Rayleigh ratio of aqueous protein mixtures that results from combining the multicomponent sticky-sphere mixture model with refractive index properties. In Section III A we describe our choice of model parameters and relate them to the molecular properties of α- and γB-crystallin. In Section III B we model the needed refractive index increments in concentrated γB-α mixtures in terms of their measured low-concentration refractive index increments. In Section III C we compare the overall model with the concentration-, composition-, and temperature-dependence of light scattering from α- and γB-crystallin mixtures.¹¹ In Section IV A we use the model to analyze the role of the near-orthogonality of prominent composition fluctuations to refractive index gradients in producing very low light scattering intensity in concentrated γB-α mixtures, at body temperature. In Section IV B we use the model to further identify free energy contributions to light scattering in the region that is concentrated in γB-crystallin, but dilute in γ-crystallin, and where an interesting temperature dependence of the light scattering intensity occurs.¹¹ In Section IV C we explore the extent of the dilute solution realms within which light scattering can be well-represented with use of the γB and γ-crystallin molecular weights and the second and third virial coefficients. In Section V, we use the model to study potential molecular origins of increased or decreased light scattering, relevant to lens transparency, by varying molecular parameters. We discuss prospects for extending the work and conclude in Section VI.

II. THEORY

A. Light scattering from isotropic fluid mixtures

Light is scattered because of spatial variations in the optical polarizability of a medium. Within the eye lens, some polarizability variations result from spontaneous, local equilibrium fluctuations of molecular concentrations; the present work focuses on modeling the magnitude of such fluctuations in single-phase concentrated lens protein mixtures. Cytoskeletal components, cell membranes, and gaps between fibre cells represent other important sources of light scattering in the lens that are not considered in this work.

In fluid mixtures, the second composition derivatives of the free energy set the amplitude of local concentration fluctuations that scatter light. Smaller values of the second derivatives of the free energy correspond to lower free energy costs of spontaneous fluctuations, and thus to more intense light scattering. In particular, for the fluid mixtures of interest here, the Rayleigh ratio $\mathrm{\Delta }\mathcal{R}(0)$ in excess of that from solvent, which measures the efficiency of forward scattering of light, can be written as^48,49

$$\mathrm{\Delta }\mathcal{R}(0)=\left(\frac{{\pi }^2{k}_{B}T}{{\lambda }^4}\right){\nabla }_{\rho }{\epsilon }^T\cdot H_{\rho }{\left[G/V\right]}^{-1}\cdot {\nabla }_{\rho }\epsilon =\left(\frac{{\pi }^2{k}_{B}T}{{\lambda }^4}\right){\parallel {\nabla }_{\rho }\epsilon \parallel }^2\left(\frac{{\cos }^2{\theta }_1}{{\lambda }_{H1}}+\frac{{\cos }^2{\theta }_2}{{\lambda }_{H2}}\right)$$ (1)

in which $\lambda$ is the vacuum wavelength of the incident and scattered light, $H_{\rho }[G/V]$ is the Hessian matrix of second partial derivatives of the Gibbs free energy G per unit volume V, with respect to the number densities of the components $\{{\rho }_1,{\rho }_2\}$, and $H_{\rho }{[G/V]}^{-1}$ is its inverse, ${\nabla }_{\rho }\epsilon$ is the gradient of the dimensionless dielectric coefficient ε with respect to number densities, at the incident light wavelength, ${\lambda }_{H1}$ and ${\lambda }_{H2}$ are the eigenvalues of $H_{\rho }[G/V]$, and ${\theta }_1$ and ${\theta }_2$ are the angles between ${\nabla }_{\rho }\epsilon$ and the eigenvectors of $H_{\rho }\left[G/V\right]$ belonging to ${\lambda }_{H1}$ and ${\lambda }_{H2}$, respectively. In the derivation of Eq. (1) from the form given by Kirkwood and Goldberg,⁴⁸ we assume that the molecular volumes are constant and additive, as detailed in Ref. 49. Eq. (1) is written for two macromolecular components 1 and 2; the multicomponent version has a completely analogous form.

The first expression for $\mathrm{\Delta }\mathcal{R}(0)$ in Eq. (1) shows the relationship between scattering intensity and second composition derivatives of the free energy. Note that the proportionality of $\mathrm{\Delta }\mathcal{R}(0)$ to the inverse of the Hessian matrix means that smaller second derivatives correspond to more intense scattering. The second expression for $\mathrm{\Delta }\mathcal{R}(0)$ in Eq. (1) illustrates in more detail how the amount of light scattered depends on the dielectric gradient orientation, relative to the eigendirections of the Hessian. For example, if the dielectric gradient is nearly parallel to the most prominent composition fluctuation directions, that is, along the eigendirection corresponding to the smaller of the eigenvalues, say, ${\lambda }_{H1}$, then ${\cos }^2({\theta }_1)=1$ while ${\cos }^2({\theta }_2)=0$ and more light will be scattered, while less would be scattered if a dielectric gradient of the same magnitude were instead along the eigendirection for the larger eigenvalue, ${\lambda }_{H2}$. These considerations turn out to be important for understanding the light scattering from concentrated γ-$\alpha$ mixtures.

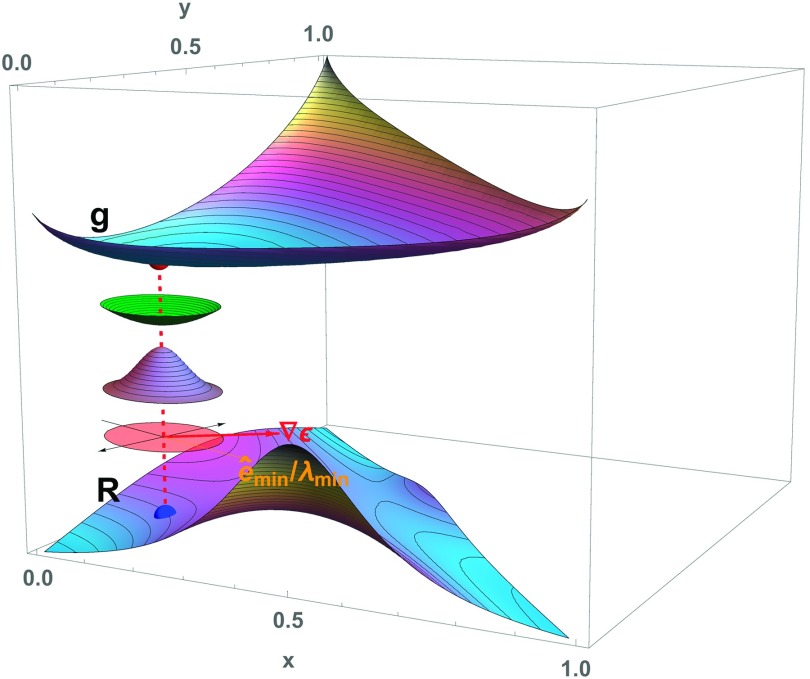
The relationships expressed in Eq. (1) are illustrated in Figures 1 and 2. In each, a succession of surfaces, from a model, regular solution free energy g at the top, to the corresponding excess Rayleigh ratio R at the bottom, calculated according to Eq. (1), are plotted above the ternary composition triangle. In each of the three panels in the two figures, the functions g and R are identical, while the composition being considered changes from panel to panel.

FIG. 1.

Relationships among the Gibbs free energy, the dielectric gradient, and the scattering of light: The upper surface, labeled g, is the graph of a model free energy for a ternary mixture, plotted above the ternary composition triangle. The lower surface, labeled R, is the graph of a function proportional to the Rayleigh ratio given by Eq. (1). The intermediate surfaces illustrate Eq. (1), which details how spontaneous, thermally driven local fluctuations in composition, together with the dielectric gradient, determine the amount of light that is scattered. At the concentration of the vertical dashed red line, the green surface, which has been displaced for visibility, is the local, second-order Taylor series approximation to the free energy, as specified by the Hessian matrix H[g]. The blue surface, which is also displaced, is proportional to the corresponding Gaussian probability density function for local composition fluctuations, whose variance-covariance matrix is proportional to the inverse of H[g]. The boundary of the pink surface is a level curve of the Gaussian. The red arrow $\mathbf{\nabla }\epsilon$ points in the direction of the dielectric gradient vector, while the orange ray labeled ${\widehat{e}}_{min}/{\lambda }_{min}$ points in the direction of the minimum eigenvector of H[g], and is weighted by the reciprocal of the corresponding eigenvalue, in accordance with Eq. (1). The vector ${\widehat{e}}_{max}/{\lambda }_{max}$ is shown by the black arrows, which are perpendicular to ${\widehat{e}}_{min}$.

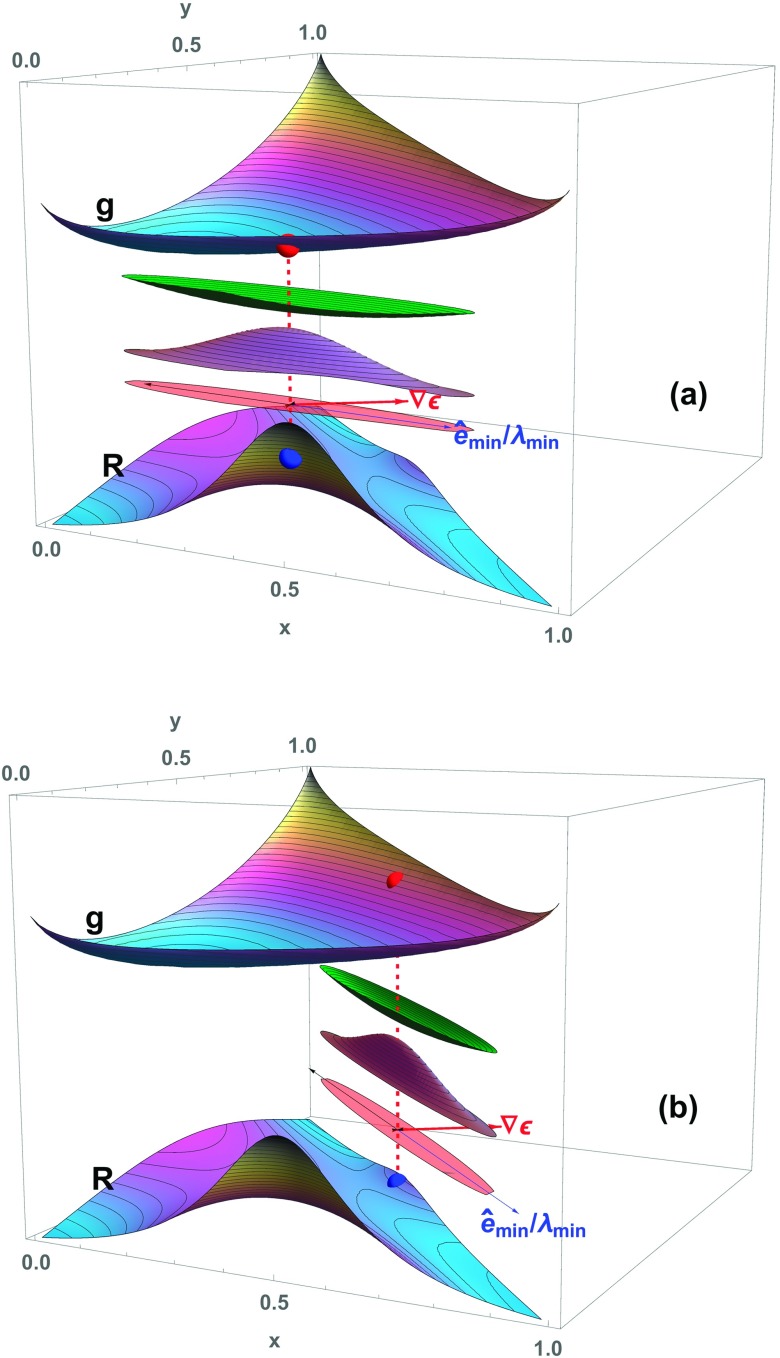
FIG. 2.

Two different ternary compositions, equidistant in temperature and composition from liquid-liquid phase separation, can give rise to dramatically different light scattering efficiencies, high (in (a)), and low (in (b)). The contrast can be understood via Eq. (1) as illustrated here. In (a), the green, blue, and pink surfaces, as defined in Figure 1, illustrate that the most prominent local composition fluctuations have a significant component along the chosen $\mathbf{\nabla }\epsilon$, leading to relatively intense light scattering, shown by the height of the blue dot on the Rayleigh ratio surface. In (b), although the prominent local fluctuations are exactly as intense as in (a), they are nearly perpendicular to the same $\mathbf{\nabla }\epsilon$, and far less light is scattered, shown by the lower blue dot. As described below, the present model indicates that prominent fluctuations closely perpendicular to $\mathbf{\nabla }\epsilon$ occur in concentrated mixtures of γ- and $\alpha$-crystallins, while a situation like that in (a) occurs near the γ-crystallin/buffer axis.

We introduce the relevant geometry by considering Fig. 1, for which the highlighted composition is near a vertex of the composition triangle. The Hessian matrix H[g] determines the local shape of the second-order part g⁽²⁾ of g, which is shown as the green surface displaced vertically down from that of the full g itself. In turn, g⁽²⁾ determines the nature of spontaneous, thermally driven composition fluctuations within given regions of space in a physical sample at that composition. The corresponding probability density function is represented by a blue surface, just under the green surface. Because the actual width of such probability density functions also depends on the volume of the portion of the sample under consideration (see, e.g., Ref. 50), the blue surfaces are representative in the sense that regardless of that volume, they nevertheless show the appropriate aspect ratio of the contours of constant probability density. The shape of a selected contour is shown by the pink ellipse, underneath the blue surface. Clearly, the ellipse in Fig. 1 is nearly circular. Because, as noted above, the angles ${\theta }_1$ and ${\theta }_2$ between the Hessian eigenvectors and the dielectric gradient vector $\nabla \epsilon$ are key to determining the Rayleigh ratio in Eq. (1), as are the corresponding reciprocal eigenvalues $1/{\lambda }_{H1}$ and $1/{\lambda }_{H2}$, Fig. 1 indicates each Hessian eigenvector, weighted by the reciprocal of its eigenvalue, by orange and black arrows, along with a red arrow depicting $\nabla \epsilon$.

Unlike Fig. 1, Fig. 2 considers compositions near liquid-liquid phase separation. It shows that two different ternary compositions, equidistant in temperature and composition from liquid-liquid phase separation, can give rise to dramatically different light scattering efficiencies, high (in Fig. 2(a)) and low (in Fig. 2(b)). To show this, the free energy model g in Figs. 1 and 2 was selected to have equal phase separation temperatures on the near binary axis that extends between x = 0 to x = 1 for y = 0, and on the diagonal axis that extends between (x, y) = (1, 0) and (0, 1). The compositions for which fluctuations are depicted in panels (a) and (b) of Fig. 2 are in precisely equivalent locations, relative to their neighboring binary critical points.

Why is the scattering higher for the composition in panel (a) of Fig. 2, but lower for the composition in panel (b), despite their equivalent proximities to a nearby critical point for liquid-liquid phase separation? The key consideration is the relationship between the direction of prominent composition fluctuations and that of $\nabla \epsilon$. Although the composition fluctuations have the same magnitude in the two cases, the directions of the prominent fluctuations, determined by the Hessian eigenvector with minimum eigenvalue, are not the same; in each case they are predominantly along the neighboring binary axis direction. As a result, the fluctuations shown in panel (b) are more nearly perpendicular to $\nabla \epsilon$, and much less light is scattered. We will find in Section IV B that conditions qualitatively similar to those depicted in panel (a) of Fig. 2 occur in concentrated solutions of γB- and $\alpha$-crystallins, in which γB is concentrated, but $\alpha$ is dilute. The situation in panel (b), on the other hand, is similar to that analyzed in Section IV A at high overall protein concentrations, near 300 mg/ml, within which both γB- and $\alpha$-crystallin are concentrated.

B. The sticky-sphere mixture model

We work from an analytic model of the local structure of fluid mixtures of spherical molecules with hard cores and tunable short-range attractions.²⁵ We adapt the model to capture key properties of mixtures of two prominent eye lens proteins, $\alpha$- and γ-crystallin. Although theories of the dielectric response relate it as well to local fluid structure,^21,51,52 here we instead use measured index of refraction increments for γ-crystallin and $\alpha$-crystallin in Eq. (1) as input to a model Lorenz-Lorentz relation, as detailed in Section III B.

The sticky-sphere mixture model evolved from the studies of hard spheres with infinitely short-range attractions by Baxter and colleagues.^22,47,53,54 Baxter discovered a factorization of the Ornstein-Zernike relations for the structure of a disordered fluid that applies in the case in which the direct correlation function is assumed to vanish beyond a finite radial separation.⁵³ Baxter applied the factorization to study systems of hard spheres with infinitely short-range attractions,^47,54 and generalized the factorization to apply to mixtures of molecules assumed to have spherically symmetric pairwise potentials.²²

To represent sticky-sphere mixtures, Barboy,²³ Perram and Smith,²⁴ and Barboy and Tenne²⁵ applied Baxter’s multicomponent factorization to a set of Mayer f-functions, f_ij(r), constructed to model infinitely short-range attractions between sphere types that can have a variety of diameters. The Mayer f-function, the difference between the Boltzmann factor of the intermolecular potential energy and unity, is the central building block for models of how intermolecular potentials u_ij(r) affect correlations of molecular positions in liquids (see, e.g., Ref. 21). Here r is the radial separation between the centers of spheres of types i and j. In the sticky-sphere mixture model

$$f_{ij}(r)\equiv e^{-u_{ij}(r)/k_{B}T}-1=\left(\frac{d_{ij}}{2{\tau }_{ij}}\right){\delta }_{-}(d_{ij}-r)+(H_{-}(r-d_{ij})-1),$$ (2)

in which u_ij(r) is the intermolecular potential at center-to-center distance r between species i and j, $d_{ij}=\frac{1}{2}(d_{ii}+d_{jj})$ is the smallest center-to-center distance between species i and j, that have diameters d_ii and d_jj, respectively, ${\delta }_{-}(x)$ is the asymmetric Dirac delta function, and $H_{-}(x)$ is the asymmetric Heaviside step function, which is 0 for $x<0$ and 1 for $x\ge 0$. Through the function $H_{-}(r-d_{ij})$, Eq. (2) expresses the fact that the centers of spheres of types i and j cannot come closer than d_ij. The term $(d_{ij}/2{\tau }_{ij}){\delta }_{-}(d_{ij}-r)$ represents infinitely short-range attractions that can be modulated by varying ${\tau }_{ij}$, for each pair of sphere types. Thus, the parameters ${\tau }_{ij}={\tau }_{ji}$ are reciprocal measures of the strength of the attractive interactions; they measure stickiness.

The value ${\tau }_{ij}=\mathrm{\infty }$ corresponds to hard-sphere interactions between components i and j, and the resulting Percus-Yevick hard-sphere model is capable of modeling the light, X-ray, and neutron scatterings from $\alpha$-crystallin solutions.^{2,3,12,14,44,55} Progressively smaller values of ${\tau }_{ij}$ increase the coefficient of the Dirac delta function in Eq. (2), and thus correspond to increasingly attractive interactions. Ultimately, low enough values of the ${\tau }_{ij}$ correspond to separation of the mixture into more than one phase, as is found experimentally for pure γ crystallin solutions,^4,5,7,9 as well as in mixtures of γ with $\alpha$-crystallin.^11,20 In the pure component case, the compressibility equation of state in the Percus-Yevick approximation predicts separation into more than one phase²³ for values of ${\tau }_{ii}<2-\sqrt{2}\simeq 0.586$. In addition, the recently found implications of short-range γ-$\alpha$ attractions for phase separation^12,13 can be represented in the present model by suitable values of an inter-species ${\tau }_{ij}$. It is important to note that in the context of building successful models of physical systems, the ${\tau }_{ij}$ can be functions of temperature, as was found in light scattering studies of pure bovine γB-crystallin solutions.⁹

C. Obtaining spatial correlation function parameters from stickiness parameters

While the consequences of Eq. (2) can be approached through other liquid-state theory approaches^34,35 as well as through simulation,^33,56 here we use the Barboy and Tenne version of the model,^23,25 which makes use of the Percus-Yevick closure of the Ornstein-Zernike equations.²¹ In that version, it turns out that the liquid-structure, thermodynamic and light scattering predictions of the model are expressed in terms of parameters, the ${\lambda }_{ij}$, that are related to the ${\tau }_{ij}$ by the following set of coupled quadratic equations:

$$\frac{\pi d_{ij}}{12(1-{\xi }_3)}\sum _k{\rho }_k{d}_{kk}^2({\lambda }_{ik}-6)({\lambda }_{jk}-6)-{\tau }_{ij}{\lambda }_{ij}=\frac{9d_{ij}{\xi }_2}{(1-{\xi }_3)}-\frac{6d_{ij}^2}{d_{ii}{d}_{jj}},$$ (3)

in which the sum is over species k, ${\rho }_k$ is the number of k-type spheres per unit volume, and the quantities ${\xi }_l$ are moments of the distribution of sphere sizes given by

$${\xi }_l=\frac{\pi }{6}\sum _k{\rho }_k{\left(d_{kk}\right)}^l.$$ (4)

That is, to use the model for a given set of stickiness parameters $\{{\tau }_{ij}\}$, one needs to solve Eqs. (3) to find the corresponding set $\{{\lambda }_{ij}\}$ that applies at each composition and temperature of the mixture; then one is in a position to explore scattering and thermodynamic predictions. Note that because Eqs. (3) remain the same when the indices i and j are interchanged, they imply that ${\lambda }_{ij}={\lambda }_{ji}$. Appendix A shows that Eqs. (3) can also be put into the form of a quadratic matrix equation,

$$Y^2+\tau ◦Y=B+\tau ◦C\text{,}$$ (5)

where Y, $\tau$, B, and C are defined there, and where $A◦B$ is the Schur (Hadamard) matrix product defined by ${(A◦B)}_{ij}=A_{ij}{B}_{ij}$. Appendix B details the numerical methods we have used for solving Eqs. (3) or equivalently Eqs. (5), and for selecting the appropriate root.

In this paper we apply the sticky-sphere mixture model to a two-protein component mixture, $\gamma$-crystallin, or species 1, and $\alpha$-crystallin, species 2. Consistent with the hard-sphere-like scattering properties of concentrated $\alpha$-crystallin solutions,² we take ${\tau }_{22}=\mathrm{\infty }$ in Eq. (2). Under these circumstances, we show in Appendix B that Eqs. (3) then imply that ${\lambda }_{22}=0$, and reduce to the following two equations that relate ${\tau }_{11}$ and ${\tau }_{12}$ to ${\lambda }_{11}$ and ${\lambda }_{12}$:

$$\frac{\pi }{12}\frac{d_{11}}{1-{\xi }_3}({\rho }_1{d}_{11}^2{({\lambda }_{11}-6)}^2+{\rho }_2{d}_{22}^2{({\lambda }_{12}-6)}^2)-{\tau }_{11}{\lambda }_{11}=\frac{9d_{11}{\xi }_2}{1-{\xi }_3}-6,$$ (6)

$$\frac{\pi }{12}\frac{d_{12}}{1-{\xi }_3}({\rho }_1{d}_{11}^2({\lambda }_{11}-6)({\lambda }_{12}-6)-6{\rho }_2{d}_{22}^2({\lambda }_{12}-6))-{\tau }_{12}{\lambda }_{12}=\frac{9d_{12}{\xi }_2}{1-{\xi }_3}-\frac{6d_{12}^2}{d_{11}{d}_{22}}.$$ (7)

In Appendix B, we show that the solution of Eqs. (6) and (7) can be further reduced to the solution of a fourth-order polynomial in ${\lambda }_{11}-6$, given by

$${({\lambda }_{11}-6)}^4+D_3{({\lambda }_{11}-6)}^3+D_2{({\lambda }_{11}-6)}^2+D_1({\lambda }_{11}-6)+D_0=0,$$ (8)

where the D_i are also defined in Appendix B, where we also discuss our method of solving this equation. With use of each value of ${\lambda }_{11}$ resulting from a solution of Eq. (8), the corresponding value of ${\lambda }_{12}$ can be obtained as detailed in Appendix B.

D. Light scattering intensity in the sticky-sphere mixture model

To calculate the predictions of the sticky-sphere mixture model for the intensity of the scattered light, one needs to evaluate integrals of functions q_ij(r); each such integral is an entry in Q, a matrix that can be used to compute the Hessian matrix in Eq. (1). The needed relationships are derived in Appendix C. First, the Gibbs free energy of the three-component mixture of aqueous solvent, $\gamma$-crystallin and $\alpha$-crystallin is shown to be analogous to the Helmholtz free energy of the hypothetical two sticky-sphere component mixture. The Hessian of the intensive Gibbs free energy then corresponds to a matrix of chemical potential derivatives of the two-component system, as follows:

$$H_{\rho }\left[\frac{G}{V}\right]=\left[\begin{array}{cc}\hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_2}\hfill \end{array}\right]$$ (9)

in which ${\mu }_1^{(2)}$ and ${\mu }_2^{(2)}$ are chemical potentials in the two-component system, related to the chemical potentials in the three-component mixture with solvent as detailed in Appendix C. Barboy and Tenne²⁵ obtain

$$\left[\begin{array}{cc}\hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_2}\hfill \end{array}\right]=\frac{1}{\beta }{\sqrt{𝝆}}^{-1}{𝑸}^T𝑸{\sqrt{𝝆}}^{-1},$$ (10)

in which $𝝆$ is the diagonal matrix of number densities. The matrix $𝑸$ is shown in Appendix C to have the entries

$$Q_{ij}={\delta }_{ij}+x_j\sqrt{\frac{{\rho }_i}{{\rho }_j}}\left(1+{\gamma }_{ij}{l}_{ij}+\sum _k{x}_k{\gamma }_{ik}{l}_{ik}\right),$$ (11)

in which ${\delta }_{ij}$ is the Kronecker delta, ${\gamma }_{ij}=d_{ii}/d_{jj}$, $l_{ij}=3-{\lambda }_{ij}$, $x_i=\frac{{\varphi }_i}{1-{\xi }_3}$, and in turn ${\varphi }_i=\frac{\pi }{6}{\rho }_i{d}_{ii}^3$, the volume fraction of the i-type spheres. It follows that Q has the form

$$\text{𝐐}=\sqrt{𝝆}{\text{𝑿}}^{-1}(\text{𝑰}+\text{𝑿𝑳}◦\mathbf{\gamma })(\text{𝑰}+\text{𝑿𝑼})\text{𝑿}{\sqrt{𝝆}}^{-1},$$ (12)

in which

$$𝝆=\left[\begin{array}{ccc}\hfill {\rho }_1\hfill & & \\ & \hfill {\rho }_2\hfill & \\ & & \hfill \ddots \hfill \end{array}\right],𝑿=\left[\begin{array}{ccc}\hfill x_1\hfill & & \\ & \hfill x_2\hfill & \\ & & \hfill \ddots \hfill \end{array}\right],𝑳=\left[\begin{array}{ccc}\hfill l_{11}\hfill & \hfill l_{12}\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill l_{12}\hfill & \hfill l_{22}\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right],𝑼=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill \end{array}\right],𝜸=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill \frac{d_{11}}{d_{22}}\hfill & \\ \hfill \frac{d_{22}}{d_{11}}\hfill & \hfill 1\hfill & \\ & & \hfill \ddots \hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill {\gamma }_{12}\hfill & \\ \hfill {\gamma }_{21}\hfill & \hfill 1\hfill & \\ & & \hfill \ddots \hfill \end{array}\right].$$ (13)

The full multicomponent excess Rayleigh ratio for a sticky-sphere mixture system can now be obtained by substituting the expressions given in Eqs. (9), (10), and (12) into Eq. (1),

$$\frac{{\lambda }^4\mathrm{\Delta }\mathcal{R}(0)}{{\pi }^2{k}_{B}T}={\nabla }_{\rho }{\epsilon }^T\cdot H_{\rho }{\left[G/V\right]}^{-1}\cdot {\nabla }_{\rho }\epsilon ={\nabla }_{\rho }{\epsilon }^T\cdot \beta \sqrt{𝝆}{𝑸}^{-1}{\left({𝑸}^{-1}\right)}^T\sqrt{𝝆}\cdot {\nabla }_{\rho }\epsilon .$$ (14)

In the case of the two sticky-sphere components in the present model, it is shown in Appendix C that $𝑸$ can be written as

$$𝑸=\left[\begin{array}{cc}\hfill 1+x_1{J}_{11}\hfill & \hfill \frac{\sqrt{x_1{x}_2}}{{\gamma }_{12}^{3/2}}{J}_{12}\hfill \\ \hfill {\gamma }_{12}^{3/2}\sqrt{x_1{x}_2}{J}_{21}\hfill & \hfill 1+x_2{J}_{22}\hfill \end{array}\right],$$ (15)

where the J_ij are given by

$$J_{11}=1+l_{11}+x_1{l}_{11}+x_2{l}_{12}{\gamma }_{12},J_{12}=1+x_1{l}_{11}+(l_{12}{\gamma }_{12})(1+x_2),J_{21}=1+x_2{l}_{22}+(l_{12}/{\gamma }_{12})(1+x_1),J_{22}=1+l_{22}+x_2{l}_{22}+(x_1/{\gamma }_{12})l_{12}.$$ (16)

For this two-component case, with use of Eq. (15), we find

$$H_{\rho }{\left[\frac{G}{V}\right]}^{-1}=\frac{\beta }{{(\text{det}𝑸)}^2}\sqrt{𝝆}\left[\begin{array}{cc}\hfill a\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill c\hfill \end{array}\right]\sqrt{𝝆},$$ (17)

where

$$a={(1+x_2{J}_{22})}^2+\frac{x_1{x}_2}{{\gamma }_{12}^3}{J}_{12}^2,b=-\sqrt{x_1{x}_2}\left(\frac{J_{12}}{{\gamma }_{12}^{3/2}}(1+x_1{J}_{11})+{\gamma }_{12}^{3/2}{J}_{21}(1+x_2{J}_{22})\right),c={(1+x_1{J}_{11})}^2+{\gamma }_{12}^3{x}_1{x}_2{J}_{21}^2.$$ (18)

The determinant of Q takes the remarkably simple form

$$\text{det}𝑸=(1+x_1+x_2)(1+l_{11}{x}_1+l_{22}{x}_2+(l_{11}{l}_{22}-l_{12}^2)x_1{x}_2).$$ (19)

Eqs. (8) and (17)–(19) provide the sticky-sphere mixture model expressions needed for evaluating the excess Rayleigh ratio, Eq. (1).

For comparison with experimental data, it is convenient to express $H_{\rho }{\left[G/V\right]}^{-1}$ in terms of dimensionless variables. To do so we define a dimensionless, intensive Gibbs free energy

$$\stackrel{\sim }{g}=\frac{\overline{v_0}G}{V{k}_{B}T}$$ (20)

and use the volume fractions ${\varphi }_1={\rho }_1\overline{v_1}$ and ${\varphi }_2={\rho }_2\overline{v_2}$, where $\overline{v_0}$, $\overline{v_1}$, and $\overline{v_2}$ are the partial molecular volumes of the solution associated with single molecules of water, γ, and α crystallin, respectively; note that $x_1={\varphi }_1/(1-({\varphi }_1+{\varphi }_2))$ and $x_2={\varphi }_2/(1-({\varphi }_1+{\varphi }_2))$. It is shown in Appendix D that

$$H_{\rho }{\left[\frac{G}{V}\right]}^{-1}=\frac{\overline{v_0}}{k_{B}T}\left[\begin{array}{cc}\hfill \frac{1}{\overline{v_1}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\overline{v_2}}\hfill \end{array}\right]{[H_{\varphi }[\stackrel{\sim }{g}]]}^{-1}\left[\begin{array}{cc}\hfill \frac{1}{\overline{v_1}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\overline{v_2}}\hfill \end{array}\right]$$ (21)

in which the entries of $H_{\varphi }[\stackrel{\sim }{g}]$ are the second derivatives of $\stackrel{\sim }{g}$ with respect to the volume fractions. The corresponding expressions for $H_{\varphi }[\stackrel{\sim }{g}]$ and $H_{\varphi }[\stackrel{\sim }{g\ast }]$, where $\stackrel{\sim }{g\ast }=(\overline{v_1}/\overline{v_0})\stackrel{\sim }{g}$, will be useful in the analysis below and are given by

$$\frac{1}{\overline{v_0}}[H_{\varphi }[\stackrel{\sim }{g}]]=\frac{1}{\overline{v_1}}[H_{\varphi }[\stackrel{\sim }{g\ast }]]=\left[\begin{array}{cc}\hfill \frac{c}{{\rho }_1{\overline{v_1}}^2}\hfill & \hfill \frac{-b}{\sqrt{{\rho }_1{\rho }_2}\overline{v_1}\overline{v_2}}\hfill \\ \hfill \frac{-b}{\sqrt{{\rho }_1{\rho }_2}\overline{v_1}\overline{v_2}}\hfill & \hfill \frac{a}{{\rho }_2{\overline{v_2}}^2}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \frac{c}{{\varphi }_1\overline{v_1}}\hfill & \hfill \frac{-b}{\sqrt{{\varphi }_1{\varphi }_2\overline{v_1}\overline{v_2}}}\hfill \\ \hfill \frac{-b}{\sqrt{{\varphi }_1{\varphi }_2\overline{v_1}\overline{v_2}}}\hfill & \hfill \frac{a}{{\varphi }_2\overline{v_2}}\hfill \end{array}\right].$$ (22)

Because refractive index increments are commonly reported in terms of derivatives of the index of refraction n with respect to the mass per unit volume of the solutes, we express ${\nabla }_{\rho }\epsilon$ in terms of the mass per unit volume concentrations $c_1={\rho }_1{m}_1$ and $c_2={\rho }_2{m}_2$, in which m₁ and m₂ are the masses of single molecules of $\gamma$- and $\alpha$-crystallin, respectively. Using $\epsilon =n^2$, we have

$${({\nabla }_{\rho }\epsilon )}^T=(\frac{\partial (n^2)}{\partial {\rho }_1},\frac{\partial (n^2)}{\partial {\rho }_2})=2n(m_1\frac{\partial n}{\partial c_1},m_2\frac{\partial n}{\partial c_2}).$$ (23)

By substituting the expressions from Eqs. (21) and (23) into Eq. (1), and defining a dimensionless refractive index gradient vector by

$$\nabla \stackrel{\sim }{n}=\frac{1}{2n\overline{v_1}}{\nabla }_{\rho }\epsilon =(\frac{m_1}{\overline{v_1}}\frac{\partial n}{\partial c_1},\frac{m_2}{\overline{v_2}}\frac{\partial n}{\partial c_2}),$$ (24)

we obtain

$$\mathrm{\Delta }\mathcal{R}(0)=\left(\frac{4{\pi }^2{n}^2\overline{v_0}}{{\lambda }^4}\right)\nabla {\stackrel{\sim }{n}}^T\cdot {[H_{\varphi }[\stackrel{\sim }{g}]]}^{-1}\cdot \nabla \stackrel{\sim }{n}$$ (25)

Because $\stackrel{\sim }{g}$, ${\varphi }_1$, ${\varphi }_2$, and $\nabla \stackrel{\sim }{n}$ are each dimensionless, the factor $\overline{v_0}/{\lambda }^4$ in Eq. (25) clearly shows that $\mathrm{\Delta }\mathcal{R}(0)$ has the required dimensions of inverse length.

Two convenient, alternative forms of the Rayleigh ratio will be used in the analysis below. First, if a dimensionless free energy is obtained by multiplying by a volume different from $\overline{v_0}$, for example, $\stackrel{\sim }{g\ast }=\overline{v_1}G/V{k}_{B}T$, Eq. (25) still holds but with $\stackrel{\sim }{g}$ replaced by $\stackrel{\sim }{g\ast }$ and $\overline{v_0}$ replaced by $\overline{v_1}$. In particular, we shall use the following dimensionless scattering intensity $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$, obtained from Eq. (25), for further analysis of the scattering both near the $\gamma$-crystallin axis and for concentrated mixtures of $\alpha$ with $\gamma$:

$$\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }=\frac{{\lambda }^4\mathrm{\Delta }R(0)}{4{\pi }^2{n}^2{\overline{v}}_1{|\nabla \stackrel{\sim }{n}|}^2}={\xi }^{\text{T}}\cdot {[H_{\varphi }[{\stackrel{\sim }{g}}^{\ast }]]}^{-1}\cdot \xi$$ (26)

in which $\theta$ is the angle between $\nabla \stackrel{\sim }{n}$ and the $\gamma$-crystallin axis, along which ${\varphi }_2=0$, and $\xi =(\cos \theta ,\sin \theta )$ is the unit vector in the direction of $\nabla \stackrel{\sim }{n}$. Specializing to the context of the current model, noting that $H_{\varphi }{[{\stackrel{\sim }{g}}^{\ast }]}^{-1}=(\overline{v_0}/\overline{v_1})H_{\varphi }{[\stackrel{\sim }{g}]}^{-1}$, and using Eqs. (17) and (21), we have

$$\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }={\xi }^{\text{T}}\cdot {[H_{\varphi }[{\stackrel{\sim }{g}}^{\ast }]]}^{-1}\cdot \xi ={\xi }^{\text{T}}\cdot \frac{1}{{(\text{det}𝑸)}^2}\left[\begin{array}{cc}\hfill {\rho }_1\overline{v_1}a\hfill & \hfill \sqrt{{\rho }_1{\rho }_2}\overline{v_2}b\hfill \\ \hfill \sqrt{{\rho }_1{\rho }_2}\overline{v_2}b\hfill & \hfill {\rho }_2({\overline{v_2}}^2/\overline{v_1})c\hfill \end{array}\right]\cdot \xi =\frac{1}{{(\text{det}𝑸)}^2}[{\rho }_1\overline{v_1}a{\cos }^2\theta +\sqrt{{\rho }_1{\rho }_2}\overline{v_2}b\sin 2\theta +{\rho }_2({\overline{v_2}}^2/\overline{v_1})c{\sin }^2\theta ].$$ (27)

Second, another instructive form of $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$, one closely connected with the concepts illustrated by Figs. 1 and 2, can be obtained in a form like the one appearing in the last line of Eq. (1), by re-expressing the right-hand side in the orthogonal curvilinear coordinate system that is created by the eigendirections of the Hessian matrix⁴⁹

$$\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }=\frac{{\cos }^2{\theta }_{+}}{{\lambda }_{+}}+\frac{{\cos }^2{\theta }_{-}}{{\lambda }_{-}},$$ (28)

where ${\lambda }_{+}$ and ${\lambda }_{-}$ are the maximum and minimum eigenvalues of $H_{\varphi }[{\stackrel{\sim }{g}}^{\ast }]$, respectively, and ${\theta }_{+}$ and ${\theta }_{-}$ are the angles between their respective eigendirections and $\xi$. Thus, if the smaller eigenvalue of the Hessian approaches 0, much light could be scattered, unless ${\theta }_{-}$ is close to $\pi /2$. We will use Eq. (28) below in analyzing light scattering in concentrated $\gamma$-$\alpha$ mixtures with the sticky-sphere mixture model.

III. MODEL OF LIGHT SCATTERING FROM AQUEOUS $\gamma$B AND $\alpha$ CRYSTALLIN MIXTURES

A. Molecular parameters for $\gamma$B and $\alpha$-crystallin

To apply the sticky-sphere mixture model predictions for light scattering given in Eq. (27) to mixtures of the eye-lens proteins $\gamma$B-crystallin (species 1) and $\alpha$-crystallin (species 2), we need to adopt suitable values of the diameters d₁₁, d₂₂, and d₁₂, the attractive interaction parameters ${\tau }_{11}$, ${\tau }_{12}$, ${\tau }_{22}$, as well as the refractive index increments. The values of both the attraction and the size parameters were chosen to give a good fit to the principal features of previously reported¹¹ light scattering data on $\gamma$B-crystallin and $\alpha$-crystallin mixtures, replotted in Figure 3 below, while also being compatible with previous work. In the following paragraphs we describe these parameters; the values adopted in this work are listed in Table I. As stated in Ref. 11, the static light scattering measurements being modeled here were obtained from aqueous solutions containing 0.1 molar sodium phosphate buffer, pH 7.1, with fresh 20 millimolar dithiothreitol (DTT) added to minimize dimerization of $\gamma$B-crystallin, and 0.02% sodium azide as a preservative. Because some of the previous work made use of D₂O in small-angle neutron scattering experiments, it is also important to note that the water used for the measurements reported in Ref. 11 was entirely H₂O, a fact not explicitly stated in Ref. 11. We note the use of closely related, yet differing buffer conditions in each of the comparisons with previous work below.

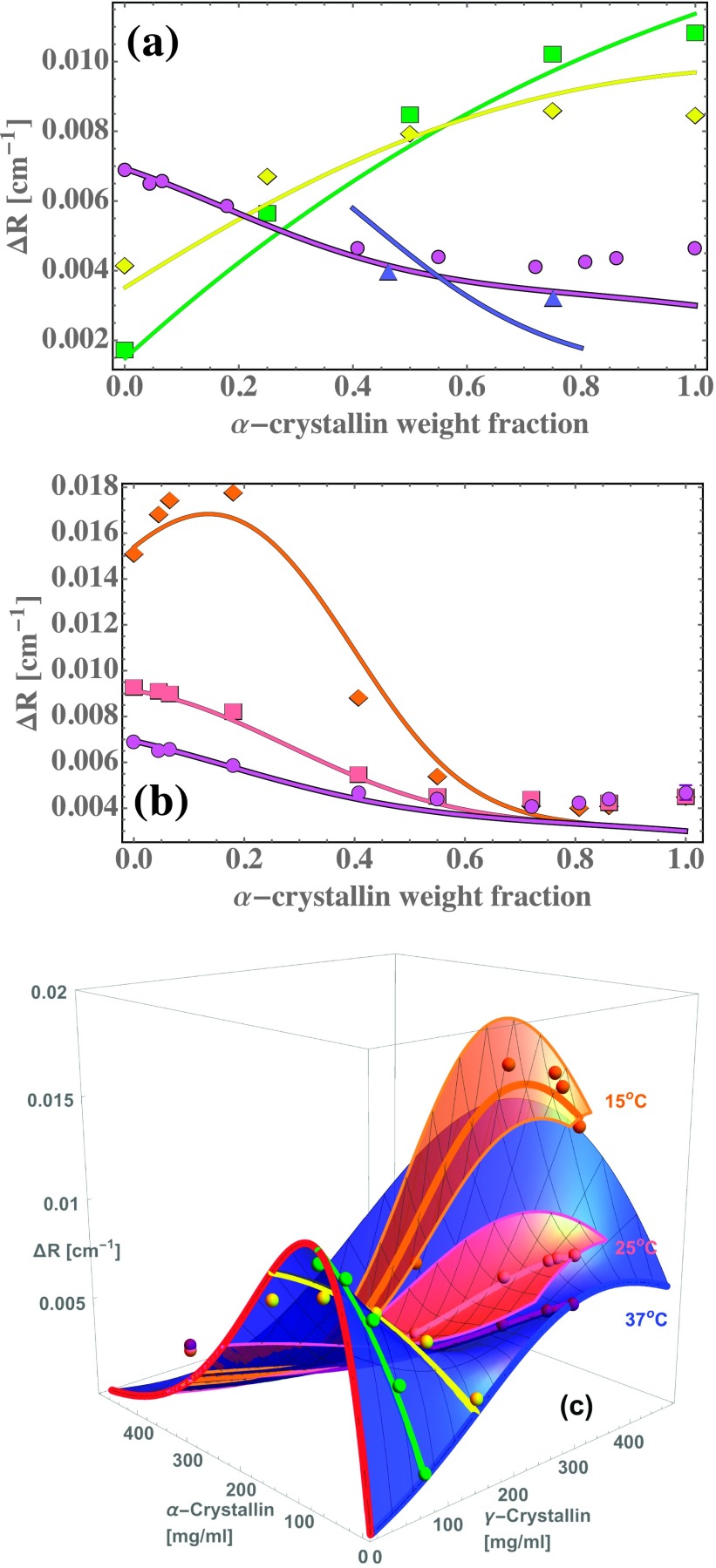
FIG. 3.

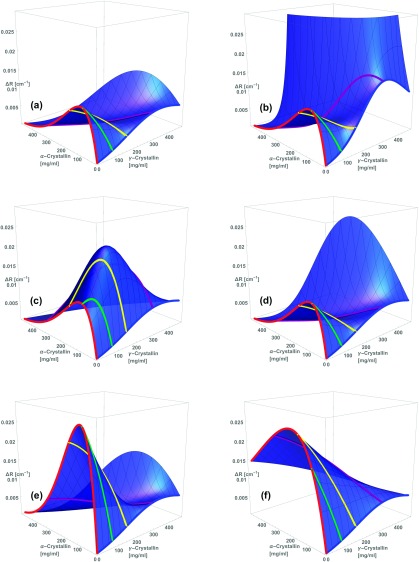
The present model quantitatively reproduces several features of the excess Rayleigh ratio $\mathrm{\Delta }R$ of concentrated and dilute mixtures of $\gamma$ and $\alpha$ crystallin. Each panel shows $\mathrm{\Delta }R$ vs. weight/volume concentrations $c_{\alpha }$ and $c_{\gamma }$, measured (points)¹¹ and calculated (surfaces and curves) from the model. (a): Modeled $\gamma$-$\alpha$ scattering at 37 °C is concave down at relatively low (75 mg/ml green) and intermediate (150 mg/ml yellow) concentrations, and concave up at higher concentrations at body temperature (300 mg/ml purple), in approximate agreement with experiment. (b): Temperature dependence of scattering at 300 mg/ml; purple points and curve repeat 37 °C data and model from (a). 25 °C (pink) and 15 °C (orange) data and model curves show intense scattering near the $\gamma$-crystallin binary axis as phase separation is approached; note that at 37 °C $\mathrm{\Delta }R$ decreases as $\alpha$-crystallin is added to concentrated $\gamma$-crystallin solutions, while at 15 °C $\mathrm{\Delta }R$ at first increases as $\alpha$-crystallin is added. In (c) $\mathrm{\Delta }R$ data (points) and model (surfaces and curves) are plotted vs. $c_{\gamma }$ and $c_{\alpha }$. Red curve: $\alpha$-crystallin $\mathrm{\Delta }R$ rises quickly at low $c_{\alpha }$ due to its large molecular weight. At higher $c_{\alpha }$, liquid packing constrains molecule positions and suppresses concentration fluctuations, slowing and reversing the increase of $\mathrm{\Delta }R$ with $c_{\alpha }$.^2,3 Blue curve: $\gamma$-crystallin $\mathrm{\Delta }R$ rises at low $c_{\gamma }$ at about 1/40 the rate shown by $\alpha$, because of its much smaller molecular weight. However, at higher $c_{\gamma }$, $\mathrm{\Delta }R$ from $\gamma$-crystallin solutions is comparable to that from $\alpha$. The surfaces in (c) show that the model predicts $\gamma$-$\alpha$ mixtures to have sharply increased $\mathrm{\Delta }R$ at high protein concentrations.

TABLE I.

Molecular parameters used in the model, discussed in the text.

Quantity	$\gamma$B-	$\alpha$-	$\alpha$-$\gamma$
	Crystallin	Crystallin	Interaction
(dij)a	1	4.33	2.67
$M_{\text{W}}$(g/mole)	$2.1\times {10}^4$	$7.9\times {10}^5$
${\tau }_{ij}$:b
37 °C	0.99	$\mathrm{\infty }$	6.4
25 °C	0.88	$\mathrm{\infty }$	6.4
15.1 °C	0.75	$\mathrm{\infty }$	6.4
${(\partial n/\partial c)}_0$ (cm3/g)	$0.21\pm 0.004$ c	$0.165\pm 0.005$ d
$v_{\text{eff}}$ (cm3/g)e	0.71	1.52

^aMinimum hard-core center separation (dimensionless).

^bStickiness parameters; (attractions $\propto$ 1/${\tau }_{ij}$).

^cFrom Ref. 57.

^dReference ⁵⁹.

^eEffective volume per unit mass (see text).

For d₁₁, d₂₂, and the corresponding $v_{eff}$ values, we use values similar to those adopted in Ref. 12 and described there; briefly, d₁₁ corresponds to the diameter of a sphere with the volume of one molecule of $\gamma$B-crystallin. With use of the value for $\gamma$B-crystallin⁵ of $v_{eff}=\mathrm{\hspace{0.17em}0.71}$ cm³/g, typical of globular proteins, together with the known molecular weight $M_{W,\gamma }$ of bovine $\gamma$B-crystallin, $\mathrm{20\hspace{0.17em}993}$ g/mole,⁵⁸ one obtains $d_{11}=\mathrm{\hspace{0.17em}36.2}$ Å. However, the sticky-sphere model light scattering predictions can be written so that the diameter values enter in terms of ratios, and so we take d₁₁ = 1 in Table I. d₂₂ corresponds to a diameter consistent with small-angle X-ray and neutron scattering data for $\alpha$-crystallin. The present value d₂₂ = 4.33 (in units of d₁₁), slightly smaller than the corresponding value 4.53 in Ref. 12, provided for a better fit to the Rayleigh ratio data of Ref. 11 being modeled. d₁₂ is the distance of closest approach of the centers of the different size model hard-sphere cores, and is therefore given by d₁₂ = (d₁₁ + d₂₂)/2. Whereas actual bovine $\alpha$-crystallin preparations are typically polydisperse (see, for example, Ref. 44), here we use a value for $M_{W,\alpha }$ that is typical of the molecular weight of the bovine $\alpha$-crystallin preparations of the present type, $\mathrm{790\hspace{0.17em}000}$ g/mole.

The values of the attraction parameters, ${\tau }_{11}(T)$, ${\tau }_{22}$, and ${\tau }_{12}$, were chosen to give a good fit to the principal features of the light scattering data reported previously in Ref. 11, while also being consistent with (i) the nearby liquid-liquid phase separation of these aqueous $\gamma$B crystallin solutions,¹¹ (ii) the weak attractions between $\gamma$B and $\alpha$-crystallin found in previous work, that modeled and simulated small-angle neutron scattering data from concentrated $\gamma$B and $\alpha$ crystallin mixtures in D₂O,^12–14 and (iii) the fact that hard-sphere models have long been found to provide good fits to X-ray and neutron scattering data for $\alpha$-crystallin.^{2,3,12–14,44,55} Accordingly, we take ${\tau }_{22}=\mathrm{\infty }$, for which $\alpha$-$\alpha$ interactions are hard-core. We now discuss the attraction parameters ${\tau }_{11}(T)$ and ${\tau }_{12}$ in more detail.

The adopted, temperature-dependent values of ${\tau }_{11}(T)$ correspond to an increasingly strong, attractive effective potential as temperature decreases. Although there are only three temperatures for $\tau$ in Table I, their compatibility with the nearby liquid-liquid upper consolute point is illustrated by the fact that a linear fit to the three $\tau$ values vs. temperature intersects the upper consolute critical point $\tau$ value for the compressibility route to the equation of state, ${\tau }_c=2-\sqrt{2}$, appropriate for the definition of $\tau$ used here, at −1 °C, not far from the critical temperature of 1 °C–2 °C observed in the H₂O, DTT-containing phosphate buffer used (see Fig. 3 of Ref. 11).

The resulting, approximate rate of change of ${\tau }_{11}$ with temperature is a factor of 1.7 larger than that found by Fine et al.^9,57 in their sticky-sphere model for solutions of $\gamma$B-crystallin. This may be due to the fact that the buffer used for obtaining the data analyzed here, previously published in Ref. 11, contained 20 mM dithiothreitol, as noted above, unlike the buffer used for the high concentration measurements analyzed in Ref. 9. Both buffers used H₂O.

We converted the values of ${\tau }_{11}(T)$ into effective square well depths, to compare with previous analyses of $\gamma$-crystallin phase diagrams.^10,46 To do so, we equated second virial coefficients of sticky-sphere and square-well models; as derived below in Eq. (48), for the sticky-sphere model the mixed or pure second virial coefficients are

$$B_{ij}^{(p,f)}(T)(\text{sticky}-\text{sphere model})=\frac{2\pi }{3}{d}_{ij}^3\left(1-\frac{3}{2{\tau }_{ij}}\right).$$ (29)

The square-well model second virial coefficients are

$$B_{ij}^{(p,f)}(T)(\text{square}-\text{well model})=\frac{2\pi }{3}{d}_{ij}^3(1-(e^{-u_{ij}/k_{B}T}-1)({(1+{\lambda }_{ij})}^3-1)),$$ (30)

in which u_ij is the square well depth beyond its inner wall, d_ij is the radial separation between centers when the inner, hard-core walls are in contact, and $(1+{\lambda }_{ij})d_{ij}$ is the radial separation of the centers at the outer wall of the square-well. The quantity $(1+\lambda )$ used here and below, and in Ref. 12, corresponds to the quantity $\lambda$ in Ref. 10.

By equating the expressions for $B_{ij}^{(p,f)}$ in Eqs. (29) and (30), one finds that the effective square well depth corresponding to given values of ${\tau }_{ij}$ and ${\lambda }_{ij}$, $(u_{\text{eff,}ij})/k_{B}T$, is

$$\frac{u_{\text{eff},ij}}{k_{B}T}=\log \left(1+\frac{3}{2{\tau }_{ij}\left({(1+{\lambda }_{ij})}^3-1\right)}\right),$$ (31)

and ${\tau }_{\text{eff,}ij}$ for given square-well parameters is

$${\tau }_{\text{eff,}ij}=\frac{3}{2\left({(1+{\lambda }_{ij})}^3-1\right)\left(e^{u_{ij}/k_{B}T}-1\right)}.$$ (32)

With use of Eq. (31) and ${\lambda }_{ij}=0.25$, corresponding to the square-well widths used in both Refs. ¹⁰ and ¹², the values of ${\tau }_{11}$ from Table I yield $u_{\text{eff}}/k_{B}T$ values of 0.95, 1.03, and 1.13 for T = 37 °C, 25 °C, and 15 °C, respectively. A linear fit to the corresponding $u_{\text{eff}}$ values as a function of temperature intersects the critical value reported in Table I of Ref. 10 for $\lambda =\mathrm{\hspace{0.17em}0.25}$, $u_{\text{eff,c}}/k_B{T}_c=\mathrm{\hspace{0.17em}1.27}$, at $T=-0.8$ °C, which is again compatible with the experimental T_c of 1 to 2 °C for the solutions modeled here. We note that the coexistence curve measurements⁷ analyzed in Ref. 10 were obtained in an H₂O-based phosphate buffer like the one used in Ref. 11, but without added DTT.

Second, we find that the values of ${\tau }_{11}(T)$ found here are compatible with the analysis of the phase diagram of a closely related protein, bovine $\gamma$IIIb-crystallin, one of those also analyzed in Ref. 10, in terms of a model of orientation-dependent protein interactions.⁴⁶ Eq. (2) of Ref. 46, which we state here for convenience in Eq. (33), models an effective, temperature-dependent square-well potential depth, ${\epsilon }_{\text{eff}}(T)$, in terms of (i) the depth $\epsilon$ of small attractive potential well patches on a central sphere and (ii) the fraction a of the area of the central sphere covered by those patches

$${\epsilon }_{\text{eff}}(T)=2k_{B}T\ln \left[a\exp \left(\frac{\epsilon }{2k_{B}T}\right)+(1-a)\right].$$ (33)

The values $\epsilon =9k_B{T}_c$ and a = 0.01, again with use of $\lambda =0.25$, provided for a good fit to the $\gamma$IIIb-crystallin phase diagram,⁴⁶ a phase diagram quantitatively quite similar⁷ to that of bovine $\gamma$B-crystallin,⁴ the protein used for the data modeled here;¹¹ note that at the time of Refs. ⁴ and ⁷, bovine $\gamma$B-crystallin was called bovine $\gamma$II-crystallin. With use of $\epsilon =\mathrm{\hspace{0.17em}9}$ and a = 0.01 in Eq. (33), and using T_c = 2 °C appropriate here, we find ${\epsilon }_{\text{eff}}/k_{B}T$ values of 0.85, 0.97, and 1.09 for T = 37 °C, 25 °C, and 15 °C, respectively. These compare well with the corresponding values 0.95, 1.03, and 1.13 of $u_{\text{eff}}/k_{B}T$ found above to correspond to the present values of ${\tau }_{11}(T)$; changes in either a or $\epsilon$ of only about 10% are sufficient to bring ${\epsilon }_{\text{eff}}(T)$ and $u_{\text{eff}}$ into agreement. Thus the present values of ${\tau }_{11}(T)$ are compatible with this previous analysis of $\gamma$-crystallin phase diagrams in terms of orientation-dependent interactions.

The value of ${\tau }_{12}=6.4$ that provided for a good fit to the observed Rayleigh ratio data also corresponds to an effective, square-well $\gamma$-$\alpha$ attraction strength not far from that previously found to provide a good match between molecular dynamics and small-angle neutron scattering data on concentrated $\gamma$-$\alpha$ mixtures.^12–14 However, it should be noted that D₂O was used as the water portion in the aqueous buffer for the experiments analyzed in Ref. 12, whereas H₂O was used for the experiments of Ref. 11 modeled here, and as a result the effective protein-protein interaction strengths can be expected to be slightly different. Again using Eq. (31), together with the present value ${\lambda }_{\gamma \alpha }=0.094$, we find $u_{\text{eff},\gamma \alpha }=0.57k_{B}T$, close to the value 0.70k_BT in Ref. 12; the latter value may be found by dividing the dimensionless value of $u_{\alpha \gamma }=0.55$ found in Table I of Ref. 12 by the dimensionless temperature $T^{\ast }=\mathrm{\hspace{0.17em}0.7875}$ used for the simulations discussed there. Whereas in principle ${\tau }_{12}$ might depend on temperature, we did not include such a dependence in order to reduce the number of parameters.

B. Refractive index model

We now consider the refractive index increments needed for use in Eq. (25). Ref. 57 reports data showing that for bovine $\gamma$B-crystallin, $\partial n/\partial c_{\gamma }=0.211\pm 0.004$ cm³/g; here we have converted from the volume fraction units used in Ref. 57 to the present weight/volume units using the partial molecular volume 0.71 cm³/g for $\gamma$B-crystallin.⁵ There is a range of reported values of $\partial n/\partial c$ in the literature for $\alpha$-crystallin. Recent measurements of the refractive index of bovine $\alpha$-crystallin solutions that were prepared in the same manner as that for the data analyzed here,¹¹ and analyzed with use of the same UV extinction coefficient, found $\partial n/\partial c_{\alpha }=0.165\pm 0.005$ cm³/g.⁵⁹

These available measurements were taken for the respective pure protein solutions, and we do not have data for the index of refraction, n, over the entire concentration and composition range for which light scattering efficiency data were obtained. Therefore, we adopt a model for the index of refraction of the mixtures, by using the measurements of the refractive index increments of $\gamma$B- and $\alpha$-crystallin just stated to construct a model for the optical-frequency polarizability of their concentrated mixtures.

Many models for the indices of refraction of liquids and liquid mixtures, as functions of concentration and composition, have been studied experimentally and theoretically.^52,60,61 In the case of a single-component gas, the Lorentz-Lorenz relationship takes the form⁵²

$$\frac{n^2-1}{n^2+2}=\rho (A_r+B_r\rho +C_r{\rho }^2+\mathrm{\cdots }).$$ (34)

In Eq. (34), $\rho$ denotes the number density and A_r, B_r, and C_r are called the refractivity virial coefficients, and are related to various aspects of the polarizability of the molecules.⁵² Measurements of the first, second, and some third and fourth-order terms have been carried out for some gases.^62,63 However, relevant to the system being analyzed here, measurements of the index of refraction of aqueous $\gamma$B-crystallin solutions⁵⁷ showed their refractive indices to remain close to linear as a function of $\gamma$B-crystallin concentration up to concentrations of nearly 300 mg/ml, which are close to the maximum concentrations used in the data we analyze here. Such a dependence can be accommodated by using only the first-order term in molecule number density in Eq. (34).

Even so, a number of forms are in use for representing the corresponding Lorentz-Lorenz relationships for fluid mixtures,^60,61 even in the context of an assumed first-order dependence of expressions closely related to that in Eq. (34) on number density. Each of these models comes close to representing measured refractive indices, while refractive index increments are more difficult to represent accurately.^60,61 We adopt the following model, essentially one of those studied in Refs. ⁶⁰ and ⁶¹ and termed there the Lorentz-Lorenz mixing rule, in which we assume that the optical polarizability per unit volume of the mixture is linear in the number densities of each of the molecules

$$\frac{n^2-1}{n^2+2}=\frac{1}{3}({\rho }_w{\gamma }_{\text{w}}+{\rho }_1{\gamma }_1+{\rho }_2{\gamma }_2).$$ (35)

In Eq. (35) the number densities and polarizabilities of the water, $\gamma$B-crystallin, and $\alpha$-crystallin molecules are denoted by ${\rho }_w$ and ${\gamma }_{\text{w}}$, ${\rho }_1$ and ${\gamma }_1$, and ${\rho }_2$ and ${\gamma }_2$, respectively, the molecular polarizabilities ${\gamma }_{\text{i}}$ are defined as the ratios of the average molecular dipole moment to the permittivity of vacuum, ${\epsilon }_0$, times the applied field at that molecule, as in Section 4.5 of Ref. 64, and SI units are used. We model the polarizabilities ${\gamma }_i(\omega )$ as fixed quantities, independent of concentration. Note that in Eq. (35) each of the ${\gamma }_i(\omega )$ has the dimensions of volume, and is often nearly proportional to the volume of that molecule (see, e.g., Appendix C of Ref. 51). Thus Eq. (35) effectively models the optical-frequency polarizability of the protein-water mixture as a linear function of the respective volume fractions, the form in which it is written in Refs. ⁶⁰ and ⁶¹.

We now re-express Eq. (35) in terms of the measured, low concentration refractive index increments of aqueous $\gamma$B-crystallin and $\alpha$-crystallin solutions. Noting that $1={\rho }_w{\mathrm{\Omega }}_w+{\rho }_1{\mathrm{\Omega }}_1+{\rho }_2{\mathrm{\Omega }}_2$, in which ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$, and ${\mathrm{\Omega }}_w$ are the partial molecular volumes of $\gamma$B-crystallin, $\alpha$-crystallin, and water, respectively, the number density of water can be rewritten in the form ${\rho }_w=(1/{\mathrm{\Omega }}_w)(1-{\rho }_1{\mathrm{\Omega }}_1-{\rho }_2{\mathrm{\Omega }}_2)$. Also, the refractive index of pure water, n_w, is given in the model by $(n_w^2-1)/(n_w^2+2)=(1/3)({\gamma }_{\text{w}}/{\mathrm{\Omega }}_w)$. With use of these relationships for ${\rho }_w$ and n_w, together with ${\rho }_1=c_1/m_1$ and ${\rho }_2=c_2/m_2$, Eq. (35) becomes

$$\frac{n^2-1}{n^2+2}-\frac{n_w^2-1}{n_w^2+2}=\frac{1}{3}\left[\frac{c_1}{m_1}\left({\gamma }_1-{\gamma }_{\text{w}}\frac{{\mathrm{\Omega }}_1}{{\mathrm{\Omega }}_w}\right)+\frac{c_2}{m_2}\left({\gamma }_2-{\gamma }_{\text{w}}\frac{{\mathrm{\Omega }}_2}{{\mathrm{\Omega }}_w}\right)\right].$$ (36)

At the same time, to linear order in c₁ and c₂, n and the refractive index increments also satisfy

$$n=n_w\left(1+{\frac{c_1}{n_w}\frac{dn}{d{c}_1}|}_0+{\frac{c_2}{n_w}\frac{dn}{d{c}_2}|}_0\right).$$ (37)

When Eq. (37) is substituted into Eq. (36), again to linear order in the concentrations one obtains

$$\frac{6n_w\left[c_1{\left(\frac{dn}{d{c}_1}\right)}_0+c_2{\left(\frac{dn}{d{c}_2}\right)}_0\right]}{{(n_w^2+2)}^2}=\frac{1}{3}\left[\frac{c_1}{m_1}\left({\gamma }_1-{\gamma }_{\text{w}}\frac{{\mathrm{\Omega }}_1}{{\mathrm{\Omega }}_w}\right)+\frac{c_2}{m_2}\left({\gamma }_2-{\gamma }_{\text{w}}\frac{{\mathrm{\Omega }}_2}{{\mathrm{\Omega }}_w}\right)\right].$$ (38)

Therefore, because of the identity of the coefficients of c₁ and c₂ on both sides of Eq. (38), the model of Eq. (35) implies that each of the low concentration refractive index increments of $\gamma$B and $\alpha$-crystallin is related to the relevant molecular polarizabilities by

$${\left(\frac{dn}{d{c}_i}\right)}_0=\frac{{(n_w^2+2)}^2}{18n_w{m}_i}\left({\gamma }_{\text{i}}-{\gamma }_{\text{w}}\frac{{\mathrm{\Omega }}_i}{{\mathrm{\Omega }}_w}\right).$$ (39)

The relationships represented by Eq. (39) now put us in a position to rewrite Eq. (36) for the mixture refractive index, at both low and high concentrations, in terms of the measured, low-concentration refractive index increments as follows:

$$\frac{n{(c_1,c_2)}^2-1}{n{(c_1,c_2)}^2+2}=\frac{n_w^2-1}{n_w^2+2}+\frac{6n_w\left[c_1{\left(\frac{dn}{d{c}_1}\right)}_0+c_2{\left(\frac{dn}{d{c}_2}\right)}_0\right]}{{(n_w^2+2)}^2}\equiv f(c_1,c_2).$$ (40)

Therefore, in terms of the function f defined in Eq. (40), the mixture model for the polarizability in Eq. (35) finally results in the following model for the index of refraction n(c₁, c₂) as a function of composition:

$$n(c_1,c_2)=\sqrt{\frac{1+2f(c_1,c_2)}{1-f(c_1,c_2)}}.$$ (41)

The corresponding model for the refractive index increments as functions of composition can be found by differentiating both sides of the first line of Eq. (40) with respect to either c_i. This gives

$$\left(\frac{dn}{d{c}_i}\right)(c_1,c_2)=\frac{{(n{(c_1,c_2)}^2+2)}^2}{{(n_w^2+2)}^2}\frac{n_w}{n(c_1,c_2)}{\left(\frac{dn}{d{c}_i}\right)}_0,$$ (42)

in which n(c₁, c₂) is given by Eq. (41).

In this work we use Eqs. (41) and (42), which we have just shown to follow from the polarizability mixture model of Eq. (35), to calculate n² and the concentration-dependent values of dn/dc_i. These in turn are needed to find the Rayleigh ratio using Eqs. (24) and (25), to compare the sticky-sphere mixture model with the data.

In this context, it is interesting to note that the complications represented by Eqs. (41) and (42) can at first seem unwarranted, because, with use of the parameters given in Table I, the linear form for the refractive index given by Eq. (37) is actually very close to the more complicated dependence given by Eq. (41), deviating by at most 0.1%, even for solutions that have protein concentrations of 300 mg/ml. However, at the same time the refractive index increments calculated with use of Eq. (42) deviate much more strongly at high concentrations from their low concentration values, by 3%–4% at the same concentrations. As a consequence, because the refractive index increments enter quadratically into Eq. (25), the use of Eq. (42) instead of the strictly constant values of the refractive index increments in Eq. (37) changes the predicted Rayleigh ratio by 6%–8% at 300 mg/ml. Because of this sensitivity, it would be useful to obtain very accurate measurements of the indices of refraction of the concentrated protein mixtures, so as to be able to refine the present refractive index model, represented by Eq. (35).

C. Comparison of model with experiment

With use of the parameters and index of refraction model presented above, we find that the sticky-sphere mixture model can quantitatively reproduce several key features of the excess Rayleigh ratio observed from concentrated and dilute mixtures of $\gamma$- and $\alpha$-crystallin.¹¹ Figure 3 shows the excess Rayleigh ratio $\mathrm{\Delta }R$ of aqueous mixtures of $\alpha$- and $\gamma$-crystallin vs. weight/volume concentrations $c_{\alpha }$ and $c_{\gamma }$, calculated from the sticky-sphere mixture model using the parameters detailed above in Sections III A and III B. Away from the binary $\gamma$B-water and $\alpha$-water axes, the most prominent feature of the scattering is a pronounced valley in the high concentration scattering, which the model reproduces (panel (c)). Second, the model reproduces the temperature-dependent $\alpha$/$\gamma$ composition dependence of the Rayleigh ratio at high protein concentrations (panel (b)). Third, the model reproduces the concave-down dependence of the Rayleigh ratio on composition at lower concentrations (panel (a)). Below, we use the model to analyze the molecular sources of these interesting features of the scattering in more detail.

IV. ANALYSIS OF LIGHT SCATTERING IN SPECIFIC REGIONS IN THE COMPOSITION TRIANGLE

A. Scattering from concentrated $\gamma$-$\alpha$ mixtures

Here we study the origin of the pronounced “valley” in the scattering intensity from $\gamma$-$\alpha$ mixtures near total protein concentrations of 300 mg/ml, which is apparent from the blue surface and purple curve of Fig. 3(c). In Fig. 4, we study this reduction in scattering in the context of Eqs. (1) and (28), which describe how the intensity of the scattered light depends on the magnitude of local composition fluctuations and to what extent fluctuations are aligned with the dielectric gradient; these factors are illustrated in Fig. 2.

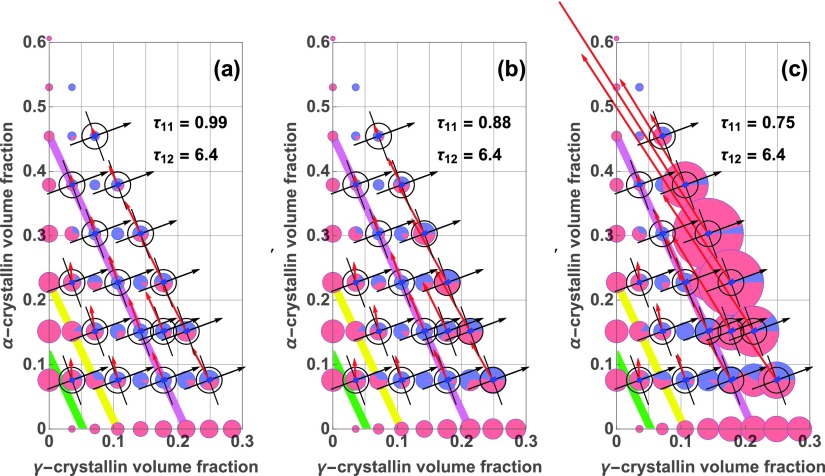
FIG. 4.

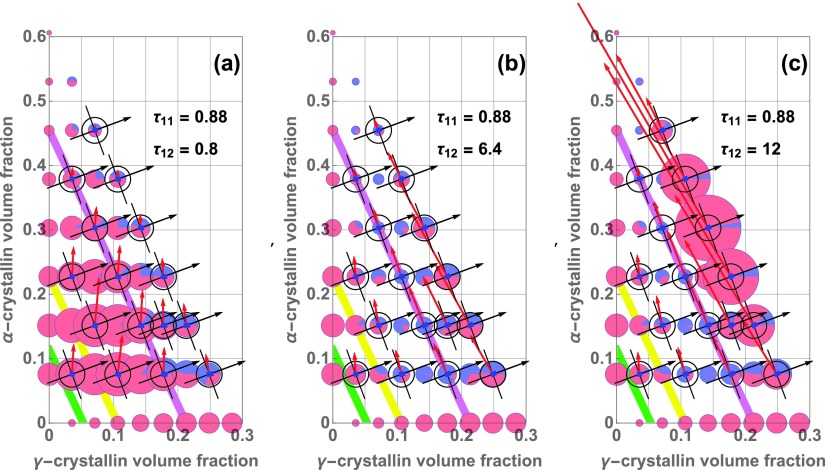
Temperature dependence, via ${\tau }_{11}$, of $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$ contributions in Eq. (28); 37 °C (a); 25 °C (b); 15.1 °C (c). Red arrows show the minimum Hessian eigenvector directions, ${\widehat{e}}_{min}$, and are plotted with lengths proportional to $1/{\lambda }_{min}$. Small blue rectangles at each composition are aligned along the directions of ${\widehat{e}}_{max}$, perpendicular to ${\widehat{e}}_{min}$, and their lengths are proportional to $1/{\lambda }_{max}$. Black arrows show $\mathbf{\nabla }\epsilon$ directions, and black crosshairs show directions perpendicular to $\mathbf{\nabla }\epsilon$. Pie chart areas are proportional to $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$, and show scattering associated with ${\widehat{e}}_{min}$ (red) and ${\widehat{e}}_{max}$ (blue). In all three panels, ${\widehat{e}}_{min}$ can be nearly perpendicular to $\mathbf{\nabla }\epsilon$, and as a result prominent composition fluctuations can scatter little light. At 37 °C, the prominent “valley” in scattering at 300 mg/ml, apparent from the blue surface and purple curve of Fig. 3(c), corresponds to compositions on the purple lines in (a)–(c); 150 and 75 mg/ml mixtures are shown by yellow and green lines, respectively. For most of the two-protein mixtures at 300 mg/ml, ${\widehat{e}}_{min}$ is closely perpendicular to $\mathbf{\nabla }\epsilon$, and less light is scattered than for higher or lower compositions. In panel (c), especially at concentrations higher than 300 mg/ml, $1/{\lambda }_{min}$ increases, ${\widehat{e}}_{min}$ and $\mathbf{\nabla }\epsilon$ are less perpendicular, and much more light is scattered.

The three panels in Fig. 4 show how the light scattering contributions associated with the minimum and maximum Hessian eigenvalues depend on protein concentration and composition at ${\tau }_{11}$ values of (a) 0.99 (37 °C), (b) 0.88 (25 °C), and (c) ${\tau }_{11}=0.75$ (15.1 °C). In each panel, the area of each of the colored pie charts is proportional to the total excess Rayleigh ratio at that composition, while the red and blue sector areas are proportional to the parts of that Rayleigh ratio associated with the minimum and maximum Hessian eigenvalues, respectively, according to Eq. (28). The purple, yellow, and green diagonal lines are drawn at total protein concentrations of 300 mg/ml, 150 mg/ml, and 75 mg/ml, respectively, the concentrations of the mixtures for which the Rayleigh ratio is modeled and displayed in Fig. 3. In particular, compositions along the purple diagonal are approximately in the middle of the light scattering valley in Fig. 3(c).

For most of the two-protein mixtures along the purple diagonal line in Fig. 4, ${\widehat{e}}_{min}$ is closely perpendicular to $\mathbf{\nabla }\epsilon$, and there is relatively little scattering, most of which may be associated with the maximum Hessian eigenvector. Hence those pie charts are small and mostly blue. For example, consider the pie charts for a volume fraction of $\gamma$-crystallin just above 0.1, and a volume fraction of $\alpha$-crystallin close to 0.23. There, the angle between $\mathbf{\nabla }\epsilon$ and ${\widehat{e}}_{min}$ is very close to 90°, and the scattering associated with the maximum eigenvalue (blue) almost completely accounts for the modeled intensity, at both 37 °C and 25 °C. This occurs despite the fact that $1/{\lambda }_{min}$ is about 10 times larger than $1/{\lambda }_{max}$, as can be seen from the ratio of the lengths of the red arrow and the small blue rectangle. In contrast, if one traverses the valley from lower to higher concentrations, the minimum eigenvector rotates counterclockwise, and crosses the direction perpendicular to the dielectric gradient.

That is, the more intense scattering on either side of the scattering valley, which appears in Fig. 4 in the form of larger colored pie charts on either side, can be associated with a transition in the alignment of the prominent composition fluctuations, from being closely aligned with the $\alpha$-crystallin axis at lower volume fractions to becoming more parallel to exchanges of $\gamma$- with $\alpha$-crystallin, at volume fractions above those of the valley. In this connection it is interesting to note that along the yellow and green lines in each of the panels of Fig. 4, there is more light scattering than for compositions along the higher concentration, purple line, even though the values of $1/{\lambda }_{min}$ are smaller at the lower concentrations. This is because the prominent fluctuation directions along the yellow and green lines, shown by ${\widehat{e}}_{min}$, are no longer well-aligned with the perpendicular to $\mathbf{\nabla }\epsilon$.

Another important feature of Fig. 4 is that as the temperature is lowered, following the sequence of panels (a) to (b) to (c), the light scattering intensity increases dramatically for the high-volume fraction mixtures of $\gamma$ and $\alpha$-crystallin. Indeed, the light scattering increase for the highest volume fractions far exceeds that on the $\gamma$-crystallin axis. This greatly increased light scattering is consistent with the approach of the mixtures towards a liquid-liquid phase separation boundary that can be highly elevated in the mixtures, many 10s of °C above the phase separation temperature of $\gamma$-crystallin alone.¹¹ Note also that the only parameter that changes between the panels of Fig. 4 is ${\tau }_{11}$, the $\gamma$-$\gamma$ stickiness parameter. Thus the scattering increase with temperature underlines the importance of $\gamma$-$\gamma$ attraction strength in controlling light scattering from high concentration $\gamma$-$\alpha$ mixtures.

Figure 5, constructed in a similar manner to Fig. 4 with use of the same symbol meanings, explores the role of $\gamma$-$\alpha$ attractions in producing light scattering from their mixtures, by varying ${\tau }_{12}$ instead of ${\tau }_{11}$; for each panel, ${\tau }_{11}=0.88$, corresponding to 25 °C. In panel (a), ${\tau }_{12}=0.8$. Such a strong $\gamma$-$\alpha$ attraction gives rise to very prominent scattering at relatively low overall protein concentrations, peaking at overall protein volume fractions of 0.075–0.15, as shown by the large red circles in that region. An increase in scattering with increasingly strong $\gamma$-$\alpha$ attraction strength corresponds to the previous identification of a cataractogenic mutation that appears to act by increasing $\alpha$-$\gamma$ attractions.²⁰

FIG. 5.

Light scattering intensity contributions vs. $\alpha$-$\gamma$ attraction strength, from strong (${\tau }_{12}=0.8$, in (a)) through Fig. 3 value (${\tau }_{12}=6.4$, in (b)), to weak (${\tau }_{12}=12$, in (c)). As $\alpha$-$\gamma$ attractions weaken, the minimum Hessian eigenvectors (red arrows) rotate counterclockwise relative to $\mathbf{\nabla }\epsilon$ (black arrows), and can become perpendicular to $\mathbf{\nabla }\epsilon$ in (b) and (c), dramatically reducing light scattering (see Eqs. (1) and (28)). Light scattering efficiency (colored circle areas) changes from peaking at low concentrations, in (a), to high concentrations, in (c); thus the peak light scattering intensity is nonmonotonic as a function of $\gamma$-$\alpha$ attraction strength, consistent with previous findings.^12–14 Symbols as in Fig. 4; fixed ${\tau }_{11}=0.88$ corresponds to T = 25 °C (Table I).

In panel (b) of Fig. 5, the $\gamma$-$\alpha$ attraction strength has been reduced by increasing ${\tau }_{12}$ to the value 6.4, and the low concentration scattering peak in panel (a) has been largely suppressed. Fig. 5(b) is the same as Fig. 4(b), and is included to illustrate both the transition and the connection with the $\tau$ values used to model the experimental data in Fig. 3. Note that decreasing the $\gamma$-$\alpha$ attraction strength is associated with a marked counterclockwise rotation of the minimum eigenvectors of the Hessian, towards the direction perpendicular to $\mathbf{\nabla }\epsilon$, as shown especially in the transition from Fig. 5(a) to Fig. 5(b). Thus, for example, for mixtures near the $\gamma$ axis, along the purple line in Fig. 5(b), less light is scattered than for the ${\tau }_{12}=0.8$ of Fig. 5(a), even though the values of $1/{\lambda }_{min}$ there are larger for ${\tau }_{12}=6.4$ in panel (b).

In panel (c) of Fig. 5, ${\tau }_{12}$ has been increased to 12, a value that corresponds to very little attraction between $\gamma$- and $\alpha$-crystallin. In panel (c), scattering at high volume fractions is greatly increased, very much like that which happens when $\gamma$-$\gamma$ attractions are increased, as was shown Fig. 4(c). Note that a similar progression of the pattern of light scattering upon going from low to high values of ${\tau }_{12}$ may also be seen by following the progression in Fig. 9 from panel (c) to (a) to (d) there, although the graphs in Fig. 9 are computed for T = 37 °C. In Fig. 5(c), the very long red arrows at high concentration correspond to small values of ${\lambda }_{min}$ that are associatedwith exchange of protein species. That is, the free energy is very gently curved in that direction, corresponding to the tendency of mixtures of different size particles to be near instability towards segregation by size.

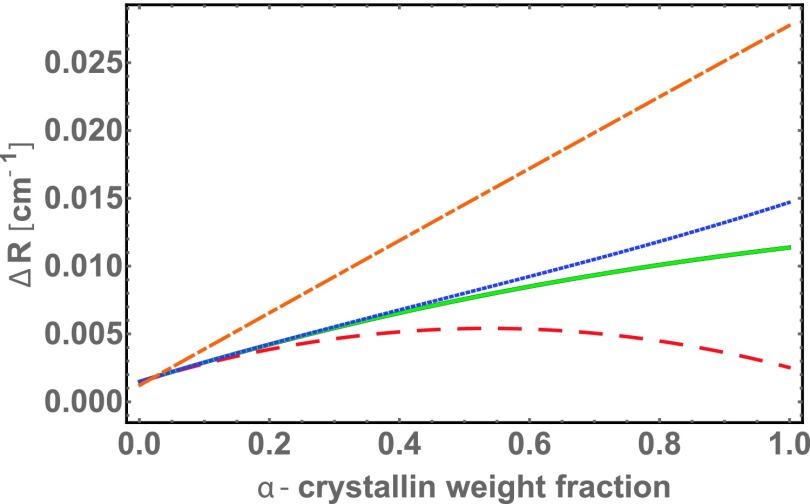
FIG. 9.

The present model can be used to study how observed and hypothetical changes in γ- and α-crystallin could affect light scattering from dilute and concentrated γ-α mixtures. The baseline case shown in panel (a) is the modeled body-temperature light scattering cross-section, $\mathrm{\Delta }R$, vs. γ-α-buffer ternary mixture composition, that is compared with the data in Fig. 3. Panel (b): Increased proximity to γ-crystallin phase separation, here going from $T-T_c=32$ °C to $T-T_c=10$ °C, not only increases scattering from pure γ solutions, but also, and in fact much more dramatically, increases light scattering from high concentration γ-α mixtures. Panel (c) illustrates the effect of an increase in γ-γ attractions, here from ${\tau }_{12}=6.4$ to ${\tau }_{12}=1$, to make a qualitative comparison with previous modeling and simulation,^12,13 and a proposed mechanism for a congenital cataract.²⁰ Panel (d) illustrates the effect of a small decrease in γ-α attraction, from ${\tau }_{12}=6.4$, as in (a) to ${\tau }_{12}=9$, which would greatly increase scattering, consistent with previous findings about phase separation instability.^12,13 The sequence of panels (c), (a), and (d) illustrates that the light scattering cross-section is non-monotonic in decreasing α-γ attraction strength. Panel (e) illustrates that low-concentration scattering would also greatly increase from that in panel (a) if the molecular weight of α-crystallin were closer to $2\times {10}^6$ g/mole rather than $8\times {10}^5$ g/mole, though the current model can only accommodate hypothetical growth into a larger sphere, which is unlikely (see, e.g., Ref. 45). Panel (f) illustrates another hypothetical change, that of making α more compact, by lowering its effective volume from its open, chaperone-protein structure to the 0.7 ml/g typical of globular proteins.⁶⁸ Interestingly, while such a change would dramatically increase light scattering at low $\gamma$-crystallin concentrations, for a large range of $\alpha$-crystallin concentrations, it would reduce light scattering in high-concentration mixtures.

Thus Fig. 5 shows that the value of ${\tau }_{12}$ that models the experimental data well is in a range for which light scattering is much lower than what could occur in the presence of stronger or weaker $\alpha$-$\gamma$ attractions. This finding of a nonmonotonic behavior of the Rayleigh ratio as a function of $\alpha$-$\gamma$ attraction strength is consistent with the results of the perturbation-theory and molecular dynamics findings presented previously.^12–14

B. Scattering from concentrated $𝜸$/dilute $𝜶$ mixtures

The Rayleigh ratio of sufficiently concentrated bovine $\gamma$B-crystallin solutions is lowered by adding small amounts of $\alpha$-crystallin near body temperature, at fixed overall protein concentration, but is raised by such additions at lower temperatures, as shown in Fig. 3(b). A qualitative rationale for this contrast was given in Ref. 11. Here we use the sticky-sphere model to study this contrast more quantitatively, and to do so we also supplement the previous analysis to allow for different refractive index increments and partial specific volumes for each protein.

As described in Ref. 11, near the $\gamma$-crystallin axis the sources of light scattering can be conveniently divided into four terms, that give the magnitudes of (i) the on-axis scattering, (ii) the change in scattering that would otherwise occur because of the larger molecular weight of $\alpha$-crystallin, (iii) scattering that can be associated with changing proximity to phase separation, and (iv) a reduction in scattering associated with prominent fluctuations that are nearly perpendicular to the dielectric gradient, like those described in Section IV A above. Because the first contribution refers to scattering in the absence of $\alpha$-crystallin, the temperature dependence of the change in scattering because of added $\alpha$ must result from a changing balance between the latter three contributions. As in Ref. 11 we start with the asymptotic form of the chemical potential for solutions in which $\gamma$-crystallin can be dilute or concentrated, but $\alpha$-crystallin is dilute⁶⁵

$${\stackrel{\sim }{g}}^{\ast }({\varphi }_1,{\varphi }_2\ll 1,T)=\frac{{\overline{v}}_{1}G({\varphi }_1,{\varphi }_2\ll 1,T)}{V{k}_{B}T}=\left(\frac{{\overline{v}}_1}{{\overline{v}}_2}\right){\varphi }_2\ln {\varphi }_2+r({\varphi }_1,{\varphi }_2,T),$$ (43)

where we assume that $r({\varphi }_1,{\varphi }_2,T)$ can be expanded in a Taylor series in ${\varphi }_1$, ${\varphi }_2$, and T near ${\varphi }_2=0$. Note that r will not have such an expansion at (i) ${\varphi }_1=0$, (ii) right at ${\varphi }_1={\varphi }_{1,c}$, the critical point for $\gamma$-crystallin/water liquid-liquid phase separation,^5,6 nor (iii) at any critical points that have ${\varphi }_2\ne 0$. However, the light scattering data we analyze in this section are for ${\varphi }_1\ne 0$ and were taken under conditions well away from critical loci.

By substituting the expression for ${\stackrel{\sim }{g}}^{\ast }({\varphi }_1,{\varphi }_2\ll 1,T)$ in Eq. (43) into that for $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$ in Eq. (26), then expanding in a Taylor series in ${\varphi }_2$ about ${\varphi }_2=0$, for fixed ${\varphi }_1$ and T, and assuming that the dielectric gradient direction $\theta$ does not vary with ${\varphi }_2$, one obtains

$$\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }({\varphi }_1,{\varphi }_2\ll \mathrm{\hspace{0.17em}1},T)={\cos }^2\theta /r_{20}+({\sin }^2\theta )({\overline{v}}_2/{\overline{v}}_1){\varphi }_2+({\cos }^2\theta )[(({\overline{v}}_2/{\overline{v}}_1)r_{11}^2-r_{21})/r_{20}^2]{\varphi }_2-(\sin 2\theta )({\overline{v}}_2/{\overline{v}}_1)(r_{11}/r_{20}){\varphi }_2+\mathcal{O}({\varphi }_2^2)$$ (44)

in which $r_{ij}=\left[{\partial }^{i+j}r/{(\partial {\varphi }_1)}^i{(\partial {\varphi }_2)}^j\right]({\varphi }_1,0,T)$.

The origin of the terms in a simplified form of Eq. (44) has been discussed in Ref. 11; we summarize briefly here for convenience. The binary axis term, ${\cos }^2\theta /r_{20}({\varphi }_1,0)$, is the scattering cross section on the $\gamma$-crystallin axis. Note that it becomes large near a binary system thermodynamic spinodal, defined by r₂₀ = 0.

The second, dilute component molecular weight term, $({\sin }^2\theta )\left({\overline{v}}_2/{\overline{v}}_1\right){\varphi }_2$, would be the only additional term in $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$ of a dilute $\alpha$-crystallin sample in buffer. It is proportional to the number density ${\rho }_2$ of $\alpha$-crystallin multiplied by the square of its volume, ${\overline{v}}_2$, because ${\overline{v}}_2{\varphi }_2={\rho }_2{\overline{v}}_2^2$, or alternatively, it is proportional to the weight/volume concentration of $\alpha$-crystallin times its molecular weight, just as in dilute solution. The factor of $1/{\overline{v}}_1$ results from the normalization adopted here for the dimensionless quantity $\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }$; see Eq. (26).

The third and fourth terms in Eq. (44) become prominent at higher concentrations of $\gamma$-crystallin, ${\varphi }_1$. The third, phase-separation approach term, $({\cos }^2\theta )\left[\left(({\overline{v}}_2/{\overline{v}}_1)r_{11}^2-r_{21}\right)/r_{20}^2\right]{\varphi }_2$, reflects changing proximity of a thermodynamic spinodal temperature T_sp to the fixed measurement temperature,¹¹ as ${\varphi }_2$ increases from 0. Sufficiently close to $T_{sp}({\varphi }_1,{\varphi }_2)$, it is positive if T_sp approaches T upon increasing ${\varphi }_2$, and negative otherwise. The magnitude of either effect increases near T_sp, because of the factor $1/r_{20}^2$.

In the fourth, ternary mixture fluctuation-direction term, $-(\sin 2\theta )\left({\overline{v}}_2/{\overline{v}}_1\right)\left(r_{11}/r_{20}\right){\varphi }_2$, the local saddle-like part of the free energy is proportional to $r_{11}({\varphi }_1,0,T)$. If r₁₁ is positive, the free energy is concave up in directions $0<\theta <\pi /2$, and thus suppresses local concentration fluctuations in those directions, because they cost more in free energy. If the dielectric gradient vector is also in the first quadrant, as it is for $\gamma$-$\alpha$ mixtures (see, e.g., Figs. 4 and 5), the fluctuation-direction term decreases the light scattering intensity.

It is very interesting to note that the fluctuation-direction term, like the phase-separation approach term, increases in magnitude near the binary spinodal, because of the factor 1/r₂₀; r₂₀ approaches 0 at the thermodynamic spinodal for liquid-liquid phase separation on the $\gamma$-crystallin/buffer axis. Thus, the fact that eye-lens $\gamma$-crystallins are near conditions for liquid-liquid phase separation, which leads to very intense light scattering when $\gamma$-crystallin is the only protein component in solution, at the same time amplifies a contribution that reduces light scattering intensity, when $\alpha$-crystallin is added. This is a striking way in which the mixture properties are not simple combinations of those of the components.

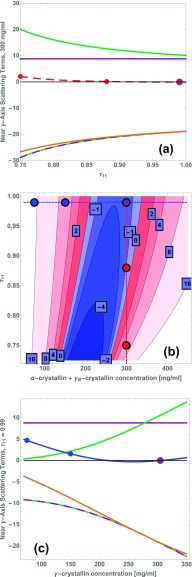
In Figures 6(a) and 6(c) we show representative plots of the contributions of the three mixture terms on the right-hand side of Eq. (44) while Fig. 6(b) is a contour plot of the resulting derivative of the Rayleigh ratio along lines of constant protein weight/volume concentration.

FIG. 6.

The sticky-sphere mixture model shows a delicate balance of the $d(\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast })/d{\varphi }_2$ contributions in Eq. (44). Blue and red points show concentrations and temperatures of $\mathrm{\Delta }R$ measurements near the $\gamma$-crystallin axis.¹¹ Panels (a) and (c): $d(\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast })/d{\varphi }_2$ contributions of the $\alpha$-crystallin molecular weight term (purple), approach to phase separation term (green), fluctuation direction term (orange), and the negative of the sum of the molecular weight and phase separation approach terms (dashed purple and green). Panel (a): $0.75<{\tau }_{11}<0.99$ at $c_{\gamma }=300$ mg/ml; the dashed red curve shows $d(\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast })/d{\varphi }_2$. Panel (c): $70\text{mg/ml}<c_{\gamma }<350\text{mg/ml}$ at ${\tau }_{11}=0.99$, corresponding to T = 37 °C; the blue curve shows the overall sum. Panel (b): contours of $d(\mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast })/d{x}_{\alpha }$ (see text) vs. $c_{\gamma }$ and ${\tau }_{11}$, with negative (blue) and positive (red) regions. Dashed lines in panel (b) correspond to the paths of panels (a) and (c).

In panels (a) and (c), the vertical coordinate shows the contributions of the molecular weight (purple), phase-separation approach (green), and fluctuation-direction terms (orange) to $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial {\varphi }_2$ at fixed ${\varphi }_1$, and evaluated at ${\varphi }_1=0$. The negative of the sum of the molecular weight and phase-separation approach terms is shown by the dashed purple and green curve. In panel (a) the contributions are plotted vs. ${\tau }_{11}$, and thereby vs. temperature, at $c_{\gamma }=$ 300 (mg/ml). In panel (c) the same contributions are plotted vs. $c_{\gamma }$ at body temperature.

The proximity of the orange curves to the dashed green and purple curve in Figs. 6(a) and 6(c) illustrates that in the present model, the positive molecular weight and phase separation approach terms in Eq. (44) are quite remarkably balanced by a negative fluctuation-direction term. We now describe these contributions in more detail. In panel (a), the molecular weight term, shown in purple, is positive and independent of ${\tau }_{11}$, while the phase-separation approach term, shown in green, is also positive but increases upon decreasing ${\tau }_{11}$, corresponding to the approach to liquid-liquid phase separation on the binary $\gamma$-crystallin axis. The fluctuation-direction term, shown in orange, is negative and its magnitude also increases with decreasing ${\tau }_{11}$. This corresponds to an increasing suppression of overall protein concentration fluctuations, with a concomitant amplification of composition fluctuations. It is interesting that although the phase separation approach term is proportional to $1/r_{20}^2$, while the fluctuation-direction term’s magnitude is instead proportional to 1/r₂₀, the presence of the molecular weight term enables the fluctuation-direction term to nevertheless remain relatively close to the negative of the sum of the other two terms over a large range of ${\tau }_{11}$. The dashed red curve shows the overall derivative $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial {\varphi }_2$ vs. ${\tau }_{11}$. The ${\tau }_{11}$ values corresponding to the three temperatures in Fig. 3 are indicated by the circles.

Panel (c) of Fig. 6 studies the concentration dependence of contributions to $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial {\varphi }_2$, at a fixed value of ${\tau }_{11}$ that corresponds to 37 °C. As expected, as the concentration is decreased, the phase separation approach and fluctuation direction terms become smaller, and the molecular weight term eventually dominates. Thus, it is only at low concentrations that the intense scattering from the high molecular weight of $\alpha$-crystallin controls the overall scattered intensity. This can be seen in Fig. 3, and is explored further in panel (e) of Fig. 9, below.

Panel (b) of Fig. 6 shows the contours of the derivative $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial x_{\alpha }$, as a function of both starting $\gamma$-crystallin concentration and ${\tau }_{11}$. For comparison with the path taken in the experiments, this derivative is taken along a path that follows a constant overall weight/volume concentration, $c_{\gamma }+c_{\alpha }=$ 300 (mg/ml), whereas Eq. (44) instead delineates contributions to $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial {\varphi }_2$. Thus to construct Fig. 6(b) we combined the sum of the first order coefficients of ${\varphi }_2$ in Eq. (44) appropriately with $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial c_{\gamma }$ along the original $\gamma$-crystallin axis. Blue and red are used to indicate negative and positive $\partial \mathrm{\Delta }{\stackrel{\sim }{R}}^{\ast }/\partial x_{\alpha }$, respectively, and contours are labeled with its value. The vertical and horizontal lines and circles show the cross-sections studied in panels (a) and (c), respectively.

In summary, compositional fluctuations, aided by proximity to phase separation, reduce $\gamma$-$\alpha$ mixture light scattering near the $\gamma$-crystallin axis well below that which would otherwise result from proximity to phase separation and from $\alpha$-crystallin’s high molecular weight.

C. Scattering from dilute mixtures: Virial coefficients

Because the light scattering prediction method presented above makes use of the Percus-Yevick approximation in the context of the sticky-sphere mixture model, it is useful to compare its predictions with those that are independent of this approximation. Toward this end, we present the second and third mixed virial coefficients of the sticky-sphere mixture model, and investigate the question of how well the low-order virial series corresponding to Eq. (2) accurately represents observed light scattering intensity from mixtures of $\gamma B$ and $\alpha$-crystallin. It is important to note that strictly, the comparisons given here only provide an assessment of how well the Percus-Yevick approximation reproduces the corresponding light scattering that would result from use of the second and third order virial coefficients, with use of the same size and attraction strength parameters. However, because the model resulting from the Percus-Yevick approximation turned out to provide a reasonably accurate representation of the low and high concentration light scattering data from this system, the comparisons also suggest how high in concentration the second and third-order virial coefficients can serve as good representations of the light scattering cross-section. From that point of view, the comparisons can provide information that may be helpful for the design of experiments on aqueous mixtures of globular protein solutions that aim to determine second and third mixed virial coefficients.

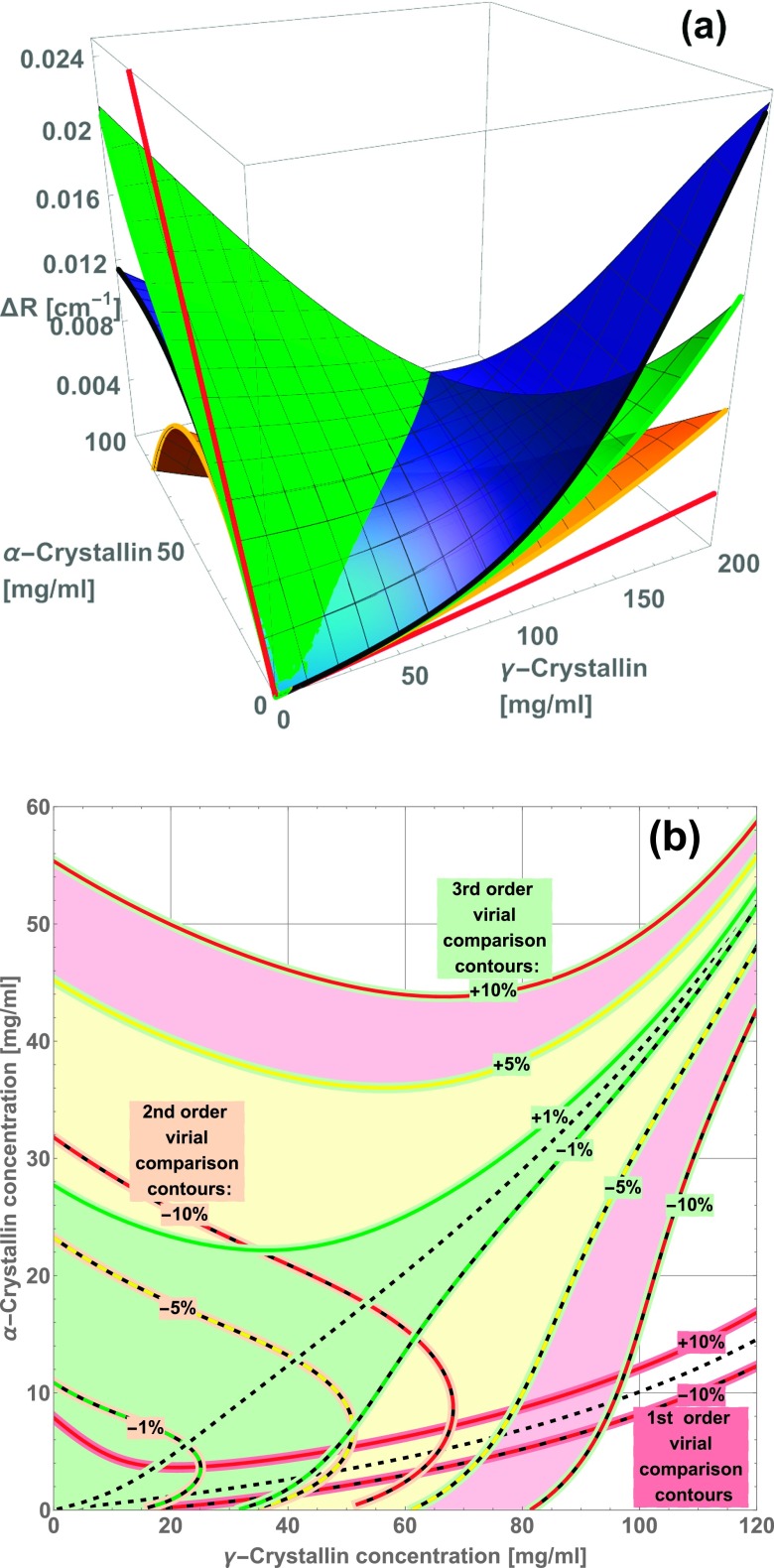
As detailed below, somewhat to our surprise we found that in contrast to the full model, the virial contributions through third-order only work well to represent the Rayleigh ratio up to protein concentrations of 60–80 mg/ml, quite low compared to concentrations in a large portion of the eye lens. This is illustrated in Fig. 7. In panel (a), the blue surface shows $\mathrm{\Delta }R$ for the full sticky-sphere mixture model, corresponding to a temperature near that of the $\gamma$-crystallin phase separation. The red lines show molecular-weight terms, while yellow and green surfaces show the second and third virial light scattering models, respectively. Note that the ideal solution and the third-order virial series models for $\mathrm{\Delta }R$ include a narrow, but extended region that agrees with the full model, associated with the fact that they underestimate $\mathrm{\Delta }R$ along the pure $\gamma$B-crystallin axis, while they overestimate $\mathrm{\Delta }R$ along the pure $\alpha$-crystallin axis. The contours plotted in panel (b) show the percentages by which each of the three virial series formulations of $\mathrm{\Delta }R$ for the sticky-sphere mixture deviate from the $\mathrm{\Delta }R$ calculated using the full sticky-sphere mixture model. As an example, in the union of the green and yellow regions, virial terms up to and including 3rd order represent $\mathrm{\Delta }R$ to within $\pm$5%. The molecular weight plus second virial contributions get within 10% of the full model up until about 60 mg/ml on the $\gamma$ axis, and through about 30 mg/ml on the $\alpha$ axis. The molecular weight plus second virial plus third virial contributions get within 10% up until about 100 mg/ml on the $\gamma$ axis, and through about 50 mg/ml on the $\alpha$ axis. Again, these concentrations are quite low compared to 300 mg/ml concentrations for which the full model represents the experimental data, as shown in Fig. 3.

FIG. 7.

The third-order virial expansion agrees well with the full model light scattering only up to concentrations of 60–80 mg/ml. Here ${\tau }_{11}=0.65$, near the component 1 critical point ${\tau }_{11}=2-\sqrt{2}$; other parameters from Table I. In panel (a): blue surface: $\mathrm{\Delta }R$ for the full model; red lines: molecular-weight contributions; yellow and green surfaces: second and third virial models, respectively. Contours in panel (b) show percentage deviations of virial series $\mathrm{\Delta }R$ values from the full model; red: +10%, yellow: +5%, green: +1%, black dotted: 0%, dashed green and black: −1%, dashed yellow and black: −5%, dashed red and black: −10%.

On the other hand, the calculations to be presented below do give some insight into the origins of the low-concentration, concave-down dependence of the scattered intensity on the relative proportions of $\alpha$ and $\gamma$-crystallin, as we describe below in connection with Eq. (59).

We now describe the calculations and considerations used to construct Fig. 7. The low-density, intensive Helmholtz free energy of a two-component mixture can sometimes be accurately expressed in a series of increasing powers of the number densities ${\rho }_1$ and ${\rho }_2$ as follows:⁶⁶

$$f=\frac{F}{V{k}_{B}T}={\rho }_1\ln {\rho }_1+{\rho }_2\ln {\rho }_2+B_{11}^{(f)}{\rho }_1^2+2B_{12}^{(f)}{\rho }_1{\rho }_2+B_{22}^{(f)}{\rho }_2^2+C_{111}^{(f)}{\rho }_1^3+\mathrm{\hspace{0.17em}3}{C}_{112}^{(f)}{\rho }_1^2{\rho }_2+3C_{122}^{(f)}{\rho }_1{\rho }_2^2+C_{222}^{(f)}{\rho }_2^3+\mathrm{\cdots }.$$ (45)

In Eq. (45), k_B is Boltzmann’s constant, T is the absolute temperature, and $B_{ij}^{(f)}$, $C_{ijk}^{(f)}$ are the second and third virial coefficients, respectively. The virial coefficients measure low-order corrections to the ideal free energy that result from intermolecular interactions, and are functionals of the intermolecular potential and functions of the temperature. It is worth noting that although the virial series can often provide a good representation of the low-density free energy, whether it converges or is accurate can be an involved question, and its applicability can be confounded by self-association equilibria.

It is also important to note that the third virial coefficients in the virial expansion of the Helmholtz free energy differ by a factor of 2 from the third virial coefficients of the corresponding virial expansion of the pressure,⁶⁷ p. The relationship between the two expansions can be readily obtained with use of

$$p=-{\left(\frac{\partial F}{\partial V}\right)}_{T,N_1,N_2}=-k_{B}T\left[f-\left({\rho }_1{\left(\frac{\partial f}{\partial {\rho }_1}\right)}_{T,{\rho }_2}+{\rho }_2{\left(\frac{\partial f}{\partial {\rho }_2}\right)}_{T,{\rho }_1}\right)\right],$$

giving

$$\frac{p}{k_{B}T}={\rho }_1+{\rho }_2+B_{11}^{(f)}{\rho }_1^2+2B_{12}^{(f)}{\rho }_1{\rho }_2+B_{22}^{(f)}{\rho }_2^2+\mathrm{\hspace{0.17em}2}{C}_{111}^{(f)}{\rho }_1^3+6C_{112}^{(f)}{\rho }_1^2{\rho }_2+6C_{122}^{(f)}{\rho }_1{\rho }_2^2+\mathrm{\hspace{0.17em}2}{C}_{222}^{(f)}{\rho }_2^3+\mathrm{\cdots };$$ (46)

that is, $B_{ij}^{(p)}=B_{ij}^{(f)}$, and $C_{ijk}^{(p)}=(2C_{ijk}^{(f)})$.

The second virial coefficients $B_{ij}^{(p)}(T)$ are given by⁶⁶

$$B_{ij}^{(p)}(T)=-2\pi {\int }_0^{\mathrm{\infty }}{f}_{ij}(r)r^{2}dr.$$ (47)

Substituting the Mayer f-function from Eq. (2) into Eq. (47), one finds

$$B_{ij}^{(p)}(T)=\frac{2\pi }{3}{d}_{ij}^3\left(1-\frac{3}{2{\tau }_{ij}}\right).$$ (48)

Similarly, each of the third pressure virial coefficients can be expressed as⁶⁶

$$3V{C}_{ijk}^{(p)}(T)=-\int f_{ij}(|{𝒓}_{ij}|)f_{jk}(|{𝒓}_{jk}|)f_{ik}(|{𝒓}_{ik}|)d{𝒓}_{i}d{𝒓}_{j}d{𝒓}_k,$$ (49)

where ${𝒓}_{ab}={𝒓}_b-{𝒓}_a$. A generating function for the $C_{ijk}^{(p)}$ for multicomponent mixtures of sticky spheres is shown in Appendix F, and is then specialized to the present two-component mixtures and evaluated as functions of the d₁₁, d₁₂, d₂₂, ${\tau }_{11}$, ${\tau }_{12}$, and ${\tau }_{22}$, while as indicated above we take ${\tau }_{22}=\mathrm{\infty }$ in the present model.

With use of the virial expansion analyzed above and in Appendix F, we now give the expressions for the light scattering intensity (Eq. (1)) through the second and third virial coefficients, in terms of the quantities $B_{ij}^{(f)}$ and $C_{ijk}^{(f)}$. The relationship presented in Eq. (D4) between the Helmholtz free energy F⁽²⁾ per unit volume of a two-component system and the Gibbs free energy G⁽³⁾ per unit volume of the modeled three-component system has the consequence that $H_{\rho }(G^{(3)}/V)=H_{\rho }(F^{(2)}/V)$. The latter Hessian can be computed from Eq. (45). Including terms up to the third virial coefficient, and not yet specializing to any particular free-energy model, we obtain

$$H_{\rho }{\left[\frac{F^{(2)}}{V{k}_{B}T}\right]}^{-1}=\frac{1}{{\rho }_1{\rho }_{2}det{H}_{\rho }\left[f\right]}\left\{\left[\begin{array}{cc}\hfill {\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_2\hfill \end{array}\right]+2{\rho }_1{\rho }_2\left[\begin{array}{cc}\hfill B_{22}^{(f)}\hfill & \hfill -B_{12}^{(f)}\hfill \\ \hfill -B_{12}^{(f)}\hfill & \hfill B_{11}^{(f)}\hfill \end{array}\right]+\mathrm{\hspace{0.17em}6}{\rho }_1{\rho }_2\left[\begin{array}{cc}\hfill C_{122}^{(f)}{\rho }_1+C_{222}^{(f)}{\rho }_2\hfill & \hfill -C_{112}^{(f)}{\rho }_1-C_{122}^{(f)}{\rho }_2\hfill \\ \hfill -C_{112}^{(f)}{\rho }_1-C_{122}^{(f)}{\rho }_2\hfill & \hfill C_{111}^{(f)}{\rho }_1+C_{112}^{(f)}{\rho }_2\hfill \end{array}\right]\right\},$$ (50)

where

$${\rho }_1{\rho }_2\text{det}{H}_{\rho }\left[f\right]=\left(1+2B_{11}^{(f)}{\rho }_1+6C_{111}^{(f)}{\rho }_1^2+6C_{112}^{(f)}{\rho }_1{\rho }_2\right)\times \left(1+2B_{22}^{(f)}{\rho }_2+6C_{222}^{(f)}{\rho }_2^2+6C_{122}^{(f)}{\rho }_1{\rho }_2\right)-{\rho }_1{\rho }_2{\left(2B_{12}^{(f)}+6C_{112}^{(f)}{\rho }_1+6C_{122}^{(f)}{\rho }_2\right)}^2.$$ (51)

Using Eqs. (23) and (1),

$$\mathrm{\Delta }\mathcal{R}(0)=\left(\frac{{\pi }^2{k}_{B}T}{{\lambda }^4}\right){\nabla }_{\rho }{\epsilon }^T\cdot H_{\rho }{\left[G^{(3)}/V\right]}^{-1}\cdot {\nabla }_{\rho }\epsilon =\left(\frac{{\pi }^2}{{\lambda }^4}\right){\nabla }_{\rho }{\epsilon }^T\cdot H_{\rho }{\left[F^{(2)}/V{k}_{B}T\right]}^{-1}\cdot {\nabla }_{\rho }\epsilon .$$ (52)

We now combine Eqs. (50) and (51) to evaluate the right-hand side of Eq. (52), and expand in a power series in the number densities of the components, keeping terms to third order in the number densities, to obtain

$$\frac{{\lambda }^4\mathrm{\Delta }\mathcal{R}(0)}{{\pi }^2}={\nabla }_{\rho }{\epsilon }^T\cdot \{\left[\begin{array}{cc}\hfill {\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_2\hfill \end{array}\right]-2\left[\begin{array}{cc}\hfill {\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_2\hfill \end{array}\right]\left[\begin{array}{cc}\hfill B_{11}\hfill & \hfill B_{12}\hfill \\ \hfill B_{12}\hfill & \hfill B_{22}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill {\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\rho }_2\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill c_{11}({\rho }_1,{\rho }_2)\hfill & \hfill c_{12}({\rho }_1,{\rho }_2)\hfill \\ \hfill c_{21}({\rho }_1,{\rho }_2)\hfill & \hfill c_{22}({\rho }_1,{\rho }_2)\hfill \end{array}\right]\}\cdot {\nabla }_{\rho }\epsilon ,$$ (53)

in which

$$c_{11}({\rho }_1,{\rho }_2)={\rho }_1^3\left(4B_{11}^2-6C_{111}^{(f)}\right)+\left(4B_{12}^2-6C_{112}^{(f)}\right){\rho }_1^2{\rho }_2;c_{12}({\rho }_1,{\rho }_2)=c_{21}({\rho }_1,{\rho }_2)={\rho }_1^2{\rho }_2\left(4B_{11}{B}_{12}-6C_{112}^{(f)}\right)+{\rho }_1{\rho }_2^2\left(4B_{22}{B}_{12}-6C_{122}^{(f)}\right);c_{22}({\rho }_1,{\rho }_2)={\rho }_2^3\left(4B_{22}^2-6C_{222}^{(f)}\right)+\left(4B_{12}^2-6C_{122}^{(f)}\right){\rho }_1{\rho }_2^2.$$ (54)

Eqs. (53) and (54) put us in a position to examine the molecular origins of the low concentration features of Fig. 3 in more detail. First, we note that the lowest-order terms in $\mathrm{\Delta }\mathcal{R}(0)$, which we denote by $\mathrm{\Delta }\mathcal{R}{(0)}_{\left(1\right)}$, are

$$\mathrm{\Delta }\mathcal{R}{(0)}_{\left(1\right)}=\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)\left[{\left(\frac{\partial n}{\partial c_1}\right)}^2{\rho }_1{m}_1^2+{\left(\frac{\partial n}{\partial c_2}\right)}^2{\rho }_2{m}_2^2\right]=\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)\left[{\left(\frac{\partial n}{\partial c_{\gamma }}\right)}^2{c}_{\gamma }{m}_{\gamma }+{\left(\frac{\partial n}{\partial c_{\alpha }}\right)}^2{c}_{\alpha }{m}_{\alpha }\right],$$ (55)

where we have used $c_{\gamma }={\rho }_{\gamma }{m}_{\gamma }$ and $c_{\alpha }={\rho }_{\alpha }{m}_{\alpha }$. Eq. (55) is the expression appropriate for low-concentration vertically polarized scattering of vertically polarized incident light. Thus, in Fig. 3, the dramatically larger initial rate of increase of light scattering intensity with concentration for $\alpha$-crystallin, as compared with that for $\gamma$-crystallin, is reflected in Eq. (55) by the fact that the molecular weight of $\alpha$-crystallin, $m_{\alpha }$, is approximately 35–40-fold that of $\gamma$-crystallin, $m_{\gamma }$, while the ratio of the squares of their respective refractive index increments (Table I) is much closer to 1.

The second-order terms in Eq. (53), similarly, can be written as

$$\mathrm{\Delta }\mathcal{R}{(0)}_{\left(2\right)}=-2\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)\times \left[n_{\gamma }^2{c}_{\gamma }^2{B}_{\gamma \gamma }+2n_{\gamma }{n}_{\alpha }{c}_{\gamma }{c}_{\alpha }{B}_{\gamma \alpha }+n_{\alpha }^2{c}_{\alpha }^2{B}_{\alpha \alpha }\right],$$ (56)

where we have used $n_{\gamma }=\partial n/\partial c_{\gamma }$ and $n_{\alpha }=\partial n/\partial c_{\alpha }.$Because the light scattering vs. composition depicted in Fig. 3 is given as a function of the mixing ratio of stock solutions of $\alpha$- and $\gamma$-crystallin, at overall concentrations of 75, 150, and 300 mg/ml, we rewrite Eq. (56), letting $c_{\gamma }^0$ denote the concentration of a stock solution of $\gamma$-crystallin, $c_{\alpha }^0$ denote the concentration of a stock solution of $\alpha$-crystallin, and $0\le f_{\alpha }\le 1$ denote the fraction of the volume of a mixed solution that is taken from the relevant $\alpha$-crystallin stock, $1-f_{\alpha }$ being the fraction taken from the relevant $\gamma$ stock. Thus, in the mixed solution, $c_{\alpha }=f_{\alpha }{c}_{\alpha }^0$ and $c_{\gamma }=\left(1-f_{\alpha }\right)c_{\gamma }^0$. For convenience we define $b_{\gamma \gamma }=n_{\gamma }^2{\left(c_{\gamma }^0\right)}^2{B}_{\gamma \gamma }$, $b_{\gamma \alpha }=n_{\gamma }{n}_{\alpha }\left(c_{\gamma }^0\right)\left(c_{\alpha }^0\right)B_{\gamma \alpha }$, and $b_{\alpha \alpha }=n_{\alpha }^2{\left(c_{\alpha }^0\right)}^2{B}_{\alpha \alpha }$. With these substitutions, we obtain

$$\mathrm{\Delta }\mathcal{R}{(0)}_{\left(2\right)}=\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)\times \left[-2\left(b_{\gamma \gamma }\left(1-f_{\alpha }\right)+b_{\alpha \alpha }{f}_{\alpha }\right)-4B{f}_{\alpha }\left(1-f_{\alpha }\right)\right],$$ (57)

where $B\equiv b_{\gamma \alpha }-\frac{1}{2}\left(b_{\gamma \gamma }+b_{\alpha \alpha }\right)$.

The term $-2\left(b_{\gamma \gamma }\left(1-f_{\alpha }\right)+b_{\alpha \alpha }{f}_{\alpha }\right)$ in Eq. (57) represents a linear dependence of second-order light scattering on relative composition $f_{\alpha }$, dependent only on the pure second virial coefficient magnitudes and signs. This second-order mixture term adds or subtracts from the corresponding linear dependence on composition that results from a similar treatment of Eq. (55), namely $\left(a_{\gamma \gamma }\left(1-f_{\alpha }\right)+a_{\alpha \alpha }{f}_{\alpha }\right)$ with $a_{\gamma \gamma }=n_{\gamma }^2{m}_{\gamma }{c}_{\gamma }^0$ and $a_{\alpha \alpha }=n_{\alpha }^2{m}_{\alpha }{c}_{\alpha }^0$. In the present case, as is well-known, $B_{\alpha \alpha }>0$, making $b_{\alpha \alpha }>0$, so that the effect of the net repulsive interactions between $\alpha$-crystallins is to reduce the light scattering intensity on the $\alpha$-crystallin axis, while $B_{\gamma \gamma }<0$, leading to an increase in light scattering intensity on the pure $\gamma$-crystallin axis, over what it would be for an ideal solution.

Thus, because $B_{\alpha \alpha }>\mathrm{\hspace{0.17em}0}$ while $B_{\gamma \gamma }<\mathrm{\hspace{0.17em}0}$, the dramatic difference in intensity between the two pure protein solutions at a given weight/volume concentration is gradually reduced with increasing concentration, because of the term $-2\left(b_{\gamma \gamma }\left(1-f_{\alpha }\right)+b_{\alpha \alpha }{f}_{\alpha }\right)$. This occurs to an extent that is quadratic in overall protein concentration, because of the dependences of the b_ij on concentration. Physically, the large excluded volume of the $\alpha$-crystallins increasingly reduces the amplitude of spontaneous composition fluctuations that are created by their thermal motion. While the $\gamma$-crystallins also have excluded-volume interactions, their mutual attractions are strong enough to overcome the excluded-volume effect and lead to successively larger, evanescent clusters from which scattered waves are in phase with one another. Specifically, note that the model virial coefficient in Eq. (48), $B_{ij}^{(p)}(T)=\left(2\pi /3\right)d_{ij}^3\left(1-\left(3/2{\tau }_{ij}\right)\right)$, expresses the excluded-volume effect in the term $\left(2\pi /3\right)d_{ij}^3$, while that of the attractions alters the excluded-volume contribution in proportion to $-\left(3/2{\tau }_{ij}\right)$. In the present case, at all the temperatures studied here, ${\tau }_{\gamma \gamma }<1.5$ and the attraction term dominates.

We turn now to the remaining term in Eq. (57), $-4B{f}_{\alpha }\left(1-f_{\alpha }\right)$, which is proportional through B to a symmetric difference between second-order virial coefficients, modulated by refractive index increments. If $B<0$, then as overall protein concentration is increased, this term, by itself, would make $\mathrm{\Delta }\mathcal{R}(0)$ gradually become more concave down as a function of relative composition $f_{\alpha }$. While this might appear to be qualitatively consistent with the concave-down 75 mg/ml $\mathrm{\Delta }\mathcal{R}(0)$ found experimentally, as shown in the top panel of Fig. 3, at the same time it is clear from Fig. 7 that in the present case, at such a large overall concentration, third-virial contributions are quite important for setting concavity with respect to $f_{\alpha }$ at that concentration. We therefore examine this situation more quantitatively.

To identify the molecular properties that determine B in the present model, we use the second virial coefficient expressions in Eq. (48) to obtain

$$B=\frac{2\pi }{3}[n_{\gamma }{n}_{\alpha }\left(c_{\gamma }^0\right)\left(c_{\alpha }^0\right)d_{\gamma \alpha }^3\left(1-\frac{3}{2{\tau }_{\gamma \alpha }}\right)-\frac{1}{2}\left(n_{\gamma }^2{\left(c_{\gamma }^0\right)}^2{d}_{\gamma \gamma }^3\left(1-\frac{3}{2{\tau }_{\gamma \gamma }}\right)+n_{\alpha }^2{\left(c_{\alpha }^0\right)}^2{d}_{\alpha \alpha }^3\right)],$$ (58)

which for the case $c_{\gamma }^0=c_{\alpha }^0=c^0$ relevant here, becomes

$$B=\frac{2\pi }{3}{n}_{\gamma }^2{\left(c^0\right)}^2[n_{\alpha \gamma }{\left(\frac{d_{\gamma \gamma }+d_{\alpha \alpha }}{2}\right)}^3\left(1-\frac{3}{2{\tau }_{\gamma \alpha }}\right)-\frac{1}{2}\left(d_{\gamma \gamma }^3\left(1-\frac{3}{2{\tau }_{\gamma \gamma }}\right)+n_{\alpha \gamma }^2{d}_{\alpha \alpha }^3\right)]=\frac{2\pi }{3}{n}_{\gamma }^2{\left(c^0\right)}^2{d}_{\alpha \alpha }^3[n_{\alpha \gamma }{\left(\frac{1+{\gamma }_{\gamma \alpha }}{2}\right)}^3\left(1-\frac{3}{2{\tau }_{\gamma \alpha }}\right)-\frac{1}{2}\left({\gamma }_{\gamma \alpha }^3\left(1-\frac{3}{2{\tau }_{\gamma \gamma }}\right)+n_{\alpha \gamma }^2\right)],$$ (59)

where we have defined $n_{\alpha \gamma }=n_{\alpha }/n_{\gamma }$ and assumed, consistent with the present model, that ${\tau }_{\alpha \alpha }=\mathrm{\infty }$. With use of the values in Table I, which give ${\gamma }_{\gamma \alpha }=0.23$ and $n_{\alpha \gamma }=0.79$, and taking ${\tau }_{\gamma \gamma }=0.99$ and ${\tau }_{\gamma \alpha }=6.4$, the square bracket in Eq. (59) has the value −0.165, so that indeed $B<0$, potentially compatible with the concave-down dependence of $\mathrm{\Delta }\mathcal{R}(0)$ on $f_{\alpha }$ at 75 mg/ml as indicated above, depending on the magnitudes of the third-order contributions, which we now analyze.

The third-order terms in the virial expansion of the light scattering intensity can be written in the form

$$\mathrm{\Delta }\mathcal{R}{(0)}_{\left(3\right)}=\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)[c_{\gamma \gamma \gamma }{\left(1-f_{\alpha }\right)}^3+c_{\gamma \gamma \alpha }{\left(1-f_{\alpha }\right)}^2{f}_{\alpha }+c_{\gamma \alpha \alpha }\left(1-f_{\alpha }\right)f_{\alpha }^2+c_{\alpha \alpha \alpha }{f}_{\alpha }^3]$$ (60)

with

$$c_{\gamma \gamma \gamma }=\left(n_{\gamma }^2/m_{\gamma }\right){\left(c_{\gamma }^0\right)}^3\left(4B_{\gamma \gamma }^2-6C_{\gamma \gamma \gamma }^{(f)}\right)c_{\gamma \gamma \alpha }={\left(c_{\gamma }^0\right)}^2\left(c_{\alpha }^0\right)[\left(n_{\gamma }{n}_{\alpha }/m_{\gamma }\right)\left(8B_{\gamma \gamma }{B}_{\gamma \alpha }-12C_{\gamma \gamma \alpha }^{(f)}\right)+\left(n_{\gamma }^2/m_{\alpha }\right)\left(4B_{\gamma \alpha }^2-6C_{\gamma \gamma \alpha }^{(f)}\right)]c_{\gamma \alpha \alpha }=\left(c_{\gamma }^0\right){\left(c_{\alpha }^0\right)}^2[\left(n_{\gamma }{n}_{\alpha }/m_{\alpha }\right)\left(8B_{\alpha \alpha }{B}_{\gamma \alpha }-12C_{\gamma \alpha \alpha }^{(f)}\right)+\left(n_{\alpha }^2/m_{\gamma }\right)\left(4B_{\gamma \alpha }^2-6C_{\gamma \alpha \alpha }^{(f)}\right)]c_{\alpha \alpha \alpha }=\left(n_{\alpha }^2/m_{\alpha }\right){\left(c_{\alpha }^0\right)}^3\left(4B_{\alpha \alpha }^2-6C_{\alpha \alpha \alpha }^{(f)}\right).$$ (61)

While Eqs. (60) and (61) apply more generally, the relevant third virial coefficients $C_{ijk}^{(p)}=2C_{ijk}^{(f)}$ in the sticky-sphere mixture model are given in Eqs. (F66), (F67), (F69), and (F70). With use of these equations one can construct the third virial analogue of Eq. (59).

First, however, it is convenient to rewrite Eq. (60) to identify linear ($L_{\left(3\right)}$), quadratic ($Q_{\left(3\right)}$), and cubic ($C_{\left(3\right)}$) dependences on $f_{\alpha }$ as follows:

$$\mathrm{\Delta }\mathcal{R}{(0)}_{\left(3\right)}=\left(\frac{4{\pi }^2{n}^2}{{\lambda }^4}\right)\left[L_{\left(3\right)}+Q_{\left(3\right)}+C_{\left(3\right)}\right]\text{, in which}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} }{L}_{\left(3\right)}=c_{\gamma \gamma \gamma }\left(1-f_{\alpha }\right)+c_{\alpha \alpha \alpha }{f}_{\alpha },Q_{\left(3\right)}=-\left(2c_{\gamma \gamma \gamma }+c_{\alpha \alpha \alpha }\right)f_{\alpha }\left(1-f_{\alpha }\right),C_{\left(3\right)}=c_{\gamma \gamma \alpha }{\left(1-f_{\alpha }\right)}^2{f}_{\alpha }+\left(c_{\gamma \alpha \alpha }+c_{\gamma \gamma \gamma }-c_{\alpha \alpha \alpha }\right)\left(1-f_{\alpha }\right)f_{\alpha }^2.$$ (62)

Eqs. (61) and (62) clearly show how terms in the light scattering that are cubic in concentration, as indicated by the definitions of the c_ijk in Eq. (61), contribute to the concave up or down nature of the composition ($f_{\alpha }$) dependence of the light scattering through $Q_{\left(3\right)}$ (Eq. (62)). With increasing protein concentration, $Q_{\left(3\right)}$ thus progressively alters the contribution proportional to B from the quadratic concentration terms, shown above in Eqs. (57) and (59).

Eqs. (61) and (62) show further that with increasing concentration, one expects to find two light scattering contributions that are cubic in the relative composition variable $f_{\alpha }$. One, the term $\left(c_{\gamma \gamma \alpha }-c_{\gamma \gamma \gamma }\right){\left(1-f_{\alpha }\right)}^2{f}_{\alpha }$, has a peak amplitude (positive or negative) at a composition that is relatively high in $\gamma$-crystallin, at $f_{\alpha }=1/3$. The other, $\left(c_{\gamma \alpha \alpha }-c_{\alpha \alpha \alpha }\right)\left(1-f_{\alpha }\right)f_{\alpha }^2$, has a peak amplitude nearer to the $\alpha$-crystallin axis, at $f_{\alpha }=2/3$.

To summarize, in the present case, despite our initial expectation that the observed concave-down dependence of the light scattering intensity on $f_{\alpha }$ at the overall protein concentration of 75 mg/ml would be straightforward to interpret, this analysis suggests that the scattering at this protein concentration involves a complicated mixture of at least second and third virial contributions, especially for $\alpha$-crystallin rich mixtures. This situation is illustrated in Figure 8, which shows the Rayleigh ratio contributions that result from use of the fitted model (green), in comparison with the contributions from the molecular weight terms (Eq. (55)) alone, the molecular weight plus second virial contributions (Eq. (57)), and the contributions including the third mixed virial terms (Eqs. (60) and (61).

FIG. 8.

Modeled Rayleigh ratios at an overall protein concentration of 75 mg/ml, from the full sticky-sphere model in the Percus-Yevick approximation (green solid curve), compared with the contributions from the molecular weight terms alone (Eq. (55), dotted-dashed orange curve), the molecular weight plus the second mixed-virial terms (Eq. (57), red dashed curve), and the molecular weight, second, and third mixed-virial terms (Eqs. (60) and (61), dotted blue curve). The full model curve (green) is the same as that shown in green in Fig. 3, panel (a), in comparison with the data.

Figure 8 suggests that to measure B (Eqs. (57)–(59)), which sets the magnitude of the second derivative of the dashed red curve in that figure, and to measure analogous third-virial quantities, one would need a series of light scattering measurements at lower concentrations than those probed in the data analyzed here, as functions of $f_{\alpha }$, and also that very accurate data would be needed. Again, as described at the outset of this section, we emphasize that in view of the nature of the comparisons being made, this is only a suggestion. The third-virial analogues of B become very complicated as functions of the $\tau$ and size parameters, and are not included here.

V. LIGHT SCATTERING FROM $\gamma$B-$\alpha$ MIXTURES: DEPENDENCE OF PREDICTIONS ON $\gamma$-$\alpha$, $\gamma$-$\gamma$, AND $\alpha$-$\alpha$ INTERACTIONS

We now use the sticky-sphere mixture model to explore how hypothetical changes in molecular properties could affect light scattering from concentrated $\gamma$-$\alpha$ mixtures. In Fig. 9, starting from panel (a), which repeats the blue surface in Fig. 3(c) for reference, these are (b) a $\gamma$-crystallin that has a higher phase separation temperature than the $\gamma$B-crystallin modeled above, (c) increased attraction between $\alpha$- and $\gamma$B-crystallin, (d) reduced attraction between $\alpha$- and $\gamma$B-crystallin, (e) a higher molecular weight of $\alpha$-crystallin, and (f) a more compact form of $\alpha$-crystallin. Changes of the types (b) and (c) have been previously linked to the occurrence of cataract.^20,69 Changes of type (d) can also be expected to cause cataract. The hypothetical changes of types (e) and (f) are presented because of the striking contrast they show between the low- andhigh-concentration dependences of light scattering on changing the molecular weight or compactness of $\alpha$-crystallin.

Panel (b) of Fig. 9 illustrates how light scattering increases as the solution conditions become nearer to a $\gamma$-crystallin phase separation temperature, T_c. Whereas $T-T_c=32$ °C for the baseline panel (a), which corresponds to the blue surface in Fig. 3, $T-T_c$ is instead 10 °C in panel (b). Bringing T_c and T closer by a factor of 3 increases the peak Rayleigh ratio on the $\gamma$-crystallin axis by approximately a factor of 3, but it is particularly striking that the scattering from mixtures of $\alpha$- and $\gamma$- crystallin changes by a much larger factor than 3 in response to the illustrated reduction in $T-T_c$. That is, an increased phase separation temperature on the $\gamma$-crystallin binary axis can increase light scattering more dramatically in $\alpha$/$\gamma$ mixtures, than it does in the pure $\gamma$-crystallin solution, and can result in intense scattering from the mixtures even in the single-phase realm. It is important to note that such a reduction in $T-T_c$ can be brought about not just by changing actual temperature, but in the living organism can occur with T fixed at body temperature while T_c rises, as happens during some forms of cataractogenesis.⁶⁹

Panel (c) of Fig. 9 shows the effect of increasing the strength of attractions between $\alpha$- and $\gamma$-crystallins. We changed the $\gamma$-$\alpha$ stickiness parameter, ${\tau }_{12}$, from 6.4, as in panel (a), to 1. In this case the excess Rayleigh ratio for the mixtures increases, but there is no change on either binary axis, as must be the case. This increase in light scattering is a single-phase counterpart of the role of increased $\alpha$-$\gamma$ attractions in destabilizing concentrated $\alpha$/$\gamma$ mixtures.^12–14 Indeed, an increased strength of $\alpha$-$\gamma$ attractions that alters their ternary phase boundaries has been connected with the human congenital cataract associated with the human $\gamma$D-crystallin mutation, E107A.²⁰ Physically, the increased $\alpha$-$\gamma$ attractions, in combination with the attractions between the $\gamma$-crystallins that are already present, enable the $\gamma$-crystallins to effectively act as a glue that can hold large conglomerates of $\alpha$ and $\gamma$ together, thereby increasing light scattering. Contributing to this light scattering increase, the minimum eigenvector of the Hessian is rotated clockwise, as illustrated upon going from panel (b) to panel (a) of Fig. 5.

Panel (d) of Fig. 9 shows the effect of decreasing the strength of attractions between $\alpha$- and $\gamma$-crystallins. We changed the $\gamma$-$\alpha$ stickiness parameter, ${\tau }_{12}$, from 6.4, its value in panel (a), to 9. Due to the inverse relationship between $\tau$ and the strength of attractions, such a change serves to reduce the attraction between $\gamma$ and $\alpha$. Again, there is no light scattering change on either binary axis, as must be the case. The Rayleigh ratio increases, as it does in the case of increasing $\alpha$-$\gamma$ attraction. However, note that a very different pattern of increased light scattering as a function of protein concentration and composition now results. Thus, a comparison of panel (d) with panel (a) illustrates that attractions between $\alpha$- and $\gamma$-crystallin are very effective in reducing the light scattering from their concentrated mixtures that would otherwise occur. This reduction in light scattering is a single-phase counterpart of the role of $\alpha$-$\gamma$ attractions in stabilizing concentrated $\alpha$/$\gamma$ mixtures with respect to phase separation, that has previously been investigated using neutron scattering, molecular dynamics simulation, and thermodynamic perturbation theory.^12–14 Physically, the $\gamma$-$\alpha$ attractions compensate for the tendency of mixtures of hard-spheres that differ in size to show fluctuations that involve segregation by type, known as depletion attraction.⁷⁰

Note that the concentration and composition dependence of the increased light scattering intensity in the concentrated mixtures of panel (b) of Fig. 9 has a qualitative similarity to that shown in panel (d), in which $\alpha$-$\gamma$ attractions are less effective at counteracting the tendency of these two proteins to segregate by size. The changes shown in the mixture scattering in panel (b) can be given a similar interpretation; that is, increasing $\gamma$-$\gamma$ attractions, provided that the $\alpha$-$\gamma$ attraction is sufficiently low, will also enhance their segregation from $\alpha$-crystallins, and thereby can enhance scattering. Thus the $\gamma$-crystallin phase separation temperature, even though it may remain well below body temperature, can nevertheless represent a key element controlling the transparency of concentrated $\alpha$/$\gamma$ mixtures.

The sequence of panels Figs. 9(c), 9(a), and 9(d) illustrates that the light scattering cross-section is non-monotonic as a function of $\alpha$-$\gamma$ attraction strength, in accord with previous molecular dynamics simulations and perturbation theory work on these systems;^12,13 for these three panels the pure $\alpha$ and $\gamma$-crystallin component parameters were left unchanged. That is, consistent with previous work, the sticky-sphere mixture model shows two distinct mechanisms by which light scattering at body temperature from $\gamma$-$\alpha$ mixtures can greatly exceed that from the pure component protein solutions: decreasing or increasing $\gamma$-$\alpha$ attraction strength. Thus, just as a human $\gamma D$-crystallin mutation has been identified for which an increase in $\gamma$-$\alpha$ attraction has been implicated as cataractogenic,²⁰ Fig. 9 suggests that other cataractogenic mutations will be found that instead act through decreasing $\gamma$-$\alpha$ attraction.

Panel (e) illustrates that low-concentration scattering would also greatly increase from that in panel (a) if the molecular weight of $\alpha$-crystallin were closer to $2\times {\mathrm{\hspace{0.17em}10}}^6$ g/mole rather than $8\times {10}^5$ g/mole. Here, it should be noted that the current model is only set up to accommodate hypothetical growth of $\alpha$-crystallin into a larger sphere, which is unlikely (e.g., see Ref. 45). Nevertheless, in the context of the current model, it is interesting to note that the light scattering effect of this increase in molecular weight is largely confined to the region near the $\alpha$-crystallin axis, for in comparison the concentrated $\alpha$-$\gamma$ mixture light scattering shows a relatively small increase. While much larger increases in molecular weight than that depicted here have long been observed in aging lenses, the contrast that panels (a) and (e) show between low- and high-concentration light scattering changes illustrates that high concentration eye lens protein mixtures can substantially reduce the light scattering impact of a considerable growth in molecular weight. This feature may be of importance for evaluating hypotheses about how growing aggregates could affect light scattering in the lens.

Panel (f) illustrates another hypothetical change, that of making $\alpha$-crystallin more compact, by lowering its effective volume from its open, chaperone-protein structure to the 0.7 ml/g typical of globular proteins.⁶⁸ Interestingly, while such a change would dramatically increase light scattering at low $\gamma$-crystallin concentrations, for a large range of $\alpha$-crystallin concentrations, it would reduce light scattering in high-concentration mixtures. The physical reason for the increased scattering on the $\alpha$-crystallin axis is that compact $\alpha$ crystallin would require higher protein concentrations in order to constrain relative protein molecule positions so as to suppress concentration fluctuations, and thereby reduce light scattering intensity. Thus, the contrast between Figs. 9(a) and 9(f) illustrates that a chaperone-like, relatively open structure of $\alpha$-crystallin, used implicitly in the construction of Fig. 9(a) via the parameters of Table I, dramatically reduces light scattering intensity at low and intermediate protein concentrations. However, Fig. 9(f) predicts that light scattering in high concentration $\gamma$-$\alpha$ mixtures would actually be reduced from its values in Fig. 9(a), if $\alpha$ crystallin were more compact than it is. Therefore, just as for the molecular weight considerations illustrated by panel (e), there is a contrast between the low- and high-concentration effects of this hypothetical change, further underlining the importance of mixture light scattering considerations.

In connection with the construction of Figs. 9(e) and 9(f), it is important to note that to make the given comparisons in the context of the present sticky-sphere mixture model, we needed to assume that the $\alpha$-crystallin remained spherical. For the molecular-weight change case shown in panel (e) we adjusted its diameter accordingly, while assuming that its partial specific volume remained the same. On the other hand, for the change in partial specific volume illustrated in panel (f), we assumed that the molecular weight remained the same. For example, for panel (f) we reduced the diameter of the assumed-spherical $\alpha$-crystallin accordingly by a factor of (0.7/1.52)^1/3. These choices then left the question of also choosing an appropriate, plausible adjustment for the effective stickiness parameter ${\tau }_{12}$, to accompany the two size changes. The underlying consideration was that if the spatial range of the $\alpha$-$\gamma$ attraction—for example, 1 D electrostatic screening length—were to remain the same between the normal $\alpha$-crystallin and the hypothetical contracted version of panel 9(f), there would now be a smaller volume in which $\gamma -\alpha$ attractions could occur, while there would be a correspondingly larger volume for $\gamma -\alpha$ attractions if the $\alpha$-crystallin molecular weight were presumed to increase, as in panel 9(e). By equating the respective second mixed virial coefficients, and using the relationships in Eqs. (31) and (32), we first found the parameters of a square-well attraction model like that used in Ref. 10 that would reproduce the value of ${\tau }_{12}$ used in panel (a), kept that square well width and depth constant for the smaller protein radius that corresponded to the more compact protein of panel (f), then again equated second mixed virial coefficients to find the new value of ${\tau }_{12}$ that corresponded to the shrunken square well. A similar procedure was used for panel (e).

VI. CONCLUSIONS

This work shows that a simple model that incorporates hard-sphere interactions of $\alpha$-crystallins, spherically symmetric sticky-sphere interactions of $\gamma$-crystallins, and spherically symmetric sticky-sphere interactions of $\alpha$-crystallins with $\gamma$-crystallins, yields nearly quantitative agreement with experimentally observed, temperature-dependent absolute light scattering cross sections of $\gamma$-$\alpha$-crystallin mixtures, including those obtained at realistically high concentrations that are not readily modeled with dilute or semi-dilute solution approaches. Thus, the present model is a step towards building an experimentally tested, quantitative theory of transparency of the eye lens cytoplasm that is based on measured molecular properties.

Clearly, additional molecular components and features are needed to build a more comprehensive theory of light scattering from the eye lens cytoplasm at equilibrium. From the present perspective of studying light scattering from controlled, concentrated mixtures of eye lens cytoplasmic components, among the key features expected to be of importance, beyond those of $\gamma$-$\alpha$ mixtures, are the roles of $\beta$-crystallins, oligomerization and high-molecular-weight aggregate formation of crystallins, aeolotopic or orientation-dependent interactions between crystallins, cytoskeletal components, and membrane components. In each of these additional contexts, one can expect that the high-concentration light scattering consequences of given molecular interaction potentials may be qualitatively different from those at more easily prepared low concentrations, as has turned out to be the case for $\gamma$-$\alpha$ mixtures (cf. Fig. 3). In this context, it is important to note that the light scattering changes we investigate here do not yet approach those that would lead to substantial scattering-angle dependence of the light scattering intensity. Angular dependence of the Rayleigh ratio does occur upon close approach to liquid-liquid phase separation and upon formation of very high molecular weight aggregates, and can also result from cytoskeletal and membrane structures. Because light scattering from the living lens does exhibit dramatic angular dependence,⁷¹ extending the present model to include these phenomena would clearly be of interest.

A model of equilibrium light scattering properties, such as the present one, can inform quantitative models of cataractogenic effects of chemical modifications and mutations of lens crystallins and other components. It is also an important starting point for models of the thermodynamic driving forces for the non-equilibrium dynamics of molecular change that are also crucial in cataract development.

APPENDIX A: SCHUR MATRIX PRODUCT FORM OF THE $\lambda -\tau$ QUADRATIC EQUATION SYSTEM

Let $\stackrel{\sim }{\tau }=\tau \frac{12(1-{\xi }_3)}{\pi d_{ij}}$. First, we divide both sides of Eq. (3) by $\frac{\pi d_{ij}}{12(1-{\xi }_3)}$ and add $6{\stackrel{\sim }{\tau }}_{ij}$ to both sides, obtaining

$$\sum _k{\rho }_k{d}_{kk}^2({\lambda }_{ik}-6)({\lambda }_{jk}-6)-{\stackrel{\sim }{\tau }}_{ij}({\lambda }_{ij}-6)=\left(\frac{9d_{ij}{\xi }_2}{(1-{\xi }_3)}-\frac{6d_{ij}^2}{d_{ii}{d}_{jj}}\right)\left(\frac{12(1-{\xi }_3)}{\pi d_{ij}}\right)+6{\stackrel{\sim }{\tau }}_{ij}.$$ (A1)

Define the matrices L, D, $\stackrel{\sim }{B}$, and $\stackrel{\sim }{C}$ as follows:

$$L=\left[\begin{array}{ccc}\hfill {\lambda }_{11}-6\hfill & \hfill {\lambda }_{12}-6\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill {\lambda }_{12}-6\hfill & \hfill {\lambda }_{22}-6\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill \mathrm{⋮}\hfill & \hfill \mathrm{⋮}\hfill & \hfill \mathrm{\ddots }\hfill \end{array}\right],$$

$$D=\left[\begin{array}{ccc}\hfill {\sqrt{\rho }}_1{d}_{11}\hfill & & \\ & \hfill {\sqrt{\rho }}_2{d}_{22}\hfill & \\ & & \hfill \mathrm{\ddots }\hfill \end{array}\right],$$

$$\stackrel{\sim }{B}=\left[\begin{array}{ccc}\hfill \left(\frac{9d_{ij}{\xi }_2}{(1-{\xi }_3)}-\frac{6d_{ij}^2}{d_{ii}{d}_{jj}}\right)\left(\frac{12(1-{\xi }_3)}{\pi d_{ij}}\right)\hfill & \hfill \mathrm{\cdots }\hfill & \\ \hfill \mathrm{⋮}\hfill & \hfill \mathrm{\ddots }\hfill & \end{array}\right],$$

$$\stackrel{\sim }{C}=\left[\begin{array}{ccc}\hfill 6\hfill & \hfill 6\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill 6\hfill & \hfill 6\hfill & \hfill \mathrm{\cdots }\hfill \\ \hfill \mathrm{⋮}\hfill & \hfill \mathrm{⋮}\hfill & \hfill \mathrm{\ddots }\hfill \end{array}\right].$$

Then with use of the substitution $Y=-DLD$ one obtains a matrix form of Eq. (3),

$$Y^2+\stackrel{\sim }{\tau }°Y=B+\stackrel{\sim }{\tau }°C,$$ (A2)

where $A°B$ is the Schur (Hadamard) matrix product defined by ${(A°B)}_{ij}=A_{ij}{B}_{ij}$.

APPENDIX B: FOURTH-ORDER POLYNOMIAL REDUCTION OF QUADRATICS FOR HARD-SPHERE $\alpha$-$\alpha$ INTERACTIONS

In this appendix, we show that the solution of Eq. (3), for the two-component case in which ${\tau }_{22}=\mathrm{\infty }$, can be reduced to the solution of a fourth-order polynomial in ${\lambda }_{11}-6$. Here, as in the text, we let component 1 stand for $\gamma$-crystallin, while component 2 is $\alpha$-crystallin, and we define ${\varphi }_i=\frac{\pi }{6}{\rho }_i{d}_{ii}^3$, $x_i=\frac{{\varphi }_i}{1-{\xi }_3}$, and ${\gamma }_{12}=\frac{d_{11}}{d_{22}}$.

First, in the i = j = 2 instance of Eq. (3), ${\tau }_{22}=\mathrm{\infty }$ implies either that ${\lambda }_{22}=0$ or that ${\lambda }_{22}=\mathrm{\infty }$. The latter possibility is unphysical, and therefore we conclude that ${\lambda }_{22}=0$. The i = j = 1 and i = 1; j = 2 equations become

$$x_1{({\lambda }_{11}-6)}^2+{\gamma }_{12}{x}_2{({\lambda }_{12}-6)}^2-2{\tau }_{11}({\lambda }_{11}-6)=12{\tau }_{11}+18(x_1+{\gamma }_{12}{x}_2)-12$$ (B1)

and

$$({\lambda }_{12}-6)\left[(1+{\gamma }_{12})(x_1({\lambda }_{11}-6)-6{\gamma }_{12}{x}_2)-4{\gamma }_{12}{\tau }_{12}\right]=18(1+{\gamma }_{12})(x_1+{\gamma }_{12}{x}_2)-6{(1+{\gamma }_{12})}^2+24{\gamma }_{12}{\tau }_{12}.$$ (B2)

By solving Eq. (B2) for $({\lambda }_{12}-6)$ we find

$$({\lambda }_{12}-6)=\frac{18(x_1+{\gamma }_{12}{x}_2)-6(1+{\gamma }_{12})+{\displaystyle \frac{24{\gamma }_{12}{\tau }_{12}}{1+{\gamma }_{12}}}}{x_1({\lambda }_{11}-6)-6{\gamma }_{12}{x}_2-{\displaystyle \frac{4{\gamma }_{12}{\tau }_{12}}{1+{\gamma }_{12}}}}.$$ (B3)

Writing

$$A=18(x_1+{\gamma }_{12}{x}_2)-6(1+{\gamma }_{12})+\frac{24{\gamma }_{12}{\tau }_{12}}{1+{\gamma }_{12}},$$ (B4)

$$B=-6{\gamma }_{12}{x}_2-\frac{4{\gamma }_{12}{\tau }_{12}}{1+{\gamma }_{12}},$$ (B5)

$$C=12{\tau }_{11}+18(x_1+{\gamma }_{12}{x}_2)-12,$$ (B6)

and substituting Eq. (B3) into Eq. (B1) yields

$$x_1{({\lambda }_{11}-6)}^2+{\gamma }_{12}{x}_2\frac{A^2}{{[x_1({\lambda }_{11}-6)+B]}^2}-2{\tau }_{11}({\lambda }_{11}-6)=C.$$ (B7)

Upon multiplying Eq. (B7) by $x_1({\lambda }_{11}-6)+{B]}^2/x_1^3$ and collecting coefficients, we obtain

$${({\lambda }_{11}-6)}^4+D_3{({\lambda }_{11}-6)}^3+D_2{({\lambda }_{11}-6)}^2+D_1({\lambda }_{11}-6)+D_0=0,$$ (B8)

where

$$D_3=\frac{2B{x}_1^2-2x_1^2{\tau }_{11}}{x_1^3},D_2=\frac{x_1{B}^2-4B{\tau }_{11}{x}_1-C{x}_1^2}{x_1^3},D_1=\frac{-2B^2{\tau }_{11}-2BC{x}_1}{x_1^3},D_0=\frac{A^2{\gamma }_{12}{x}_2-C{B}^2}{x_1^3},$$

which is a fourth order monic polynomial in $({\lambda }_{11}-6)$. We find the roots of Eq. (B8), as well as more complex $\lambda -\tau$ equations, by starting at “high temperature”—that is, high values of $\tau$. We use a parameter t to scale the entire set of $\tau$ values by the same factor, where t = 0 corresponds to $\tau =\mathrm{\infty }$, for all particle pair types, and t = 1 corresponds to the desired set of ${\tau }_{ij}$ values. When t = 0, ${\lambda }_{ij}=0$ for all pairs. Starting at t = 0 we step t up by small increments, $\delta t$, and gradually increase the value of t up to 1. At each point we use a combination of secant and Newton’s fixed-point methods to find the new sets of roots, while decreasing $\delta t$ as necessary to ensure convergence of Newton’s method, or increasing it so as to speed up the process. This method is described further under the subject of parameter homotopy continuation in Refs. ⁷² and ⁷³.

APPENDIX C: MATHEMATICAL DETAILS INVOLVED IN EVALUATING THE MATRIX $𝑸$

From Eq. (51) in Ref. 25, we have

$$Q_{ij}(r)={\delta }_{ij}-2\pi {({\rho }_i{\rho }_j)}^{1/2}{\int }_{m_{ij}}^{d_{ij}}{q}_{ij}(r)dr,$$ (C1)

in which m_ij = (1/2)(d_ii − d_jj), d_ij = (1/2) (d_ii + d_jj), and ${\rho }_i$ is the number density of component i. Eqs. (11)–(15) of Ref. 25 specify the q_ij(r) as

$$q_{ij}(r)=[\frac{1}{2}{a}_i(d_{ij}^2-r^2)+b_i(d_{ij}-r)+t_{ij}]H_{-}(d_{ij}-r)$$ (C2)

in which

$$a_i=\frac{1}{{(1-{\xi }_3)}^2}\left(1-{\xi }_3+3{\xi }_2{d}_{ii}-\frac{\pi }{6}{d}_{ii}\sum _k{\rho }_k{d}_{kk}{\lambda }_{ki}\right),$$ (C3)

$$b_i=\frac{1}{2}{d}_{ii}\left(\frac{1}{1-{\xi }_3}-a_i\right).$$ (C4)

Here, the quantities ${\xi }_i$ are moments of the distribution of sphere sizes as described in the text, and

$$t_{ij}={\lambda }_{ij}{d}_{ii}{d}_{jj}/(12(1-{\xi }_3)).$$ (C5)

The expressions given in Eqs. (C1)–(C3) can be simplified using $x_k=(\pi /6){\rho }_k{d}_{kk}^3/(1-{\xi }_3)$, ${\gamma }_{ij}=d_{ii}/d_{jj}$, and $l_{ij}=3-{\lambda }_{ij}$, to obtain

$$a_i=\frac{1}{1-{\xi }_3}\left(1+\sum _k{x}_k{\gamma }_{ik}{l}_{ik}\right)$$ (C6)

and

$$Q_{ij}={\delta }_{ij}+x_j\sqrt{\frac{{\rho }_i}{{\rho }_j}}\cdot \left[\left(1+{\gamma }_{ij}{l}_{ij}+\sum _k{x}_k{\gamma }_{ik}{l}_{ik}\right)\right].$$ (C7)

It is convenient to note that the diagonal and off-diagonal elements from Eq. (C7), identical to Eq. (11) in the text, are

$$Q_{ii}=1+x_i+x_i{l}_{ii}+x_i\sum _k{x}_k{\gamma }_{ik}{l}_{ik},\text{and}$$ (C8)

$$Q_{ij}=x_j\sqrt{\frac{{\rho }_i}{{\rho }_j}}\left[1+{\gamma }_{ij}{l}_{ij}+\sum _k{x}_k{\gamma }_{ik}{l}_{ik}\right].$$ (C9)

If we let

$$J_{11}=1+l_{11}+x_1{l}_{11}+x_2{l}_{12}\gamma ,$$ (C10)

$$J_{12}=1+x_1{l}_{11}+l_{12}\gamma (1+x_2),$$ (C11)

$$J_{21}=1+x_2{l}_{22}+\frac{x_2{l}_{12}}{\gamma }(1+x_1),$$ (C12)

$$J_{22}=1+l_{22}+x_2{l}_{22}+\frac{x_1{l}_{12}}{\gamma },$$ (C13)

then the two-component matrix $𝑸$ can be written as

$$𝑸=\left[\begin{array}{c}\hfill \frac{\sqrt{{\rho }_1}}{x_1}\hfill \\ & \hfill \frac{\sqrt{{\rho }_2}}{x_2}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill 1+x_1{J}_{11}\hfill & \hfill x_1{J}_{12}\hfill \\ \hfill x_2{J}_{21}\hfill & \hfill 1+x_2{J}_{22}\hfill \end{array}\right]\left[\begin{array}{c}\hfill \frac{x_1}{\sqrt{{\rho }_1}}\hfill \\ & \hfill \frac{x_2}{\sqrt{{\rho }_2}}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1+x_1{J}_{11}\hfill & \hfill \sqrt{\frac{{\rho }_1}{{\rho }_2}}{x}_2{J}_{12}\hfill \\ \hfill \sqrt{\frac{{\rho }_2}{{\rho }_1}}{x}_1{J}_{21}\hfill & \hfill 1+x_2{J}_{22}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1+x_1{J}_{11}\hfill & \hfill \frac{\sqrt{x_1{x}_2}}{{\gamma }^{3/2}}{x}_2{J}_{12}\hfill \\ \hfill {\gamma }^{3/2}\sqrt{x_1{x}_2}{J}_{21}\hfill & \hfill 1+x_2{J}_{22}\hfill \end{array}\right].$$ (C14)

APPENDIX D: TRANSFORMATION OF KEY QUANTITIES BETWEEN THE MODEL 2-COMPONENT STICKY-SPHERE MIXTURE AND THE 3-COMPONENT EXPERIMENTAL MIXTURES

In the present implementation of the sticky-sphere mixture model, it is assumed that there are just two components, the $\gamma$ and $\alpha$ crystallin proteins. In this model the solvent is regarded as a featureless continuum that fills the space between the proteins. As a consequence, in order to compare the model predictions with experiments that use aqueous buffer together with the proteins, we need to consider the correspondence between the thermodynamics of the two-component model and the properties of the experimental mixture. For this purpose, we use relationships that stem from the McMillan-Mayer theory of solutions.⁵⁰ One could of course treat the water as a third component directly, which is an interesting possible extension of the present work.

We use a superscript (⁽²⁾) to identify thermodynamic properties of the two-component model system, to distinguish them from those of the three-component experimental system. The latter are written with no superscript, as are quantities taken as common to both two-component and three-component systems. The Helmholtz free energy, F⁽²⁾, of the two-component model system is extensive in the variables V, N₁, and N₂ and therefore can be written as

$$F^{(2)}=N_1{\left(\frac{\partial F^{(2)}}{\partial N_1}\right)}_{T,V,N_2}+N_2{\left(\frac{\partial F^{(2)}}{\partial N_2}\right)}_{T,V,N_1}+V{\left(\frac{\partial F^{(2)}}{\partial V}\right)}_{T,N_1,N_2}=N_1{\mu }_1^{(2)}+N_2{\mu }_2^{(2)}-V{p}^{(2)},$$ (D1)

where ${\mu }_1^{(2)}$ and ${\mu }_2^{(2)}$ are the chemical potentials of components 1 and 2, respectively, and p⁽²⁾ is the two-component model pressure.

In the McMillan-Mayer theory, the pressure p⁽²⁾ of the two-component system corresponds to the osmotic pressure $\pi$ of the corresponding system containing solvent.⁵⁰ If, as we assume, the partial molecular volume of a water molecule, ${\overline{v}}_w$, does not significantly change with pressure in the applicable range, the osmotic pressure is given by $\pi {\overline{v}}_w={\mu }_w^0-{\mu }_w$, in which ${\mu }_w$ denotes water chemical potential in the solution, while ${\mu }_w^0$ denotes the chemical potential of pure water.

Now we assume throughout that in the experimental liquid mixture, the partial molecular volumes are constant; that is, we use $V=N_1{\overline{v}}_1+N_2{\overline{v}}_2+N_w{\overline{v}}_w$ with constant values of ${\overline{v}}_1$, ${\overline{v}}_2$, and ${\overline{v}}_w$. As mentioned in the text, this is an assumption in the derivation⁴⁹ of Eq. (1) from the excess Rayleigh ratio form given by Kirkwood and Goldberg.⁴⁸ Therefore, if a molecule of type 1 is added to the model two-component mixture at constant overall volume, as in the evaluation of the two-component chemical potential ${\mu }_1^{(2)}={\left(\frac{\partial F^{(2)}}{\partial N_1}\right)}_{T,V,N_2}$, in the corresponding three-component system $({\overline{v}}_1/{\overline{v}}_w)$ water molecules would have to be removed. Therefore, we take

$${\mu }_1^{(2)}={\mu }_1-({\overline{v}}_1/{\overline{v}}_w){\mu }_w{\mu }_2^{(2)}={\mu }_2-({\overline{v}}_2/{\overline{v}}_w){\mu }_w.$$ (D2)

We now substitute the expressions for p⁽²⁾, ${\mu }_1^{(2)}$, and ${\mu }_2^{(2)}$ into Eq. (D1) to obtain

$$F^{(2)}=N_1{\mu }_1-(N_1{\overline{v}}_1/{\overline{v}}_w){\mu }_w+N_2{\mu }_2-(N_2{\overline{v}}_2/{\overline{v}}_w){\mu }_w-(V/{\overline{v}}_w)({\mu }_w^0-{\mu }_w)=N_1{\mu }_1+N_2{\mu }_2+N_w{\mu }_w-(V/{\overline{v}}_w)({\mu }_w^0)=G(N_1,N_2,N_w)-(V/{\overline{v}}_w)({\mu }_w^0).$$ (D3)

From Eq. (D3) it follows that in the present model, the Gibbs free energy per unit volume of the three-component mixture, the quantity appearing in the excess Rayleigh ratio in Eq. (1), can be written as

$$G(N_1,N_2,N_w)/V=F^{(2)}/V+({\mu }_w^0/{\overline{v}}_w).$$ (D4)

That is, the three-component Gibbs free energy per unit volume corresponds to the two-component Helmholtz free energy per unit volume, plus a quantity that is independent of the solute concentrations, ${\mu }_w^0/{\overline{v}}_w$.

To find a convenient form for the Rayleigh ratio of the scattered light in terms of the model, 2-component sticky-sphere mixture system, we now evaluate the Hessian matrix needed in Eq. (1), and its inverse. With use of

$${\mu }_w={\left(\frac{\partial (Vg)}{\partial N_w}\right)}_{T,p,N_1,N_2}={\overline{v}}_w\left[g+\left(\frac{\partial g}{\partial {\rho }_1}\right)(-{\rho }_1)+\left(\frac{\partial g}{\partial {\rho }_2}\right)(-{\rho }_2)\right],$$ (D5)

in which g = G/V is the Gibbs free energy per unit volume, and differentiating each of Eqs. (D2) with respect to ${\rho }_j(j=\mathrm{1,2})$ and using Eq. (D5), we obtain

$$\left(\begin{array}{cc}\hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_2}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \frac{\partial {\mu }_1}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2}{\partial {\rho }_2}\hfill \end{array}\right)+\left(\begin{array}{cc}\hfill {\overline{v}}_1{\rho }_1\hfill & \hfill {\overline{v}}_1{\rho }_2\hfill \\ \hfill {\overline{v}}_2{\rho }_1\hfill & \hfill {\overline{v}}_2{\rho }_2\hfill \end{array}\right)H_{\rho }[g],$$ (D6)

where

$$H_{\rho }[g]=\left(\begin{array}{cc}\hfill \frac{{\partial }^{2}g}{\partial {\rho }_1^2}\hfill & \hfill \frac{{\partial }^{2}g}{\partial {\rho }_1{\rho }_2}\hfill \\ \hfill \frac{{\partial }^{2}g}{\partial {\rho }_1{\rho }_2}\hfill & \hfill \frac{{\partial }^{2}g}{\partial {\rho }_2^2}\hfill \end{array}\right)$$ (D7)

is the Hessian of the intensive Gibbs free energy with respect to number density. Further, with use of

$${\mu }_1={\left(\frac{\partial (Vg)}{\partial N_1}\right)}_{T,p,N_2,N_w}={\overline{v}}_1\left[g+\left(\frac{\partial g}{\partial {\rho }_1}\right)((1/{\overline{v}}_1)-{\rho }_1)+\left(\frac{\partial g}{\partial {\rho }_2}\right)(-{\rho }_2)\right]{\mu }_2={\left(\frac{\partial (Vg)}{\partial N_2}\right)}_{T,p,N_1,N_w}={\overline{v}}_2\left[g+\left(\frac{\partial g}{\partial {\rho }_1}\right)(-{\rho }_1)+\left(\frac{\partial g}{\partial {\rho }_2}\right)((1/{\overline{v}}_2)-{\rho }_2)\right],$$ (D8)

one obtains

$$\left(\begin{array}{cc}\hfill \frac{\partial {\mu }_1}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2}{\partial {\rho }_2}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1-{\rho }_1{\overline{v}}_1\hfill & \hfill -{\rho }_2{\overline{v}}_1\hfill \\ \hfill -{\rho }_1{\overline{v}}_2\hfill & \hfill 1-{\rho }_2{\overline{v}}_2\hfill \end{array}\right)H_{\rho }[g].$$ (D9)

Substituting Eq. (D9) into Eq. (D6) yields

$$\left(\begin{array}{cc}\hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_1^{(2)}}{\partial {\rho }_2}\hfill \\ \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_1}\hfill & \hfill \frac{\partial {\mu }_2^{(2)}}{\partial {\rho }_2}\hfill \end{array}\right)=H_{\rho }[g].$$ (D10)

Eq. (D10) now gives the expression in the two-component, sticky-sphere mixture model to be used for the Hessian matrix of the corresponding three-component system, that appears in the light scattering intensity given by Eq. (1).

In the present model, expressions for the needed partial derivatives of the chemical potentials with respect to number densities are given by

$$\frac{\partial {\mu }_i^{(2)}}{\partial {\rho }_j}=\frac{1}{\beta }{({\rho }_i{\rho }_j)}^{-1/2}\sum _k{Q}_{ki}{Q}_{kj}.$$ (D11)

The Q_ki are given above in Eqs. (C7) and (C14).

APPENDIX E: CHANGE TO DIMENSIONLESS QUANTITIES IN THE HESSIAN MATRIX

In order to recast Eq. (1) into a more convenient, dimensionless form, as described in the text we use the volume fractions ${\varphi }_1={\rho }_1\overline{v_1}$ and ${\varphi }_2={\rho }_1\overline{v_2}$, and define a dimensionless, intensive Gibbs free energy

$$\stackrel{\sim }{g}=\frac{\overline{v_0}G}{V{k}_{B}T}.$$

We can then write the second partial derivatives of the intensive Gibbs free energy, with respect to number density, as

$$\frac{{\partial }^2\left(\frac{G}{V}\right)}{\partial {\rho }_1^2}={\overline{v_1}}^2\frac{k_{B}T}{\overline{v_0}}\frac{{\partial }^2\stackrel{\sim }{g}}{\partial {\varphi }_1^2},\frac{{\partial }^2\left(\frac{G}{V}\right)}{\partial {\rho }_1\partial {\rho }_2}=\overline{v_1}\overline{v_2}\frac{k_{B}T}{\overline{v_0}}\frac{{\partial }^2\stackrel{\sim }{g}}{\partial {\varphi }_1\partial {\varphi }_2},\frac{{\partial }^2\left(\frac{G}{V}\right)}{\partial {\rho }_1^2}={\overline{v_2}}^2\frac{k_{B}T}{\overline{v_0}}\frac{{\partial }^2\stackrel{\sim }{g}}{\partial {\varphi }_2^2}.$$

Therefore, the Hessian matrix can be written as

$$H_{\rho }\left[\frac{G}{V}\right]=\frac{k_{B}T}{\overline{v_0}}\left[\begin{array}{cc}\hfill \overline{v_1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \overline{v_2}\hfill \end{array}\right][H_{\varphi }[\stackrel{\sim }{g}]]\left[\begin{array}{cc}\hfill \overline{v_1}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \overline{v_2}\hfill \end{array}\right],$$

which gives

$$H_{\rho }{\left[\frac{G}{V}\right]}^{-1}=\frac{\overline{v_0}}{k_{B}T}\left[\begin{array}{cc}\hfill \frac{1}{\overline{v_1}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\overline{v_2}}\hfill \end{array}\right]{[H_{\varphi }[\stackrel{\sim }{g}]]}^{-1}\left[\begin{array}{cc}\hfill \frac{1}{\overline{v_1}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\overline{v_2}}\hfill \end{array}\right]$$ (E1)

as used in the text.

APPENDIX F: STEPS IN THE DERIVATION OF THE THIRD VIRIAL COEFFICIENTS FOR STICKY-SPHERE MIXTURES

It can be shown (see Ref. 66, Section 12-5) that the integral in Eq. (49) can be written as

$$C_{ijk}^{(p)}(T)=-\frac{4\pi {(2\pi )}^{3/2}}{3}{\int }_0^{\mathrm{\infty }}{\gamma }_{ij}(t){\gamma }_{jk}(t){\gamma }_{ik}(t)t^{2}dt,$$ (F1)

where ${\gamma }_{\alpha \gamma }(t)$ is the Fourier transform of $f_{\alpha \gamma }(|𝒓|)$. Taking the Fourier transform of the Mayer  f-function given in Eq. (2), we obtain

$${\gamma }_{\alpha \gamma }(t)={\left(\frac{2}{\pi }\right)}^{1/2}{d}_{\alpha \gamma }^3\left[\frac{\sin d_{\alpha \gamma }t}{2d_{\alpha \gamma }{\tau }_{\alpha \gamma }t}+\frac{\cos d_{\alpha \gamma }t}{{(d_{\alpha \gamma }t)}^2}-\frac{\sin d_{\alpha \gamma }t}{{(d_{\alpha \gamma }t)}^3}\right].$$ (F2)

With use of Eq. (F2), Eq. (F1) becomes

$$C_{ijk}^{(p)}(T)=-\frac{32\pi }{3}{d}_{ij}^3{d}_{jk}^3{d}_{ik}^3{\int }_0^{\mathrm{\infty }}\left[\frac{\sin d_{ij}t}{2d_{ij}{\tau }_{ij}t}+\frac{\cos d_{ij}t}{{(d_{ij}t)}^2}-\frac{\sin d_{ij}t}{{(d_{ij}t)}^3}\right]\times \left[\frac{\sin d_{jk}t}{2d_{jk}{\tau }_{jk}t}+\frac{\cos d_{jk}t}{{(d_{jk}t)}^2}-\frac{\sin d_{jk}t}{{(d_{jk}t)}^3}\right]\times \left[\frac{\sin d_{ik}t}{2d_{ik}{\tau }_{ik}t}+\frac{\cos d_{ik}t}{{(d_{ik}t)}^2}-\frac{\sin d_{ik}t}{{(d_{ik}t)}^3}\right]t^{2}dt.$$ (F3)

The integral appearing in Eq. (F3) is of the form

$$I=I(A,B,C,{\tau }_A,{\tau }_B,{\tau }_C)={\int }_0^{\mathrm{\infty }}\left[\frac{\sin At}{2A{\tau }_{A}t}+g(At)\right]\left[\frac{\sin Bt}{2B{\tau }_{B}t}+g(Bt)\right]\times \left[\frac{\sin Ct}{2C{\tau }_{C}t}+g(Ct)\right]t^{2}dt$$ (F4)

in which

$$g(x)=\frac{\cos x}{x^2}-\frac{\sin x}{x^3}$$ (F5)

and $A,B,C,{\tau }_A,{\tau }_B,{\tau }_C$ are positive, real parameters. We note that each bracketed expression in the integrand of Eq. (F4) is an even function of t, and therefore

$$I=\frac{1}{2}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left[\frac{\sin At}{2A{\tau }_{A}t}+g(At)\right]\left[\frac{\sin Bt}{2B{\tau }_{B}t}+g(Bt)\right]\times \left[\frac{\sin Ct}{2C{\tau }_{C}t}+g(Ct)\right]t^{2}dt.$$ (F6)

Expanding the integrand of Eq. (F6) yields

$$I=\frac{1}{2}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\frac{\sin At\sin Bt\sin Ct}{8{\tau }_A{\tau }_B{\tau }_{C}ABCt}+\frac{\sin At\sin Bt}{4{\tau }_A{\tau }_{B}AB}g(Ct)+\frac{\sin At\sin Ct}{4{\tau }_A{\tau }_{C}AC}g(Bt)+\frac{\sin Bt\sin Ct}{4{\tau }_B{\tau }_{C}BC}g(At)+\frac{\sin At}{2{\tau }_{A}A}g(Bt)g(Ct)t+\frac{\sin Bt}{2{\tau }_{B}Bt}g(At)g(Ct)t+\frac{\sin Ct}{2{\tau }_{C}Ct}g(At)g(Bt)t+g(At)g(Bt)g(Ct)t^2]dt.$$ (F7)

The integral in Eq. (F7) is the sum of integrals of four distinct types, namely,

$$T_1(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(\sin At\sin Bt\sin Ct/t)dt,$$ (F8)

$$T_2(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin At\sin Btg(Ct)dt,$$ (F9)

$$T_3(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin Atg(Bt)g(Ct)tdt,$$ (F10)

$$T_4(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}g(At)g(Bt)g(Ct)t^{2}dt,$$ (F11)

which can all be evaluated in closed form, as we shall demonstrate using the technique of differentiation under the integral sign. The following two lemmas will be useful.

Lemma 1 (Riemann-Lebesgue Lemma). Let f be an L¹ integrable function. Then

$$\underset{\lambda \to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x)\sin (\lambda x)dx=0$$

and

$$\underset{\lambda \to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x)\cos (\lambda x)dx=0.$$

Lemma 2. Let f be an L¹ integrable function. Then

$$\underset{\lambda \to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin (\lambda x)}{x}f(x)dx=\underset{x\to 0}{lim}f(x)\pi .$$

Proofs of Lemmas (1) and (2) can be found in most introductory analysis texts, such as Ref. 74. Additionally, we define

$$Y_n(A,B,C)=\frac{\pi }{4n!}[{((A+B+C))}^{n-1}|(A+B+C)|+{((A-B-C))}^{n-1}|(A-B-C)|+{(-1)}^n{((-A+B-C))}^{n-1}|(-A+B-C)|+{(-1)}^n{((-A-B+C))}^{n-1}|(-A-B+C)|]$$ (F12)

for non-negative integers, n, and note that

$$\frac{\partial Y_n(A,B,C)}{\partial A}=Y_{n-1}(A,B,C).$$ (F13)

1. Type I integrals

To evaluate integrals of the first type, we note that by expressing $\sin x$ in terms of complex exponentials, we can derive the identity

$$\sin At\sin Bt\sin Ct=-\frac{1}{4}[\sin ((A+B+C))t+\sin ((A-B-C))t+\sin ((-A+B-C))t+\sin ((-A-B+C))t].$$ (F14)

Thus, Eq. (F8) becomes

$$T_1=-\frac{1}{4}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\frac{\sin ((A+B+C))t}{t}+\frac{\sin ((A-B-C))t}{t}+\frac{\sin ((-A+B-C))t}{t}+\frac{\sin ((-A-B+C))t}{t}]dt.$$ (F15)

Using the well-known result

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin \sigma t}{t}dt=\text{sgn}(\sigma )\cdot \pi$$ (F16)

a proof of which can be found in most introductory complex analysis texts, such as Ref. 75, we find

$$T_1(A,B,C)=-\frac{\pi }{4}[\text{sgn}((A+B+C))+\text{sgn}((A-B-C))+\text{sgn}((-A+B-C))+\text{sgn}((-A-B+C))].$$ (F17)

In light of the fact that $\text{sgn}(x)=\frac{x}{|x|}$, for non-zero x, we obtain

$$T_1(A,B,C)=-Y_0(A,B,C).$$ (F18)

This notation will be convenient in the evaluation of the remaining integrals.

2. Type II integrals

If we make the observation that

$$g(Ct)=\frac{1}{C{t}^2}\frac{\partial }{\partial C}\left(\frac{\sin Ct}{Ct}\right),$$ (F19)

then the integral of the second type, given by Eq. (F9), can be written as

$$T_2(A,B,C)=\frac{1}{C}\frac{\partial }{\partial C}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{C{t}^3}dt.$$ (F20)

If we now define

$$I_3(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{t^3}dt,$$ (F21)

differentiating Eq. (F21) twice with respect to the parameter A yields

$$\frac{\partial I_3(A,B,C)}{\partial A}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\cos At\sin Bt\sin Ct}{t^2}dt$$ (F22)

and

$$\frac{{\partial }^2{I}_3(A,B,C)}{\partial A^2}=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{t}dt=-T_1(A,B,C).$$ (F23)

From Eq. (F18) we obtain

$$\frac{{\partial }^2{I}_3(A,B,C)}{\partial A^2}=Y_0(A,B,C).$$ (F24)

Integration with respect to A yields

$$\frac{\partial I_3}{\partial A}=Y_1(A,B,C)+{\eta }_1(B,C),$$ (F25)

where ${\eta }_1$ is an arbitrary function of B and C. Taking the limit of Eq. (F22) as A goes to infinity,

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_3}{\partial A}=\underset{A\to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos At\frac{\sin Bt\sin Ct}{t^2}dt=0$$ (F26)

by Lemma 1. Taking the same limit of Eq. (F25) gives

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_3}{\partial A}=\underset{A\to \mathrm{\infty }}{lim}-\frac{\pi }{4}[|A+B+C|+|A-B-C|-|-A+B-C|-|-A-B+C|]+{\eta }_1(B,C)={\eta }_1(B,C)$$ (F27)

because the bracketed term in Eq. (F27) vanishes for $A>B+C$. Hence ${\eta }_1(B,C)\equiv 0$, which gives

$$\frac{\partial I_3}{\partial A}=Y_1(A,B,C)$$ (F28)

and

$$I_3(A,B,C)=Y_2(A,B,C)+{\eta }_2(B,C).$$ (F29)

If we take the limit as $A\to \mathrm{\infty }$ of Eq. (F21) and apply Lemma 2, we obtain

$$\underset{A\to \mathrm{\infty }}{lim}{I}_3(A,B,C)={lim}_{A_{\mathrm{\infty }}}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\cdot \frac{\sin Bt\sin Ct}{t^2}dt=\pi {lim}_{t\to 0}\left[\frac{\sin Bt\sin Ct}{t^2}\right]=\pi BC.$$ (F30)

Taking the same limit of Eq. (F29), we find

$$\underset{A\to \mathrm{\infty }}{lim}{I}_3(A,B,C)=\underset{A\to \mathrm{\infty }}{lim}\frac{\pi }{8}[{(A+B+C)}^2+{(A-B-C)}^2-{(-A+B-C)}^2-{(-A-B+C)}^2]+{\eta }_2(B,C)=\underset{A\to \mathrm{\infty }}{lim}\frac{\pi }{8}[2{(B+C)}^2-2{(B-C)}^2]+{\eta }_2(B,C)=\pi BC+{\eta }_2(B,C),$$ (F31)

which, by Eq. (F30) gives ${\eta }_2\equiv 0$ and so

$$I_3(A,B,C)=Y_2(A,B,C)$$ (F32)

and

$$T_2(A,B,C)=\frac{1}{C}\frac{\partial }{\partial C}\frac{Y_2(A,B,C)}{C}.$$ (F33)

3. Type III integrals

Making use of Eq. (F19) we can write

$$T_3(A,B,C)=\frac{1}{BC}\frac{\partial }{\partial C}\frac{\partial }{\partial B}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{BC{t}^5}dt.$$ (F34)

We observe that the integral in Eq. (F34) does not converge. However, we may add a regularization term inside the integrand which does not depend on B, because the derivative with respect to B will cause these terms to vanish. Specifically, we have

$$T_3(A,B,C)=\frac{1}{BC}\frac{\partial }{\partial C}\frac{\partial }{\partial B}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}[\frac{\sin At\sin Bt\sin Ct}{BC{t}^5}-\frac{\sin At\sin t\sin Ct}{C{t}^5}]dt$$ (F35)

$$=\frac{1}{BC}\frac{\partial }{\partial C}\frac{\partial }{\partial B}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{Ct}dt.$$ (F36)

If we let

$$I_5(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{Ct}dt,$$ (F37)

then

$$\frac{\partial I_5}{\partial A}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos At\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{Ct}dt,$$ (F38)

$$\frac{{\partial }^2{I}_5}{\partial A^2}=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin At\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{C}dt.$$ (F39)

Expanding the integrand in Eq. (F39) we find

$$\frac{{\partial }^2{I}_5}{\partial A^2}=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{BC{t}^3}-\frac{\sin At\sin t\sin Ct}{C{t}^3}dt=-\frac{1}{BC}{I}_3(A,B,C)+\frac{1}{C}{I}_3(A,1,C)=-\frac{1}{BC}{Y}_2(A,B,C)+\frac{1}{C}{Y}_2(A,1,C),$$ (F40)

where we have used the result obtained in Eq. (F32). Integrating, we find

$$\frac{\partial I_5}{\partial A}=-\frac{1}{BC}{Y}_3(A,B,C)+\frac{1}{C}{Y}_3(A,1,C)+{\eta }_1(B,C),$$ (F41)

$$I_5=-\frac{1}{BC}{Y}_4(A,B,C)+\frac{1}{C}{Y}_4(A,1,C)+A{\eta }_1(B,C)+{\eta }_2(B,C),$$ (F42)

where ${\eta }_1$ and ${\eta }_2$ are arbitrary functions of integration, which we will again determine by comparing the limits of Eqs. (F37) and (F38)–Eqs. (F41) and (F42) as $A\to \mathrm{\infty }$. We begin by noting that the function

$$h(t)=\frac{1}{t^2}\left[\frac{\sin Bt}{Bt}-\frac{\sin t}{t}\right]\frac{\sin Ct}{Ct}$$

is bounded, smooth, and integrable, which can be shown by performing a Taylor’s series expansion of the terms in the square brackets near t = 0, and hence by Lemma 1,

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_5}{\partial A}=0$$ (F43)

and by Lemma 2,

$$\underset{A\to \mathrm{\infty }}{lim}{I}_5=\pi \underset{t\to 0}{lim}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{Ct}=\pi \underset{t\to 0}{lim}[\left(\frac{Bt}{B{t}^3}-\frac{{(Bt)}^3}{3!B{t}^3}+\frac{{(Bt)}^5}{5!B{t}^3}+\mathrm{\cdots }\right)-\left(\frac{t}{t3}-\frac{{(t)}^3}{3!t^3}+\frac{{(t)}^5}{5!t^3}+\mathrm{\cdots }\right)]\frac{\sin Ct}{t}=\frac{\pi }{6}(1-B^2).$$ (F44)

Furthermore, taking the limit as $A\to \mathrm{\infty }$ of Eq. (F41) yields

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_5}{\partial A}=\underset{A\to \mathrm{\infty }}{lim}-\frac{\pi }{24BC}[{(A+B+C)}^3+{(A-B-C)}^3+{(-A+B-C)}^3+{(-A-B+C)}^3]+\frac{\pi }{24BC}[{(A+1+C)}^3+{(A-1-C)}^3+{(-A+1-C)}^3+{(-A-1+C)}^3]+{\eta }_1(B,C)=-\frac{\pi }{24BC}[6A{(B+C)}^2-6A{(B-C)}^2]+\frac{\pi }{24C}[6A{(1+C)}^2-6A{(1-C)}^2]+{\eta }_1(B,C)=-\frac{\pi A}{8BC}[4BC]+\frac{\pi A}{8C}[4C]+{\eta }_1(B,C)={\eta }_1(B,C),$$ (F45)

which implies ${\eta }_1(B,C)\equiv 0$. As $A\to \mathrm{\infty }$, Eq. (F42) becomes

$$\underset{A\to \mathrm{\infty }}{lim}{I}_5=\underset{A\to \mathrm{\infty }}{lim}-\frac{\pi }{96BC}[{(A+B+C)}^4+{(A-B-C)}^4-{(-A+B-C)}^4-{(-A-B+C)}^4]+\frac{\pi }{96C}[{(A+1+C)}^4+{(A-1-C)}^4-{(-A+1-C)}^4-{(-A-1+C)}^4]+{\eta }_2(B,C)=\underset{A\to \mathrm{\infty }}{lim}-\frac{\pi }{96BC}[12A^2{(B+C)}^2-12A^2{(B-C)}^2+2{(B+C)}^4-2{(B-C)}^4]+\frac{\pi }{96C}[12A^2{(1+C)}^2-12A^2{(1-C)}^2+2{(1+C)}^4-2{(1-C)}^4]+{\eta }_2(B,C)=\underset{A\to \mathrm{\infty }}{lim}-\frac{\pi }{96BC}[48A^{2}BC+16BC+16B{C}^3]+\frac{\pi }{BC}[48A^{2}C+16C+16C^3]+{\eta }_2(B,C)=\frac{\pi }{6}(1-B^2)+{\eta }_2(B,C).$$ (F46)

Comparing with Eq. (F44), we deduce that ${\eta }_2(B,C)\equiv 0$, which gives

$$I_5(A,B,C)=-\frac{1}{BC}{Y}_4(A,B,C)+\frac{1}{C}{Y}_4(A,1,C).$$ (F47)

Hence,

$$T_3(A,B,C)=\frac{1}{BC}\frac{\partial }{\partial C}\frac{\partial }{\partial B}[-\frac{1}{BC}{Y}_4(A,B,C)+\frac{1}{C}{Y}_4(A,1,C)]=-\frac{1}{BC}\frac{{\partial }^2}{\partial B\partial C}\left[\frac{Y_4(A,B,C)}{BC}\right].$$ (F48)

4. Type IV integrals

The fourth type of integral can be expressed as

$$T_4(A,B,C)=\frac{1}{ABC}\frac{\partial }{\partial A}\frac{\partial }{\partial B}\frac{\partial }{\partial C}\frac{1}{A}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{BC{t}^7}dt.$$ (F49)

Using the same reasoning as we did above for the Type III integrals, while the integral in Eq. (F49) does not converge, we are able to introduce regularization terms into the integrand of Eq. (F49) as long as they are not functions of A, B, and C simultaneously. Thus we can write

$$T_4(A,B,C)=\frac{1}{ABC}\frac{\partial }{\partial A}\frac{\partial }{\partial B}\frac{\partial }{\partial C}\frac{1}{A}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\{\frac{\sin At\sin Bt\sin Ct}{BC{t}^7}-\frac{\sin At\sin Bt\sin t}{B{t}^7}-\frac{\sin At\sin t\sin Ct}{C{t}^7}+\frac{\sin At{\sin }^{2}t}{t^7}\}dt=\frac{1}{ABC}\frac{\partial }{\partial A}\frac{\partial }{\partial B}\frac{\partial }{\partial C}\frac{1}{A}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{c{t}^3}-\frac{\sin t}{t^3}\right]dt.$$ (F50)

Let

$$I_7(A,B,C)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]dt,$$ (F51)

which gives

$$\frac{\partial I_7}{\partial A}={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos At\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]dt$$ (F52)

and

$$\frac{{\partial }^2{I}_7}{\partial A^2}=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos At\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^2}-\frac{\sin t}{t^2}\right]dt=-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\{\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin Ct}{Ct}-\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\frac{\sin t}{t}\}dt=-I_5(A,B,C)+I_5(A,B,1)=\frac{1}{BC}{Y}_4(A,B,C)-\frac{1}{C}{Y}_4(A,1,C)-\frac{1}{B}{Y}_4(A,B,1)+Y_4(A,\mathrm{1,1}).$$ (F53)

Integrating, we find

$$\frac{\partial I_7}{\partial A}=\frac{1}{BC}{Y}_5(A,B,C)-\frac{1}{C}{Y}_5(A,1,C)-\frac{1}{B}{Y}_5(A,B,1)+Y_5(A,\mathrm{1,1})+{\eta }_1(B,C),$$ (F54)

$$I_7(A,B,C)=\frac{1}{BC}{Y}_6(A,B,C)-\frac{1}{C}{Y}_6(A,1,C)-\frac{1}{B}{Y}_6(A,B,1)+Y_6(A,\mathrm{1,1})+A{\eta }_1(B,C)+{\eta }_2(B,C).$$ (F55)

As usual, to determine ${\eta }_1$ and ${\eta }_2$, we take ${lim}_{A\to \mathrm{\infty }}$ of Eqs. (F51)–(F54). Because

$$\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]$$

is Riemann integrable, Lemmas 1 and 2 apply, giving

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_7}{\partial A}=\underset{A\to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\cos At\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]dt=0$$ (F56)

and

$$\underset{A\to \mathrm{\infty }}{lim}{I}_7(A,B,C)=\underset{A\to \mathrm{\infty }}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At}{t}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]dt=\pi \underset{t\to 0}{lim}\left[\frac{\sin Bt}{B{t}^3}-\frac{\sin t}{t^3}\right]\left[\frac{\sin Ct}{C{t}^3}-\frac{\sin t}{t^3}\right]=\frac{\pi }{36}(1-B^2)(1-C^2).$$ (F57)

From Eq. (F56), we also have

$$\underset{A\to \mathrm{\infty }}{lim}\frac{\partial I_7}{\partial A}=\underset{A\to \mathrm{\infty }}{lim}\frac{1}{BC}{Y}_5(A,B,C)-\frac{1}{C}{Y}_5(A,1,C)-\frac{1}{B}{Y}_5(A,B,1)+Y_5(A,\mathrm{1,1})+{\eta }_1(B,C)=\underset{A\to \mathrm{\infty }}{lim}\frac{\pi }{480BC}\left[10A({(B+C)}^4-{(B-C)}^4)+20A^3({(B+C)}^2-{(B-C)}^2)\right]-\frac{\pi }{480C}\left[10A({(1+C)}^4-{(1-C)}^4)+20A^3({(1+C)}^2-{(1-C)}^2)\right]-\frac{\pi }{480B}\left[10A({(B+1)}^4-{(B-1)}^4)+20A^3({(B+1)}^2-{(B-1)}^2)\right]-\frac{\pi }{480}\left[160A+80A^3\right]+{\eta }_1(B,C)=\underset{A\to \mathrm{\infty }}{lim}\frac{\pi }{480BC}\left[10A(8B^{3}C+8B{C}^3)+80A^{3}BC\right]-\frac{\pi }{480C}\left[10A(8C+8C^3)+80A^{3}C\right]-\frac{\pi }{480B}\left[10A(8B^3+8B)+20A^3(80A^{3}B)\right]-\frac{\pi }{480}\left[160A+80A^3\right]+{\eta }_1(B,C)={\eta }_1(B,C)$$ (F58)

implying ${\eta }_1\equiv 0$. Similarly, in the limit of large A, Eq. (F55) becomes

$$\underset{A\to \mathrm{\infty }}{lim}{I}_7(A,B,C)=\frac{1}{BC}{Y}_6(A,B,C)-\frac{1}{C}{Y}_6(A,1,C)-\frac{1}{B}{Y}_6(A,B,1)+Y_6(A,\mathrm{1,1})+{\eta }_2(B,C)=\underset{A\to \mathrm{\infty }}{lim}\frac{\pi }{2880BC}[2({(B+C)}^6-{(B-C)}^6)+30A^2({(B+C)}^4-{(B-C)}^4)+\mathrm{\hspace{0.17em}30}{A}^4({(B+C)}^2-{(B-C)}^2)]-\frac{\pi }{2880C}[2({(1+C)}^6-{(1-C)}^6)+30A^2({(1+C)}^4-{(1-C)}^4)+30A^4({(1+C)}^2-{(1-C)}^2)]-\frac{\pi }{2880B}[2({(B+1)}^6-{(B-1)}^6)+30A^2({(B+1)}^4-{(B-1)}^4)+30A^4({(B+1)}^2-{(B-1)}^2)]-\frac{\pi }{2880}[128+480A^2+120A^4)]+{\eta }_2(B,C)=\frac{\pi }{36}[B^2{C}^2-C^2-B^2+1]+{\eta }_2(B,C)=\frac{\pi }{36}(1-B^2)(1-C^2)+{\eta }_2(B,C).$$ (F59)

Eqs. (F59) and (F57) imply ${\eta }_2=0$. Therefore,

$$I_7(A,B,C)=\frac{1}{BC}{Y}_6(A,B,C)-\frac{1}{C}{Y}_6(A,1,C)-\frac{1}{B}{Y}_6(A,B,1)+Y_6(A,\mathrm{1,1})$$ (F60)

and

$$T_4(A,B,C)=\frac{1}{ABC}\frac{\partial }{\partial A}\frac{\partial }{\partial B}\frac{\partial }{\partial C}[\frac{1}{ABC}{Y}_6(A,B,C)-\frac{1}{AC}{Y}_6(A,1,C)-\frac{1}{AB}{Y}_6(A,B,1)+\frac{1}{A}{Y}_6(A,\mathrm{1,1})]=\frac{1}{ABC}\frac{\partial }{\partial A}\frac{\partial }{\partial B}\frac{\partial }{\partial C}\frac{Y_6(A,B,C)}{ABC}.$$ (F61)

5. Evaluation of the third virial coefficients for the present sticky-sphere mixture model

In summary, we have found

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{t}dt=-Y_0(A,B,C){\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin At\sin Btg(Ct)dt=\frac{1}{C}\frac{\partial }{\partial C}\frac{Y_2(A,B,C)}{C}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\sin Atg(Bt)g(Ct)tdt=-\frac{1}{BC}\frac{{\partial }^2}{\partial B\partial C}\frac{Y_4(A,B,C)}{BC}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\sin At\sin Bt\sin Ct}{t}dt=\frac{1}{ABC}\frac{{\partial }^3}{\partial A\partial B\partial C}{Y}_6(A,B,C)ABC,$$ (F62)

where Y_n is given above in Eq. (F12), and g(x) is given by Eq. (F5). We can therefore write Eq. (F4) as

$${\int }_0^{\mathrm{\infty }}\left[\frac{\sin At}{2A{\tau }_{A}t}+g(At)\right]\left[\frac{\sin Bt}{2B{\tau }_{B}t}+g(Bt)\right]\times \left[\frac{\sin Ct}{2C{\tau }_{C}t}+g(Ct)\right]t^{2}dt=\frac{1}{16ABC}[-\frac{Y_0(A,B,C)}{{\tau }_A{\tau }_B{\tau }_C}+\frac{2}{{\tau }_A{\tau }_B}\frac{\partial }{\partial C}\frac{Y_2(A,B,C)}{C}+\frac{2}{{\tau }_A{\tau }_C}\frac{\partial }{\partial B}\frac{Y_2(A,C,B)}{B}+\frac{2}{{\tau }_B{\tau }_C}\frac{\partial }{\partial A}\frac{Y_2(B,C,A)}{A}-\frac{4}{{\tau }_A}\frac{{\partial }^2}{\partial B\partial C}\frac{Y_4(A,B,C)}{BC}-\frac{4}{{\tau }_B}\frac{{\partial }^2}{\partial A\partial C}\frac{Y_4(B,A,C)}{AC}-\frac{4}{{\tau }_C}\frac{{\partial }^2}{\partial A\partial B}\frac{Y_4(C,A,B)}{AB}+8\frac{{\partial }^3}{\partial A\partial B\partial C}\frac{Y_6(A,B,C)}{ABC}].$$ (F63)

It turns out that for the two-component system we model, all of the quantities inside the second and succeeding absolute value signs in Eq. (F12) are negative, for any of the eventual substitutions of d_ij values for A, B, and C, as appropriate. Therefore, for this system, even before differentiation Eq. (F12) can be usefully rewritten as

$$Y_n(A,B,C)=\frac{\pi }{4n!}[{((A+B+C))}^n-{((A-B-C))}^n-{(-1)}^n{((-A+B-C))}^n-{(-1)}^n{((-A-B+C))}^n].$$ (F64)

This simplifies the consideration of the needed derivatives that appear in Eq. (F63). After taking the indicated derivatives, any of the four third virial coefficients for the two-component sticky-sphere mixture model can be evaluated by taking, for $C_{ijk}^{(p)}$, A = d_ij, B = d_jk and C = d_ik. We find

$$C_{ijk}^{(p)}=\frac{{\pi }^2}{54{\tau }_{ij}{\tau }_{jk}{\tau }_{ik}}\{d_{ij}^6({\tau }_{ij}-3){\tau }_{jk}{\tau }_{ik}-\mathrm{\hspace{0.17em}9}{d}_{ij}^4({\tau }_{ij}-2)\left[d_{ik}^2({\tau }_{ik}-1){\tau }_{jk}+d_{jk}^2{\tau }_{ik}({\tau }_{jk}-1)\right]+\mathrm{\hspace{0.17em}4}{d}_{ij}^3(2{\tau }_{ij}-3)\left[d_{ik}^3(2{\tau }_{ik}-3){\tau }_{jk}+d_{jk}^3{\tau }_{ik}(2{\tau }_{jk}-3)\right]-\mathrm{\hspace{0.17em}9}{d}_{ij}^2({\tau }_{ij}-1)[d_{ik}^4({\tau }_{ik}-2){\tau }_{jk}-2d_{ik}^2{d}_{jk}^2({\tau }_{ik}-1)({\tau }_{jk}-1)+d_{jk}^4{\tau }_{ik}({\tau }_{jk}-2)]+{\tau }_{ij}{(d_{ik}-d_{jk})}^2[d_{ik}^4({\tau }_{ik}-3){\tau }_{jk}+2d_{ik}^3{d}_{jk}({\tau }_{ik}-3){\tau }_{jk}+\mathrm{\hspace{0.17em}3}{d}_{ik}^2{d}_{jk}^2[{\tau }_{ik}(3-2{\tau }_{jk})+3({\tau }_{jk}-2)]+2d_{ik}{d}_{jk}^3{\tau }_{ik}({\tau }_{jk}-3)+d_{jk}^4{\tau }_{ik}({\tau }_{jk}-3)]\}.$$ (F65)

For the present model of mixtures of the $\gamma$B- and $\alpha$-crystallin lens proteins, in which we take ${\tau }_{22}=\mathrm{\infty }$, Eq. (F65) gives the following expressions for the four third mixed virial coefficients:

$$\frac{C_{111}^{(p)}}{{(\pi d_{11}^3/6)}^2}=10\left(1-\frac{3}{{\tau }_{11}}+\frac{18}{5{\tau }_{11}^2}-\frac{6}{5{\tau }_{11}^3}\right),$$ (F66)

which reduces correctly to the hard-sphere value, 10, when ${\tau }_{11}=\mathrm{\infty }$. Note that for the $\gamma$-crystallin third virial coefficient C₁₁₁ just given, clearly ${\tau }_{12}$ cannot contribute. Again for ${\tau }_{22}=\mathrm{\infty }$, the mixed virial coefficient C₁₁₂ is given by

$$C_{112}^{(p)}=\frac{{\pi }^2{d}_{11}^3}{108}(d_{11}^3(1-\frac{3}{{\tau }_{12}}+\frac{9}{4{\tau }_{12}^2}-\frac{9}{4{\tau }_{11}{\tau }_{12}^2})+\mathrm{\hspace{0.17em}6}{d}_{11}^2{d}_{22}(1-\frac{3}{{\tau }_{12}}(1+\frac{1}{2{\tau }_{12}})(1-\frac{1}{{\tau }_{11}}))+\mathrm{\hspace{0.17em}15}{d}_{11}{d}_{22}^2(1-\frac{6}{5{\tau }_{11}}-\frac{9}{5{\tau }_{12}}+\frac{12}{5{\tau }_{11}{\tau }_{12}}+\frac{9}{10{\tau }_{12}^2}-\frac{9}{10{\tau }_{11}{\tau }_{12}^2})+8d_{22}^3(1-\frac{3}{2{\tau }_{11}}-\frac{3}{2{\tau }_{12}}+\frac{9}{4{\tau }_{11}{\tau }_{12}}+\frac{9}{8{\tau }_{12}^2}-\frac{9}{8{\tau }_{11}{\tau }_{12}^2})+\frac{d_{22}^4}{d_{11}}(\frac{4}{9{\tau }_{12}^2}-\frac{4}{9{\tau }_{11}{\tau }_{12}^2})).$$ (F67)

This reduces correctly to the corresponding, mixed hard-sphere third virial coefficient, given by⁷⁶

$$C_{112}^{(p)HS}=\frac{{\pi }^2{d}_{11}^3}{108}(d_{11}^3+6d_{11}^2{d}_{22}+15d_{11}{d}_{22}^2+8d_{22}^3).$$ (F68)

For ${\tau }_{22}=\mathrm{\infty }$, the coefficient C₁₂₂ becomes

$$C_{122}^{(p)}=\frac{{\pi }^2{d}_{22}^2}{108}[d_{22}^4(1-\frac{3}{{\tau }_{12}}+\frac{9}{4{\tau }_{12}^2})+\mathrm{\hspace{0.17em}6}{d}_{22}^3{d}_{11}(1-\frac{3}{{\tau }_{12}}+\frac{3}{2{\tau }_{12}^2})+15d_{22}^2{d}_{11}^2(1-\frac{9}{5{\tau }_{12}}+\frac{9}{10{\tau }_{12}^2})+\mathrm{\hspace{0.17em}8}{d}_{11}^3{d}_{22}(1-\frac{3}{2{\tau }_{12}}+\frac{9}{8{\tau }_{12}^2})+9d_{11}^4\frac{1}{4{\tau }_{12}^2}].$$ (F69)

Finally, with ${\tau }_{22}=\mathrm{\infty }$, C₂₂₂ takes on the appropriate hard-sphere value,

$$\frac{C_{222}^{(p)}}{{(\pi d_{22}^3/6)}^2}=10.$$ (F70)