Highly Predictive and Interpretable Models for PAMPA Permeability

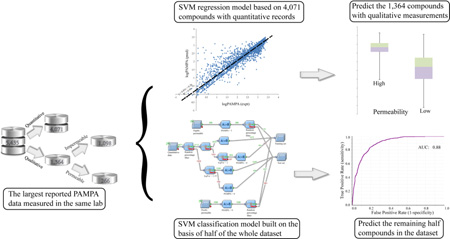
Abstract

Cell membrane permeability is an important determinant for oral absorption and bioavailability of a drug molecule. An in-silico model predicting drug permeability is described, which is built based on a large permeability dataset of 7488 compound entries or 5,435 structurally unique molecules measured by the same lab using parallel artificial membrane permeability assay (PAMPA). On the basis of customized molecular descriptors, the support vector regression (SVR) model trained with 4,071 compounds with quantitative data is able to predict the remaining 1,364 compounds with the qualitative data with an area under the curve of receiver operating characteristic (AUC-ROC) of 0.90. The support vector classification (SVC) model trained with half of the whole dataset comprised of both the quantitative and the qualitative data produced accurate predictions to the remaining data with the AUC-ROC of 0.88. The results suggest that the developed SVR model is highly predictive and provides medicinal chemists a useful in-silico tool to facilitate design and synthesis of novel compounds with optimal drug-like properties, and thus accelerate the lead optimization in drug discovery.

Graphical Abstract

Introduction

The oral route of administration is desirable for most drugs due to the convenience, patient compliance and cost concerns. After a drug is orally administrated, it is dissolved in gastrointestinal fluids and then absorbed by the digestive system. Drug absorption primarily takes place in the small intestine, where drug molecules can penetrate the cell membrane on the intestine wall to enter the blood circulation. Before drug molecules reach the systemic circulation, they are carried via the portal vein to the liver where drug molecules might be metabolized by either phase I or/and II enzymes (the first-pass effect) in hepatocytes.

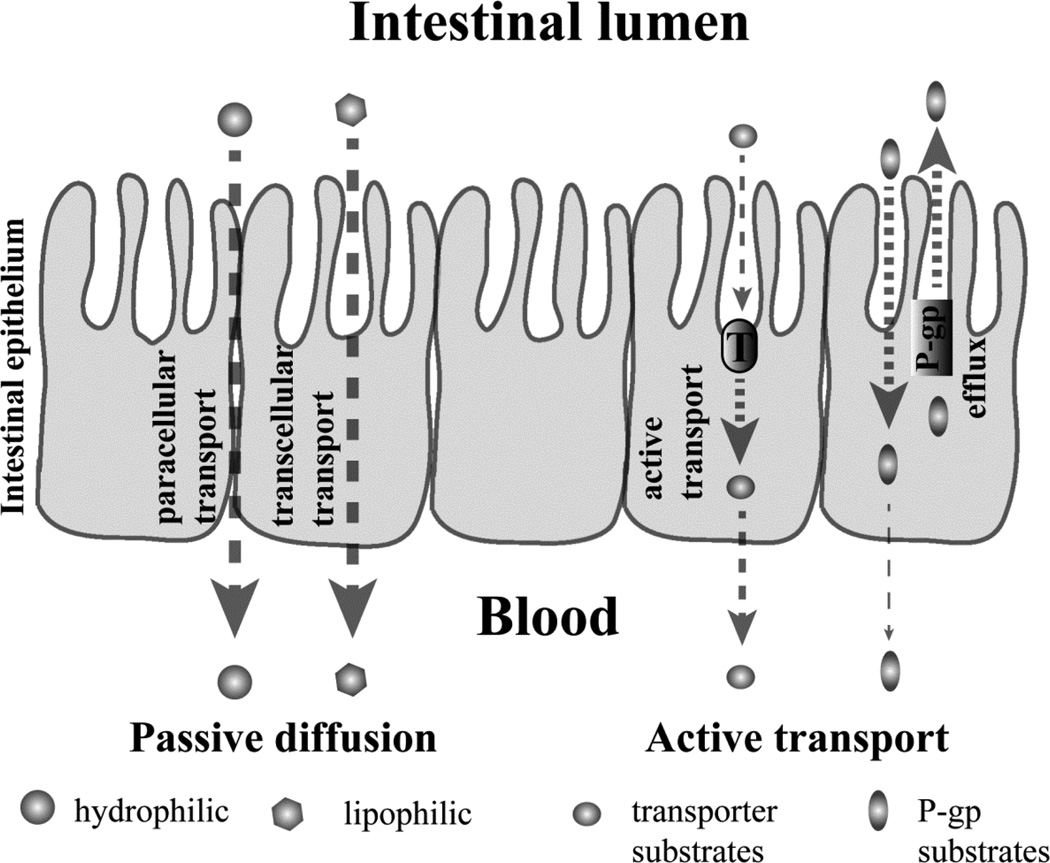
The small intestine is composed of duodenum, jejunum, and ileum sections. The luminal folding and villi structure (Figure 1) in the human small intestine greatly enlarge the effective absorption surface area by 600-fold.¹ Most drugs are absorbed through the intestinal epithelium to enter the systemic circulation primarily by passive diffusion, which is driven by the concentration gradient.^{2, 3} Lipophilic drugs mainly diffuse transcellularly, due to their high permeability across the plasma lipid membrane. Hydrophilic drugs with a low molecular weight might diffuse primarily via the paracellular route (Figure 1). In addition to passive diffusion, some drugs as well as endogenous compounds such as dipeptides, pass through the intestinal epithelium via active transporters including OCTs (organic cation transporter), OATPs (organic anion-transporting polypeptide) and PEPT1 (H⁺/peptide co-transporter), just to name a few. On the other hand, drug molecules, after entering the epithelial cells or reaching systemic circulation, can also be pumped back to the intestinal lumen by efflux transporters, such as P-gp (P-glycoprotein, MDR1), BCRP (breast cancer resistance protein) and MRP2 (multidrug resistance-associated protein) expressed on the small intestine epithelial cells, if the drug is a substrate for the transporter.²

Figure 1.

A simplified cartoon representation of different mechanisms involved in intestinal absorption of a drug molecule. After oral administration, drug uptake through the intestinal epithelium follows either passive diffusion or active transport. Lipophilic drugs favor transcellular transport, while hydropholic drugs prefer to paracellular transport. P-gp, an efflux transporter engaged in pumping drugs back to intestinal lumen, is used as an example to represent active transport processes.

Because absorption is one of the key physico-chemical properties that determine oral bioavailability, several in vitro methods such as Caco-2 and PAMPA (parallel artificial membrane permeability assay) have been developed to evaluate drug permeability across the cellular membrane. Caco-2 cells are derived from human colorectal adenocarcinomas, and they express a number of transporters such as P-gp and BCRP, and also exhibit characteristics that resemble intestinal epithelial cells such as the formation of a polarized monolayer, well-defined brush border on the apical surface and tight intercellular junctions. Therefore, Caco-2 permeability assay has been widely used by pharmaceutical companies in absorption screening for preclinical drug selection.⁴ PAMPA is a non-cell-based and low-cost alternative to cellular models. Compared to cell-based methods, PAMPA has the advantages of cost and time effectiveness, high tolerance to a wider pH range and higher DMSO content, and amenability to high throughput.^5–7 A limitation of PAMPA is that neither active nor efflux transporters are modeled by the artificial PAMPA membrane. Despite this limitation, PAMPA provides permeability values that are useful for absorption prediction, because the majority of drugs are absorbed by passive diffusion through the membrane.^{2, 8} The high intestinal concentrations of drugs after oral administration greatly exceed the intestinal transporter K_m values and they are saturated, whereas passive diffusion is not saturable and is thus the primary permeation mechanism. Strong correlations have been observed between PAMPA and Caco-2 assay results.^{6, 9, 10} Although both Caco-2 and PAMPA measurements provide valuable drug permeability data after compound synthesis, an in-silico model that predicts permeability of structurally diversified compounds can provide medicinal chemists a useful tool to facilitate pre-synthesis design of novel compounds with optimal permeability, and thus accelerate lead optimization in drug discovery. A quantitative structure-permeability relationships (QSPR) prediction approach using previously measured PAMPA values from a large diverse compound set would be a useful contribution to translational pharmaceutical sciences.

A typical QSPR approach for PAMPA data was carried out by Akamatsu’s group in 2005:¹¹

$${\mathit{\text{log}}P}_{\mathit{\text{app}}-\mathit{\text{pampa}}}=0.43(\pm 0.09)\mathit{\text{log}}{P}_{\mathit{\text{oct}}}-0.25(\pm 0.08)|p{K}_a-pH|-1.07(\pm 0.49)S{A}_{HA}-1.00(\pm 0.42)S{A}_{HD}-4.98(\pm 0.31)$$

n = 57, s = 0.33, r² = 0.76, q² = 0.72. where logP_oct is the logarithm of the octanol-water partitioning coefficient, pK_a is the negative logarithm of the acid dissociation constant (K_a), SA_HA and SA_HD are surface area of hydrogen bond acceptors and hydrogen bond donors, n is the number of training compounds, s is the standard deviation, r and q are the correlation coefficient and the cross-validation (CV) correlation coefficient, respectively. Twenty two peptidic compounds and 38 commercial drugs comprised the training data, with three drugs, Desipramine, Imipramine, and Testosterone, excluded from the model development.¹¹

Addition of 37 organic compounds to the training set led the group to conclude a bilinear QSPR model:¹²

For compounds with logP_app-pampa ≤ −4.5,

$${\mathit{\text{log}}P}_{\mathit{\text{app}}-\mathit{\text{pampa}}}=0.42(\pm 0.09)\mathit{\text{log}}{P}_{\mathit{\text{oct}}}-0.28(\pm 0.07)|p{K}_a-pH|-1.20(\pm 0.47)S{A}_{HA}-1.11(\pm 0.40)S{A}_{HD}-4.79(\pm 0.30)$$

n = 71, s = 0.35, r² = 0.76, q² = 0.72.

For compounds with logP_app-pampa > −4.5,

$${\mathit{\text{log}}P}_{\mathit{\text{app}}-\mathit{\text{pampa}}}=0.40(\pm 0.16)\mathit{\text{log}}{P}_{\mathit{\text{oct}}}+0.24(\pm 0.15)|p{K}_a-pH|-3.68(\pm 0.51)$$

n = 26, s = 0.30, r² = 0.54, q² = 0.42.

It is noted that the PAMPA models published to date are mostly based on small datasets; thus, it bears less predictive power for today’s diversified chemical spaces.^13–15 A number of physical models have been proposed to predict passive membrane permeation, in an attempt to simulate the underlying physical permeation process.¹⁶ The majority of the physical models exhibited poor predictability based on the small datasets, partly due to complexity of the permeation process and lack of reliable parameters to formulate the equations associated with the process.¹⁶

The current study presents an in-silico model for predicting drug permeability based on experimental PAMPA data collected at NCATS. This model is built based on a dataset of more than 4,000 structurally diverse compound entries, a large permeability dataset generated by the same lab under exactly the same assay conditions. Based on the large dataset, both regression (SVR) model and classification (SVC) model are developed to predict PAMPA permeability for public use (https://tripod.nih.gov/adme/pampar/ppp.html).

Experiments

The stirring double-sink PAMPA method patented by pION Inc. (Billerica, MA) was employed to determine the permeability of compounds via PAMPA passive diffusion.^{17, 18} The PAMPA lipid membrane, which consisted of an artificial membrane of a proprietary lipid mixture and dodecane (Pion Inc.), was optimized to predict gastrointestinal tract (GIT) passive diffusion permeability. This membrane was immobilized on a plastic matrix of a 96 well “donor” filter plate placed above a 96 well “acceptor” plate. This artificial membrane mimicked the GIT membrane in the human body. Both “donor” and “acceptor” wells were buffered to pH 7.4. The test articles, stocked in 10 mM DMSO solutions, were diluted to 0.05 mM in aqueous buffer (pH 7.4) and the concentration of DMSO was 0.5% in the final solution. During the 30-minute permeation period at room temperature the test samples in the donor compartment were stirred using the Gutbox technology (Pion Inc.) to reduce the unstirred water layer. The test article concentrations in the “donor” and “acceptor” compartments were measured using a UV plate reader (Nano Quant, Infinite^® 200 PRO, Tecan Inc., Männedorf, Switzerland). Permeability calculations were performed using Pion Inc. software and were expressed in the units of 10⁻⁶cm/s.

Data preparation

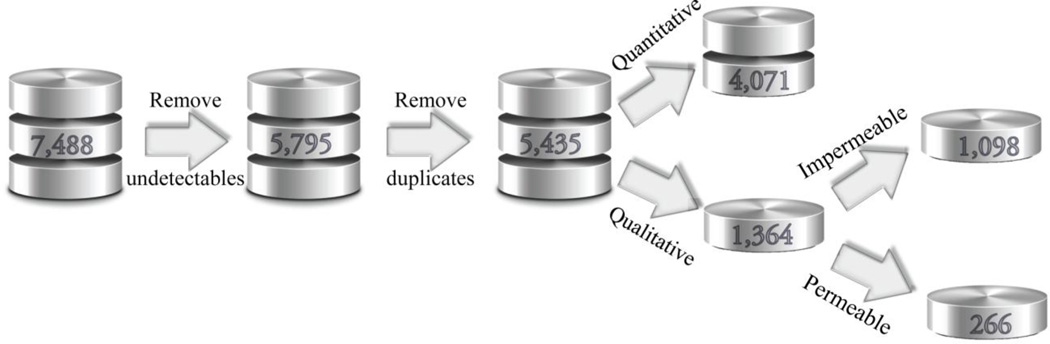
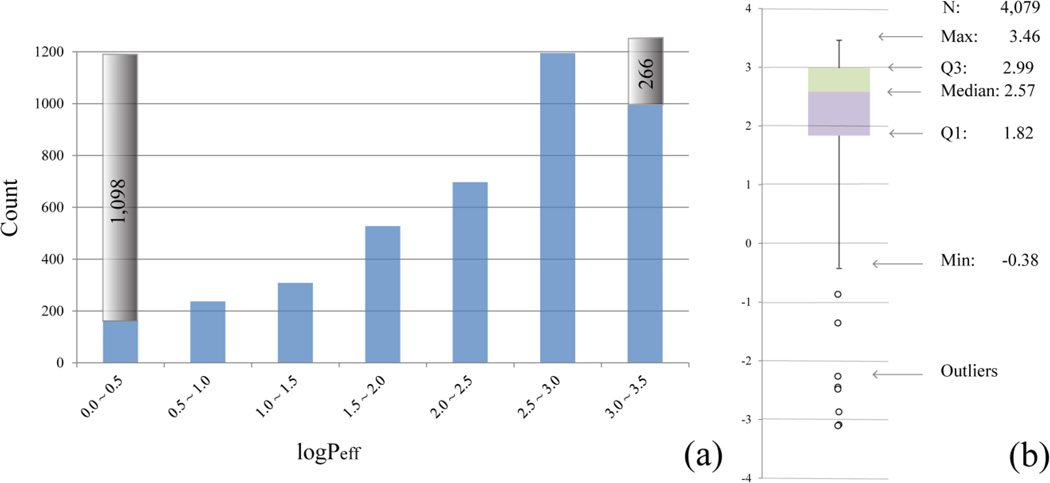
The original dataset contains 7,488 compound entries, among which 1,693 compounds were not detectable presumably due to their UV-inactivity. The remaining compound entries in the dataset were standardized by removing different salt forms, isotopes, and organometallic compounds. The duplicated compounds were either excluded from the dataset or kept as single copies, depending on the consistency of the measurements: if the Z scores (mean/standard deviation) were less than 3.0, the mean values were calculated to replace the individual logP_eff values; otherwise, the duplicates were rejected. The cleansed dataset contains 4,079 compounds with quantitative P_eff readouts and 1,364 compounds with qualitative records (eg. P_eff < 1.0 × 10⁻⁶ cm/s), among which 266 compounds were referred to as highly permeable with logP_eff greater than 3.0, and the rest were poorly permeable with logP_eff smaller than 1.0 (Figures 2 and 3a). The boxplot of the quantitative data demonstrates that the measured PAMPA values span nearly four orders of magnitude without including the 8 outliers, and the data skew toward lower logP_eff portion (Figure 3b).

Figure 2.

The flowchart describing the preprocessing of the PAMPA dataset.

Figure 3.

(a) Histogram plot depicting the distribution of quantitative data of logP_eff. The two gray columns represent the counts of poorly and highly permeable compounds in the dataset. (b) Boxplot of the quantitative PAMPA data, where Q1 and Q3 present the first and third quartiles.

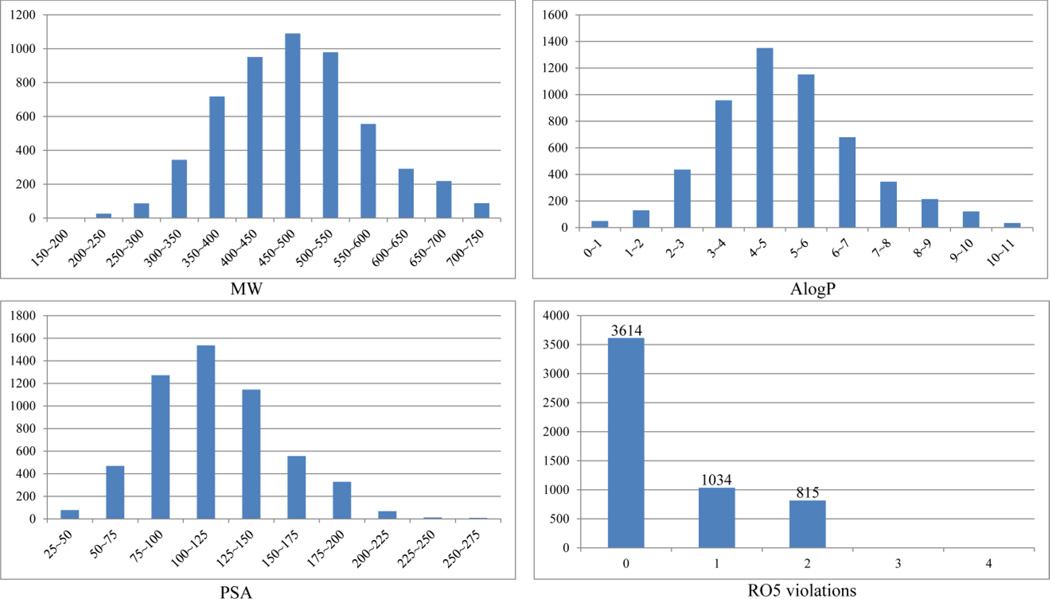
It is noted that the current PAMPA P_eff dataset is mostly comprised of drug-like molecules resulting from multiple drug discovery projects, and majority of these compounds were synthesized by NCATS. Molecular weight (MW), AlogP, and polar surface area (PSA) of the compounds in the dataset follow normal distribution, peaking at 450 ~ 500 Daltons, 4 ~ 5, and 100 ~ 125 Ų, respectively (Figure 4). A majority of the collection (84.8%) can be characterized as drug-like compounds, with zero or single violation of Lipinski’s rule-of-5 (RO5) (Figure 4). Consequently, the PAMPA permeability models based on these drug-like compounds are expected to be of pharmaceutical interest.

Figure 4.

Distributions of molecular weight (MW), lipophilicity (AlogP), polar surface area (PSA), and rule-of-five (RO5) violations of the PAMPA dataset generated by NCATS.

Based on the characteristics of the dataset, i.e. a mixture of quantitative and qualitative data, two strategies were adopted to compose the training and test datasets in order to construct the predictive QSPR models. The first strategy was to utilize all the 4,071 quantitative data to train a regression model to predict the PAMPA permeability, logP_eff, of the test set containing all the 1,364 qualitative data; the second strategy was to develop a classification model with 50% of the data randomly selected from the combined dataset of quantitative and qualitative data (5,473 compounds in total after excluding the 8 outliers) and validate the model with the remaining half of the data. For the quantitative data, those compounds with logP_eff values (in the units of 10⁻⁶ cm/s for P_eff) greater than 2.5 in the training set were assigned as permeable; those lower than 2.0, as non-permeable; and the 387 compounds with logP_eff values in between 2.0 and 2.5 were discarded (Figure S1). The 304 compounds with their logP_eff values falling between 2.0 and 2.5 are remained in the test set, and binned into high or low permeable by using cutoff of 2.25 log units.

Molecular descriptors

An atom-type-based molecular descriptor system was used to derive the structure-permeability relationships. An atom-type casting tree was designed to assign atom types according to each atom’s own chemical properties and its chemical environment within the molecule.¹⁹ The structure of the original tree was subject to recursive optimizations to improve its performance in predicting lipophilicity of the compounds (logP) in the Pomona College Masterfile subset, Starlist (2004 version), a high-quality dataset containing nearly 11,000 structurally diverse compounds. In addition to the 218 atom types, 41 correction factors were introduced to recruit the whole-molecule properties, such as molecular globularity, flexibility, etc. The atom-type casting tree was implemented by using OEChem toolkits from OpenEye (OpenEye, Santa Fe, NM). The same set of molecular descriptors has been applied to produce highly predictive models for a variety of molecular properties.^19–22

Support vector machine (SVM)

SVM is an elegant machine learning algorithm that has been successfully applied to many pattern recognition problems.²³ SVM has been proven to outperform other machine learning methods because of its outstanding generalization capability.^24–26 Actually, SVM is one of the few machine learning algorithms to address the generalization problem, i.e., how well a derived model performs on unseen data. It is not trivial to estimate the generalization error solely based on a training data set. According to Novikoff’s Theorem, minimizing the generalization error is equivalent to maximizing the separating margin in support vector classification (SVC).²⁴ Therefore, the binary classification with minimized generalization error problem is transformed to a constrained optimization problem:

Maximizing the margin

$$\frac{2}{\Vert \mathit{w}\Vert },\text{or minimize}\frac{1}{2}{\Vert \mathit{w}\Vert }^2,\text{ subject to}$$

$$y_i(\langle \mathit{w}·\mathit{x}\rangle +b)\ge 1.$$

When the training data are not separable, the concept of soft margin is applied to allow data points misclassified but at a cost. By introducing slack variables ξ_i, the constrained optimization problem becomes:

$$\text{Minimizing }\frac{1}{2}{\Vert \mathit{w}\Vert }^2+C{\sum }_{i=1}^m{\xi }_i,\text{ subject to}$$

$$y_i(\langle \mathit{w}·\mathit{x}\rangle +b)\ge 1-{\xi }_i,$$

$${\xi }_i\ge 0,i=1,2,\dots ,m,$$

where C is a penalty parameter applied to misclassified compounds, which is the major parameter affects the performance of a SVC model.

The final piece of the puzzle in SVC is “kernel trick”, which enables a smooth introduction of nonlinearity thus allows application of linear algorithm to solve nonlinear problems. A common choice of kernel function is a Gaussian Radial Basis Function (RBF):

$$k({\mathit{x}}_i,{\mathit{x}}_j)=e^{-\gamma {\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert }^2}$$

which has a single parameter γ. The best combination of C and γ is often selected by a grid search with exponentially growing sequences of C and γ, for example, ∈ {2⁻⁵, 2⁻³, …, 2⁵}; γ ∈ {2⁻⁵, 2⁻³, …, 2⁵}.

The principle of SVM can be readily extended to regression through Vapnik’s ε–insensitive loss function:

$$L_{\epsilon }(y_i,\langle \mathit{w}·\mathit{x}\rangle )=\{\begin{array}{cc}0\hfill & \mathit{\text{if }}|y_i-\langle \mathit{w}·\mathit{x}\rangle |\le \epsilon \hfill \\ \hfill |y_i-\langle \mathit{w}·\mathit{x}\rangle |-\epsilon & \hfill \mathit{\text{otherwise}}\end{array}$$

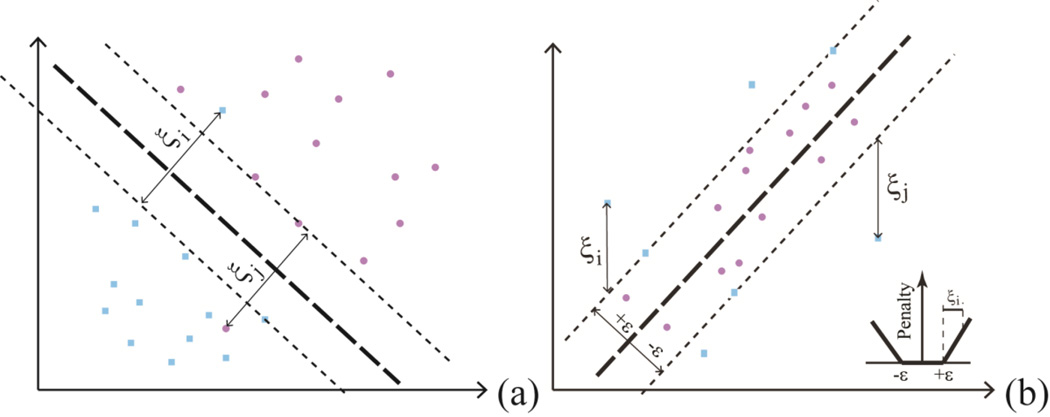
Support vector regression (SVR) is similar to SVC in the sense that SVC segregates data points belonging to different classes into different sides of hyper-planes and maximizes the margin between the planes, whereas SVR drives the data points in between the minimized ε-tube (Figure 5). The parameterization was accomplished on a grid-based search to minimize the mean standard error (MSE) of 5-fold cross-validation (CV) on the training data. LIBSVM, a software implementation of SVM developed by Chang and Lin,²⁷ was employed in this the study.

Figure 5.

(a) The slack variables in a SVC model; and (b) the ε–insensitive tube, ε–insensitive loss function, and slack variables for a SVR model.

Model development

A typical protocol for SVM is to first train the learner with a set of compounds with known classification – “to learn”, and then to use the trained model to classify previously unseen compounds – “to predict”. Before parameter optimization, the counts of atom types and correction factors were center-normalized and scaled to the space of [0, 1]. Parameterization was then conducted in order to maximize the effectiveness of SVM models. For a SVR model, three parameters influence the performance of generalization, the soft margin penalty, C, the kernel parameter, γ, and ε.

The parameter ε is useful if the desired accuracy of the approximation is specified beforehand. However, lacking of a priori information about the accuracy of the y values makes it difficult to determine the value of ε a priori. The sparsity parameter ν is equivalent to the fraction of data points outside the ε–tube, which can be chosen in accordance with the noise in y values.²⁸ The optimal ν is negatively correlated to the noise in data and the tube width ε. The parameter ν is also shown largely insensitive to the choice of the other two parameters (Figure S2).

The surface chart in Figure S3 provides a clear picture illustrating the interplay of the soft margin penalty, C, and the sparsity parameter, ν, and the joint effects on the MSE, when the kernel parameter, γ, is set to 0.25. The concave shape of the surface revealed a relatively flat bottom corresponding to the C and ν combinations, which offer optimal performance.

The similar protocol has been followed in parameterization of the SVC models.

Results

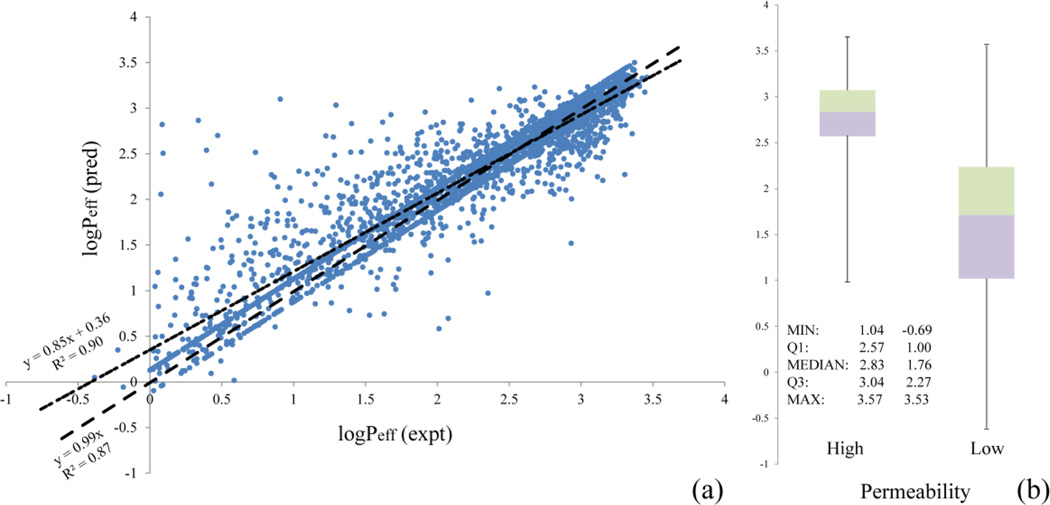
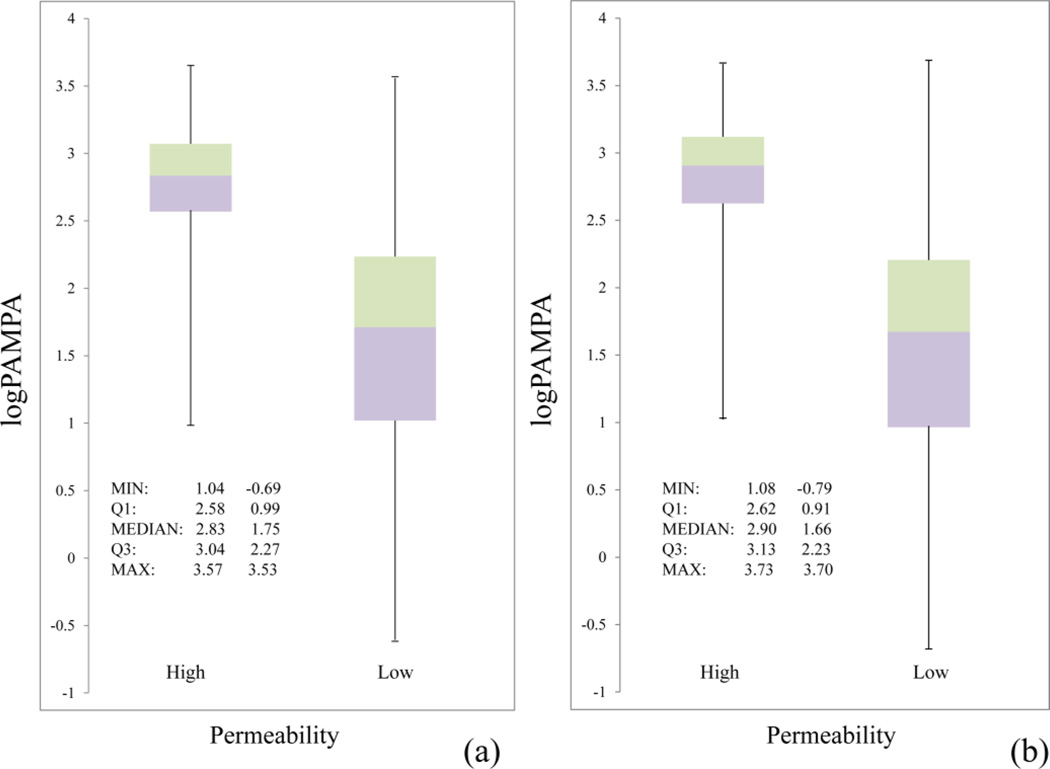
Adopting the optimized parameters (C = 8, γ = 0.25, and ν = 0.125), the SVR model was highly predictive for the compounds in the training set, with the regression coefficient r² of 0.90 (or 0.87 by setting interception to 0.0) and the MSE of 0.07 log units (Figure 6a). Examination of the boxplots of the predicted logP_eff values for the compounds in the two categories of low and high permeability leads to the primary conclusion that the SVR model was capable of separating the two groups of compounds in the test set (Figure 6b).

Figure 6.

(a) Correlation between the observed and predicted logP_eff values over the 4,071-compound training set for the SVR model; (b) Boxplots of the predicted logP_eff values for the poorly and highly permeable compounds in the test set.

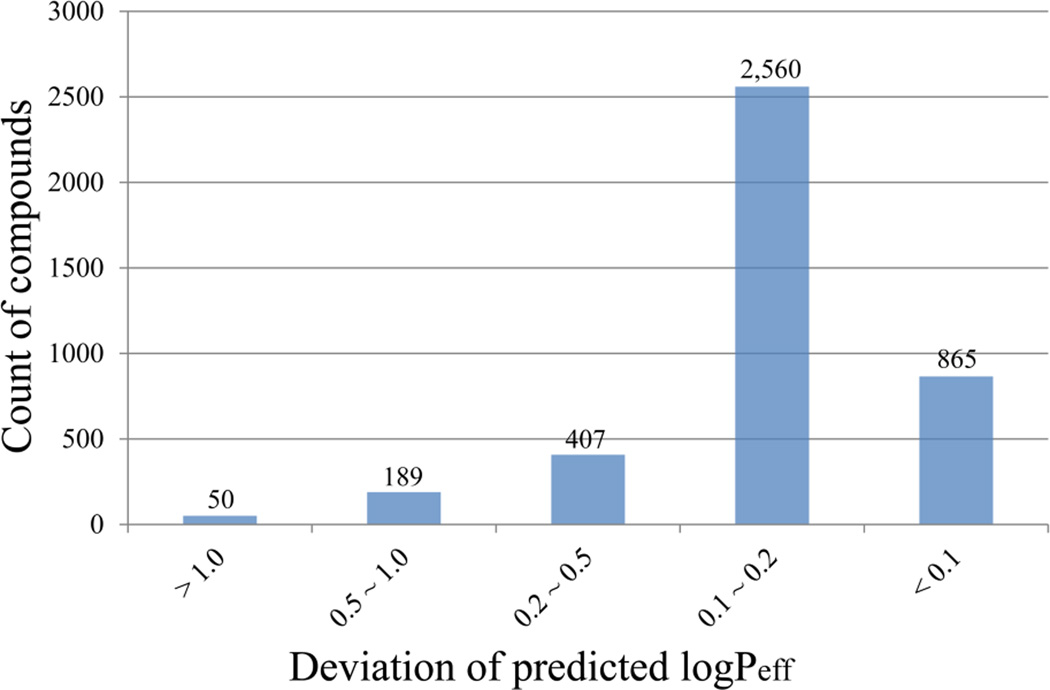
Figure 7 illustrates the count of the compounds falling into the different categories in terms of accuracy of the predictions. The majority of the 4,071 compounds (3,425 of which, or 84.1%) were accurately predicted by the SVR model with a deviation of logP_eff smaller than 0.2 log units, whereas only 239 compounds, or 5.9%, were poorly predicted with the predicted logP_eff diverging from the experimental values greater than 0.5 log units. Among the most poorly predicted 50 compounds, 27 (or 54.0%) are less permeable with a logP_eff lower than 1.0, while the whole dataset contains only 401, or 9.9%, of less permeable compounds.

Figure 7.

Distribution of 4,071-compound dataset, according to the deviation of the predicted logP_eff values.

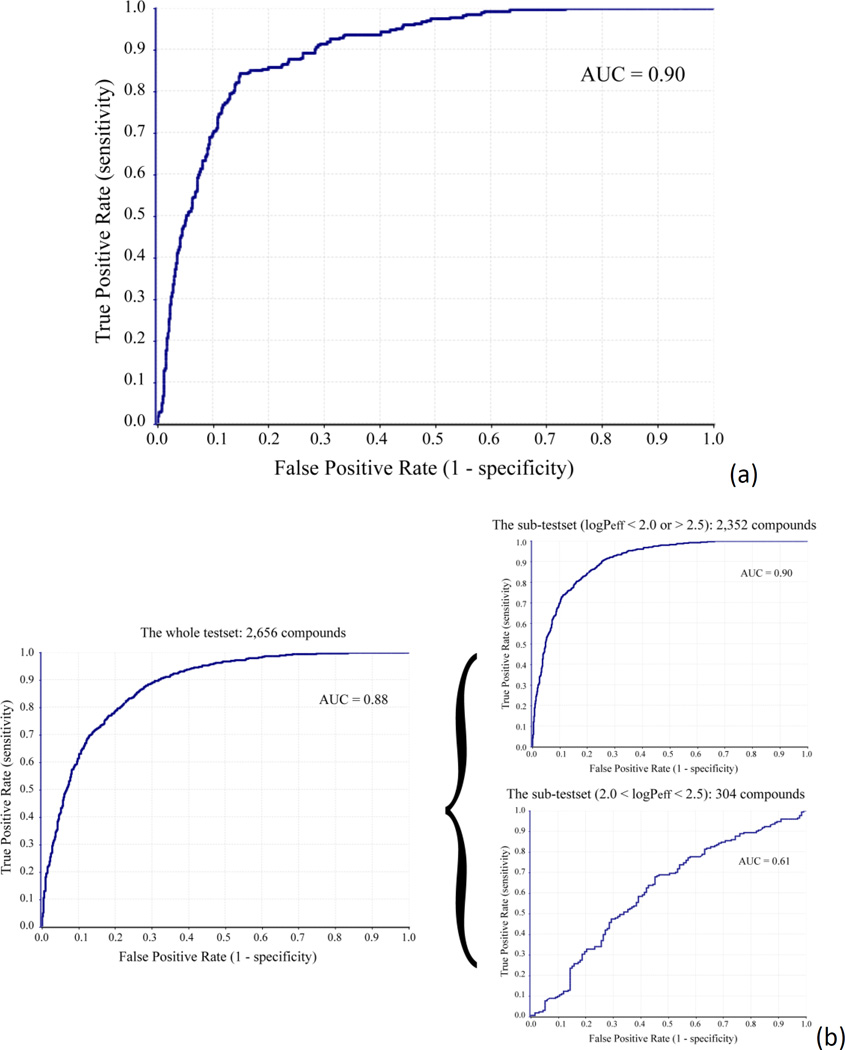
The simplicity and insensitiveness to changes in class distribution and error costs of the receiver operating characteristic (ROC) curve make it suitable for assessing and comparing the discerning power of QSPR models. The area under the ROC curve (AUC-ROC) provides objective “single value” estimation of the accuracy of machine learning models.²⁹ Rank-ordering the compounds in the test set with the predicted logP_eff values yielded the ROC curve, as shown in Figure 8. The AUC-ROC value of 0.90 indicates the highly predictive power of the SVR PAMPA model. Among the first third (454 compounds) top ranking compounds with the smallest predicted logP_eff values, there are only 2 highly permeable compounds, whereas screening the one third compounds with the highest predicted logP_eff values will retrieve 228 of 266 (85.7%) highly permeable compounds (Figure 8a).

Figure 8.

The ROC curves representing the predictive power of (a) the SVR logP_eff predictor and (b) the SVC PAMPA permeability classifier.

In the second strategy, an SVC model was built on the basis of randomly selected half of the 5,435 compounds. The SVC model was trained with 2,406 compounds, among which 50.0% compounds were labelled as permeable. In order to minimize the impact of the uncertainties associated with experimental errors on the model performance, the compounds with logP_eff values between 2.0 and 2.5 were excluded from the training data. The excellent prediction was achieved when applying the PAMPA classifier to predict the permeability of the test set compounds, with the AUC-ROC of 0.88 (Figure 8b). The binary classifier lose the prediction power significantly on the 304 compounds with logP_eff values between 2.0 and 2.5 (AUC = 0.61, Figure 8b), while improved performance was observed on the remaining test compounds (AUC = 0.90, Figure 8b).

Discussions

QSPR models are only as good as the data on which they are based. The quality of a QSPR model is determined by three key components – quality of datasets to train and validate the model; molecular descriptors to decipher and extract the relevant structural features; and sound statistical methods.

The quality of a dataset is assessed by at least three factors – size, integrity, and diversity. The optimal size of a dataset for a model depends on its application. If a particular QSPR model is a local model to cover a subset of structure space, a small dataset might be sufficient. Based on our experience, for QSPR models to cover drug-like chemical space, a couple of thousands to tens of thousands of diverse compounds are required. Optimal size is also dependent on the choice of molecular descriptors: atom-type-based and functional-group-based molecular descriptors tend to have a better coverage of chemical space than finger-print-based ones; thus atom-type-based QSPR models may require fewer training data to cover more space.

Data integrity refers to compatibility of subsets from different resources. Some properties can be determined with different experimental methods, and most properties are sensitive to experimental conditions, such as temperature; so it is not encouraged to combine datasets from different laboratories, unless the exact protocols are followed. Many experimental errors are associated with the skills and experience of the experimenters, so the datasets with the best integrity are produced when the same scientist carries out the experiment under the same study conditions by following the same protocols, which was how PAMPA data were collected in this study. Even though this PAMPA dataset represents the largest collection of drug-like compounds with great integrity, experimental errors are inevitable, which will be discussed in the next session.

Structural diversity is a double-edged sword to a QSPR model. High diversity of a dataset implies a more efficient coverage of the chemical space; on the other hand, high diversity leads to sparseness of data points and singletons in the space, especially for small datasets. The sparsely distributed data points may pose challenges in machine learning, due to the lack of pattern repetition for learning. The PAMPA dataset generated by NCATS consist of over 5,400 in-house compounds from multiple projects, together with marketed drugs, representing a suitable structural diversity to cover a good portion of chemical space of drug-like compounds. This dataset represents so-far the largest reported PAMPA dataset measured by the same lab. In addition, the atom type based molecular descriptor greatly expands the coverage of the chemical space through fragmentalizing compounds into atoms and functional groups. The normal distributions of MW, AlogP, and PSA (Fig. 4) also indicate a good coverage of the PAMPA dataset over the space of drug-like compounds.

Impact of outliers on the SVR model and classification

In the training set, eight compounds were excluded as outliers (Figure 3b). The reported PAMPA values of these compounds were beyond the sensitivity that the assay can reach, thus they were most likely due to data entry errors. Since experimental errors are inevitable in research, evaluation of the impact of these outliers on the performance of the model provides useful information. The SVR model trained with the 4,079-compound dataset exhibited a significant deterioration in terms of the correlation coefficient, since most outliers were poorly predicted with an averaged deviation of logP_eff being as high as 3.72 log units (Figure S4). These outliers contributed dramatically to the residual sum of squares (SS_res), thus significantly influencing the value of the regression coefficient r² ($r^2=1-\frac{S{S}_{\mathit{\text{res}}}}{S{S}_{\mathit{\text{tot}}}}$, where SS_tot is the total sum of squares). However, the impact of the outliers on the prediction of the permeability of the test set compounds was minimal – both the boxplots (Figure 9) and ROC curve (figure not shown) resembled the model trained without the outliers. The insensitiveness of the predictive performance to the outliers is primarily attributed to the big size of the training set, which dilutes the noises introduced by the very small fraction of the outliers.

Figure 9.

Comparison of boxplots of the predicted logP_eff values for the poorly and highly permeable compounds in the test sets (a) without and (b) with eight outliers.

Outliers with abnormal responses, such as the 8 outliers with lower-than-anticipated permeability in this study, are easy to observe, while other outliers associated with different types of experimental errors, such as incorrect chemical structures, and human mistakes in handling the data are more difficult to recognize. The incorrect data in the training sets have great impact on the performance of QSPR models, especially when the datasets are relatively small. Therefore, chemical data curation has been listed as a key element in QSPR modeling workflow, since a QSPR model is only as good as the data on which it is based.³⁰

Error analysis of the SVR model

Experimental errors, which deteriorate a QSPR model, are inevitable in reality. The top ten poorly predicted compounds are listed in Table 1. Interestingly, the predicted permeability is higher than the observed in 8 of the 10 cases. Eight of the ten molecules are organic bases (4) or acids (4). The impact of ionization of a substance on its permeability is complicated. It has been reported that PAMPA permeability is negatively correlated to the |pK_a − pH| value for poorly permeable compounds, whereas a positive correlation is observed for those with high permeability (logP_eff > 1.5 when logP_eff is recorded in the unit of 10⁻⁶ cm/sec).³¹ |pK_a − pH| value is directly associated with the amount of the unionized form of the compound (|pH − pK_a| = −log (fraction of unionized substance)). Due to the amphiphilic nature of the artificial membrane used in PAMPA experiment, the ionized form of the compounds generally have low permeability because of the higher energy required for the charged form to permeate the membranes. On the other hand, the ionized form of a compound is generally more soluble than its neutral form. Indeed, the 499 organic acids in the dataset have an averaged logP_eff of 1.44 log units, much lower than the averaged logP_eff of the whole dataset, which are 2.32 log units. Since higher level of experimental uncertainty is usually observed for low permeable compounds, the less accurate predictions of logP_eff for the ionizable compounds might be attributed to the experimental errors associated with these compounds. The higher deviations are observed for less permeable compounds, as clearly illustrated in Fig. 6a. Among the ten poorly predicted compounds, seven compounds are measured less permeable with logP_eff lower than 1.2 log units. Therefore, the loss of predictivity for the ionizable compounds is presumably due to the experimental fluctuations associated with the low permeability of such compounds.

Table 1.

The structures of the top 10 poorly predicted compounds with their observed and predicted logP_eff. The compounds in the table were purchased and characterized at NCATS.

Structures	Obs.	logPeff Pred.	Diff.	New	Known
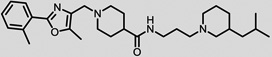	0.47	2.70	2.22	N	Y
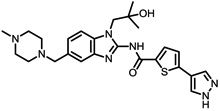	0.08	2.05	1.98	N	Y
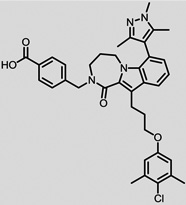	0.74	2.51	1.78	N	Y
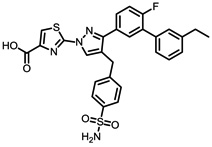	2.08	0.69	1.38	N	Y
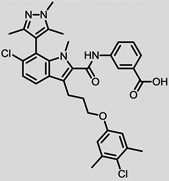	2.35	0.97	1.38	N	Y
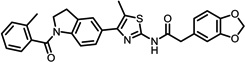	1.04	2.31	1.27	N	Y
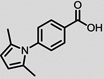	0.06	1.20	1.14	N	Y
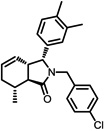	1.24	2.34	1.10	N	Y
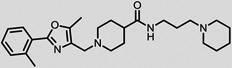	1.54	2.64	1.10	N	Y
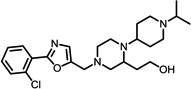	1.20	2.27	1.07	N	Y

Interpretability of the models

A good QSPR model is not only statistically solid, but also instructive and interpretable. Interpretability of a QSPR model depends on both molecular descriptors and statistical tools. One major advantage of using atom types as molecular descriptor is its excellent interpretability. SVM employs kernel transformation; thus it is considered a “black box” technique. A correlation matrix, created by calculating the correlations between each column of the input data with that of each row of the kernel matrix, will express the contribution of each input variable to the kernel matrix.³² This technique resumes the interpretability of SVM, making it a transparent and comprehensible algorithm.

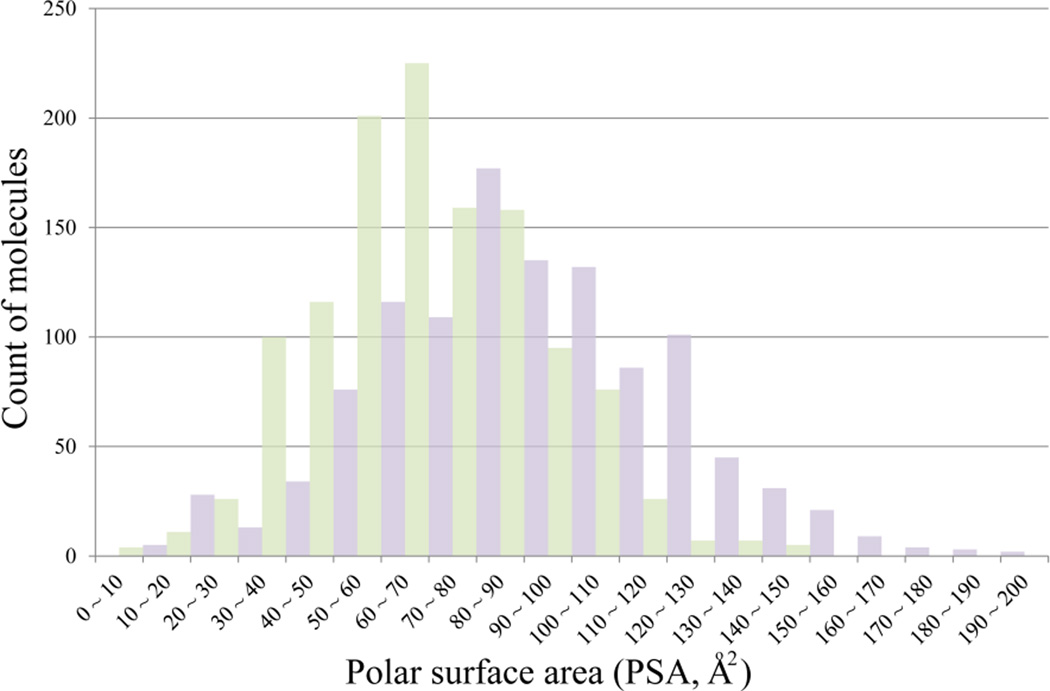
The features with the top discriminating power to separate highly from poorly permeable compounds include polar surface area (PSA), counts of hydrogen bond donors (HBD) and acceptors (HBA), count of aromatic rings, molecular weight, hydroxyl oxygen and hydrogen in an acidic group (O6 and H4). The distribution of PSA of permeable compounds in the training set shifted significantly to the larger side in comparison with the impermeable ones, with the mean PSA values changing from 68 Ų to 92 Ų (Figure 10).

Figure 10.

The distribution of polar surface area (PSA) for permeable (colored in light green) and impermeable (colored in light purple) compounds in the training data.

Significant deviation was also observed for the occurrence of the acidic oxygen O6 in the permeable and impermeable compound sets. 20 of 1216 (1.6%) permeable compounds in the training set carry an acidic group, whereas the ratio of acidic compounds is much higher in the impermeable set (246 of 1130, or 21.8%). This observation is in good agreement with Akamatsu’s QSPR model concluded from a small set of drugs and peptide-related compounds.³¹ Drugs carrying acidic groups might be actively transported by OATPs, which is beyond the capability of PAMPA models, since transporters are not expressed in the PAMPA membranes.

Summary

Both regression and classification models built for PAMPA permeability, on the basis of a large dataset generated by NCATS, exhibit high predictive ability. The SVR model trained with 4,071 drug-like compounds with quantitative PAMPA measurements predicted the 1,364 qualitative data points with an AUC-ROC of 0.90. The SVC model trained with half of the dataset produced accurate predictions to the remaining half of data with the same AUC-ROC of 0.88. The key features influencing the permeability of a compound include PSA, counts of HBD and HBA, MW, and occurrence of acidic group in the molecule. Smaller molecules with low PSA are more likely to penetrate the biomembrane through passive diffusion mechanism. Introduction of an ionizable group to a highly lipophilic compound tends to improve its permeability, since its low aqueous solubility might become the dominant factor for its poor permeability, and addition of ionizable group usually enhance the solubility of the parent compound.