Canny Edge-Based Deformable Image Registration

Abstract

This work focuses on developing a 2D Canny edge-based deformable image registration (Canny DIR) algorithm to register in vivo white light images taken at various time points. This method uses a sparse interpolation deformation algorithm to sparsely register regions of the image with strong edge information. A stability criterion is enforced which removes regions of edges that do not deform in a smooth uniform manner. Using a synthetic mouse surface ground truth model, the accuracy of the Canny DIR algorithm was evaluated under axial rotation in the presence of deformation. The accuracy was also tested using fluorescent dye injections, which were then used for gamma analysis to establish a second ground truth. The results indicate that the Canny DIR algorithm performs better than rigid registration, intensity corrected Demons, and Distinctive Features for all evaluation matrices and ground truth scenarios. In conclusion Canny DIR performs well in the presence of the unique lighting and shading variations associated with white-light-based image registration.

1. Introduction

1.1 Non-invasive imaging modalities

Optical imaging systems are a crucial modality for observing in vivo functional changes. Optical imaging techniques have emerged to track organ system responses to endogenous or exogenous changes. Small animal optical imaging in vivo models are often used to test drug accumulation, drug response, toxicity, metastatic behavior, tumor progression/regression, changes in metabolism, and inflammatory response (Hilderbrand and Weissleder, 2010; Rao et al., 2007).

In vivo imaging modalities that are non-invasive are often preferred for small animal longitudinal studies (Balas, 2009). Generally, non-invasive imaging systems can be divided into structural and functional modalities. Structural modalities provide anatomical and morphological information, such as computed tomography (CT), magnetic resonance imaging (MRI), white light optical imaging, and ultra sound. Whereas functional modalities, such as positron emission tomography (PET), single photon emission computed tomography (SPECT), and optical imaging (fluorescence and bioluminescence), provide biological molecular activity information. All of these imaging modalities come with their own unique blend of advantages and limitations.

Micro CTs can have high spatial resolution and fast acquisition times (Holdsworth and Thornton, 2002). However CTs, can be expensive and are associated with increased hazards, such as ionizing radiation exposure (Carlson et al., 2007). To achieve high contrast and spatial resolution large photon fluences are required which leads to high integral radiation dose for the subject, which can affect the immune system and potentially influence the outcome of some in vivo studies (Jawhara and Mordon, 2004; Anderson and Warner, 1976; Kroeker et al., 2011). MRIs can produce high quality 3D images without the use of ionizing radiation. However, MRIs can have long image acquisition times, suffer from low spatial resolution, require special electromagnetic shielding, and are expensive (Kobayashi et al., 2004). To achieve high spatial resolution while simultaneously preserving good signal to noise rations, long slice acquisition times are required. Ultrasound imaging techniques can acquire images at high image acquisition frequencies. Ultrasound imaging provides a low cost, non-invasive, in vivo imaging modality that has been implemented as a complement to fluorescent imaging (Snyder et al., 2009). Although useful for 3D in vivo tumor localization imaging applications, ultrasound imaging may present challenges when used for full in vivo surface imaging (Kepshire et al., 2009). Also, high spatial resolution, low contrast, full small animal imaging can be challenging with this modality (Qin et al., 2015). White light imaging techniques are non-ionizing, very low cost, easy to mobilize, and have fast image acquisition times. However, white light imaging techniques are limited to surface information, and are sensitive to lighting and shading variations (Maier-Hein et al., 2013). For these reasons, white light imaging modalities are not currently used for quantitative longitudinal studies.

PET scanners have been developed for use in small animals. However, in order to obtain high spatial resolution with high signal contrast, high radiation doses are needed, which have the potential to damage healthy tissues (Johnson et al., 2005). High costs and additional regulation due to the presence of radioactive tracers are also factors for PET imaging. SPECT is similar to PET in its use of a radioactive γ-ray tracer material but are much cheaper than PET scans, as longer half-life radionuclides can be used. Fast acquisition times are possible with SPECT, allowing for cardiac or respiratory image gating. However, since SPECT does not rely on coincidence timing, it suffers from poor spatial resolution (about 1cm), which makes SPECT not suitable for small animal imaging (Kung et al., 1990).

Optical imaging using fluorescence or bioluminescence can have fast acquisition times and achieve high spatial resolution (Balas, 2009). Optical imaging modalities do not rely on radioactive tracers so are subject to less stringent regulations. Fluorescent tracer molecules can be less costly and less biologically harmful than their radioactive counterparts. An optical imaging small animal model can be made portable with greater ease than PET or SPECT imaging modalities (Rodriguez et al., 2014). However, optical imaging techniques can only image near surface signals and must rely on reconstructive techniques for 3D localization (Werner et al., 2012).

To help facilitate cross institutional collaboration, commercial demonstration, and proof of principal modeling, portable multimodal structural and functional imaging systems have begun to gain attention (Rodriguez et al., 2014). As the demand for portable imaging systems has increased, low cost optical imaging modalities have become increasingly attractive (Okusanya et al., 2014; Ye et al., 2016). White light in vivo anatomical tracking is attractive as a light weight versatile tool for clinical imaging research. However, it is currently very difficult conduct longitudinal quantitative optical imaging-based studies as anatomical mapping from day to day is challenging (Zhu et al., 2013).

1.2 Deformable Image Registration Methods

In order to track inflammatory responses, immunological behavior, or metastatic behavior, images must be assessed at various time points along a span of time sufficient to characterize the time dependent biological event. To quantitatively measure signal and compare it in a meaningful way, corresponding regions between images taken at different time points must be compared. To compare corresponding regions between images, structural information must be used as a surrogate to track functional information.

Conventional small animal in vivo tracking methods include direct voxel/pixel to voxel/pixel tracking based on intensity and gradient information or atlas matching, which relies on an a-priori digital model (Joshi et al., 2010; Wang et al., 2012a; Wang et al., 2012b). The atlas matching method relies on iteratively deforming a digital mouse model to match simulated x-ray projections with measured x-ray projections. The deformations of the digital mouse are typically optimized using a steepest decent model until convergence is reached (Avriel, 2003; Bonnans et al., 2013). This method has two major drawbacks, it relies on x-ray information which makes it unusable for a pure optical system and it will not meaningfully converge if the solution space of the optimization problem is non-convex (Horst and Tuy, 2013). Also, recalculating the simulated x-ray projections at every iteration is extremely computationally expensive, and thus very time consuming (Folkerts, 2015).

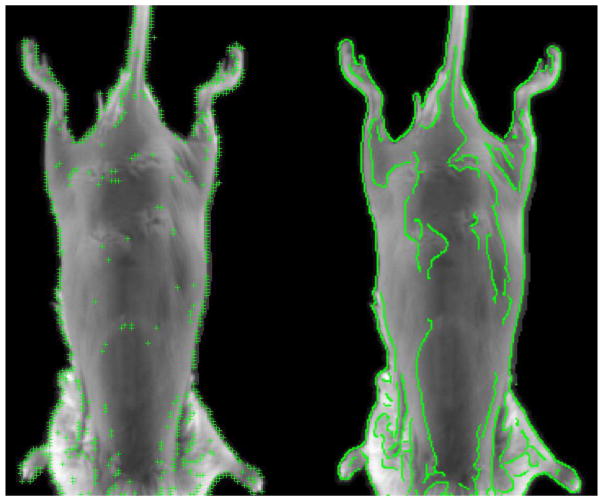
Another class of algorithms utilizes feature extraction methods for image registration. These methods rely on steepest decent optimization to minimize a non-linear least squares function (Yuille et al., 1992). This style of registration includes facial recognition, facial expression extraction, finger print identification, and palm print recognition. These distinct feature methods are all based on the scale-invariant feature transform (SIFT) method (Lowe, 2004; Xiong and Torre, 2013; de la Torre et al., 2015; Chu et al., 2013). Local gradient information around each district feature is transformed into a representation that allows for high levels of local shape distortion and change in illumination. Using district features, as opposed to conventional deformable image registration (DIR) techniques, allows for less susceptibility to noise, and lighting variations. However, distinct feature extraction techniques currently rely heavily on disjointed features, which causes sparsity in features within the image (Naveen, 2013). This is in part caused by a stability feature removal step, which helps ensure feature reliance. In the case of white light image registration, it is favorable to use complete edges of an image instead of using a scattered subset of features (Canny, 1986; Qian and Huang, 1996; Worthington, 2002; Wang and HE, 2004; Luo and Duraiswami, 2008; Wang and Fan, 2009; Chen and Lo, 2012). If each point along the canny edge is treated as a feature, then edge continuity can be used for stability discrimination. The differences between the SIFT method and the canny edge feature extraction method is demonstrated in figure 1.

Figure 1.

Posterior mouse surface with superimposed SIFT method (left), and Canny edge feature extraction method (right).

Small animal white light based DIR is uniquely challenging, as minor changes in the mouse’s anatomical position can lead to big changes in shading and lighting. Similarly, features such as implantation swelling, and lesions on the skin can vary from day to day. Weight loss or weight gain can also make tracking the surface of a mouse difficult.

Conventional DIR algorithms using uniform grid based approaches can be error prone in regions with low contrast information such as the smooth surfaces on the skin or low quality regions of the image. However, strong features on the mouse skin surface such as the ridges of the spine, shoulders, ribs, and hind legs can often be seen even in the presence of lighting, shading, and noise variation. Recently, a new form of non-grid based DIR algorithms have emerged, called Landmark-Guided DIR, which uses a sparse subset of points to deformably register noisy images (Kearney et al., 2015). This style of registration is well suited for images that have high noise contamination and large intensity inconsistencies between time points.

This paper demonstrates the feasibility of using canny edges, embedded in a sparse DIR framework, to overcome the challenges of small animal in vivo white light based anatomical tracking.

2. Methods and Materials

2.1 In Vivo Setup

All images were acquired using Progenitec’s portable imaging device (Progenitec Inc., Arlington, Tx). White light and fluorescent images where acquired using a 100μm isotropic pixel size. Fluorescent images where obtained using a 635nm LED source at 30mA for 60 seconds.

7 BALB/c, 8–10 week old mice were subcutaneously injected with CY5 tagged EPO. CY5 is a near infrared fluorescent dye with an emission wavelength of 630–700nm (Veiseh et al., 2007). All mice were imaged in prone position.

2.2 The Algorithm

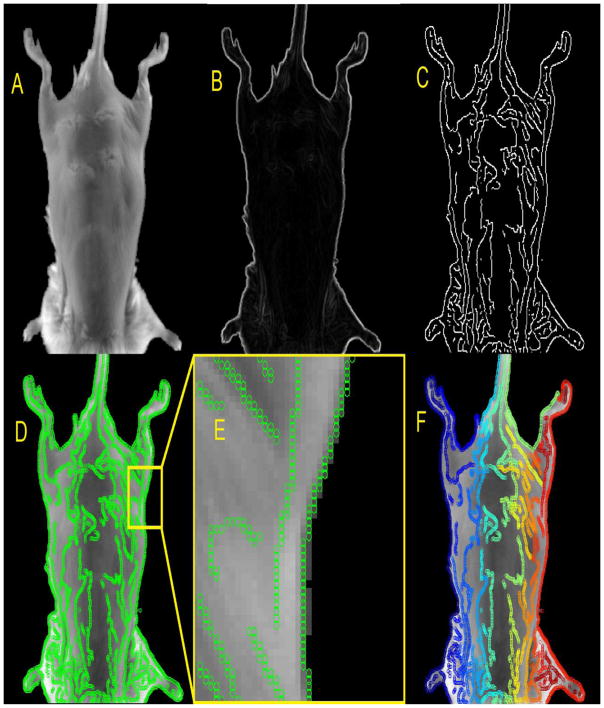
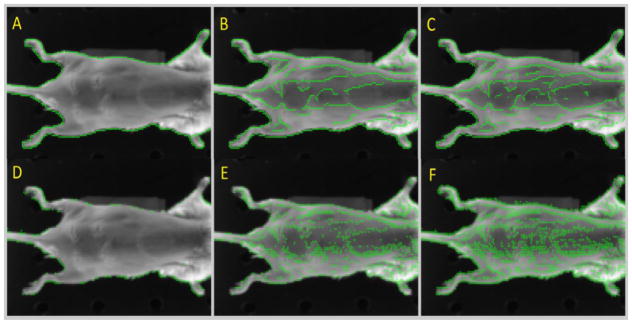
A cross correlation based algorithm was used to rigidly register the image at time zero (I_stsatic) with an image acquired at a later time (I_moving). Once a rigid registration is determined, canny edges are generated on the I_static set (Wang and Fan, 2009; Luo and Duraiswami, 2008; Wang and HE, 2004; Canny, 1986). The canny edges are then separated using connected component analysis (Samet and Tamminen, 1988). The various steps associated with generating points from and separating the Canny edges can be seen in figure 2.

Figure 2.

The static image (A). The magnitude of the gradients (B). The Canny edge extraction (C). The points associated with the Canny edges superimposed on the static image (D). Zoomed in region of image D (E). Color coded separated canny edges, are shown superimposed on the static image (F).

Each point (P) associated with the canny edges is used to match corresponding regions between I_static and I_moving, as these edges will all have strong gradient information associated with them. To help ensure that the canny edge does not represent noise, a line filtration algorithm is implemented. The line (L) must be above a certain length α. Once a set of filtered canny edges is defined, a local small area (LSA) around each P on the static image (LSA_static) is defined with an initial size of 500μm × 500μm. Each LSA is registered to a corresponding area on the moving image (LSA_moving). An optimization scheme is implemented to determine the optimal (i,j) shift of each LSA_moving until E is minimized for every P, where

$$\begin{array}{l}E{(i,j)}^P=\Vert {(\nabla {\mathit{LSA}}_{\mathit{static}}-\nabla {\mathit{LSA}}_{\mathit{moving}}^{i,j})}^2{({\mathit{LSA}}_{\mathit{static}}-{\mathit{LSA}}_{\mathit{moving}}^{i,j})}^2\Vert \\ i^P,j^P=argmin\mathit{E}{(i,j)}^P\end{array}$$

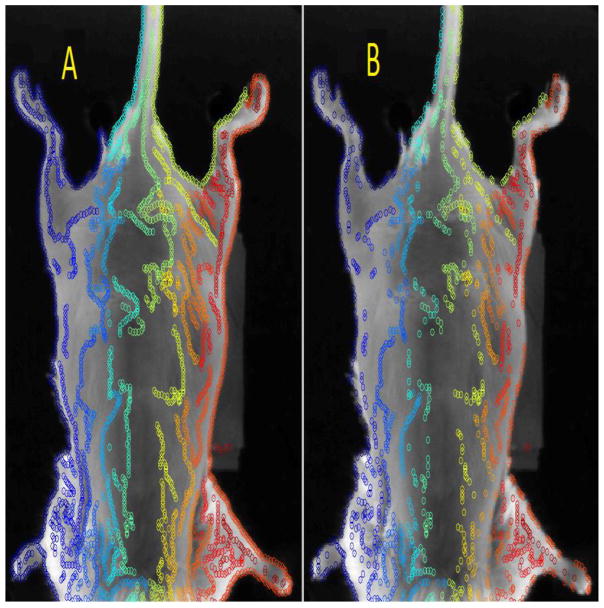
The set of offsets i^P and j^P are then tested for stability. The deformation vectors at all points along an individual canny line are tested for smoothness by comparing neighboring offsets. If |i_p−i^p±1,2| or |j_p−j^p±1,2| is greater than δ then the p^th point is considered unstable, and is subsequently removed. The removed points will be discarded and will not be considered during the deformation process, since these points have been labeled unstable. Figure 3 shows the original set of control points derived from the canny edge, with the corresponding stable set of control points.

Figure 3.

The original set of all points are shown (left). The stable set once all the unstable points have been removed (right).

The new set of stable offsets i^P and j^P are used to populate the complete 2D deformation vector field (DVF). To populate the DVF, the convex hull is calculated to find the boundary of the data set (Jarvis, 1973; Stein et al., 2012; Srikanth et al., 2009). Then Delaunay triangulation is used to compute a bounding triangle for the interpolated area (Rong et al., 2008; Qi et al., 2013). Next, sparse bi-linear interpolation is applied to extract the value at every unknown voxel (Kearney et al., 2015; Kaltofen and Yagati, 1989; Cuyt and Lee, 2008). The complete DVF is then used to deform I_moving. The whole process is repeated iteratively, using the Vercauteren method, until the stopping criterion S at iteration I is reached, where $S\ge {\displaystyle \sum _{\#\mathit{po}ints}}{E}_I^{P+1}/{\displaystyle \sum _{\#\mathit{po}ints}}{E}_I^P$ (Vercauteren et al., 2008; Vercauteren et al., 2009).

The various steps of the Canny DIR algorithm are implemented as follows:

Algorithm 1.

Initiate Multiscale Loop

Canny Edge Extraction

Canny Edge Refinement and Separation

Initiate Canny-Edge-Based Sparse Interpolation Loop

Initiate Canny-Edge Smoothness Loop

LSA Similarity Search

End Loop

Compute Sparse Interpolant

Accumulate DVFs and Deform Imoving

Evaluate Stopping Criterion

End Loop

End Loop

2.3 Evaluations

Several DIR methods were compared with the Canny DIR algorithm, such as rigid registration, the Demons based method, and the distinct feature method. A modified open source version of the Demons algorithm was used, with an intensity correction step, called intensity corrected Demons (IC Demons) (Kroon, 2011). The distinct feature extraction method was based on an open source code (Naveen, 2013). The Canny DIR method was developed in-house.

The distinct feature extraction method relies on detecting blobs with associated scale levels, derived from scale-space extrema on the scale-normalized Laplacian ${\nabla }_{\mathit{norm}}^{2}L(x,y;s)$. The scale-space extrema are extracted from the points (x, y; s) in scale-space. Comparisons are then made in relation to local neighbors over space and scale. If a point falls within a cutoff criterion over the scale-space local neighborhood, then it is considered to be a district feature (Lowe, 2004).

Common methods of establishing a ground truth include, using a known DVF applied to a reference image then applying Monte Carlo noise contamination, Gaussian noise contamination, and or an intensity transformation (Liu, 2008; Shen et al., 2005; Brock et al., 2005; Sharp et al., 2007; Kearney, 2012; Zhen et al., 2013; Kearney et al., 2015). Other popular methods include using an entirely digital phantom with a known DVF (Segars et al., 2008; Segars and Tsui, 2009; Segars et al., 2010).

Monte Carlo noise contamination can be challenging in a 2D white light image, as there is no 3D surface information to base shading characteristics. Gaussian noise does not account for shading and lighting artifacts. Intensity transformations that simulate lighting and shading variations can be unrealistic. To overcome these challenges, two different ground truth models were created. A synthetic 3D mouse surface model, and a 2D fluorescence accumulation model were used to evaluate the accuracy of the algorithm.

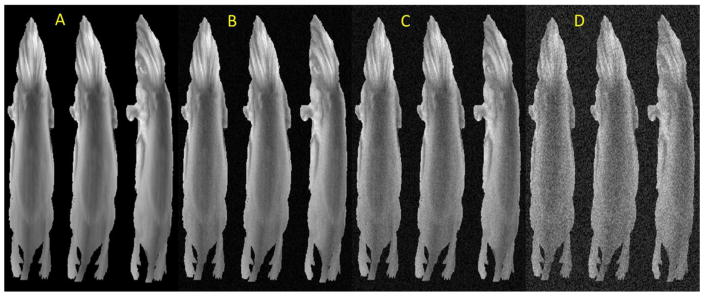
For the synthetic 3D mouse surface model, a microCT scan was taken with the Skyscan 1178 (Bruker, Kontich, Belgium), using an isotropic resolution of 200μm. A surface mesh was generated using marching cubes (Lorensen and Cline, 1987; Ho et al., 2005). A white light image, taken from the portable imager, then mapped on to the surface of the mouse. A line was drawn from each surface face on the mouse surface, which passed through the white light image to a virtual source. The pixel that each line passes through was used to shade a corresponding surface face. All the faces of the mouse surface are shaded using this method, until the mouse skin texture is fully mapped to the reconstructed mouse surface. The mouse surface was then deformed using a 15mm half sine wave in the right-left (LR) direction, from the apex of the head to most posterior aspect of the feet. The mouse surface was then rotated about the superior-inferior axis, from 0° to 40°. Figure 4 shows the various synthetic mouse surface scenarios.

Figure 4.

The synthetic mouse surface (A), with 15mm deformation at 0° rotation (B), 10° rotation (C), 20° rotation (D), 30° rotation (E), and 40° rotation (F).

In order to evaluate the performance of the various DIR algorithms in the presence of noise contamination, 3 different noise contamination scenarios were introduced, in the presence of deformation and/or rotational transformation, as described in figure 4. Figure 5 shows the various synthetic mouse surface scenarios with various levels of Gaussian noise contamination. In figure 5, noise contamination levels 1, 2, and 3, correspond respectively to standard deviations of 2.3%, 4.6% and 11.59% of the maximum white light signal intensities.

Figure 5.

The synthetic mouse surface with no noise (A), with noise contamination level 1 (B), with noise contamination level 2 (C), and with noise contamination level 3 (D). All four noise contamination scenarios are shown with no deformation (left), deformation with no rotation (middle), and 40° rotation with deformation (right), as described in figure 4.

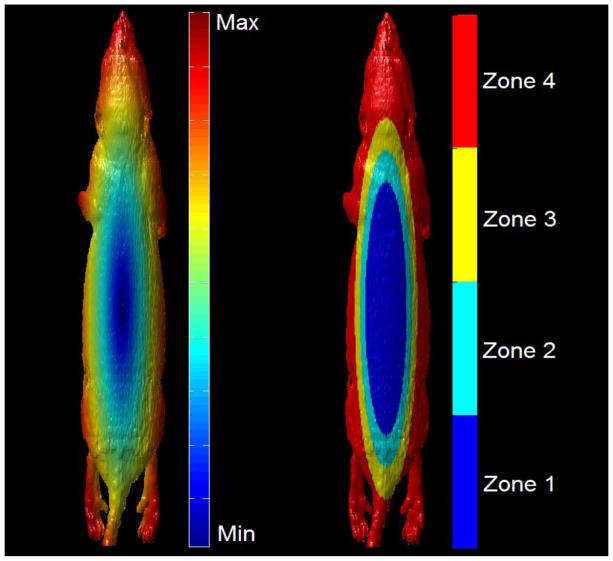
In order to test the local accuracy of the various DIR methods, the surface of the mouse was divided into multiple zones, to help understand the effects of rotation on different local regions of the mouse surface. Figure 6 shows the various zones of the mouse surface.

Figure 6.

The mouse surface distance from centermost vertex on the posterior abdomen (left). The 4 local zones of the mouse from centermost (zone 1) to outermost (zone 4).

For the second ground truth testing case, the Canny DIR will be used to deformably register white light image sets. The resulting DVFs will then be applied to the corresponding fluorescent image sets. The similarity of the original fluorescent image and the deformed fluorescent image are then evaluated using the gamma analysis technique (Harms Sr et al., 1998). If a direct spatial comparison between images is done, two corresponding pixels that are offset by a pixel width can lead to big discrepancies using direct spatial comparison (Depuydt et al., 2002; Spezi and Lewis, 2006; Gu et al., 2011). For this reason it is favorable to use a technique that searches locally for a best match. Gamma analysis searches a specified area around each pixel until a best match is found. The smallest difference from each pixel is recorded for a given region of interest.

If i, and j represent the indexes of the image being analyzed, k, and l represent the search range specified, R represents the search range, and D represents the percent error threshold, the gamma equation can be represented as, G(i, j) = arg min ||Ga(k,l)||, where, $Ga(k,l)=\sqrt{\frac{r{(i,j)}^2}{R^2}+\frac{d{(i,j)}^2}{D^2}}$, r represents the radial distance squared, and d represents the signal difference squared. The cutoff criterion used was 95% of all pixels within a 3×3 pixel search range, are within 3% error (Depuydt et al., 2002).

To test the spatial congruence between the various registration algorithms, several intensity evaluation metrics were used, root mean square error of the Canny edge (RMSE_CE), root mean square error of the mouse boundary (RMSE_B), normalized mutual information (NMI), and feature similarity index metric (FSIM). RMSE_CE between the Canny edges C₁ and the Canny edges C₂ in corresponding images, are defined as, ${\text{RMSE}}_{\text{CE}}=\sqrt{{{\displaystyle \sum _i^N}[{C_2}^i-{C_1}^i]}^2/{{\displaystyle \sum _i^N}[{C_2}^i]}^2}$ (Qian and Huang, 1996; Zhen et al., 2012). RMSE_B between the mouse boundary B₁ and the mouse boundary B₂ in corresponding images, are defined as, ${\text{RMSE}}_{\mathrm{B}}=\sqrt{{{\displaystyle \sum _i^N}[{B_2}^i-{B_1}^i]}^2/{{\displaystyle \sum _i^N}[{B_2}^i]}^2}$. The mouse boundaries, and are extracted using the marching squares algorithm on the intensity thresholded white light images, once small areas outside the central mouse boundary have been removed (Ho et al., 2005). NMI is a measurement of the mutual information between corresponding images (Wells et al., 1996; Skouson et al., 2001; Pluim et al., 2003; Torkkola, 2003). FSIM evaluates gradient and phase information between corresponding images (Zhang et al., 2011).

To help evaluate the accuracy of the fluorescent signal mapping between image sets, confined NMI is used. By confining the NMI algorithm to a region of interest conforming to the 50 percentile margin of fluorescent signal on the static image, the relative distribution of signal intensities can be used as a measure of fluorescent signal mapping congruence. Confined NMI provides a metric that relies on intensity frequency distribution rather than the intensity spatial distribution, which can be useful when regions of interest undergo morphological transformations (Kearney et al., 2015).

3. Results

3.1 Ground Truth Results

A deformed grid superimposed on the static image is shown for IC Demons, SIFT, and Canny DIR methods in figure 7.

Figure 7.

A deformed grid superimposed on the static image is shown for IC Demons (A), SIFT (B), and Canny DIR (C).

Figure 8 shows an absolute difference comparison between the static and deformed images using rigid registration, SIFT, and Canny DIR methods, with its corresponding deformed fluorescent image sets.

Figure 8.

White light absolute value difference comparison between the static and deformed images for rigid registration (A), SIFT (B), and Canny DIR (C). Fluorescence absolute value difference comparison between the static and deformed images for rigid registration (D), SIFT (E), and Canny DIR (F).

To get a better understanding of the intensity congruence between image sets a gamma analysis was done between the various image sets. Figure 9 shows a gamma analysis between the static and deformed images using rigid registration, SIFT, and Canny DIR methods.

Figure 9.

The white light image with the fluorescence superimposed on the static image (A). The static image with the superimposed fluorescence gamma comparison between the static and rigid registration (B), SIFT (C), and Canny DIR (D). The yellow box shows the area under consideration.

3.2 Evaluation Metrics Results

The synthetic mouse surface ground truth scenarios were evaluated using the 90 percentile error margin for the IC Demons, SIFT and Canny DIR algorithms. Table 2 shows the DVF accuracy for all synthetic scenarios using various DIR methods.

Table 2.

The DVF 90 percentile error for IC Demons, SIFT, and Canny DIR methods for all synthetic scenarios.

		0°	10°	20°	30°	40°
zone 1	IC Demons 90% error (μm)	240.3	310.2	398.5	530.6	618.7
	SIFT 90% error (μm)	291.4	304.4	376.0	435.2	503.4
	Canny DIR 90% error (μm)	258.2	276.4	289.4	310.1	395.5
zone 2	IC Demons 90% error (μm)	248.1	300.9	371.0	529.1	781.8
	SIFT 90% error (μm)	279.7	316.5	387.9	410.6	566.2
	Canny DIR 90% error (μm)	251.2	281.0	297.1	357.3	442.1
zone 3	IC Demons 90% error (μm)	234.8	283.0	408.8	581.0	738.6
	SIFT 90% error (μm)	269.6	297.8	358.6	481.9	703.1
	Canny DIR 90% error (μm)	259.3	268.1	284.7	392.8	569.0
zone 4	IC Demons 90% error (μm)	221.8	298.1	387.9	577.0	807.7
	SIFT 90% error (μm)	304.5	312.6	353.1	433.3	758.8
	Canny DIR 90% error (μm)	232.2	261.0	297.3	401.4	631.9

The synthetic mouse surface ground truth scenarios were also evaluated using various noise contamination levels at the 90 percentile error margin for the IC Demons, SIFT and Canny DIR algorithms. Table 3 shows the DVF accuracy for all noise contamination scenarios at 0° and 40°, with deformation, using various DIR methods.

Table 3.

The DVF 90 percentile error for IC Demons, SIFT, and Canny DIR methods at 0° and 40° using various DIR methods scenarios for all noise contamination levels. Noise level 1, 2, and 3, correspond to standard deviations of 2.3%, 4.6%, and 11.59% respectively, of the maximum signal intensity.

		No Noise		noise level 1		noise level 2		noise level 3
		0°	40°	0°	40°	0°	40°	0°	40°
zone 1	IC Demons 90% error (μm)	240.3	618.7	255.9	691.1	295.1	754.2	511.1	801.1
	SIFT 90% error (μm)	291.4	503.4	300.1	551.1	361.9	602.1	410.2	690.0
	Canny DIR 90% error (μm)	258.2	395.5	259.8	403.2	272.1	457.4	301.0	540.1
zone 2	IC Demons 90% error (μm)	248.1	781.8	272.6	779.3	342.2	784.1	522.1	815.0
	SIFT 90% error (μm)	279.7	566.2	281.2	591.8	301.9	653.8	367.2	699.9
	Canny DIR 90% error (μm)	251.2	442.1	250.2	459.4	283.9	483.5	283.9	501.3
zone 3	IC Demons 90% error (μm)	234.8	738.6	240.1	792.7	369.1	806.1	561.7	810.1
	SIFT 90% error (μm)	269.6	703.1	272.2	762.3	347.1	792.6	407.6	808.7
	Canny DIR 90% error (μm)	259.3	569.0	260.5	581.2	290.1	604.2	367.2	637.6
zone 4	IC Demons 90% error (μm)	221.8	807.7	241.7	801.9	391.7	810.4	581.1	809.2
	SIFT 90% error (μm)	304.5	758.8	321.2	771.2	376.2	790.0	431.9	810.9
	Canny DIR 90% error (μm)	232.2	631.9	236.1	657.2	298.9	701.9	389.1	742.8

Table 4 shows the registration results from 7 mice evaluated with NMI, RMSE_CE, and FSIM evaluation metrics.

Table 4.

The evaluation matrix results from 7 mice with their corresponding mean values are shown for NMI, RMSE_CE, and FSIM. The values for the various registration methods are shown, including rigid, intensity corrected Demons, SIFT, and canny edge registration.

		1	2	3	4	5	6	7	mean
NMI	Rigid	0.56	0.51	0.59	0.62	0.61	0.63	0.49	0.57
	IC Demons	0.61	0.55	0.67	0.66	0.65	0.70	0.67	0.64
	SIFT	0.78	0.74	0.70	0.87	0.71	0.80	0.72	0.76
	Canny	0.85	0.83	0.84	0.89	0.81	0.89	0.75	0.84
RMSECE	Rigid	0.42	0.34	0.38	0.41	0.40	0.43	0.42	0.40
	IC Demons	0.39	0.35	0.45	0.43	0.43	0.46	0.44	0.42
	SIFT	0.30	0.30	0.29	0.36	0.29	0.32	0.30	0.31
	Canny	0.20	0.20	0.16	0.21	0.19	0.21	0.18	0.19
FSIM	Rigid	0.63	0.53	0.56	0.59	0.59	0.65	0.52	0.58
	IC Demons	0.60	0.54	0.69	0.71	0.66	0.68	0.62	0.64
	SIFT	0.89	0.83	0.82	0.83	0.82	0.89	0.78	0.84
	Canny	0.91	0.91	0.99	0.96	0.87	0.98	0.83	0.92

To evaluate the intensity congruence of the various registration algorithms the maximum gamma error was used as well as the overall gamma passing rate. A gamma passing rate of 3% error with a (300 × 300) μm² search range was used. For maximum gamma a (300 × 300) μm² search range was also used. Table 5 shows the gamma evaluation results.

Table 5.

The gamma analysis results from 7 mice with their corresponding mean values are shown for the maximum gamma error and the gamma passing rate. The values for the various registration methods are shown, including rigid, intensity corrected Demons, SIFT, and canny edge registration.

		1	2	3	4	5	6	7	mean
Max Gamma	Rigid	29.47	23.87	26.82	28.67	28.32	29.86	29.84	28.12
	Parametric	31.78	24.82	31.48	30.51	21.80	32.21	31.45	29.15
	SIFT	12.38	11.95	8.40	14.38	11.44	12.94	7.90	11.34
	Canny	5.96	9.50	4.87	6.23	5.66	6.35	5.37	6.28
Failing %	Rigid	21.07	16.84	19.22	20.24	19.90	21.51	21.59	20.05
	Parametric	25.65	17.07	22.60	21.19	21.01	22.88	21.96	21.77
	SIFT	7.34	10.10	4.30	8.34	6.85	7.42	3.90	6.89
	Canny	2.89	4.90	2.45	3.23	2.84	3.21	2.68	3.17

In addition to the NMI, canny edge RMSE_CE, and FSIM, the mouse body boundary RMSE_B was used to evaluate the anatomical accuracy of the various registration algorithms. To provide additional evaluation of the fluorescent signal mapping accuracy, confined NMI was used to evaluate the fluorescent intensity congruence of the various registration algorithms. Table 6 shows the mouse body RMSE_B and confined NMI evaluation results.

Table 6.

The mouse body boundary RMSE_B and the confined NMI analysis results from 7 mice with their corresponding mean values are shown. The values for the various registration methods are listed, including rigid, intensity corrected Demons, SIFT, and canny edge registration.

		1	2	3	4	5	6	7	mean
Confined NMI	Rigid	0.48	0.56	0.31	0.61	0.47	0.49	0.40	0.47
	Parametric	0.49	0.52	0.46	0.58	0.58	0.48	0.57	0.53
	Feature	0.62	0.68	0.54	0.59	0.57	0.63	0.65	0.61
	Canny	0.69	0.86	0.79	0.62	0.72	0.74	0.76	0.74
RMSEB	Rigid	0.38	0.29	0.38	0.40	0.39	0.41	0.38	0.38
	Parametric	0.41	0.35	0.36	0.39	0.43	0.37	0.38	0.38
	Feature	0.30	0.28	0.29	0.35	0.28	0.25	0.23	0.28
	Canny	0.25	0.26	0.20	0.25	0.19	0.19	0.20	0.22

4. Discussion

The ground truth accuracy for the synthetic scenarios for IC Demons, SIFT, and Canny DIR were all evaluated at the 90% error margin. For the 0° scenario, all the algorithms performed well for all zones and were within 305μm at the 90% error margin. For the 10° scenario all the algorithms performed fairly well overall and the Canny DIR slightly outperformed all other algorithms. For the 20° scenario, the IC Demons and SIFT algorithms performed poorly for some zones, while the Canny DIR algorithm performed well for all zones and was within 300μm for all zones. At 30° rotation, most of the methods for all the zones did not perform well, except for zones 1 and 2 of the Canny DIR method. Zone 1 is within 310.1μm at the 90% error margin. For the 40° scenario, all algorithms for all zones perform poorly but the Canny Edge method performs far better than all other algorithms, especially for zone 1, which stays within 395.1μm at the 90% error margin. The synthetic ground truth test demonstrates that the Canny DIR method is accurate in the presence of rotations (≤ 20°). However, under larger rotations, between 20° and 30°, the surface tracking should be limited to zone 1. Rotations larger than 30° should be avoided.

The ground truth accuracy for the noise contamination scenarios for IC Demons, SIFT, and Canny DIR were all evaluated at the 90% error margin. For the level 1 noise contamination scenario, all three algorithms performed well with no rotation for all zones. Level 1 noise contamination combined with 40° rotation caused some degradation of the accuracy for the IC Demons and SIFT algorithms for all zones. For level 1 noise contamination, the Canny DIR method maximum accuracy degradation was 26μm at the 90% error margin for zone 4 with a 40° rotational transformation. For the level 2 noise contamination, with no rotation, the SIFT and Canny DIR algorithms remained accurate for all zones but the IC Demons algorithm had a large accuracy degradation for all zones. For level 3 noise contamination, all the algorithms had large accuracy degradations for all zones, except for Canny DIR, which stayed within 42.8μm at the 90% error margin, with no rotation for zones 1 and 2.

In general, large noise contamination should be avoided and care should be taken to ensure sufficient and consistent illumination conditions. If large lighting variations are present, additional care should be taken during setup and positioning to reduce the degree of rotational variation between measurements. Also, experiments should be limited to zones 1 and 2 if there are large uncertainties in lighting and rotational conditions.

For the evaluation matrices, the IC Demons performed near as well as rigid registration for the RMSE_CE evaluation method and only slightly better than the rigid registration method for the NMI and FSIM. Although the intensity distribution is transformed towards the target image, the resulting DVF is not a good representation of the physical morphological deformation (Castillo et al., 2009). The deformed grid may warp unrealistically in the presence of intensity incongruence between the image sets. This effect can be seen in figure 7. Since the objective function of the Demons method is minimizing intensity difference distribution between the deformed and static image, intensity evaluation metrics can give artificially good results (Leow et al., 2005). The RMSE_CE method, produces poor results in this case because it is a representation of how well the edges between the images are aligned (Oliveira and Tavares, 2014).

The SIFT performance was generally much better than IC Demons. This method will perform particularly well when evaluated with NMI or FSIM because the distinct features are chosen on regions of the image that have rich intensity and gradient features. So when these regions are selected for intensity matching they will have a somewhat better performance. This method performs only slightly better than IC Demons method when evaluated using RMSE_CE, because the edges between the deformed and static image do not match up well. This is in part because the distinct features are not dense along the image edges. If the distinct feature extraction method is less discriminatory, more features will be used but they will be less stable and will produce more deformation errors (Lowe, 2004). There will always be a tradeoff between the amount of distinct features being used and the quality of the overall quality of the features (Naveen, 2013). For this study the removal criteria was calibrated to achieve the best possible NMI performance.

There is an effect on the Canny edge sensitivity ε and the SIFT removal tolerance ω. The effects of changing the canny edge and SIFT constants can be seen in figure 10.

Figure 10.

Canny edges with an ε_lower of 0.1 and an ε_upper of 0.9 (A), an ε_lower of 0.01 and an ε_upper of 0.1 (B), and an ε_lower of 0.001 and an ε_upper of 0.01 (C). SIFT points with an ω of 0.1 (D), an ω 0.01 (E), and an ω 0.001 (F).

Although the optimal values for the upper threshold ε_upper and lower threshold ε_lower will vary somewhat depending on the imaging environment, a normalized ε_upper value of 0.1 and an ε_lower value of 0.01, tend to produce the best tradeoff between edge density and edge quality. Similarly, using an ω of 0.01 offered a good tradeoff between distinct feature density and quality.

The canny DIR method performed better than all other methods for every evaluation metric used. It performed only slightly better than the SIFT method for the NMI evaluation metric. This is in part due to the distinct feature selection criteria bias towards NMI performance, which stems from the removal criteria calibration (Torkkola, 2003). It had the largest performance increase over all other methods for the RMSE_CE evaluation metric. Since the Canny DIR method uses stable edges, it is expected that an edge-based evaluation matrix would give good results.

For the gamma analysis evaluation methods, it can be seen that the IC Demons method performed the worst, which suggests that the DVFs are not accurate. This method sacrifices spatial congruence for intensity congruence. As a result, the quality of the DVFs can suffer, in the presence of lighting and shading variations.

The SIFT method performed far better than the rigid registration method for both the maximum gamma and the gamma passing rate tests. This method had a mean maximum gamma of roughly twice as small as the rigid registration method and about triple the gamma passing rate. This is a good indication that this method had realistic DVFs.

The canny DIR method outperformed the district feature method for both the maximum gamma and the gamma passing rate tests. This method had a mean maximum gamma of roughly twice as small as the SIFT method and about 2x better gamma passing rate. This is a strong indication that the canny DIR method has the most accurate DVFs.

It is important to note that, all the Canny DIR mice passed the gamma analysis test and that only two mice passed the gamma analysis test for the SIFT method. Also, none of the mice passed the gamma test for the IC Demons or rigid registration methods.

The confined NMI method showed the rigid registration and IC Demons methods performing the worst in most cases. In some cases the IC Demons performed worse than the rigid registration method. This is in part due to unrealistic DVFs resulting from Demons bias towards intensity congruence over spatial congruence. The Canny DIR algorithm outperformed all other methods for all mice. The Canny DIR method only performed slightly better than the SIFT method for mice 1 and 4. The SIFT distinct features were visually inspected for these cases and found to correspond well with the NMI region of interest. This helped the SIFT algorithm accurately map the fluorescent signal between image sets. For mouse 4 the rigid registration performed almost as well as the Canny DIR algorithm. This case was visually inspected and was found to not match anatomically very well but the fluorescent signals did spatially correspond to each other well.

The RMSE_B method showed that the rigid registration and parametric algorithms performed on average nearly the same. The SIFT method had a large increase in performance compared with the rigid and parametric algorithms. For the SIFT method, the RMSE_B evaluation metric accuracy depends heavily on the placement of the distinct features. If regions near the boundary do not have distinct features, those portions of the boundary will have to rely on sparse interpolation only and may not get registered accurately. The Canny DIR method performed better than all other algorithms for the RMSE_B evaluation method. This is partially because it is likely that a Canny edge will form continuously around the boundary of the mouse.

Since, 2D white light images are based on 3D surface projections of mice, there are some limitations to using the Canny DIR method. Canny DIR, will not account for large mouse rotations, since the region of the skin surface being image can change between time points. Care must be taken during setup and positioning to help minimize rotation. The mice should be oriented such that the fluorescent implants are not too far from the center of the mouse surface, with respect to the imager. Future work will be directed at comprehensively analyzing the setup, and implantation imaging limitation of this method.

5. Conclusion

Canny DIR presents a possible solution to overcome the challenges of in vivo deformable image registration using optical imaging. The ground truth results, and the evaluation matrices, demonstrate that Canny DIR is capable of achieving high spatial accuracy between image sets in the presence of illumination changes, due to anatomical deformation, and low levels of axial rotation, due to setup errors. Furthermore, an in vivo metastatic cancer tracking experiment is underway which will shed light on the effectiveness of various cancer trap devices. This work has taken advantage of the capabilities of optical imaging systems, to provide the initial steps towards an in vivo, non-invasive, portable, fluorescent signal tracking solution.