Abstract
This paper introduces explicit dependence of atomic polarizabilities on intermolecular interactions within the framework of a polarizable force field AMOEBA. Polarizable models used in biomolecular simulations often poorly describe molecular electrostatic induction in condensed phase, in part, due to neglect of a strong dependency of molecular electronic polarizability on intermolecular interactions at short distances. Our variable polarizability model parameters are derived from quantum chemical calculations of small clusters of atoms and molecules, and can be applied in simulations in condensed phase without additional scaling factors. The variable polarizability model is applied to simulate a ligand exchange reaction for a Mg2+ ion solvated in water. Explicit dependence of water polarizability on a distance between a water oxygen and Mg2+ is derived from in vacuum MP2 calculations of Mg2+−water dimer. The simulations yield a consistent description of the energetics of the Mg2+−water clusters of different size. Simulations also reproduce thermodynamics of ion solvation as well as kinetics of a water ligand exchange reaction. In contrast, simulations that used the additive force field or that used the constant polarizability models were not able to consistently and quantitatively describe the properties of the solvated Mg2+ ion.
Graphical abstract
INTRODUCTION
Atomistic molecular mechanics methods are routinely employed to model biological macromolecular systems. Simulations are widely used in structure refinement and interpretation of spectroscopic experiments, analysis of ligand binding and conformational rearrangements of macromolecules, and in many other applications.1,2 Currently additive fixed atomic charge models are used predominantly to describe electrostatic interactions in biomolecular simulations, and such models often perform remarkably well. However, multiple studies indicate that accurate description of many biochemical processes requires models with explicit representation of electronic polarization.3–6
One important class of biological systems, in which fixed charge models have limited applicability are biological membrane ion channel and transporter proteins. These remarkable molecular machines achieve a highly selective control of ion permeation through hydrophobic lipid bilayer membranes by means of formation of finely tuned web of molecular interactions involving ions, protein amino acids, lipids and water.7,8 Fixed charge models have difficulty reproducing critical properties of ion channels such as free energy profiles of ions in protein pore.9–12 Ions, especially divalent cations, e.g., Ca2+ and Mg2+, strongly polarize electrons of coordinating molecular groups. Therefore, to achieve a quantitative level of description for the ion channel conduction properties, such as ion selectivity, binding affinity, and rates of permeation,13,14 it is necessary to model the electronic polarization accurately. First molecular mechanics simulations of biomolecules with explicit account of polarizability have been reported more than 40 years ago.15,16 Since then numerous methods to model electronic polarization within the framework of empirical force fields have been developed. Among them point polarizable dipoles (PPD), charge on the spring (COS) or Drude oscillator model and a fluctuating charge (FC) model received the most attention and were implemented in popular molecular mechanics software packages such as AMBER,17 CHARMM,18 TINKER,19 GROMACS,20 and NAMD.21 A summary of progress in development of advanced force fields can be found in a number of recent reviews.3,4,6,22–27 Systematic efforts to develop new advanced force fields for biopolymers have greatly accelerated during the past decade. Recently new polarizable force fields for proteins and DNA have been reported.28–31 Testing showed, however, that these more sophisticated and computationally expensive models do not always increase accuracy of the simulations.29,31,32
A number of problems were identified that complicate development of a successful scheme for modeling electronic polarization within the molecular mechanics framework. For example, when electronic polarizability is modeled via induced point dipoles a mutual interaction between the induced dipoles located at neighboring atoms can result in a divergence of polarization energy, the so-called “polarization catastrophe”. A common remedy to this problem is provided by the Thole method.33 In the Thole procedure polarizable dipole densities are smeared around the atom centers using a Gaussian or another analytical 3D function.34 Electrostatic interaction between polarizable centers is thus reduced at small distances, and “polarization catastrophe” is avoided.
Another problem in modeling electronic polarization that attracted significant attention but proved harder to solve is accounting for dependency of a molecular electronic polarizability on the presence of other molecules in close proximity of a polarizable molecule. Polarizability of molecules is generally diminished in condensed phase compared to vacuum because orbital space available to the excited states is reduced due to exchange interactions with electrons of surrounding molecules.35 One approach proposed to remedy this problem is to uniformly scale atomic polarizability values derived from quantum mechanical calculations of isolated molecules. Lowering atomic polarizabilities improved condensed phase simulation results for anions,36–38 water,39,40 and other molecular systems.41,42 It was found, however, that optimal polarizability scaling factors differ for different types of organic compounds.43 A systematic procedure has been suggested to derive optimal condensed phase atomic polarizabilities from QM/MM simulations.44 One significant limitation of such approach however is lack of parameter transferability, because different environments may require different optimal polarizability scaling constants for the same molecules. At the same time the need for a costly optimization procedure involving series of condensed matter simulations greatly complicates the task. A different approach to the problem was proposed by Kaminsky et al.,35 in which a basis set without diffuse functions in quantum chemical calculation was used to derive polarizability parameters, thus emulating limitations on the space of virtual orbitals of a molecule in a condensed phase environment. Another approximation, a sublinear dependency of polarization from the strength of an applied electric field has been used45 to avoid overpolarization of molecules; although, quantum calculations show that polarizability increases with the increasing electric field strength, rendering such proposal unsatisfying.
In this work we present a modification of a popular AMOEBA force field that introduces an explicit dependence of atomic polarizabilities on positions of atoms of surrounding molecules. Our approach preserves the idea of developing an empirical force-field that is rigorously derivable from purely electronic properties of molecules and thus, transferable between the gas phase and condensed phase systems. At the same time the proposed model is simple and allows for an analytical form of the energy derivatives, which is important to maintain efficiency of molecular dynamics simulations. An implementation of a proposed method was developed using the AMBER/AMOEBA PMEMD program17 and our own software HARLEM46
We demonstrate the usefulness of our approach by modeling energetics of solvation and ligand exchange rates of a Mg2+ ion solvated in water. A problem of a water exchange in the first solvation shell of a divalent ion is of great importance to many processes in biological systems. A magnesium ion is involved in regulation and catalysis of numerous enzymes of different types,47 it plays a major role in nucleic acid biochemistry,48 and in regulating excitatory transmission in brain.49–51 Yet, it proved to be one of the most difficult systems for the existing empirical methods of modeling including polarizable force-fields. Structural chemistry of Mg2+ interaction with water is well established.52 In bulk water magnesium ion coordinates six ligand molecules in a stable configuration. The water-ligand exchange reaction around Mg2+ proceeds via a dissociative mechanism53 with the rate of about 106 s−1. The rate of water exchange near Mg2+ is much slower than that of, for example, Ca2+ another biologically ubiquitous divalent ion. Water exchanges in the first solvation shell of Ca2+ at a rate of 1010 s−1.53 In part, the slow exchange rate of the ligands is a manifestation of a very strong electric field that Mg2+ exerts on its ligands. Electronic polarization effects are known to be important for Mg2+ modeling. Several sets of parameters have been suggested for Mg2+−water interaction both for fixed charge and polarizable empirical force-fields.36,54–58 Quantum chemical calculations59 have shown that electronic polarizability of the water molecules in the vicinity of Mg2+ are significantly different from that of bulk water or of the isolated water molecules. Masiaet al.59 suggested to use ion–water specific Thole parameters to describe ion solvation within polarizable force field model. Specifically it was found that rather small value of Thole coefficient 0.05 is needed to fit position dependence of dipole moment of water near Mg2+. In the framework of the popular AMOEBA force field Mg2+−water polarization interactions were fit using somewhat larger Thole coefficients 0.08858 and 0.09555,60 that were still much smaller than 0.39 value used as a standard in AMOEBA. Calculations with reduced Thole coefficient showed a good description of Mg2+−water potential curve in vacuum, predicted correctly the first peak position for the Mg2+−O distance for the solvated ion, the water coordination number, and other experimental observables. However, subsequent calculations with this model60 showed water residence time 1.9 × 10−9 s, which is much smaller than the experimentally observed 2 × 10−6 s− 10−5 s.53,61
Below we analyze how different models for electronic polarizability affect the computed rate for a water ligand exchange around Mg2+. We introduce modifications to AMOEBA force field that introduce explicit dependence of the water electronic polarizability from its position relative to the Mg2+ ion. We argue that such modified force field provides a better description of the Mg2+−water interactions than the existing empirical models and that our approach opens a path for development of a more systematic and consistent treatment of electronic polarizability in molecular mechanics simulations.
METHODS
Variable Polarizability Model
Electronic polarizability of an atom is a property typically modeled as a constant parameter. However, molecular polarizability is not a constant but varies in the presence of other molecules in the vicinity of an atom. It is also a field-dependent property in a strong electric field. In some cases, i.e., in the vicinity of an ion exerting a strong electric field, the effect is non-negligible. In such cases, the energetics, kinetics and structure of the system are modeled poorly if polarizability of atoms is taken as constant.
The origin of molecular polarizability dependence on the nonbonded interactions with other molecules can be illustrated by examining a sum over states expression for electronic polarizability tensor α of a molecule (see also discussion elsewhere62):
where Ψ0 and Ψj are the ground and excited electronic states of the molecule, E0 and Ej are their corresponding energies and µ is the dipole moment operator. On one hand, closed electronic shells of the surrounding molecules reduce electron polarizability of the molecule by limiting the space of the excited states Ψj through Fermi repulsion. On the other hand, surrounding molecules with low energy empty orbitals may increase electronic polarizability. The former effect is similar in origin to the atom−atom repulsion at close distances. In empirical force-fields simple pairwise formulas have been very successful in describing such atomic repulsion. This indicates that it is possible to design an analytical formalism that adequately describes a reduction of the electronic polarizability due to nonbonded interactions with nearby molecules.
A variable electronic polarizability model (identified further with a VAR POLAR tag) introduced in this work takes into account the nonbonded interactions with other molecules in the vicinity of an atom via the following expression for the position-dependent atomic polarizability αi(ri) of an atom i with coordinates ri:
| (1) |
In eq 1 Σj is the sum over all atoms j of the nonbonded interaction list of an atom i; rj is a position of an atom j; is the polarizability of an atom i in the absence of nonbonded interactions. and are parameters to control an influence of an atom j on a polarizability of an atom i. Namely, is a coefficient describing how strongly an atomic polarizability of an atom i is reduced by the presence of an atom j (it is further termed a polarizability damping strength); and is the radius at which an atom j is affecting the polarizability of an atom i. is a sensitivity constant, a parameter coupling a polarizability of an atom i to the presence of other atoms.
A general form of the expressions for electrostatic and polarization energies Uel−pol (r1, … , rN) are taken as in the AMOEBA force field. However, atom electronic polarizabilities in this work are not constant but expressed as multidimensional functions of atomic coordinates.
| (2) |
where
In eq 2 the sums are performed over all atoms i, j, and n = n1a1 + n2a2 + n3a3 where a1, a2, a3 are the unit lattice vectors and (n1, n2, n3) are the integer triplets with i = j and n = 0 omitted. qi and qj are charges; Qi and Qj are quadrupoles; and are permanent dipoles; and are induced dipoles of the atoms i and j, respectively.
| (3) |
where E(ri) is the electric field at a position of an atom i.
The values αi of the induced atomic dipoles are obtained self-consistently with the electric field E(ri); therefore the electrostatic energy of the system is stationary relative to the small changes of the polarizable dipole components:
| (4) |
where index m indicates Cartesian components of the dipole moment. Thus, the only additional term to the force due to the coordinate dependence of the polarization constant αi (r1, …, rN) arises from the differentiation of the last term in eq 2:
| (5) |
Substituting in eq 5 the expression (1) for αi (r1, …, rN) we obtain the following expression for an additional force exerted on the atom i due to the coordinate dependence of the atomic polarizability:
| (6) |
Molecular Dynamics Simulations
Two types of molecular dynamics (MD) simulations were performed in this work: direct unrestricted simulations and umbrella sampling simulations. In all simulations a modeled system consisted of a single Mg2+ ion in a periodical box of 5120 water molecules (37 × 37 × 37 Å). All simulations were performed at constant temperature of 300 K and a constant pressure of 1 atm. Langevin thermostat was used for maintaining temperature and Berendsen barostat was used to maintain pressure. Several force-fields were used in simulations as described in corresponding sections of the manuscript. These force-fields included an additive force-field with TIP3P water and Mg2+ as supplied with AMBER 12, an AMOEBA force-field as supplied with AMBER 12 and with Thole screening parameters as described in55 and a force-field based on AMOEBA and modified with variable polarizability as described in this work.
Three unrestricted MD simulations with the AMBER 10 force-field were performed for 300 ns each with the charge on Mg ion set respectively to 1.3, 1.4, and 1.5 electron units. A single 10 ns unrestricted simulation of Mg2+ ion in water with the AMOEBA force-field and Thole coefficient 0.095 was also performed to compute the ligand exchange rates by direct counting of ligand switching events and compare such results with the TST theory.
Umbrella sampling simulations were performed to compute potential of mean force (PMF) of a water molecule removal (or insertion) from (or to) the first solvation shell of an ion. Harmonic umbrella constraints of 100 kcal/mol Å2 were centered at incremental water−ion distances with the step of 0.1 Å, and 1 ns production simulations were run for each umbrella window. The PMF profiles were calculated using the weighted histogram analysis method (WHAM).63
Rates of the Ligand Exchange Reactions
To compute a rate of a ligand exchange reaction, kexch, we used the transition state theory (TST) formalism:
| (7) |
where ΔG# is an activation energy of a ligand exchange reaction, k0 is an exponential prefactor constant, R is the gas constant, and T is temperature. An activation energy ΔG# for the ligand exchange reaction was derived from the PMF profiles of the water removal or insertion computed with WHAM method63 with parameters described in the molecular dynamics section.. Two possible mechanisms of the ligand-exchange reaction are possible: an associative and a dissociative mechanism. In order to determine the reaction rate of a reaction of interest as well as its preferred mechanism the rates for both mechanisms need to be estimated. The mechanism with the highest rate can then be chosen. Therefore, two different types of the US simulations were performed in this work. To compute activation energy for the dissociative mechanism of the ligand exchange reaction one of the Mg2+ water ligands was “pulled out” of the first solvation shell. This was performed by setting harmonic umbrella restrains on the distance between Mg2+ and a water ligand oxygen. To compute activation energy for an associative mechanism of the ligand exchange, we kept loose restraints on the six Mg2+ ligands not allowing them to move away from the ion while an extra water ligand was “pulled” into the first solvation shell. This has also been performed applying a single one-dimensional harmonic restraining potential between Mg2+ and a water molecule oxygen atom.
Ab Initio Quantum Chemical Calculations
Ab initio quantum chemical calculations of energetics of Mg2+−water molecules clusters were performed on MP2 level of theory with 6-311G(3d,3p) basis set. Calculations with higher level CCSD(T) method and a basis set with larger number of diffuse function have not changed significantly computed relative energies of ion−water clusters. While computing energies of withdrawal of the water molecule from Mg2+ ion or from Mg2+−(H2O)6 cluster Mg2+−O distance for one water molecule was fixed while other degrees of freedom of the system were allowed to relax during energy optimization.
RESULTS
The VAR POLAR model described in the previous section is applied here to model energetics and kinetics of the ligand exchange in the first solvation shell of a magnesium ion in bulk water. A magnesium ion solvated in water is an important test system for modeling electronic polarization. While it is a simple system in composition (only Mg2+ and pure water are involved), it proves notoriously difficult to model with empirical models. Numerous studies were dedicated to modeling various aspects of Mg2+−water coordination, energetics and the rates of exchange (see references in the Introduction). However, no empirical model that faithfully reproduces behavior of this system in all its complexity has been designed. We demonstrate below that development of a successful empirical force-field for this, and similar systems are possible from the first-principles if variable polarizability of water is accounted for systematically.
Polarizability of a water molecule in an electric field of a Mg2+ ion varies as the water molecule approaches Mg2+. For example, Figure 1a shows the diagonal components of a polarizability tensor of a Mg2+−H2O dimer as a function of Mg2+−oxygen (O) distance computed ab initio (MP2/6-311++G(3d,3p)). The αZZ component of the polarizability tensor along the Mg2+−O axis increases initially as the water approaches the ion up to the distances of about 3 Å, apparently due to hyperpolarizability of water in a strong electric field of Mg2+.59 However, as the water approaches Mg2+ even closer, αZZ decreases sharply starting at a distance of ca. 2 Å. This decrease of the water polarizability at the approach of an atom is significant, it has a very specific origin but it is typically not accounted for in empirical models. In order to separate the effects of an electric field due to the magnesium ion charge, and a Fermi repulsion exerted on the approaching water molecule by the magnesium atom electronic density it is useful to examine a system that is similar in electronic structure but lacks the excess electric charge. In the case of magnesium, neon represents such a similar system. Figure 1b shows polarizability of a water molecule located in the vicinity of a neon atom as a function of an external electric field. It can be seen that the polarizability of water depends strongly on the distance of the oxygen to the neon for all values of the electric field. Specifically, water polarizability is strongly damped when the Ne−O distances are below 3 Å. At weak fields this effect is solely due to the presence of the Ne electrons in the vicinity of the water oxygen. The hyperpolarizability of water in the strong electric fields is reduced as well; i.e., the water molecule polarizability is less dependent on the electric field when the neon is close to the oxygen. Figure 1c shows the ratio of the total induced dipole of water in the Mg2+−H2O dimer and the value of the electric field induced by Mg2+ at the oxygen position. Thus, defined “averaged” water polarizability increases slightly at 3 Å and drops significantly at small Mg − O distances demonstrating that decrease of the polarizability due to repulsion of the magnesium ion electrons overcomes both polarization and hypolarization due to the strong electric field of Mg2+ at these distances.
Figure 1.
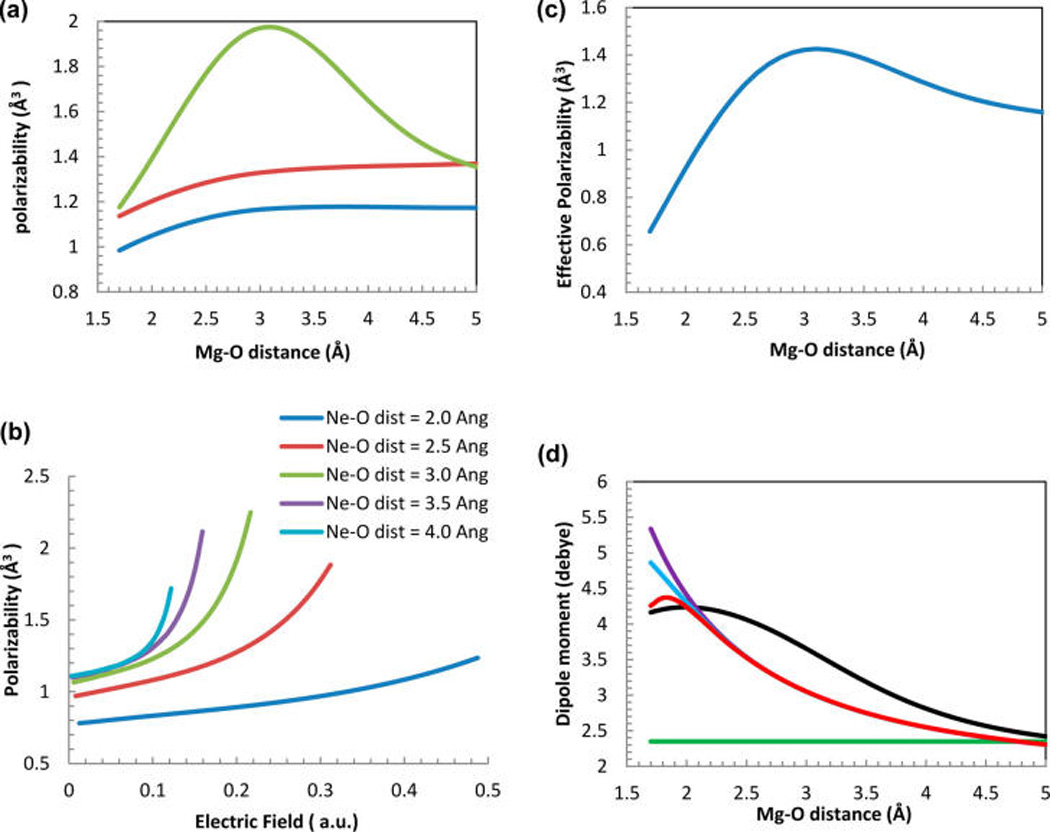
(a) Components of the polarizability tensor of the Mg2+−H2O dimer shown as a function of the Mg − O distance. αxx is shown in blue, αyy is shown in red, and αzz is shown in green line. (b) Polarizability of Ne − H2O dimer as a function of the applied electric field at different distances between Ne and water. (c) Effective H2O polarizability pind(R)/E(R) in Mg2+−H2O dimer computed by MP2/6-311++G(3d,3p). See the definition in text. (d) Dipole moment of Mg2+−H2O as a function of Mg−O distance. The line colors are as follows: AMBER10 force-field is shown in green, AMOEBA with the Thole coefficient of 0.39 is shown in purple, AMOEBA with the Thole coefficient 0.095 is light blue and AMOEBA with variable polarizability (this work) is shown in red.
Figure 1d shows the dipole moment of the Mg2+−H2O dimer as a function of the Mg2+ − O distance computed using the quantum chemical and molecular mechanics methods. MP2/6-311G(3d,3p) calculations show that the dipole moment of a water molecule increases in the strong electric field of Mg2+ at intermediate distances. However, at distances below 2.2 Å the dipole moment does not increase further due to the decrease of water electronic polarizability (as shown in Figures 1, parts a and c). Comparing to the ab initio result, the AMOEBA force-field calculations with the standard Thole damping coefficient (0.39) show an overpolarization of a water molecule at small Mg2+−O distances. Recently, AMOEBA parameters for Mg2+−water interaction with a reduced Thole coefficient (0.095) has been introduced in an attempt to account for water overpolarization55 Thus, we include the AMOEBA with the reduced Thole coefficient in present analysis. Calculations with the reduced Thole coefficient (0.095) reduced the overpolarization of the water molecule at Mg2+−O distances below 2.1 Å. However, in contrast to the quantum chemical data, the water dipole moment value does not reach a maximum.
To develop parameters for the AMOEBA force-field with the variable polarizability model (VAR POLAR, introduced in Methods section) we adjusted the coefficients in eq 1 to match the quantum chemically (QM) computed value of the Mg2+− H2O dimer dipole moment at a distance of 2 Å. This distance corresponds to the Mg2+−O separation in the first solvation shell. The system dipole moment (which is predominantly water dipole moment)computed with the VAR POLAR model reaches a maximum as a function of Mg2+−O distance below 2 Å as expected from the QM calculations. The values of the parameters of the VAR POLAR model are presented in Table 1. In the current work only Mg2+ ions have a nonzero damping strength and only oxygen atoms of water have a nonzero polarizability sensitivity thus polarizability of the oxygen atom of the water molecule is a function of the Mg2+−O distance only. The value of the dipole moment computed using additive force-field (AMBER10) is also included in Figure 1d (green line) for comparison.
Table 1.
Parameters of VAR POLAR Model Eq 1 Used in the Calculations
| 0.6 | |
| 1.0 | |
| 1.0 |
It must be noted that the value of a dipole moment of a water molecule computed with all empirical models presented in this study is underestimated for the Mg2+−O distances between 2.5 and 4 Å due to the neglect of the hyperpolarizabilty of water. This work follows a traditional approach to neglect a dependence of the water polarizability on the strength of the electric field. It can be reasonably expected that the hyperpolarizability is less pronounced in the condensed phase than in vacuum (as computed in Figure 1d for the Mg2+−H2O dimer) because the electric field acting on water molecules in condensed phase is significantly lower than in vacuum due to the dielectric screening.
Figure 2a compares dissociation energy of the Mg2+−H2O dimer as a function of the Mg2+−O distance computed using quantum chemical and empirical methods. The additive force-field AMBER model (alternatively termed here a fixed charge model) gives a dimer dissociation curve that is too soft as compared to the QM results. The AMOEBA model with the standard Thole screening (the Thole coefficient 0.39) predicts an equilibrium Mg2+-O distance that is too small (1.7 Å (the purple line in Figure 2a) vs 2.0 Å in QM (the black line)). The AMOEBA model with the reduced Thole coefficient (shown in light blue line) follows the QM curve closely at distances between 1.8 and 2.8 Å but diverges from it at larger distances. The dissociation energy of the Mg2+−water dimer computed using AMOEBA VAR POLAR model is shown in Figure 2a as a red line. For the VAR POLAR model developed in this work the Lennard-Jones (van der Waals) parameters are chosen to best reproduce the equilibrium position and the asymptotic behavior for the Mg2+−H2O dissociation energy curve computed quantum mechanically (after parameters of polarizability damping in Table 1 were chosen to fit changes of the system electric dipole at small Mg2+−H2O distances). It can be seen in Table 2 that to reproduce the QM curve in Figure 2a the VAR POLAR requires smaller van der Waals (VdW) radius for Mg2+ than other AMOEBA force field versions. In fact van der Waals radius of Mg2+ in the VAR POLAR model is close to reported ionic radius of Mg2+ (between 0.67 and 1.1 and depending on coordination) and the van der Waals radius value of 1.05 Å derived from the electronic density of Mg2+. At small Mg2+−O distances, polarizability of the water molecule is reduced due to the interaction with the Mg2+ closed shell electrons resulting in a repulsive force between Mg2+ and the water molecule. The VAR POLAR model reproduces this repulsive force via eq 5, while the standard AMOEBA model with fixed polarizability attempts to compensate for the lack of this force by employing an unreasonably large Mg2+ VdW radius, which is equivalent to extending the VdW repulsion contribution to longer distances. It should be noted, however, that both the asymptotic behavior and the electric field dependence of the van der Waals interactions and the repulsive force arising from polarizability changes differ substantially, and one may not be successfully used in lieu of the other. A repulsive force in eq 5 arising from a position dependence of the molecular polarizability is proportional to the square of an induced dipole moment, and depends on the value of the electric field at the atom position, while the repulsive VdW force depends only on the distance between atoms. Thus, one can expect the VdW term cannot fully describe changes of the interatomic repulsions in different molecular environments, e.g. polar and nonpolar environments.
Figure 2.
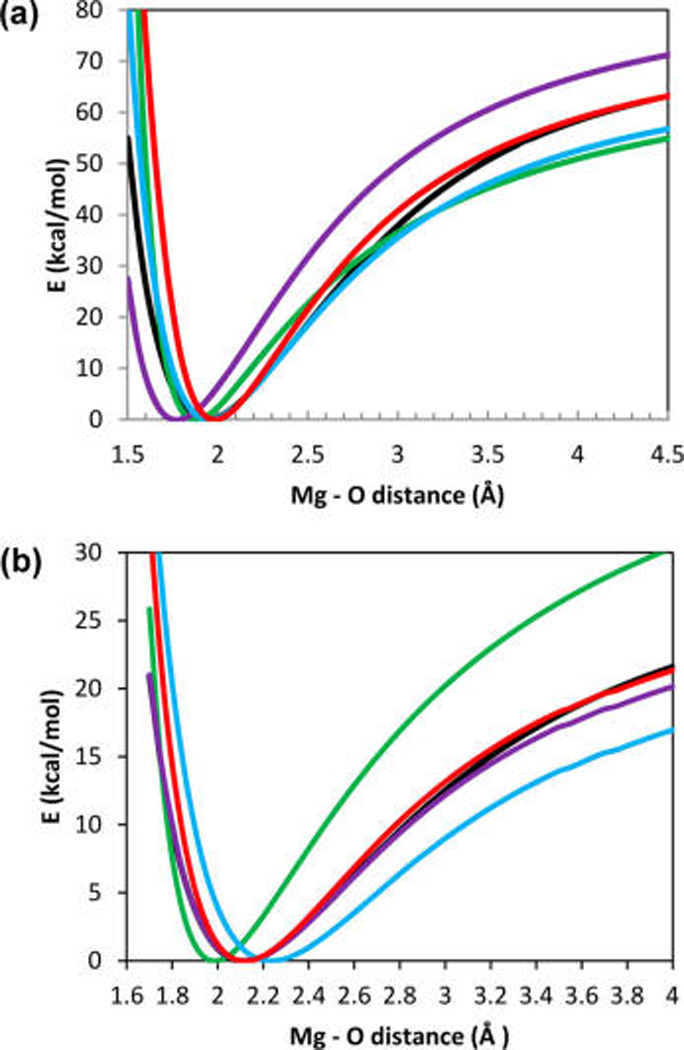
(a) Mg2+−H2O dimer energy vs Mg−O distance computed with different empirical force-fields as described in text and compared with ab initio calculation using MP2 method with the 6-311+ +G(3d,3p) basis set (shown as a black line) The line colors are the same as in Figure 1d. (b) Energy of the Mg2+−(H2O)6 cluster vs Mg− O distance for pulling of one of the ligands out of the equilibrium cluster (see the description of the calculation set up in text). Colors are the same as in Figure 1d.
Table 2.
Mg2+ VdW Parameters for Empirical Force-Field Models Tested in This Work
| AMBER | AMOEBA Thole = 0.39 |
AMOEBA Thole = 0.095 |
AMOEBA VAR POLAR |
|
|---|---|---|---|---|
|
rvdw = r0/2 (Å) |
0.78 | 1.275 | 1.605 | 1.0 |
|
Evdw (kcal/mol) |
0.88 | 0.85 | 0.28 | 0.15 |
In the following paragraphs, we apply the VAR POLAR model developed and parametrized above using dissociation energy and the dipole moment distance dependency of the Mg2+−H2O dimer in vacuum to simulations in larger ion−water clusters in vacuum and in bulk water. We will compare the dissociation and activation energies, and rates of ligand exchange reactions predicted by the new model to the standard force-fields and ab initio calculations where possible. It is well established that the Mg2+ ion solvated in water has a stable six ligand configuration, and the first coordination shell water exchange reaction proceeds via a dissociative mechanism.53 Thus, it is reasonable to expect that the activation free energy for the water exchange reaction around Mg2+ is correlated with the energy of a removal of one water molecule from a Mg2+− (H2O)6 cluster in vacuum. Figures 2b shows that VAR POLAR model reproduces well an ab initio computed distance dependence of removal of a water ligand from the Mg2+− (H2O)6 cluster; while a nonpolarizable force field overestimates thi dependence strongly, and AMOEBA with a reduced Thole coefficient underestimates it. AMOEBA with the standard Thole coefficient failed to reproduce the energy of the Mg2+− H2O dimer dissociation but works quite well for the Mg2+-(H2O)6 cluster. Indeed, these results emphasize that constant polarizability models can be parametrized using larger cluster calculations but such parametrization will result in limited transferability between environments with different polarity. Figure 3 shows dissociation energy of a water molecule from the Mg2+−water clusters containing from one to six water molecules. The energies in Figure 3 were computed using the MP2 quantum chemical method, the fixed charge AMBER force field, and the polarizable AMOEBA force field (including the fixed polarizability and the VAR POLAR model). Overall, the energy of removal of a water molecule from a cluster decreases as the number of the water molecules in a cluster increases. This trend is due to screening of electrostatic interaction between Mg2+ and a leaving water molecule by both permanent and induced dipole moments of the water ligands remaining in the cluster. The fixed charge AMBER force field underestimates the energy of a removal of a water molecule from the Mg−H2O dimer because this model disregards polarization energy of a water molecule in the Mg2+ electric field. Polarization effect strongly contributes to the binding of Mg2+ and H2O. In contrast, the energy of a removal of a ligand from the Mg2+−(H2O)6 cluster is strongly overestimated because the fixed charge model underestimates screening of the Mg2+ electrostatic field by the water ligands. The energies of a single water removal computed using the AMOEBA force field with the standard Thole coefficient 0.39 are overestimated for the Mg2+−H2O cluster and are underestimated for Mg2+−(H2O)6 due to the overpolarization of the water ligands in this force-field. The AMOEBA force field with the reduced Thole coefficient of 0.095 systematically underestimates energies of a water ligand dissociation from all clusters. The VAR POLAR model with a position dependent water polarizability predicts the water removal energies in excellent agreement with the energies obtained in ab initio calculations for all Mg2+−(H2O)n clusters.
Figure 3.
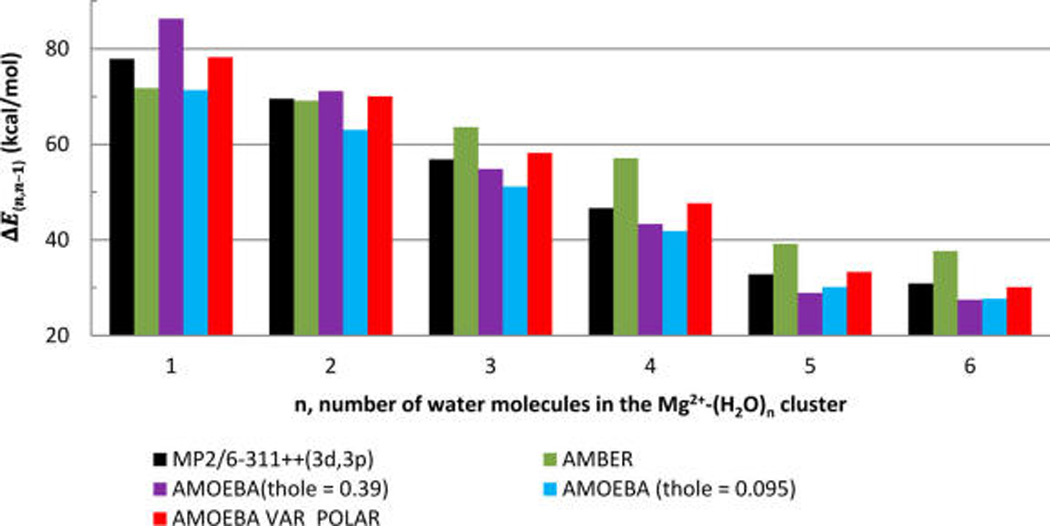
ΔEnn−1 = EMg2+(H2O)n − EMg2+(H2O)n−1 Energies of a water molecule removal from Mg2+(H2O)n clusters, where n is the number of water molecules in the cluster. Energies are computed using different force-fields as indicated in the legend in the graph.
In order to compute rates of reactions in the condensed phase where direct simulations are intractable for the majority of the systems of interest we resort to the formalism of the transition state theory, eq 7. In order to compute a rate of a reaction two parameters, an activation free energy and a prefactor are needed. Activation free energies can be computed using enhanced sampling methods to compute potential of mean force (PMF) along a relevant reaction coordinate (umbrella sampling is used in this work as described in Methods). These were simulated using all force-fields tested in this work and will be described in the following paragraph. To estimate a value of a prefactor k0 using eq 7 in this work, we initially performed a series of long unrestrained MD simulations of the magnesium in bulk water using the TIP3P water model and ions with a reduced electric charge from 1.3 to 1.5e. With thus reduced charges the simulated magnesium-like ion still has a stable six ligand configuration of the first solvation shell. At the same time the activation energy of the ligand-exchange reaction is reduced sufficiently, such that it is possible to observe ligand exchange events in direct unrestrained simulations. We assume that a value of a prefactor k0 for the dissociative water exchange with these fixed charge models is similar to that for other models (including the VAR POLAR model) because the mechanism of the process is similar. The following results support such an assumption. Figures 4, section A and B, show time traces of the Mg−O distances of the seven water molecules closest to the magnesium in which representative ligand exchange events are observed. It is clearly seen from these figures that indeed in this case water exchange proceeds via a dissociative mechanism. Table 3 shows the rates of the ligand exchange reaction computed from these long unrestrained MD simulations for the three simulated systems. Table 3 also lists the ligand exchange activation free energies computed using the umbrella sampling (US) simulations of the same three reduced charge ion systems. The US simulations were performed as described in the Methods section. The PMF profiles of a water molecule leaving the first solvation shell of an ion via dissociative mechanism are shown in Figure 5. From the Table 3 data we can see that the value of the prefactor k0 in the TST formula for the ligand exchange eq 7 is relatively constant for the three simulated systems and is close to the classical Eyring value k0 ≈ (kBT/h) = 0.6 × 1013 (s−1).
Figure 4.
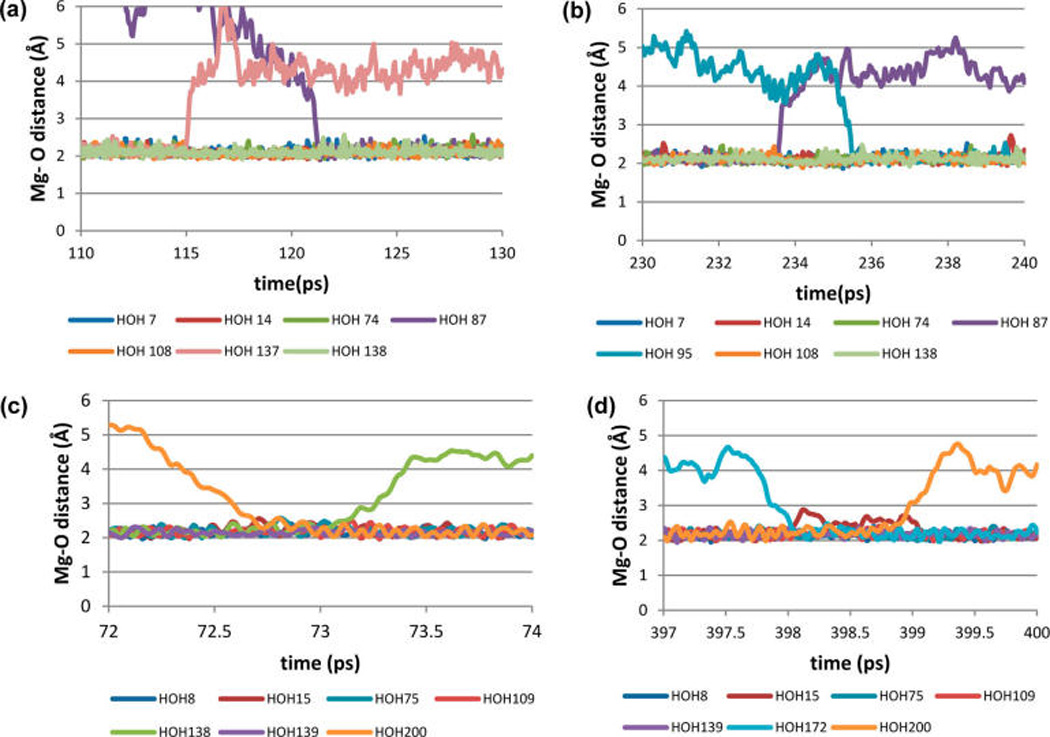
Direct observation of the water ligand exchange events near Mg2+ in water. (a, b) (top) AMBER force field (TIP3P water), Mg charge =1.3e (Dissociative mechanism). (c, d) (bottom) AMOEBA force field Thole coefficient = 0.095 (associative mechanism). Trajectories of individual water molecules are shown as lines of different colors as marked on the graphs.
Table 3.
Ligand Exchange for Reduced Charge Models of Mg Ion Solvated in TIP3P Water
| Mg charge (e) | k0 (s−1) | ||
|---|---|---|---|
| 1.3 | 4.7 | 3.4 × 109 | 1.0 × 1013 |
| 1.4 | 5.8 | 5.7 × 108 | 1.1 × 1013 |
| 1.5 | 7.2 | 3.4 × 107 | 0.6 × 1013 |
Figure 5.
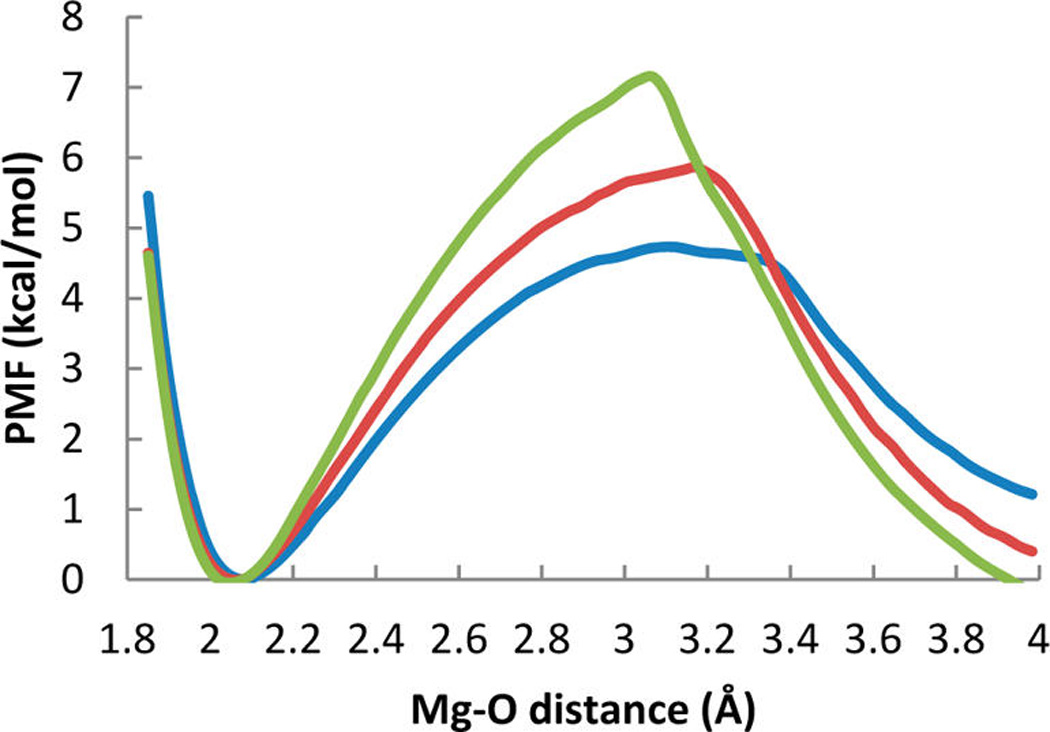
Potential of mean force (PMF) for removal of one water molecule ligand from the first solvation shell of the Mg ion. PMFs for the Mg-like ion models with the reduced electric charge are shown respectively in blue for qMg = 1.3e, in red for qMg = 1.4e, and in green for qMg = 1.5e The US/WHAM simulations of Mg-like ion in bulk water were performed using AMBER force field with TIP3P water as described in text.
Table data are for , activation free energies for water ligand exchange in the coordination shell of Mg ion model (dissociative mechanism) computed using the umbrella sampling and WHAM method. PMF profiles are shown in Figure 5. , the rates of the water ligand exchange computed from direct observation of ligand exchange event in MD simulations, and k0, values of prefactor in eq 7, were computed from and .
Lastly, we describe here the results of the molecular dynamics umbrella sampling simulations of the Mg2+ ion in bulk water to compute the PMFs of a single water dissociation or association in the first solvation shell of the ion. The PMFs for the dissociative and associative mechanisms of the water ligand exchange around Mg2+ ion were computed as described in Methods section and are shown in Figure 6, parts a and b.
Figure 6.
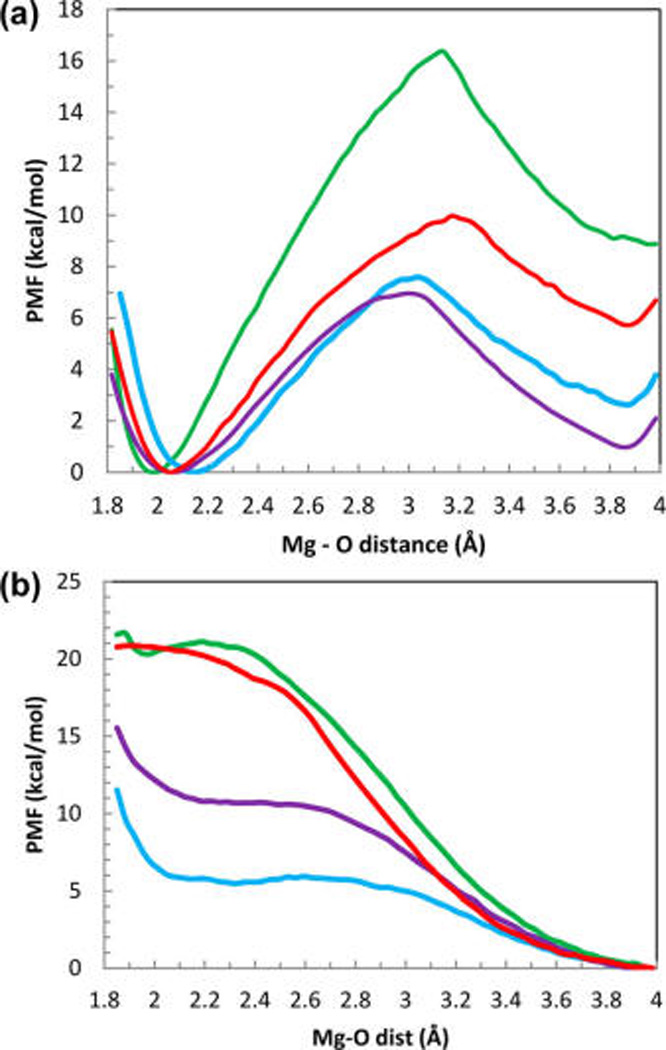
(a) Potential of mean force of the removal of a H2O ligand in bulk water (dissociative mechanism of the ligand exchange). The line colors are as follows: AMBER10 force-field is shown in green, AMOEBA with the Thole coefficient of 0.39 is shown purple, AMOEBA with the Thole coefficient 0.095 is light blue and AMOEBA with variable polarizability (this work) is shown in red. (b) Potential of mean force for insertion of an extra H2O ligand into the Mg2+ first solvation shell in bulk water (associative mechanism of ligand exchange). Simulations in both parts a and b were performed using the US method as described in the text. Colors are the same as in part a.
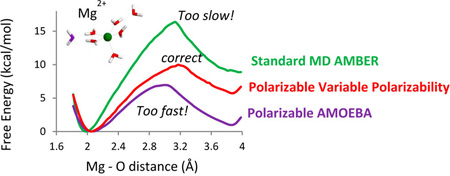
The force-fields used in these simulations are AMBER10 force field, and three versions of the AMOEBA force field described above (including the model with variable polarizability, VAR POLAR, introduced in this work). The activation free energies for the corresponding ligand-exchange reaction were estimated as a difference energy in the PMF profiles between the minimum and the maximum of the curve. As seen from Figure 6, parts a and b, the activation free energies computed with the nonpolarizable AMBER force-field are excessively large 16.4 kcal/mol for the dissociative mechanism, and 21.4 kcal/mol for the associative mechanism respectively resulting in a very slow predicted rate of the ligand exchange of about 6 s−1 as compared to the experimental value of 6.7 × 105 s−1. Calculations using AMOEBA model with the reduced Thole coefficient of 0.095 for the Mg−O interactions predicted a low activation barrier for the associative mechanism of the ligand exchange (ca. 6.0 kcal/mol) corresponding to the exchange rate of 2.5 × 108 s−1. The predicted ligand exchange rate is in good agreement with the water ligand residence time 1.9 × 10−9 s computed for the same Mg2+−water AMOEBA interaction model in ref 60. Indeed, a direct observation of the ligand exchange events in unrestrained MD simulations with this force-field showed that in contrast to the experimental data, the ligand exchange for the AMOEBA model with the reduced Thole coefficient of 0.095 proceeds via the associative mechanism (Figure 4 C , D). Moreover, the exchange events are observed on a nanosecond time scale consistent with the rates predicted using the TST theory with the activation energies and prefactors computed in Table 3 and Figure 6b. Calculations using the standard AMOEBA Thole coefficient of 0.39 correctly predicted the dissociative mechanism for the water exchange reaction, however computed activation barrier was only about. Seven kcal/mol resulting in a predicted ligand exchange rate of 4.6 × 107 s−1. This AMOEBA predicted rate of the ligand exchange is 2 orders of magnitude faster than the experimental value. The AMOEBA model with the position dependent polarizability (VAR POLAR) developed in this work predicts that activation energy for the associative mechanism of the water-ligand exchange in the first solvation shell of a magnesium ion is significantly higher than that for the dissociative mechanism. Namely, the corresponding energies are approximately 20 and 10 kcal/mol. Thus, our model correctly predicts that the exchange of the ligands in the first solvation shell of a Mg2+ ion preferentially occurs by the dissociative mechanism. A water ligand exchange rate is predicted to be 3 × 105 s−1 in this model, which in an excellent agreement with the experiment.
We also computed solvation energy of Mg2+ in water with all force field models applied in the ligand exchange activation energies calculations (Table 4). The additive nonpolarizable Amber force field (TIP3P water and Aquist model for Mg2+) and AMOEBA Thole = 0.39 calculations are in excellent agreement with the experimental values, because Mg2+ parameters were chosen to reproduce solvation energy. The AMOEBA force-field with the reduced Thole coefficient (Thole = 0.095) underestimates Mg2+ solvation energy by about 20 kcal/mol. The VAR POLAR model is also in excellent agreement with the experiment. However, unlike the additive AMBER model and the original AMOEBA the parameters for the Mg2+−water interaction were derived only from quantum chemical calculations of Mg2+−H2O dimer. No refitting of parameters to reproduce experimental energies were performed in this case.
Table 4.
Solvation Free Energies of Mg2+ Ion in Water Computed with Different Force Fields
DISCUSSION AND CONCLUSIONS
Modeling electronic polarizability of molecules in liquid phase simulations continues to be a challenge for molecular mechanics methods. One of the issues that hinders the systematic development of an accurate empirical force field is the dependence of electronic polarizabilities on intermolecular interactions. Atomic parameters deduced from quantum mechanical calculations on isolated molecules often do not reproduce polarizabilities in the condensed phase. Strong overpolarization of molecules in the vicinity of the charged species have been observed in simulations with constant polarizability polarizable force fields. To remedy this problem and better reproduce condensed phase properties a variety of empirical scaling procedures for in vacuo derived constant polarizabilities have been proposed. However, such empirical scaling reduces the range of applicability and transferability of a force-field. A better approach is to redesign the force-field to account for this effect explicitly using a polarizability function that is responsive to the presence of other molecules in the vicinity of a polarizable atom. Molecular processes that involve substantial changes of electronic polarization and polar-izabilities cannot be described accurately with constant atomic polarizability models. Coordinate dependence of the molecular polarizabilities can also result in additional interatomic forces that may be difficult to model consistently within the framework of conventional force fields. Attempts to address this problem included a number of ad hoc procedures, e.g., the atomic polarizability parameters obtained in ab initio calculations have been scaled to reproduce experimental observables. Complex procedures involving multiple cluster quantum chemical/MD calculations have been suggested to derive polarization parameters optimal for condensed phase simulations. Modification of the Thole damping parameters has also been proposed to compensate for erroneous molecular overpolarization in constant polarizability model simulations.
In this work we proposed a new approach that introduces a coordinate dependence of the atomic polarizabilities into a popular AMOEBA force field (the VAR POLAR model). We discussed a proposed modification of the force field in the context of modeling of water ligand exchange reactions in the first solvation shell of a solvated Mg2+ ion. Water ligands of Mg2+ are strongly polarized in the electrical field of the divalent ion. At the same time polarizabilities of the water molecules are reduced in the immediate vicinity of Mg2+ and are changing substantially in the course of the ligand exchange reaction.
Simulation results described in this work clearly demonstrate the feasibility as well as the advantages of an explicit treatment of coordinate dependence of electronic polarizability in molecular mechanics simulations. In conventional fixed polar-izability and fixed charge force fields, this effect is typically ignored or factored into models designed to account for other properties of molecular systems. We have found that constant atomic polarizability AMOEBA model fails to consistently describe the energetics of the Mg2+−water clusters with different number of water molecules. Compensating for overpolarization of the water molecules in the vicinity of the Mg2+ ion by reducing the Thole coefficient for the Mg2+−water interactions as was suggested in the literature55,58–60 results in a qualitatively incorrect description of the water ligand exchange around Mg2+. Namely, a ligand exchange by associative instead of dissociative mechanism results from such an approximation. A reduction of the Thole coefficients in the calculations of the electrostatic interactions between atoms affects the charge distributions of the interacting molecules; i.e., the smaller a Thole coefficient of an atom is, the larger is an effective radius of the multipole densities of the atom. While using the smaller values for Thole coefficients resulted in a reduction of the electrostatic interactions between the Mg2+ ion and the water ligand, the effect is not identical to that occurring because of the reduction of the molecular polarizability.
Another indication that the VAR POLAR model provides a more consistent description of the Mg2+−water interactions than the constant polarizability AMOEBA models is that the optimal parametrization in this case is possible with the small value of the Mg2+ van der Waals radius. The value VdW radius of Mg2+ is close to the value derived from electronic density of the ion. Significantly larger Mg2+ VdW radii used in AMOEBA models are indicative that an additional repulsive force arising from the reduction of water polarizability at close Mg2+−water distances (see eq 5) partially accounted for in the repulsive part of VdW interactions. This short-range repulsive force eq 5 depends on the value of polarization of water, thus it will depend on the value of dielectric screening in the system and presence of charges species in the vicinity Thus, the VAR POLAR model can be expected to be more transferable than the standard AMOEBA between systems of different polarity as well as better suited for the systems with the heterogenic charge distributions such as in a protein environment.
Compared to the standard AMOEBA model VAR POLAR model adds atom pairwise sum in the denominator of (1) to compute instantaneous atom polarizabilities. For the system considered in the paper, only Mg2+ ion had nonzero index, thus an increase in computational costs compared to standard AMOEBA calculations was negligible (less than 5% increase in computational time). When all atoms in the systems affect each other polarizabilities via eq 1 an expected increase in the computational time will be only moderate. This is because AMOEBA calculations involve only several atom pairwise sums, and, most importantly, the most time-consuming part of calculations: the iterative convergence of the atom polarizable dipoles, is not affected by eq 1.
The VAR POLAR model, in which electronic polarizability of water dependent on the distance between water oxygen and Mg2+ allowed us to consistently reproduce a number of properties of Mg2+ interaction with water, namely (i) energetics of the ion-water complexes of different sizes and (ii) free energy of ion solvation in water, as well as (iii) the rate and the mechanism of water-ligand exchange in the Mg2+ first solvation shell. The results presented in this work indicate that introduction of an explicit dependence of atomic polarizabilities into molecular mechanics energy functionals may allow us to develop an empirical force-fields capable of much more accurate description of the important biochemical processes, such as an ion propagation in the biological membrane channels, than is presently possible. Also, the suggested modifications of the functional form of the force field may be useful in simplifying the development of the force field parameters for the condensed matter simulations. An introduction into the force-field of the electronic polarizability damping parameters obtained in quantum chemical calculations performed on small clusters may result in a parameter set with a better transferability of the atomic polarizability parameters derived from vacuum quantum chemical calculations on isolated molecules.
Acknowledgments
The authors are grateful to Jon Johnson for bringing this problem to our attention, educating us about the NMDA receptors, and patiently supporting this project. This work was in part supported by the NIH, Grant R01MH04581722.
Footnotes
The authors declare no competing financial interest.
REFERENCES
- 1.Karplus M. Molecular dynamics of biological macromolecules: A brief history and perspective. Biopolymers. 2003;68:350–358. doi: 10.1002/bip.10266. [DOI] [PubMed] [Google Scholar]
- 2.Adcock SA, McCammon J. A Molecular dynamics: Survey of methods for simulating the activity of proteins. Chem. Rev. 2006;106:1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ponder JW, Case DA. Force fields for protein simulations. Adv. Protein Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 4.Warshel A, Kato M, Pisliakov AV. Polarizable force fields: History, test cases, and prospects. J. Chem. Theory Comput. 2007;3:2034–2045. doi: 10.1021/ct700127w. [DOI] [PubMed] [Google Scholar]
- 5.van der Vaart A, Bursulaya BD, Brooks CL, Merz KM. Are many-body effects important in protein folding? J. Phys. Chem. B. 2000;104:9554–9563. [Google Scholar]
- 6.Mackerell AD. Empirical force fields for biological macro-molecules: Overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 7.Jiang YX, Lee A, Chen JY, Ruta V, Cadene M, Chait BT, MacKinnon R. X-ray structure of a voltage-dependent K+ channel. Nature. 2003;423:33–41. doi: 10.1038/nature01580. [DOI] [PubMed] [Google Scholar]
- 8.MacKinnon R. Potassium channels. FEBS Lett. 2003;555:62–65. doi: 10.1016/s0014-5793(03)01104-9. [DOI] [PubMed] [Google Scholar]
- 9.Roux B. Theoretical and computational models of ion channels. Curr. Opin. Struct. Biol. 2002;12:182–189. doi: 10.1016/s0959-440x(02)00307-x. [DOI] [PubMed] [Google Scholar]
- 10.Mamonov AB, Coalson RD, Nitzan A, Kurnikova MG. The role of the dielectric barrier in narrow biological channels: A novel composite approach to modeling single-channel currents. Biophys. J. 2003;84:3646–3661. doi: 10.1016/S0006-3495(03)75095-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bucher D, Raugei S, Guidoni L, Dal Peraro M, Rothlisberger U, Carloni P, Klein ML. Polarization effects and charge transfer in the KcsA potassium channel. Biophys. Chem. 2006;124:292–301. doi: 10.1016/j.bpc.2006.04.008. [DOI] [PubMed] [Google Scholar]
- 12.Simakov NA, Kurnikova MG. Soft wall ion channel in continuum representation with application to modeling ion currents in alpha-hemolysin. J. Phys. Chem. B. 2010;114:15180–15190. doi: 10.1021/jp1046062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roux B, Berneche S. On the potential functions used in molecular dynamics simulations of ion channels. Biophys. J. 2002;82:1681–1684. doi: 10.1016/S0006-3495(02)75520-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Boiteux C, Kraszewski S, Ramseyer C, Girardet C. Ion conductance vs. pore gating and selectivity in KcsA channel: Modeling achievements and perspectives. J. Mol. Model. 2007;13:699–713. doi: 10.1007/s00894-007-0202-y. [DOI] [PubMed] [Google Scholar]
- 15.Warshel A, Levitt M. Theoretical studies of enzymatic reactions - dielectric, electrostatic, and steric stabilization of carbonium-ion in reaction of lysozyme. J. Mol. Biol. 1976;103:227–249. doi: 10.1016/0022-2836(76)90311-9. [DOI] [PubMed] [Google Scholar]
- 16.Pullman B, Claverie P, Caillet J. Interaction energies in hydrogen-bonded purine-pyrimidine triplets. Proc. Natl. Acad. Sci. U. S. A. 1967;57:1663–1669. doi: 10.1073/pnas.57.6.1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ponder JW. TINKER: Software tools for molecular design; 5.0 ed. Saint Louis, MO: Washington University School of Medicine; 2009. [Google Scholar]
- 20.Kunz APE, Allison JR, Geerke DP, Horta BAC, Hunenberger PH, Riniker S, Schmid N, van Gunsteren WF. New functionalities in the GROMOS biomolecular simulation software. J. Comput. Chem. 2012;33:340–353. doi: 10.1002/jcc.21954. [DOI] [PubMed] [Google Scholar]
- 21.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Halgren TA, Damm W. Polarizable force fields. Curr. Opin. Struct. Biol. 2001;11:236–242. doi: 10.1016/s0959-440x(00)00196-2. [DOI] [PubMed] [Google Scholar]
- 23.Rick SW, Stuart SJ. Potentials and algorithms for incorporating polarizability in computer simulations. In: Lipkowitz KB, Boyd DB, editors. Reviews in Computational Chemistry. Vol. 18. New York: Wiley-VCH, Inc; 2002. pp. 89–146. [Google Scholar]
- 24.Cieplak P, Dupradeau FY, Duan Y, Wang JM. Polarization effects in molecular mechanical force fields. J. Phys. Condens. Matter. 2009;21:21. doi: 10.1088/0953-8984/21/33/333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ren P, Wu C, Ponder JW. Polarizable atomic multipole-based molecular mechanics for organic molecules. J. Chem. Theory. Comput. 2011;7:3143–3161. doi: 10.1021/ct200304d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gresh N, Cisneros GA, Darden TA, Piquemal JP. Anisotropic polarizable molecular mechanics studies of inter- and intramoecular interactions ligand-macromolecule complexes A bottom-up strategy. J. Chem. Theory Comput. 2007;3:1960–1986. doi: 10.1021/ct700134r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lopes PEM, Roux B, MacKerell AD. Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability: theory and applications. Theor. Chem. Acc. 2009;124:11–28. doi: 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shi Y, Xia Z, Zhang J, Best R, Wu C, Ponder JW, Ren P. Polarizable atomic multipole-based AMOEBA force field for proteins. J. Chem. Theory Comput. 2013;9:4046–4063. doi: 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lopes PEM, Huang J, Shim J, Luo Y, Li H, Roux B, MacKerell AD. Polarizable force field for peptides and proteins based on the classical drude oscillator. J. Chem. Theory Comput. 2013;9:5430–5449. doi: 10.1021/ct400781b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Savelyev A, MacKerell AD. All-atom polarizable force field for DNA based on the classical drude oscillator model. J. Comput. Chem. 2014;35:1219–1239. doi: 10.1002/jcc.23611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ponder JW, Wu C, Ren P, Pande SV, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Jr, et al. Current status of the AMOEBA polarizable force field. J. Phys. Chem. B. 2010;114:2549–2564. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cisneros GA, Karttunen M, Ren PY, Sagui C. Classical electrostatics for biomolecular simulations. Chem. Rev. 2014;114:779–814. doi: 10.1021/cr300461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Thole BT. Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys. 1981;59:341–350. [Google Scholar]
- 34.Ren PY, Ponder JW. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B. 2003;107:5933–5947. [Google Scholar]
- 35.Kaminski GA, Stern HA, Berne BJ, Friesner RA. Development of an accurate and robust polarizable molecular mechanics force field from ab initio quantum chemistry. J. Phys. Chem. A. 2004;108:621–627. [Google Scholar]
- 36.Yu HB, Whitfield TW, Harder E, Lamoureux G, Vorobyov I, Anisimov VM, MacKerell AD, Roux B. Simulating monovalent and divalent Ions in aqueous solution using a drude polarizable force field. J. Chem. Theory Comput. 2010;6:774–786. doi: 10.1021/ct900576a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bauer BA, Lucas TR, Krishtal A, Van Alsenoy C, Patel S. Variation of ion polarizability from vacuum to hydration: Insights from Hirshfeld partitioning. J. Phys. Chem. A. 2010;114:8984–8992. doi: 10.1021/jp103691w. [DOI] [PubMed] [Google Scholar]
- 38.Coker H. Polarizability changes on ion hydration. J. Phys. Chem. 1976;80:2084–2091. [Google Scholar]
- 39.Lamoureux G, MacKerell AD, Roux B. A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys. 2003;119:5185–5197. [Google Scholar]
- 40.Yu HB, Hansson T, van Gunsteren WF. Development of a simple, self-consistent polarizable model for liquid water. J. Chem. Phys. 2003;118:221–234. [Google Scholar]
- 41.Geerke DP, Van Gunsteren WF. The performance of non-polarizable and polarizable force-field parameter sets for ethylene glycol in molecular dynamics simulations of the pure liquid and its aqueous mixtures. Mol. Phys. 2007;105:1861–1881. [Google Scholar]
- 42.Anisimov VM, Vorobyov IV, Roux B, MacKerell AD. Polarizable empirical force field for the primary and secondary alcohol series based on the classical drude model. J. Chem. Theory Comput. 2007;3:1927–1946. doi: 10.1021/ct700100a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Baker CM, MacKerell AD. Polarizability rescaling and atom-based Thole scaling in the CHARMM Drude polarizable force field for ethers. J. Mol. Model. 2010;16:567–576. doi: 10.1007/s00894-009-0572-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vosmeer CR, Rustenburg AS, Rice JE, Horn HW, Swope WC, Geerke DP. QM/MM-based fitting of atomic polarizabilities for use in condensed-phase biomolecular simulation. I. Chem. Theory Comput. 2012;8:3839–3853. doi: 10.1021/ct300085z. [DOI] [PubMed] [Google Scholar]
- 45.Kunz APE, van Gunsteren WF. Development of a nonlinear classical polarization model for liquid water and aqueous solutions: COS/D. J. Phys. Chem. A. 2009;113:11570–11579. doi: 10.1021/jp903164s. [DOI] [PubMed] [Google Scholar]
- 46.Kurnikov IV, Simakov N, Speranskiy K, Kurnikova M. HARLEM. Pittsburgh PA: Carnegie Mellon University; 2014. [Google Scholar]
- 47.The Biological Chemistry of Magnesium. First. New York: Wiley-VCH; 1995. [Google Scholar]
- 48.Draper DE, Grilley D, Soto AM. Ions and RNA folding. Annu. Rev. Biophys. Biomol. Struct. 2005;34:221–243. doi: 10.1146/annurev.biophys.34.040204.144511. [DOI] [PubMed] [Google Scholar]
- 49.Nowak L, Bregestovski P, Ascher P, Herbet A, Prochiantz A. Magnesium gates glutamate-activated channels in mouse central neurones. Nature. 1984;307:462–465. doi: 10.1038/307462a0. [DOI] [PubMed] [Google Scholar]
- 50.Dingledine R, Borges K, Bowie D, Traynelis SF. The glutamate receptor ion channels. Pharmacol. Rev. 1999;51:7–61. [PubMed] [Google Scholar]
- 51.Siegler Retchless B, Gao W, Johnson JW. A single GluN2 subunit residue controls NMDA receptor channel properties via intersubunit interaction. Nat. Neurosci. 2012;15:406–413. doi: 10.1038/nn.3025. S401–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Caminiti R, Licheri G, Piccaluga G, Pinna G. X-ray-diffraction study of Mg-Cl2 aqueous solutions. J. Appl. Crystallogr. 1979;12:34–38. [Google Scholar]
- 53.Helm L, Merbach AE. Inorganic and bioinorganic solvent exchange mechanisms. Chem. Rev. 2005;105:1923–1959. doi: 10.1021/cr030726o. [DOI] [PubMed] [Google Scholar]
- 54.Allner O, Nilsson L, Villa A. A Magnesium ion-water coordination and exchange in biomolecular simulations. J. Chem. Theory Comput. 2012;8:1493–1502. doi: 10.1021/ct3000734. [DOI] [PubMed] [Google Scholar]
- 55.Jiao D, King C, Grossfield A, Darden TA, Ren PY. Simulation of Ca2+ and Mg2+ solvation using polarizable atomic multipole potential. J. Phys. Chem. B. 2006;110:18553–18559. doi: 10.1021/jp062230r. [DOI] [PubMed] [Google Scholar]
- 56.Guardia E, Sese G, Padro JA, Kalko S. G Molecular dynamics simulation of Mg2+ and Ca2+ ions in water. J. Solution. Chem. 1999;28:1113–1126. [Google Scholar]
- 57.Aaqvist J. Ion water interaction potentials derived from free-energy perturbation simulations. J. Phys. Chem. 1990;94:8021–8024. [Google Scholar]
- 58.Piquemal JP, Perera L, Cisneros GA, Ren PY, Pedersen LG, Darden TA. Towards accurate solvation dynamics of divalent cations in water using the polarizable amoeba force field: From energetics to structure. J. Chem. Phys. 2006;125:7. doi: 10.1063/1.2234774. [DOI] [PubMed] [Google Scholar]
- 59.Masia M, Probst M, Rey R. On the performance of molecular polarization methods. II. Water and carbon tetrachloride close to a cation. J. Chem. Phys. 2005;123:13. doi: 10.1063/1.2075107. [DOI] [PubMed] [Google Scholar]
- 60.Wu JC, Piquemal JP, Chaudret R, Reinhardt P, Ren PY. Polarizable molecular dynamics simulation of Zn(II) in water using the AMOEBA force field. J. Chem. Theory Comput. 2010;6:2059–2070. doi: 10.1021/ct100091j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Neely J, Connick R. Rate of water exchange from hydrated magnesium ion. J. Am. Chem. Soc. 1970;92:3476. [Google Scholar]
- 62.Lamoureux G, Roux B. Absolute hydration free energy scale for alkali and halide ions established from simulations with a polarizable force field. J. Phys. Chem. B. 2006;110:3308–3322. doi: 10.1021/jp056043p. [DOI] [PubMed] [Google Scholar]
- 63.Ferrenberg AM, Swendsen RH. Optimized Monte-Carlo data-analysis. Phys. Rev. Lett. 1989;63:1195–1198. doi: 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- 64.Schmid R, Miah AM, Sapunov VN. A new table of the thermodynamic quantities of ionic hydration: values and some applications (enthalpy-entropy compensation and Born radii) Phys. Chem. Chem. Phys. 2000;2:97–102. [Google Scholar]
- 65.Marcus Y. Thermodynamics of solvation of ions 0.5. Gibbs free-energy of hydration at 298.15 K. J. Chem. Soc., Faraday Trans. 1991;87:2995–2999. [Google Scholar]


