Abstract
Transcranial magnetic stimulation (TMS) delivers highly localized brain stimulations via non-invasive externally applied magnetic fields. This non-invasive, painless technique provides researchers and clinicians with a unique tool capable of stimulating both the central and peripheral nervous systems. However, a complete analysis of the macroscopic electric fields produced by TMS has not yet been performed. In this paper, we addressed the importance of the secondary E-field created by surface charge accumulation during TMS using the boundary element method (BEM). 3D models were developed using simple head geometries in order to test the model and compare it with measured values. The effects of tissue geometry, size and conductivity were also investigated. Finally, a realistically shaped head model was used to assess the effect of multiple surfaces on the total E-field. Secondary E-fields have the greatest impact at areas in close proximity to each tissue layer. Throughout the head, the secondary E-field magnitudes typically range from 20% to 35% of the primary E-field's magnitude. The direction of the secondary E-field was generally in opposition to the primary E-field; however, for some locations, this was not the case (i.e. going from high to low conductivity tissues). These findings show that realistically shaped head geometries are important for accurate modeling of the total E-field.
1. Introduction
Transcranial magnetic stimulation (TMS) is a non-invasive, painless technique, which has provided researchers and clinicians a unique tool capable of stimulating both the central and peripheral nervous systems (Barker et al 1985, Ilmoniemi et al 1999). In TMS, intense pulses of current flow through a coil located at the surface of the head. This current creates a time-varying magnetic field, which induces a primary electric field (E-field) in the space surrounding the TMS coil. When a conductive medium (i.e. the head) is exposed to this induced E-field, charges accumulate at surfaces with different electrical conductivities (Tofts and Branston 1991) creating a secondary E-field. While several theoretical models have been developed to elaborate on the primary E-field distributions generated by TMS coils (Cohen et al 1990, Grandori and Ravazzani 1991, Davey et al 1991, Kim et al 2006, Salinas et al 2007), little work has been done regarding the influence of the secondary E-field.
Tofts (1990) modeled induced current density—using primary and secondary E-fields—during magnetic stimulation of an infinite planar surface; current density may be determined using Ohm's law . This study found that only tangential currents (parallel to the coil's surface) were induced in the surface. As the size of the tissue surface approaches that of the TMS coil, more boundary effects will arise. Therefore, the validity of this model is limited to cases in which the coil's size is much smaller than the tissue surface—since that is the only scenario where the surface may be considered to be planar. This paper laid the groundwork for further investigation into modeling of the total E-field—both the primary and secondary E-fields.
Some research groups used a three-shell head model (Rush and Driscoll 1969) in TMS E-field modeling. This model was originally used for electro-encephalographic (EEG) and magneto-encephalographic (MEG) studies. The transition from EEG and MEG field modeling to TMS is relatively seamless, since the physics involved in the calculations is very similar—due to reciprocity. In the forward problem, the source and properties of the volume conductor are known whereas the fields are unknown—which is the case for TMS field calculations inside the head. In the inverse problem, the fields and conductors are known, and the source is unknown; this is the case for EEG and MEG field calculations. The source in TMS is much stronger than that in EEG and MEG; therefore, some of the assumptions in EEG and MEG field modeling (e.g. removing scalp and skull layers from the calculation) may not directly transfer to TMS E-field modeling.
Roth et al (1991a, 1991b) addressed the effect of the secondary E-field (due to TMS induced E-fields) in spherical volume conductors. These studies used the finite difference method (FDM) to calculate the E-fields. The FDM is an iterative numerical solution (coupled with relaxation techniques) which calculates the potential at each point as the average of its neighbors, and then repeats the process until the solution converges (i.e. further iterations do not change the result). Because this method is an approximation technique, it may oversimplify the computation in complex tissue geometries (Johnson 2006). These studies asserted that the secondary E-field created by charge accumulation on tissue surfaces may shield the nerve from the induced E-field. The spherical head models in these studies consisted of three concentric spherical shells—representing the scalp, skull and cortex (Rush and Driscoll 1969). They concluded that the inclusion of the scalp and skull tissue layers was not necessary since these layers ‘have no influence on the electrical field distribution in the three-sphere model’ (Roth et al 1991b). The primary E-field calculations (which would not be affected by tissue layers) were not presented for a quantitative comparison with the total E-field; also, only axial views (i.e. the xy-plane) were displayed. Therefore, it was not possible to decipher whether or not the statement was valid across the volume.
Heller and van Hulsteyn (1992) agreed that Roth's omission of the scalp and skull layers was valid; however, their reasoning was quite different. They assumed that the E-field at any position inside of a spherically symmetric volume conductor primarily depends only on the magnetic moment produced by the TMS coil and its position relative to the origin of the volume conductor. This approach is independent of electrical conductivity because it is assumed to be spherically symmetric—via an analytical solution. They reason that the maximum E-field strength will occur at a boundary where the conductivity changes from one tissue to the next and that any changes in conductivity inside this boundary are inconsequential. One caveat to this approach is that the volume conductor is spherically symmetric—realistically shaped head models (such as magnetic resonance (MR)-based tissue segmentations) are not. However, this paper has provided the TMS community (as well as EEG and MEG groups) a solid theoretical/analytical framework for calculating electromagnetic fields.
Recently, Toschi et al (2008, 2009) calculated the total E-fields induced by TMS in a realistically shaped head model. They used the FDM (described earlier) and concluded that complex head geometries provide more accurate estimates of the secondary E-field, resulting in a better estimate for the total E-field. These estimates can have a profound impact on the coil's observed focality as well as the direction and magnitude of the E-fields being produced. Unlike Roth et al (1991a, 1991b), these studies used realistic coil geometries—providing more accurate estimates of the induced primary E-field. However, because the FDM is an approximation technique, a more accurate solution is needed to verify the need to use the secondary E-field.
Wang and Eisenberg (1994), Miranda et al (2003), Wagner et al (2004) and De Lucia et al (2007) proposed solutions for calculating the total E-field using the finite element method (FEM) which provides an exact solution to the E-field calculation. The FEM supports user-defined tissue geometries to which anisotropic tissue characteristics may be assigned. Also, the FEM is very effective when modeling tissues with continuously varying tissue conductivities. For example, De Lucia et al (2007) used diffusion tensor imaging (DTI) to create anisotropic conductivity models of each tissue in a realistically shaped head model. However, most commercial FEM software programs are expensive and much time is spent generating the meshes of the volume conductor. Because of this, some studies simplify the calculation by reducing the resolution of the model (Wagner et al 2004). In doing so, important anatomical features such as gyri and sulci have been excluded from these head models. An alternative to the FEM is the boundary element method (BEM).
The BEM is a numerical technique used to calculate surface potentials everywhere inside a volume conductor due to a known current source (Ferguson and Stroink 1997). In the BEM, only the boundaries are discretized whereas in the FEM, the whole volume must be discretized. This greatly decreases the number of nodes involved in the calculations thereby reducing the computational load while still offering an exact solution to the boundary value problem. A complete description of the BEM is beyond the scope of this paper; however, a thorough description of the technique may be found in Stenroos et al (2007). Assuming that each boundary encloses an isotropic, homogeneous region of the volume conductor, the entire problem may be treated as a piecewise homogeneous volume conductor. In such a volume conductor, the BEM may be used to address any gross effects on the macroscopic induced E-field—i.e. to determine whether or not the secondary E-field must be included in the total E-field calculation. The BEM should not be used to model anisotropic tissues; the FEM is more suitable for these modeling scenarios.
In this study we address the importance of the secondary E-field created by surface charge accumulation at conductivity interfaces using the BEM with detailed TMS coil models. Calculations were performed using simple head geometries to test the model and compare it with measured values. The effects of coil orientation, tissue geometry and size were also investigated. A four-shell head model (similar to Cuffin and Cohen (1979)) was used to assess the effect of multiple surfaces on the total E-field. Finally, a realistically shaped head model was created to calculate the total E-field induced by TMS.
2. Theoretical background
The E-field induced by a TMS current pulse has a low frequency spectrum (less than 10 kHz). At these quasistatic frequencies, typical high-frequency effects—propagation delays, shielding effects and capacitive effects—may be neglected (Wang and Eisenberg 1994, Miranda et al 2003). Therefore, when a volume conductor is exposed to a TMS pulse, the electromagnetic wave effects—skin depth, displacement currents, etc—may be neglected.
By assigning a uniform bulk conductivity (σ) to each homogeneous conductor, we see that their macroscopic current density should be equivalent to Ohm's law (Geselowitz 1967):
| (1) |
where σ is the inverse of resistance (i.e. conductance in S m−1), assuming that the conductor is purely resisitive and contains no point-like sources (i.e. singularities). In the quasistatic limit, the divergence of the induced current density is zero; therefore,
| (2) |
Using the Lorenz gauge (Jackson 1999), we see that the total electric field in the tissue is the sum of the primary and secondary electric fields:
| (3) |
Therefore, (1) becomes
The vector potential is used to model the primary E-field and is a direct result of the magnetic field created by the coil's rapidly changing current (Salinas et al 2007). The scalar potential (φ) is due to surface charge buildup—due to the primary E-field—at interfaces where conductivity changes. Combining (2) and (3) we see that
| (4) |
which is essentially the Poisson equation . The current density normal to each surface must be zero, so (4) becomes
| (5) |
where is the unit normal vector directed outward from the surface. Further investigation shows that each surface has an effect on the scalar potential in a volume conductor (Ferguson and Stroink 1997). The continuity conditions state that the scalar potential on one side of the interface equals that of the other side:
| (6) |
| (7) |
where the prime and double prime notations refer to the conductive media on each side of an internal surface (Liu and Ueno 2000)—note that the charges used to calculate each scalar potential are of opposite sense; (6) and (7) are in accordance with the quasistatic limit. We must also account for the contribution from the coil's current; therefore,
| (8) |
At all locations across the interface, the following condition should be valid:
| (9) |
Using (9) and Neumann boundary conditions, (8) becomes
| (10) |
leaving us with a suitable boundary condition for all internal surfaces. Using this boundary condition, we may now solve Laplace's equation
| (11) |
for the scalar potential (φ) throughout the volume conductor.
3. Materials and methods
3.1. Measuring secondary E-fields
A small dipole probe (figure 1(A), top) was fabricated to measure the total E-field created by the TMS coil in a saline volume conductor (i.e. the tissue phantom). The design of the probe was similar to previous studies (Glover and Bowtell 2007); however, our probe had a 6.15 mm—rather than 50 mm—tip separation. The smaller tip separation supported more detailed measurements in the volume conductor since at some locations the TMS coil's induced E-field can change very rapidly.
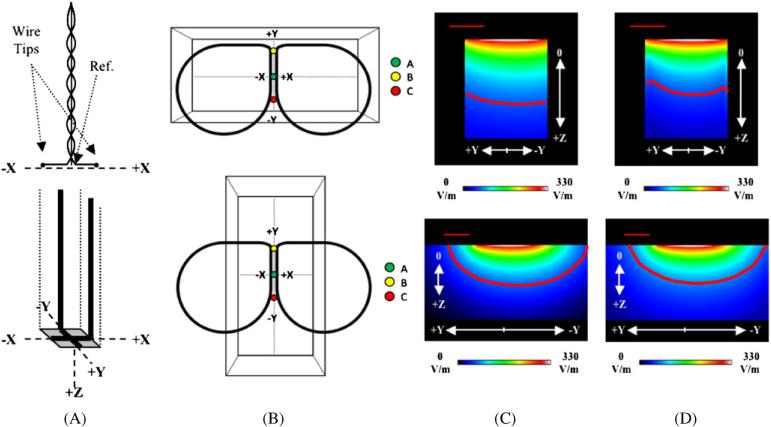
Figure 1.
(A) Schematic of the straight dipole (top) and 3D Eddy current probe (bottom). The dipole probe's wire tips and reference electrode are labeled and the coordinate systems of each probe are provided. The dipole probe's measurements are performed in one dimension; recordings in other dimensions required a rotation of the dipole probe. (B) Phantom orientations for the ‘Horizontal Box’ (top) and ‘Vertical Box’ (bottom) models. Points ‘A’, ‘B’ and ‘C’ were used for E-field measurements with the two E-field probes. The points are the same locations in both orientations. Sagittal views (yz-plane) are presented for the modeled magnitude images of the (C) primary and (D) total E-fields for the ‘Horizontal Box’ (top) and ‘Vertical Box’ (bottom) phantoms at a TMS stimulator intensity of 50%; sagittal views are at X = 0 mm. Primary E-field strengths at cortical depths—Z = 30 mm—have modeled values (on-axis) of up to 23% of the maximum E-field strength. Therefore, red contour lines (representing magnitudes greater than 20% of the maximum E-field strength) were drawn for the primary and total E-fields to show the distribution of these E-field strengths. The straight, red line in the upper left corners of the image represents a distance of 2 cm.
The dipole probe was constructed from two insulated copper wires. Each wire tip was bent at a 90° angle creating a 3 mm long straight dipole element. The two wires were twisted together at their bases and a reference electrode was positioned in the center of the probe. The wires were placed in a rectangular carbon fiber rod to which the wire tips were secured at one end by non-conductive epoxy cement. Only the wire tips—the dots in figure 1(A) (top)—and the centrally located reference electrode were exposed to the conductive medium when measurements were performed. The probe's wires attach to balanced/shielded coaxial cables, which provided input signals to a digital oscilloscope (Tektronix TDS 320). Waveforms were measured using a 1 μs sampling rate.
The dipole probe was calibrated using a known electric field at the center of a trough of saline with a square cross-section; the calibration factor was very close to unity. This probe was then used for measurements of the total E-field created by the TMS coil and the phantom. E-fields measured with the dipole probe had an accuracy of ± 2.6 V m−1 (a 0.93% difference). Since the dipole probe has straight elements, the primary component is also included in the measurement (Tofts and Branston 1991). To account for this, a calibrated 3D Eddy current probe (Salinas et al 2007; figure 1(A) (bottom)) was used to measure the primary component; the 3D Eddy current probe had an accuracy of ± 1.6 V m−1 (a 0.58% difference). Subtraction provides a measurement of the secondary component. Since we are using a quasistatic approximation, the effect of waveforms of the E-fields induced by TMS can be neglected. Thus, in order to simplify calculations, we selected a particular point in time (i.e. the maximum , typically between 7 μs and 10 μs) for each waveform as the representative induced E-field value. All measurements were performed using a Cadwell High Speed magnetic stimulator (at 50% intensity) and a B-shaped TMS coil (Cadwell, Inc., Kennewick, WA, USA). A full description of the B-shaped coil may be found in Salinas et al 2007.
3.2. Phantom construction and utilization
Previous studies used large saline tanks (Durand et al 1992, Kobayashi et al 1997)—which simulated a semi-infinite medium—to reduce edge (boundary) effects in their calculations. In an effort to provide a rigorous test of our numerical model, we purposefully exaggerated edge effects by making one dimension of the phantom smaller than the TMS coil (i.e. short axis). When the phantom's short axis is aligned with the TMS coil's maximum primary E-field vector, large secondary E-fields will arise at the boundaries. Measurements of the total E-field at sites near these boundaries provided a means for calibrating our modeled data.
A rectangular phantom was constructed using 2.50 mm thick flat polymer sheets. The phantom's dimensions were 128 mm × 48 mm × 60 mm (i.e. length, width and height, respectively). The phantom was filled with a 0.9% NaCl solution (saline). Three locations—labeled ‘A’, ‘B’ and ‘C’ in figure 1(B)—were designated as test points to assess the accuracy of measured and modeled values. The center test point (‘A’) of the phantom was placed at the designated origin—i.e. site of maximum E-field strength—of the B-shaped TMS coil. The long axis of the phantom was aligned horizontally with the long axis of the TMS coil (‘Horizontal Box’ in figure 1(B)). A second test was performed with the long axis of the phantom aligned perpendicular to the TMS coil's long axis (‘Vertical Box’ in figure 1(B)).
Dipole and 3D Eddy current probe E-field (Ex and Ey) measurements were performed at a 50% TMS stimulator intensity setting at ‘A’, ‘B’ and ‘C’ locations in the phantom. Although there should be no induced E-field in the Z direction for a flat TMS coil (Branston and Tofts 1991), the dipole probe is capable of measuring the total E-field in that direction—this requires a simple rotation of the dipole elements. However, due to the geometry of our phantom this was not possible. Thus, we are only reporting Ex and Ey measurements. However, the secondary E-field in the Z direction is reported in the modeled data.
Tofts and Branston 1991 stated that loop probes (e.g. the 3D Eddy current probe) may not be used to measure induced effects off of the coil's main axis of symmetry since there would be different potentials on each side of the loop. In order to correct for this, measurements taken using the 3D Eddy current probe were performed twice (once at 0° with respect to each axis, and then at 180°). Also, by keeping the tangential length of the probe wire small (~5 mm), we significantly reduced effects due to E-field averaging across the wires. The signs of the primary E-field measurements were verified using the reported direction of current through the wires of the TMS coil.
3.3. Size dependence
Previous studies (Sarvas 1987, Eaton 1992, Miranda et al 2003) used spherical models to represent the shape of the head. Because of the B-shaped TMS coil's limited penetration depth (Salinas et al 2007), most of the points on the lower half of a sphere's boundary would be exposed to negligible primary E-fields—assuming a realistic head radius (~100 mm). While these distant points have little effect on the total E-field, including them in the model drastically increases the computational load. By focusing on the section of the volume conductor exposed to significant primary E-fields (i.e. greater than 1%), we can drastically decrease the computation times needed in each calculation. We created ‘Hemisphere’ and ‘Sphere’ models—both with a 100 mm radius—to test the geometric dependence of the total E-field calculation. Since we are using the BEM—a numerical solution—irregular shapes (even those in open form) may be modeled. We used the conductivity of the 0.9% NaCl solution—1.744 S m−1 (Tay et al 1989)—in each model; air had a conductivity value of 1.0 × 10−15 S m−1.
A ‘Small Hemisphere’ model (radius = 10 mm) was also constructed—simulating a small animal head model. Again, the conductivity of the 0.9% NaCl solution was used in the calculation. We compared the results of the animal and human head models to demonstrate the importance of the TMS coil's size with respect to the volume conductor's on the total E-field calculation.
3.4. Hemisphere models
A symmetric ‘One-Shell Hemisphere’ model was created to simulate an air–scalp interface—which is assumed to have the largest effect on the scalar potential (Tofts 1990). A more complete ‘Four-Shell Hemisphere’ model was also created to study the impact of multiple surfaces on the secondary E-field—also on the total E-field; the four tissue layers were scalp, skull, cerebrospinal fluid (CSF) and cortex. The radii of each tissue layer (Cuffin and Cohen 1979) are 88 mm (scalp), 85 mm (skull), 81 mm (CSF) and 79 mm (cortex). The electrical conductivity values (Geddes and Baker 1967, Rush and Driscoll 1969) for the scalp, skull, CSF and cortex were 0.33 S m−1, 0.0042 S m−1, 1.79 S m−1 and 0.33 S m−1, respectively.
3.5. The realistically shaped head model
3.5.1. Human subject imaging data
T1-weighted magnetic resonance (MR) and computed tomography (CT) images of one subject were obtained from the Research Imaging Center's (RIC) image archive. MR images were obtained using a 1.9 T GE/Elscint Prestige MRI scanner (GE/Elscint, Haifa, Israel) at the RIC, University of Texas Health Science Center at San Antonio (UTHSCSA, San Antonio, TX, USA); the CT image was acquired using a Picker PQ5000 CT Scanner (Picker International, Cleveland, OH, USA) at the Cancer Therapy and Research Center, UTHSCSA. The subject in these imaging studies was a healthy male with no neurological deficits. The imaging data were acquired in accordance with UTHSCSA's Institutional Review Board (IRB) regulations and the subject was informed that his images would be used for a post hoc analysis.
3.5.2. Image segmentation
We used the FMRIb's Automated Segmentation Tool (FAST; Zhang et al 2001), a part of the FMRIb Software Library (FSL; Smith et al 2004). FAST segments a three-dimensional image of the brain into different tissue classes (gray matter, white matter, CSF, etc). This segmentation algorithm is based on a hidden Markov random field model and an Expectation-Maximization algorithm (Zhang et al 2001). The program also checked and corrected each MR image for RF-inhomogeneities (bias fields). The program is fully automated and produces segmented tissue images organized by tissue class. Since MR images are not ideal for bone visualization, we segmented a CT scan of the subject's head using a bone threshold (greater than 1500 HU); the MR and CT images were aligned using specific bony features (i.e. nasion, inion, etc). The CT skull segmentation was used to define the bone regions in the MR image segmentation. We made mask images of each tissue class to define each tissue as a 3D volume.
All images were viewed using the RIC's in-house visualization software: MANGO (Lancaster and Martinez 2008). This visualization tool supports 3D viewing and rendering as well as several image processing applications—such as the region of interest (ROI), histogram and image analysis. Each tissue class was assigned a conductivity value according to the layer of the head it represented. Six tissue layers were modeled including scalp, skull, cerebrospinal fluid (CSF), gray matter, white matter and the ventricles (i.e. CSF). The electrical conductivity values (Geddes and Baker 1967, Rush and Driscoll 1969) for the scalp, skull, CSF, gray matter, white matter and ventricles were 0.33 S m−1, 0.0042 S m−1, 1.79 S m−1, 0.33 S m−1, 0.14 S m−1 and 1.79 S m−1, respectively. The segmented mask images were combined to create a realistic conductivity head model (e.g. ‘Realistically Shaped Head’) with an isotropic 1 mm spacing.
3.6. Computer implementation of the BEM
Stenroos et al (2007) developed a BEM library of computer algorithms for use in MATLAB (The MathWorks, Inc., Natick, MA, USA). The original source code in this library was designed to solve boundary-value problems (BVPs) for EEG, MEG and electrocardiographic applications. This library offers many users a straightforward way to solve BVPs; however, a solution involving magnetic stimulation was not included.
We developed an image-based approach appropriate for the TMS boundary-value problem using the BEM library's element integral kernel—with linear basis functions. Several computer programs were written in Matlab to perform the necessary calculations of the BEM for TMS E-field modeling. Salinas et al (2007) calculated the primary E-field of the B-shaped coil; the x, y and z components of the primary E-field were saved as individual images. Each surface was modeled—using 1 mm × 1 mm × 1 mm voxels—and then its surface normals were found using 3D gradient image filters; the normals were directed outward from each surface. All images were saved in the Neuroimaging Informatics Technology Initiative (NIfTI) file format using the NIfTI Matlab Toolbox created by Shen (2005). Neumann's boundary conditions—similar to Miranda et al (2003)—were applied to the BVP and the resulting scalar potential distributions were obtained for each surface. The scalar potential images were then combined to show one potential distribution across the volume conductor. The negative gradient of the potential distribution image generated a vectorized secondary E-field image, which could be combined with the primary E-field image to obtain a total E-field image. All calculations were performed using a Power Mac G5 with 1 GB of RAM and a dual 1.8 GHz processor.
4. Results
4.1. Phantom measurements
The dipole and 3D Eddy current probe measurements were highly correlated with modeled data at the points shown in figure 1(B)—0.9992 (P > 0.001) and 0.9985 (P > 0.001), respectively; the BEM models were calibrated using the probe measurements. Figures 1(C) and (D) show the sagittal views of the primary and total E-field magnitudes for the two orientations of the box phantom. Differences can be seen between the primary and total E-field's respective contour lines, particularly at the edges of the box. Table 1 lists the primary and total E-field vector components for points ‘A’, ‘B’ and ‘C’ at the horizontal and vertical phantom orientations. Table 1 also shows that the ‘Horizontal Box’ model's total E-field magnitude is 19.74% lower than that of the primary E-field (at Z = 30 mm). The ‘Vertical Box’ has a small difference (5.68%) between the primary and total E-field magnitudes (at Z = 30 mm). We found that at these locations, the secondary E-field was larger when the boundaries were closer together (‘Horizontal Box’, table 1) which is consistent with the distribution of the scalar potential.
Table 1.
Modeled primary and total E-field vector components for the B-shaped TMS coil in various phantom and head models. Values are modeled for a TMS stimulator setting of 50% and are reported in V m−1. These values were taken at (X = 0 mm, Y = 0 mm, Z = 30 mm) in each model unless otherwise noted.
| Primary |
Total |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Ex (V m−1) | Ey (V m−1) | Ez (Vm−1) | Magnitude (V m−1) | Ex (V m−1) | Ey (V m−1) | Ez (V m−1) | Magnitude (V m−1) | ||
| Horizontal boxa | A | −0.07 | 263.20 | 0 | 263.20 | −0.07 | 252.47 | −0.52 | 252.47 | 4.08 |
| B | −0.28 | 219.34 | 0 | 219.34 | −0.28 | 211.43 | 14.49 | 211.93 | 3.38 | |
| C | 0.17 | 255.99 | 0 | 255.99 | 0.16 | 244.05 | −10.90 | 244.29 | 4.57 | |
| Vertical boxa | A | −0.07 | 263.20 | 0 | 263.20 | −0.09 | 258.88 | 0.86 | 258.89 | 1.64 |
| B | −0.28 | 219.34 | 0 | 219.34 | −0.31 | 216.63 | 1.95 | 216.64 | 1.23 | |
| C | 0.17 | 255.99 | 0 | 255.99 | 0.19 | 251.20 | −0.24 | 251.20 | 1.87 | |
| Horizontal box | −0.05 | 77.01 | 0 | 77.01 | −0.05 | 61.81 | 0.27 | 61.81 | 19.74 | |
| Vertical box | −0.05 | 77.01 | 0 | 77.01 | −0.05 | 72.63 | −0.72 | 72.64 | 5.68 | |
| Sphere | −0.05 | 77.01 | 0 | 77.01 | −0.05 | 71.82 | −0.18 | 71.82 | 6.74 | |
| Hemisphere | −0.05 | 77.01 | 0 | 77.01 | 0.02 | 71.78 | −0.20 | 71.78 | 6.79 | |
| Small hemispherea | −0.07 | 263.20 | 0 | 263.20 | −0.07 | 224.66 | 0.17 | 224.66 | 14.64 | |
| Hemispherea | −0.07 | 263.20 | 0 | 263.20 | 0.13 | 251.53 | 0.10 | 251.53 | 4.43 | |
| One-shell hemisphere | −0.05 | 77.01 | 0 | 77.01 | −0.05 | 71.54 | −0.36 | 71.54 | 7.10 | |
| Four-shell hemisphere | −0.05 | 77.01 | 0 | 77.01 | −0.04 | 56.88 | −1.13 | 56.89 | 26.12 | |
| Realistic head | −0.05 | 77.01 | 0 | 77.01 | −4.23 | 56.58 | 0.42 | 56.74 | 26.32 | |
These values were taken at Z = 3 mm.
4.2. Size dependence
The results for the ‘Sphere’ model using the BEM solution were similar to purely analytical solutions (Eaton 1992); the total E-field magnitudes were 6.74% (using the BEM) and 8.56% (using analytical solutions) lower than the primary E-field magnitude for the ‘Sphere’ model. In addition, similar results were obtained when using either the ‘Sphere’ or ‘Hemisphere’ models (see table 1). Since hemispherical head model computations take much less time, they were used to model the human head; the computational load was reduced by a factor of 4.
We also modeled a small animal's head (‘Small Hemisphere’). We estimated that a typical small animal's cortical region is one-tenth as deep as that of a human's. Thus, any charge accumulation at the surface would be in close proximity to all other locations in the model; therefore, large secondary effects in small animal head models were not surprising. Table 1 shows that the ‘Small Hemisphere’ model's total E-field magnitude is 14.64% lower than their primary E-field's magnitude at that location (0 mm, 0 mm, 3 mm); the ‘Hemisphere’ model's total E-field magnitude is only 4.43% lower at Z = 3 mm. The ‘Small Hemisphere’ model's total E-field at Z = 10 mm—the center of the model—still has a large secondary effect: 10.77%. The ‘Hemisphere’ model's secondary E-field at Z = 10 mm is only 5.27% of the primary E-field.
4.3. Hemisphere models
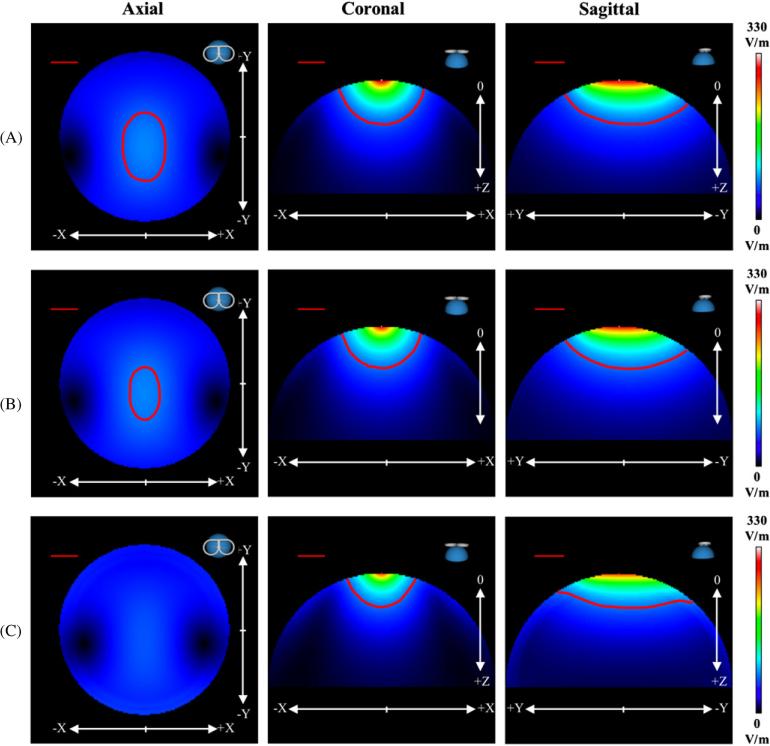
Figure 2 shows the 3D magnitude images of the primary E-fields for the hemisphere models. All contour lines represent magnitudes that are 20% of the maximum E-field strength; however, the (3D) shape of each contour line changes as more layers are included. In the coronal plane, the depth of the ‘Four-Shell Hemisphere’ model (red ROI) decreased indicating that multiple conductivity layers have a damping effect on the total E-field. At 0 mm, 0 mm and 30 mm, the ‘One-Shell Hemisphere’ model has a magnitude difference of 7.10%, whereas the ‘Four-Shell Hemisphere’ model has a large on-axis difference of 26.12% (table 1). These differences in E-field magnitudes indicate that the secondary E-field is relatively stronger in areas very close to the surface of each tissue layer—especially at the layers of scalp, skull and CSF.
Figure 2.
Modeled 3D magnitude images of the (A) primary E-field, (B) ‘One-Shell Hemisphere’ total E-field and (C) ‘Four-Shell Hemisphere’ total E-field for a TMS stimulator intensity of 50%. The axial (xy-plane; Z = 30 mm), coronal (xz-plane; Y = 0 mm) and sagittal (yz-plane; X = 0 mm) views are presented. The red ROIs in each image represent magnitudes greater than 20% for each respective model. The ‘Four-Shell Hemisphere’ total E-field ROI is not present in the axial slice. The straight, red line in the upper left corner represents a distance of 2 cm.
4.4. Realistically shaped head model
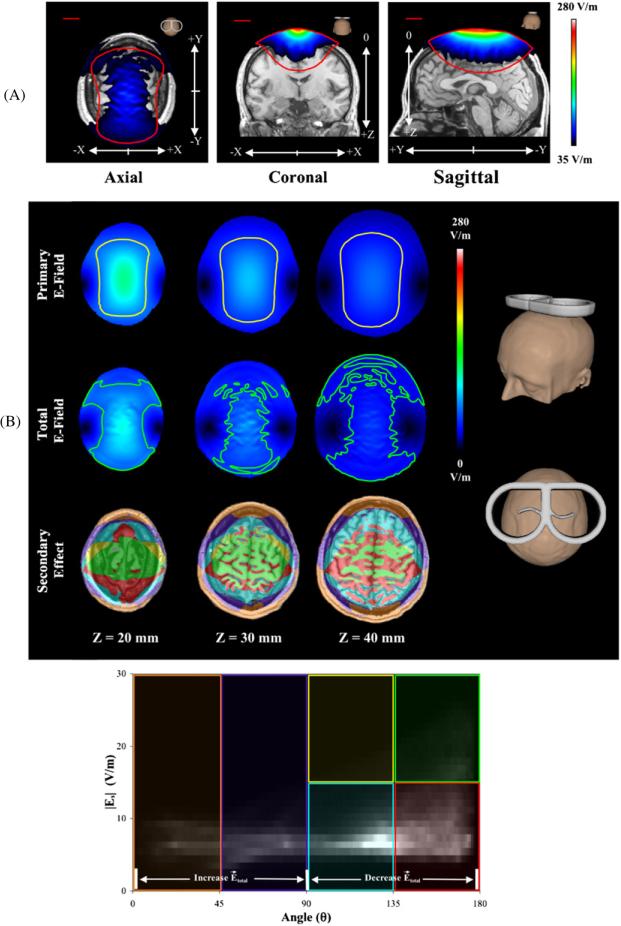
To better illustrate the total E-fields, they were overlaid onto an MR image of the subject (figure 3(A)) with values modeled for 50% TMS stimulator intensity setting . The total E-field has contributions from both inner and outer tissue surfaces; in addition, at the center of the total E-field's axial image, we can see the outline of the sulci and gyri in the modeled data, indicating that at depth Z = 30 mm, the secondary E-field is large enough to significantly change the total E-field. The red outlines represent the primary E-field at a threshold of 35 V m−1. The on-axis (i.e. center of the image) magnitude—at this TMS coil position/orientation—of the total E-field is much lower than that of the primary E-field at the same location, indicating that the secondary E-field has a quenching effect on the penetration depth of the TMS coil; the coronal view also demonstrates this effect. Therefore, the TMS stimulator setting would have to be adjusted to increase the total E-field's penetration depth; for this head model and TMS coil position/orientation, a TMS stimulator setting of 65% would be needed for the total E-field to have the same penetration depth (i.e. magnitude) as the primary E-field at a 50% TMS stimulator setting.
Figure 3.
(A) Modeled 3D intensity images of the total E-field for the ‘Realistically Shaped Head’ model at a TMS stimulator intensity of 50%. (A, left) Axial views are at z = 30 mm; (A, middle) coronal views are at y = 0 mm; (A, right) sagittal views are at x = 0 mm. Each model is overlaid onto an MR image of the subject's head. The red lines in each image represent the primary E-field at the same threshold. (B) E-field comparisons of the ‘Realistically Shaped Head’ model. (B, top) Axial views of the primary and total E-fields at three cortical depths. The yellow (primary) and green (total) ROIs represent values at 50% of each slice's maximum value. (B, bottom) 2D histogram plot of the secondary E-field magnitude versus the angle between the secondary and primary E-field vectors. The six color-coded sections in the 2D histogram designate specific secondary E-field magnitude/angle relationships shown in the ‘Secondary Effect’ images. For example, the green box represents sections of the image where the secondary E-field magnitude is large—greater than 15 V m−1—and its direction is in opposition (near 180°) to the primary E-field vector; whereas the light blue box has a low secondary E-field magnitude—less than 15 V m−1—and its direction slightly opposes (between 90° and 135°) that of the primary E-field vector.
Figure 3(B) compares the primary, secondary and total E-fields of the ‘Realistically Shaped Head’ model at three cortical depths. The primary and total E-field axial slices have outlines depicting the distribution of each E-field at half of that slice's maximum E-field strength. At each depth, the total E-field was more focal than the primary E-field (in the x-direction). However, at this TMS coil position/orientation, the total E-field had a larger distribution in the y-direction with increasing depth—since more tissue interfaces contribute to the secondary E-field at these cortical locations.
At on-axis locations (i.e. center of the ‘Secondary Effect’ images in figure 3(B))—where the primary E-field is the strongest—we see that the vast majority of the secondary E-fields are in opposition to the primary E-field (figure 3(B), bottom). Thus, the total E-field is always lower than the primary E-field at on-axis locations (for this TMS coil position/orientation). On-axis, the relative magnitudes of the secondary E-field are between 20% and 30% of the primary E-field magnitudes. At cortical locations, local surface charge accumulation can change drastically from one voxel to the other; the amount of surface charge accumulation depends on the surface normals of each tissue layer. However, at cortical sites—where the tissue layers are highly convoluted—the changes appear to be muted by neighboring tissue layers.
At the TMS coil's periphery, the secondary E-field is additive (orange and purple boxes; figure 3(B), bottom) at sites close to the TMS coil, but in opposition (light blue box) at depth for these same lateral locations; the relative magnitudes of the secondary E-fields (at the TMS coil periphery) are between 8% and 62% of the primary E-field magnitudes. At depth, the neighboring cortical tissues have a larger effect on the secondary E-field than the air–scalp interface (at these lateral locations). Thus, at lateral locations (near the TMS coil), the total E-field is slightly higher than the primary E-field; whereas deeper lateral locations have lower total E-fields than primary E-fields (for this TMS coil position/orientation). Observations at on-axis and peripheral sites indicate that the influence of surface charge accumulation on the secondary E-field is highly localized at sites near each tissue interface. Therefore, it is very important for the head model to include each tissue layer so that accurate estimates of the total induced E-field may be made throughout the volume.
5. Discussion
Our results show that the geometry and orientation of the TMS coil play an important role when calculating the total E-field induced by magnetic stimulation in several models with varying conductivity. Because the total E-field includes the secondary component—the second term in (3)—the gradient of the scalar potential may (theoretically) produce an Ez component. Many studies have concluded that there will not be a total E-field in the Z direction (Branston and Tofts 1991; Cohen and Cuffin 1991, Roth et al 1991a, 1991b, Heller and van Hulsteyn 1992). However, each of these studies used spherically symmetric head models. The Ez components (table 1) found using the ‘Realistically Shaped Head’ model were very small when compared to the other components but it may be larger in other (clinically relevant) coil orientations.
5.1. Orientation
Previous studies (Grandori and Ravazzani 1991, Roth et al 1991b, Eaton 1992) have found that the orientation of the TMS coil plays an important role in the calculation of the primary E-field at a particular point in space. Since the primary E-field is calculated using the TMS coil's wire geometry, it makes sense that changing (even slightly) the orientation of the TMS coil will alter the primary E-field. A 90° rotation of the TMS coil (in our box experiment) produced different surface interactions—since the sides of the box were separated by a different distance—thereby producing a different total E-field. Also, the secondary E-fields cancel the primary E-field at sites where the surface normal aligns with the primary E-field vector—along the periphery of the volume conductor. Therefore, reorienting the TMS coil (i.e. laterally) or changing the shape of the volume conductor (i.e. asymmetric models) will change these values. Because these orientations may potentially affect the total E-field calculation, it is important to note that any changes in the total E-field may not be consistent across the volume conductor. Therefore, it is important to accurately model the whole volume conductor (i.e. as an image) so that these changes may be visualized and addressed.
5.2. Simple head models
The secondary E-field is largest when in close proximity to tissue surfaces. However, it is important to remember that the ‘Four-Shell Hemisphere’ model is not a true representation of the human head. Realistically shaped head tissues have folds and dimples in their surfaces. Thus, realistically shaped head geometries yield more accurate estimates of the secondary E-field (e.g. the total E-field).
5.3. Realistically shaped head model
Spherical (and even hemispherical) head models are not anatomically correct approximations. The human brain has many gyri and sulci; thus, at cortical depths there may be tissue surfaces at (or at least near) the site of stimulation. Since the secondary E-field is greatest near a surface, we must correctly model the geometry of each tissue surface to obtain the most accurate estimates of the total E-field throughout the brain. Several recent studies (Starzynski et al 2002, Wagner et al 2004, Wagner et al 2006) incorporated realistically shaped head models—using magnetic resonance images—to estimate the total E-fields induced by TMS. However, the level of anatomical detail involved in these simulations was not sufficient for a detailed assessment of the secondary E-field. The ‘Realistically Shaped Head’ model is a tissue-segmented MR image (with 1 mm voxel spacing), with realistic anatomical features (such as gyri and sulci). Using such a model enabled more accurate estimation of the total E-field throughout the brain—but especially at the cortical locations where neural activations are believed to be occurring during TMS. Our findings indicate that the magnitude and direction of the secondary E-field vary widely throughout the brain. In some locations, it directly opposes the primary E-field whereas in others it has an additive effect (see figure 3(B)). These conclusions were also observed by Toschi et al (2008). We cannot hypothesize the magnitude or direction of the secondary E-field at a particular location without an accurate description of the head's local tissue geometry and conductivity values.
5.4. Impact on human TMS studies
Accurate total E-field estimates are especially needed when using TMS for clinical applications. For example, repetitive TMS (rTMS) has generated much interest as a treatment for psychiatric disorders such as depression, schizophrenia and anxiety (Grisaru et al 1994, Pascual-Leone et al 1996, George et al 1997, 2003). Greater accuracy in the total E-field estimates will provide better per-pulse dose approximations (especially at depth) for these clinical studies. Accurate, quantitative dosage estimates are needed to monitor patient progress and/or treatment effectiveness over time. Accurate dosage information would also be useful when comparing treatments across patient groups (i.e. normal and impaired patients), instead of using TMS stimulator output settings, where stimulator/coil parameters may be different, or resting motor threshold values—which vary from person to person.
5.5. Impact on small animal TMS studies
The ‘Small Hemisphere’ model is not an accurate representation of a small animal's head; however, it does provide a rough estimate regarding the effect of the secondary E-field on the total E-field calculations. Because of its small radius, each point on the surface is within close proximity to every other point in the volume—thereby having the capacity to influence each point's scalar potential (14.64% difference). In larger volumes, surface points have less effect at the same depth (4.43% difference) because they are separated by larger distances. In addition, as the volumes change size, their exposure to the TMS coil's primary E-field also changes (since the coil is asymmetric).
Small animal TMS coils have been developed by some TMS manufacturers (Magstim; Woburn, MA, USA) and they provide more focal primary E-fields for small animal TMS (Salinas et al 2007); yet there have not been any studies on how small animal TMS—using the proper TMS coils—will affect the secondary E-field. Since the E-field should be more focal in a small animal TMS coil, less of the peripheral surface locations will be exposed to the primary E-field—at least the magnitude at those locations should be much lower. Whether or not the secondary E-field is lower depends on the location of the small animal TMS coil, its orientation and the size/shape of the small animal head model. Using the 3D modeling technique described in this paper should prove to be useful for TMS studies in small animals.
6. Conclusion
Using the image-based BEM described in this paper, we now have the ability to accurately model the total E-field induced by TMS throughout a volume conductor. We have shown that size and geometric complexity of the volume conductor are very important when calculating the total E-field. More explicit (i.e. realistic) volume conductor geometries provide more accurate total E-field estimates than simple head models. The inclusion of the secondary E-field is important in total E-field calculations and should not be overlooked.
Acknowledgments
This work was supported by NIH grant T32MH065728-03 and the Research Imaging Center, UTHSCSA. We would like to thank John Roby and Wei Zhang for their assistance in probe fabrication and data acquisition.
References
- Barker AT, Jalinous R, Freeston IL. Non-invasive magnetic stimulation of the human motor cortex. Lancet. 1985;1:1106–7. doi: 10.1016/s0140-6736(85)92413-4. [DOI] [PubMed] [Google Scholar]
- Branston NM, Tofts PS. Analysis of the distribution of currents induced by a changing magnetic field in a volume conductor. Phys. Med. Biol. 1991;36:161–8. [Google Scholar]
- Cohen D, Cuffin BN. Developing a more focal magnetic stimulator. Part I: some basic principles. J. Clin. Neurophysiol. 1991;8:102–11. doi: 10.1097/00004691-199101000-00013. [DOI] [PubMed] [Google Scholar]
- Cohen LG, Roth BJ, Nilsson J, Dang N, Panizza M, Bandinelli S, Friauf W, Hallett M. Effects of coil design on delivery of focal magnetic stimulation: technical considerations. Electroencephalogr. Clin. Neurophysiol. 1990;75:350–7. doi: 10.1016/0013-4694(90)90113-x. [DOI] [PubMed] [Google Scholar]
- Cuffin BN, Cohen D. Comparison of the magnetoencephalogram and electroencephalogram. Electroencephalogr. Clin. Neurophysiol. 1979;47:132–46. doi: 10.1016/0013-4694(79)90215-3. [DOI] [PubMed] [Google Scholar]
- Davey KR, Cheng CH, Epstein CM. Prediction of magnetically induced electric fields in biological tissue. IEEE Trans. Biomed. Eng. 1991;38:418–22. doi: 10.1109/10.81560. [DOI] [PubMed] [Google Scholar]
- De Lucia M, Parker GJM, Embleton K, Newton JM, Walsh V. Diffusion tensor MRI-based estimation of the influence of brain tissue anisotropy on the effects of transcranial magnetic stimulation. NeuroImage. 2007;36:1159–70. doi: 10.1016/j.neuroimage.2007.03.062. [DOI] [PubMed] [Google Scholar]
- Durand D, Ferguson AS, Dalbasti T. Effect of surface boundary on neuronal magnetic stimulation. IEEE Trans. Biomed. Eng. 1992;39:58–64. doi: 10.1109/10.108128. [DOI] [PubMed] [Google Scholar]
- Eaton H. Electric field induced in a spherical volume conductor from arbitrary coils: application to magnetic stimulation and MEG. Med. Biol. Eng. Comput. 1992;30:433–40. doi: 10.1007/BF02446182. [DOI] [PubMed] [Google Scholar]
- Ferguson AS, Stroink G. Factors affecting the accuracy of the boundary element method in the forward problem—I. calculating surface potentials. IEEE Trans. Biomed. Eng. 1997;44:1139–55. doi: 10.1109/10.641342. [DOI] [PubMed] [Google Scholar]
- Geddes LA, Baker LE. The specific resistance of biological material—a compendium of data for the biomedical engineer and physiologist. Med. Biol. Eng. 1967;5:271–93. doi: 10.1007/BF02474537. [DOI] [PubMed] [Google Scholar]
- George MS, Nahas Z, Kozel FA, Li X, Yamanaka K, Mishory A, Bohning D. Mechanisms and the current state of transcranial magnetic stimulation. CNS Spectrums. 2003;8:496–514. doi: 10.1017/s1092852900018976. [DOI] [PubMed] [Google Scholar]
- George MS, Wassermann EM, Kimbrell TA, Little JT, Williams WE, Danielson AL, Greenberg BD, Hallett M, Post RM. Mood improvement following daily left prefrontal repetitive transcranial magnetic stimulation in patients with depression: a placebo-controlled crossover trial. Am. J. Psychol. 1997;154:1752–6. doi: 10.1176/ajp.154.12.1752. [DOI] [PubMed] [Google Scholar]
- Geselowitz DB. On biolelectric potentials in an inhomogeneous volume conductor. Biophys. J. 1967;7:1–11. doi: 10.1016/S0006-3495(67)86571-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover PM, Bowtell R. Measurement of electric fields due to time-varying magnetic field gradients using dipole probes. Phys. Med. Biol. 2007;52:5119–30. doi: 10.1088/0031-9155/52/17/001. [DOI] [PubMed] [Google Scholar]
- Grandori F, Ravazzani P. Magnetic stimulation of the motor cortex—theoretical considerations. IEEE Trans. Biomed. Eng. 1991;38:180–91. doi: 10.1109/10.76385. [DOI] [PubMed] [Google Scholar]
- Grisaru N, Yarovslavsky U, Abarbanel J, Lamberg T, Belmaker RH. Transcranial magnetic stimulation in depression and schizophrenia. Eur. Neuropsychopharmacol. 1994;4:287–8. [Google Scholar]
- Heller L, van Hulsteyn DB. Brain stimulation using electromagnetic sources: theoretical aspects. Biophys. J. 1992;63:129–38. doi: 10.1016/S0006-3495(92)81587-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilmoniemi RJ, Ruohonen J, Karhu J. Transcranial magnetic stimulation—a new tool for functional imaging of the brain. Crit. Rev. Biomed. Eng. 1999;27:241–84. [PubMed] [Google Scholar]
- Jackson JD. Classical Electrodynamics. 3rd edn Wiley; Hoboken, NJ: 1999. [Google Scholar]
- Johnson C. In: Computational methods and software for biolelectric field problems The Biomedical Engineering Handbook: Biomedical Engineeing Fundamentals. 3rd edn. Bronzino JD, editor. Vol. 1. CRC Press; Hoboken, NJ: 2006. chapter 23. [Google Scholar]
- Kim DH, Georghiou GE, Won C. Improved field localization in transcranial magnetic stimulation of the brain with the utilization of a conductive shield plate in the stimulator. IEEE Trans. Biomed. Eng. 2006;53:720–5. doi: 10.1109/TBME.2006.870244. [DOI] [PubMed] [Google Scholar]
- Kobayashi M, Ueno S, Kurokawa T. Importance of soft tissue inhomogeneity in magnetic peripheral nerve stimulation. Electroencephalogr. Clin. Neurophysiol. 1997;105:406–13. doi: 10.1016/s0924-980x(97)00035-0. [DOI] [PubMed] [Google Scholar]
- Lancaster JL, Martinez M. Mango: Multi-Image Analysis GUI. 2008 http://ric.uthscsa.edu/mango/
- Liu R, Ueno S. Calculating the activating function of nerve excitation in inhomogeneous volume conductor during magnetic stimulation using the finite element method. IEEE Trans. Magn. 2000;36:1796–9. [Google Scholar]
- Miranda PC, Hallett M, Basser PJ. The electric field induced in the brain by magnetic stimulation: a 3D finite-element analysis of the effect of tissue heterogeneity and anisotropy. IEEE Trans. Biomed. Eng. 2003;50:1074–85. doi: 10.1109/TBME.2003.816079. [DOI] [PubMed] [Google Scholar]
- Pascual-Leone A, Rubio B, Pallardo F, Catala MD. Rapid-rate transcranial magnetic stimulation of left dorsolateral prefrontal cortex in drug-resistant depression. Lancet. 1996;347:233–7. doi: 10.1016/s0140-6736(96)01219-6. [DOI] [PubMed] [Google Scholar]
- Roth BJ, Cohen LG, Hallett M. The electric field induced during magnetic stimulation. Electroencephalogr. Clin. Neurophysiol. 1991a;43(Suppl.):268–78. [PubMed] [Google Scholar]
- Roth BJ, Saypol JM, Hallett M, Cohen LG. A theoretical calculation of the electric field induced in the cortex during magnetic stimulation. Electroencephalogr. Clin. Neurophysiol. 1991b;81:47–56. doi: 10.1016/0168-5597(91)90103-5. [DOI] [PubMed] [Google Scholar]
- Rush S, Driscoll D. EEG electrode sensitivity—an application of reciprocity. IEEE Trans. Biomed. Eng. 1969;16:15–22. doi: 10.1109/tbme.1969.4502598. [DOI] [PubMed] [Google Scholar]
- Salinas FS, Lancaster JL, Fox PT. Detailed 3D models of the induced electric field of transcranial magnetic stimulation coils. Phys. Med. Biol. 2007;52:2879–92. doi: 10.1088/0031-9155/52/10/016. [DOI] [PubMed] [Google Scholar]
- Sarvas J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys. Med. Biol. 1987;32:11–22. doi: 10.1088/0031-9155/32/1/004. [DOI] [PubMed] [Google Scholar]
- Shen J. Tools for NIfTI (ANALYZE) MR image MATLAB Central File Exchange. 2005 http://www.mathworks.com/matlabcentral/fileexchange/loadFile.do?objectId=8797&objectType=file.
- Smith SM, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage. 2004;23:S1 208–19. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- Starzynski J, Sawicki B, Wincenciak S, Krawczyk A, Zyss T. Simulation of magnetic stimulation of the brain. IEEE Trans. Mag. 2002;38:1237–40. [Google Scholar]
- Stenroos M, Mantynen V, Nenonen J. A Matlab library for solving quasi-static volume conduction problems using the boundary element method. Comp. Methods Prog. Biomed. 2007;88:256–63. doi: 10.1016/j.cmpb.2007.09.004. [DOI] [PubMed] [Google Scholar]
- Tay G, Chilbert M, Battocletti J, Sances A, Swiontek T, Kurakami C. Measurement of magnetically induced current density in saline and in vivo. IEEE Eng. Med. Biol. Soc. 1989:1167–8. [Google Scholar]
- Tofts PS. The distribution of induced currents in magnetic stimulation of the nervous system. Phys. Med. Biol. 1990;35:1119–28. doi: 10.1088/0031-9155/35/8/008. [DOI] [PubMed] [Google Scholar]
- Tofts PS, Branston NM. The measurement of electric field, and the influence of surface charge, in magnetic stimulation. Electroencephalogr. Clin. Neurophysiol. 1991;81:238–9. doi: 10.1016/0168-5597(91)90077-b. [DOI] [PubMed] [Google Scholar]
- Toschi N, Welt T, Guerrisi M, Keck ME. A reconstruction of the conductive phenomena elicited by transcranial magnetic stimulation in heterogeneous brain tissue. Phys. Med. 2008;24:80–6. doi: 10.1016/j.ejmp.2008.01.005. [DOI] [PubMed] [Google Scholar]
- Toschi N, Welt T, Guerrisi M, Keck ME. Transcranial magnetic stimulation in heterogeneous brain tissue: clinical impact on focality, reproducibility and true sham stimulation. J. Psychiatr. Res. 2009;43:255–64. doi: 10.1016/j.jpsychires.2008.04.008. [DOI] [PubMed] [Google Scholar]
- Wagner T, Fregni F, Eden U, Ramos-Estebanez C, Grodzinsky A, Zahn M, Pascual-Leone A. Transcranial magnetic stimulation and stroke: a computer-based human model study. NeuroImage. 2006;30:857–70. doi: 10.1016/j.neuroimage.2005.04.046. [DOI] [PubMed] [Google Scholar]
- Wagner TA, Zahn M, Grodzinsky AJ, Pascual-Leone A. Three-dimensional head model simulation of transcranial magnetic stimulation. IEEE Trans. Biomed. Eng. 2004;51:1586–98. doi: 10.1109/TBME.2004.827925. [DOI] [PubMed] [Google Scholar]
- Wang W, Eisenberg SR. A three-dimensional finite element method for computing magnetically induced currents in tissues. IEEE Trans. Mag. 1994;30:5015–23. [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]