Hydrogen isotope fractionation in methane plasma

Significance

Large variations in light element isotope ratios (H, N, C) are routinely observed in meteorite organic matter. The origin of these so-called anomalies is not accounted for by the classical theory of isotope fractionation. In the case of H, micrometer-size areas within the insoluble organic matter (IOM) isolated from meteorites by acid treatment, exhibit extreme deuterium enrichment. They are generally interpreted as components exogenous to the solar system and attributed to surviving interstellar grains. In the present paper, these H isotope anomalies were reproduced in the IOM synthesized through laboratory reactions involving CH_x^• radicals formed in CH₄ plasma. Therefore, these anomalies may result from the chemistry occurring in the disk surrounding the Sun during its formation.

Abstract

The hydrogen isotope ratio (D/H) is commonly used to reconstruct the chemical processes at the origin of water and organic compounds in the early solar system. On the one hand, the large enrichments in deuterium of the insoluble organic matter (IOM) isolated from the carbonaceous meteorites are interpreted as a heritage of the interstellar medium or resulting from ion−molecule reactions taking place in the diffuse part of the protosolar nebula. On the other hand, the molecular structure of this IOM suggests that organic radicals have played a central role in a gas-phase organosynthesis. So as to reproduce this type of chemistry between organic radicals, experiments based on a microwave plasma of CH₄ have been performed. They yielded a black organic residue in which ion microprobe analyses revealed hydrogen isotopic anomalies at a submicrometric spatial resolution. They likely reflect differences in the D/H ratios between the various CH_x radicals whose polymerization is at the origin of the IOM. These isotopic heterogeneities, usually referred to as hot and cold spots, are commensurable with those observed in meteorite IOM. As a consequence, the appearance of organic radicals in the ionized regions of the disk surrounding the Sun during its formation may have triggered the formation of organic compounds.

Carbonaceous meteorites are regarded as the most pristine state of the volatile-rich building blocks of solar system planets. The abiotic insoluble organic matter (IOM) isolated from these meteorites hosts most of the volatile elements (H, C, N) that constitute the Earth hydrosphere and biosphere (1). Planetary hydrogen, in organic molecules or in water, exhibits systematic deuterium (D) enrichment relative to the protosolar H₂ (2). For example, the IOM displays D enrichments relative to the protosolar H₂ [noted (D/H)_H2] with (D/H)_IOM ≈ 15–30 × (D/H)_H2 and (D/H)_H2 = 20 ± 5 × 10⁻⁶ (3–6).

The IOM is also systematically enriched in D relative to the water [(D/H)_IOM ≈ 2 × (D/H)_Water] that was circulating on meteorite parent body during hydrothermal events (7, 8). Because all types of isotopic exchange between water and organic bonds, under equilibrium or not, should result in the opposite distribution [i.e., (D/H)_Organic < (D/H)_Water], this observation can be regarded as a signature acquired before the accretion of the meteorite parent body.

In the IOM, submicrometric domains were detected by nanoscale secondary ion mass spectrometry (NanoSIMS) (9, 10). They exhibit enrichments or depletions in D (referred to as hot or cold spots, respectively) compared with the bulk D/H ratio of the IOM. The D/H variations (up to a factor of 3) exceed, by far, any known isotope fractionation mechanism that could have taken place between organic bonds. They are thus interpreted as remnants of interstellar grains (9–12), mechanically mixed with the IOM. In summary, the D/H ratio of the IOM raises two questions: (i) What is the origin of the bulk enrichment in D, and (ii) what is the origin of the isotopic heterogeneities at the micrometer scale? Answering these questions should provide information about the physicochemical conditions of the organosynthesis in the early solar system. Because there is no scientific consensus about these questions, we explore another origin for these isotopic enrichments, associated with organic radical reactions.

A major role of organic radicals in the formation of the IOM is supported by the reconstruction of its molecular structure (13). The proposed pathway involves successive additions of CH_x^• radicals (x = 0–3; the dot designates a radical) leading to short chains followed by their aromatization. Moreover, UV photodissociation is known to induce bond homolytic cleavage, leading to organic radicals. The T-Tauri Sun being an intense UV source, such a strong generation of organic radicals could have taken place at the surface of the protosolar nebula. If this mechanism would account for the isotopic enrichments and heterogeneities observed in the IOM, it would imply a profound change in the broad perspective about the origin for the solar system. Indeed, an interstellar D-rich source would be no longer a prerequisite. We therefore tested this hypothesis in an experiment in which organic radicals, produced by the dissociation of CH₄, govern the condensation reactions. Experimental devices based on microwave-induced plasma of CH₄ were shown to produce radicals in the gas phase, which yield macromolecular organic matter through condensation reactions (14). At this stage, it is important to note that the experimental device (plasma vapor deposition) is not supposed to reproduce the physical conditions or the chemical compositions of the protosolar nebula but to produce, in a gas phase, a high density of organic radicals. In this respect, CH₄ should be considered only as a source of radicals rather than actually present in the protosolar nebula.

Results

In the present experiment, the formation of the CH₄ plasma led to the deposition of a black residue onto the glass walls of the reactor (Materials and Methods). This residue was mechanically scraped from the glass walls and submitted to organic solvent extraction to remove the soluble organic molecules. The insoluble leftover fraction (referred to as IOM) was prepared for NanoSIMS analyses.

The D/H ratio and the ionic intensities of the molecular ions C⁻, CH⁻, CH₂⁻, and CH₃⁻, emitted from the IOM surface sample were recorded with the mass spectrometer of the NanoSIMS in 20 × 20 μm² images divided in nine regions of interest (ROI ≈ 45 μm²). The average isotopic composition of all analyses (552 ROI) was calculated as δD(‰)_{Measured-SMOW} = −473‰ ± 70, i.e., D/H = 82 × 10⁻⁶. Although most areas of the IOM are isotopically homogeneous (Fig. 1 A and B), 134 and 224 areas were shown to exhibit D enrichment and depletion, respectively, termed hot and cold spots (Fig. 1C). The isotopic ratios of the ROI are hereafter expressed in δD(‰)_IOM relative to the average D/H ratio, with δD(‰)_IOM = {[(D/H)/82 × 10⁻⁶] − 1}0.1000. The ROI show δD_IOM values ranging from −590‰ up to +965‰ (Table S1), markedly out of the range (0 ± 110‰) defined by the average δD value.

Fig. 1.

NanoSIMS ion images of the D/H ratio. The 20 × 20 μm² images are expressed in δD units relative to the D/H ratio of the bulk sample (for comparison purposes, color scale bars for δD all range between −1,000 and +4,000‰). (A and B) Data collected from the same image of IOM produced from a CH₄ plasma, illustrating the routine quality of imaging the D/H ratio. (A) H intensity is expressed in counts per second. The H variations reflect the H ionic emissivity related to the topography of the sample surface. (B) The statistical δD distribution is shown for an isotopically homogeneous area. The statistical error on the average δD value for this image was ±30‰ (1 SD). At the pixel level of the image, the variations in δD are unrelated with H intensity, ruling out any possible topographic effect on the determination of δD values. (C) Contrary to the homogeneous δD distribution commonly observed in terrestrial samples and standards, the IOM collected from CH₄ plasma exhibits δD heterogeneities in some rare areas rich in hot spots. (D) Example of the IOM isolated from the Murchison meteorite exhibiting hot spots [bulk IOM δD_SMOW = +970‰ (5); NanoSIMS data are from ref. 19].

Table S1.

The δD_IOM(‰) measured in 45-μm² ROI are ranked in 100‰ step variations

δD range	−600 to −500‰ (N = 29)	−500 to −400‰ (N = 22)	−400 to −300‰ (N = 58)	−300 to −200‰ (N = 33)	−200 to −100‰ (N = 82)	−100 to 100‰ (N = 194)	100 to 200‰ (N = 61)	200 to 300‰ (N = 14)	300 to 400‰ (N = 12)	400 to 500‰ (N = 15)	500 to 600‰ (N = 13)	600 to 700‰ (N = 4)	700 to 800‰ (N = 3)	800 to 900‰ (N = 6)	900 to 1000‰ (N = 6)
δD values	−590.2	−499.4	−394.2	−295.1	−199.7	0 ± 110	100.4	200.0	308.2	401.5	506.3	606.6	722.2	808.5	900.4
	−581.8	−496.3	−393.2	−293.8	−197.3		101.9	201.9	341.9	401.5	512.4	635.4	781.6	839.2	923.5
	−572.1	−495.9	−392.8	−289.0	−194.3		103.4	205.8	357.8	413.2	519.5	653.3	786.6	840.5	924.0
	−569.5	−495.0	−392.3	−286.6	−190.7		103.9	206.2	358.9	416.7	525.5	670.3		846.3	925.1
	−569.4	−494.4	−388.1	−284.4	−189.9		105.8	220.3	361.5	421.7	531.3			868.2	931.9
	−565.3	−487.6	−384.2	−277.4	−188.4		106.0	229.3	362.9	424.2	535.0			889.7	965.2
	−563.5	−486.9	−384.0	−268.4	−187.2		106.4	235.8	366.4	427.8	547.9
	−561.2	−483.2	−383.2	−268.1	−186.9		110.7	240.4	374.6	438.9	554.8
	−559.8	−480.7	−381.0	−265.4	−186.3		114.3	242.3	374.6	472.3	563.3
	−555.7	−480.5	−380.6	−265.3	−185.1		116.5	248.4	385.5	472.8	564.5
	−555.1	−480.1	−378.3	−265.0	−184.9		118.5	250.1	390.4	474.0	598.8
	−552.9	−467.0	−373.5	−264.5	−178.9		119.4	254.7	398.3	483.2
	−544.8	−466.3	−372.9	−262.4	−178.8		120.3	257.5		485.8
	−541.9	−465.6	−371.7	−251.7	−178.5		121.3	260.3		488.1
	−539.3	−456.5	−369.3	−250.8	−176.6		121.8			490.7
	−537.7	−434.6	−365.6	−247.6	−174.9		122.1
	−536.8	−417.7	−365.0	−244.6	−171.1		123.0
	−533.2	−415.0	−364.8	−238.0	−170.9		125.9
	−530.2	−406.9	−364.7	−237.0	−170.8		128.5
	−528.9	−403.6	−363.8	−233.4	−170.6		129.0
	−528.9	−401.8	−362.6	−232.2	−170.6		129.1
	−527.9	−400.0	−362.4	−228.2	−169.9		130.2
	−527.8		−362.1	−228.1	−169.9		135.8
	−526.4		−361.1	−225.7	−168.3		136.1
	−524.3		−358.8	−224.6	−165.7		136.6
	−516.4		−358.8	−222.6	−165.7		137.0
	−513.6		−358.7	−220.6	−164.7		138.9
	−512.4		−358.1	−218.7	−164.3		142.2
	−507.9		−353.7	−217.9	−162.6		144.2
			−352.5	−212.8	−162.2		144.5
			−351.4	−209.6	−160.5		144.9
			−350.6	−206.1	−160.1		145.5
			−350.3	−203.9	−157.6		146.4
			−346.0		−157.2		147.1
			−346.0		−157.1		147.2
			−344.3		−156.7		148.9
			−344.1		−155.1		151.0
			−344.0		−151.8		151.8
			−343.7		−150.0		151.9
			−339.3		−149.8		152.2
			−335.1		−149.7		153.2
			−334.0		−149.6		153.4
			−331.0		−148.8		155.3
			−330.5		−147.2		158.6
			−327.3		−143.7		160.1
			−324.8		−139.1		160.6
			−323.8		−137.9		165.0
			−323.7		−136.8		165.6
			−319.8		−135.5		166.2
			−318.6		−133.6		166.9
			−318.6		−133.1		170.4
			−316.8		−132.6		174.3
			−315.5		−132.3		175.4
			−315.5		−129.1		176.0
			−315.2		−128.9		183.4
			−313.4		−128.3		186.7
			−309.9		−127.7		187.3
			−306.8		−127.0		187.4
					−126.9		198.8
					−126.6		198.9
					−124.5		199.4
					−123.8
					−122.9
					−122.4
					−122.4
					−120.5
					−120.0
					−119.7
					−117.3
					−116.9
					−116.1
					−114.1
					−113.1
					−112.8
					−112.6
					−111.1
					−108.8
					−104.9
					−103.8
					−102.3
					−101.7
					−100.7

The numbers of ROI are used to construct Fig. 2.

The distribution of the ROI δD_IOM values listed in Table S1 is shown as a histogram (Fig. 2). In this histogram, the aforementioned 134 and 224 areas show, respectively, positive and negative departures in δD values. Because our analyses were focused on these isotopically anomalous zones, their relative contribution to the bulk sample cannot be precisely calculated from the present data but should not exceed 1%.

Fig. 2.

The histogram of D/H ratio is compared with variations in ¹²CH₃⁻/¹²C⁻ ionic ratios. Steps of 100‰ rank the δD values. (A) Histogram of the isotopic compositions of CH₄ plasma deposited IOM. The shaded central area represents ≥99% of the sample surface with a domain a variation defined by 2 sigma error (±110‰) around the mean D/H ratio (R₀) defining δD_IOM = 0‰ {δD_IOM (‰) = [(R/R₀) − 1] × 1,000 with R = D/H}. The curve of the density distribution highlights the five modes of the isotopic pattern. (B) The ¹²CH₃⁻/¹²C⁻ ratios are reported versus δD values. The bulk atomic H/C sample value determined by elemental analyses is 1.34. Error bars on ¹²CH₃⁻/¹²C⁻ stand for the statistical error, and the 100‰ bars on δD values stand for the width of the step (the +250‰ data point is not reported because of its large errors on the ¹²CH₃⁻/¹²C⁻ ratio).

The δD_IOM distribution function (100‰ steps) shows five occurrences (five peaks) of high (+180‰, +520‰, and +980‰) and low (−280‰ and −480‰) δD_IOM values (Fig. 2A). Because the data were, on purpose, recorded randomly, these five peaks in the distribution must correspond to five different isotopic compositions of the IOM. The weighted average for all of the positive and negative δD_IOM values lying outside 0 ± 110‰ is equal to −52‰, showing that the isotope mass balance is achieved between the five compounds.

In Fig. 2B, the ionic ratio ¹²CH₃⁻/¹²C⁻ measured on the same ROI was reported. This ionic ratio can be regarded as a proxy of H/C atomic ratio. However, note that these two ratios are not linearly correlated. Despite rather large error bars on these measurements, it can be assessed from Fig. 2B that the ROI exhibiting enrichment and depletion in D correspond to small domains of IOM depleted in H (i.e., with a higher aromaticity than the bulk sample) and thus should result from H abstraction reactions.

Discussion

Chemical Reactions Accounting for the Isotope Fractionation.

In the plasma, the dissociation of CH₄ is achieved by electron impact. A high density of neutral molecular radicals CH_x^• is maintained in steady state at 1,600 K (14−16) (Fig. S1). Because δD values vary with the H/C ratio (Fig. 2B), it can be supposed that the isotopic fractionation is associated with variations in the molecular structures of the deposited matter. Molecular analyses of the bulk IOM revealed the occurrence of aliphatic linkages between aromatic units (17). The formation of aliphatics being precluded in the gas phase where the temperature is around 1,600 K, these linkages are consistent with a formation onto the cold (350 K) surface of the reactor walls, through radical polymerization.

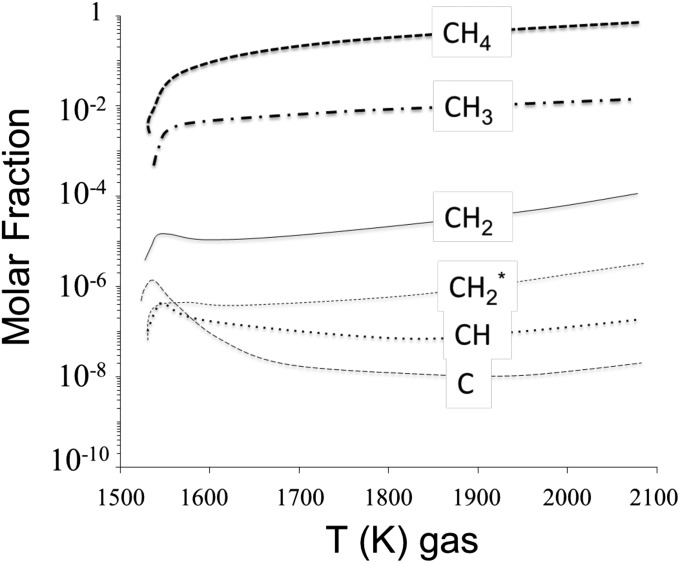
Fig. S1.

The relative molar abundances of CH_x radicals in a plasma of CH₄ calculated as a function of the plasma temperature. At 1,600 K, CH₃^• is the main radical produced from the dissociation of CH₄ by electronic impact, whereas the other radicals result from the reactions H + CH_x → H₂ + CH_x-1.

The origin of the isotopic fractionation in the IOM can be attributed to the isotope exchange reaction

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_x{\mathrm{D}}^{\mathrm{•}}\rightleftarrows {\left[\mathrm{C}{\mathrm{H}}_{x+1}\mathrm{D}\right]}^{\mathrm{•}}\to \mathrm{D}+\mathrm{C}{\mathrm{H}}_{x+1}^{\mathrm{•}}.$$ [1a]

The decomposition of the complex [CH_x+1D]^• is also possible via

$${\left[\mathrm{C}{\mathrm{H}}_{x+1}\mathrm{D}\right]}^{\mathrm{•}}\to \mathrm{HD}+\mathrm{C}{\mathrm{H}}_x^{\mathrm{•}}\hspace{0.17em}\text{or}\hspace{0.17em}\to {\mathrm{H}}_2+\mathrm{C}{\mathrm{H}}_{x\text{-}1}{\mathrm{D}}^{\mathrm{•}},$$ [1b]

with x ranging from 0 to 2 (18). The radicals CH₃^•, CH₂^•, and CH^• are then involved in successive reactions (Eq. 2) with other organic molecules yielding different IOMs that ultimately condense on the walls of the apparatus while H/H₂ or CH₄ remain in the gas phase.

$$\mathrm{C}{\mathrm{H}}_x^{\mathrm{•}}+{\mathrm{C}}_y{\mathrm{H}}_z\to \to \mathrm{IOM}\mathrm{.}$$ [2]

The origin of the isotope effect could be explained by trajectory calculations for the atom−molecule collisions described in more detail in Supporting Information. However, applying an isotopic mass balance to reactions 1a and 1b, we can write

$${\left(\mathrm{D}/\mathrm{H}\right)}_{\mathrm{C}{\mathrm{H}}_{x+1}}=y\hspace{0.17em}\alpha {\left(\mathrm{D}/\mathrm{H}\right)}_{\mathrm{C}{\mathrm{H}}_{x+1}}+\left(1\text{-}y\right){\left(\mathrm{D}/\mathrm{H}\right)}_{\mathrm{C}{\mathrm{H}}_x}.$$ [3]

The D/H ratio refers to the IOM formed from the radicals designated by the subscripts, α stands for the isotopic fractionation factor, and y and 1 − y are the relative proportions of CH_x+1^• and CH_x^•, respectively. The two parameters α and y govern the decomposition of the complex and the stabilization of the radicals under the form of IOM.

Considering CH₄ as an infinite reservoir, the steady state can be applied to all of the reactions involving CH_x and CH_x+1. The five peaks in Fig. 2A are ascribed to five types of IOM resulting from the condensation of five types of radicals having different δD_IOM values (see Supporting Information). As a first approximation, we assume that α and y are constant for all of the reactions; α is related to the measured isotopic variations via α = 1 + δD_IOM/1,000. Adjusting numerically α = 0.4 and y = 0.3 in Eq. 3, we found (i) for CH₃D+H, δD(CH₃) = +260‰ (measured peak at +180‰; note that CH₄ and CH₃D do not condense), (ii) for CH₂D^•+H, δD(CH₃) = −487‰ and δD(CH₂) = +580‰ (measured peak at −480‰ and +520‰, respectively), and (iii) for CHD^•+H, δD(CH₂) = −370‰ and δD(CH) = +987‰ (measured peak at −280‰ and +980‰, respectively). These results are in reasonable agreement with the present experimental data (Fig. 3). The details and significance of this calculation are reported in Supporting Information.

Fig. 3.

Comparison between the numerical results obtained from Eq. 3 and the experimental data (i.e., the peak δD values reported in Fig. 2 at +180‰, +520‰, +980‰ and at −280‰ and −480‰). The 1:1 line is drawn for reference. The black dots correspond to α = 0.4 and y = 0.3. The precision on the calculated δD_IOM values was calculated from ±0.05 random variations on α and y. The precision on the measured δD_IOM values is ±100‰, i.e., the width of the step used to construct the histogram reported in Fig. 2.

Cosmochemical Implications.

Fig. 1D shows an example of a NanoSIMS image of the D/H ratio in hot spots measured in the IOM isolated from Murchison meteorite. As in Fig. 1C, it exhibits microdomains where the D/H ratio exceeds, by far, the statistical distribution of this ratio recorded in isotopically homogeneous regions as in Fig. 1A. In the IOM from Murchison, the domains appear as spots, contrary to the IOM from CH₄ where the domains exhibit a more diffuse aspect; this is likely because, in the meteorite sample, these domains are present as distinct grains in the mineralogical matrix and are mechanically mixed with the bulk IOM. Nevertheless, the chondritic IOM shows clear isotopic similarities with the presently synthesized IOM.

As shown experimentally, the polymerization of organic radicals can yield isotopic heterogeneities in the D/H ratio of the condensed organic matter. In addition, organic radicals account for the simultaneous occurrence of hot and cold spots that are also commonly observed at a micrometer spatial resolution in the chondritic IOM. Taking, for example, the data from ref. 19, the Murchison meteorite exhibits 1-μm²-size cold (δD_SMOW = −460‰) and hot (δD_SMOW = +3,710‰) spots, with an average IOM bulk composition of δD_SMOW = +970‰ (13). Using δD (‰) = [(R/R₀) − 1] × 1,000, with R the D/H ratio and R₀ the D/H ratio of the SMOW (155.76 × 10⁻⁶), we can calculate the δD_IOM in the Murchison cold and hot spots relative to +970‰. The obtained values, −725‰ and + 1390‰, respectively, are in the range of the δD_IOM values observed for the synthesized IOM. The experimentally produced isotopic heterogeneities are thus commensurable with those observed in the chondritic IOM.

Another similarity lies on the molecular structure of both chondritic and synthetic IOM. In a side experiment, the IOM synthesized from octane plasma was investigated through various spectroscopic and degradative techniques and was shown to reproduce most of the hydrocarbon skeleton features of the chondritic IOM (20). The synthetic IOM from the CH₄ plasma is also similar to that synthesized from octane plasma (17). Taken together, these isotopic and molecular similarities suggest that radical reactions have played a major role in the formation of the natural chondritic IOM.

Moreover, some rare micrometeorites and interplanetary dust particles exhibit δD values in organic matter even higher than in hotspots [up to +14,300‰ and +30,000‰, respectively (10, 21)]. Such huge isotopic fractionation may be due to a much larger contribution of the reactions H+CH_x than that in the present experiment performed with pure CH₄. Indeed, theoretical calculations show that the CH₂^•/CH₄ ratio increases by a factor of 5 for an H₂/CH₄ mixing ratio increasing from 0:100 to 95:5 (14).

Although the physical process at the origin of the production of organic radicals in the protosolar nebula (UV photodissociation, cosmic rays …?) should still be considered as an open question (22), the significant isotopic fractionation associated with polymerization reactions of organic radicals must be considered as a possible additional process playing a role in the D enrichment observed in solar system organic compounds. A chemistry involving radicals would account for the two issues mentioned in the Introduction, namely (i) the isotope exchange reaction between CH₃^• and H₂ is likely fast, even below 200 K, resulting in deuterium-rich CH₄ in the gas phase (23), and (ii) the IOM condensation would yield both isotopic hot and cold spots.

Materials and Methods

Synthesis Device.

Irradiation experiments were performed in a high-vacuum glass line equipped with two pressure gauges to control the pressure of the gases on the way in and way out of the reaction. The glass line was fitted with molecular and primary pumps on the way out, as all of the experiments are performed during the constant flow of the gases. The reaction setup, similar to the so-called Nebulotron (4), includes a removable U-shaped Pyrex tube where the synthesis takes place (1.2 cm diameter, 10 cm in length). A flow of methane was dynamically pumped, and the pressure was maintained at 3 mbar. An Evenson cavity (24) was used to excite microwave discharges with a 2,450-MHz microwave generator (Opthos Instruments), and the reflected power on the microwave generator was close to 0 W.

In the absence of refrigeration, the temperature of the glass walls measured on the outer surface of the Pyrex glass rises up to 72 °C. Before each experiment, the high-vacuum glass line was cleared of any possible contaminants. The entire system was heated to 100 °C under the vacuum for several hours to remove water and other trace gases that may adsorb on the surfaces of the chamber. After 3 h of reaction with CH₄, 130 mg of organic matter were deposited. The synthesized material was extracted with a mixture of dichloromethane/methanol (2/1 vol/vol) by magnetic stirring at room temperature, and the IOM represented 99% of the total collected organic matter.

NanoSIMS Analyses.

Elemental and isotopic measurements were performed with the Cameca NanoSIMS 50 at Muséum National d'Histoire Naturelle. The powdered sample was deposited on gold sample holders. Secondary ions were imaged in two different sessions, using a cesium primary beam. The determination of the secondary ions intensity for ¹²C⁻, ¹²CH⁻, ¹²CH₂⁻, and ¹²CH₃⁻ was performed in the daily session after D⁻ and H⁻, with almost no change in the preset of the instrument. Therefore, the two sets of data correspond almost exactly to the same location on the sample (±0.5 μm).

Before H⁻, D⁻ analysis, a 25 × 25 μm² surface area was presputtered for 8 min using a high primary beam current (i.e., 500 pA) and a 750-μm-aperture diaphragm. For ¹²CH_x⁻ analysis, the 25 × 25 μm² surface area was presputtered for only 2 min using a primary beam current (i.e., 50 pA) and a 300-μm-aperture diaphragm. The primary beam was rastered over a (20 × 20) μm² surface area divided in (256 × 256) pixels² with a 200-μm-aperture diaphragm for 80 cycles. The counting time was set to of 1 ms per pixel.

The mass resolution power was ∼4,300. The summation, pixel by pixel, of the 80 cycles yields one single image, then divided in nine ROI. For each image, the counts per second (cps) for H were of the order of 3 × 10⁵ cps by ROI. The cumulated H⁻ and D⁻ counts for the 80 cycles were around 3 × 10⁷ and 1,800, respectively. The corresponding statistical error on the D/H ratio was about ±50‰ (2 sigma) in each ROI. The present study was focused on the abnormally D-enriched or depleted regions of the studied sample.

A kerogen sample having a known δD_SMOW value (−81‰ ± 2) was used to calibrate the instrumental isotope fractionation. Using the same procedures as those used to determine the IOM deposited from CH₄, we found, for this kerogen sample, δD(‰)_{Measured-SMOW} = −362 ± 20‰. Using the instrumental fractionation between measured and known δD values for this kerogen, we found, for the IOM deposited from CH₄, a δD(‰)_SMOW = −202 ± 37‰. This value is in agreement with the δD(‰)_SMOW (−227 ± 2‰) determined by standard methods on gaseous CH₄ and confirms that, at a bulk scale, no isotopic fractionation takes place during the condensation of the radicals from the gas phase.

Radical Densities in the Plasma of CH₄

The relative molar fractions of the neutral radicals were computed by the code adapted from ref. 15 and are reported in Fig. S1. This model relies on the description of a CH₄ microwave plasma obtained under moderate pressure discharge conditions in a tubular quartz reactor. The transport in the reactor was described using a Nusselt model for a radially quasi-homogeneous (0 D) plasma. Three types of equations are solved in the model: (i) a continuity equation to calculate species mole fraction, (ii) an electron energy equation to calculate electron temperature and then average electron energy, and (iii) a total energy equation to calculate the gas temperature, required for the reaction rates, which are temperature-dependent.

The chemistry in the CH₄ plasma was described using 28 species involved in 130 reactions (14). Methane decomposition can lead to carbon-containing fragments (13 neutral species, and 7 ions). The most abundant radicals are CH₄, CH₃, ³CH₂ (triplet state; noted with * on Fig. S1), ¹CH₂ (singlet state), CH, and C for radicals containing one carbon atom. Due to hydrogen abstraction, pure hydrogen species are also taken into account: H₂, H, H⁺, H₂⁺, and H₃⁺, as well as electrons. Rate constants for the reactions are listed in ref. 14.

The experimental parameters of the calculation are 1 mbar of pure CH₄ for an input microwave power of 60 W in a 10-cm-long glass tube (diameter 1.2 cm) and with a glass surface temperature of 350 K. The steady-state temperature of the gas is calculated to be 1,600 K. On Fig. S1, it can be seen that CH₃^• is the most abundant radical produced upon CH₄ dissociation by electron impact. The relative abundance of CH₂^• shows that the reactions of deprotonation of radicals such as H^•+CH_x^• → CH_x-1^• + H₂, contributes less than 1% to the production of the radicals. The relative abundance of CH₂^• to CH₃^• is close to 1%, supporting the fact that, at most, 1% of the deposited IOM exhibits isotopic anomalies. Note that C₂ hydrocarbons are also produced in the discharge in commensurable amounts compared with those of CH_x radicals but are not condensible, and hence are not collected in the present experiment.

A Possible Origin for the Isotopic Fractionation.

According to the theoretical approach developed by ref. 25, when the activated complex of a chemical reaction has two different reactive channels, the overall isotopic fractionation factor α can be written as

$$\alpha ={\alpha }_{\text{Mass-dependent}}\cdot \eta .$$ [S1]

The term α_{Mass-dependent} is the classical mass-dependent term. Because the temperature of the plasma is close to 1,600 K, α_{Mass-dependent} should be close to 1 in the gas phase (23). However, the polymerization of the carbon takes place on the walls of the apparatus where the temperature is close to 350 K; it cannot thus be ruled out that α_{Mass-dependent} is ≠ 1. The term η in S1 can be interpreted as a consequence of the mass-independent fractionation effect (26–28). It is proposed that this effect results from the interaction between the indistinguishable H atoms involved in reaction 1a when H replaces D. This interpretation relies on the theoretical approach developed by ref. 25 according to which the probability of the reactions differs when it involves distinguishable or indistinguishable isotopes, for example, H + CH₃D compared with H + CH₄.

Few reactions in the plasma could be relevant to this isotope effect (14–16).

The dissociation of methane is primarily due to electron (e) impact,

$$\mathrm{e}+\mathrm{C}{\mathrm{H}}_4\to \mathrm{C}{\mathrm{H}}_{\mathrm{3}}^{\mathrm{•}}+\mathrm{H}+\mathrm{e}\mathrm{.}$$ [S2]

The radical CH₃^• is the precursor of a whole family of IOM formed in the gas phase and deposited on the walls of the plasma chamber. We first assume that this family stands for the large variety of compounds having δD_IOM around 0 ± 110‰.

Additional radicals CH₃^•, CH₂^•, and CH^• are also produced via chemical reactions with H,

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_{\mathrm{x}}^{\mathrm{•}}\rightleftarrows {\left[\mathrm{C}{\mathrm{H}}_{\mathrm{x}+1}\right]}^{\mathrm{•}}\to {\mathrm{H}}_2+\mathrm{C}{\mathrm{H}}_{\mathrm{x}\text{-}1}^{\mathrm{•}}.$$ [S3a]

[CH_x+1] ^• stands for the intermediate complex. As shown in Eq. 1a, an isotopic exchange reaction can take place during the formation of the complex,

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_{x\text{-}1}{\mathrm{D}}^{\mathrm{•}}\underset{\mathrm{NR}}{\rightleftarrows }{\left[\mathrm{C}{\mathrm{H}}_x\mathrm{D}\right]}^{\mathrm{•}}\underset{\mathrm{R}}{\to }\mathrm{D}+\mathrm{C}{\mathrm{H}}_x^{\mathrm{•}}.$$ [S3b]

Because of the low abundance of D in its natural abundance, the doubly (or higher) deuterated species are neglected. Following the reactions (S3a and S3b), the radicals CH_x^• and CH_x-1^• (and their isotopic counterparts) condense under the form of IOMs by polymerization reactions on the walls of the apparatus. These condensation reactions can be schematically written as

$$\mathrm{C}{\mathrm{H}}_{\mathrm{x}}^{\mathrm{•}}+{\mathrm{C}}_y{\mathrm{H}}_{\mathrm{z}}\to \mathrm{IO}{\mathrm{M}}_1$$ [S4a]

$$\mathrm{C}{\mathrm{H}}_{x\text{-}1}^{\mathrm{•}}+{\mathrm{C}}_y{\mathrm{H}}_z\to \mathrm{IO}{\mathrm{M}}_2.$$ [S4b]

The term η can be understood as follows.

Suppose that we have an observable w averaged over the classical trajectories sampling all of the collision parameters (spatial orientation, relative collision energy, and impact parameter following respective Boltzmann distributions for a given temperature). Some of the trajectories will show an isotope exchange (R standing for “reactive” in the forward reaction S3b) whereas some will be elastic or inelastic collisions but without exchange (NR standing for “nonreactive” in reaction S3b). The relative abundances of each reaction channel X_R and X_NR are calculated as the average of w in each reaction channel R or NR, taking into account all of the possible trajectories weighted by their respective Boltzmann contribution; this procedure yields X_R + X_NR = 1.

For modeling the quantum mechanical indistinguishability, we neglect for simplicity the mass difference between H and D and we introduce the scaling factors P_R and P_NR, which take into account only the trajectories corresponding to w larger than a threshold value allowing the polymerization reactions S4a and S4b to take place. If all of the trajectories involved in the Boltzmann distribution are considered, the scaling factors are normalized to 1, i.e., P_R = P_NR = 1.

The classical weighted mean value < w > for the complex [CH_xD]^• is

$$\langle w\rangle =\left(w_{\text{R}}\hspace{0.17em}{X}_{\text{R}}\hspace{0.17em}{P}_{\text{R}}+w_{\text{NR}}{X}_{\text{NR}}{P}_{\text{NR}}\right)/\left(X_{\text{R}}{P}_{\text{R}}+X_{\text{NR}}{P}_{\text{NR}}\right),$$ [S5a]

where w_R stands for the average of w taken only over the reactive collisions, and w_NR stands for the average of w taken only over the nonreactive collisions. In the case of indistinguishable isotopes, one cannot decide anymore whether an isotope exchange took place or not during the formation of the complex, and thus P_R and P_NR take the common value 1/2(P_R + P_NR). Therefore, for H in place of D in reaction S3b, the weighted mean value < w_I > (subscript I stands for “indistinguishable”) becomes

$$\langle w_{\text{I}}\rangle =w_{\text{R}}.X_{\text{R}}.+w_{\text{NR}}.X_{\text{NR}}.$$ [S5b]

The mass-independent isotopic fractionation factor η is

$$\eta =\langle w\rangle /\langle w_{\text{I}}\rangle .$$ [S6]

Contrary to the reactions involved in ozone formation (25) where w stands for the lifetime of the complex, the reactions taking place during the collisions between radicals and hydrogen atoms are too fast to yield measurable lifetimes. One has therefore to look to another observable standing for w, but the principle of an isotopic fractionation caused by the isotopic indistinguishability in scattering processes remains unaltered.

The actual theoretical determination of α is beyond the purpose of this paper.

The Mass Balance Calculations Reported as Fig. 3.

The proposed model describing the isotopic fractionation is mostly inspired by the one proposed for ozone by ref. 25. We use the reaction H + CH₃ to illustrate the model of IOM polymerization:

The mass balance equation for this reaction is written as

$$\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\right)=y.\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3,\mathrm{IOM}1\right)+\left(1\text{-}y\right).\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_2,\mathrm{IOM}2\right).$$ [S7]

The isotopic fractionation factor between the reactant CH₃ and the product CH₃, IOM1 is noted α, and Eq. S7 becomes

$$\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\right)=y.\alpha .\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\right)+\left(1\text{-}y\right).\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_2\right).$$ [S8]

Omitting the terms IOM2 in S8 for simplicity yields Eq. 3. The reactions leading to S7 can be written as

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_3\rightleftarrows {\mathrm{H}}_2+\mathrm{C}{\mathrm{H}}_2.$$ [S9]

Similarly, the other two reactions of H abstraction can be written as

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_4\rightleftarrows {\mathrm{H}}_2+\mathrm{C}{\mathrm{H}}_3$$ [S10]

$$\mathrm{H}+\mathrm{C}{\mathrm{H}}_2\rightleftarrows {\mathrm{H}}_2+\mathrm{CH}\mathrm{.}$$ [S11]

In reaction S10, CH₄ remains in the gas phase and does not yield condensible IOM. We have therefore a set of three mass balance equations,

$$\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_4\right)=y.\alpha .\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_4\right)+\left(1\text{-}y\right).\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\text{-}\mathrm{S}10\right)$$

$$\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\mathrm{-S}10\right)=y.\alpha .\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_3\mathrm{-S}9\right)+\left(1\text{-}y\right).\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_2\text{-}\mathrm{S}9\right)$$

$$\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_2\mathrm{-S9}\right)=y.\alpha .\mathrm{D}/\mathrm{H}\left(\mathrm{C}{\mathrm{H}}_2\mathrm{-S}11\right)+\left(1\text{-}y\right).\mathrm{D}/\mathrm{H}\left(\mathrm{CH}\text{-}\mathrm{S}11\right).$$

The five products CH₃ in S10, CH₃ in S9, CH₂ in S9, CH₂ in S11 and CH in S11 are ascribed to the D/H values of the five peaks of Fig. 2. i.e., to δD values equal to +180‰, −280‰, +520‰, −480‰, and +980‰, respectively. In these three equations, the two remaining unknowns are y and α that we have adjusted numerically to reproduce the five δD values of the five peaks. Note that the mass-dependent (α_{Mass-dependent}) and the mass-independent (η) terms cannot be identified in the α value calculated with this procedure.