Significance
The relationship between a population’s antibiotic consumption and the frequency of antibiotic resistance among bacteria colonizing that population is not fully understood. Antibiotic resistant and sensitive strains compete for available hosts—we would therefore expect the fitter strain to dominate. Instead, we observe stable coexistence of both strains. In this work, we propose an explanation for this coexistence by showing the fitness advantage of resistance depends on a bacterial strain’s duration of carriage. This finding ties the evolution of resistance to any genetic mechanism affecting duration of carriage. These insights could allow more accurate prediction of future resistance levels and play a role in informing strategies to prevent the spread of resistance.
Keywords: antibiotic resistance, coexistence, Streptococcus pneumoniae, epistasis, multistrain model
Abstract
Understanding how changes in antibiotic consumption affect the prevalence of antibiotic resistance in bacterial pathogens is important for public health. In a number of bacterial species, including Streptococcus pneumoniae, the prevalence of resistance has remained relatively stable despite prolonged selection pressure from antibiotics. The evolutionary processes allowing the robust coexistence of antibiotic sensitive and resistant strains are not fully understood. While allelic diversity can be maintained at a locus by direct balancing selection, there is no evidence for such selection acting in the case of resistance. In this work, we propose a mechanism for maintaining coexistence at the resistance locus: linkage to a second locus that is under balancing selection and that modulates the fitness effect of resistance. We show that duration of carriage plays such a role, with long duration of carriage increasing the fitness advantage gained from resistance. We therefore predict that resistance will be more common in strains with a long duration of carriage and that mechanisms maintaining diversity in duration of carriage will also maintain diversity in antibiotic resistance. We test these predictions in S. pneumoniae and find that the duration of carriage of a serotype is indeed positively correlated with the prevalence of resistance in that serotype. These findings suggest heterogeneity in duration of carriage is a partial explanation for the coexistence of sensitive and resistant strains and that factors determining bacterial duration of carriage will also affect the prevalence of resistance.
Antibacterial resistance is a serious threat to public health, with resistant strains emerging in numerous pathogens. Although estimates of resistance levels vary by region, pathogen, and antibiotic type, a common feature is that fixation of resistance is rarely observed: sensitive and resistant strains tend to coexist robustly. For example, according to the European Antimicrobial Resistance Surveillance Network (EARS-Net; available at ecdc.europa.eu) (1), the prevalence of penicillin and macrolide nonsensitivity in Streptococcus pneumoniae has been stable at around 10 and 15% respectively for the past 15 years in Europe. Similarly, EARS-Net estimates of multidrug resistance in Klebsiella pneumoniae have varied around 20% since 2009 and those for methicillin resistance in Staphylococcus aureus have ranged between 15 and 25% from 1999 onwards, with no persisting directional trend.
The stable coexistence of sensitive and resistant strains is unexpected: because these strains compete for the same hosts, simple ecological models predict that the fitter strain would dominate and the weaker strain become extinct (“competitive exclusion”). Understanding how coexistence is maintained is therefore important for predicting the prevalence of resistant strains and for explaining the approximately linear relationship between regional antibiotic consumption and resistance (2). Predicting the prevalence of resistance is, in turn, crucial for evaluating its impact. For example, recently published worst case estimates from the Review on Antimicrobial Resistance commissioned by the UK government, which put the cumulative cost of antimicrobial resistance at $100 trillion by 2050, assumed resistance would eventually reach 100% (3). Moreover, identifying the factors that determine the prevalence of resistance will play a role in informing strategies to limit its spread.
In general, diversity at a locus can be maintained through selective processes that introduce balancing selection (negative frequency-dependent selection for example) (4), but the inclusion of such processes into models of strain dynamics should be informed by the ecology of the strains (5). Because no such mechanisms are known for antibiotic resistance, models of resistance should be structured in a way that does not build them in (i.e., “structurally neutral”) (5). Colijn et al. explored whether coexistence of sensitive and resistant strains in the pneumococcus could be reproduced using a number of structurally neutral coexistence-promoting mechanisms (including habitat heterogeneity, within-host competition and lowered competition for hosts) (6). Although coexistence was possible in all models, it was highly sensitive to antibiotic consumption rate and the fitness cost of resistance. Such sensitivity is at odds with observed patterns of resistance: coexistence occurs at a wide range of antibiotic consumption rates (2), in a number of different bacterial species (1), and most probably for a range of fitness costs (because coexistence is observed for a number of different antibiotics and resistance mechanisms).
Thus, while coexistence of sensitive and resistant strains has not been satisfactorily explained using structurally neutral models, there is an absence of evidence for mechanisms justifying departures from structural neutrality.
In this work, we propose a mechanism of coexistence in the absence of balancing selection on antibiotic resistance: diversity at the resistance locus can be maintained by balancing selection at a linked locus if the linked locus modulates the fitness effect of resistance. We show that the fitness advantage of resistance for a strain depends on its duration of carriage, with strains with long durations of carriage gaining more from resistance. Coexistence of antibiotic sensitivity and resistance can therefore be maintained by coexistence of different durations of carriage and the evolution of antibacterial resistance is tied to any genetic mechanism affecting duration of carriage.
Results
Fitness Effect of Resistance Depends on Duration of Carriage.
We begin by considering a one-locus, two-allele model of resistance in a bacterial species with asymptomatic carriage, such as S. pneumoniae, where the probability of receiving antibiotics can be considered independent of carriage status. The resistant and sensitive strains (r and s, respectively) compete directly for hosts, with no balancing selection (Fig. 1). The dynamics of this model are described by
| [1] |
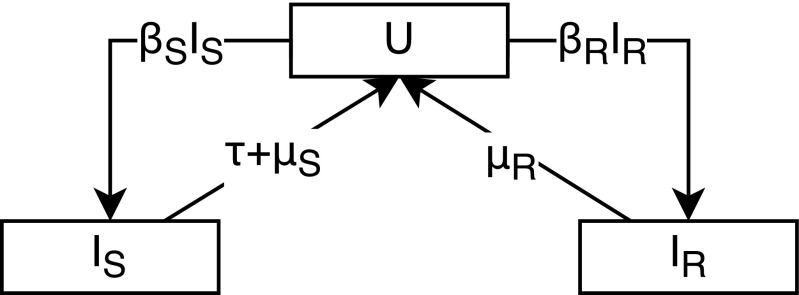
where , , and are uninfected individuals and individuals infected with the sensitive and resistant strains, respectively, and are transmission and clearance rates, is the population antibiotic consumption rate (we assume instant treatment), and . We use the terms infected and carrier synonymously throughout the paper. Resistance carries a fitness cost, which is modeled as either decreased transmission () or increased clearance (), with and .
Fig. 1.
Model of competition between antibiotic sensitive and resistant strains (Eq. 1). represents uninfected hosts, represents hosts infected with the sensitive strain, represents hosts infected with the resistant strain, is the transmission rate, is the clearance rate, is the population antibiotic consumption rate, and , where and represent the cost of resistance.
At equilibrium, the resistance and sensitive strains only coexist when : in a single-locus model, coexistence is only possible if two strains have the same . This occurs when the population antibiotic consumption rate is
| [2] |
Below this consumption rate, the sensitive excludes the resistant strain, whereas the resistant strain dominates above the threshold. The longer the duration of carriage (i.e., the smaller the clearance rate), the lower the antibiotic consumption rate at which it becomes advantageous for strains to be resistant. This is because a long duration of carriage is associated with a greater risk of antibiotic exposure per carriage episode. There is therefore epistasis between resistance and duration of carriage: the resistance allele confers a greater fitness advantage in a genetic background associated with longer duration of carriage.
Heterogeneity in Duration of Carriage Can Maintain Coexistence of Sensitivity and Resistance.
We now consider a model that includes a second locus, with alleles and , which differ in duration of carriage, under some form of balancing selection that allows coexistence of these two alleles (for example, A and B could represent serotypes with serotype-specific acquired immunity). Because of the difference in duration of carriage, the antibiotic consumption rate at which resistance is selected for will be different for strains and (Eq. 2). Coexistence of antibiotic sensitivity and resistance will occur between these two consumption thresholds: the strain with longer duration of carriage will be resistant, whereas the strain with shorter duration of carriage will be sensitive (Fig. 2). Thus, diversity in antibiotic sensitivity can be maintained by balancing selection at a linked locus.
Fig. 2.
Parameter space for coexistence in a two-allele two-locus model of resistance. One locus determines resistance ( or ), and the other determines duration of carriage ( or ). The coexistence space is constrained by the lines and , with , where is the antibiotic consumption rate, is a strain’s clearance rate, is the cost of resistance in transmission, and is the cost of resistance in clearance. In this plot, . We use cost to mean proportional multiplicative cost: corresponds to no cost.
To further explore the relationship between heterogeneity in duration of carriage and coexistence of sensitivity and resistance, we construct a model with strains with different durations of carriage (D-types). Each strain has a two-locus genotype: a two-allele resistance locus ( or ) and an allele D-type locus. To maintain the coexistence of multiple D-types, we introduce balancing selection by scaling transmission by , a term depending on the frequency of D-type , . does not have a direct mechanistic interpretation: it can be any function that decreases as the frequency of a D-type increases. In the results presented here, we model balancing selection as a function that drives the frequency of all D-types toward :
| [3] |
where and sets the strength of balancing selection.
The dynamics of each D-type are described by
| [4] |
where , and is the clearance rate for D-type . This model is structurally neutral for the resistance locus: within each D-type, the model has the structure presented in Fig. 1. When , and Eq. 4 become identical to Eq. 1. We assume no recombination (however, the results we present are robust to inclusion of recombination at realistic rates; see below).
This model reproduces the approximately linear relationship between antibiotic consumption rate and prevalence of resistance that has been observed in data (2). As predicted by Eq. 2, whether a D-type is sensitive or resistant at a given antibiotic consumption rate depends on its duration of carriage (Fig. 3). As antibiotic consumption increases, an increasing number of D-types will switch from sensitivity to resistance, leading to an increase in the prevalence of resistance. A small total number of D-types produces a stepped relationship between antibiotic consumption and the frequency of resistance, with each step corresponding to another D-type switching to resistance. As the number of D-types increases, the relationship becomes smoother (Fig. 4). These results are robust to how balancing selection is modeled, except when balancing selection acts solely by increasing clearance rate as strain prevalence increases, thus abolishing differences in carriage duration between D-types (SI Appendix, Supporting Text 1 and Fig. S1). Because the prevalence of resistance at a given antibiotic consumption rate depends on the relative frequencies of resistant and sensitive D-types, the strength of balancing selection determines how steeply resistance rises with increasing antibiotic consumption: the stronger the balancing selection, the smaller the differences in D-type prevalence and therefore the more linear the relationship between antibiotic consumption and resistance (SI Appendix, Supporting Text 1 and Fig. S1).
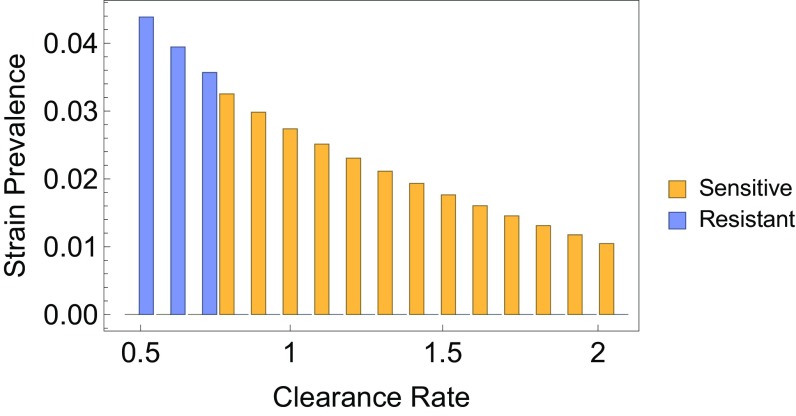
Fig. 3.
Prevalence of sensitive and resistant D-types, in a model with 16 D-types (). The bars represent the prevalence of a D-type, stratified by antibiotic resistance (yellow and blue). Clearance rates for D-types were evenly spaced in the range . Other parameters are .
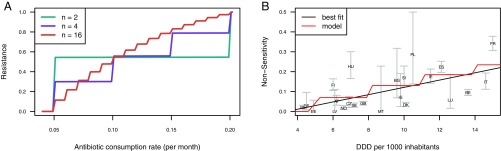
Fig. 4.
Increase in resistance with increasing antibiotic consumption. (A) Effect of number of modeled D-types on the relationship between antibiotic consumption and resistance. Clearance rates for D-types were evenly spaced in the range and other parameters were . (B) Relationship between penicillin nonsensitivity in S. pneumoniae and primary care beta-lactam prescriptions, in defined daily doses (DDD) per 1,000 inhabitants, in European countries in 2007 [chosen to avoid confounding by 2008 changes in Clinical and Laboratory Standards Institute breakpoints for S. pneumoniae implemented in some countries (7)]. . We excluded Portugal, which reported 0 beta-lactam prescriptions. Error bars represent 95% confidence intervals (CIs). The “best fit” line is from a linear regression, the model line shows the relationship between consumption and resistance in a model with 40 D-types, with clearance rates evenly spaced in the range and with (parameters chosen to approximately replicate the best fit line; SI Appendix, Supporting Text 3). Antibiotic consumption rate (per month; Materials and Methods) was transformed into DDDs by assuming a course of treatment consists of 10 DDDs.
For diversity in duration of carriage to act as a mechanism of coexistence, selection must be able to act on combinations of D-type and resistance status. Thus, duration of carriage must be inherited: introducing the possibility that D-type alleles change during transmission decreases coexistence. While our results are robust to low probabilities of allele change (such as those arising from mutation or recombination, SI Appendix, Supporting Text 2), higher rates abolish coexistence (SI Appendix, Figs. S2 and S3).
Longer Duration of Carriage Is Associated with Higher Prevalence of Resistance in Pneumococcal Serotypes.
One of the model’s key predictions is that resistance will be more commonly observed for strains with longer duration of carriage. We tested this prediction by examining the relationship between resistance and serotype in S. pneumoniae. Pneumococcal serotype is determined by the bacterium’s polysaccharide capsule and is highly diverse. This diversity is thought to be maintained by balancing selection arising from serotype-specific immunity (8). Serotypes differ in both duration of carriage (9, 10), likely due to differences in how well capsules protect the bacterium from neutrophil-mediated killing (11), and level of antibiotic resistance (12).
We computed the correlation between duration of carriage and resistance in three sets of isolates collected at different locations: Maela (13), using Maela-based duration of carriage estimates by Turner et al. (14) (Dataset S1); and Massachusetts (15) and Malawi (16), using duration of carriage calculated from rates estimated by Lipsitch et al. (17), based on data collected in Kilifi, Kenya (Materials and Methods). There was a significant positive correlation between resistance and duration of carriage for seven out of the eight tested dataset/antibiotic combinations (Table 1 and Fig. 5).
Table 1.
Prevalence of resistance () and Kendall’s rank correlation coefficient tau (SI Appendix, Supporting Text 4) for the relationship between serotype mean duration of carriage and resistance
| Antibiotic | Dataset | tau (95% CI) | P | |
| Penicillin | Massachusetts | 0.39 | 0.34 (− 0.04, 0.61) | 0.045 |
| Penicillin | Malawi | 0.21 | 0.49 (− 0.09, 0.79) | 0.035 |
| Penicillin | Maela | 0.49 | 0.46 (0.27, 0.58) | 8.6 10-6 |
| Penicillin | Combined | — | — | 2.4 10-6 |
| Co-trimoxazole | Malawi | 0.46 | − 0.14 (− 0.62, 0.41) | 0.70 |
| Co-trimoxazole | Maela | 0.81 | 0.22 (0.03, 0.39) | 0.012 |
| Co-trimoxazole | Combined | — | — | 0.049 |
| Trimethoprim | Massachusetts | 0.14 | 0.38 (0.01, 0.64) | 0.027 |
| Erythromycin | Massachusetts | 0.19 | 0.34 (− 0.04, 0.61) | 0.045 |
| Ceftriaxone | Massachusetts | 0.13 | 0.35 (− 0.03, 0.62) | 0.047 |
Number of isolates and serotypes for which carriage duration could be calculated: Massachusetts, 180 and 19; Malawi, 300 (Materials and Methods) and 9; and Maela, 2,923 and 51. P values are one-tailed, which is why 95% CIs sometimes overlap zero for P < 0.05. Combined P values were calculated using Fisher’s method for all three datasets for penicillin and Malawi and Maela for co-trimoxazole (we treated trimethoprim and co-trimoxazole as different drugs). Bold P values are below 0.05. Values of tau for antibiotics in the Massachusetts dataset are similar because there is a strong association between resistance to different antibiotics (e.g., odds ratio for penicillin and erythromycin nonsensitivity: 10; 95% CI: 6–21).
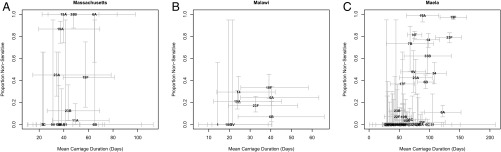
Fig. 5.
Relationship between mean duration of carriage and the prevalence of penicillin resistance across serotypes in Massachusetts (n = 16) (A), Malawi (n = 9) (B), and Maela (n = 50) (C). Values of n differ slightly from those given in Table 1 because data for penicillin resistance was missing for some serotypes. Error bars represent 95% CIs. Error is underestimated for duration of carriage in A and B because estimates of uncertainty were not available for all quantities used in making these estimates and for the prevalence of resistance in the Malawi (B) dataset because of uneven serotyping of resistant and sensitive isolates (Materials and Methods).
Discussion
Using a simple model of strain dynamics, we have shown that in bacterial species with asymptomatic carriage, heterogeneity in duration of carriage can maintain diversity in antibiotic sensitivity because the fitness effect of resistance depends on duration of carriage. Strains with a long duration of carriage have a greater risk of antibiotic exposure per carriage episode and therefore more to gain from resistance. Balancing selection that maintains strains with different durations of carriage will therefore allow coexistence of sensitive and resistant strains at a range of antibiotic consumption rates. This model reproduces the previously unexplained gradual increase in resistance with increasing antibiotic consumption.
As predicted by this model, we find that duration of carriage in pneumococcal serotypes is a predictor of resistance. This result suggests that coexistence of serotypes differing in carriage duration is indeed a mechanism maintaining the coexistence of antibiotic sensitivity and resistance in the pneumococcus. A significant association between duration of carriage and resistance was found for all antibiotics and datasets, with the exception of co-trimoxazole (trimethoprim/sulfamethoxazole) in Malawi. The absence of a significant association may relate to the small number of serotypes in the Malawi dataset (n = 9) and large uncertainty in resistance estimates due to a small number of isolates for some of these serotypes. Additionally, duration of carriage for both Malawi and Massachusetts was calculated using Kilifi-based estimates of immune clearance and serotype “knockout” (i.e., replacement by another serotype within the host; Materials and Methods). Such estimates may be setting-specific (beyond differences in rate of serotype knockout due to setting-specific serotype distribution and overall pneumococcal carriage, which we accounted for). Although there is a reasonable correlation between Kilifi-based duration of carriage estimates for the Maela dataset and those reported by Turner et al. (14) [Pearson’s r = 0.56; 95% CI: 0.18–0.79; SI Appendix, Supporting Text 5], it is possible that our estimates do not accurately reflect duration of carriage for Massachusetts and Malawi.
Duration of carriage measured at the serotype level was a relatively weak predictor of resistance, even in the Maela dataset where carriage duration and resistance were measured as part of the same study. Although uncertainty in both resistance and duration of carriage estimates likely contributes to the weakness of the association, the weak correlation could also point to factors other than duration of carriage playing a role in the prevalence of resistance.
Diversity in serotype duration of carriage is not a sufficient explanation for coexistence of antibiotic sensitivity and resistance because coexistence is also observed within serotype. It is possible that this within-serotype coexistence arises because of within-serotype diversity in some other genetic factor affecting duration of carriage. Indeed, there is evidence for noncapsular factors contributing to duration of carriage: Weinberger et al. have reported within-serotype variation in resistance to neutrophil-mediated killing in vitro (a likely predictor of duration of carriage) for isolates with different genetic backgrounds (11). Possible candidates for genetic factors influencing duration of carriage include bacterial adhesins (as suggested by Weinberger et al.), metabolic genes and bacteriocins, which likely mediate killing of nonisogenic strains and could therefore play a role in strain knockout (18).
The role of duration of carriage in the coexistence of antibiotic sensitivity and resistance represents a specific example of a more general mechanism previously described by Wade (19): the presence of epistasis between loci ties the fitness effect of alleles at one locus to allelic frequencies at the other. Epistasis therefore allows balancing selection on one locus to maintain allelic diversity at another. In the case of resistance, the fitness effect is also modulated by the cost of resistance, meaning that mechanisms maintaining variability in the fitness cost of resistance would also maintain diversity in antibiotic sensitivity. Although compensatory mutations that decrease the fitness cost of resistance could potentially play this role, we are not aware of any mechanisms that would introduce balancing selection on these mutations.
Our model predicts linkage disequilibrium between loci determining resistance and duration of carriage, with resistance alleles associating with long duration of carriage. In S. pneumoniae, beta-lactam resistance has been shown to associate with a number of variants outside the direct target of beta-lactams (the peptidoglycan biosynthesis pathway) (20). It seems plausible that some of these variants may play a role in determining duration of carriage. Furthermore, we would expect to see substantial overlap between variants associated with a resistant phenotype and variants associated with a long duration of carriage (subject to some caveats; SI Appendix, Supporting Text 8).
More generally, we would expect to observe linkage disequilibrium between any two loci, where one locus is under balancing selection and modulates the fitness effect of the other. These results bear some similarity to previous multistrain models where linkage disequilibrium between loci emerges from the epidemiological properties of strains (21, 22). In these models, unlike the model presented here, balancing selection is present for both loci and linkage emerges because, once allele combinations have been established, discordant combinations will be suppressed by competition. Nevertheless, both models represent mechanisms that maintain linkage disequilibrium in bacterial populations and thus contribute to explaining why strain structure persists despite the presence of recombination.
In theory, the mechanism of coexistence we describe could also arise from characteristics of the host rather than the pathogen: host properties are “inherited” if the host populations are assortatively mixing. A model with assortatively mixing classes of host that differ in duration of carriage is therefore structurally near-equivalent to the model presented in Eq. 4, with the difference that heterogeneity in carriage duration is maintained through the host population structure, rather than balancing selection on D-type. Pneumococcal carriage duration varies with age (10, 17); host age, combined with assortative mixing between age groups, could therefore act as a mechanism of coexistence in S. pneumoniae (SI Appendix, Supporting Text 7). Other host factors, such as socioeconomic groups, could also play this role.
The effect of duration of carriage on resistance has potential public health implications: as the fitness advantage of resistance depends on absolute (rather than relative) duration of carriage, we would expect interventions that lower a bacterial species’ duration of carriage to also lower the prevalence of antibiotic resistance in that species. On the other hand, if carriage episodes are often terminated by replacement with a different strain (knockout), rather than by immune clearance, we would expect interventions that decrease transmission to decrease knockout and therefore increase duration of carriage and antibiotic resistance. This effect could explain the increase of resistance in nonvaccine serotypes observed after introduction of the pneumococcal conjugate vaccine PCV7 in 2000 (15). Vaccination was followed by an increase in prevalence of nonvaccine types (23). If this increase was at least partially due to longer duration of carriage in nonvaccine types (because of decreased knockout by vaccine types), we would predict increased prevalence of resistance in the nonvaccine types. A caveat here is that there is stronger evidence for the postvaccination increase in prevalence of nonvaccine serotypes being related to increased acquisition rates than prolonged duration of carriage (24).
We have shown that epistasis between resistance and duration of carriage loci ties the fate of resistance alleles to genetic mechanisms affecting duration of carriage. This effect is a partial solution to the problem of coexistence and provides mechanistic insight into the relationship between antibiotic consumption and resistance levels, with significant implications for public health.
Materials and Methods
Parametrization.
Model parameter values have been chosen from ranges presented in Colijn et al. (6) to correspond to reasonable values for S. pneumoniae, with all rates in units of per month.
Antibiotic-Resistance Datasets.
Analysis of the relationship between duration of carriage and resistance was performed on datasets from three studies that reported both serotype-specific prevalence of resistance and either serotype duration of carriage (Maela) or overall pneumococcal carriage rate (Malawi and Massachusetts), required for calculating duration of carriage (see below). The Maela data, collected from a refugee camp on the border of Thailand and Myanmar from 2007 to 2010, were obtained from Chewapreecha et al. (13). The Malawi data, collected in Dwanga in 1997, were obtained from Feikin et al. (16). The study serotyped a greater proportion of the resistant than sensitive isolates (89 vs. 25%). We weighted the number of sensitive isolates to recover the correct overall prevalence of resistance. The Massachusetts data, collected as part of the SPARC (Streptococcus pneumoniae Antimicrobial Resistance in Children) project (25), were obtained from Croucher et al. (15). To avoid confounding by vaccine-associated changes and changes in the rate of antibiotic consumption, only data from 2007 was included (the largest dataset of the available years). For Massachusetts, resistance data were provided in terms of minimum inhibitory concentrations (MICs). Penicillin, erythromycin, ceftriaxone, and trimethoprim nonsensitivity were defined in accordance to Clinical and Laboratory Standards Institute breakpoints as MICs above 0.06, 0.25, 0.5, and 1 g/mL, respectively (26).
Estimating S. pneumoniae Mean Carriage Duration.
For the Maela dataset, we used mean carriage duration (in infants) estimates based on longitudinal sampling in Maela by Turner et al. (14) (SI Appendix, Supporting Text 5 and Dataset S1). Because longitudinal sampling was not available for Malawi and Massachusetts, we derived clearance rates (and hence mean carriage duration as the reciprocal of clearance rate) for these datasets using estimates by Lipsitch et al. based on data collected in Kilifi, Kenya (17). Lipsitch et al. estimated serotype-specific rates of immune clearance and knockout (for serotype replacing serotype within the host), where , with being susceptibility of serotype to competition and being the force of infection for serotype (, where is the proportion of the population carrying serotype in the Lipsitch et al. dataset). To calculate the clearance rate for serotype in resistance dataset , we adjusted for setting-specific rates of knockout due to differences in serotype distribution and overall pneumococcal carriage by scaling the rate of knockout by the relative proportion of the population carrying the knocking out serotype in the Lipsitch and resistance datasets (, where is the proportion of the population carrying serotype in the resistance dataset). Estimates of , , and were not available for serotypes making up 35% of the Massachusetts and 29% of the Malawi datasets. Simply excluding these serotypes from the calculation of clearance rates would underestimate the rate of knockout. We calculated the contribution of these serotypes to competition as the overall force of infection (where is the full set of serotypes for which has been estimated) weighted by the relative prevalence of carriage in the resistance () and Lipsitch datasets () and the frequency of serotypes for which estimates of , , and were missing (), giving
| [5] |
For the Massachusetts dataset, overall rates of carriage were obtained from Huang et al. (27).
This method assumes that rates of immune clearance () and susceptibility to knockout () are transferable between context. To verify our estimates, we calculated clearance rates for Maela using the method above and compared them to those calculated directly from longitudinal sampling in Maela. The correlation between the two was reasonable (Pearson’s = 0.56; 95% CI: 0.18–0.79; SI Appendix, Fig. S4). We also corroborated our results by using serotype frequency in a dataset as a proxy for carriage duration in that dataset, with results consistent with those in Table 1 (SI Appendix, Table S1). In calculating the correlation between resistance and carriage duration, we do not differentiate between carriage ending through immune clearance () and strain knockout (). If the fitness cost of resistance is very different for these two modes of clearance, treating the two as equivalent would not be appropriate (SI Appendix, Supporting Text 6).
Supplementary Material
Acknowledgments
We thank Sarah Cobey for comments on the manuscript. S.L. and C.F. were supported by the Models of Infectious Disease Agent Study [NIH National Institute of General Medical Sciences (NIGMS) Grant U01GM110721], F.B. was supported by Marie Skłodowska-Curie Individual Fellowship 657768, N.J.C. was supported by a Sir Henry Dale Fellowship (jointly funded by the Wellcome Trust and Royal Society; Grant 104169/Z/14/Z), P.T. was supported by Wellcome Trust Training Fellowship 083735/Z/07/Z, and M.L. was supported by NIH Grants R01AI048935 and U54GM088558. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIGMS or NIH.
Footnotes
Conflict of interest statement: M.L. has received consulting fees/honoraria from Merck, Pfizer, Affinivax, and Venable LLC and grant support not related to this paper from Pfizer and PATH Vaccine Solutions.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1617849114/-/DCSupplemental.
References
- 1. European Centre for Disease Prevention and Control (2015) Antimicrobial Resistance Surveillance in Europe 2015 (European Centre for Disease Prevention and Control, Stockholm).
- 2.Goossens H, Ferech M, Vander Stichele R, Elseviers M, ESAC Project Group Outpatient antibiotic use in Europe and association with resistance: a cross-national database study. Lancet. 2005;365(9459):579–587. doi: 10.1016/S0140-6736(05)17907-0. [DOI] [PubMed] [Google Scholar]
- 3.Taylor J, et al. Model and Results. RAND Corporation; Cambridge, UK: 2014. Estimating the economic costs of antimicrobial resistance. [Google Scholar]
- 4.Chesson P. Mechanisms of maintenance of species diversity. Annu Rev Ecol Syst. 2000;31(1):343–366. [Google Scholar]
- 5.Lipsitch M, Colijn C, Cohen T, Hanage WP, Fraser C. No coexistence for free: neutral null models for multistrain pathogens. Epidemics. 2009;1(1):2–13. doi: 10.1016/j.epidem.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Colijn C, et al. What is the mechanism for persistent coexistence of drug-susceptible and drug-resistant strains of Streptococcus pneumoniae? J R Soc Interface. 2010;7(47):905–919. doi: 10.1098/rsif.2009.0400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goossens MC, Catry B, Verhaegen J. Antimicrobial resistance to benzylpenicillin in invasive pneumococcal disease in Belgium, 2003–2010: the effect of altering clinical breakpoints. Epidemiol Infect. 2013;141(3):490–495. doi: 10.1017/S0950268812001057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cobey S, Lipsitch M. Niche and neutral effects of acquired immunity permit coexistence of pneumococcal serotypes. Science. 2012;335(6074):1376–1380. doi: 10.1126/science.1215947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sleeman KL, et al. Capsular serotype–specific attack rates and duration of carriage of Streptococcus pneumoniae in a population of children. J Infec Dis. 2006;194(5):682–688. doi: 10.1086/505710. [DOI] [PubMed] [Google Scholar]
- 10.Högberg L, et al. Age-and serogroup-related differences in observed durations of nasopharyngeal carriage of penicillin-resistant pneumococci. J Clin Microbiol. 2007;45(3):948–952. doi: 10.1128/JCM.01913-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weinberger DM, et al. Pneumococcal capsular polysaccharide structure predicts serotype prevalence. PLoS Pathog. 2009;5(6):e1000476. doi: 10.1371/journal.ppat.1000476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McCormick AW, et al. Geographic diversity and temporal trends of antimicrobial resistance in Streptococcus pneumoniae in the United States. Nat Med. 2003;9(4):424–430. doi: 10.1038/nm839. [DOI] [PubMed] [Google Scholar]
- 13.Chewapreecha C, et al. Dense genomic sampling identifies highways of pneumococcal recombination. Nat Genet. 2014;46(3):305–309. doi: 10.1038/ng.2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Turner P, et al. A longitudinal study of Streptococcus pneumoniae carriage in a cohort of infants and their mothers on the Thailand-Myanmar border. PLoS One. 2012;7(5):e38271. doi: 10.1371/journal.pone.0038271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Croucher NJ, et al. Population genomics of post-vaccine changes in pneumococcal epidemiology. Nat Genet. 2013;45(6):656–663. doi: 10.1038/ng.2625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Feikin DR, et al. Antibiotic resistance and serotype distribution of Streptococcus pneumoniae colonizing rural Malawian children. Pediatr Infect Dis J. 2003;22(6):564–567. [PubMed] [Google Scholar]
- 17.Lipsitch M, et al. Estimating rates of carriage acquisition and clearance and competitive ability for pneumococcal serotypes in Kenya with a Markov transition model. Epidemiology. 2012;23(4):510–519. doi: 10.1097/EDE.0b013e31824f2f32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dawid S, Roche AM, Weiser JN. The blp bacteriocins of Streptococcus pneumoniae mediate intraspecies competition both in vitro and in vivo. Infect Immun. 2007;75(1):443–451. doi: 10.1128/IAI.01775-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wade MJ. A gene’s eye view of epistasis, selection and speciation. J Evol Biol. 2002;15(3):337–346. [Google Scholar]
- 20.Chewapreecha C, et al. Comprehensive identification of single nucleotide polymorphisms associated with beta-lactam resistance within pneumococcal mosaic genes. PLoS Genet. 2014;10(8):e1004547. doi: 10.1371/journal.pgen.1004547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gupta S, et al. The maintenance of strain structure in populations of recombining infectious agents. Nat Med. 1996;2(4):437–442. doi: 10.1038/nm0496-437. [DOI] [PubMed] [Google Scholar]
- 22.Watkins ER, et al. Vaccination drives changes in metabolic and virulence profiles of Streptococcus pneumoniae. PLoS Pathog. 2015;11(7):e1005034. doi: 10.1371/journal.ppat.1005034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Weinberger DM, Malley R, Lipsitch M. Serotype replacement in disease after pneumococcal vaccination. Lancet. 2011;378(9807):1962–1973. doi: 10.1016/S0140-6736(10)62225-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mehtälä J, Antonio M, Kaltoft MS, O’Brien KL, Auranen K. Competition between Streptococcus pneumoniae strains: implications for vaccine-induced replacement in colonization and disease. Epidemiology. 2013;24(4):522–529. doi: 10.1097/EDE.0b013e318294be89. [DOI] [PubMed] [Google Scholar]
- 25.Finkelstein JA, et al. Antibiotic-resistant Streptococcus pneumoniae in the heptavalent pneumococcal conjugate vaccine era: predictors of carriage in a multicommunity sample. Pediatrics. 2003;112(4):862–869. doi: 10.1542/peds.112.4.862. [DOI] [PubMed] [Google Scholar]
- 26.Jorgensen JH, Turnidge JD. Manual of Clinical Microbiology. 11th Ed. American Society of Microbiology; Washington, DC: 2015. Susceptibility test methods: dilution and disk diffusion methods; pp. 1253–1273. [Google Scholar]
- 27.Huang SS, et al. Continued impact of pneumococcal conjugate vaccine on carriage in young children. Pediatrics. 2009;124(1):e1–e11. doi: 10.1542/peds.2008-3099. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.