Modeling the role of voyaging in the coastal spread of the Early Neolithic in the West Mediterranean

Significance

The Neolithic expansion in Europe took place at an average rate of 1 km⋅y⁻¹. In the West Mediterranean, the archaeological record yields a much faster rate of spread, one that cannot be explained by classical overland models. Voyaging has been put forward as an alternative line of explanation. Here, we develop a computational model to identify the key elements and mechanisms and to estimate the values that yield outcomes that fit the observations. The results show that voyaging is indeed required to explain the pattern. We have also found that interactions with local hunter-gatherers played a lesser part in the fast rate of spread.

Abstract

The earliest dates for the West Mediterranean Neolithic indicate that it expanded across 2,500 km in about 300 y. Such a fast spread is held to be mainly due to a demic process driven by dispersal along coastal routes. Here, we model the Neolithic spread in the region by focusing on the role of voyaging to understand better the core elements that produced the observed pattern of dates. We also explore the effect of cultural interaction with Mesolithic populations living along the coast. The simulation study shows that (i) sea travel is required to obtain reasonable predictions, with a minimum sea-travel range of 300 km per generation; (ii) leapfrog coastal dispersals yield the best results (quantitatively and qualitatively); and (iii) interaction with Mesolithic people can assist the spread, but long-range voyaging is still needed to explain the archaeological pattern.

The Neolithic transition in Europe spread at an average rate of about 1 km⋅y⁻¹ (1, 2). This process can be modeled by the so-called wave-of-advance model, which describes a progressive land-based expansion due to population growth and short-range migratory activity (3). Ancient DNA studies provide support for a mainly demic expansion in many parts of Europe (4), involving two main pathways: one up the Danube, connected with the spread of the Linearbandkeramic (LBK) culture (5, 6), and the other along the Mediterranean shores (7).

Current radiocarbon dates indicate a coastal spread in West Mediterranean Europe taking place at a much faster rate (above 5 km⋅y⁻¹) than one would expect on the basis of the classical wave-of-advance model. An alternative approach is needed to explain this process. The maritime pioneer colonization model (8, also refs. 9, 10) postulates a sea-based expansion that involves voyaging along the coast in the form of cabotage (with the possibility of making a short stop here and there along the way). This model drew upon new and more reliable carbon-14 dates [including accelerator mass spectrometry (AMS) determinations on short-lived samples to avoid the old wood effect], and is consistent with a demic expansion and the observed pattern (alternative approaches to the West Mediterranean spread are discussed in ref. 11). During the past 15 y, quality dates for the Early Neolithic in the West Mediterranean have continued to come in. As a result, the overall pattern is now more refined but remains consistent with the maritime pioneer model.

Voyaging during the Early Neolithic is well documented in the Eastern Mediterranean (e.g., refs. 12–14). From the distribution of obsidian artifacts in the Cyprus, Aegean, and Tyrrhenian basins, we know that its quantity tends to fall off with distance from a given source and that long-distance crossing of the open sea between these three basins is extremely rare (15). In short, it is fair to say that early voyaging in the eastern and central parts of the Mediterranean was kept on a comparatively short leash. In the West Mediterranean, obsidian is far less common at Early Neolithic sites; it occurs in small numbers at the sites of this age in southern France (16), and it has yet to be documented in the case of the Iberian Peninsula (17). In other words, obsidian from the island of Sardinia did not reach the east coast of Spain. Accordingly, it is reasonable to think that the initial spread of the Neolithic in the west took place along coastal routes by first farmers ultimately coming from northwest Italy (proposed alternative routes, which are not supported by reliable evidence, are discussed in ref. 18).

The purpose of this article is to put forward a new and more quantitative approach to the question of the exceptionally fast spread of the Neolithic in the west, one that focuses on the role of voyaging. We perform computational simulations to identify the underlying mechanisms of voyaging and estimate the associated parameters that can account for the archaeological pattern. Previous computational approaches that included sea travel only analyzed its average effect on a continental scale (19). Thus, this modeling exercise is needed to understand better the processes at work in the coastal spread of first farmers in the West Mediterranean.

Although the models considered here are principally demic in character, such a fast coastal spread may well have entailed some interactions with local Mesolithic populations. Interaction can take place in a range of different forms, from exchanges of information and material culture to the adoption of farming as a way of life by a Mesolithic community. As a first step, we explore briefly two aspects of population interaction: cross-mating and acculturation [also called vertical and oblique/horizontal cultural transmission, respectively (20)].

Methods

Neolithic Chronology.

The database used in this study (available as Dataset S1) contains high-quality dates from 42 Early Neolithic sites of the West Mediterranean, including northwest Italy, southern France, Spain, Portugal, and northern Morocco, most of which have a coastal location. For each site, the earliest date has been selected to estimate the time when the Neolithic first arrived in a given area.

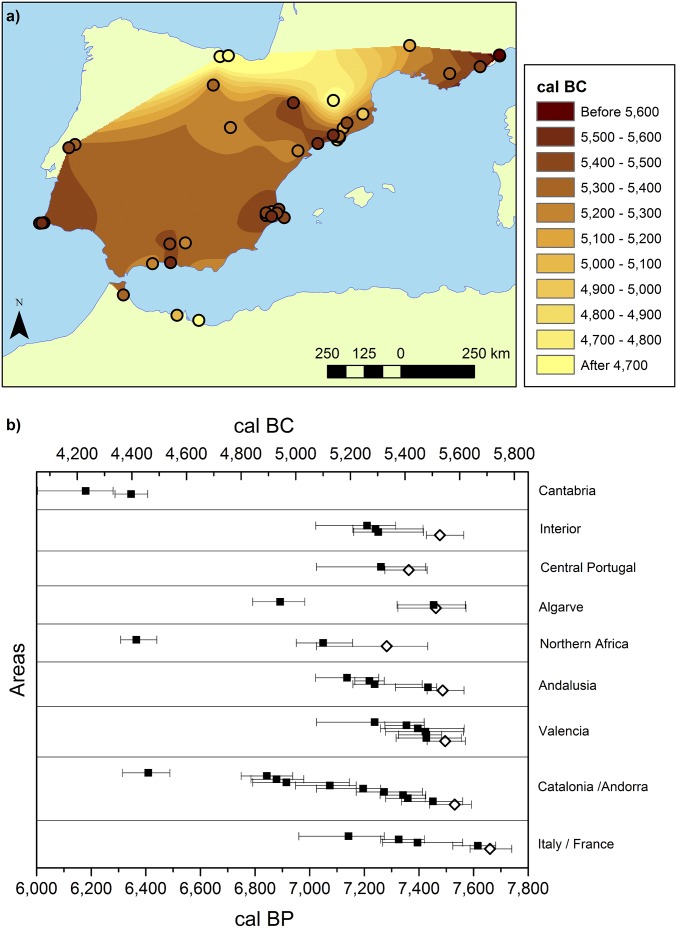
The sites are represented in Fig. 1A as circles, colored according to their calibrated dates. We analyze the dates by applying natural neighbor interpolation (background color scale in Fig. 1A), which provides a basic picture of the Neolithic spread. The map suggests an inland expansion from nearly coeval discrete locations along the coast. It also shows that the expansion into the Cantabrian region is an independent process, probably taking place from the interior toward the coast and at a later time; thus, this area is not taken into consideration below.

Fig. 1.

Early Neolithic sites and chronology of the Neolithic spread in the West Mediterranean. (A) Archaeological sites (circles) are colored according to the median of the calibrated age range of their earliest date. The interpolation map has been obtained by using the natural neighbor technique and disregarding coastal sites with medians younger than 5000 BC to avoid masking effects. Those sites disregarded in the interpolation are Vale de Boi (4943 BC), La Draga (4966 BC), Pou Nou 3 (4930 BC), Cova de St Llorenç (4894 BC), and El Zafrín (Islas Chafarinas; 4416 BC). (B) Database dates represented by areas and chronologically (following, from bottom to top, the order in Dataset S1). Symbols represent the calibrated dates before Christ (cal BC), and the error bars indicate their 2σ error ranges. The dates shown as diamonds are the earliest for each area and are the dates used to test the validity of the different models; they are also shown as diamonds in Figs. 2–4.

The dates in Fig. 1A are basically clustered in areas. Accordingly, we show in Fig. 1B the median of each site’s 2σ calibrated age range (given by error bars) arranged in terms of space and time. Because we are interested in being able to reproduce the time of first arrival, only the earliest date per coastal area (excluding Cantabria) is compared with the simulation results. The eight sites yielding such dates (listed in SI Appendix, Table S1) are represented as diamonds in Fig. 1B. The predicted arrival time in the interior area is given for purposes of reference.

Computational Simulations.

We have written four computational models that aim to simulate the Neolithic spread in the West Mediterranean. A model is always a simplification of the complex processes taking place in human events; in this case, we use models that follow a dispersion-interaction-reproduction scheme, which allows us to study different possibilities for each of these three steps. We apply a deterministic approach, which gives a good approximation to the averaged stochastic process, because we are not trying to reconstruct the exact processes that took place but, rather, to assess the range of scenarios that may have led to the observed pattern.

We run the simulations on a Cartesian grid of 50-km × 50-km cells, which are classified as inland, coastal, or sea cells. The size of a cell is obtained from ethnographic data on mobility (21), and it is consistent with the spatial framework used in a recent land-based computational analysis for the Iberian Peninsula (22, also ref. 23). In agreement with the hypothesis that first farmers spread by means of cabotage voyaging, the starting point chosen for the simulations is, in space, the cell that contains the oldest and easternmost site in the database, Arene Candide (7660 calibrated B.P.) in northern Italy, and, in time, 7700 calibrated B.P. (5751 BC). From there, the simulation runs for a series of iterations (e.g., 50 for the slowest spreads), with each iteration corresponding to one generation, for which we use the realistic value of 32 y (24). During a given iteration, three steps are performed as described below (a more detailed description is provided in SI Appendix).

Step 1: Dispersion.

Land dispersion takes place so that 38% of the population stays put in a cell. This value, which is called the persistence in demography, is taken from ethnographic data (21). The rest of its population relocates homogeneously to the four nearest neighbors. When one (or more) of the four neighbors is a sea cell, the population that should move there will be redistributed according to one of the four models that we used. Model 1 does not allow travel by sea, so the population that cannot “settle” in a sea cell does so in its other habitable neighbors (land/coastal cells). Model 2 allows voyaging along the coast up to a certain range, but with preferential attachment to the nearest cells (we use a Gaussian curve as the dispersal probability function). Model 3 allows for voyaging along the coast within a certain range, with all distances having an equal probability. Model 4 is based on a leapfrog process, with all voyagers relocating at a given distance measured along the coast (reached by means of cabotage), skipping over several cells between a starting place and a destination. Seagoing takes place in models 2–4 by means of cabotage [i.e., sea-travel distances are measured along the coast instead of along straight lines as in previous simulation models (19, 25)] and moves in an outward direction.

Step 2: Population interaction.

When both farmer and hunter-gatherer populations are present in a given cell, they can interact. In broad terms, this interaction can involve rich and complex processes. Here, we consider two main forms of interaction: vertical and horizontal/oblique cultural transmission (20).

Vertical cultural transmission relates to cross-mating between late hunter-gatherers (M) and first farmers (N), whose children we take to become farmers in agreement with ethnographic evidence (26, 27). We compute the number of cross-matings per generation as

$$I_{VT}=\eta \frac{N\cdot M}{N+M},$$ [1]

where $\eta \in \left[\mathrm{0,1}\right]$ indicates the degree of interbreeding (28).

Horizontal/oblique cultural transmission relates to hunter-gatherers who adopt farming; we compute the number of acculturated Mesolithic individuals per generation as

$$I_{HT}=f\frac{N\cdot M}{N+\gamma M},$$ [2]

where the ratio $C=f/\gamma$ gives the number of hunter-gatherers that a pioneer farmer (i.e., for $N<<M$) teaches or converts to farmers (29). Note that, in general, acculturation could also take place at different levels, with the local population acquiring certain traits but not becoming full farmers in one generation; however, here we use Eq. 2 as a first approximation to the process.

Step 3: Population growth.

Finally, we compute the new generation in each cell by applying population growth to the parent generation (couples of farmers, mixed couples, and couples of hunter-gatherers who have adopted farming). We compute the new size of the population as

$$\{\begin{array}{cc}N(t+T)=R_{0}N\left(t\right)& if\hspace{0.17em}N<N_{\max }\\ N(t+T)=N_{\max }& if\hspace{0.17em}N\ge N_{\max }\end{array},$$ [3]

where the maximum population per cell is $N_{\max }=\mathrm{3,200}\hspace{0.17em}\text{individuals}$. This value is obtained from a maximum population density of $1.28\hspace{0.17em}\hspace{0.17em}{\text{individuals/km}}^2$ (30) and the size of the cells. The reproduction coefficient is $R_0=\exp \left(aT\right)$ (21), where a is the intrinsic growth rate and $T$ is the generation time. Using a logistic approach instead of Eq. 3 will yield the same results; however, in more general cases, Eq. 3 avoids negative population numbers, whereas a logistic treatment does not (21, 31).

The position of the Neolithic front is identified as the cells that have reached, for the first time, a population of 300 Neolithic individuals during a given iteration. We have chosen this value (about 10% of the maximum cell population) as a practical threshold to compare the simulation outcomes with the archeological pattern. The simulated arrival times for the respective cells can be plotted on a map and then compared with the observed archeological dates to evaluate the goodness of fit between the two.

Results and Discussion

Our main interest is in reproducing the earliest arrival of the Neolithic in areas along the West Mediterranean coasts. For this reason, we compare the simulation results with a database consisting of the earliest high-quality Neolithic dates in the region (Dataset S1). As explained in Methods, we compare the simulation results with the earliest date for each area of interest (diamonds in Fig. 1B). We consider a model to predict the observed arrival time correctly if the simulated arrival time falls within the 2σ calibrated range (represented by a white diamond in Figs. 2 and 4). Otherwise, we consider the simulation to arrive either “too late” (the modeled expansion is too slow; represented by a black diamond) or “too early” (the modeled expansion is too fast; none of our maps contain such a case).

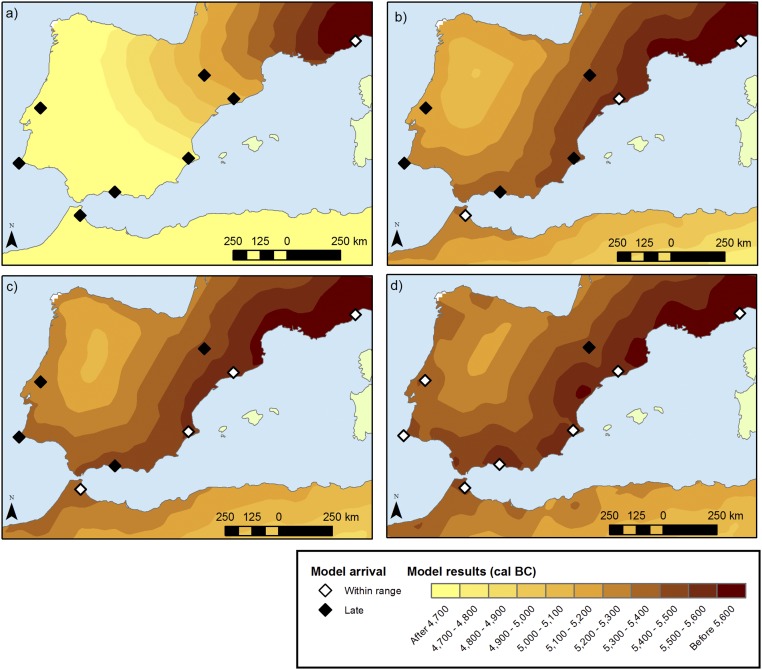
Fig. 2.

Model predictions for the Neolithic expansion. (A) Model 1: no voyaging. (B) Model 2: voyaging along the coast within 350 km with preference for closer destinations. (C) Model 3: voyaging along the coast with all destinations within 350 km being equally probable. (D) Model 4: leapfrog voyaging with jumps of about 350 km. White diamonds represent areas reached within the calibrated 2σ range; black diamonds represent areas reached by the model later than the calibrated range. (In all panels, voyage distances are computed along the coast and a = 2.8%.)

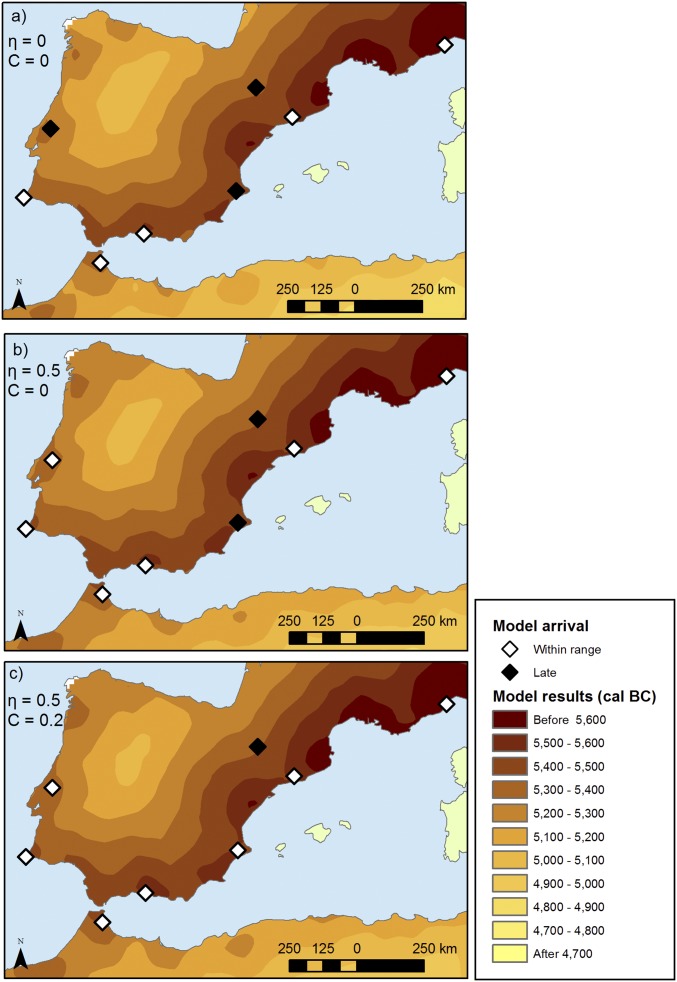
Fig. 4.

Effect of Neolithic–Mesolithic interaction on the expansion process. The results derive from the use of model 4, with a voyage range of 350 km and an intrinsic growth rate of a = 1.8% for three cases: no interaction (A; η = 0, C = 0), vertical cultural transmission only (B; η = 0.5, C = 0), and vertical and horizontal cultural transmission (C; η = 0.5, C = 0.2). We assume Mesolithic bands of 50 people, but the results for 80 people are similar (SI Appendix). White diamonds represent areas reached within the calibrated 2σ range; black diamonds represent areas reached by the model later than the calibrated range.

Below, we study the effects of each of the three steps in the simulation process (dispersal, interaction, and reproduction) to identify the necessary conditions for the spread to reach each of the respective areas at the right time.

Voyaging Mechanisms.

We first study and try to characterize the importance and dynamics of coastal voyaging in the West Mediterranean expansion. The analysis of the database by interpolation (Fig. 1A) supports the inference of a process of inland expansion from nearly coeval coastal source points. This pattern fits with a fast coastal expansion characterized by long-distance jumps. However, for the sake of completeness, we explore four different dispersal mechanisms, taking into consideration voyages that range from 50 to 1,000 km. In all cases, we use a growth rate of a = 2.8%. This value is taken from data on preindustrial farming populations (32), and it is consonant with other independent estimates of preindustrial farming populations, a = 2.5% (33), as well as with estimations obtained from Neolithic skeletal remains, a = 2.4% (34).

When no maritime dispersal is taken into account (model 1), the predicted Neolithic front is much slower than the observed arrival times, reaching Portugal more than 1,000 y too late. Indeed, comparing Fig. 2A with Fig. 1A shows that this model does not fit the archaeological data. This result is, of course, expected (supporting the position that overland dispersion cannot explain the data), and voyaging has to enter the picture.

Any model in which first farmers can travel by sea improves the previous simulation results. Considering a kernel where voyagers settle at successive locations along the coast within a specified range of distances (models 2 and 3) can yield “perfect” coastal fits (i.e., with all coastal areas reached within the 2σ range) when voyaging is of sufficient length. Model 2 requires voyages of up to 600 km to reach all of the coastal areas by observed arrival dates, whereas in the case of model 3, one can obtain a similar result with somewhat lower voyage ranges (over 450 km). For lower ranges, the simulations provide better results when a larger fraction of the population traveling by sea settles away from its point of departure. This behavior can be seen in Fig. 2, where for a given range of 350 km, model 3 (Fig. 2C) yields a slightly better fit (white diamonds) than model 2 (Fig. 2D).

Model 4, which takes a leapfrog approach, is the one that yields the best results with lower voyaging ranges. Indeed, assuming jumps of 350 km, all coastal areas are reached by the time of their observed arrival dates (Fig. 2D). For this model, good simulation results can also be obtained for coastal jumps of 450 km, and other jump distances between 350 km and 600 km are marginally consistent with the observed data, reaching one or two coastal areas either slightly too late (less than one generation) or else too early (less than two generations).

Thus, we find that model predictions improve when more individuals relocate to the most distant places within a given range (model 4). This scenario, in turn, allows us to obtain good fits with lower voyaging ranges. We can also see in Fig. 2 that only in this scenario (model 4; Fig. 2D) can we recover a pattern with multiple points of coastal entry similar to the data (Fig. 1). In contrast, the other models yield a progressive expansion. In short, model 4 yields the best results, both from a qualitative point of view and from a quantitative one.

Note that although we are using a deterministic treatment where all sea jumps happen to have the same length (model 4), we do not mean to imply that this treatment reproduces exactly how the process took place. What we have found is that, to account for the coastal spread of the Early Neolithic across the whole of the West Mediterranean, first farmers must have advanced by means of cabotage jumps of at least 350 km, but the exact length of a given voyage may well have been determined by socioecological factors [e.g., presence of river mouths (22)] not included in model 4.

In addition, we can see that areas in the Iberian interior are often reached too late on the basis of the voyage ranges considered above (e.g., black diamond in Fig. 2D), implying that the land-based part of the expansion in these areas needs a more refined treatment. For the northeast, in particular, the role of the Ebro River in facilitating inland expansion along its banks, as suggested for the Danube-Rhine corridor in the LBK expansion (35), needs to be considered. A fuller study of this dynamic, however, is beyond the purpose of this article.

Coastal Speed.

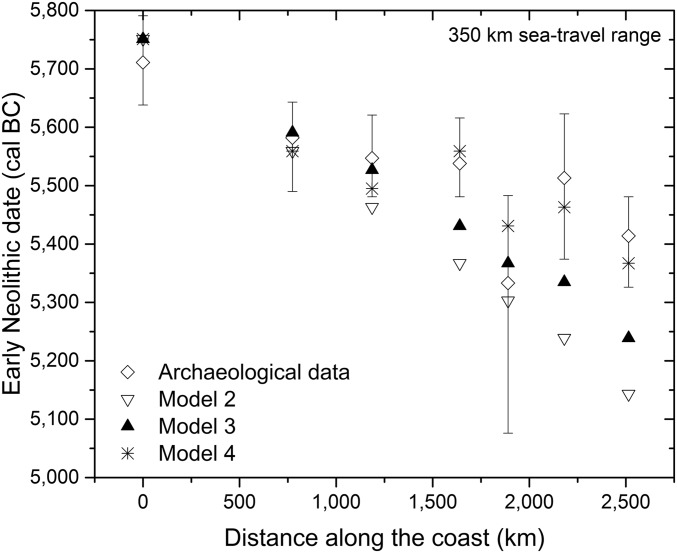
As a complementary visualization to the simulation results shown in Fig. 2 and to compute the coastal rate of spread, arrival times versus coastal distance to Arene Candide (the origin of the simulation) are plotted in Fig. 3 for each of the seven coastal areas (the much slower model 1 is excluded because it would fall out of range; note that distances are measured following the coastline and not from straight lines between locations). Fig. 3 shows that up to about 1,000 km from the origin, the three models that involve voyaging behave much the same and that it is only at further distances that a leapfrog scenario (model 4) provides a better fit.

Fig. 3.

Early Neolithic dates against distance along the coast to Arene Candide. For each area defined in Fig. 1B, its earliest date is represented (diamonds) with its 2σ error range (error bars). Simulation results at the same location as the archaeological data are also plotted for the three models with maritime voyaging: model 2 (inverted triangles), model 3 (triangles), and model 4 (stars). All simulations have been computed with the same parameters as Fig. 2 (a = 2.8% and sea-travel ranges of 350 km).

Computing the speed from the archeological data, we obtain that the coastal expansion took place at about 8.66 km⋅y⁻¹ (R = 0.830). For the parameters considered (a = 2.8% and voyage ranges of 350 km), the predicted rates of spread are: 1.70 km⋅y⁻¹ (R = 0.925) for model 1, 4.22 km⋅y⁻¹ (R = 0.999) for model 2, 5.02 km⋅y⁻¹ (R = 0.998) for model 3, and 7.66 km⋅y⁻¹ (R = 0.918) for model 4. Thus, model 4 agrees best with the observed spread rate. Note how a voyage range of 350 km does not imply that the coastal front advances at a speed of 350 km per generation (i.e., about 10.9 km⋅y⁻¹). On the contrary, the front is substantially slower. Because only a fraction of the population living at a coastal site will travel by sea, the population at the front will sometimes be only a few individuals; thus, the Neolithic front may be stalled until the population number has grown. In fact, a general feature of reproduction-dispersal models is that the front speed is equal to the jump length divided by the time between successive jumps (350 km per generation in our case) only if the reproduction rate is sufficiently high; otherwise, the front travels at a slower speed (36).

Sensitivity to Simulation Origin.

As argued earlier, the choice of a starting point located on the mainland (Arene Candide) is consistent with the distribution of obsidian artifacts in the region (obsidian from sources on the off-shore island of Sardinia are not found at Early Neolithic sites in Spain) and with voyaging in the form of cabotage as the means of the coastal spread (18). Because the choice of the cell of origin can affect the locations where the pioneer voyagers arrive in the models, it might modify, in principle, the ranges that yield the best fit. Therefore, we have repeated the simulations for model 4, shifting the origin first one or two cells eastward and then likewise to the west, while keeping the starting year at 7700 B.P. (5751 BC). Recall that the distance between the centers of two adjacent cells is 50 km. Studying the results from these other possible origins, the best fits are still obtained with leaps of 350–450 km (although “jumps” of up to 600 km may also yield agreement with the observed data). In other words, our results are not affected by the exact origin chosen for the simulation runs.

Growth Rate.

We have also tested a wider range of growth rates in the case of model 4 to learn more about their effect. In short, increasing the growth rate improves the results when shorter jumps are involved, but not for values of voyaging below 300 km (even considering a = 4%, which is an unrealistically fast reproduction rate for human populations). Clearly, this finding implies that a minimum jump length is necessary.

In addition, we have evaluated the extent to which the growth rate could be lower than the maximum values reported in the ethnographic and archeological literature (a = 2.8%). In the case of model 4, we find that for jumps in the range of 350–450 km, we could lower the growth rate to a = 2.3%, close to the value of a = 2.4% (34) estimated on the basis of the archaeological record, and still obtain much the same goodness of fit.

Population Interaction.

Although the archaeological record for the Late Mesolithic in many areas of the West Mediterranean is still quite modest, there are Late Mesolithic sites on the coast of Portugal that provide good evidence of the side-by-side coexistence of late hunter-gatherers and first farmers over a fair arc of time (8). On the other hand, there is still a shortage of good evidence for the nature and temporal length of Mesolithic and Neolithic coexistence along the Spanish coast (37). On the Mediterranean coasts of France and northern Italy, the evidence so far does not support the idea of coexistence of any real length of time (38, 39). In short, given the paucity of evidence on the Late Mesolithic currently available for most of the region, we explore a few basic scenarios in this section rather than test a specific hypothesis.

So far, all of the Late Mesolithic sites found in Iberia are located either near the coast or else on a river valley (e.g., the Ebro Valley), with no evidence for Mesolithic populations in the central Meseta (37). In this light, and with the aim of evaluating the effects of interaction, we consider that Mesolithic populations were restricted to coastal cells. Following the ethnographic evidence for populations of hunter-gatherers living on the coasts of southwest Tasmania (40), we assume a band of 50 hunter-gatherers per cell (50 km on each side; the results for a larger band size, 80 individuals, are given in SI Appendix).

Let us consider that Neolithic individuals relocate according to model 4 (with voyages of 350 km). Because the two processes of population interaction discussed briefly here (cross-mating and acculturation) result in the incorporation of Mesolithic people into Neolithic communities, the effective population growth is increased (i.e., not all of population growth is due simply to childbearing on the Neolithic side). Accordingly, in this section, for the first farmers’ side of the interaction, we consider the growth rate of a = 1.8%; for example, Fig. 4A shows the results for a purely demic spread under such conditions.

The first form of interaction, known as vertical cultural transmission (20), assumes that some newcomers (first farmers) mate with individuals in the local Mesolithic population. For example, in accord with ethnographic parallels, we expect voyaging male farmers to mate with local female hunter-gatherers, who will then become part of the farmer population (27). Such cross-mating, which is taken into account in Fig. 4B, will give rise to a slightly faster rate of spread (compare Fig. 4 A and B, especially in the Portuguese case, where the effect is more pronounced due to the cumulative effect of continually adding population at the front). In this case, the arrival times for the respective coastal areas are correctly predicted only for the maximum possible value of the interbreeding parameter, $\eta =1$ (28). It is, however, important to note that such a high interbreeding level is highly unlikely when we bear in mind that only a small proportion of female hunter-gatherers will be available for interbreeding (i.e., women between, say, 15 and 30 y old who do not already have a partner).

The other form of interaction, as mentioned above, is acculturation or recruitment [known also as horizontal/oblique cultural transmission (20)], that is, Mesolithic individuals or families who adopt first farming and become part of the Neolithic community. Because values for the acculturation parameter $C$ (the number of hunter-gatherers incorporated in this way into the farming community per pioneer farmer per generation) are not well known today, we have chosen three values to illustrate three quite different scenarios: $C=0.2$, $C=1$, and $C=10$. Again, as expected, the incorporation of acculturated farmers in Neolithic populations gives rise to a faster spread. When no vertical cultural transmission is taken into account, the model requires that at least one hunter-gatherer adopts farming per pioneer farmer ($C=1$) in order for the expansion to reach all coastal areas in agreement with their observed arrival times. Interestingly, increasing the acculturation parameter to $C=10$ yields almost no change in the simulations’ arrival times. The reason for this result is that the number of Mesolithic individuals per cell (e.g., up to 50 individuals) is relatively small, so the potential contribution of Mesolithic acculturation to increases in the rate of spread is limited.

Finally, we can combine these two forms of interaction by using somewhat lower intensities for each process in a simulation run. For example, as shown in Fig. 4C, we obtain a good fit with the observed arrival dates for an interbreeding level of $\eta =0.5$ and an acculturation level of $C=0.2$ (one Mesolithic individual brought into first farming for every five pioneer farmers per generation). Again, further increasing the value of C yields little change in the simulation outcomes (maps are provided in SI Appendix).

From these results, we see that including such interactions gives rise to faster rates of spread with somewhat lower rates of population growth intrinsic to the spreading farmers. However, it does not eliminate the need for voyages that involve a distance of at least 300 km. In addition, it is worth adding that rates of interbreeding and incorporation that are too high will yield the complete acculturation of Mesolithic populations within one or two generations of first contact. However, this rate of acculturation is clearly at odds with the evidence for the coexistence of the two populations in Portugal over a notable span of time. Even for areas with shorter spans of coexistence, such a high pace of incorporation is probably unwarranted. In other words, it is more likely that cross-mating and acculturation took place at lower levels of intensity alongside other forms of interaction, such as a hunter-gatherer acting as a guide with local knowledge or else participating in a voyage led by a first farmer with a boat. The latter kinds of interaction are called mutualism (3), and they too would have made positive contributions to such things as choosing the new place for a first farmer to settle or having enough crew members on hand to set out on a voyage.

Conclusions

The initial spread of the Neolithic in the West Mediterranean shows a clear pattern: a rapid expansion that involved multiple points of entry along the coast. This pattern led to the formulation of a model based on voyaging, which provides both a confirmation and an extension of the maritime pioneer model (8). In this article, we have explored several quantitative models of the spread (with and without voyaging) and found that (i) sea travel, as opposed to a land-based expansion, is necessary to explain the spread of the Early Neolithic in the West Mediterranean and (ii) the best fit with the observed pattern of arrival times is one in which voyaging, in the form of cabotage, takes place by means of long-distance relocations. These findings now make it possible to put forward distances of voyage dispersal in the range of 300–450 km. Although such distances might appear to be extreme (they came as a surprise to us), they are necessary to match the observed pattern of arrival dates. In fact, no value of voyaging below 300 km can fit with this pattern.

We have also found that to achieve a fast enough spread, an effective growth rate of at least 2.3% is called for. This growth rate can be achieved directly by means of reproduction and also through some level of interaction with local Mesolithic populations. Here, we have considered two cases: incorporation of Mesolithic individuals either by means of mating or by means of acculturation. The results show that population interaction can play a positive role in the rapid spread of the Early Neolithic, although its contribution is limited by the small size of Mesolithic populations. On the other hand, the level of incorporation called for to achieve a major effect on the rate of spread would be higher than what is consistent with the coexistence between the early Neolithic and the final Mesolithic observed in Portugal (8). Nonetheless, we think that some level of interaction was required to sustain such a high rate of spread over a span of some 300 y; thus, other mechanisms not requiring the adoption of early farming, such as mutualism, may have played a role as well.

In summary, our results point toward a spread driven by small groups of first farmers who relocated by means of voyaging over distances of 300–450 km at the expanding front. Interaction with local hunter-gatherers, in the form of cross-mating, acculturation, or mutualism (or some combination of the three), would have facilitated the growth of farming populations and, in turn, their rapid spread in the West Mediterranean.

Future Perspectives

The results presented here define some boundaries for the interpretation of population history; they also provide a basis for future inferences with respect to questions that have yet to be explored in greater depth. To develop a better knowledge of how the spread of first farming took place in the West Mediterranean, further research needs to be done along four main lines: (i) We need more and better dates for those areas where high-quality AMS dates are still not available; (ii) the best computational scenario obtained so far (model 4) can now serve as the starting point for a new generation of models with more complex dynamics (including a fuller treatment of the question of population interactions); (iii) in future work, it will be useful to incorporate more geographic detail (e.g., rivers, mountains) in modeling the inland spread; and (iv) the study of the DNA in Neolithic populations (to be done when more individuals come to light than the very limited sample available today) will provide an independent line of evidence for evaluating the conclusions reached in this article.