Harmonic template neurons in primate auditory cortex underlying complex sound processing

Significance

Harmonicity is a fundamental element of music, speech, and animal vocalizations. How the brain extracts harmonic structures embedded in complex sounds remains largely unknown. We have discovered a unique population of harmonic template neurons in the core region of auditory cortex of marmosets, a highly vocal primate species. Responses of these neurons show nonlinear facilitation to harmonic complex sounds over inharmonic sounds and selectivity for particular harmonic structures. Such neuronal selectivity may form the basis of harmonic processing by the brain and has important implications for music and speech processing.

Abstract

Harmonicity is a fundamental element of music, speech, and animal vocalizations. How the auditory system extracts harmonic structures embedded in complex sounds and uses them to form a coherent unitary entity is not fully understood. Despite the prevalence of sounds rich in harmonic structures in our everyday hearing environment, it has remained largely unknown what neural mechanisms are used by the primate auditory cortex to extract these biologically important acoustic structures. In this study, we discovered a unique class of harmonic template neurons in the core region of auditory cortex of a highly vocal New World primate, the common marmoset (Callithrix jacchus), across the entire hearing frequency range. Marmosets have a rich vocal repertoire and a similar hearing range to that of humans. Responses of these neurons show nonlinear facilitation to harmonic complex sounds over inharmonic sounds, selectivity for particular harmonic structures beyond two-tone combinations, and sensitivity to harmonic number and spectral regularity. Our findings suggest that the harmonic template neurons in auditory cortex may play an important role in processing sounds with harmonic structures, such as animal vocalizations, human speech, and music.

Many natural sounds, such as animal vocalizations, human speech, and the sounds produced by most musical instruments, contain spectral components at frequencies that are integer multiples (harmonics) of a fundamental frequency ($f_0$). Harmonicity is a crucial feature for perceptual organization and object formation in hearing. Harmonics of the same $f_0$ tend to fuse together to form a single percept with a pitch of $f_0$. The perceptual fusion of harmonics can be used for segregating different sound sources (1–3) or to facilitate the discrimination of vocal communication sounds in noisy environments (4–6). Harmonicity is also an important principle in the context of music perception. Two tones one octave apart are perceived to be more similar than tones at any other musical intervals, usually known as the octave equivalence in the construction and description of musical scales (7, 8). It has also been shown that harmonicity is correlated with preferences for consonant over dissonant chords (9–11). Therefore, understanding how the brain processes harmonic spectra is critical for understanding auditory perception, especially in the context of speech and music perception.

In the peripheral auditory system, a harmonic sound can be represented by its constituent parts that are decomposed (or resolved) into separate tonotopically organized frequency channels (12). The tonotopic organization starting from the cochlea is preserved at different stages up to the primary auditory cortex (A1) along the ascending auditory pathway, where many neurons are narrowly tuned to pure tones and can represent individually resolved frequency components in a harmonic sound with high precision (13–18). To form an auditory object based on harmonic spectral patterns, a central process is required to integrate harmonic components from different frequency channels. Such processing might be responsible for extracting pitch through template matching as has been previously suggested (19, 20), although the physiological evidence for such harmonic templates has been lacking. Auditory cortex has been shown to play an important role in harmonic integration in processing complex sounds. Patients with unilateral temporal lobe excision showed poorer performance in a missing fundamental pitch perception task than normal listeners but performed as normal in the task when the $f_0$ was presented (21). Auditory cortex lesions could impair complex sound discrimination, such as animal vocalizations, and vowel-like sounds without affecting responses to relative simple stimuli, like pure tones (22–24).

Primate auditory cortex is subdivided into a “core” region, consisting of A1 and the neighboring primary-like rostral (R) and rostral–temporal areas, surrounded by a belt region, which contains multiple distinct secondary fields (Fig. S1A) (25). Neurons in the core region are tonotopically organized and typically tuned spectrally to individual components of resolved harmonics or temporally to the modulation frequency of summed unresolved harmonics (13–16). Although a cortical region for representing low-frequency pitch (<1,000 Hz) near the low-frequency border between A1 and R has been implicated in both humans (26–29) and nonhuman primates (27), it remains unclear whether neurons in the core region can detect complex harmonic patterns across a broader frequency range. Previous studies using two tones showed that some neurons in A1 were tuned to more than one frequency, and those frequencies were sometimes harmonically related (30–32). Such findings suggest a neural circuitry in A1 for detecting harmonic structures more complex than two-tone combination, which may underlie the perceptual fusion of harmonic complex tones (HCTs). However, no study has provided direct evidence for such harmonic template processing at the single-neuron level in auditory cortex.

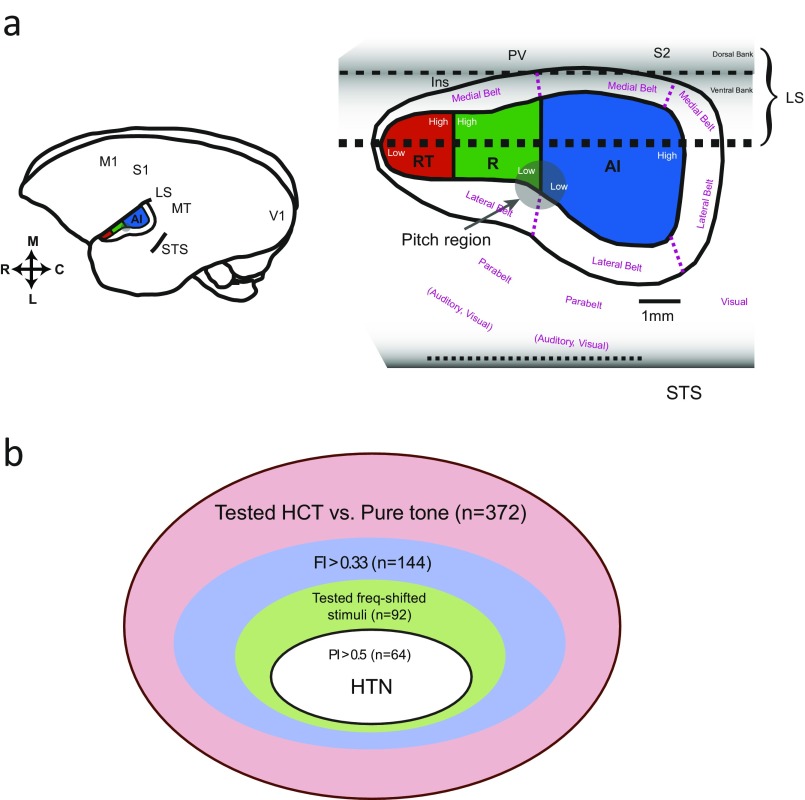
Fig. S1.

(A) A schematic drawing showing the organization of marmoset auditory cortex and the location of pitch region. Adapted from refs. 27 and 64. Inset shows the location of auditory cortex on the marmoset brain. C, caudal; Ins, insula; L, lateral; LS, lateral sulcus; M, medial; M1, primary motor cortex; MT, middle-temporal area; PV, parietal ventral area; RT, rostral temporal field; S1, primary somatosensory cortex; STS, superior temporal sulcus; S2, secondary somatosensory cortex. (B) A Venn diagram illustrating the criteria of identifying HTNs. C, caudal; L, lateral; LS, lateral sulcus; M, medial; RT, rostral–temporal.

In this study, we systematically evaluated harmonic processing by single neurons in the core area (A1 and R) of auditory cortex of the marmoset (Callithrix jacchus). The marmoset is a highly vocal New World primate, and its vocal repertoire contains rich harmonic structures (33). It has recently been shown that marmosets perceive harmonic pitch in a similar manner as humans (34). Using HCTs and other comparison stimuli, we identified a subpopulation of neurons that exhibited preference to particular HCTs over pure tones or two-tone combinations. Responses of these neurons were selective to fundamental frequencies ($f_0$) of HCTs over a broad range (400 Hz to 12 kHz) and sensitive to harmonic number and spectral regularity. Our findings suggest a generalized harmonic processing organization in primate auditory cortex that can be used to effectively extract harmonic structures embedded in complex sound sources, such as music and vocal communication signals.

Results

Identification of Harmonic Template Neurons.

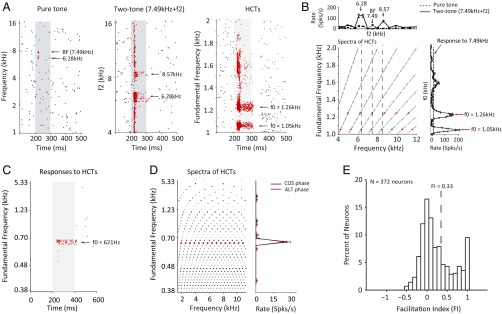
Most of the neurons in the core region of marmoset auditory cortex are responsive to pure tones, some only weakly. Fig. 1A shows an A1 neuron’s response to pure tones (Fig. 1A, Left), two tones (Fig. 1A, Center), and HCTs (Fig. 1A, Right). The level of individual components of an HCT or a two-tone combination matched the level of pure tones. This neuron responded weakly to pure tones near two frequencies (7.49 and 6.28 kHz), with the maximal firing rate at 7.49 kHz [determined as best frequency (BF)] (Fig. 1A, Left). When the BF tone was presented simultaneously with a second tone at varying frequency, this neuron’s response was enhanced at several f₂ frequencies (Fig. 1A, Center). The two-tone response profile shows higher firing rates than those of pure tones with two facilitatory peaks flanking the BF at 6.28 and 8.57 kHz, respectively (Fig. 1B, Upper). The response of this neuron was further enhanced when HCTs with varying $f_0$ values were presented. Fig. 1B, Lower Left illustrates the array of HCTs used in the testing, each having several spectral components, all of which are multiples of $f_0$. We systematically varied $f_0$ values and limited all harmonics within a two-octave frequency range centered at BF. At some $f_0$ values (e.g., 1.05 and 1.26 kHz), the responses were much stronger than the maximal responses to pure tones or two-tone stimuli and became sustained through stimulus duration (Fig. 1 A, Right and B, Lower Right). Because sustained firing is usually evoked by the preferred stimulus (or stimuli) of a neuron in auditory cortex of awake marmosets (35), we may consider that this example neuron preferred HCTs with particular $f_0$ values. The $f_0$ at which the maximal firing rate is evoked by an HCT is referred to as the best $f_0$ ($B{f}_0$). The neuron shown in Fig. 1 A and B, therefore, has a $B{f}_0$ at 1.05 kHz (Fig. 1B, Lower Right). Its $f_0$ tuning profile also has a smaller peak at 1.26 kHz. A close examination shows that the two HCTs corresponding to the two largest peaks at $f_0$ of 1.05 and 1.26 kHz both contain three spectral components that aligned with the BF (7.49 kHz) and the two frequencies (6.28 and 8.57 kHz) at the facilitatory peaks of the two-tone response profile (Fig. 1B, Upper and Lower Left, vertical dashed lines). The HCT at $f_0$ of 1.26 kHz is slightly misaligned from the HCT at $f_0$ of 1.05 kHz, resulting in a smaller firing rate in the $f_0$ tuning profile. These observations suggest that this neuron is tuned to a particular harmonic template.

Fig. 1.

Examples of neuronal responses to HCTs in A1. (A) Raster plots of an example neuron’s (M79u-U472) responses to (Left) pure tone, (Center) two tone, and (Right) HCTs. (B) Same neuron as shown in A. (Upper) Pure-tone and two-tone response curves. (Lower Right) Firing rate vs. f₀ tuning profile for HCTs. (Lower Left) Spectral components of HCTs (y axis: $f_0$; x axis: frequency of individual harmonics) used to test the neuron. Each row represents an HCT, with each dot representing a harmonic in the stimulus. Components in the HCTs corresponding to the two largest peaks in the firing rate vs. $f_0$ curve as shown in Lower Right plot are colored in red. Three vertical black dashed lines indicate BF and the two frequencies corresponding to the two facilitatory peaks in the two-tone response curve as shown in Upper plot. The firing rate curves are derived from the raster plots in A. Error bars represent SD of the mean firing rate. (C) Raster plots of another example neuron’s (M6x-U175) responses to HCTs. (D, Left) Spectral components of HCTs used to test the neuron shown in C. Harmonics of the preferred $f_0$ are colored in red. (D, Right) Firing rate vs. $f_0$ curves of the same neuron shown in C. The black curve is the f₀ tuning profile when all harmonics were added in cosine (COS) phase. The red curve is the f₀ tuning profile when all harmonics were added in alternating (ALT) phase (i.e., odd harmonics in sine phase, even harmonics in COS phase). (E) Distribution of the FI for all 372 neurons tested with HCTs. The vertical dashed line indicates the threshold FI value to identify HTNs (FI = 0.33; corresponding to 100% facilitation).

Another example of a neuron showing harmonic template tuning is shown in Fig. 1 C and D. This neuron did not respond to pure tones but was highly selective to HCTs with a $B{f}_0$ at 621 Hz (Fig. 1C) and was not sensitive to the phases of individual harmonics (Fig. 1D). Because the phases of individual harmonics determine the temporal envelope of an HCT and envelope modulation dominates the pitch perception of unresolved harmonics, the insensitivity to the phase of an HCT suggests a representation of resolved harmonics.

The examples described above show that a neuron’s selectivity to harmonic templates cannot be adequately predicted from its responses to pure tones or even two tones. They also suggest that some A1 neurons integrate multiple frequency components in HCTs in a nonlinear fashion. The increased firing rate to HCTs cannot be explained by the change in overall sound level because of the high selectivity to particular HCTs by these neurons. Although the overall sound level of an HCT increased monotonically with decreasing $f_0$, the firing rate evoked by an HCT did not change monotonically as shown by the example neurons in Fig. 1 B and D. We use a facilitation index (FI) to quantify the difference between the responses to HCTs and pure tones (Materials and Methods) for 372 single neurons recorded from A1 and R in four hemispheres of three awake marmosets (Fig. 1E). FI is defined as $({\text{R}}_{\text{HCT}}-{\text{R}}_{\text{Tone}})/({\text{R}}_{\text{HCT}}+{\text{R}}_{\text{Tone}})$. When FI is positive, it indicates a stronger response to HCTs than pure tones. FI equals one if a neuron only responds to HCTs but does not respond to pure tones and zero if a neuron has equal responses to HCTs and pure tones. Fig. 1D shows that a large proportion of sampled neurons showed response enhancement to HCTs over pure tones (FI > 0), a substantial minority (∼10%) of which only responded to HCTs (FI = 1).

Fig. 1D also indicates the diversity in neural responses to HCTs, with some neurons showing similar or even reduced firing rates compared with pure tones. One such example is shown in Fig. S2B (FI = 0.12). This neuron responded to the HCTs only when the stimuli contained the BF, and its responses decreased as the $f_0$ decreased, likely because of side-band inhibition evoked by dense spectral components surrounding BF (36). To illustrate such diversity, we show several more example neurons in Fig. S2. Some neurons showed enhanced responses to HCTs (FI > 0) but weak selectivity to $f_0$ values as shown by the example in Fig. S2A (FI = 0.59). The firing rate decreased monotonically as the $f_0$ increased. Because when the $f_0$ of HCTs increases, the number of harmonics within a neuron’s receptive field decreases, this neuron’s response reflects the preference for spectrally dense stimuli but not harmonic structures.

Fig. S2.

Examples of diverse responses to HCTs by non-HTNs. (A–D) Four examples of non-HTNs. (Lower Left) Spectral components of HCTs (y axis: $f_0$; x axis: frequency of individual harmonics), (Lower Center) raster plot of responses to HCTs in Lower Left, and (Lower Right) averaged firing rates at different $f_0$ derived from the raster plot. In the HCT spectra plots, each row represents an HCT, with a dot representing a harmonic in the stimulus. The black dashed lines indicate BF, corresponding to the frequency with the maximal firing rate in the pure tone tuning (Upper). Error bars represent SD of the mean firing rate.

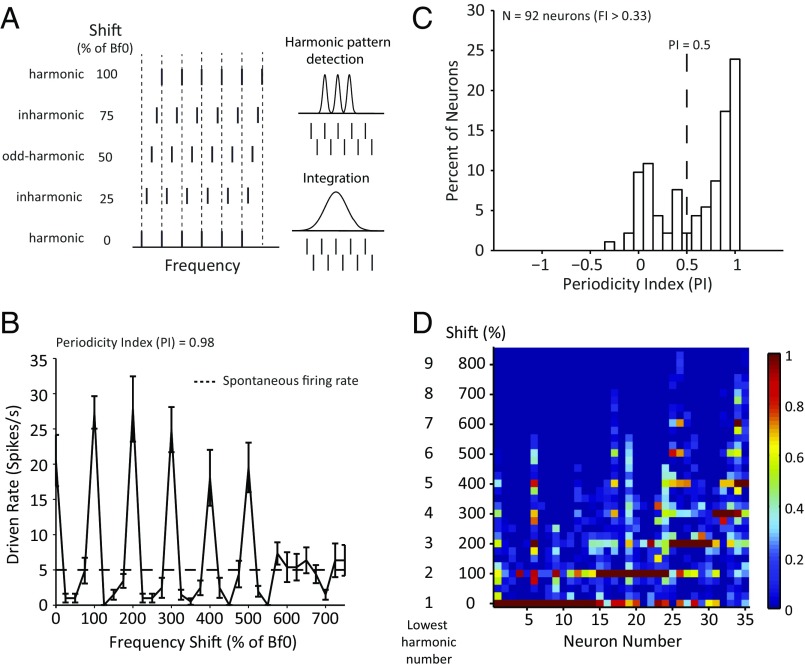
We use FI > 0.33 (representing >100% response enhancement to HCTs over pure tones) as one of two criteria to identify neurons that are selective to harmonic spectra; 144 of 372 tested neurons (38%) met this criterion. However, as examples in Fig. 1 and Fig. S2 show, the response enhancement for HCTs alone is not sufficient to distinguish harmonic pattern detection from spectral integration within receptive fields. We next used frequency-shifted complex tones to further test all candidate neurons. These stimuli were generated by adding frequency shifts to an HCT containing the first six harmonics of $B{f}_0$ (Fig. 2A). The shifts were proportional to $B{f}_0$, with an increment of $25\%\times B{f}_0$. In all shifted conditions, the spectral space between adjacent components remained the same, as did the envelope modulation of the complex tone. However, only at harmonic shifts (100, 200, and 300%…) were all components aligned with the original HCT. When the shifts were odd integer multiples of $50\%\times B{f}_0$ (“odd shifts”; $50\%\times B{f}_0$, $150\%\times B{f}_0$, and $250\%\times B{f}_0$,…), the tones were still harmonics of $B{f}_0/2$ but spectrally farthest from those in the original HCT. Therefore, if a neuron detects a specific harmonic pattern, its responses should be largest to harmonic shifts and smallest to odd shifts, whereas neural responses based on within-receptive field integration (either overall sound level or envelope modulation) should be insensitive or less sensitive to the frequency shifts as illustrated in Fig. 2A.

Fig. 2.

Selective responses to periodic spectra by HTNs. (A) An illustration of the spectra of HCTs and spectrally shifted tones relative to two different receptive fields. In this example, the first six harmonics are shifted in frequency by an increment of 25% × $B{f}_0$. All frequency components are summed in COS phase. (B) The responses of an HTN to HCTs and spectrally shifted tones. Error bars represent SD of the mean firing rate. The black dashed line indicates the spontaneous firing rate. (C) Distribution of the PI for 92 neurons with FI > 0.33. The vertical dashed line indicates the threshold PI value for defining HTNs. (D) More examples of the periodic response patterns to frequency shifts. Each column represents the data from an HTN neuron. Neurons are organized sequentially by the preferred harmonic numbers. The firing rates were normalized by the maximal firing rate for each neuron and are represented by a heat map.

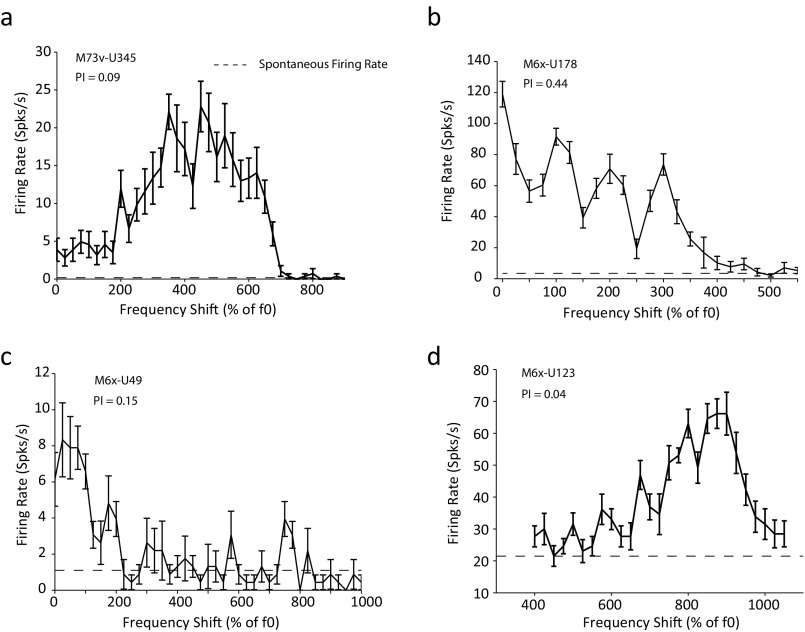
Fig. 2B shows an example neuron that exhibited a periodic response pattern as a function of the frequency shift, achieving maximal firing rates at harmonic shifts and minimum firing rates at odd shifts. Such response pattern indicates that this neuron detects harmonic patterns embedded in the stimuli and that the harmonics in the preferred pattern are resolved. A periodicity index (PI), defined as the averaged firing rate difference between each harmonic shift and adjacent odd shifts (Materials and Methods), was used to quantify a neuron’s sensitivity to harmonic patterns. PI equals one if a neuron only responds to harmonic shifts but shows no response to the odd shifts or zero if a neuron responds equally well to harmonic and odd shifts. The example neuron shown in Fig. 2B had a PI of 0.98. Of 144 neurons that had FI > 0.33, we were able to hold 92 neurons long enough to further test their responses to frequency shift stimuli. Fig. 2C shows the distribution of PI values of these 92 neurons. We used PI > 0.5 as the second criterion to define a class of neurons that are facilitated by and selective for harmonic complex sounds; 64 of 92 neurons (∼70%) had PI values greater than 0.5 (Fig. 2C). We will hereafter refer to the neurons that met both criteria (FI > 0.33 and PI > 0.5) as “harmonic template neurons” (HTNs). A Venn diagram illustrating the criteria of identifying HTNs is shown in Fig. S1B. Properties of the neurons that failed to qualify as HTNs will be systematically analyzed and reported in a separate publication. To contrast properties of HTNs, Fig. S3 shows some example neurons that satisfied the facilitation criterion (FI > 0.33) but failed to meet the periodicity criterion (PI > 0.5). The neurons shown in Fig. S3 A, C, and D do not show periodic response patterns to the frequency shift stimuli (PI = 0.09, 0.15, and 0.04, respectively), whereas the neuron shown in Fig. S3B shows a clear but weaker periodic response pattern (PI = 0.44) compared with the example neuron in Fig. 2B (PI = 0.98) that is classified as an HTN.

Fig. S3.

Additional examples of responses to frequency shifts by non-HTNs. (A–D) The responses of non-HTNs to HCTs and spectrally shifted tones. Error bars represent SD of the mean firing rate. The black dashed lines indicate the spontaneous firing rate.

Thus, for a neuron to qualify as an HTN, it must (i) show at least 100% response enhancement to HCTs over pure tones (FI > 0.33) and (ii) exhibit a clear periodic pattern to frequency-shifted HCTs (PI > 0.5). We would point out that these two criteria are stringent. We chose the threshold values of these two criteria to ensure that HTNs reflect the detection of harmonic spectral patterns. The number of neurons that qualified as HTNs under these experimental conditions likely represents an underestimate of the neuronal population that functions to detect harmonic spectral patterns in the core region of marmoset auditory cortex. Below, we will further analyze the properties of HTNs.

Sensitivity of HTNs to Spectral Jitter.

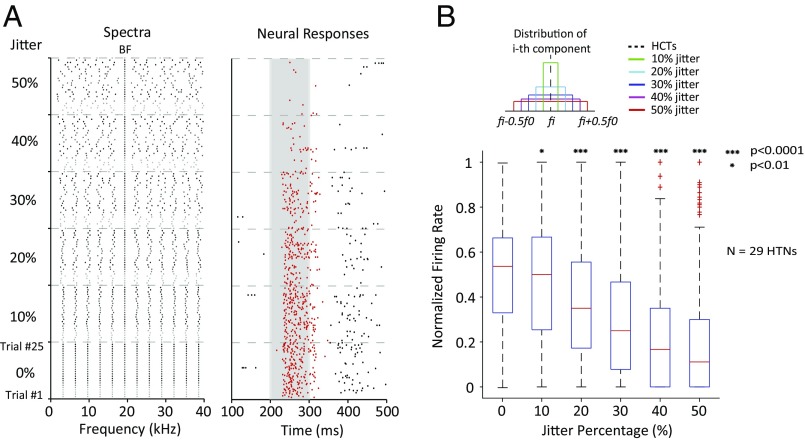
If HTNs were to play a role in encoding harmonic spectral patterns, one would like to know its sensitivity to variations in spectral regularity. It has been suggested that the auditory system could derive pitch information from the spectrum where resolved harmonics need to be taken into account (19). Perceptually, frequency variations in individual spectral components of an HCT will change the perceived pitch of the complex tone (37, 38). A complex tone containing nonharmonically related frequencies elicits a less definite pitch than HCTs (“pitch ambiguity”) (39, 40). To examine how sensitive HTNs are to spectral variations, we also tested these neurons by systematically perturbing the equal spacing between the spectral components of an HCT. A spectrally jittered HCT was generated by fixing the component at BF while adding random frequency shifts (drawn from a uniform distribution) to other harmonics independently (Fig. 3A, Left). The SD of the frequency shifts was determined by the amount of the jitter to be introduced: between 10 and 50% in our experiments (Fig. 3B, Inset). As the jitter amount increases, the spectrum becomes more irregular (Fig. 3A, Left).

Fig. 3.

Responses of HTNs degrade with spectral jitter. (A) An HTN’s (M73v-U307) responses to spectrally jittered HCTs. (Left) The spectral components of HCTs and corresponding jittered tones at five different jitter amounts; 25 stimuli were generated for each jitter amount. The HCT was also repeated 25 times. (Right) Raster plot of the neuron’s responses to the stimuli shown in Left. Note the decreasing firing rate with increasing jitter amount. (B) Distributions of normalized firing rates of 29 HTNs to repeated HCTs and jittered tones at different jitter amounts. The red lines represent the medians. The boxes indicate the upper and lower quartiles. Error bars show the upper and lower extremes. Red markers (+) indicate outliers. Wilcoxon signed rank test was used to determine whether the responses to jittered tones were significantly different from those of the HCTs. Inset shows the uniform frequency distribution of jittered components at different jitter amounts.

The responses of an example HTN to the spectrally jittered HCT are shown in Fig. 3A, Right. The firing rate was decreased and eventually ceased when the spectrum of the jittered HCTs became too irregular (Fig. 3A, Right). We were able to test spectrally jittered HCTs in 29 of 64 HTNs that we could hold long enough during recording sessions. For each neuron, 150 stimuli were played in a random order, which included 25 independently generated stimuli at each jitter amount and 25 repetitions of the original HCT. Each stimulus was played once, and the corresponding firing rate was normalized by the maximal firing rate of the responses to all 150 stimuli in a neuron. Fig. 3B compares distributions of the normalized firing rates of all 29 neurons between each jitter amount and original HCT (0% jitter). The median firing rate to the jittered HCTs was significantly less than that to original HCTs when the jitter amount was larger than 10% (Wilcoxon signed rank test, P < 0.0001). The sharp change in firing rate with increasing jitter amount indicates that HTNs have limited tolerance for spectral jitter.

Relationship Between BF and $\mathit{B}{\mathit{f}}_0$ and Distribution of HTNs in A1 and R.

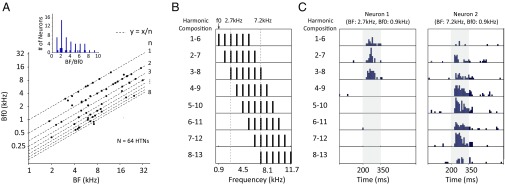
For most HTNs, such as the two examples shown in Fig. 1 A and C, the $B{f}_0$ does not equal the BF but a subharmonic of BF (BF/2, BF/3,…). Fig. 4A plots the relationship between $B{f}_0$ and BF for all HTNs. The ratio of BF to $B{f}_0$ is close to integer numbers between one and nine (Fig. 4A, Inset). It is possible to have HTNs with the same $B{f}_0$ but different BFs. Two such examples are shown in Fig. 4C. The BFs of these two neurons were the third and eighth harmonics of their $B{f}_0$. A set of HCTs of $B{f}_0$ but with different harmonic compositions was used to test both neurons (Fig. 4B). The first neuron responded only to HCTs comprising lower harmonics where its BF (the third harmonic) was included (Fig. 4C, Left). The second neuron selectively responded to HCTs containing the eighth harmonic (Fig. 4C, Right). These examples show that HTNs were also sensitive to harmonic number: the ratio of BF to $B{f}_0$. The selectivity to harmonic numbers is also reflected in different local maxima in the responses of HTNs studied with the frequency shift test (Fig. 2D).

Fig. 4.

HTNs showed sensitivity to harmonic numbers. (A) The relationship between BF and $B{f}_0$ is plotted on the logarithm scale for 64 HTNs. Inset is the distribution of the BF to $B{f}_0$ ratios of the same 64 neurons. The $B{f}_0$ of an HTN is either equal to the BF or a subharmonic of the BF. (B) The spectra of a set of HCTs with the same $f_0$ but different harmonic compositions. All harmonics have equal amplitude of 40 dB SPL. (C) Peristimulus time histograms (PSTHs) of two neurons’ responses to the stimuli shown in B. (Left) M73v-U66. (Right) M73v-U288. PSTHs were computed from responses to 10 repetitions of the same stimulus and calculated as the firing rate within each 20-ms time window. Stimuli were presented from 200 to 350 ms, indicated by the shaded regions on the two plots.

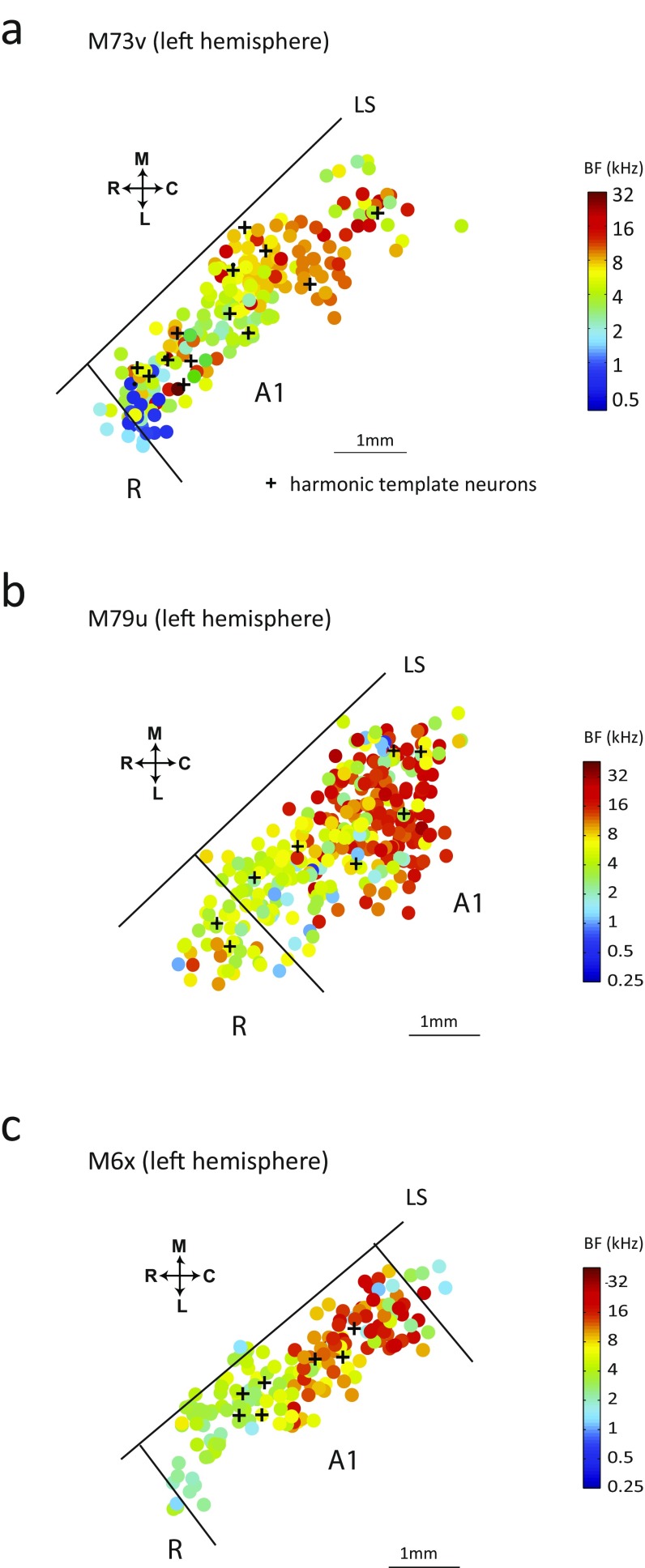
For 64 HTNs identified in these experiments, $B{f}_0$ values varied from 400 Hz to 12 kHz (Fig. 4A, y axis), and BFs spread over the entire frequency range of marmosets’ hearing. The BF distribution of the population of HTNs is highly overlapping with that of non-HTNs (Fig. 5A). Mapping data show that HTNs are organized tonotopically by their BFs in A1 and R and intermingled with non-HTNs (Fig. 5B and Fig. S4).

Fig. 5.

Distributions of the BF and locations of HTNs in marmoset auditory cortex. (A) BF distributions of HTNs and non-HTNs in auditory cortex based on data from three marmosets. (B) Tonotopic map of one recorded hemisphere (marmoset M73v, right hemisphere). HTNs (black crosses) are distributed across a broad frequency range and intermingled with other neurons in A1 and R. The border between A1 and R is identified at the low-frequency reversal. C, caudal; L, lateral; LS, lateral sulcus; M, medial.

Fig. S4.

Distributions of the BF and locations of HTNs in marmoset A1. (A–C) Additional tonotopic maps of three hemispheres of two marmosets reported here. HTNs (black crosses) are distributed across a broad frequency range in A1 and R. C, caudal; L, lateral; LS, lateral sulcus; M, medial.

Balanced Excitatory and Inhibitory Inputs Generate Harmonic Selectivity.

One possible mechanism for forming harmonic templates in A1 and R is by combining sharply tuned and harmonically related excitatory inputs from the medial geniculate body (MGB) or different frequency regions of auditory cortex. However, excitatory inputs alone cannot explain the suppression of the responses below spontaneous firing rate (likely caused by inhibition) induced by odd shifts in frequency-shifted HCTs as shown by the example neuron in Fig. 2B. To further investigate this issue, we compared the responses of each HTN with HCTs at $B{f}_0$ and $B{f}_0/2$. An HCT at $B{f}_0/2$ has twice as many spectral components as an HCT at $B{f}_0$ and contains all of the harmonics in an HCT at $B{f}_0$ as even harmonics. Fig. 6A shows this comparison for all 64 HTNs. The larger responses of HTNs to HCTs at $B{f}_0$ values but smaller or no response to HCTs at $B{f}_0/2$ cannot be explained if HTNs are constructed by integrating harmonically related excitatory inputs alone. The fact that the additional odd harmonics of $B{f}_0/2$ reduced the firing rate suggests inhibitory inputs that are sandwiched between harmonically related excitatory inputs.

Fig. 6.

Excitatory and inhibitory inputs to HTNs. (A) A comparison between the responses to HCTs at $B{f}_0$ and $B{f}_0/2$ for all 64 HTNs. Responses to $B{f}_0$ were always greater than those to $B{f}_0/2$. (B, Left) An example of the adjusted level matrix for RHSs is shown in gray scale. Each row represents a stimulus. Individual harmonics are plotted in columns. The gray level indicates the relative amplitude of each harmonic to the reference level. The SD is 20 dB in this plot. B, Right shows three exemplar stimuli with different harmonic amplitudes from the matrix. (C and D) Two examples of the linear weights estimated from the responses to RHSs. For the neuron in C (M79u-U375), the $f_0$ of RHS was set to $B{f}_0/2$. For the neuron in D (M79u-U572), the $f_0$ was set to $B{f}_0/4$.

For six HTNs that were held long enough, we used the random harmonic stimuli (RHSs) and a linear weighting model to estimate the spectral distribution of their excitatory and inhibitory inputs (41). RHSs were generated by randomly and independently roving the sound level of each harmonic in an HCT, so that every stimulus contained the same harmonics but was different in its spectral profile (Fig. 6B). The $f_0$ of RHS was set to $B{f}_0/2$ (Fig. 6C) or $B{f}_0/4$ (Fig. 6D), so that there were also sample frequencies between adjacent harmonics in the preferred template. For each HTN, typically 2N + 20 (N = total number of harmonics) RHSs were delivered, and their responses were recorded. A linearly optimal weighting function was computed from RHS responses (41). The polarity of the linear weight indicates whether each frequency excites or inhibits a neuron (positive: excitatory; negative: inhibitory). As shown in Fig. 6 C and D, the estimated linear weights near BF showed an alternating pattern of excitation and inhibition, with positive weights at BF, adjacent harmonics in the preferred template, and negative weights in between those harmonics. We performed the above RHS analyses in six HTNs. Fig. S5 shows the averaged linear weights of this group of neurons at six components (BF, two adjacent harmonics, and three components between these harmonics). More than one-half of six neurons had significant weights (Materials and Methods) at those components. A similar alternating pattern of excitation and inhibition in the linear weight profile was observed. These results also suggest a role of inhibition in forming harmonic templates in auditory cortex. Other methodologies, such as intracellular or whole-cell recordings and anatomical tracing techniques, will be needed to reveal the input sources and organizations of HTNs.

Fig. S5.

The distribution of estimated linear weights from six neurons at six components, including BF and two adjacent harmonics in the preferred template, as well as three components between those harmonics. x Axis shows the harmonic number of each component in relation to BF. The space between components was $B{f}_0/2$. Only integer numbers are harmonics in the template. Other numbers were components at frequencies between two adjacent harmonics in the template. The red lines represent the medians. The boxes indicate the upper and lower quartiles. Error bars show the upper and lower extremes. The red plus symbol indicates outliers.

Discussion

HTNs and Marmosets’ Auditory Perception.

Harmonicity is an important grouping cue used by the auditory system to determine what spectral components are likely to belong to the same auditory object. HTNs described in this study could be the neural substrates underlying such perceptual grouping. The $B{f}_0$ of HTNs covers a wide range from 400 Hz to 12 kHz, which is much broader than the range for pitch in speech and music. The marmoset hearing range, extending from 125 Hz to 36 kHz, is similar to that of humans, although broader on the high-frequency side (42). BFs of HTNs fall well within marmosets’ hearing range. Marmosets have a rich vocalization repertoire that contains a variety of harmonic structures (33, 43, 44). Their vocalizations contain harmonic sounds with both high-frequency $f_0$ values (>2–3 kHz; e.g., “phee” and “twitter” calls) and low-frequency $f_0$ values (<2 kHz; covering the range of pitch; e.g., the “egg” calls, “moans,” and “squeals” calls). Therefore, HTNs could function to detect harmonic patterns in marmoset vocalizations. Other than their own vocalizations, harmonic structures are also commonly found throughout the marmoset’s natural acoustic environment in the South American rainforest, including the vocalizations of various heterospecific species, such as insects, birds, amphibians, mammals, etc. Therefore, we would expect marmosets to hear a broader range of $f_0$ values than those of their own vocalizations. It is, therefore, not surprising to find HTNs with $f_0$ selectivity that extends to frequency out of the vocalization range. Either as predator or prey, marmosets may take advantage of harmonic structures in sounds for their survival in their natural habitat. We, therefore, believe that HTNs reported in this study likely play an important role in marmoset’s auditory perception.

A recent behavioral study showed that marmosets exhibit human-like pitch perception behaviors (34). In this study, marmosets were trained on pitch discrimination tasks, and the minimal difference limen of $f_0$ ($f_{0}DL$) was measured with resolved and unresolved harmonics of $f_0$ at 440 Hz. It was found that the first 16 harmonics dominated the pitch perception, and marmosets showed no sensitivity to the adding phases of individual harmonics (cosine or Schroder phase) when only the first 16 harmonics were used. The $f_{0}DL$ increased when the harmonics were mistuned. These findings suggest that the first 16 harmonics of 440-Hz $f_0$ are resolved, which is consistent with the estimation from marmoset’s auditory filter bandwidth measured in another behavior study in marmosets (45). The HTNs found in our study provide templates for coding resolved harmonics at varying $f_0$ above 400 Hz. The preferred harmonic numbers of HTNs are usually smaller than eight (Fig. 4A, Inset), consistent with both behavior studies.

The broad distribution of BF and $B{f}_0$ of HTNs suggests that the primate auditory cortex uses a generalized harmonic processing organization across a species’ entire hearing frequency range to process sounds rich in harmonics, including not only species-specific vocalizations but also, sounds produced by other species or devices, such as speech and music. Although there is little evidence of music perception by marmoset monkeys, rhesus monkeys showed octave generalization to children’s songs and tonal melodies in a study by Wright et al. (46), which suggests potentially similar processing of musical passages in monkeys and humans. A recent study has revealed distinct cortical regions selective for music and speech in non-A1 of the human brain (47). A similar population of HTNs in the core area of human auditory cortex may serve as the basis for forming a pathway for music processing at higher stages of auditory pathway. Whether HTNs in auditory cortex arise from exposure to the acoustic environment during early development or as a consequence of natural evolution to adapt to the statistics of natural sounds is a fascinating topic for additional investigations.

HTNs and Pitch-Selective Neurons.

An earlier study identified pitch-selective neurons in marmoset auditory cortex (27). A similarly located pitch center has also been identified in human auditory cortex (26–29). HTNs found in this study are distinctly different from the pitch-selective neurons in several important ways. First, pitch-selective neurons are localized within a small cortical region (∼1 × 1 mm in size) lateral to the low-frequency border between areas A1 and R (Fig. S1A) (27, 29), whereas HTNs are distributed across A1 and R (Fig. 5B and Fig. S4). Second, pitch-selective neurons have BFs < 1,000 Hz, whereas HTNs have BFs ranging from ∼1 to ∼32 kHz, which covers the entire hearing range of the marmoset. Third, pitch-selective neurons are responsive to pure tones and tuned to a BF, and they are responsive to “missing fundamental harmonics” and tuned to a best $f_0$ equal to BF (27, 29). In contrast, not all HTNs respond (or only respond weakly) to pure tones (21 of 64 HTNs had FI of 1.0 and were unresponsive to pure tones). An HTN typically responds maximally to harmonic complex sounds of a particular $f_0$ with their spectra covering its BF (or would-be BF). For those HTNs that are responsive to pure tones and tuned to a BF, the $B{f}_0$ is often not equal to BF (usually much smaller) (Fig. 4A). Although HTNs were not required to respond to missing fundamental harmonics by the selection criteria, some of them did respond to HCTs with or without the fundamental component. Fourth, the range of the best $f_0$ of pitch-selective neurons is below 1,000 Hz, whereas the $B{f}_0$ of HTNs has a broader distribution (400 Hz to 12 kHz). Fifth, pitch-selective neurons have a preference for low harmonic numbers, which have greater pitch salience than high harmonic numbers. HTNs, however, may prefer low or high harmonic numbers depending on the ratio of BF to $B{f}_0$ as shown by the examples in Fig. 4C. Therefore, HTNs do not encode pitch per se. They are selective to a particular combination of harmonically spaced frequency components (referred to as “harmonic templates”). However, HTNs do share one important characteristic with a subset of pitch-selective neurons that extract pitch from resolved harmonics: both are sensitive to spectral regularity and show reduced firing rates to spectral jitters (Fig. 3).

HTNs can be used to extract pitch information from a particular harmonic pattern in a template matching manner as suggested by a maximum likelihood model (19). The estimation of $f_0$ from harmonics with such an operation may have a certain degree of ambiguity as predicted by the model. We also observed such ambiguity in the responses of HTNs to HCTs depending on the tuning width of the frequency receptive fields. As the example show in Fig. 1B, the neuron responded strongly at two different $f_0$ values (indicated by red arrows in Fig. 1B), because the preferred template matched either the fourth, fifth, and sixth harmonics of the first $f_0$ (1.05 kHz) or the fifth, sixth, and seventh harmonics of the second $f_0$ (1.26 kHz). Similar ambiguity in pitch perception was also observed in human psychophysics studies (39, 48). Although some HTNs could be precursors of pitch-selective neurons, HTNs seem to represent a larger class of neurons selective for harmonic structures beyond pitch. The responses of HTNs represent a transformation from coding individual components of complex sounds to coding features (harmonicity in our case) and eventually, form representations of objects in auditory processing, analogous to the transformation from coding of lines to coding of curvatures in visual processing. Such an integral representation of harmonic structures can be used in (but not limited to) pitch extraction. Because of their selectivity to harmonic numbers, HTNs also encode information for extracting timbre, and they could also be a preprocessing stage for the coding of complex sounds, such as animal vocalizations.

Nonlinear Spectral Integration by HTNs.

A number of previous studies have shown nonlinear integration in multipeaked neurons and two-tone responses of single-peaked neurons in A1 of several species, including the marmoset (31, 32, 49). There are, however, major differences between HTNs and these previous findings. Multipeaked neurons can be strongly driven by pure tones at its primary BF (31), but HTNs are not necessarily driven or can only be weakly driven by pure tones. Therefore, HTNs exhibit much greater nonlinearity than previously reported single-peaked and multipeaked neurons. In addition, the complex spectral tuning property that HTNs exhibit is a reflection of the nonlinear spectral integration, where a combination of pure tones evokes maximal responses. Individual components of this combination are either suboptimal (evoke weak responses) or subthreshold (elicit no response). In other words, such complex spectral tuning does not always show as the multiple peaks (even if the HTN responds to pure tones). Finally, the multipeaked neurons do not necessarily show facilitation to multiple harmonically related pure tones, but HTNs always do by definition. Some single-peaked neurons show nonlinear facilitation when stimulated by two-tone stimuli (sometimes harmonically related) (31), whereas HTNs by definition always show nonlinear facilitation when stimulated by harmonic complex sounds. Two-tone stimuli may reveal some harmonic interactions in an HTN but do not reveal the optimal stimulus for an HTN, which is usually a combination of three or more harmonics with a particular $f_0$ (example neurons are shown in Fig. 1 B and C). Thus, the unique properties of HTNs are not necessarily predictable from previously reported multipeaked neurons and two-tone responses (31, 32). Of 64 HTNs reported in this study, only 11 showed multipeak tuning in their pure tone response.

The two-tone stimuli are usually based on the pure tone tuning to decide the fixed frequency of one tone while varying the frequency of the second tone. This approach would miss those HTNs that do not respond to pure tones at all. Multiple peaks in pure tone tuning do not necessarily imply nonlinear spectral integration either as indicated by the responses of the neuron shown in Fig. S2C. This neuron responded to any HCT when at least one harmonic overlaps either of the two peaks in pure tone tuning. The larger peaks appeared when there were components near both peaks in pure tone tuning. There were also smaller peaks that corresponded to HCTs, which contained only a component near the second peak. This type of response to HCTs is closer to a sum of two single-peak neurons shown in Fig. S2B. By contrast, HTNs by definition always show nonlinear facilitation when stimulated by harmonic complex sounds. However, it is possible that HTNs receive inputs from such multipeaked neurons to form their harmonic selectivity.

In summary, our findings revealed more complicated and harmonically structured receptive fields for extracting harmonic patterns than previous studies. These findings provide direct biological evidence for previously proposed harmonic template matching models at the single-neuron level for the central processing of pitch and other harmonic sounds (19, 20). In the peripheral auditory system, single auditory nerve fibers encode individual components of harmonic sounds. In contrast, HTNs found in marmoset auditory cortex can represent combinations of multiple harmonics. Such a change in neural representation of harmonic sounds from auditory nerve fibers to auditory cortex reflects a neural coding principle in sensory systems: neurons in the later stage of sensory pathway transform the representation of physical features, such as frequencies of sounds in hearing or luminance of images in vision, into the representation of perceptual features, such as pitch in hearing or curvature in vision, which eventually lead to the formation of auditory or visual objects (50, 51). Such transformations could simplify decoding for purposes of sound source recognition (52, 53).

Distributions of HTNs in Auditory Cortex.

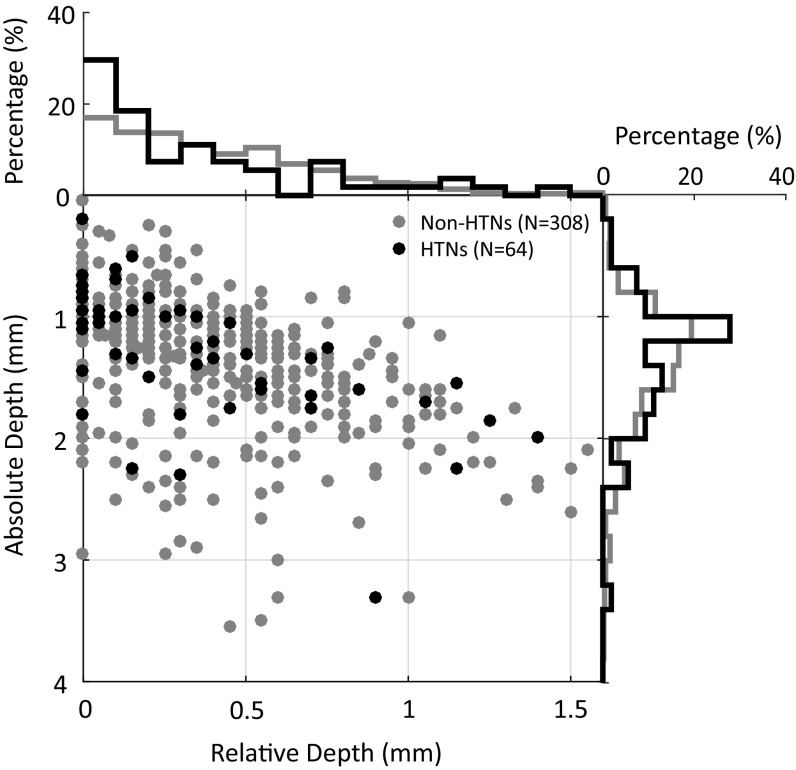
We did not find any functional clusters of HTNs among a large number of neurons recorded in A1 and R. Instead, HTNs were intermixed with other non-HTNs (Fig. 5B and Fig. S4). They had frequency preference (BFs) such as their neighboring neurons, except for their harmonically structured receptive fields. Those findings are consistent with previous studies, which did not reveal any functional clusters for multipeaked neurons in A1, except in the specialized cortical areas of echo-locating bats (31, 32, 54). Such an organization is analogous to the coexistence of simple and complex cells in primary visual cortex (55). Although we were unable to determine the exact laminar location of each recorded neuron because of the limitation of the chronic extracellular recording method, we recorded the depth of each neuron relative to the location of the first neuron encountered in each recording track. Fig. S6 shows the depth distributions of both HTNs and non-HTNs studied in these experiments. The majority of neurons in our study were recorded at superficial cortical depths, most likely in layers II/III (median relative depth: 0.2 mm for HTNs and 0.3 mm for non-HTNs). A previous study in awake marmosets found a high proportion of combination-selective, nontone-responsive, and low spontaneous-firing neurons at superficial cortical depths in A1 (49). A two-photon imaging study showed that A1 neurons in layer IV respond more strongly to pure tones than neurons in upper layers (56). To fully understand the hierarchical auditory processing of harmonic information, it will be important to investigate the circuitry basis of HTNs and their connectivity to other neurons in auditory cortex in future studies. It will also be important to examine harmonic selectivity in subcortical stations, such as the inferior colliculus (IC) and MGB, to determine whether the harmonic selectivity shown by HTNs is inherited from previous stages or emerges at cortical level, preferably using similar stimulus paradigms used in this study. Hitherto, there has not been evidence of HTNs in neural structures below auditory cortex. Kostlan (57) has conducted single-neuron recording experiments in the IC of awake marmosets using the same stimuli used in our study and did not find any evidence of HTNs.

Fig. S6.

Distribution of absolute depth (from dura surface) and relative depth (from first neuron encountered) of HTNs (black dots; n = 64) and non-HTNs (gray dots; n = 308). Histograms of absolute and relative depths are shown on the margins. The medians of the relative depth are 0.2 and 0.3 mm for HTNs and non-HTNs, respectively. The median of the absolute depth is 1.25 mm for both groups.

It will also be interesting to test harmonic selectivity in neurons of higher cortical areas, such as belt and parabelt, which receive inputs from A1 and R. Previous studies have shown that neurons in those areas selectively respond to complex features, such as species-specific vocalizations or narrowband noises (50, 58), and typically do not respond well to pure tones. However, a recent multiunit study in macaques showed that responses to pure tones in parabelt were comparable with the responses to bandpass noise (59). How the neurons outside the core region respond to HCTs would provide additional insights into the roles that HTNs play in processing sounds containing harmonic structures, such as music and speech. It has been suggested that neurons in the lateral belt area of macaque monkeys may process harmonic sounds (60). In light of the observations of harmonically related multipeak frequency tuning (61) and cortical regions selective for music sounds (47) in human auditory cortex, one would expect that the harmonic selectivity performed by the HTNs described in this study may form the basis for harmonic processing across primate auditory cortex.

Materials and Methods

Neurophysiology.

All experimental procedures were approved by the Johns Hopkins University Animal Use and Care Committee. Singe-unit neural recordings were conducted in a double-walled soundproof chamber (Industrial Acoustics). Single-neuron responses were recorded from four hemispheres of three marmoset monkeys. Details of the chronic recording preparation can be found in previous publications from our laboratory (62). Marmosets were adapted to sit quietly in a primate chair with the head immobilized. A tungsten electrode (2–5 MΩ; A-M System) was inserted into the auditory cortex perpendicularly to the surface through a 1-mm craniotomy on the skull. The electrode was manually advanced by a hydraulic microdrive (Trend Wells). Each recording session lasted 3–5 h. Animals were awake but were not required to perform a task during recordings. Spike waveforms were high-pass filtered (300 Hz to 3.75 kHz), digitized, and sorted in a template-based online sorting software (MSD; Alpha Omega Engineering). We recorded neurons from A1 and R. A1 was identified by the tonotopic map and the frequency reversal at the rostral part dividing A1 and R (Fig. S1A). HTNs were found in both A1 and the R high-frequency region after the frequency reversal (Fig. 5B and Fig. S4).

Acoustic Stimuli.

All acoustic stimuli were generated digitally and delivered by a free-field loudspeaker (Fostex FT-28D or B&W-600S3) 1 m in front of the animal. All stimuli were sampled at 100 kHz and attenuated to a desired sound pressure level (SPL) (RX6, PA5; Tucker-Davis Technologies). Tones at different frequencies (1–40 kHz; 10 steps per octave) were typically played at a moderate sound level (between 30 and 60 dB SPL) to measure the frequency selectivity. If neurons did not respond, other sound levels (20 and 80 dB SPL) were tested. BF was defined as the pure tone frequency that evoked the maximal firing rate. The threshold of a neuron was estimated from the rate-level function at BF tone (from −10 to 80 dB SPL in steps of 10 dB). Threshold was defined as the lowest sound level that evoked a response significantly larger than spontaneous firing rate (t test, P < 0.05).

Three types of complexes tones were used to study the spectral selectivity: HCTs, spectrally shifted tones, and jittered tones. For all complex tones, individual components were kept at the same sound level and added in cosine phases. The sound intensity per component was initially set to 10 dB above the threshold of a tone at the BF. If a neuron did not respond to pure tone, a 40-dB SPL sound level per component was used. HCTs at different $f_0$ values were generated that contained harmonics within a three-octave frequency range centered at BF. For neurons that preferred low-frequency $f_0$ values, a smaller two-octave range was also tested to balance the number of harmonics to high-frequency $f_0$ values. For neurons that did not respond to pure tones, BF was estimated from adjacent neurons in the same recording track. Five different jitter amounts (10, 20, 30, 40, and 50%) were used for the jittered tones. Twenty-five stimuli were independently generated for each jitter amount. The RHSs used here were adapted from random spectrum stimuli (41, 63). Each stimulus consisted of a sum of harmonics of a chosen $f_0$, typically $B{f}_0/2$ or $B{f}_0/4$, within a three-octave range centered at the BF. In an RHS set, every stimulus differed from every other stimulus in the spectral profiles, which were determined by the mean sound level and the level SD. The spectral profile was generated by randomly and independently roving sound level of each harmonic, so that the RHS set as a whole was “white” (i.e., the stimuli were uncorrelated to each other). The mean sound level, also called the reference level, was the level used for HCTs and inharmonic tones. The most common level SD used was 10 dB. If time permitted, other SDs, like 5, 15, and 20 dB, were also tested. Each RHS set consisted of N + 10 pairs of stimuli with various spectral profiles, where N is the number of harmonics. The amplitude levels of the first stimulus in each pair were inverted in the second stimulus. Additionally, 10 flat spectrum stimuli, in which all harmonics had equal amplitude, were used to estimate the reference firing rate ${\text{R}}_0$.

Typically, stimuli were 100 ms in duration, with a 500-ms interstimulus interval (ISI) and 5-ms onset and offset ramps. Longer durations (150, 200, and 500 ms) with longer ISIs (>1,000 ms) were used for HCTs at $f_0$ values less than 1 kHz. Every stimulus was presented for 10 repetitions in a random order with other stimuli.

Data Analysis.

Firing rates were calculated over the time window from 15 ms after stimulus onset to 50 ms after stimulus offset. An FI is defined as $({\text{R}}_{\text{HCT}}-{\text{R}}_{\text{Tone}})/({\text{R}}_{\text{HCT}}+{\text{R}}_{\text{Tone}})$ to quantify the response difference between HCTs and BF tones, where ${\text{R}}_{\text{HCT}}$ is the firing rate to the preferred HCT, and ${\text{R}}_{\text{Tone}}$ is the firing rate to BF tones. FI is a measure of neural preference to combinations of tones. FI equals 1 if the neuron only responds to HCTs but does not respond to pure tones, 0 if the maximal response to complex tones is the same as that to pure tones, and −1 if the neuron only responds to pure tones but does not respond to complex tones.

A PI is the averaged firing rate difference between harmonic shifts and adjacent odd shifts as defined in Eq. 1:

$$\text{PI}=\frac{{\displaystyle \sum _{\text{i}=1}^{\text{N}}}\frac{(2\times {\text{R}}_{{\mathrm{n}}_{\text{i}}}-{\text{R}}_{{\mathrm{n}}_{\text{i}}+50\text{\%}}-{\text{R}}_{{\mathrm{n}}_{\text{i}}-50\text{\%}})}{(2\times {\text{R}}_{{\mathrm{n}}_{\text{i}}}+{\text{R}}_{{\mathrm{n}}_{\text{i}}+50\text{\%}}+{\text{R}}_{{\mathrm{n}}_{\text{i}}-50\text{\%}})}}{\text{N}},$$ [1]

where $\text{N}$ is the total number of harmonic shifts that evoke a firing rate significantly larger than spontaneous rate (t test, P < 0.05). $\text{R}$ is the firing rate, and ${\mathrm{n}}_{\text{i}}$ for ${\text{R}}_{{\mathrm{n}}_{\text{i}}}$ is the $i\text{th}$ harmonic shift. For example, ${\mathrm{n}}_{\text{i}}$ for the example neuron shown in Fig. 2B would be 0, 100, 200, 300, 400, and 500% for $i=1,\dots ,\hspace{0.17em}6$, respectively. ${\text{R}}_{{\mathrm{n}}_{\text{i}}+50\text{\%}}$ and ${\text{R}}_{{\mathrm{n}}_{\text{i}}-50\text{\%}}$ are responses to the two adjacent odd shifts 50% up or down from the harmonic shift ${\mathrm{n}}_{\text{i}}$. If a neuron only responds to harmonic shifts but shows no response to the odd shifts, the PI will be one. If a neuron responds equally well to harmonic shifts and odd shifts, the PI will be zero.

The relationship between the firing rate $r$ and the spectral shape of each stimulus in an RHS set is modeled as the given function:

$$\text{r}={\text{R}}_0+{\displaystyle \sum _{\text{i}=1}^{\text{N}}}{\mathrm{w}}_{\text{i}}{\mathrm{S}}_{\text{i}},$$ [2]

where ${\mathrm{R}}_{\text{0}}$ is the reference firing rate estimated from the response to all flat stimuli, ${\mathrm{S}}_{\text{i}}$ is the relative decibel level of each harmonic to the reference level, and ${\mathrm{w}}_{\text{i}}$ is the linear weight. The linear weights can be estimated by recording the responses to RHSs and solving Eq. 2 by using a least squares method. To maximize the ratio of data to model parameters, weights were computed only for a limited number of harmonics around BF. Those harmonics were chosen by estimating first-order weights over all harmonics but only selecting continuous harmonics with significant weights (the absolute value of the weight >1 SD from zero; bootstrapping).