Summary
A near-ubiquitous pathology in very low birth weight infants is neonatal apnea, breathing pauses with slowing of the heart and falling blood oxygen. Events of substantial duration occasionally occur after an infant is discharged from the NICU. It is not known whether apneas result from a predictable process or from a stochastic process, but the observation that they occur in seemingly random clusters justifies the use of stochastic models. We use a hidden-Markov model to analyze the distribution of durations of apneas and the distribution of times between apneas. The model suggests the presence of four breathing states, ranging from very stable (with an average lifetime of 12 hours) to very unstable (with an average lifetime of 10 seconds). Although the states themselves are not visible, the mathematical analysis gives estimates of the transition rates among these states. We have obtained these transition rates, and shown how they change with post-menstrual age; as expected, the residence time in the more stable breathing states increases with age. We also extrapolated the model to predict the frequency of very prolonged apnea during the first year of life. This paradigm – stochastic modeling of cardiorespiratory control in neonatal infants to estimate risk for severe clinical events – may be a first step toward personalized risk assessment for life threatening apnea events after NICU discharge.
Keywords: apnea, preterm infants, Markov model, ALTE
Introduction
Apnea of prematurity is the occasional breathing cessation and accompanying bradycardia and oxyhemoglobin desaturation that is experienced by nearly all infants born at very low birth weight (<1500 grams, VLBW). While clinically significant apnea events usually resolve by 9 months from conception, apparent life-threatening events (ALTEs) occasionally occur after discharge from the neonatal intensive care unit (NICU) (Darnall, 2009, Ramanathan et al., 2001). Such prolonged apnea events have been postulated to be related to sudden infant death syndrome (SIDS), the leading cause of infant death after the neonatal period (Kinney and Thach, 2009, Willinger et al., 1991).
Foreknowledge of impending apnea in premature infants might lead to better management and earlier safe discharge. However, some clinical experience and scientific study suggest that prolonged apnea events may appear without warning (Darnall, 2009, Ramanathan et al., 2001), making their prediction and prevention impossible. On the other hand, it is known that apneas often appear in clusters, and these clusters of apnea events have been modeled as transient combinations of oscillatory breathing dynamics (Waggener et al., 1982, Waggener et al., 1984). The observation of clustering raises fundamental questions about the nature of neonatal apnea – is it a deterministic and predictable process, with a proximate cause for every individual apnea, or, on the other hand, does it result from a random or stochastic process? Control of breathing is maintained in the brain stem through gating of CO2 and pH sensitive ion channels – a mesoscale process at the borderline between true quantum unpredictability, (e.g. radioactive decay), and randomness in the sense of Laplace (Laplace, 1840), (that is, too many processes to account for) – and we therefore reasoned that apneas might also have random kinetics. Indeed, stochastic switching of respiratory drive between normal rhythm and attenuated or abolished respiration has been demonstrated in animal models (Paydarfar and Buerkel, 1995). Clustering of apneas viewed in this way takes on features of a random walk – the best predictor of whether an inebriated gentleman will appear beneath a solitary streetlight in the next few minutes is that he had appeared there a short time ago.
In this paper we develop a predictive statistical model based on the hypothesis that apneas can be described by a stochastic hidden-Markov model. The model works well, but nevertheless, we warn in advance that success of a stochastic model is not proof that apneas can only occur randomly, and such success should not deter search for deterministic models with better predictors of prolonged apnea. Indeed, algorithmic complexity theory indicates that distinction between random and deterministic mechanisms in long time series can rarely be achieved (Chaitin, 1975).
In this paper, we study the kinetics of apnea events in the data set used to validate an apnea detection algorithm (Lee et al., 2012). We begin by presenting the empirical distributions of apnea events and the time between events in a large, clinically-annotated database. We next build statistical models for neonatal breathing and apnea as a function of post-menstrual age using a hidden Markov model – this type of model represents internal states of neonatal breathing as transitions among hidden states having varying degrees of stability. We present the concordant relation between model estimates and empirical values of apnea duration and burden. These parameters show steady development toward more stable neonatal breathing with PMA, represented by transitions in the models to favor more stable (longer-lived) breathing states and away from the apnea and the proximal (shortest-lived) breathing state. Finally, we extrapolate the rates obtained from hidden Markov modeling to estimate the rate of substantial breathing cessations within the first year of life. We suggest that measuring transition rates for neonatal breathing control might identify infants at increased risk for prolonged, potentially-fatal apnea events.
Materials and Methods
Ethical approval
The UVA Institutional Review Board approved this study under a waiver of consent. Computerized apnea detection results were not available to the patient care team, and decisions about apnea management and discharge readiness were based on nursing documentation of events and standard NICU monitor alarm data.
Patient population
We analyzed cardiorespiratory waveforms from 298 VLBW infants consecutively admitted to the UVA NICU between January 2009 and June 2011. Demographic information, including birth weight, gestational age at birth, birth date, and types and times of respiratory support, were collected from patient medical records. Table 1 shows the demographic characteristics of the infants. Median gestational age at birth was 27 weeks and median birth weight 1010 grams. The number of infants discharged home includes those that were discharged with respiratory support. Figure 1 shows a histogram of the number of patients with data available at each postmenstrual age (PMA, gestational age plus age from birth), with distinction made by disposition at discharge.
Table 1.
Demographic characteristics of the population used to model apnea (2nd column) as a function of PMA and (3rd column) in the eight days prior to discharge home. Data are presented as median (25th, 75th percentile).
| Infants studied … | As a function of PMA | Prior to discharge home |
|---|---|---|
| N | 298 | 196 |
| Gestational age (weeks) | 27 (25, 29) | 28 (26, 29) |
| Birth weight (grams) | 1010 (788, 1263) | 1025 (795, 1298) |
| Males | 143 | 108 |
| Discharged home | 223 | 196 |
| Died | 19 | 0 |
| Transferred | 56 | 0 |
| PMA at discharge (weeks) | 37 (35, 39) | 37 (35, 39) |
| Days in NICU | 52 (26, 93) | 62 (36, 93) |
| Days on mechanical ventilation | 3 (0, 29) | 2 (0, 24) |
| ABDs: Apneas >10 sec with bradycardia (<100 bpm) and O2 desaturation (<80%) | 26,088 | 1,577 |
| ABDs >10 sec with bradycardia (<100 bpm) and O2 desaturation (<80%), after additional filtering | N/A | 724 |
| ABD events per patient per day of analyzable data | 1.48 (0.37, 3.4) | 0.7 (0.1, 2)† |
ABDs per day during last 8 days of stay
Fig. 1.
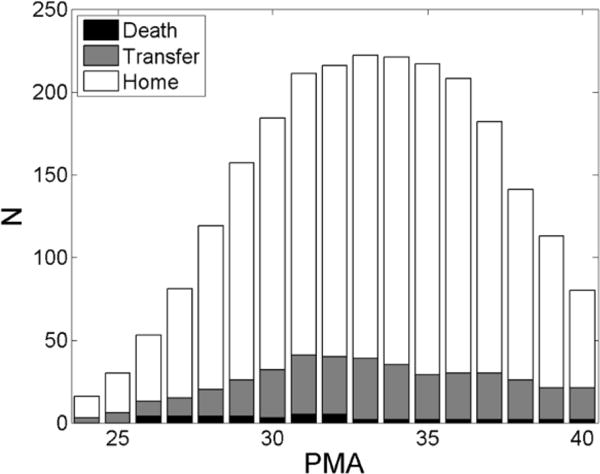
Patient data histogram. The histogram shows of the number of patients that had data available for analysis at each PMA. Distinction is made between infants who were discharged to home (white), those who were transferred to another unit or hospital (grey), and those who died (black). Only PMA up to term (40 weeks) are represented.
We also analyzed patients within the 8 days preceding discharge to home: we found 196 VLBW infants that had data available for analysis immediately preceding discharge to home. Table 1 shows the demographic characteristics of this sample of infants.
Data Acquisition
All patients in the UVA NICU have continuous cardiorespiratory monitoring. We collected signals from 3 electrocardiograph leads digitized at 240 Hz, the chest impedance pneumograph digitized at 60 Hz, and pulse oximetry digitized at 120 Hz from the GE bedside monitors using a central network server (Bedmaster Ex, Excel Medical, Jupiter, FL) behind the clinical firewall. We also collected heart rate, respiratory rate, and oxygen saturation vital signs derived by the monitor. Data were transmitted to our centralized computing and storage cluster and analyzed in parallel.
Of the total NICU stay for all patients (55 patient years) (Clark et al., 2012), 51% of data were deemed unsuitable for analysis due to epochs where recording was interrupted. Data were analyzed in 16 minutes epochs, and we required continuous time series of 3 ECG leads, chest impedance, and heart rate from the physiological monitor to define epochs as suitable for analysis. Missing chest impedance and dropped data packets from the data acquisition system were the most common causes for excluding an epoch. Of the remaining data (26.5 patient years), 10% were excluded to avoid the times during which the infants were being treated with mechanical ventilation.
Apnea detection
Apnea events were identified in this data set as part of a previous study by our group – the apnea detection algorithm has been validated with accuracy > 90% by comparison with clinical inspection of waveform time series (Lee et al., 2012, Vergales et al., 2013). Briefly, apnea was detected as low variance epochs in the chest impedance pneumograph after notch filtering in heart-clock time to eliminate cardiac artifact and high-pass filtering to remove movement artifact. Heartbeats were detected using a threshold-based algorithm (Pan and Tompkins, 1985) as implemented by Clifford and co-workers (Li et al., 2008, Tarassenko et al., 2001). For the current analysis, apnea was defined as breathing cessation of at least 10 seconds with both associated bradycardia and desaturations. We consider this definition for apnea clinically relevant because the breathing cessation caused both a decrease in heart rate and a decline in oxygen level in the blood – this is a stricter definition than that given by Finer et al. (Finer et al., 2006) in order to assure clinical relevance. The thresholds for bradycardia (HR<100, within 50 seconds from the beginning of the apnea or 25 seconds from the end of the apnea) and desaturation (SPO2<80%, within 55 seconds from the beginning of the apnea or 38 seconds from the end of the apnea) are based on detailed inspection of 932 central apnea events by clinical personnel, see the Appendix of (Lee et al., 2012). This apnea detection method is based on chest movement and therefore identifies only central apnea events (obstructive events as breathing identified as breathing). While this algorithm does not explicitly exclude epochs of periodic breathing (Poets and Southall, 1991, Barrington and Finer, 1990), breathing pauses in periodic breathing epochs are shorter than 10 seconds and seldom induce sufficient bradycardia and desaturation to meet our thresholds (Khan et al., 2005, Wilkinson et al., 2007).
The results of (Lee et al., 2012) show an acceptable false positive rate (5%) throughout a NICU stay. Near discharge, however, the rate of false positives may be higher due to the reduced apnea rate and increased noise due to movement. We filtered out false positive apnea events within 8 days of NICU discharge as detailed in Appendix A, section Filtering out false positive apnea events near discharge.
Empirical distribution of apnea and inter-apnea epochs
We studied the duration and timing of 26,088 apnea events occurring from admission through discharge for the patient population in Table 1. Figure 2(a) shows the cumulative distribution of the apnea durations (dots). For each patient we identified sequential apnea events and calculated the time between each – the inter-apnea epochs. Inter-apnea epochs that started or ended at missing data were excluded as these are periods where apnea may occur but not be detected. Figure 2(b) shows the cumulative distribution of observed inter-apnea epochs for all infants regardless of PMA (dots).
Fig. 2.
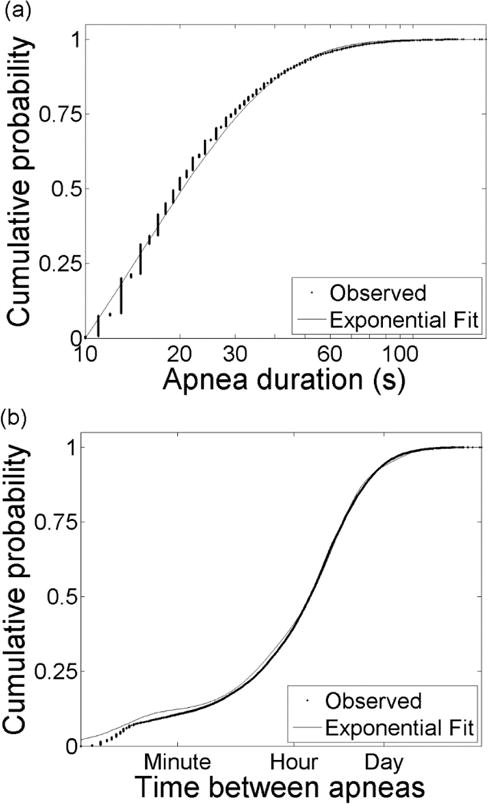
Statistics of apnea events. (a) Cumulative distribution of 26,088 apnea durations. Vertical banding in observed data (dots) results from rounding of apnea durations to integer values. The distribution is well-described by an exponential distribution (lines). (b) Cumulative distribution of the logarithm of times between apnea. The data (dots) are well-described by a sum of four exponential distributions (line).
Statistical modeling of neonatal apnea
We modeled apnea of prematurity as a Markov process based on the interpretation of apnea as the result of transitions through decreasingly stable breathing states. One type of Markov model is a Markov chain, which has a large or infinite number of states and transitions only between adjacent neighbors. These models have diffusion-like behavior and have been used to model the tail of inter-breath interval distributions in infants (Frey et al., 1998). These models result in power law distributions that may be useful for fitting apnea durations (Frey et al., 1998) but are not appropriate for fitting multimodal distributions (McManus et al., 1988) – no single power law can fit the distribution of inter-apnea epochs in Figure 2(b), thus no solvable diffusion or fractal model describes the statistics of apnea in VLBW infants.
In the second type of Markov model a small number of states are postulated, with transitions occurring randomly from each state to others. Generally transitions are allowed directly from every state to every other state. Models of this type are used in a wide range of fields, e.g., speech recognition (Lee and Jean, 2013, Schafer and Jin, 2014), disease tracking (Robertson et al., 2011, Detilleux, 2008), and ion channel recording (Colquhoun and Hawkes, 1982). In ion channel models, states are defined for open, closed, and blocked channels and transition rates are determined empirically. Knowledge of these transition rates allows for determination of important behaviors, for example mean open lifetime, mean time between openings, and number of ion channel openings per cluster. This type of Markov modeling also has important applications in medicine (Sonnenberg and Beck, 1993) and has been used to evaluate obstructive sleep apnea in adults (Kim et al., 2009) and detect apnea of prematurity in short heart rate time series for preterm infants (Altuve et al.).
Markov model parameter estimation
Parameters of Markov models were derived following methods from analysis of single ion channel recordings (Colquhoun and Hawkes, 1977, Colquhoun and Hawkes, 1982). A Markov model is specified by the number of distinct observables M, the number of states N, the observation symbol probability distribution B = bj, the state transition probability distribution C or the related transition rate matrix K, and the initial state distribution P(0) (Rabiner, 1989). We define M = 2 distinct observables for neonatal breathing: breathing and apnea. Derivation of parameters N and bj are given in the following section. Details on the remaining parameters are provided in Appendix A.
Neonatal breathing Markov model definition
The number of states N in a Markov model is chosen from study of the distribution of dwell times and transition rates (Sigworth and Sine, 1987), in our case apnea durations and time between apnea events, the dots in Figure 2. If a Markov model with discrete states and continuous time is correct, then the probability q that an infant will stay in any given state for time t with no transition to another state decreases with time exponentially, q(t)=exp(−t/τ) where τ is the expected duration in the state. The corresponding cumulative distribution, which in our case is the probability that the duration is less than t, is given by Q(t) = 1 − exp(−t/τ). Similarly, the probability that the infant will stay among m hidden breathing states is a superposition of exponentials, and the corresponding cumulative distribution for the time between apneas is
| (1) |
Here τi and αi are the mean of the distribution and relative magnitude for exponential mode i, respectively.
The cumulative distribution of apnea durations was modeled with a single exponential, Eq. (1) with α=m=1 (Figure 2(a), solid curve), with parameter τA, the mean apnea duration, by maximizing the log likelihood of the parameter given the observed durations (Sigworth and Sine, 1987). The mean apnea duration based on the model for apnea events greater than 10 seconds was τ = 24.9 seconds, and a single exponential function provided an accurate fit (R2 = 0.99).
In contrast, multiple distributions are evident in the cumulative distribution of inter-apnea epochs, Figure 2(b) dots. We fit the data with increasing number of exponentials until the goodness-of-fit R2 ≥ 99.9%. The goal was to minimize the complexity of the model (i.e. as few states as possible) while accurately fitting the data. We optimized the parameters using maximum likelihood and found that the sum of four exponentials, Eq. (1) with m=4 (Figure 2(b), solid curve), adequately describes the data. The parameters are provided in Table 2. Based on these results we defined the number of states in the Markov model for neonatal breathing to be N = 5, including 4 breathing states and one apnea state, S = [B1, B2, B3, B4, A].
Table 2.
Model parameters for time between apnea based on all patients at all times.
| Bi | Percent of distribution (100 α) | Mean time between apneas (τi) |
|---|---|---|
| 1 | 12.9 % | 31.9 hours |
| 2 | 59.5 % | 3.9 hours |
| 3 | 16.4 % | 16 minutes |
| 4 | 11.1 % | 9.7 seconds |
As stated above, the observables are that the infant is breathing or that the infant is not breathing, and the observation matrix B gives the probability of observing Oj given that the model is in state Si. For the apnea model this is trivial; the probability of observing breathing is 1 in each breathing state and 0 in the apnea state,
| (2) |
In order to characterize changes in breathing control with post-natal development, we created Markov models at weekly post-menstrual ages – for each, we used a 3-week epoch centered on the one of interest. Specifically, we optimized the transition rate matrix K of a Markov model for each PMA from 25 to 40 weeks, 16 models in all. At each PMA a time series was created for each infant with data at that PMA, where each time series was a number each second: “0” if the infant is breathing and “1” if the infant is apneic. It is possible to have multiple time series per patient due to missing data or excluded epochs of mechanical ventilation. Each model was developed using B from Eq. (2) and the initial state distribution P(0) was taken to be,
| (3) |
where τi were determined using the exponential distribution fits to the data in Figure 2, and are listed in Table 2. Note that the same observation matrix B and initial state distribution P(0) were used for each PMA and these were not allowed to vary during optimization. The transition rate matrix K for each PMA was determined using the optimization technique described in Appendix A using the initial estimate from Eq. (A4). The transition probability density C was calculated as the matrix exponential of the transition rate matrix K.
Transition rate confidence intervals
At each PMA 40 bootstrap runs were completed (Harrell, 2001, Feng et al., 1996). For each run the n patients at that PMA (see Figure 1) were randomly resampled with replacement – for each run some patients were used multiple times and some patients not used. For each bootstrap run we calculated the transition rates using the same procedure described above and in the Appendix. At each PMA, and for each transition rate, we calculated the 95% confidence interval by identifying the 2.5 and 97.5 %-tiles of the 40 samples – for 40 samples, the 95% confidence interval is defined by the minimum and maximum values.
Results
Apnea in VLBW infants
Inspection of the waveform data from bedside monitors revealed clusters of apnea separated by longer periods without apnea. Figure 3(a) shows a cluster of three clinically significant apneas within three minutes. Only the events labeled with black bars were identified as apnea by the algorithm (because, as stated above, the algorithm selects breathing cessations of at least 10 seconds accompanied by bradycardia and desaturation). Throughout, we use ABDX to indicate apnea events of at least X seconds accompanied by bradycardia and oxygen desaturation. The first apnea is an ABD20. This is followed by two subclinical apneas, or breathing cessations that do not cause critical slowing of heart rate and declining oxygen saturation in the blood. Subsequently there are two clinical apneas; the first is 30 seconds and the second is 25 seconds, an ABD30 and an ABD25. Figure 3(b) depicts the number of ABD10 events for a single preterm infant from 33 to 35 weeks PMA. Each half hour is represented by a vertical band, with the intensity of the band indicating the number of ABD events longer than 10 seconds during that time period (0 events per half hour is white, 6 is black). In this example apnea occurs at highly variable intervals; there are instances of multiple apneas within a half-hour as well as days without apnea. From day 21–24 there are no apnea events (the infant was not on mechanical ventilation during this time, and data were available more than 90% of the time). Subsequently, there is another cluster of apnea. These results suggested breathing states of varying stability, with apnea accessible from any state.
Fig. 3.
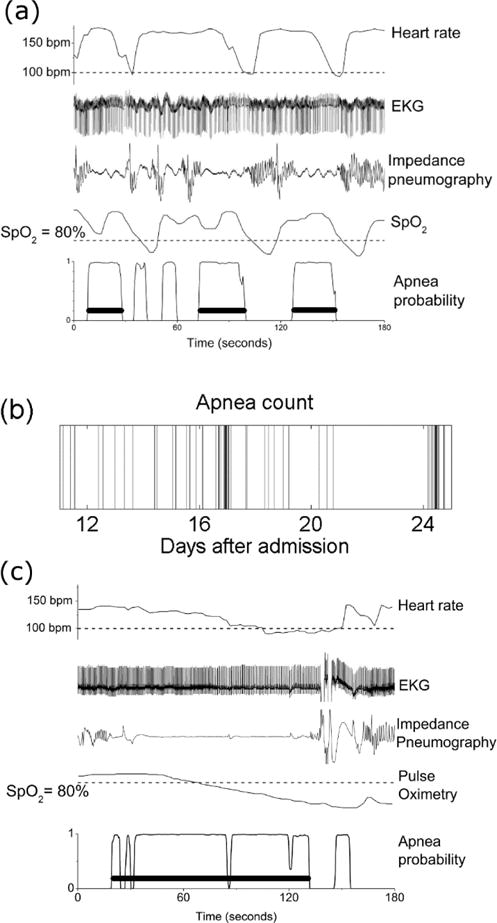
Physiological time series during apnea events. (a) Heart rate, EKG, impedance pneumography, peripheral oxygen saturation (SpO2), and apnea probability for three minutes from a preterm infant. There is a cluster of three clinically significant apnea events within three minutes. (b) Time series of apnea events for a preterm infant over a two week period, from 33 to 35 weeks post-menstrual age. Each band represents the number of apnea events longer than 10 seconds in one half-hour; increasing density indicates more apnea. (c) Heart rate, EKG, impedance pneumography, peripheral oxygen saturation (SpO2), and apnea probability for three minutes from a preterm infant. A prolonged period of apnea with associated bradycardia and oxygen desaturation lasting nearly two minutes is apparent. Isolated breaths during this episode may allow the prolongation.
We also identified breathing cessations of substantial duration, many times longer than the 30 second duration characterized as ALTE (Ramanathan et al., 2001). Figure 3(c) shows an example of an epoch of abnormal breathing control lasting nearly two minutes with bradycardia and oxygen desaturation. The detected event is labeled with a horizontal black bar. This epoch comes from an infant born at 27 weeks with a birth weight of 850 grams who was eventually discharged to home from the NICU. This event was detected as an ABD110 by the automated detection algorithm, starting at 20 seconds and ending at 131 seconds. It is important to note that, although this episode represents a period of apnea detected as an ABD, isolated tiny fluctuations in the impedance signal may occur in long ABDs. This may permit these episodes to reach substantial lengths (Mohr et al., 2014).
Statistical models for central apnea in preterm infants
We studied Markov models with the state diagram shown in Figure 4(a), with one apneic state (A) and four breathing states (Bi, i=1,2,3,4) numbered from most to least stable. For each PMA we optimized the transition rate matrix K of a Markov model. Figure 4b and 4c show the dominant transitions (arrows) and states (bold) for 27 and 40 weeks PMA, respectively. The important findings are that the earlier PMA has higher probabilities of transitions towards and residence in less stable breathing and apnea states. The model at higher PMA is characterized by larger probability of the second-most stable breathing state, and lower probability of apnea.
Fig. 4.
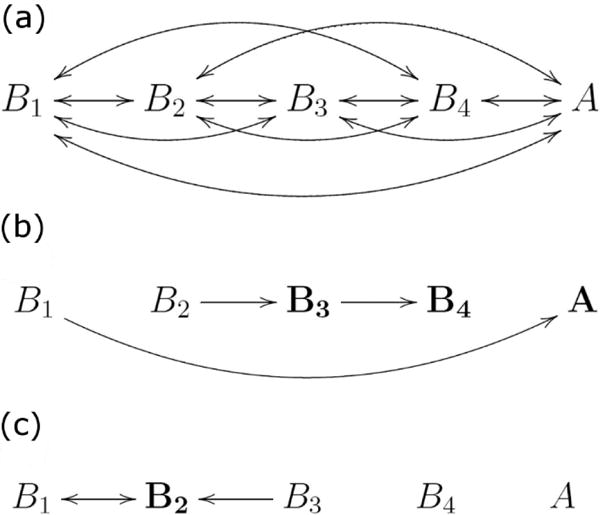
Markov state diagrams. The diagrams show (a) all possible transitions, (b) 27 weeks PMA, (c) 40 weeks PMA. In (b) and (c) only the most probable transitions are shown. Major differences between residence times in the two cases are identified by bold symbols.
The Markov model transition rates are shown in Figure 5 as a function of PMA. We found the average durations of these breathing states to be on the order of 10 seconds (B4), 10 minutes (B3), 2 hours (B2), and 12 hours (B1), see Figure 5 and Appendix section Calculating apnea burden and mean apnea duration from a Markov model. Confidence intervals are shown for the transition rates and percent residence for each state.
Fig. 5.
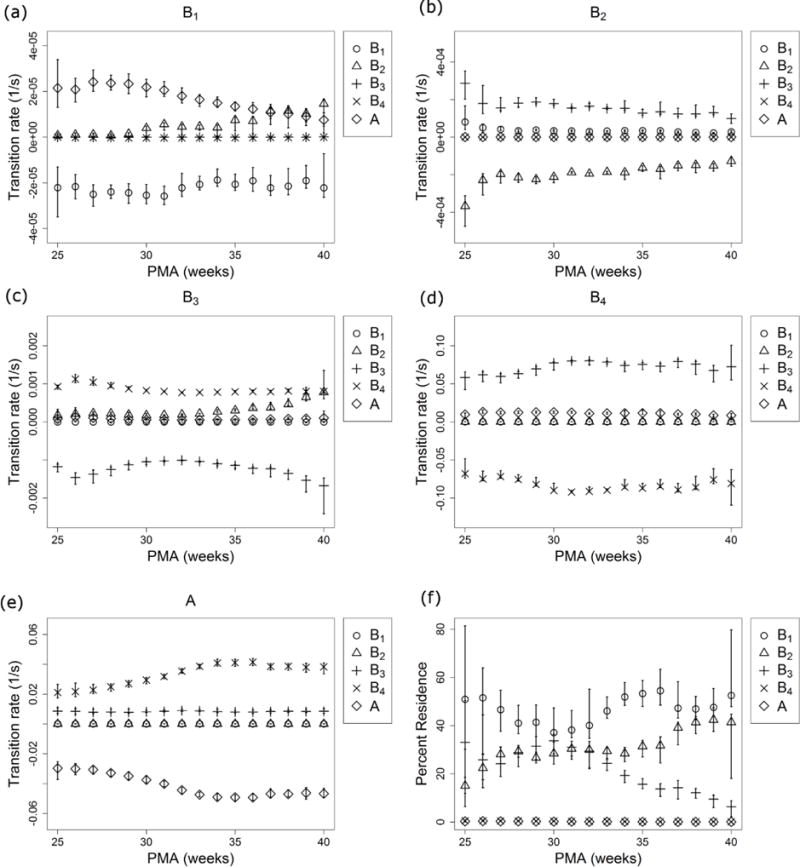
Transition rates vs PMA. Transitions are shown from B1 (a), B2 (b), B3 (c), B4 (d), and A (e) into B1 (circles), B2 (triangles), B3 (plusses), B4 (crosses), and A (diamonds) as a function of PMA. The percentage of time spent in each state is shown in (f) as a function of PMA. Segments above and below each symbol identify the 95% confidence interval and are sometimes smaller than the symbol.
The suitability of the model can be assessed by comparing its predictions to the observed data. We tested the goodness-of-fit of the model by comparing predicted and observed apnea burdens and the average duration of individual apneas. For each PMA, we calculated the apnea burden based on observed data as the number of seconds of apnea divided by the total monitoring time in days. We repeated the process for each Markov model being careful to censor apneas shorter than 10 seconds first, as apnea shorter than 10 seconds is not clinically significant (Finer et al., 2006). Details are described in Appendix A sections Calculating apnea burden and mean apnea duration from a Markov model and Censoring short apnea from the model. Figure 6 shows very good agreement between the predictions of the model and the observed data for apnea duration (Figure 6a) and apnea burden (Figure 6b). Observed data are shown as mean (circles) and 95% confidence interval (error bars) for the sample of patients at each PMA. This agreement is evidence that a Markov model with 5 (4 breathing and 1 apnea) states and 2 observables (breathing and not breathing) can accurately characterize the kinetics of apnea in VLBW infants.
Fig. 6.
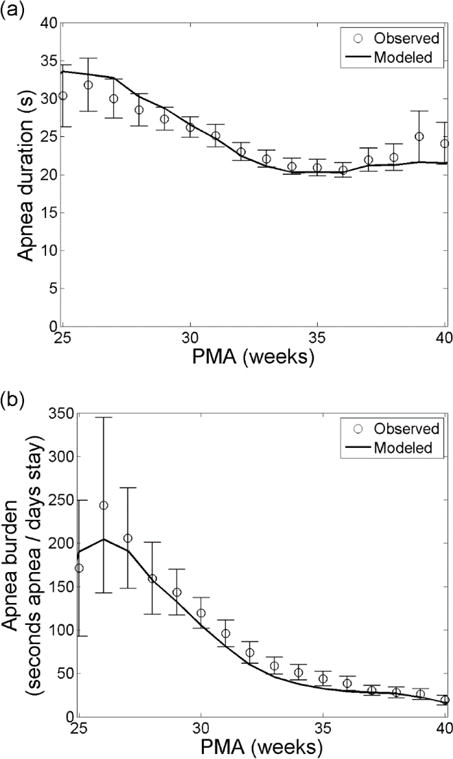
Apnea trends with PMA. Apnea duration (a) and apnea burden (b) as a function of PMA based on observation (circles) and modeling (solid). Error bars on the observations are 95% confidence intervals. The model results are adjusted to censor apnea events shorter than 10 seconds.
The rate of severe apnea after NICU discharge
Rare but clinically significant apnea events occur after discharge from the NICU. These ALTEs often lead to rehospitalization. We wish to estimate the rate of ALTE after NICU discharge. Thus we constructed a Markov model based on data from the eight days before discharge home, see Table 1. We optimized the transition rate matrix K of a Markov model using the same methods described above: the mean residence time in each Markov state in this model are 18.1 hours (B1), 2.2 hours (B2), 13.9 minutes (B3), and 12.3 seconds (B4).
We used the optimal transition rate constants from the discharge Markov model to estimate the rate of prolonged apnea after discharge. An analytical expression to estimate the rate of extreme apnea after NICU discharge is derived in Appendix A section Estimating the rate of extreme apneas after discharge. This estimate is shown in Figure 7 – the figure addresses the question, “given that an infant is discharged from the NICU to home, what is the probability that that infant will go X days and have at least one apnea of duration at least Y”. The rate of an apnea event is shown as a function of days after NICU discharge on the abscissa and duration on the ordinate. For example, our model estimates that the rate at which infants discharged to home have at least one apnea > 128s within the first 6 months after NICU discharge is 1 in 100. This extrapolation predicts that the rate of severe apnea (~180 seconds) occurring after discharge is on the order of 1 per 1000. This is on the order of the occurrence rate of SIDS in the US population (Moon and Syndrome, 2011).
Fig. 7.
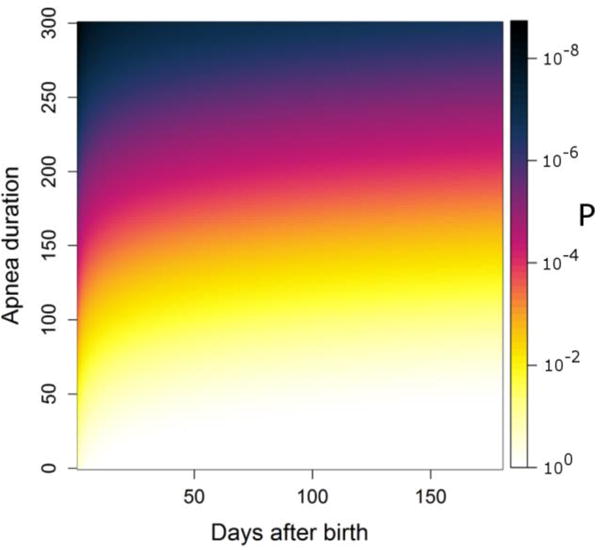
Apnea rate (In color online). The rate of apnea in post-neonatal patients based on a Markov model of all patients discharged home during their last week in the NICU. Grayscale is the probability of having at least one apnea with duration at least that on the ordinate between NICU discharge and the day on the abscissa.
Discussion
We modeled neonatal apnea in VLBW infants in intensive care using stochastic Markov type models. The choice of a stochastic model was motivated by the simplicity of such models. This choice does not require that the underlying mechanisms of neonatal breathing control actually be stochastic as opposed to deterministic and high order. Our model accurately fit the trend of declining apnea duration and apnea burden with post-natal development in a large clinical dataset, and allowed for the observations of apnea bursts as well as long apnea-free epochs terminated by severe apnea events. We find that a small number of states, 4 breathing and 1 apnea state, are sufficient to accurately model apnea durations and the return time to apnea, and the development of these transitions with PMA. An interesting extension would be to develop models based only on RR intervals, where bradycardia alone would act as surrogate for apnea with bradycardia and desaturation (Altuve et al.). Bradycardia duration and rate of descent are directly related to apnea duration and may be used to enhance such a model (Mohr et al., 2014).
The longest breathing state, with transitions at about 12 hours, is the most frequently occupied state regardless of PMA and most preferably transfers to apnea until 38 weeks PMA, Figure 5a. In Figure 5f, it is interesting that the moderately stable state, B3 with transitions at tens of minutes, is occupied 30% of the time until approximately 32 weeks PMA, after which it becomes less frequently occupied. Transitions from B3 into more stable breathing state B2 become increasingly likely with postnatal development in Figure 5c. These transitions may reflect the developing circadian and sleep cycles in neonatal brainstem physiology during this time. Circadian variations have been observed in the oxygen consumption of 31 week PMA infants (Bauer et al., 2009), but this physiology may not measurably begin developing until after 32 weeks PMA (Chen, 2010). The development of sleep-wake cycles has been observed as early as 28 weeks (Kuhle et al., 2001, Olischar et al., 2004), though sleep states develop in stability and occupancy over a longer period (Giganti et al., 2006).
One speculative interpretation is that the most stable breathing state B1 represents wakefulness, the second most stable state B2 represents residence in various stages of sleep, and B3 and B4 represent transition states where the feedback from central and peripheral chemoreceptors to the respiratory centers in the neonatal brainstem may cause breathing to become unstable, leading to apnea. Early in neurological development the neonatal control centers do not vary oxygen consumption with day-night activity cycles and do not transition to stable sleep. This corresponds to the high probability of transition from the wakeful state B1 into apnea, a frequently occupied unstable state B3, and frequent transitions from unstable breathing B3 into apnea before 29 weeks PMA (see Figure 5(a), (c), and (f)). As circadian variation in oxygen consumption and control of breathing develop an infant spends more time in the stable sleep breathing state and less in unstable breathing, Figure 5(f) starting at 30 weeks PMA. As sleep-wake cycles begin to develop transitions from wakefulness into stable sleep become more likely, Figure 5(a) starting at 29 weeks PMA. Transitions out of stable sleep into unstable breathing (B2 to B3, Figure 5(b)) become increasingly likely to transition into another sleep cycle (B3 to B2, Figure 5(c)). If these changing transition rates of Markov models are indicative of more stable sleep and circadian patterns approaching discharge, investigating the model for an individual patient may inform on that patient’s postnatal brainstem development.
The rate of severe apnea events occurring after discharge from the NICU remains an unknown in neonatology. Though the data were collected during the 8 days prior to discharge from the NICU, we extrapolated our model to estimate the rate of such apparent life threatening events. Prolonged, potentially fatal apnea events after NICU discharge were studied by the CHIME study in the 1990’s. A surprising result was the very high incidence of apneas exceeding 30 seconds accompanied by bradycardia and O2 desaturation that were not associated with obvious untoward effects (Ramanathan et al., 2001). Our study also found clinically significant apnea events in the eight days prior to discharge home; many of these infants went home with respiratory support or on an apnea monitor. This suggests a great deal of resiliency in infants: our estimate of the rate of apnea lasting longer than 180 seconds during the first year of life is 1 in 1000, as shown in Figure 7.
The implication is that information from breathing patterns might serve to identify infants that are more likely to experience prolonged potentially fatal apnea events during the first year of life. It is, counter-intuitively, the breathing durations and not the apnea durations that hold the information. Apnea durations were well-described by a single exponential decay function, a convincing argument for a single apnea state at all stages that allows for infrequent events of substantial duration. What is clinically important is how likely the current breathing state is to transition into apnea. On average, more stable breathing states are more likely with advancing development. A finding of improper maturation of transition rate constants might serve to identify the infants at highest risk for prolonged apnea after discharge to home.
Limitations and strengths
A limitation of our study is the inconsistent quality of neonatal breathing measurements – a large proportion of patient data were missing or not of suitable quality for analysis. More accurate and robust monitoring would improve the estimate for severe apnea occurring after NICU discharge, and would allow the stability of neonatal breathing control to be more accurately assessed. Another limitation is that additional filtering was performed only for apnea events within 8 days of discharge. Filtering all 26,088 would likely increase the transition rates out of apnea in Figure 5 and reduce the residual apnea burden and duration at higher PMA in Figure 6. Another limitation is that, were data excluded due to movement, this may have led to a non-random distribution of missing data. If the more active infant is less likely to experience apnea, this would tend to skew our results towards shorter time periods between apneas. Whatever the imperfections of our algorithm, we emphasize that this continuous-monitoring system is far more accurate than nursing records.
Another limitation of our approach is that central apnea events are identified without distinction by cause. Some apneas near discharge may reflect poor sucking-swallowing-breathing coordination during feeds, or changing sleep architecture. Other normal physiologic processes contribute to apnea, notably anemia (Zagol et al., 2012) and gastro-esophageal reflux (Poets, 2004). Both of these normal physiologic phenomena may be progressing at the time of NICU discharge and may play a role in the stochastic distribution of apnea, with the possibility of very long time between apnea events as the chemoreceptors and other elements of the respiratory control system mature. Another limitation of our study is that we have considered only one of many manifestations of pathologic cardiorespiratory control. Future models for transitions between stable and abnormal cardiorespiratory control should include not only apnea (Darnall, 2009, Martin et al., 2002, Di Fiore et al., 2013), but also, for example, periodic breathing (Khan et al., 2005, Wilkinson et al., 2007, Mohr et al., 2015), cardiorespiratory uncoupling (Clark et al., 2012, Godin and Buchman, 1996), and transient heart rate decelerations (Moorman et al., 2011, Dorostkar et al., 2005). A final limitation is that we model the rate of prolonged apnea after discharge using data from the last 8 days in the NICU, thus extrapolating the data as if neurological development were complete at discharge.
A major strength of this study is the use of computer algorithm-detected apnea based on chest impedance waveforms rather than nursing documentation or a tally of bedside monitor alarms, thus allowing us to accurately quantify occurrence and duration of events (Muttitt et al., 1988, Southall et al., 1983, Vergales et al., 2013). Automated detection algorithms could be continuously implemented at the bedside of preterm infants in intensive care, where all such infants already have routine cardiorespiratory monitoring. Such implementation would allow online estimation of the risk for apparently random transitions to isolated and severe apnea events following extended periods without apnea.
Press Release.
Apnea of prematurity is the occasional breathing cessation that is experienced by nearly all very premature infants. These events usually become uncommon by 9 months from conception, but apparent life-threatening events occasionally occur even after discharge from neonatal intensive care units. Such prolonged apnea events have been postulated to be related to sudden infant death syndrome (SIDS), the leading cause of infant death after the neonatal period. Foreknowledge of impending apnea in premature infants might lead to better management and earlier safe discharge.
It is not known whether apneas result from a deterministic and predictable process, with a proximate cause for every individual apnea, or whether they result from a random or stochastic process. We use a stochastic model to analyze the distribution of lengths of apneas and the distribution of lengths between apneas. The model (called a hidden-Markov model) suggests the presence of four breathing states, ranging from very stable (with an average lifetime of 12 hours) to very unstable (with an average lifetime of 10 seconds). Although the states themselves are not visible, the mathematical analysis gives estimates of the transition rates among these states.
We have obtained these transition rates, and shown how they change with post-menstrual age. As expected, the residence time in the more stable breathing states increases with age. We also obtained transition rates for the last 8 days prior to discharge home from the NICU. Extrapolating these rates, we obtain a prediction of the rate of long apneas in the first year of life. This extrapolation shows that the probability that an apnea lasting more than three minutes occurs in the first year of an infant’s life (an event that is likely to be fatal) is about one in 1000. This is close to the observed rate of SIDS.
Acknowledgments
Funding: MTC, JBD, DEL, HL, JK, and JRM were funded by NIH GO grant 1RC2HD064488. JBD was partially supported by NSF grant 1068344.
Glossary
- A
Markov state representing apnea
- αi
Relative magnitude of exponential mode i
- ABDX
Apnea event lasting at least X seconds with bradycardia and desaturation
- ALTE
Apparent life threatening event
- Bi
Markov state i representing breathing
- B
Observation symbol probability density
- C
Transition probability density
- K
Transition rate matrix
- Kij
Transition rate from i to j
- M
Number of distinct observables
- N
Number of Markov states
- NICU
Neonatal intensive care unit
- Ok
Observable k
- P
Transition probability
- P(t)
State probability vector at time t
- PMA
Post-menstrual age
- q(t)
Exponential probability distribution
- Q(t)
Exponential cumulative distribution
- ROC
Receiver operating characteristic
- Si
Markov state i
- SpO2
Peripheral oxyhemoglobin saturation
- τi
Expected value for exponential mode i
- VLBW
Very low birth weight, < 1500 grams
Appendix A
Hidden Markov modeling
Hidden Markov models represent time series data as random transitions between states that are not visible to the observer. At each instant the probability that an infant is in any one of N states is described by a vector with N components, P(t)=(P1,P2,…,PN). In the context of neonatal apnea, there are states that represent apnea and others that represent breathing states with varying levels of stability that are hidden from observers. The change of that probability vector is given by,
| (A1) |
where C is a matrix that represents transition probabilities: the probability P that the system is in state j at time t + 1 given that it was in state i at time t is
| (A2) |
where S(t) represents the state of the system at time t. In a stationary Markov model, this transition probability matrix does not depend on time. After each step, there is a finite probability that the infant remains in the same state (i=j), and for each initial state Si
| (A3) |
The general theory of hidden Markov models includes also a collection of observables (Ok, k=1,2,…), and there is another matrix B that converts the state probability vector P(t) into the probability of observing each particular outcome (Ok). In our case this matrix is trivial: the two outcomes are breathing or not-breathing. If an infant is in any of the breathing states the probability of observing breathing is 1, while if the infant is in an apnea state the probability of observing breathing is 0. Thus, “hidden” refers to the fact that we cannot identify the stability of an infant’s respiratory control system solely by observing that the infant is breathing.
Maximum likelihood calculation of transition probabilities
Several algorithms are available for obtaining maximum likelihood estimates of the one-step transition probability matrix C and from that its matrix logarithm K. Here K is a time-invariant N × N matrix of rate coefficients. The diagonal elements of K are negative, all others are positive, and each row of the matrix sums to zero. We used the Baum-Welch maximization algorithm to determine the optimal transition rate matrix K (Baum et al., 1970, Juang and Rabiner, 1991) as implemented in MatLab® (The MathWorks, Natick, MA), though the Viterbi algorithm is also an option (Shinghal and Toussaint, 1979). These optimization algorithms allow for non-zero transition rates between any pair of states. This method requires an initial estimate of C and of the initial vector of probabilities P(0). The initial estimate C0 was derived from an initial estimate K0 that was chosen to be,
| (A4) |
The transition rates were determined as a function of PMA using these parameters. The resulting coefficients of the transition rate matrix K are shown in Figure 5a–e. Note that the diagonal elements of K are negative to maintain a zero row sum. The coefficients are shown for the longest lifetime breathing state B1 (a), the next longest lifetime breathing state B2 (b), the third longest lifetime breathing B3 (c), the shortest lifetime breathing state B4 (d), and the apneic state A (e). The percentage of time spent in each state is shown in Figure 5f.
Calculating apnea burden and mean apnea duration from a Markov model
To check the consistency between the model and the data, we estimate the apnea burden and the mean apnea duration. At steady state, the probability of apnea is the value of the corresponding element of the normalized left-eigenvector of the transition rate matrix K having eigenvalue equal to zero. If this probability is multiplied by the number of seconds in a day, it gives the apnea burden (seconds of apnea per days of monitoring) predicted by the Markov model. The average apnea duration predicted by the model is −1/KAA, where KAA is the transition rate from the apnea state into the apnea state. For any state Si the average residence time in that state is −1/Kii.
Censoring short apnea from the model
A Markov model assumes the dwell time in each state is exponentially distributed. Apnea durations are censored below 10 seconds. Censoring an exponential probability distribution below a value x has the effect of increasing the mean of that distribution by x. The average residence time in the apnea state (A) must be decreased by 10 seconds to account for this fact. This is achieved by modifying transition rates KAi, i=1…N representing transitions out of apnea as,
| (A5) |
Filtering out false positive apnea events near discharge
When modeling apnea during the 8 days prior to discharge home, the apnea detection algorithm produced a larger false positive rate than that during the rest of the stay. This is a result of the lower apnea rate and increased infant activity at this point in neonatal care. In order to reduce the rate of false positives and more accurately estimate the rate of apnea, we filtered events using an automated algorithm. For each apnea event we calculated two parameters: the area under the apnea probability (Lee et al., 2012) divided by the apnea duration, and the power in the chest impedance between 0.5 Hz and 2.0 Hz. These two parameters were calculated for 500 automatically-identified apnea events randomly selected throughout the entire stay of all infants in the study. Of these, 471 events were adjudicated as true apnea or false positive by agreement of two neonatologists. A logistic regression model was created using maximum likelihood estimation. The ROC area of this model is 0.93.
We used this model as an additional filter for apnea events, and determined a threshold below which apnea events were censored from our analysis. This threshold was determined by randomly selecting 100 events from the 8 days prior to discharge in 196 infants, of which 96 events were adjudicated. We selected a threshold for the apnea filter such that the false positive rate was equal to the false negative rate: we used an apnea filter threshold of 0.81.
Estimating the rate of extreme apneas after discharge
We also computed a K matrix based on time series from the last 8 days prior to discharge home. We extrapolated the rate of apnea occurring after discharge from the NICU. We wish to estimate the probability that an infant will have at least one apnea event within N days after discharge, and that at least one of those events will have duration greater than d. Figure A1 shows the distribution of apnea durations in the 8 days before discharge (circles) and the modeled distribution (dashed). The rate of apneas longer than about 1 ½ minutes is extrapolated.
We now model the probability of having n apnea events in N days using a Poisson distribution. We consider each day as a trial, and estimate the probability of n “successes” (apnea events) based on the expected number of successes v. In this context, the probability of having exactly n apneas in N days is the Poisson probability density distribution,
| (A6) |
Here v, the expected number of apneas in N days, is
| (A7) |
where α= 86,400 seconds per day, KAA is the diagonal element of the rate matrix corresponding to the apneic state (i.e. the negative inverse of the mean apnea duration), and pA is the probability of apnea. At steady state, this probability of apnea pA is the value of the corresponding element of the normalized left-eigenvector of the transition rate matrix K having eigenvalue equal to zero. The probability that an apnea is shorter than d seconds is the cumulative of the exponential distribution,
| (A8) |
The proposition that there are no apneas within N days of discharge, or that any apnea events occurring within N days are shorter than d, is,
| (A9) |
We use the distributions in Eqs. (A6) and (A8) to find the probability of this proposition,
| (A10) |
This simplifies to,
| (A11) |
| (A12) |
The proposition of having at least one apnea with duration greater than d is the negation of the proposition in Eq. (A9),
| (A13) |
The probability of prolonged apnea after discharge is therefore one minus the probability in Eq. (A11),
| (A14) |
This result is shown in Figure 7.
Fig. A1.
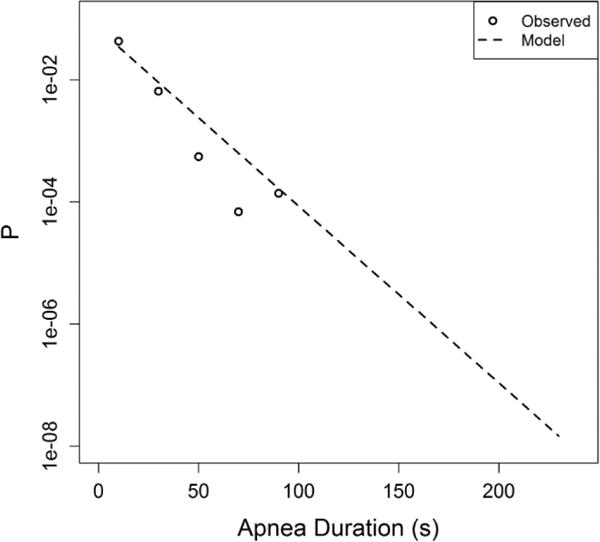
Probability density of automatically identified apnea durations during the eight days prior to discharge for 196 VLBW infants. Events longer than 60 seconds were identified as false positives by manual inspection, and were censored.
Footnotes
Author contributions: MTC, DEL, and JRM designed the study and performed the analysis. JBD and HL developed the apnea detection algorithm and its refinement described in the appendix. KDF and JK performed validation of the apnea detection algorithm and its refinement, and provided clinical context for the results. All authors contributed to the writing of the manuscript.
Competing interests: JBD and HL have filed for a patent on the apnea detection algorithm.
Data and materials availability: Per the NIH requirements, data from this study are available through an MTA.
References and Notes
- ALTUVE M, CARRAULT G, BEUCHEE A, PLADYS P, HERNANDEZ AI. On-line apnea-bradycardia detection using hidden semi-Markov models. Conf Proc IEEE Eng Med Biol Soc. 2011:4374–7. doi: 10.1109/IEMBS.2011.6091085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- BARRINGTON KJ, FINER NN. Periodic breathing and apnea in preterm infants. Pediatr Res. 1990;27:118–21. doi: 10.1203/00006450-199002000-00003. [DOI] [PubMed] [Google Scholar]
- BAUER J, JANECKE A, GERSS J, MASJOSTHUSMANN K, WERNER C, HOFFMANN G. Circadian variation on oxygen consumption in preterm infants. J Perinat Med. 2009;37:413–7. doi: 10.1515/JPM.2009.067. [DOI] [PubMed] [Google Scholar]
- BAUM LE, PETRIE T, SOULES G, WEISS N. A Maximization Technique Occurring in Statistical Analysis of Probabilistic Functions of Markov Chains. Annals of Mathematical Statistics. 1970;41:164–&. [Google Scholar]
- CHAITIN GJ. Randomness and Mathematical Proof. Scientific American 1975 [Google Scholar]
- CHEN A. The circadian rhythm of expression of Bmal1 and Cry1 in peripheral blood mononuclear cells of preterm neonates. J Matern Fetal Neonatal Med. 2010;23:1172–5. doi: 10.3109/14767051003677947. [DOI] [PubMed] [Google Scholar]
- CLARK MT, RUSIN CG, HUDSON JL, LEE H, DELOS JB, GUIN LE, VERGALES BD, PAGET-BROWN A, KATTWINKEL J, LAKE DE, MOORMAN JR. Breath-by-breath analysis of cardiorespiratory interaction for quantifying developmental maturity in premature infants. J Appl Physiol. 2012;112:859–67. doi: 10.1152/japplphysiol.01152.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- COLQUHOUN D, HAWKES AG. Relaxation and Fluctuations of Membrane Currents That Flow through Drug-Operated Channels. Proceedings of the Royal Society of London Series B-Biological Sciences. 1977;199:231–262. doi: 10.1098/rspb.1977.0137. [DOI] [PubMed] [Google Scholar]
- COLQUHOUN D, HAWKES AG. On the Stochastic Properties of Bursts of Single Ion Channel Openings and of Clusters of Bursts. Philosophical Transactions of the Royal Society of London Series B-Biological Sciences. 1982;300:1–59. doi: 10.1098/rstb.1982.0156. [DOI] [PubMed] [Google Scholar]
- DARNALL RA. ALTEs: still a puzzle after all these years. J Pediatr. 2009;154:317–9. doi: 10.1016/j.jpeds.2008.09.041. [DOI] [PubMed] [Google Scholar]
- DETILLEUX JC. The analysis of disease biomarker data using a mixed hidden Markov model (Open Access publication) Genet Sel Evol. 2008;40:491–509. doi: 10.1186/1297-9686-40-5-491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DI FIORE JM, MARTIN RJ, GAUDA EB. Apnea of prematurity – Perfect storm. Respir Physiol Neurobiol. 2013 doi: 10.1016/j.resp.2013.05.026. [DOI] [PubMed] [Google Scholar]
- DOROSTKAR PC, ARKO MK, BAIRD TM, RODRIGUEZ S, MARTIN RJ. Asystole and severe bradycardia in preterm infants. Biol Neonate. 2005;88:299–305. doi: 10.1159/000087627. [DOI] [PubMed] [Google Scholar]
- FENG Z, MCLERRAN D, GRIZZLE J. A comparison of statistical methods for clustered data analysis with Gaussian error. Stat Med. 1996;15:1793–806. doi: 10.1002/(SICI)1097-0258(19960830)15:16<1793::AID-SIM332>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
- FINER NN, HIGGINS R, KATTWINKEL J, MARTIN RJ. Summary proceedings from the apnea-of-prematurity group. Pediatrics. 2006;117:S47–51. doi: 10.1542/peds.2005-0620H. [DOI] [PubMed] [Google Scholar]
- FREY U, SILVERMAN M, BARABÁSI AL, SUKI B. Irregularities and power law distributions in the breathing pattern in preterm and term infants. J Appl Physiol (1985) 1998;85:789–97. doi: 10.1152/jappl.1998.85.3.789. [DOI] [PubMed] [Google Scholar]
- GIGANTI F, FICCA G, CIONI G, SALZARULO P. Spontaneous awakenings in preterm and term infants assessed throughout 24-h video-recordings. Early Hum Dev. 2006;82:435–40. doi: 10.1016/j.earlhumdev.2005.11.005. [DOI] [PubMed] [Google Scholar]
- GODIN PJ, BUCHMAN TG. Uncoupling of biological oscillators: a complementary hypothesis concerning the pathogenesis of multiple organ dysfunction syndrome. Crit Care Med. 1996;24:1107–1116. doi: 10.1097/00003246-199607000-00008. [DOI] [PubMed] [Google Scholar]
- HARRELL FE. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. Berlin: Springer; 2001. [Google Scholar]
- JUANG BH, RABINER LR. Hidden Markov-Models for Speech Recognition. Technometrics. 1991;33:251–272. [Google Scholar]
- KHAN A, QURASHI M, KWIATKOWSKI K, CATES D, RIGATTO H. Measurement of the CO2 apneic threshold in newborn infants: possible relevance for periodic breathing and apnea. J Appl Physiol. 2005;98:1171–6. doi: 10.1152/japplphysiol.00574.2003. [DOI] [PubMed] [Google Scholar]
- KIM JW, LEE JS, ROBINSON PA, JEONG DU. Markov analysis of sleep dynamics. Phys Rev Lett. 2009;102:178104. doi: 10.1103/PhysRevLett.102.178104. [DOI] [PubMed] [Google Scholar]
- KINNEY HC, THACH BT. The sudden infant death syndrome. N Engl J Med. 2009;361:795–805. doi: 10.1056/NEJMra0803836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- KUHLE S, KLEBERMASS K, OLISCHAR M, HULEK M, PRUSA AR, KOHLHAUSER C, BIRNBACHER R, WENINGER M. Sleep-wake cycles in preterm infants below 30 weeks of gestational age. Preliminary results of a prospective amplitude-integrated EEG study. Wien Klin Wochenschr. 2001;113:219–23. [PubMed] [Google Scholar]
- LAPLACE PS. Essai Philosophique sur les probabilities. Paris: Paris Bachelier; 1840. [Google Scholar]
- LEE H, RUSIN CG, LAKE DE, CLARK MT, GUIN L, SMOOT TJ, PAGET-BROWN AO, VERGALES BD, KATTWINKEL J, MOORMAN JR, DELOS JB. A new algorithm for detecting central apnea in neonates. Physiol Meas. 2012;33:1–17. doi: 10.1088/0967-3334/33/1/1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LEE LM, JEAN FR. Adaptation of Hidden Markov Models for Recognizing Speech of Reduced Frame Rate. IEEE Trans Cybern. 2013 doi: 10.1109/TCYB.2013.2240450. [DOI] [PubMed] [Google Scholar]
- LI Q, MARK RG, CLIFFORD GD. Robust heart rate estimation from multiple asynchronous noisy sources using signal quality indices and a Kalman filter. Physiol Meas. 2008;29:15–32. doi: 10.1088/0967-3334/29/1/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MARTIN RJ, ABU-SHAWEESH JM, BAIRD TM. Pathophysiology mechanisms underlying apnea of prematurity. Neoreviews. 2002;3:e59–e65. [Google Scholar]
- MCMANUS OB, WEISS DS, SPIVAK CE, BLATZ AL, MAGLEBY KL. Fractal models are inadequate for the kinetics of four different ion channels. Biophys J. 1988;54:859–70. doi: 10.1016/S0006-3495(88)83022-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MOHR M, VERGALES B, LEE H, CLARK MT, LAKE DE, MENNEN AC, KATTWINKEL J, SINKIN R, MOORMAN JR, FAIRCHILD KD, DELOS JB. Very long apnea events in preterm infants: systems failures in the NICUs. J Appl Physiol. 2014 doi: 10.1152/japplphysiol.00144.2014. Revision submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MOHR MA, FAIRCHILD KD, PATEL M, SINKIN RA, CLARK MT, MOORMAN JR, LAKE DE, KATTWINKEL J, DELOS JB. Quantification of periodic breathing in premature infants. Physiol Meas. 2015;36:1415–27. doi: 10.1088/0967-3334/36/7/1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MOON RY, SYNDROME, T. F. O. S. I. D. SIDS and other sleep-related infant deaths: expansion of recommendations for a safe infant sleeping environment. Pediatrics. 2011;128:1030–9. doi: 10.1542/peds.2011-2284. [DOI] [PubMed] [Google Scholar]
- MOORMAN JR, CARLO WA, KATTWINKEL J, SCHELONKA RL, PORCELLI PJ, NAVARRETE CT, BANCALARI E, ASCHNER JL, WHIT WALKER M, PEREZ JA, PALMER C, STUKENBORG GJ, LAKE DE, MICHAEL O’SHEA T. Mortality reduction by heart rate characteristic monitoring in very low birth weight neonates: a randomized trial. J Pediatr. 2011;159:900–6 e1. doi: 10.1016/j.jpeds.2011.06.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MUTTITT SC, FINER NN, TIERNEY AJ, ROSSMANN J. Neonatal apnea: diagnosis by nurse versus computer. Pediatrics. 1988;82:713–20. [PubMed] [Google Scholar]
- OLISCHAR M, KLEBERMASS K, KUHLE S, HULEK M, KOHLHAUSER C, RÜCKLINGER E, POLLAK A, WENINGER M. Reference values for amplitude-integrated electroencephalographic activity in preterm infants younger than 30 weeks’ gestational age. Pediatrics. 2004;113:e61–6. doi: 10.1542/peds.113.1.e61. [DOI] [PubMed] [Google Scholar]
- PAN J, TOMPKINS WJ. A real-time QRS detection algorithm. IEEE Trans Biomed Eng. 1985;32:230–6. doi: 10.1109/TBME.1985.325532. [DOI] [PubMed] [Google Scholar]
- PAYDARFAR D, BUERKEL DM. Dysrhythmias of the respiratory oscillator. Chaos. 1995;5:18–29. doi: 10.1063/1.166067. [DOI] [PubMed] [Google Scholar]
- POETS CF. Gastroesophageal reflux: a critical review of its role in preterm infants. Pediatrics. 2004;113:e128–32. doi: 10.1542/peds.113.2.e128. [DOI] [PubMed] [Google Scholar]
- POETS CF, SOUTHALL DP. Patterns of oxygenation during periodic breathing in preterm infants. Early Hum Dev. 1991;26:1–12. doi: 10.1016/0378-3782(91)90038-5. [DOI] [PubMed] [Google Scholar]
- RABINER LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of IEEE. 1989:257–286. [Google Scholar]
- RAMANATHAN R, CORWIN MJ, HUNT CE, LISTER G, TINSLEY LR, BAIRD T, SILVESTRI JM, CROWELL DH, HUFFORD D, MARTIN RJ, NEUMAN MR, WEESE-MAYER DE, CUPPLES LA, PEUCKER M, WILLINGER M, KEENS TG. Cardiorespiratory events recorded on home monitors: Comparison of healthy infants with those at increased risk for SIDS. JAMA. 2001;285:2199–2207. doi: 10.1001/jama.285.17.2199. [DOI] [PubMed] [Google Scholar]
- ROBERTSON C, SAWFORD K, GUNAWARDANA WS, NELSON TA, NATHOO F, STEPHEN C. A hidden Markov model for analysis of frontline veterinary data for emerging zoonotic disease surveillance. PLoS One. 2011;6:e24833. doi: 10.1371/journal.pone.0024833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SCHAFER PB, JIN DZ. Noise-robust speech recognition through auditory feature detection and spike sequence decoding. Neural Comput. 2014;26:523–56. doi: 10.1162/NECO_a_00557. [DOI] [PubMed] [Google Scholar]
- SHINGHAL R, TOUSSAINT GT. Experiments in text recognition with the modified viterbi algorithm. IEEE Trans Pattern Anal Mach Intell. 1979;1:184–93. doi: 10.1109/tpami.1979.4766904. [DOI] [PubMed] [Google Scholar]
- SIGWORTH FJ, SINE SM. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys J. 1987;52:1047–54. doi: 10.1016/S0006-3495(87)83298-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SONNENBERG FA, BECK JR. Markov models in medical decision making: a practical guide. Med Decis Making. 1993;13:322–38. doi: 10.1177/0272989X9301300409. [DOI] [PubMed] [Google Scholar]
- SOUTHALL DP, LEVITT GA, RICHARDS JM, JONES RA, KONG C, FARNDON PA, ALEXANDER JR, WILSON AJ. Undetected episodes of prolonged apnea and severe bradycardia in preterm infants. Pediatrics. 1983;72:541–51. [PubMed] [Google Scholar]
- TARASSENKO L, CLIFFORD G, TOWNSEND N. Detection of ectopic beats in the electrocardiogram using an auto-associative neural network. Neural Processing Letters. 2001;14:15–25. [Google Scholar]
- VERGALES BD, PAGET-BROWN AO, LEE H, GUIN LE, SMOOT TJ, RUSIN CG, CLARK MT, DELOS JB, FAIRCHILD KD, LAKE DE, MOORMAN R, KATTWINKEL J. Accurate Automated Apnea Analysis in Preterm Infants. Am J Perinatol. 2013;31 doi: 10.1055/s-0033-1343769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WAGGENER TB, FRANTZ ID, STARK AR, KRONAUER RE. Oscillatory breathing patterns leading to apneic spells in infants. J Appl Physiol Respir Environ Exerc Physiol. 1982;52:1288–95. doi: 10.1152/jappl.1982.52.5.1288. [DOI] [PubMed] [Google Scholar]
- WAGGENER TB, STARK AR, COHLAN BA, FRANTZ ID. Apnea duration is related to ventilatory oscillation characteristics in newborn infants. J Appl Physiol Respir Environ Exerc Physiol. 1984;57:536–44. doi: 10.1152/jappl.1984.57.2.536. [DOI] [PubMed] [Google Scholar]
- WILKINSON MH, SKUZA EM, RENNIE GC, SANDS SA, YIALLOUROU SR, HORNE RS, BERGER PJ. Postnatal development of periodic breathing cycle duration in term and preterm infants. Pediatr Res. 2007;62:331–6. doi: 10.1203/PDR.0b013e3180db29e5. [DOI] [PubMed] [Google Scholar]
- WILLINGER M, JAMES LS, CATZ C. Defining the sudden infant death syndrome (SIDS): deliberations of an expert panel convened by the National Institute of Child Health and Human Development. Pediatr Pathol. 1991;11:677–84. doi: 10.3109/15513819109065465. [DOI] [PubMed] [Google Scholar]
- ZAGOL K, LAKE DE, VERGALES B, MOORMAN ME, PAGET-BROWN A, LEE H, RUSIN CG, DELOS JB, CLARK MT, MOORMAN JR, KATTWINKEL J. Anemia, apnea of prematurity, and blood transfusions. J Pediatr. 2012;161:417–421 e1. doi: 10.1016/j.jpeds.2012.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]


