To the Editor:
North et al. (2002) discussed the estimation of a P value on the basis of computer (i.e., Monte Carlo) simulations. They emphasized that such a P value is an estimate of the true P value. This is essentially their only point with which we agree. The letter from North et al. is more likely to confuse than enlighten.
Consider an observed test statistic, x, that under the null hypothesis follows some distribution, f. Let X be a random variable following the distribution f. We seek to estimate the P value, p=Pr(X⩾x). Let y1,…,yn be independent draws from f, obtained by computer simulation. Let r=#{i:yi⩾x} (i.e., the number of simulated statistics greater than or equal to the observed statistic). Let 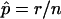 and
and 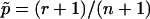 .
.
North et al. (2002) stated that 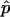 is “not strictly correct” and that
is “not strictly correct” and that 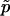 is “the most accurate estimate of the P value.” They further called
is “the most accurate estimate of the P value.” They further called 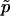 “the true P value.”
“the true P value.”
We strongly disagree with this characterization. First, minor differences in P-value estimates on the order of Monte Carlo error should not be treated differently in practice, and so it is immaterial whether one uses 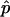 or
or 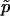 . Second,
. Second, 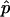 is a perfectly reasonable estimate of p. Indeed, in many ways
is a perfectly reasonable estimate of p. Indeed, in many ways 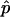 is superior to
is superior to 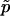 . Given the observed test statistic, x, r follows a binomial (n,p) distribution, and so
. Given the observed test statistic, x, r follows a binomial (n,p) distribution, and so 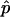 is unbiased, whereas
is unbiased, whereas 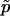 is biased. (The bias of
is biased. (The bias of 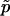 is (1-p)/(n+1).) Further,
is (1-p)/(n+1).) Further, 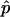 has smaller mean square error (MSE) than
has smaller mean square error (MSE) than 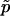 , provided that p<n/(1+3n)≈1/3. (The MSE of
, provided that p<n/(1+3n)≈1/3. (The MSE of 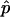 is p(1-p)/n, whereas that of
is p(1-p)/n, whereas that of 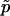 is (1-p)(np+1-p)/(n+1)2.)
is (1-p)(np+1-p)/(n+1)2.)
These results are contrary to those of North et al. (2002) because they evaluate the performance of 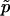 under the joint distribution of both the observed and Monte Carlo data, whereas we prefer to condition on the observed value of the test statistic. Evaluating P-value estimates conditionally on the observed data is widely accepted when the estimation is performed via analytic approximations.
under the joint distribution of both the observed and Monte Carlo data, whereas we prefer to condition on the observed value of the test statistic. Evaluating P-value estimates conditionally on the observed data is widely accepted when the estimation is performed via analytic approximations.
Regarding the question of how many simulation replicates to perform, we recommend consideration of the precision of the estimate, 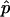 , using the properties of the binomial distribution, rather than adherence to a rule such as r⩾10. Standard statistical packages, such as R (Ihaka and Gentleman 1996), allow one to calculate a CI for the true P value and to perform a statistical test, such as whether the true P value is <.01.
, using the properties of the binomial distribution, rather than adherence to a rule such as r⩾10. Standard statistical packages, such as R (Ihaka and Gentleman 1996), allow one to calculate a CI for the true P value and to perform a statistical test, such as whether the true P value is <.01.
References
- Ihaka R, Gentleman R (1996) R: a language for data analysis and graphics. J Comp Graph Stat 5:299–314 [Google Scholar]
- North BV, Curtis D, Sham PC (2002) A note on the calculation of empirical P values from Monte Carlo procedures. Am J Hum Genet 71:439–441 [DOI] [PMC free article] [PubMed] [Google Scholar]


