Mathematical Modeling of the Methionine Cycle and Transsulfuration Pathway in Individuals with Autism Spectrum Disorder

Abstract

Previous research has shown a connection between metabolic abnormalities in the methionine cycle and transsulfuration pathway and autism spectrum disorder. Using clinical data from a case-control study investigating measurements of transmethylation and transsulfuration metabolites, a steady-state model of these metabolites in liver cells was developed and participant-specific parameters were identified. Comparison of mean parameter values and parameter distributions between neurotypical study participants and those on the autism spectrum revealed significant differences for four model parameters. Sensitivity analysis identified the parameter describing the rate of glutamylcysteine synthesis, the rate-limiting step in glutathione production, to be particularly important in determining steady-state metabolite concentrations. These results may provide insight into key reactions to target for potential intervention strategies relating to autism spectrum disorder.

1. Introduction

Autism spectrum disorder (ASD) is a general diagnosis for a group of neurodevelopmental disabilities that appear in the early years of childhood, typically before the age of two (American Psychiatric Association, 2013). Although the disorder can be associated with a large array of symptoms, the two primary criteria for diagnosis of ASD are difficulties with social interaction and communication and the display of restricted, repetitive behaviors (American Psychiatric Association, 2013). The Center for Disease Control’s most recent estimate of ASD prevalence among children in the United States is 1 in 68 (Christensen et al., 2016). This is a substantial increase from its 1996 estimate of 1 in 294 (Yeargin-Allsopp et al., 2003), and even more so from international estimates in the early 1970s of approximately 1 in 2300 (Gillberg and Wing, 1999).

The significant rise in ASD prevalence has prompted research into certain risk factors for the disorder. While there is clearly a genetic component involved in the development of ASD (Abrahams and Geschwind, 2008; Bailey et al., 1995; Rai, 2016), recent twin studies indicate that heritability of the disorder is potentially lower than previously estimated (Gaugler et al., 2014; Hallmayer et al., 2011). Environmental factors are also suggested to contribute to increased ASD susceptibility through a variety of mechanisms (Rossignol et al., 2014). For example, a recent study found significant correlations between the concentrations of organic pollutants, such as pesticides, in the blood of children and the severity of ASD-associated behaviors in those children with the disorder potentially also affected by a child’s genetic susceptibilities (Boggess et al., 2016). The results of another study indicated a significant association between maternal antidepressant treatment before pregnancy and ASD risk in children (Castro et al., 2016). Correlations have also been found between concentrations of certain toxic metals in blood and urine and ASD severity (Adams et al., 2012; Adams et al., 2016). While there is an ongoing debate on what factors contribute to ASD (and in what capacity), these findings provide evidence that the factors involved in ASD risk are much more complex than just genetic predisposition alone.

Recent research has also pointed to a critical connection between incidence of ASD and irregularities in folate-dependent one-carbon metabolism and transsulfuration. Several studies have found evidence for reduced methylation capacity and increased oxidative stress in people with ASD compared to age-matched controls (Adams et al., 2011; James et al., 2006; Melnyk et al., 2012). Since the metabolic pathways directly responsible for these abnormalities are the methionine cycle and transsulfuration pathway, these results suggest that some dysfunction in these pathways might be associated with ASD. While the methionine cycle is found in all cells in the body, transsulfuration is limited to the liver, pancreas, small intestine, kidney, and brain (Finkelstein and Martin, 2000; Vitvitsky et al., 2006). Combined, these pathways have many diverse functions in the human body, including the regulation of gene expression through addition of methyl groups to DNA (Ulrey et al., 2005), myelin protein stabilization in nerve cells (Miller, 2003), and synthesis of glutathione, one of the body’s major antioxidants (Wu et al., 2004). Glutathione plays an important role in detoxification and removal of reactive oxygen species in the body. In mammals, glutathione is found in all tissue types, with high concentrations found in the liver (Lu, 1999) where it is primarily synthesized. The main function of glutathione is antioxidant defense against reactive oxygen species, including free radicals (Fang et al., 2002), and detoxification of environmental toxins, including heavy metals (Adams et al., 2011). Metabolic abnormalities and deficiency of glutathione can result in increased intracellular oxidative stress. Studies suggest that elevated levels of oxidative stress are associated with the pathophysiology of a number of diseases, including Alzheimer’s disease (Markesbery, 1997), diabetes (Giugliano et al., 1996), and cystic fibrosis (Roum et al., 1993), as well as ASD (James et al., 2006). Although the link between glutathione, oxidative stress, and disease has been well-studied, exact explanations for why these relationships exist have yet to be found (Ballatori et al., 2009).

This paper seeks to contribute to our understanding of how metabolites of the methionine cycle and transsulfuration pathway interact by creating a mathematical model where the probability density functions (PDFs) of the parameter values are determined from clinical data. Detailed models of the methionine cycle and transsulfuration pathway exist (Duncan et al., 2013a, 2013b; Reed et al., 2008; Reed et al., 2004) that include complex nonlinear formulas for the rates of each of the reactions, as well as inhibitory and excitatory effects of metabolites on enzymes. These models have a large number of parameters which cannot all be estimated by measuring only a small number of metabolites in the blood. Instead, we chose to develop a smaller model of the pathways with unidirectional linear kinetics. This model does not have the biological detail of the larger models, but it has the advantage of having only 8 parameters (the kinetic rate constants), which can be determined from clinical data. Estimation of the PDFs of these parameters for both neurotypical study participants and participants with ASD, as well as performing sensitivity analysis on the model, allows for identification of important reactions that could potentially be manipulated for future intervention strategies for ASD.

2. Materials and Methods

2.1. Plasma metabolite data

The clinical data used in this model come from the Integrated Metabolic and Genomic Endeavor (IMAGE) study at Arkansas Children’s Hospital Research Institute (Melnyk et al., 2012). The IMAGE study protocol was approved by the University of Arkansas for Medical Sciences’ Institutional Review Board, and parents provided written informed consent. Data for 82 neurotypical study participants (control) and 93 participants on the autism spectrum (case) were used for the model in this work. These data reflect plasma concentrations of transmethylation and transsulfuration metabolites, as well as those of tyrosine, nitrotyrosine, and chlorotyrosine, quantified with high performance liquid chromatography (HPLC) (Melnyk et al., 1999; Melnyk et al., 2000). Amounts of cytosine, 5-methylcytosine, and 8-oxo-deoxyguanosine in DNA were also quantified using a HPLC-ultraviolet system and HPLC electrochemical detection (Helbock et al., 1998). The interested reader is referred to (Melnyk et al., 2012) for further information regarding data collection and experimental procedures.

2.2. Model development

The components and structure of the methionine cycle and transsulfuration pathway can be found in the public literature (Reed et al., 2008). The mathematical model developed here is based upon the structure of these metabolic pathways in liver cells, where 8 metabolites measured in the clinical study are modeled. The model consists of the component balances of the individual metabolites at steady state, is based on mass action kinetics, and can be mathematically described as a set of linear algebraic equations. Molar concentrations of metabolites (c), participant-specific rate parameters (p), and efflux rate constants (f) represent the inputs to the system.

A compartmental model, where the concentrations of the metabolites within each compartment are considered to be well-mixed, is used. There are potentially fluxes of components into and out of each compartment, resulting in a net flux rate. Similarly, reactions within each compartment can result in the concentration of a metabolite being increased or decreased. This is represented by the general component balance:

$$\frac{d}{dt}\left(\mathit{amount}\mathit{of}\mathit{metabolite}i\mathit{in}\mathit{compartment}\right)=\left(\mathit{net}\mathit{flow}\mathit{rate}\mathit{of}\mathit{metabolite}i\mathit{into}\mathit{or}\mathit{out}\mathit{of}\mathit{compartment}\right)+\left(\mathit{net}\mathit{rate}\mathit{of}\mathit{production}\mathit{or}\mathit{depletion}\mathit{of}\mathit{metabolite}i\mathit{in}\mathit{compartment}\right).$$ (1)

The structure of the metabolic reactions described by the mathematical model is shown in Figure 1. Methionine, S-adenosylmethionine (SAM), S-adenosylhomocysteine (SAH), and homocysteine make up the methionine cycle. Cysteine, glutamylcysteine, glutathione (GSH), and glutathione disulfide (GSSG) are the modeled components of the transsulfuration pathway. Cystathionine, an intermediate in the reaction of homocysteine converting to cysteine, was omitted from the transsulfuration pathway due to lack of available measurements for it.

Figure 1.

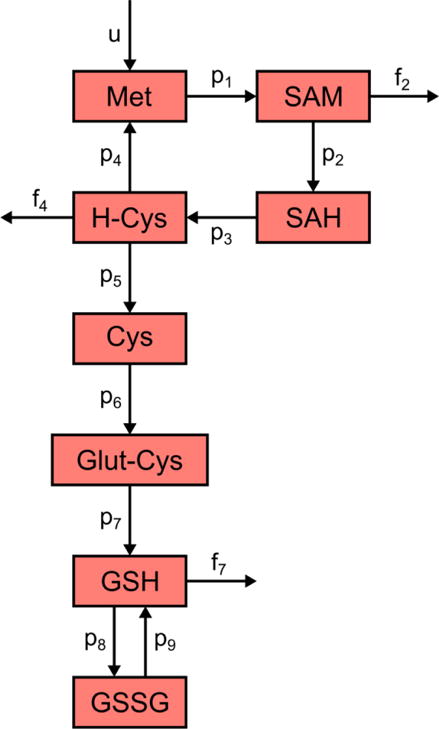
The structure of the methionine cycle and transsulfuration pathway as described by the mathematical model. Met: methionine, SAM: S-adenosylmethionine, SAH: S-adenosylhomocysteine, H-Cys: homocysteine, Cys: cysteine, Glut-Cys: glutamylcysteine, GSH: glutathione, GSSG: glutathione disulfide. The p variables represent participant-specific rate parameters, while the f variables correspond to flux rate constants. Variable u is a zero-order, participant-dependent methionine influx used to keep the system at steady state.

The model consists of 8 equations (Table 1) and contains 9 participant-specific parameters represented by variables p₁ through p₉, each having units of hr⁻¹. Included are also 3 global efflux rate constants representing the removal rates of SAM, homocysteine, and GSH from the compartment. These flux rates are represented by variables f₂ = 9 hr⁻¹ (Duncan et al., 2013a; Stabler and Allen, 2004), f₄ = 0.001 hr⁻¹ (Chwatko and Jakubowski, 2005; Duncan et al., 2013a; Refsum et al., 1985), and f₇ = 3.8 hr⁻¹ (Hong et al., 2005). To maintain the steady state properties of the model, a zero-order influx rate constant u is used to supply methionine to the system. This variable has units of μM/hr and is equal to the sum of a participant’s three efflux rates to achieve a steady state balance:

$$u=f_2{c}_2+f_4{c}_4+f_7{c}_7$$ (2)

with f₂, f₄, and f₇ being the removal rates (in hr⁻¹) of SAM, homocysteine, and GSH, respectively, and c₂, c₄, and c₇ being the concentrations (in μM) of SAM, homocysteine, and GSH, respectively.

Table 1.

Metabolites included in and linear algebraic equations of the model.

Metabolite	Concentration Variable	Model Equation
Methionine	c1	0 = p4c4 − p1c1 + f2c2 + f4c4 + f7c7
S-adenosylmethionine (SAM)	c2	0 = p1c1 − p2c2 − f2c2
S-adenosylhomocysteine (SAH)	c3	0 = p2c2 −p3c3
Homocysteine	c4	0 = p3c3 − p4c4 − p5c4 − f4c4
Cysteine	c5	0 = p5c4 −p6c5
Glutamylcysteine	c6	0 = p6c5 − p7c6
Glutathione (GSH)	c7	0 = p7c6 − p8c7 + p9c8 − f7c7
Glutathione disulfide (GSSG)	c8	0 = P8c7 − p9c8

In this model, methionine enters the system at the rate defined in Equation 2, and is converted into SAM with rate constant p₁. SAM is then converted to SAH in a DNA methylation reaction with rate constant p₂, while some of it is also lost via breakdown or excretion (represented by efflux rate constant f₂). SAH turns into homocysteine according to the rate constant p₃. Homocysteine then follows several paths: it is re-methylated to form methionine with rate constant p₄, contributes to the transsulfuration pathway by converting to cysteine with rate constant p₅, and leaves the system with rate constant f₄. Cysteine is converted to glutamylcysteine according to rate constant p₆, with glutamylcysteine subsequently being depleted to form GSH with rate constant p₇. GSH is transported out of liver cells or degraded (represented by flux rate constant f₇) or is oxidized to GSSG at a rate defined by p₈. GSSG is reduced back to GSH according to rate constant p₉.

Each participant-specific rate parameter in the model represents the activity of an enzyme associated with the methionine cycle or transsulfuration pathway. For example, p₁ corresponds to the combined activities of methionine adenosyltransferase I (MAT-I) and methionine adenosyltransferase III (MAT-III), two enzymes responsible for the conversion of methionine to SAM. p₂ describes the combined rate of the enzymes DNA methyltransferase (DNMT), glycine N-methyltransferase (GNMT), and other methyltransferases, while p₃ characterizes the activity of S-adenosylhomocysteine hydrolase (SAHH) and p₄ captures the combined effects of methionine synthase (MS) and betaine-homocysteine methyltransferase (BHMT). p₅ describes a lumped reaction of homocysteine being converted directly to cysteine with no cystathionine intermediate; this parameter is taken to represent solely the activity of cystathionine β-synthase (CBS), which is responsible for the conversion of homocysteine to cystathionine. Parameter p₆ corresponds to glutamate-cysteine ligase (GCL), while p₇ describes the activity of glutathione synthetase (GS). p₈ captures the rate of glutathione peroxidase (GPX), and p₉ describes the action of glutathione reductase (GR). These model enzymes are summarized in Table 2.

Table 2.

Enzymes and fluxes represented by parameters used in the mathematical model.

Parameter	Representative Enzyme(s) or Flux	Abbreviation
p1	methionine adenosyltransferase I	MAT-I
	methionine adenosyltransferase III	MAT-III
p2	DNA methyltransferases	DNMT
	glycine N-methyltransferase	GNMT
p3	S-adenosylhomocysteine hydrolase	SAHH
p4	methionine synthase	MS
	betaine-homocysteine methyltransferase	BHMT
p5	cystathionine β-synthase	CBS
p6	glutamate-cysteine ligase	GCL
p7	glutathione synthetase	GS
p8	glutathione peroxidase	GPX
p9	glutathione reductase	GR
f2	SAM efflux	–
f4	homocysteine efflux	–
f7	GSH efflux	–

2.3. Parameter estimation

When estimating parameters for each study participant, the values of c and f as given in Table 1 are known; these are the measured metabolite concentrations and defined efflux rates, respectively. The values of p represent the unknown participant-specific rate parameters and need to be computed. Since the relationship between GSH and GSSG is underdetermined in this system, however, the individual values of p₈ and p₉ cannot be computed; instead, only the ratio of p₈ to p₉ (expressed p₈:p₉ or GPX:GR) can be calculated. This ratio was thus considered to be one combined term describing the relative values of p₈ and p₉. To account for this, the component balance equation for GSSG (Table 1) was rewritten as:

$$0=(p_8/p_9)c_7-c_8.$$ (3)

This effectively reduces the model to 8 parameters. Given that the model is still linear, it can be written such that the c values are in an 8×8 coefficient matrix multiplied by an 8×1 vector of unknown p variables. This product is then summed with an 8×1 vector of the f·c efflux terms, and this sum is set equal to the 8×1 zero vector. Formulating the model in this manner allows for estimation of the 8 unknown p values by solving a system of linear equations. Estimation of model parameters was performed for each study participant in the neurotypical and ASD groups using their individual measured values of c from the clinical data.

2.4. Model assumptions

Certain assumptions needed to be made for this work to develop the mathematical structure of the model and explain how it is affected by the availability of data:

1. The derived model has a linear structure and includes 8 parameters to allow for the distributions of the parameter values to be estimated from the clinical data. While a more detailed model of the pathway may allow for a more accurate description, it is assumed that a model of the chosen complexity can reflect the pathway behavior reasonably well.

2. The model system is at steady state, so the concentrations of metabolites are not changing over time. This has to be assumed because each study participant only had metabolite measurements taken at one point in time. Along with this, it is assumed that the combined contributions of an enzyme’s concentration and activity do not change over time.

3. Changes in concentrations of metabolites in plasma are reflected by proportional changes in concentrations of metabolites in liver cells, although this is not always true in some cases (Duncan et al., 2013a). However, this assumption must be made here because the clinical data consist of measurements taken in plasma while the model structure describes the metabolic pathways in liver cells.

Other assumptions were made to explain the biological implications of each reaction in the model and how these were also affected by the available data:

• 4The conversion of methionine to SAM is due to the combined effects of MAT-I and MAT-III. Having only a single measurement in time for each metabolite does not allow for understanding the effects of individual enzymes acting in parallel, so only the combined effect is modeled.
• 5The conversion of SAM to SAH is due to the combined contributions of DNMT enzymes, GNMT, and approximately 150 other methyltransferases. For reasons given in Assumption 4, only the combined effect of these enzymes is modeled. Additionally, GNMT uses glycine as a second substrate, but the associated reaction is treated as pseudo first order so only the effects of SAM concentration are considered.
• 6While the reaction converting SAH to homocysteine by the enzyme SAHH is reversible, it is represented by one net forward rate constant in the model. At steady state, it is not possible to determine the individual rate constants of the forward and reverse reactions. However, the rate of the forward reaction must be greater than the rate of the reverse reaction for the system to remain at steady state.
• 7The conversion of homocysteine to methionine is due to the combined contributions of MS and BHMT. This assumption is made for reasons similar to Assumption 4, so again only the combined contribution of these enzymes is modeled. Additionally, BHMT uses betaine as a second substrate, but the associated reaction is treated as pseudo first order so only the effects of homocysteine concentration are considered.
• 8The reactions involving the conversion of homocysteine to cystathionine and the conversion of cystathionine to cysteine are represented by a single lumped reaction where homocysteine is directly converted to cysteine. This is due to no measurements being taken for cystathionine.

Furthermore, an assumption was made to focus the analyses on just the model system of interest:

• 9There are no indirect inhibitory or regulatory effects between metabolites in the described pathways. In addition, it is assumed that there are no interaction effects from other metabolic pathways. While it is known that other pathways and metabolites, such as folate, have long-range regulatory effects (Reed et al., 2008), these mechanisms are ignored in this model so that parameters can be estimated as stated in Section 2.3.

The final assumption was needed to reflect that certain information is not readily available for subsets of participants:

• 10The rates of SAM removal, homocysteine excretion, and GSH degradation are identical in neurotypical and ASD study participants. No reported numbers for the values of these rates are available for participants on the autism spectrum. Therefore, the reported values of these rates for neurotypical individuals were assumed to be identical to those for participants on the autism spectrum.

2.5. Sensitivity analysis

The sensitivity of a model to a specific parameter is commonly measured as the change in the model’s output due to a perturbation of that parameter (Frey and Patil, 2002). Local sensitivity analysis can be performed by individually perturbing each parameter from its baseline value while keeping the values of all other parameters constant. This is also referred to as a one-factor-at-a-time approach (Hamby, 1994; Saltelli and Annoni, 2010). A simple method for perturbing a chosen parameter is to add or subtract a percentage of its base value (Hamby, 1994).

The baseline value of each model parameter was taken to be the mean value of that parameter among all neurotypical participants. The resulting set of baseline parameters, which were then known, corresponded to a particular unknown set of metabolite concentrations, which were treated as the outputs of the system. However, calculating the output’s sensitivity to changes in parameters required knowledge of the baseline concentrations that would serve as a point of reference for the model output. This required calculating the metabolite concentrations that corresponded to the baseline parameter values.

To solve for these unknown baseline concentrations, an approach similar to that described in Section 2.3 was taken. Using the model equations in Table 1, an 8×8 matrix of average p and f terms was constructed and multiplied by an 8×1 vector of unknown baseline c values. Their product was then set equal to an 8×1 zero vector to form a homogeneous system of linear equations. Given that any row of the matrix is equal to the negative sum of all other rows, all rows are not linearly independent; the calculated rank of the matrix was then found to be 7. Since the largest potential rank of this matrix is 8, the rank-nullity theorem states there exists one solution for the right null space of this matrix. The right null space was then solved for by using the null command in MATLAB. The absolute values of these vector elements were taken to be the baseline metabolite concentrations for the purposes of sensitivity analysis.

Each model parameter, as well as each efflux rate constant, was perturbed according to the one-factor-at-a-time approach. To observe the output’s response to small perturbations, parameters were increased and decreased by 1% of their baseline value. The metabolite concentrations corresponding to each new perturbation were then recalculated by finding the right null space of the parameter matrix as described above. Each new metabolite concentration resulting from a given perturbation was compared to its baseline value using the relative change, which was used to account for large differences in magnitude between metabolite concentrations. The sensitivity measure for a particular perturbation was taken to be the Euclidean norm of the vector containing these 8 relative changes (one for each metabolite). Total sensitivity of the output to changes in a certain parameter was calculated as the average of this sensitivity measure for the negative and positive perturbations of that parameter.

2.5.1 Sensitivity analysis and cross validation

The many model assumptions and the uncertainties in model parameter estimates may limit the confidence with which the results of sensitivity analysis can be interpreted. Thus, these results were validated using a leave-one-out cross validation approach (Kohavi, 1995). The cross-validation procedure was applied by removing the first neurotypical participant’s set of parameters from the data – this participant was treated as the test set, while the remaining 81 participants were treated as the training set. Sensitivity analysis was performed, as described above, independently for the training set and the test set. The obtained sensitivity measures were recorded, the first participant’s data were replaced, and the process was repeated one at a time for each of the other neurotypical participants. Thus, sensitivity analysis was performed for 82 training sets and 82 test sets. The averages of the sensitivity measures between the training sets and test sets were then compared. Performing the analysis in this manner helped to ensure that the sensitivity results were robust to changes in the available sample set. Efflux rates were also considered in this cross-validation.

3. Results

3.1. Parameter estimation

The 8 participant-specific parameters were estimated for the 82 neurotypical participants and 93 participants with ASD for who concentrations of all 8 model metabolites were available in the clinical data. Means and standard deviations for metabolite concentrations among the participants included in this study are provided in Table 3. Significant statistical differences were observed between the neurotypical and ASD groups for all metabolites except homocysteine (α = 0.01).

Table 3.

Means and standard deviations of metabolite concentrations for the neurotypical and ASD groups.

Metabolite	Concentration Mean ± SD (μM)		p-value
	Neurotypical (n = 82)	ASD (n = 93)
Methionine	23.1 ± 3.6	19.0 ± 2.9	< 0.0001
SAM	0.0696 ± 0.0100	0.0600 ± 0.0104	< 0.0001
SAH	0.0152 ± 0.0036	0.0186 ± 0.0047	< 0.0001
Homocysteine	4.74 ± 1.01	5.10 ± 1.20	0.0323
Cysteine	209 ± 17	190. ± 18	< 0.0001
Glutamylcysteine	2.33 ± 0.59	1.85 ± 0.48	< 0.0001
GSH	2.31 ± 0.70	1.71 ± 0.36	< 0.0001
GSSG	0.147 ± 0.058	0.236 ± 0.100	< 0.0001

Following the methodology outlined in Section 2.3, a system of linear equations was constructed using a coefficient matrix of c values, a vector of unknown p values, and a vector of efflux terms f·c. However, the matrix of c values was found to be rank deficient (for reasons identical to those given in Section 2.5 for a matrix of p and f terms). The four components describing the methionine cycle were specifically responsible for this condition. Finding a unique solution for the associated parameters required that a constraint be placed on one of the four parameters in the methionine cycle. To determine the optimal parameter to constrain, an equality constraint was applied to one parameter in the cycle, and values of the remaining parameters were estimated. The constraint was then removed and placed on another parameter in the methionine cycle, and the new group of unconstrained parameters was estimated. This process was repeated for all four parameters in the methionine cycle. Estimates of all model parameters resulting from each of the constraints for neurotypical participants were compared with approximated biological values of these rate constants from the literature. The lsqlin routine in MATLAB was used to define each constraint and estimate the parameters such that the constraints were satisfied.

The equality constraint used to estimate parameters relates the rate of each reaction in the methionine cycle to a nominal rate, given in μM/hr. Each constraint has the form:

$$p_i{c}_i=p_{\mathit{nom}}{\overline{c}}_i$$ (4)

where p_i is a participant’s estimated value of the i-th rate constant (to be solved), c_i is that participant’s concentration of the i-th metabolite, p_nom is a nominal value for the rate parameter being estimated (taken from the literature), and ${\overline{c}}_i$ is the average concentration of the i-th metabolite for the group that the participant belongs to (neurotypical or ASD). Each constraint is only applied to a reaction within the methionine cycle, i.e., i ranges from 1 to 4.

During the process of determining the optimal constraint, only data for neurotypical participants were considered. When the constraint described by Equation 4 was applied to each methionine cycle parameter in turn, the parameter estimates in Table 4 were obtained. Approximate nominal values from the literature are also provided. The linear structure of the transsulfuration pathway results in the estimates for parameters p₅ through p₈:p₉ remaining unchanged across the different constraints. Placing a constraint on p₁ produces very large values for the other methionine cycle parameters. Constraining p₂ gives much smaller estimates of p₁ and p₃, with unacceptable negative values for p₄. The constraint on p₃, however, produces parameter estimates that are most similar to the values from the literature. Values for p₂ and p₃ resulting from the constraint on p₄ are too large to consider acceptable. Thus, constraining p₃ is the preferred approach to estimating parameters for the methionine cycle.

Table 4.

Estimates of control parameters when p₁ through p₄ are individually constrained. All parameters have units of hr⁻¹ except for p₈:p₉, which is dimensionless.

	Mean Parameter Value ± SD				Literature value
Parameter	p1 constrained	p2 constrained	P3 constrained	P4 constrained		Reference
p1	4.90 ± 0.78	0.412 ± 0.064	1.90 ± 0.30	2.97 ± 0.46	4.78	(Broxson et al., 1989; del Pino et al., 2000; Nijhout et al., 2006; Sullivan and Hoffman, 1983)
p2	1610 ± 218	127 ± 17	620. ± 84	976 ± 140.	125	(Castro et al., 2003; Flynn and Reich, 1998; Luka and Wagner, 2003; Nijhout et al., 2006)
p3	7720 ± 2215	610. ± 175	2970 ± 852	4680 ± 1410	2780	(Castro et al., 2003; Døskeland and Ueland, 1982; Nakanishi et al., 2001)
p4	22.3 ± 4.6	−0.0210 ± 0.5858	7.38 ± 1.62	12.7 ± 2.6	12.2	(Castro et al., 2003; Finkelstein and Martin, 1984)
p5	1.93 ± 0.70	1.93 ± 0.70	1.93 ± 0.70	1.93 ± 0.70	10.4	(Castro et al., 2003; Finkelstein and Martin, 1984)
p6	0.0421 ± 0.0125	0.0421 ± 0.0125	0.0421 ± 0.0125	0.0421 ± 0.0125	0.0276	(Davis et al., 2006; Huang et al., 1988; Toroser et al., 2006)
p7	3.82 ± 0.77	3.82 ± 0.77	3.82 ± 0.77	3.82 ± 0.77	10.0	(Lyons et al., 2000; Martensson, 1987)
p8:p9	0.0660 ± 0.0244	0.0660 ± 0.0244	0.0660 ± 0.0244	0.0660 ± 0.0244	0.0118	(Blanco et al., 2007; López-Barea and Lee, 1979; Maddipati and Marnett, 1987)

Using the optimal constraint on p₃, parameter values for ASD participants were then estimated. A comparison of the estimates for control and ASD participants is provided in Table 5. Significant statistical differences can be seen between the neurotypical and ASD groups for all parameters except p₃ and p₇ (α = 0.01). Additional insight into these differences can be gained from observing the respective PDFs of each parameter for the control and ASD groups. Using kernel density estimation with a normal kernel (using the ksdensity command in MATLAB), PDFs were constructed for each parameter (Figure 2). The most apparent differences between neurotypical and ASD distributions are seen for parameters p₁ (Figure 2A), p₂ (Figure 2B), p₄ (Figure 2D), and p₈:p₉ (Figure 2H). Although p₅ and p₆ (Figure 2E and 2F, respectively) displayed significant statistical differences, there are not observable differences in the distributions for the two groups of participants. The two distributions for p₃ (Figure 2C) are nearly identical, which is a consequence of the constraint placed upon the parameter.

Table 5.

Comparison of model parameter estimates for control and ASD participants. All parameters have units of hr⁻¹ except for p₈:p₉, which is dimensionless.

Parameter	Parameter Mean ± SD		p-value
	Neurotypical (n = 82)	ASD (n = 93)
p1	1.90 ± 0.30	2.81 ± 0.42	< 0.0001
p2	620. ± 84	889 ± 154	< 0.0001
p3	2970 ± 852	3020 ± 1020	0.726
p4	7.38 ± 1.62	9.32 ± 2.00	< 0.0001
p5	1.93 ± 0.70	1.35 ± 0.47	< 0.0001
p6	0.0421 ± 0.0125	0.0346 ± 0.0088	< 0.0001
p7	3.82 ± 0.77	3.59 ± 0.63	0.031
p8:p9	0.0660 ± 0.0244	0.144 ± 0.065	< 0.0001

Figure 2.

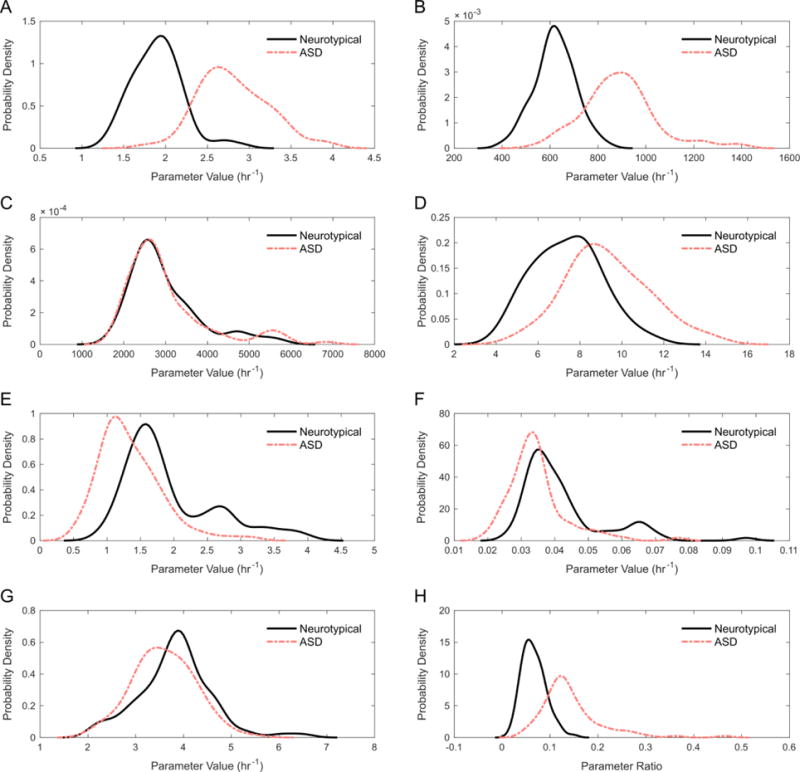
PDFs of the eight participant-specific model parameters for the neurotypical and ASD participant groups. (A) Rate parameter p₁ for MAT-I + MAT-III. (B) Rate parameter p₂ for DNMT + GNMT. (C) Rate parameter p₃ for SAHH. (D) Rate parameter p₄ for MS + BHMT. (E) Rate parameter p₅ for CBS. (F) Rate parameter p₆ for GCL. (G) Rate parameter p₇ for GS. (H) Ratio of rate parameters p₈ and p₉ for GPX:GR.

3.3. Sensitivity analysis

Metabolite concentrations were considered to be the outputs of the system for local sensitivity analysis. Since the system is linear, local sensitivity analysis results for positive and negative 1% perturbations should be identical. However, both perturbations were performed for each parameter to ensure the results were not affected by numerical inaccuracies. The results of both perturbations were indeed found to be almost identical, and the average results are reported in Table 6.

Table 6.

Results of sensitivity analysis from perturbing each parameter and efflux rate constant by 1%. Also shown are the results of leave-one-out cross validation for this analysis.

Parameter or Efflux Rate Constant	Sensitivity (all samples)	Mean Training Sensitivity ± SD	Mean Test Sensitivity ± SD
p1	0.0099	0.0099 ± 0.0000	0.0099 ± 0.0000
p2	0.0100	0.0100 ± 0.0000	0.0100 ± 0.0000
p3	0.0100	0.0100 ± 0.0000	0.0100 ± 0.0000
p4	0.0136	0.0136 ± 0.0000	0.0136 ± 0.0011
p5	0.0168	0.0168 ± 0.0000	0.0168 ± 0.0008
p6	0.0261	0.0261 ± 0.0000	0.0261 ± 0.0001
p7	0.0100	0.0100 ± 0.0000	0.0100 ± 0.0000
p8: p9	0.0100	0.0100 ± 0.0000	0.0100 ± 0.0000
f2	0.0001	0.0001 ± 0.0000	0.0001 ± 0.0000
f4	0.0000	0.0000 ± 0.0000	0.0000 ± 0.0000
f7	0.0141	0.0141 ± 0.0000	0.0141 ± 0.0000

The metabolite concentrations were found to be most sensitive to changes in parameter p₆, which describes the rate at which cysteine is converted to glutamylcysteine. In other words, altering the value of p₆ causes the largest cumulative relative change in the steady state metabolite concentrations. It is thus an important parameter and has the most influence on the model output. After p₆, the output was most sensitive to changes in parameter p₅, which defines the rate of production of cysteine from homocysteine, and to changes in efflux rate constant f₇, which represents the removal rate of GSH from the system. The model output also showed relatively high sensitivity to changes in parameter p₄, which describes the rate at which homocysteine is converted to methionine. These results indicate that these parameters also have a greater effect on the model concentrations. The remaining participant-specific parameters, having equally low measures of sensitivity, were indicated to have less effect on steady state metabolite concentrations. Efflux rate constants f₂ and f₄ appeared to have minimal influence on the concentrations of metabolites. Additionally, the cross-validation results (Table 6) revealed no effective differences between the parameter sensitivity measures as calculated from all samples, from the averaged training results, and from the averaged test results.

4. Discussion

This work developed a model of the methionine cycle and transsulfuration pathway and this is the first effort which estimates parameters for such a model using clinical data from both neurotypical and ASD study participants. Furthermore, the distributions of the parameters were estimated and compared between the groups of study participants, as each participant had different metabolite concentrations, resulting in different model parameters.

Development of the presented model was based on a number of assumptions. Some of these assumptions may limit the accuracy of the model, while others may have little or no bearing on the model’s ability to describe true metabolic behavior. The assumption of a steady state system can be particularly limiting since biological systems are rarely, if ever, in this state of equilibrium. That being said, few physiological measurements, especially if they involve metabolites in clinical studies, are taken over time and as such this is a reasonable assumption for this particular application. Additionally, assuming linear interactions between enzymes and substrates may neglect to capture the true behavior of these reactions. Michaelis-Menten equations are often used to describe the nonlinear kinetics of enzymes, but the kinetic parameters of these equations are difficult to estimate without available time-series data. In general, the assumptions made are based upon the state-of-the-art of what can be done in a clinical research trial. Regardless of the implications of these assumptions, the overall purpose of this study was to characterize and model metabolic differences between neurotypical and ASD participants. The current model provides a starting point for describing the interactions of the studied metabolic pathways in ASD.

The most significant limitation of the model is that the efflux rate constants are not necessarily specific to each participant. Given the variability in metabolite concentrations between participants, it is unlikely that these efflux rates are identical for participants within the same group, let alone identical between the neurotypical and ASD participant groups. Differences in these efflux rates could explain the differences observed for certain participant-specific rate parameters; using a one-size-fits-all approach could result in forced parameter differences that would not be present if the efflux rates had been specific to each participant. However, the lack of data describing these individualized effluxes makes this problem difficult to address. There are also very limited studies investigating these processes in individuals with ASD, so it is challenging to characterize any flux differences for those participants compared to the neurotypical group. Thus, the efflux rate constants must be assumed to be the same for every participant until more data regarding the rates of these processes become available.

The mean values for many of the estimated parameters in the neurotypical group are close to the biological activity rates of their corresponding enzymes that are found in the literature. Referring to the literature values in Table 4, it can be seen that the approximate rate constant for MAT-I + MAT-III activity is fairly close to the mean estimated value for control participants. The estimates for the DNMT+GNMT and MS+BHMT rate constants are also within acceptable ranges of their literature values. Additionally, the mean estimate of the rate constant for SAHH is very close to the true rate constant, although this is expected due to the constraint applied during estimation. The estimated rate constants for GCL, GS, and the GPX:GR ratio are close to their approximate nominal values as well. However, the mean estimate for CBS is significantly different from its nominal value. It is unlikely that this discrepancy is a consequence of the lumped homocysteine-cystathionine-cysteine reaction used in the model. At steady state, the theoretical metabolic flux from homocysteine to cystathionine will be equivalent to the flux from cystathionine to cysteine; since the flux throughout the transsulfuration pathway needs to be the same at every reaction step, the lumped reaction rate from homocysteine to cysteine will also be equal to either of these two individual reaction rates. Therefore, the product of the homocysteine concentration and rate constant p₅ still reflects the actual conversion rate of homocysteine to cystathionine, and p₅ should be a valid approximation of CBS activity. A more likely reason for the discrepancy is the fact that cysteine is used in many other metabolic processes besides the transsulfuration pathway; it is also involved in the synthesis of taurine, pyruvates, sulfates, and sulfites, for example (Stipanuk et al., 2006). The model does not describe these alternative pathways, and thus does not account for the higher levels of cysteine that would be required to carry out all of these reactions. This may explain why the rate of cysteine synthesis is underestimated in the model.

Parameter estimation revealed observable differences in parameters p₁, p₂, p₄, and p₈:p₉ between neurotypical and ASD participants. This suggests some degree of difference in activity rate for MAT-I+MAT-III, DNMT+GNMT, MS+BHMT, and GPX:GR in participants with ASD as compared to neurotypical participants. The GPX:GR difference is expected; the ratio of reduced to oxidized glutathione as a marker of oxidative stress has been well-documented (Asensi et al., 1999; James et al., 2006) and there is evidence to suggest that a decreased ratio is present in participants with ASD (Adams et al., 2011; James et al., 2006; Melnyk et al., 2012). The DNMT+GNMT parameter represents the rate at which SAM is converted into SAH, and reflects the SAM/SAH ratio, which is an indicator of DNA methylation capacity (Yi et al., 2000). In participants with ASD, the SAM/SAH ratio has been found to be significantly reduced (Adams et al., 2011; James et al., 2006; Melnyk et al., 2012). With regards to the differences in MAT-I + MAT-III, oxidative stress has been linked to a down-regulation of the methionine adenosyltransferase enzymes (Avila et al., 1998). Given that increased oxidative stress is characteristic of ASD, it is possible that there could be altered MAT rates in participants on the spectrum. Finally, it has been found that increased oxidative stress can be responsible for reduced MS activity (Muratore et al., 2013). This mechanism leaves more homocysteine available to be eventually converted to glutathione, which can then be used to lower oxidative stress. These observations are in line with the finding that the participants with ASD had different values of the p₄ parameter as compared to their neurotypical counterparts.

Model metabolite concentrations were found to be most sensitive to changes in parameter p₆, followed by parameter p₅, efflux rate constant f₇, and parameter p₄. These correspond to the first-order rate constants of the enzymes GCL and CBS, the removal of GSH, and the enzymes MS+BHMT, respectively. GCL is responsible for the conversion of cysteine to glutamylcysteine, so the sensitivity results suggest that the formation of glutamylcysteine has an important role in the model. This is somewhat surprising because the formation of GSH was expected to have a significant impact on the model predictions; instead the synthesis of its precursor was identified as more important. That being said, the synthesis of a GSH precursor will ultimately affect GSH formation, and formation of glutamylcysteine is considered to be the rate-limiting step of GSH synthesis (Hamilton et al., 2003; Lu, 2009; Shi et al., 1994). In addition, the relatively high sensitivity to the removal of GSH does suggest that levels of GSH have a significant effect on other metabolites in the methionine cycle and transsulfuration pathway; this could be supported by findings of redox levels (which are influenced by GSH) affecting synthesis of certain metabolites in these pathways (Mosharov et al., 2000; Richman and Meister, 1975). The other important model enzymes, CBS and MS+BHMT, are involved in the synthesis of cysteine and methionine, respectively, both from homocysteine. Given that these enzymes form the juncture between the methionine cycle and transsulfuration pathway, and determine the fate of homocysteine, it is not as surprising that these are among the most important parameters in the model.

The robustness of the most important sensitivity analysis results to changes in the study participants was verified by leave-one-out cross validation, where no substantial differences in sensitivity measures were observed between the averaged training and test set results (Table 6). The sensitivity results were nearly identical across training sets since each training set’s baseline parameter values were averaged from the parameters of all neurotypical participants except one, and removing one different participant from the average of 81 participants in each training set is unlikely to have a significant effect on the average parameter values. This explains why the variations in the sensitivity measures between training sets are below the used cutoff. Unlike the training set, however, the test sets did show some variation in their sensitivity measures for certain parameters. Despite this difference, the test sets’ averaged results were very close to those from the averaged training results, suggesting that the parameters’ sensitivity measures are much less dependent on individual parameter values than on the structure of the model itself.

Model robustness is further suggested by the small values of the sensitivity measures for each parameter. However, a potential drawback of these small sensitivities is poor observability of the parameters in the experimental data. One possible way to address this issue could be to implement a different measure of sensitivity, perhaps by considering a relationship among the metabolites’ relative changes other than the Euclidean norm, or by replacing the relative change of a metabolite with a different calculation of change altogether. Another solution is to employ regularization methods, such as Tikhonov regularization (Engl et al., 1996), that can deal with poor observability by providing more stable estimates of model parameters (Golub et al., 1999). Experimentation with Tikhonov regularization (using neurotypical participants and values of the regularization parameter up to 0.1) yielded parameter values that, on average, varied by less than 6% of their current solutions. This was the case for all parameters except p₈:p₉, which had an average percent change of 89.1%. These results indicate that the parameters are robust with respect to the parameter observability, with the exception of p₈:p₉. However, the p₈:p₉ ratio is not one of the key variables in the model as determined by sensitivity analysis, and thus the conclusions do not change as a result of this analysis.

Analysis of the raw plasma concentration data in (Melnyk et al., 2012) yielded many important observations of metabolic abnormalities in study participants with ASD. Among the primary outcomes of that study were significant measured differences for methionine, SAM, SAH, total cysteine, GSH, and GSSG concentrations in control and case participants. The study concluded that participants with ASD have genome-wide reduced DNA methylation, in addition to finding evidence for increased oxidative stress in participants with ASD. While the current model does not provide any insight into genome-wide trends, it does offer some results similar to those obtained by analysis of the raw data. Mainly, observed differences in the p₁, p₂, p₄, and p₈:p₉ rate parameters point to equivalent metabolic differences identified in (Melnyk et al., 2012). An important distinction to make, however, is that those analyses focused directly on the metabolite concentrations, while the model analyses here are aimed toward the rates at which the metabolic reactions take place. With this in mind, the model also produced some novel results that were not previously extracted from the data. Sensitivity analysis found two parameters relating to the fate of homocysteine to be very important, while no significant difference in homocysteine concentration was found in the raw data. While this could be an important finding, it could also be an artifact of the model; the idea of homocysteine metabolism being altered in response to oxidative stress (Muratore et al., 2013) suggests the former, however. The parameter pertaining to glutamylcysteine synthesis (by GCL) was indicated to be of even greater importance, but no analysis of glutamylcysteine concentrations in the raw data was performed. Future investigations should explore in more detail the importance of GCL, and its rate-limiting reaction, in GSH synthesis.

5. Conclusions

This study developed a model for two pathways of potential importance to ASD and identified model parameters, as well as their PDFs, from clinical data from neurotypical participants and those on the spectrum. Significant statistical differences can be seen in four of the parameters between the two groups through comparison of their mean parameter values and their parameter distributions. Almost all estimated rate parameters were found to match with corresponding experimental values from the literature, with the exception of the rate constant for cystathionine β-synthase. Sensitivity analysis revealed parameter p₆, which reflects the activity of the enzyme glutamate-cysteine ligase, to be especially important to the model’s predictions. This finding aligns with the observation that the reaction the enzyme is responsible for, i.e., the formation of glutamylcysteine, is the rate-limiting step in glutathione synthesis. Development of this model serves as the first step for identifying targets for potential future intervention strategies. Reactions with significant differences among the two participant groups can serve as a potential starting point for future investigations.

Highlights.

• Previous studies linked autism spectrum disorder (ASD) to metabolic irregularities.

• A model describing transmethylation and transsulfuration pathways was developed.

• Case-control clinical data were used to estimate distribution of model parameters.

• Sensitivity analysis identified potential metabolic reactions of interest.

• Results of this study hint at potential intervention strategies for ASD.