Longitudinal patterns of glycemic control and blood pressure in pregnant women with type 1 diabetes mellitus: phenotypes from functional data analysis

Abstract

Objective

To identify phenotypes of type 1 diabetes control and associations with maternal/neonatal characteristics based on blood pressure (BP), glucose and insulin curves during gestation, using a novel functional data analysis approach that accounts for sparse longitudinal patterns of medical monitoring during pregnancy.

Methods

We performed a retrospective longitudinal cohort study of women with type 1 diabetes whose BP, glucose and insulin requirements were monitored throughout gestation as part of a program-project grant. Scores from sparse functional principal component analysis (fPCA) were used to classify gestational profiles according to degree of control for each monitored measure. Phenotypes created using fPCA were compared with respect to maternal and neonatal characteristics and outcome.

Results

Most of the gestational profile variation in the monitored measures was explained by the first principal component (82%–94%). Profiles clustered into three subgroups of high, moderate or low heterogeneity, relative to the overall mean response. Phenotypes were associated with baseline characteristics, longitudinal changes in glycohemoglobin A1 and weight, and to pregnancy-related outcomes (P<0.01).

Conclusion

Three distinct longitudinal patterns of glucose, insulin and BP control were found. By identifying these phenotypes, interventions can be targeted for subgroups at highest risk for compromised outcome, to optimize diabetes management during pregnancy.

Maintaining glucose and blood pressure control is essential during pregnancy for women with type 1 diabetes. Poor control has long been associated with poor maternal and neonatal outcomes.^1–3 Variability in glucose, insulin requirement and blood pressure experienced throughout gestation has been studied for decades as a proxy for diabetes control, and is typically expressed through use of summary measures. The most commonly-reported summary measures are standard deviation, coefficient of variation, and mean amplitude of glycemic excursion, all of which have been used as clinical indicators for decades.⁴ Although these summary statistics provide a value for variation around the mean, the underlying longitudinal structure—the mean response function and natural variation over pregnancy—is ignored. Furthermore, summary measures generally yield misleading results if portions of the longitudinal data are missing for a given individual.^5,6 Despite the advent of continuous glucose monitoring and more advanced statistical techniques to combat heterogeneous data, summary measures are still often used to estimate variability throughout the course of gestation, notwithstanding the risk of providing biased findings. Few studies have shed light on glucose mean response and variability over gestation without the use of these summary measures.⁷ To our knowledge, no studies have been conducted to gain insight into rich, longitudinal data collected simultaneously on glucose, insulin requirements and blood pressure throughout the course of pregnancy.

Functional principal components analysis (fPCA) is a classical functional data analysis tool that has been applied to individual profiles forming dense collections of data⁸; however, this approach requires complete measurements or a large number of repeated measurements taken over common time points across individuals. Indeed, classical fPCA was used in a recent study to examine glucose variation obtained from dense collections of continuous glucose monitoring data.⁹ Although the study revealed substantial between- and within-individual heterogeneity, as in real-world clinical settings, continuous glucose monitoring was performed only for brief periods of time during pregnancy on each individual (as opposed to the entire duration). Many women with type 1 diabetes who become pregnant will commence more intensive monitoring at different times in gestation, may miss scheduled visits for monitoring and assessment, or could exempt from measurements randomly (e.g. glucometer malfunctions). These settings produce unequal numbers of repeated measurements and mistimed measurements, often known in the statistics literature as sparse longitudinal data. The number of observations per individual could range from small to large. Failing to account for these sources of missing data through appropriate estimation methods will lead to biased results¹⁰, potentially hampering the introduction of new therapies or development of revised or new clinical regimens to optimize care during pregnancies complicated by diabetes.

Patterns of longitudinal data, such as the clinical measures monitored during diabetic pregnancy, may be classified using fPCA developed for sparse longitudinal data.^11,12 This type of approach enables prediction of individual smoothed trajectories, even if only a few measurements are available for a given individual, while simultaneously accounting for longitudinal correlation. This so-called sparse fPCA is a variant of the traditional PCA that finds linear combinations of a small number of features to maximize variance across data. As an extension to the classical PCA dimensionality reduction tool and an analogue to classical fPCA, sparse fPCA significantly improves the interpretability and relevance of the components, and is more likely to reveal the underlying structure of longitudinal data. In addition, with the advent of statistical software, sparse components can be computed faster for high-dimensional datasets.^13,14 In this retrospective cohort study, we aimed to characterize the timing and degree of variability in clinical measures monitored over the course of gestation in women with type 1 diabetes using a novel statistical approach and implementation to accommodate sparse longitudinal data commonly found in these settings.

METHODS

Study cohort

This is a retrospective study of a longitudinal cohort of women with type 1 diabetes who were followed prospectively as part of a 17-year interdisciplinary program of diabetes in pregnancy. Care management for insulin therapy and glucose control performed throughout the study has been reported elsewhere.³ The study presented here has been approved by the local IRB.

There were four monitored measures of interest in this study. Briefly, each study subject was asked to monitor her glucose level four to six times per day throughout the course of pregnancy; these observed concentrations were aggregated into subject-specific, ordered weekly values. Insulin requirements (expressed as units of insulin) and systolic and diastolic blood pressure (SBP and DBP, respectively, expressed as mmHg) readings were collected at each weekly or bi-weekly clinical visit.

Baseline study characteristics of interest included White classification¹⁵, race, parity, any previous non-live births, age, age at diabetes diagnosis, years since diabetes diagnosis, and BMI. Longitudinal measures for this analysis included HbA1 at each trimester and weight recorded pre-pregnancy and at weeks 9, 14, 16, and 26 during gestation. Measures specific to pregnancy outcome included pregnancy-associated hypertension, preeclampsia, and infant weight at birth (in grams).

Longitudinal pattern classification via sparse functional principal components

Prior to conducting the sparse fPCA, we chose a suitable basis for representing the eigenfunctions using cubic B-spline basis functions^16,17,18. We used a routine from the R package “fpca” to implement the restricted maximum likelihood estimation through a Newton-Raphson procedure, in order to estimate functional principal components from sparse longitudinal data.¹⁴ This approach addresses the selection of the number of basis functions, as well as the dimension of the process (i.e., number of nonzero eigenvalues) used in the model by minimizing an approximation of the leave-one-curve-out cross-validation score. We implemented the algorithm for each subject’s monitored glucose-, insulin- and BP-specific collection of longitudinal data, in order to obtain smooth individual functions across gestation for each measure.

The individually fitted curves formed the basis for the fPCA for each monitored measure. The maximum number of functional principal components (fPCs) retained in each analysis was based on the eigenvalue criterion (≥80% of variance explained).¹⁹ The individual curve-fitting routine and sparse fPCA implementation code are available from the authors upon request.

Comparisons between phenotypes

For each monitored measure (glucose, insulin and BP), bivariate associations between classification membership (phenotype) and continuous variables of interest were examined using linear regression with an overall F-test for fixed effects; if statistically significant, pairwise comparisons were conducted in post-hoc analysis by comparing least-square means. Bivariate associations between phenotype and categorical variables of interest were examined using Chi-square analysis or Fisher’s exact test as appropriate.

To determine the extent to which longitudinal changes in weight and HbA1 were related to phenotype, we performed a repeated measures analysis, in which weight or HbA1 served as the response variable; phenotype and time (in terms of gestation) were included as main effects; an interaction term between phenotype and time was included in each model. To account for longitudinal correlation, we selected a covariance structure for each response variable based on fit statistics. Results corresponding to P<0.01 were considered statistically significant, to account for multiple testing. Analyses for comparisons and repeated measures analyses were implemented using SAS 9.3 (SAS Institute, Cary, NC).

RESULTS

Study cohort

There were 147 women in the analysis cohort who had repeated monitoring of glucose, insulin and blood pressure during pregnancy across all trimesters. Median (IQR) age at initial visit was 26.0 (5.0) years; 87.1% of subjects were Caucasian and had been diagnosed with type 1 diabetes at 13.4 (6.8) years of age. There were 40 subjects (27.2%) who had at least one previous live birth; 73 subjects (nearly 50%) had never been pregnant prior to the study. A third of the subjects had prior pregnancies that resulted in non-live births, 12.2% had a previous delivery via cesarean section.

Longitudinal pattern classification via sparse functional principal components

Median times for beginning and ending monitoring of the four measures during gestation were 8 and 39 weeks, respectively, which gave the temporal range for subject-specific curve fitting of each monitored measure. For each monitored outcome, over 95% of the variation between individually fitted curves could be expressed in the first two fPCs, and further analyses were therefore restricted to the first three fPCs. For each of the monitored outcomes, the first fPC, referred to as fPC₁, explained ≥80% of the variation between the fitted curves. As a result, for each analysis, we classified the fitted curves into three clusters according to the first and third quartiles (Q1 and Q3, respectively) of the fPC₁ scores as follows. Subjects with scores < Q1 were classified into one group; subjects with scores between Q1 and Q3 were in a second group; subjects with scores >Q3 were classified into a third group. This classification resulted in a consistent number of the 147 subjects being categorized into the three clusters or subgroups (N=37, 73 and 37); however, these classifications did not imply that the same subjects were consistently clustered into the same subgroups across glucose, insulin, SBP and DBP.

Insulin patterns

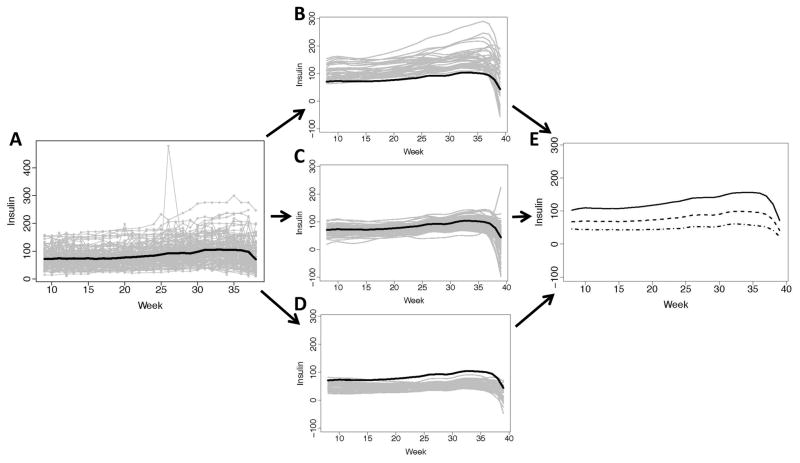
There were a median (IQR) of 27 (24–29) weekly measurements for subject insulin observed during gestation. The subject-specific observations show that insulin variation increased with gestation (Figure 1A) with an extreme observation of insulin occurring around the 27^th week for an individual woman; the sample mean for insulin over time indicates a tendency for insulin to increase later in gestation and end with a slight decline.

Figure 1. Observed insulin requirements (Units) and individually fitted curves at gestational weeks 8–39.

(A) Observed insulin trajectories over time (gray lines) for the 147 women during pregnancy with the overall mean insulin over time (black); (B) Individually fitted trajectories (gray curves) of women with higher mean and variability over pregnancy, relative to the overall mean insulin (black curve); (C) Individually fitted trajectories (gray curves) of women with moderate mean insulin and less variability over pregnancy, relative to the overall mean insulin (black curve); (D) Individually fitted trajectories (gray curves) of women with lower mean glucose and moderate variability over pregnancy, relative to the overall mean insulin (black curve); (E) The three mean fitted curves for the corresponding insulin-specific classifications (solid, dash and dash-dot).

The subject-specific functions obtained from sparse longitudinal fPCA were each classified into one of three subgroups using fPC scores. Nearly 82% of the variation between fitted insulin curves was explained by fPC₁. Based on mean glucose and variation over time, we found that the groups could be characterized as high, moderate and low. The high-insulin subgroup exhibited larger mean response and variation (Figure 1B), particularly towards the end of gestation, compared to the more moderate subgroup that exhibited steadier, lower mean levels of insulin (Figure 1C). The low-insulin subgroup had the least variation, and, on average, had lower insulin throughout gestation (Figure 1D). The subgroup mean response functions also indicate that differences with respect to mean insulin levels increase over gestation, but all showed decline at the end of gestation (Figure 1E).

Glucose patterns

The number of weeks with measurements per subject was 24 (18–28) for average glucose concentration. Ninety-nine subjects (67.3%) reported glucose level via written record, while the remaining subjects monitored glucose electronically, a method of measurement that was made available later in the 17-year study.

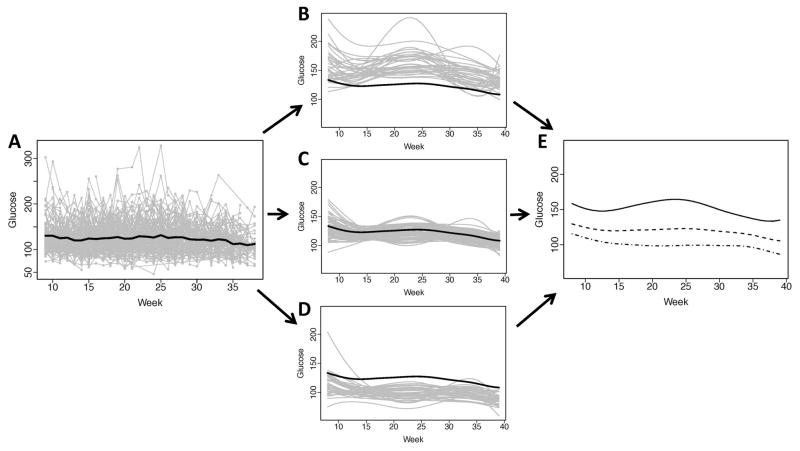
There was substantial within- and between-subject heterogeneity in glucose level over gestation (Figure 2A). Prior to classification analysis, the sample mean curve showed a relatively stable glucose trend over gestation. About 86.5% of the variation between fitted glucose curves was explained by fPC₁. The fitted subject-specific curves, which were obtained with sparse longitudinal fPCA of the raw glucose observations, were categorized into three clusters based on fPC scores, and tended to appear as high, moderate and low with regard to subject-specific glucose variation during pregnancy. There was a subgroup (N=37) with higher glucose mean response and variability over gestation (Figure 2B). Several of the subjects (N=73) were clustered as having moderate glucose mean response over gestation and exhibited tighter control (Figure 2C), as indicated by a low level of glucose fluctuations over gestation, relative to the other two subgroups (Figures 2B and 2D); furthermore, this subgroup tended to have relatively lower within-subject variability. The remaining subjects fell into a subgroup that exhibited lower mean glucose response throughout gestation (Figure 2D), relative to the mean glucose curve, with the exception of one profile early in pregnancy that had a higher mean glucose response function than the other subjects in the subgroup. This subgroup exhibited within-patient variation that was similar to the moderate subgroup, but lower than the high-glucose subgroup. The cluster-specific response functions for glucose over gestation also indicate differences with regard to mean glucose over gestation between the subgroups (Figure 2E). The degree of overlap between similar high/moderate/low classifications for glucose and insulin phenotypes ranged from 7 subjects (4.8%) to 39 subjects (26.5%).

Figure 2. Observed glucose (mg/dL) and individually fitted curves at gestational weeks 8–39.

(A) Observed glucose trajectories over time (gray lines) for the 147 women during pregnancy with the overall mean glucose over time (black); (B) Individually fitted trajectories (gray curves) of women with higher mean and variability over pregnancy, relative to the overall mean glucose (black curve); (C) Individually fitted trajectories (gray curves) of women with moderate mean glucose and less variability over pregnancy, relative to the overall mean glucose (black curve); (D) Individually fitted trajectories (gray curves) of women with lower mean glucose and moderate variability over pregnancy, relative to the overall mean glucose (black curve); (E) The three mean fitted curves for the corresponding glucose-specific classifications (solid, dash and dash-dot).

Blood pressure patterns

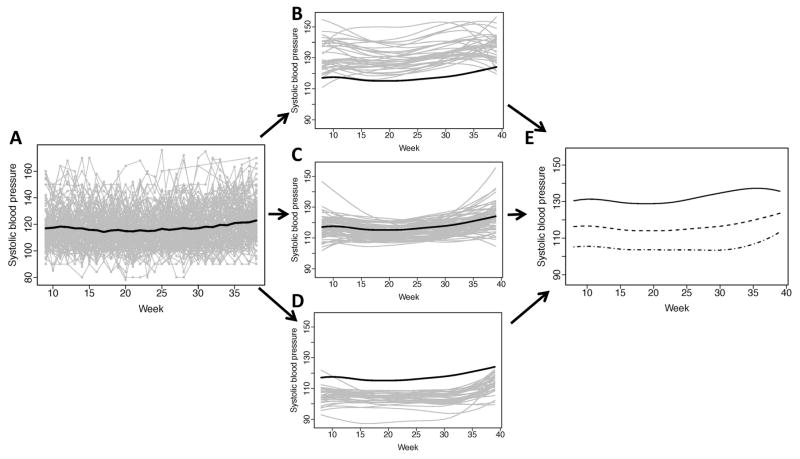
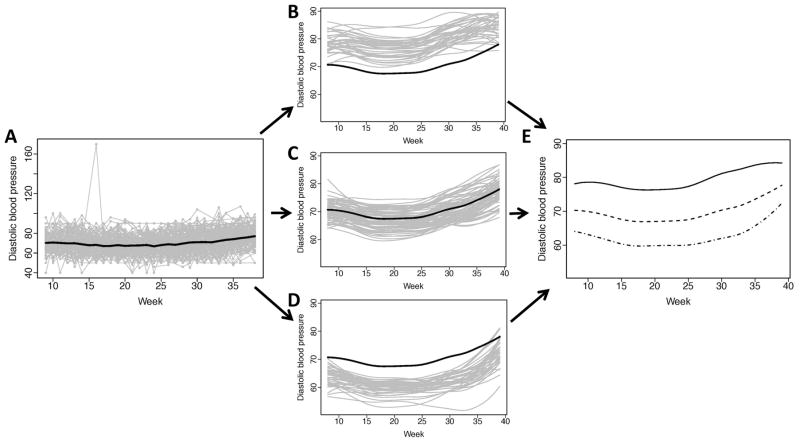
The number of weekly measurements per subject was 27 (24–29) for both DBP and SBP; FPC₁ explained roughly 94% and 92% of the variation between the fitted curves, respectively. The observed profiles of DBP exhibited tight variation around the sample mean (Figure 4A), with the exception of an outlying DBP value observed in the first trimester of pregnancy.

Figure 4. Observed systolic blood pressure (mmHg) and individually fitted curves at gestational weeks 8–39.

(A) Observed glucose trajectories over time (gray lines) for the 147 women during pregnancy with the overall mean systolic blood pressure (SBP) over time (black); (B) Individually fitted trajectories (gray curves) of women with higher mean and variability over pregnancy, relative to the overall mean SBP (black curve); (C) Individually fitted trajectories (gray curves) of women with moderate mean SBP and less variability over pregnancy, relative to the overall mean SBP (black curve); (D) Individually fitted trajectories (gray curves) of women with lower mean SBP and moderate variability over pregnancy, relative to the overall mean SBP (black curve); (E) The three mean fitted curves for the corresponding SBP-specific classifications (solid, dash and dash-dot).

The overall mean response indicated that DBP remained relatively stable through the first 24 weeks of gestation, but began to increase until the end of pregnancy. The sparse longitudinal fPCA scores were used to generate subject-specific curves of DBP over gestation and classify patients into one of three subgroups corresponding to high, moderate and low DBP (N=37, 73, and 37, respectively). The high-level DBP subgroup had profiles that exceed the overall mean DBP curve (Figure 3B). The moderate subgroup of DBP curves were above and below the mean (Figure 3C), but had variation over gestation time that was similar their high-subgroup counterparts. The low subgroup of DBP also had similar variation (Figure 3D) with curves that fell below the mean DBP response function. The subgroup-specific mean DBP curves suggest that profiles are shifted according to DBP at the beginning of pregnancy; however, nearing the end of pregnancy, the mean response of DBP in the low-level subgroup appears to increase at a higher rate than the other two subgroups (Figure 3D).

Figure 3. Observed diastolic blood pressure (mmHg) and individually fitted curves at gestational weeks 8–39.

(A) Observed glucose trajectories over time (gray lines) for the 147 women during pregnancy with the overall mean diastolic blood pressure (DBP) over time (black); (B) Individually fitted trajectories (gray curves) of women with higher mean and variability over pregnancy, relative to the overall mean DBP (black curve); (C) Individually fitted trajectories (gray curves) of women with moderate mean DBP and less variability over pregnancy, relative to the overall mean DBP (black curve); (D) Individually fitted trajectories (gray curves) of women with lower mean DBP and moderate variability over pregnancy, relative to the overall mean DBP (black curve); (E) The three mean fitted curves for the corresponding DBP-specific classifications (solid, dash and dash-dot).

Scores from fPC₁ were again used to classify each subject into one of three subgroups according to SBP mean and variability over gestation (N=37, 73 and 37, respectively).

Unlike previous findings, subject-specific SBP curves appeared to have large within- and between-subject variability (Figure 4A), regardless of subgroup. The high-level SBP subgroup exhibited the greatest heterogeneity of all the subgroups (Figure 4B); however, the variation did not appear to change over gestation. The moderate SBP group had few subjects with large deviations in their profiles at the beginning and end of pregnancy; overall, this subgroup had the lowest degree of variation (Figure 4C). The last subgroup reflected lower mean SBP over gestation; similar to the other two subgroups, these subjects also had curves with large variation (Figure 4D). All three subgroups tended to have mean SBP functions that slightly increased over gestation, but appeared to differ according to SBP level both at the beginning and end of pregnancy (Figure 4E).

Comparisons between phenotypes

Insulin phenotypes were associated with White classification (Table 1). The subgroup with higher mean insulin and variability (Figure 1B) had the highest mean BMI at baseline, and differed from the low-insulin subgroup (Figure 1D) with respect to mean infant birth weight. Subjects who were experiencing their first pregnancy tended to be in the moderate glucose phenotype (Figure 2C). The more extreme phenotypes of glucose (Figures 2B and 2D) differed according to mean infant birth weight.

Table 1.

Insulin/glucose phenotypes and associations with baseline characteristics and pregnancy outcome

	Insulin				Glucose
	I (N=37)	II (N=73)	III (N=37)	P*	I (N=37)	II (N=73)	III (N=37)	P*
Baseline Characteristics
White class, n (%)				0.0088				0.57
B	4 (10.8)	10 (13.7)	5 (13.5)		3 (8.1)	10 (13.7)	6 (16.2)
C	13 (35.1)	25 (34.3)	10 (27.0)		10 (27.0)	26 (35.6)	12 (32.4)
D	16 (43.2)	24 (32.9)	5 (13.5)		11 (29.7)	24 (32.9)	10 (27.0)
>D	4 (10.8)	14 (19.1)	17 (46.0)		13 (35.1)	13 (17.8)	9 (24.3)
First Pregnancy, n (%)				0.60				0.0044
Yes	18 (48.7)	34 (46.6)	21 (58.8)		15 (40.5)	46 (63.0)	12 (32.4)
No	19 (51.3)	39 (53.4)	16 (43.2)		22 (59.5)	27 (37.0)	25(67.6)
Pre-pregnancy BMI, kg/m2, mean±SD (n)	24.5±4.4 (37)†;‡	22.7±2.8 (72)	21.7±1.6 (36)	0.0001	23.2±3.8 (35)	22.9±3.3 (73)	22.6±2.5 (37)	0.86
Outcome at Pregnancy
Infant weight at birth, in g, mean±SD (n)	3565±648 (35)‡	3396±676 (70)	3024±812 (36)	0.0018	3294±910 (35)‡	3366±694 (71)	3345±606 (35)	0.79

^*Reported for differences in means or proportions in which P<0.01 with subjects missing information not included;

^†P<0.01 for I vs. II;

^‡P<0.01 for I vs. III;

^⋄P<0.01 for II vs. III based on least-square means comparisons.

Both DBP and SBP phenotypes had associations with White classification, pregnancy-associated hypertension and preeclampsia (Table 2). Both low-blood pressure phenotypes (Figures 3D and 4D) differed from their two corresponding subgroups (Figures 3B, 3C and 4B, 4C, respectively) regarding mean BMI at baseline. Subjects in the low-SBP subgroup (Figure 3D) were diagnosed with type 1 diabetes at a younger age, on average, but were living with the disease for a shorter period of time, on average, compared to the other SBP subgroups (Figures 3B and 3C).

Table 2.

Blood pressure phenotypes and associations with baseline characteristics and pregnancy outcome

	DBP				SBP
	I (N=37)	II (N=73)	III (N=37)	P*	I (N=37)	II (N=73)	III (N=37)	P*
Baseline Characteristics
White class, n (%)				<0.0001				<0.0001
B	1 (2.7)	12 (16.4)	6 (16.2)		3 (8.1)	6 (8.2)	10 (27.0)
C	8 (21.6)	22 (30.1)	18 (48.6)		5 (13.5)	24 (32.9)	19 (51.4)
D	8 (21.6)	25 (34.2)	12 (32.4)		9 (24.3)	29 (39.7)	7 (18.9)
>D	20 (54.1)	14 (19.2)	1 (2.7)		20 (54.1)	14 (19.2)	1 (2.7)
Age at type 1 diabetes diagnosis, in years, mean±SD (n)	11.9±5.8 (37)	13.7±6.9 (73)	14.4±7.4 (37)	0.25	11.6±7.2 (37)‡	12.8±5.6 (73)⋄	16.4±7.6 (37)	0.0053
Years since type 1 diabetes diagnosis, mean±SD (n)	13.7±6.8 (37)	11.9±6.6 (73)	10.2±7.0 (37)	0.09	14.8±7.6 (37) ‡	12.6±5.6 (73)⋄	7.7±6.3 (37)	<0.0001
Pre-pregnancy BMI, kg/m2, mean±SD (n)	24.4±4.6 (35)‡	22.9±2.6 (73)⋄	21.4±2.1 (37)	0.0004	24.3±4.1 (35) ‡	23.2±2.9 (73)⋄	21.0±2.0 (37)	<0.0001
Pregnancy-associated hypertension, n (%)				<0.0001				<0.0001
Yes	24 (66.7)	19 (26.0)	6 (16.2)		23 (63.9)	23 (31.5)	3 (8.1)
No	12 (33.3)	54 (74.0)	31 (83.8)		13 (36.1)	50 (68.5)	34 (91.9)
Pregnancy Outcomes
Preeclampsia, n (%)				<0.0001				<0.0001
Yes	18 (50.0)	13 (17.8)	3 (8.1)		17 (47.2)	15 (20.5)	2 (5.4)
No	18 (50.0)	60 (82.2)	34 (91.9)		19 (52.8)	58 (79.5)	35 (94.6)

Abbreviations: Diastolic and systolic blood pressure (DBP and SBP, respectively);

^*Reported for differences in means or proportions in which P<0.01 with subjects missing information not included;

^†P<0.01 for I vs. II;

^‡P<0.01 for I vs. III;

^⋄P<0.01 for II vs. III based on least-square means comparisons

Repeated measures analysis of HbA1 revealed changes according to trimester but not based on any of the phenotype subgroups. There was a significant interaction between maternal weight change over time and SBP phenotype (P=0.0024); post-hoc analysis revealed significant differences at baseline, as the low SBP subgroup (Figure 4D) had lower mean±SE weight (123.3±3.7 lbs) than the high and moderate SBP subgroups (144.0±3.7 and 140.3±2.6 lbs, respectively, both P<0.0001). Each subgroup appeared to have similar weight gain over gestation, although the baseline shift remained (results not shown).

There were no significant interaction effects in the models involving DBP or insulin phenotypes, but there were overall differences in the main effects. The low-DBP phenotype (Figure 3D) had lower mean weight (131.4±3.8 lbs) than the high and moderate DBP phenotypes (153.6±3.8, P<0.0001, and 145.6±2.7 lbs, P=0.0025, respectively). The high-insulin phenotype (Figure 1D) had higher mean weight (156.1±3.8 lbs), compared to moderate- and low-insulin phenotypes (142.6±3.8, P=0.0041, and 134.8±2.7 lbs, P=0.0001, respectively).

DISCUSSION

Results from this novel application build upon aforementioned research examining summary measures of glucose variability. This is the first study, to our knowledge, to extract profile-level information across entire pregnancy on blood pressure, glucose and insulin control, while simultaneously accounting for sparse longitudinal data that is typical in medical monitoring. Our approach has implications for clinical use to assess degree in which a mother with type 1 diabetes and her offspring may be at risk for adverse outcomes. This study adds important information on the specific timing and degree of diabetes control during gestation by identifying phenotypes related to variation and offering insights into the optimal time for clinical monitoring. In addition, the findings reaffirm the importance of entering pregnancy with healthy levels of glucose, insulin requirements and BP. Indeed, SBP exhibited the highest degree of variability, but revealed that having a lower baseline value may lead to better control throughout pregnancy, thereby improving odds of better maternal, fetal and neonatal outcomes.

The current study has limitations. It is possible that the findings could be confounded by differences related to reporting glucose via written record in a book, as opposed to use of a glucometer. Since a subset of subjects used the former method, we performed a sensitivity analysis of key findings by including book use as a covariate in each regression model; conclusions from our phenotype comparisons did not change as a result. It is possible that this source of confounding is related to obstetric practices, which evolved during the course of the study period. Although we found temporal associations between phenotypes and other longitudinal data collected throughout gestation, complex models are needed to evaluate the interplay between these large collections of outcomes.²⁰ The analysis approach accommodates incomplete longitudinal data in the form of missing at random (known as MAR). Although this approach is often used in intent-to-treat analyses, it is possible that the missing data mechanism is more complex, given the irregular monitoring of clinical measures over pregnancy. Such assumptions may be implemented in standard software, but there are no formal methods to examine their validity.²¹ Despite these limitations, this data source provides a unique opportunity to precisely evaluate mean changes and variability in clinical measures that are still relevant in modern diabetes and perinatal care.

Overall, this is the first diabetes in pregnancy study to leverage intensive amounts of medical monitoring data for phenotypic classification related to glucose, insulin and blood pressure control. Phenotypes based on functional data analysis, like those identified from this study, are likely to generalize to other chronic conditions that require frequent clinical monitoring and complex care regimens during pregnancy, including type 2 diabetes and gestational diabetes, and should be evaluated in these populations. Examining longitudinal patterns using this methodology may lead to innovations, potentially including interactive web-based tools, in the care and monitoring of diabetes during pregnancy.