Tropomyosin Controls Sarcomere-like Contractions for Rigidity Sensing and Suppressing Growth on Soft Matrices

Abstract

Cells test the rigidity of the extracellular matrix by applying forces to it through integrin adhesions. Recent measurements show that these forces are applied via local micrometre-scale contractions, but how contraction force is regulated by rigidity is unknown. Here we performed high temporal- and spatial-resolution tracking of contractile forces by plating cells on sub-micron elastomeric pillars. We found that actomyosin-based sarcomere-like contractile units (CUs) simultaneously moved opposing pillars in net steps of ~2.5 nm, independent of rigidity. What correlated with rigidity was the number of steps taken to reach a force level that activated recruitment of α-actinin to the CUs. When we removed actomyosin restriction by depleting tropomyosin 2.1, we observed larger steps and higher forces that resulted in aberrant rigidity sensing and growth of non-transformed cells on soft matrices. Thus, we conclude that tropomyosin 2.1 acts as a suppressor of growth on soft matrices by supporting proper rigidity sensing.

Introduction

The rigidity of the extracellular matrix (ECM) plays critical roles in cell apoptosis, proliferation, and differentiation^1,2. Accordingly, aberrant rigidity sensing is involved in many medical disorders^3,4. For example, the anchorage-independent growth of cancer cells^5,6 indicates that their rigidity sensing machinery is malfunctioning. Importantly, while the effects of ECM rigidity on cell fate are observed on timescales of hours to days, rigidity sensing is a rapid and cyclic process that occurs on much shorter timescales^7,8.

According to the current model, during cell spreading and migration, when the cell edge protrudes forward, nascent integrin adhesions are built upon initial contact with the matrix. This is followed by generation of traction forces on the adhesions through local actomyosin-based contractile units (CUs)⁹, and subsequent linkage of these adhesions to the general rearward flow of actin towards the centre of the cell (the integrin ‘clutch’ model^10,11). At its most basic sense, rigidity sensing is manifested as the decision to reinforce the adhesions during the initial period of force application¹². On stiffer substrates, stronger adhesions are built, thereby allowing them to resist the forces from actin flow^12,13. When measured at the sub-micrometre scale, cells displace matrix-coated 0.5 μm diameter flexible pillars to a constant distance irrespective of rigidity⁹. This indicates that there is a well-developed mechanism to link rigidity sensing, force production, and adhesion reinforcement, through sub-micrometre contractions in a few tens of seconds.

Hence, in this study, we analysed cellular forces during rigidity sensing with a new high resolution technology. Using arrays of Polydimethylsiloxane (PDMS) micropillars as substrates (Supplementary Movie 1), we find that mouse embryo fibroblast (MEF) CUs resemble sarcomeres and pull opposing pillars in nanometre-level myosin-II-generated stepwise contractions as verified by different analytical tools. What determines rigidity sensing is the number of steps taken before reaching a ~20 pN force level, which activates adhesion reinforcement. The stepwise movements are dramatically altered after the knock-down of tropomyosin 2.1 (Tpm2.1, formerly known as Tm1¹⁴), indicating that it has a critical role in controlling force production and rigidity sensing. We further link the role of Tpm2.1 in rigidity sensing to suppression of cellular growth on soft matrices.

Results

Molecular organization of CUs resembles sarcomeres

When plated on 0.5 μm diameter fibronectin-coated pillars, fibroblasts use CUs at the cell edge (Fig. 1a,b) to pull on neighbouring pillars and test their rigidity⁹ (similar CUs were observed on collagen-coated pillars; Supplementary Fig. 1a). This is a transient process that typically lasts 20–40 seconds, and involves local contractions of 5–10%^9,15, resembling muscle sarcomere contractions within their ‘normal’ range¹⁶. Therefore, we tested if sarcomere-resident proteins localized to CUs during local contractions. This included α-actinin and myosin, as well as Tpm¹⁷ and tropomodulin3 (Tmod3)¹⁸.

Figure 1.

Contractile Units (CUs) at cell edges require myosin. (a) Cartoon illustration of a CU at the cell edge. (b) Left: Actual CUs observed at the edge of a cell spreading on 8.4 pN/nm pillars (Experiment was repeated 7 times, 45 videos taken altogether). Arrows represent pillar movement vectors: red, contractile pairs; yellow, non-paired pillars. Cell edge is marked in blue. Right: Typical displacement vs. time of two 0.5 μm diameter pillars that were part of a CU. Experiment was repeated (c) α-actinin localizes to the cell edge during P2 stage of spreading (~15 minutes after initial attachment) but is distributed evenly during P1 (from initial attachment up to ~15 minutes). Experiment was repeated three times (10 videos altogether). (d) GFP-myosin-IIA as well as immunolabelled myosin-IIA localize to the cell edge. Experiment was repeated twice. (e) Myosin-IIA is required for force production in CUs. Typical forces generated by myosin-IIA-KD cells²¹ show a significant reduction of the inward-directed forces (see also Supplementary Fig. 1b); only ~25% of the pillars show inward movements compared to >80% in WT cells. CUs are rarely observed, and even in such cases they are short lived and cause small pillar displacements (average maximum displacement = 23±2 nm). Experiment was repeated twice (9 videos altogether). (f) Treatment of the cells with blebbistatin (50 μM) leads to a rapid halt in pillar displacement. Experiment was repeated twice (6 videos altogether).

Consistent with previous studies^19,20, α-actinin was concentrated at the cell edge only after ~15 minutes of spreading (Fig. 1c), at the onset of the slow spreading, rigidity sensing phase¹⁹, P2, when local contractions occurred⁹. Myosin-IIA, the isoform relevant for mechanosensing²¹, simultaneously localized to the active cell edges (Fig. 1d). In myosin-IIA knockdown cells, local contractions were dramatically reduced (Fig. 1e, Supplementary Fig. 1b), and treatment of wild-type cells with 50 μM blebbistatin blocked local contractions (Fig. 1f).

To visualize active myosin molecules, we immunostained for phosphorylated myosin light chain (p-MLC), and found that it localized with GFP-α-actinin at the cell edge (Fig. 2a). Typically, α-actinin concentrated around the edges of the pillars, whereas p-MLC appeared as small clusters between the pillars (Fig. 2a). Bleaching analysis (Supplementary Fig. 1c) showed that the clusters contained between 16 and 36 myosin heads, which is in the known range of the number of heads present in myosin mini-filaments²². Immunostaining for Tpm [using an antibody for high molecular weight (HMW) Tpm, which included Tpm2.1, Tpm1.6, and Tpm1.7, the major HMW isoforms expressed in MEFs²³], overlapped with α-actinin at the pillar edges (Fig. 2a). Tpm was also present between the pillars (Fig. 2a), overlapping with p-MLC (Supplementary Fig. 1d). Further, Tmod3 was located between the pillars (Supplementary Fig. 2a), indicating that the actin filaments terminated in those locations.

Figure 2.

Distribution of sarcomeric proteins in CUs. (a) Top: Patches of p-MLC localize between pillars at the cell edge, whereas α-actinin is localized around the pillars. Middle: Tpm overlaps with α-actinin at the edges of the pillars (arrow in zoom-in image) and is also located between pillars (arrowhead). Experiment was repeated 3 times. Bottom: Normalized average fluorescence intensities of α-actinin, p-MLC, and Tpm on 0.5 μm pillars measured from line-scans between two adjacent pillars. (n = 20 traces from 4 cells in each case). (b) Localization of sarcomeric proteins with respect to nascent adhesions in cells plated on 2D surfaces. Cells transfected with GFP-β3-integrin (marker for nascent adhesions) were fixed after 15 minutes of spreading on fibronectin-coated coverslips. p-MLC and Tpm (both imaged after immunostaining), localized between nascent adhesions (with some overlap of Tpm with the adhesions); mCherry-α-actinin co-localized with β3-integrin and also extended out of the adhesions. Experiment was repeated twice.

To verify that the localization of the different sarcomeric proteins was not pillar dependent, we analysed cells on fibronectin-coated coverslips after 15 minutes of spreading and observed similar distributions relative to β3-integrin adhesion sites. Tmod3 (Supplementary Fig. 2b) and p-MLC (Fig. 2b) appeared between nascent adhesions, Tpm appeared between adhesions with some overlap with β3-integrin (Fig. 2b), and α-actinin co-localized with β3-integrin (Fig. 2b).

Since the CU-generated forces were relatively low (maximum force ~400 pN), we postulated that the p-MLC clusters corresponded to single myosin filaments that drove the local contractions. To test this, we tracked the pillar movements by GFP-α-actinin-expressing cells, fixed and then stained for p-MLC. After analysis to find contractile pillar pairs (see below), we performed super-resolution analysis (3B-microscopy²⁴) and observed that α-actinin was concentrated on the pillar edges and that p-MLC between the contracted pillars had a dumbbell shape that resembled that of bipolar mini-filaments²⁵ (Fig. 3a). The average size of these filaments, 377±16 nm, matched the known size of myosin-II mini-filaments²⁵ (Fig. 3b).

Figure 3.

Myosin mini-filaments appear in CUs. (a) 3B super-resolution image of p-MLC (red) and α-actinin (green) in a contractile pair where the displacement of the pillars was tracked (right traces) and the final displacement vectors (about 35 nm) are marked by the arrows. Note the dumbbell shape of p-MLC, consistent with the known shape of myosin mini-filaments. Experiment was repeated 3 times (7 videos altogether). (b) Left: additional examples of dumbbell-shaped p-MLC filaments from super-resolution fluorescence analyses. Right: The length histogram of these dumbbell shapes matches the known size of myosin mini-filaments. n = 30 patches from 5 cells. (c) Schematic of a CU with the relevant molecular components.

Overall, these results were consistent with a sarcomeric organization within CUs. In this, α-actinin anchored force-bearing, Tpm-decorated actin filaments at the pillars, while an active myosin-IIA filament was in the centre, producing contractile forces on the pillars (Fig. 3c).

Pillar displacement occurs by nanometre-level steps that are constant regardless of rigidity

Since myosin moved by nanometre-scale steps^26,27, and the velocity of pillar displacement was relatively low (2.5–3.5 nm/s), it seemed possible to analyse the contractions at the nanometer level. Videos taken at a frame rate of 100 Hz were used to analyse individual pillar positions using a cross-correlation technique that enabled nanometer-level tracking over time²⁸. To test the accuracy of this method, we used a piezo-device to move the pillar array in steps of 0.6 or 1.2 nm at frequencies of up to 4 steps/s (Fig. 4a, Supplementary Fig. 3a). With a step-fitting algorithm²⁹ as well as pairwise distance analysis^30,31 we were able to detect the steps reliably (Fig. 4a, Supplementary Fig. 3b).

Figure 4.

Cells pull on pillars with nanometre-level steps. (a) Top: Median-averaged tracking data of a single pillar displaced by a piezo-device with 1.2 nm steps at 2 steps/s (blue), along with fitting data using the step-detection algorithm (black). Bottom: the frequency of detection and average step sizes detected (±SEM) using the step-fitting algorithm on data obtained by piezo-controlled movements with 0.6 and 1.2 nm steps at different rates. n=102,96,99 steps from 12,10,11 pillars for the 0.6 nm steps at 2,3,4 steps per second data, respectively; the mean detected step sizes were insignificantly different from 0.6 nm: p-values=0.11, 0.57, and 0.22, one-sample t-test. n=90,92,94 steps from 10,11,11 pillars for the 1.2 nm steps at 2,3,4 steps per second data, respectively; the mean detected step sizes were insignificantly different from 1.2 nm: p-values=0.19,0.27.0.3, one-sample t-test. All piezo-driven experiments were repeated 4 times for each case. (b) Top: Median-averaged displacement data of a single pillar which was part of a CU at the cell edge (green) with the raw 100 Hz measurements in grey, along with fitting data using the step-detection algorithm in black. Bottom: Negative control data along with its step-fitting data for the same pillar (grey and black, respectively). (c) Histograms of the steps detected in the real and negative control data (n=527 steps from 24 pillars in 7 cells; experiment was repeated 4 times).

Next, as cells spread on arrays of 1.3 μm high, 0.5 μm diameter pillars (pillar stiffness=8.4 pN/nm), we tracked pillar movements during P2 in the lamellipodium. In local CUs, we analysed movements of two opposing pillars as they were pulled together, defining a contractile pair (Supplementary Movie 2). The high-frequency displacement curves contained abrupt transitions (steps) from one pillar position to another (Fig. 4b) and pairwise distance analysis showed a step size of 1.1±0.2 nm (Supplementary Fig. 3c). As a control for thermal vibrations, light fluctuations, and detector noise, for each pillar we analysed a “step-free” curve derived from a polynomial fit to the displacement curve with added noise from a pillar outside the cell (Fig. 4b, Supplementary Fig. 3d). These negative control curves contained many fewer steps than the real ones (Fig. 4b), and pairwise distance analysis did not detect the 1.1 nm steps seen in the real cell displacement data (Supplementary Fig. 3e). When we applied the step-detection algorithm, we found that on average, each negative control curve contained ~45% ramps, compared to ~12% in the real curves (see Supplementary Fig. 3f for definition of steps vs. ramps). The steps that were found in the negative control curves (the remaining ~55%) were described by a single Gaussian distribution centred at 0.4 nm, with ~90% of the steps below 0.6 nm (Fig. 2c), providing a threshold below which the steps detected were attributed to noise. When we applied the step-detection algorithm to the real cell displacement curves, the distribution of detected steps was well-fitted with two Gaussians, one centred at 0.4 nm and the other at 1.2 nm (Fig. 2c). When the noise-dependent steps were subtracted from the real data, the remaining steps had an average value of 1.2±0.6 nm (mean±SD). We also performed negative control measurements to verify that no contribution to the steps came from optical or pillar configuration effects (Supplementary Fig. 4), as well as an additional positive control experiment in which >90% of the steps were detected (188/207 steps from 16 pillars in 8 runs) when the piezo-device was programmed to better mimic the real pillar displacements (1 nm steps separated by random, exponentially-distributed, time intervals).

Taken together, these results showed that contractions of CUs involved nanometre-scale steps at a frequency of ~2–3 steps/s and were reliably detected with our method.

Next, cells were plated on soft pillars (2.3 μm high, 0.5 μm diameter; stiffness=1.6 pN/nm). Since in vitro data showed bigger myosin step sizes under lower loads³², we expected larger steps on the softer pillars. However, the mean step size was indistinguishable on both rigidities: 1.2±0.7 nm for soft (n=344 steps from 20 pillars) vs. 1.2±0.6 nm for stiff pillars (n=307 steps from 20 pillars).

Early contractile steps are simultaneous

To further characterize the CUs, we analysed the very early stages of CU displacements toward each other, during which only a few myosin molecules were expected to be involved (see Methods). We observed simultaneous steps (within <100 ms) towards the centre of the CU (inward) in both pillars (Fig. 5a, Supplementary Fig. 5a). A plot of the time between the inward and outward steps showed a normal distribution centred at zero time (Fig. 5b). The sum of simultaneous steps gave an average total displacement of 2.5±0.6 nm on the stiff pillars and 2.4±0.7 nm on the soft ones (Fig. 5c), approximately 2-fold larger than the mean step size for single pillars. Not all steps were simultaneous, but the lack of pairing for some steps was attributed to interactions of filaments with other neighbouring pillars or with the general flow of actin rearward. Simultaneous steps were not found in anti-parallel displacements of neighbouring pillars that were not part of CUs (a completely random time-difference between the steps was found in such pillars; Fig. 5a,b).

Figure 5.

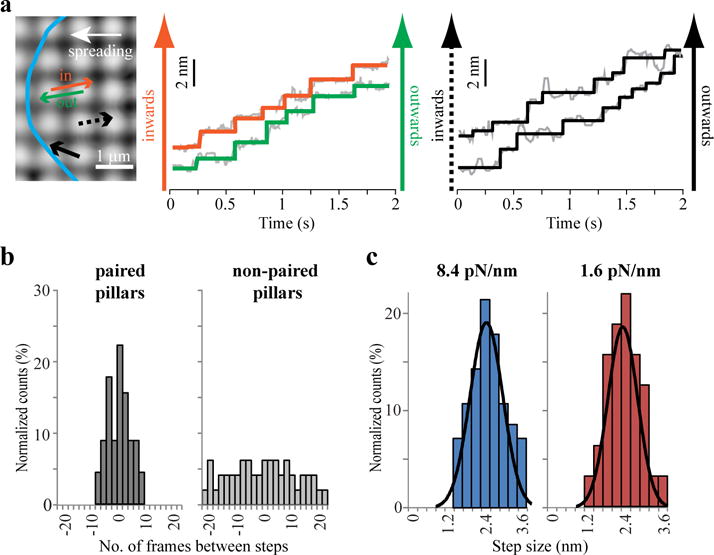
Steps of paired pillars are simultaneous and antiparallel. (a) Image of paired pillars that began to move at the same time (orange and green arrows in image on left; cell edge shown in blue) show simultaneous anti-parallel steps during early phases of displacement. Black arrows represent the movement vectors of unpaired pillars that were being displaced at the same time (see displacement curves on the right) when the simultaneous steps of the pillar pair were detected; these were used as controls to verify that the correlated steps did not arise from similar fits of neighbouring pillar movements. (b) Histogram of the time difference between simultaneous steps in paired pillars has a peak around 0, whereas for unpaired pillars in the same field it is random. In paired pillars ~70% of the steps were correlated within the first 5 seconds of displacement compared to ~20% in unpaired pillars. (n=144 and 152 steps from 17 paired and non-paired pillars, respectively). (c) Histograms of the sum of the displacements for simultaneous steps from paired pillars on stiff (8.4 pN/nm) and soft (1.6 pN/nm) pillars. (n=70 and 74 steps from 8 and 9 CUs for the stiff and soft pillars, respectively; experiment was repeated three times).

These results indicated that an actomyosin structure connecting the pillars contracted by steps of ~2.5 nm about every 300 ms, and displaced each pillar approximately equally, providing strong evidence that the displacements were driven by a single bipolar myosin filament.

Rigidity sensing is regulated by the level of force

Since step sizes and maximal displacement of the pillars⁹ were the same regardless of rigidity, we postulated that rigidity sensing was related to a difference in the pattern of steps between the stiff and soft pillars. Overall kinetics of pillar movements (measuring from the start to the maximal displacement values), were similar for rigid and soft pillars at 2.5–3.5 nm/s. However, careful examination of early stages of pillar displacement revealed that contraction of stiffer pillars began with 3–5 steps within 1–2 seconds, followed by a stall period of ~1–2 seconds, and then a subsequent series of steps. In contrast, contraction of the softer pillars began with 10–12 steps before the pause (Fig. 6a; Supplementary Fig. 5b). This was observed clearly in >65% of the pillars. In both cases, the pause was at a force of ~20 pN, and lasted a similar time: 1.8±0.7 s (n=20 pillars) and 1.6±0.5 s (n=21 pillars) for the stiff and soft pillars, respectively (mean±SD). In comparison, before the pause, the mean time between steps was nearly an order of magnitude smaller than the pause time, at 0.25–0.28 s (Supplementary Fig. 5c).

Figure 6.

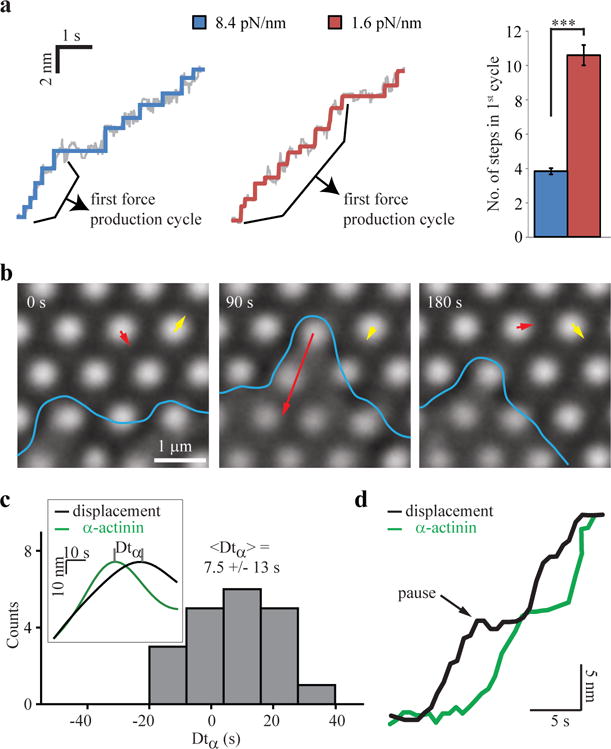
Adhesion reinforcement at a specific force level is critical for rigidity sensing. (a) Typical early displacement traces showing first force production cycles on stiff and soft pillars, along with plots of the mean±SEM number of steps during such cycles (n=12,14 pillars from 4,5 cells, respectively; experiment was repeated three times). (b) Adhesion breakage observed on 0.85 pN/nm pillars (See also Supplementary Movie 3). Cell edge is marked in blue; yellow vector shows the noise level of pillar movements. Notice that the pillar marked with a red vector is released by the cell and returns to zero force position at 180 s. Experiment was repeated three times (9 videos altogether). (c) Histogram of the time interval between the peak in GFP-α-actinin intensity and the peak in pillar displacement (Δt_α, see inset time traces) shows that α-actinin recruitment precedes the peak in force production by 7.5±13 s (mean±SD; n = 20 pillars from 3 cells). Experiment was repeated twice. (d) Typical time traces of pillar displacement (stiffness: 1.6 pN/nm) and GFP-α-actinin intensity show a considerable increase in α-actinin recruitment during the pause in displacement, followed by subsequent force production. Experiment was repeated twice (8 videos altogether). ***p-value < 0.001, two-tailed, equal variance t-test.

Importantly, when extremely soft pillars were used (0.85 pN/nm), there were a large number of steps without a pause and adhesive contacts often broke, releasing the force on pillars (Fig. 6b, Supplementary Movie 3). This resembled previous optical trap experiments using fibronectin-coated beads where adhesions broke when the trap stiffness was very low³³; however, with a high stiffness trap, there was reinforcement of the cytoskeleton-ECM linkage following a stall period of a few seconds¹². Therefore, we suggest that the rate of rise of force with the ultra-soft pillars was too slow and linkages broke before the force threshold for reinforcement could be reached.

If reinforcement of the adhesions occurred during the pause, then proteins that could strengthen the integrin-actin interaction such as α-actinin (which binds both to actin and integrin) might have been recruited. Indeed, cross-correlation analysis between pillar displacements and GFP-α-actinin intensity around pillars showed that its recruitment correlated strongly with force development, whereas the recruitment of vinculin (binds to actin but not to integrin) did not (Supplementary Fig. 6a–c). Initial forces were developed seemingly without α-actinin, possibly mediated by talin¹⁵ (Supplementary Fig. 6d), but the peak in α-actinin fluorescence (and not talin) preceded the peak in force development by ~7.5 s (Fig. 6c), indicating that it was required to reach peak force. Consistent with this, α-actinin recruitment typically increased dramatically during pauses in displacement (Fig. 6d). We suggest that the pause at a force level of ~20 pN was for adhesion reinforcement that was needed for further force development.

Tpm2.1 affects force, step size, step rate, and rigidity sensing

The constant step size indicated that there was a structural restriction of motor movement, perhaps due to Tpm, which mechanically alters myosin binding to actin in muscle^17,34,35. To determine which Tpm isoform was present at the cell edge, we transfected the cells with YFP- or GFP-tagged Tpm2.1, Tpm1.6, or Tpm1.7, and found that the latter two localized primarily to central regions of cells, whereas YFP-Tpm2.1 localized to the cell edges (Supplementary Fig. 7a). When we knocked-down Tpm2.1 expression (Tpm2.1-KD; Supplementary Fig. 7b) and immunostained the cells for HMW Tpms, we observed that the edge localization was lost (Supplementary Fig. 7c). Live imaging of spreading of YFP-Tpm2.1-expressing cells showed that Tpm2.1 gradually assembled at protruding cell edges and then retracted with the membrane (Supplementary Movie 4), consistent with a possible involvement of Tpm2.1 in local contractions for rigidity sensing.

To test this, we analysed the effect of Tpm2.1-KD on cell spreading on different rigidities. Whereas Tpm2.1-KD cells spread equally on both stiff and soft pillars after 1 hour, control cells spread to ~1.5-fold greater area on stiff pillars compared to soft ones (Fig. 7a). Also, control cells were polarized and elongated, but Tpm2.1-KD cells were typically round (Supplementary Fig. 7d). These results indicated that Tpm2.1-KD cells were defective in their rigidity sensing³⁶. Importantly, after Tpm2.1-KD, the local contractions were highly disorganized (Supplementary Fig. 7e) and pillar displacements were significantly larger than in control cells (with even higher displacements on softer pillars; Fig. 7b). Further, the rate of pillar movement increased 2-fold compared to control rates (Fig. 7c, Supplementary Fig. 7f). Analysis of stepping movements in Tpm2.1-KD cells revealed step sizes of up to ~5 nm that were not observed in controls, and an average step size of 2.2±0.7 nm (Fig. 7d, Supplementary Fig. 7g). In many cases, high forces caused release of pillars (similar to the ultra-soft pillars) and halted further spreading, possibly due to impaired adhesion development. Indeed, control cells plated on fibronectin-coated coverslips for 1 hour formed large, elongated adhesions, but the Tpm2.1-KD cells formed only small, round adhesions at the cell edge (Fig. 7e), indicating that CUs were important for the development of focal adhesions and cell spreading. As a control for the specificity of Tpm2.1, we knocked down Tpm1.7 and found that pillar movements had the same step size as controls (Supplementary Fig. 7h), consistent with the absence of these isoforms from the cell edge.

Figure 7.

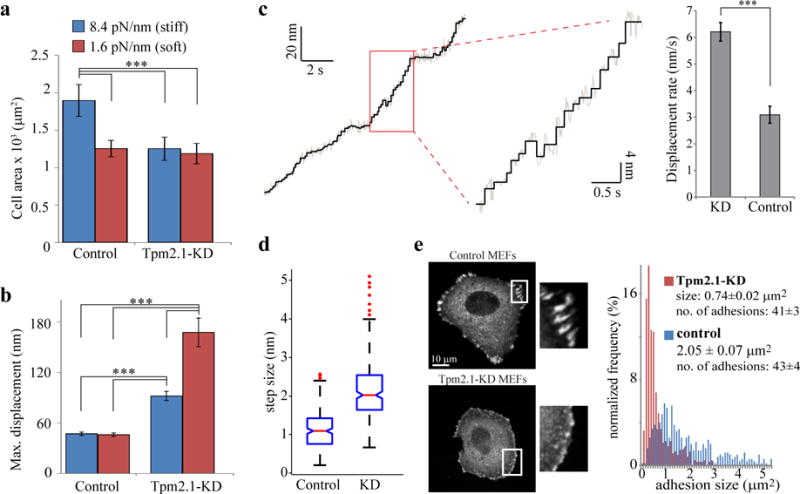
Tpm2.1 regulates force production, step size, and adhesion growth. (a) Average area ±SEM of cells transfected with non-targeting SiRNA (control) and Tpm2.1-KD cells after 1 hour of spreading on stiff and soft pillars (n=50,52,51,54 cells). Experiment was repeated three times. (b) Mean±SEM of the maximal displacements of pillars when control and Tpm2.1-KD cells were plated on stiff and soft pillars (n=81,79,70,71 pillars from at least 5 cells in each case). Experiment was repeated twice. (c) Left: Typical pillar displacement by a Tpm2.1-KD cell, showing high displacement rate and large steps. Right: quantification of pillar displacement rates (mean±SEM) by Tpm2.1-KD and control cells (n=20 pillars from 3 cells in each case). Experiment was repeated three times. (d) Average step sizes for control and Tpm2.1-KD cells. Red lines are the median values, the edges of the blue boxes are the 25^th and 75^th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers (data greater than 3 SD than the median) are plotted individually as red dots; comparison between boxes is done by the overlap of the notches: if they do not overlap, the conclusion with 95% confidence is that the true medians do differ. (n=344 and 316 steps from 20 and 15 pillars for control and KD cells, respectively). Experiment was repeated three times. (e) Adhesions are much smaller after Tpm2.1-KD. Left: Micrographs showing the distribution of paxillin-GFP in Tpm2.1-KD and control cells. Right: Quantification of adhesion sizes in Tpm2.1-KD and control cells (n=245 and 256 adhesions from 6 cells in each case). ***p-value < 0.001, two-tailed, equal variance t-test. Experiment was repeated twice.

Taken together, these results indicated that Tpm2.1 controlled myosin stepping on anti-parallel actin filaments and was linked to the systems that regulated overall displacement in contractile units, as well as matrix rigidity sensing.

Tpm2.1 suppresses growth on soft matrices by supporting rigidity sensing

Many cancer cells that were anchorage-independent for growth displayed very low Tpm2.1 levels, and its re-expression restored their ability to grow on soft matrices^37,38. Thus, we postulated that anchorage-independence was linked to an aberrant rigidity response. To test this, we analysed malignant MDA-MB-231 and non-malignant MCF-10A breast epithelial cells. Immunostaining of these cells showed that Tpm was present at the edges of MCF-10A cells but not of MDA-MB-231 cells (Fig. 8a). CUs were observed in MCF-10A cells but not in MDA-MB-231 cells (Supplementary Fig. 7i). Forces produced by MDA-MB-231 cells were significantly higher than MCF-10A cells (maximal displacements of 1.6 pN/nm pillars by MDA-MB-231 and MCF-10A cells were 187±53 and 49±20 nm, respectively; n=39,35 pillars), and there was considerable adhesion breakage by MDA-MB-231 but not by MCF-10A cells. High-resolution analysis of the pillar movements indicated that the average step size for MCF-10A cells was the same as wild-type MEFs, whereas for MDA-MB-231 cells it was 2-fold larger, similar to Tpm2.1-KD MEFs (Fig. 8b). MCF-7 cells, another malignant breast epithelial cell line with low Tpm2.1 levels³⁹, had a similar step size as MDA-MB-231 cells (Fig. 8b), and high maximal displacements (92±21 nm, n=38 pillars). When we knocked-down Tpm2.1 expression in MCF-10A cells (Supplementary Fig. 7j), the maximal displacements increased to 103±15 nm (n=40 pillars) and step sizes to 1.9±0.8 nm (Fig. 8b). Conversely, when we transfected MDA-MB-231 cells with YFP-Tpm2.1, the average step size decreased 2-fold (Fig. 8b) and the maximal displacements dropped to controls, 50±18 nm (n=45 pillars). Also, YFP-Tpm2.1-expressing MDA-MB-231 cells formed larger adhesions than non-expressing cells (Fig. 8c).

Figure 8.

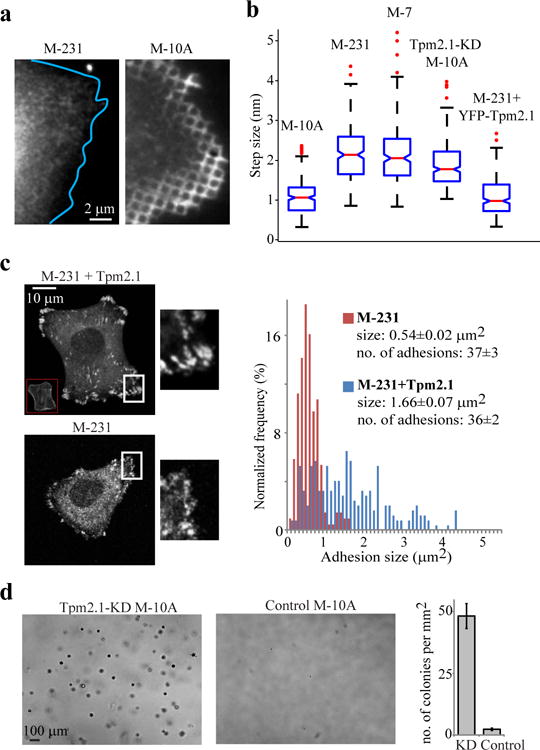
Tpm2.1 differentiates between normal and malignant cell lines and controls growth on soft matrices. (a) Examples of MCF-10A and MDA-MB-231 cells plated on pillars and immunostained for Tpm. Experiment was repeated twice. (b) Average step sizes for MCF-10A cells (M-10A), MDA-MB-231 cells (M-231), MCF-7 cells (M-7), Tpm2.1-KD MCF-10A cells, and MDA-MB-231 cells with YFP-Tpm2.1 expressed. (n=231,248,245,311,270 steps from at least 12 pillars in each case). Experiment was repeated twice for each case. Red lines are the median values, the edges of the blue boxes are the 25^th and 75^th percentiles, the whiskers extend to the most extreme data points not considered outliers, and outliers (data greater than 3 SD than the median) are plotted individually as red dots; comparison between boxes is done by the overlap of the notches: if they do not overlap, the conclusion with 95% confidence is that the true medians do differ. (c) Adhesion sizes are larger in MDA-MB-231 cells when Tpm2.1 is expressed. Left: Micrographs showing the distribution of paxillin-GFP in MDA-MB-231 and MDA-MB-231+Tpm2.1 cells. Right: Quantification of adhesion sizes in Tpm2.1-KD and control cells (n=220 and 217 adhesions from 6 cells in each case). Experiment was repeated twice. (d) Soft agar assay showing growth of Tpm2.1-KD MCF-10A cells but not of control cells. Cells were stained with Crystal Violet. Experiment was repeated twice.

To test the involvement of Tpm2.1 in anchorage-independent growth, we performed a soft agar assay and observed that control MCF-10A cells did not survive after two weeks in culture whereas Tpm2.1-KD MCF-10A cells proliferated and formed colonies (Fig. 8d), confirming that defective rigidity sensing in the absence of Tpm2.1 contributed to the ability of cells to grow on soft matrices.

Discussion

Rigidity sensing is a fundamental function that is highly dynamic, occurs on small length-scales, and affects many cell processes. In these studies, sarcomere-like CUs contract 500 nm pillars by nanometre-level steps for rigidity sensing. Applying our analysis method to lamellipodial CUs, we reliably find single pillar steps of about 1.2 nm at low and intermediate rigidities that differ significantly from noise. In contractile pairs of pillars, there are simultaneous, anti-parallel displacements of ~2.5 nm. This step size is smaller than the working stroke size of myosin-II reported from single-molecule in vitro studies²⁷; however, it is consistent with the fact that the stroke size decreases when the velocity of actin filament sliding is low⁴⁰ and when Tm is present⁴¹. Our measurements also correlate well with the in vitro movements of actin filaments by myosin filaments that occur in steps of 2.7 nm⁴².

Nanometre-level movements could theoretically originate from several different mechanisms, including conformational changes of adhesion proteins, receptor movements, subtraction of single actin monomers from filaments attached to pillars, or myosin contractions. While we cannot completely rule out other possibilities, several observations indicate that the steps are due to myosin contraction: I. simultaneous anti-parallel steps of pillar pairs indicate that the pairs are joined by a single CU of about 2 μm in length. II. The CUs contain many sarcomere proteins and a single bipolar myosin filament. III. A bipolar myosin filament with only few myosin heads engaged can produce ~30–50 pN³² and the pause force of 20–30 pN fits well with this stall force^43,44. IV. The depletion of Tpm changes the step length as expected for myosin movements controlled by Tpm.

Assuming that contractile steps are myosin dependent, there are two different mechanisms that could account for the 2.5 nm step size. The first possibility is that the steps we detect are not the full myosin working stroke; this is in line with recent X-ray interference and mechanical measurements of sarcomeres that suggest that the myosin stroke size occurs by sub-steps of ~2.75 nm^40,45. The second possible mechanism is based on recent measurements that show that Tpm limits the binding of myosin to actin^34,35. Under this model, a myosin filament effectively moves from one actin monomer on a single strand to the next on the neighbouring strand, thus displacing the actin filament by half the length of an actin monomer, i.e., ~2.7 nm. This latter model is more favourable since Tpm depletion not only increases step size, but also the velocity. Thus, under this model, in the absence of Tpm2.1 there are more available binding locations for myosin on the actin filaments, allowing it to produce high forces rapidly (Supplementary Fig. 8a).

The speed of pillar movement, 2.5–3 nm/s, is significantly lower than the stepping rates of myosin molecules found in vitro, but is consistent with the movement velocities of actin nodes by myosin in fibroblasts⁴⁶, as well as with measurements and computational models that show that the behaviour of single myosin molecules is vastly different than small myosin ensembles (mini-filaments)^44,47. In the latter case, increased load significantly reduces the movement velocities of actin filaments, to the range of several nanometres per second^44,46,47. Further, when we test a wider range of pillar rigidities, we find that there is an inverse relationship between force and velocity (Supplementary Fig. 8b), in line with the known behaviour of sarcomeres, which contract slower with increased load.

In terms of the molecular mechanism of rigidity sensing, we propose that it is not the step size or rate of stepping, but rather exceeding a force threshold of ~20 pN that triggers a pause for reinforcement and establishment of a strong adhesion. This pause is best explained by the fact that under high loads the lifetime of myosin-actin attachment increases substantially⁴⁸ (another process that could contribute to the pause is the ‘latch state’ of myosin heads, which can occur when light chains of bound myosin heads are de-phosphorylated, leaving myosin bound and still generating tension^49,50). Since the force-producing mini-filaments contain a small number of myosin heads, the ~20 pN force level puts each head under a high load where it is in a strongly actin-bound state⁴⁸, resulting in a plateau in the displacement curve. Since the step length is constant regardless of rigidity, the myosin heads need to move many more steps on softer pillars to develop the same tension. Once the threshold force is reached, there is reinforcement of the integrin adhesions that involves recruitment of α-actinin and presumably other adhesion proteins⁵¹. After reinforcement, forces on adhesions continue to increase, perhaps through further activation or recruitment of myosin (Supplementary Fig. 8a). On ultra-soft surfaces the force does not rise rapidly enough to induce a pause, and the adhesions dissociate without reinforcement. Conversely, adhesion breakage is observed also in the absence of Tpm2.1 due to the very high forces that are produced rapidly.

Notably, these observations may explain the involvement of Tpm2.1 as a repressor of cancer^38,52. When plated on soft matrices, non-transformed cells produce low forces, leaving the adhesions small^53,54, and thus the integrin-mediated signals that promote cell-cycle progression are absent; instead, apoptotic signals are activated. Cancer cells override the requirement for stable adhesions in order to proliferate, and thus they can grow on soft matrices. We propose that signaling cascades would be repeatedly activated by the high forces that are being produced in the absence of Tpm2.1 (presumably through activation of mechanosensory proteins⁵⁵). Hence, the cells would not be dependent on the formation of strong adhesions. This is indeed what we observe in the case of non-malignant MCF-10A Tpm2.1-KD cells. This model suggests there is an accumulation of mechanically-activated signals over time. Thus, the connection between force and vital cellular signals should be further studied by long-term tracking of forces, protein dynamics, and activation of signalling cascades.

Methods

Cell culture, transfections, and spreading experiments

Sources for WT and Myosin-IIA-KD MEFs were described previously^17–19. MDA-MB-231 and MCF-10A cells were obtained from Jay Groves (University of California, Berkeley, and Mechanobiology Institute, National University of Singapore), MCF-7 cells were from ATCC. MEFs, MCF-7, and MDA-MB-231 cells were cultured at 37° C in a 5% CO2 incubator in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% fetal bovine serum, 100 IU/ml Penicillin-Streptomycin, 2 μM L-Glutamine, and 2 μM HEPES; MCF-10A cells were cultured at 37° C in a 5% CO2 incubator in DMEM supplemented with 20 ng/ml EGF, 10 ng/ml Bovine insulin, 500 ng/ml Hydrocortisone, 5% horse serum albumin, and 100 IU/ml Penicillin-Streptomycin (all reagents were from Life Technologies).

Transfections were carried out 1 day before measurements using the Amaxa Nucleofector System (Lonza) according to the manufacturer’s instructions, with ~10⁶ cells per reaction and 4–5 μg DNA.

One day prior to spreading experiments, cells were sparsely plated to minimize cell-cell interactions prior to re-plating. The following day, cells were trypsinized using TrypLE (Life Technologies), centrifuged with growth medium, and then resuspended and pre-incubated in Ringer’s buffer (150 mM NaCl, 5 mM KCl, 1 mM CaCl₂, 1 mM MgCl₂, 20 mM Hepes and 2 g/L D-Glucose at pH 7.4) for 30 min prior to the experiment. Cells were then spread on pillar arrays, or on silanized cover glasses [2 hours in 20% nitric acid, followed by exposure to gaseous 1, 1, 1, 3, 3, 3-Hexamethyldisilazane (Sigma)] that were pre-coated with 10 μg/ml human plasma full-length pure fibronectin (Roche) or collagen I (Corning) for 1 hour at 37° C. In all cases we made sure that the cells were not clustered when plated on the substrates.

Plasmids and siRNA oligonucleotides

GFP- and YFP-tagged Tpm plasmids were a generous gift from Peter Gunning (The University of New South Wales, Sydney, Australia); mCherry-tropomodulin3 was a generous gift from Carol Gregorio (University of Arizona, Tucson, USA); GFP-α-actinin was a generous gift from Carol Otey (University of North Carolina, Chapel Hill, NC); GFP-vinculin was a generous gift from Kenneth Yamada (National Institutes of Health, Bethesda, MD); RFP-paxillin was a generous gift from Michael Partridge (Columbia University, New York, NY); GFP-VASP was a generous gift from Juergen Wehland (German Research Center for Biotechnology, Braunschweig, Germany).

Knockdown of Tpm2.1 was performed with siRNA oligonucletides (target sequence: AAGCACATCGCTGAGGATTCA) labelled with Alexa-488 (Qiagen). Cells in 35 mm plates were transfected with 2,100 ng oligonucleotide duplexes using GeneSilencer’s siRNA transfection reagent (Gene Therapy Systems) according to the manufacturer’s instructions. After transfection, cells were incubated for 72 h for efficient depletion of the target protein. Specific knockdown of Tpm2.1 was then tested by Western blotting using TM-311 (Sigma) as a primary antibody. Although on average the knockdown was not complete (~70–75%), single cell analysis showed that the effects of Tpm2.1-KD were most prominent in cells that showed high fluorescence levels of the transfected siRNA.

For verification of the effect of Tpm2.1 knockdown, an shRNA plasmid (Mission shRNA®, sigma) was used (target sequence: TTGTTACCAACAACTTGAAAT) for transfecting the cells (transfection was carried out using the Amaxa system); experiments were performed 72 h following transfection.

Knockdown of Tpm1.7 was carried out using shRNA plasmids (Sigma; target sequences: sh1 –AGCTGACGTAGCTTCTCTGAAC, sh2 – GGATCAGACTTTACTGGAGCTA).

Myosin-IIA knockdown cell line (target sequence: GGTGAAGGTGAACAAGGAC) was previously described¹⁹. For verification of the effect of myosin-IIA knockdown, an shRNA plasmid (Sigma; target sequence: CGGTAAATTCATTCGTATCAACT) was used. Western blot was used to test knockdown levels using a primary antibody against myosin IIA (Abcam, ab24762). Load controls for the Western blots were done using a tubulin antibody.

High frequency brightfield microscopy and pillar displacement measurements

Time-lapse imaging of pillars was performed with bright-field microscopy using an ORCA-Flash2.8 CMOS camera (Hamamatsu) attached to an inverted microscope (Olympus IX-81), controlled by Micromanager software²⁰. Images were recorded continuously at 100 Hz using a 100× 1.4 NA, oil immersion objective (yielding a pixel size of 36 nm/pixel). For each cell, a movie of ~5 minutes (corresponding to 30,000 frames) was recorded; stage drift and focus changes were minimized by using a controlled 37°C chamber.

To minimize the noise arising from the imaging conditions, we removed the shutter from the illumination path and used a >600 nm filter that allowed us to increase the light intensity significantly in order to reach high pillar-to-background contrast without significant photo-damage to the cells. Because we were analysing the position of the pillars 100 times per second, the noise for a 1 second period was ten-fold lower than in our previous work²¹ where only 1 image per second was analysed. All these improvements resulted in typical noise amplitude that ranged between 0.8 and 1.2 nm, with generally lower noise for the softer pillars (theoretically, increasing the pillar length should also increase the thermal noise of the pillar tip, however, we find that the noise level depends mostly on the contrast between the pillars and background, which is higher with the 2.3 μm pillars and therefore their noise amplitude is lower).

Tracking pillar movements

Pillar tracking over time was performed with ImageJ (National Institutes of Health) using the Nano Tracking plugin^22,23. In this technique, two regions of interest (ROIs) were used: one containing an image of a pillar of interest and another containing the surrounding area through which this pillar moved during the movie (typically the latter ROI was ~2-fold larger than the former even though the movements were much smaller than twice the size of a pillar). Next, calculation of the cross-correlation between the pillar image in every frame of the movie was performed with an image of the same pillar (called the ‘kernel’) from the first frame of the movie. The cross-correlation of the pillar image with the kernel had a peak centered at the position in the pillar image where the surrounding intensity most closely matched the intensity distribution in the kernel. Next, an intensity threshold value, T, was subtracted from the cross-correlation, and the negative pixels were discarded, isolating only those pixels that contributed to the central peak. The centroid (x_c,y_c) of these remaining pixels was then calculated according to: ${\mathrm{x}}_{\mathrm{c}}=\frac{\sum \mathrm{x}\left\{\mathrm{C}\right(\mathrm{x},\mathrm{y}\left)\right\}}{\sum \left\{\mathrm{C}\right(\mathrm{x},\mathrm{y}\left)\right\}}{\text{ y}}_{\mathrm{c}}=\frac{\sum \mathrm{y}\left\{\mathrm{C}\right(\mathrm{x},\mathrm{y}\left)\right\}}{\sum \left\{\mathrm{C}\right(\mathrm{x},\mathrm{y}\left)\right\}}$. In this way, the relative position of the pillar in every frame of the movie was obtained. To account for stage drift, the average displacement of a set of pillars far from any cell was subtracted from the data. After analysis, a displacement map on each frame in the movie was generated by Matlab (MathWorks), which allowed detection of contractile pairs (see Supplementary Movie 2).

Using this technique, the overall precision of position measurements made every 10 milliseconds (based on the standard deviation of the frame-by-frame differences in the movements of a pillar not in contact with the cells, see Schnapp et al., 1988²²) was 0.8–1.2 nm. Since the time between steps was on average 0.25–0.28 s, we could reduce this noise level 2.5–3-fold by averaging over multiple frames without blurring the steps using a 15-pt. linear moving-median filter (similar result were obtained when we used a 21-pt. non-linear Savitky-Golay filter²⁴).

In general, factors that might affect the accuracy of the measurements are changes in focus and uneven illumination of a pillar²³. We made sure that the focus was stable by analysing a reference pillar outside the cell in each movie; changes in focus would result in changes in the apparent movement of a reference pillar, and so we verified that its movement was stable on average throughout the measurement (i.e. the overall seconds-scale movement, not the rapid millisecond-scale fluctuations). The uneven illumination of a pillar might result in a skewed representation of the pillar’s centroid. While typically the illumination was even over regions larger than a single pillar, a local effect could occur when the cell was not completely covering a pillar, resulting in one side of the pillar being brighter than the other. This resulted in some cases in an apparent outward “movement” of pillars upon cell-pillar contact which we referred to in our previous publication as a ‘lensing effect’²¹. We estimated that this effect could account for a maximum displacement value of ~25 nm²¹; therefore, in the current work we only analysed the nano-steps after the cell edge has passed the pillars completely. Another concern that we took into account was the possibility that tracking the movements of a pillar using pixelated images might lead to inaccuracies; however, digitization of the image (i.e., its representation as a pixelated array) in fact had very negligible effects. The error in calculating the centroid of a digitized cross-correlation peak was shown to be ~0.03% of the pixel size²³, i.e. ~0.01 nm in our case (which is the contribution digitization alone).

Images shown in Figs. 1 and 5 are representative frames from movies taken on an 8.4 pN/nm pillar array. For each of the 1.6 and 8.4 pN/nm stiffnesses, at least 40 videos were taken from at least 6 separate experiments. Image shown in Fig. 6 is a representative frame from a movie taken on a 0.85 pN/nm pillar array; 9 videos were taken on these pillars from 3 separate experiments.

Step-fitting algorithm

Fitting the median-filtered pillar movements data (either cell- or piezo-generated) was done using the L1-PWC algorithm described by Little et al.²⁵. This algorithm detects steps generated by molecular motors in noisy data series. The only parameter that can be changed in this algorithm is γ, which controls the smoothing of the data and should be set to at least 2σ, where σ is the standard deviation of the noise²⁵. In practice, analysis of data series of pillar movements by cells yielded the same steps using γ values ranging from 2 to 15; therefore, we used a γ value of 10 for all the analyses of pillar movements.

In some cases, a clear transition from one pillar position to the next was fitted by the algorithm as a large step (of ~1 nm) with a much smaller step immediately adjacent to it; thus, if we were to simply subtract the pillar position in one frame from the previous, this would have resulted in an underestimation of the step size (see Supplementary Fig. 3f). Therefore, we performed a post-fitting procedure in which a step was defined as a transition from one pillar position to the next, where the transition lasts less than 5 frames, and the second pillar position is being held for more than 10 frames. This enabled the distinction between transitions that occurred by steps and those that occurred by ramps (see Supplementary Fig. 3f for examples).

Piezo-controlled measurements

For the piezo-device experiments, movements of pillar arrays by the piezo stage (PI, model P-517) were controlled by a Modular Piezo Controller (PI, model E-500) and a 10 MHz DDS function generator (Wavetek, model 29). Step sizes were first calibrated by verifying a linear relationship between function generator voltage and step size. In this way it was determined that 0.1 V corresponded to a step size of 0.6 nm. In a typical experiment using the piezo-device, we took movies of areas of ~6×6 pillar arrays. Within a single sequence, there were very little pillar-to-pillar variations (see Supplementary Fig. 3a). In these experiments, the piezo-device moved 9 steps (of 0.6 or 1.2 nm) in varying rates (2–4 steps per second) and at the end of this cycle it jumped back to its starting position to start another cycle with the same parameters.

As an additional positive control, to better mimic the pillar displacements, we programmed the piezo device to move by 1 nm steps with time intervals which were randomly selected from an exponential distribution ranging from 20 to 50 frames between the steps and an overall pillar movement velocity of 2.5–3 nm/s. Each run lasted 5 seconds and contained 13–15 steps (see main text).

Construction of negative control data

As a negative control, for each pillar that we analysed we used Matlab to construct a curve that mimicked the original data by taking the overall pillar displacement trend (a 5^th degree polynomial fit of the displacement) and adding it to the noise during the time of the displacement. The noise was taken from a pillar that was not in contact with the cell. We also verified that the fluctuations of pillars which were not in contact with cells were the same as those of pillars underneath cells while the latter were not being displaced (see Supplementary Fig. 4d).

Thus, this data contained a realistic signal and was subjected to the identical data analysis as the real data. We did this in order to test the alternative hypothesis that the steps arose from the analysis method or from some stage/instrument noise (thus considering possible systematic errors that might exist in the real data). In this alternative scenario the pillars were moving in a smooth manner and the steps that we were detecting were the result of the pillar noise. If the alternative scenario were true, there would have been no difference in the steps between our real data and the negative control data. However, a significant difference between the steps in the real and negative control data was observed, thus rejecting the alternative hypothesis.

Notably, noise alone contributed almost no steps, rather it was the combination of noise and the slope of the displacement (the 5^th degree polynomial) that gave rise to the small steps (up to ~0.6 nm).

Pairwise-distance analysis

Analyses of the pairwise differences between data points in pillar displacement curves was performed for a given filtered record (filtered using a 15-point median filter) by considering all possible inter-point amounts (i.e., by 1, 2, 3,…, N frames, where N was the final frame number of a record) and then plotting the histogram of all the resulting pairwise distance differences (i.e., the pairwise distance distribution function, PDF) between −25 and +25 nm, with a bin size of 0.1 nm. The PDFs of all records were then normalized between 0 and 1 and averaged, resulting in the PDFs presented in Supplementary Figs. 3 and 7. Next, fast Fourier transform was performed using Matlab on each single PDF after removing the so-called “DC component” by subtracting a 10-point moving average of each PDF from itself (the peaks in the power spectra were observed also when applying the Fourier transform directly to the original PDFs, but they were more pronounced after the removal of the DC component). The resulting power spectra were then averaged, followed by smoothing of the average power spectrum with a 10-point moving average window, and normalization to unity at a spatial frequency of 0 nm⁻¹. Identical power spectrum was obtained when applying the Fourier transform to the averaged PDF and when applying it to each individual PDF and then averaging the resulting power spectra. To compute the error in the peak location in the Fourier transforms, we recorded the spatial frequency which corresponded to the peak in each individual curve and calculated the SEM of all these values.

Fluorescence microscopy

For immunofluorescence microscopy, cells were plated for 15 minutes on fibronectin-coated pillars, fixed with 4% paraformaldehyde, and permeabilized with 0.1% Triton X-100. Immunolabeling was performed with primary antibodies overnight at 4°C, and with Cy3- or Alexa-488-conjugated secondary polyclonal antibodies (Jackson ImmunoResearch Laboratories and Invitrogen, respectively) for 1 h at room temperature. Primary antibodies used were against Thr18/Ser19 p-MLC (Santa Cruz Biotechnology, sc-12896), HMW Tpm (Sigma; TM-311), and α-actinin 4 (Alexis Biochemicals, ALX-210-356-C050).

Images of immunolabelled cells or cells transfected with fluorescently-labelled proteins were taken using an Olympus IX-81 fluorescence microscope, 100× or 60×, 1.45 NA oil objective, an electron multiplied-CCD camera (model Cascade-II:512, Photometrics), and a further 2× magnification, or with a Zeiss 700 confocal microscope, 63x, 1.4 NA oil objective. Images were background subtracted using the ImageJ ‘rolling ball’ plugin. Representative images presented in Figures 1, 2, 3, 7, and 8, and Supplementary Figures 1, 2, and 7 were from experiments that were repeated at least twice.

Quantification of adhesion size was performed with ImageJ after applying a threshold for background subtraction using the MultiThresholder plugin. Quantification of cellular circularity was performed using the ‘Shape descriptors’ option in the Measure menu.

Counting the number of p-MLC molecules between pillars

For analysis of the number of active myosin molecules present in the clusters between pillars, continuous movies of labelled cells were taken to completely bleach the Cy3 fluorophores attached to the secondary antibodies (which in turn were attached to the primary anti-p-MLC antibodies). Next, the fluorescence time traces of single clusters were plotted to track the bleaching process; this enabled determination of the size of a single bleaching step (SBS) in arbitrary fluorescence units. Each secondary antibody carried on average 6 fluorophores (information available from Jackson ImmunoResearch Laboratories), and thus 6xSBS was equivalent to a single secondary antibody. In this way, we determined that on average ~18 secondary antibodies were present in each isolated cluster, i.e., 9 for each half myosin mini-filament. The epitope used for producing the p-MLC antibody was small enough so that each MLC molecule could bind to two primary antibodies (information available from Santa Cruz Biotechnology). Thus, 9 secondary polyclonal antibodies could label a maximum number of 18 p-MLC molecules (if two p-MLC molecules in a myosin dimer carry two primary antibodies that bind to one secondary antibody). However, the distance between two myosin dimers (~14 nm) could be bridged by a single secondary antibody (~15 nm between the antigen binding sites within a single antibody), and therefore another likely scenario is that each primary antibody binds to two secondary antibodies, and thus 9 secondary antibodies would label 8 p-MLC molecules in a half mini-filament. Hence we concluded that on average between 16 and 36 p-MLC molecules (myosin heads) were present in the clusters observed between the pillars.

Imaging for 3B analysis

3B microscopy uses Bayesian analysis of blinking and bleaching events in a sample of data with many overlapping fluorophores, to calculate the structure of the system at enhanced resolution²⁶. Imaging for 3B analysis was performed using an Olympus IX-81 fluorescence microscope maintained at 37 °C with a 60x/1.45 NA oil-immersion objective and an electron multiplied-CCD camera (model Cascade-II:512, Photometrics). 3B analysis was done as described in by Cox et al.²⁶. Because of the computational cost, the 3B software was run on the Titan cluster at the Center for Computational Biology and Bioinformatics (Columbia University); http://wiki.c2b2.columbia.edu/systems/index.php/Documentation/Titan_cluster.

Pillar and soft gel fabrication

Moulds for making PDMS pillars were fabricated using electron beam lithography in hard Poly(methyl methacrylate) (PMMA) substrates. PMMA was first spun-coated onto a silicon substrate and then hard-baked on a hot plate for 10 hours. An electron beam lithography tool (NanoBeam nB5) was then used to pattern holes in the PMMA. The depth of holes was dependent on the thickness of the PMMA. PDMS (mixed at 10:1 with its curing agent, Sylgard 184; Dow Corning) was then poured onto the PMMA moulds, cured at 70 °C for 12 h to reach a Young modulus of 2±0.1 MPa, and peeled off while immersed in isopropanol. All pillars had diameter D = 500 nm, except for the 0.85 pN/nm pillars that due to the fabrication process had a diameter of ~650 nm. The centre-to-centre spacing between pillars was twice the pillar diameter. Increasing the distance between the pillars did not affect the formation of CUs and the forces produced by them (unpublished results). The top surfaces of the pillars were flat, with a height variation of only ~10% of pillar diameter²¹. Pillar bending stiffness, k, was calculated by Euler–Bernoulli beam theory:

$$k=\frac{3}{64}\pi E\frac{D^4}{L^3}$$

where D and L are the diameter and length of the pillar, respectively, and E is the Young’s modulus of the material (PDMS).

Fluorescent labelling of pillar tops was done by stamping highly hydrophobic Quantum-dots (Life technologies) after peeling off the PDMS pillars from the moulds in the air.

Soft agar assay

Soft Agar assay was performed using the Cell Transformation Assays, Standard Soft Agar kit from Cell Biolabs according to the manufacturer’s instructions. 5,000 cells were seeded in each well of a 96-well plate. Experiment was repeated twice with triplicates of each condition in each experiment.

Statistics & Reproducibility

Sample sizes were chosen to test if the distributions of the populations were normal. Indeed, the samples step sizes and cell areas had normal distribution, which justified the use of Student’s t-test [Figs. 4a (one-sample t-test), 6, 7, and 8, and Supplementary Figs. 3, 4, and 5 (two-tailed, equal variance t-tests)].

All pillar displacement experiments were performed at least three times on different days. All fluorescence imaging of immunostained or transfected cells and the soft agar assay were repeated twice on different days. Immunostainings and western blots were performed using established antibodies which were previously used in published manuscripts.

MCF-10A, MDA-MB-231, and MCF-7 cells that were used in this study are highly established cell lines which are typically used for comparing malignant vs. non-malignant breast epithelial cells. The MEF cells were previously described^18,19 and have been used in the Sheetz lab in the last decade for cell spreading experiments. All cells were kept at a low passage number and passed 2–3 times a week.

Analyses of pillar movements were performed only in cases where two pillars were moving primarily towards each other, which was true in ~1/3 of the CUs that we analysed; in the majority of the CUs there were three or more pillars that moved during the contraction events (see also Ghassemi et al., 2012²¹).

Cross correlation analysis

Pillar displacements and fluorescence traces were obtained from time-lapse movies taken at 1 frame per second with a 60× objective in an Olympus Fluoview FV500 laser-scanning confocal microscope, maintained at 37 °C.

For each pillar analysed, the cross correlation function between pillar deflection and protein localization, c(τ), was calculated:

$$c\left(\tau \right)=\frac{\langle \left[\langle d\left(t+\tau \right)-\langle d\rangle \right][I_{\mathit{\text{max}}}\left(t\right)-\langle I_{\mathit{\text{max}}}\rangle ]\rangle }{{\sigma }_d{\sigma }_I}$$

where d is the pillar deflection, I_max is the maximum intensity of GFP-α-actinin or GFP-vinculin within distance 0.75D of the centre of the pillar, and <…> indicates a time average. σ_d and σ_I are the standard deviations of d and I_max over time. Time traces were low-pass-filtered with a cut-off frequency of 0.15 Hz. For each offset time, τ, the cross-correlation takes a value between -1 and 1. Cross correlation functions from different pillars were averaged, and then the time delay of protein localization compared to pillar deflection was defined to be the offset time of the maximum of the averaged cross correlation function. Because this quantity is affected also by negative (correlation) contributions coming from secondary displacement peaks we also used the temporal distance between the first peak in pillar displacement and the first peak in protein intensity to further characterize the relation between these two events.

Code availability

The plugin for pillar tracking and the code for pillar movement analyses are available upon request.