Using noise to shape motor learning

Many theories argue that we choose to make the specific movements that minimize motor noise. Here, by changing the relationship between movements and noise, we show that people actively learn to make movements that minimize noise. This not only provides direct evidence for the theories of noise minimization but presents a way to use noise to teach specific movements to improve rehabilitative therapies and human-machine interface control.

Abstract

Each of our movements is selected from any number of alternative movements. Some studies have shown evidence that the central nervous system (CNS) chooses to make the specific movements that are least affected by motor noise. Previous results showing that the CNS has a natural tendency to minimize the effects of noise make the direct prediction that if the relationship between movements and noise were to change, the specific movements people learn to make would also change in a predictable manner. Indeed, this has been shown for well-practiced movements such as reaching. Here, we artificially manipulated the relationship between movements and visuomotor noise by adding noise to a motor task in a novel redundant geometry such that there arose a single control policy that minimized the noise. This allowed us to see whether, for a novel motor task, people could learn the specific control policy that minimized noise or would need to employ other compensation strategies to overcome the added noise. As predicted, subjects were able to learn movements that were biased toward the specific ones that minimized the noise, suggesting not only that the CNS can learn to minimize the effects of noise in a novel motor task but also that artificial visuomotor noise can be a useful tool for teaching people to make specific movements. Using noise as a teaching signal promises to be useful for rehabilitative therapies and movement training with human-machine interfaces.

NEW & NOTEWORTHY Many theories argue that we choose to make the specific movements that minimize motor noise. Here, by changing the relationship between movements and noise, we show that people actively learn to make movements that minimize noise. This not only provides direct evidence for the theories of noise minimization but presents a way to use noise to teach specific movements to improve rehabilitative therapies and human-machine interface control.

when we reach for a glass of milk, we must choose one movement from all of the possible movements that would bring our hand to the glass (Bernstein 1967). This is far from a trivial problem, as it relies on the simultaneous coordination of many degrees of freedom. In fact, there are infinite coordination patterns that are seemingly equivalent to complete the task (Mussa-Ivaldi et al. 1988). Despite this complexity, people are able to consistently reach for the glass with low error.

Standard theories postulate that the central nervous system (CNS) chooses movements that are energetically efficient but also lead to low noise (Berniker et al. 2013; Harris and Wolpert 1998; Osu et al. 2004; Sternad et al. 2014; Todorov and Jordan 2002)—after all, we do not want to spill the milk. Indeed, some evidence suggests that people “exploit” the redundancy in the motor system to either reduce task variability (van Beers et al. 2004; Latash et al. 2002; Scholz and Schöner 1999) or find specific control policies that are more robust to variability (Cohen and Sternad 2009; Sternad et al. 2011), often in concert with minimizing effort (O'Sullivan et al. 2009; Todorov 2004). These theories usually present the process by which we select movements as an optimization problem in which a cost function, consisting of noise, effort, or both, is minimized through the choice of movement. These models have been remarkably strong at predicting which movement subjects choose. However, these approaches are often criticized for the fact that the evidence can be indirect, as it is often difficult to dissociate minimization of quantities such as effort, noise, or jerk. As such, many of the common features of human movement have been successfully explained by minimizing effort (Fagg et al. 2006; Farshchiansadegh et al. 2016), noise (Harris and Wolpert 1998), kinematic qualities of the movement such as smoothness (Flash and Hogan 1985; Morasso 1981), or some combination of these factors (Mistry et al. 2013; O'Sullivan et al. 2009; Todorov 2004).

These theories usually assume that the level of noise depends on the movement, often through signal dependence, where stronger motor commands give rise to more noise (Hamilton et al. 2004; Jones et al. 2002; Schmidt et al. 1979). This dictates that the amount of noise present in a movement is a function of what movement is selected; however, this relationship between movement and noise is not varied in the majority of experiments. The central prediction of the theories of noise minimization is that if the dependence of noise on the movement changed, the chosen movement would also change in a predictable manner. If the CNS does indeed learn to make the specific movements that are least affected by noise, then one should be able to manipulate visuomotor noise to elicit desired movement patterns.

Earlier studies have in fact shown that by changing the relationship between movements and noise it is possible to change people's behavior in a targeted way (Chu et al. 2013; Hasson et al. 2016; Manley et al. 2014). For instance, Manley and colleagues (2014) showed that for a planar reaching movement it is possible for noise to bias the reach direction. They also found, however, that the ability to find the reach direction that minimized noise depended on one's conscious awareness of the direction dependence of the noise. This suggests that biasing a well-practiced movement may rely on more complex interactions; however, it remains to be seen whether, when first learning to move in a novel geometry where people must learn from scratch how to complete the task, people can use noise as a feature to guide learned movements. Chu et al. (2013) used a task in which the participants had no previous experience and found that they changed their behavior in response to increased or decreased levels of noise. Here, we aimed to build on these results by assessing whether people will actively seek low-noise movements or compensate for increased noise in other ways when learning a motor task in a novel geometry.

Using noise to bias the control policy that users learn to coordinate high-dimensional movements in a novel task would not only be a direct test of whether the CNS can learn to minimize noise but also has the potential to bring about new approaches in neurorehabilitation. Specifically, the use of visuomotor noise could benefit individuals with severe motor impairments by encouraging them to practice specific functionally effective movements (Ellis et al. 2005; Pierella et al. 2015; Taub et al. 1999; Thorp et al. 2016). As such, it is important to test whether visuomotor noise directly affects which coordination patterns people learn to use.

Here, participants learned a novel redundant motor mapping, from high-dimensional control movements to a low-dimensional task space. When learning to complete this task, users must form a control policy or learn a relationship between end-point (cursor) movements and body movements. Specifically, they must learn appropriate body configurations to achieve desired cursor locations. We tested two groups of subjects where the relationship between movements and noise differed between groups to quantify how this relationship may alter the movements subjects learn. The noise is designed such that there are specific movements that minimize task relevant noise (cursor jitter). We found that in the presence of noise users learned to make movements that were less affected by the noise. Additionally, our approach improved generalization to trials without visual feedback. These results support the hypothesis that the CNS can learn specific movements to minimize the effects of noise and provide exciting evidence that artificially shaping the relationship between movements and task-relevant noise can be used to teach individuals to adopt specific coordination strategies.

MATERIALS AND METHODS

Participants.

Sixteen able-bodied young adults (6 women; mean age = 23.2 ± 4.5 yr) participated in this study. All participants provided informed written consent for protocols approved by the Northwestern University Institutional Review Board.

Motor task.

Participants held two inertial measurement units (IMUs) (3-Space Wireless Sensors, YEI), one in each hand (Fig. 1A). They formed a fist around each of the IMUs so as to not introduce redundancy between the hand configuration and the IMU measurements. They were instructed to make relatively small hand movements and were informed that only changes in the roll and pitch of the sensors were being recorded, as yaw was subject to substantial drift. The four-dimensional control signal (roll and pitch from each sensor) was linearly mapped to the two-dimensional location of a computer cursor with a specific forward map (A) according to the equation below (Liu et al. 2011; Mosier et al. 2005):

$$p=\left[\begin{array}{c}{p}_1\\ p_2\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\end{array}\right]\ast \left[\begin{array}{c}{h}_1\\ h_2\\ h_3\\ h_4\end{array}\right]=\mathrm{Ah}$$ (1)

Fig. 1.

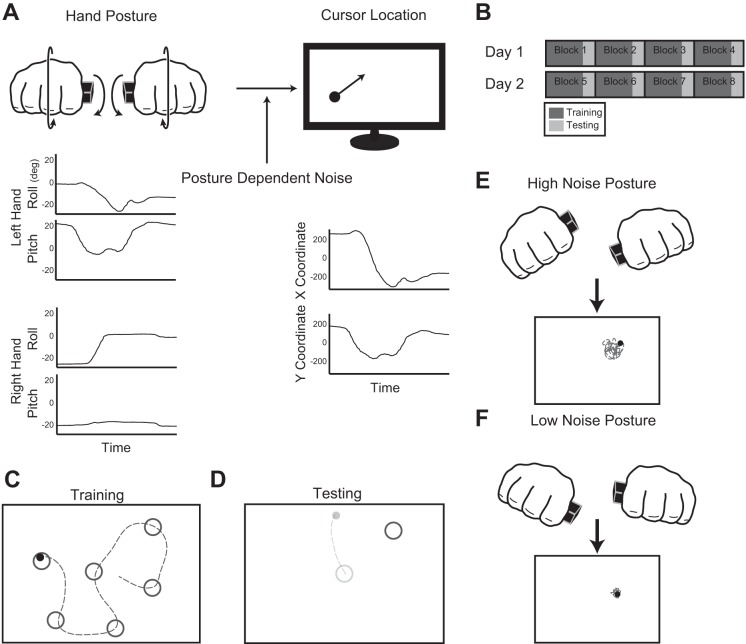
Experimental paradigm. A: participants manipulated the pose of 2 inertial measurement units with their hands to control the location of a cursor on a computer screen. The task was redundant in that hand motions had 4 degrees of freedom but there were only 2 degrees of freedom for the computer cursor. For half of the participants, posture-dependent noise was added into the interface between movements and visual feedback. B: participants practiced using the interface over 2 consecutive days. During each day, participants alternated between 50 training trials and 8 testing trials. C: during training, participants reached to 50 targets, always an equal distance from the previous target. D: during testing, visual feedback was removed from the onset of movement until the participant stopped moving. Here, the faint colors indicate when visual feedback was removed. E and F: since the task is redundant and the amount of noise was posture dependent, there were independent hand postures that would produce the same cursor location with varying noise. E shows a high-noise posture, and F shows a low-noise posture. We predict that through training subjects will learn to adopt low-noise postures to complete the task.

Here h is the vector of measurements from the IMUs at a given time and p is the corresponding location of the computer cursor. The forward map A was identical for all participants, A = $\left[\begin{array}{cccc}11.68& -1.45& -11.48& -0.85\\ -1.83& 11.24& -3.93& 8.72\end{array}\right]$, and was formulated with a single calibration process performed by an additional user who did not participate in the study. For the calibration process, random hand movements, well within the comfortable range, were recorded for 1 min. Principal components analysis was then performed on the data to identify the orthogonal axes or principal components (PCs) that best described the variability in the data. The forward map (A) was then simply constructed from the two PCs that accounted for the highest percentage of the total variance in the hand movements scaled by the variance along each PC to make cursor movement comparable in both dimensions.

This method creates a hand-to-cursor mapping in which a single hand posture results in a single cursor position but a single cursor position can be achieved through a multitude of hand postures. Because the two-dimensional location of the cursor is a linear combination of four IMU measurements, there is an infinite set of hand postures that produce the same cursor location (e.g., rotate the left hand more and the right hand less). This motor task mimics how we learn to make even simple movements but eliminates any prior biases and allows us to study how the CNS initially learns to resolve redundancy. To become proficient at this task, subjects learn the relation of their hand movements to cursor movements (Mosier et al. 2005), analogous to how the CNS forms internal models for well-practiced movements (Kawato 1999; Wolpert et al. 1998; Wolpert and Kawato 1998).

Procedure.

Participants completed eight blocks, four per day for two consecutive days. Each block consisted of first training trials followed by testing trials (Fig. 1B). During the training trials (Fig. 1C) targets randomly appeared on the screen, always 11.5 cm from the previous target. Participants were instructed to move the cursor as quickly and accurately as possible to the target and maintain the cursor in the target location for 500 ms. At this point, the current target would disappear and the next target would appear. Each block consisted of 50 training trials. For the testing trials (Fig. 1D), participants made center-out reaches to four target locations, 11.5 cm from the center of the screen. The target locations in the testing trials were not experienced during the training trials; however, both sets of targets were uniformly distributed around the center of the screen. When participants left the center target, visual feedback was removed until the movement was completed. The end of the movement was taken as the time when the cursor position was held sufficiently static for 500 ms (total movement < 1 cm). Participants were instructed to make a movement that they thought would bring the cursor to the target and then stop moving. Each block consisted of eight testing trials, where subjects made two reaches to each of the four targets. For both training and testing trials, the target was a circle with a diameter of 2 cm.

Signal-dependent noise.

Participants were divided into two experimental groups, the noise group (n = 8) and the control group (n = 8). For participants in the noise group, artificial signal-dependent noise was added to the IMU measurements (h) only during the training trials of the protocol. For the control group, no additional noise was added during the entirety of the experiment. During the testing trials, no noise was added for either group. When noise was added, for each channel an independent random variable was drawn at 50 Hz and low-pass filtered at 3 Hz to ensure smoothness of the visual feedback. Random samples were drawn from a Gaussian distribution with zero mean and variance equal to the magnitude of the measurement for that channel scaled by a constant factor. Under this condition, Eq. 1 became

$$p=A\left(h+w\right)$$ (2)

where w_i = N(0,k_i|h_i|). Here, N(x,y) represents a random value from a normal distribution with mean x and standard deviation y and k_i is the scale factor for channel i. In this context, the noise level was posture dependent, or for any hand posture there would be a well-defined level of cursor jitter. The covariance of the cursor at any hand posture could be calculated with the hand posture and the scale factors for each channel: Cov[p] = A∑A^T, where

$${\displaystyle \sum =\left[\begin{array}{cccc}{k}_1^2{h}_1^2& 0& 0& 0\\ 0& k_2^2{h}_2^2& 0& 0\\ 0& 0& k_3^2{h}_3^2& 0\\ 0& 0& 0& k_4^2{h}_4^2\end{array}\right]}$$ (3)

From the covariance matrix, we quantified the noise level as the maximum deviation from the mean cursor position with 95% confidence. We calculated the eigenvalues of the covariance matrix for a given hand posture and took the maximum deviation due to noise as twice the square root of the largest eigenvalue. This value was then scaled down by 1/3 to account for the effects of the low-pass filter. To quantify the effect of the low-pass filter, we ran simulations to compare the nonfiltered variance of the noise and the filtered variance of the noise for the noise levels that we expected given the constraints of the experiment (i.e., no angle was >90°). For each hand posture, we could thus calculate a single value that would represent the maximum likely distance that the noise would take the cursor from the mean cursor position.

The scale factors (k_i) were chosen to ensure that even at relatively high-noise postures the task was still possible. To do this, we generated random control strategies, i.e., random generalized inverses of A. Each of these generalized inverses could be used to translate cursor positions to a specific hand posture. If the hand postures calculated using a generalized inverse did not violate the constraints of the experiment, i.e., that no angle be >90° at the four most extreme cursor locations (the corners of the screen), this was kept as a valid control policy. Generalized inverses were generated and tested until there was a random sampling of 10,000 possible control strategies. The scale factors were tuned such that for 95% of the control policies the task would still be possible, or that at the four corners of the screen (where the noise was greatest) the noise level was not greater than the target radius. The scaling factors chosen for the present experiment were k = [0.1 0.001 0.001 0.11]. As such, two degrees of freedom (h₁ and h₄) contributed greater to cursor noise and were thus discouraged in the present paradigm. We thus refer to these as the noisy degrees of freedom. The scale factors were the same for all participants and constant throughout the experiment.

Within this framework, the level of noise was dependent on the position of the hands such that there arose high-noise hand postures as well as low-noise hand postures (Fig. 1, E and F). In fact, there was a single collection of hand postures, or a single control policy, that minimized cursor noise for every cursor location (the optimal control policy). By seeing how similar participants' movements were to the optimal ones, we could directly observe whether the added noise biased movements toward the ones that minimized noise.

Data analysis.

During training, we quantified task performance by measuring the time it took participants to move between target locations, the path length of the cursor from the beginning to the end of the movement, and the initial direction error. To ensure that path length was not confounded by the level of noise, we removed the noise from the path length calculations for participants in the noise group. Specifically, we recreated the cursor trajectories based on the actual hand movements but did not add noise into the calculations. For initial direction error, we measured the angle between two vectors, one going from the starting location to the target location and one going from the starting location to the cursor location corresponding to the first peak in the speed profile of the cursor. Peaks were detected only if the speed was >25% of the maximum speed. These measures allowed us to assess the effect that adding noise had on participants' ability to learn to complete the task.

To quantify the accuracy of participants' control policies, we measured error during the testing trials. We measured the Euclidean distance between the target location and the cursor location at the end of the movement as well as the angle error, or the angle between the vector going from the center to the target and the vector going from the center to the cursor position at the end of the movement, or the point when visual feedback was restored.

To measure the effect that the noise had on which control policy participants learned, we needed to estimate the specific control policy participants used. We assumed that participants learned a linear model to determine an appropriate hand posture given a desired cursor location. This mapping was defined by the control policy B^ and can be computed by using maximum likelihood estimation on the data set consisting of all testing trials in each block. From a set of N body vectors, H = [h⁽¹⁾, h⁽²⁾,… h^(N)], and N desired cursor vectors, P = [p^⁽¹⁾, p^⁽²⁾,… p^^(N)], we could calculate B^ according to

$$\widehat{B}=H{P}^T{\left(P{P}^T\right)}^{-1}$$ (4)

This analysis was only performed on testing trials in which the desired cursor vectors were the target locations and the body vectors were the hand configurations when the participant stopped moving. This allowed us to directly assess the feedforward control policy without the ability to make feedback corrections. We then calculated the difference between the estimated control policy and the optimal control policy for all participants by taking the matrix norm of the difference between the two matrices. For subjects in the control group, the optimal control policy had no meaning; however, this group was included in this analysis to ensure that changes in control policy selection were driven solely by the added noise and were outside the range of arbitrary control policy selections. We did not expect this measure to change for the control group through training.

To successfully complete the task, subjects in the noise group had to keep the sum of their systematic error (the distance from the cursor to the center of the target at the end of the trial) and random error (the level of the noise) less than the target radius. To ensure that it would be feasible for the subjects to complete the task by reducing either or both of these, we measured the systematic error and the random error at baseline and throughout training. To quantify random error we used the noise level as described above, and to quantify systematic error we used the distance between the final cursor position without noise and the center of the target. The measures of systematic and random error allowed us to quantify whether the task would be possible if subjects did not converge to low-noise postures given the baseline levels of noise and to observe how these values changed through training.

Finally, we sought to describe how noise may change the way participants distribute their variability when learning the task. Previous experiments suggest that when learning a similar task subjects converge to a single control policy or confine their variability to mainly two degrees of freedom (Casadio et al. 2010; Liu et al. 2011; Mosier et al. 2005). While adding noise should have had no effect on this behavior, we felt it was important to ensure that this behavior was conserved in the presence of noise. Specifically, we measured the planarity of movements by performing principal components analysis on the hand postures during training blocks and calculating the variance accounted for by the first two PCs. If planarity was not sufficiently high, it would suggest that participants were not learning a single control policy and thus our estimates of this policy would not be valid. While our hypothesis did not predict that noise would cause changes in the planarity of movements, we did, however, predict that the distribution of this variance would be changed. To quantify whether participants in the noise group were learning to more optimally distribute their variability, we measured the percent variance along degrees of freedom that resulted in high levels of noise.

Statistical analysis.

For each of the metrics described above, excluding the noise level, we performed a mixed-model ANOVA with training block (1–8) as the within-subject factor and group (additional noise vs. no added noise) as the between-subjects factor. Post hoc pairwise testing was performed on significant factors, using Tukey's test when appropriate. For noise level, we performed a one-way repeated-measures ANOVA with training block as the between-subjects factor only for participants in the noise group. We did not measure the noise level for control participants, as no noise was added during the experiment. All statistical tests were performed using an α level of 0.05 for significance.

RESULTS

Effect of noise on task performance.

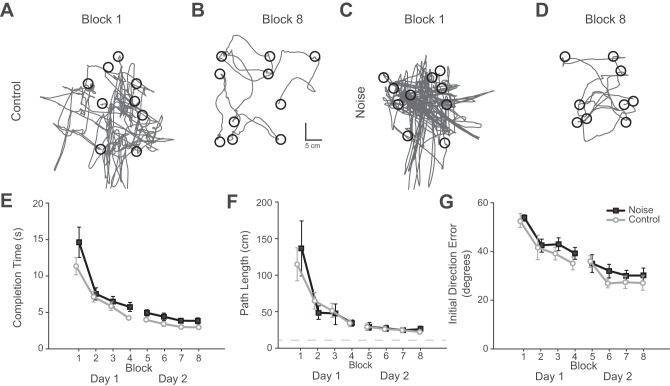
We first sought to verify whether subjects were able to learn to successfully complete the task despite the added noise. Example cursor trajectories are shown in Fig. 2 for a typical participant from each group during for the first 10 reaches of the first block (Fig. 2, A and C) and the final block (Fig. 2, B and D). With practice, all subjects showed a significant decrease in completion time (F_1,7 = 64.2, P < 0.001; Fig. 2E), path length (F_1,7 = 22.4, P < 0.001; Fig. 2F), and initial direction error (F_1,7 = 27.7, P < 0.001; Fig. 2G). Adding signal-dependent noise did not have a significant effect on completion time (F_1,7 = 2.43, P = 0.14), path length (F_1,7 = 1.13, P = 0.30), or initial direction error (F_1,7 = 0.95, P = 0.35). However, during the final session, completion time, path length, and initial direction error were slightly higher for participants in the noise group (completion time: 3.9 s, SD = 1.2; path length: 23.6 cm, SD = 11.4; initial direction error: 30.2°, SD = 8.5) compared with those in the control group (completion time: 3.0 s, SD = 0.3; path length: 20.8 cm, SD = 2.7; initial direction error: 27.0°, SD = 8.3). This was not unexpected, as the task was inherently more difficult in the presence of noise. Nonetheless, this demonstrated that even in the presence of additional signal-dependent noise subjects were able to become skilled at the task.

Fig. 2.

Task performance. A–D: cursor trajectories for the first 10 reaches of the first block (A and C) and the last block (B and D) for a typical subject in the control group (A and B) and a subject in the noise group (C and D). E–G: the average completion time (E), path length (F), and initial direction error (G) are shown for each group across training blocks. All subjects in both groups showed significant increases in performance by reducing completion time (P < 0.001), path length (P < 0.001), and initial direction error (P < 0.001) from the first block to the last block. There was no significant difference between the 2 groups for completion time (P = 0.14), path length (P = 0.30), or initial direction error (P = 0.92). Thus noise did not have an effect on the ability of subjects to become skilled at the motor task. Error bars represent 1 SE.

Analysis of control policy selection.

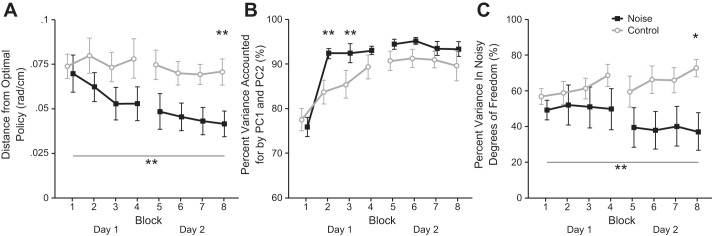
To test the hypothesis that users would learn to make movements that reduced task specific variability, we calculated the difference between their estimated control policy and the control policy that minimized cursor covariance, i.e., the desired control policy (Fig. 3A). We found a significant effect of the interaction between group and block on the distance from the desired control policy (F_1,7 = 2.416, P = 0.02). Post hoc tests revealed that through training participants in the noise group used movement policies that became significantly closer to the desired policy (studentized range statistic: q = 6.85, P < 0.001) while participants in the control group did not (q = 0.41, P = 1). Also, during the final block, participants in the noise group used movement policies that were significantly closer to the desired policy than participants in the control group (q = 3.77, P = 0.01). This suggested that the CNS actively learned to make movements that minimized noise and that by manipulating the relationship between movements and noise one can teach users to adopt specific control policies.

Fig. 3.

Control policy analysis. A: through training, noise caused subjects to be biased toward the desired control policy. By the end of the experiment, subjects in the noise group had significantly reduced their distance from the optimal control policy (P = 0.001) and were significantly closer to the optimal control policy than subjects in the control group (P = 0.01). B: all participants distributed variability largely in 2 dimensions, indicating that they were learning a single control policy. Specifically, all subjects significantly increased the variance accounted for by the first 2 PCs from the first to the final block (P < 0.001). However, participants in the noise group were significantly more planar than participants with no noise in the second and third training blocks (P = 0.005 and P = 0.006, respectively). C: as predicted, subjects in the noise group decreased variability in degrees of freedom that resulted in higher task noise while those in the control group did not. Error bars represent 1 SE. Asterisks indicate significance: *P < 0.05, **P < 0.01.

The design of the forward map and the pattern of noise led to the possibility that participants in the noise group would adopt a strategy in which they made unimanual movements to control the x- and y-directions of the cursor independently. Despite the existence of this straightforward strategy, we observed that only one of the eight subjects fully adopted this strategy, with two other participants adopting a less extreme version. The majority of subjects adopted complex bimanual movements while still reducing the cursor noise.

Our hypothesis did not predict that the distribution of the variance of movements would change but did predict that subjects would learn to avoid movements along dimensions that led to increased noise. If this were the case, we expected to find that subjects in the noise group reduced the variance of movements along dimensions that lead to high noise while still learning a single control policy. Indeed, when we analyzed the distribution of variance of the movements (Fig. 3B), it was the same between the two groups. The high levels of variance accounted for by the first two PCs in both groups indicated that all participants learned a single control policy, with the only difference being that subjects in the noise groups converged to this behavior slightly faster. However, when we analyzed the variance of movements only along the directions that resulted in large task noise (Fig. 3C), we found far less variance in the noise group than in the control group. There was a significant interaction between group and training block for variance along the noisy degrees of freedom (F_1,7 = 4.24, P < 0.001). Post hoc tests revealed that subjects in the noise group significantly decreased their variance along these dimensions (q = 5.5, P = 0.004) while those in the control group did not, and during the final block their variance in these dimensions was significantly less than in the control group (q = 3.5, P = 0.02). This was important to verify that the structure of how the CNS represents learning the task does not change with noise, only which control policy is learned.

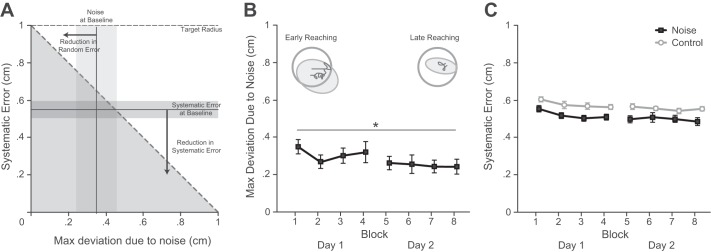
To ensure that this bias in movement policy was not simply done out of necessity, we measured the level of noise and the systematic error throughout training. We wanted to verify that, given the level of noise at baseline, subjects would have been able either to reduce their systematic error by moving the mean cursor position closer to the center of the target or to reduce their random error by adopting low-noise postures. Figure 4A shows the baseline level of noise (mean ± 1 SD) and the systematic error (mean ± 1 SD) for subjects in the noise group. The average noise level for subjects in the noise group was 0.35 cm (SD = 0.1 cm), and the average systematic error was 0.55 cm (SD = 0.05 cm). This validates that if subjects had maintained their baseline level of noise throughout training they would have been able to complete the task by reducing their systematic error. We found that there was a significant effect of training block on the noise level (F_7,49 = 3.342, P = 0.005; Fig. 4B). Post hoc tests revealed that subjects significantly reduced their noise level from the first block to the final block (q = 5.00, P = 0.019). Noise levels were reduced on average by 30%. For systematic error (Fig. 4C), the ANOVA revealed main effects of both session (F_1,7 = 12.3, P = 0.003) and training group (F_1,7 = 4.15, P < 0.001); however, the interaction between training session and group was not significant (F_1,7 = 0.028, P = 0.962). This suggests that while subjects in the noise group had lower systematic errors than subjects in the control group, there was no difference in the extent or rate to which they reduced their systematic error through training.

Fig. 4.

Changes in random and systematic error. A: baseline random and systematic errors for subjects in the noise group. The horizontal rectangle represents the mean ± 1 SD of the noise level during the first training session, and the vertical rectangle represents the mean ± 1 SD of the systematic error during the first training session. The sum of the systematic error and random error must be <1 cm for the task to be possible; thus only for configurations in the shaded triangular region was the task possible. Subjects could move further into this region by reducing random error (shifting the vertical box left), systematic error (shifting the horizontal box down), or both. B: subjects in the noise group significantly decreased the level of noise during training from the first block to the final block (P = 0.018). Top: example of a typical subject in the noise group holding the target early (left) and late (right) in training. The large circle represents the target radius, the dark line is the actual movement of the cursor, and the light ellipse is the 95% confidence interval for the covariance at the mean hand posture. The confidence intervals were calculated with the covariance matrix from Eq. 3. C: the systematic error is shown for subjects in the noise group and the control group across training sessions. There were significant main effects of session (P = 0.003) and group (P < 0.001), but the interaction between group and session was not significant (P = 0.962). Error bars represent 1 SE. Asterisk indicates significance: *P < 0.05.

Generalization to test trials.

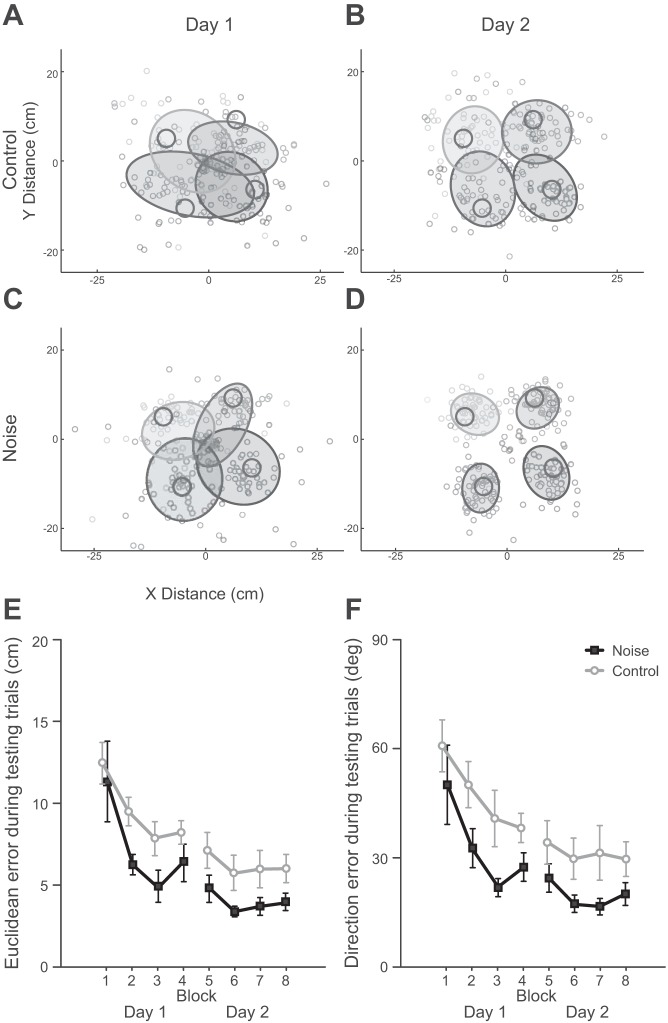
Furthermore, to see if adding signal-dependent noise hindered the ability of the CNS to form an accurate control policy, we compared both Euclidean and direction error during test trials between groups (Fig. 5, E and F). In Fig. 5 the distribution of all final cursor positions for each target during the test trials is shown for subjects in the control group (Fig. 5, A and B) and the noise group (Fig. 5, C and D) during the first day (Fig. 5, A and C) and the second day (Fig. 5, B and D) of training. The magnitude of errors during testing trials allowed us to directly measure the quality of the control policy that participants formed, independent of the participants' ability to make online corrections using visual feedback. Larger errors indicated that the control policy formed by participants was less accurate. For both error measures, there was a significant main effect of session, as both groups reduced error throughout the experiment (Euclidean error: F_1,7 = 14.9, P < 0.001; direction error: F_1,7 = 10.6, P < 0.001). The ANOVAs also revealed a main effect of training group on both Euclidean error (F_1,7 = 6.88, P = 0.036) and direction error (F_1,7 = 6.54, P = 0.023) during the testing trials. However, we found that in fact it was participants in the noise group who had significantly lower errors during the testing trials. Participants in the noise group had an average Euclidean error of 5.6 cm (SD = 3.9), while participants in the control group had an average Euclidean error of 8.0 cm (SD = 3.5). Similarly, average direction error was 26.3° (SD = 11.0) for the noise group and 39.3° (SD = 11.0) for the control group. This rejected the hypothesis that signal-dependent feedback noise hinders the formation of an accurate control policy and in fact suggested the opposite, that signal-dependent feedback noise during training may enhance the ability of the CNS to form a control policy and thus enhance feedforward motor planning.

Fig. 5.

Feedforward task performance. A–D: distributions of final positions are shown for subjects in the noise group (C and D) and control participants (A and B) for the first day (blocks 1–4, A and C) and the second day (blocks 5–8, B and D). Each shade of gray represents 1 of the 4 targets, and the dark circles indicate the actual target locations. The ellipses are 75% confidence ellipses for the final positions for each target across all subjects. E: participants in both groups showed a significant decrease in Euclidean error during testing from the first block to the final block (P < 0.001). However, participants experiencing signal-dependent noise had significantly lower Euclidean errors than the control group (P = 0.036) across all testing blocks. F: similarly, both groups reduced direction error from the first to the final block (P < 0.001), but subjects in the noise group had significantly lower direction errors overall (P = 0.023). Error bars represent 1 SE.

DISCUSSION

Here, we manipulated the relationship between movements and noise in a novel redundant motor task such that there arose a single desired control policy that minimized task-specific variability (cursor noise). We tested whether this would cause subjects to learn specific movements that minimized the noise and indeed found that subjects learned to make movements that were less affected by noise. Subjects learned to avoid movement dimensions that were responsible for task-specific noise. Moreover, subjects who trained with the additional noise generalized better to unseen movements. Our results thus suggest that motor noise is an important factor that can guide how the CNS forms control policies and that visuomotor noise can thus be used as a tool to shape motor learning.

In this study, we were not trying to reproduce “physiological noise” in the sense that it exists in the motor system. Instead, we tested whether the CNS is able to learn to reduce noise in a broader sense. Our results indirectly support the notion that the CNS cares about reducing noise not only when its source is physiological and show that this is even the case when people learn a motor task that is in a previously unexperienced geometry.

To further highlight this result, it is important to make the distinction between minimizing noise and minimizing overall error in the present study. The goal of the task was to hold the cursor in the target for 0.5 s. Thus we can assume that the main measure of error was the distance between the cursor and the center of the target. This error can be broken into two components, systematic error, or the distance between the mean cursor position and the center of the target, and random error, or the distance between the cursor and its mean position due to random fluctuations. To successfully complete the task, the sum of these components had to be less than the target radius; however, there were no restrictions on each component independently. The noise paradigm here creates additional random error but does not require that participants subsequently reduce random error to reduce overall error. To complete the task accurately in the presence of noise, one could have reduced either or both of the components of error by choosing movement policies that result in low noise and/or by aiming closer to the center of the target. An important factor for the interpretation of the present results is that these possibilities were realistic for participants. Indeed, if they did not reduce the level of noise from the baseline, they would have only needed to reduce their systematic error by an additional 0.18 cm in order to achieve the same final total error. Given that the baseline systematic error was 0.55 cm, there was ample opportunity for subjects to become proficient at the task without choosing low-noise postures.

Our work argues that the CNS learns to choose movements that are less affected by motor noise. This per se is far from a novel concept, as many previous studies have shown that the movements we make are the ones that lead to low noise or high noise tolerance (van Beers et al. 2004; Berniker et al. 2013; Cohen and Sternad 2009; Harris and Wolpert 1998; Latash et al. 2002; Osu et al. 2004; Scholz and Schöner 1999; Sternad et al. 2011; Todorov and Jordan 2002). However, our approach provides particularly direct evidence for this theory. And while others have shown that noise can be manipulated to influence the movements people make (Chu et al. 2013; Hasson et al. 2016; Manley et al. 2014), we show that people can actively learn to reduce noise when performing a motor task in a novel geometry. For the two experimental groups, the only difference in the task was the added noise. If, in choosing movements, the CNS only acted to minimize effort or some quality of movement other than noise, we would predict no systematic difference between the movements learned by the two groups. Instead, we found a stark and systematic difference between the movements of the two groups, suggesting that noise minimization can drive motor learning.

Nonetheless, we cannot rule out the possibility that there are other qualities of movement that the CNS may be trying to optimize. In fact, because we found that subjects did not perfectly converge to the desired solution, there are likely factors besides task-specific noise that are important in choosing movement patterns. Previous studies speculate that the motor system may try to optimize effort (Nakano et al. 1999; Ranganathan et al. 2013; Soechting et al. 1995) or even a combination of effort and variability (O'Sullivan et al. 2009). For the present experiment, and, arguably, for any experiment, there is no method for directly measuring effort. As the movements here were relatively small, effort may not have been a primary concern for subjects. However, the general noise paradigm presented here in a more effort-intensive task coupled with measures of metabolic cost would offer a simple means for developing a more complete understanding of the relationship between minimizing variability and effort when learning to make high-dimensional movements. Specifically, one could completely dissociate the two, by making the minimum variance control policy be orthogonal to the minimum effort control policy. Additionally, there are many other costs, such as smoothness, stability, or predictability, that could and probably do play a role in the movements people choose (Burdet et al. 2006; Flash and Hogan 1985; Nasseroleslami et al. 2014; Soechting and Lacquaniti 1981; Sternad et al. 2014). Nevertheless, the results here confirm that, regardless of other factors, the CNS can use noise alone as a driving force for learning movement coordination patterns.

When we designed our experiment we wondered whether subjects would even be able to exhibit proper motor learning in the presence of high levels of noise. After all, high levels of feedback noise lead to less precise estimates of state. This should make the formation of an internal model, which many assume that the brain uses for motor control (Kawato 1999; Wolpert et al. 1998), more difficult. However, we not only found that subjects exposed to noise learned quickly, they even generalized to movements without visual feedback better than the control group. This suggests that the brain can learn its control policies efficiently, even in the presence of high feedback noise.

The fact that the subjects who were exposed to noise generalized to movements without visual feedback better was particularly surprising. Statistically, they have actually obtained worse feedback information than control subjects, which, in a Bayesian system, e.g., a Kalman filter, which has become a popular framework for how the brain handles the uncertainty in sensory feedback, should lead to slower learning (Burge et al. 2008; Izawa and Shadmehr 2008; Korenberg and Ghahramani 2002). However, the noise also makes subjects uncertain about their current state, which places a greater emphasis on quickly forming a more accurate control policy (Wei and Körding 2010), which, because of the novelty of our motor task, participants could not have formed before the experiment. As such, our finding could be interpreted as an interplay between the quality of feedback and the necessity to have an accurate control policy. Alternatively, it may be seen as the reflection of a broad set of psychological factors that are increasingly getting attention (Galea et al. 2015; Taylor and Ivry 2012). Furthermore, it could be a result of increased exploration of the space of hand movements or a result of altered training, as the task was more difficult for subjects in the noise group. While we cannot currently confirm the accuracy of these hypotheses, the ability to improve generalization is important, as generalization is a chief objective in any form of training, including those practiced in clinical interventions.

Determining how the CNS learns to control the many dimensions of body motion is a central objective in understanding the neural control of movement. It not only matters for broadening our fundamental knowledge of motor behavior but also can be beneficial in improving motor learning within a rehabilitation context. Our findings suggest the possibility to “design” and exploit artificial visuomotor noise as a tool for shaping and enhancing learning. Learning to produce appropriate neural signals (Carmena et al. 2003; Diez et al. 2013; Radhakrishnan et al. 2008; Wolpaw et al. 2000;) or body motions (Casadio et al. 2010; Dewald and Beer 2001; Ellis et al. 2005; Farshchiansadegh et al. 2014; Raineteau and Schwab 2001; Taub et al. 1999; Thorp et al. 2016), whether in the context of learning to use a brain-machine interface after paralysis or relearning coordination after a stroke, is often difficult when many degrees of freedom are involved. The work here has the direct potential both to lessen this burden and to teach specific coordination patterns that can improve clinical rehabilitation outcomes. Overall, our work shows that noise has a direct effect on how the CNS organizes high-dimensional movements and that it can be a powerful tool for shaping the learning of such movements.

GRANTS

The work was funded by National Institutes of Health Grants R01 HD-072080, T32 HD-07418, F31 NS-096878, and NIDRR H133E120010.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

E.B.T. and F.A.M.-I. conceived and designed research; E.B.T. performed experiments; E.B.T. analyzed data; E.B.T., K.P.K., and F.A.M.-I. interpreted results of experiments; E.B.T. prepared figures; E.B.T. drafted manuscript; E.B.T., K.P.K., and F.A.M.-I. edited and revised manuscript; E.B.T., K.P.K., and F.A.M.-I. approved final version of manuscript.