The Caudate Nucleus Mediates Learning of Stimulus–Control State Associations

Abstract

A longstanding dichotomy in cognitive psychology and neuroscience pits controlled, top-down driven behavior against associative, bottom-up driven behavior, where cognitive control processes allow us to override well-learned stimulus–response (S–R) associations. By contrast, some previous studies have raised the intriguing possibility of an integration between associative and controlled processing in the form of stimulus–control state (S–C) associations, the learned linkage of specific stimuli to particular control states, such as high attentional selectivity. The neural machinery mediating S–C learning remains poorly understood, however. Here, we combined human functional magnetic resonance imaging (fMRI) with a previously developed Stroop protocol that allowed us to dissociate reductions in Stroop interference based on S–R learning from those based on S–C learning. We modeled subjects' acquisition of S–C and S–R associations using an associative learning model and then used trial-by-trial S–C and S–R prediction error (PE) estimates in model-based behavioral and fMRI analyses. We found that PE estimates derived from S–C and S–R associations accounted for the reductions in behavioral Stroop interference effects in the S–C and S–R learning conditions, respectively. Moreover, model-based fMRI analyses identified the caudate nucleus as the key structure involved in selectively updating stimulus–control state associations. Complementary analyses also revealed a greater reliance on parietal cortex when using the learned S–R versus S–C associations to minimize Stroop interference. These results support the emerging view that generalizable control states can become associated with specific bottom-up cues, and they place the caudate nucleus of the dorsal striatum at the center of the neural stimulus–control learning machinery.

SIGNIFICANCE STATEMENT Previous behavioral studies have demonstrated that control states, for instance, heightened attentional selectivity, can become directly associated with, and subsequently retrieved by, particular stimuli, thus breaking down the traditional dichotomy between top-down and bottom-up driven behavior. However, the neural mechanisms underlying this type of stimulus–control learning remain poorly understood. We therefore combined noninvasive human neuroimaging with a task that allowed us to dissociate the acquisition of stimulus–control associations from that of stimulus–response associations. The results revealed the caudate nucleus as the key brain structure involved in selectively driving stimulus–control learning. These data represent the first identification of the neural mechanisms of stimulus-specific control associations, and they significantly extend current conceptions of the type of learning processes mediated by the caudate.

Introduction

“Cognitive control” describes a collection of mechanisms that coordinate our thoughts and actions in line with internal goals (Miller and Cohen, 2001). Traditionally, control is conceptualized in juxtaposition to associative processing, because it allows us to override well-learned behaviors to produce responses that are more suitable to the current context (Ach, 1910; Schneider and Shiffrin, 1977; Norman and Shallice, 1986; Cohen et al., 1990). For instance, the classic Stroop task requires subjects to name the ink color of color words (Stroop, 1935; MacLeod, 1991), thus pitting a temporary instructed goal (color naming) against an overlearned behavior (word reading). Slowed responses on incongruent trials (e.g., the word “RED” printed in blue ink) compared to congruent trials (e.g., “RED” in red) reflect the difficulty of overriding the habitual word-reading process. Running into such difficulty, in turn, is thought to elicit a strategic upregulation in control, enhancing the top-down override of the word-reading associations triggered by the bottom-up stimulus (Botvinick et al., 2001). However, this historical dichotomy of controlled versus memory-guided responding ignores the fact that context-sensitive application of cognitive control requires one to associate particular situations or stimuli with appropriate control states. Thus, cognitive control itself must rely on learning (Braver and Cohen, 2000; Botvinicket al., 2001; Frank et al., 2001; Egner, 2014).

Accordingly, previous behavioral work has demonstrated that attentional control states can be directly associated with, and subsequently retrieved by, particular bottom-up stimuli or contextual cues (Crump et al., 2006; Spapé and Hommel, 2008; Crump and Milliken, 2009; Crump and Logan, 2010; Cosman and Vecera, 2013). Here, rather than having to experience performance difficulty to strategically adjust controlled processing in response to that difficulty, features of the stimulus itself appear to directly trigger the retrieval of the appropriate control state. This type of bottom-up priming of control states therefore has the merit of combining the speed of “automatic” processing with the flexibility and generalizability of controlled processing (Egner, 2014). The neural mechanisms mediating this integration of bottom-up and top-down processing are presently not well understood, however. The extant neuroimaging studies interrogating this type of control learning have investigated the linking of spatial contexts (stimulus location) or temporal contexts (trial type history) to varying control demands (King et al., 2012; Jiang et al., 2015a,b). However, no study to date has examined the neural mechanisms underlying stimulus–control (S–C) learning—the acquisition of associations between specific stimuli and appropriate control states—and assessed how these mechanisms may differ from classic stimulus–response (S–R) learning.

The present study pursued this goal by adapting a recently developed experimental approach (Bugg et al., 2011) that allowed us to dissociate S–C learning from S–R learning in the context of a single task (see Materials and Methods, Experimental rationale). We combined this protocol with functional magnetic resonance imaging (fMRI) in healthy human participants to isolate the neural mechanisms of S–C learning. To this end, we used an associative learning algorithm (Sutton and Barto, 1998) to model subjects' learning of S–C and S–R associations. After modeling each individual subject's learning, we then used the trialwise S–C and S–R prediction error (PE) estimates in model-based fMRI analyses to identify brain regions that selectively mediate the acquisition of stimulus–control state associations. To preview the results, we found that the caudate nucleus is the key structure for associating stimuli with appropriate attentional control states (but not with specific responses).

Materials and Methods

Experimental rationale.

Excitement about the possibility of S–C associations first arose from the demonstration of an “item-specific proportion congruency” (ISPC) effect in the Stroop task (Jacoby et al., 2003). While keeping the overall proportion of congruent versus incongruent trials [proportion congruency (PC)] at 50%, the authors manipulated the frequency with which the task-irrelevant stimulus feature (i.e., the color words) appeared as congruent or incongruent stimuli. In other words, the PC was manipulated at the stimulus/item level. Thus, particular color words could be either frequently incongruent (e.g., the word “RED” is paired with green ink 75% of the time) or rarely incongruent (e.g., the word “BLUE” is paired with blue ink 75% of the time). The key finding was that Stroop interference [incongruent vs congruent trial response time (RT)] was attenuated in the frequently incongruent items compared to the rarely incongruent ones (Jacoby et al., 2003). While this finding could in theory be an expression of S–C learning, whereby frequently incongruent items become associated with a stronger attentional focus on ink color (Jacoby et al., 2003), it has subsequently been shown that this modulation of Stroop interference was instead an expression of S–R learning: In reference to the above example, subjects simply learned to associate the word “RED” with a “green” response (Schmidt and Besner, 2008).

Importantly, Bugg et al. (2011) introduced a novel variation on the ISPC design that deconfounds the cuing of PC from the cuing of the correct response. Specifically, their design contrasts an S–R learning condition, where the source of PC cuing is the task-irrelevant stimulus feature [as in the study by Jacoby et al. (2003)], with an S–C learning condition, where it is the task-relevant feature that cues PC. The rationale is that when the task-irrelevant feature is associated with a biased PC (e.g., signaling 75% congruent stimuli), this is accompanied by a corresponding biased signaling of the correct response. However, when the task-relevant feature is associated with a biased PC, this does not alter the association between that stimulus feature and the correct response, because the task-relevant stimulus feature is always associated with the correct response, regardless of whether it is more frequently accompanied by a congruent or an incongruent task-irrelevant feature. Thus, any reduction in Stroop interference for frequently incongruent as compared to rarely incongruent stimuli where the task-relevant feature cues PC cannot be driven by S–R associations and therefore is attributable to S–C learning. Using this design, Bugg et al. (2011) successfully demonstrated an ISPC pattern that was driven by S–C learning.

To investigate the neural mechanism associated with the acquisition of stimulus–control state associations, we here adapted this protocol to a face–name Stroop task and combined it with fMRI. Participants had to indicate the identity of famous actors' faces via button press while ignoring congruent or incongruent names written across the faces (Fig. 1). Unbeknownst to the participants, in one condition it was the task-irrelevant feature (names) that predicted congruency (S–R learning condition; Fig. 1, Table 1), whereas in another condition, it was the task-relevant feature (faces) that was predictive of congruency (S–C learning condition; Fig. 1, Table 2). By contrasting S–C and S–R learning conditions, we aimed to reveal the neural substrates that selectively support the linking of specific stimuli with optimal control states.

Figure 1.

Task design and stimuli. Example of frequently incongruent and rarely incongruent stimuli used in the face–name Stroop task. In the S–C learning condition, targets (face stimuli) are predictive of proportion congruency, whereas in the S–R learning condition, distracters (names) are predictive of proportion congruency and responses. See Tables 1 and 2 for the exact trial numbers for each stimulus. Note that these images are for illustration purpose only and are not the exact same ones used in the experiment (see Materials and Methods). The images used in this example are work in the public domain; for details, see https://commons.wikimedia.org/wiki/File:George.Clooneywiki1.jpg, https://commons.wikimedia.org/wiki/File:Leonardo_DiCaprio_June_2014.jpg, https://commons.wikimedia.org/wiki/File:Matt_D a m o n _ T I F F _ 2 0 1 5 . j p g, and https://commons.wikimedia.org/wiki/File:Tom_Hanks_2014.jpg.

Table 1.

Trial numbers for each face–name stimulus compound in the stimulus–response learning condition

	Name 5	Name 6	Name 7	Name 8	p (incongruent|facej)
Face 5	63	30	3	30	0.5
Face 6	9	21	9	3	0.5
Face 7	3	30	63	30	0.5
Face 8	9	3	9	21	0.5
p (incongruent|namei)	0.25	0.75	0.25	0.75

Table 2.

Trial numbers for each face–name stimulus compound in the stimulus–control learning condition

	Face 1	Face 2	Face 3	Face 4	p (incongruent|namei)
Name 1	63	30	3	30	0.5
Name 2	9	21	9	3	0.5
Name 3	3	30	63	30	0.5
Name 4	9	3	9	21	0.5
p (incongruent|facej)	0.25	0.75	0.25	0.75

Participants.

Twenty-eight right-handed volunteers (15 females, 13 males; age, 20–38; mean, 26.7; SD, 5.4) gave written informed consent to participate in this study, which was approved by the Duke University Healthy System Institutional Review Board. All participants had normal or corrected-to-normal vision and reported no history of neurological or psychiatric disorders. Participants were compensated with $30 for their time (1.5 h). Data from six participants were excluded, three due to excessive motion and three due to poor behavioral performance (accuracy <70%).

Stimuli.

The face–name Stroop task used eight well-known male actors' face images and their printed last names (actors Brad Pitt, Tom Cruise, Matt Damon, George Clooney, Tom Hanks, Morgan Freeman, Will Smith, and Leonardo DiCaprio). Names were overlaid on faces to produce compound face–name stimuli, which could be congruent (e.g., Brad Pitt's face paired with a “Pitt” name label) or incongruent (e.g., Brad Pitt's face combined with a “Hanks” name label; Fig. 1). The images were collected from the Internet; cropped to reveal only face, hair, and ear features; turned into gray-scaled images; and resized to 324 × 405 pixels (6.9 × 8.6°). For each participant, each face image was randomly assigned to one of the experimental conditions.

Procedure.

Each participant performed two sets (three consecutive scan runs per set) of a face–name Stroop task in the scanner, with one of the sets comprising the S–C learning condition and the other one the S–R learning condition. Each set involved four actors' faces and their corresponding names. The order in which the two sets/conditions were administered was counterbalanced across participants. For both sets, the participants were instructed to identify, via a button press, the actor whose face (target) was shown in the presented compound stimulus, while ignoring the name (distracter) written on the face. Participants were not informed about any contingency manipulation (Tables 1, 2) in the task. Thus, from the participants' perspective, they performed the same task (identifying actor's faces) throughout all six runs of the experiment, with a change in stimulus set occurring halfway through the experiment.

Each trial started with a central fixation cross shown for 300 ms, followed by a face–name compound stimulus shown for 1000 ms, during which participants had to make a manual button press response to identify the face (i.e., RT limit, 1000 ms). After stimulus offset, a blank screen was shown during a variable intertrial interval randomly drawn from a pseudoexponential distribution of 2.5–3.75 s (mean, 3 s; step size, 250 ms). No trialwise feedback was provided, but the mean accuracy and response time was provided at the end of each run. Participants were encouraged to be as accurate as possible while responding within the response deadline (1000 ms).

Before each set, participants received written instructions about the S–R mapping and were given a short practice block of 40 trials to familiarize themselves with the goal of the task and the assigned S–R mapping. For the first set, the practice block was performed outside of the scanner, and for the second set, the practice block was performed during the anatomical scan in the scanner. During the practice blocks, to facilitate the learning of the assigned S–R mapping, the distracter names were replaced with “XXXX” (i.e., neutral distractors). There were four different actors in each set, which mapped onto four different response buttons. In the scanner, participants held two MR-compatible response boxes, one in each hand. They were instructed to use their index and middle finger of each hand to press the designated buttons.

Design.

In both sets, half of the trials were face–name congruent trials, and half were incongruent trials (Tables 1, 2). With four faces and four names in each set, there were a total of 16 unique face–name combinations per set. However, unbeknownst to the participants, the frequency of each face–name combination was biased, and the type of frequency manipulation differentiated the two sets into S–C learning versus S–R learning conditions (Tables 1, 2; Fig. 1). Specifically, in the S–C learning condition, two of the faces (i.e., the target feature) were associated 75% of the time with incongruent distracters (“frequently incongruent faces”), whereas the other two faces were associated only 25% of the time with incongruent distracters (“rarely incongruent faces”), while none of the names was predictive of proportion congruency. In contrast, in the S–R learning condition, two of the names (i.e., the distracter feature) were associated with incongruent targets 75% of the time (“frequently incongruent names”), whereas the other two names were associated with incongruent targets only 25% of the time (“rarely incongruent names”), while none of the faces were predictive of proportion congruency.

Thus, both conditions involved predictive associations based on PC, with the only difference between the two learning conditions being the source of the PC prediction: in the S–C learning condition, it was the task-relevant feature (i.e., the face) that signaled PC, whereas in the S–R learning condition, it was the task-irrelevant feature (i.e., the name) that signaled PC. This means that in the S–R learning condition, the distracter name was probabilistically tied to both the PC and the correct response (e.g., the distracter name “Pitt” assigned to signal 75% congruency also signaled a 75% chance of being paired with Brad Pitt's face, and thus a “Pitt” response). This should result in faster responses for more probable face–name combinations than less probable ones. Importantly, while this distracter–PC association could in theory facilitate both the linking of distracters with control states (S–C learning) and with response selection (S–R learning), previous studies have shown that behavioral effects in this type of manipulation are driven predominantly by S–R learning, presumably because exploiting direct S–R links is less effortful than retrieving appropriate control states for facilitating performance (Schmidt and Besner, 2008). By contrast, since faces are the task-relevant stimulus feature, a given face is associated with a particular face response 100% of the time, and therefore any performance benefit derived from faces predicting PC in the S–C learning condition cannot be attributed to S–R learning, but instead must derive from the association between the face and the appropriate control state (Bugg et al., 2011). By contrasting behavioral effects and neural substrates between the S–C and S–R learning conditions, we could therefore isolate the mechanism that mediates stimulus-driven control learning.

With this design, the S–R and S–C learning face–name stimulus sets yielded four experimental conditions each: (1) congruent trials for stimuli associated with incongruent distracters 75% of the time (frequently incongruent/congruent), (2) incongruent trials for stimuli associated with incongruent distracters 75% of the time (frequently incongruent/incongruent), (3) congruent trials for stimuli associated with incongruent distracters 25% of the time (rarely incongruent/congruent), and (4) incongruent trials for stimuli associated with incongruent distracters 25% of the time (rarely congruent/incongruent). Behavioral and neural data could therefore be analyzed according to a factorial 2 (learning condition, S–C vs S–R) × 2 (PC association, frequently incongruent vs rarely incongruent) × 2 (current trial congruency, congruent vs incongruent) design. In addition, to explore the time course of the acquisition of the ISPC effect, we divided the response time data into three blocks of 112 trials each and calculated the ISPC effect for each block separately. The data were then analyzed with a 2 (learning condition, S–C vs S–R) × 3 (block) ANOVA.

Importantly, this protocol additionally allowed us to directly model the putative associative learning process taking place for each type of stimulus. To this end, we used a standard reinforcement learning (RL) modeling approach (Sutton and Barto, 1998), which assumes that the participants form associations between the faces (or names) and proportion congruency (and responses, in the S–R learning condition), i.e., the likelihood of encountering a given face or name in the context of a congruent or incongruent trial. The strength of these associations is updated as a function of the difference between expected (based on previous co-occurrence) and observed congruency, i.e., a prediction error (PE). Thus, if a participant had formed an expectation of a specific face predicting a congruent trial and this prediction is violated (that face occurs in the context of an incongruent trial), the prediction is updated, in this case by reducing the expectation that this face would occur in the context of a congruent trial in the future. The degree to which prediction errors update associations is a function of the participant's learning rate, which is fit by the associative learning model, as described below. Therefore, in line with a large prior literature on RL (Seymour et al., 2004; Daw et al., 2006), we used condition-specific PEs to track subjects' learning process and to reveal the underlying neural mechanisms of S–C versus S–R learning.

Modeling of prediction error.

To quantitatively model how the S–C and S–R associations were acquired, one associative learning model was used for each face stimulus and each name label, in each participant. In other words, for each face/name, we extracted all trials in which that face/name was presented to form a new trial vector. In this trial vector, the learning process that associated each face/name to PC was modeled as p_{i + 1} = p_i + α(c_i − p_i), where p_{i + 1} is the predicted congruency (specifically, the predicted probability of encountering an incongruent face–name compound) at trial i + 1, which is given by the predicted congruency in the last trial, p_i, and an updating term based on the previous-trial PE (c_i − p_i), weighted by a learning rate α. For each participant, two αs were used, one for all faces (i.e., the learning rate for forming face–PC associations) and one for all names (i.e., the learning rate for forming name–PC/response associations). Note that the two learning conditions were modeled together. Thus, the learning rates (one for all faces and one for all names) were the same across the S–C and S–R learning conditions in a given participant. To determine the best-fitting αs, we conducted an exhaustive search (α = 0.01 – 0.99; step size, 0.01): for each pair of αs, the trial-by-trial predicted congruency was calculated separately using the associative learning models based on the faces and names, respectively. The unsigned PE of congruency was then used to account for RT in a trial-by-trial fashion using a linear model with a least-square objective function (Jiang et al., 2015a), namely, RT = [|PE_face|, |PE_name|,|1].

We used RT to fit the model parameters based on the hypothesis that if participants used the stimulus–PC and stimulus–response associations to adjust their information processing strategy, this should be reflected in their RT. In model fitting, to account for the main effect of congruency on RT, we modeled congruent and incongruent trials separately. We also maximized the correlation between RT and unsigned PE based on the theoretical prediction that the behavioral ISPC effect is manifested as slower responses when there is a mismatch between the expected and observed congruency (e.g., longer RT in congruent/incongruent trials with a larger unsigned PE). Therefore, as ISPC is a joint effect of congruent and incongruent trials, the best model-fitting parameters were searched while keeping the correlation coefficient across congruent and incongruent trials positive or at least zero. Our modeling approach focuses on independent contributions from PE_face and PE_name to learning, rather than a combined contribution (e.g., using the linear weighted sum to generate a unified PE), based on two key theoretical considerations: First, our design intentionally discourages an integration of face and name features in the service of predicting congruency, as only one of the two stimulus features is ever predictive of congruency at any one time (i.e., names in the S–R learning runs and faces in the S–C learning runs, respectively; Tables 1, 2). Second, and most importantly, the two conditions are of course assumed to foster qualitatively different kinds of associations (S–R vs S–C associations), as supported by a number of previous studies (Schmidt and Besner, 2008; Bugg et al., 2011), and the present study is specifically targeted at differentiating the neural substrates of those different learning strategies. Nonetheless, we conducted a formal model comparison to establish that an independent PE model resulted in a superior fit of behavior than a combined PE model (see below, Alternative model and model comparison).

Following exhaustive search, the learning rates that accounted for the most variance in RT were then used in the associative learning models to generate trial-by-trial PE estimates of congruency in each participant, for the faces (PE_face) and names (PE_name) separately. The trial-by-trial PE values were then used as the parametric modulators in the fMRI analyses, which allowed us to pinpoint neural substrates of learning (prediction updates) to link stimuli to either a heightened attentional control state (PE_face in the S–C learning condition) or to specific responses (PE_name in the S–R learning condition), and to directly contrast the two. Note that because the learning rates were obtained within each participant, this procedure did not violate the assumption of independence of data in the group-level model-based behavioral analysis described below in Model-based behavioral analysis.

Model-based behavioral analysis.

We conducted a model-based behavioral analysis relating the associative model PE parameter to participants' mean RT ISPC effects to corroborate that ISPC effects are adequately captured by this type of associative learning model. Specifically, to obtain an estimate of the amount of variance in RT across all trials that was explained by the trial-by-trial PE derived from faces versus from names in the S–C versus S–R learning conditions, we performed a multiple regression analysis. Here, RT served as the dependent variable, and the trial-by-trial PE_face and PE_name obtained from the above modeling, along with four binary “bottom-up factors,” served as predictor variables, resulting in a total of six regressors for each learning condition. The first binary factor coded for the congruency of the current trial, the second coded for potential repetition of the face, the third coded for potential repetition of the name, and the fourth factor coded for whether both stimulus features repeated or changed simultaneously (complete repetitions/alternations) versus whether only one of the two was repeated from the previous trial (partial repetitions). Although these factors were not of interest here, we included them to account for variance in RT that could be attributable to well-known trial sequence effects (cf. Notebaert and Verguts, 2007), to isolate the variance explained by PE_face and PE_name above and beyond these bottom-up stimulus factors. To be consistent with the model-fitting approach described above, we also constrained the correlation between RT and unsigned PE to be positive. Finally, for the following group-level model-based behavioral analysis, we extracted the standardized coefficients (t) of PE_face and PE_name from the multiple regression analysis.

To test whether the ISPC effects in the S–C learning and S–R learning conditions were in fact driven by the hypothesized face–PC and name–PC/response associations, respectively, we performed four cross-subject correlations: two correlation analyses assessed the relationships between the behavioral ISPC effect (RT) in the S–C learning condition and the regression weights of PE_face and PE_name on RT in that condition, and another two correlation analyses assessed the relationships between the behavioral ISPC effect (RT) in the S–R learning condition and the regression weights of PE_face and PE_name on RT in that condition. If the putative associative learning model offers an appropriate account of these ISPC effects, we would expect a significant correlation between the ISPC effect and the regression weight of PE_face (but not PE_name) in the S–C learning condition as well as a significant correlation between the ISPC effect and the regression weight of PE_name (but not PE_face) in the S–R learning condition.

Alternative model and model comparison.

Despite having a strong theoretical rationale for assuming independent PE contributions in model fitting, we nonetheless performed a formal model comparison between independent PE versus combined PE model variants. Specifically, we performed a model comparison using a threefold cross-validation procedure (Efron, 1983) with respect to whether a model can account for the variance in the trial-by-trial RT. This cross-validation procedure insures against overfitting and allows for an unbiased comparison between models with varying numbers of free parameters (the combined PE models have one additional parameter). Data were divided into three folds. In each cross-validation, two folds of data served as the training set to obtain the optimal free parameters (i.e., learning rates and weights), which were then used to derive the trial-by-trial PE estimates in the remaining fold of data (i.e., the test set). We then calculated the amount of variance in terms of the trial by trial RT in the test set that was accounted for by a particular model. This procedure was repeated until each fold served as the test set once for each model. The extent to which a particular model accounted for a subject's trial RT was quantified by the mean squared error and was taken as (negative) model evidence at the subject level. Individual model evidence was then submitted to a group-level Bayesian model selection analysis to evaluate the likelihood that a specific model generated the data of a randomly chosen subject and to compute the exceedance probability of one model being more likely than any other models (Stephan et al., 2009). The exceedance probability of the independent PE model was 1.00, suggesting that data from 22 out of 22 subjects favored the independent PE model over the combined PE model. As a result, we used the parameters estimated by the independent PE model in the subsequent fMRI analyses.

fMRI acquisition.

Images were acquired on a 3.0T GE MR750 Scanner with an eight-channel head coil. Functional images were acquired with a T2*-weighted gradient-echo EPI sequence of 40 contiguous axial slices (TR, 2000 ms; TE, 28 ms; flip angle, 90°; FoV, 192 × 192 mm; voxel size, 3 × 3 × 3 mm). Anatomical images were acquired with a T1-weighted Spoiled Gradient Echo (SPGR) acquisition in a steady state axial sequence of 120 1-mm-thick slices (TR, 7.668 ms; TE, 2.936 ms; FoV, 256 × 256 mm; voxel size, 1 × 1 × 1 mm). The face–name Stroop task was acquired in six runs (three runs of S–C learning and three runs of S–R learning) of 176 images each.

fMRI preprocessing.

All preprocessing and statistical analysis was performed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) with the exception that spatial normalization to the MNI template was performed using Advanced Normalization Tools (ANTS) (Avants et al., 2011). The first four images of each functional run were discarded, as these were acquired to allow for saturation of the MR signal. Functional data were slice-time and motion corrected. Each participant's EPI volumes were coregistered to that participant's anatomical scan. Each anatomical scan was then normalized to the MNI template brain, and the resulting transformation was applied to each EPI volume to achieve alignment to the common space. Normalized functional data were resampled into 3 × 3 × 3 mm voxel size and were smoothed using an 8 mm Gaussian kernel. The standard general linear model (GLM) approach (Friston et al., 1994) with participants treated as random effects was used to estimate parameter values.

fMRI analyses.

The face–name Stroop task was modeled in the GLM framework using a design matrix with eight event regressors of interests, which modeled the full-factorial design described above [i.e., 2 (learning condition, S–C vs S–R) × 2 (PC association, frequently incongruent vs rarely incongruent) × 2 (current trial congruency, congruent vs incongruent)]. Importantly, we added to each of these conditions four parametric modulators that modeled trial-by-trial congruency prediction error (PE_face and PE_name) and whether the face or name stimuli were repeated from the previous trial. Specifically, the PE regressor modeled trial-to-trial variance in fMRI signal that varied linearly with trial-to-trial variance in the PE as determined by an associative learning model with a subject-specific learning rate (see Modeling of prediction error). The last two modulators were binary regressors included to control for nuisance priming effects due to possible repetition of the same physical face/name from the previous trial. Note that we entered the PE modulator of interest (i.e., PE_face in the S–C learning condition and PE_name in the S–R learning condition) as the last parametric modulator in the GLM model and imposed serial orthogonalization. This approach ensured that we obtained the specific and unique variance accounted for by the PE modulator of interest (Mumford et al., 2015). Finally, error trials were modeled in two separate nuisance regressors (one for each learning condition). All regressors (except for the modulators) were created by convolving a canonical hemodynamic response function (HRF) with an impulse function marking the temporal onset of each event. For the parametric modulators, the magnitude of these regressors modulated the amplitude of an impulse function, which was then convolved with a HRF. In addition, six realignment parameters and six run constants were also included in the GLM to account for participant motion and differences in mean activity across runs. Note that all six runs of fMRI data were modeled and analyzed with a single design matrix to facilitate direct within-subject contrasts between the two learning conditions.

The following within-subject contrasts were performed on the first-level GLM result. As our main question lay with determining distinct neural learning mechanisms underlying the formation of S–C as compared to S–R learning, we focused on model-based fMRI analysis to assess the neural signature of PE in the S–C and S–R learning conditions. To this end, we first report the main effects of PE_face in the S–C learning condition and PE_name in the S–R learning condition separately. Next, to identify regions that selectively mediate stimulus–PC associations in the S–C learning condition but not in the S–R learning condition, and vice versa, we performed a conjunction (Nichols et al., 2005) between the contrast of PE_face > baseline and PE_face > PE_name. This conjunctive analysis thus identified brain regions that were significantly associated with S–C learning, and significantly more so than with S–R learning. For completeness sake, we also performed a conjunction between the contrast of PE_name > baseline and PE_name > PE_face.

Second, we also performed conventional, condition-based contrasts to pinpoint neural substrates of the ISPC effect (i.e., attenuated interference for frequently incongruent items as compared to rarely incongruent items) in the S–C and S–R learning conditions, respectively. This analysis mirrors the behavioral analysis as outlined above. Furthermore, it complements the model-based, learning-focused analysis above by examining the difference in mean activity between trial types across the two learning conditions. The ISPC contrasts were obtained by subtracting the trial congruency effect (incongruent > congruent) in the frequently incongruent items from the trial congruency effect in the rarely incongruent items, which should reveal neural correlates of attenuated interference as a result of learning. We then conducted a direct comparison between the two, to determine regions that were selectively more involved as a result of one type of association than the other. All of these within-subject contrasts were entered into a second-level group analysis where participants were treated as random effects. All group-level results were corrected for multiple comparisons to yield a whole-brain familywise error rate at 0.05 by combining a voxelwise threshold of p < 0.005 with a cluster size threshold determined using SPM8 and the CorrClusTh script (http://www2.warwick.ac.uk/fac/sci/statistics/staff/academic-research/nichols/scripts/spm/spm8/corrclusth.m). The estimated intrinsic smoothness was based on residual images in the analysis. Cluster size thresholds ranged from 67 to 72, depending on the specific contrast.

Results

Behavioral data

Mean RT and accuracy

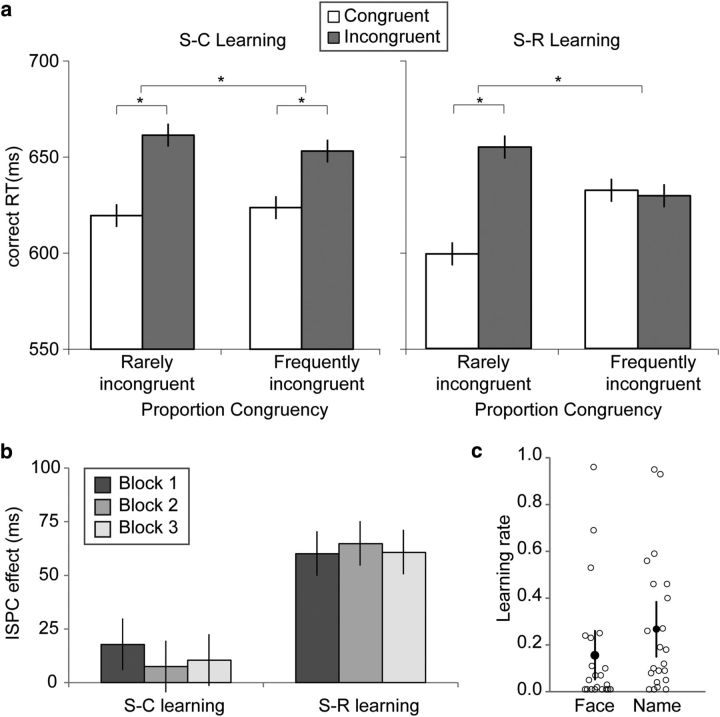
Mean RT and accuracy were analyzed in separate 2 (learning condition, S–C vs S–R) × 2 (PC association, frequently incongruent vs rarely incongruent) × 2 (current trial congruency, congruent vs incongruent) repeated-measures ANOVAs. Only RT data from correct trials were analyzed. As expected, we observed a main effect of congruency (F_{(1, 21)} = 48.04, p < 0.001, η_p = 0.70), as participants responded faster on congruent trials (mean, 621; 95% CI, [597, 649]) than on incongruent trials (mean, 653; 95% CI, [626, 683]; Fig. 2a, Table 3). Also as expected, the congruency effects was modulated by PC, as indicated by a PC by congruency interaction (F_{(1, 21)} = 25.79, p < 0.001, η_p = 0.55), which was due to a significant congruency effect in the rarely incongruent condition (t₍₂₁₎ = 9.45, p < 0.001, Cohen's d = 2.06), accompanied by a lack of a congruency effect in the frequently incongruent condition (t₍₂₁₎ = 1.98, p > 0.05, Cohen's d = 0.43). This finding represents the classic ISPC effect, which, importantly, was significant in both the S–R learning condition (F_(1,21) = 17.77, p < 0.001, η_p = 0.46) and the S–C learning condition (F_(1,21) = 4.44, p = 0.047, η_p = 0.18). In line with previous findings, the relative benefits derived from the predictive associations were greater in the S–R learning condition (ISPC mean, 62; 95% CI, [34, 90]) than in the S–C learning condition (ISPC mean, 13; 95% CI, [1, 25]), as evidenced by a significant three-way interaction effect (F_{(1, 21)} = 8.21, p < 0.01, η_p = 0.28; Fig. 2a, Table 3). No other RT main effects and two-way interactions were significant (F values < 2.32, p values >.05). Finally, the main effect of block as well as the interaction did not approach significance (block, F_(2,42) = 0.06, p > 0.05, η_p = 0.003; interaction, F_(2,42) = 0.22, p > 0.05, η_p = 0.01). This result indicates that in both learning conditions, the ISPC effect is acquired fairly quickly and is stable over time (Fig. 2b), which is in line with previous findings (Jacoby et al., 2003).

Figure 2.

Behavioral results. a, Correct RTs as a function of item-specific proportion congruency and trial congruency in the S–C learning condition (left) and in the S–R learning condition (right). b, Behavioral ISPC effect as a function of block separately for the S–C and S–R learning condition. c, Learning rates for face–PC associations and name–PC/response associations across the S–C and S–R learning conditions. Each open circle represents a single participant. Error bars show mean ± within-subject SEs (Franz and Loftus, 2012).

Table 3.

Response time (ms) and accuracy (%) for S–C and S–R learning conditions

	Learning condition	Rarely incongruent		Frequently incongruent
		Congruent trial	Incongruent trial	Congruent trial	Incongruent trial
Accuracy (%)	S–C	94 [92, 97]	89 [84, 94]	95 [92, 98]	91 [88, 94]
	S–R	96 [95, 98]	91 [88, 95]	95 [91, 97]	93 [91, 95]
Response Time (ms)	S–C	621 [593, 653]	663 [628, 703]	622 [595, 653]	651 [620, 686]
	S–R	604 [584, 626]	662 [636, 691]	639 [612, 668]	635 [611, 659]

Data are means with 95% confidence intervals.

Participants performed the face–name Stroop task with high accuracy (mean, 93; 95% CI, [91, 95]), and they were more accurate on congruent trials (mean, 95; 95% CI, [93, 97]) than on incongruent trials (mean, 91; 95% CI, [88, 94]; main effect of trial congruency, F_{(1, 21)} = 18.33, p < 0.001, η_p = 0.47; Table 3). No other main effects or interactions involving accuracy were significant (F values < 3.59, p values >.05).

In sum, the basic analyses of mean performance data suggest that our task manipulations were successful in producing two varieties of ISPC effect, one driven primarily by S–R learning, and the other one driven by S–C learning. To corroborate this conclusion, we next conducted a set of RL model-based analyses that directly related the associative learning of target (face) and distracter (name) stimuli to the ISPC effects in the two learning conditions.

Model-based analyses

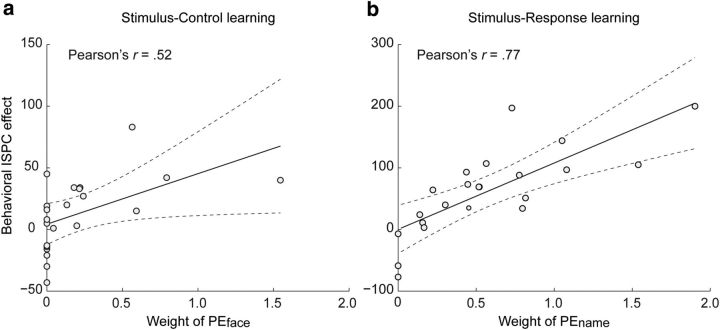
First, to ensure that participants had used face–PC associations and name–PC/response associations in adjusting behavior in a similar fashion, we performed a paired t test on the learning rates (α) for faces and names. The learning rates were indeed highly similar (t₍₂₁₎ = 1.51, p > 0.05; α_face, mean, 0.16, 95% CI, [.06, 0.26]; α_name, mean, 0.27; 95% CI, [.15, 0.39]; Fig. 2c). Next, to corroborate that the ISPC effects we observed in the two learning conditions were in fact the result of learned face–PC associations in the S–C learning condition, and of learned name–PC/response associations in the S–R learning condition, we correlated the regression weights of PE_face and PE_name on RT with the behavioral ISPC effects from both learning conditions across subjects (see Materials and Methods, Model-based behavioral analysis). Figure 3 displays the degree to which participants' behavior was affected by the contingency manipulation (i.e., the behavioral ISPC effect) as a function of the degree to which a participants' trial-by-trial RT can be explained by the putative association learning model (i.e., the weights of PE_face or PE_name, or face–PC association vs name–PC/response association). Participants who successfully formed associations between the faces (or names) and PC/responses and used these associations to optimize their responding would have larger weights of PE_face/PE_name, whereas participants who did not form these associations or used sub-optimal strategies would have zero or near zero weights. As hypothesized, these analyses revealed a significant positive correlation for the behavioral ISPC effect in the S–C learning condition with the regression weight of PE_face (r = 0.52, p < 0.05; Fig. 3a) but not with the regression weight of PE_name (r = −0.05, p > 0.05). Conversely, in the S–R learning condition, the behavioral ISPC effect was highly correlated with the regression weight of PE_name (r = 0.77, p < 0.001; Fig. 3b) but not with the regression weight of PE_face (r = −0.17, p > 0.05). These results validate the modeling of congruency PE using a simple associative learning model. Furthermore, they demonstrate that our task design successfully dissociated the two signaling sources of PC (face vs name) because, as shown in Figure 2a, the ISPC effects in RT in the S–C and S–R conditions are primarily attributed to S–C versus to S–R learning, respectively.

Figure 3.

a, Behavioral dissociation of PE_face and PE_name in the S–C and in the S–R learning conditions. In the S–C learning condition, a large portion of variance in the behavioral ISPC effect across subjects is accounted for by the individual differences in learning of the face–PC associations (i.e., regression weight of PE_face). b, By contrast, in the S–R learning condition, a large portion of variance in the behavioral ISPC effect across subjects is accounted for by the individual differences in learning of the name–PC/response associations (i.e., regression weight of PE_name). Dashed lines indicate the 95% confidence interval for the regression line.

fMRI data

A selective role for the caudate nucleus in the acquisition of stimulus–control state associations

To determine neural mechanisms underlying the acquisition of S–C compared to S–R associations, we derived trial-by-trial estimates of item-level PE of congruency using an associative learning model and entered them as parametric regressors in the GLM (see Material and Methods). Based on our task design and the double dissociation that face–PC associations accounted for S–C learning whereas name–PC/response accounted for S–R learning (Fig. 3), we focused on the PE_face regressor to identify regions whose activity tracks the updating of face–PC associations (i.e., trial-to-trial variation in PE_face) in the S–C learning condition. By contrast, we focused on the PE_name regressor to identify regions whose activity tracks the updating of name–PC/response associations in the S–R learning condition. We found that S–C learning was associated with activation in a prominent cluster in the right head of the caudate nucleus, extending into the inferior frontal gyrus and anterior cingulate cortex (Fig. 4a, Table 4), whose activity scaled positively with PE_face in the S–C learning condition. By contrast, we did not find significant voxel clusters whose activity scaled with PE_name in the S–R learning condition. Critically, to test whether the brain regions implicated in S–C learning were in fact selectively associated with processing prediction error in the context of stimulus–control state associations, we performed a conjunction between a direct contrast of S–C versus S–R learning and the main effect of S–C learning. This analysis identified the right caudate as the exclusive brain structure with a selective, dissociable role in mediating S–C versus S–R learning (Fig. 4b, Table 4). For completeness sake, we also performed the analogous reverse analysis to probe any selective involvement in S–R learning; however, no regions were detected in this analysis. Together, these analyses reveal a selective role for the caudate nucleus in learning to associate the PC-signaling face stimuli with appropriate control states in the S–C learning condition.

Figure 4.

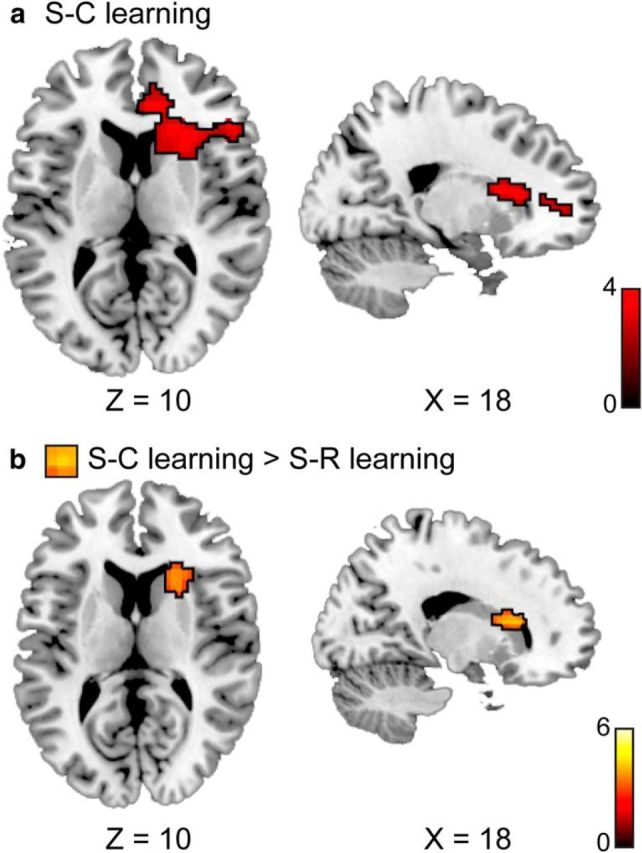
Brain regions associated with model-based prediction error estimates. a, In the S–C learning condition, activity in a cluster encompassing the right caudate nucleus, part of the inferior frontal gyrus, and anterior cingulate cortex appeared to track the updating of face–PC associations. b, The conjunction of a direct contrast between the neural correlates of S–C and S–R learning and the main effect of S–C learning revealed a cluster in the right head of the caudate nucleus, suggesting its distinct role in updating stimulus–control state associations. All maps were whole-brain corrected to α < 0.05.

Table 4.

Activation clusters for the contrasts

	MNI Coordinates			Peak t	No. of voxels	Hemisphere	Region
	x	y	z
Main effect of PEface (S–C learning)	24	17	13	4.42	264	R	Caudate/anterior cingulate/inferior frontal gyrus
Main effect of PEname (S–R learning)	n.s.
PEface > PEname and PEface > baseline	21	14	13	4.27	107	R	Caudate head
ISPC effecta in the S–C learning condition	−27	−76	52	4.57	225	L	Inferior parietal lobule
	−39	2	31	4.69	148	L	Inferior frontal gyrus
	−48	−52	−17	4.44	231	L	Fusiform gyrus/temporal lobe
	0	17	52	3.96	125	L/R	Supplementary motor area
	54	11	46	5.79	91	R	Middle frontal gyrus
	69	−28	−8	4.49	148	R	Middle temporal gyrus
ISPC effect in the S–R learning condition	−33	−43	67	5.26	2069	L	Inferior parietal lobule
	−51	32	22	4.41	117	L	Middle frontal gyrus
	−48	−58	−20	5.49	885	L	Fusiform gyrus
	33	−1	64	4.04	123	R	Middle frontal gyrus
	45	−49	26	5.84	972	R	Fusiform gyrus
ISPC effect S–C learning > S–R learning	n.s.
ISPC effect S–R learning > S–C learning	−51	−37	55	3.62	94	L	Inferior parietal lobe

R, Right; L, left.

^aThe ISPC effect is rarely incongruent (incongruent versus congruent) > frequently incongruent (incongruent versus congruent).

A potential caveat concerning the above conclusion is that, because of our specific paradigm, any selective activation revealed in the above S–C versus S–R contrast could in theory be due to differences in learning associations involving faces versus words rather than due to differences in S–C versus S–R learning. While prima facie a preferential involvement of the caudate in learning face rather than word associations seems unlikely, to probe whether this hypothetical confound may nevertheless contribute to the finding described above, we assessed the observed caudate region's involvement in face or word processing using a term-based meta-analysis tool in Neurosynth (http://neurosynth.org; Yarkoni et al., 2011). Specifically, we generated two forward inference maps [i.e., P(activation|Term)], one based on the term “face” and another one based on the term “word.” We then examined whether voxels in these meta-analysis maps overlapped with the caudate region identified by the S–C versus S–R learning contrast. As suspected, this region contained neither face nor word hotspots from the meta-analytic maps. This suggests that the caudate activation that we attributed to the S–C learning mechanism is very unlikely due to differences in learning associations with faces versus words.

Learned stimulus–response associations are preferentially represented in parietal cortex

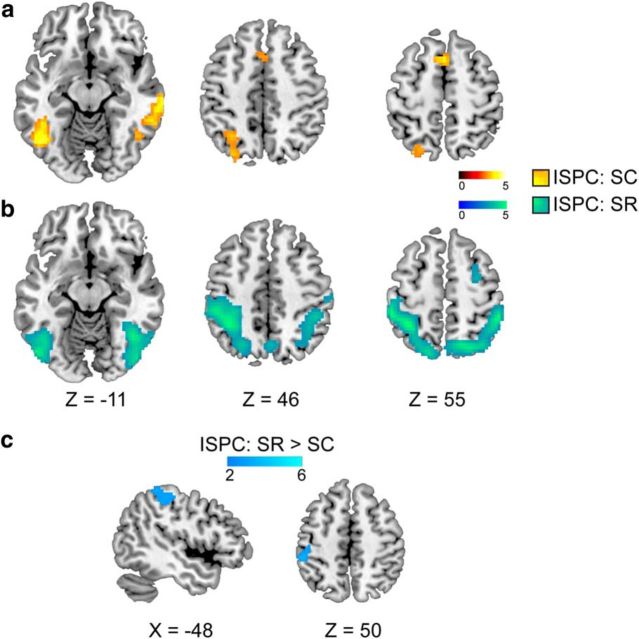
In addition to the model-based characterization of S–C learning mechanisms in the above analysis, we also examined the mean activity difference between trial types in the two learning conditions; that is, to identify regions that exhibited greater activation for attenuated interference as a result of learning (i.e., the ISPC effect in RT), we performed a contrast between the congruency effect (incongruent vs congruent) in the frequently incongruent items and the congruency effect in the rarely incongruent items, separately for the S–C and for the S–R learning conditions. For the S–C learning condition, this type of interaction effect was observed in the frontoparietal network (i.e., middle frontal gyrus, inferior parietal lobe) as well as in the supplementary motor area and in the fusiform gyrus (Fig. 5a, Table 4). For the S–R learning condition, this interaction effect was observed in larger swathes of parietal cortex and fusiform gyrus as well as surrounding temporo-occipital areas (Fig. 5b, Table 4). Comparing the neural substrates of the ISPC effects between the two learning conditions directly, we observed greater activity in the left superior parietal cortex for the S–R learning condition as compared to the S–C learning condition (Fig. 5c, Table 4). However, while the ISPC effect appeared to engage more frontal involvement in the S–C learning condition than in the S–R learning condition (Fig. 5, compare a, b), these frontal activations did not survive statistical correction in the direct contrast. Both the frontal and parietal regions revealed in the above analyses have been reported in previous studies of the ISPC effect (Blais and Bunge, 2010; Grandjean et al., 2013; Xia et al., 2015). These studies, however, were unable to clearly disambiguate regions associated with item-specific stimulus–control learning versus stimulus–response learning. Instead, here we show that greater parietal involvement in minimizing Stroop interference is likely primarily a reflection of the parietal cortex' role in representing S–R associations.

Figure 5.

Brain regions associated with ISPC effects. a, b, Cortical activations associated with attenuated Stroop interference as a result of (a) S–C learning and (b) S–R learning. c, A direct comparison between the two above patterns revealed greater activity in the left superior parietal cortex as a result of using the stimulus–response associations to reduce Stroop interference. All maps were whole-brain corrected to α < 0.05.

Discussion

Previous work in experimental psychology has shown that individual stimuli can become associated with context-appropriate control states (for review, see Bugg, 2012). The neural substrates underlying the learning of stimulus–control state associations (or “item-level” control), however, have remained unknown. To characterize the brain mechanism mediating this phenomenon, we adapted a design by Bugg et al. (2011) that allowed us to obtain two varieties of ISPC effect, one dominated by S–R learning and the other exclusively mediated by S–C learning. We tracked the acquisition of S–C and S–R associations in these conditions using associative learning modeling and used trial-by-trial S–C and S–R PE estimates in model-based fMRI analyses to reveal a selective role for the caudate nucleus of the dorsal striatum in updating stimulus–control state associations. Moreover, using conventional fMRI analyses, it was also found that reduced interference effects observed for frequently incongruent stimuli were associated with more posterior (parietal) involvements in the S–R learning condition.

Our finding that the caudate nucleus appears to be responsible for associating stimuli with control states whereas activity in frontoparietal regions scales with interference reduction based on that learning is consistent with the general notion that cognitive control involves an intimate interplay between (especially frontal) neocortex and the basal ganglia (Frank et al., 2001; Bar-Gad et al., 2003; Chatham et al., 2014). Most relevant to the present findings, prior nonhuman and human studies have implicated the caudate nucleus in aiding goal-directed learning, as opposed to stimulus–response, or habit learning, which is thought to be subserved by the putamen (for review, see Balleine and O'Doherty, 2010; Grahn et al., 2008). The key distinction between these two learning processes in this literature is that goal-directed learning depends on the representations of goal value and of the contingencies between actions and their consequences. Crucially, the present work represents an important conceptual extension of the type of associations the caudate may be involved in forming, because in the context of the current study, the “action” to be learned is not a specific response (e.g., the pressing of a particular button). Rather, it is the retrieval of an item-appropriate control state, most likely in the form of a more selective attentional filter that reduced the impact of incongruent task-irrelevant information on behavior. Therefore, our results suggest that the caudate nucleus plays a role in associating desired outcomes not only with concrete actions, but also with abstract, higher-order control states, which can be generalized across stimulus particulars. For instance, the benefit derived from retrieving a more selective attentional set when encountering a target that has frequently been paired with incongruent distracters is not dependent on the precise nature of the distracters (cf. Bugg et al., 2011; Egner, 2014).

It is also worth noting that the nature of the item-specific control adjustments delineated in the present protocol is “reactive” as opposed to “proactive” or anticipatory (Braver, 2012), as the control state can only be retrieved upon the presentation of a particular stimulus. The observed involvement of the caudate nucleus in acquiring S–C associations in the service of such reactive control extends prior work showing that the caudate is also engaged in predicting control demands proactively to adjust attentional selectivity before the onset of a forthcoming stimulus (Jiang et al., 2015a). Similarly, another previous study (DePasque Swanson and Tricomi, 2014) showed that activity in the caudate not only is modulated by the valence of feedback during learning but is also sensitive to expectations about task difficulty. This result implicates the caudate's unique role in tracking and integrating outcomes along with other contextual information that is pertinent to achieving optimal performance (e.g., difficulty expectation). Our finding of selective caudate involvement in item-level S–C learning thus dovetails with previous studies implicating the caudate in aiding long-term adaption to dynamically changing control demands (McGuire et al., 2014; Jiang et al., 2015a) to confer a central role onto the caudate in a variety of control learning processes.

Subcortically, despite finding a clear dissociation of S–C learning from S–R learning in the caudate nucleus, we did not find a selective involvement of the putamen for S–R learning. The most likely explanation for this null finding is a lack of sensitivity, as the distracters in our S–R learning condition were not 100% predictive of responses (Table 2). It is possible that a deterministic mapping or more extensive training might be required to more robustly drive S–R learning in the putamen (Tricomi et al., 2009; but see Liljeholm et al., 2015).

Cortically, we observed an anterior versus posterior (or frontal vs parietal) gradient of involvement in the ISPC effect as a function of whether that effect represents the result of S–C or S–R learning (although only the parietal activation survived statistical correction in the direct contrast). This finding is congruent with much prior work that has implicated the prefrontal cortex as the primary neocortical source of cognitive control signals (Miller and Cohen, 2001), whereas parietal cortex has been found to facilitate cognitive reconfiguration based on retrieved contextual information (King et al., 2012) as well as in the retrieval of well-learned stimulus–response associations (Sakai et al., 1998). In addition to the selective parietal involvement in S–R learning, the neural ISPC effects for both S–C and S–R learning were largely overlapping within the frontoparietal network (Fig. 5a,b). This is not surprising, because, setting aside their differences in the signaling source of proportion congruency, the two learning conditions in our study were expected to partly recruit the same attentional control processes for conflict detection and resolution as well as similar episodic retrieval mechanisms for learned associations.

In conclusion, the present study revealed a selective role for the caudate nucleus in the acquisition of stimulus–control state associations. This finding is consistent with the broader literature implicating the caudate nucleus in aiding goal-directed learning by forming the contingencies between actions and their consequences. Importantly, we significantly extend this literature by showing that these goal-directed associations can entail links between stimuli and control states, in addition to associations between specific stimuli, motor responses, and outcomes. Our study therefore highlights the close relationship between associative learning and cognitive control processes and adds to an emerging understanding of the underlying neural mechanisms of control learning (King et al., 2012; Jiang et al., 2015a,b).