Abstract
Pitch and timbre are two primary dimensions of auditory perception, but how they are represented in the human brain remains a matter of contention. Some animal studies of auditory cortical processing have suggested modular processing, with different brain regions preferentially coding for pitch or timbre, whereas other studies have suggested a distributed code for different attributes across the same population of neurons. This study tested whether variations in pitch and timbre elicit activity in distinct regions of the human temporal lobes. Listeners were presented with sequences of sounds that varied in either fundamental frequency (eliciting changes in pitch) or spectral centroid (eliciting changes in brightness, an important attribute of timbre), with the degree of pitch or timbre variation in each sequence parametrically manipulated. The BOLD responses from auditory cortex increased with increasing sequence variance along each perceptual dimension. The spatial extent, region, and laterality of the cortical regions most responsive to variations in pitch or timbre at the univariate level of analysis were largely overlapping. However, patterns of activation in response to pitch or timbre variations were discriminable in most subjects at an individual level using multivoxel pattern analysis, suggesting a distributed coding of the two dimensions bilaterally in human auditory cortex.
SIGNIFICANCE STATEMENT Pitch and timbre are two crucial aspects of auditory perception. Pitch governs our perception of musical melodies and harmonies, and conveys both prosodic and (in tone languages) lexical information in speech. Brightness—an aspect of timbre or sound quality—allows us to distinguish different musical instruments and speech sounds. Frequency-mapping studies have revealed tonotopic organization in primary auditory cortex, but the use of pure tones or noise bands has precluded the possibility of dissociating pitch from brightness. Our results suggest a distributed code, with no clear anatomical distinctions between auditory cortical regions responsive to changes in either pitch or timbre, but also reveal a population code that can differentiate between changes in either dimension within the same cortical regions.
Keywords: auditory cortex, fMRI, Heschl's gyrus, perception, pitch, timbre
Introduction
Pitch and timbre play central roles in both speech and music. Pitch allows us to hear intonation in a language and notes in a melody. Timbre allows us to distinguish the vowels and consonants that make up words, as well as the unique sound qualities of different musical instruments. Combinations of pitch and timbre enable us to identify a speaker's voice or a piece of music.
Several studies have been devoted to elucidating the cortical code for pitch; less attention has been paid to timbre. Bendor and Wang (2005) identified pitch-selective neurons in the marmoset cortex near the anterolateral border of primary auditory cortex (A1), the rostral field, and anterolateral and middle lateral nonprimary belt areas. These neurons responded selectively to a specific fundamental frequency (F0, the physical correlate of pitch), independent of the overall spectral content of the sound. Anatomically analogous regions have been identified in anterolateral Heschl's gyrus (HG) of humans that seem particularly responsive to pitch (Gutschalk et al., 2002; Patterson et al., 2002; Penagos et al., 2004; Norman-Haignere et al., 2013), while posterior regions of HG, superior temporal sulcus (STS), and insula have been found to be active in timbre processing (Menon et al., 2002). Other studies have failed to observe distinct, or modular, processing of pitch (Bizley et al., 2009; Hall and Plack, 2009). A combined MEG/EEG study by Gutschalk and Uppenkamp (2011) of cortical processing of pitch and vowels (which have different timbres due to variations in spectral shape) found overlapping responses in anterolateral HG, suggesting a lack of spatial distinction across these dimensions. However, conclusions regarding spatial location using MEG or EEG are necessarily limited, given their generally poor spatial resolution. In a single-unit physiological study, Bizley et al. (2009) used stimuli that varied in F0 (corresponding to pitch), spectral envelope peak (corresponding to brightness, an important dimension of timbre), and spatial location, to identify neurons in the ferret auditory cortex that were selective for one or more of these dimensions. They found a distributed population code in the auditory cortices of ferrets with over two-thirds of the units responding to at least two dimensions, most often, pitch and brightness. In summary, the degree to which cortical representations of pitch and timbre are spatially separated in the auditory cortex remains unclear.
Here we investigated whether variations in pitch and brightness elicit activity in distinct regions of the temporal lobes during a passive listening task, using functional magnetic resonance imaging (fMRI). A similar question was posed by Warren et al. (2005). They found overlapping bilateral regions of activation in the temporal lobes to sounds that varied in either F0 or spectral envelope shape, but found additional activation when spectral envelope shape was varied along with alternations between harmonic and noise stimuli. Based on their results, Warren et al. (2005) suggested that the mid-portion of the right STS contains a specific mechanism for processing spectral envelopes, the acoustic correlate of brightness, which extended beyond the regions responsive to pitch or spectrotemporal fine structure. However, Warren et al. (2005) did not attempt to equate their changes in pitch or spectral shape in terms of perceptual salience, making the direct comparisons difficult to interpret. In our paradigm, inspired by the experimental design of Zatorre and Belin (2001), we generated sound sequences that varied in either F0 (pitch) or spectral peak position (brightness), where the changes in either dimension were equated for perceptual salience. The range of the sequence in the dimension of interest (pitch or brightness) was parametrically varied, and the BOLD responses were measured. Our hypothesis was that regions selective for pitch or brightness should show increases in activation with increases in the variance or range of pitch or timbre within each sequence, and that modular processing of the two dimensions would be reflected by spatially distinct regions of the temporal lobe being selectively responsive to changes in the two dimensions.
Materials and Methods
Participants.
Ten right-handed subjects (mean age, 23.8 years; SD, 2.0; five females and five males) were included in the analysis. An 11th subject was discovered to have been left handed, and his data were subsequently excluded from analysis. All subjects had normal hearing, which was defined as audiometric pure-tone thresholds of 20 dB hearing level or better at octave frequencies between 250 Hz and 8 kHz, and were recruited from the University of Minnesota community. The musical experience of the subjects ranged between 0 and 23 years. Three subjects had musical experience of ≤2 years, while seven subjects had at least 9 years of experience.
Stimuli and procedure.
Tone sequences were 30 s in duration, containing 60 notes each. Each tone had a total duration of 300 ms, including 10 ms raised-cosine onset and offset ramps, and consecutive tones were separated by 200 ms silent gaps. Stimuli were presented binaurally (diotically) at 85 dB SPL. The 30 s tone sequences were interspersed with 15 s of silence to provide a baseline condition. Sequences were generated from scales created with steps that were multiples of the average F0 difference limen (DL) of 1.3% for pitch or the average spectral centroid DL of 4.5% for timbre, as established in an earlier study (Allen and Oxenham, 2014). This approach was used to equate for perceptual salience across the two dimensions. All harmonics of the complex tone up to 10,000 Hz were generated and scaled to produce slopes of 24 dB/octave around the center frequency (CF), or spectral centroid, with no flat bandpass region. The F0 values and spectral centroids in each sequence were geometrically centered around 200 and 900 Hz, respectively (Fig. 1A). In each sequence, the scale step size was selected to be 1, 2, 5, or 10 times the average DL. Each scale consisted of five notes spaced apart by one scale step. The note sequence on each trial was created by randomly selecting notes (with replacement) from the five-note scale, with the constraint that consecutive repeated notes were not permitted. Each level of variation (i.e., step size) was presented once per scan in random order (Fig. 1B). Each scan contained all step sizes across both dimensions. The presentation order of the dimensions and step sizes was generated randomly for each scan and for each subject separately. The scans were 6 min in duration, and a total of six scans were run consecutively for each subject (Fig. 1C).
Figure 1.
Schematic diagrams of the stimuli. A, Spectral representation of the stimuli used in this study (plotted on log–log axes). Changing the F0 value results in changes in the frequencies of the harmonics (represented by the vertical lines). Changing the CF of the filter results in changes in the spectral centroid of the sound and hence in changes in the amplitudes (but not frequencies) of the harmonics. Lighter-colored arrows indicate that shifting in the rightward direction results in a sound with a higher pitch (increase in F0) or a brighter timbre (increase in spectral centroid). B, Tone sequences with small and large step sizes. For the pitch sequences, the y-axis is F0, centered around 200 Hz; for the timbre sequences, the y-axis is spectral centroid, centered around 900 Hz. C, Experimental block design layout. Thirty second pitch- and timbre-varying sequences are indicated in blue and green, respectively. Fifteen second silent gaps for a baseline measure are indicated in gray. The presentation order of step sizes, indicated in white text, was randomized. All possible step sizes across both dimensions were included in each scan.
Subjects listened passively to the stimuli while watching a silent video. MATLAB (MathWorks) and the Psychophysics Toolbox (www.psychtoolbox.org) were used to generate the stimuli and control the experimental procedures. Sounds were presented via MRI-compatible Sensimetrics S14 model earphones with custom filters.
Data acquisition.
The data were acquired on a 3 T Prisma Scanner (Siemens) at the Center for Magnetic Resonance Research (University of Minnesota, Minneapolis, MN). Anatomical T1-weighted images and field maps were acquired. The MPRAGE T1-weighted anatomical image parameters were as follows: TR = 2600 ms; TE = 3.02 ms; matrix size = 256 × 256; 1 mm isotropic voxels. The pulse sequence for the functional scans used slice-accelerated multiband echoplanar imaging (Xu et al., 2013) and sparse temporal acquisition (Hall et al., 1999). The acquisition parameters for the functional scans were as follows: TR = 6000 ms; time of acquisition (TA) = 2000 ms; silent gap = TR − TA = 4000 ms; TE = 30 ms; multiband factor = 2; number of slices = 48; partial Fourier 6/8; matrix size = 96 × 96; 2 mm isotropic voxels. A total of 60 volumes were collected in each of the six scans. Slices were angled in effort to avoid some of the motion from eye movement and covered the majority of the brain. However, for most subjects the top of the parietal and part of the frontal cortices were excluded.
Data analysis.
Data were preprocessed using the Analysis of Functional NeuroImages (AFNI) software package (Cox, 1996) and FSL 5.0.4 (http://fsl.fmrib.ox.ac.uk/). Statistical analyses and visualization were performed with AFNI and SPSS (IBM). Preprocessing included distortion correction using FUGUE in FSL, six-parameter motion correction, spatial smoothing (3 mm FWHM Gaussian blur), and prewhitening.
For each subject, a general linear model (GLM) analysis was performed that included regressors for each experimental condition (i.e., each of the four step sizes for pitch and timbre), six motion parameters, and Legendre polynomials up to the fourth order to account for baseline drift (modeled separately for each run). Each subject's brain was transformed into Montreal Neurological Institute (MNI) space (Mazziotta et al., 1995). Beta weights (regression coefficients) for individual voxels were estimated by the GLM for each condition for each subject, as were contrasts comparing pitch, timbre, and step size conditions, and a contrast comparing all sounds to baseline.
Group-level analyses with subject as a random effect included a one-sample t test performed on the unmasked, unthresholded β weights for each dimension (i.e., separately for pitch and timbre, averaged across all step sizes) using the AFNI function 3dttest++. A paired t test was performed in the same manner, comparing the pitch condition to the timbre condition.
To determine whether BOLD response increased linearly with increasing step size, the Pearson product-moment correlation between BOLD response to step size and a linear trend were computed in each voxel for each subject, separately for pitch and timbre. These correlation coefficients were then Fisher z transformed and submitted to a one-sample t test compared with zero, within a mask created by the union of all subjects' individual regions of interest (iROIs), to test the average correlation for significance across subjects.
For all analyses in AFNI, in light of the inflated false-positive findings by Eklund et al. (2016), smoothness values were obtained using the AFNI 3dFWHMx spherical autocorrelation function (acf) parameters at the individual level and then averaged for the group level. These acf values were then used in the AFNI 3dClustSim function (AFNI 16.1.27) to obtain nearest-neighbor, faces-touching, two-sided cluster thresholds via a Monte Carlo simulation with 10,000 iterations. This determined the probability of clusters of a given size occurring by chance if each voxel has a 1% chance of displaying a false positive. Based on these probabilities, clusters smaller than those that would occur by chance >5% of the time were filtered out of the results to achieve a cluster-level α = 0.05.
Multivoxel pattern analysis (MVPA) was performed using the Princeton MVPA toolbox for MATLAB with the backpropagation classifier algorithm for analysis (http://code.google.com/p/princeton-mvpa-toolbox/). To restrict the number of voxels in our analyses, we added a functionally defined mask, based on our univariate analysis results, containing voxels that were active for a particular subject during the sound conditions (pitch or timbre). We then thresholded this starting voxel set to contain only the 2000 most responsive voxels across both hemispheres for each subject, making the number of voxels in each mask consistent across subjects as well as reducing the number of voxels used for classification, in an attempt to improve classifier performance (De Martino et al., 2008; Schindler et al., 2013). Functional volumes sampled within 5 s of a transition between conditions were eliminated to account for the lag in the hemodynamic response. Functional volumes during rest conditions were also eliminated in order for the classifier to be trained exclusively on the pitch and timbre conditions. Data were z scored, and each run was treated as a separate time course to eliminate any between-run differences caused by baseline shifts. An n − 1 (leave-one-out) cross-validation scheme was used, with six iterations, accounting for the six runs. Each iteration trained a new classifier on five of the six runs and tested it on the remaining run. A feature selection function was used to discard uninformative voxels, with a separate ANOVA run for each iteration.
Results
Whole-brain analyses of pitch and timbre
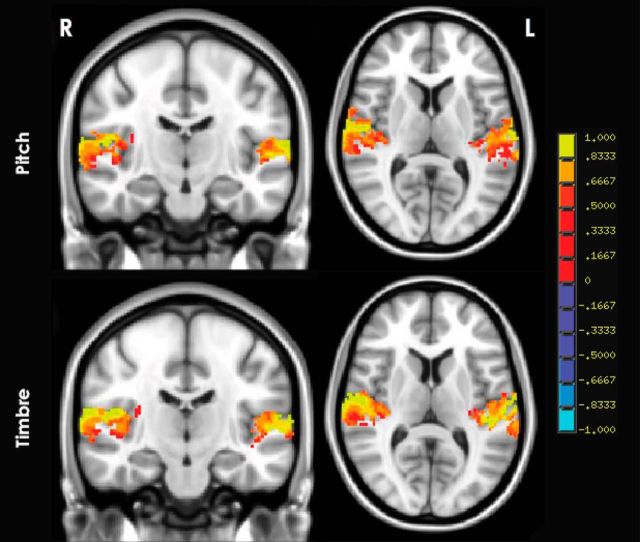
Figure 2 shows BOLD activity at the group level separately for pitch and timbre variation conditions contrasted with silence with single-sample t tests. Similar bilateral activation can be seen, with the strongest activation occurring in and around HG for both dimensions. A paired t test revealed no significant differences (no surviving voxels) between the pitch and timbre conditions at the group level, with a cluster threshold of 1072 microliters (134 voxels). At the individual level, only 2 of the 10 subjects showed any significant differences between the pitch and timbre conditions (pitch-timbre), and neither of them had any significant clusters within the auditory cortex. There was no connection between these two subjects in terms of musicianship, as one had 2 years of musical training, while the other had 16 years.
Figure 2.
Group-level statistical maps of pitch (top) and timbre (bottom), pooled across all step sizes, both contrasted with silence. A cluster in each of right and left superior temporal gyri for pitch [center of mass: right (R), 56, −16, 8; left (L), −53, −22, 9) and timbre (center of mass: R, 56, −18, 9; L, −53, −24, 9) conditions, respectively. Color scale values range from −1 to 1, in units of percentage change relative to baseline. No voxels survive the contrast of pitch and timbre (pitch-timbre).
ROI analysis
Two auditory ROIs in the temporal lobes were functionally defined in individual subjects (iROIs) based on the contrast of all sound conditions versus baseline (silence), one in each hemisphere. The average (±SEM) cluster size of these iROIs was 2507 voxels ± 135.4 [left hemisphere (LH), 2451 ± 171.1; right hemisphere (RH), 2564 ± 217.7]. A two-tailed paired t test revealed no significant difference in cluster size between hemispheres (t(9) = 0.60, p = 0.565).
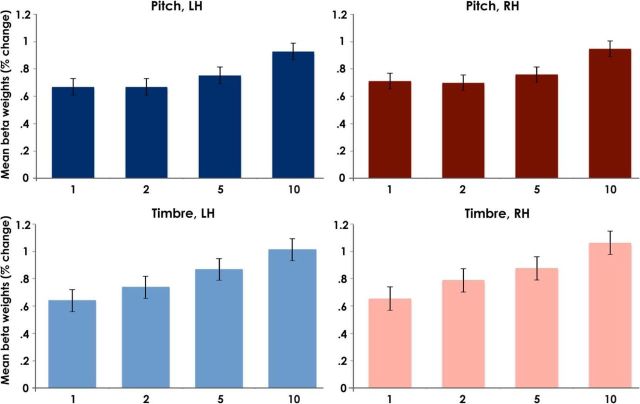
Within each iROI, the subject β weights for acoustical dimension (pitch and timbre) at each step size were averaged across voxels. A repeated-measures 2 × 2 × 4 ANOVA with average BOLD response within each subject's iROIs as the dependent variable and factors of acoustical dimension (pitch and timbre), hemisphere (right and left), and step size (1, 2, 5, and 10 times the DL) showed no main effect of hemisphere (F(1,9) = 1.2, p = 0.3) or dimension (F(1,9) = 2.2, p = 0.172), indicating that the overall level of activation in the ROIs was similar across hemispheres and across the pitch and timbre conditions. There was, however, a main effect of step size (F(3,27) = 14.7, p = 0.0001) as well as a significant linear trend (F(1,9) = 31.5, p = 0.0001), indicating increasing activity with increasing step size. No significant interactions were observed, indicating that the effect of step size was similar in both hemispheres (F(3,27) = 1.3, p = 0.302) and for both dimensions (F(3,27) = 1.2, p = 0.346). Figure 3 depicts the mean β weight for each step size for pitch and timbre within each of the left and right hemisphere ROIs.
Figure 3.
Bar graphs showing mean β weights in the percentage change across all subjects' iROIs at each step size (1, 2, 5, and 10 DL) for pitch (top row) and timbre (bottom row) in each hemisphere (left and right). Error bars indicate ± 1 SEM across subjects.
Correlations between BOLD and step size in pitch and timbre
The main purpose of the experiment was to identify regions that were selectively sensitive to either pitch or timbre variations. We reasoned that such regions would show increased activation with increasing step size (and hence sequence range and variance) in the relevant dimension. Results of the single-sample t test of Fisher z-transformed r coefficients compared with 0 within the union of iROI masks, with a cluster threshold of 464 μl (58 voxels), are shown in Figure 4A. Results are limited to voxels within the MNI template. In line with the linear trends in activation with increasing step size observed in the analysis of iROI means, the heatmap shows that voxels within the union mask were positively correlated with step size in both the pitch and timbre dimensions. In addition, there was no clear spatial separation between the regions most sensitive to pitch changes and those most sensitive to timbre changes, either within or between hemispheres. This point is illustrated further with binary versions of each map in Figure 4A overlaid to show which voxels the two maps have in common (Fig. 4B). Previous studies found pitch to be represented in the anterior-lateral portion of Heschl's gyrus (Patterson et al., 2002; Penagos et al., 2004; Norman-Haignere et al., 2013); however, the large degree of spatial overlap we found across these dimensions does not strongly support the modular processing of pitch or timbre within this region.
Figure 4.
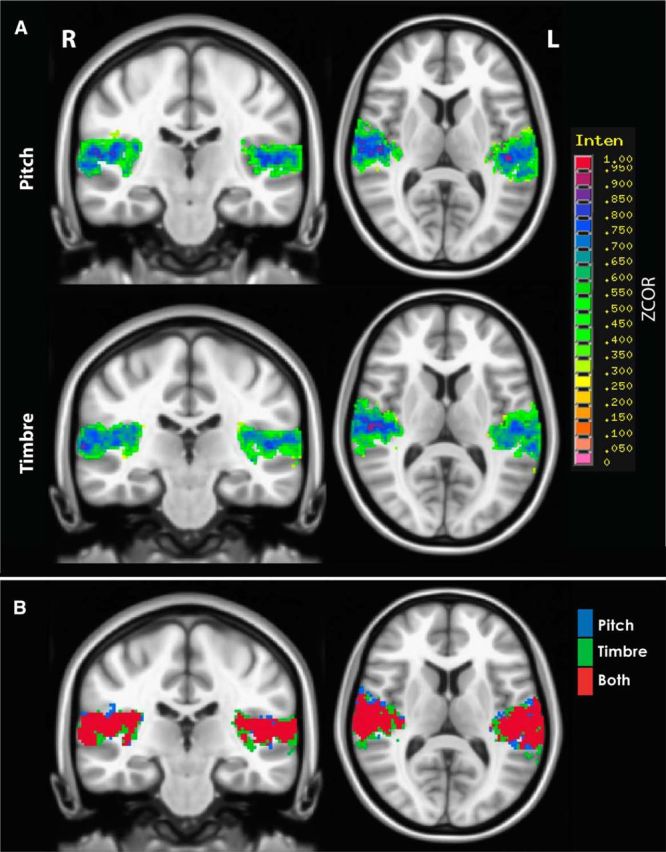
A, B, Group-level correlation coefficient maps. A, Heat maps of positive mean Fisher's z-transformed correlation coefficients (ZCOR) for pitch (top) and timbre (bottom), limited to voxels within a union of all subjects' iROI masks. No significant negative correlations were found. A cluster is shown in each hemisphere for pitch [peak: right (R), 52, −10, 6; left (L), −46, −24, 10] and timbre (peak: R, 48, −20, 12; L, −52, −18, 6) conditions, respectively. B, Maps indicating which voxels the maps in A have in common. The significant correlation coefficients within the pitch map (blue), the significant correlation coefficients within the timbre map (green), and the voxels these two maps have in common (red).
Surface-based analyses
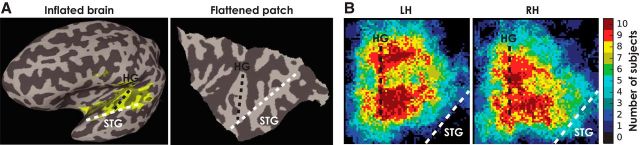
To determine whether there were any significant differences between the spatial distributions of these correlation coefficients, we identified the anterior-lateral and posterior-medial coordinates of HG on a flattened patch of auditory cortex in each hemisphere for each subject (Fig. 5). Right hemisphere coordinate systems were mirrored in the medial-lateral dimension to align with the left hemisphere. Fisher z-transformed correlations coefficients and iROI masks were transformed to the cortical surface (using AFNI 3dVol2Surf), using the “median” sampling option to assign the median of the volume values found along the surface normal to each surface vertex, and were aligned for each subject to this new coordinate system.
Figure 5.
Spatial distribution of the iROI masks in the auditory cortex in each hemisphere with respect to Heschl's gyrus. A, Individual subject's inflated brain (left) with iROI mask and a flattened patch (right) of the auditory cortex. Heschl's gyrus (black dashed line) and superior temporal gyrus (STG; white dashed line) are labeled for this subject. B, Summation of iROI masks across all subjects in the left hemisphere (left) and right hemisphere (right), color coded to indicate the number of subjects for which each surface vertex was inside their iROI.
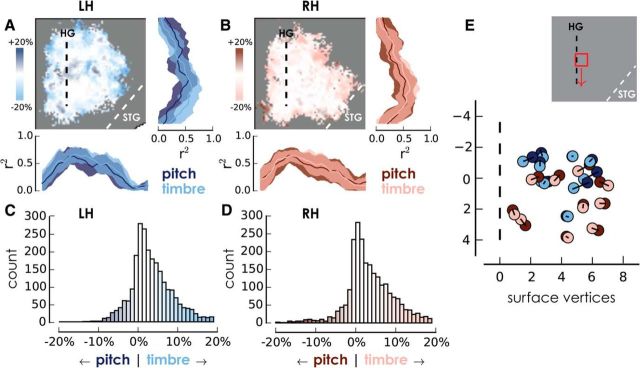
Surface maps of the contrast between pitch and timbre illustrate that there was no systematic difference between representations of the two dimensions in the left (Fig. 6A) or right (Fig. 6B) hemisphere. Contrast was computed as (rpitch2 − rtimbre2)/(rpitch2 + rtimbre2), where each r represents the average (across subjects) correlation between the BOLD signal and step size. Projections of the data onto axes parallel to and orthogonal to HG also reveal nearly complete overlap of pitch and timbre correlations.
Figure 6.
Spatial distribution of correlation coefficients for pitch and timbre. A, B, Left hemisphere (blues) and right hemisphere (reds) contrast maps within the sound mask (vertices inside the auditory ROI of at least five subjects), with darker colors indicating that pitch had a higher correlation coefficient in a given voxel. To the right and bottom are projections of the mean (SD) proportion of variance explained, parallel and perpendicular to Heschl's gyrus. C, D, Distribution of the contrast between variance explained by pitch and timbre step size across all voxels within the mask in each hemisphere. E, Variance-weighted COM for each subject for each dimension in each hemisphere. Black lines connect the center of mass for each condition within a hemisphere for each subject. Inset above demonstrates how small the spatial range is for the COMs. STG, Superior temporal gyrus.
Histograms of pitch/timbre contrast for left (Fig. 6C) and right (Fig. 6D) hemispheres show that strong correlations with timbre were more common than strong correlations with pitch. This finding is also reflected in the steeper slopes for timbre relative to pitch in Figure 3. Therefore, while the spatial distribution of pitch and timbre responses is largely overlapping, the BOLD response shows stronger correlation with timbre scales, despite the fact that the step sizes were perceptually matched to the pitch step sizes.
As a final test of the spatial distribution of responses, a weighted center of mass (COM) was calculated for each subject, weighting each surface vertex by the square of the correlation coefficient (i.e., accounted variance) for either pitch step sizes or timbre step sizes (Fig. 6E). After Bonferroni correction for multiple comparisons, paired t tests indicated that the left hemisphere showed a significant difference in the direction running along (parallel to) HG, going from anterior-lateral to posterior-medial in the cortex [t(9) = −3.9, p = 0.016 (p = 0.004, uncorrected)], but no difference in the direction running across (perpendicular to) HG [t(9) = 2.3, p = 0.18 (p = 0.045, uncorrected)]. The right hemisphere showed no significant differences in either direction [along HG: t(9) = −1.9, p = 0.36 (p = 0.09, uncorrected); across HG: t(9) = 2.4, p = 0.172 (p = 0.043, uncorrected)]. The slight divergence between the location of strong pitch and timbre correlations is also evident in the projection of the pitch/timbre contrast running parallel to HG (Fig. 6A). The weighted COM of timbre responses was more anterior and lateral than pitch responses, but the overall spatial similarity of the pitch and timbre responses and the very small difference between the COMs suggest caution in interpreting this outcome. Overall, the results do not provide support for the idea of a pitch region in the anterior portion of the auditory cortex that is not responsive to changes in other dimensions.
Excitation-pattern analysis
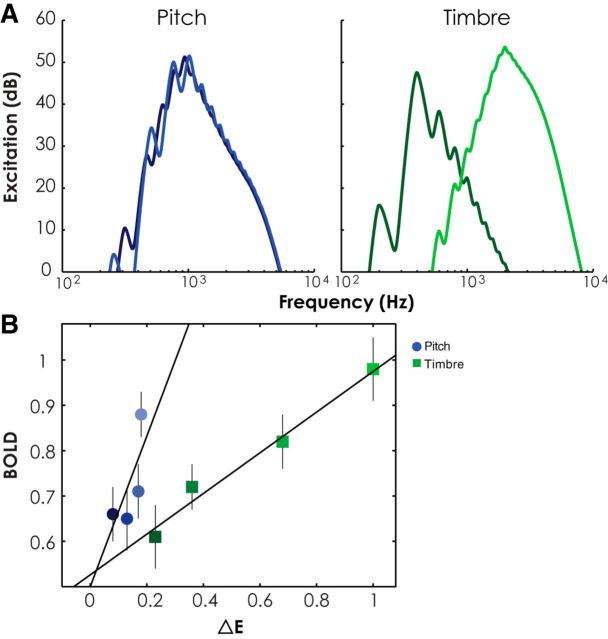
The general similarity in responses to variations in pitch and timbre suggested the possibility of a single representation, perhaps based on the tonotopic organization within the auditory pathways that begins in the cochlea. Changes in both the F0 and the spectral centroid produce changes in the tonotopic representation of sound. It may be that the activation differences measured by our fMRI study reflect tonotopy rather than the extraction of higher-level features, such as pitch or timbre. We tested this hypothesis by deriving the predicted changes in tonotopic representation, based on the differences in the auditory excitation pattern between successive notes produced by the pitch and timbre sequences. The predicted changes in excitation were derived using the recent model of Chen et al. (2011), which itself is based on the earlier model of Moore et al. (1997) (for review, see Moore (2014)). An example of the excitation patterns generated by notes that differ in either F0 or spectral centroid is shown in Figure 7A.
Figure 7.
A, Excitation patterns for the highest and lowest steps of the largest step size (10× DL) for the pitch and timbre conditions, respectively. Lighter colors indicate the higher pitch and brighter timbre, respectively. B, Scatter plot showing mean β weight across all 10 subjects at each step size, averaged across hemispheres as a function of ΔE with a linear regression line for each dimension. Lighter colors indicate larger step sizes. Error bars indicate ±1 SEM across subjects.
The change in excitation from one note to the next (ΔE) was quantified as the sum of the absolute differences in specific loudness across frequency. The average change in excitation (ΔE) between successive notes in the melody for each step size was estimated by running simulations of sequences containing 1000 notes per step size. This enabled us to predict the average changes in excitation at different step sizes for both dimensions.
The predictions show that the changes in excitation are larger and vary more with step size for changes in spectral centroid than for changes in F0 (Fig. 7B). If BOLD responses simply reflected the average changes in excitation based on tonotopy, rather than a response to the features of pitch and timbre (where step sizes were equated for perceptual salience across the two dimensions), then there should be a monotonic relationship between the BOLD response and the predicted excitation change (ΔE). The fact that the data do not fall on a single line, and instead separate based on whether pitch or timbre was varying, suggests that the BOLD responses are not simply a reflection of the tonotopic changes in activation produced by the stimuli.
Multivoxel pattern analysis
Although the univariate analyses do not support the existence of anatomically distinct pitch and timbre processing within auditory cortex, this finding does not rule out the possibility that the patterns of activity across the regions can still code for variations in the two dimensions. As suggested in the single-unit study of ferrets by Bizley et al. (2009), the same population of neurons could be used to code for both dimensions (or more). To explore this possibility, we used MVPA (for procedural details, see Materials and Methods).
Average classifier performance for predicting pitch versus timbre conditions was 61.6% across subjects, which was significantly above chance (50%), based on a two-tailed t test (p = 0.015). For 8 of the 10 subjects, the classifier performed significantly above chance (p < 0.0001) for accurately discriminating pitch from timbre conditions, with performance from individual subject data ranging from 55% to 86% correct. These results suggest that there is a distinguishable difference in activation patterns across voxels for these conditions.
To determine whether our results were strongly affected by the masks used, we compared our functionally defined ROI mask, based on our univariate analysis results, which was cluster thresholded and limited to the 2000 most responsive voxels, to results using other mask types, as follows: (1) an ROI mask not limited to 2000 voxels, but thresholded at p = 0.01 and cluster thresholded (resulting in a greater number of voxels); (2) a mask containing voxels strongly correlated with step size (created with correlation coefficient data from the correlations between BOLD and step size in pitch and timbre section; p = 0.01, cluster thresholded); and (3) a mask containing voxels strongly correlated with step size, intersected with the 2000 voxel mask (further reducing the number of voxels in each subject's mask). Classifier performance results across masks can be seen in Table 1. Paired t tests revealed no significant differences across mask types, suggesting that the differences between voxels included in each mask type did not have a strong effect on classifier performance and that classifier performance remained reasonably consistent within subjects.
Table 1.
Princeton's MVPA toolbox classifier performance (in percent) distinguishing pitch from timbre conditions using four different masks
| Subject | ROI mask thresholded to 2000 voxels | ROI mask | Step size correlated voxel mask intersected with 2000 voxel mask | Step size correlated voxel mask | Mean classifier performance (%) for each subject | SD |
|---|---|---|---|---|---|---|
| 1 | 73 | 70 | 71 | 68 | 70.5 | 2.08 |
| 2 | 45 | 43 | 47 | 38 | 43.25 | 3.86 |
| 3 | 49 | 53 | 50 | 47 | 49.75 | 2.50 |
| 4 | 55 | 52 | 51 | 57 | 53.75 | 2.75 |
| 5 | 65 | 63 | 66 | 64 | 64.5 | 1.29 |
| 6 | 69 | 72 | 69 | 63 | 68.25 | 3.77 |
| 7 | 56 | 56 | 61 | 60 | 58.25 | 2.63 |
| 8 | 86 | 80 | 70 | 74 | 77.5 | 7.00 |
| 9 | 56 | 56 | 55 | 56 | 55.75 | 0.50 |
| 10 | 62 | 66 | 60 | 63 | 62.75 | 2.50 |
| Mean classifier performance (%) for each mask | 61.6 | 61.1 | 60 | 59 | 60.4 | 1.16 |
| SD | 12.17 | 11.11 | 8.91 | 10.34 | 10.3 |
Values in bold indicate best classifier performance for each subject.
Finally, we examined classifier performance when comparing only the largest step sizes. Given that the largest step sizes produce the most salient perceptual changes, these may be the easiest conditions for the classifier to differentiate. A repeated-measures 3 × 2 ANOVA comparing the step sizes (all, 5 and 10, or 10) and mask types (2000 voxel mask or standard mask) showed no main effect of step sizes or mask type and no interactions (Table 2), indicating that including only the step sizes with the greatest perceptual variation did not improve classifier performance, perhaps due to the reduced amount of data when only a subset of step sizes was considered.
Table 2.
Classifier performance comparing all step sizes to step size 5 and 10 only, and 10 only, across two ROI masks (ROI mask thresholded to 2000 voxels, and the standard functional mask)
| Subject | All step sizes |
Step sizes 5 and 10 |
Step size 10 |
|||
|---|---|---|---|---|---|---|
| ROI mask thresholded to 2000 voxels | ROI mask | ROI mask thresholded to 2000 voxels | ROI mask | ROI mask thresholded to 2000 voxels | ROI mask | |
| 1 | 73 | 70 | 71 | 71 | 71 | 71 |
| 2 | 45 | 43 | 49 | 46 | 50 | 42 |
| 3 | 49 | 53 | 49 | 56 | 53 | 54 |
| 4 | 55 | 52 | 59 | 56 | 56 | 53 |
| 5 | 65 | 63 | 64 | 65 | 66 | 64 |
| 6 | 69 | 72 | 69 | 71 | 70 | 70 |
| 7 | 56 | 56 | 59 | 53 | 55 | 58 |
| 8 | 86 | 80 | 88 | 79 | 88 | 80 |
| 9 | 56 | 56 | 54 | 55 | 56 | 49 |
| 10 | 62 | 66 | 60 | 69 | 61 | 68 |
| Mean classifier performance (%) for each mask | 61.6 | 61.1 | 62.2 | 62.1 | 62.6 | 60.9 |
| SD | 12.17 | 11.11 | 11.71 | 10.37 | 11.45 | 11.68 |
Values in bold indicate best classifier performance for each subject.
Discussion
In this study, we compared human cortical processing of the auditory dimensions of pitch and timbre. Conventional univariate analyses revealed no significant differences in terms of the regions dedicated to processing variations in these two dimensions, with the exception of a slight difference in the weighted center of mass of the clusters of voxels whose responses were correlated with step size in the direction parallel to the HG (anterior-lateral to posterior-medial) in the LH. These results provide no evidence for modular and exclusive processing of the two dimensions in separate regions of auditory cortex, at least on the coarse level of analysis available with fMRI.
While previous studies of pitch found active regions in the anterior portion of HG, bilaterally, providing converging evidence that these regions are important for pitch processing, we found broader bilateral regions throughout the auditory cortices that were responsive to pitch as well as timbre variation. It is possible, however, that had we contrasted our periodic stimuli with aperiodic stimuli, such as noise, we would have found elevated activation in anterior regions for pitch and timbre, consistent with dipole locations found by Gutschalk and Uppenkamp (2011) using MEG. Instead, our results focus exclusively on the contrast between pitch and timbre and suggest that the pitch-sensitive regions in the aforementioned studies may not be uniquely dedicated to pitch processing.
Although our univariate results indicate that pitch and timbre processing takes place in common anatomical regions of the auditory cortices, their decodability using MVPA suggests that they may engage distinct circuitries within these regions. In this respect, our results are consistent with the conclusions of the single-unit study in the auditory cortex of ferrets, which also suggested population-based codes for pitch and timbre, with many neurons showing sensitivity to changes in both dimensions (Bizley et al., 2009).
We found evidence supporting our hypothesis that regions selective for pitch or timbre show increases in activation with increases in the size of the range covered within each sequence. In other words, larger variations in either pitch or timbre within the sequences led to larger changes in BOLD in both dimensions, akin to the findings of Zatorre and Belin (2001) for spectral and temporal variations.
It is worth considering how the use of melodies may have affected our results. Our stimulus sets for both pitch and timbre variations were presented in the form of tone sequences that could be perceived as pitch melodies and timbre “melodies.” It has been found that pitch, loudness, and brightness (i.e., timbre) can all be used to identify familiar melodies, which suggests a substrate for detecting and recognizing patterns of sound variations that generalizes beyond pitch (McDermott et al., 2008; Graves et al., 2014). If the recognition of pitch and timbre melodies is subserved by similar cortical circuits, it seems reasonable to expect similar regions of activation. Further, melody processing is considered a higher level of auditory processing, which may be represented in nonprimary auditory cortical regions (Patterson et al., 2002). Thus, it is possible that the regions active in this study include higher-level processing than basic pitch or timbre processing, which might explain the spread of activation along the superior temporal gyri. Contrary to expectations based on higher-level processing, the activation we found was relatively symmetric across hemispheres and covered large regions of Heschl's gyrus; other studies have found limited and more right-lateralized processing of pitch melodies (Zatorre et al., 1994; Griffiths et al., 2001).
In studies of auditory perception, pitch and timbre are often treated as separable dimensions (Fletcher, 1934; Kraus et al., 2009; McDermott et al., 2010). However, several studies have also shown that the two can interact (Krumhansl and Iverson, 1992; Warrier and Zatorre, 2002; Russo and Thompson, 2005; Marozeau and de Cheveigné, 2007). A recent psychoacoustic study showed that pitch and brightness variations interfered with the perception of the other dimension, and that the interference effects were symmetric; in other words, variations in pitch affected the perception of brightness as much as variations in brightness affected pitch perception (Allen and Oxenham, 2014). The finding held for both musically trained and musically naive subjects. The strong overlap in cortical activation of the two dimensions found in the present study may also reflect the perceptual difficulty in separating the two dimensions. Although our study was not designed to investigate potential differences between people with and without extensive musical training, comparing a subset of subjects with the most training (three subjects with 15, 16, and 23 years of training) with a subset of subjects with the least training (three subjects with 0, 1, and 2 years of training) did not reveal any significant differences or clear trends within these groups either in terms of the degree of activation or the correlation with melody range in either dimension.
Finally, one potential limitation of the study is that it involved a passive listening task. It is possible that the results may have been different if subjects had been engaged in a task that involved either pitch or brightness discrimination. Auditory attention has also been found to modulate activity in the superior temporal gyrus (Jäncke et al., 1999). Attention to auditory stimuli has been found to produce stronger activity throughout large areas in the superior temporal cortex, compared with when attention is directed toward visual stimuli (Degerman et al., 2006). When subjects were instructed to discriminate between tones and identify the brighter timbre, Reiterer et al. (2008) found activity in a bilateral network including cingulate and cerebellum, as well as core and belt areas of the auditory cortices. This same network was active when subjects were performing loudness discrimination tasks, again highlighting the existence of overlapping neural networks for processing sound. However, for timbre, Broca's area was also active, resulting in a left hemisphere dominance, highlighting the connection between timbre discrimination and processing of vowels in language. It may be that similar dissociations between pitch and timbre would become apparent in an active version of the task undertaken in this study.
Footnotes
This research was supported by National Institutes of Health Grant R01-DC-005216 and by the Brain Imaging Initiative of the College Liberal Arts, University of Minnesota. We thank Andrea Grant, Ingrid Johnsrude, Michelle Moerel, Juraj Mesik, Zeeman Choo, and Jordan Beim for helpful advice and assistance.
The authors declare no competing financial interests.
References
- Allen EJ, Oxenham AJ (2014) Symmetric interactions and interference between pitch and timbre. J Acoust Soc Am 135:1371–1379. 10.1121/1.4863269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendor D, Wang X (2005) The neuronal representation of pitch in primate auditory cortex. Nature 436:1161–1165. 10.1038/nature03867 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bizley JK, Walker KM, Silverman BW, King AJ, Schnupp JW (2009) Interdependent encoding of pitch, timbre, and spatial location in auditory cortex. J Neurosci 29:2064–2075. 10.1523/JNEUROSCI.4755-08.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z, Hu G, Glasberg BR, Moore BC (2011) A new method of calculating auditory excitation patterns and loudness for steady sounds. Hear Res 282:204–215. 10.1016/j.heares.2011.08.001 [DOI] [PubMed] [Google Scholar]
- Cox RW. (1996) AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res 29:162–173. 10.1006/cbmr.1996.0014 [DOI] [PubMed] [Google Scholar]
- Degerman A, Rinne T, Salmi J, Salonen O, Alho K (2006) Selective attention to sound location or pitch studied with fMRI. Brain Res 1077:123–134. 10.1016/j.brainres.2006.01.025 [DOI] [PubMed] [Google Scholar]
- De Martino F, Valente G, Staeren N, Ashburner J, Goebel R, Formisano E (2008) Combining multivariate voxel selection and support vector machines for mapping and classification of fMRI spatial patterns. Neuroimage 43:44–58. 10.1016/j.neuroimage.2008.06.037 [DOI] [PubMed] [Google Scholar]
- Eklund A, Nichols TE, Knutsson H (2016) Cluster failure: why fMRI inferences for spatial extent have inflated false-positive rates. Proc Natl Acad Sci U S A 113:7900–7905. 10.1073/pnas.1602413113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher H. (1934) Loudness, pitch and the timbre of musical tones and their relation to the intensity, the frequency and the overtone structure. J Acoust Soc Am 6:59–69. 10.1121/1.1915704 [DOI] [Google Scholar]
- Graves J, Micheyl C, Oxenham A (2014) Preferences for melodic contours transcend pitch. J Acoust Soc Am 133:3366 10.1121/1.4805757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths TD, Uppenkamp S, Johnsrude I, Josephs O, Patterson RD (2001) Encoding of the temporal regularity of sound in the human brainstem. Nat Neurosci 4:633–637. 10.1038/88459 [DOI] [PubMed] [Google Scholar]
- Gutschalk A, Uppenkamp S (2011) Sustained responses for pitch and vowels map to similar sites in human auditory cortex. Neuroimage 56:1578–1587. 10.1016/j.neuroimage.2011.02.026 [DOI] [PubMed] [Google Scholar]
- Gutschalk A, Patterson RD, Rupp A, Uppenkamp S, Scherg M (2002) Sustained magnetic fields reveal separate sites for sound level and temporal regularity in human auditory cortex. Neuroimage 15:207–216. 10.1006/nimg.2001.0949 [DOI] [PubMed] [Google Scholar]
- Hall DA, Plack CJ (2009) Pitch processing sites in the human auditory brain. Cereb Cortex 19:576–585. 10.1093/cercor/bhn108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall DA, Haggard MP, Akeroyd MA, Palmer AR, Summerfield AQ, Elliott MR, Gurney EM, Bowtell RW (1999) “Sparse” temporal sampling in auditory fMRI. Hum Brain Mapp 7:213–223. 10.1002/(SICI)1097-0193(1999)7:3%3C213::AID-HBM5%3E3.0.CO;2-N [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jäncke L, Mirzazade S, Shah NJ (1999) Attention modulates activity in the primary and the secondary auditory cortex: a functional magnetic resonance imaging study in human subjects. Neurosci Lett 266:125–128. 10.1016/S0304-3940(99)00288-8 [DOI] [PubMed] [Google Scholar]
- Kraus N, Skoe E, Parbery-Clark A, Ashley R (2009) Experience-induced malleability in neural encoding of pitch, timbre, and timing: implications for language and music. Ann N Y Acad Sci 1169:543–557. 10.1111/j.1749-6632.2009.04549.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krumhansl CL, Iverson P (1992) Perceptual interactions between musical pitch and timbre. J Exp Psychol Hum Percept Perform 18:739–751. 10.1037/0096-1523.18.3.739 [DOI] [PubMed] [Google Scholar]
- Marozeau J, de Cheveigné A (2007) The effect of fundamental frequency on the brightness dimension of timbre. J Acoust Soc Am 121:383–387. 10.1121/1.2384910 [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J (1995) A probabalisitc atlas of the human brain: theory and rationale for its development. Neuroimage 2:89–101. 10.1006/nimg.1995.1012 [DOI] [PubMed] [Google Scholar]
- McDermott JH, Lehr AJ, Oxenham AJ (2008) Is relative pitch specific to pitch? Psychol Sci 19:1263–1271. 10.1111/j.1467-9280.2008.02235.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH, Keebler MV, Micheyl C, Oxenham AJ (2010) Musical intervals and relative pitch: frequency resolution, not interval resolution, is special. J Acoust Soc Am 128:1943–1951. 10.1121/1.3478785 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon V, Levitin DJ, Smith BK, Lembke A, Krasnow BD, Glazer D, Glover GH, McAdams S (2002) Neural correlates of timbre change in harmonic sounds. Neuroimage 17:1742–1754. 10.1006/nimg.2002.1295 [DOI] [PubMed] [Google Scholar]
- Moore BC. (2014) Development and current status of the “Cambridge” loudness models. Trends Hear 18:2331216514550620. 10.1177/2331216514550620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore BCJ, Glasberg BR, Baer T (1997) A model for the prediction of thresholds, loudness, and partial loudness. J Audio Eng Soc 45:224–240. [Google Scholar]
- Norman-Haignere S, Kanwisher N, McDermott JH (2013) Cortical pitch regions in humans respond primarily to resolved harmonics and are located in specific tonotopic regions of anterior auditory cortex. J Neurosci 33:19451–19469. 10.1523/JNEUROSCI.2880-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson RD, Uppenkamp S, Johnsrude IS, Griffiths TD (2002) The processing of temporal pitch and melody information in auditory cortex. Neuron 36:767–776. 10.1016/S0896-6273(02)01060-7 [DOI] [PubMed] [Google Scholar]
- Penagos H, Melcher JR, Oxenham AJ (2004) A neural representation of pitch salience in nonprimary human auditory cortex revealed with functional magnetic resonance imaging. J Neurosci 24:6810–6815. 10.1523/JNEUROSCI.0383-04.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiterer S, Erb M, Grodd W, Wildgruber D (2008) Cerebral processing of timbre and loudness: fMRI evidence for a contribution of Broca's area to basic auditory discrimination. Brain Imaging Behav 2:1–10. 10.1007/s11682-007-9010-3 [DOI] [Google Scholar]
- Russo FA, Thompson WF (2005) An interval size illusion: the influence of timbre on the perceived size of melodic intervals. Percept Psychophys 67:559–568. 10.3758/BF03193514 [DOI] [PubMed] [Google Scholar]
- Schindler A, Herdener M, Bartels A (2013) Coding of melodic gestalt in human auditory cortex. Cereb Cortex 23:2987–2993. 10.1093/cercor/bhs289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren JD, Jennings AR, Griffiths TD (2005) Analysis of the spectral envelope of sounds by the human brain. Neuroimage 24:1052–1057. 10.1016/j.neuroimage.2004.10.031 [DOI] [PubMed] [Google Scholar]
- Warrier CM, Zatorre RJ (2002) Influence of tonal context and timbral variation on perception of pitch. Percept Psychophys 64:198–207. 10.3758/BF03195786 [DOI] [PubMed] [Google Scholar]
- Xu J, Moeller S, Auerbach EJ, Strupp J, Smith SM, Feinberg DA, Yacoub E, Uğurbil K (2013) Evaluation of slice accelerations using multiband echo planar imaging at 3 T. Neuroimage 83:991–1001. 10.1016/j.neuroimage.2013.07.055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatorre RJ, Belin P (2001) Spectral and temporal processing in human auditory cortex. Cereb Cortex 11:946–953. 10.1093/cercor/11.10.946 [DOI] [PubMed] [Google Scholar]
- Zatorre RJ, Evans AC, Meyer E (1994) Neural mechanisms underlying melodic perception and memory for pitch. J Neurosci 14:1908–1919. [DOI] [PMC free article] [PubMed] [Google Scholar]