Sequence Affects the Cyclization of DNA Minicircles

Abstract

Understanding how the sequence of a DNA molecule affects its dynamic properties is a central problem affecting biochemistry and biotechnology. The process of cyclizing short DNA, as a critical step in molecular cloning, lacks a comprehensive picture of the kinetic process containing sequence information. We have elucidated this process by using coarse-grained simulations, enhanced sampling methods, and recent theoretical advances. We are able to identify the types and positions of structural defects during the looping process at a base-pair level. Correlations along a DNA molecule dictate critical sequence positions that can affect the looping rate. Structural defects change the bending elasticity of the DNA molecule from a harmonic to subharmonic potential with respect to bending angles. We explore the subelastic chain as a possible model in loop formation kinetics. A sequence-dependent model is developed to qualitatively predict the relative loop formation time as a function of DNA sequence.

Graphical abstract

The formation of circular DNA is critical to many molecular cloning technologies, in particular, for certain gene therapies.¹ A central question is how the sequence of a DNA molecule affects its various dynamic and structural properties when there are geometric restrictions.² The circularization or looping of short DNA segments^3–5 has drawn considerable experimental attention.^6–9 DNA looping is also a critical step in cellular processes such as gene transcription and expression. Under many circumstances, transcription is regulated by binding a protein to a DNA loop. Interestingly, the DNA loop can be very short (<150bp) and form quickly. A typical example is the Lac Repressor–DNA loop. Thus, studying the looping of short DNA segments^3–5 is central to a variety of processes. Within the 150 base pair (bp) persistence length,¹⁰ unconstrained double-stranded DNA (dsDNA) has been often described by the wormlike chain (WLC) model; however, the cyclization rate of DNA fragments <100 bps is orders magnitude larger than the WLC predictions in experimental studies.^11–14 There are several hypotheses to explain this phenomenon that involve some form of nonlinear elasticity, including forming transient kinks^15,16 (KWLC model), bubbles,¹⁷ and the linear subelastic chain model¹² (LSEC).

Many previous theoretical works have treated DNA as a sequence nonspecific polymer. Thus, a central question, how the sequence of a DNA molecule affects its various dynamic properties, has not been well addressed. Understanding the consequences of coupling mechanical defects such as kinks and bubbles to the kinetics could allow one to manipulate the looping rate by sequence variations. We show that sequence determines possible mechanical geometries that dictate the kinetics of cyclization. We find that experimentally measured DNA looping rates are consistent with locally sublinear elasticity created by specific transient sequence dependent defects. Our theory qualitatively predicts the relative loop formation time as a function of DNA sequence.

Here we first investigate the cyclization process using molecular dynamics simulations with a coarse-grained model. Simulations provide a route to study the dynamic consequences from structural information at the base pair level^18–20 and include the sequence information. Through simulations, we identify the critical sequential positions in the cyclization process. Next, we will use this information to develop a Markov model to predict the looping time for various sequences.

The issue for simulating the cyclization process is the long time scale (up to hours). We consider a sequence-dependent a coarse-grained (CG) model.^21–24 We note that results from this CG model are not strictly representative of real time, but the time elapsed can be considered to scale roughly with the number of integration time steps. In addition, we sample with a biasing potential to further accelerate the simulations. The biased potential was devised to be weak enough to reduce but not eliminate the free-energy barrier to cyclization.

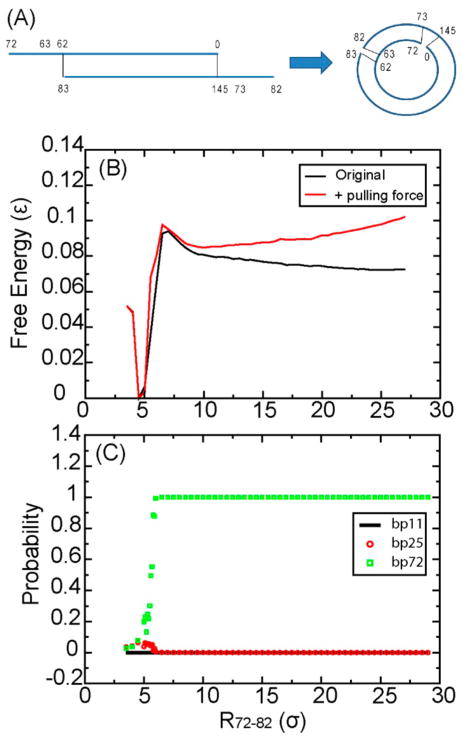
DNA sequence named “TA” (see supplement or ref 14) was chosen to compare with experiments,¹⁴ which provide the looping time of “TA” and four other DNA molecules with the same length of “TA” but with different sequences. This makes it possible for us to compare our analytical predictions directly to the experimental observations. The total length of “TA” is 73bp (63bp +10-nt overhang), considerably shorter than the average persistence length. During cyclization, the two complementary overhangs can form contacts if they are spatially close enough, leading to a stable loop (Figure 1A).

Figure 1.

(A) Illustration of the cyclization process of a dsDNA with total bp =73. The numbers in the Figure show the bp index. Two overhangs are at nucleotides 63–72 in one strand and nt73–82 in its complementary strand. (B) Free-energy profile of DNA TA as a function of the distance between bp72 and bp82, R_72–82. (C) Base pair opening probability of bp11, 25, and 72. ε = 25 kJ/mol. σ = 8.52 Å.

The free-energy profile for DNA cyclization is shown in Figure 1B (black curve). It is clear that there is a modest free-energy barrier during the cyclization process. Because of increasing curvature, the free energy gradually increases when the distance between residues 72 and 82, R_72–82, reduces from 27σ to 6σ. When R_72–82 < 6σ, the free energy decreases sharply because new complementary contacts begin to form and stabilize the system. This can be inferred from the fact that the probability of base-pair opening for bp72 (Figure 1C) quickly decreases from one to close to zero at this region; however, this contact still has ~5% probability to reopen. This is not surprising considering that the nick between bp72 and bp0 should increase the instability (Figure 1A). In contrast, for bp11 that is far away from the nick, the probability of bp opening remains essentially at zero. Interestingly, bp25, which is also far away from the nick, has ~5% probability to open. Those results indicate that the probability of base-pair opening depends on sequence. After the pulling force was assigned, the free-energy barrier still exists in the range from R_72–82 = 6–10σ (Figure 1B, red curve). Thus, although our cyclization simulation is biased, it provides useful information on how a linear-shaped DNA molecule searches dynamically to form a loop.

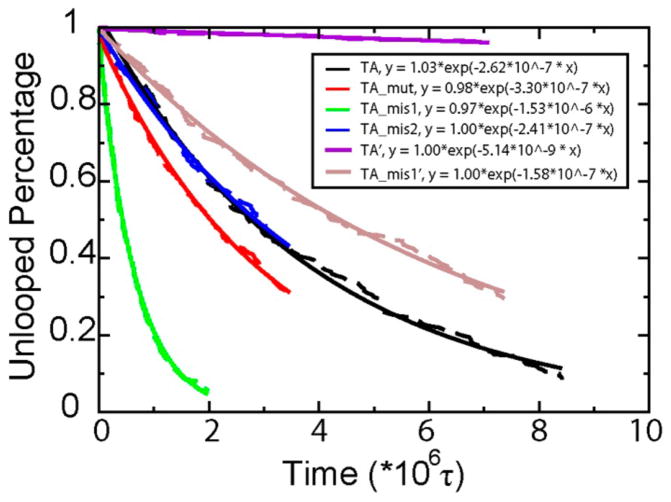
Next, cyclization simulations were performed (see Supporting Information). The percentage of unlooped structures as a function of time is shown in Figure 2. The looping rate can be obtained by fitting the curve to a single exponential function (R > 0.99), which matches with experiments. Structural defects were found to be inevitable in the cyclization process. In all 200 looping trajectories, we found no single successful cyclization trajectory with an absence of kinks or bubbles (Supplemental Figure 1).

Figure 2.

Percentage of unlooped structures as a function of time for four DNA sequences. Raw simulation data are shown in dashed lines, and solid lines fit results with a single exponential function. TA, TA_mut, TA_mis1, and TA_mis2 are results with a biased potential 0.003 ε/σ² = 0.001 kJ/mol/Ų. TA′ and TA_mis1′ are results with a biased potential 0.0015 ε/σ². τ = 200 integration steps.

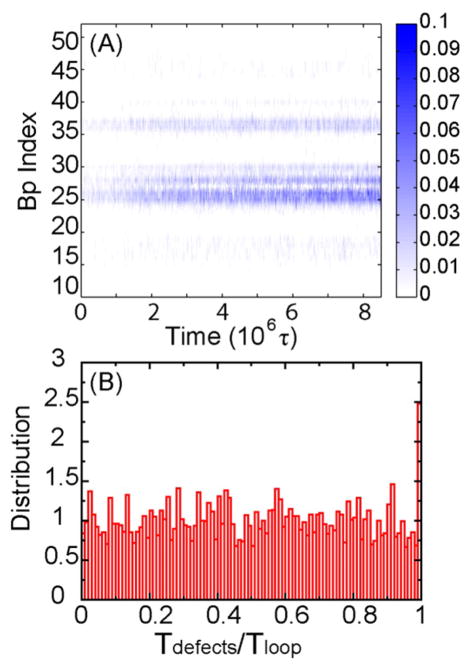
The probability of each base pair of sequence TA to open as a function of time is shown in Figure 3A. We found that the two dominant regions having bp openings are 24–26 and 35–37, while other base pairs are quite stable. This result remains the same regardless of the strength of the external biased potential k = 0.003 or 0.0015 ε/σ². AT tracts are known to be the thermodynamic “weak points” along a dsDNA based on multiple previous studies;^25,26 kinks have been observed to concentrate at TpA base stacks in both simulations^27,28 and experiments.^29–31 Thus, one might assume that bp24–26 and bp35–37 would be weak points; however, bp24–26 is “CCA” and bp35–37 is “GCA”, both thermodynamically more stable than bp15–20 (ATTTT).

Figure 3.

(A) Probability of each base pair of DNA TA to open as a function of time. (B) Distribution of the time for the appearance of structural defects T_defects (bp 24–26) divided by the time of looping T_loop for model sequence TA.

A probable explanation for this phenomenon is that for a highly bent structure, the location of the structural defects is controlled by a positive correlation along a DNA minicircle for bp i and bp i+N/2, in conjunction with its local thermodynamic stability. This positive correlation was also observed in a previous experimental study.³² For the sequence TA, bp0 and bp63 are unstable because there are nicks next to them (Figure 1A). Because of the positive correlation, base pairs near bp36 (= 0 + 73/2) and bp26 (= 63–73/2) would be predicted to be unstable as well.

The relation between the relative time of structural defects appearing, T_defects, and looping T_loop is shown in Figure 3B. When T_defects/T_loop = 1, loop formation happens as structural defects occur, suggesting that those defects are critical in the cyclization process. For a random sequence location bp16–18, the distribution of T_defects/T_loop is near that expected for a random process (Supplemental Figure 2A). In contrast, for bp24–26 and bp35–37, the probability is dramatically increased, T_defects/T_loop ≈ 1, especially for bp24–26 (Figure 3B). Our results demonstrate for our test sequence that bp24–26 and bp35–37 are two critical positions for the cyclization process. Note that when the length of overhang equals zero, the two critical positions merge into one position locating the center of the sequence.

Because bp24–26 and bp35–37 have the highest frequency of bp openings and they are strongly correlated with the final cyclization, we hypothesize that mutation at those places will greatly affect the loop closure rate. Three sequences were designed: TA_mut, mutation from C/G to A/T at bp24–26 and bp35–37; TA_mis1, mutation from CC to AA in one strand of TA at bp24 (so there are 2 bp mismatched); and TA_mis2, similar to TA_mis1 but the mutation is at bp11. For TA_mut, the looping rate is increased 1.5 times compared with TA (Figure 2, red curve). This is because the mutation from stable base pairs C/G to less stable base pairs A/T at bp24–26 and bp35–37 increases the probability to form defects at those positions. In addition, creating bp mismatches at those two places would further accelerate the looping process because a bubble is highly probable. Indeed, TA_mis1 loops 1 order of magnitude faster than TA (Figure 2). To exclude other possible influences brought by bp mismatches, we created similar mismatches at bp11, and its looping rate was found to be about the same as the original TA model sequence. Our results clearly show that in cyclization, position bp(x+N/2) controls the cyclization rate, where x is an unstable position (such as having nicks nearby) and N is the total bp number. This is a geometric result that allows a sharp bend to bring the ends together kinetically in the most thermodynamically economical way.

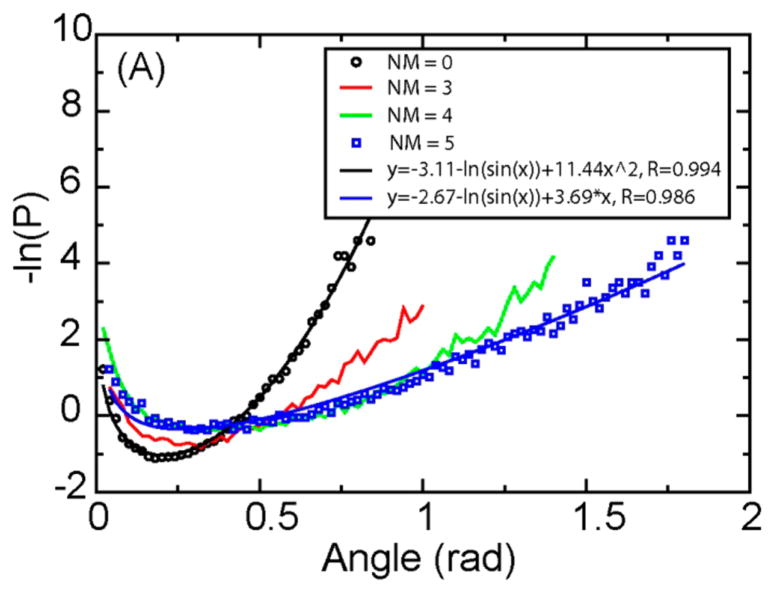
To investigate how structural defects affect the elastic properties of a DNA molecular, we ran simulations for an 18bp dsDNA with different bp mismatches (see Supporting Information). The angular distribution of DNA segments with 7bp length is shown in Figure 4. For NM (number of mismatched bps) = 0, it is widely accepted that free DNA behaves like an elastic rod so the bending energy is approximately E = kθ² with probability P ≈ sin θ*e^−βkθ2. Thus, its potential of mean force −ln(P) should be well fit by y = A − ln(sin θ) + Bθ². Indeed, the fitting quality is very good (R = 0.994), fully supporting the idea that the bending energy varies essentially quadratically with the bending angle. When NM increases, the fitting quality decreases, indicating that the bending energy gradually deviated from the harmonic assumption. When NM = 5, a linear elasticity model y = A − ln(sin θ) + Bθ provides a higher quality fit. We fitted the resulting angular distribution using the form y = A − ln(sin θ) + Bθ^a (Supplemental Figure 3B). When NM = 0, a = 2.1, close to the harmonic model. When NM = 5, a decreases to 1.2, close to the linear model. Our results demonstrate that structural defects can change the elastic properties of a DNA molecule from harmonic to subharmonic (linear) behavior, which greatly favors the cyclization.

Figure 4.

Probabilities of angles between DNA segments, with different numbers of mismatched base pairs (NM). The length of the DNA segment is 7bp. Black line: results using y = A − ln(sin θ) + Bθ²; blue line: results using y = A − ln(sin θ) + Bθ.

A so-called subelastic chain model¹² (LSEC) was proposed to explain the high bendability of certain DNA molecules. LSEC is based on the observation that if a long DNA molecule is divided into small segments ~7bp, the bending energy increases linearly, instead of quadratically, with the bending angle; however, LSEC is an empirical energy function with an unclear mechanistic origin. Our CG simulations show that, a “bare” or unconstrained DNA is well described by the WLC model. Only when the total number of mismatches, NM, is large enough can the elasticity of the DNA be approximately described by the LSEC model. This also probably explains why the WLC model is good enough for studies without considering the magnesium;^33,34 the probability of transient structural defects decreases in the absence of magnesium. LSEC model is powerful when the probability of defects is large enough (large NM); however, moderate NM can cause the elasticity of a DNA molecule to display a behavior between harmonic and linear form (Supplemental Figure 3B). Thus, many conditions such as the concentration of magnesium or the length of an AT track in the circle can affect the validity of the LSEC model.

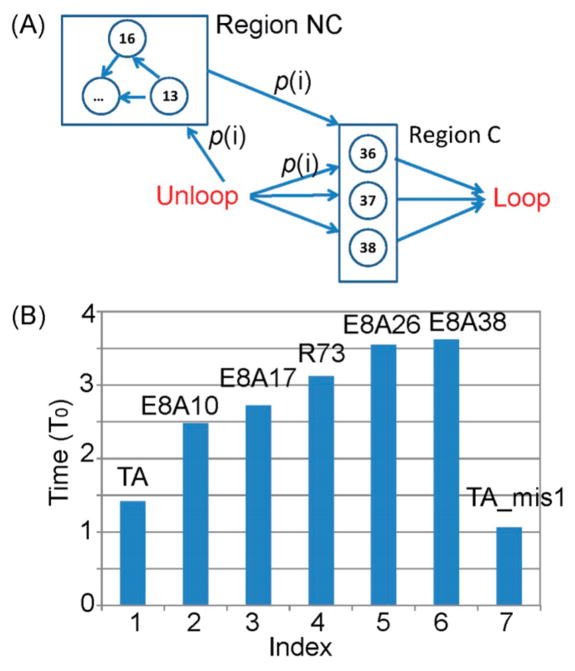
On the basis of the above discussions, a sequence-dependent model (Figure 5A) is proposed to predict the looping time for a given DNA sequence. The sequence positions were divided to two regions: (1) Region C, the critical position to affect the looping time. This region contains the bp index |i − N/2| < δ₁ and |i − (N/2−s)| < δ₁. N is the total bp number, s is the length of overhangs (= 10bp in our simulation), and δ₁ describes the region width. (2) Region NC, this region is adjacent to the region C. If any base pair has defects in the region NC, the local stress will be released by local melting or kinking, and the probability of forming defects in region C actually decreases. In other words, region NC is negatively correlated with region C. This negative correlation has been studied in our previous work.²³ This region includes bp i satisfying δ₁ < |i − N/2| < δ₂, and δ₁ < |i − (N/2 − s)| < δ₂. We take δ₁ = 1 and δ₂ = 5 in this work, but it will not affect the results qualitatively. We neglect all other regions except region N and NC because they have a minor influence on the cyclization time (Figure 2, black and blue curves).

Figure 5.

(A) Markov model to represent the looping process. (B) Prediction on the looping time for different DNA sequences. T₀ is a time unit to match the CG time to real time. The error is <0.01 T_0..

We modeled the looping as a Markov process searching positions that have structural defects. Any base pair i can have a defect with a probability p(i). If i belongs to region C, then the structure will loop immediately. If i belongs to region NC; then, the structure cannot loop and has to wait for the next search until a defect happens in the region C. Normalized p(i) satisfies

$$p(i)={\mathrm{e}}^{-\mathrm{\Delta }G(i-1,i,i+1)/k_{\mathrm{B}}T}/\sum _{i\in C,i\in NC}{\mathrm{e}}^{-\mathrm{\Delta }G(i-1,i,i+1)/k_{\mathrm{B}}T}$$

ΔG(i − 1, i, i + 1) is the free energy of having defects at base pair i, when its neighbor is i − 1 and i + 1. Note that the negative correlation is implied by this normalization process because p(i ∈ NC) increases will lead to p(i ∈ C) decreases. As we have noted before, ΔG can be decomposed as Kirkwood superposition relationship

$$\mathrm{\Delta }G(i-1,i,i+1)=\mathrm{\Delta }G(i-1,i)+\mathrm{\Delta }G(i,i+1)-\mathrm{\Delta }G°(i)$$

The values of ΔG(i−1, i), ΔG(i, i + 1), and ΔG⁰ (i) can be found in our previous work.²³ To reduce the error of estimation in region C, we assume

$$p(i)=max(p(k)),i\in C,k\in C$$

The looping time T is approximated as T = X * T₀. X is how many positions have ever been chosen during the Markov searching process before loop finishes and T₀ is a time unit chosen to scale the CG time to real time. We cannot determine the exact value of T₀, but it should not qualitatively affect the result. Predictions on six different DNA sequences are shown in Figure 5B. We predicted that the looping time order should be TA < E8A10 ~ E8A17 < R73 < E8A26 ~ E8A38, matching with the experimental result¹⁴ very well.

In conclusion, both kinks and bubbles were observed in the dynamic simulations, which provides the mechanical origin of the subelastic model. As long as there are these types of structural defects, the subelastic model is valid to describe the looping process of small DNA circles or so-called mini circles. Several conditions are correlated to induce such structural defects; they depend on the size the loop, external torsional stress, magnesium concentrations, and many other factors. Here we point out that the defects related to the looping process happen in specific, critical sequential positions. The probability to have structural defects can be affected by the sequence in the critical regions and the sequence in the adjacent regions through negative correlations. This appears to be a general rule and could be used in studies of the relative looping time of various sequences with similar lengths.