The fan-beam short-scan FBP algorithm is not exact

Abstract

The fan-beam short-scan filtered backprojection (FBP) algorithm is popular in the computed tomography (CT) industry and in clinical applications. This paper points out that the fan-beam short-scan FBP algorithm is not exact, even in an ideal noiseless situation. The error depends on the focal length of the imaging geometry. When the focal length is long enough, the error is small and can therefore be ignored.

1. Introduction

Short-scan in fan-beam tomography has wide industry and health care applications; it can acquire sufficient line-integral measurements by scanning the object 180° plus the fan-beam full fan angle (Parker 1982, Crawford and King 1990, Silver 2000). The most popular fan-beam short-scan filtered backprojection (FBP) technique was developed by Parker (Parker 1982, Wesarg et al 2002). The main strategy of Parker’s method is to wisely scale the redundant measurements so that the weighting function in the sinogram is smooth.

In the next section, we will point out that the short-scan fan-beam FBP algorithm is not exact, even when the projections are ideal and noiseless. The reconstruction error depends on the reconstruction location and the focal length of the imaging geometry. The cause of the error is the inconsistency of the ramp filter’s cut-off frequency (Pan 1999, Pan and Yu 2003, Zeng 2004). This inconsistency is made worse by fan-beam short-scan.

Computer simulations are presented in the results section, which reveal that the errors are larger with a shorter focal length. When the focal length is extremely long, the errors are small and can be neglected. Parallel-beam half scan, on the other hand, is mathematically exact.

2. Methods

In the fan-beam FBP algorithm, the fan-beam projections are first filtered by a ramp filter. In order to make the FBP algorithm more computationally efficient, the ramp filtration is made shift invariant. The following relationship is an important step to achieve this shift (Zeng 2009):

$$h_{\Omega }\left(at\right)=\frac{1}{a^2}{h}_{a\Omega }\left(t\right)$$ (1)

where h is the inverse Fourier transform of the ramp filter, which has a bandwidth Ω. The bandwidth Ω is commonly set to ½. To be precise,

$$h_{\Omega }\left(t\right)={\displaystyle \underset{-\Omega }{\overset{\Omega }{\int }}\left|\omega \right|}{\mathrm{e}}^{\mathrm{j}2\pi \omega t}\mathrm{d}\omega ,$$ (2)

and

$$h_{\Omega }\left(at\right)={\displaystyle \underset{-\Omega }{\overset{\Omega }{\int }}\left|\omega \right|}{\mathrm{e}}^{\mathrm{j}2\pi \omega at}\mathrm{d}\omega$$ (3)

If a > 0, let x = a ω and we have:

$$h_{\Omega }\left(at\right)=\frac{1}{a^2}{\displaystyle \underset{-a\Omega }{\overset{a\Omega }{\int }}\left|x\right|}{\mathrm{e}}^{\mathrm{j}2\pi xt}\mathrm{d}x=\frac{1}{a^2}{h}_{a\Omega }\left(t\right).$$ (4)

It is straightforward to show that (4) also works for a < 0.

For the curved fan-beam imaging geometry, the FBP algorithm is expressed as (Zeng 2009):

$$f\left(r,\phi \right)=\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(D\text{cos}\alpha \right)g\left(\alpha ,\beta \right)h_{\Omega }\left(D\prime \text{sin}\left(\alpha \prime -\alpha \right)\right)\mathrm{d}\alpha \mathrm{d}\beta ,}}$$ (5)

or, by using (1),

$$f\left(r,\varphi \right)=\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\frac{\text{cos}\alpha }{D}}g\left(\alpha ,\beta \right)}{h}_{\Omega }\left(\frac{D\prime }{D}\text{sin}\left(\alpha \prime -\alpha \right)\right)\mathrm{d}\alpha \mathrm{d}\beta ,$$ (6)

where f(r, φ) is the reconstructed image, g(α β) is the curved fan-beam projection, α is the projection ray angle with respect to its central fan-beam ray, β is the focal point rotation angle, D′ and α′ are parameters related to the reconstruction point (r, φ) as illustrated in figure 1.

Figure 1.

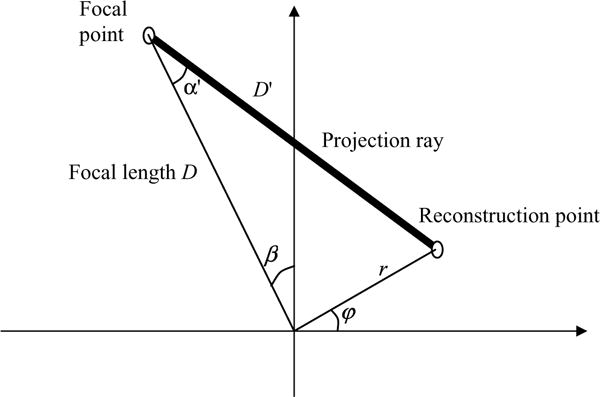
The reconstruction point (r, φ) defines the angle α′ and distance D′. The origin of the coordinate system is the center of rotation for the focal point and the virtual detector.

The fan-beam algorithm (6) is not in the form of a convolution backprojection algorithm and is not computationally efficient, because the filter depends on the parameter D′, which is reconstruction point dependent. One common solution is to use the relation (1) to move the parameter D′ out from the variable of h, obtaining:

$$f\left(r,\varphi \right)=\frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{1}{{(D\prime )}^2}{\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(D\text{cos}\alpha \right)g\left(\alpha ,\beta \right)h_{\frac{D\prime }{D}\Omega }\left(\text{sin}\left({\alpha }^{\prime }-\alpha \right)\right)\mathrm{d}\alpha \mathrm{d}\beta .}}$$ (7)

Even though algorithm (7) is exact, it is still not computationally efficient, because the cut-off frequency of the ramp filter is reconstruction point dependent. Therefore, an approximation is made:

$$h_{\frac{D\prime }{D}\Omega }\left(t\right)\approx h_{\Omega }\left(t\right),$$ (8)

and then

$$f\left(r,\varphi \right)\approx \frac{1}{2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{1}{{(D\prime )}^2}{\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(D\text{cos}\alpha \right)g\left(\alpha ,\beta \right)h_{\Omega }\left(\text{sin}\left(\alpha \prime -\alpha \right)\right)\mathrm{d}\alpha \mathrm{d}\beta .}}$$ (9)

The error of this approximation is fairly small for the full-scan fan-beam imaging. For any fan-beam line integral, it associates with two D′ parameters, usually one small (D′ < D) and one large (D′ > D); their effects are opposite and roughly cancel each other out.

However, in short-scan fan-beam imaging, the projections are acquired when the fan-beam rotation angle β is in the range of [0°, 180° + 2δ] or in a larger range, where δ is half of the fan angle. The redundant measurements in the range of [0°, 180° + 2δ] are weighted by the Parker weights (Parker 1982). The non-redundant measurements are only measured once and only one D′ parameter is associated with each fan-beam line integral.

Let us consider a reconstruction point, A, that is close to the focal point location and the measurement is not redundant. Figure 2 shows this situation with a non-redundant fan-beam ray g(α,β). The correct formula (7) uses the filter h_D′/DΩ for this fan-beam ray, with a small D′, D′ < D. On the other hand, the approximated formula (9) uses the filter h_Ω for this fan-beam ray. Notice that h_Ω has a wider bandwidth than h_D′/DΩ and allows some extra frequency components or structures to be added to the image.

Figure 2.

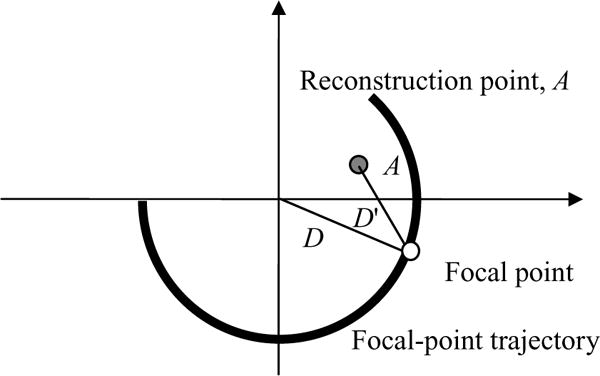
Reconstruction point, A, is close to the focal point and is on a ray which is only measured once.

A bandwidth change in a filter can change the value of the reconstructed image (Zeng 2014). It is expected that in the reconstructed image, the image value at point A is greater than its true value, due to the higher cut-off frequency.

In a more complex way, the Parker weighting function can also influence the error pattern. In a fan-beam full-scan each ray is measured twice. The approximation effects of (8) are opposite and balanced. In a short-scan, however, the redundant measurements are weighted differently, and the balance is destroyed. A weighting function dependent error pattern will appear in the reconstructed image. This phenomenon will be demonstrated in the next section.

In this paper, we use a large uniform phantom (see figure 3) to illustrate the fan-beam short-scan errors. The imaging geometry is a curved fan-beam. The detector has 512 detector channels (i.e. detector bins). The angular gap between acquisition views is 360°/6000 = 0.01°. This angular gap is much smaller than that in any practical imaging system. We deliberately chose this small angular gap to eliminate any under-sampling effects. The line-integral measurements are generated analytically without any discretization effects and are noise-free. The ideal fan-beam data are generated over the focal-point rotation angle range of [0°, 180° + 2δ], where 2δ is the fan-beam detector’s full angle. The fan-beam focal length D is a varying parameter, and the half fan-angle δ changes accordingly as

$$\delta =\frac{256}{D}.$$ (10)

Figure 3.

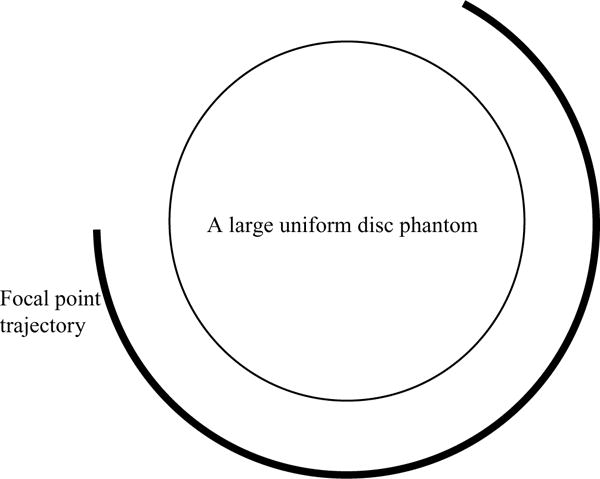
A large uniform disc phantom and the focal-point trajectory for a fan-beam short scan.

The image reconstruction algorithm for the computer simulations is

$$f\left(r,\varphi \right)=\frac{1}{2}{\displaystyle \underset{0}{\overset{2\delta }{\int }}\frac{1}{{(D\prime )}^2}{\displaystyle \underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left(D\text{cos}\alpha \right)P\left(\alpha ,\beta \right)g\left(\alpha ,\beta \right)h_{\Omega }\left(\text{sin}\left(\alpha \prime -\alpha \right)\right)\mathrm{d}\alpha \mathrm{d}\beta ,}}$$ (11)

where the Parker weighting function (Parker 1982) is defined as

$$P\left(\alpha ,\beta \right)=\{\begin{array}{cccc}{\text{sin}}^2\left(\frac{\pi }{4}\frac{\pi +2\delta -\beta }{\delta +\alpha }\right),& \text{if}& \pi -2\delta \le \beta \le \pi +2\delta & 0\le \frac{\pi +2\delta -\beta }{\delta +\alpha }\le 2,\\ {\text{sin}}^2\left(\frac{\pi }{4}\frac{\beta }{\delta -\alpha }\right),& \text{if}& 0\le \beta \le 4\delta & 0\le \frac{\beta }{\delta -\alpha }\le 2,\\ 1,& \text{otherwise}.& & \end{array}$$ (12)

3. Results

In the computer simulations, the focal length is changed from 270 to 400 units. The unit is the arc-length of each detector bin, which is also the image pixel size. The large uniform disc phantom has a radius of 230 units. The true image value within the disc is 1. The detector size is not limited and can be large enough to avoid data truncation.

The computer simulation results are shown in figures 4–11, for focal lengths 270, 300, 350, and 400 units, respectively. The display windows for the figures on the left are from the minimum value in the disc (black) to the maximum value in the disc (white).

Figure 4.

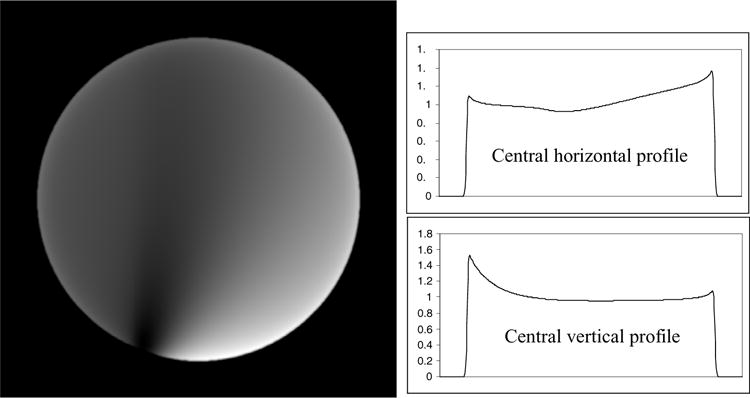
Reconstruction with short-scan data with D = 270 units. The display window is [0.76, 1.57].

Figure 11.

Reconstruction with full-scan data at D = 400 units. The display window is [1.00, 1.0005].

In figures 4–7, the short-scan results using Parker weights are shown. The largest error is observed at 57% when the focal length is the shortest at D = 270. When the focal length increases to D = 400, the largest error is reduced to 3%.

Figure 7.

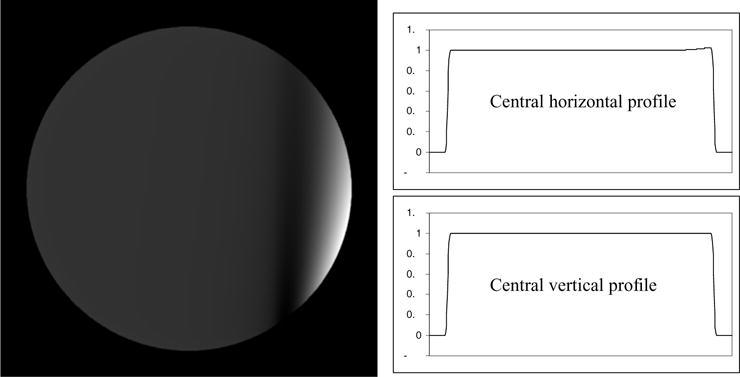
Reconstruction with short-scan data at D = 400 units. The display window is [0.99, 1.03].

As a comparison, the full-scan fan-beam reconstruction results are shown in figures 8–11. The reconstruction algorithm for the full-scan data is given by (9). It can be seen that the approximation error caused by (8) is small for the full-scan and can be neglected, thanks to the cancellation of the two opposite approximation errors. At D = 270, the largest error is 11%. At D = 400, the largest error is 0.05%. However, for the fan-beam short-scan, the error is large enough to be noticed. In both the full-scan and short-scan cases, the errors are smaller when the focal length is longer.

Figure 8.

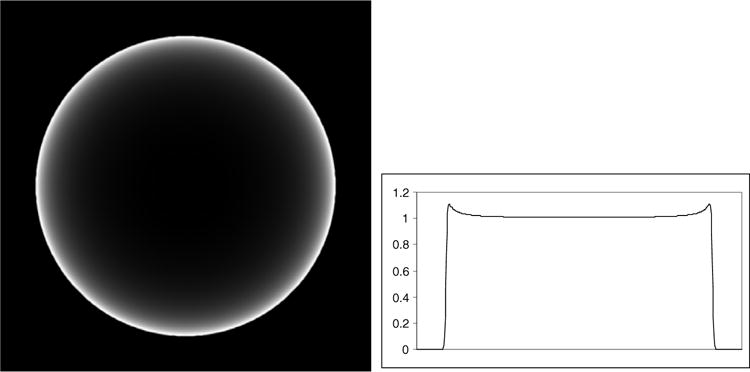
Reconstruction with full-scan data at D = 270 units. The display window is [1.01, 1.11].

4. Conclusions

The key argument in this paper is summarized as follows. Equation (7) is exact and should give an exact reconstruction. The problem is that the convolution kernel h_D′/DΩ(t) has a bandwidth D′/DΩ, depending on the variable D′. This results in an inefficient FBP algorithm. By using the approximation (8), an efficient FBP algorithm can be obtained. As for the parallel-beam imaging geometry, the relationship h (at) = 1/a²h (t) is never needed. Thus, the parallel-beam FBP algorithm is exact, using either the full-scan or half-scan data.

In the fan-beam FBP algorithm, in order to improve the computational efficiency, an approximation (8) is made, so that a fixed ramp filter is used to filter all fan-beam projections before backprojection. The error caused by this approximation is small for the fan-beam full-scan, thanks to the fact that each projection ray is measured twice with two focal-point positions. The approximation effects at these two positions are opposite; they somehow (but not completely) cancel each other out.

Unfortunately, for the fan-beam short-scan, this error cancellation phenomenon does not occur. The error can be as large as 57% when the focal length is short. This error is less severe as the focal length gets longer. The error pattern is influenced by the weighting function for the redundant measurements.

The curved-detector fan-beam imaging geometry is considered in this paper. A similar principle can be applied to the flat-detector fan-beam imaging geometry; however, the error patterns and percent errors may be different from the curved-detector case.

This paper points out that the short-scan fan-beam FBP algorithm is not exact. However, this error is very small and can only be observed with a short focal-length. Nowadays the medical x-ray CT systems have a long focal-length. The short-scan fan-beam FBP errors can be neglected.

Figure 5.

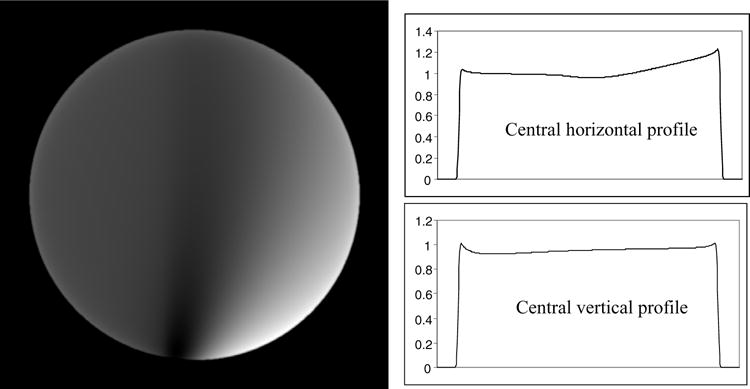
Reconstruction with short-scan data at D = 300 units. The display window is [0.87, 1.34].

Figure 6.

Reconstruction with short-scan data at D = 350 units. The display window is [0.96, 1.11].

Figure 9.

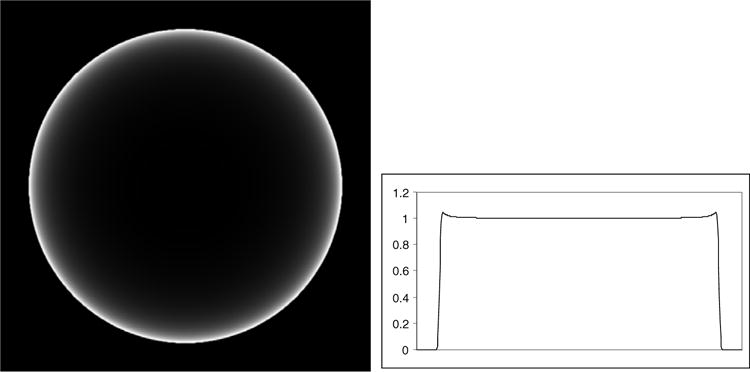
Reconstruction with full-scan data at D =300 units. The display window is [1.00, 1.05].

Figure 10.

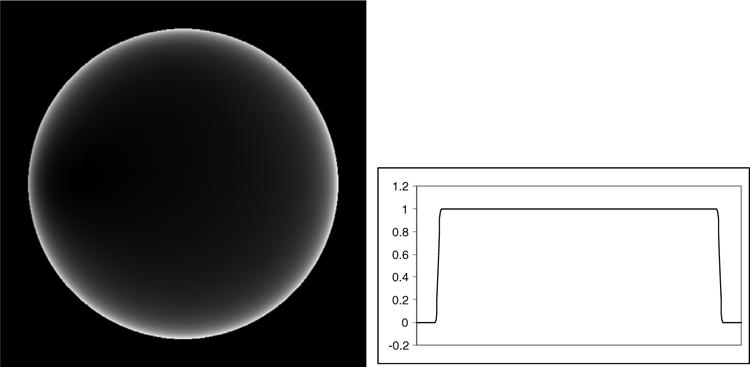
Reconstruction with full-scan data at D =350 units. The display window is [1.00, 1.001].