Assessment of viscous energy loss and the association with three‐dimensional vortex ring formation in left ventricular inflow: In vivo evaluation using four‐dimensional flow MRI

Abstract

Purpose

To evaluate viscous energy loss and the association with three‐dimensional (3D) vortex ring formation in left ventricular (LV) blood flow during diastolic filling.

Theory and Methods

Thirty healthy volunteers were compared with 32 patients with corrected atrioventricular septal defect as unnatural mitral valve morphology and inflow are common in these patients. 4DFlow MRI was acquired from which 3D vortex ring formation was identified in LV blood flow at peak early (E)‐filling and late (A)‐filling and characterized by its presence/absence, orientation, and position from the lateral wall. Viscous energy loss was computed over E‐filling, A‐filling, and complete diastole using the Navier‐Stokes energy equations.

Results

Compared with healthy volunteers, viscous energy loss was significantly elevated in patients with disturbed vortex ring formation as characterized by a significantly inclined orientation and/or position closer to the lateral wall. Highest viscous energy loss was found in patients without a ring‐shaped vortex during E‐filling (on average more than double compared with patients with ring‐shape vortex, P < 0.003). Altered A‐filling vortex ring formation was associated with significant increase in total viscous energy loss over diastole even in the presence of normal E‐filling vortex ring.

Conclusion

Altered vortex ring formation during LV filling is associated with increased viscous energy loss. Magn Reson Med 77:794–805, 2017. © 2016 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine. This is an open access article under the terms of the Creative Commons Attribution‐NonCommercial License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.

INTRODUCTION

Evaluation of vortex ring formation in left ventricular (LV) blood flow during diastolic filling has recently emerged as a potential novel approach for characterization of LV blood flow efficiency and cardiac chamber (dys‐)function 1, 2, 3, 4, 5. A vortex is characterized by a flow pattern with compact vorticity (the curl of velocity). During LV filling, vortical flow is organized in a ring‐like shape enclosing the inflow jet. During both LV filling phases, a vortex ring is formed in the shear layer at the distal tip of the mitral valve (MV) leaflets 6 and eventually pinches off from these leaflets and propagates toward the apex. While propagating, the vortex ring dissipates in the bulk flow due to viscosity‐driven friction between the vortex ring and the lateral LV wall 7.

Vortical flow in the LV cavity is thought to preserve momentum and kinetic energy in intra‐LV blood flow and to help redirect mitral inflow toward the aortic valve and, therefore, minimizing the LV mechanical energy needed to eject the blood during systole 2, 6, 8. Viscous dissipation of the vortex ring may contribute to or attenuate this flow organization 8, 9. Viscous energy dissipation/loss is essentially kinetic energy converted into thermal energy due to viscosity‐driven friction 10. Consequently, in healthy hearts the viscous energy loss is proportional to the amount of kinetic energy produced in the flow which is in turn proportional to the amount of the inflow, i.e., the stroke volume 10.

The normal dissipation of the vortex ring in the LV is mainly driven by the asymmetric shape of MV leaflets and the annulus position 3, 7. The MV setup is found to be optimal for minimizing viscous kinetic energy loss in LV blood flow 8, 9. Using an idealized LV model, computational fluid dynamics (CFD) studies have shown that a breakup in the natural MV setup, by either displacing the annulus closer to the lateral wall 8 or changing the natural MV asymmetry 9, can alter the formed vortex ring orientation and/or position relative to the lateral wall. Such unnatural vortex ring formation is found to be associated with an increase in viscous energy loss during LV filling which then may require more mechanical energy from the LV to preserve the cardiac output during systole 3, 8, 9. However, it has not been shown that a similar association between three‐dimensional (3D) vortex ring formation and viscous energy loss during LV filling is present in vivo.

Patients after atrioventricular septal defect (AVSD) correction are exemplary to have an unnatural MV/left atrioventricular valve (LAVV) setup with a more laterally positioned annulus and a smaller posterior leaflet compared with normal hearts 11, 12, 13. This setup has shown to result in altered 3D vortex ring formation characterized by a more lateral position, more inclined orientation and more frequent absence of vortex ring formation compared with healthy controls 14. Moreover, the inflow jet was found to be directed toward the lateral wall in these patients 15. Nevertheless, it is currently unclear whether these disturbed vortex ring parameters would correspond with different levels of viscous energy loss during LV filling in these patients compared with healthy volunteers.

Recently, 4DFlow MRI (also known as three‐directional, 3D, and time‐resolved velocity‐encoded MRI) has enabled quantitative 3D vortex ring analysis during both early and late LV filling in healthy volunteers and patients including measurements of vortex ring orientation and radial position (i.e., distance from lateral wall) 14, 16, 17. Given the role of natural vortex ring formation in minimization of viscous energy loss, previously reported in in vitro studies 8, 9, we hypothesized that disturbed vortex ring formation in patients would be associated with increased viscous energy loss in LV blood flow due to increased friction with the lateral wall. Therefore, the aim of this study was to use 4DFlow MRI to evaluate viscous energy loss and assess the association with 3D vortex ring formation during LV filling in vivo in healthy volunteers and patients with altered vortex flow.

THEORY

Mechanical energy can be described as the ability to move the mass of an object over some distance. In case of idealized flow in which no frictional forces are present, the total mechanical energy in the system (i.e., circulatory system) is conserved 10. This means that any increase in potential energy (i.e., pressure) will be compensated by a decrease in kinetic energy and vice versa and the exchange of energy occurs without energy loss. In the LV, the blood flow is nonidealized and with blood being a viscous fluid, frictional forces exist, resulting in irreversible mechanical energy loss mainly in the form of thermal energy (heat) 10. Viscous energy loss corresponds to the mechanical kinetic energy irreversibly lost (converted) to thermal energy due to frictional forces induced by fluid viscosity and no‐slip condition 10, 18.

4DFlow MRI can provide the three‐directional velocity flow field $\mathrm{v}$ over the three principal directions x, y, z and over the complete cardiac cycle 19. Given the acquired velocity field $v$, the instantaneous rate of viscous energy loss ( $\dot{EL}$) in watt (W) and the total energy loss ( $E{L}_{total}$) in joule (J) over a given period of time $T$ can be computed using the viscous dissipation function ${Ф}_v$ in the Newtonian Navier‐Stokes energy equations 20, 21, 22:

$${Ф}_{\mathit{v}}=\frac{1}{2}{\displaystyle \sum }_{\mathit{i}=1}^3{\displaystyle \sum }_{\mathit{j}=1}^3{\left[\left(\frac{\partial {\mathit{v}}_{\mathit{i}}}{\partial {\mathit{x}}_{\mathit{j}}}+\frac{\partial {\mathit{v}}_{\mathit{j}}}{\partial {\mathit{x}}_{\mathit{i}}}\right)-\frac{2}{3}(\nabla \mathit{\nabla }.\mathit{v}){\mathit{\delta }}_{\mathit{i}\mathit{j}}\right]}^2,\{\begin{array}{c}{\mathit{\delta }}_{\mathit{i}\mathit{j}}=1, if i=j\\ {\mathit{\delta }}_{\mathit{i}\mathit{j}}=0, if i\ne j\end{array}\left[{\mathrm{s}}^{-2}\right]$$ (1)

The viscous dissipation function ${Ф}_{\mathrm{v}}$ represents the rate of viscous energy dissipation per unit volume. $\mathrm{i},\mathrm{j}$ correspond to the principal velocity directions x, y, z. $\nabla .\mathrm{v}$ is the divergence of the velocity field. Hence, the volumetric rate of viscous energy loss ( $\dot{\text{EL}}$) in watt at time instance $\mathrm{t}$ can be computed as:

$${\dot{\mathbf{E}\mathbf{L}}}_{\mathbf{t}} = \mathbf{\mu }{\displaystyle \sum }_{\mathbf{w}=1}^{\mathbf{N}}{Ф}_{\mathbf{v}}{\mathbf{L}}_{\mathbf{w}}\left[\text{watt (W)}\right]$$ (2)

with the dynamic viscosity $\mu$ = 0.004 Pa·s, assuming the blood as a Newtonian fluid, $\mathrm{N}$ as the total number of voxels in the given domain of interest (e.g., LV), ${\mathrm{L}}_{\mathrm{w}}$ as the voxel volume.

Consequently, the total viscous energy loss ( $\text{EL}$) in joules over time period $\mathrm{T}$ starting at phase ${\mathrm{t}}_{\text{start}}$ and ending at ${\mathrm{t}}_{\text{end}}$ can be computed as:

$$\mathbf{E}{\mathbf{L}}_{\mathbf{T}}={\displaystyle \sum }_{\mathbf{d}=\mathbf{t}{}_{\mathbf{s}\mathbf{t}\mathbf{a}\mathbf{r}\mathbf{t}}}^{\mathbf{t}{}_{\mathbf{e}\mathbf{n}\mathbf{d}}}{\dot{\mathbf{E}\mathbf{L}}}_{\mathbf{d}}{\mathbf{p}}_{\mathbf{d}}\left[\text{joule (J)}\right]$$ (3)

with ${\mathrm{p}}_{\mathrm{d}}$ the time step (temporal resolution) of the 4DFlow MRI acquisition.

Given the three‐directional velocity vector field $\mathrm{v}$, the kinetic energy ( $\text{KE}$) over a domain of interest with $\mathrm{N}$ voxels of volume $\mathrm{L}$ at time instance $\mathrm{t}$ can be computed as

$$\mathbf{K}{\mathbf{E}}_{\mathbf{t}}=\frac{\mathbf{\rho } }{2}{\displaystyle \sum }_{\mathbf{k}=1}^{\mathbf{N}}\Vert {\mathbf{v}}_{\mathbf{k}}\Vert { }^2{\mathbf{L}}_{\mathbf{k}}\left[\text{J}\right]$$ (4)

with blood assumed as incompressible fluid with density $\rho$ = 1025 kg/m³.

METHODS

Study Population

The study was approved by the local ethical committee and written informed consent was obtained from all participants or their parents. Thirty‐two patients with a history of corrected‐AVSD were prospectively enrolled 23. Thirty controls with a similar age and without history of cardiac disease were included for comparison. Patients underwent electrocardiography and ECG and their details were analyzed. All patients were in sinus rhythm. Forty‐four percent of the patients presented with a right bundle branch block and six (19%) with some form of left bundle branch block. Data from patients and/or controls were previously reported in studies with the aim to characterize and quantify diastolic trans‐atrioventricular valve flow 15, 24, providing reference values for 3D vortex flow in the LV 16 and evaluating LV inflow propagation velocity 25. Two more recent publications have used the 4D flow MRI data to evaluate the intracardiac blood flow organization in the same populations of corrected AVSD patients and healthy controls 17, 26 and to evaluate vortex ring formation in patients after AVSD‐repair 17. However, none of these publications reported viscous energy loss, kinetic energy or its association with vortex ring parameters. For clarity, the term mitral valve (MV) will be used in both healthy subjects and patients (instead of LAVV).

4DFlow MRI Protocol and Data Preparation

Whole‐heart 4DFlow MRI was obtained on a 3 Tesla (T) MRI scanner (Ingenia 3T MRI with Software Stream 4.1.3.0, Philips Healthcare, Best, The Netherlands), using a combination of FlexCoverage Posterior coil in the table top with a dStream Torso coil, providing up to 32‐coil elements for signal reception. Velocity encoding of 150cm/s was used in all three directions, with spatial resolution 2.3 × 2.3 × 3.0–4.2 mm³, flip angle 10 °, echo time (TE) 3.2 ms, and repetition time (TR) 7.7 ms, resulting in a maximal true temporal resolution of 4 × TR = 31 ms. Retrospective ECG‐gating was used and 30 cardiac phases were reconstructed to represent one average heartbeat. Parallel imaging was performed using SENSE with factor 2 and echo planar imaging with factor 5 for acquisition acceleration. Furthermore, to quantify LV volumes and ejection fraction as well as facilitating LV segmentation, a left two‐chamber and four‐chamber cine view and a short‐axis cine stack of slices were acquired with steady‐state free‐precession with echo time/repetition time (TE/TR) 1.5/3.0; 8mm section thickness; 45 ° flip angle; spatial resolution 1.0 × 1.0 × 8.0 mm³; three signal averages and parallel imaging with SENSE factor 2. Typical volume for a whole‐heart 4DFlow MRI acquisition was 396 mm (right–left) × 336 mm (anterior–posterior) × 117 mm (feet–head). However, the field‐of‐view in anterior–posterior direction was adapted to the size of each subject. 4DFlow MRI acquisition took on average 8 min (range, 5–12 min). Concomitant gradient correction and local phase correction were applied using the software available on the MRI system.

To enable a reasonable acquisition time (8–10 min), free breathing was allowed for both patients as well as controls, without using motion compensation techniques such as navigators. For each voxel, 4D flow MRI data were obtained in retrospectively gated time‐resolved manner, using one velocity‐compensated and three velocity‐sensitive (in three orthogonal directions) recordings. No additional signal averaging was performed. For short‐axis cine data, three signal averages were obtained to compensate for breathing motion.

Using in‐house developed MASS software (Leiden University Medical Center), the LV endocardial contours were manually traced on short‐axis slices over all acquired phases. Contours were then projected on the whole‐heart 4DFlow data. To reduce possible translation errors between cine short‐axis and whole‐heart 4DFlow acquisitions, automated image registration using Elastix 27 was performed between cine short‐axis data and velocity magnitude reconstructed images of the 4DFlow data using a single phase that visually showed the best depiction of the LV in the velocity magnitude 4DFlow image. Registration was restricted to translation only. This registration result was then propagated to all 4DFlow phases. Registered 4DFlow MRI contours were then visually reviewed for any possible registration or projection errors and manually corrected whenever needed. The 3D velocity data within the segmented LV volume were then used to compute energy parameters as described in the Theory section. Segmented LV endocardial boundaries were also used to compute the LV end‐diastolic volume, end‐systolic volume, stroke volume (SV), and ejection fraction. Cardiac output (CO) was computed as CO = (SV × HR), with HR as the heart rate.

LV inflow was quantified from 4DFlow MRI data using retrospective mitral valve tracking 28. The time points corresponding to peak early filling (E‐peak) and peak late filling (A‐peak) were defined from the flow‐time curves which resulted from velocity mapping as previously described 15, 24. E/A ratio was computed from flow rate values at E‐peak and A‐peak. To study the association with diastolic vortex formation, the inflow area and peak velocity during E‐peak were quantified at the level of peak inflow velocity as previously described 15.

Image analysis was performed by one observer (E.C.) with 2 years of experience in cardiac MRI and verified by one observer (J.W.) with over 15 years of experience.

3D Vortex Core Identification Using the Lambda2 (λ₂)‐Method

Using the previously validated 3D vortex analysis workflow 16, the 3D vortex cores within the segmented LV blood pool were identified from the 4DFlow MRI data at both LV filling phases using the Lambda2‐method and visualized as 3D isosurfaces 29. In short, the Lambda2‐method is a well‐established fluid‐dynamics‐based method that uses the gradient properties of the velocity field to generate a 3D scalar (λ2) field. The λ2‐field implicitly describes the fluid pressure at each voxel. Voxels with extreme negative values, i.e., below a predefined λ2 threshold are labeled as part of a vortex core in the flow. Vortex cores are then visualized as isosurfaces of some negative λ2 threshold. In this work, the threshold was defined using a previously validated interactive method 16. Qualitative visual inspection of the shape of detected 3D vortex core isosurfaces were performed by a single observer (ME) to determine whether a ring‐shaped vortex core (a vortex core with a donut‐like (torus) shape enclosing the inflow jet) was present. If such vortex ring core was detected during E‐filling and/or A‐filling, its normalized radial position and orientation relative to the LV long‐axis were calculated as described previously 16 (Fig. 1).

Figure 1.

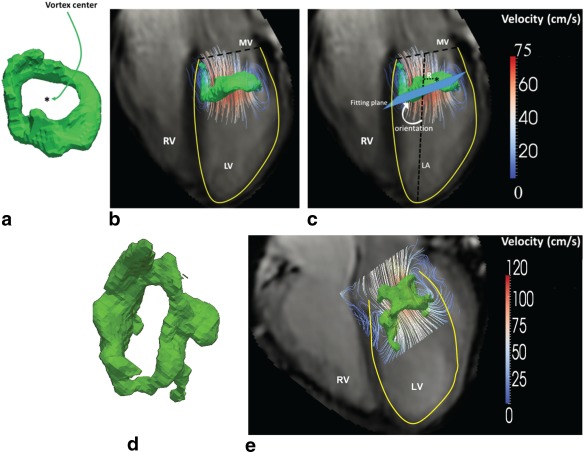
a: Example of vortex ring isosurface (in green) at E‐peak filling phase as identified using Lambda2‐based vortex core detection 16 from a healthy volunteer. b: Streamlines superimposed on vortex ring isosurface (a) in a four‐chamber view. c: Definition of vortex ring orientation and normalized radial position relative to the LV long‐axis: The LV long‐axis is defined as the line from the mid of the mitral valvular opening to the LV apex. The normalized radial position was calculated as the distance of the vortex ring center (marked by “*”) to the LV long‐axis normalized by the basal endocardial radius. Vortex ring orientation was measured as the angle between the fitting plane of the vortex ring isosurface and the LV long‐axis (LA). d: Example vortex ring isosurface (in light green) at E‐peak filling phase from an AVSD‐repaired patient with an inclined E‐peak vortex ring orientation, showing a more elliptical vortex ring compared with controls. This deviated shape can be due to the restricted valve opening known to occur in AVSD patients after repair 17. e: Streamlines superimposed on vortex ring isosurface presented in (d) showing the inclined inflow and vortex ring orientation in this patient in a four‐chamber view.

Vortex Formation Time Index

The vortex formation time (VFT), a dimensionless index previously proposed to quantify the process of vortex progression during early filling 30, was determined as follows:

$$VFT = \frac{V_{avg}\times E_{duration} }{D}$$ (5)

with $V_{avg}$ as the average speed of the blood flow during E‐filling, $E_{duration}$ as the duration of E‐filling and $D$ as the maximum diameter of the MV opening. $D$ was computed at E‐peak from the area of the MV flow on retrospective valve tracking at peak inflow velocity level (i.e., approximately at the tip of the valves), using $D$ =  $2\sqrt{Area/\pi }$, assuming a circular inflow area.

Energy Analysis

To quantify viscous energy loss in the LV during diastolic filling, the instantaneous volumetric rate of viscous energy loss ( $\dot{\text{EL}}$) was computed for each time point during LV filling using Eq. (2). To quantify the viscous energy loss over both E‐ and A‐filling phases, the average rate of viscous energy loss over both periods ( ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$) and ( ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$) was computed. The average viscous energy loss rate was used instead of the total viscous energy loss to account for the variation in E‐ and A‐filling durations among different subjects. The peaks $\dot{\text{EL}}$ during E‐filling ( ${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$) and A‐filling ( ${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$) were calculated as well as the ratio ${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$/ ${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$, reported as ${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$.

The total viscous energy loss over diastole ( ${\text{EL}}_{\text{diastole}}$) was computed using Eq. (3). To account for the variation in inflow volumes between different subjects, all computed viscous energy loss measurements were normalized by stroke volume (SV). This resulted in viscous energy loss measurements per unit volume $\text{EL}$ (in J/m³) and the rate of viscous energy loss $\dot{\text{EL}}$ per unit volume (in W/m³). To compare with previously reported studies on viscous energy loss based on other modalities 31, 32, the absolute (i.e., not SV normalized) ${\text{EL}}_{\text{diastole}}$ is also reported as $\text{abs}\_{\text{EL}}_{\text{diastole}}$.

To quantify the change of kinetic energy (KE) over the period of LV filling, the instantaneous volumetric KE was quantified at each time point during LV filling (defined from the flow‐time curve) using Eq. (4). The average KE over E‐filling ( ${\text{KE}}_{\mathrm{E}-\text{avg}}$) and A‐filling ( ${\text{KE}}_{\mathrm{A}-\text{avg}}$) was computed. Also peak KE over E‐filling ( ${\text{KE}}_{\mathrm{E}-\text{peak}}$) and A‐filling ( ${\text{KE}}_{\mathrm{A}-\text{peak}}$) was calculated.

The amount of KE is proportional to the amount of LV inflow volume. Similar to EL, all computed KE were normalized by SV resulting in KE per unit volume (in J/m³) to account for the variation in inflow volumes among subjects. To compare with previously reported KE 33, the absolute (i.e., not SV normalized) ${\text{KE}}_{\mathrm{E}-\text{peak}}$ and ${\text{KE}}_{\mathrm{A}-\text{peak}}$ are also reported as $\text{abs}\_{\text{KE}}_{\mathrm{E}-\text{peak}}$ and $\text{abs}\_{\text{KE}}_{\mathrm{A}-\text{peak}}$.

Energy analysis was performed with an in‐house software module developed using MATLAB (MathWorks Inc., version R2013b). Time‐resolved segmented LV volumes were used in all provided analysis.

Statistical Analysis

Data analysis was performed using SPSS Statistics (version 20.0 IBM SPSS, Chicago, IL). Variables were tested for normal distribution using the Shapiro‐Wilk test. Continuous variables are expressed as mean ± standard deviation (SD) or as median with inter‐quartile range (IQR) where appropriate. Comparison of variables amongst different groups was performed using unpaired Student's t‐test or Mann‐Whitney U‐test where appropriate, and P < 0.05 was considered statistically significant.

The normal limits of vortex ring's radial position and orientation were obtained from the 95% confidence interval (95%CI) in the controls group. For each of the two vortex parameters, the patients were divided into three groups: patients with data within, below, or above 95%CI of controls. One additional group was constructed which included patients with a normal vortex ring, i.e., both radial position and orientation within 95%CI normal limits. For each group, the values of aforementioned parameters of $\dot{\text{EL}}$ and $\text{EL}$ were compared with corresponding values in controls using Mann‐Whitney U‐test.

Correlations of ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ with ${\text{KE}}_{\mathrm{E}-\text{avg}}$, ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ with ${\text{KE}}_{\mathrm{A}-\text{avg}}$, stroke volume with $\text{abs}\_{\text{EL}}_{\text{diastole}}$, ejection fraction with $\text{abs}\_{\text{EL}}_{\text{diastole}}$, VFT with ${\text{EL}}_{\text{diastole}}$, ${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$ with inflow E/A, and ${\text{EL}}_{\text{diastole}}$ with HR were assessed from linear regression analysis (Pearson's R²).

RESULTS

Clinical Characteristics

Clinical characteristics of the studied subjects are summarized in Table 1.

Table 1.

Characteristics of Healthy Controls and Corrected‐AVSD Patients^a

	Controls	Corrected‐AVSD patients
Age (years)	23 [13–38]	26 ± 12
Male (%)	14 (46)	9 28
Heart rate (bpm)	68 [60–78]	76 ± 13
Diastasis (ms)	116 ± 89	26 [0–67]b, c
Stroke volume (mL)	89 ± 23	85 ± 19
Cardiac output (L/min)	6.01 ± 1.3	6.39 ± 1.4
EDV (mL)	146 ± 42	155 ± 33
Early filling fraction (%)	76 ± 5	73 ± 13
Ejection fraction (%)	61 ± 5	56 [52–58]d
E/A ratio peak flow rate	2.5 ± 0.8	2.1 [1.7–2.6]b
VFT index	2.6 ± 0.6 (N = 30)	2.4 [1.9–3.1] (N = 32)

^aNormally distributed data are presented as mean ± SD, while non‐normally distributed data are presented as median [interquartile range].

^bexcluding two cases without A‐peak.

^cindicates P < 0.01.

^dindicates P < 0.001.

EDV = end‐diastolic volume; VFT = vortex formation time.

LV Viscous Energy Loss over Diastole

Detailed results are listed in Table 2. In all controls, the timing of the peaks in viscous energy loss (EL) rate $\dot{\text{EL}}$ over diastole appeared in good alignment with the peaks in the flow rate‐time curves (one example shown in Figure 2a). Two distinct peaks of viscous EL during diastole were discriminated: the first during early filling and the second during late filling. The peak E‐filling viscous energy loss was significantly higher than A‐peak ( ${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$ = 14.7 ± 4.6 W/m³, ${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$ = 5.1 ± 2.8 W/m³, P < 0.001). The ratio between the EL peaks ${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$ was 3.4 ± 1.6. The normal limits of 95%CI of ${\text{EL}}_{\text{diastole}}$ were [1.97–4.92 J/m³].

Table 2.

Quantitative Analysis of Viscous Energy Loss and Kinetic Energy during LV Filling

	Controls (N = 30)	Patients (N = 32)	P‐Value
${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ (W/m3)	6.6 [5.5–9.0]	12.2 ± 7.2	<0.001
${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (W/m3)	3.9 ± 2.2	8.1 ± 3.8a	<0.001
${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$ (W/m3)	14.7 ± 4.6	18.3 [13.9–28.6]	0.002
${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$ (W/m3)	5.1 ± 2.8	10.4 ± 5.3 a	<0.001
${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$	3.4 ± 1.6	1.9 [1.3–2.9] a	0.003
${\text{EL}}_{\text{diastole}}$ (J/m3)	2.7 [2.3‐3.2]	4.9 ± 2.0	<0.001
$\text{abs}\_{\text{EL}}_{\text{diastole}}$ (mJ)	0.24 [0.19–0.28]	0.37 [0.26–0.53]	<0.001
${\text{KE}}_{\mathrm{E}-\text{avg}}$ (J/m3)	25.1 ± 7.8	34.1 ± 18.8	0.03
${\text{KE}}_{\mathrm{A}-\text{avg}}$ (J/m3)a	9.3 [7.0–13.2]	21.4 ± 11.2 a	<0.001
${\text{KE}}_{\mathrm{E}-\text{peak}}$ (J/m3)	57.2 ± 16.6	55.2 [46.4–76.5]	0.65
${\text{KE}}_{\mathrm{A}-\text{peak}}$ (J/m3)a	15.9 ± 8.0	28.9 ± 16.0 a	<0.001
$\text{abs}\_{\text{KE}}_{\mathrm{E}-\text{peak}}$ (mJ)	5.0 ± 1.9	5.5 ± 2.7	0.73
$\text{abs}\_{\text{KE}}_{\mathrm{A}-\text{peak}}$ (mJ)a	1.3 ± 0.5	2.26 [1.3–3.2] a	<0.001

^aTwo patients had no A‐wave and were excluded.

Figure 2.

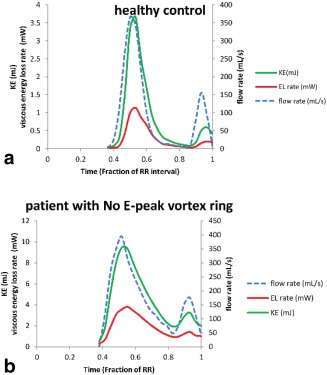
Temporal evolution of viscous energy loss rate ( $\dot{\text{EL}}$), kinetic energy (KE), and inflow rate over LV diastole of a typical healthy subject (a) and a patient who did not present E‐vortex ring formation but rather a complex irregular flow instead (b). Viscous energy loss characterized by E‐ and A‐peaks is significantly elevated (with more than two‐fold increase) in the patient (b) compared with the healthy control subject (a).

In patients, similar to controls, two peaks could be detected in $\dot{\text{EL}}$ during diastole in good alignment with the peaks in the flow rate‐time curves (Fig. 2b). The ${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$ was significantly higher than in controls (patients ${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$ = 18.3 [13.9–28.6] W/m³, P = 0.002). Similarly, the peak of energy loss rate during A‐filling in patients was significantly increased compared with controls (patients ${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$ = 10.4 ± 5.3 W/m³, P < 0.001). Furthermore, the E/A ratio between $\dot{\text{EL}}$ peaks was significantly reduced in patients compared with controls (patients ${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$ = 1.9 [1.3–2.9], P = 0.003). In two patients, no A‐wave was discriminated and, therefore, in those cases, no results for A‐peak were obtained. Compared with controls, patients showed a significant increase (P < 0.001) in viscous energy loss over complete diastole ${\text{EL}}_{\text{diastole}}$.

LV Kinetic Energy over Diastole and the Association with Viscous Energy Loss

Detailed results are listed in Table 2. Similar to EL, two peaks ${\text{KE}}_{\mathrm{E}-\text{peak}}$ and ${\text{KE}}_{\mathrm{A}-\text{peak}}$ of kinetic energy (KE) could be detected in controls and patients with the timing of these peaks in good alignment with the flow rate‐time curves (Fig. 2). Both ${\text{KE}}_{\mathrm{E}-\text{avg}}$ and ${\text{KE}}_{\mathrm{E}-\text{peak}}$ were significantly higher (P = 0.03) in patients compared with controls. Similarly, both ${ \text{KE}}_{\mathrm{A}-\text{avg}}$ and ${\text{KE}}_{\mathrm{A}-\text{peak}}$ were significantly increased in patients compared with controls (P < 0.001).

In controls, strong correlations were found between ${\text{KE}}_{\mathrm{E}-\text{avg}}$ and ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ during E‐filling (R² = 0.81) and between ${\text{KE}}_{\mathrm{A}-\text{avg}}$ and ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ during A‐filling (R² = 0.88) (Fig. 3). This was similar for patients where strong correlations were found between ${\text{KE}}_{\mathrm{E}-\text{avg}}$ and ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ during E‐filling (R² = 0.88) and between ${\text{KE}}_{\mathrm{A}-\text{avg}}$ and ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ during A‐filling (R² = 0.88) (Fig. 3).

Figure 3.

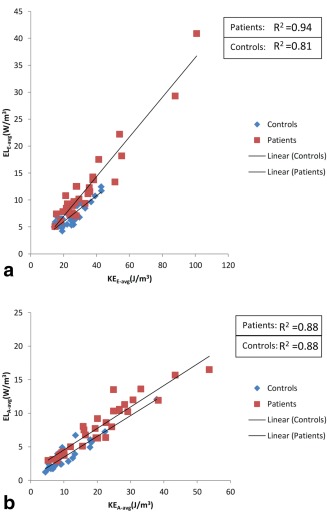
Correlation between average viscous energy loss rate during E‐filling (EL_E‐avg) (a) and late filling (EL_A‐avg) (b) with corresponding kinetic energy (KE), i.e., KE_E‐avg and KE_A‐avg, respectively, in controls (blue) and patients (red).

LV Vortex Ring Formation and Viscous Energy Loss

In all controls, a compact vortex ring core was identified in the LV blood flow during E‐filling and quantitatively characterized. In 26 patients (81%), a vortex ring core was present but with different characteristics from controls (Tables 3, 5). Among these patients, 17 (65%) patients had significantly tilted vortex ring orientation beyond the 95%CI of controls' vortex orientation (Table 4): in 14 patients below the lower limit and in 3 patients above the upper limit of the 95%CI of controls. Compared with controls, patients with E‐peak vortex ring orientation within the normal limits (N = 9) presented with nonsignificantly different E‐filling viscous energy loss rate ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ but showed significantly higher ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (P < 0.01) and ${\text{EL}}_{\text{diastole}}$ (P = 0.04) (Table 5). Patients with E‐peak vortex ring orientation beyond normal limits (N = 17) presented significantly increased viscous energy loss during E‐filling, A‐filling and complete diastole (P < 0.01). Detailed results are listed in Table 5.

Table 3.

Quantitative Energy Parameters in Patients Presented with Vortex Ring Core vs. Those without Vortex Ring

	Patients with vortex ring (E‐filling: N = 26, A‐filling: N = 19)	Patients without vortex ring (E‐filling: N = 6, A‐filling: N = 13)	P‐Value
${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ (W/m3)	9.3 [7.5–12.4]a	21.0 ± 11.6a	0.003
${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (W/m3)b	1.6 ± 1.1c	2.2 ± 0.9a, b	0.04
${\dot{\text{EL}}}_{\mathrm{E}-\text{peak}}$ (W/m3)	17 [13.8–22.5]c	41.8 ± 20.0a	0.001
${\dot{\text{EL}}}_{\mathrm{A}-\text{peak}}$ (W/m3)b	9.4 [6–13.3]a	12.1 ± 5.5a, b	0.16
${\text{EL}}_{\text{diastole}}$ (J/m3)	4.2 ± 1.3a	7.60 ± 2.2a	0.005
${\text{KE}}_{\mathrm{E}-\text{avg}}$ (J/m3)	26.8 [22.8–34.9]d	54.4 ± 31.8a	0.03
${\text{KE}}_{\mathrm{A}-\text{avg}}$ (J/m3)b	19.0 ± 11.4c	25.5 ± 10.1a, b	0.13
${\text{KE}}_{\mathrm{E}-\text{peak}}$ (J/m3)	57.8 ± 0.2d	101.6 ± 59.2c	0.05
${\text{KE}}_{\mathrm{A}-\text{peak}}$ (J/m3)b	24.9 [16.0–40.8]c	34.5 ± 16.2a, b	0.07

^a P < 0.01 compared with controls.

^bTwo patients had no A‐wave and were excluded.

^c P < 0.05 compared with controls.

P > 0.05 compared with controls.

Table 5.

Viscous Energy Loss in Corrected‐AVSD Patients with Normal or Abnormal E‐Peak Vortex Ring Orientation and/or Radial Position

	Phase	N	Vortex Orientation (degrees)	${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ (W/m3)	${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (W/m3)	${\text{EL}}_{\text{diastole}}$ (J/m3)
Patients with Orientation within 95%CI	E‐filling	9	71 ± 10a	8.4 ± 1.8a	8.3 ± 3.9b	3.8 [2.6–4.0]c
	A‐filling	10	71 ± 7a	9.7 ± 2.6b	6.7 ± 3.9b	3.7 ± 0.8b
Patients with Orientation below 95%CI	E‐filling	14	37 ± 11b	10.0 ± 3.2b	8.3 ± 4.2b	4.4 ± 1.30b
	A‐filling	9	35 ± 13b	10.0 ± 3.7b	8.3 ± 4.0b	4.8 ± 1.1b
Patients with Orientation above 95%CI	E‐filling	3	118 ± 16b	16.1 ± 5.2b	8.1 ± 5.3c	5.8 ± 1.6b
	A‐filling	0	–		–	–

		N	Normalized radial position	${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ (W/m3)	${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (W/m3)	ELdiastole(J/m3)
Patients with radial position within 95%CI	E‐filling	20	0.29 ± 0.06a	9.5 [7.4–12.5]b	8.1 ± 4.1b	4.1 ± 1.4b
	A‐filling	12	0.25 ± 0.07a	10.5 ± 3.4b	6.5 ± 3.3b	4.0(3.4‐5.2)b
Patients radial position below 95%CI	E‐filling	0	–	–	–	–
	A‐filling	0	–	–	–	–
Patients with radial position above 95%CI	E‐filling	6	0.43 ± 0.03b	9.0 ± 1.8c	8.8 ± 4.2b	4.6 ± 1.0b
	A‐filling	7	0.47 ± 0.04b	8.7 ± 2.0c	9.3 ± 4.5b	4.2 ± 0.7b
Patients with both radial position and orientation within 95%CI	E‐filling	8	0.28 ± 0.05a	8.5 ± 1.9a	7.8+‐3.9b	3.7 [2.5–4.0]c
	A‐filling	7	0.25 ± 0.08a	9.6 ± 2.9c	4.8 ± 1.7c	3.±1.0c

^a P > 0.05.

^b P ≤ 0.01 when compared with controls.

^c0.01 < P < 0.05 when compared with controls.

Table 4.

Controls' Vortex Ring Parameters and Normal Limits^a

Phase	Vortex ring parameter	95%CI range
		Lower limit (2.5%)	Upper limit (97.5%)	N (total=30)	Noutside
E‐filling peak	Orientation	55°	87°	28	2
	Normalized Radial Position	0.14	0.39	28	2
A‐filling peakb	Orientation	57°	84°	25	2
	Normalized Radial Position	0.05	0.39	25	2

^aThe 95% confidence interval (CI) represents the interval [2.5%–97.5%]. N is the number of subjects that presented a vortex ring core within the 95%CI range. N_outside is the number of subjects with detected vortex ring core but outside the 95%CI range. Radial position is normalized to the basal endocardial radius (measured on a short‐axis slice).

Three subjects did not present vortex ring core at peak late filling.

In eight patients with both radial position and orientation of E‐peak vortex ring within the normal limits, ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ was not significantly different from controls but ${\text{EL}}_{\text{diastole}}$ was still different from controls (P < 0.01). Patients with E‐peak vortex ring positioned significantly more lateral (radial position > 95%CI), showed a significant increase in viscous energy loss during E‐filling, A‐filling and over complete diastole.

In the remaining six patients (19%), no well‐formed E‐peak vortex ring core was detected but rather a complex flow with isolated vortex cores of irregular shape. These patients showed a significant increase in viscous energy loss over complete diastole $({\text{EL}}_{\text{diastole}})$ compared with controls (P < 0.01) as well as compared with the other patients (P = 0.002) (Figure 2b; Table 4). Moreover, these patients presented significant increase in energy loss rate during E‐filling ( ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$) compared with controls (P < 0.01). Five of these six patients showed $\text{EL}$ per unit volume above the 95%CI [1.97–4.92 J/m³] of controls (Fig. 4). In addition, these five patients showed significantly higher vortex formation time (VFT) compared with controls [VFT (six patients without E‐vortex ring = 6.4 ± 1.3 versus VFT (controls) = 2.6 ± 0.6; P = 0.002] and compared with other patients [VFT (26 patients with E‐vortex ring] = 2.4 ± 0.6; P = 0.002). The one remaining patient with no E‐peak vortex ring presented with an abnormal valve anatomy with double orifice for which it was not feasible to determine the orifice diameter D (in Eq. (5)). In controls, the values for VFT presented with a narrow range, therefore, low correlation was found between ${\text{EL}}_{\text{diastole}}$ and VFT (R² = 0.03; P = 0.35) (Fig. 5). However, in patients, with a wider range for VFT, this parameter showed good correlation with ${\text{EL}}_{\text{diastole}}$ (R² = 0.864; P < 0.001) (Fig. 5).

Figure 4.

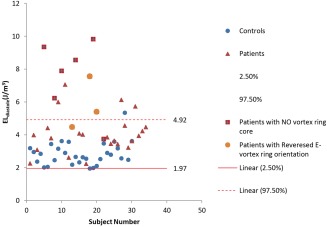
Normal limits [95%CI (confidence interval)] of the total viscous energy loss integrated over complete diastole and normalized by stroke volume (EL_diastole) as derived from thirty healthy controls (in blue circles). Solid red horizontal line represents the 2.5% (lower limit) and dashed red horizontal line represents 97.5% (upper limit). Five (out of the six) patients who showed no vortex ring formation during E‐filling presented elevated viscous energy loss considerably beyond the upper limit of the healthy controls. Likewise, two (out of the three) patients who presented E‐peak vortex ring orientation above the 95%CI showed significant increase in viscous energy loss beyond the upper limit with the remaining patient approaching the upper limit.

Figure 5.

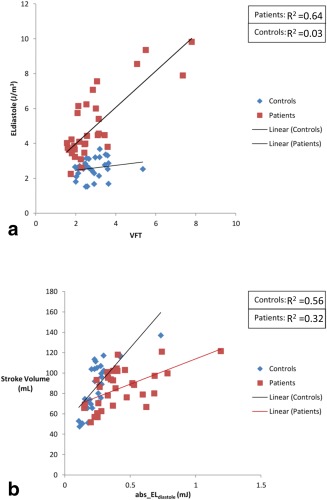
a: Correlation between total viscous energy loss integrated over diastole (EL_diastole) with vortex formation time (VFT) in controls (blue) and patients (red). b: Correlation between total viscous energy loss integrated over diastole but not normalized by stroke volume (abs_EL_diastole) with stroke volume in controls (blue) and patients (red).

In 27 (90%) controls, a vortex ring core was identified during late filling. In the remaining three controls with no identified A‐filling vortex ring, a short or no diastasis was observed 16.

During A‐filling, a vortex ring core was identified in 19 patients (59%). In the other 13 patients (41%), only irregular isolated vortex cores were present. Although ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ was significantly increased in patients with absent A‐peak vortex ring compared with controls, it was not significantly different from the other patients who presented with A‐peak vortex ring. Detailed results are presented in Tables 3 and 5.

During A‐filling, patients with A‐peak vortex ring orientation and/or radial position within the normal limits still presented significant increase in viscous energy loss rate ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (P < 0.05) compared with controls. These patients showed significant increase in the corresponding E‐filling energy loss rate ( ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$) with P < 0.01. There was no significant difference of ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ between patients with significantly laterally positioned A‐peak vortex ring and those within 95%CI.

Only three patients had both E‐peak and A‐peak vortex rings with orientation and radial position within normal limits. Compared with controls, these patients presented comparable viscous energy loss of ${\dot{\text{EL}}}_{\mathrm{E}-\text{avg}}$ (P = 0.5), ${\dot{\text{EL}}}_{\mathrm{A}-\text{avg}}$ (P = 0.2) and ${\text{EL}}_{\text{diastole}}$ (P = 0.3).

Association between Viscous Energy Loss with Global Functional Parameters

No correlation was found between ejection fraction and $\text{abs}\_{\text{EL}}_{\text{diastole}}$ in controls (R² = 0.04; P = 0.31) or patients (R² = 0.001; P = 0.7). Good correlation was found between $\text{abs}\_{\text{EL}}_{\text{diastole}}$ and stroke volume in controls (R² = 0.56; P < 0.001). This correlation was moderate in patients (R² = 0.32; P = 0.001) (Fig. 5). E/A ratio showed moderate correlation with ${\dot{\text{EL}}}_{\mathrm{E}/\mathrm{A}}$ in both controls (R² = 0.31; P = 0.001) and patients (R² = 0.36; P = 0.001). No correlation was found between ${\text{EL}}_{\text{diastole}}$ and HR in controls (R² = 0.008; P = 0.97) or patients (R² = 0.11; P = 0.55).

DISCUSSION

The present study quantitatively evaluates the viscous energy loss during LV filling in healthy volunteers and patients with altered 3D vortex ring formation (corrected‐AVSD patients) in LV blood flow by means of 4DFlow MRI. The main finding of this study is that viscous energy loss during LV filling is significantly elevated in patients with altered diastolic vortex ring parameters characterized by an abnormal orientation and/or position of the vortex ring relative to the lateral wall. The highest viscous energy loss was found in patients who presented without ring‐shaped vortex during early filling in combination with a VFT significantly beyond the normal limit.

Previous in vitro 22 and in vivo 20 studies showed the feasibility of MRI‐derived viscous energy loss calculation. However, no studies have reported in vivo viscous energy loss in 3D (+time) in the LV using 4DFlow MRI and no gold standard currently exists. Nevertheless, the reported quantitative values of viscous energy loss for healthy volunteers in this study are in good agreement with those reported in recent in vitro studies. A CFD study using an echo‐derived LV model 32 reported a mean total viscous energy loss over diastole from 20 volunteers (age 19 ± 4 years) of 0.17 ± 0.07 mJ. This is in the same order of magnitude of our results ( $\text{abs}\_{\text{EL}}_{\text{diastole} }$ = 0.24 [0.19–0.28] mJ). Similarly, the reported mean viscous energy loss in patients in the current study ( $\text{abs}\_{\text{EL}}_{\text{diastole} }$ = 0.37 [0.26–0.53] mJ) is in good agreement with the calculated in vitro energy loss (0.39 mJ) reported from a CFD simulation in a patient with unnatural mitral valve 31. Moreover, the appearance of the viscous energy loss‐time curves agree with previously reported in vitro results 8, 9. Likewise, our reported results of kinetic energy in LV blood flow in healthy volunteers for both E‐peak ( $\text{abs}\_{\text{KE}}_{\mathrm{E}-\text{peak}}$ = 5.0 ± 1.9 mJ) and A‐peak ( $\text{abs}\_{\text{KE}}_{\mathrm{A}-\text{peak}}$ = 2.26 [1.3–3.2] mJ) agree well with those reported by Carlsson et al 33 as 6.0 ± 0.6 mJ and 1.3 ± 0.2 mJ, respectively. Using a time‐resolved KE measurements, similar to the current study, Hussaini et al 34 reported peak KE from 10 healthy volunteers to be 4.90 ± 1.49 mJ which is again in good agreement with our reported results ( $\text{abs}\_{\text{KE}}_{\mathrm{E}-\text{peak}}$ = 5.0 ± 1.9 mJ). Furthermore, the obvious strong correlation found in this study between viscous energy loss and kinetic energy during both early and late filling as well as the good correlation with the stroke volume may further emphasize the feasibility of 4DFlow MRI for in vivo computation of kinetic energy and viscous energy loss in the LV.

During normal LV filling, vortex ring formation in LV blood flow is thought to contribute to organizing the inflow and its kinetic energy by preserving momentum, rearranging flow direction and minimizing collision of flow with the LV wall and, therefore, minimizing energy loss 6, 8, 9, 18. In AVSD patients, the connection between the atria and ventricles is characterized by a common atrioventricular valve 12, 13. Compared with the normal MV, the LAVV in AVSD hearts is characterized by a smaller posterior leaflet which is positioned more laterally 11, 12, 13. Surgical correction of an AVSD may also result in a restricted opening of the LAVV 35 causing the inflow jet to be directed toward the lateral wall 15. The abnormal LAVV morphology in corrected‐AVSD patients compared with the MV in healthy controls is associated with altered vortex ring orientation and shifted radial position toward the lateral wall 14. In this study, we demonstrated that these different vortex characteristics are also associated with an increase in viscous energy loss compared with healthy controls. A possible explanation may be that the deformed asymmetry of the MV leaflets in corrected‐AVSD patients 11, 12, 13 inclines the inflow jet more toward the lateral wall 8, 9, 15. Consequently, the vortex ring originates with an abnormal orientation during LV filling and propagates toward (instead of along) the lateral wall, eventually colliding with it. Friction due to vortex‐wall interaction increases the viscous dissipation 8. Also, the shifted position of the vortex ring brings the lateral vortex side in close interaction with the lateral wall.

The associations between vortex characteristics and viscous energy loss reported in this study are in agreement with previous studies. Using idealized LV models with a circular mitral annulus and CFD experiments, Pedrizzetti and Domenichini 8 showed that a shift of the annulus toward the lateral wall altered vortex ring formation during diastole which was associated with elevated viscous energy loss. Furthermore, in vitro experiments 9, 36 showed that a change in the natural MV asymmetry corresponded with altered vortex ring formation and increase in viscous energy loss. Moreover, simulations using an abnormal symmetric prosthetic mitral valve orifice resulted in reversed vortex ring orientation which was associated with increased viscous energy loss 9, 18, similar to the findings in three patients in this study. Additionally, in an in vivo study using particle image velocimetry and ultrasound, abnormal vortical flow associated with increased energy dissipation was found in patients with an unnaturally oriented or positioned prosthetic mitral valve 37. Finally, in another CFD simulation of a patient with mitral valve stenosis, de Vecchi et al 31 reported the formation of an abnormally skewed vortex ring toward the lateral wall which was associated with increased viscous energy loss during diastole.

Highest viscous energy loss was found in patients who presented without a ring‐shaped vortex during early filling. Given the suggested role of vortex ring formation in minimizing inflow collision with the LV wall 3, 6, 8, 9, 18, the absence of vortex ring formation in patients could lead to a disorganized LV inflow with increased blood–wall interaction as a result and associated increased viscous energy loss. In this study, the absence of vortex ring formation during E‐filling in patients was further confirmed by a high VFT. This agrees with previous studies showing that in the presence of elevated VFT, the vortex ring will not pinch off from the MV leaflets, i.e., the vortex ring does not form efficiently 18, 37, 38 which was associated with increased viscous energy loss 37. Furthermore, VFT is proportional to mitral inflow velocity and inversely proportional to mitral inflow diameter 30, therefore, the reported good correlation between VFT with diastolic viscous energy loss in patients might implicate similar association between energy loss and mitral inflow diameter and velocity.

In this study, patients with a normal E‐peak vortex ring orientation and radial position presented comparable viscous energy loss to controls. However, this was not the case in patients with normal A‐peak vortex ring orientation and/or radial position as significantly higher levels of energy loss during A‐filling were presented compared with controls. In these patients, viscous energy loss was significantly elevated during E‐filling which might have an additional effect to the viscous energy loss during A‐filling and subsequently increasing its total viscous energy loss. Although only in three patients, normal vortex characteristics for both E‐ and A‐filling did show comparable viscous energy loss during E‐ and A‐filling compared with the normal subjects. Reported results of ${\text{EL}}_{\text{diastole}}$ in association with E‐ and A‐vortex ring formation suggest that normal vortex ring formation during both E‐ and A‐filling might be necessary to maintain normal levels of total viscous energy loss over diastole. Accordingly, presence of only normal E‐vortex ring formation might not be sufficient to retain or indicate normal total diastolic viscous energy loss. This could suggest the need to extend vortex flow analysis in the LV to A‐filling vortex ring formation which is not included in recent analyses of vortex formation 30, 38.

Despite the normal ranges of conventional global diastolic and systolic functional parameters in the studied patients, viscous energy loss was significantly increased and discriminative in patients compared with healthy controls. This included a more pronounced decrease in ÉL_E/A compared with the conventional E/A ratio. This may suggest that viscous energy loss could be more sensitive to altered LV inflow than conventional global diastolic parameters.

The reported association between viscous energy loss and vortex ring formation emphasizes the previously suggested role of vortex ring formation in optimizing blood flow in the LV 1, 18. This knowledge can be important for all heart disease, congenital or acquired, leading to cardiac failure. With respect to AVSD patients, this study shows that the surgeon correcting these defects should be aware of the influence of valve abnormalities on energy balance within the LV. Although, currently, the main concern in correcting an AVSD is avoiding regurgitation and/or stenosis, ensuring a more natural orientation/position of the LAVV may encourage normal inflow vortex ring formation and associated minimization of viscous energy loss. Furthermore, altered vortex ring interaction with the lateral wall might influence the wall shear stress which serves as an epigenetic factor in cardiac remodeling 1, 18. However, future follow‐up studies are needed to assess the impact of abnormal vortex ring formation and its associated increase in viscous energy loss on cardiac function.

This study has some limitations. The typical limited spatiotemporal resolution of 4DFlow MRI may influence the accuracy of the velocity gradients used in the viscous energy loss equations and, therefore, affect the accuracy of the computed viscous energy loss. However, in this study both controls and patients underwent similar 4DFlow MRI protocols with similar spatiotemporal resolutions to minimize possible discrepancy and to allow for comparative analysis. The aim of this study was to provide relative comparative analysis of viscous energy loss in association with vortex ring formation in subjects acquired under the same resolution/protocol, and not to provide absolute values for viscous energy loss which can be resolution dependent. In this study, the noise level ( ${\sigma }_{\mathrm{V}}$), the standard deviation of the signal intensity (i.e., velocity) in the stationary chest wall, was measured and found in the order of 0.75 cm/s in all three directions (0.5% of the velocity sensitivity VENC = 150 cm/s). Noise level is expected to be similar among subjects of this study where the 4D flow MRI protocol was maintained similar and, therefore, allowing for the relative comparison.

Furthermore, the reported strong correlation with kinetic energy, for which no derivatives are involved in its calculation, may further indicate feasibility of the computed viscous energy loss. However, future studies are needed to evaluate the impact of spatial resolution and noise on in vivo viscous energy loss calculations. The viscous energy loss and kinetic energy computations are automated calculations without observer dependency. Only the LV segmentation from cine short‐axis slices required manual interaction. However, this has previously shown to have low inter‐ and intraobserver variability 39. The registration of the cine short‐axis contours to the 4DFlow MRI was performed automatically using the Elastix image registration toolbox 27.

The presence and absence of vortex rings was visually scored. Nevertheless, a previous study 16 showed that vortex detection can be done with low inter‐ and intraobserver variation. Moreover, the absence of vortex ring formation in some patients in this study was further confirmed by the significantly high VFT values which are in good agreement with previous literature. Analysis of vortex ring formation was limited to only E‐peak and A‐peak, subsequently no data were available on the timing, forming, and disappearance of the vortex rings. It was the objective of this work to mainly characterize and quantify the viscous energy loss globally by means of average and total viscous energy loss (over E‐, A‐filling, and complete diastole), to associate with vortex ring formation at peak E‐filling, peak A‐filling as full vortex ring development occurs at these phases 16.

Analysis of the association between the instantaneous viscous energy loss rate over the cardiac cycle and corresponding instantaneous vortex ring evolution/deformation could provide more insights on vortex–energy association but was beyond the focus of this work. Future studies are needed to assess the impact of vortex ring time evolution on viscous energy loss. The presence of elevated kinetic energy as reported in patients with absent E‐vortex, may yield turbulent flow which increases energy loss by means of turbulence 10, 18. Whenever turbulent energy loss is present in the flow, it can dominate the viscous dissipation by orders of magnitude, becoming the main source of energy loss 10, 18. Turbulent energy loss 40 was not investigated in this study and is left for future work.

In this study, a possible effect of the left bundle branch block observed in six patients cannot be ruled out, but we expect that this will predominantly influence LV ejection during systole and not the LV inflow during diastole, which is the focus of this work.

In the current MRI study, the VFT values in controls were lower than previously reported range (3.5–5.5) with echocardiography and CFD 30. This might be due to differences between modalities and their measurement of valve diameter. However, our results are in agreement and may further confirm the recent Echo publication by Stewart et al 41 who studied VFT of sixty volunteers using echocardiography and reported a mean of 1.6, much below the previously reported CFD‐derived and experimentally observed VFT, suggesting that the vortex ring pinch‐off in the human left ventricle occurs before the end of E‐filling, i.e., earlier than the experimentally observed and CFD‐derived time range. Moreover, in this study, VFT measurements were comparable and not significantly different between controls and patients who presented an E‐vortex ring core. Meanwhile, the considerably higher VFT values in patients with an absent E‐ vortex ring confirm that patients with a narrow mitral valve diameter and higher peak velocity develop abnormal vortex flow 30, 36.

In this work, stroke volume was used to normalize the in vivo‐derived LV energetics. A similar approach was used in a recent study where Mangual et al 32 have normalized energy dissipation to account for stroke volume differences between subjects. However, a previous in vitro CFD study of Fontan patients 42 suggested a different normalization of energy dissipation by $\rho \frac{{\text{CO}}^3}{\text{BSA}}$ with ρ as the blood density, CO as cardiac output and BSA as body surface area. Future in vivo studies are needed to evaluate the impact of different normalizations on energy loss (dissipation) for inter‐subject analysis.

4D flow MRI was acquired without respiratory gating. However, a recent publication showed that 4D flow MRI acquired without respiratory gating yields comparable quantitative measurements, both kinetic energy and vortex ring formation, to 4D flow MRI with respiratory gating 43. Furthermore, possible errors due to motion blurring from breathing are expected to be similar in magnitude between patients and controls.

CONCLUSIONS

Altered vortex ring formation in the blood flow during LV filling is associated with elevated viscous energy in the LV in the studied patient cohort. Further work is needed to understand the connection between increased viscous energy loss in the LV and clinical outcomes.