Measurement of Mechanical Tension at Cell-cell Junctions Using Two-photon Laser Ablation

Abstract

The cortical actomyosin cytoskeleton is found in all non-muscle cells where a key function is to control mechanical force (Salbreux et al., 2012). When coupled to E-cadherin cell-cell adhesion, cortical actomyosin generates junctional tension that influences many aspects of tissue function, organization and morphogenesis (Lecuit and Yap, 2015). Uncovering the molecular mechanisms underlying the generation of junctional tension requires tools for measuring it in live cells with a high spatio-temporal resolution. For this, we have set up a technique of laser ablation, in which we use the high power output of a two-photon laser to physically cut the actin cortex at the sites of cell-cell adhesion labeled with E-cadherin-GFP. Tension, thus is visualized as the outwards recoil of the vertices that define a junction after this was ablated/cut. Analysis of recoil versus time allows extracting parameters related to the amount of contractile force that is applied to the junction before ablation (initial recoil) and the ratio between elasticity of the junction and viscosity of the media (cytoplasm) in which the junctional cortex is immersed. Using this approach we have discovered how Src protein-tyrosine kinase (Gomez et al., 2015); actin-binding proteins such as tropomyosins (Caldwell et al., 2014) and N-WASP (Wu et al., 2014); Myosin II (Priya et al., 2015) and coronin-1B (Michael et al., 2016) contribute to the molecular apparatus responsible for generating tension at the cell-cell junctions. This protocol describes the experimental procedure for setting up laser ablation experiments and how to optimize ablation and acquisition conditions for optimal measurements of junctional tension. It also provides a full description, step by step, of the post-acquisition analysis required to evaluate changes in contractile force as well as cell elasticity and/or cytoplasm viscosity.

Background

Physical tension on junctions has been revealed by a variety of microscopy methods. These include laser ablation (Ratheesh et al., 2012; Smutny et al., 2015; Michael et al., 2016), optical tweezers (Bambardekar et al., 2015), FRET tension sensors (Grashoff et al., 2010; Borghi et al., 2012; Conway et al., 2013; Leerberg et al., 2014) and immunofluorescence for protein epitopes that are revealed under tension (Yonemura et al., 2010). Among these, laser ablation has become the most popular method, as it is easy to implement and provide a direct measurement of mechanical tension compared with other methods (e.g., FRET or immunofluorescence where the evidence for mechanical tension is more indirect). However, special considerations need to be taken to set up these experiments as well as its analysis, which are important for the correct interpretation of results. This protocol, provides the basic steps needed for the setup and optimization of laser ablation experiments in confluent monolayers of epithelial cells as well as a complete description of the image analysis procedure for measurements of initial recoil after ablation, which is an index of junctional tension.

Materials and Reagents

1. MCF-7 or Caco-2 cells from ATCC^®

   Note: This protocol can be easily extended to any other endothelial or epithelial cell line with well defined cell-cell junctions like AML12 cells.

2. Plasmids (or lentivirus) to express a junctional marker like E-cadherin-GFP.

   See Bio-protocol e937 by Priya and Gomez (2013) for lentivirus preparation for expression of mouse E-cadherin-GFP in cells knockdown for endogenous human E-cadherin. In this protocol, we describe the transfection of cells for overexpression of E-cadherin-GFP.

3. Purified plasmid DNA encoding E-cadherin-GFP (Addgene, catalog number: 67937) or any other junctional protein like ZO-1 (Addgene, catalog number: 30313), vinculin (Addgene, catalog number: 30312), MRLC (Addgene, catalog number: 35680), or the actin marker Utrophin (Addgene, catalog number: 26737)

4. Lipofectamine 3000 and P3000 reagent (Thermo Fisher Scientific, Invitrogen™, catalog number: L3000015)

5. Dulbecco’s modified Eagle’s medium high glucose with stable L-glutamine (DMEM) (Thermo Fisher Scientific, Gibco™, catalog number: 11995-073)

6. Fetal bovine serum (FBS) (Thermo Fisher Scientific, Gibco™, catalog number: 26140079)

7. PBS without Ca²⁺ and Mg²⁺ (Astral Scientific, catalog number: 09-8912-100)

8. Opti-MEM media (Thermo Fisher Scientific, Gibco™, catalog number: 31985070)

9. Hank’s balanced salt solution (HBSS) (Sigma-Aldrich, catalog number: H8264)

10. CaCl₂

11. Imaging media (See Recipes)

Equipment

1. Laser scanning confocal microscope, LSM 510 Meta Zeiss confocal microscope (Zeiss, Jena, Germany) equipped with:

   An acoustic optical tunable filter (AOTF) for bleaching of selected areas

   A heated chamber (37 °C) for live cell imaging

   A tunable two-photon laser (700-1100 nm, > 2,000 mW power, Chameleon Laser, Coherent Inc.)

   A 30 mW argon laser (458, 488 and 514 nm laser lines)

   A 60x objective, 1.4 NA oil Plan Apochromat (Zeiss) immersion lens

   Dichroic and emission filters for the use of the 488 nm laser lines and detection of GFP fluorescence

2. Glass bottom dishes, No. 1.5 Coverslip (35 mm diameter, MATTEK, catalog number: P35G-1.5-20-C or 29 mm diameter, Shengyou Biotechnology, catalog number: D29-10-1.5-N)

Software

1. ImageJ software (https://imagej.nih.gov/ij/)

2. Fiji software (http://imagej.net/Fiji)

3. MTrackJ pluging (http://www.imagescience.org/meijering/software/mtrackj/manual/)

4. Microsoft Excel (https://products.office.com/en-au/excel)

5. GraphPad PRISM software (http://www.graphpad.com/scientific-software/prism/)

Procedure

1. Cell preparation

   Expression of GFP-Tagged proteins to label cell-cell junctions could be achieved by endogenously tagging a gene of interest using genome editing tools like CRISPR, virus transduction (see Priya and Gomez, 2013) or transient transfection of a plasmid encoding a junctional protein fused to GFP using Lipofectamine 3000 as it is described below (See Appendix I).

   Note: The overexpression of plasmids should not cause any gain of function and/or alter cell’s physiology (i.e., abrupt changes in morphology).

   1. Plating and transfection of cells with E-cadherin-GFP constructs

      1. For ablation experiments, MCF-7 cells are cultured in DMEM supplemented with 10% FBS and transfected with a plasmid encoding E-cadherin-GFP.

      2. Cells are incubated at 37 °C in DMEM + 10% FBS and when these are ~80% confluent harvested by trypsinization.

      3. Single-cell suspensions are seeded on glass bottom dishes at 75% confluence and allowed to grow for 24 h for transfection with plasmids using Lipofectamine 3000.

      4. On the day of transfection, medium of cells is changed to Opti-MEM (1 ml) in the absence of serum and antibiotics and transfection performed as described in Appendix I.

      5. 24 to 48 h after transfection, and once cells are 90 to 100% confluent, cells were washed and incubated in the presence of imaging media for microscopy analysis. Figure 1 shows a representative image of the morphology of cells before ablation using 60x magnification.

         Note: The imaging media is used as it does not have phenol red, which can interfere with live cell imaging by increasing the fluorescence background. This leads to the use of higher laser power for imaging and the production of reactive species that might result toxic for cells.

2. Image acquisition

   Notes:

   • a.For the use of multiphoton lasers read carefully the Safety considerations associate to its use (Appendix IV)
   • b.For recoil measurements, please ensure analyze cells with consistent level of expression of the E-cadherin-GFP construct. Ideally overexpression levels should be kept at minimal to prevent overexpression artifacts (see also Appendix I) and being compatible with live cell imaging.
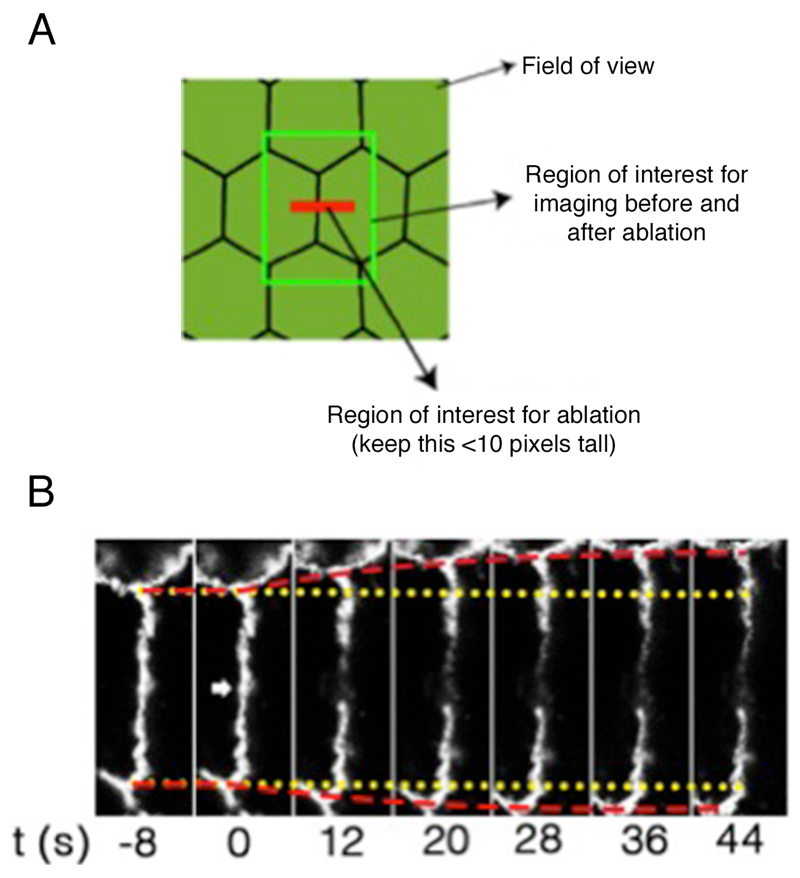
   • 1.Once identified the target cells, acquire time-lapse images of GFP fluorescence in a region of interest of 270 x 270 pixels, 0.1860119 μm/pixel (at 4x digital zoom, 0.8 μm optical section) before (2 frames) and after (5 frames, or until no more changes in junctional length are observed, ~1 min). Images are acquired with a time interval of 8 sec for a total time of 44 sec using a 488 nm laser line of an argon laser (30 mW) at 1-3% transmission (Figures 2A and 2B; Supplementary Video 1; Appendix II).

     Note: This region of interest is sufficient to acquire a single cell-cell junction to analyze its changes in length after ablation without the need of acquiring the entire field of view (512 x 512 pixels, Figure 2A) that would slow down the speed at which junctional recoil can be monitored.

   • 2.A constant region of interest of 2.8 x 1.7 μm with the longer axis parallel to the cell-cell contact (Figure 2A) was marked for ablation using 30 iterations of the Chameleon laser set at 790 nm with 40% transmission (See Supplementary Video 1 and Appendix II). This resulted in efficient ablation without significant cell damage (Figure 2B, see also Supplementary Video 2 for a case where cell damage is significant).

     Note: For quantifications and statistical analysis this acquisition procedure is repeated between 15 and 25 times per condition per experiment in at least 3 independent experiments (See also Figure 14).

3. Optimization of laser power and iterations for the ablation step (see Appendix V).

   Note: This optimization should be done using the cell line of interest expressing the preferred junctional marker in sufficient amount for efficient detection using a laser confocal microscope and perform time lapse imaging. If the marker is overexpressed, the experimentalist should try to express it at minimal levels enough for imaging and avoid any gain of function effect due to overexpression.

   1. To set up this optimization step, it is imperative to start with cells that have tension on their junctions, as a successful ablation would lead to observable elongation of the junction, i.e., recoil of the vertices that define it (Supplementary Videos 1, 2 and 4).

   2. In practice, perform initial tests with ablation settings using a high number of iterations (> 20 and increase more if necessary) and high laser power (~70% and increase more if necessary). Under these harsh conditions, significant cell damage should be observed, which will show that laser power of the infrared laser is effective and it is properly collimated (See also Appendix III, Supplementary Video 3).

   3. Once this laser power and iterations have been attained, then these parameters could be reduced stepwise until recoil of junctions is observed but with much less cell damage.

   4. While keeping constant iterations (~10-20) the laser could be reduced until a level where no more recoil is observed, but bleaching of fluorescence occurs instead. These tests would help to identify the minimal laser power needed for an efficient ablation protocol.

   5. Once this is achieved, it is possible to obtain settings in which damage to the cell membrane is minimal. This could be done by doing additional controls ablating a junction (labeled with apical junctional marker) between a cell that expresses cytoplasmic mCherry and a cell that does not. Under these conditions, it should be possible to perform ablation experiments in which observable recoil is observed but no significant flow of mCherry fluorescence from one cell to another is observed (see Supplementary Videos 2 and 3).

   6. Moreover, acquisition of a DIC image together with GFP fluorescence images allow for checking that laser power is not too high to cause damage.

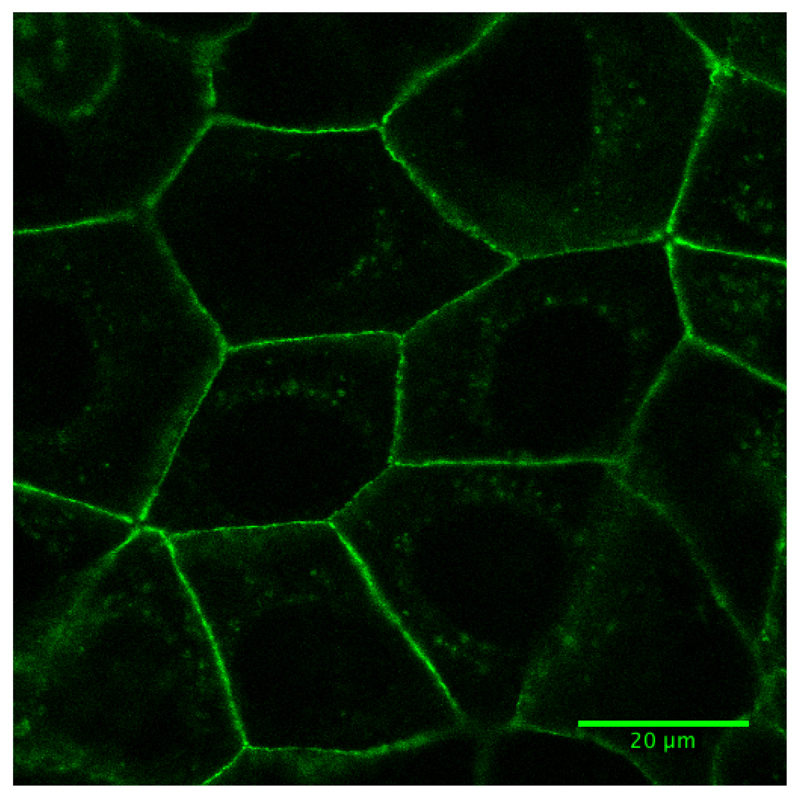
Figure 1. Fluorescence image of Caco-2 cells expressing E-cadherin-GFP.

See also Supplementary Video 4.

Figure 2. Regions of interest acquired during ablation experiments and representative still images of a junction before and after ablation.

A. Scheme of different regions of interest used for laser ablation and measurements of junctional tension; B. Slices of movie stills of a laser ablation experiment to measure tension on cell-cell junctions. Yellow lines: the original positions of vertices before laser ablation; Red lines: the real-time positions of vertices; Arrowhead: the site of ablation.

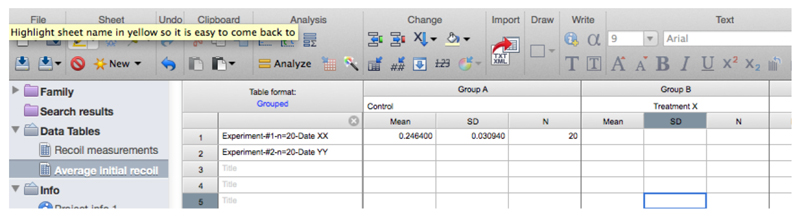
Figure 14. Table with initial recoil values and its errors obtained from non-linear regression analysis of recoil data.

Here the data is pasted into a new grouped table within the GraphPad PRISM file (see also this PRISM file provided as Supplementary File 1 for this protocol).

Data analysis

1. Image analysis

   1. Measurements of distances between vertices over time

      1. One at the time, open acquired time-lapse images (n = 15 - 25 per condition per experiment) in ImageJ software. A median filter (1 pixel) should be applied if the images are noisy and a maximal projection if Z-stacks were acquired at each time point.

      2. Use the MTrackJ plugin to measure the strain or deformation ε(t) of the cell-cell junction as a function of time after ablation. In particular, using this plugin we track the XY coordinates of each vertex that defines the ablated junction over time (see MTrackJ manual available at http://www.imagescience.org/meijering/software/mtrackj/manual/). Then, copy the X and Y values into an excel sheet. For each ablated junction we will obtain 4 columns: X(top), Y(top), X(bottom) and Y(bottom) and n rows, where n is the number of time points present in the movie (This ranges from 6 to 20, depending on how fast the system reaches the plateau).

   2. Using the tracking data generated by the MTrackJ plugin, calculate the length of the contact L(t) for each time point t as:

      $$L\left(t\right)=\sqrt{{\left[X\left(top\right)-X\left(bottom\right)\right]}^2+{\left[Y\left(top\right)-Y\left(bottom\right)\right]}^2}$$ (Eq.1)

      which in Excel can be done using the following formula

      $$\text{L}\left(\text{t}\right)=\text{sqrt}\left(\left(\text{Xtop}\left(\text{t}\right)-\text{Xbottom}\left(\text{t}\right)\right)^2+\left(\text{Ytop}\left(\text{t}\right)-\text{Ybottom}\left(\text{t}\right)\right)^2\right)$$ (Eq. 2)
   3. The amount of recoil or strain ε(t) after ablation is then measured at each time point (row) as the difference between the length of the contact at any time [L(t)] and the length of the contact before ablation [L(0)].

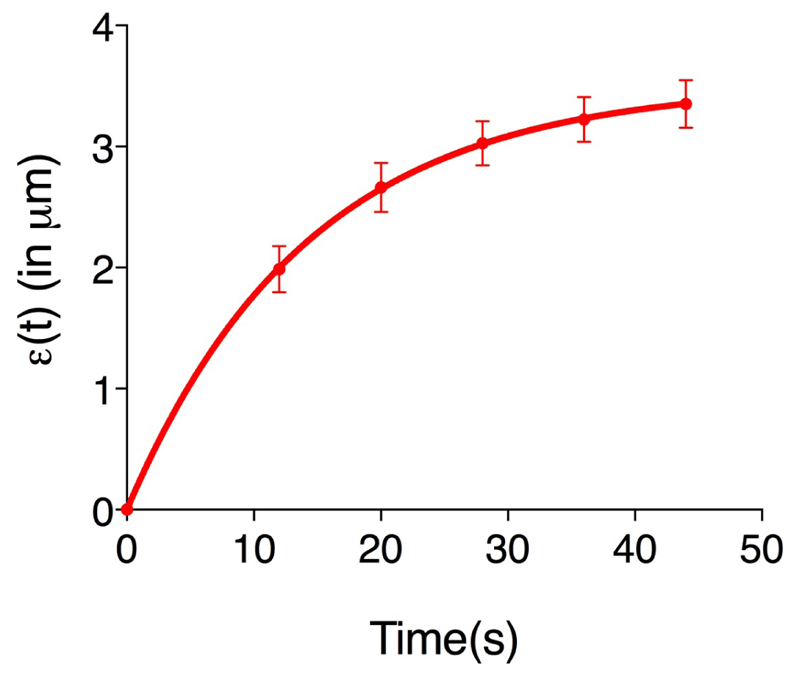
      $$\epsilon \left(t\right)=L\left(t\right)-L\left(0\right)$$ (Eq. 3)

   4. Figure 3 shows an example of experimental data obtained using Eq. 3. Where it is plotted the average recoil value from 20 ablations (See also Supplementary File 1).

2. Fitting of the data: extraction of initial recoil and k values

   Rationale: Within the time scales of the ablation experiments, if junctional strain exhibits a single exponential growth with a defined plateau after ablation, then it can be modeled as a Kelvin-Voigt fiber (Fernandez-Gonzalez et al., 2009) by fitting it to the following equation.

   $$\epsilon \left(t\right)=L\left(t\right)-L\left(0\right)=\frac{F_0}{E}\cdot \left(1-e^{-\left[\left(\frac{E}{\mu }\right)\ast t\right]}\right)$$ (Eq. 4)

   Where,

   F₀ is the tensile force present at the junction before ablation,

   E is the elasticity of the junction,

   μ is the viscosity coefficient related to the viscous drag of the cell cytoplasm.

   As fitting parameters for the above equation we introduced

   $$initialrecoil=\frac{d\epsilon \left(0\right)dt}{\mathit{dt}}=\frac{F_0}{\mu }$$ (Eq. 5)

   And

   $$k=\frac{E}{\mu }$$ (Eq. 6)

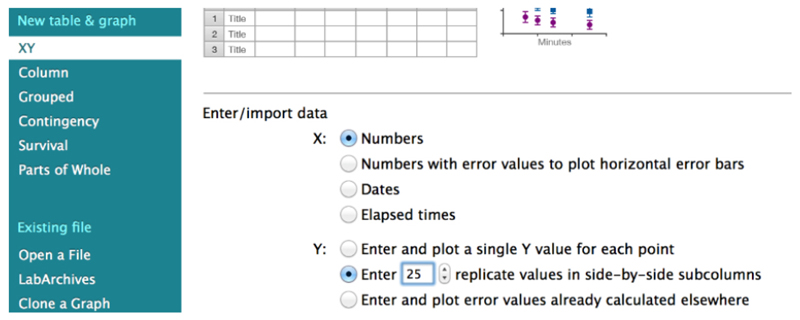
   1. From the fitting results then it is possible to extract two quantities: initial recoil, which is a measure of the underlying contractile tension on the junction before ablation and the k value, which is the ratio between the junctional elasticity and viscosity of the media.
      Note: When ablations are performed on different conditions, a change in initial recoil but not in k value is a strong indication that the tension on the junctions is affected. In contrast, simultaneous changes in initial recoil and k values are more difficult to interpret. For this last case, to could infer changes in physical tension (i.e., the amount of force) on cell-cell junctions first is needed to obtain an independent measurement of junctional elasticity (or stiffness). This can be done for example using atomic force microscopy or optical tweezers. Values of elasticity or stiffness are then used to calculate μ from the k values obtained from laser ablation experiments μ = Ek. Then, values of μ obtained in this manner, allow the calculation of the average amount of force on cell-cell junctions before ablation (F₀ = initial recoil ∗ μ) even in conditions where elasticity and or viscosity are altered.
      Fitting of the recoil data (Eq. 3) can be done using GraphPad PRISM software. The file from where the snapshots displayed in Figures 4-14 is provided as Supplementary File 1. To start the analysis, first create a new XY table project where replicate Y (n = 20 to 30) values are entered and plotted for each time point (Figure 4).
   2. Then paste the ε(t) values obtained in Excel (Eq. 3, see steps A1-A4 of the Image analysis section) into the GraphPad PRISM table (Figure 5, see also the Data Table: ‘recoil measurements’ within the Supplementary File 1 provided together with this protocol).
   3. Using this software plot the average ε(t) values by going to insert → New graph of existing data → Mean ± SEM (Figure 6).
   4. Then perform the fitting by going to the ‘fit non linear’ button (Figure 7). This will open a new window with the different options to use already available equations or to create a new equation for fitting of the data. Please note that for this and the following steps it might be useful having read the general guidelines for non-linear regression using GraphPad Prism available at: http://www.graphpad.com/guides/prism/7/curve-fitting/index.htm?reg__curve_fitting_with_prism_6.htm
   5. In the new dialog window, create a new equation for fitting (Figure 8).
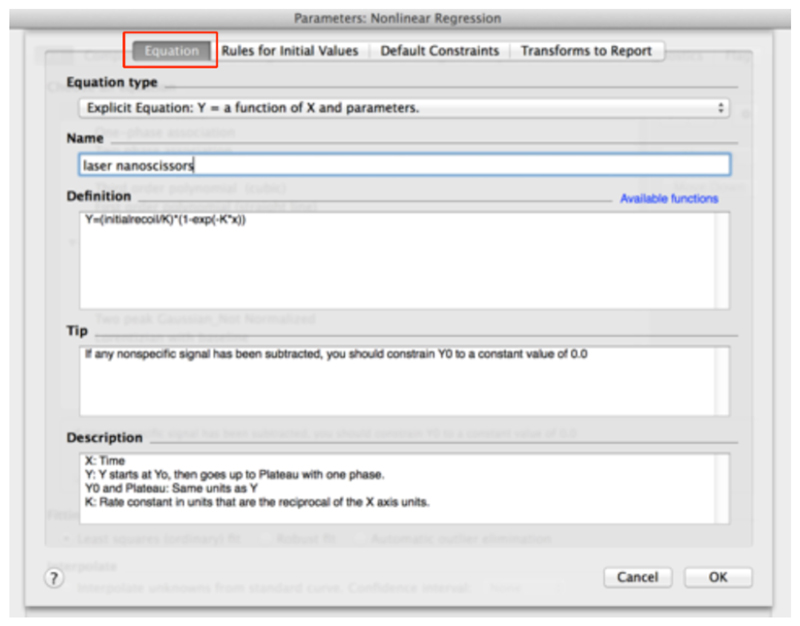
   6. In the ‘Equation’ menu (see top of Figure 9)
      1. Assign a Name to the new Equation, for example ‘laser nanoscissors’.
      2. Paste the following equation within the Definition field:

         $$\text{Y}=\left(\text{initialrecoil}/\text{K}\right)*\left(1-\text{exp}\left[-\text{K}*\text{x}\right]\right)$$

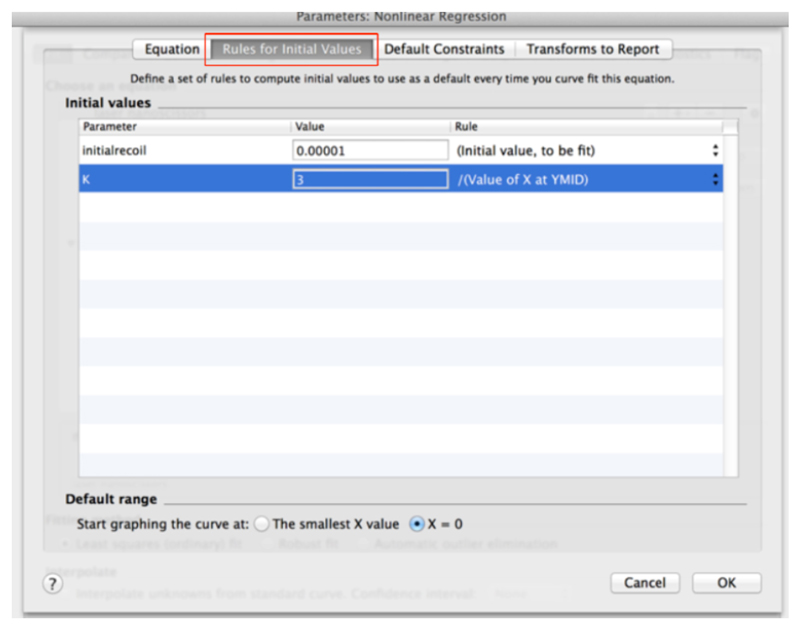
         (see also Figure 9)
      3. Then, go to the next tab ‘Rule for Initial Values’ in the same window and select the following conditions for the initial values of parameters for fitting (Figure 10).
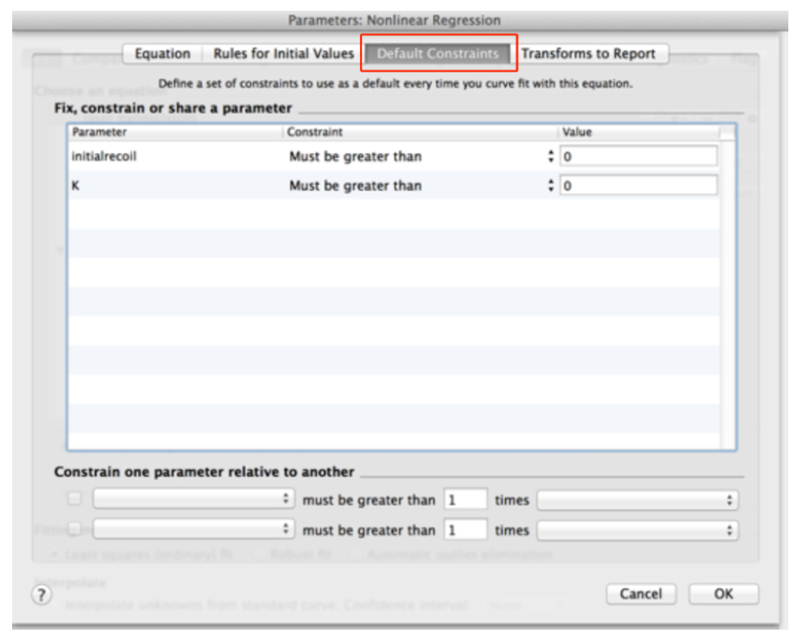
      4. Go to the ‘Default constraints’ tab and assign values greater than zero for the fitting parameters initial recoil and k (Figure 11).
      5. Clear any transformation to be reported in the last tab of this window (Transform to report, Figure 12). These are not further required for this analysis.
      6. Accept all the changes by pressing the ‘ok’ button.
      7. Fit the data (least squares and without interpolation of unknowns). You will obtain a table with the results of the fitting (Figure 13).
      8. Copy the row with the different ‘initial recoil’ (3rd row of the results, see also Figure 13) and ‘k’ values (4^th row of results) together with their standard errors (SD, rows 6 and 7, respectively) of the different experimental conditions and paste them into another sheet in GraphPad PRISM (see sheet ‘Average initial recoil’ within the Supplementary File 1, see also Figure 14). From there it is possible to calculate average values of initial recoil and k values from different conditions and for independent experiments (different dates) and perform statistical tests across these to evaluate differences in recoil velocity (i.e., tension).
      9. From the above model, it can be deduced that differences in the tensile force present on junctions can be estimated by comparing initial recoil values between different conditions assuming that the viscosity is not significantly different between them. In order to assess whether this assumption is valid during these experiments, it is important to compute the rate constant, k, between different conditions as this would change if viscosity or elasticity of the junctions were significantly altered. No significant change in k values between different experimental conditions (assessed by t-test or ONE-WAY ANOVA) suggests that changes in tensile force are the dominant contributors to the changes in initial recoil velocity.

Figure 3. The records of ε(t), vertex separation minus vertex separation at time = 0.

The plots are mean values of 20 junctions analyzed. Error bars are ± SEM (See also Supplementary File 1).

Figure 4. Snapshot of the GraphPad PRISM dialog window for the creation of a new XY project for the analysis of junctional recoil data.

Figure 5. Snapshot of a XY table that contains the recoil data from an experiment.

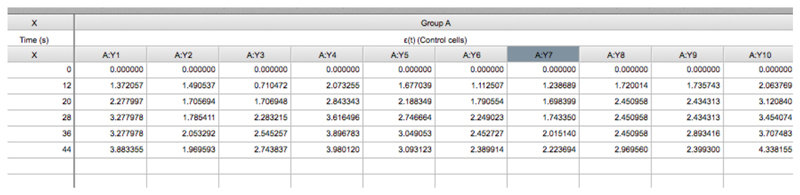
The X column contains the values of time (in seconds) at which images were acquired. Time = 0 seconds corresponds to the time point acquired just before ablation. The Y component correspond to the ε(t) data derived from control cells (Eq. 3) and this data is grouped within group A. The values A:Y1, A:Y2, A:Yn corresponds to the recoil values from single junctions that were ablated. See also Supplementary File 1.

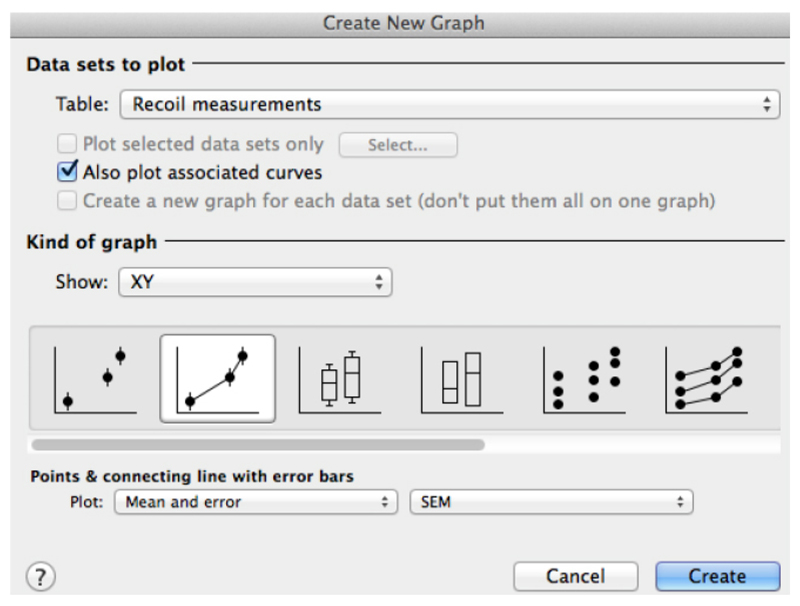
Figure 6. Snapshot of the ‘Create a new graph’ window in GraphPad PRISM for the plot of recoil results.

Figure 7. Snapshot of the fitting analysis options in GraphPad PRISM software.

Figure 8. Snapshot of the non-linear fitting menu within the GraphPad Prism software.

Figure 9. Adding the equation for initial recoil measurements within the non-linear functions of GraphPad PRISM.

Figure 10. ‘Rule for Initial Values’ for fitting parameters of recoil measurements within the non-linear regression menu in GraphPad PRISM.

Figure 11. Definition of default constrains for fitting parameters of recoil data using non-linear regression.

Figure 12. ‘Transform to Report’ menu within the ‘create New Equation’ window in Non-linear regression analysis.

Figure 13. Snapshot of the results from the non-linear regression of the recoil data showing the values for initial recoil and k.

Recipes

1. Imaging media

   Hank’s balanced salt solution supplemented with 10 mM HEPES pH 7.4 and 5 mM CaCl₂