Positron Emission Tomography: Current Challenges and Opportunities for Technological Advances in Clinical and Preclinical Imaging Systems

Abstract

Positron emission tomography (PET) imaging is based on detecting two time-coincident high-energy photons from the emission of a positron-emitting radioisotope. The physics of the emission, and the detection of the coincident photons, give PET imaging unique capabilities for both very high sensitivity and accurate estimation of the in vivo concentration of the radiotracer. PET imaging has been widely adopted as an important clinical modality for oncological, cardiovascular, and neurological applications. PET imaging has also become an important tool in preclinical studies, particularly for investigating murine models of disease and other small-animal models. However, there are several challenges to using PET imaging systems. These include the fundamental trade-offs between resolution and noise, the quantitative accuracy of the measurements, and integration with X-ray computed tomography and magnetic resonance imaging. In this article, we review how researchers and industry are addressing these challenges.

1. INTRODUCTION

In vivo structural imaging provides valuable data in clinical and preclinical studies, but to reveal the true structures of the physiological time-varying processes that explain disease phenomena it is necessary to combine morphological information with in vivo molecular imaging. Of all the tomographic molecular imaging modalities, positron emission tomography (PET) imaging probably offers more translational possibilities than any other modality due to its combination of sensitivity and quantitative accuracy. PET is a noninvasive imaging modality that provides physiological information through the injection of radioactive compounds (radiotracers), detection of radiation, and reconstruction of the distribution of the radiotracer. PET imaging has evolved from an imaging modality used for research to become a standard component of diagnosis and staging in oncology; it is also used for specific neurological and cardiovascular indications. This is due to the clinically useful information that it provides about tissue and organ function, and status, through the use of radiolabeled molecular imaging agents. The type of information provided depends on the imaging agent and the disease and can include detection, classification, staging, prognosis, treatment planning, assessing response to therapy, and surveillance.

Combining PET imaging with the anatomical imaging delivered by X-ray computed tomography (CT) or magnetic resonance imaging (MRI) provides the synergistic combination of information about what (from PET) with information about where (from CT or MRI). In addition, the anatomical information from CT and MRI can often be used to provide estimates of the quantitative corrections needed for accurate PET imaging. These synergies, when combined with advances in PET technologies, have led to a fertile area for the development of new imaging methods and applications. This review outlines the technological advances made in clinical and preclinical PET imaging systems, as well as the major current challenges, and opportunities for further advancement. These advances and challenges are summarized in Table 1.

Table 1.

Positron emission tomography (PET): new applications and their readiness for implementation

New technology	Problem addressed	Readiness level	Application	Comments
Faster and cheaper scintillators	Increases count-rate performance, light output (with higher energy and better spatial resolution), and usability; enables time-of flight PET imaging	In production, widely available	Cost reduction in clinical scanners; higher image quality in preclinical systems	Radioactive isotopes in the formulation introduce background noise that could limit the signal-to-noise ratio in very low count applications
Subsurface laser engraving of scintillators	Facilitates the manufacture of crystal arrays, reduces costs, increases sensitivity by avoiding the need for reflectors in between crystals	Prototypes are being tested, mainly for preclinical applications	Clinical and preclinical, but more relevant for preclinical use due to the higher complexity of the crystal matrices	Great potential for introducing alternative, affordable coding schemes for depth-of-interaction and light sharing
Solid-state photodetectors	Reduces the cost of the detectors; enables magnetic compatibility for combined PET–MR imaging	In production; several manufacturers offer alternatives and yearly updates	Used in combined PET–MR scanners; they reduce the cost of the PET gantry; new applications may be based on more compact detectors	Semiconductor technology is highly competitive; newer and better devices will appear, and their cost will be reduced over time
Dual-energy CT attenuation correction	Quantitative accuracy of PET imaging	Already developed for CT, but clinical need for combined PET–CT imaging not demonstrated yet	Clinical quantitative imaging	Already applied in preclinical imaging, but no applications yet
Scatter correction in systems with long axial extent	Larger field of view increases the scatter fraction	To be developed	Clinical systems	Monte Carlo simulations and single-scatter approximation approaches will require intensive computation
Clinical 4D (time-varying or gated) imaging	Difficulty of adopting 4D techniques into clinical routines	Widely used for preclinical applications; already adopted in some clinical applications, including cardiology and planning for radiation oncology treatment	Relevant to any imaging requiring suppression of respiratory-motion effects	Clinical applications are limited to simple models due to limitations in the signal-to-noise ratio; movement suppression is slowly being adopted
Multi-isotope PET imaging	Limitations of single-radiotracer imaging	Under development	Simultaneous imaging of different physiological processes	Several approaches have been reported in the literature, but none has been adopted in clinical or preclinical applications
PET–MR imaging	Soft-tissue contrast in anatomical imaging, e.g., brain	Commercially available	Under development	Attenuation correction issues not completely resolved

Abbreviation: CT, computed tomography; MR, magnetic resonance.

2. THE PHYSICS OF PET IMAGING

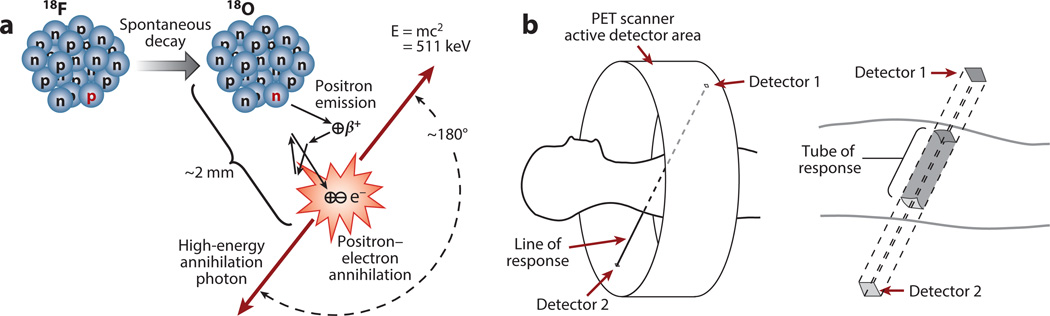
The physics that enable PET imaging are based on the emission of a positron by a neutron-deficient radioisotope. This is illustrated in Figure 1a for fluorine-18 (¹⁸F), the most commonly used radioisotope. As the radioisotope decays to a stable state, the emitted positron travels a short distance (typically 1–2 mm) and interacts with an electron; this interaction annihilates both the electron and the positron, thus producing two high-energy photons. The photons travel in opposite directions along an approximately straight line, and can be detected outside the body by the PET scanner.

Figure 1.

(a) Creation of two anticollinear 511 keV annihilation photons following positron emission by the radioactive decay of fluorine-18 (¹⁸F) (half-life, 110 min). The neutron-deficient ¹⁸F isotope decays to the stable isotope oxygen-18 (¹⁸O) by converting a proton to a neutron and thus emitting a positron (a process known as conservation of charge). After losing most of its kinetic energy via random scattering while traveling a short distance (i.e., the positron’s range is 2 mm in this case), the positron encounters its antiparticle, the electron. The resulting annihilation of both particles generates two 511 keV annihilation photons traveling in opposite directions. The small deviations from 180° are due to random variations in the residual momentum at the time of annihilation. (b) Schematic of the positron emission tomography (PET) imaging process. The patient is placed inside the gantry and surrounded by a ring of detectors that define the scanner’s active sensor area. When two annihilation photons are detected within a few nanoseconds of each other, the two points of interaction define a line of response. Because the detector’s elements have finite dimensions, the line of response schematically represents the ensemble of coincidences that fall inside the tube of response, which is defined by the size of the detector’s elements.

The detectors use scintillator crystals coupled to photomultipliers (discussed in Section 3). A review of the properties of these detectors can be found in Reference 1. The first limitation in PET imaging is the noise, which is driven by the number of individual 511 keV photons detected. In turn, this is determined by the density of the scintillator, the count-rate capabilities of the scanner, and the amount of radiation injected into the patient. The second limitation is the spatial resolution, which is determined by the variability in estimating the interaction point of the 511 keV photon in the scintillator. In turn, this is affected by the optics of the scintillator, the number of optical photons emitted, and the fidelity of the photomultiplier tubes and associated electronics. These factors impose the noise and resolution characteristics of the PET imaging process.

If two photons are detected in a short-coincidence time window (typically 1–10 ns), the joint detection is called a true-coincidence event for the line of response (LOR) joining the two detectors (Figure 1b). More accurately, the parallelepiped joining the two detector elements is called a tube of response. The total number of true-coincidence events detected by the two detector elements will be proportional to the total amount of radiotracer contained in the tube of response. This is the key to PET imaging. Based on this relationship, one can process the coincidence events to accurately reconstruct the distribution of the radioisotope. For time of flight (TOF) PET imaging systems, the differential timing of the detection of the two photons is used to localize the annihilation along the LOR.

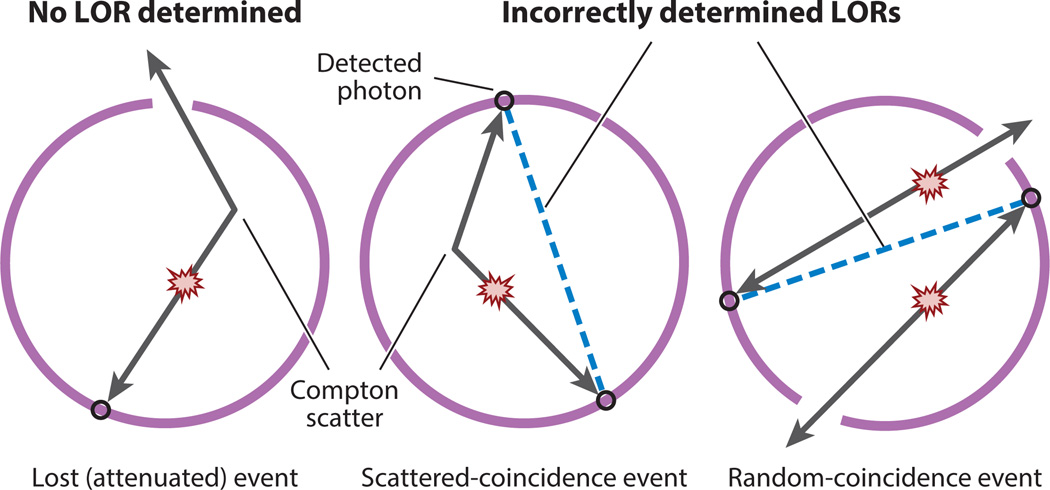
However, before this can happen, confounding physical effects must be estimated and compensated for. The most important confounding effects are patient-specific, and they have to be reestimated for each scan; these confounding effects are attenuation, scattered coincidences, and random coincidences (see Figure 2 and Section 4). It is also possible to consider the patient’s motion (e.g., movements caused by respiration) as a confounding effect (Section 6). More detailed descriptions of the physics of PET imaging can be found in Reference ².

Figure 2.

Confounding physical effects that cause bias in positron emission tomography (PET) coincidence imaging. (Left to right) Attenuation: One of the annihilation photons does not reach the detector either because it has undergone absorption or Compton scattering that deflects it away from the detectors or because it does not interact in a measureable way with a scanner detector. Scattered-coincidence event: One of the two photons undergoes Compton scattering and changes its trajectory, but both photons are still detected, thus defining an incorrect line of response (LOR). Random-coincidence event: Two simultaneous annihilations produce two pairs of photons; if for any reason two of the photons belonging to different annihilations are detected in a time coincidence, they will define a randomly oriented (i.e., incorrect) LOR.

In practice, with patients or animals, a biologically functional compound is first labeled with a positron-emitting radioisotope. Then the radiotracer is injected into the living subject, and it preferentially accumulates where the compound is metabolized. The biodistribution of the radiotracer varies over time, and this dynamic information is sometimes used to analyze the image (Section 5).

3. NEW DETECTOR TECHNOLOGIES

Improvements to the quality of PET images are made by increasing the sensitivity and spatial resolution of the image, which requires an array of detectors that can capture the largest possible fraction of the photons emitted by the target object at the highest possible rate and with the best possible spatial accuracy. In addition, the detectors should possess the highest possible energy resolution to reduce the effects of scattered radiation (3).

Accordingly, new designs for detectors begin with new scintillator materials because this is the preferred method for detecting annihilation photons. Scintillation crystals produce fluorescent light after being excited by a 511 keV photon that has been scattered by or absorbed into the crystal. The intensity of the pulse of visible light contains information about the energy of the original photon that caused the scintillation. Therefore, annihilation photons can be characterized by detecting and counting the visible light photons with a photodetector. A good scintillator crystal should have high stopping power for 511 keV annihilation photons and high efficiency for converting the energy from the annihilation photon into detectable light; it is also desirable that the resulting light pulse occurs within a very short time, and the intensity should be proportional to the energy of the annihilation photon. The optical properties of the crystal are also important: The crystal must be transparent to the wavelength of the fluorescent light to avoid self-attenuation, the index of refraction must match that of the photodetector to optimize the collection of light, and the crystal should be rugged enough to be processed and manipulated during manufacturing.

Modern scintillators produce shorter and more intense light pulses compared with earlier crystals, such as BGO (bismuth germanate), which used to dominate PET-detector technology. BGO has a high density and high atomic number, so the 511 keV photons have a large probability of interacting with the crystal, but the BGO low light production limits the energy resolution of the detector, thus resulting in more scatter in the final image, and its long decay time precludes its use in applications with high count rates. Newer, more luminous, and faster scintillator crystals, such as LSO (lutetium oxyorthosilicate) and LYSO (lutetium yttrium oxyorthosilicate) (4, 5), have been used to build detectors that have better energy resolution and faster light decay times that can reduce undesired effects, such as the piling up of events on the detector, degradation of event timing, or background scatter. These new scintillators also enable clinical TOF PET imaging (6–8), and they are being used in layered combinations (known as phoswichs)—of LSO, LYSO, LuYAP (cerium-doped lutetium yttrium perovskite), GSO (gadolinium oxyorthosilicate), LaBr3:Ce (cerium-doped lanthanum bromide), Ce:GAGG (cerium-doped gadolinium aluminum gallium garnet) (9), and others (10)—in small-animal PET scanners to implement depth of interaction (DOI) corrections on long crystals (11), which increases spatial resolution and reduces parallax error (12).

A drawback of using scintillator crystals made from lutetium (¹⁷⁶Lu) is that it is a radioactive contaminant that produces a natural background coincidence count rate, which increases the noise in low count-rate applications (13). Another drawback to using modern scintillators is their high cost. Alternative ceramic scintillators may ameliorate this limitation (for example, BaAl4O7:Eu²⁺); although they are too slow for PET time-coincidence imaging, they compete with currently used scintillator crystals when used for single-photon imaging (14). The mass production of transparent, ceramic scintillators may make them more affordable than current scintillators, and this may open new opportunities to confront the design of next-generation PET scanners (Section 3.3).

Pixelated scintillator crystals covered by reflectors perform better as detectors than those that use monolithic crystals (15). However, the need to individually manipulate the pixelated crystals, and to paint or apply the reflector surfaces, makes their production time consuming and expensive. An alternative to using pixelated crystals is to use monolithic crystals with sophisticated algorithms to resolve the scintillation point of occurrence in 3D space (16). More recently, a process called subsurface laser engraving (SSLE, also known as a laser-processed boundary) has been used to build arrays of scintillator pixels from monolithic crystals (17, 18). Because an automated laser engraver processes the crystals, manufacturing should become more affordable and reliable. In addition, creating reflective surfaces using SSLE rather than by cutting material away, allows scintillation material to be retained between crystals. As a result, the sensitivity of the detector is increased. A further advantage of SSLE is that the shapes of detector elements can be optimized, for example by combining continuous sections with pixelated ones that have been multilayered, tapered, or texturized to introduce DOI encoding schemes (19). Finally, it should also be noted that 3D printing techniques, using different materials, have been devised to efficiently manufacture reflectors and light guides that extract the maximum light from monolithic and pixelated scintillator arrays.

3.1. Solid-State Photodetectors

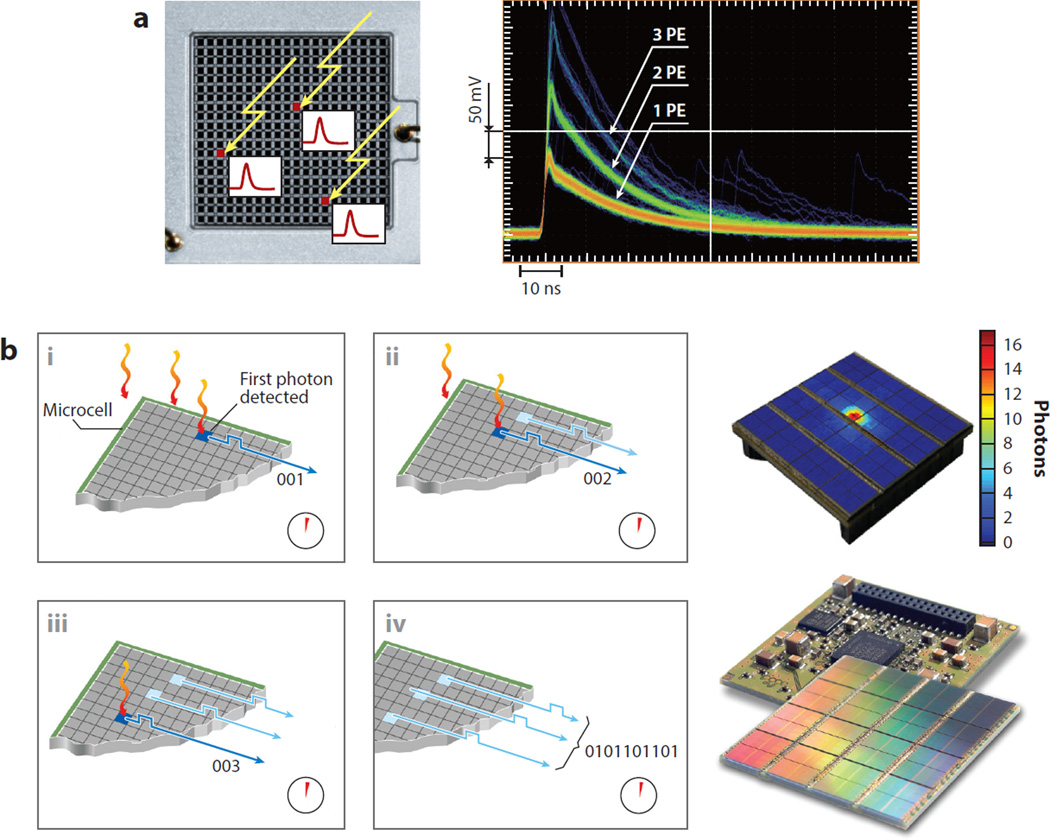
The mass production of semiconductor photodetectors in radiation detector engineering has enabled new molecular imaging modalities, such as simultaneous PET imaging and MRI (20). Different manufacturers name their photodetectors differently, depending on the manufacturing process and mode of operation. Examples include the silicon photomultiplier, multipixel photon counter, single-photon avalanche diode, and avalanche photodiode (21), all of which use a matrix of individual photodiodes that operate in or near avalanche mode. The sum of the signals from all individual diodes is a measurement of the amount of light deposited in the array, and this, in turn, is related to the light produced by the scintillator (Figure 3a). These new devices have had important impacts on detector design: They have an improved, effective sensing area in comparison with traditional photomultipliers; the time resolution increases their potential in terms of TOF capabilities; their power requirements are lower; their packaging is more robust and compact; and they are compatible with the high magnetic and electric fields present inside an MR scanner.

Figure 3.

(a) (Left) Semiconductor photodetectors using an ensemble of photodiodes; in this case, a matrix of 20 × 20 elements produces an electrical analog signal that is proportional to the number of scintillation photons reaching the sensor. The signal is built by adding the contributions of each individual photodiode avalanche. Three γ-rays impinging on the three red pixels will produce a signal (labeled as “3 PE”) that is the result of the addition of the three avalanches produced at each individual element. (Right) The output pulse is labeled in photoelectrons (PE). Images courtesy of Hamamatsu Photonics K.K. (Hamamatsu City, Japan). (b) In digital photocounters, each individual signal from each photodiode is treated as a discrete or integer (i.e., digital) increment. The time of arrival of the first scintillation photon at the digital semiconductor photodetector (i) marks the beginning of the period for counting the total number of arrivals during a given interval (ii). Once the period ends (iii), the total count of individual contributions becomes a digital number (iv) that is proportional to the number of photons reaching the detector, and that number, in turn, relates to the energy of the γ-photon that originated the scintillation. All processing is done using digital electronics. Drawings courtesy of Philips GmbH (Herrsching, Germany).

The digital photon counter (DPC) is a variant of conventional silicon photomultiplier (SiPM) detectors, and it operates intrinsically in a digital mode (22). The DPC treats the signal from individual photodiodes as the basic quantum of information and, instead of adding them in analog mode, counts them to produce a digital code that is related to the number of photons (Figure 3b). In principle, this method should produce noise-free data that are precisely timed with respect to a master clock, thus producing high-resolution measurements of time. These novel characteristics of the DPC have created high expectations about the performance of the PET scanners that use them, and the first commercial clinical systems are appearing.

Detectors based on CZT (cadmium zinc telluride) do not use scintillators because they directly convert ionizing radiation to charge production, providing higher energy and spatial resolutions than scintillator-based PET detectors. However, their poor spectroscopic performance at high energies and their performance in terms of timing are lower. To overcome the lower efficiency in photopeak detection, designers have stacked these devices, providing the additional advantage of gaining DOI information. However, the poor timing performance and the complexity of the system are difficult to compensate for, limiting the potential application of these devices (23).

In summary, the selective combination of these new scintillators coupled with silicon photo-multipliers presents new alternatives for designing detector modules with very high energy and spatial resolutions (<1 mm), increased sensitivity, and more accurate timing. These capabilities are important in highly demanding applications, such as rubidium-82 chloride (⁸²Rb) cardiac imaging (24), oncological head and neck imaging (25), radiation therapy procedures in which detecting a hypoxic region is crucial for determining prognosis, radioimmunotherapy imaging (26, 27), or for the early detection of neurodegenerative dementias, for example by imaging tau proteins to detect Alzheimer’s disease using highly specific radiotracers (28).

3.2. Improved Data-Acquisition Systems

Signals coming from PET detectors carry information about the detected event in the characteristics of the electrical pulse generated by the charge collection. After determining the precise timing of the pulse’s arrival, the pulse’s waveform is integrated and digitized. In this process, the full description of the original shape of the pulse is lost. However, it is known that the shape of the pulse contains additional information that could be extracted and used to improve the processing of the pulse and, in turn, the quality of the image reconstructed from the ensemble of pulses. New, fast, free-running analog-to-digital converters are ubiquitous in modern communication systems. They can be used to implement waveform digitization of the detector pulses, and from that, researchers can derive additional information that can be used by the binning and image-reconstruction algorithms. This extra information can also be used, for example, to remove pulse pileups in situations with a high count rate (29), in TOF imaging (30), and to implement DOI correction (31).

An alternative to analog-to-digital converters is the time-over-threshold converter, which obtains accurate information about timing and energy by converting the charge measurement to a time measurement. This technique allows for significant simplification of the electronics by reducing circuitry and power consumption, characteristics that become relevant to applications such as handheld probes, MRI that is compatible with PET detectors, or large-scale systems with a high number of channels. One of the drawbacks of the time-over-threshold method has been the intrinsic nonlinearity of the method, although recent implementations have compensated for that inconvenience, improving its performance to the point where it can be used in TOF systems (32).

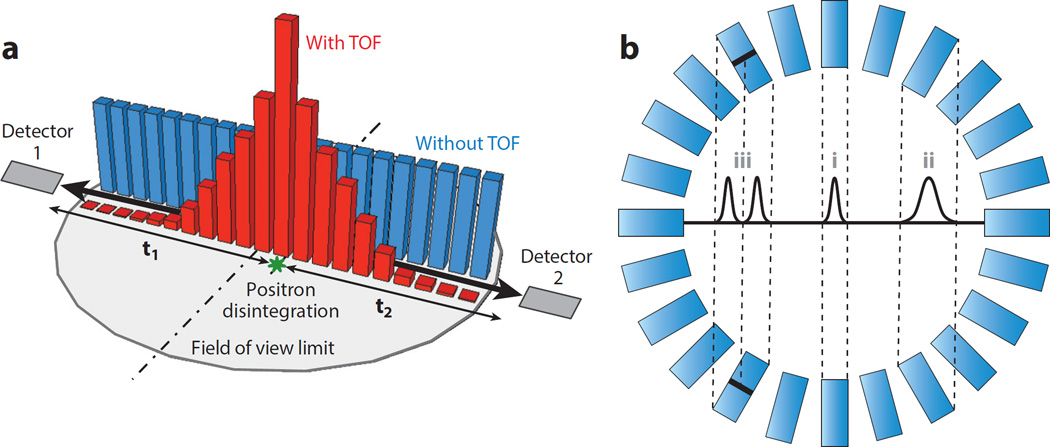
In TOF PET imaging, the measurement of the precise difference in the arrival times of the two 511 keV annihilation photons (Figure 1) can be used to reduce uncertainty about the location of the annihilation locus and thus improve image quality. In the situation depicted in Figure 4a, the offset in distances from the annihilation point to the detectors causes a difference in detection times, described by Δt = t₂ − t₁, albeit with some variability due to the timing resolution. This information enables localization of the annihilation to a limited region between the two detectors. This small time difference is Δt = 2d/c, where d is the distance from the scintillation to the center of the segment defined by the two detectors, and c is the speed of light (6). Currently, detectors and instrumentation technology in clinical scanners can provide a timing resolution no better than 200 ps, which translates into a 3 cm spatial difference that is not small enough to allow direct reconstruction of a high-resolution image. However, when TOF measurements are fed into the reconstruction algorithms as a priori information, the image quality is significantly improved (33).

Another challenge of current detector technology is the DOI effect, or parallax error: This appears when attempts are made to increase the sensitivity of a PET system by reducing the diameter of the ring or increasing the thickness of the crystal. As the relative thickness of the detector increases, the spatial resolution degrades increasingly as one moves from the center to the edge of the field of view (FOV) (12). Such nonuniformity in resolution across the FOV has adverse consequences for the visualization and the quantification of target activity. Different techniques can be used to deal with this problem by estimating the DOI: Previously mentioned combinations of different scintillators can be used in a phoswich (34) (Figure 4b), or stacks of photodetectors and scintillators with properly treated surfaces can be configured (35). Although DOI is very important for high-resolution preclinical imaging, it may not be that relevant in clinical scanners because its effect is small compared with the overall resolution of the scanner itself. However, in high-resolution brain imaging, the DOI may become more important.

Figure 4.

(a) The time of flight (TOF) is defined as the interval between the arrival (t₁ and t₂) at their respective detectors of the two photons resulting from the disintegration of the positron. Both photons travel at the speed of light, and if positron annihilation occurs at the midpoint of the line of response (LOR), t₁ will be equal to t₂. If that is not the case, then the time difference (t₁-t₂) can be translated into a distance from the LOR midpoint to the most probable annihilation point, and that will be the location where the probability density function should be centered (red) for the disintegration occurrence used in the reconstruction model, instead of using a less accurate uniform distribution (blue). (b) The detector sensitivity is directly proportional to the crystal thickness, but thicker crystals produce larger cross sections when the LOR defined by the two detectors in coincidence does not cross the detector ring center. The resulting effect is a deterioration in the effective resolution from the center (i) toward the edges (ii). The Gaussian profiles depict the LOR spatial response to a point source placed in the center of the cross section: The narrower the cross section, the better. A scintillator crystal that can estimate the depth of interaction (DOI) defines several LORs for the same non-DOI LOR. This is depicted here for a two-layered crystal that defines two narrower LORs (iii) instead of just one (ii). Black lines in the scintillator crystals indicate the separation between the front layer and the back layer.

3.3. System Designs: New Geometries

An alternative to the basic PET scanner, which uses rings or ring sections of opposing detectors, is to use different geometrical configurations for specific applications in different organs. These geometrical configurations optimize the positioning of the detectors to improve spatial resolution and sensitivity in the region of interest (ROI), thus increasing the detection ability and quantitative accuracy of the resulting image. An example is the case of brain imaging, for which a proposal based on the geometry of a helmet with the addition of chin detectors has been shown to increase the supported solid angle of the scanner, thus maximizing its geometric efficiency (36).

A promising alternative to organ-adapted designs is the use of inserts or probes with high-resolution detectors that can be used as magnifiers (37) to define virtual PET pinholes (38) or implement zoom-in capabilities (39). In these configurations, a conventional PET scanner is set in coincidence with the high-resolution insert detector or endoscopic probe in such a way that the new set of LORs oversamples the area of interest. This new information is used by the reconstruction algorithm to complement the simultaneous collection of standard data performed by the detector ring in such a way that the ROI can be reconstructed with higher resolution and sensitivity. This approach may not be as optimal as using customized geometry, but it has the advantage of improving imaging in the breast (40, 41), prostate (42), and other organs of interest using existing PET scanners, with investment needed only for an additional imaging probe.

Whole-body (WB) PET imaging is an option that could benefit from technological advances (43). Currently, WB imaging is achieved by moving the patient’s bed from head to toe, thus exposing different body sections to the detectors and then stitching together those sections to present a WB image. The problems with this approach are obvious: Different parts of the body are scanned at different time points; thus, there are differing biodistributions of the radiotracer. The idea of covering the full length of the human body with detectors (44, 45), or even with a spherical PET scanner (46), is not new, but there has been a revival of interest in WB PET imaging. This is motivated by its potential to evaluate the pharmacological kinetics of new imaging radiotracers in different organs of interest simultaneously as well as by the tremendous increase in sensitivity that occurs due to the much larger, solid angle. However, the increase in sensitivity comes with an increase in the scatter fraction along with the requirement for a data-acquisition system capable of coping with enormous event rates. Initiatives are being undertaken to address these issues as well as the high cost of building WB scanners with available technology. A recent study evaluated many of these issues, trying to optimize the design of a viable WB scanner (47).

4. NEW ALGORITHMS FOR IMAGE RECONSTRUCTION AND DATA PROCESSING

4.1. Quantitative Corrections

Ensuring quantitative accuracy requires estimating the confounding effects described in Section 2. These include, in rough order of effect size, attenuation; random coincidences; scattered coincidences; patients’ movements; geometry-based variations in efficiency; the system’s dead time; radioisotope decay time and branching ratio; detector resolution; and variations specific to the detector element in efficiency, signal gain, coincidence timing, energy resolution, and event positioning. A description of these effects is beyond the scope of this review, but useful overviews are provided in References 48 and 49.

These effects must first be estimated before they can be corrected. Scanner-dependent effects can be complex and time-consuming to estimate, but in general they require only infrequent updates—for example, quarterly, annually, or only once for a class of scanners using calibration procedures. Patient-dependent confounding effects, however, have to be estimated for each imaging session, and so are much more time sensitive. There is no fixed guideline for processing times because images are analyzed and interpreted after the imaging session. However, a useful rule of thumb for clinical systems is that to prevent delays in the data queue, the total time for image processing and reconstruction should match the duration of the imaging session. Clinical imaging sessions typically last from 30 to 60 min, depending on local protocols. For preclinical or research imaging protocols, there is much more flexibility, depending on scanner usage. Here we focus on three patient-dependent effects that present unique challenges: attenuation, scattered coincidences, and random coincidences. Respiratory motion is covered in Section 6.2.

4.1.1. Attenuation

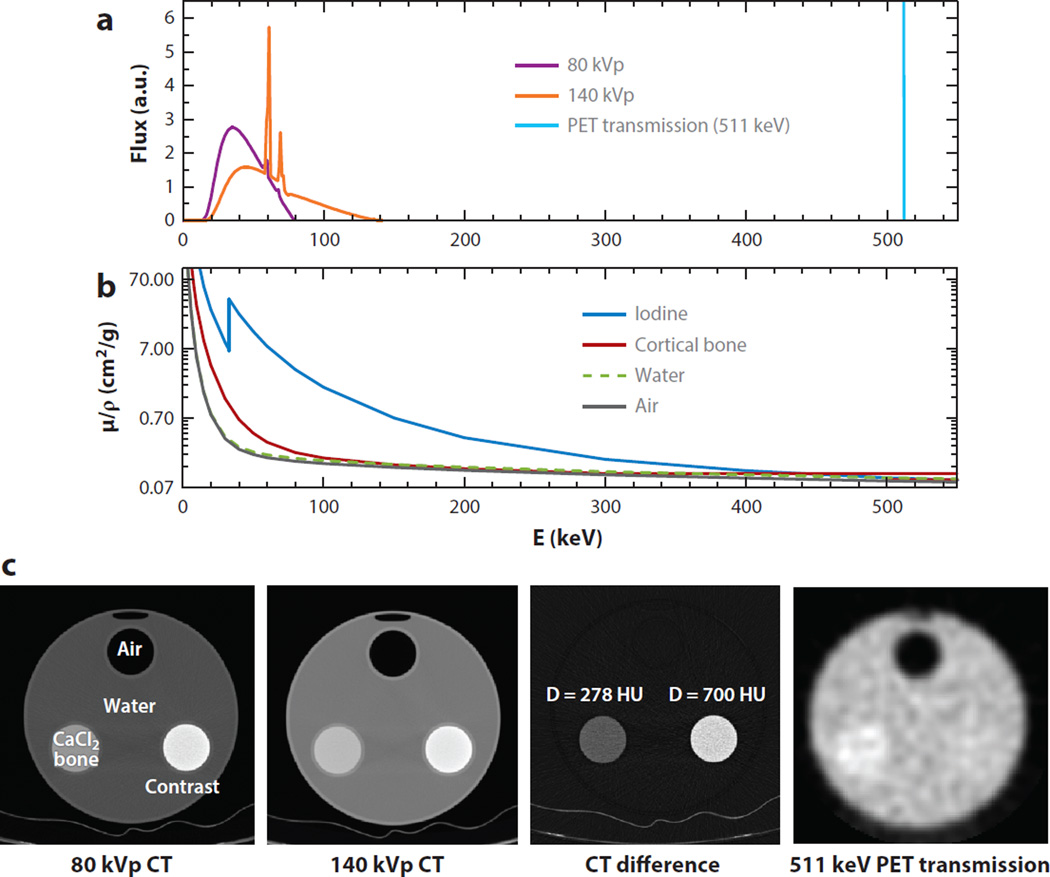
Stand-alone PET systems (i.e., those used without CT) obtain their attenuation maps of a transmission scan by rotating a positron-emitting rod source around the subject (2). However, with the advent of combined PET and CT scanners roughly 15 years ago, standalone PET scanners have disappeared from the clinical market. The standard approach used by dual-mode PET–CT scanners is to convert the CT image to attenuation coefficients for 511 keV photons using a bilinear transformation with different scale factors for soft tissue and bone. This approach has also been applied to preclinical imaging systems that have separate PET and CT scanners. The bilinear transformation method is based on the observation that the mass attenuation coefficient (the linear attenuation coefficient divided by density) is the same for all soft tissue but not for bone, due to the higher photoelectric absorption cross section. In addition, the attenuation of PET coincidence data at 511 keV primarily occurs due to Compton scattering, which is determined by density, so the mass attenuation coefficient for all materials at 511 keV is constant. Thus, only scale factors for bone and soft tissue are needed (50). Although this works well for soft tissue, CT-based attenuation correction is challenging in bone imaging and when nonbiological materials are present, such as iodine-based contrast agents, implants, or other devices (51). In addition, when combined PET–MRI scanners are used then CT is not available, as is further discussed in Section 6. To address the challenges of CT-based attenuation correction, several multienergy algorithms have been developed for use in both clinical and preclinical imaging. The fundamental physics are illustrated in Figure 5, which shows three closely related components: the CT and PET transmission spectra of photon fluence versus energy, and the mass attenuation coefficients over the same energy range. Note that air and water are very similar, unlike bone and iodine. Also shown are corresponding measured attenuation images for a 20 cm diameter water cylinder with 5 cm cylindrical inserts containing air, a bone-equivalent solution of calcium chloride (CaCl₂), and diluted iodine. Iodine and barium-based contrast agents are commonly used with CT scans to enhance organ delineation and perfusion. Note that at 511 keV the cylindrical insert containing diluted iodine has essentially the same attenuation coefficient as water, but at CT energies it exhibits a noticeably higher attenuation, and the relative amount of attenuation compared with bone depends on the peak kilovoltage (kVp) setting. The PET transmission image is noisier and has lower resolution than the CT images, but it has far lower bias (50).

Figure 5.

(a) Computed tomography (CT) and positron emission tomography (PET) transmission energy spectra. The purple and orange spectra correspond to the typical polychromatic emission of a standard X-ray tube operating at 80 peak kilovoltage (kVp) and 140 kVp, respectively, and the monochromatic blue spectra is the 511 kV emission from one of the photons resulting from a positron–electron annihilation. (b) Mass attenuation coefficients µ/ρ (note the log scale) versus energy for four different media; notice the variations that occur as a function of the energy. (c) Measured attenuation images for a water cylinder with inserts containing air, a bone-equivalent calcium chloride (CaCl₂) solution, and diluted iodine. The CT difference image in Hounsfield units (HU) and a PET transmission image done at 511 keV (from annihilation photon energy) show how the resulting attenuation image from which the attenuation map will be derived will differ unless the correct energy scaling is used.

By using two CT scans with different energy ranges (e.g., 80 and 140 kVp), several approaches have been developed to provide more accurate attenuation correction. The first of these includes classifying iodine versus bone using the principles illustrated in Figure 5. This approach can be used to account for soft tissue, bone, and any third material, such as iodine (52).

When there are more than three types of materials, alternative methods based on the seminal dual-energy CT method developed by Alvarez & Macovski (53) can be used. In the modified dual-energy approach, the raw data from the two CT scans are decomposed using material basis functions, which are then separately reconstructed. The two basis images are then converted to attenuation images at 511 keV using known material properties (54).

These dual-energy methods, and their variations, suffer from noise amplification in the estimated attenuation image due to the large degree of similarity between the two data sets. In principle, the noise can be mitigated through the use of iterative image-reconstruction methods, similar to those described in Section 4.2 (55). Over the past few years, manufacturers have successfully introduced dual-energy CTs that use different approaches (56, 57); however, these innovations have not yet been introduced on the CT components of combined PET–CT scanners. Although there is an obvious advantage in the accuracy of the attenuation correction, the clinical need has not been demonstrated. This may change as attention is increasingly paid to quantitative accuracy in PET imaging (58, 59). It is interesting that CT-based attenuation correction has been used for a decade in preclinical PET–CT scanners (60) and that dual-energy CT methods have been successfully applied in preclinical imaging systems (61). However, we are not aware of dual-energy CT-based attenuation correction being applied to the preclinical use of PET–CT scanners.

4.1.2. Scatter

The second major quantitative correction is for the Compton-scattered photons that are detected in coincidence; the Compton scattering reduces contrast. In modern PET systems these Compton-scattered photons can account for 30–50% of the desired true coincidences. Because photons can undergo multiple scatters prior to detection, scatter is most accurately estimated using Monte Carlo photon-tracking simulations (62). However, these simulations are still computationally intractable (63). The distribution of scattered photons can be estimated much more quickly by using single-scatter approximation (SSA), which can be analytically calculated using the Klein–Nishina equation, as first proposed by Barney et al. (64). This analytical SSA method has been accelerated and extended by others (65–67) and has replaced all other scatter-estimation methods used for clinical and PET–CT scanners and preclinical scanners (68). Although the SSA method works well for objects with uniform attenuation, it is less accurate for cases in which there is nonuniform attenuation, such as in the lung (66). A remaining challenge for the SSA method is that most implementations neglect scatter that occurs outside of the transaxial plane. However, newer commercial systems with longer axial extent have oblique angles that are larger by a factor of 2 (69, 70), which may potentially invalidate the small-angle approximations used to date, but this remains to be evaluated. Finally, we note that the SSA method can be extended to TOF PET imaging, albeit with an added requirement that computing the ray integrals between detector pairs will depend on the position along the ray, thus increasing computation time by a factor of 3 to 7 (67).

Random-coincidence events from the detection of photons from separate annihilations also lead to reduced image contrast. The most common method for estimating the rate of random events is to use the product of the singles counting rates for a given detector pair and the coincidence time window. This provides an accurate and noise-free estimate of the random-coincidence rate for all LORs (71).

The estimates for attenuation, scattered coincidences, and random coincidences can be directly used to correct the raw data to give an estimate of true-coincidence events, or the corrections can be incorporated in the iterative reconstruction methods described in Section 4.2. The latter approach is preferred because this preserves the Poisson statistical distribution of the raw data.

4.2. Image Reconstruction

The goal of PET image reconstruction is to provide cross-sectional images of the radiotracer distribution within an object by using the coincidence events detected by a scanner. Detailed mathematical formulations of the problem are presented in several reviews (48, 72, 73). There are several important differences between PET image reconstruction and most other tomographic imaging modalities (e.g., CT, MRI, ultrasound), the first being the Poisson statistical distribution of the measured data. This distribution enables the use of an accurate noise model in the reconstruction process, but only if the raw data have not been precorrected—for example, for attenuation, scattered coincidences, and random coincidences. The second difference is the redundancy of the acquired data, which can be understood by analyzing a sampling of the Fourier transform of the object, which leads to unique image-reconstruction algorithms (72). There are two classes of image-reconstruction algorithms: analytical and iterative. Analytical algorithms are fast and well understood due to their linearity. Iterative algorithms are slower and nonlinear; thus, their behavior is often poorly understood.

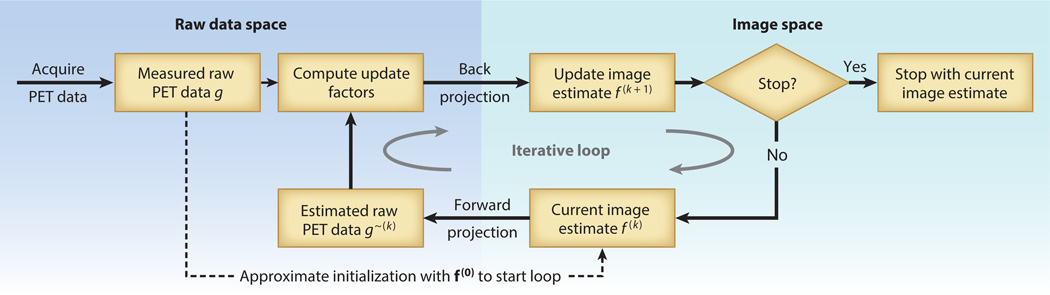
Despite their drawbacks, the use of iterative algorithms is becoming standard in most clinical and preclinical imaging due to their ability to suppress statistical noise by modeling the statistical distribution of the raw data, as well as their ability to include more detailed models of the imaging physics and radiotracer distribution. Additionally, advances in computer speeds have made iterative approaches feasible, following the rule of thumb described above—that is, the total time for image processing and reconstruction should match the typical duration of the imaging session. For this reason, we focus on iterative image-reconstruction algorithms, starting with a model of the image process as the matrix equation g = Hf, where f = (f₁, …, f_j, …, f_M) is an M-dimensional vector representing the image values, and g = (g₁, …, g_i, …, g_N) is an N-dimensional vector representing the photon count data from the PET detector. The system model H has elements H_ij that represent the probability that a photon pair emitted from voxel j is detected by the i-th pair of detectors. Thus, the matrix equation g = Hf presents a forward projection of the image values into the data space. In general, the system model H is very large (e.g., N × M ≈ 10⁶ × 10⁸), so the H_ij elements are computed as needed, and several methods are used to reduce computation time. The general process of iterative image reconstruction is illustrated in Figure 6.

Figure 6.

General process for iterative tomographic image reconstruction. A key characteristic is the alternation back and forth between (left) the data space and (right) the image space. The process starts with the raw data acquired from positron emission tomography (PET) and an initial estimation of the reconstructed image, f⁽⁰⁾, which can be derived from the acquired data, by assuming a uniform distribution, or by another method. The first image estimation is projected into the raw data space (i.e., it is a forward projection that simulates the data-acquisition process), and the result is compared with the measured PET data. Differences are used to calculate updates, which are projected back into the image space (i.e., back projection is the adjoint operation to forward projection). This produces an updated image estimate, f⁽¹⁾. The process is repeated until the difference in estimates of sequential images reaches a convergence criteria previously defined, or a preset number of iterations occurs. Although several hundred variations of iterative algorithms have been proposed, common approaches are now used.

Because the PET data have a Poisson distribution, the equation above models only the average behavior of the imaging system, and a more accurate description is E{g} = Hf, where E{·} denotes the expectation operator. To preserve the statistical properties of raw PET data, the estimates for the confounding effects of attenuation (A), scattered coincidences (s), and random coincidences (r) can be included in the forward projection step as E{g} = AHf + s + r. To make use of the known statistical properties of raw PET data, the most widely used approach is maximum-likelihood (ML) estimation. This is a standard statistical method that produces an estimate that maximizes the likelihood function. This gives an estimated image that would have most likely led to the data that were actually measured. The use of such iterative reconstruction methods based on statistical principles can lead to improved image signal-to-noise ratios (SNRs). The most useful methods are, in some manner, connected to the expectation maximization (EM) algorithm, which is an efficient algorithm for finding the ML estimate. Thus, maximum likelihood–expectation maximization (ML-EM) image reconstruction uses ML as the optimization criterion and the EM algorithm to find the optimal solution. The EM algorithm was first described in detail in 1977 (74) and was introduced for emission-tomography reconstruction in 1982 (75). A key step on the path to clinical feasibility was the development of ordered-subset ML-EM [typically called OSEM (76)], which increases algorithmic speed by factors of roughly 20–30. These developments, along with increased computational power and fast numerical forward-projection algorithms (77), have enabled the routine clinical use of statistical iterative algorithms that suppress statistical noise in images.

5. APPLICATION DEVELOPMENTS

5.1. Time-Varying Imaging

The imaging theory described so far assumes that the object and the radiotracer distribution are stationary. In practice, the radiotracer distribution changes over time, and there is patient motion, which can include cardiac motion, respiratory motion, and general motion. Depending on the degree of change during the imaging period, there is the potential to extract more information from the PET images if motion is included in the analysis or otherwise compensated for. If the radiotracer distribution changes over time but the patient is otherwise stationary, the imaging is typically referred to as dynamic imaging. If the radiotracer distribution is constant but the patient moves substantially in a regular pattern owing to respiratory or cardiac motion, then gated imaging methods can be used to suppress motion artifacts. The suppression of respiratory motion effects is discussed in Section 6.2, and similar methods are used to compensate for cardiac motion.

5.1.1. Acquiring dynamic images

Static 3D PET images represent a single, static snapshot of the distribution of the radiotracer at a given time. Applications in drug development, cardiology, neurology, or oncology often require an understanding of the dynamics underlying the process of radiotracer biodistribution in order to reveal the true biochemical process, and this information cannot be obtained from static imaging. The trade-off that occurs with the simplicity of using static imaging is that the dynamic information related to the kinetics of the radiotracer is lost for further analysis.

Dynamic imaging (or 4D imaging, or time-varying 3D) is a PET imaging mode in which instead of acquiring a single, fixed-time 3D image, a series of 3D images (frames) are individually registered at different intervals, creating a time-varying sequence, which is the 4D image (that is, 3D plus time). The 3D sequences can be analyzed by extracting the time–activity curves (TACs) that describe the radiotracer accumulation in a specific voxel or group of voxels. TACs can be studied by using kinetic modeling analysis for the radiotracer biodistribution (78), which results in a valuable description of the physiological parameters governing the radiotracer uptake. Examples of applying this technique include imaging cardiac perfusion using ¹³N-ammonia or ⁸²Rb, monitoring the metabolism rate of glucose in tumors using 2-deoxy-2-[fluorine-18]fluoro-D-glucose (¹⁸FDG), assessing blood flow using oxygen-15 (¹⁵O), assessing cellular proliferation using ¹⁸FLT, and evaluating dopamine receptors using ¹¹C-PHNO.

Issues that impose practical limitations in dynamic 4D PET imaging (Figure 7, left) include those listed below.

• ■The time resolution of the data acquisition compared with the time characteristics of the physiological process: The 3D PET frame requires a minimum amount of accumulated counts, and thus an acquisition time that is long enough to reach an acceptable SNR. If the time required for imaging is longer than the transients of the radiotracer kinetics in the tissue, the relevant dynamic information will be lost. Myocardial perfusion imaging using ⁸²Rb is an extreme example in which the radiotracer’s dynamics and the isotope’s half-life require very short time frames in the 4D imaging process; thus, the resulting sequence is difficult to analyze due to a lack of counts per frame.
• ■The confounding results from resolution loss and spillover between the tissue of interest and the blood pool or other adjacent tissues: This problem is present on any PET image. In static images, the activity of the background due to the blood pool is low, but in the early frames of a dynamic study all of the activity is in the blood pool, although this situation changes at later time points. The redistribution of the radiotracer affects the spillover in a different manner at different time points.
• ■The assumptions made during the kinetic modeling itself: Modeling, by definition, is a simplification of real phenomena, and in the case of PET the data-limited SNR limits the capability of the numerical algorithms to resolve the kinetic model.
• ■The difficulty of measuring the arterial input function that is required for the kinetic modeling process in order to provide quantitative results (79): The most commonly used method for measuring arterial input function relies on obtaining arterial blood samples from the patient throughout the duration of the scan. This is an invasive and costly procedure that precludes the widespread use of kinetic modeling in clinical applications. Newer approaches that try to extract the same information from the data set (such as the image-derived input function) are still under development.

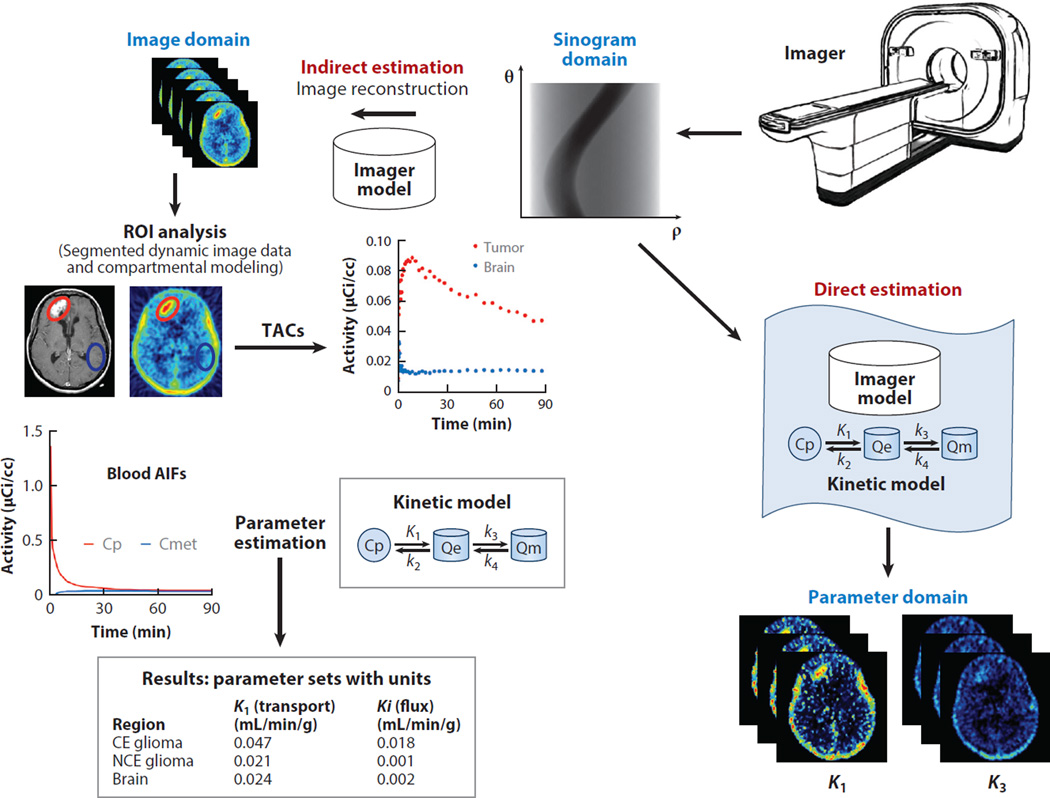
Figure 7.

Dynamic analysis of data from positron emission tomography (PET) is used to determine critical metabolic, transport, and proliferation variables. (Left) The standard protocol relies on delineating regions of interest (ROIs) on a summed PET image reconstructed using the imager model, or a coregistered anatomical image (from computed tomography or magnetic resonance). Time–activity curves (TACs) from the ROIs applied to previously reconstructed time-series images are extracted, and they become the input to the kinetic-modeling programs that estimate physiologically relevant parameters for each of the tissues defined in the kinetic model. The reconstruction step could be avoided by redefining the objective function used for the reconstruction process: In the standard indirect model, the objective function is the relationship between the projection data sets measured by the PET system and the 3D image sequence, and that information is contained in the imager model. (Right) In the direct estimation method, the new objective function relates the projection data sets measured by the PET imager to the kinetic parameters defined in the kinetic model. This new parametric model solves directly for the kinetic parameters and produces less noisy estimations of the physiological variables. Modified from a figure courtesy of Mark Muzi, University of Washington. Other abbreviations: AIF, arterial input function; CE, contrast-enhanced; NCE, non-contrast-enhanced.

Other important issues are errors that arise owing to unavoidable patient movement originated by respiration, the heartbeat, or involuntary muscular movements (80).

In conclusion, 4D PET imaging provides more complete and valuable information than does static 3D imaging, but challenges remain, including the need to optimize acquisition protocols to collect data of sufficient quality—which are needed to obtain enough information to perform the kinetic modeling—and the increased complexity of data processing. These challenges will need to be addressed before dynamic 4D PET imaging can permeate into clinical practice.

5.1.2. 4D processing and kinetic analysis

The conventional analysis of data from 4D PET imaging proceeds in four steps: time framing, 3D image reconstruction of each frame, ROI segmentation on a time-integrated image or an anatomical reference (such as a registered CT or MR image), and, finally, kinetic modeling. The framing resulting from the first two steps is a time-varying sequence with a single 3D image per time point.

The size of the time bins becomes a critical parameter in ensuring there are sufficient samples for the TAC while simultaneously minimizing the number of time points (frames). If the physiological process being studied is known, one can optimize the duration of the frames by choosing short time frames for the initial fast section of the TAC, when the activity in the FOV is high because of the first pass of the initial bolus, and by using longer time frames later, when biological washout has cleared part of the radiotracer from the FOV and slow kinetics dominate the TAC plot (Figure 7).

The third step, segmentation, produces ROIs from which the TACs are obtained, representing, for example, the time-varying uptake of radiotracer in tumor tissue or perfusion in an organ. The complexity in this step stems from the tedious and error-prone manual segmentation or definition of the ROIs on the image sequences, which challenges even experienced investigators in sequences with low SNRs. Automatic image segmentation offers a potential solution to this problem, especially the techniques that provide more than simple anatomical ROI identification. These algorithms may be based on principal-component analysis or multidimensional clustering, in which the time–activity voxels and the spatial arrangement of those voxels are considered in an iterative segmentation process before being assigned to a given cluster that defines an ROI (81, 82). New combined PET–MR imaging systems offer an alternative that ameliorates the difficulties of segmentation by taking advantage of the high contrast of soft tissue provided by MRI to help define the ROI.

An interesting alternative to the conventional protocol—which is based on image-domain segmentation and TAC generation, followed by kinetic modeling analysis—is the generation of parametric images from the raw sinogram or LOR histogram data by means of direct estimation without previous image reconstruction (83, 84). Direct estimation can be used to reformulate the reconstruction process described in Section 4.2, solving for the kinetic parameters instead of the image itself, thus combining kinetic modeling with a scanner model into a new model (Figure 7). More recently, direct-estimation methods have begun to incorporate corrections for patients’ movements (85). The computational cost of these methods is high, and although they are still under development, preliminary results suggest they offer several advantages: When applied to challenging models, such as dynamic myocardial perfusion with ⁸²Rb used to evaluate coronary flow reserve, the method produced results with improved resolution and contrast recovery and also reduced quantitative bias (83). Better precision and lower bias have also been found for brain-receptor imaging (84) with these methods.

5.2. Dosimetry and Image Monitoring

Targeted radionuclide therapy for cancer treats the disease by administering radiopharmaceuticals that selectively deliver the radiation dose to the targeted tissue. The accuracy of 3D patient-specific dosimetry depends on the quality of the 3D dose estimations. These estimations are usually obtained using a combination of single-photon emission computerized tomography (SPECT) and CT images that enable estimation of tumor volumes and 3D imaging of radionuclide distribution over time.

PET imaging is becoming a potentially useful tool for dosimetry in therapeutic procedures because it can provide 3D estimations of many radio labeled therapeutic and imaging agents. As an example, iodine-131 (¹³¹I)-labeled antibody for therapy can be combined with iodine-124 (¹²⁴I) for PET imaging in patients with thyroid cancer, in a process in which 3D PET imaging–based dosimetry provides dose–volume histograms of the absorbed dose, and therefore of the tumor’s response and of toxicity in normal organs (86). Similarly, yttrium-90 (⁹⁰Y) TOF PET imaging is used to precisely quantify ⁹⁰Y-DOTATOC (edotreotide) in somatostatin-receptor-based radionuclide therapy; it is also used on microspheres for radioembolization of liver tumors (87), even though the ⁹⁰Y branching ratio for pair production yielding PET events is extremely low (34 disintegrations per min) (88).

Knowledge of the 3D distribution and quantification of a radiopharmaceutical are needed to accurately estimate the efficacy of the treatment. The development of new, optimized PET imaging protocols has provided valid dosimetry procedures that are compatible with clinical practice in terms of the time required for preparation and acquisition (89). PET imaging is particularly useful for precisely parameterizing lesion TACs to estimate the cumulated activity concentration of a lesion using monoexponential models (90). However, there remain a significant number of cases in which PET imaging fails to predict the uptake of radiotherapeutic agents (91). The challenges remaining for imaging dosimetry in targeted radionuclide radiotherapy or in charged particle-beam therapy are in predicting and correcting the positron range of the isotopes used and in providing better scattering estimation and correction, issues that are exacerbated by unavoidable patient movement.

5.3. Multi-Isotope PET

Multi-isotope imaging is a common protocol in SPECT imaging and is used to visualize two different physiological processes simultaneously. This is done by administering two radiotracers with isotopes whose photon emissions have different energies. The isotope images are disentangled with the appropriate energy windowing for each isotope. However, this technique is based on distinguishing between different photon energies and will not work in standard PET imaging because all annihilation photons resulting from positron annihilation have the same energy (Figure 1). To overcome this limitation, alternative techniques have been proposed, including the following:

• ■simultaneous injection of or sequential close-in-time injections of two radiotracers that do not interfere with each other (92);
• ■dynamic imaging of timed injections followed by constrained kinetic modeling to separate the particular dynamics of each radiotracer (93) using generalized factor analysis of the dynamic sequences (94); or
• ■the use of a combination of radiotracers, one of which emits an additional photon simultaneously with the annihilation photons. The two radiotracers can be differentiated by measuring the energy of the third photon (which has to be different from 511 keV) (95).

A recent proposal is to use what has been termed the triple coincidence, which works with any third photon because it can be distinguished from random or scatter; therefore, the triple coincidences can be included in iterative reconstruction models (96). Events coming from triple-photon isotopes can be detected separately from pure positron emitters using precalculated double-coincidence probabilities that are used to assign the triple event to one of the possible LORs. Then, by labeling two compounds, one with a pure positron emitter and the other with a complex-decay isotope, simultaneous multitracer imaging can be done (Figure 8) without losing sensitivity or image quality. Because this method does not require specialized detectors or additional energy-resolution requirements, it is being explored for implementation on clinical scanners (97). Simultaneously imaging several molecular or physiological targets using different radiotracers may provide valuable prognostic information and improve disease diagnosis and classification. Some examples of these applications include the simultaneous evaluation of tumor hypoxia and perfusion, which have been demonstrated to impact the efficacy of chemotherapy and radiotherapy, the determination of tumor grade in patients with neuroendocrine tumors, or the simultaneous evaluation of myocardial angiogenesis and hypoxia or metabolism (98).

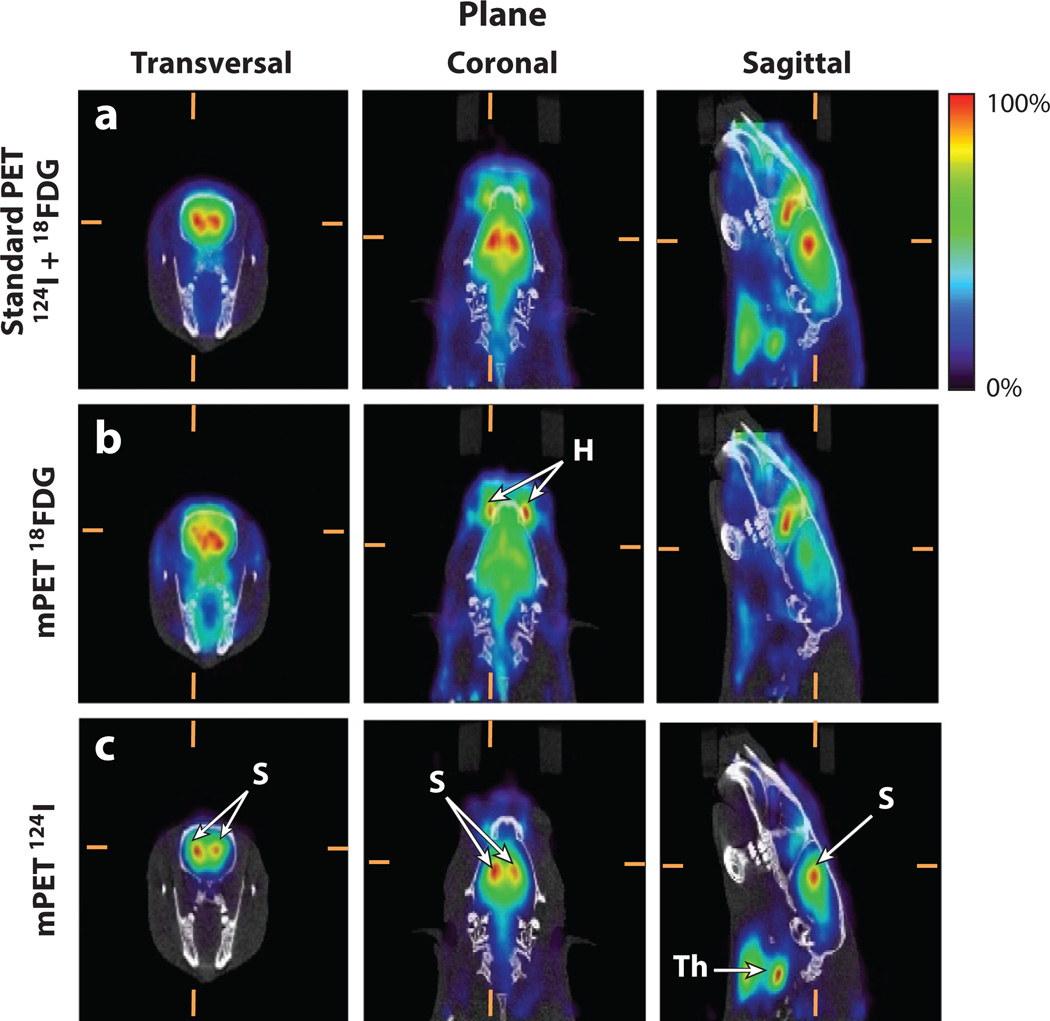
Figure 8.

Multi-isotope in vivo brain positron emission tomography and computed tomography (PET–CT) imaging. All images show the same approximate anatomical slice in the three orthogonal views (columns). CT image values are represented using a gray scale, and PET image values are represented using a rainbow color scale. (Top row) Standard PET image (using only double coincidences) from a rat injected with iodine-124 (¹²⁴I)-β-CIT (dopamine transporters) and ¹⁸FDG (glucose metabolism). Because standard PET data processing does not allow signal multiplexing, the combined signal from both radiotracers is shown as a single, mixed image. (Middle row) Separated ¹⁸FDG signal obtained by multiplexed PET (mPET) showing homogeneous uptake in the brain and a high, nonspecific uptake in the Harderian gland (H), which is typical of this radiotracer. (Bottom row) Separated ¹²⁴I-β-CIT signal obtained by mPET showing specific, dopamine transporter binding in the striatum (S) and nonspecific uptake in the thyroid glands (Th). The top row shows the result of adding information from the middle and bottom rows; mPET is capable of separating both independent components. Images courtesy of Stephen Moore, Brigham and Women’s Hospital, Boston.

6. MULTIMODALITY IMAGING

In the late 1980s and early 1990s, several investigators conceived the idea of a multimodal medical imaging system that could merge the more readable anatomical images from CT and MRI with the functional information provided by PET (or SPECT). After a period of development [and skepticism (99)], a new range of imaging tools was enabled by combining different modalities. Pairing anatomical and functional information increases the accuracy of the information, and different combinations of modalities have been proposed in the literature. However, only some of these—specifically the combinations of PET and CT, PET and MRI, and SPECT and CT—have proven to be of clinical and commercial interest. In preclinical imaging, similar considerations are applicable, albeit with a broader range of combinations of PET, SPECT, MRI, and CT, and even triple-modality systems (100). As articulated by Cherry (101), multimodality systems should provide added value, such as addressing scientific or clinical questions that would be impossible to answer using separate scanners, or improving throughput for clinical or preclinical studies. However, the use of multimodality systems comes with trade-offs between imaging performance and cost when compared with stand-alone systems, and the use of multimodality systems requires expertise across both, or all, of the combined modalities.

6.1. PET–CT Imaging

The primary goal of using combined PET–CT imaging is to accurately align the PET and CT images, which provide complementary information on function (PET) and anatomy (CT), as illustrated in Figure 9. Clinical PET–CT imaging has demonstrated its added value, and it is now the standard approach for diagnosing and staging many cancers (102). Near-simultaneous PET and CT imaging provides information that is not available in separate PET and CT scans; thus, it improves the assessment of the primary tumor, and nodal and distant metastases (103). Although PET–CT imaging is primarily used in oncology, it has also been used to identify brown fat (104), which potentially has important implications for metabolic disorders related to diabetes. It also has applications in clinical and research cardiology (105). Preclinical PET–CT imaging has also become a standard imaging tool that is used in studies using mouse models (106). The structure of a typical PET–CT scanner is shown in Figure 9. As discussed in Section 4, a CT image can also be used as the basis for correcting attenuation and scatter, along with offering substantial reductions in transmission imaging time and other secondary benefits (50).

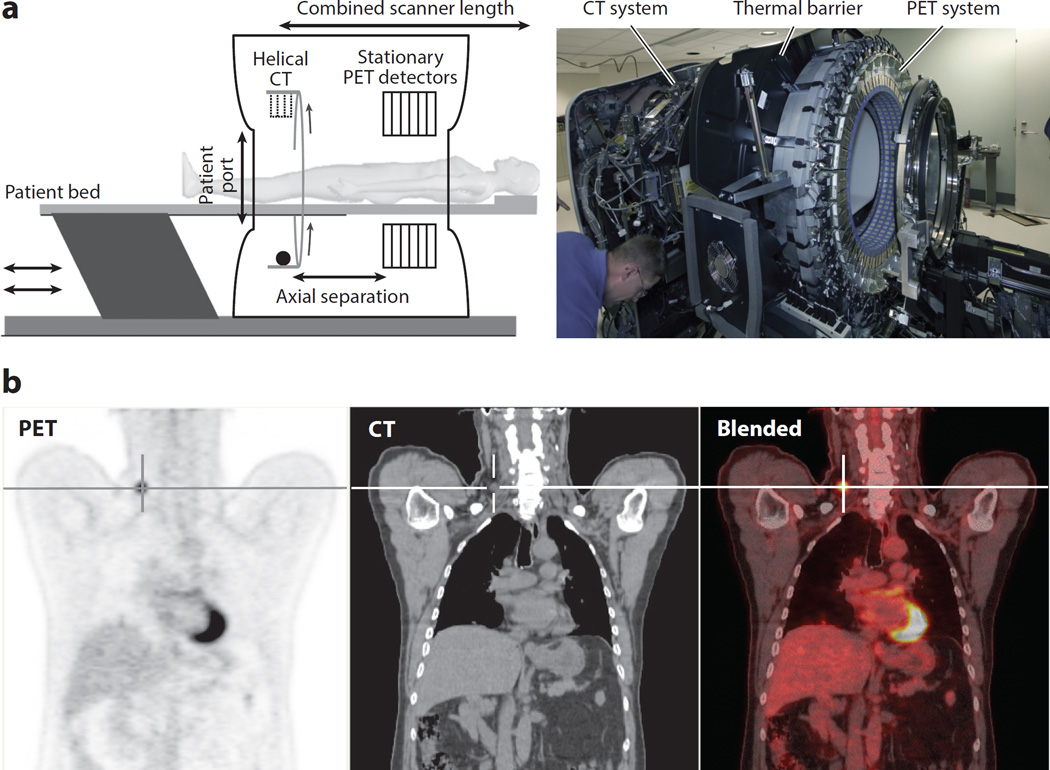
Figure 9.

(a) Schematic and photograph of a combined positron emission tomography and computed tomography (PET–CT) scanner used for clinical applications. Although the concept of aligning in tandem a CT scanner and a PET scanner is simple, the technical and practical complexities pose challenges that range from the footprint size of the resulting system to the spatial and temporal alignment of the resulting data sets. (b, left to right) The coronal view of a clinical ¹⁸FDG PET scan clearly shows a recurrent thyroid cancer tumor (crosshair), the CT image shows detailed anatomy in which the tumor is hardly distinguishable, and the blended image shows the precise anatomical localization (from the CT image) of the active tumor (from the PET image).

Although in a combined system the PET and CT images are nearly simultaneous, they cannot be acquired contemporaneously because the CT X-ray photon flux would overwhelm the PET detector system. Thus, there is a short time delay (e.g., approximately 30 s) between the CT image—which is typically acquired first—and the PET image. This allows for the possibility of motion occurring between the CT and PET images. Such motions, when they do occur, can lead to different errors.

1. An unknown spatial offset between the CT and PET images can lead to a change in the diagnosis or in staging criteria. For example, it may be difficult to differentiate whether a lung tumor is near to, or invading, the chest wall or pleura.

2. An error may also arise from a shift in the attenuation correction, especially if PET radio-tracer uptake occurs near a boundary between tissues that have large attenuation differences, such as the top of the liver or the skin surface.

3. If there are artifacts or errors in the CT image, these will propagate to the PET image through the attenuation-correction process. The impact of these artifacts on the PET images is hard to predict a priori because the attenuation- correction process and the iterative image-reconstruction algorithms are nonlinear (107).

In addition to the delay occurring between the acquisition of the CT and the PET images, the images themselves also require different durations. A modern CT scanner can acquire an image similar to that shown in Figure 9 in a few seconds (e.g., approximately 10 s), but PET scanners may require 5–20 min, depending on the acquisition protocol. These differences in the duration of acquisition time can lead to errors due to respiratory motion, which are discussed in the next section.

6.2. Respiratory Motion in Multimodality Imaging

Multimodality imaging of the lung and abdomen requires consideration of respiratory motion. There are two major respiratory motion effects in PET–CT imaging. The first is the blurring caused by respiratory motion during the acquisition of PET images, which leads to shape distortion and loss of signal. The second effect, described in the previous section, is the potential for a positional mismatch between the different modalities, which can impact the use of CT images to correct attenuation in the PET data. A mismatch in PET–CT imaging is illustrated in Figure 10, where a detailed computer simulation shows several effects that result from a patient breathing during a PET scan and from using a single breath-hold CT for attenuation correction. Although the tumor is still clearly visible, its shape and values are distorted (108), as is the left ventricle, both of which might impact the tracking of disease status.

Figure 10.

Simulated coronal slice of a human torso obtained by positron emission tomography (PET) illustrating the impact of respiratory motion effects during combined acquisition of PET and computed tomography (CT) data. (Left) If there is no motion, the lung tumor, liver boundaries, and the left ventricle of the heart are well delineated. (Right) However, when respiratory movement is present, the blurring and mismatches in attenuation correction introduce artifacts and numerical errors, which also obscure clinical evaluations.

Considerable efforts have been made to develop methods to compensate for the effects of respiratory motion (109). The most direct approach is to use phase-matched respiratory-gated CT and PET images to jointly solve for both blurring caused by respiratory motion and a PET–CT mismatch. One of the difficulties with this approach, however, is the multitude of noisy images that are produced. This has led to the development of more sophisticated methods that remove respiratory-motion artifacts of both types while preserving quantitative accuracy without increasing noise (52).

Similar considerations apply to combined MR and PET imaging. Although the multimodality aspects of compensation for respiratory motion with PET–MR imaging are less advanced, MR imaging does offer the potential of using simultaneous PET and MR imaging to provide accurate respiratory-gating signals (110).

6.3. PET–MR Imaging

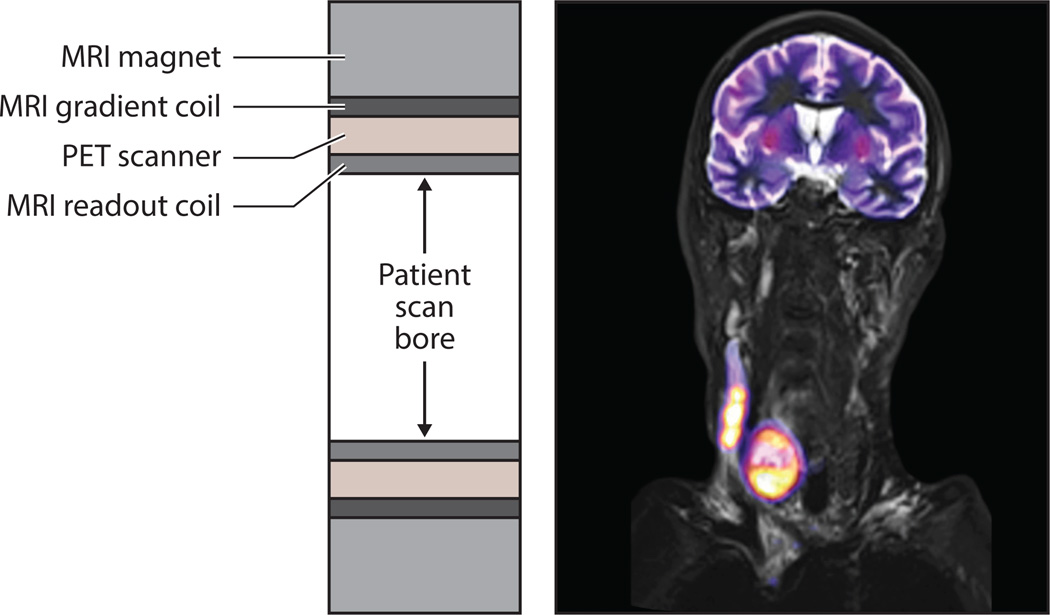
Although combined PET–CT scanners quickly became established as clinical tools, the development of combined PET and MR imaging has been slower because of technical challenges arising from both modalities when they are paired. The potential value gained by combining PET and MR imaging is attributed to the superior capabilities of MR for soft-tissue imaging compared with CT, as well as the different types of imaging that can be performed. Additionally, unlike PET–CT imaging, PET–MR imaging is capable of achieving truly simultaneous imaging. This is enabled by its integrated inline design, which is shown in the cross section in Figure 11.

Figure 11.

(Left) Cross section along the patient scan axis for an integrated inline design used by clinical positron emission tomography–magnetic resonance (PET–MR) scanners. The PET detectors are placed between the different MR coils to reduce cross-system interference. (Right) PET–MR image of an anaplastic thyroid carcinoma formed from an MR T2-weighted turbo inversion recovery magnitude image showing high contrast in the soft tissue (gray) fused with an ¹⁸FDG PET image (color). Courtesy of Siemens Healthcare and University Hospital of Tubingen.

The simultaneous acquisition of PET and MRI data was first demonstrated in vivo in small animals in the late 1990s (111). Initially, most of the progress in the field was made in preclinical scanners. It took a full decade for the first imaging systems for human brains to be developed. These systems had poor PET imaging performance (112) but were a key step in developing the current WB systems in clinical use. With the introduction of clinical PET–MR scanners, early work has focused on comparing the diagnostic value of PET–MR images with those from PET–CT imaging. Published studies of PET–MR imaging demonstrate that the PET image data are somewhat comparable to those obtained from PET–CT scanners (113). However, the equivalency of standardized uptake value quantification from PET–MR scans has been variable (114). Two important technical challenges that have not yet been resolved are attenuation correction for and calibration of the PET scanner.

6.3.1. Attenuation correction

For combined PET–CT imaging, the attenuation factors can be conveniently derived from the CT image because the same processes affect photon scattering in PET and CT. For MR imaging, however, the image values typically represent a weighted average of hydrogen proton density and T1 and T2 relaxation times, which are influenced by the local environment (115). This mismatch between the physics of PET and MRI means that there is no simple scaling method that can be used to convert the MR image to a CT-equivalent attenuation map. The current approach to attenuation correction, which circumvents the different physics of PET and MR imaging, is to use image segmentation to discriminate between air, lungs, fat, and soft tissue in the MR image, and then assign estimated attenuation coefficients to the regions. Although this approach can lead to errors in estimating the uptake of PET radiotracer in bone, it is currently the most robust method for estimating PET radiotracer uptake in the lung from PET–MR data (116). Several other methods have been proposed for using the MR image to estimate the attenuation image (117). In general, there are trade-offs between reliability and quantitative accuracy, especially when estimating radiotracer uptake in bone. This is an active area of research and development.

6.3.2. PET calibration

For PET–CT imaging, PET calibration and quality control are simplified by the use of water-filled phantoms. However, this is challenging because MR images of water-filled phantoms show artifacts and in homogeneities when imaged at the 3T field strength of current PET–MRI systems (118). This, in turn, causes challenges for MRI-based attenuation correction (described above). The search for fluids other than water—for example, oil—is challenging because FDG does not dissolve well in oils (119). Phantom fluids that enable image quality testing in PET, MRI, and PET–MRI hybrid imaging are currently under development and will be a necessary step toward standardization of calibration and qualification procedures in PET–MRI.

The immediate value of PET–MRI in oncology, not surprisingly, appears to come from the improved diagnostic information regarding soft-tissue lesions that is obtained from the MR images. In these cases, PET is the first option for clinical functional imaging because it is considered the most sensitive technology, but for the anatomical component, MRI is becoming an alternative to CT because of the higher contrast resolution for soft tissue. Further potential applications are reviewed in Reference 120.

7. SUMMARY

Before the full potential of the sensitivity and accuracy of PET imaging can be exploited, challenges must be resolved, including the limited SNR, the development of cost-effective technologies, and the development of efficient workflows for clinical and research imaging. These limitations arise not only from the physics of PET imaging but also from limitations in the technology.

The continued introduction of new detector technologies that use new, faster scintillators, along with the introduction of semiconductor detectors, has enabled simultaneous hybrid PET–MR imaging. Recent advances in processing scintillator crystals and coupling these to photodetectors have improved the performance of scanners built using these technologies, enabling new applications in cardiology, oncology, neurology, and pediatrics.

Advanced algorithms that can be used for image reconstruction and correction are improving the accuracy of quantitative imaging, and more sophisticated CT techniques, such as dual energy CT, have been successfully applied in preclinical imaging. Scatter and random effects, which have historically limited the image SNR, are being corrected by incorporating improved estimations of these effects in iterative image-reconstruction methods. These new, albeit computationally intensive, algorithms are demonstrating improved quantitative properties and improved lesion detection.

Improvements in detector technology combined with enhanced image-reconstruction algorithms are enabling clinical applications of 4D (that is, 3D plus time) imaging, kinetic modeling, dosimetry, and even multi-isotope PET applications that provide more complete and accurate information about the physiology being studied.

Finally, multimodality imaging has been widely adopted by the scientific community as a way to gain a more comprehensive understanding of the effects of diseases and treatments. The PET–CT revolution has initiated a new way of looking at physiology and morphology simultaneously, and the new class of PET–MR systems is broadening the landscape of opportunities for clinical and preclinical applications, while at the same time presenting new challenges for clinicians using PET–MR systems and the engineers who are developing them.

The continued introduction of new detector technologies, hybrid imaging, and advanced algorithms for image reconstruction and analysis make it clear that there will continue to be exciting developments in the technology. These developments will both address the challenges and enable new uses of PET in research and clinical imaging.

Glossary

CT

X-ray computed tomography

keV

kiloelectronvolt; a measurement of the energy of a γ-ray or X-ray

Line of response (LOR)

line defined by the centers of the two detectors that have near-simultaneous scintillations from the two 511 keV annihilation photons

Time of flight (TOF)

the difference between the arrival times at the detectors of the two photons resulting from a positron annihilation

Depth of interaction (DOI)

the distance from the surface crystal to the precise location of the scintillation crystal along its longitudinal axis

Digital photon counter (DPC)

a semiconductor detector that counts individual photons and outputs a digital code representing the number of photons that arrived during a specific time

Field of view (FOV)

the area covered by the scanner from which images can be reconstructed

Region of interest (ROI)

the defined area of an image that is being analyzed or characterized

Whole-body (WB) image

image that covers the whole body (or most) of the subject under study

Peak kilovoltage (kVp)

the maximum voltage applied across an X-ray tube, which determines the peak energy of the X-ray emission spectrum

Single-scatter approximation (SSA)

an analytical technique for estimating the distribution of scattered photons in PET systems

Maximum likelihood (ML)

a statistically based method for estimating the parameters of a model

Signal-to-noise ratio (SNR)

the ratio of the signal level to the noise level measured in intensity or power

ML-EM

maximum likelihood (ML) estimation using the expectation maximization (EM) algorithm

Time–activity curve (TAC)

activity concentration as a function of time for a defined region of interest