Abstract.
Ultrasound-guided diffuse optical tomography (DOT) is a promising imaging technique that maps hemoglobin concentrations of breast lesions to assist ultrasound (US) for cancer diagnosis and treatment monitoring. The accurate recovery of breast lesion optical properties requires an effective image reconstruction method. We introduce a reconstruction approach in which US images are encoded as prior information for regularization of the inversion matrix. The framework of this approach is based on image reconstruction package “NIRFAST.” We compare this approach to the US-guided dual-zone mesh reconstruction method, which is based on Born approximation and conjugate gradient optimization developed in our laboratory. Results were evaluated using phantoms and clinical data. This method improves classification of malignant and benign lesions by increasing malignant to benign lesion absorption contrast. The results also show improvements in reconstructed lesion shapes and the spatial distribution of absorption maps.
Keywords: ultrasound-guided diffuse optical tomography, image reconstruction, NIRFAST
1. Introduction
Diffuse optical tomography (DOT) is a noninvasive functional imaging modality that utilizes near-infrared (NIR) light in the wavelength range of 650 to 900 nm to probe tissue optical properties.1,2 In DOT, tissue is illuminated by a set of laser diodes of different optical wavelengths, the reflected or transmitted light is detected at the surface of the tissue. These measurements are then used to estimate (recover) optical proprieties of the tissue.1–20 Minimal light absorption in this wavelength range, allows for several centimeters of light penetration in soft tissue, such as breast and brain.3 Utilizing multiple wavelengths in the NIR range enables this technology to quantify tissue characteristics, such as oxygenated, deoxygenated, and total hemoglobin (HbO2, HbR, and HbT) concentrations as well as hemoglobin oxygen saturation () and lipid and water concentrations.4,5
The ability of DOT to probe these specific tissue optical properties demonstrates its potential to detect and monitor functional changes related to blood flow, blood oxygenation, and tumor angiogenesis for different applications. DOT is emerging in many fields, such as brain imaging, monitoring of cerebral hemodynamics, diagnosis of rheumatoid arthritis, breast cancer detection, and treatment monitoring.6–10
In addition to all of the promising applications of the DOT, it has not been widely used in clinics because of strong light scattering in biological tissues. Light scattering causes poor spatial resolution and location uncertainty of reconstructed lesions. To overcome this challenge, several research groups have investigated the use of other imaging modalities, such as ultrasound (US), magnetic resonance imaging (MRI), and x-ray, to guide DOT imaging reconstruction or recovery of optical proprieties.11–15 In these approaches, a suspicious lesion is localized using either US, MRI, or x-ray, and a region of interest (ROI) is identified in the corresponding modality, which is used to segment imaging volume for DOT image reconstruction. As a result, the DOT inverse problem is well conditioned and lesion localization and reconstruction accuracy are significantly improved.
The DOT image reconstruction or inversion estimates the optical properties of interior tissue by iteratively matching the boundary measurements with the predicted model data. To stabilize the solution, many different regularization techniques were studied, such as Tikhonov regularization and Levenberg Marquardt regularization.16–18 In general, regularization techniques can be grouped into two different types. The first group is applied when there is an absence of prior information. Application of a spatially variant regularization parameter was examined.17 Most recently, regularization approaches based on the model of the problem, named model-resolution based penalty, was presented.19 This group of regularization techniques is valuable when the prior information is unavailable. The second group is based on the available prior information, which is, in general, the anatomical information obtained from high resolution imaging modalities.20 Implementation of spatially encoded regularization using images obtained from MRI was introduced and investigated, where two-step image reconstruction procedure is required.21,22 In the first step, a suspicious lesion is segmented from the rest of the tissue. Then, this prior information is imposed to regularize the matrix inversion. More recently, a direct regularization imaging (DRI) technique has been proposed in which the grayscale values of MRI images are directly used to regularize the reconstruction process, without the need for image segmentation.23
In this paper, we evaluate the DRI using US images to regulate the inversion matrix. The performance of the reconstruction method is evaluated using phantom targets and clinical data. Clinical results using DRI are further compared to those obtained from US-guided dual-zone mesh method using Born approximation and conjugate gradient optimization referred as US-guided dual-zone mesh method, which was developed in our laboratory.11 Although the DRI was introduced in MRI imaging guided DOT approach,23 the use of US images to regulate the inversion matrix has not been investigated. This study will systemically evaluate the performance of this method using US priors and the improvement of this method in target quantification and cancer diagnosis.
2. Method
2.1. Reconstruction Algorithms
There are mainly two problems involved with the DOT: a forward and an inverse problem. In the forward problem, boundary data () are generated or measured using assumed or measured optical proprieties of absorption coefficient and reduced scattering coefficient . The diffusion approximation of the radiative transport equation is used to model light transport in tissue. In the inverse problem, optical proprieties of a target or a lesion are iteratively reconstructed from the boundary data (). This is achieved by minimizing an objective function (), which is the difference between the measured data () and the forward calculated (modeled) data, . Using the Tikhonov minimization technique, the objective function is defined as
| (1) |
where is the Tikhonov regularization parameter, is a prior estimate of the optical properties of the imaged medium, and is a regularization matrix. In the case when there is no prior anatomical information available, the is set to the identity matrix.23,24 Researchers have investigated the use of spatial priors in two different approaches: soft priors and hard priors.17,19,20,25 In the soft prior approach, the -matrix encodes spatial information, where Laplacian-type and Helmholtz-type structures can be used. Unlike soft prior approach where segmented regions are allowed to have local variations, the hard prior approach assumes segmented regions to have same optical properties. This allows for significant reduction in the number of unknowns, so the inverse problem is well-determined. However, accuracy of this approach highly depends on the segmentation process of the tissues. Errors or uncertainty in the segmentation process may be increased, which causes reduced accuracy in target or lesion quantification.17,18 In the DRI approach,23 the method directly encodes the anatomical information from the grayscale image vales () into the regularization matrix :
| (2) |
Here we used coregistered US images to compute . Each grayscale US image value () corresponds to FEM node . is a characteristic grayscale difference parameter, and is a normalization factor for each row that satisfies , where is the number of finite element nodes.
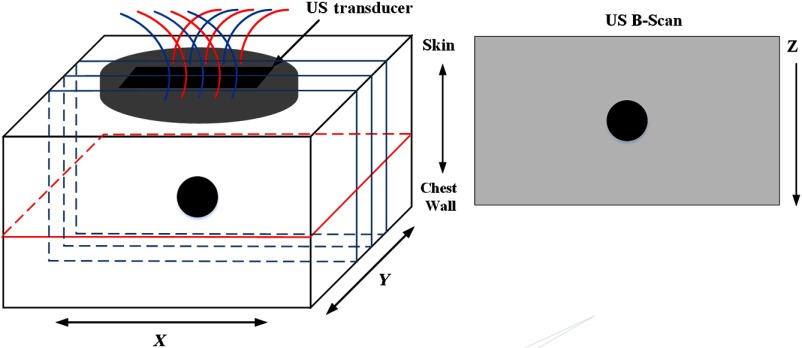
Coregistered US images were two-dimensional in plane; however, we need three-dimensional (3-D) regularization to reconstruct tomographic images. To compensate for the limited US priors in the lesion region along the direction, we have repeated a coregistered US image to obtain an estimate of a 3-D mapping of the US priors (Fig. 1). Because one-dimensional (1-D) US transducer arrays have about 1 cm height in direction, each image covers about 1 cm tissue thickness. Assuming lesions are approximately spherical in shape, we repeat 1 to 2 times in 0.5 cm step in both positive and negative directions depending on lesion size. This procedure effectively covers a 3-D volume for up to 3 to 4 cm in and provides an estimated 3-D map of the lesion. Although this mapping is not the exact 3-D reflection of the lesion region, it provides a reasonable estimate for 3-D regularization of the -matrix, especially when the lesions are not too large. In this study, the finite element discretization scheme of widely used NIRFAST software was adopted to solve the diffusion equation and perform the DOT image reconstruction.24,26
Fig. 1.
The 3-D geometry of the imaging volume. Several B-scan images were used to provide an estimate of a 3-D target map. The presented reconstructed optical images are the lesion middle layer in the plane.
2.2. US-Guided Dual-Zone Mesh Method
The reconstructed results with the US-guided dual-zone mesh scheme introduced by our group11,27 early was used to compare with the results of proposed regularization technique. In this method, the imaging volume was segmented into two regions consisting of the US-identified lesion and the background region. The coregistered US image was used to measure the lesion size in spatial and depth dimensions. The lesion size in dimension was assumed the same as dimension. Because diffused light probes a larger lesion volume than that of US, the ROI used for optical reconstruction was typically 2 to 3 times larger than the lesion in spatial dimensions and about the same in depth dimension. The tighter prior in depth improves the reconstruction accuracy due to a greater degree depth uncertainty of the diffused light. As a result, the total number of voxels with unknown optical properties is significantly reduced because of the use of the smaller voxel size for lesion region and a larger coarse voxel size for background. Additionally, the total absorption of each voxel is reconstructed, which provides balanced values in lesion region (higher absorption and smaller voxel size) and background (lower absorption and larger voxel size) for improving inversion. Finally, the total absorption is divided by the voxel size to obtain the absorption map at each wavelength. Born approximation is used for computing the weight matrix and conjugate gradient method was used for the iterative optimization of the inverse problem. Details of this method were described elsewhere.11,27
2.3. Phantom and Clinical Experiments
The US-guided DOT system was used to conduct both the phantom and the clinical experiments. The DOT system consists of four laser diodes of wavelength 740, 780, 808, and 830 nm and 14 photomultiplier (PMT) detectors. Laser diodes were modulated at 140 MHz and the light at each wavelength was sequentially delivered to nine positions on a handheld probe through optical fibers. Fourteen light guides couple the reflected light from tissue to 14 PMT detectors simultaneously. The details of the NIR system can be found in Ref. 27.
Clinical data were obtained from patients recruited from UConn Health Center and Hartford Hospital, and the protocol was approved by the Institutional Review Boards and Health Insurance Portability and Accountability Act compliant. All patients signed the informed consent form and data used for this study were deidentified.
3. Results
3.1. One Target Phantom Experiment
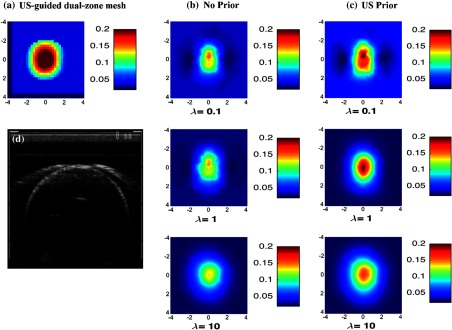
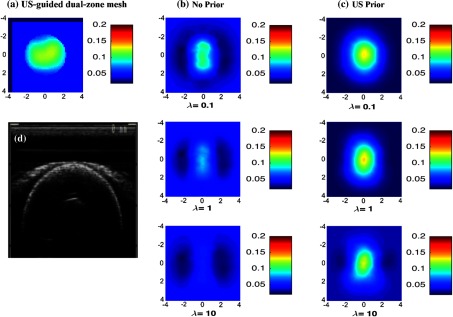
Phantom experiments were performed to evaluate the performance of this method using coregistered US images as prior for the regularization matrix. Two phantom targets of high and lower optical contrasts of diameter 3 cm were used for experiments. The calibrated values for the two targets were and , and and , respectively. The different optical proprieties of the targets were used to emulate high contrast malignant tumors and low contrast benign lesions. The optical proprieties of background intralipid solution were measured as and , which were typical values of normal breast tissue.28 In the first part of this experiment, the high contrast target was submerged in the solution and located at different depths of 2.0 to 3.5 cm in 0.5 cm increments. In the second part, the lower contrast target was imaged with the same procedure. Figures 2 and 3 show the reconstructed absorption distributions of high and low contrast targets at 2.5 cm depth, respectively. The reconstructed images for the no prior and US prior are shown for three different values of 0.1, 1, and 10. A small value () was used. We have tried different values (0.01, 0.1, 1, and 10) with the phantom experiments and found 0.01 is optimal. It was also reported in Ref. 23 that the high reconstruction contrast occurred with small value, no matter which regularization parameter “” was selected.
Fig. 2.
Reconstructed absorpstion map of the high contrast phantom target ( and ) at 780 nm at the 2.5-cm target depth. The maps at rest of the depths were not shown. (a) Reconstruction result of US-guided dual-zone mesh method. (b) Reconstruction result of NIRFAST with no prior using different . (c) NIRFAST with US prior. (d) Coregistered US B-scan image.
Fig. 3.
Reconstructed absorpstion map of the low contrast phantom target ( and ) at the 2.5-cm target depth. The maps at rest of the depths were not shown. (a) Reconstruction result of US-guided dual-zone mesh method. (b) Reconstruction result of NIRFAST with no prior using different . (c) NIRFAST with US prior. (d) Coregistered US B-scan image.
The two figures show the results with no prior in the regularization matrix and with US prior. In the same figure and at the same depth, the results are further compared to the US-guided dual-zone mesh reconstruction method.
By applying the US prior to the regularization matrix, the absorption contrast has been improved for different values used (Fig. 2). For , the maximum reconstructed optical absorption values are 0.148 and for no prior and US prior methods, respectively. Similarly, the reconstructed value has improved by for and by for when US prior is used.
As shown in Fig. 3, the low contrast phantom experiment showed significant improvement in the reconstructed target shape with US prior. In this case, a small value of 0.1 showed a better shape; however, its reconstructed absorption value is overestimated by as shown in Fig. 3(c) first row.
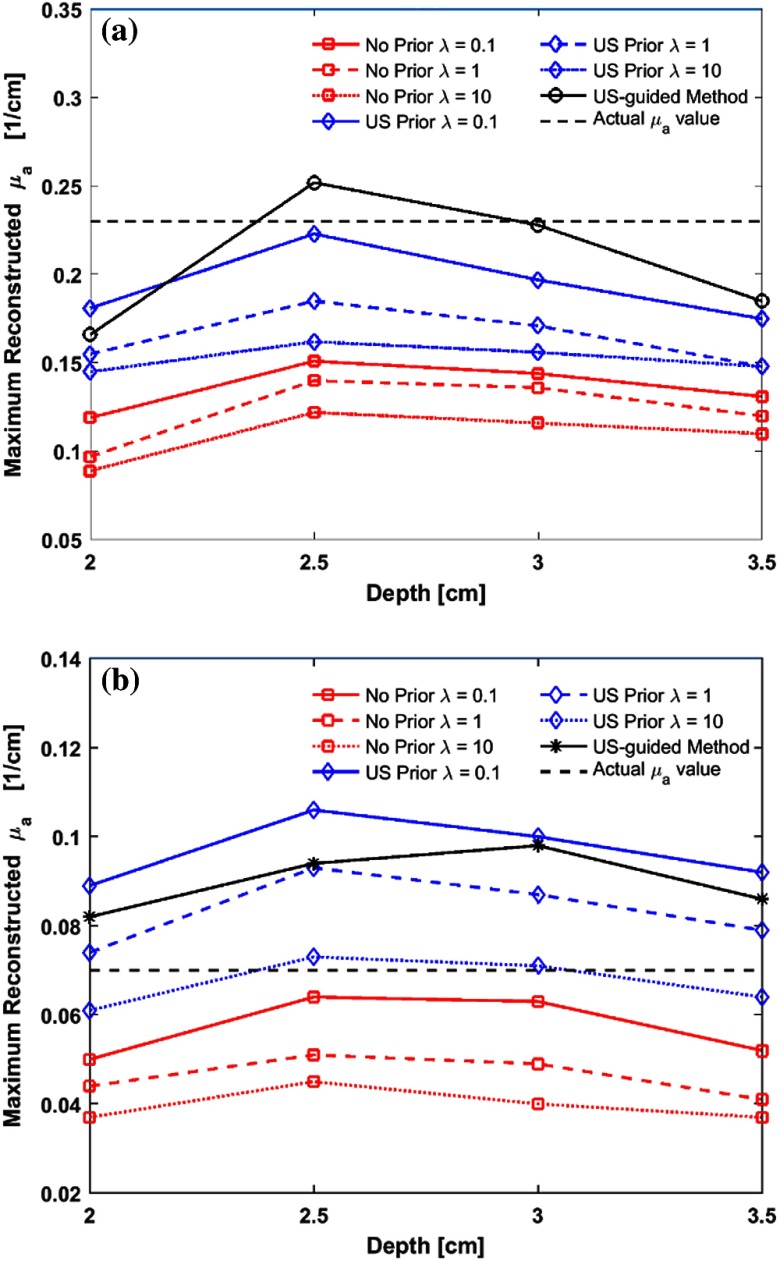
Figures 4(a) and 4(b) show the maximum recovered absorption coefficients of different for high and low contrast targets located at various target depths, respectively. Since we know the actual absorption coefficients of the phantom targets, we also calculated the percentage error of the maximum recovered absorption coefficient for each reconstruction method. The errors were averaged for different target depths and results are presented in Table 1. In comparison to the no prior method, US prior shows better estimate of the recovered absorption coefficients for different values. For the high contrast target, the reconstructed absorption values are more accurate with small values. Results with US-guided dual-zone mesh method are similer to those obtained from US prior method with small (Table 1). For the low contrast target, large values provide better estimate of the target optical properties. When the target was located deeper, results show consistent improvement in absorption values with US prior (Fig. 4).
Fig. 4.
Maximum reconstructed absorption coefficients for targets located at different depths from the probe surface. (a) High contrast target and (b) low contrast target.
Table 1.
Percentage error of maximum reconstructed absorption coefficients for both high and low contrast targets.
| Reconstruction methods | High contrast target % error | Low contrast target % error | |
|---|---|---|---|
| US-guided dual-zone | 14.4 | 28.5 | |
| No prior | 40.7 | 18.2 | |
| 46.4 | 33.9 | ||
| 52.5 | 43.9 | ||
| US prior | 15.6 | 28.2 | |
| 28.3 | 18.9 | ||
| 33.5 | 10.7 | ||
We have evaluated the accuracy of reconstruction using different layer thickness in direction from phantom experiments. Both high and low contrast targets of 3 cm located at 2.5 cm depth were used and step sizes in were 0.5, 1.0, and 1.5 cm. For a high contrast target, the maximum reconstructed absorption values obtained () were 0.21, 0.19, and , respectively, for the corresponding step size. The reconstructed values for the 0.5- and 1.0-cm layer thickness are very similar. Although the reconstructed value for the 1.5-cm layer thickness dropped, this value is more accurate in comparison with no prior method, which was . For the low contrast 3 cm target, the maximum reconstructed absorption values obtained were 0.11, 0.097, and , respectively, for the corresponding step sizes. The value obtained for no prior method was . Thus for phantom and clinical data, 0.5-cm spacing was used.
3.2. Two Targets Phantom Experiment
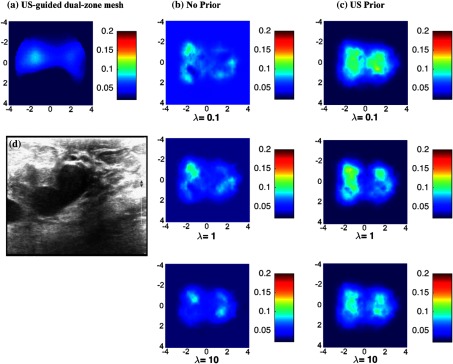
Some patients have more than one lesion of different characteristics. In this set of experiments, phantom targets of 2 cm diameters of calibrated values and , and and were embedded in the intralipid solution. The two targets mimic malignant and benign lesion characteristics.
The two targets of the same size but different absorption contrasts were located at the same depth. The depth from the target center to the probe surface differed for each experiment. The targets of 2 cm diameter and 3 cm center-to-center separation were located at 2 cm depth. The reconstructed absorption distributions at the center depth of targets (2 cm) are shown in Fig. 5 and other layers with different depths were not shown in this figure. US-guided dual-zone method and US prior show better distinction between the high and the low contrast targets. The low contrast target in Fig. 5(a) seems to be smaller than its actual size. This is due to the lower sensitivity of the system to low contrast targets compared to that of high contrast targets. Since a single mesh was used to reconstruct both high and low contrast targets, the reconstructed image of low contrast target was dominated by the high contrast target and it showed lower accuracy for low contrast target in terms of shape. The US prior method was able to improve this lower sensitivity as seen in Fig. 5(c) where the reconstructed target shape has been improved as evaluated by size. Using US-guided dual-zone method, the maximum reconstructed absorption coefficient values for the high and low contrasts are 0.19 and , respectively. These values are similar to the reconstructed values when US prior is used. The reconstructed values (using , as an example) are 0.171 and for the high and low contrasts, respectively. US prior method has shown good contrast values for all values. In this case, smaller values show optimal results for estimating the high contrast target, (Fig. 5). Values obtained with higher are best estimate for the low contrast target, (Fig. 5).
Fig. 5.
Phantom targets of 2 cm diameter with different absorption coefficients. (a) Reconstruction result of US-guided dual-zone mesh method. (b) Reconstruction result of NIRFAST with no prior using different . (c) NIRFAST with US prior. (d) Coregistered US B-scan image.
In contrast, when no prior is used for regularization matrix, absorption contrast between the two targets is very poor. The maximum reconstructed values for the two targets obtained for are 0.129 and . The no prior method showed poor contrast values for all (Fig. 5).
3.3. Clinical Cases
Clinical examples are given to illustrate the performance of the proposed method, where US images are used to regulate the inversion matrix. Once a lesion was located with the US-guided DOT system, optical measurements as well as coregistered US images were acquired simultaneously. In addition, images and measurements from the normal contralateral breast of the same quadrant as the lesion were also acquired as the reference to compute the bulk tissue optical properties for weight matrix calculation.
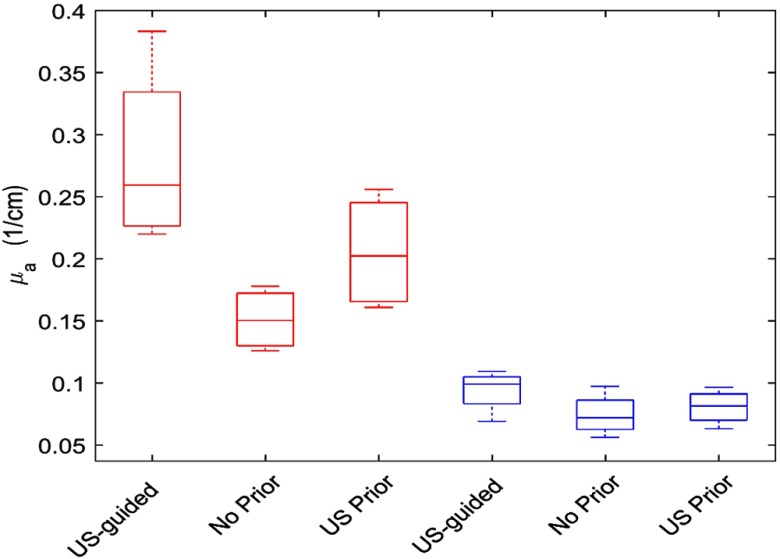
In this study, we have analyzed a total of eight patients of four malignant and four benign cases and the diagnosis was based on biopsy results. The size of the malignant group ranges from 0.9 to 1.8 cm and the size of benign is from 0.9 to 2.2 cm. We used the US-guided dual-zone method to compare the NIRFAST results of no prior and the proposed US prior method. In Fig. 6, we present the average maximum reconstructed absorption coefficients. For the no prior and US prior methods, the maximum reconstructed absorption coefficients values are averaged for the three values (, 1, and 10). Red and blue boxes represent the malignant and benign cases, respectively.
Fig. 6.
Maximum reconstructed absorption coefficient for eight clinical cases at 780 nm. Red and blue boxes indicate the malignant and benign cases, respectively.
The average maximum reconstructed absorption coefficient for malignant cases is using the US-guided dual-zone mesh method (Fig. 6). In contrast, the value obtained with NIRFAST with no prior is . Applying the US prior with 0.5 cm layer thickness in Y direction has improved the reconstructed value to . For the benign cases, the maximum reconstructed absorption coefficients are similar for all three methods used. These values are 0.11, 0.085, and obtained with the US-guided dual-zone mesh method, no prior, and US prior, respectively.
The ratio of the maximum reconstructed absorption values of malignant to benign lesions is 1.7 when no prior was applied to the NIRFAST reconstruction. This ratio is improved to 2.3 when the US prior is applied. In contrast, the US-guided dual-zone mesh method still provides the highest malignant to benign ratio of 2.5 (Table 2).
Table 2.
Ratio of maximum reconstructed absorption coefficients of malignant to benign.
| Reconstruction methods | Ratio |
|---|---|
| US-guided dual-zone | 2.5 |
| No prior | 1.7 |
| US prior | 2.3 |
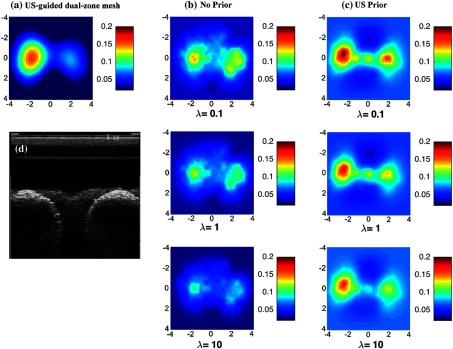
Figure 7(d) shows an example of an US B-scan of a suspicious lesion located in the left breast of a 56-year-old patient. The size measured by US is 1.8 cm in -dimension. The biopsy result revealed high grade invasive ductal carcinoma. Using US-guided dual-zone reconstruction method, the reconstructed maximum absorption coefficient is [Fig. 7(a)]. Using NIRFAST with no-prior regularization [Fig. 7(b)] and US prior [Fig. 7(c)], the average maximum absorption coefficients reconstructed (with , 1, and 10) are 0.136 and , respectively.
Fig. 7.
Malignant lesion located in the left breast of a 56-year-old patient shown in ultrasound B-scan. Reconstructed absorption coefficient with (a) US-guided dual-zone mesh method, (b) no prior, and (c) US prior are shown for different regularization parameter .
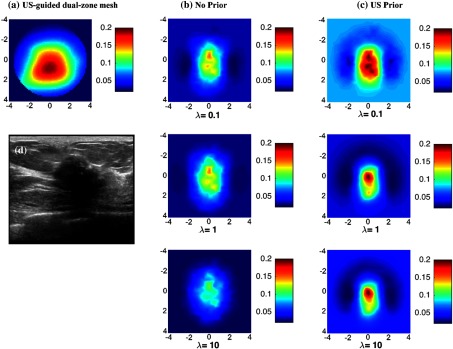
Figure 8(d) shows another example of a suspicious lesion seen in the right breast of a 44-year-old patient. The size measured by US is 2.2 cm in -dimension. Biopsy result revealed benign fibrocystic changes. The maximum reconstructed absorption coefficient is using the US-guided dual-zone reconstruction method. Similar results are obtained using NIRFAST with no prior and with US prior, the maximum absorption coefficients reconstructed (averaged for , 1, and 10) are 0.072 and , respectively.
Fig. 8.
A benign lesion in the right breast of a 44-year-old patient shown in ultrasound B-scan. Reconstructed absorption coefficient with (a) US-guided dual-zone mesh method, (b) no prior, and (c) US prior are shown for different regularization parameter .
4. Discussion and Summary
We have evaluated the performance of direct regularization method where US images were used to regularize the inversion matrix. The results of this method were compared with those obtained where no prior was used for regularization. We further compared these two methods to the US-guided dual-zone mesh method developed by our group and successfully used to characterize malignant and benign lesions of more than 400 patient data.29–31
In single-target phantom experiments, applying US prior provides more accurate absorption coefficient of the targets and good agreement with results obtained from US-guided dual-zone mesh method. Furthermore, the reconstructed target shape (for both the high and the low contrast targets) is closer to the original spherical target shape. Smaller provides better estimate of the optical properties for high contrast targets while larger provides better estimate for low contrast targets. Using average results of three different values could be a good choice for clinical data where the lesion optical contrast is unknown.
In the dual-target experiments, using US prior improves the optical contrast of the two targets. We see the effects of applying different regularization parameters, , in each method, but we clearly see the improvements using all values when US regularization prior is applied. Although, smaller overestimates targets optical properties, it is evident that the improved results for better distinction between the high and low optical absorption targets are obtained from all regularization parameters. In comparison to the results with no prior, applying US regularization prior helps to clearly distinguish the low and high contrast targets.
All three reconstruction methods provide similar optical proprieties of low contrast benign lesions; however, the US-guided dual-zone method provides the highest absorption contrast of malignant lesions. We believe its superior performance is related to the use of dual-voxel scheme to enhance the lesion quantification. US prior has improved the malignant to benign lesion ratio by as compared with no prior. Even though, the choice of has an effect on the quality of the reconstructed optical images, the malignant to benign ratio is always higher for US prior method regardless of the choice of .
The use of US prior has a limitation because the lesion size and map in dimension are estimated based on a symmetry assumption of dimension. However, since 1-D US array in dimension has about 1 cm in size and an image in slice is a map of a thick tissue layer of same size in dimension. Therefore, the use of symmetry assumption in for small lesions of 1 to 2.5 cm in size should not affect the results much as demonstrated in phantom studies. Ideally, a 3-D US map should provide a more precise ROI for optical imaging reconstruction.
This study has assessed the DRI technique using US images. This method has demonstrated an improvement in the characterization of malignant and benign breast lesions. Phantom experiments and clinical data have showed that results obtained from this method are closer to the US-guided dual-zone mesh method. Because NIRFAST is widely used by researchers in DOT field, the addition of US prior could be a valuable tool for this community.
Acknowledgments
The authors acknowledge and thank the funding supports of this work from NIH (EB002136), Connecticut Bioscience Fund. Murad Althobaiti acknowledges the funding support of fellowship from Saudi Arabian Cultural Mission of the Royal Embassy of Saudi Arabia.
Biographies
Murad Althobaiti is a PhD student in the Biomedical Engineering Department at the University of Connecticut, Storrs. He received his BS and MS degrees in biomedical engineering from Wright State University in Dayton, Ohio, in 2011 and 2013, respectively. His current research interests include diffuse optical tomography (DOT) applied for clinical diagnosis of breast cancers. He is a student member of SPIE.
Hamed Vavadi is currently a PhD student at the University of Connecticut. His current research includes development of systems and algorithms for optical imaging methods for cancer detection and diagnosis. He is specifically working on combining ultrasound and NIR imaging modalities for clinical diagnosis of breast cancers. He has expertise in vital signal processing, system design, and modeling.
Quing Zhu joined Washington University in St. Louis as a professor of the Department of Biomedical Engineering and Radiology in July 2016. Previously, she was a professor of Electrical and Computer Engineering at the University of Connecticut. She has been named fellow of Optical Society of America, and fellow of SPIE. Her research is focused on ultrasound and optical techniques for breast and ovarian cancer diagnosis and treatment monitoring.
Disclosures
Authors have no conflict of interest on this study.
References
- 1.Gibson A. P., et al. , “Recent advances in diffuse optical tomography,” Phys. Med. Biol. 50(4), R1–R30 (2005). 10.1088/0031-9155/50/4/R01 [DOI] [PubMed] [Google Scholar]
- 2.Taroni P., et al. , “In vivo absorption and scattering spectroscopy of biological tissues,” Photochem. Photobiol. Sci. 2(2), 124–129 (2003). 10.1039/b209651j [DOI] [PubMed] [Google Scholar]
- 3.Boas D. A., et al. , “Imaging the body with diffuse optical tomography,” IEEE Signal Process. Mag. 18(6), 57–75 (2001). 10.1109/79.962278 [DOI] [Google Scholar]
- 4.Chance B., et al. , “Breast cancer detection based on incremental biochemical and physiological properties of breast cancers: a six-year, two-site study,” Academic Radiol. 12(8), 925–933 (2005). 10.1016/j.acra.2005.04.016 [DOI] [PubMed] [Google Scholar]
- 5.Quarto G., et al. , “Estimate of tissue composition in malignant and benign breast lesions by time-domain optical mammography,” Biomed. Opt. Express 5(5), 3684–3698 (2014). 10.1364/BOE.5.003684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Eggebrecht A. T., et al. , “Mapping distributed brain function and networks with diffuse optical tomography,” Nat. Photonics 8(8), 448–454 (2014). 10.1038/nphoton.2014.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chitnis D., et al. , “Functional imaging of the human brain using a modular, fibre-less, high-density diffuse optical tomography system,” Biomed. Opt. Express 7(10), 4275–4288 (2016). 10.1364/BOE.7.004275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Durduran T., et al. , “Diffuse optics for tissue monitoring and tomography,” Rep. Prog. Phys. 73(076701), 1–44 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wu H., et al. , “Development of a multi-wavelength diffuse optical tomography system for early diagnosis of rheumatoid arthritis: simulation, phantoms and healthy human studies,” Biomed. Opt. Express 7(11), 4769–4786 (2016). 10.1364/BOE.7.004769 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Xu C., et al. , “Ultrasound-guided diffuse optical tomography for predicting and monitoring neoadjuvant chemotherapy of breast cancers: recent progress,” Ultrason. Imaging 38(1), 5–18 (2015). 10.1177/0161734615580280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhu Q., et al. , “Imaging tumor angiogenesis by use of combined near-infrared diffusive light and ultrasound,” Opt. Lett. 28(5), 337–339 (2003). 10.1364/OL.28.000337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang Q., et al. , “Co-registered tomographic x-ray and optical breast imaging: initial results,” J. Biomed. Opt. 10(2), 024033 (2005). 10.1117/1.1899183 [DOI] [PubMed] [Google Scholar]
- 13.Brooksby B., et al. , “Imaging breast adipose and fibro glandular tissue molecular signatures by using MRI-guided near-infrared spectral tomography,” Proc. Natl. Acad. Sci. U. S. A. 103(23), 8828–8833 (2006). 10.1073/pnas.0509636103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fang Q., et al. , “Combined optical and X-ray tomosynthesis breast imaging 1,” Radiology 258(1), 89–97 (2011). 10.1148/radiol.10082176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ntziachristos V., et al. , “MRI-guided diffuse optical spectroscopy of malignant and benign breast lesions,” Neoplasia 4(4), 347–354 (2002). 10.1038/sj.neo.7900244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yalavarthy P. K., et al. , “Weight matrix structured regularization provides optimal generalized least squares estimate in diffuse optical tomography,” Med. Phys. 34(6), 2085–2098 (2007). 10.1118/1.2733803 [DOI] [PubMed] [Google Scholar]
- 17.Pogue B. W., et al. , “Spatially variant regularization improves diffuse optical tomography,” Appl. Opt. 38(13), 2950–2961 (1999). 10.1364/AO.38.002950 [DOI] [PubMed] [Google Scholar]
- 18.Davis S., et al. , “Image-guided diffuse optical fluorescence tomography implemented with Laplacian-type regularization,” Opt. Express 15 (7), 4066–4082 (2007). 10.1364/OE.15.004066 [DOI] [PubMed] [Google Scholar]
- 19.Katamreddy S. H., et al. , “Model-resolution based regularization improves near infrared diffuse optical tomography,” J. Opt. Soc. Am. 29(5), 649–655 (2012). 10.1364/JOSAA.29.000649 [DOI] [PubMed] [Google Scholar]
- 20.Guven M., et al. , “Diffuse optical tomography with a priori anatomical information,” Phys. Med. Biol. 50(12), 2837–2858 (2005). 10.1088/0031-9155/50/12/008 [DOI] [PubMed] [Google Scholar]
- 21.Brooksby B., et al. , “Combining near-infrared tomography and magnetic resonance imaging to study in vivo breast tissue: implementation of a Laplacian-type regularization to incorporate magnetic resonance structure,” J. Biomed. Opt. 10(5), 051504 (2005). 10.1117/1.2098627 [DOI] [PubMed] [Google Scholar]
- 22.Azar F. S., et al. , “Standardized platform for coregistration of nonconcurrent diffuse optical and magnetic resonance breast images obtained in different geometries,” J. Biomed. Opt. 12(5), 051902 (2007). 10.1117/1.2798630 [DOI] [PubMed] [Google Scholar]
- 23.Zhang L., et al. , “Direct regularization from co-registered anatomical images for MRI-guided near infrared spectral tomographic image reconstruction,” Biomed. Opt. Express 6(9), 3618–3630 (2015). 10.1364/BOE.6.003618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dehghani H., et al. , “Near infrared optical tomography using NIRFAST: algorithm for numerical model and image reconstruction,” Commun. Numer. Met. Eng. 25(6), 711–732 (2009). 10.1002/cnm.v25:6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yalavarthy P. K., et al. , “Structural information within regularization matrices improves near infrared diffuse optical tomography,” Opt. Express 15(3), 8043–8058 (2007). 10.1364/OE.15.008043 [DOI] [PubMed] [Google Scholar]
- 26.Jermyn M., et al. , “Fast segmentation and high-quality three-dimensional volume mesh creation from medical images for diffuse optical tomography,” J. Biomed. Opt. 18(8), 086007 (2013). 10.1117/1.JBO.18.8.086007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhu Q., et al. , “Optimal probing of optical contrast of breast lesions of different size located at different depths by U.S. localization,” Technol. Cancer Res. Treat. 5(4), 365–380 (2006). 10.1177/153303460600500408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Durduran T., et al. , “Bulk optical properties of healthy female breast tissue,” Phys. Med. Biol. 47(16), 2847–2861 (2002). 10.1088/0031-9155/47/16/302 [DOI] [PubMed] [Google Scholar]
- 29.Zhu Q., et al. , “Ultrasound-guided optical tomographic imaging of malignant and benign breast lesions: initial clinical results of 19 cases,” Neoplasia 5(5), 379–388 (2003). 10.1016/S1476-5586(03)80040-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhu Q., et al. , “Assessment of functional differences in malignant and benign breast lesions and improvement of diagnostic accuracy by using US-guided diffuse optical tomography in conjunction with conventional US,” Radiology 280(2), 387–397 (2016). 10.1148/radiol.2016151097 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhu Q., et al. , “Early-stage invasive breast cancers: potential role of optical tomography with US localization in assisting diagnosis,” Radiology 256(2), 367–378 (2010). 10.1148/radiol.10091237 [DOI] [PMC free article] [PubMed] [Google Scholar]