Spatiotemporal Filter for Visual Motion Integration from Pursuit Eye Movements in Humans and Monkeys

Abstract

Despite the enduring interest in motion integration, a direct measure of the space–time filter that the brain imposes on a visual scene has been elusive. This is perhaps because of the challenge of estimating a 3D function from perceptual reports in psychophysical tasks. We take a different approach. We exploit the close connection between visual motion estimates and smooth pursuit eye movements to measure stimulus–response correlations across space and time, computing the linear space–time filter for global motion direction in humans and monkeys. Although derived from eye movements, we find that the filter predicts perceptual motion estimates quite well. To distinguish visual from motor contributions to the temporal duration of the pursuit motion filter, we recorded single-unit responses in the monkey middle temporal cortical area (MT). We find that pursuit response delays are consistent with the distribution of cortical neuron latencies and that temporal motion integration for pursuit is consistent with a short integration MT subpopulation. Remarkably, the visual system appears to preferentially weight motion signals across a narrow range of foveal eccentricities rather than uniformly over the whole visual field, with a transiently enhanced contribution from locations along the direction of motion. We find that the visual system is most sensitive to motion falling at approximately one-third the radius of the stimulus aperture. Hypothesizing that the visual drive for pursuit is related to the filtered motion energy in a motion stimulus, we compare measured and predicted eye acceleration across several other target forms.

SIGNIFICANCE STATEMENT A compact model of the spatial and temporal processing underlying global motion perception has been elusive. We used visually driven smooth eye movements to find the 3D space–time function that best predicts both eye movements and perception of translating dot patterns. We found that the visual system does not appear to use all available motion signals uniformly, but rather weights motion preferentially in a narrow band at approximately one-third the radius of the stimulus. Although not universal, the filter predicts responses to other types of stimuli, demonstrating a remarkable degree of generalization that may lead to a deeper understanding of visual motion processing.

Introduction

Differences in motion across space are highly informative about the structure of a visual scene. For example, spatially localized motion discontinuities differentiate objects from background (Braddick, 1993) and the distribution of motion vectors across the visual field form a cue for heading direction (Gibson, 1950). By reconfiguring how motion signals are weighted across space, the brain could extract motion contrast or sum motion across a portion of the visual field to subserve different perceptions and actions as needed. Here, we focus on global motion summation. Much of what we know about motion summation comes from analysis of perceptual thresholds for detection or discrimination (van Doorn and Koenderink, 1984; de Bruyn and Orban, 1988; Watamaniuk and Sekuler, 1992; Fredericksen and Verstraten, 1994; Watamaniuk and Heinen, 1999; Tadin et al., 2003; Tadin and Lappin, 2005). Thresholds represent net signal-to-noise and thus make it challenging to recover the underlying weighting of motion signals across space and time. Correlation analyses can differentiate spatial (Neri and Levi, 2009) or temporal (Tadin et al., 2006) contributions to perceptual motion estimates, but the enormous data samples involved limit sampling resolution. Our goal is to analyze global motion processing jointly in space and time at high resolution, so we take a different experimental approach. We used smooth pursuit eye tracking as a proxy for the brain's internal estimate of motion direction. We created spatial and temporal variation in motion direction and correlated motion at different locations and time lags with the eye direction. We find the linear model that best predicts pursuit, and we explored how the filter changes with stimulus size and form. We show that the filter reflects visual summation that is shared with perception rather than visual–motor processing specific to pursuit (Krauzlis and Adler, 2001; Wilmer and Nakayama, 2007).

The visual system determines many features of the initial pursuit response. The initial eye acceleration is performed open loop, driven by feedforward visual motion estimates without extraretinal feedback (Lisberger and Westbrook, 1985; Movshon et al., 1990). Visual estimates for pursuit and perception arise in the extrastriate middle temporal cortical area (MT), where neurons respond selectively to visual motion and are tuned for direction and speed (Maunsell and Van Essen, 1983; Newsome et al., 1985; Newsome and Pare, 1988; Komatsu and Wurtz, 1989; Britten et al., 1996; Groh et al., 1997; Lisberger and Movshon, 1999; Rudolph and Pasternak, 1999; Born et al., 2000; Pack and Born, 2001; Hohl and Lisberger, 2011). For motion that drives pursuit well, downstream motor processing of the visual signal adds little noise such that stimulus motion is faithfully translated into eye movement (Osborne et al., 2005; Osborne et al., 2007; Lisberger, 2010; Mukherjee et al., 2015). Under these conditions, the eye movement is correlated both with perceptual estimates of stimulus motion (Stone and Krauzlis, 2003; Mukherjee et al., 2015) and with motion-sensitive cortical neuron responses (Groh et al., 1997; Pack and Born, 2001; Hohl and Lisberger, 2011; Hohl et al., 2013). Taken together, these properties suggest that pursuit can be a good proxy for system-level estimates of visual motion. Indeed, we find that the spatiotemporal filter for pursuit predicts perceptual judgments of motion direction.

Pursuit responds both to the motion of small objects and to spatially distributed motion such as random dot kinematograms (Lisberger et al., 1987). In this sense, pursuit bridges two different scales of spatial motion processing, one operating on local motion contrast and another that sums motion over larger visual regions. In theory, motion contrast and motion summation require different cortical processing and therefore might be modeled by different spatiotemporal filters (Born and Tootell, 1992; Born et al., 2000). To focus on global motion integration, we employ high-contrast, dot motion stimuli that are well suited to the correlation analysis, drive a robust pursuit response, and require motion signals to be pooled across space and time to estimate the direction of travel. We also explore the filter's dependence on stimulus size and form.

Materials and Methods

Procedures.

All experimental procedures adhered to the guidelines of the University of Chicago's Institutional Review Board and Institutional Animal Care and Use Committee and were in strict compliance with the National Institutes of Health's Guide for the Care and Use of Laboratory Animals.

Data acquisition.

We recorded eye movements from four adult male rhesus monkeys that had substantial prior training on pursuit tasks. Not all monkeys participated in all experiments. Monkeys viewed stimuli in a dimly lit room on a Sony GDM-FW9011 fast CRT display (display mode 100 frames/s (fps), 1024 × 768 pixels) subtending 57° × 38° at a viewing distance of 48 cm or a Dell P1130 (100 fps, 1024 × 768) subtending 35° × 32° at a viewing distance of 51 cm. We measured the horizontal and vertical position of one eye with an implanted scleral coil (Robinson, 1963). Eye position was sampled at 1 ms intervals, vertical and horizontal eye velocity signals were passed through a double-pole, low-pass filter that differentiated frequencies <25 Hz and rejected higher frequencies with a roll-off of 20 dB per decade to yield velocity signals that were then stored for later analysis (Mukherjee et al., 2015).

We also recorded eye movements in three adult (one male, two female) human subjects who gave informed consent. The human subjects had normal or corrected to normal vision and had some prior experience in psychophysical and eye-tracking tasks. Not all subjects participated in all experiments. We measured the vertical and horizontal positions of the right eye with a dual Purkinje image infrared eye tracker (Ward Electro-Optics Gen 6). Eye positions were sampled every 1 ms and then filtered and stored using the same electronics described above. Subjects viewed stimuli in a dimly lit room on a Sony GDM-FW900 fast CRT display (100 fps, 1024 × 768 pixels) subtending 35° × 21° at a viewing distance of 68 cm.

Pursuit experiments.

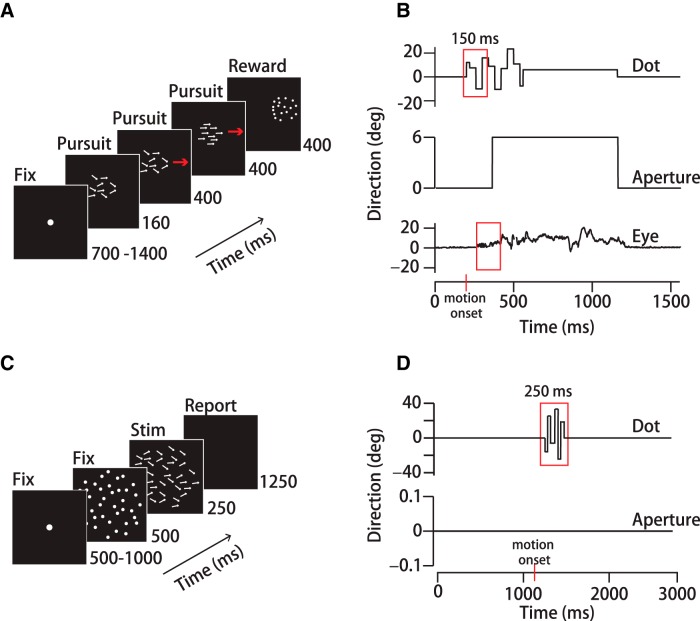
Pursuit experiments were organized into trials lasting 2–3 s that consisted of an initial fixation period of random duration (700–1400 ms), a pursuit period (960 ms), and a final fixation period (400 ms) (Fig. 1A). The fixation target was a small (0.25° or 0.5°), uniformly illuminated circle. The fixation target extinguished as a pursuit target appeared synchronously with motion onset. Pursuit targets appeared either centered on the fixation location or 2–3° eccentric from it and then translated back toward the former fixation point in the classic step-ramp experimental design that minimizes the frequency of saccades (Rashbass, 1961). Pursuit experiments with spatiotemporal noise targets (described below) had motion within a stationary aperture for 160 ms to initiate pursuit, after which the pattern and aperture translated together for the remaining pursuit period (Fig. 1A). The “motion-within” period allowed calculation of the spatiotemporal filter based on dot motion without contribution from aperture translation. The translation period maintained a high pursuit gain throughout the experiment. Monkeys were rewarded at the end of each successfully completed trial. Human subjects did not receive performance feedback. Both monkeys and humans were required to maintain fixation within 2° of a stationary spot for 700 ms before motion onset and to be within 3° of the target center during the final 200 ms of pursuit. We expanded the accuracy windows for large targets as needed. We did not penalize gaze accuracy during time windows used for data analysis. To minimize anticipatory eye movements, we randomized the initial fixation interval duration by 700 ms and we balanced the directions of target motion about the center. Target directions ranged from −6° to +6° from rightward or leftward in 3° increments except where noted. We used one target form for each day's experiment. We presented stimuli in blocks rather than interleaving target forms based on our observation that pursuit movements reach a steady-state gain when the target form is expected, whereas alternating target forms can cause strong stimulus history effects in eye speed (Heinen et al., 2005). Monkeys performed ∼1500–3000 trials per daily session. Humans typically performed ∼300 trials per session, so we pooled multiple sessions to reach the necessary sample size. We inspected each trial record and discarded trials with saccades or blinks during the analysis window. We collected data until we accumulated ∼100 repetitions of each experimental condition for analysis.

Figure 1.

Experimental design. A, Schematic representation of a step-ramp pursuit trial sequence. Stimuli consisted of 3-pixel “dots” randomly positioned within a circular aperture. B, Top, Direction of a single dot in a noisy dot stimulus over time during the pursuit task. Each dot's direction fluctuated randomly within ±40° of the mean, updated synchronously every 40 ms. Middle, Aperture motion over time. Dots moved within a stationary aperture for 160 ms before both translated together across the screen at 15°/s. Bottom, Eye direction over time on an example trial. The red boxes represent the 150 ms analysis windows. C, Schematic representation of the perceptual task. After a 500 ms interval during which the dot pattern was stationary, the dots underwent a step change in speed, moving behind a stationary 30°-diameter aperture for 250 ms. Human subjects then had 1250 ms to indicate their up/down judgments of the average motion direction by button press. D, Top, Direction of a single dot in the noisy dot stimulus (40 ms update) over time. Red box indicates the 250ms analysis window. Bottom, Aperture did not translate in the perception experiment.

Perceptual discrimination experiments.

We performed a series of perceptual motion discrimination experiments in two of the human subjects for whom we recorded pursuit (H1, H3). The perceptual discrimination experiments used the same noisy dot direction stimuli as the pursuit tasks. We configured the perceptual experiments as two-alternative-forced-choice (2AFC) tasks. Subjects reported whether the time-averaged center-of-mass motion direction was upward or downward with respect to horizontal (0°). For these experiments, we presented only rightward directions (0°, ±6°, ±12°). Perceptual trials began with a randomized fixation interval (500–1000 ms). Then, a stationary, 30° circular diameter random dot pattern appeared on screen for 500 ms, after which the dots moved (see description of noisy dot direction stimuli) within the stationary aperture for 250 ms (Fig. 1C). Subjects then reported motion direction by button press in a 1250 ms period. The purpose of the 500 ms stationary interval was to minimize the contribution of visual activity driven by stimulus appearance rather than motion.

Neurophysiology experiments.

To measure neural filters for motion integration, we recorded extracellularly from well isolated units in MT of two adult male rhesus monkeys (Macaca mulatta) that had performed pursuit tasks (M2, M3). We implanted a recording chamber, head restraint, and eye coil under anesthesia using sterile technique. Monkeys maintained fixation during physiology experiments to stabilize stimuli in each neuron's receptive field (RF). Extracellular recordings were made with quartz-coated tungsten microelectrodes (TREC). Signals were filtered, amplified, digitized, and recorded through the Plexon OmniPlex system. Initially, we isolated single units using the Plexon online sorter, and we inspected and refined the isolation using Plexon's offline sorter. Once we isolated a unit, we mapped its direction and speed tuning functions and the location and size of its excitatory RF using coherent random dot pattern stimuli. We then created visual stimuli online that had a time-averaged mean direction centered on the flank of the isolated unit's direction tuning curve and that moved at the neuron's preferred speed.

Monkeys were required to maintain fixation of a 0.5° spot within a 2° window throughout the trial (∼1–4 s) for a juice reward. Visual stimuli were projected in the RF of the neuron after an initial fixation period of 200 ms. The stimuli remained stationary on screen for another 200 ms to allow for the neural response to stimulus appearance to decay (Osborne et al., 2004). Stimuli were spatiotemporal noise targets as described below or, more typically, coherent motion dot patterns undergoing randomized direction changes about a constant mean motion direction. In both cases, dot directions were updated every 20 or 40 ms as in the pursuit experiments and stimuli moved for 500–4000 ms. We recorded 44 MT neurons (n = 26 M2; n = 18 M3) using multiple levels of motion direction variation to yield multiple data points per neuron.

Spatiotemporal noise stimuli.

To provide the spatial and temporal variation in motion direction needed to compute a spatiotemporal filter, we added a stochastic component to random dot kinematograms, modeled on stimuli developed by Williams and Sekuler (1984) (see also Heinen and Watamaniuk, 1998; Watamaniuk and Heinen, 1999; Osborne and Lisberger, 2009; Watamaniuk et al., 2011; Mukherjee et al., 2015). The “noisy dots” stimuli comprised high-intensity “dots” (3 pixels) positioned randomly within a circular aperture displayed against the dark background of the CRT monitor (Fig. 1). Aperture diameters ranged from 5° to 30°. Dot density was 1 dot/deg² except where noted. Each dot had a common base direction and speed with an individually added stochastic perturbation in direction. Each dot's direction was updated synchronously with a random draw (with replacement) from a uniform direction distribution of −40° to +40° around the base direction in 1° increments. The interval between direction updates was 40 ms (4 frames). Between update intervals, each dot moved across the screen along a different direction. The noisy dots targets resemble the motion of a swarm of bees or a flock of birds in which each has a random trajectory but there is also overall cohesion in swarm translation. The spatial resolution of our displays limited the actual direction resolution to ∼3–6° between updates. The effects of limited display resolution were not apparent when watching the stimulus or in the movements of the eye even when tracking a single dot. If a dot's updated position fell outside of the aperture, it was repositioned randomly along the opposite edge. For pursuit experiments, the dots moved within a stationary aperture for 160 ms before dots and aperture began translating together. All targets except for the 30° noisy dots stimulus had an aperture speed of 15°/s for pursuit tasks and base directions of −6°, −3°, 0, +3°, or +6° rightward and leftward. The 30° diameter noisy dots stimuli had motion within a stationary aperture for the entire duration of the pursuit experiment. Because the direction varies across dots, the apparent translational speed of the dot swarm is slower than that of the aperture. To keep the dot pattern in register with the aperture as they translated, dot speed was increased to 16.4°/s, a correction equivalent to the SD of the direction distribution (Watamaniuk and Heinen, 1999; Osborne and Lisberger, 2009; Mukherjee et al., 2015).

For human perceptual direction discrimination experiments, we used the same 30° diameter noisy dot direction stimulus as in the pursuit experiments. The range of dot directions remained −40° to +40° around rightward base directions of 0°, ±6°, and ±12°. Dot directions updated synchronously every 40 ms. Dots moved at 16.4°/s within the stationary aperture.

Coherent motion stimuli for physiology and pursuit.

We created coherent motion versions of the noisy dots stimuli to compare temporal motion filters in MT neurons and pursuit. The statistics of direction updates were similar to those for noisy dots (−40° to +40° uniform direction distribution, 20 ms or 40 ms update interval), but there was no spatial variation in dot direction within the aperture. Rather, the directions of all dots updated synchronously and identically to create a coherent, time-varying motion direction (Osborne and Lisberger, 2009). For the pursuit experiments that accompanied the physiology recordings, the target aperture had a 4° diameter, with 100 dots moving with the aperture at 15–20°/s, set according to the optimum pursuit speed for each monkey. Targets appeared 2–3° eccentric to the fixation spot and immediately began translating toward it as the fixation point was extinguished. The pursuit interval lasted for 650 ms. The MT recordings were performed while monkeys maintained fixation within 2° and the motion stimulus was projected onto the unit's RF. The stimulus aperture was positioned, scaled, and motion speed was chosen to drive the unit maximally. The base direction of motion was positioned on a flank of the direction tuning ∼45° from the neuron's preferred direction, where sensitivity to direction fluctuations is maximal.

Additional stimulus forms.

We performed a limited number of experiments with alternate stimulus forms to determine to what degree the filter generalizes to other motion stimuli. We used several translating Gabor stimuli, all of which were 100% contrast, odd symmetric, 1 cycle/° sinusoids that translated at 15°/s. Grating orientation was always perpendicular to the direction of motion. The single Gabor stimulus had a 14° diameter aperture with a 2D Gaussian envelope SD of 2.75° and was either presented against a dark background or against a uniformly illuminated background set to the average intensity of the Gabor. We also used an array of 13 small, 2° diameter Gabors (SD = 0.75°) positioned 1–2° apart to create an overall stimulus diameter of 14° in a diamond formation. The array was presented against a background set to the mean luminance of each Gabor. We also created a 100% contrast, 14° diameter square aperture checkerboard pattern, with 1.8° squares that alternated black and white, that translated together against the dark screen of the CRT. Additionally, we tested a range of fully coherent dot pattern stimuli in apertures of 5–14° diameter and a dot density of 1 dot/deg² that translated at 15°/s, and a 0.5° circular spot target moving at 16°/s. The motion directions of all targets were pseudorandomly interleaved, 0°, ±3°, and ±6° leftward and rightward.

Behavioral filter calculation.

We performed a linear analysis of the correlation between fluctuations in eye direction and fluctuations in stimulus direction during the first 150 ms of pursuit. We chose this time period to emphasize the portion of the eye movement that is dominated by retinal image motion while the eye is still. After the target begins to move, there is a latency interval of 75 ± 7 ms (SD) for monkeys (n = 40 datasets; 4 subjects) and 160 ± 11 ms (SD) for humans (n = 9 datasets; 3 subjects) before the eye begins to accelerate. The visually driven open loop interval is longer than the latency period, ranging from 93 to 139 ms in monkeys and from 236 to 320 ms in humans based on past experimental measurements for which the measurement criterion was known to us (Lisberger and Westbrook, 1985; Osborne et al., 2007; Mukherjee et al., 2015). The duration of the open loop interval in monkeys is often standardized to 100 ms when a measurement is lacking and a very conservative measure is desired. Here, our primary concern was computing the extent of the linear filter rather than restricting analysis to the open-loop interval. We chose an analysis time window of 150 ms as a compromise between the typical duration of the pursuit open-loop interval and adequate movement duration to characterize the motion filter fully. We used a 150 ms window in two ways: the time vector of pursuit considered on each trial was limited to the first 150 ms of pursuit and the filter at stimulus–response time lags was computed up to 150 ms. A longer time window ensured that we could truly observe stimulus–behavioral correlations go to zero for the shortest and longest time lags. Before analysis, we shifted the eye trace with respect to the stimulus trace by 50 ms to compensate partially for the average pursuit latency and thereby center the filter within the 150 ms analysis window. Then, at each time point starting from pursuit onset, we computed the correlation between eye and the preceding dot direction values at time lags from 0 ms to 150 ms in the past (actually 50 ms to 200 ms). As expected, these correlations were zero for the shortest and longest lags. At pursuit onset, the stimulus has not been moving for 200 ms, so the stimulus was extended with zeros. The algorithm steps through the first 150 ms of pursuit computing the correlation at all lags, and then averages all samples at given time lag to determine the temporal filter. Therefore, each trial in a day's experiment contributes up to 150 measurements of the correlation at each lag value. We tested the degree to which eye movements just beyond the true open-loop interval affected our results and found that the structure of the filter was stable across the first 200 ms of monkey pursuit, in agreement with a previous study (Osborne and Lisberger, 2009). We describe this calculation in more detail below.

The pursuit response can be described as a velocity vector $\overrightarrow{v}(t)=({\overrightarrow{v}}_H(t),{\overrightarrow{v}}_V(t))$ where $\overrightarrow{v}$ indicates an eye velocity vector and the subscripts “H” and “V” label horizontal and vertical, respectively. We sampled the eye velocity at 1 ms intervals. To relate the eye movement to the direction perturbations in the stimuli, we converted the vector eye velocities into time-varying eye direction: $\overrightarrow{e}(t)={\text{tan}}^{-1}({\overrightarrow{v}}_V(t)/{\overrightarrow{v}}_H(t))$. For each target condition, we then subtracted the trial averaged mean eye direction over time from each pursuit trial to create an array of residuals. The eye direction residual for the i^th trial is given by the following: $\delta {\overrightarrow{e}}_i(t)={\overrightarrow{e}}_i(t)-<{\overrightarrow{e}}_i(t)>$ where <…> denotes an average across trials with the same target motion. We performed a similar operation on the stimulus. First, we up-sampled the stimulus to 1 ms resolution, creating an array of residual dot directions over time with respect to each dot's mean direction with a target condition. We used the arrays of eye movement and stimulus residuals to compute a 3D linear filter F(R, θ, T), which describes the spatial and temporal relationship between motion and eye movement. The filter is defined in discrete time by the following equation:

where ê(T) represents the estimated instantaneous eye direction at time T, R and θ are spatial coordinates of eccentricity and direction in visual space with respect to the fovea, τ is the time lag between the stimulus and the predicted response, and S is the motion stimulus defined relative to the fovea (Weiner, 1949, Mulligan, 2002; Papoulis, 1991; Osborne and Lisberger, 2009; Tavassoli and Ringach, 2009). The filter is the function that minimizes the summed squared error between the estimated and actual eye direction over time. When applied to the dot motion on a single trial, the filter predicts the eye direction over time. The quality of the prediction is a measure of how linear the visual to motor transformation is in pursuit. As defined by Equation 1, F(R, θ, T) has no explicit units, but rather represents the relative weighting of motion at different spatial locations and time lags with respect to the eye direction at some point in time.

We solved Equation 1 for F(R, θ, T) using a modified version of MATLAB's tfe function (The MathWorks), which is based on Welch's averaged periodogram method. The algorithm divides the input (fluctuations in dot direction) and output (fluctuations in eye direction) into overlapping 150 ms sections that are detrended, padded with zeros to a length of 256 (or 512) data points, and convolved with a 256-point (or 512-point) Hann window (“Hanning”) to compute the discrete Fourier transform. Most of our analyses were confined to the first 150 ms of pursuit. We computed the power spectral densities as the squared magnitude of the Fourier transform averaged over the overlapping sections and over trials. The algorithm normalizes the cross power spectrum between stimulus and response by the power spectrum of the stimulus. We used a cutoff frequency of 30 Hz for the spatiotemporal noise stimuli and a cutoff frequency of 35 Hz for the coherent dot motion stimuli. This operation is mathematically equivalent to walking millisecond by millisecond through the first 150 ms of pursuit, computing the correlation between the motion stimulus and the eye movement (and the stimulus autocorrelation) at each point at time lags from 0 to 150 ms, and then averaging the results for each time lag and dividing the cross-correlation by the autocorrelation. The zero padding compensates for the fact that at early times in the pursuit response there were not 150 ms of prior stimulus.

There was not a sufficiently large data sample to measure the filter at the pixel resolution of our display. Instead, we divided visual space into a polar grid centered on the fovea at each time step. We divided the visual field eccentrically into 59 overlapping concentric annuli (0 to 0.5 visual degrees of spatial arc, 0.25° to 0.75°, 0.5° to 1°, …, 14.5° to 15°) and angularly into 12, 30° pie slice segments (−15° to +15°, +15° to +45°, …) (see Fig. 2A). Annuli of increasing eccentricity encompass a greater area of the visual field, and hence a larger number of dots. To ensure that the filter structure was not affected by the spatial binning, we normalized by number of dots for each location and time step in the calculation (Fig. 2C, red trace). As a control, we also confirmed that segmenting visual space such that equal numbers of dots fell within each area produced an identical spatiotemporal filter (Fig. 2C, gray trace). To analyze the filter's directional structure, we flipped the sign of the horizontal component of target and eye velocity on leftward trials. This operation oriented the angular coordinate frame with respect to the direction of motion set to 0° while preserving upward and downward motion components across all stimulus directions. We then computed F(R, θ = θ_i, T) separately for each section i (Fig. 2D,E).

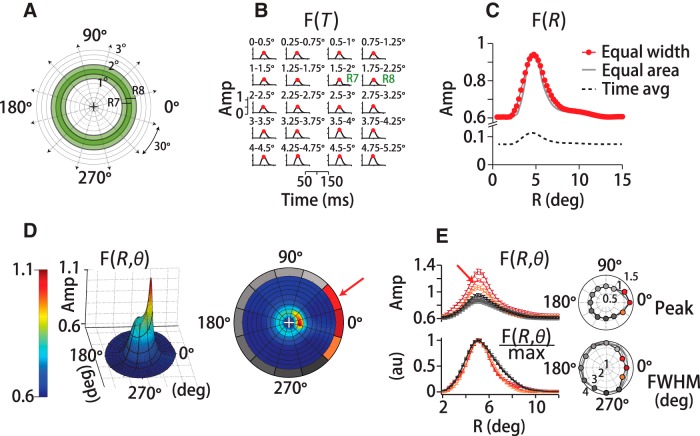
Figure 2.

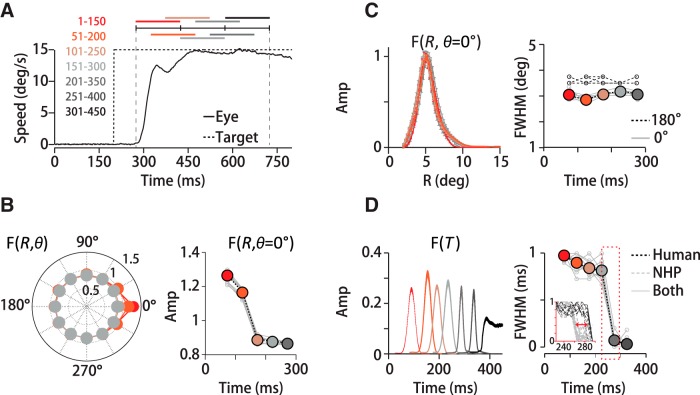
Spatiotemporal filter for motion integration. A, We defined the motion stimulus on a polar grid centered on instantaneous eye position (+), dividing visual space into 59 concentric overlapping annuli of 0.5° (visual degrees of spatial arc) width that span 15° of eccentricity. Green rings (R7, R8) exemplify the overlap in adjacent annuli. We further subdivided space into 12, 30° pie-slice segments. B, At each spatial location, we computed a temporal filter between eye and dot-averaged motion direction, here shown only for eccentricities up to 5.25° of 15°. Red circles indicate the peak of the temporal filter, F(R = R_i, T)_max. Each temporal filter represents a unitless weight corresponding to a dot's contribution to eye direction based on its position and the time delay. The peak temporal filter amplitudes (Amp) sweep out the spatial filter based on motion eccentricity, F(R), in C, red trace. Reconfiguring the annuli to equalize the number of dots in each grid region does not change the form of the spatial filter (gray trace). Defining F(R) by the time-averaged amplitude rather than the peak reduces the scale, but does not change the filter's form (dotted black trace). D, 3D spatial filter, F(R, θ, T), shows a pronounced directional anisotropy, with high amplitudes in front, below and above the eye. Color and height indicate the relative contribution to pursuit of different portions of the visual field in a 3D projection (left) and a top-down view (right). The red arrow points to the same example segment (15–45 degrees of spatial arc) in D and E. The gray-red colors of the polar plot's outer sections (right) represent the relative spatial filter amplitudes in each angular segment. The contribution of many segments was nearly identical, reflected in the similarity in outer-section shading. E, Top left, Set of spatial filters from each directional segment from one experiment (M1), colors correspond to the right panel in D. Amplitudes are high along the direction of motion (red-orange shades), but similar otherwise (gray shades). Top right polar plot, Peak amplitude versus direction segment for three humans and two monkeys. The traces overlap. Bottom left, Normalizing by the peak amplitude illustrates that the filter is narrowing in segments where amplitudes are high. Bottom right polar plot, Spatial filter FWHM for five subjects (black, gray lines).

We used a cross-validation resampling technique, measuring the filter with a random draw of 70% of the sample and then using the filter to predict the eye's response to the remaining 30% of the stimuli. We repeated this process many times to generate a mean and error (SD) for all measurements. We created an array of residuals, or prediction errors, by subtracting the predicted eye direction over time from the actual eye movement. We inspected the residual differences between the filter-predicted and measured eye movements for evidence of response saturation or other static (time independent) nonlinearities. To quantify the predictive power of the linear filter, we calculated the correlation coefficient between the predicted and actual eye movements over time as part of the cross-validation analysis.

Analysis of spatial anisotropy and dynamics in the motion filter.

To determine whether there are any rotational anisotropies in motion integration, we analyzed pursuit data as a function of direction with 30°-diameter aperture noisy dots stimuli. As described above, we divided the visual field into 12 sections, each subtending 30 visual degrees of spatial arc. We centered the analysis frame on the eye's position at each time step. We flipped the sign of the horizontal components of the stimulus and eye velocity on leftward trials to keep the coordinate frame consistent across all motion directions. The filter calculation proceeded as described above. To determine how the form of the spatial and temporal filter components changed over time, we performed the analysis in overlapping 150 ms windows that spanned the first 450 ms of the pursuit response.

Comparison of pursuit and perception.

Because we could not compute the spatiotemporal filter directly from our 2AFC perceptual data, we instead quantified how well the pursuit filter predicted subjects' perceptual choices compared with other filter shapes. We analyzed data from 0° or 180° trials only from experiments with 30° diameter stimuli. First, we fit each subject's temporal filter with a Gaussian function, f(x) = a₁e^{−(x−b₁/c₁)2} and each spatial filter was fit with the sum of two normal functions to capture the skew, f(x) = a₁e^{−(x−b₁/c₁)2} + a₂e^{−(x−b₂/c₂)2}. All fits had R² values of 0.99. Subject H1's temporal filter fit parameters were a₁ = 0.61, b₁ = 48, c₁ = 13, The spatial filter fit parameters were a₁ = 0.31, b₁ = 4.8, c₁ = 1.7, a₂ = 0.64, b₂ = 8.2, c₂ = 28. Subject H2's temporal filter had fit parameters a₁ = 0.61, b₁ = 43, c₁ = 13 and spatial filter fit parameters a₁ = 0.33, b₁ = 4.5, c₁ = 1.8, a₂ = 0.64, b₂ = 9.5, c₂ = 24. Then, a set of 209 (19 × 11) spatial and 208 (16 × 13) temporal filter forms was generated by changing the peak eccentricity or delay (b₁, b₂) and the width (related to c₁, c₂) systematically. We tested different spatial filter forms while keeping the temporal filter constant and vice versa. Nine examples from the spatial filter set are illustrated in the margins of Figure 5A by colored dashed lines holding the other fit parameters constant.

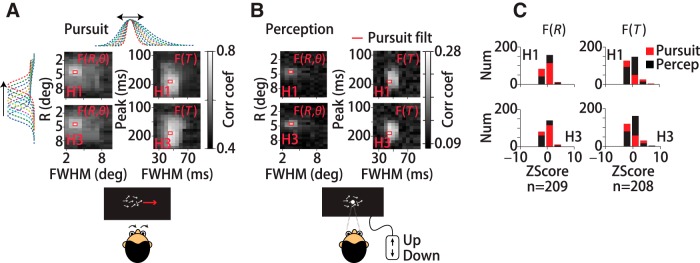
Figure 5.

Same spatiotemporal filter predicts pursuit and perceptual reports of motion direction. We compared the predictive power of the actual spatial and temporal filters (red rectangles) and synthetic filters created by shifting (y-axes) and stretching (x-axes) the measured filter forms (top, side dotted lines, A). Each grayscale element in the density plots represents the linear correlation coefficient between predicted and measured eye direction or perceptual reports using a different filter shape; white indicates high and black low correlation. The elements outlined in red correspond to the best prediction, obtained in each case by the actual pursuit filter. A, Pursuit data for two human subjects (H1, H3). Data in left panels were generated by holding the temporal filter constant and manipulating the spatial filter; for right panels, the opposite was done. The pattern of near white values indicates the sensitivity of prediction quality to the shape of the filter. B, Perceptual data for the same subjects using the same filter set. As with pursuit, the actual spatial and temporal filters yield the best prediction of perceptual reports. C, Histogram plots of the z-scored correlation coefficients for pursuit and perception for manipulations in the spatial filter form (left) or temporal filter forms (right) from the same data.

To evaluate the predictive performance of each filter form, we convolved the spatiotemporal filters, F_model(R)F_model(T)^T, with the dot motion on each trial to predict the pursuit or perceptual response and then we computed the linear correlation between the predicted responses and the actual responses over all trials. We assigned perceptual responses +1 for upward and −1 for downward choices. For the pursuit data, we computed the mean eye direction in a 5 ms window centered at 250 ms after motion onset and assigned the trial +1 if the eye direction was rotated upward and −1 if it was rotated downward with respect to the mean. For the perception data, we used each filter form to predict the time-averaged motion direction over the 250 ms interval, as per the task we assigned the subjects. Then, we computed the correlation coefficient between the binary behavioral data (eye direction or perceptual report) and the predicted responses from the filters in degrees. The correlation calculation was therefore identical for the pursuit and perceptual data. We converted the correlation value for each filter shape into a z-score by subtracting the mean value of the correlation coefficient across all model filter forms and dividing by the SD of the values across the set. The z-score transformation simplified comparison between pursuit and perception predictions. To quantify how similar the pursuit data and perception data matrices were, we formed distributions of z-scored correlation coefficients for all model filters and compared the RMS variance of those distributions for each subject. We performed a control analysis to ensure that the pattern of behavioral predictions by the different spatial and temporal filter forms did not arise by chance. We took multiple random draws of 50% of the pursuit or perception data samples, convolving each of the 208 or 209 filter shapes with the stimulus set, to predict behavioral responses. We then computed the correlation coefficient between the predicted and actual behavioral responses and the correlation coefficient between the predicted responses and a random permutation of the responses. We defined the p-value of each filter form as the fraction of times that the correlation with the randomly permuted values equaled or exceeded the actual correlation coefficient. The p-values were ≤0.01 for all correlation coefficients plotted in Figure 5.

We performed a second control analysis to ensure that differences in how we used each filter form to predict eye directions or perceptual reports did not affect the results. To generate the results in Figure 5, we used the filter sets differently to predict the perceptual and pursuit responses based on the difference between the tasks. In the perception tasks, subjects reported whether the time-averaged motion direction was upward or downward from horizontal, so we used each model filter form to predict the time-averaged dot direction across the 250 ms motion interval. In pursuit, the eye reports the estimated direction at each time point, so we used each filter to predict the eye direction at 250 ms after pursuit onset. To ensure that the data-handling difference did not contribute to the grayscale patterns of correlation values in Figures 5, A and B, we reanalyzed the data to test both prediction methods on each dataset. We generated matrices like the right panels in Figures 5A, but we used the temporal filter set to estimate the time-averaged pursuit stimulus direction over 250 ms. The pursuit prediction results were not statistically different from the data in Figure 5A (p = 0.41, two-sample t test, H1; p = 0.37, H3). Next, we used the temporal filter set to predict the perceptual stimulus direction at 250 ms to correlate with the perceptual reports. Again, the results were not statistically different from the right panels in Figure 5B (p = 0.43, two-sample t test, H1; p = 0.39, H3). Therefore, the method used to characterize the stimulus for pursuit and perception data did not affect the results reported in Figure 5.

Neural temporal filter calculation.

We computed the temporal filter relating fluctuations in spike count to stimulus direction as a function of time lag using the same methods described above for the behavioral filters. We counted spikes in overlapping 20 ms time windows centered at 1 ms intervals starting from stimulus motion onset and extending over a 250–2000 ms motion segment for each trial. The calculation of the neural filter then proceeds identically to the methods described for the behavioral filter using a cutoff frequency of 30 Hz and replacing eye direction with spike count in the time window. We computed the correlation between the count values and motion direction at 1 ms intervals up to lags of 200 ms.

Separability analysis.

We performed singular value decomposition to determine the extent to which motion filters were space–time separable; that is, the degree to which the full spatial temporal filter is captured by the outer product of a 2D spatial and 1D temporal filter, F(R, θ) ⊗ F(T). We analyzed both F(R, T) (59 eccentricity annuli by 150 time points) and the full 3D filter, F(R, θ, T), after reorganizing into a sparse, 2D array of 708 spatial points (12 direction segments × 59 annuli) by 150 time points. The relative squared weight of the first singular value σ₁ with respect to the others; that is, σ₁²/Σ_iσ_i² defines the separability index (SI). An SI of 1 indicates that variance in the filter form is perfectly captured by a single mode and thus its space–time separability is exact.

Optic flow score.

To determine whether the filter computed with noisy dots stimuli also predicts responses to novel stimuli, we compared the filter predictions with measured eye movements. We convolved the filter with each new stimulus and then integrated over space and time from motion onset to 150 ms to generate a scalar value termed the optic flow score. The optic flow score summarizes the net motion energy in a stimulus as weighted by the visual system (Mukherjee et al., 2015). To perform the convolution, we first converted each new motion stimulus into a pixel flow field using an algorithm based on Sun et al., 2010. The pixel flow field is a luminance-weighted vector field describing the translation of each pixel from one frame to the next. For dot pattern stimuli, the pixels were either on (1) or off (0), so the optic flow for adjacent frames was simply the fraction of illuminated pixels per frame times their speed along the base direction of motion summed over dots and frames. The optic flow for a stimulus with intermediate luminance values such as a Gabor is determined by the speed-weighted difference in pixel intensity with respect to the background for each pair of frames normalized by the total pixel number. For non-zero background illumination, darker pixels within a stimulus such as a grating create negative flow values with respect to the background. However, the same grating stimulus against a dark background will have non-negative flow scores. For all frames in the first 150 ms of motion, we measured the position of illuminated pixels with respect to eye position and applied the MATLAB function conv2 to compute the 2D convolution between the filter F(R,θ,T) and the luminance-weighted pixel flow for each pair of frames and at each spatial grid location. The convolution operation produces a scalar flow score for each stimulus form that we compared to the measured peak eye acceleration. The scores that we report are averages across all trials in a dataset (n ≥ 200). The stimuli for which we computed flow scores matched the sizes of the noisy dots stimuli that generated the set of filters, so no interpolation of the filter form was necessary except for a 2° aperture dot stimulus and a 0.5° spot target. We generated a flow score for a 2° aperture stimulus by extrapolating the foveal eccentricity of the spatial filter peak based on the observed linear relationship between the location of the spatial filter peak and stimulus radius. The spot target was so small compared with the stimuli for which we computed filters that we had to estimate the score differently. We used two scores based on different assumptions: one without any filtering (i.e., the number of illuminated pixels (180 × 16°/s × 150 frames = 4.32 × 10⁵ °/s) and another multiplying the unfiltered score by a factor equal to the extrapolated estimate of filter amplitude for a 0.5° stimulus (4.32 × 10⁵ °/s × 0.4 = 17.3 × 10⁴ °/s) using the filter peak location versus size relationship (defined above) that we derived based on larger stimuli.

Results

To determine how visual motion signals are integrated across space and over time, we performed experiments to measure pursuit eye movements in response to stochastic motion stimuli composed of random dot kinematograms. We base our approach on the “noisy dots” stimuli developed by Williams et al. to study global motion integration (Heinen and Watamaniuk, 1998; Watamaniuk and Heinen, 1999; Osborne and Lisberger, 2009; Watamaniuk et al., 2011; Mukherjee et al., 2015) (Fig. 1A). To drive pursuit effectively, each dot in the stimulus pattern has a constant drift direction and speed, but with an added stochastic direction perturbation that we updated every 40 ms (4 frames) (Fig. 1B; see Materials and Methods). The stochastic component of each dot's motion generates a random walk around the constant motion vector. Dot perturbations update independently but synchronously, which differentiates the stimulus direction across space and time. The overall stimulus appearance is of a swarm that translates together, but with each member executing its own randomized flight path. The spatial and temporal variation in the stimulus allows us to correlate eye direction with stimulus direction as a function of location in the visual field and time delay to compute the spatiotemporal motion filter. With the exception of the stochastic element of dot motion, our experiments were otherwise standard pursuit tasks (Materials and Methods). We focus our analysis on the first 150 ms of pursuit that is driven by visual motion estimates without a substantial contribution from extraretinal feedback (Lisberger and Westbrook, 1985; Mukherjee et al., 2015).

Spatiotemporal filter for motion direction

From the eye and target direction over time, we used linear analysis to compute the spatiotemporal filter for motion integration within this experimental context (see Materials and Methods). We sampled the motion stimulus and the eye velocity at 1 ms intervals. We also divided visual space into overlapping 0.5°-wide annuli. Each annulus was centered on the position of the fovea and then subdivided into 12 segments spanning 30 visual degrees of spatial arc (see Materials and Methods; Fig. 2A). We then stepped through the eye movement time vector on each trial and computed the linear correlation between fluctuations in eye direction and the vector-average of the dot directions at each spatial location in the visual field (R,θ) as a function of time delay, T, from 0 to 150 ms in the past in 1 ms increments. At each step in the calculation, we normalized by the autocorrelation of the motion stimulus (see Materials and Methods). This calculation solves Equation 1 to find F(R, θ, T), a unitless function of space and time that best predicts the eye direction at each time point from past stimulus motion in each region of the visual field. Although dot density is uniform within the stimulus aperture on average, the number of dots falling within each spatial region at each time point and trial is not identical. Throughout the analysis, we correct for varying dot number by normalizing by the number of dots falling within each spatial region at each time step. Therefore, the filter that we derive represents the contribution that each dot will make to the eye movement based on its spatial location over time.

The filter that we derive captures the relationship between fluctuations in stimulus direction and fluctuations in eye direction, our proxy for visual motion estimates. We present the motion filter in several ways. The 20 panels in Figure 2B are a set of temporal filters, F(R = R_i, T), from a monkey pursuit experiment with a 30°-diameter noisy dot stimulus. The filters were computed on a grid of concentric annuli (Fig. 2A) at eccentricities of R_i = 0–14.75°, although only the first 20 bands R_1–20 = 0–4.75° are shown. The overlap between annuli is illustrated by the green-shaded bands in Figure 2A. To generate the temporal filters in Figure 2B, we stepped through time points and trials, computing the correlation between eye direction and vector mean dot direction within each annulus as a function of time lag (see Materials and Methods). The red dots mark the peak amplitude at each eccentricity and collectively trace out the rotationally averaged spatial filter, F(R) (red trace; Fig. 2C). If we represent F(R) as the time-averaged amplitude instead of the peak value of each temporal filter in Figure 2B, we change the scale, but not the form of the spatial filter (black dashed line; Fig. 2C). The most striking feature of the spatial filter is that its amplitude peaks eccentric to the fovea, at ∼5° (visual degrees of spatial arc) for the 30°-diameter stimulus in this experiment. Contributions from motion at eccentricities >10° and <2.5° with respect to gaze position are only ∼60% of the peak. Using alternate spatial partitions that equalized the number of illuminated pixels (i.e., dots) within each segment produced a nearly identical spatial filter (gray trace; Fig. 2C; see Materials and Methods). The preferential weighting of eccentric motion was consistent across the range of stimuli that we tested.

The full spatial filter, F(R, θ), shows a pronounced directional anisotropy. In Figure 2D, both color and height indicate the relative contribution of motion signals at different spatial locations within the visual field to global direction estimates. The coordinate frame is centered on the eye's position, and 0° corresponds to spatial locations along the axis of stimulus motion. The data are drawn from the same example experiment as the other panels. To calculate the rotational component of the spatial filter, we divided visual space into 12 pie-slice segments of 30 degrees of spatial arc (i.e., −15° to +15°, +15° to +45°, etc.; see Fig. 2D, right) and computed the spatial filter within each slice separately using the same eccentricity annuli described above. We oriented the coordinate frame on the target direction so that the 0° segment always represented locations “ahead” of the eye along the direction of stimulus motion. We used both leftward and rightward trials, so we flipped the sign of the horizontal components of leftward motion to align with the same coordinate frame. Therefore, the vertical segments (labeled 90° and 270°) always represent spatial locations above and below the eye, respectively. We found substantial direction-dependent anisotropy in the spatial filter (Figs. 2D,E). Figure 2D, left, presents the spatial filter F(R, θ) as a pseudo-3D projection and the right panel the same data as if viewed from above. The colors (orange to red, grays) of the outer borders of the direction segments around the right panel of Figure 2D identify the region of the visual field from which the filter traces in Figure 2E were derived. For example, a red arrow points to the +15° to +45° spatial segment in Figure 2D and to the corresponding plot of F(R, θ = θ_i) in Figure 2E. The filter amplitudes are higher in the spatial segments centered from −30° to +30° (Fig. 2D,E, orange-red colors, right panel) compared with all other segments (Fig. 2D,E, gray colors). Filter amplitudes are so similar in all other direction segments that the grayscales are difficult to differentiate. The largest contribution to pursuit is from the 0° segment, representing motion in front of the eye (Fig. 2E, top left panel, and top polar plot). We find the same directional pattern whether we analyze the stimulus motion or the retinal image motion, the difference between eye and target velocity. The directional enhancement has a very similar pattern of spatial weighting for all human (H1–H3) and monkey (M1–M2) subjects, such that the traces in Figure 2E's polar plots are difficult to resolve. The directional enhancement is not solely a multiplicative rescaling because the filters from each direction segment do not superimpose after normalization, F(R, θ)/max(F(R, θ)). The motion filters in spatial direction segments in front of the eye are narrower as well as higher in amplitude. We present the normalized data for all five subjects in the bottom left panel and bottom polar plot in Figure 2E. Before normalization, the filter's full width, measured at half maximum (FWHM), is slightly narrower in the same segments in which amplitudes are enhanced (Fig. 2E, red colors, bottom panel). The filter width in the spatial segment in front of the eye (0°) was 27 ± 4% (SD) smaller than the width of the segment behind the eye (180°) (n = 12 datasets, H1–H3, M1–M2). The narrowing of the leading versus trailing direction spatial filters was statistically significant across subjects (p < 3 × 10⁻⁴, n = 12 datasets, paired t test). The difference in normalized filter amplitudes was somewhat smaller, 18 ± 3% (SD), but still statistically different from zero (p = 3 × 10⁻⁴; n = 12 datasets, paired t test). The directional anisotropy that we observed suggests both a gain enhancement and a slight spatial sharpening for motion integration in and near the direction of motion.

We did not find a corresponding directional difference in the temporal filters that would indicate that motion integration time scales differed by spatial direction. We performed a paired t test on five subjects (H1–H3, M1–M2) comparing temporal filters from the 0° and 180° direction segments and found that there were no significant differences in the temporal filter peak time delay (p = 0.65, n = 12 datasets) or duration (FWHM) (p = 0.74, n = 12 datasets).

Predictive power for pursuit

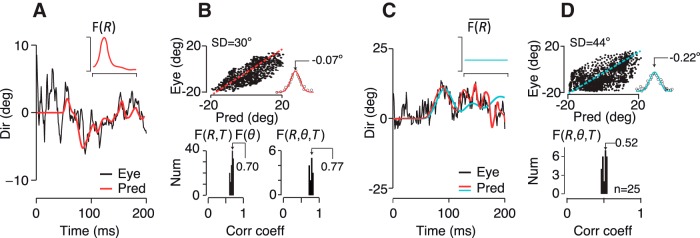
The narrow peak of the spatial filter is surprising because it indicates that the visual system is down weighting motion information from a large part of the visual field. That seems counterintuitive because all of the dots in the pattern are equally informative about the global motion direction. However, we found that the spatial filter predicts the eye direction over time quite well, whereas an “ideal observer” spatial filter that sums motion uniformly over the visual field does not (Figs. 3A,C, top insets). We tested filter performance by applying the filter to trial data left out of the filter calculation to predict the eye direction over time. The prediction for an example trial with a 30°-diameter noisy dots stimulus using the 3D pursuit filter, F(R, θ, T), is shown in Figure 3A (red trace) and is quite similar to the actual eye direction over time (black trace). The relationship between the predicted and actual eye direction at many time points throughout the dataset is plotted in Figure 3B (top). Although we calculated the filter by relating fluctuations in stimulus direction to fluctuations in eye direction around the mean, we found that the same filter form also predicts the time-averaged eye direction correctly (Fig. 3B, top). Therefore, the spatiotemporal filter in Figure 2 captures global direction estimates for pursuit, not just the eye's response to small direction fluctuations. The prediction errors have a Gaussian distribution and a near-zero bias of 0.07° (Fig. 3B, inset, top), indicating that the filter accounts for the structured variation in motion estimation leaving only residual noise. We computed the linear correlation coefficient, ρ, between the predicted and actual eye direction over the first 150 ms of pursuit to summarize the quality of the filter's prediction for each dataset (Fig. 3B, bottom). We found that the full 3D spatiotemporal filter, F(R, θ, T), accounts for almost 60% of the variance (ρ²) in eye direction (Fig. 3B, bottom right) in monkeys (ρ = 0.77 ± 0.4 SD, n = 10 datasets, M1–M2) and 62% in humans (ρ = 0.79 ± 0.3 SD, n = 5 datasets, H1–H3). If we include only open-loop pursuit (125 ms) the fraction of variance predicted was slightly lower: 55% in monkeys (ρ = 0.74 ± 0.3 SD, n = 10 datasets, M1–M2) and 56% in humans (ρ = 0.75 ± 0.3 SD, n = 5 datasets, H1–H3). We had sufficient dot numbers to generate the full 3D filter only for 30°-diameter noisy dots stimuli, but we found that the direction weighting, F(θ), derived from the large stimuli improved filter predictions across the full range of stimulus sizes we tested. The directionally averaged 2D filter, F(R, T), accounts for 46% of the variance (ρ = 0.68 ± 0.3 SD, n = 120 datasets, M1–M2, H1–H3), whereas using the directional weighting with the 2D filter, F(R, T) ⊗ F(θ), makes slightly better predictions of eye direction over time across all stimulus sizes (49%, ρ = 0.70 ± 0.2 SD, n = 120 datasets, M1–M2, H1–H3) (Fig. 3B, bottom left). The difference is small but statistically significant across all subjects and stimulus sizes (p = 2.1 × 10⁻¹¹, n = 120, paired t test).

Figure 3.

Predictive power of the spatiotemporal filter for pursuit. A, Predicted eye direction over time with respect to pursuit onset for an example trial (red) compared with the monkeys' actual eye direction (black). The inset shows the eccentricity dependence of the spatial filter, but the full 3D filter, F(R, θ, T) was used for the reconstruction (black trace). B, Although we calculated the filter by relating fluctuations in stimulus direction with eye direction around the mean, we found that the same filter form is able to predict the time averaged eye direction throughout the dataset (top) The predictive errors have a Gaussian distribution and near-zero bias (inset) indicative of a noise process. The dashed red line has a slope of 1. Bottom, Population data showing the distribution of correlation coefficients between predicted and actual eye direction over time across many datasets and subjects. The bottom left panel shows the correlation coefficients using F(R, T) ⊗ F(θ) for experiments with 5–30°-diameter stimuli. The right panel shows just the 30°-diameter experiments from which we derived F(R, θ, T). C, Eye direction prediction is poor with a flat spatial filter, F(R) (cyan line, inset) despite pooling motion over all dots to estimate the mean direction. Predicted (cyan) and measured eye direction (black) across time for an example trial are shown with the actual pursuit filter's prediction in red. D, Top, Predicted versus actual eye direction as in B. The distribution of residuals shows that the filter produces both systematic and random prediction errors. Bottom, as in B. The flat filter accounts for only 27% of the variance of eye direction over time compared with 59% for the filter itself.

How well does motion across all parts of the visual field predict pursuit? Because the random walk of each dot is drawn from the same distribution, all dots are equally informative about the average direction of motion. An ideal motion estimator would therefore average over all dots uniformly to determine the global motion direction. The nonuniformity of the spatial filter suggests that the brain does not act as an ideal observer and that predictions of eye direction based on the ideal observer model should be poorer than the filter shown in Figure 3A (inset). We tested the predictive power of a flat eccentricity filter, F(R), scaled to the mean spatial filter amplitude (cyan line, inset; Fig. 3C) with the same example dataset shown in Figures 2 and 3A. We preserved the direction weighting plotted in Figure 2E to isolate the eccentricity filter's effect on prediction quality. The flat filter model can be written as follows: (F(R) ⊗ F(θ)) ⊗ F(T) where ⊗ indicates an outer product. We found that the flat filter (cyan trace) did not predict the eye direction over time as well as the actual pursuit filter (Fig. 3C, red trace). The distribution of residuals suggests that the flat filter produces both systematic and random prediction errors (Fig. 3D, top). Across datasets, the flat filter accounts for only 27% of the variance of eye direction over time (ρ = 0.52 ± 0.3 SD, n = 25 datasets, all subjects; ρ = 0.50 ± 0.3 SD, n = 18 datasets, M1–M2; ρ = 0.52 ± 0.2, n = 7 datasets, H1–H3). Although a flat spatial filter pools motion equally over all dots, as would an ideal observer, its predictive power is poorer than the spatially anisotropic filter that we measured from pursuit. The visual system's emphasis on a portion of the visual field is curious because it means that all available information is not being used to estimate the global motion direction to initiate pursuit. To determine whether the filter that we measured from pursuit indeed arises from internal motion estimates rather than a pursuit-specific process, we compared the motion filters in human and monkey subjects and then tested the filter's ability to predict perceptual direction estimates.

Comparison between humans and monkeys

We find that human and monkey pursuit filters are quite similar, although there is an overall time shift corresponding to the difference in pursuit latencies. For 30°-diameter stimuli, the peak eccentricity of the spatial filter, F(R), falls at R_peak = 4.4 ± 0.12° (SD) for humans (n = 4 datasets, H1–H3) and R_peak = 4.8 ± 0.1° (SD) for monkeys (n = 8 datasets, M1–M2) (Fig. 4A, top left). The dotted lines in Figure 4A are meant only to emphasize the species differences and similarities in the filter parameters. The peak eccentricity of monkey and human spatial motion filters are close and that is also true if we subdivide space into 12 directional segments to compute F(R, θ) (see Fig. 2): R_peak = 4.8 ± 0.2° (SD) for monkeys (n = 96, 12 direction segments, 8 datasets, M1–M2, p = 0.54, one-way ANOVA), R_peak = 4.5 ± 0.2° (SD) for humans (n = 48, 12 directions, 4 datasets, H1–H3, p = 0.77, one-way ANOVA). We characterize the width of the spatial filters by the FWHM. FWHM values in visual degrees of spatial arc are 3.2 ± 0.1° (SD) for monkeys (n = 8 datasets, M1–M2) and 3.1 ± 0.2° (SD) for humans (n = 4 datasets, H1–H3) (Fig. 4A, left). There is a more marked species difference in the temporal filters. Monkeys' temporal filters peak at shorter delays compared with humans (solid vs dotted lines; Fig. 4A, top right; Fig. 4B, bottom). The delay at which the temporal filter peaks is a measure of the time lag of the eye's response to fluctuations in motion direction. Considering just the 30° stimuli, monkeys' temporal filters peaked at T_peak = 95 ± 4 ms (SD) (n = 8 datasets, M1–M2) compared with T_peak = 185 ± 7 ms (SD) for humans (n = 4 datasets, H1–H3) (Fig. 4A, top right), but in fact the temporal filters were very similar across all stimulus sizes, T_peak = 92 ± 6 ms (SD) (n = 114 datasets, M1–M2) for monkeys. Although pursuit latencies tend to be somewhat longer than visual response delays while the eye is in flight (Krauzlis and Lisberger, 1994), the species difference in temporal filter delays is consistent with the species difference in pursuit latencies. Average pursuit latencies in monkeys with dot motion stimuli are 75 ± 7 ms (SD) (n = 40 datasets, M1–M2) and in humans are 160 ± 13 ms (SD) (n = 15 datasets, H1–H3), a difference of 85 ms on average, which is close to the 90 ms difference in peak delays. Because visual perception in macaques and humans is quite similar (Orban et al., 2004), the differences in temporal filters likely arise from species differences in motor processing or eye movement execution.

Figure 4.

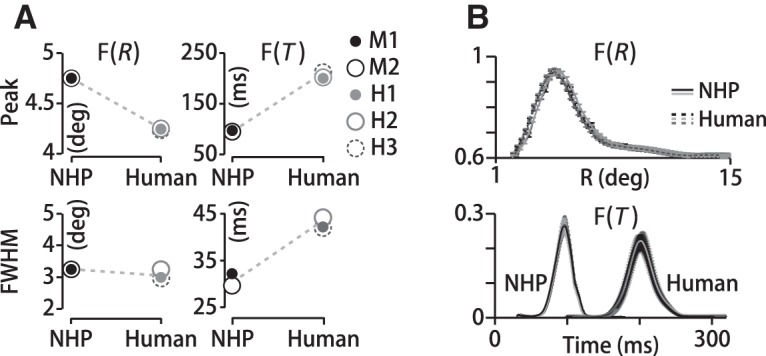
More similarity in spatial than temporal motion integration in humans and monkeys. A, Left, Peak eccentricities of monkey (NHP) and human spatial filters differ by only 0.5° and they both span 3° (FWHM). Right, Temporal filters differ by (top) 90 ms in peak delay and (bottom) about 14 ms in duration. Data points represent mean values across datasets per subject; errors (SD) are smaller than marker sizes. B, Top, F(R) for three human (H1–H3) and two monkey (M1–M2) subjects. Error bars are SDs from cross-validation resampling. Bottom, Temporal filters for the same subjects as the top panel. Although the spatial filters are similar, there is an overall time shift between human and monkey temporal filters corresponding to the difference in pursuit latencies.

The duration of the temporal filters is more similar in monkeys and humans and consistent across all stimuli. The duration or width of the temporal filter describes the time window over which past motion is summed to estimate target direction and drive pursuit—the sensory–motor integration time. Pursuit filter durations average 42 ± 4 ms (SD) for humans (n = 4 datasets, H1–H3) and 28 ± 5 ms (SD) for monkeys (n = 8 datasets, M1–M2) with 30° diameter stimuli (Fig. 4A, bottom right) and do not differ with stimulus size (FWHM = 27 ± 5 ms (SD), n = 114 datasets, M1–M2, p>0.9, two-sided Wilcoxon rank-sum test). The filter durations for the noisy dot stimuli are comparable to those measured for coherent motion stimuli (Osborne and Lisberger, 2009).

Motion filter predicts perception

Is the spatiotemporal pursuit filter dominated by visual or motor processing? Smooth eye movements, especially during the initial open-loop interval, are guided by visual cortical inputs but generated by downstream motor circuits. Therefore, both sensory integration and motor processing may shape the filter forms we measure from eye movements. To determine the extent of the visual system's contribution to the filter, we performed two types of experiments. First, we performed psychophysical experiments with human subjects to test how well the spatiotemporal filter that we derived from pursuit predicts perceptual judgments of motion direction compared with other filter forms (Fig. 5). Second, we recorded MT unit activity in nonhuman primates to compare the temporal filters for motion integration in cortical neurons mediating pursuit with the behavior itself (Fig. 6).

Figure 6.

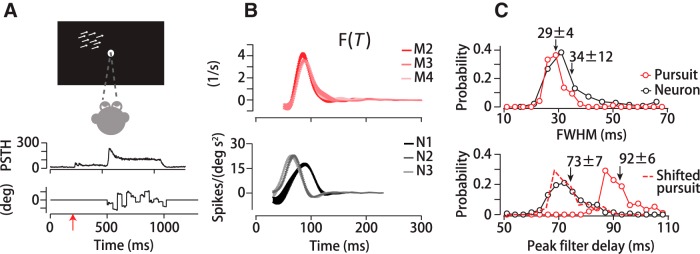
Temporal motion integration in MT neurons. A, Top, Neurophysiology experimental design. Monkeys maintained fixation while a dot stimulus moved in the neuron's RF. Middle, PSTH of a single neuron Bottom, Stimulus direction over time. Red arrow represents stimulus appearance. Dots appeared and remained stationary for 200 ms to allow visual onset responses to decay. B, Temporal filters computed from pursuit in three monkeys (top) and three MT neurons from the same monkeys (bottom). C, Top, Population distribution of temporal filter durations, FWHM, of MT neurons (black) and pursuit (red) from the same monkeys. Bottom, Distribution of temporal filter peaks for MT neurons (black solid line) and pursuit (red solid line). Matching the mean delay of the pursuit distribution to the neural data (dashed red line) shows that the distributions overlap.

The motion filter must arise from the joint activity of a population of cortical neurons, each with a limited RF. Although the collective spatial filter is difficult to access physiologically, perceptual estimates are often used as a proxy for internal sensory estimates. To determine whether the filter that we compute from eye movements represents visual processing shared with perception, we quantified how well the pursuit filter predicts subjects' perceptual choices compared with other filter shapes. We performed parallel pursuit and perception experiments in two human subjects (H1, H3) using a 30°-diameter noisy dots stimulus. In the 2AFC perceptual discrimination experiment, subjects were asked to indicate whether the average stimulus direction over the 250 ms motion interval was upward or downward with respect to horizontal (see Materials and Methods). We assigned responses +1 for upward and −1 for downward choices. To put the eye movement data on the same footing as the binary perceptual reports, we averaged the eye direction in a 5 ms time window centered at 250 ms and assigned the value a +1 if rotated upward and −1 if downward. We only analyzed trials in which the time-averaged stimulus direction was horizontal (0° or 180°). See Materials and Methods for a detailed description of the experiments and analysis.

The filter that we compute from eye movements will be the function that best predicts pursuit, but it may not be the function that best predicts perceptual judgments of motion direction. To find the spatial and temporal filter forms that best predict perceptual judgments of motion direction, we created a set of 209 spatial filters and 208 temporal filters. The filter sets were based on Gaussian fits to the actual spatial, F(R, θ), and temporal, F(T), pursuit filters, but with different means (peak locations or delays) and widths (FWHM, in visual degrees or ms; see Materials and Methods). The spatial filter peak locations spanned 0.5° to 9.5° in 0.5° (degrees of spatial arc) increments and temporal filter delays ranged from 90 to 240 ms in 10 ms increments. The widths (FWHM) for the spatial filter set ranged from 2° to 9.5° in 0.75° increments, or 25 to 85 ms in 5 ms increments for the temporal filters. We held F(θ), the weighting as a function of spatial direction, constant for all tested filter forms. The set of synthetic spatial filters are illustrated in the margins of Figure 5A by colored dashed lines. We used each spatial and temporal filter form to generate trial-by-trial predictions of the behavioral response 250 ms after motion onset by convolving the filter with the dot motions. To quantify the quality of the prediction, we computed the linear correlation coefficient between the predicted and actual (binary) eye directions or perceptual reports (Fig. 3). Figure 5A shows linear correlation coefficients for two subjects' pursuit (see Materials and Methods), with spatial filter predictions on the left and temporal filters on the right. Each grayscale element in the density plots corresponds to a single filter form. Lighter shades indicate better prediction. Along each column, the filter peaks at a different location (or delay) and, along each row, the filters have a different width. When changing the spatial filter form, we held the temporal filter fixed and vice versa. The patterns of correlations across the different filter shapes were quite similar for both human subjects (H1, H3). In each case, the best predictions (Fig. 5A, bold red boxes) were made with the actual spatial or temporal pursuit filter, as expected. Subject H1's pursuit filter has a correlation coefficient with binary eye direction of 0.77 ± 0.04 (SD) (n = 100 random samples of 50% of total dataset), indicating that the filter accounts for 59% of the eye direction variance. Subject H3's pursuit filter has a correlation coefficient of 0.78 ± 0.04 (SD) (n = 100) representing 61% of the variance. The region of near-white pixels indicates the range of filter forms with a correlation coefficient within 2 SDs of the best prediction. Eye direction estimates were somewhat more sensitive to the shape of the spatial than the temporal filter, seen by the smaller white patch on the left versus the larger white patches on the right in Figure 5A for both subjects. The lowest correlation values were 0.44 and 0.46 (H1, H3), reflecting the background level of correlations in the predictions due to the similarity in the tested filter shapes and the dot direction statistics (see Materials and Methods). Although the motion of each dot is stochastic, the time-averaged motion direction is the same for all dots. Therefore, averaging dot motions under overlapping filters centered at different spatial locations will produce correlated results by the law of averages and the direction update interval creates correlations in dot directions over time. All matrix elements in Figure 5A represent statistically significant correlation coefficients with p ≤ 0.01 with respect to a random permutation of the pursuit responses. See Materials and Methods for a detailed description of all analyses.

We performed a parallel analysis on the perceptual data from the same subjects. To predict perceptual direction estimates from trial to trial, we used each spatial and temporal filter in the set to estimate the perceived time-averaged motion direction over the 250 ms interval (see Materials and Methods) and computed the linear correlation coefficient with the actual binary perceptual reports. If perception pools signals over a different spatial region of the stimulus or over a different time interval, then the spatial and temporal filter that best predicts perception may differ from the pursuit filter. However, we found that the pursuit filter was the best predictor of the perceptual data (Fig. 5B, red boxes). If all motion directions are analyzed, the pursuit filter predicts perception with comparable predictive power as for pursuit. Subject H1's pursuit filter had a correlation coefficient of 0.76 ± 0.06 (SD) (n = 100 random samples of 50% of total dataset) with reported stimulus direction, accounting for 58% of his perceptual report variance. Subject H3's pursuit filter had a correlation coefficient of 0.77 ± 0.06 (SD) (n = 100) accounting for 60% of the perceptual variance. When only the 0° (rightward) trials are included in the analysis, the fluctuations in stimulus global motion direction (0.05 ± 0.08° (SD), n = 210 trials) are below human discrimination threshold (de Bruyn and Orban, 1988; Mukherjee et al., 2015; ∼1.7°), so subjects perform at chance levels. Chance level performance means that perceptual choices will be less well correlated with the stimulus, so no motion filter will predict perceptual choices well. However, restricting the data analysis to the 0° (rightward) trials is advantageous for minimizing the contribution of the time-averaged motion direction that can create spurious patterns of correlation in Figure 5B. Using just 0° trials, the pursuit filter is still the best predictor of perceptual choice (Fig. 5B, red boxes), with correlation coefficients of 0.26 ± 0.03 (SD) for subject H1 and 0.25 ± 0.02 (SD) for subject H3 (n = 100 random samples of 50% of data). All matrix elements in Figure 5B represent statistically significant correlation coefficients with p ≤ 0.01 with respect to a random permutation of the perceptual responses. The fact that the best predictor of perceptual choices at chance-level performance is the pursuit filter is a strong indication that the spatiotemporal filter that we derive from eye movements reflects visual motion processing that is shared between pursuit and perception.

Prediction quality rolls-off with deformations of the pursuit filter in a similar way for the pursuit and perception data. Both subjects' data showed remarkably similar patterns of correlation for pursuit and perception for different spatial filter forms (Fig. 5A,B, left). Prediction quality falls by >2 SD units for shifts in the spatial filter peak of >1.5 degrees of spatial arc and for spatial filter widths that are >2.75° narrower or 4.25° wider than the pursuit filter for both subjects' pursuit and perception data (Figs. 5A,B, left). Compared with the narrow range of spatial filters that gave good behavioral predictions, a somewhat larger range of temporal filter forms predicted both subjects' pursuit and perceptual responses well. The area of lighter pixels is larger in the right compared with the left panels in Figure 5, A and B. Pursuit and perception prediction quality were within 2 SD units of the peak over a 40 ms range of temporal filter peak delays for H1; that is, −20 ms to +20 ms around 190 ms for pursuit (Fig. 5A, top right) and −10 ms to +30 ms for perception (Fig. 5B, top right). The same 40 ms range of temporal filter peak delays (−10 ms to +30 ms) predicted H3's perceptual choices well (Fig. 5B, bottom right), but a larger range of filter delays predicted H3's pursuit within 2 SD units of the highest correlation coefficient (−40 ms to +40 ms; Fig. 5A, bottom right). Overall, the changes in behavioral prediction quality with deformations of the spatial and temporal filter shapes were consistent between pursuit and perception data and between subjects.

We summarized the similarity in the predictions of pursuit and perceptual responses by plotting the distributions of correlation coefficients. The histogram plots in Figure 5C represent the distributions of all correlation coefficient values in Figure 5, A and B, converted to z-scores by subtracting the mean and normalizing by the SD within each panel. The extent to which the distributions for the pursuit versus perceptual data overlap indicates the similarity in filter performance. For both subjects, the span of spatial filter forms with good prediction performance was similar for pursuit and perception (RMS variance of z-scored correlation coefficients; H1: 1.3 z-score units for pursuit, 1.0 for perception, top left; H3: 1.2 pursuit, 1.1 perception, bottom left; Fig. 5C). The span of temporal filter forms that predict pursuit and perception well is also similar, but less so than for the spatial filter predictions (RMS variance of z-scored correlation coefficients; H1: 1.8 z-score units pursuit, 1.2 perception, top right panel; H3: 1.7 pursuit, 1.2 perception; Fig. 5C, bottom right) for both subjects. The similarity in temporal filtering for pursuit and perception is not expected because the dynamics of generating the eye's responses need not match the time scale of generating perceptual reports from visual estimates. Therefore, two pieces of evidence support a visual origin for the spatiotemporal filter. The best predictor of perceptual performance is the pursuit filter and deforming the pursuit filter degrades prediction quality for both pursuit and perception in the same way.

Temporal integration in MT neurons versus pursuit

To further test the hypothesis that the motion filter that we computed from pursuit eye movements arises primarily from visual rather than motor processing, we compared temporal motion filtering in MT with pursuit. We performed parallel pursuit and neurophysiology experiments to compare temporal filters for motion integration in single MT neurons with pursuit eye movements in monkeys. We used both the noisy dots stimuli and coherent motion versions of those stimuli that shared the same temporal statistics but without the variation across space (see Materials and Methods). For the coherent stimuli, all dots updated to the same randomly drawn direction value every 20 or 40 ms to produce time-varying motion (see Materials and Methods). We found no significant differences in neural filters based on stimulus form. We projected motion stimuli onto each unit's excitatory RF while the monkeys fixated. We rotated the time-averaged or base directions of stimulus motion to the flanks of the neuron's direction tuning curve where motion sensitivity is largest. In this way, we made several measurements of the temporal filter for each recorded MT unit. We computed neural temporal filters by relating spike count and motion direction over time using the same analysis technique as described for eye movements. We counted spikes in overlapping 20 ms time windows and then computed the correlation between the count values and motion direction at 1 ms intervals up to lags of 200 ms. The temporal filters for three example MT neurons from two monkeys are plotted in Figure 6B (bottom). We also used the translating versions of the same stimuli to compute pursuit temporal filters, shown in Figure 6B, top. The temporal filter forms were quite similar between individual MT units and pursuit behavior, although the MT filters have shorter peak delays than pursuit, as expected. Figure 6C, top, shows the distribution of filter durations (FWHM) for the MT units (red trace) and pursuit data (black trace). The population-mean width of the pursuit temporal filters is 29 ± 4 ms (SD, n = 96 datasets, M2–M4), only 5 ms shorter than the population mean for the MT sample, 34 ± 12 ms (SD, n = 138 measurements from 44 neurons, M3–M4). The distributions of neural and behavioral temporal filter durations are highly overlapped though still statistically distinct with a p < 3.1 × 10⁻⁵ (two-sample t test). The distributions of peak delays are also similar in the MT and pursuit data. The population mean peak delay of the MT neurons was 73 ± 7 ms (SD, n = 138 measurements from 44 neurons, M2–3) and for pursuit was 92 ± 6 ms (SD, n = 96 datasets, M2–M4; bottom panel; Fig. 6C). The overall latency shift between the neural and behavioral filters is expected, but what is notable is that the range of delays is similar for pursuit and MT neurons. If we shift the behavioral distribution to match the mean delays (Fig. 6C, red dashed line, bottom), then the MT and pursuit distributions of peak filter delays overlap (p = 1, two-sample t test). Our results suggest that pursuit could be driven by the full range of MT neurons, as could motion perception presumably. Therefore, we cannot explain the different pattern of temporal filter predictions for pursuit and perception in Figure 5 from obvious differences in cortical motion inputs. These results do not rule out contributions from downstream visual or motor processing to the form of the pursuit motion filter (Grinvald et al., 1994; Sincich et al., 2009; Butts et al., 2011), but they suggest that little such refinement is necessary to account for pursuit.

Our experiments were not designed to test response scaling with RF location because we sized the motion stimuli to the RF of each MT unit. Nevertheless, we tested for neural filter differences based on RF eccentricity. We found no statistical dependencies in either neural filter amplitude (R² = 0.1, n = 115 datasets from 44 neurons) or duration (R² = 2 × 10⁻⁴, n = 115) based on RF location. Because we did not use the same stimulus aperture sizes for the neurophysiological recordings, it is difficult to interpret the lack of eccentricity dependence of MT filters in terms of the spatial motion filters for pursuit and perception.

Dynamics in motion integration for pursuit

How motion is integrated across space need not be the same over time. Dynamics in MT neural responses, downstream motor processing, or execution of the eye movement itself could all potentially alter the form of the measured motion filter over time (Lisberger and Movshon, 1999; Osborne et al., 2004). We tested the stationarity of motion integration by computing the pursuit filter in different time intervals of the eye movement response (Fig. 7A, inset). Here, we only analyzed experiments with 30°-diameter noisy dot stimuli. We computed the spatiotemporal filter in overlapping 150 ms time windows spanning the first 450 ms of pursuit (Fig. 7A) using the spatial segmentation described in Figure 2. We were able to compute motion filters throughout the first 300 ms of pursuit, but at later times, the filter calculation became unstable, perhaps because of the diminishing differences between the eye and target direction with ongoing pursuit.

Figure 7.

Dynamics of spatial and temporal motion integration. A, Target (dotted line) and eye speed (solid line) over time. Diagram indicates the overlapping 150 ms time windows in which we computed filters. B, Left, Polar plot of the directional dependence of the peak filter amplitude in the time windows defined in A for M1. The directional bias is strongest early in pursuit (red-orange symbols), diminishing to uniform weighting at 175 ms (red-gray symbols). Right, Time evolution of peak filter amplitude in the θ = 0° segment in front of the eye. Colored circles indicate mean values, thin gray lines data from 12 datasets (M1–M2, H1–H3). C, Filter widths for the spatial direction segment in front of the eye, F(R, θ = 0°), do not change over the time period. Left, Example traces (M1). Right, Population mean spatial filter FWHM (n = 12 datasets, M1–M2, H1–H3) as a function of time window center (colored circles). Error SDs are smaller than the symbol size. Gray lines represent individual datasets. D, Left, Example of the time evolution of the temporal filter, F(T) (M1). Right, Filter duration (FWHM; n = 12 datasets, M1–M2, H1–H3) is stable over the first 225 ms of pursuit, but narrows in later time windows. Error SDs are smaller than symbol size. Inset expands the area surrounded by the red dotted line. Upping the time resolution to 10 ms from 50 ms intervals reveals a species difference in the time at which the temporal filters narrow (red arrow). Temporal filter duration (FWHM) drops at 260 ± 6 ms (SD) (n = 8 datasets, M1–M2) in monkeys (gray dotted lines) and 295 ± 8 ms (SD) (n = 4 datasets, H1–H3) in humans (black dotted lines).

We find that the directional anisotropy in the pursuit spatial filter amplitude is highly dynamic, but other features of the spatial filter are less so. The preferential weighting of motion in spatial locations along the direction of motion is transient in monkeys and humans. We plotted the amplitude of subject M1's spatial filter as a polar function of spatial direction segment in Figure 7B. Each connected curve represents a different 150 ms time window, colored as per Figure 7A. We found that the direction bias is strongest at pursuit onset, when motion in the spatial regions “downstream” of the fovea along the direction of motion are weighted most strongly (also see Fig. 2E). The anisotropy decays to rotationally uniform weighting over time. We quantified the deviation from circularity across the population by computing the circular variance in the peak filter amplitude in each time window. Higher values of the circular variance indicate more directional anisotropy. The circular variance decreased from 0.26 ± 0.07 (SD) (n = 12 datasets, 5 subjects, M1–M2, H1–H3) in the earliest time window centered at 75 ms to 0.18 ± 0.07 (SD) at 275 ms (p < 6 × 10⁻⁹, two-sample t test, n = 12). For both the monkeys and humans, spatial filters became rotationally invariant in time windows starting later than 100 ms after pursuit onset (centered at ≥175 ms).

Although the spatial filter's amplitude along the direction of motion changes during pursuit, other features are stable over time. For example, the eccentricity at which the spatial filter peaks has the same value in all spatial direction segments throughout the first 300 ms of pursuit. We plot the spatial filters for just the 0°-segment over time in Figure 7C (left) for all 12 datasets (M1–M2, H1–H3), showing that the spatial filters nearly superimpose when we normalize to the peak amplitude. The differences in spatial filter peak eccentricity were not statistically significant across all monkey and human datasets (monkeys p = 0.92, n = 576, 12 directions, 8 datasets, and 6 time windows; one-way ANOVA; humans p = 0.98, n = 288, 12 directions, 4 datasets, 6 time windows; one-way ANOVA). The width of the 0°-segment's spatial filter (FWHM) is also constant over the first 300 ms of pursuit (p = 0.28, n = 12 datasets from 5 subjects, paired t test), but it remains significantly narrower than the spatial filter for all except the adjacent direction segments even when filter amplitudes are normalized. We plot the spatial filter width (FWHM) for the 0°-segment (gray lines) and the 180°-segment (black dotted lines) as a function of time window center for all datasets and subjects in Figure 7C, right. The closed circles represent the sample mean (FWHM of the 0°-segment spatial filters) and are colored by time window identity according to Figure 7A. The closed circles occlude the individual dataset values somewhat (gray lines) because they are tightly clustered. The difference between the FWHM of the 0°-segment and 180°-segment filters was −0.5 ± 0.2 degrees of spatial arc (SD, n = 12 datasets from 5 subjects, p = 4.3 × 10⁻²², paired t test). Together, these data suggest that global motion estimates are transiently more sensitive to motion in downstream locations along the motion axis, but that the pooling region is smaller there compared with elsewhere in the visual field for a more sustained period.

The temporal filter is stable across the first 300 ms of pursuit, but the peak delay decreases and filter duration narrows later in the eye movement. Example data from M1 are plotted in Figure 7D, left. In the example data and across monkey datasets, we found that the temporal filter peak delay decreases gradually from 94 ± 3 ms (SD) to 87 ± 2 ms (SD) (n = 8 datasets, M1–M2) between the first time window centered at 75 ms (Fig. 7D, red trace, left) and the last time window centered at 325 ms (Fig. 7D, dark gray trace, left). For humans, the peak delay changes from 98 ± 5 ms (SD) to 88 ± 6 ms across the same time interval (n = 4 datasets, H1–H3). The temporal filter duration (FWHM), a measure of the motion integration time, also decreases after ∼275 ms of pursuit, but the transition is more abrupt than the change in peak delay (Fig. 7D). Monkey temporal filter durations are 28 ± 0.8 ms (SD) for early time windows (n = 8 datasets, M1–M2), narrowing to 18 ± 1 ms (SD) (n = 8 datasets, M1–M2; gray lines, Fig. 7D, right). Human temporal filter durations drop from 39 ± 2 ms to 29 ± 1 ms (SD) (n = 4 datasets, H1–H3; gray lines, Fig. 7D, right). To better resolve the times at which each subject's temporal filter narrows, we computed the temporal filters in 150 ms time windows centered at 10 ms intervals throughout the pursuit response. The drop in temporal filter duration occurs at 260 ± 6 ms (SD) (n = 8 datasets, M1–M2) in monkeys (gray dotted lines, right panel inset, Fig. 7D) and 295 ± 8 ms (SD) (n = 4 datasets, H1–H3) in humans (Fig. 7D, black dotted lines, right inset). The transition in temporal filter duration and the change in peak delay over time may be due to a switch from open-loop to closed-loop control that is thought to happen earlier in monkeys than in humans (Lisberger and Westbrook, 1985; Goldreich et al., 1992; Churchland and Lisberger, 2001). However, the abrupt shift in filter duration suggests a sharp transition between control states rather than a gradual takeover of nonvisual signals in the oculomotor control loop (Churchland and Lisberger, 2001). Another possibility is that the dynamics might arise from visual processing, caused perhaps by sharpening in MT temporal filters over time. To test this idea, we performed the same sliding time-window analysis on the MT neural data and found that neural temporal filters do not display changes in duration over time. We defined the time windows for the physiological analysis with respect to the average response latency of each unit. We computed the difference in the FWHM of the temporal filter computed in the first time window (1–150 ms) and the last time window (300–450 ms) across our sample. We found that neural filter durations did not change significantly, measuring 36 ± 15 ms (SD) (n = 74 measurements from n = 44 neurons) in the first time window and 34 ± 14 ms (SD) in the last time window (p = 0.41, rank sum test, two-tailed). The stability of MT neural filters over time suggests that the narrowing that we observed in pursuit temporal filters after the first 200 ms of pursuit has a nonvisual origin.

The extent to which the motion filter changes over time determines how well the 3D spatiotemporal filter can be described as space–time separable. We quantified the filter's separability by computing a separability index (SI) using singular value decomposition (DeAngelis et al., 1992; Peña and Konishi, 2001; Grunewald and Skoumbourdis, 2004; Malone and Ringach, 2008; see Materials and Methods). We analyzed the space–time separability of both the 2D filter F(R, T) and the full 3D filter, F(R, θ, T). We found that, although the 2D filter, F(R, T), is separable (SI = 0.98 ± 0.04 SD, n = 120 datasets, M1–M2, H1–H3), the full spatiotemporal filter, F(R, θ, T) is not (SI = 0.87 ± 0.04 SD, n = 12 datasets, M1–M2, H1–H3). We illustrate the separability of the 2D filter F(R, T) in Figure 8. The color density representation of filter amplitude is very similar between the actual filter F(R, T) and the outer product of two single parameter filters, F(R)F(T)^T, where the “T” superscript indicates a transpose operation. The reduced separability of the full motion filter is consistent with the dynamics that we observed in the directional anisotropy of the spatial filter.

Figure 8.

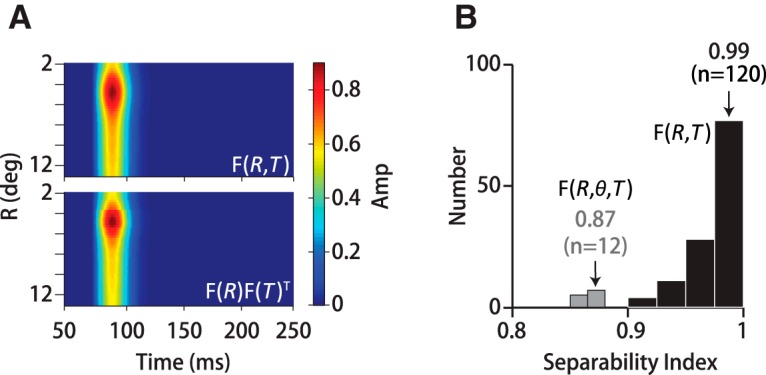
Separability of spatial and temporal motion integration. A, 2D, rotationally averaged filter, F(R, T), is well approximated by the outer product of separate 1D spatial and temporal filters, F(R)F(T)^T, seen in the similar color patterns in the top and bottom panels. Data from subject M1 are shown. B, Population distribution of separability index values for the rotationally averaged filter F(R, T) (black) and the full filter F(R, θ, T) (gray). Although F(R, T) is separable (SI = 0.98 ± 0.04, n = 120), the full motion filter, F(R, θ, T), is not (SI = 0.87 ± 0.04, n = 12). Changes in F(θ) over time link spatial and temporal motion processing.

Dependence based on stimulus size

The spatial or temporal span over which motion signals are pooled might adapt to the visual scale of the moving object. We tested for stimulus-size adaptability in spatial motion filtering by changing the aperture diameter of our noisy dot direction targets from 5 to 30° holding dot density fixed (Fig. 9A, colored circles). We computed F(R) in the same manner described previously by dividing the visual field into 59 fovea-centered annuli and computing the per-dot contribution at each eccentricity. Each colored curve in Figure 9B represents the spatial filter for the corresponding colored stimulus size. The spatial filter peaks at more eccentric values with increasing aperture size. For the smallest aperture (5° diameter, red trace), the spatial filter peaks close to the fovea (∼1°), but the larger the stimulus, the more eccentric the peak (up to 4.75° for a 30°-diameter aperture). The location of the filter peak scales nearly linearly with target radius such that the peak amplitude falls at ∼1/3 of the distance between the fovea and the aperture boundary. The linear fit in Figure 9C has a slope of 0.31 with an R² value of 0.94 (n = 10 datasets from M1–M2). Note that F(R) is always positive, implying a lack of inhibition from peripheral motion signals often termed surround suppression. This is consistent with studies of spatial motion integration of dot pattern stimuli in perception (Linares et al., 2012) and pursuit (Heinen and Watamaniuk, 1998). The temporal filters were nearly identical for all aperture sizes for 2 monkeys (FWHM = 27 ± 5 ms (SD), n = 114 datasets, M1–M2; p > 0.9 two-sided Wilcoxon rank-sum test).

Figure 9.

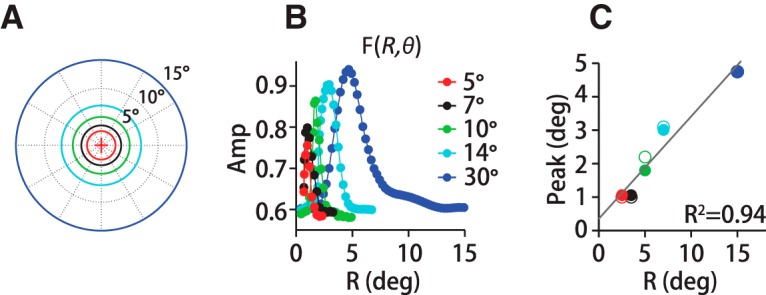
Spatial motion integration depends on stimulus size. A, We tested stimulus diameters from 5 to 30°, indicated by the colored circles. For each stimulus size, we measured the filter on the same polar grid, always centered on the eye's instantaneous position (+). B, The spatial filter, F(R), computed for each stimulus size (colored traces) for subject M1; the larger the size, the more eccentric the filter's peak. C, Foveal eccentricity of the spatial filter's peak scales linearly with stimulus radius, (f(x) = 0.30x + 0.35; R² = 0.94). Closed circles indicate data from monkey M1; open circles M2.

We did not have the statistical power to estimate the 3D spatiotemporal filter for the smaller noisy dot stimuli (see Materials and Methods), so we could not evaluate directly whether the directional anisotropy in motion integration depends on stimulus size. As displayed in Figure 3B, bottom, the pseudo-3D filter, F(R, T) ⊗ F(θ), accounts for only 2% more variance on average than the 2D filter, F(R, T) for stimulus diameters <30°. To determine whether another function of spatial direction would yield better predictive power for smaller motion stimuli, we tested a range of direction weights. We contracted the number of spatial direction segments to four and then allowed the filter amplitude in each segment to change by 0%, ±25%, ±50%, and ±75% (7⁴ combinations) and computed the correlation coefficient between the predicted and actual global motion direction over time for each model F(θ). We found that the best predictor of pursuit was the function F(θ) measured from the 30° stimuli. Although this analysis is not conclusive, it does suggest that the directional anisotropy in motion weighting is not dependent on stimulus size.

Optic flow content predicts pursuit gain for novel stimuli

There are many reasons why the motion filter might vary for different visual stimuli. Differences in spatial and temporal frequency content, contrast, and the strength of the optic flow might drive different patterns and degrees of cortical activation, leading to different stimulus–behavior relationships. Ideally, we would compute a filter for a variety of stimulus forms, but many commonly used laboratory stimuli such as drifting gratings or coherent dot patterns do not have the spatiotemporal variation necessary for the analysis. To test the generality and predictive power of the filter we compute from the spatiotemporal noise stimulus, we investigated how well the filter predicts the pursuit response to different stimuli.

Pursuit gain varies as a function of stimulus size, contrast, coherence, etc.—all factors that affect motion energy (Lisberger et al., 1987; Heinen and Watamaniuk, 1998; Schütz et al., 2010; Yang et al., 2012; Mukherjee et al., 2015). In previous work, we quantified motion energy by measuring the movement of pixels across adjacent frames weighted by their luminance (see Materials and Methods, Sun et al., 2010; Mukherjee et al., 2015). Here, we introduce the additional step of convolving the filter, F(R, θ, T), with its optic flow field to create an optic flow score to represent the effective motion energy of the stimulus. As long as the filter, or rather set of filters for different noisy dots stimulus sizes, remains descriptive of internal motion estimates, the flow score should predict the effective drive for pursuit initiation for each target form. The logic underlying this analysis is that the time course of smooth eye acceleration can be predicted from motion-driven cortical activity (Kawano et al., 1994; Lisberger and Movshon, 1999) and therefore, if the filter represents the interpretation of the cortical population activity, then it may predict the gain of the pursuit response. We tested this hypothesis by comparing the predicted and measured pursuit gains for a variety of motion stimuli with a fivefold range in flow scores. To generate a flow score for each stimulus, we used a single set of 2D filters, F(R,T), computed from noisy dots experiments with a dot density of 1 dot/deg² and speed of 15°/s displayed in Figure 9B. Because we could only compute the full, 3D motion filter, F(R, θ, T), with the 30° noisy dots stimulus, we had to assume that the pattern of directional weighting in time was consistent across aperture sizes to generate flow scores. With two exceptions (2° dot pattern, spot target), we generated new stimuli with the same aperture diameters (5°, 7°, 10°, 14°) for which we had measured spatiotemporal filters to minimize the need for interpolation. For the two small stimuli, we shifted the 5° stimulus filter to the peak location predicted by the linear relationship plotted in Figure 9C.

Figure 10A shows an example of how stimulus motion energy affects the initiation of pursuit. Peak eye acceleration in response to a motion step is generally higher for a high-score stimulus (black dotted trace) than a low-score stimulus (black solid trace), even though the average eye speeds after 200 ms of pursuit are nearly identical. The trial-averaged eye movements in Figure 10A are both from experiments with 15°/s noisy dots targets with the same dot density but different aperture sizes. The sinusoidal ringing in the eye speed trace for the high-score stimulus (Fig. 10A, black dotted trace) is the predicted result of an increase in open-loop gain (Churchland and Lisberger, 2001). Drawing on experiments with noisy dot stimuli of different sizes (5–30°), dot densities (1, 2, and 4 dots/deg²), and speeds (10–20°/s), we performed a linear regression between the measured trial-averaged peak eye acceleration and optic flow score (Fig. 10B, solid black circles and solid red line). Each symbol in Figure 10B represents the average pursuit gain over multiple datasets with the same stimulus and subject. With the noisy dot experiments alone, a linear regression explains 96% of the gain variance (solid red line, R² = 0.96, n = 33, M1–M2, H1–H3; Fig. 10B). We performed additional pursuit experiments with alternate stimulus forms to determine whether the motion filter derived for the noisy dots targets also predicts pursuit gain for different motion stimuli (Fig. 10B, colored circles). See Materials and Methods for a complete description of each stimulus. We found that pursuit gain was well predicted for all but two of the stimuli. The eight solid circles in shades of orange to brown (symbol group #2; Fig. 10B) represent coherent-motion random dot patterns with different aperture diameters (5°-14°). Dot density was 1 dot/deg² and dot speed was 15°/s for all experiments within this group (M1, M2). The five solid circles in shades of blue represent variations on Gabors (M1, M2). The darkest blue shade is a 14°-diameter Gabor (100% contrast, SD = 2.75°; 1 cycle/deg) that translated at 15°/s against a gray background set to the mean luminance of the target (see Materials and Methods). The medium blue symbols represent a 5°-diameter Gabor (SD = 1.2°) that was otherwise identical. Cyan circles represent an array of 13, 2°-diameter Gabors (SD = 0.75°) spaced 1–2° apart to create a target diameter of about 14°. The magenta circles represent experiments with a 14° checkerboard pattern of 1.8° alternating black and white squares (M1, M2). A linear regression that includes both the noisy dots data (black circles) and the new stimuli is very similar to the relationship derived for the noisy dots data alone (see legend in Fig. 10B) and explains 83% of the gain variation (dashed red line, R² = 0.83, n = 48 data points, M1–M2, H1–H3).

Figure 10.

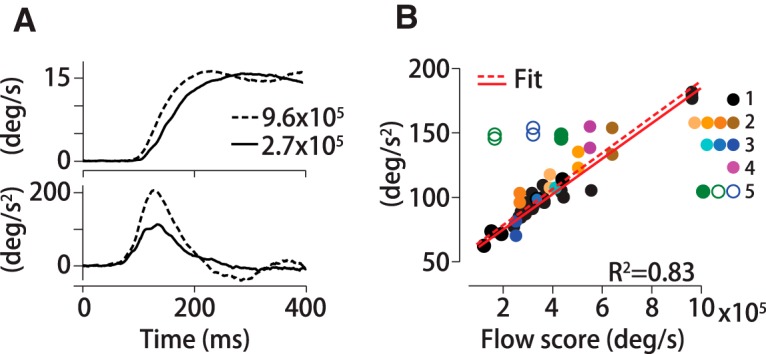
Motion filter predicts the effective drive for pursuit across several stimulus forms. Convolving the motion filter with pixel flow generates a scalar optic flow score related to the visual drive for pursuit. A, Trial-averaged eye speed (top) and acceleration (bottom) over time for a noisy dot stimulus with high (dotted line) and low flow score (solid line). B, Pursuit gain (peak eye acceleration) is proportional to the flow score. Thirty-three closed black circles (symbol group 1) represent pursuit experiments for monkeys and humans with noisy dots targets. The solid red line (slope = 1.1 × 10⁻⁵) represents the fit for group 1 stimuli only and accounts for 96% of the variance in pursuit gain (R² = 0.96, n = 33 group 1 stimuli, M1–M2, H1–H3). Pursuit gains for additional stimuli are plotted in groups (group 2 = coherent dot motion, 3 = Gabors, 4 = checkerboards; see text). A line of slope = 1.4 × 10⁻⁵ explains 83% of the variance for all but 2 tested stimuli (red dashed line, n = 48). Pursuit gains for two stimulus forms were not well predicted by flow score (and thus by the noisy dots motion filter): a small spot target (open green circles) and a Gabor that translated against a dark background (see text, blue open circles). Using unfiltered dot motion to generate a flow score for the spot target placed it within the fitted stimulus forms (green closed circles).

The motion filter did not predict pursuit gain for two stimulus forms (Fig. 10B, open circles, symbol group #5). One of those targets was a 0.25° white circular spot target translating at 16°/s (M1, M3), represented by the green circles in Figure 10B. The spot target is so small with respect to the dot pattern stimuli from which we measured the filter we simply weighted each pixel equally (open green circles; Fig. 10B). We extrapolated the weight value from the linear relationship between peak filter amplitude and aperture radius presented in Figure 9C. If we do not apply any scaling to the spot target's flow score, that is, score = pixel speed × number of illuminated pixels, then the pursuit gains of M1 and M2 are well predicted by the linear fits in Figure 10B (solid green circles). It is therefore unlikely that the motion filter that we derived from dot stimuli generalizes to spot targets. Finally, blue open circles represent a translating Gabor, identical to the first Gabor described above (darkest blue, symbol group #3) except that the background luminance was set to zero instead of the average grayscale level. Background luminance affects the total pixel flow in our algorithm (see Materials and Methods) and thus the flow scores for the two Gabors are somewhat different. However, the pursuit gains are very different. Eye acceleration is substantially higher for a Gabor translating against a dark background (open dark blue circles) compared with a gray background (open dark blue circles; Fig. 10B, M1, M2). Overall we found that, with the exception of the spot and nonzero background Gabor stimuli, a linear model of spatiotemporal direction estimation explains a large fraction of the variance in pursuit gain for multiple visual stimuli. The predictive power is impressive given that the filter relates eye to stimulus direction over time, yet here we have used the filter to predict the relationship between motion energy and pursuit gain.

In smooth pursuit, peak eye acceleration is linearly related to target speed for the speed range used in these experiments (Lisberger and Westbrook, 1985). Could low eye accelerations arise because the brain underestimates the speed of low score stimuli? We tested this idea by measuring the time-averaged eye speed in a 50 ms window from 150 to 200 ms after pursuit onset and computing the difference between eye speed and stimulus speed. If speed estimation errors are correlated with flow score, then we would expect to see larger, more negative errors for low score stimuli and decreasing error magnitude as flow scores increase. However, we did not detect a correlation between speed error and flow score in either of our monkey's data (R² ≤ 0.02, n = 20 dot stimulus experiments, 10 with scores <3 × 10⁵ and 10 with scores >6 × 10⁵; M1, M2). Neither subject's linear regression explained enough the variance across stimuli to motivate a Bayesian model of speed estimation.

Discussion

We have focused on short-timescale integration of random dot pattern motion studied through the lens of pursuit eye movements. The spatiotemporal filter captures how the movements of point objects are integrated over space and time to estimate direction (Williams and Sekuler, 1984; Watamaniuk et al., 1989, 2011; Smith et al., 1994). Although we use eye movements to derive the filter, visual and motor processing specific to pursuit do not appear to influence its form. Rather, we found that the same filter predicts both pursuit and perceptual judgments of motion direction. Consistent with past studies of global motion perception (Watamaniuk and Sekuler, 1992; Smith et al., 1994) and pursuit (Heinen and Watamaniuk, 1998), we found that all motion within the visual field adds. The literature suggests, however, that spatial motion integration is stimulus dependent because large-sinewave gratings decrease the internal signal-to-noise ratio (Tadin and Lapin, 2005; Tadin et al., 2003), whereas large dot fields increase it (Linares et al., 2012). The spatial filter's eccentric peak (≥1°) and non-negative profile are consistent with several psychophysical studies of dot motion that found low perceptual sensitivity for near-foveal motion, then rapid improvement and leveling off with increasing stimulus size (Gorea, 1985; Anderson and Burr, 1987; Watamaniuk and Sekuler, 1992; Fredericksen et al., 1994; Morrone et al., 1995; Watson and Turano, 1995). Our spatial calculations are similar to Neri and Levi (2009), who divided their stimulus aperture into annuli and computed stimulus-report correlations in each division. They found that motion was weighted fairly uniformly across an eccentrically located 2° aperture; however, their study's surround distractor complicates comparison with our results because surround motion can affect the area over which motion is perceptually averaged (Sasaki and Uka, 2011).

A striking feature of our spatial filter is its transient directional anisotropy. There is no clear consensus in the psychophysical literature for spatial bias in motion summation based on motion direction (Ball and Sekuler, 1980; Raymond, 1994). There is a physiological analog for our behavioral results, however, from studies of attentional modulation in MT. Spatially directed attention enhances responses in MT neurons with RFs that overlap the attended area (Cook and Maunsell, 2004). If our pursuit and perceptual tasks enhance spatial attention and MT neuron firing rates at locations along the expected direction of motion, then the directional anisotropy that we observed in the motion filter is expected. A later study suggests that spatial attention creates an attractive shift in MT RF centers and narrows RF extent, providing a candidate physiological mechanism for our observation that motion weights are enhanced and the spatial filter narrows along the expected direction of motion. (Womelsdorf et al., 2008)

Motion integration times in pursuit are also consistent with perceptual studies. For large area stimuli, motion is perceivable with 30 ms presentations (van Doorn and Koenderink, 1984). Tadin et al. (2006) measured a temporal motion filter based on the correlation between stimulus motion and perceptual reports, finding a duration of ∼30 ms consistent with our pursuit-based measurement. These and other studies suggest that pursuit and perception integrate motion over time quite similarly (Kowler and McKee, 1987; Watamaniuk et al., 1989; Osborne et al., 2007, 2009; Mukherjee et al., 2015). The filter's peak delay, however, is more likely a result of pursuit-specific motor processing. Although the spatial filters that we derived for humans and monkeys are nearly identical, their temporal filters are time shifted by an amount approximately corresponding to the species difference in pursuit latencies. Furthermore, manipulating the peak delay did not affect predictions of perceptual reports, whereas manipulating the duration of the temporal filter did. Given the similarity to filter durations in MT neurons, we suggest that the temporal filter duration that we measured represents visual processing.

Motion integration is highly context dependent. Spatial and temporal summation of motion signals changes with the nature of the stimulus (contrast, spectral content, spatial scale, etc.) and the task (e.g., object segmentation vs heading perception; Braddick, 1993; Tadin et al., 2008; Burr et al., 2009). Stimulus-driven differences in motion integration should therefore give rise to different motion filters. Here, we have analyzed differences in motion integration as a function of stimulus size and found that the form of the spatial filter changes substantially with aperture diameter. The peak eccentricity for motion weighting rescales to ∼1/3 of the stimulus radius for each aperture size that we measured. Ideally, we could compute the filter for a range of stimulus forms and tasks to quantify stimulus driven changes in motion summation changes, but many commonly used laboratory stimuli, such as drifting Gabors, lack the spatial and temporal variation to compute a filter. We therefore used the less direct approach of testing for generality in the filter by predicting the gain of the pursuit response for stimuli of different size, coherence levels, and spectral bandwidth. Although far from an exhaustive study, the success of the filter to predict pursuit gain for all but a few targets indicates a measure of generalizability across stimulus forms. However, the filters that we report did not predict the high sensitivity of pursuit and perception of small, moving spot targets and one of the translating Gabors. Nor do they explain why dense stimuli like Gabor patches and speckle patterns of sizes larger than ∼1.5° suppress motion sensitivity (Tadin et al., 2003; Tadin and Lapin, 2005), whereas dot stimuli show the opposite effect (Linares et al., 2012; present study). These failures confirm the expectation generated by diverse and often conflicting results in the literature that the inherent adaptability of motion integration will restrict the degree of generalization of any single model of motion processing (Braddick, 1993). That said, the spatiotemporal filter that we measured from pursuit generates testable predictions of perceptual judgments and motor responses to some alternate stimulus forms. How behavior deviates from filter predictions may provide a clue to the nature of the underlying nonlinearities in motion integration.

Global motion estimation has been described by an averaging operation (Williams and Sekuler, 1984; Watamaniuk et al., 1989, 2011; Watamaniuk and Sekuler, 1992; Smith et al., 1994; Verghese et al., 1999), winner-take-all (Churchland and Lisberger, 2001; Sheliga et al., 2006), and by probabilistic estimation (Stocker and Simoncelli, 2006; Yang et al., 2012). The fact that a linear model can predict pursuit and perception quite well is consistent with vector averaging; however, a strict vector-average would pool all available motion signals. We found that, whereas all motion signals are used, contributions from a narrow eccentricity band are emphasized. It seems counterintuitive that the brain would devalue motion signal from much of the visual field unless it is taken as noise. Past studies have reported spatial interference effects from peripheral motion (Bex et al., 2003; Bex and Dakin, 2005) that drive attention-based contraction of the perceptual pooling area while increasing sensitivity (Sasaki and Uka, 2011). If a similar mechanism is at play here, then our results suggest that the divisive normalization that underlies the vector average can operate on both local (Chang and Julesz, 1983; Morgan, 1992) and global (Williams and Sekuler, 1984; van Doorn and Koenderink, 1984; Watamaniuk et al., 1989; Watamaniuk and Sekuler, 1992; Smith et al., 1994; Verghese et al., 1999; Sheliga et al., 2008) scales. Given the behavioral flexibility in motion integration (Braddick, 1993; Tadin et al., 2008), it seems plausible that normalization operations are either themselves flexible or that their overall contribution to behavior depends on context. Departures from linearity in global motion processing may provide clues to the nature of the normalization.

Evidence for Bayesian estimation

We used the spatiotemporal filter to investigate the relationship between stimulus optic flow content and pursuit gain. How the eye accelerates initially and the eye speed at the end of the open-loop interval is related to internal estimates of target speed (Lisberger and Westbrook, 1985; Lisberger and Movshon, 1999; Osborne et al., 2005). For example, if the brain underestimates the target's speed, the eye's acceleration and steady-state speed will be too slow until visual feedback becomes available to correct pursuit (Lisberger et al., 1981; Lisberger and Westbrook, 1985; Osborne et al., 2005). We found that scoring motion stimuli based on filter-weighted summed optic flow allowed us to predict pursuit gain over a fivefold range of optic flow scores, an indication of the filter's generality. With two exceptions, eye acceleration increases in proportion to flow score. This result is consistent with past studies linking behavioral gain to motion energy (Lisberger and Westbrook, 1985; Heinen and Watamaniuk, 1998; Sheliga et al., 2008a, 2009; Schütz et al., 2010; Mukherjee et al., 2015). Peak eye acceleration increases linearly with target speed (Lisberger and Westbrook, 1985), so lower pursuit gains could also indicate that the brain underestimates the speed of weaker motion energy stimuli. A Bayesian model of speed estimation predicts this bias by postulating that the brain expects a stationary world: a zero-speed prior (Stocker and Simoncelli, 2006; Yang et al., 2012). Priors have a stronger influence on speed estimates at low signal-to-noise, shifting speed estimates of weaker stimuli toward zero. Therefore, Bayesian models predict larger, negative speed errors for low flow score stimuli, which we did not observe. Further study with carefully chosen stimuli that tease apart contextual dependencies on motion drive will be necessary to test Bayesian theories more explicitly.