Contributions of Microtubule Dynamic Instability and Rotational Diffusion to Kinetochore Capture

Abstract

Microtubule dynamic instability allows search and capture of kinetochores during spindle formation, an important process for accurate chromosome segregation during cell division. Recent work has found that microtubule rotational diffusion about minus-end attachment points contributes to kinetochore capture in fission yeast, but the relative contributions of dynamic instability and rotational diffusion are not well understood. We have developed a biophysical model of kinetochore capture in small fission-yeast nuclei using hybrid Brownian dynamics/kinetic Monte Carlo simulation techniques. With this model, we have studied the importance of dynamic instability and microtubule rotational diffusion for kinetochore capture, both to the lateral surface of a microtubule and at or near its end. Over a range of biologically relevant parameters, microtubule rotational diffusion decreased capture time, but made a relatively small contribution compared to dynamic instability. At most, rotational diffusion reduced capture time by 25%. Our results suggest that while microtubule rotational diffusion can speed up kinetochore capture, it is unlikely to be the dominant physical mechanism for typical conditions in fission yeast. In addition, we found that when microtubules undergo dynamic instability, lateral captures predominate even in the absence of rotational diffusion. Counterintuitively, adding rotational diffusion to a dynamic microtubule increases the probability of end-on capture.

Introduction

Cell division is essential to the propagation of life. For a cell to divide successfully, each daughter cell must inherit the correct genetic material. In eukaryotes, segregation of duplicated chromosomes is performed by the mitotic spindle, a cellular machine composed of microtubules (MTs) and their associated proteins (1). Specialized sites on the chromosomes called kinetochores (KCs) attach to spindle MTs, and these KC-MT attachments are necessary for proper chromosome segregation. Understanding KC capture by spindle MTs and the subsequent chromosome movements is challenging because the process depends on multiple overlapping mechanisms (2, 3, 4), including the action of multiple KC-associated motors and highly dynamic MTs that maintain KC attachment during significant MT turnover. Numerous proteins localize to MT plus ends and KCs, but the roles of these different proteins are not yet clear (5, 6, 7). Problems in kinetochore-MT attachment and chromosome segregation can lead to aneuploidy, which is associated with birth defects and cancer progression (8).

The discovery of MT dynamic instability 30 years ago (9) led to the proposal that MT search and capture is the primary mechanism of initial KC-MT attachment in mitosis. In this picture, dynamic MTs grow in different directions from centrosomes and make end-on attachments with KCs (10, 11, 12, 13). Perturbations to MT dynamics are predicted to have significant effects on KC capture (12), suggesting that dynamic instability is a key component of any KC capture model. Search and capture has been directly observed in large cells (14). However, the simplest search-and-capture mechanism does not appear rapid enough to capture multiple chromosomes quickly enough to match measured time in mitosis. Extensions to the search-and-capture mechanism that can make KC capture more rapid in large cells or cell extracts include KC diffusion (12, 15), MT growth that is spatially biased toward chromosomes (16, 17, 18), chromosome spatial arrangements and rotation (15, 19, 20), and KC-initiated MTs that can interact with searching MTs (15, 21, 22). KCs in human cells change size and shape during mitosis, which can both speed up capture and minimize errors (20).

KC capture may occur differently in smaller cells. Lateral and end-on KC contacts have been directly observed both in budding yeast (23) and fission yeast (24). Recent work on the small cells of fission yeast found that KC attachment to MTs that rotationally diffuse about their attachment points at the spindle-pole bodies (SPBs, the yeast centrosomes) enabled rapid KC capture, even for relatively less dynamic MTs (24). Here we use the term “rotational diffusion” for diffusive movements about MT minus-end attachment points, termed “pivoting” in previous work. Based on experiments and a biophysical model, this work concluded that MT rotational diffusion was the primary determinant of the time to capture lost KCs in these cells. This important finding suggests that MT rotational diffusion may significantly contribute to efficient KC capture, an effect that has been neglected previously. Because initial KC captures are often lateral rather than end-on (14, 19, 20, 23, 24, 25), MT rotational diffusion about minus-end attachment points could be an important determinant of the capture time.

We have sought to evaluate the relative importance of MT dynamic instability versus MT rotational diffusion to KC capture. Previous theoretical work has focused either on MT dynamic instability (11, 12, 15, 17, 20, 26) or rotational diffusion (24); as a result, this work has been unable to compare the two mechanisms and determine their relative importance. One model examined the relative contributions of dynamic instability and rotational diffusion for a single parameter set and found that turning off rotational diffusion caused a modest increase in the mean capture time (27). Because MT rotational diffusion can lead to significant increases in the effective volume searched by a single MT, search-and-capture models that neglect MT rotational diffusion could lead to incorrect conclusions.

We extended the model of fission-yeast KC capture of Kalinina et al. (24) to include both MT rotational diffusion and dynamic instability to gauge their relative importance to KC capture. We modeled both relatively slow dynamic instability (using measured parameters (24)) and faster dynamic instability based on our measurements of single mitotic MTs in fission yeast. Rotational diffusion typically gave only a modest speedup of KC capture in our model. For slow dynamics, rotational diffusion decreased the KC capture time by up to 25%, while for faster MT dynamics, rotational diffusion caused at most a 16% decrease in the capture time. Our results suggest that the capture time in fission yeast is primarily determined by MT search and capture. We also found that while lateral captures are typical even in the model with no rotational diffusion, including MT diffusion made end-on attachments more likely. This occurred because rotational diffusion sweeps the tip of the MT through space, increasing the volume searched by the tip. Our findings suggest that associating search and capture with end-on attachment and rotational diffusion with lateral attachment is oversimplified.

Materials and Methods

Kinetochore capture model

We developed a computational model of KC capture in fission yeast that includes the key physical effects of MT dynamic instability and rotational diffusion. Capture occurs within the spherical nucleus of radius R = 1.5 μm. A dynamic MT has its minus end attached to the SPB (which is fixed for this study), rotationally diffuses, and has a length L(t) that changes with time due to dynamic instability (Fig. 1 and Fig. S1 in the Supporting Material). Simultaneously, a spherical KC of radius a = 100 nm diffuses in the nucleus (24). We assumed the fission yeast KC size remained constant during mitosis, in contrast to recent work on human KCs (20). KC capture occurs when the KC contacts the MT, either at its end or along its lateral wall.

Figure 1.

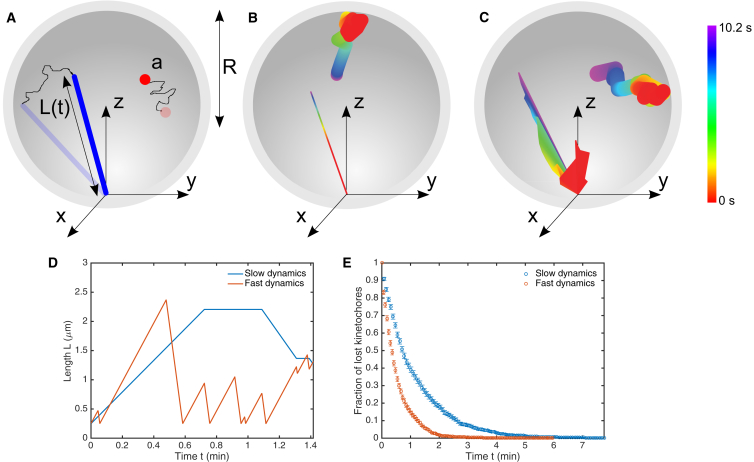
Kinetochore capture model overview. (A) Model schematic. A dynamic microtubule (blue) undergoes dynamic instability and rotational diffusion about its minus-end attachment point; a kinetochore (red) undergoes translational diffusion within the spherical fission-yeast nucleus (gray). (B and C) Images created from simulation data showing microtubule (line) and kinetochore (circle) dynamics. Color indicates time, where red reflects an early position, purple a late one. (B) Model with microtubule dynamic instability but no rotational diffusion. (C) Model with dynamic instability and microtubule rotational diffusion. (D) Microtubule length and (E) fraction of lost kinetochores versus time for slow (blue) and fast (orange) models with the reference parameters (Table 1). To see this figure in color, go online.

The simulations used a hybrid Brownian dynamics-kinetic Monte Carlo scheme approach based on our previous work (28, 29, 30, 31). Brownian dynamics model the diffusive random motion of MTs and KCs; kinetic Monte Carlo models the stochastic MT dynamic instability (Supporting Material).

Slow and fast microtubule dynamics

We studied two MT dynamic instability models that represent relatively slow and fast dynamics (Supporting Material; Fig. 1; Table 1). Kalinina et al. (24) found that MT dynamics were relatively slow and MTs spent most of their time paused. Therefore, we modeled MTs with growing, shrinking, or paused states; the fixed-length paused state is an intermediate between the growing and shrinking states (Supporting Material). In other work on single fission yeast mitotic (32) and meiotic (27) MTs and our measurements, MT dynamics were faster and pausing was rarely seen. We modeled this with growing and shrinking states only, where catastrophe is the transition from growing to shrinking, and rescue the transition from shrinking to growing.

Table 1.

Model Parameter Values

Parameter	Symbol	Reference Value	Range	Notes
Nuclear envelope radius	R	1.5 μm	—	Kalinina et al. (24)
KC diameter	σKC	200 nm	—	Ding et al. (58)
MT diameter	σMT	25 nm	—	Alberts et al. (59)
MT angular diffusion coefficient	Dθ	–	Varies with MT length	Kalinina et al. (24), Supporting Material
Force-induced catastrophe constant	α	0.5 pN−1	—	Dogterom and Yurke (37) and Janson et al. (38)
Slow dynamic instability model
Growth speed	$v_g$	2.7 μm min−1	0.7–11 μm min−1	Kalinina et al. (24)
Shrinking speed	$v_s$	3.8 μm min−1	1–16 μm min−1	Kalinina et al. (24)
Grow-to-pause frequency	$f_{+0}$	1.8 min−1	0.4–7.1 min−1	Kalinina et al. (24)
Shrink-to-pause frequency	$f_{-0}$	2.53 min−1	1.2–5 min–1	Kalinina et al. (24)
Pause-to-shrink frequency	$f_{0-}$	0.49 min−1	0.2–1 min–1	Kalinina et al. (24)
Pause-to-grow frequency	$f_{0+}$	0 min−1	—	Transitions from pausing to growing appeared infrequent in Kalinina et al. (24)
Fast dynamic instability model
Growth speed	$v_g$	4.1 μm min−1	1–10 μm min−1	This work
Shrinking speed	$v_s$	6.7 μm min−1	5–25 μm min−1	This work and Sagolla et al. (32)
Catastrophe frequency	$f_{\text{cat}}$	3.7 min−1	1–8 min−1	This work
Rescue frequency	$f_{\text{res}}$	0.175 min−1	0–8 min−1	This work

In our model, MTs in the growing or shrinking state increase or decrease in length at the constant speed v_g or v_s. For MTs that are not interacting with the nuclear envelope boundaries, the state switching frequencies are constant in time. Any shrinking MTs that reach the minimum length of 4σ_MT = 100 nm switch to the growing state (Supporting Material).

Microtubule interactions with the nuclear envelope

MTs that touch the nuclear envelope experience steric forces and torques from the interaction of the MT tip with the envelope (Supporting Material). The torque can cause the MT tip to slip along the edge of the envelope, reorienting the MT, as has been measured and modeled previously for MTs interacting with microchamber boundaries (33, 34, 35). In addition, MTs that grow into a boundary exhibit increased catastrophe frequency (36). The force component along the MT long axis increases the catastrophe frequency, as measured previously (37, 38). By combining these previous measurements of the force dependence of MT growth speed with the growth speed dependence of the catastrophe time, we wrote the catastrophe frequency $f_c\left(F_{\Vert }\right)=f_c\text{exp}\left(\alpha F_{\Vert }\right)$, where $F_{\Vert }$ is the component of the steric force along the MT long axis, α is the force sensitivity of catastrophe (Table 1), and $f_c$ is the zero-force catastrophe frequency (or the analogous grow-to-pause frequency in the model with pausing).

Initial conditions and measurements

We began simulations with a single MT of length 4σ_MT (100 nm) placed at a random angle subject to the requirement that the MT was not initially interacting with the nuclear envelope. We inserted a KC at a random position uniformly sampled within the simulation volume, with the requirement that the KC was not initially interacting with either the MT or the nuclear envelope. We ran the simulation until the KC collided with the MT (either laterally or end-on), which defined a capture. For each parameter set, we repeated simulations 2000–5000 times to determine the distribution of capture times, shown as the fraction of lost KCs as a function of time in Figs. 1 E and S2. From these data, we computed the mean capture time $\langle {\tau }_c\rangle$.

We defined reference parameter sets and wide parameter ranges around the reference for both the slow and fast dynamic instability models (Table 1). For both slow and fast models, we performed simulations of dynamic instability with no MT rotational diffusion, and dynamic instability plus MT rotational diffusion. To connect to previous search-and-capture models, MTs that shrink to the minimum length reenter the growing state with a new random orientation.

Experimental methods

To understand the difference between previous measurements of fission-yeast mitotic MT dynamics that were relatively slow (24) or fast (32), we measured MT dynamic instability in S. pombe. To facilitate these measurements, we used a strain with temperature-sensitive inactivation of kinesin-5 motors (cut7-24 in fission yeast) and low-level fluorescent tagging with mCherry-atb2 (39) (Supporting Material; Table S1). Cells carrying the cut7-ts allele are unable to form bipolar mitotic spindles at restrictive temperature (36–37°C) (40). The cells instead form monopolar mitotic spindles, in which individual fluorescently labeled mitotic MTs can be imaged (Fig. 2) (41).

Figure 2.

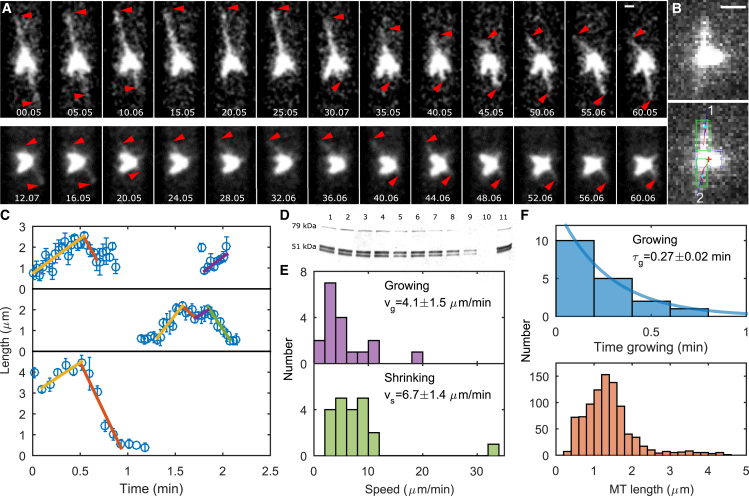
Measurements of single MT dynamics and length in monopolar mitotic spindles. (A) Image sequences. Images are pixel-interpolated maximum intensity projections of monopolar spindles with mCherry-labeled MTs. Red arrowheads indicate single MTs, time is shown in s, and the scale bar is 1 μm. (B) Example raw maximum-intensity-projected image (top) and analyzed image (lower). The red cross indicates the center of brightness of the SPB, green boxes indicate the regions analyzed near MT tips, blue lines indicate the fits to the MT backbone positions, and blue dots indicate the fits to the MT tip positions. The scale bar is 1 μm. (C) Example traces of MT length versus time (points) and fits to growing and shrinking events (lines). (D) Western blot used to quantify fraction of fluorescently labeled tubulin. The gel was loaded with serial dilutions from 100 to 10% with 100% repeated in lane 11: lane 1 = 100%, lane 2 = 90%, lane 3 = 80%, lane 4 = 70%, lane 5 = 60%, lane 6 = 50%, lane 7 = 40%, lane 8 = 0%, lane 9 = 20%, lane 10 = 10%, and lane 11 = 100%. (E) Histograms of growth speed and shrinking speed. (F) Histograms of growth time and MT length. To see this figure in color, go online.

Measurement of labeled tubulin fraction

We performed immunoblots using the TAT-1 tubulin antibody on S. pombe cell lysate with serial dilutions ranging from 100 to 10% of the original cell suspension concentration (Supporting Material) and scanned the bands for analysis. The two lower, darker bands corresponded to α-tubulin-1 (nda2) at 51 kDa and α-tubulin-2 (atb2) at 50 kDa, while the fainter third band corresponded to mCherry-atb2 at 79 kDa (Fig. 2). To analyze the scanned images, we inverted the images so that labeled regions corresponded to high intensity, drew equally sized regions of interest around each band, and determined the average pixel intensity in each region. From this, we determined the fraction of intensity in the mCherry-atb2 band relative to the total. Each lane had similar ratios (data not shown), and we averaged the results for each lane.

Cell preparation and confocal imaging

We grew cells using standard techniques (Supporting Material) and cultured them on glass-bottomed dishes at 36°C for 2–4 h to allow monopolar spindles to form. The dishes were transferred to the microscope in <60 s to prevent the monopolar spindles from becoming bipolar. Images were taken on a spinning disk (Yokogawa, Musashino, Japan) Eclipse Ti inverted confocal microscope (Nikon, Tokyo, Japan) with a 100×, 1.4 NA Plan Apo oil-immersion objective, an iXon Ultra 897 EM-CCD camera (Andor, Belfast, UK), and a TIZSH Stage Top incubator (Tokai Hit, Fujinomiya, Japan) warmed to 36°C. Three-dimensional images were obtained with an EM gain of 300, and an exposure time per plane of 40–150 ms with 595 nm laser illumination for each of five focal planes separated by 500 nm in z, and subsequent stacks are separated by 4–6 s. Images of Fig. 2 A are displayed as pixel-interpolated maximum-intensity projections.

Image and data analysis

In our images of monopolar spindles, we were able to observe dynamic MTs (Fig. 2). We quantified the dynamic instability of mitotic MTs by determining the location of the SPBs and the tip of each emanating MT with image analysis software adapted from TipTracker (42, 43). To identify the center of the monopolar spindle, we noted that near the two SPBs, many short and overlapping MTs produced a bright fluorescent region. When using this software, one selects a rectangle around this region, and our program then computes the center of intensity within that region to estimate the SPB location and determines the length of each MT in a given frame by assuming the MT formed a line between the estimated SPB location and the MT tip position. Visual inspection of each frame confirmed that MTs in the monopolar spindles formed in these cells were typically straight lines emanating from the bright spindle center region (Fig. 2 B). Each frame is analyzed separately, and the MT length data stored for analysis. The software allows us to make MT length and angle measurements with subpixel resolution and quantify the lengths and dynamics of mitotic MTs in monopolar spindles.

We identified growth and shrinking events by comparing the movies and plots of MT length versus time to identify starting and ending times of events. We then performed weighted least-squares linear fits to the MT length versus time during each event (Fig. 2). Growth and shrinking speeds were the slopes determined from the fits, and the catastrophe and the rescue times were the duration of the events before a switch.

Results and Discussion

Experimental results

Kalinina et al. (24) found that fission yeast mitotic MTs on average spent 75% of their time in a paused state and had lifetimes of 3 min, growth speed $v_g$ = 2.7 μm min⁻¹, and shrinking speed $v_s$ = 3.8 μm min⁻¹. These results differed from the results of Sagolla et al. (32), who observed highly dynamic polar MTs in early mitosis (before spindle formation), with lifetimes of seconds and a shrinking speed $v_s$ = 20 μm min⁻¹, and more recent work on meiotic MTs (27). These differences in lifetime and dynamics could be related to the stage of mitosis (before and after spindle formation), the number of MTs per bundle, and/or to the fraction of fluorescent tubulin in the cells (which affects MT dynamics (44)). The differences are most likely due to MT bundling, which alters MT dynamics (45, 46). Because KC capture could occur either by single MTs that are more dynamic or bundled MTs that are more stable, we undertook additional measurements of mitotic MT dynamic instability in S. pombe.

We adapted the strategy of Costa et al. (41), who used temperature-sensitive inactivation of the kinesin-5 motor (cut7-24) to obtain cells stably arrested in a monopolar state. Fission yeasts carrying the cut7-ts allele arrest in early mitosis at restrictive temperature (36–37°C), because bipolar spindles cannot form when cut7p is inactive (40). These cells instead form monopolar mitotic spindles, in which individual fluorescently labeled mitotic MTs can be imaged and tracked (Fig. 2, A and B) (41).

To measure MT length, we adapted the TipTracker algorithm (42, 43) to measure MT lengths in monopolar spindles (Materials and Methods, Fig. 2 B). Brighter MTs showed lengths that were more stable in time, and dimmer MTs showed more rapid dynamics (Fig. 2 A). We identified the dimmer, more dynamic MTs as single MTs, as in previous work (41). We analyzed 20 MTs from 15 cells that showed low intensity compared to other MTs in the same cell and relatively fast dynamics. We determined growth and shrinking events and their associated speeds and times (Fig. 2 C, Materials and Methods).

Fluorescent-protein fusions to tubulin in fission yeast can alter MT dynamics (44). We studied fission yeast carrying mCherry-atb2 that is an additional copy of this α-tubulin gene under a weak promoter (39). We used Western blotting to determine the fraction of tubulin our cells that was fluorescently tagged (Fig. 2 D, Materials and Methods) and found a low fraction of 8.8 ± 0.5% labeled α-tubulin.

These MTs had a median growth speed $v_g=4.1\pm 1.5$ μm min⁻¹ and shrinking speed $v_s=6.7\pm 1.4$ μm min⁻¹ (Fig. 2 E). The distribution of times in the growing state appeared exponential with a characteristic time ${\tau }_g=0.27\pm 0.02$ min, implying a catastrophe frequency of 3.7 min⁻¹ (Fig. 2 F). Measuring the rescue frequency was challenging, because it was difficult to distinguish rescue from complete shrinkage followed by regrowth of a different MT in the same area. We saw one possible rescue event, which gave a bound $f_r\le 0.175$ min⁻¹.

Our data were collected at 37°C, and MT dynamic instability is sensitive to temperature (47). However, Kalinina et al. (24) found relatively little change in fission-yeast MT dynamic instability parameters between 24 and 32°C, suggesting that S. pombe mitotic MT dynamic instability may not vary markedly with temperature in this regime. Another possible complication is that MT dynamics might be altered in the monopolar spindle system where kinesin-5 is inactive. Previous work in budding yeast found that kinesin-5s promote disassembly of longer MTs (48). However, because we found similar MT mean lengths to those of Kalinina et al. (24), it appears that our measurements do not show a strong bias toward longer MTs due to loss of kinesin-5-associated depolymerization activity.

Pooled length measurements of MTs we identified as single MTs (including all measurements, not just points identified as growing/shrinking events) had a median $\langle L\rangle =1.31\pm 0.02$ μm (Fig. 2 F). We compared this to the predicted mean length for dynamic instability in an infinite volume (neglecting boundary effects): in the bounded growth regime, $\langle L\rangle =v_g{v}_s/\left(v_s{f}_c-v_g{f}_r\right)$ (49). If we estimate the mean length using our median dynamic instability parameters with the upper bound on the rescue frequency of $f_r\le 0.175$ min⁻¹, we predict $\langle L\rangle =1.14$ μm, while using $f_r=0$ gives $\langle L\rangle =1.11$ μm. There is little difference between these values, showing that the mean MT length is primarily determined by the growth speed and catastrophe frequency in this low-rescue-frequency regime. This typical MT length estimated from the dynamic instability parameters is consistent with our direct measurements of MT length.

Model results

Kinetochore capture by single microtubules with fast or slow dynamic instability

Because KC capture could occur by either single MTs that are more dynamic or bundled MTs that are more stable, we sought to understand how these different MT arrangements affect KC capture in fission yeast. We studied two reference parameter sets that we denote slow (based on the measurements of Kalinina et al. (24)) and fast (based on our measurements). In the slow model, MTs can be growing, shrinking, or paused. The reference parameter values (Table 1) were taken from Kalinina et al. (24), assuming that transitions from pausing to growing did not occur. In the fast model, we considered only growing and shrinking states with reference parameter values determined from our measurements. Examples of the resulting MT length as a function of time and the dynamics of KC capture are shown in Fig. 1. For each model, we varied parameters around the reference values by factors of 4–20 (Table 1) so that we could study the dependence of the capture time on parameter values. We then studied both slow and fast models with and without MT rotational diffusion, to determine the contributions of dynamic instability alone and dynamic instability with rotational diffusion to the capture time.

Kalinina et al. (24) found that three polar MTs were typically visible during their KC capture experiments, and that the time of KC capture was sensitive to MT number. Here we determined capture times for a single MT. Our model results for capture by a single MT and slow dynamic instability agree well with those of Kalinina et al. (24) (Fig. S2). Studying capture by single MTs allowed us to focus on the effect of dynamic instability parameters and rotational diffusion.

Parametric study using polynomial chaos expansion

To understand how the mean capture time $\langle {\tau }_c\rangle$ and the mean MT length $\langle L\rangle$ depend on model parameters (Table 1), we used polynomial chaos (PC) expansion (50, 51), a widely used technique for uncertainty quantification. PC expansion is a type of spectral method in which we represent $\langle {\tau }_c\rangle$ and $\langle L\rangle$ as functions of the dynamic instability parameters in a high-order, multivariate, orthogonal polynomial basis, here of Legendre type. This allowed us to use a relatively small number of simulations, corresponding to random samples of input parameters generated uniformly over their allowed ranges (Table 1), to accurately approximate $\langle {\tau }_c\rangle$ and $\langle L\rangle$ over the full multidimensional parameter space (52, 53, 54). We then used this expansion to perform global and local sensitivity analysis to determine which dynamic instability parameters are of most importance to $\langle {\tau }_c\rangle$ and $\langle L\rangle$. The global sensitivity analysis provides information on the importance of each parameter in terms of its contribution to the overall solution variability, while the local analysis identifies the dependence of the solution on each parameter in the small neighborhood of its nominal value. To construct the PC expansions, here of a total degree three, we used a regression approach based on ${\ell }_1$-minimization (52, 53, 54) using 250 randomly sampled parameter sets, and the corresponding realizations of $\langle {\tau }_c\rangle$ and $\langle L\rangle$. In Figs. 3, 4, 5, and 6 below, each point corresponds to one of the 250 parameter sets.

Figure 3.

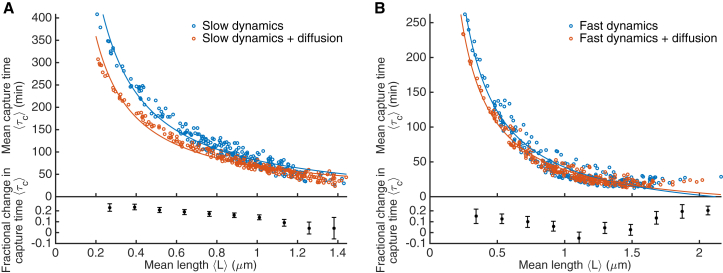
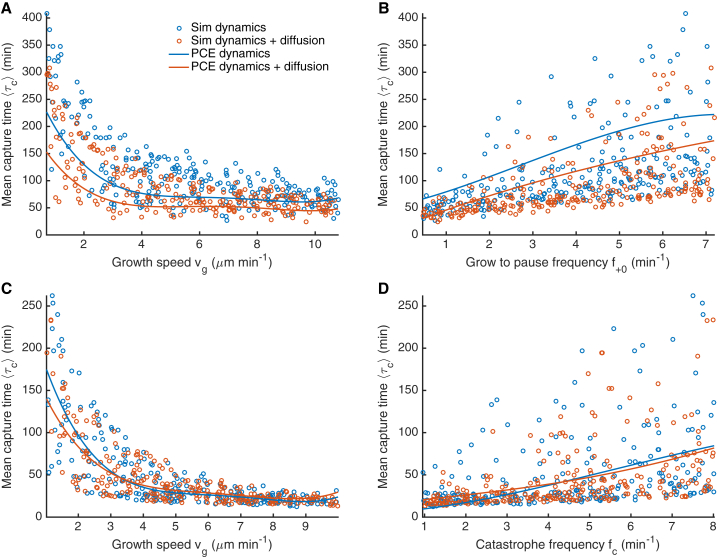
Dependence of capture time on MT length and rotational diffusion. (A) Slow model. (B) Fast model. Points are results of simulations with all dynamics parameters varied for search and capture only (blue) and search and capture with microtubule rotational diffusion (orange). Lines are fits to $\langle {\tau }_c\rangle =A{\langle L\rangle }^{-1}+B$. (Insets) Fractional decrease in capture time when rotational diffusion is added to the model. Error bars are determined using standard error propagation techniques from the standard error of the mean capture time in each bin of simulations. To see this figure in color, go online.

Figure 4.

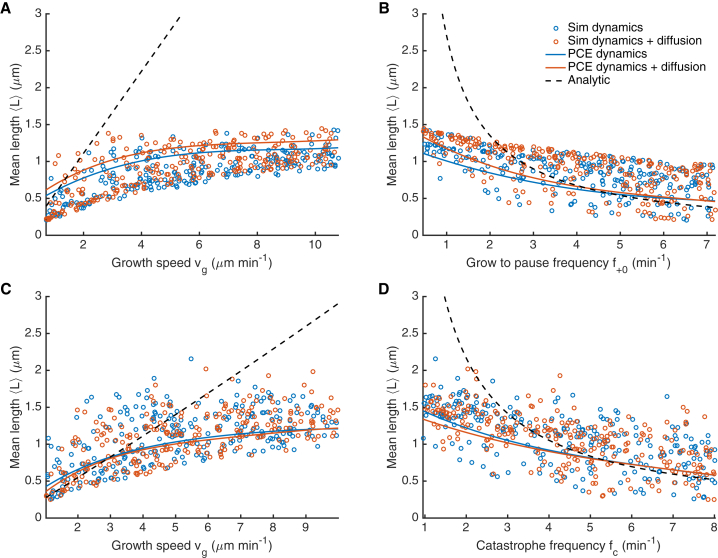
Variation of microtubule length with single parameters. (A and B) Slow model. (C and D) Fast model. Points represent individual simulations of model with dynamic instability only (blue) and model with dynamic instability and rotational diffusion (orange). (Solid lines) Projection of the polynomial chaos expansion prediction in one dimension for variation of indicated parameter with other parameters at their reference values. (Dashed line) Predicted mean microtubule length for dynamic instability in the absence of boundary effects. To see this figure in color, go online.

Figure 5.

Variation of capture time with single parameters. (A and B) Slow model. (C and D) Fast model. Points represent individual simulations of model with dynamic instability only (blue) and model with dynamic instability and rotational diffusion (orange). (Solid lines) Projection of the polynomial chaos expansion prediction in one dimension for variation of indicated parameter with other parameters at their reference values. To see this figure in color, go online.

Figure 6.

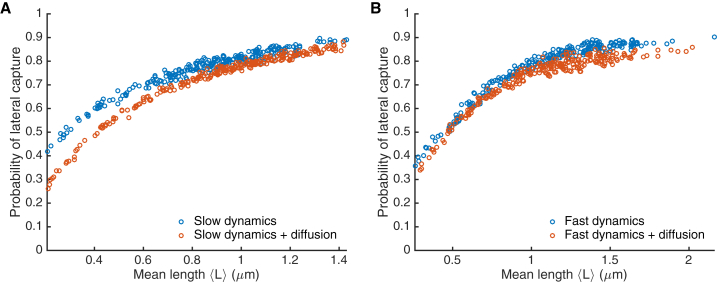
Fraction of captures that occur laterally as a function of mean microtubule length. (A) Slow model. (B) Fast model. Points represent individual simulations of model with dynamic instability only (blue) and model with dynamic instability and rotational diffusion (orange). To see this figure in color, go online.

Effects of varying mean MT length

The rotational diffusion coefficient of a rod varies as $L^{-3}$, making MT length important for KC capture by a fixed-length MT (24). We found that the MT mean length was also important for KC capture with dynamic instability. Indeed, the primary determinant of the capture time was the mean MT length (Fig. 3), for all models studied. The capture time decreased by approximately a factor of 10 as $\langle L\rangle$ increased from short ($\mathrm{\lesssim }0.3$ μm) to long ($\mathrm{\gtrsim }1.5$ μm, one-half the nuclear diameter). A longer MT increases the effective number of binding sites for a KC, lowering the capture time. If the number of binding sites were the sole factor determining the rate of KC capture, we would expect $\langle {\tau }_c\rangle \sim {\langle L\rangle }^{-1}$. The dependence in our model is more complex, because the MT dynamics also change with $\langle L\rangle$. Nevertheless, fitting the capture time as a function of the mean length to the form $\langle {\tau }_c\rangle =A{\langle L\rangle }^{-1}+B$ (solid lines in Fig. 3) gave reasonable agreement with our simulation results.

For all MT lengths and both slow and fast dynamic instability, adding MT rotational diffusion to a model with only dynamic instability reduced the capture time. The contribution of rotational diffusion depended on the MT dynamics: $\langle {\tau }_c\rangle$ decreased by 23% on average (25% at most) for the slow model, and by 9% on average (16% at most) for the fast model. The speedup due to rotational diffusion was larger for slower MT dynamics and shorter MTs (Fig. 3). For the most relevant MT lengths in fission yeast of ∼1 μm, rotational diffusion shortened the capture time by at most 14% for the slow model and 6% for the fast model. This suggests that while rotational diffusion does speed up KC capture, it makes a relatively small quantitative contribution, consistent with recent work (27).

Sensitivity analysis

We performed sensitivity analysis to check how the capture time and MT mean length vary with model parameters. For dynamic instability with no boundary effects, we would expect a mean length of $\langle L\rangle =v_g/f_{+0}$ in the slow model and $\langle L\rangle =v_g{v}_s/\left(v_s{f}_c-v_g{f}_r\right)\approx v_g/f_c$ in the fast model ((49) and the Supporting Material). While interactions of MTs with the nuclear envelope alter this relationship, we expected that the MT mean length and therefore the capture time depend primarily on the MT growth speed and the catastrophe frequency (or its analog in the slow model, the grow-to-pause frequency).

To test these relationships, we performed a global sensitivity analysis of the mean capture time and MT length to the dynamic instability parameters using the analysis of the variance of $\langle {\tau }_c\rangle$ and $\langle L\rangle$ based on the so-called Sobol decomposition (55), which we computed directly using the PC expansion ((56) and the Supporting Material). The PC expansion gave low errors of a few percent (Table S2), indicating that it accurately describes the full simulation model. As expected, $\langle {\tau }_c\rangle$ and $\langle L\rangle$ are most sensitive to the growth speed and effective catastrophe frequency, and this dependence is not altered significantly by the addition of rotational diffusion to the model (Table S3). We also determined the local sensitivity of the capture time to these parameters (Supporting Material, Fig. S3).

Variation with individual parameters

To develop better intuition for how variation of individual parameters affects capture, we used both our individual simulations and the PC expansion to study how the MT mean length and capture time depend on variation of individual parameters (Figs. 4, S4, and S5). The solid lines are the predicted dependence of $\langle L\rangle$ for the reference parameter set on the varied single parameter from the PC expansion, while the dashed line is the analytic prediction for $\langle L\rangle$ with unconstrained dynamic instability. As expected, the analytic solution that neglects boundary interactions matches the data and PC expansion well when $\langle L\rangle$ is relatively small, but differs significantly where $\langle L\rangle$ ≳ 1 μm. The points show the behavior of individual simulations with widely varying parameters, illustrating the range of behavior of our model.

The variation of the capture time with individual parameters shows qualitatively similar dependence (Figs. 5, S4, and S5). Consistent with intuitive expectations, parameter sets with higher growth speed and lower catastrophe frequency lead to shorter capture times. Growth speed is the main parameter affecting capture time, causing it to vary by up to a factor of five, consistent with its total Sobol index (Table S3). This makes sense because MTs with higher growth speeds search a given direction more quickly than slower MTs with the same orientation, resulting in lower capture time; fast-growing MTs have also typically longer mean lengths. Also as expected, catastrophe frequency affects the capture time, because high catastrophe frequency tends to reduce the mean length of MTs. However, MTs with low catastrophe frequency typically reach the nuclear envelope and undergo force-induced catastrophe, which limits the advantage gained by lowering the catastrophe frequency. The shrinking speed and rescue frequency have little effect on the capture time, because they do not significantly affect the mean MT length (Figs. S4 and S5). For simulations both with and without MT rotational diffusion, varying these parameters alone varies the capture time by ≲25%.

Lateral versus end-on capture

In fission yeast, KC capture occurs primarily via end-on attachment, with ∼75% of captures occurring <500 nm away from the MT tip (24), while other work in both large and small cells has found a high frequency of lateral attachments (14, 19, 20, 23, 25). In our model, we classified attachments as end-on if the capture occurred within 4.5σ_MT (≈113 nm) from the MT tip, and lateral otherwise. We found that lateral attachments are more likely in our model, but the fraction of captures that occur laterally depends on the mean MT length (Fig. 6). Increasing $\langle L\rangle$ increased the probability of lateral capture, because the available MT surface area for binding laterally increases.

Remarkably, we found that lateral captures predominated even in the model with dynamic instability only (no rotational diffusion). This occurred for two reasons: first, interactions of MTs with the nuclear envelope caused some MT reorientation in the absence of thermal diffusion. However, we observed significant lateral attachment even for relatively short MTs that did not interact with the nuclear envelope, because KC diffusion allowed lateral attachment even for fixed-orientation MTs.

Surprisingly, adding rotational diffusion to the model made end-on attachments more likely: diffusion decreases the probability of lateral capture, an effect that was more noticeable for shorter MTs. Rotational diffusion allows the MT to sweep through space, increasing the volume searched by the MT. This increase in effective volume searched is largest at the MT tip because the tip is furthest from the pivot point at the SPB. This effect was more important for shorter MTs where end-on attachments were more likely.

It is not clear why our model found primarily lateral captures, while Kalinina et al. (24) measured primarily end-on captures. Some difference would be expected due to the different definitions of end-on versus lateral attachment: Kalinina et al. (24) used a 500 nm distance cutoff that was limited by optical resolution. In addition, it is possible that because lost KCs were induced by a short cold treatment in these experiments, more of the KCs were close to the SPB and were captured by shorter MTs for which rotational diffusion is more important.

Conclusions

The search-and-capture model has been considered the main mechanism by which KCs are captured since the discovery of MT dynamic instability (9, 11, 12, 13). The original picture of search and capture posited that MTs undergo dynamic instability nucleated from centrosomes until they form end-on attachments with KCs. Additional effects such as diffusion of KCs (12, 15), a bias in MT growth toward chromosomes (16, 17, 18), MT nucleation from KCs (15, 21, 22), spatial distribution and rotation of chromosomes (15, 19, 20), and KC size decreases after capture (20) can make search and capture more rapid. MT rotational diffusion and lateral capture were found to be important mechanisms in fission yeast (24). This work suggested that MT rotational diffusion about centrosomes is important, but because the model assumed fixed-length MTs, it was unable to directly evaluate the relative importance of rotational diffusion and dynamic instability to KC capture.

We developed a biophysical model of KC capture in fission yeast that includes MT dynamic instability and rotational diffusion, KC diffusion, and interactions with the nuclear envelope (Fig. 1). We used the model to compare the time course of KC capture in models with and without MT rotational diffusion. The mitotic MTs measured by Kalinina et al. (24) were primarily paused, and the measured dynamics appeared slow compared to previous measurements (32). Therefore, we performed further measurements of the dynamics of MTs in fission yeast monopolar spindles with low-level fluorescent tubulin labeling. We found more rapid dynamic instability of single MTs, with little pausing (Fig. 2). This motivated us to consider two dynamic instability models: a slow model with dynamics measured by Kalinina et al. (24), and a fast model with dynamics measured in this work (Table 1).

We studied KC capture by single MTs in our model both for the reference parameter sets and for broad ranges of parameters around the reference sets. In all cases, KC capture occurred more quickly when rotational diffusion about SPBs was added to a model with only dynamic instability (Fig. 3): $\langle {\tau }_c\rangle$ decreased by 23% on average for the slow model, and by 9% on average for the fast model, similar to recent work (27). We found that the primary determinant of the capture time was the mean MT length. Longer MTs have a larger surface on which the KC can bind, which suggests that the capture time $\langle {\tau }_c\rangle \sim {\langle L\rangle }^{-1}$, as we observed. Because the MT growth speed and catastrophe frequency controlled the mean length in the parameter regimes we studied, these parameters had the biggest effect on the capture time (Table S3; Fig. S3).

For the experimentally measured mitotic polar MT lengths of ∼1 μm in fission yeast, adding rotational diffusion to our model shortened the capture time by 14% for the slow model and 6% for the fast model. This suggests that rotational diffusion causes relatively small changes to the capture time for typical conditions in fission yeast. We note that our model, like that of Kalinina et al. (24), considered the capturing MT only and neglected the bipolar spindle that assembles in prometaphase and the possibility of capturing MTs from the other spindle-pole body. Because the assembled spindle alters the rotational freedom of mitotic polar MTs, in future work it would be interesting to study how the presence of the spindle affects the kinetics of KC capture.

We further examined how MT length (Fig. 4) and capture time (Fig. 5) varied with the growth speed and catastrophe frequency. The mean length varied qualitatively as expected from the predictions of analytic theory that neglects MT interactions with the nuclear envelope. In the computational model, changes from this theory became significant for longer MTs. Parameter sets with higher growth speed and lower catastrophe frequency that lead to longer mean MT lengths had shorter capture times.

The original search-and-capture model supposed that KC attachments to MTs are end-on, consistent with the results of Kalinina et al. (24), while others observed primarily lateral attachments (14, 19, 20, 23, 25). Therefore, we studied how the probability of lateral or end-on attachment varied with MT length and the presence or absence of rotational diffusion in the model (Fig. 6). Lateral captures predominated, even in the absence of MT rotational diffusion. Somewhat counterintuitively, we found that adding rotational diffusion to the model made end-on attachments more likely. A diffusing MT searches a larger volume of space than a rotationally constrained MT, an effect that is largest for the MT tip. Therefore, rotational diffusion can decrease lateral attachment.

Recently, Magidson et al. (20) proposed that initial lateral contacts are important to the timing and low error rates of KC-spindle attachment in human cells. Although many proteins are known to contribute to KC-MT attachment, including motors and nonmotor MT-binding proteins (the Ndc80 complex, other components of the KMN network, Ska or Dam1, and others) (57), the contributions of end-on versus lateral KC-MT attachment pathways are not fully understood. Our work suggests that lateral captures are enhanced when MT rotational diffusion about SPBs is decreased or eliminated, as would be the case in large spindles with many long MTs. Future work dissecting contributions of lateral and end-on attachment mechanisms may contribute interesting additional insights into this biologically important problem.

Author Contributions

R.B., O.S.-S., C.E., Z.R.G., A.D., J.R.M., M.A.G., and M.D.B. designed research; R.B., O.S.-S., C.E., Z.R.G., P.J.F., S.M., A.C., and M.D.B. performed research; R.B., O.S.-S., C.E., Z.R.G., P.J.F., A.D., M.A.G., and M.D.B. contributed analytic tools; R.B., O.S.-S., C.E., Z.R.G., P.J.F., S.M., A.C., and M.D.B. analyzed data; and R.B., C.E., Z.R.G., P.J.F., and M.D.B. wrote the article.

Editor: Jennifer Ross.