Abstract
Transcatheter aortic valve (TAV) implantation within a failed bioprosthetic valve is a growing trend for high-risk patients. The non-compliant stent of the previous prosthesis may prevent full expansion of the TAV, which has been shown to distort the leaflet configuration, and has been hypothesized to adversely affect durability. In this study, TAV leaflet fatigue damage under cyclic pressurization in the setting of stent underexpansion by 0 (fully expanded), 1, 2 and 3 mm was simulated using finite element analysis to test this hypothesis. In the 2 and 3 mm underexpanded devices, the TAV leaflets exhibited severe pin-wheeling during valve closure, which increased leaflet stresses dramatically, and resulted in accelerated fatigue damage of the leaflets. The leaflet fatigue damage in the 1 mm underexpanded case was similar to that in the fully expanded case. Clinically a range of 10% to 15% underexpansion is generally considered acceptable; however, it was observed in this study that ≥2 mm (≥9.1%) underexpansion, will significantly impact device durability. Further study is necessary to determine the impact of various deployment conditions, i.e. non-uniform and non-circular deployments and different implantation heights, on differing TAV devices, but it is clear that the normal TAV leaflet configuration must be preserved in order to preserve durability.
INTRODUCTION
Transcatheter aortic valve (TAV) implantation into an existing bioprosthetic valve, to treat stenosis or regurgitation in either a failed surgical valve (SAV) or an ill positioned TAV, is a growing trend for high-risk patients. Multiple TAV devices have been used in these “valve-in-valve” (ViV) procedures 5, 28. TAV implantation within a failed SAV has been shown to be feasible and safe with a reported procedural success rate of 95.7% in the largest reported TAV-in-SAV meta-analysis to date with 976 patients across 25 multi-center studies 5. Considering this success rate with the morbidity and mortality associated with valve reoperation, ViV treatment for SAV failure will likely become an increasingly attractive option for both patients and clinicians 47, particularly with the recent shift towards the implantation of bioprosthetic SAVs versus mechanical SAVs 12, with bioprosthetic SAVs comprising 78.4% of the total valves used in North America over the last 10 years 5.
In ViV procedures the newly implanted TAV is typically oversized (larger in diameter) with respect to the inner diameter of the previous prosthesis to prevent paravalular leak and valve migration 6, 16. While oversizing has been shown to reduce the risk of moderate to severe paravalvular leak in patients 13, 24, 49, the degree of oversizing remains controversial. There are little guidelines in terms of proper TAV sizing and positioning for clinicians to go by. The non-deformable stent of the previous prosthesis may preclude full expansion of an excessively oversized TAV resulting in valve underexpansion 9, 33, 50. Valve underexpansion has been shown to distort the configuration of the leaflets 38, 51 and can affect transvalvular gradients and effective orifice areas 2, 16, 19, 21–23, 29, 48. ViV with small SAVs, which already have a small EOA, put patients at higher risk of patient-prosthesis mismatch where the EOA is too small in relation to the patient’s body size34 and 28. The ViV configuration is also believed to affect leaflet durability by two primary mechanisms: 1) overhanging of the leaflets over the stent during opening and 2) twisting and overhanging of the leaflets over each other during valve closure 7, 16, 47.
In our recent simulation study of TAV leaflet fatigue 25, we showed that even in the ideal deployed configuration, TAVs may be expected to have reduced durability compared to bioprosthetic SAVs due to the thinner leaflets and reduced stent-tip deflection of TAVs. TAV structural failures as early as 3 years after implantation have been cited 3, 17, 20. Furthermore, it has been shown that poor leaflet coaptation 27, 45 will reduce the durability of bioprosthetic SAVs; thus, it follows that the durability of TAVs that exhibit poor leaflet coaptation as seen under non-optimal deployment conditions (elliptical, underexpanded, non-uniformly expanded) 14, 15, 43, would be further reduced. Therefore, there is a critical need for more comprehensive studies on the long-term durability of TAV devices in various configurations to assess deployment strategies and provide insight for improved design. The objective of this study was to implement the computational framework developed previously to investigate SAV and TAV leaflet fatigue 25–27, to assess TAV fatigue in the setting of stent underexpansion.
METHODS
Constitutive modeling of tissue fatigue
In this study, GLBP was selected as a representative valve leaflet material. GLBP tissue is comprised of stiff collagen fibers embedded in a compliant matrix of elastin and proteoglycans, and thus can be considered a fiber-reinforced continuum. Accordingly, the total tissue free energy, W, was decomposed into isochoric, Wiso, and volumetric parts, W Wvol, as
| (1) |
where C is the right Cauchy-Green tensor, and C is the deviatoric right Cauchy-Green tensor, and Wiso is further decomposed into distinct matrix and fiber contributions denoted with “m” and “f” subscripts respectively giving
| (2) |
where M is a structural tensor describing the fiber orientation.
Fatigued state tissue free energy function
Details on the constitutive modeling of the soft tissue fatigue response were described previously in 26, 27. Briefly, to incorporate changes to the valve leaflet material properties as a result of fatigue damage, W, was enhanced with the addition of a stress-softening parameter, Ds, and a permanent set parameter, Dps, given by
| (3) |
where Wps is the dissipated energy due to the permanent set, and W0 indicates the initial (un-fatigued) strain energy. At the un-fatigued state, both Ds and Dps are inactive, i.e. Ds = 0 and Dps = 0, thus W reduces to the strain-energy function, W0. The parameters Ds and Dps become active with the onset of fatigue damage induced by cyclic loading.
GLBP tissue fatigue damage evolution was considered to be a function of the peak equivalent strain per cycle as in our previous studies 26, 27. The equivalent strain Ξt 35 at time t ∈ [0,T ], was defined for the matrix and fiber constituents distinctly as
| (4) |
| (5) |
The peak equivalent strains for each loading cycle were thus
| (6) |
| (7) |
where h is the frequency and n is the number of loading cycles up to a maximum number of cycles, ntotm and ntotf. The number of cycles until failure (ntot) were defined for the matrix and fiber constituents distinctly as 26:
| (8) |
where α and β are material constants governing the amount of damage incurred by a single cycle at , and ψmin and ψmax, define the boundaries of the fatigue damage evolution zone. Note that α, β, ψmin and ψmax, were also defined for the matrix and fiber constituents distinctly. The total amount of damage due to stress softening, Ds, after n tensile loading cycles was defined as
| (9) |
The tissue permanent set, Dps, was considered to be due to damage to the isotropic matrix described by 27:
| (10) |
Here the matrix permanent set is scaled by the peak strain ratio, , to enforce anisotropy, where is the Green strain at in direction ij, and . The refers to the maximum permanent set Green strain associated with tensile failure of the material. The permanent set was enforced with a plastic stress, SP27
| (11) |
The SP contribution to the overall tissue response is governed by η in Eqn. 12, which was modified from Dorfmann and Ogden’s η function 10 in order to accommodate for the dissipated equivalent strain associated with the permanent set, Ξps, defined by Eqn. 13,
| (12) |
| (13) |
The second Piola-Kirchoff stress tensor may be expressed in the following reduced form:
| (14) |
Un-fatigued strain energy function
GLBP was assumed to be an incompressible, anisotropic, nonlinear, hyperelastic material 40, thus the un-fatigued strain energy was expressed by a fiber-reinforced hyperelastic material model based on the work of Holzapfel, Gasser et al. (2000) and Gasser, Ogden et al. (2006), given by
| (15) |
| (16) |
| (17) |
where I1,4,6 are the deviatoric strain invariants, c1,2 and k1,2 are the matrix and fiber parameters respectively, D is a material constant to enforce near compressibility, and J is the determinant of the deformation gradient. The fiber orientation is defined by Mi = m0i ⊗ m0i with m01=[cos θ,sinθ,0] and m02=[cosθ,−sinθ, 0], where θ is the angle between the 11 axis and the preferred fiber orientation.
Finite element modeling of TAVs
The finite element (FE) model of a generic size 23 mm TAV developed previously 25 was adopted for this study. Briefly, the TAV model consisted of 3 leaflets, each 0.25 mm thick similar to commercial TAV devices. Each leaflet was constructed from continuum large-strain brick elements in ABAQUS (Providence, RI) FE software. The local material orientations were defined for the leaflets at each element. The leaflet material properties were defined by the constitutive law, Eq. (14), which was incorporated into a user subroutine (UMAT) using the numerical approximation of tangent moduli method proposed by Sun et al 41. The un-fatigued GLBP leaflet material parameters were determined by fitting the biaxial testing data of GLBP valve leaflets presented by Sun 39, and the GLBP leaflet fatigue response was defined by the hypothetical GLBP fatigue parameters presented in our previous works 25–27. The amount of damage per simulated cycle was scaled up to reflect approximately 10x106 cycles real-time based on the fatigue model parameters. However, due to limited experimental data, the amount of damage at certain cycle states may not be accurate, and we use the variable, N, to nominalize the simulated cycle state. Although the precise timing of fatigue events cannot be predicted, through well-controlled side-by-side comparison, the effects of valve configuration on the durability can be assessed.
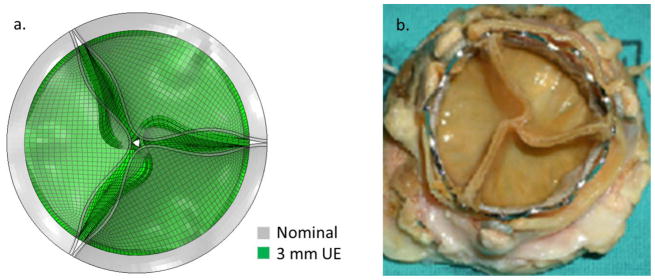
Cyclic diastolic closure of TAVs was simulated in two steps. First, the aortic side of the leaflets were slightly pressurized to 10% of the peak pressure (~12 mmHg) and the nodes along the leaflet stent-attachment lines were radially displaced towards the center of the valve by 0 mm, 0.5 mm, 1 mm, and 1.5 mm to uniformly reduce the valve radius along the whole height and achieve the nominal, and 1 mm, 2 mm, and 3 mm underexpanded (UE) cases respectively (Figure 1a). In a size 23 mm TAV with an internal diameter of 22 mm, these UE cases represent 4.5%, 9.1%, and 13.6% diameter underexpansion respectively. Note that 10% to 15% underexpansion is generally considered acceptable in clinical practice 16. Qualitatively, this approach resulted in realistic distortion of the leaflets (Figure 1b). The stent-attachment nodes were then fixed in space at this new location for the duration of the simulations to mimic attachment to a rigid stent. Then diastolic pressurization cycles from the minimum pressure of ~12 mmHg to a peak pressure of ~120 mmHg were applied to the aortic side of the leaflets to investigate the effects of repetitive loading.
Figure 1.
a) The 3 mm UE TAV FE model after inward radial displacement of the stent-attachment line overlaid with the nominal TAV model under minimum pressure. b) A failed explanted 26 mm Sapien XT TAV implanted in a 27 mm Carpentier-Edwards SAV (adapted from 3).
The simulation results (stress, strain, damage, etc.) were extracted for each loading cycle. Values from the elements along the stent-attachments were ignored to avoid potentially inaccurate boundary effects. The deformed valve geometries were imported into HyperMesh 12.0 (Altair HyperWorks, MI), for dimensional analysis. The leaflet coaptation area under the peak diastolic pressure of 120 mmHg was measured as the surface area of the contacting regions of adjacent leaflets. The degree of leaflet pin-wheeling upon valve closure was quantified in terms of the minimium bending radius (MBR) of the leaflet free edge per the methods proposed by Corden et al8. The leaflet MBR was also measured along the radial mid-line, the line bisecting the leaflet in the radial direction. Briefly, the deformed coordinates of the nodes along the leaflet free edge and radial mid-line were exported and used to generate spline curves using Matlab (Mathworks, MA). The central difference method was used to calculate the approximate derivatives of the spline curves in order to calculate the line curvatures and bending radii for each case.
RESULTS
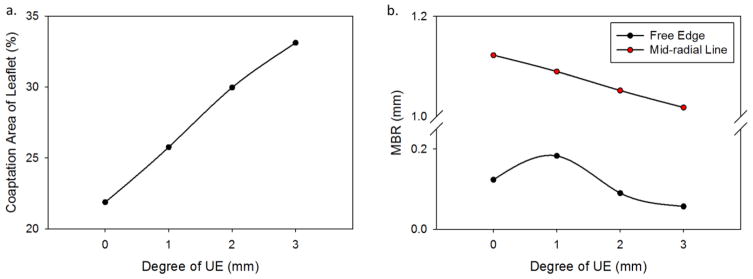
In each UE case, the leaflets exhibited leaflet redundancy and pin-wheeling upon valve closure (Figure 2b-d). The reduced valve area caused a nearly linear increase in the leaflet coaptation area with the degree of UE (Figure 3a). At the unfatigued state the coaptation increased from 21.9% of the leaflet area in the nominal case to 33.1% of the leaflet area in the 3 mm UE case. The coaptation areas increased slightly over fatigue cycling. The pin-wheeling effect also tended to increase the leaflet curvature at the free edge as shown by the decreased MBR at the free edge in the 2 mm and 3 mm UE cases (Figure 3b). The MBR was actually slightly higher at the free edge in the 1 mm UE case than the nominal, because the pin-wheeling effect was very minor. The MBR at the free edge tended to decrease slightly with continued cycling. The MBR along the radial mid-line also decreased with the degree of underexpansion because the leaflet redundancy caused the belly region to sag (Figure 3c). This effect worsened with fatigue as permanent set accumulated and the leaflets became larger.
Figure 2.
Leaflet coaptation upon full closure in the a) nominal, and b) 1 mm, c) 2 mm, and d) 3 mm stent diameter reduction cases overlaid with a circle of the original stent diameter (gray).
Figure 3.
a) The percent area of leaflet coaptation, b) the MBR of the leaflet free edge and radial mid-line versus the degree of underexpansion at the 0N state.
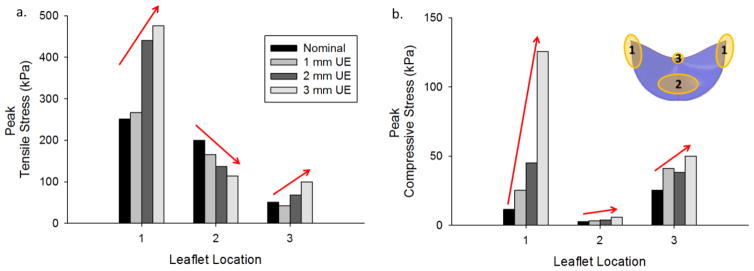
The peak leaflet stresses during closure along the commissures, belly, and nadir were compared for each case. The normalized peak stresses compared to the nominal case at the 0N state are shown in Figure 4, where regions 1, 2, and 3 in the leaflet diagram (Fig. 4b) correspond to the commissures, belly, and nadir respectively. The underexpanded configuration resulted in increased tensile stresses at the commissures and decreased tensile stresses in the belly region (Fig. 4a). The peak tensile stress was also increased in the 2 mm and 3 mm UE cases at the nadir compared to the nominal valve. The peak compressive stresses consistently increased in all regions of the leaflets with increasing degree of underexpansion (Fig. 4b). In the nominal and 1 mm UE cases the peak tensile stress was located at the commissures and the peak compressive stress was at the nadir due to coaptation. In the 2 mm and 3 mm UE cases the peak tensile and compressive stresses were both located near the commissures along the suture attachments due to significant leaflet bending in these regions.
Figure 4.
Peak a) tensile and b) compressive stress for each valve at the 0N state in different regions of the leaflet: 1) along commissures, 2) belly, and 3) nadir.
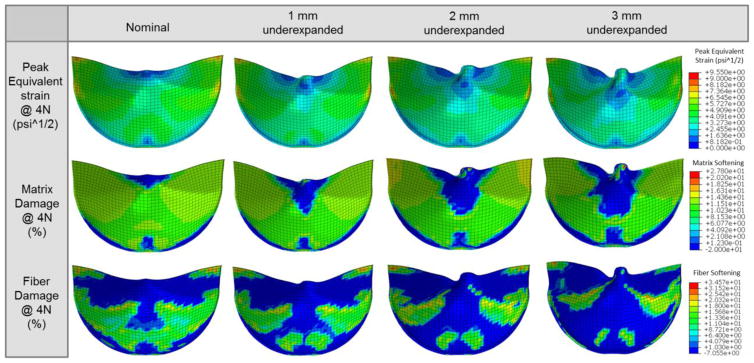
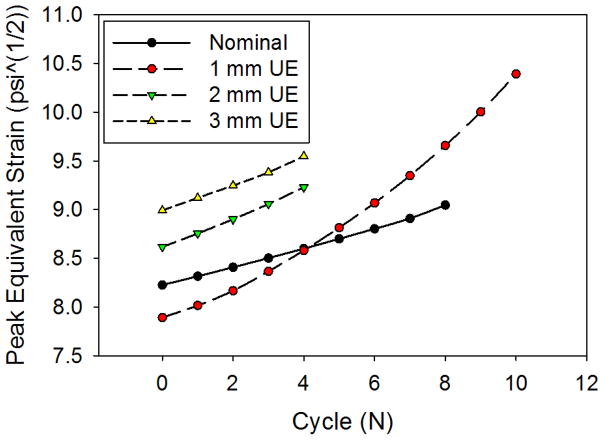
The nominal TAV had the most uniform peak equivalent strain distribution in the leaflets, which translated to the most uniform damage patterns for both the matrix and fiber components (Figure 5). In the UE cases, the overall damage area was reduced, but damage was accelerated at the free edge and suture attachments corresponding to the elevated stresses and equivalent strains in these regions. The damage became more concentrated with increasing degree of underexpansion, as the maximum peak equivalent strain values tended to increase (Figure 6). The overall peak equivalent strain was initially lowest in the 1 mm UE; however, surpassed that of the nominal valve at the 4N state (Figure 6). The maximum peak equivalent strain was initially located at the commissures in the nominal case, but shifted slightly downwards along the suture attachments at the 8N state. The maximum peak equivalent strains were located at this region along the suture attachments throughout each of the UE simulations. The maximum peak equivalent strain increased slightly more rapidly in each of the UE cases compared to the nominal fully expanded case with continued cycling.
Figure 5.
Contour plots of the peak equivalent strain and the matrix and fiber damage at the 4N cycle fatigued state for each case.
Figure 6.
The peak equivalent strain observed in the leaflets for each case and cycle.
DISCUSSION
There have been few quantitative studies on the effects of non-optimal deployment configurations on TAV mechanics. Sun et al. 42 used FE analysis to investigate the effect of elliptical stent deployment on TAV leaflet stresses and strains, which they found to be significantly increased compared to those in the nominal cylindrical stent. These simulation results were later confirmed by in vitro results reported by Gunning et al. 14, in which elliptically deployed TAVs were shown to have increased leaflet strains compared to nominally deployed valves particularly in the commissural regions. Abbasi and Azadani 1 have shown that TAV leaflet stresses and strains increase at the commissures in the underexpanded configuration as well due to sharp bending through FE analysis. Smuts et al. 38 have also used FE analysis to study the effects of leaflet design, mismatched leaflet properties, stent under and overexpansion, as well as asymmetric expansion, on the deformation of the leaflets under hypotensive (50 mmHg) pressurization. They showed that the leaflets will fold over each other in the 1 mm UE case, similar to our result. This is the first study to our knowledge which investigated TAV leaflet mechanics in the setting of stent underexpansion with the added effects of GLBP tissue fatigue.
Effect of TAV stent underexpansion on leaflet durability
The UE cases all exhibited leaflet redundancy, pin-wheeling, and sagging in the belly region upon closure, which lead to increasingly heterogeneous leaflet stress and peak equivalent strain distributions (Figs. 4 & 5). From the substantial compressive stresses (Fig. 4b) and leaflet curvatures in the UE valves (Fig. 3b&c), it is clear that tissue bending becomes a more significant loading condition during TAV closure in the UE configuration. The combination of increased coaptation and considerable leaflet pin-wheeling of the significantly underexpanded valves (≥ 2 mm), increased the leaflet free edge curvature (Fig. 3b), and resulted in stress concentrations and accelerated tissue fatigue damage at the nadirs (Fig. 5). This effect may have been exaggerated by the perfect valve symmetry assumed, which promotes pin-wheeling, whereas asymmetry, i.e. non-uniform underexpansion, may promote prolapse of one or more of the leaflets. Non-uniform expansion has been seen in patients with bicuspid aortic valves 30 particularly with self-expanding TAVs 18, 46, and could be caused by asymmetric SAV leaflet calcification in ViV procedures. The exaggerated leaflet sagging (Fig. 3c) and twisting in the UE cases also dramatically increased the peak leaflet stresses and equivalent strains at the suture attachments compared to the nominal case (Figs. 4 & 5), which is consistent with the increased commissural leaflet stresses and strains in underexpanded TAVs in 1. This finding was also in agreement with the results of our previous fatigue simulation study of SAVs, where valves that exhibited poor leaflet coaptation had accelerated damage along the suture attachments 27, and the clinical finding that poor coaptation is a predictor of poor durability in SAVs 45.
Although failure could not be simulated, the leaflet maximum peak equivalent strains in the 2 mm and 3 mm UE valves were significantly higher than those in the 1 mm UE and nominal cases at corresponding cycle states (Fig. 6). Although the peak equivalent strain was initially lower in the 1mm UE case than in the nominal case, it increased more rapidly with cycling and quickly surpassed that of the nominal case at the 4N state (Fig. 6). These results indicate that TAV underexpansion will compromise the durability of the leaflets, and that leaflet tissue fatigue damage accumulates faster with increasing degrees of underexpansion. In each of the UE cases, the maximum peak equivalent strain values were along the suture attachments just below the commissures (Fig. 5), thus, the expected mode of leaflet fatigue failure for TAVs in the ViV configuration is combined tension and flexure along the suture attachments. The maximum peak equivalent strain values in the nominal TAV leaflets were located at the commissures until the 8N fatigue state when the maximum value moved slightly further down suture attachment line. Therefore, TAVs in the fully expanded configuration are also expected to fail just below the commissures along the suture attachments, the known failure region of SAV leaflets 4, 32, 37, 44.
Clinical impacts
Clinically a range of 10% to 15% underexpansion is generally considered acceptable 16. All of the cases presented here fall within or below this range, with 3 mm of underexpansion representing only 13.6% underexpansion. The simulation results indicate that up to 5% underexpansion may be acceptable (1 mm underexpansion case), but beyond this level, leaflet tensile and compressive stresses may increase dramatically, which will compromise durability. Recent clinical results show that 50% of TAVs exhibit structural deterioration within 8 years, thus, the durability of severely underexpanded TAVs is likely less than 8 years 11. It is important to note that the degree of acceptable underexpansion is also likely dependent on the valve implantation depth and the valve design. A recent study by Simonato et al. 36 shows that higher TAV implantation height is associated with lower risk of elevated gradients because in this position, the TAV is able to expand more fully, and in turn, may increase durability. Thus, it is difficult to precisely predict the effect of TAV underexpansion on ViV durability which depends on many additional specific factors including: the SAV and TAV designs, mode of SAV failure, and TAV implantation height, etc. The leaflet curvature and coaptation areas at closure may be useful non-design specific indicators of the leaflet durability.
The results of this study suggest that the true inner diameter of a previous prosthesis is of critical importance in selecting an appropriately sized TAV. Knowing the labelled size of the SAV may not be enough: the mechanism of failure may also be of importance. Regurgitant valves with torn leaflets may have relatively larger inner diameters, while calcified or thrombosed valves may have smaller or asymmetric inner diameters 16. Conservative oversizing may also be justified in standard TAV procedures cases where the native aortic valve leaflets are heavily calcified and non-deformable. New TAV devices that are intentionally designed to be deployed within a prosthesis with a relatively larger central gap between the leaflets at the undeformed configuration may reduce the likelihood of paravalvular leak without negatively impacting the leaflet durability.
Limitations of this study
As in previous studies 25–27, a linear progression of the stress softening and permanent set parameters at a given equivalent strain as a function of the number of loading cycles was assumed, and the fatigue model parameters were not rigorously determined through experiments. The fatigue damage parameters for the matrix and fiber constituents were assumed to be equivalent. However, the equivalent strain threshold to induce fatigue for the fiber constituents is likely higher than that for the matrix, thus, the rate of matrix damage accumulation in the UE cases due to compressive stresses is likely underestimated. The lack of experimental validation of TAV fatigue damage patterns is a major limitation of this study. However, in a recent publication 25, we predicted TAVR durability to be approximately 8 years using this approach, which is in close agreement with new clinical TAVR results 11, indicating that this TAVR fatigue model can generate meaningful results. Such clinical data does not yet exist on how TAVR durability in suboptimal deployment configurations. Furthermore, although the amount of fatigue damage in each case presented here is dependent on the fatigue model parameters chosen, this approach is valid for studying the effects of TAV underexpansion on durability through well-controlled, side by side comparison.
It was difficult to obtain solution convergence particularly in the UE configurations due to the complicated and changing contact conditions between the leaflets; thus, complete leaflet tissue failure could not be simulated. Strategies to improve numerical stability should be developed in order to simulate more advanced fatigue states.
Cyclic valve opening was not simulated because we have recently shown that TAV leaflet peak equivalent strains are consistently lower during opening compared to closing, thus, opening would have a minimal impact on the leaflet tissue fatigue damage. However, clinicians have expressed concern about the valve leaflets hitting the stent during opening in the UE configuration 47. While this potential mode of damage was not modeled, this would likely exacerbate damage in the UE cases, particularly at the leaflet free edges.
Structural valve degeneration due to calcification was also not considered in this study, because the mechanism of calcification is currently not well understood. However, calcification tends to occur in the areas of high stress during function 31, so the fatigue damage areas for each case presented here may also represent areas most susceptible to calcification.
Conclusions
TAVs do not always fully expand clinically when deployed within either a heavily calcified native aortic valve or a non-compliant failed prosthesis in ViV procedures. It has been shown that the configuration of the leaflets may be altered when the TAV stent is underexpanded 51, which has been hypothesized to limit the device durability 7, 16, 47. In this study, a computational tissue fatigue damage framework developed previously 25–27 was applied to investigate the effect of TAV underexpansion on the durability of the GLBP leaflets. The simulation results show that TAV underexpansion by ≥ 2mm results in significantly higher tensile and compressive leaflet stresses which will ultimately limit the durability of the leaflets, while slight underexpansion (1 mm) has a minimal effect on the leaflet durability. However, the degree of acceptable underexpansion will likely depend on the particular valve design. The results of this study warrant further investigation of ViV mechanics.
Acknowledgments
Research for this project was funded in part by NIH HL104080 and HL108240 grants and a NIH F31 HL112632 predoctoral fellowship.
Footnotes
CONFLICTS OF INTEREST
None.
References
- 1.Abbasi M, Azadani AN. Leaflet stress and strain distributions following incomplete transcatheter aortic valve expansion. Journal of Biomechanics. 2015;48:3663–3671. doi: 10.1016/j.jbiomech.2015.08.012. [DOI] [PubMed] [Google Scholar]
- 2.Azadani AN, Tseng EE. Transcatheter Heart Valves for Failing Bioprostheses: State-of-the-Art Review of Valve-in-Valve Implantation. Circulation: Cardiovascular Interventions. 2011;4:621–628. doi: 10.1161/CIRCINTERVENTIONS.111.964478. [DOI] [PubMed] [Google Scholar]
- 3.Bruschi G, Botta L, Fratto P, Martinelli L. Failed valve-in-valve transcatheter mitral valve implantation. Eur J Cardiothorac Surg. 2014;45:e127. doi: 10.1093/ejcts/ezt633. [DOI] [PubMed] [Google Scholar]
- 4.Butany J, Nair V, Leong SW, Soor GS, Feindel C. Carpentier-Edwards Perimount Valves Morphological Findings in Surgical Explants. Journal of Cardiac Surgery. 2007;22:7–12. doi: 10.1111/j.1540-8191.2007.00336.x. [DOI] [PubMed] [Google Scholar]
- 5.Chen HL, Liu K. Clinical outcomes for transcatheter valve-in-valve in treating surgical bioprosthetic dysfunction: A meta-analysis. Int J Cardiol. 2016;212:138–141. doi: 10.1016/j.ijcard.2016.03.024. [DOI] [PubMed] [Google Scholar]
- 6.Chevalier F, Leipsic J, Genereux P. Valve-in-Valve Implantation With a 23-mm Balloon-Expandable Transcatheter Heart Valve for the Treatment of a 19-mm Stentless Bioprosthesis Severe Aortic Regurgitation Using a Strategy of “Extreme” Underfilling. Catheterization and Cardiovascular Interventions. 2014;84:503–508. doi: 10.1002/ccd.25381. [DOI] [PubMed] [Google Scholar]
- 7.Chevalier F, Leipsic J, Généreux P. Valve-in-valve implantation with a 23-mm balloon-expandable transcatheter heart valve for the treatment of a 19-mm stentless bioprosthesis severe aortic regurgitation using a strategy of “extreme” underfilling. Catheterization and Cardiovascular Interventions. 2014 doi: 10.1002/ccd.25381. n/a-n/a. [DOI] [PubMed] [Google Scholar]
- 8.Corden J, David T, Fisher J. Determination of the Curvatures and Bending Strains in Open Trileaflet Heart Valves. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 1995;209:121–128. doi: 10.1243/PIME_PROC_1995_209_329_02. [DOI] [PubMed] [Google Scholar]
- 9.Cribier A, Eltchaninoff H, Bash A, Borenstein N, Tron C, Bauer F, Derumeaux G, Anselme F, Laborde F, Leon MB. Percutaneous transcatheter implantation of an aortic valve prosthesis for calcific aortic stenosis: first human case description. Circulation. 2002;106:3006–3008. doi: 10.1161/01.cir.0000047200.36165.b8. [DOI] [PubMed] [Google Scholar]
- 10.Dorfmann A, Ogden RW. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. International Journal of Solids and Structures. 2004;41:1855–1878. [Google Scholar]
- 11.Dvir D, Eltchaninoff H, Ye J, Kan A, Durand E, Bizios A, Cheung A, Aziz M, Simonato M, Tron C, Arbel Y, Moss R, Leipsic J, Ofek H, Perlman G, Barbanti M, Seidman MA, Blanke P, Yao R, Boone R, Lauck S, Lichtenstein S, Wood D, Cribier A, Webb JG. First look at long-term durability of transcatheter heart valves: Assessment of valve function up to 10-years after implantation. Euro PCR; 2016; Paris, France. 2016. [Google Scholar]
- 12.Dvir D, Webb JG, Bleiziffer S, Pasic M, Waksman R, Kodali S, Barbanti M, Latib A, Schaefer U, Rodes-Cabau J, Treede H, Piazza N, Hildick-Smith D, Himbert D, Walther T, Hengstenberg C, Nissen H, Bekeredjian R, Presbitero P, Ferrari E, Segev A, de Weger A, Windecker S, Moat NE, Napodano M, Wilbring M, Cerillo AG, Brecker S, Tchetche D, Lefevre T, De Marco F, Fiorina C, Petronio AS, Teles RC, Testa L, Laborde JC, Leon MB, Kornowski R I Valve-in-Valve International Data Registry. Transcatheter aortic valve implantation in failed bioprosthetic surgical valves. JAMA. 2014;312:162–170. doi: 10.1001/jama.2014.7246. [DOI] [PubMed] [Google Scholar]
- 13.Faerber G, Schleger S, Diab M, Breuer M, Figulla H, Eichinger W, Doenst T. Valve-in-valve transcatheter aortic valve implantation: the new playground for prothesis-patient mismatch. J Interv Cardiol. 2014 Mar 10; doi: 10.1111/joic.12108. [DOI] [PubMed] [Google Scholar]
- 14.Gunning PS, Saikrishnan N, Yoganathan AP, McNamara LM. Total ellipse of the heart valve: The impact of eccentric stent distortion on the regional dynamic deformation of pericardial tissue leaflets of a transcatheter aortic valve replacement. Journal of The Royal Society Interface. 2015;12 doi: 10.1098/rsif.2015.0737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gunning PS, Vaughan TJ, McNamara LM. Simulation of self expanding transcatheter aortic valve in a realistic aortic root: implications of deployment geometry on leaflet deformation. Annals of Biomedical Engineering. 2014;42:1989–2001. doi: 10.1007/s10439-014-1051-3. [DOI] [PubMed] [Google Scholar]
- 16.Gurvitch R, Cheung A, Ye J, Wood DA, Willson AB, Toggweiler S, Binder R, Webb JG. Transcatheter Valve-in-Valve Implantation for Failed Surgical Bioprosthetic Valves. Journal of the American College of Cardiology. 2011;58:2196–2209. doi: 10.1016/j.jacc.2011.09.009. [DOI] [PubMed] [Google Scholar]
- 17.Harbaoui B, Courand PY, Schmitt Z, Farhat F, Dauphin R, Lantelme P. Early Edwards SAPIEN Valve Degeneration After Transcatheter Aortic Valve Replacement. JACC Cardiovasc Interv. 2016;9:198–199. doi: 10.1016/j.jcin.2015.09.034. [DOI] [PubMed] [Google Scholar]
- 18.Himbert D, Pontnau F, Messika-Zeitoun D, Descoutures F, Détaint D, Cueff C, Sordi M, Laissy JP, Alkhoder S, Brochet E, Iung B, Depoix JP, Nataf P, Vahanian A. Feasibility and Outcomes of Transcatheter Aortic Valve Implantation in High-Risk Patients With Stenotic Bicuspid Aortic Valves. The American Journal of Cardiology. 2012;110:877–883. doi: 10.1016/j.amjcard.2012.04.064. [DOI] [PubMed] [Google Scholar]
- 19.John D, Buellesfeld L, Yuecel S, Mueller R, Latsios G, Beucher H, Gerckens U, Grube E. Correlation of Device Landing Zone Calcification and Acute Procedural Success in Patients Undergoing Transcatheter Aortic Valve Implantations With the Self-Expanding CoreValve Prosthesis. JACC: Cardiovascular Interventions. 2010;3:233–243. doi: 10.1016/j.jcin.2009.11.015. [DOI] [PubMed] [Google Scholar]
- 20.Kiefer P, Seeburger J, Chu MW, Ender J, Vollroth M, Noack T, Mohr FW, Holzhey DM. Reoperative transapical aortic valve implantation for early structural valve deterioration of a SAPIEN XT valve. Ann Thorac Surg. 2013;95:2169–2170. doi: 10.1016/j.athoracsur.2012.10.072. [DOI] [PubMed] [Google Scholar]
- 21.Klotz S, Scharfschwerdt M, Richardt D, Sievers HH. Failed valve-in-valve transcatheter aortic valve implantation. JACC Cardiovasc Interv. 2012;5:591–592. doi: 10.1016/j.jcin.2012.01.022. [DOI] [PubMed] [Google Scholar]
- 22.Koos R, Mahnken AH, Dohmen G, Brehmer K, Günther RW, Autschbach R, Marx N, Hoffmann R. Association of aortic valve calcification severity with the degree of aortic regurgitation after transcatheter aortic valve implantation. International Journal of Cardiology. 2011;150:142–145. doi: 10.1016/j.ijcard.2010.03.004. [DOI] [PubMed] [Google Scholar]
- 23.Leber AW, Kasel M, Ischinger T, Ebersberger UH, Antoni D, Schmidt M, Riess G, Renz V, Huber A, Helmberger T, Hoffmann E. Aortic valve calcium score as a predictor for outcome after TAVI using the CoreValve revalving system. Int J Cardiol. 2013;166:652–657. doi: 10.1016/j.ijcard.2011.11.091. [DOI] [PubMed] [Google Scholar]
- 24.Leon MB, Smith CR, Mack M, Miller DC, Moses JW, Svensson LG, Tuzcu EM, Webb JG, Fontana GP, Makkar RR, Brown DL, Block PC, Guyton RA, Pichard AD, Bavaria JE, Herrmann HC, Douglas PS, Petersen JL, Akin JJ, Anderson WN, Wang D, Pocock S. Transcatheter Aortic-Valve Implantation for Aortic Stenosis in Patients Who Cannot Undergo Surgery. New England Journal of Medicine. 2010;363:1597–1607. doi: 10.1056/NEJMoa1008232. [DOI] [PubMed] [Google Scholar]
- 25.Martin C, Sun W. Comparison of transcatheter aortic valve and surgical bioprosthetic valve durability: A fatigue simulation study. J Biomech. 2015;48:3026–3034. doi: 10.1016/j.jbiomech.2015.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Martin C, Sun W. Modeling of long-term fatigue damage of soft tissue with stress softening and permanent set effects. Biomech Model Mechanobiol. 2013;12:645–655. doi: 10.1007/s10237-012-0431-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Martin C, Sun W. Simulation of long-term fatigue damage in bioprosthetic heart valves: effects of leaflet and stent elastic properties. Biomech Model Mechanobiol. 2014;13:759–770. doi: 10.1007/s10237-013-0532-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Milburn K, Bapat V, Thomas M. Valve-in-valve implantations: is this the new standard for degenerated bioprostheses? Review of the literature. Clinical Research in Cardiology. 2014:1–13. doi: 10.1007/s00392-013-0653-3. [DOI] [PubMed] [Google Scholar]
- 29.Muñoz-García AJ, Alonso-Briales JH, Jiménez-Navarro MF, Caballero-Borrego J, Domínguez-Franco AJ, Rodríguez-Bailón I, Such-Martínez M, Hernández-García JM, de Teresa-Galván E. Mechanisms, treatment and course of paravalvular aortic regurgitation after percutaneous implantation of the CoreValve aortic prosthesis. International Journal of Cardiology. 2011;149:389–392. doi: 10.1016/j.ijcard.2011.03.011. [DOI] [PubMed] [Google Scholar]
- 30.Perlman GY, Blanke P, Dvir D, Pache G, Modine T, Barbanti M, Holy EW, Treede H, Ruile P, Neumann FJ, Gandolfo C, Saia F, Tamburino C, Mak G, Thompson C, Wood D, Leipsic J, Webb JG. Bicuspid Aortic Valve Stenosis: Favorable Early Outcomes With a Next-Generation Transcatheter Heart Valve in a Multicenter Study. JACC: Cardiovascular Interventions. 2016;9:817–824. doi: 10.1016/j.jcin.2016.01.002. [DOI] [PubMed] [Google Scholar]
- 31.Schoen FJ, Fernandez J, Gonzalez-Lavin L, Cernaianu A. Causes of failure and pathologic findings in surgically removed Ionescu-Shiley standard bovine pericardial heart valve bioprostheses: emphasis on progressive structural deterioration. Circulation. 1987;76:618–627. doi: 10.1161/01.cir.76.3.618. [DOI] [PubMed] [Google Scholar]
- 32.Schoen FJ, Levy RJ. Tissue heart valves: Current challenges and future research perspectives. Journal of Biomedical Materials Research. 1999;47:439–465. doi: 10.1002/(sici)1097-4636(19991215)47:4<439::aid-jbm1>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 33.Schultz CJ, Weustink A, Piazza N, Otten A, Mollet N, Krestin G, van Geuns RJ, de Feyter P, Serruys PWJ, de Jaegere P. Geometry and Degree of Apposition of the CoreValve ReValving System With Multislice Computed Tomography After Implantation in Patients With Aortic Stenosis. Journal of the American College of Cardiology. 2009;54:911–918. doi: 10.1016/j.jacc.2009.04.075. [DOI] [PubMed] [Google Scholar]
- 34.Shalabi A, Spiegelstein D, Sternik L, Feinberg MS, Kogan A, Levin S, Orlov B, Nachum E, Lipey A, Raanani E. Sutureless Versus Stented Valve in Aortic Valve Replacement in Patients With Small Annulus. The Annals of Thoracic Surgery. 2016;102:118–122. doi: 10.1016/j.athoracsur.2016.01.003. [DOI] [PubMed] [Google Scholar]
- 35.Simo JC. On a fully three-dimensional finite-strain viscoelastic damage model: Formulation and computational aspects. Computer Methods in Applied Mechanics and Engineering. 1987;60:153–173. [Google Scholar]
- 36.Simonato M, Webb J, Kornowski R, Vahanian A, Frerker C, Nissen H, Bleiziffer S, Duncan A, Rodes-Cabau J, Attizzani GF, Horlick E, Latib A, Bekeredjian R, Barbanti M, Lefevre T, Cerillo A, Hernandez JM, Bruschi G, Spargias K, Iadanza A, Brecker S, Palma JH, Finkelstein A, Abdel-Wahab M, Lemos P, Petronio AS, Champagnac D, Sinning JM, Salizzoni S, Napodano M, Fiorina C, Marzocchi A, Leon M, Dvir D. Transcatheter Replacement of Failed Bioprosthetic Valves: Large Multicenter Assessment of the Effect of Implantation Depth on Hemodynamics After Aortic Valve-in-Valve. Circ Cardiovasc Interv. 2016;9 doi: 10.1161/CIRCINTERVENTIONS.115.003651. [DOI] [PubMed] [Google Scholar]
- 37.Singhal P, Luk A, Butany J. Bioprosthetic Heart Valves: Impact of Implantation on Biomaterials. ISRN Biomaterials. 2013;2013:1–14. [Google Scholar]
- 38.Smuts AN, Blaine DC, Scheffer C, Weich H, Doubell AF, Dellimore KH. Application of finite element analysis to the design of tissue leaflets for a percutaneous aortic valve. Journal of the Mechanical Behavior of Biomedical Materials. 2011;4:85–98. doi: 10.1016/j.jmbbm.2010.09.009. [DOI] [PubMed] [Google Scholar]
- 39.Sun W. Department of Bioengineering. Pittsburgh: University of Pittsburgh; 2003. Biomechanical simulations of heart valve biomaterials; p. 240. [Google Scholar]
- 40.Sun W, Abad A, Sacks MS. Simulated Bioprosthetic Heart Valve Deformation under Quasi-Static Loading. Journal of Biomechanical Engineering. 2005;127:905–914. doi: 10.1115/1.2049337. [DOI] [PubMed] [Google Scholar]
- 41.Sun W, Chaikof EL, Levenston ME. Numerical approximation of tangent moduli for finite element implementations of nonlinear hyperelastic material models. Journal of Biomechanical Engineering. 2008;130:061003. doi: 10.1115/1.2979872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sun W, Li K, Sirois E. Simulated elliptical bioprosthetic valve deformation: Implications for asymmetric transcatheter valve deployment. Journal of Biomechanics. 2010;43:3085–3090. doi: 10.1016/j.jbiomech.2010.08.010. [DOI] [PubMed] [Google Scholar]
- 43.Sun W, Li K, Sirois E. Simulated elliptical bioprosthetic valve deformation: implications for asymmetric transcatheter valve deployment. J Biomech. 2010;43:3085–3090. doi: 10.1016/j.jbiomech.2010.08.010. [DOI] [PubMed] [Google Scholar]
- 44.Trowbridge EA, Crofts CE. Pericardial heterograft valves: an assessment of leaflet stresses and their implications for heart valve design. J Biomech Eng. 1987;9:345–355. doi: 10.1016/0141-5425(87)90084-7. [DOI] [PubMed] [Google Scholar]
- 45.Vesely I. The Influence of Design on Bioprosthetic Valve Durability. 2001;11:13. [PubMed] [Google Scholar]
- 46.Watanabe Y, Chevalier B, Hayashida K, Leong T, Bouvier E, Arai T, Farge A, Hovasse T, Garot P, Cormier B, Morice MC, Lefèvre T. Comparison of multislice computed tomography findings between bicuspid and tricuspid aortic valves before and after transcatheter aortic valve implantation. Catheterization and Cardiovascular Interventions. 2015;86:323–330. doi: 10.1002/ccd.25830. [DOI] [PubMed] [Google Scholar]
- 47.Webb JG, Dvir D. Transcatheter aortic valve replacement for bioprosthetic aortic valve failure: the valve-in-valve procedure. Circulation. 2013;127:2542–2550. doi: 10.1161/CIRCULATIONAHA.113.000631. [DOI] [PubMed] [Google Scholar]
- 48.Webb JG, Wood DA, Ye J, Gurvitch R, Masson JB, Rodés-Cabau J, Osten M, Horlick E, Wendler O, Dumont E, Carere RG, Wijesinghe N, Nietlispach F, Johnson M, Thompson CR, Moss R, Leipsic J, Munt B, Lichtenstein SV, Cheung A. Transcatheter Valve-in-Valve Implantation for Failed Bioprosthetic Heart Valves. Circulation. 2010;121:1848–1857. doi: 10.1161/CIRCULATIONAHA.109.924613. [DOI] [PubMed] [Google Scholar]
- 49.Willson A, Webb J, LaBounty T, Achenbach S, Moss R, Wheeler M, Thompson C, Min J, Gurvitch R, Norgard B, Toggweiler S, Binder RK, Hague C, Freeman M, Poulter SH, Poulter R, Wood D, Jonathon L. Three-Dimensional Aortic Annular Assessment by Multidetector Computed Tomography Predicts Moderate or Severe Paravalvular Regurgitation after Transcatheter Aortic Valve Replacement: A Multicenter Retrospective Analysis. Journal of the American College of Cardiology. 2012;59:E325. doi: 10.1016/j.jacc.2011.12.015. [DOI] [PubMed] [Google Scholar]
- 50.Willson AB, Webb JG, Gurvitch R, Wood DA, Toggweiler S, Binder R, Freeman M, Madden M, Hague C, Leipsic J. Structural integrity of balloon-expandable stents after transcatheter aortic valve replacement: assessment by multidetector computed tomography. JACC Cardiovasc Interv. 2012;5:525–532. doi: 10.1016/j.jcin.2012.03.007. [DOI] [PubMed] [Google Scholar]
- 51.Zegdi R, Ciobotaru V, Noghin M, Sleilaty G, Lafont A, Latrémouille C, Deloche A, Fabiani J-N. Is It Reasonable to Treat All Calcified Stenotic Aortic Valves With a Valved Stent?: Results From a Human Anatomic Study in Adults. Journal of the American College of Cardiology. 2008;51:579–584. doi: 10.1016/j.jacc.2007.10.023. [DOI] [PubMed] [Google Scholar]