Spatial representations of granule cells and mossy cells of the dentate gyrus

Summary

Granule cells in the dentate gyrus of the hippocampus are thought to be essential to memory function by decorrelating overlapping input patterns (pattern separation). A second excitatory cell type in the dentate gyrus, the mossy cell, forms an intricate circuit with granule cells, CA3c pyramidal cells, and local interneurons, but the influence of mossy cells on dentate function is often overlooked. Multiple tetrode recordings, supported by juxtacellular recording techniques, showed that granule cells fired very sparsely, whereas mossy cells in the hilus fired promiscuously in multiple locations and in multiple environments. The activity patterns of these cell types thus represent different environments through distinct computational mechanisms: sparse coding in granule cells and changes in firing field locations in mossy cells.

eTOC Blurb

Using tetrode and juxtacellular recordings, GoodSmith et al. demonstrate distinct spatial firing and remapping properties of excitatory cell types within the dentate gyrus and CA3c and assess how these cells may support pattern separation in the dentate-CA3 circuit.

Introduction

One of the key goals of systems neuroscience is to understand specific neural circuits in terms of anatomical connectivity and computational functions of the individual cell types in those circuits. Local circuits within a small brain volume present a particular challenge to this goal when the circuits are probed with extracellular, electrophysiological techniques in freely moving animals. The inability of such techniques to identify which particular neuronal types generate which particular spikes creates a major obstacle to relating the neural correlates of single units during freely moving behavior to the exquisite circuitry revealed by anatomical studies and the sophisticated computational models inspired by the anatomy and cellular physiology.

The simple, laminated structure of the hippocampus provides a prime system that is amenable to such analyses. The dentate gyrus (DG) is the only region of the hippocampus that contains two distinct, excitatory cell types. Granule cells, located in the densely packed granule cell layer (GCL), are by far the most numerous cell type in the DG (Amaral et al., 1990). Mossy cells, located in the subjacent hilus, are the second excitatory cell type (Amaral, 1978). In the classic notion of hippocampal circuitry, the DG granule cells are the first processing stage of the “trisynaptic loop,” receiving inputs from the entorhinal cortex and sending projections to the CA3 region. Modern techniques have revealed a more complex circuitry, with the mossy cell occupying a pivotal node mediating both a disynaptic, recurrent processing loop within the DG as well as a disynaptic feedback loop from the CA3 region back to the DG granule layer (Figure 1A; Scharfman, 1994; Scharfman, 2007; Myers and Scharfman, 2009).

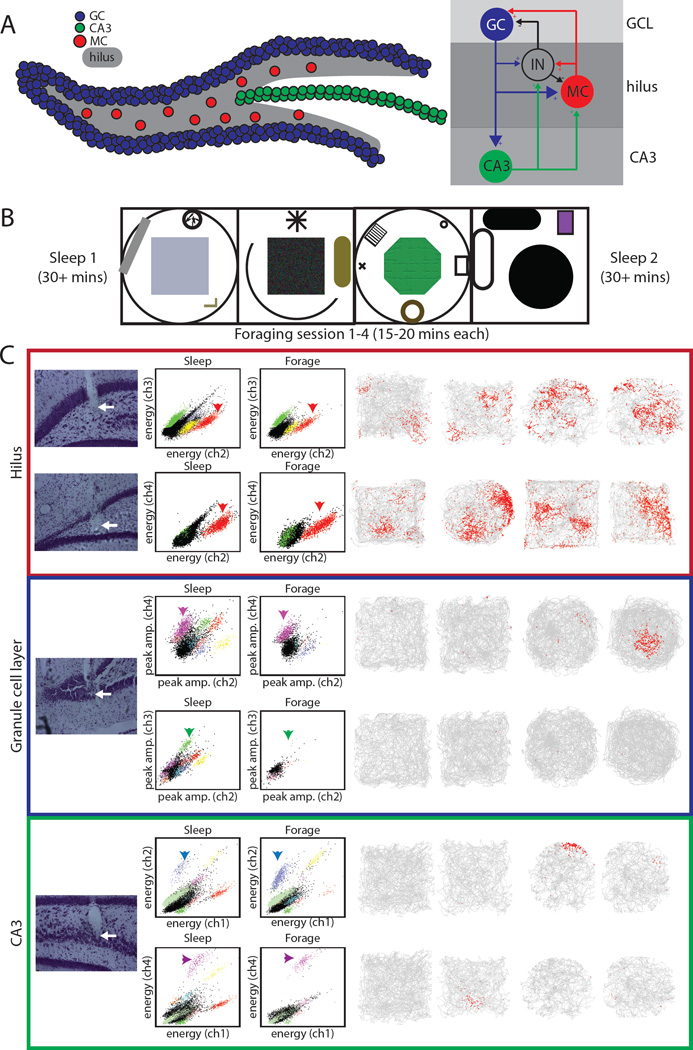
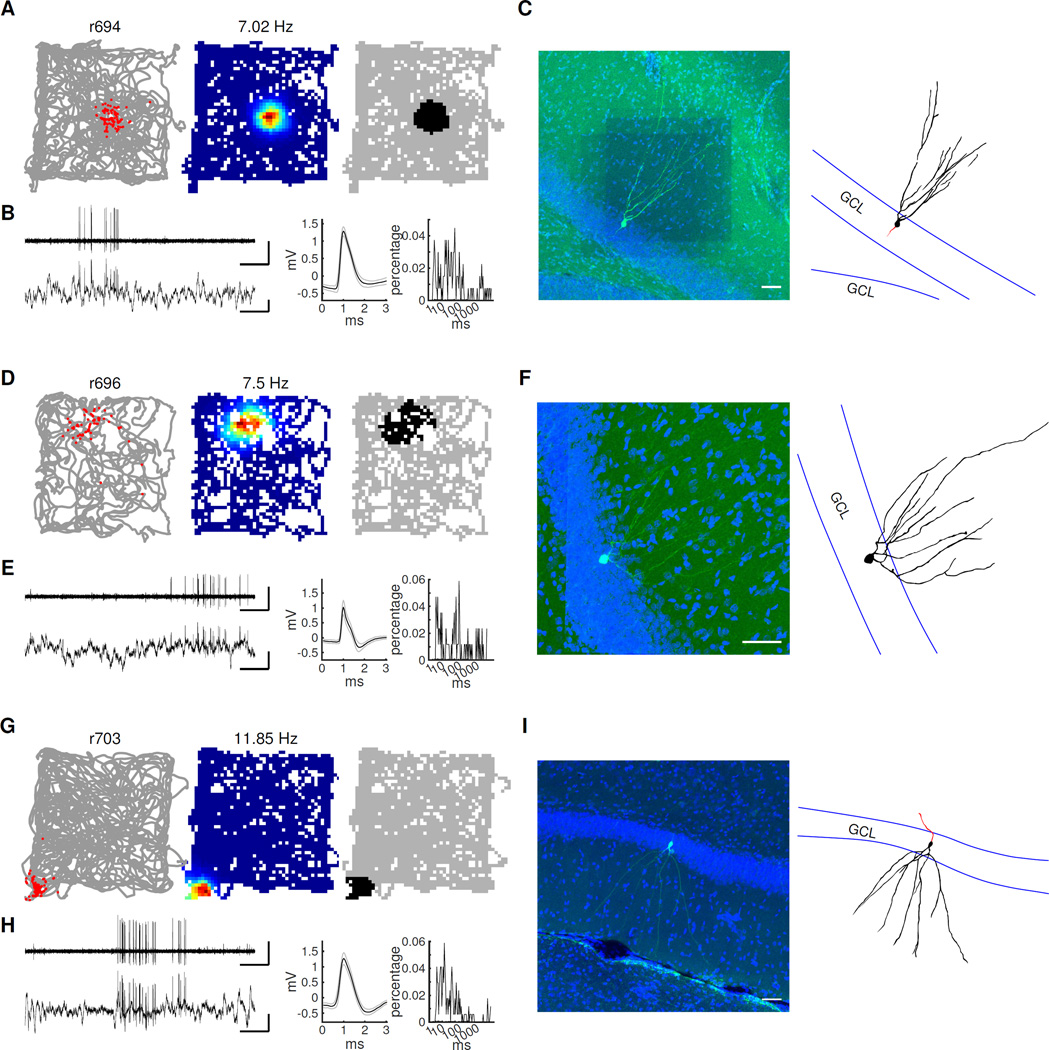
Figure 1. DG circuit, experimental design, and example cells recorded in the GCL, hilus, and CA3.

A) Schematic of the DG (left) with granule cells (blue), CA3 cells (green), and mossy cells (red) in the hilus (shaded). To the right is a simplified diagram of the numerous connections between these cell types and dentate interneurons. B) Schematic of experimental procedure including sleep sessions and four foraging sessions in 4 distinct rooms. C) Example cells recorded on the final day from tetrodes located clearly in the hilus (top), GCL (middle), and CA3 (bottom). For each cell, the deepest point of the tetrode track is shown (left, marked by arrows). In the GCL and CA3, both example cells were recorded on the same tetrode. One cluster projection is shown for each cell (middle) in both the post-behavior sleep session and during one foraging session. Note that cells in the hilus tended to be active during both sleep and behavior (dense clusters in both projections), whereas cells in the GCL and CA3 tended to be more active during sleep with only a fraction active during behavior. The firing of the cell in all four sessions is shown on the right. For each session, the grey line represents the rat’s trajectory, with the location of spikes plotted in red. The two cells in the hilus had multiple fields in multiple rooms, whereas the cells in the GCL and CA3 were mostly silent in most environments, and they had a single field in one room when they were active.

CA3 is thought to mediate memory storage and retrieval of full patterns from partial or degraded cues, a process termed pattern completion (McClelland and Goddard, 1996; O’Reilly and McClelland, 1994). However, the storage capacity of such a distributed memory system is limited and susceptible to interference if the stored patterns are too similar to each other (McNaughton and Morris, 1987; Rolls, 2013). The DG is thought to perform a complementary pattern separation computation, receiving overlapping inputs from entorhinal cortex and sending less correlated outputs to CA3 (Yassa and Stark, 2011; Neunuebel and Knierim, 2014). Early computational models of DG pattern separation, inspired by Marr’s “expansion recoding” theory of the cerebellar granule layer (Marr, 1969), suggested a particular mechanism of pattern separation in which overlapping entorhinal input patterns are projected onto the larger, sparsely firing population of dentate granule cells, thereby recruiting ensembles of active granule cells that have reduced overlap compared to the entorhinal inputs (McNaughton and Morris, 1987; McNaughton and Nadel, 1990; Rolls and Treves, 1998; Hasselmo and Wyble, 1997). The DG patterns were then imposed on the CA3 network by the powerful DG-CA3 synapses.

Although accumulating evidence strongly supports the role of the DG in pattern separation (Neunuebel and Knierim, 2014; Hunsaker et al., 2008; Nakashiba et al., 2012; Yassa and Stark, 2011; Rolls and Kesner, 2006), the precise computational and circuit mechanisms underlying this role remain under debate. In particular, the “expansion recoding” mechanism of DG pattern separation was challenged by the finding that cells recorded in the DG often have multiple place fields in a single environment and fire promiscuously in multiple environments, rather than being sparsely active and selective for a small fraction of environments (Jung and McNaughton, 1993; Leutgeb et al., 2007; Alme et al., 2010). This type of firing could still support pattern separation, but by an entirely different mechanism in which an active population discriminates environments based on changes in the spatial or temporal coincidence of firing, rather than the sparse activation of discrete subsets of cells (Leutgeb et al., 2007). Both single- and multiple-field cells can be recorded from the DG (Jung and McNaughton, 1993; Leutgeb et al., 2007), and recent evidence suggested that the multiple-field cells may be confined to the hilus (Neunuebel and Knierim, 2012). Nonetheless, limitations in the data reported in the latter study made it uncertain whether these response types represent the firing of distinct, anatomically defined cell types and how these cells would fire in multiple environments.

We recorded excitatory cells from the GCL, hilus, and CA3 while rats foraged for food in four distinct environments. Cells recorded in the GCL rarely fired during behavior and typically had single place fields in a single environment when active. In contrast, cells recorded in the hilus were active in all or most environments and usually had multiple firing fields. Juxtacellular recordings from identified granule cells and mossy cells suggest that the single-field cells recorded in the GCL correspond to granule cells and multiple-field cells recorded in the hilus correspond to mossy cells. As unique populations of putative granule cells were active in each environment, this result supports classic models of DG pattern separation (Marr, 1969; McNaughton and Morris, 1987; Rolls and Treves, 1998), while the firing of mossy cells may support pattern separation through changes in coincident firing (Leutgeb et al., 2007), demonstrating two modes of pattern separation in the distinct excitatory cell components of the same computational circuit in the DG.

Results

Spatial firing properties of cells in the GCL, hilus, and CA3

Single unit activity was recorded from the DG (GCL and hilus) and CA3 of 8 adult rats as they foraged for food in four distinct environments. Each of the four environments was in a different room, with distinct visual cues, on a platform with different shape, color, and/or texture (Figure 1B). The firing rates of granule cells when the rat was not asleep were extremely low (in some cases, zero spikes were recorded in > 15 minutes of awake resting; Figure S2, video S1). It was therefore essential to record long periods of sleep in order to identify granule cells, as it was otherwise easy to move electrodes through the GCL without recording any cells (Jung and McNaughton, 1993; Skaggs et al., 1996; Neunuebel and Knierim, 2012).

To minimize ambiguity in the recording location for each tetrode, rats were perfused on the final day of recording and only well-isolated cells recorded on the final day were analyzed initially. We excluded putative interneurons (Figure S3) and cells recorded on tetrodes that did not show, upon histological examination, tracks that ended clearly in the GCL, hilus, or CA3 (Figure 1C, S1). With these criteria, 37, 23, and 28 cells from 12, 10, and 5 tetrodes located clearly in the GCL, hilus, and CA3, respectively, were selected for initial analysis. These cells came from 4 (GCL), 5 (hilus), and 2 (CA3) rats, since the strict selection criteria excluded many cells from this initial analysis. This selection process was completely independent of any of the spatial firing properties analyzed below.

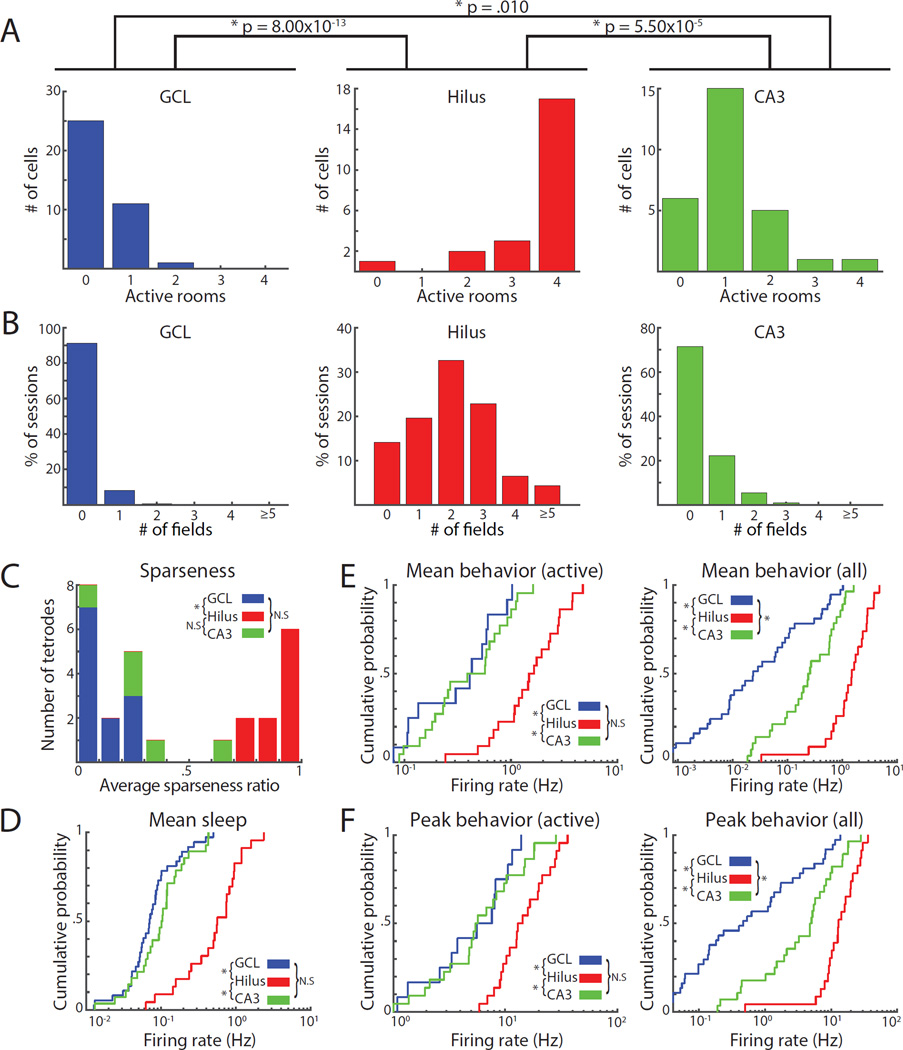
Overall, the number of environments in which cells had a place field was higher in the hilus than the GCL or CA3 (GCL: 0.35 ± 0.09; hilus: 3.52 ± 0.21; CA3: 1.14 ± 0.18; Kruskal-Wallis test across all 3 areas, p = 2.48 × 10⁻¹²; Dunn’s tests: hilus vs. GCL, p = 8.00 × 10⁻¹³; hilus vs. CA3, p = 5.50 × 10⁻⁵; GCL vs. CA3, p = .010) (Figure 2A). The majority of cells recorded in the GCL (25/37) were silent in all four environments. The proportion of silent cells in the GCL was significantly higher than the proportion in either the hilus (1/23) or CA3 (6/28) (Figure 2A; overall: χ² = 28.45, p = 6.62 × 10^−7; GCL vs. hilus: χ² = 23.09, p = 4.65 × 10⁻⁶; GCL vs. CA3: χ² = 13.60, p = 6.77 × 10⁻⁴). Only one cell in the GCL was active in more than one room, whereas the majority of cells in the hilus (17/23) were active in all four environments. Averaged over all 4 environments, only 9% of cells in the GCL were active in a given environment, compared to 88% of cells in the hilus and 29% of CA3 cells.

Figure 2. Spatial firing of cells recorded on the final day of recording and on tetrodes located clearly in the GCL, hilus, or CA3.

A) Number of rooms with place fields for cells in the GCL (left), hilus (middle), and CA3 (right). B) Number of fields in each recording session. Each cell contributed four values (one for each session). C) Histogram of average sparseness ratio for each tetrode. A value of 1 means that all cells on the tetrode were active in all rooms; values near 0 mean that most cells were silent. D) Cumulative density function (CDF) of the mean firing rates of cells during sleep. Cells in the hilus had higher mean firing rates than cells in the GCL or CA3. E-F) CDF of mean firing rates (E) and peak firing rates (F) in the most active room for cells with a field in at least one environment (left) or all cells (right).

Cells in the hilus were more likely than cells in the GCL or CA3 to have multiple firing fields in a given recording session (Figure 2B). Because each cell contributed 4 data points to Figure 2B (one for each environment), for statistical testing we calculated the average number of place fields for each cell that was active in at least one room (total fields across all environments / # of active environments). Cells in the hilus had a higher average number of place fields (2.26 ± 0.14) than cells in the GCL (1.04 ± 0.04) or CA3 (1.19 ± 0.07) (Kruskal-Wallis: p = 1.63 × 10⁻⁸; Dunn’s tests: GCL vs. hilus, p = 1.43 × 10⁻⁶; hilus vs. CA3, p = 1.27 × 10⁻⁶; GCL vs. CA3, p = 0.817). Some hilus cells had zero or one field in some sessions (Figure 2B), but these same cells often had multiple fields in other rooms (Data S1H). Thus, the presence and number of place fields in a single environment are insufficient criteria to distinguish between individual cells of the hilus and GCL.

Tetrodes in the GCL tended to record a larger number of cells during sleep, and fewer cells that were active during open-field exploration, than tetrodes in the hilus. The average sparseness ratio (defined as the number of active cells during behavior / the number of cells recorded during sleep; Neunuebel and Knierim, 2012) across all four rooms was higher (i.e., less sparse) in the hilus (median: 0.96, interquartile range [IQR]: 0.83 – 1.0) than the GCL (median: 0.05, IQR 0.0 – 0.18) (Kruskal-Wallis: p = 3.50 × 10⁻⁵; Dunn’s tests: GCL vs. hilus, p = 1.86 × 10⁻⁵; hilus vs. CA3, p = 0.079; GCL vs. CA3, p = 0.44) (Figure 2C). In contrast, cells in the hilus had 5–7-fold higher mean firing rates during sleep sessions (0.70 ± 0.11 Hz) than cells in the GCL (0.10 ± 0.02 Hz) or CA3 (0.13 ± 0.02 Hz) (Figure 2D; Kruskal-Wallis: p = 1.04 × 10⁻⁸; Dunn’s tests: GCL vs. hilus, p = 8.76 × 10⁻⁹; hilus vs. CA3, p = 2.46 × 10⁻⁵; GCL vs. CA3, p = 0.488). For cells active in at least one environment, the mean and peak firing rates of the most active session for each cell were also higher in the hilus (Figure 2E–F, left; see Table S1 for statistics). When silent cells were included, mean and peak firing rates were significantly different between CA3 and the GCL (Figure 2E–F right; see Table S1 for statistics); these differences were driven by the proportions of active cells in these areas.

Simultaneous recording of multiple cell types on anatomically ambiguous tetrodes

We next expanded our analyses to include earlier recording days and tetrodes that ended too close to the GCL-hilus boundary or the hilus-CA3 boundary to be included in our initial analyses. For each tetrode that reached the DG or CA3, we selected the recording day on which the largest number of well-isolated, putative excitatory units were recorded. This selection process generated a dataset of 242 cells from 57 tetrodes, while ensuring that individual units were not counted more than once from the same tetrode.

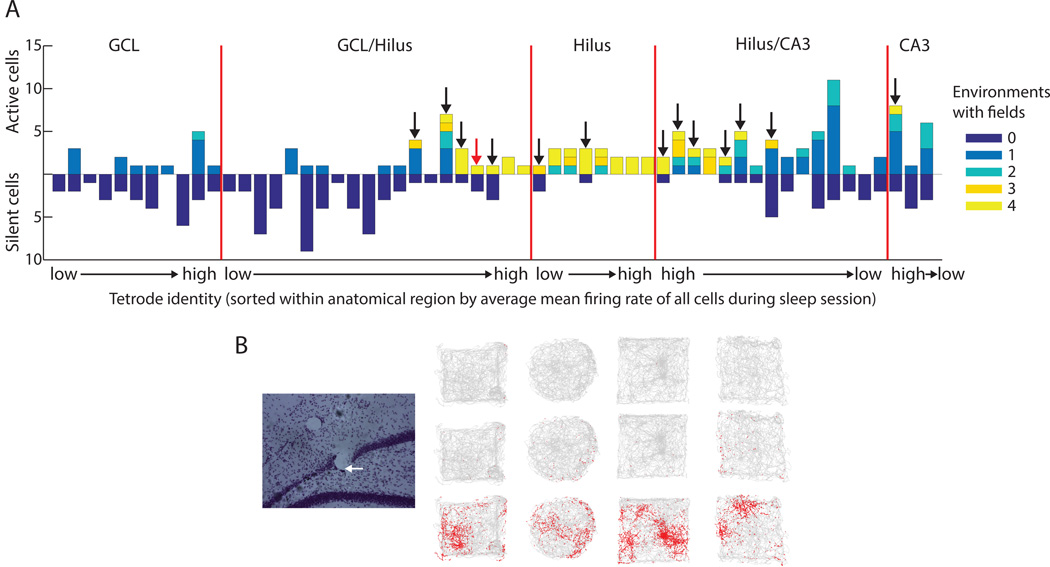
For each tetrode, the number of cells active in 0, 1, 2, 3, or 4 environments is shown in Figure 3A. A subset of the tetrodes that were used in the initial analysis (GCL, hilus, and CA3) were segregated from the more ambiguous tetrodes (i.e., tetrodes on which no cells were recorded on the last day or tetrodes judged to be too close to the layer boundaries: GCL/hilus and hilus/CA3). Each anatomically segregated group of tetrodes was sorted by the average mean firing rate of all cells recorded on the tetrode during the post-behavior sleep session. The tetrode with the lowest average firing rate within the anatomical region is labeled on the x-axis as “low,” while the tetrode with the highest rate is labeled “high”. Some tetrodes in the GCL/hilus and hilus/CA3 groups simultaneously recorded cells that were silent or active in a single room with other cells that were active in all or most rooms (Figure 3A, arrows). The firing of cells recorded on one example tetrode, marked by a red arrow in Figure 3A, is shown in Figure 3B. Simultaneous recording of both response types near layer boundaries is expected, as multiple cell types would be within the recording area of the tetrode. Since it is unlikely that a granule cell would be recorded near the hilus/CA3 border, the presence of cells active in all rooms on the hilus/CA3 tetrodes further supports the conclusion that multiple-field cells correspond to cells in the hilus rather than granule cells.

Figure 3. Distribution of response types recorded simultaneously from individual tetrodes.

For each tetrode, the recording day with the most active cells during sleep was selected. This produced a set of 242 cells from 57 tetrodes, shown here. A) Each tetrode was sorted into anatomical regions. Tetrodes that ended clearly in the GCL, hilus, or CA3, and either were recorded on the final day or had not been moved between the recording day and perfusion, were separated from tetrodes which were estimated based on histology to be near the GCL/hilus or hilus/CA3 boundaries at the time of recording. Tetrodes were sorted within each area by the average mean firing rate during sleep of all cells on the tetrode. Tetrodes in each area are arranged from lowest to highest average firing rate or vice versa (labeled low → high or high → low). Cells silent in all environments are plotted downward and cells active in at least one room are plotted upward. Some tetrodes (marked with arrows) recorded simultaneously cells that were active in all rooms and cells that were silent or only active in a single room; these recordings were most often localized to ambiguous recording sites. B) An example tetrode (marked by red arrow in A). This tetrode ended at the border between the GCL and hilus (left, white arrow). The firing of all three cells (recorded on the final day) during the 4 foraging sessions is shown on the right. One cell had multiple fields in all environments while the other two cells were mostly silent.

Decision-tree classification of cells based on baseline firing properties

Reconstruction of tetrode location based solely on histology is insufficient to reliably assign cell identity to all cells on a tetrode (Neunuebel and Knierim, 2012). Due to the proximity of the hilus to the GCL and CA3, small amounts of electrode drift between recording and perfusion can result in inaccurate classification. In addition, cells in the hilus, such as mossy cells, can be recorded on electrodes up to 300 microns apart (Henze and Buzsaki, 2007) and some tetrodes may simultaneously record cells from the hilus and either the GCL or CA3 (Figure 3). Our initial analysis minimized these issues by excluding cells recorded on days preceding the day of perfusion and on tetrodes located near area boundaries. To improve the accuracy of histological classification and assign putative cell types to the larger dataset, we used firing properties recorded during the baseline sleep/rest sessions of our initial dataset of 88 cells to train a random forests classifier (Breiman 2001; Figure S4, STAR methods). This classification technique was chosen because it is more resistant to overfitting relative to other supervised learning methods, and it generates an estimate of the classifier’s generalization error (the “out of bag” [OOB] error rate) without the need for additional cross-validation steps.

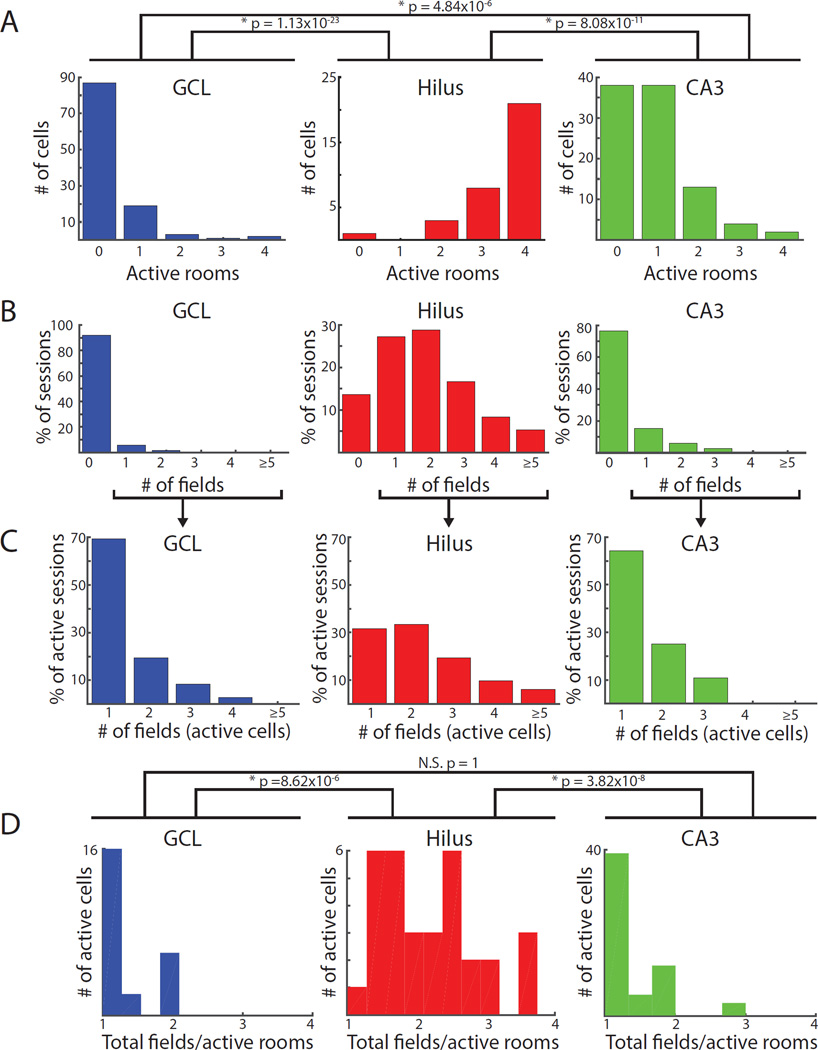
We trained the model using spiking and histological features of the initial data set (i.e., Figure 2 data) recorded during the post-behavior sleep session (Figure S4). The classifier learned to accurately assign the training set to the experimenter-defined histological regions, with an OOB error rate of 5.7% (Figure S4D). We used the trained classifier to assign cell layers to the larger dataset of 242 cells from all tetrodes with the largest number of recorded cells per day (Figure 3 data). The model classified 112 cells as GCL, 33 cells as hilus, and 97 cells as CA3 recordings. Although the class labels of the training data were based on histology alone, and the features used for random forests classification did not include any firing properties of cells recorded during foraging sessions, the spatial firing properties of the classified cells during foraging sessions (Figure 4) were very similar to the firing properties of the cells recorded on histologically unambiguous tetrodes on the final day (Figure 2A, B, Table S1). This consistency reinforced the robust differences in the spatial firing properties among the cell classes.

Figure 4. Spatial firing of cells from the larger dataset classified as putative GCL, hilus, and CA3 cells by the random forests classifier.

The 5 features used by the classifier were mean firing rate, burst index (proportion of all inter-spike intervals that are ≤ 6 ms), number of well-isolated units recorded simultaneously on the same tetrode, channel slope (slope of the best fit line through the normalized, sorted peak amplitudes of the average waveform on the four tetrode wires), and proximity of the tetrode tip to either the GCL or CA3 (Figure S4A). Classified cells had distributions of firing properties that were very similar to the initial training set based on histological classification (Figure 2). All p values represent the results of Dunn’s tests and are adjusted for multiple comparisons. A) Number of active rooms. The number of rooms with fields was higher for cells classified as hilus than cells classified as GCL or CA3, even when only considering active cells (Table S1). B) Number of fields in each recording session and C) number of fields excluding sessions with no fields. Cells in the hilus were more likely to have multiple firing fields in a recording session than cells in the GCL or CA3, which were silent in the majority of behavior sessions and typically had single fields when active. D) Number of fields per room (total number of fields divided by the number of active rooms, excluding silent cells). Cells classified as hilus cells had more fields per room (2.20 ± 0.13) than GCL (1.33 ± 0.09) or CA3 cells (1.35 ± 0.07).

Although some of the cells used for training were also included in the larger dataset, similar results were produced when we restricted classification to only cells recorded on tetrodes not used for training (Figure S5A–D). These results were not driven by any individual animals, as the firing properties of classified cells were consistent across all animals (Figure S5E). Finally, K-means clustering using the number of active rooms and total number of fields revealed two clusters that separated between hilus recordings and combined CA3 and GCL recordings (Figure S4F–I). The outputs of these two models generated the same class label for ~92% of cells (Figure S4I), suggesting that the random forests classifier is able to accurately detect patterns of activity in the sleep data that correspond to cells with distinct clusters of spatial firing properties.

Juxtacellular recordings from identified granule cells and mossy cells

Although the extracellular recordings analyzed above are highly likely to correspond to the excitatory cell types in the GCL, hilus, and CA3c region (i.e., granule cells, mossy cells, and pyramidal cell, respectively), direct evidence from identified cells would add additional support to this identification. We thus recorded and labelled single cells with juxtacellular procedures (Tang et al., 2014) as well-trained rats foraged for food reward on a square platform (95 cm × 95 cm). We only attempted to label cells that were active when rats were running on the platform; thus, these data do not provide any measures of the proportion of active cells in any region. Electrodes were often advanced through the entire GCL without encountering an active GC, consistent with the extremely sparse firing of putative granule cells observed in our tetrode recordings. Of 46 juxtacellular recording and labeling attempts (including attempts in neocortex and CA1 to establish the technique), 30 cells were recovered without ambiguity, including 23 cells in the hippocampus: 8 granule cells, 3 mossy cells, 3 CA3 pyramidal cells, 1 hilar interneuron, 6 CA1 pyramidal cells, 1 putative interneuron in the GCL, and 1 putative interneuron in CA1. We concentrate on the granule cells and mossy cells here, but all recorded hippocampal cells are presented in Data S1.

All identified granule cells (4 in the upper blade and 4 in the lower blade of the GCL) had a single firing field in the environment tested (Figure 5 A, D, G, Data S1A). The average peak rate of the granule cells was 6.44 ± 1.25 Hz (Figure S6). The peak rates and spatial firing fields were similar to the identified GCL recordings from the tetrode data (Figure 1, Data S1). Consistent with observations from other laboratories (Andrea Burgalossi and Michael Brecht, personal communication) and possibly due to their known vulnerability to cytochemical and mechanical stress (Sloviter et al., 2003; Scharfman and Myers, 2013), it was particularly difficult to label and recover the full morphology of mossy cells in freely moving rats. Instead, we used GluR2/3 as a marker to confirm the identity of the mossy cells, as mossy cells are the only cell type in the hilus to express this marker (Leranth et al, 1996), except for a very small number of ectopic granule cells (~1,000 vs 30–50,000 mossy cells; McCloskey et al., 2006; Myers and Scharfman, 2009). For the cell shown in Figure 6A, which is positive for GluR2/3, the somato-dendritic morphology could be recovered and was typical of a mossy cell. The other two hilar cells (Figure 6D, G) were also positive for GluR2/3. Additionally, the soma diameters of these two cells (~20 µm, similar to the mossy cell in Figure 6A) were larger than the identified granule cells (~10 µm), providing further evidence that the recorded cells are mossy cells rather than the extremely rare ectopic granule cells in the hilus. Of the three recorded and labelled mossy cells, two had multiple place fields, and one had a single field (Figure 6). The single-field mossy cell is consistent with tetrode recordings from the hilus, where cells had single fields in 20–30% of foraging sessions (Figure 2B). In addition, we recorded two more cells in the hilus but failed to label the recorded cells (Data S1C). The end of the electrode tracks were in the hilus (arrows in Data S1C), and a deposit of tracer was apparent in the hilus. Previous juxtacellular studies have shown that strong current pulses which fail to elicit spiking can result in a small accumulation of residual tracer at the tip of the pipette (Duque and Zaborszky, 2006; Pinault, 1996). While the exact identities of the recorded cells are uncertain, they had higher burstiness (6 ms burst index = 0.17 and 0.14, Figure S6E) than expected from hilar interneurons (Scharfman 1992). Consistent with the 3 identified mossy cells and our tetrode dataset from the hilus, these cells had multi-peaked firing fields.

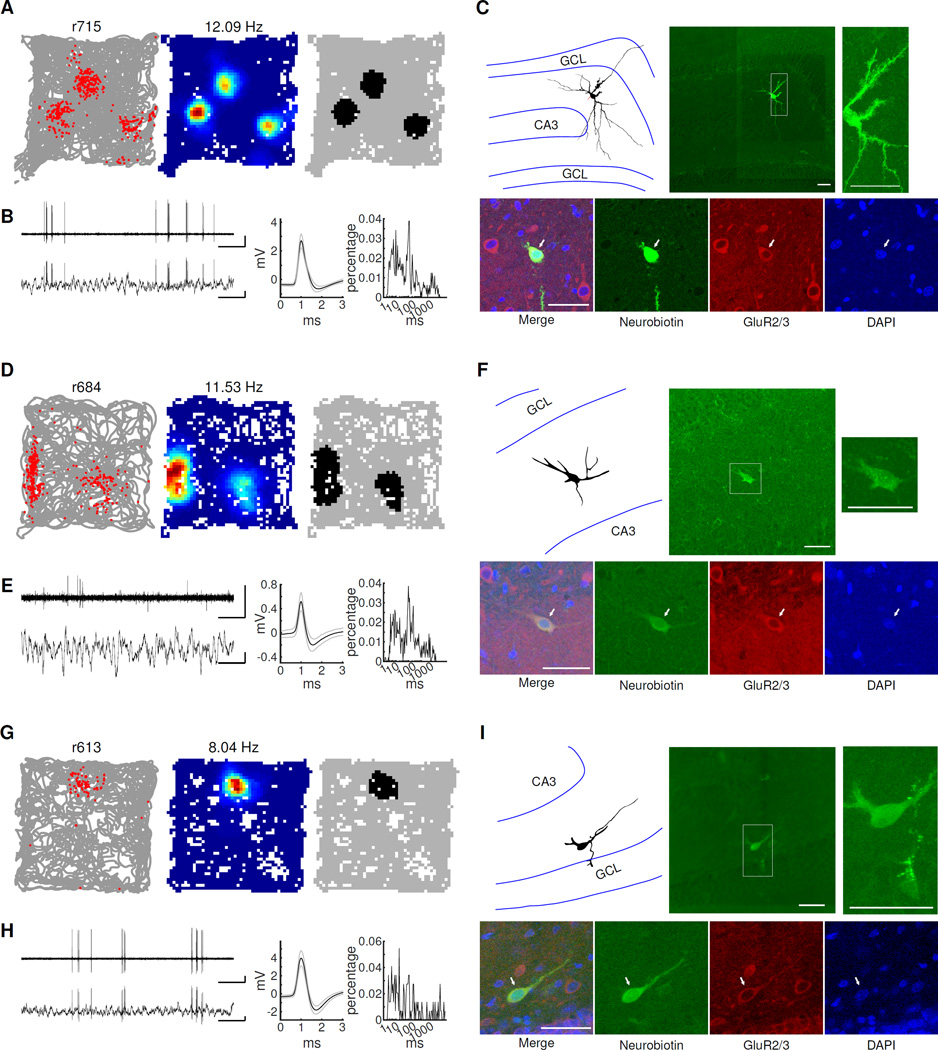
Figure 5. Spatial firing properties of juxtacellularly recorded and identified granule cells.

A) Left, rat’s trajectory (gray lines) superimposed by the firing locations of the neuron (red dots). Middle, rate map where red represents the highest firing rate and blue represents no firing. The peak firing rate is shown above each rate map. Right, binary image showing pixels where the firing rate was > 20% of the peak firing rate. B) Left, representative voltage traces recorded during freely moving behavior. Bandpass-filtered (300 Hz – 6 kHz) (top) and raw traces (bottom) are shown. Scale bars: 1 s (horizontal) and 1 mV (vertical). Middle, mean (black line) and standard deviation (gray lines) of spike waveforms. Right, inter-spike interval histograms. C) Fluorescent image showing the morphology and location of the labelled neuron (green, Neurobiotin; blue, DAPI). Right, camera lucida reconstructed morphology (soma and dendrite, black; axon, red; GCL border, blue). Scale bar: 50 µm. D–I) Further example granule cells located in upper blade (D–F) and lower blade (G–I) of the GCL are shown with the same conventions as (A–C). The 6 ms burst indices for these 3 granule cells were 0.16 (B), 0.16 (E) and 0.13 (H), respectively.

Figure 6. Spatial firing properties of juxtacellularly recorded and identified mossy cells.

A–C) One mossy cell with 3 firing fields. A-B) Same convention used for Figure 5A–B. Scale bars in B: 1 sec (horizontal) and 1 mV (vertical). C) Top middle, the morphology and location of the recorded cell. The inset to the right shows a magnified view, where large spines (“thorny excrescences”) covering the soma and proximal dendrites, typical of mossy cells, can be clearly seen. The camera lucida reconstructed morphology of the mossy cell is shown at left. The boundaries of GCL and CA3 are represented with blue lines. Bottom, antibody staining of the cell (left to right: merge, Neurobiotin, GluR2/3, DAPI). The labeled cell (indicated with arrows) is positive for GluR2/3. Scale bar: 50 µm. (D–F) A mossy cell with 2 firing fields. Note that only the soma and parts of the dendritic arbor of the cell were recovered after labeling. The identity of this mossy cell was confirmed by the location of the cell body (in the hilus), the GluR2/3+ signal, as well as some large spines on the cell body (F, top right panel). (G–I) A mossy cell close to the lower blade of the GCL with a single field. Although only one labeling attempt was made, three cells were labeled in this rat. We believe that the recorded cell was a mossy cell because the deepest labeled cell was adjacent to the pipette tip, was located in the hilus (I, top), and was GluR2/3+ (I, bottom). The 6 ms burst indices for these 3 mossy cells were 0.17 (B), 0.11 (E) and 0.19 (H), respectively.

Firing patterns in the GCL and hilus support different mechanisms of pattern separation

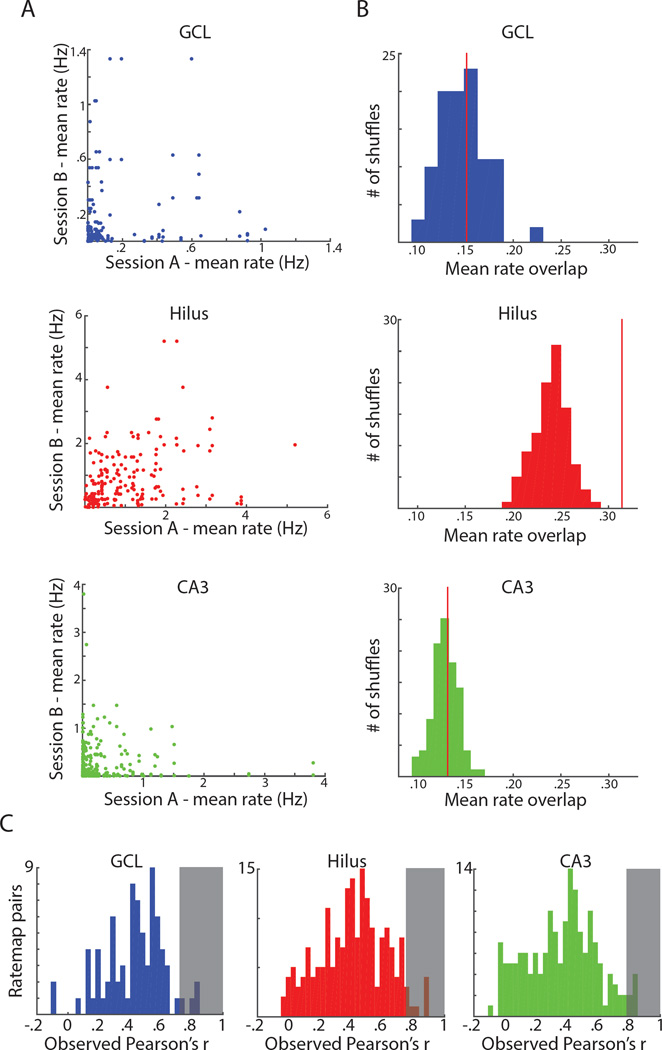
The juxtacellular results support the conclusion that cells classified as GCL recordings correspond to granule cells and cells classified as hilar recordings correspond to mossy cells, but these results cannot determine how the cell types differentiate between distinct environments. Our classified tetrode recordings show that different cells in the GCL tended to be active in each environment whereas each cell in the hilus tended to be active in most environments (Figure 7A). To quantify the overlap in firing rates in these populations, the mean firing rates of all cells active in at least one environment were normalized to the mean firing rate in the most active room. For each cell, for each pair of rooms (excluding pairs where the cell was silent in both rooms) the rate overlap was defined as the product of the normalized mean firing rates in the two rooms (Leutgeb et al., 2007). Values close to one indicate a cell that fired near its highest mean firing rate in both rooms, while values closer to zero suggest that a cell had a low rate in at least one environment. The distribution of overlap values was significantly lower for cells classified as recordings from the GCL (0.15 ± 0.02) and CA3 (0.13 ± 0.01) than in the hilus (0.31 ± 0.02) (Kruskal-Wallis: p = 2.30 × 10⁻²¹; Dunn’s tests: GCL vs. hilus: p = 3.18 × 10⁻⁹; hilus vs. CA3: p = 9.00 × 10⁻²¹; GCL vs. CA3: p = 0.538). Because these differences may reflect nonspecific differences in the firing statistics of these cell types, we generated shuffled distributions for each area by shuffling cell identification within each maze for either GCL, hilus, or CA3 cells 100 times. For each shuffle, the mean overlap value for all cells was calculated. The observed average overlap value in the hilus was higher than the average value for all hilus shuffles, but the observed values in the GCL and CA3 were not significantly different from their respective shuffled distributions (GCL p = 0.45; CA3 p = 0.43) (Figure 7B).

Figure 7. Different mechanisms to support pattern separation in putative mossy cells vs. granule cells and CA3 cells.

A) For each session pair (4 rooms, 6 pairs per cell), the mean firing rate in one session is plotted against the mean rate for the other session. This was done for all cells active in at least one environment. Cells in the GCL (top) and CA3 (bottom) were usually silent in all but one room when active, causing most points to lie near an axis. Cells in the hilus (middle) were more likely to have high firing rates in multiple sessions. B) Histogram of the mean value of rate overlap for each of 100 shuffles of active cells in the GCL (top), hilus (middle), and CA3 (bottom). The red line indicates the observed mean of rate overlap values. The observed value is not significantly different from the shuffled distributions for the GCL (p = 0.45) or CA3 (p = 0.43) but the observed value is greater than all shuffles in the hilus (p < .01). C) Histogram of observed ratemap correlations between pairs of sessions (excluding pairs with no fields in either room). The shaded region represents the 95^th percentile of correlation values obtained from shuffled distributions. In all three areas, the observed correlations exceed this value < 5% of the time (i.e., no more than as expected by chance).

While the activity of cells in the hilus cannot distinguish environments based on the group of active cells, the relative location, spacing, and number of firing fields in distinct environments may provide enough information for the population of hilar cells to differentiate between environments. For each cell, for each pair of rooms (excluding pairs where the cell was silent in both rooms), the maximum ratemap correlation following 36 10° rotations of one ratemap was calculated (Figure 7C). Using the same shuffling procedure described above, separate shuffled distributions were created for active GCL, hilus, and CA3 cells and ratemap correlations were calculated for each of 100 shuffles in each area. The observed correlations did not exceed the 95^th percentile of the shuffled distribution (Figure 7C, shaded area) any more than expected by chance in either the GCL (4/90, 4.44%), hilus (8/189, 4.23%), or CA3 (7/227, 3.08%). The low ratemap correlations demonstrate that cells in all three areas remap in different environments, with distinct spatial firing in different environments.

Discussion

In the present study, cells in the GCL fired very sparsely, with < 10% of cells having a place field in a given environment, and they almost always had a single place field when active. In contrast, cells recorded in the hilus were active promiscuously in most environments and typically had multiple firing fields. Juxtacellular recordings from identified granule cells and mossy cells were entirely consistent with the tetrode data. Identified, active granule cells fired in single place fields during free exploration in an open field. In contrast, identified, active mossy cells tended to fire in multiple locations. Although this evidence rests on a small dataset of positively identified mossy cells, these data provide the first conclusive evidence that mossy cells demonstrate spatially selective firing fields during exploration (see also Senzai and Buzsaki, in press), similar to the other excitatory cell types of the hippocampus.

Implications for mechanisms of pattern separation

For decades, the most prominent computational theory of the DG proposed that it performs pattern separation on its entorhinal inputs, thus increasing the storage capacity of the downstream CA3 network and reducing memory retrieval errors resulting from interference among memory traces. Much behavioral evidence has accumulated in favor of this theory (Hunsaker et al., 2008; Nakashiba et al., 2012; Yassa and Stark 2011; Rolls and Kesner, 2006). Nonetheless, the precise circuit mechanisms by which the DG performs pattern separation are still not clear, due in part to conflicting reports about the basic firing properties of granule cells in freely moving animals. Some studies suggested that many granule cells had multiple firing fields in an environment, in contrast to the typical single firing fields of CA1 and CA3 pyramidal cells (Jung and McNaughton, 1993; Leutgeb et al., 2007). Furthermore, the majority of putative granule cells recorded during baseline sleep sessions were reported to be active in most or all environments (Shen et al., 1998; Leutgeb et al., 2007). These data contradicted the predictions from the classic DG models that granule cells employed a very sparse coding scheme and multiple lines of evidence for sparse granule cell activity that have more recently emerged (Alme et al., 2010; Danielson et al., 2016; Chawla et al., 2005; Neunuebel and Knierim, 2012; Diamantaki et al., 2016a, b; see also Jung and McNaughton, 1993; Skaggs et al., 1996).

The current study provides strong, direct evidence in support of the classic models of granule cells’ sparse selectivity, and it definitively resolves the conflicting literature by identifying the multi-field firing patterns as corresponding to mossy cells, rather than granule cells (as hypothesized by Neunuebel and Knierim, 2012). Furthermore, both cell types showed statistically independent representations (remapping) of 4 distinct environments, but showed distinct coding mechanisms for generating the independent maps. Putative granule cells used independent ensembles of cells to represent the environments (similar to the CA3 region; Leutgeb et al., 2007; Alme et al., 2014), whereas putative mossy cells used largely overlapping ensembles of neurons, with each neuron displaying a different spatial firing pattern in each environment.

Although not the classic mechanism from the computational literature, the pattern of mossy cell remapping could also support pattern separation (a mechanism termed “pattern separation by changes in spatial and temporal coincidence” by Leutgeb et al., 2007). Currently, there are few detailed models of the computational role of mossy cells in hippocampus-dependent memory processing. Mossy cells may perform an essential role in pattern separation by regulating granule cell excitability, sparsity, and activity (Myers and Scharfman, 2009; Sloviter et al. 2003; Jinde et al., 2012; Henze and Buzsáki, 2007), and loss of mossy cells leads to deficits in context discrimination (Jinde et al., 2012). Through activation of local interneurons, mossy cell activation may ensure that only the most active granule cells within a local area of the DG have firing fields, ensuring sufficiently sparse activity to support pattern separation. CA3 back-projections to mossy cells may further regulate the activity and sparseness of granule cells (Scharfman 2007). It would be valuable to determine if the present data can be fit into these models in terms of the distinct, spatial firing properties of granule cells and mossy cells. Specifically, what is the computational significance of the property of mossy cells to tend to fire in multiple locations, rather than single fields, and the distinct forms of remapping in granule cells and mossy cells?

Entorhinal-granule cell interactions during sleep and awake activity

Cells in the GCL fired more strongly during periods of sleep than awake behavior (see also Neunuebel and Knierim, 2012). Non-REM sleep epochs are characterized by reactivations of CA1 and CA3 cells, and this activity is thought to be important for the consolidation of memories (Buzsaki, 1989; Wilson and McNaughton, 1994). These reactivations are generated through the coordinated firing of recurrently connected CA3 cells (Buzsaki, 1986), but the preferential firing of granule cells during sleep suggests a role of granule cells in the consolidation process. Perforant path stimulation generates larger LFP population spikes in the DG during sleep than during awake periods (Winson and Abzug, 1977). This enhanced drive may be mediated through a decrease in feedforward inhibition in the DG following changes in locus coeruleus activity during the transition from down states to up states in slow wave sleep (Brown et al., 2005; Eschenko et al., 2012). The increased activity of granule cells during sleep may serve a crucial role in coordinating the hippocampal-neocortical dialog that occurs during hypothesized periods of memory consolidation (Siapas and Wilson, 1998; Isomura et al., 2006; Bendor and Wilson, 2012).

The transformations between entorhinal input representations and DG representations during exploration is another key question to understanding hippocampal processing. A number of computational models of the generation of DG place fields from medial entorhinal grid cell input relied on the descriptions from the Leutgeb et al. (2007) paper that putative granule cells typically had multiple firing fields (de Almeida et al., 2009, 2012; Ujfalussy et al., 2009; Si and Treves, 2009). Although the functional relationship between grid cells and place cells is under intense debate (Bonnevie et al., 2013; Koenig et al., 2011; Bush et al., 2014), these models will nonetheless require modification to incorporate the finding that granule cells actually have single place fields in a typical laboratory experiment (consistent with other models of place field formation; Solstad et al., 2006; Rolls et al., 2006; Savelli and Knierim 2010; Monaco and Abbot, 2011). Furthermore, now that the spatial firing properties of mossy cells have been elucidated, it is incumbent to introduce into these models the role of mossy cells, which occupy a key node in the hippocampal circuitry as a component of a disynaptic, recurrent excitatory loop between granule cells and mossy cells and as the recipient of feedback projections from CA3, allowing the output of CA3 to affect the ongoing computations in the dentate gyrus.

CA3c and DG

The cells we recorded in CA3c were more likely to be active in a given environment than cells in the GCL, but the firing properties of individual, active CA3 cells during behavior were largely similar to active granule cells. This similarity reinforces the notion from previous studies that CA3c is likely to act more as a computational unit in conjunction with the DG than with the rest of CA3 (Scharfman 2007; Hunsaker et al., 2008). CA3c receives the strongest input from granule cells and provides most of the back-projection to the mossy cells (Witter, 2007; Scharfman 2007). While CA3 is often associated with pattern completion and storage due to its extensive recurrent collaterals, CA3c has a lower density of recurrent collaterals than more distal CA3a or CA3b (Ishizuka et al., 1990). According to theory, CA3 ensembles are capable of performing both pattern separation and pattern completion (Rolls and Treves, 1998; O’Reilly and McClelland 1994), and the dominance of pattern separation in CA3c and pattern completion in CA3a (Lee et al. 2015; Lu et al. 2015) suggests that the balance between these processes is differentially modulated along the CA3 transverse axis.

Utility of classifier techniques for deciphering neural circuits and function

The classification techniques described here and in Senzai and Buzsaki (in press) will allow future studies to identify, with a high degree of confidence, the different cell types recorded in the DG/CA3c region and will supply much more reliable and consistent data on the functional properties of these cells than has been possible previously. It will be of particular importance to understand the different modes of remapping among granule cells, mossy cells, and CA3c cells under different conditions to decipher the computational functions of this circuit. Senzai and Buzsaki (in press) showed that when mice explored two similar chambers in the same location, with the chambers differing only in the floor texture and the markings on the wall, granule cells may remap less than the mossy cells (in contrast to the present paper, which showed that both cell types produced independent representations in completely different rooms). There are a number of potential explanations for the difference in results. In the present experiment, both local and global cues were altered, whereas in the Senzai and Buszaki experiment, only local, intra-chamber cues were altered. These results may reflect different sensitivities of granule cells to changes in medial or lateral entorhinal inputs (Neunuebel et al., 2013). Alternatively, the greater remapping in different rooms may result from realignment of head direction cells, which has been shown to co-occur with place cell remapping (Knierim et al., 1995).

Future studies will also be required to address the firing of immature adult-born granule cells and their contribution to the DG/CA3 pattern separation circuit. Adult-born granule cells strongly influence performance on tasks thought to rely on pattern separation (Clelland et al., 2009; Sahay et al., 2011), but their spatial firing properties during normal exploration remain unclear (but see Danielson et al., 2016). Some have previously attributed the multiple-field firing patterns, seen in mossy cells in this study, to adult-born granule cells (Alme et al., 2010; Neunuebel and Knierim, 2012). Although we observed this type of firing on some tetrodes near the hilus/GCL border (Figure 3B), where adult-born neurons are present, the same firing is also apparent on tetrodes at the hilus/CA3 border, suggesting these multi-field cells represent mossy cells co-recorded with granule cells rather than adult-born granule cells (although we cannot rule out the possibility that adult-born granule cells also show this property). Direct recordings from identified, adult-born granule cells in freely moving animals will complete the picture of all excitatory cell types in the dentate gyrus, and form the basis for a complete understanding of spatial representations in the dentate and their roles in hippocampal mnemonic processing.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Requests for additional information can be directed to Dr. James J. Knierim (jknierim@jhu.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

For tetrode recordings, 8 male, Long-Evans rats (3–6 months old, 350–450 g, Harlan Laboratories) were implanted with a custom designed recording drive, with 16 independently movable tetrodes and two reference electrodes. Rats were individually housed on a 12 hour light/dark cycle with ad libitum access to water. In 3 rats, a retrovirus expressing channelrhodopsin2 was injected into the DG at the time of the drive implantation surgery for a different experiment, but the results from these rats (422, 386, 454) did not differ from those of the other rats (Figure S5E).

For juxtacellular recordings, 94 male, Wistar rats (3–4 months old, 280–380 g, Harlan Laboratories) were implanted with a recording chamber targeted to the DG, as well as a headstage holder and microdrive holder. Wistar rats were used for juxtacellular recordings (as in previous juxtacellular studies; Diamantaki et al., 2016a, b) as they are thought to be more amenable than Long-Evans rats to brief periods of head fixation. Rats were individually housed on a 12 hour light/dark cycle with ad libitum access to water.

All surgeries and animal procedures complied with National Institutes of Health guidelines and were approved by the Institutional Animal Care and Use Committees at Johns Hopkins University.

METHOD DETAILS

Tetrode experiments

Surgical procedures

During surgery, rats were anesthetized initially with ketamine (80 mg/kg) and xylazine (10 mg/kg) and maintained at a surgical plane with isoflurane (to effect). The skull was exposed and cleaned, and 9 anchor screws were attached to the skull. A craniotomy was drilled for the drive and the dura was cut. The drive was targeted to the DG of the right hemisphere, with the center of the circular drive bundle ranging from 3.5–3.7 mm posterior to bregma and 1.8–2.2 mm lateral to bregma. The craniotomy was sealed with Kwik-Sil (World Precision Instruments) and the drive was secured in place with Osteobond (Zimmer) and/or dental acrylic (Coltene).

Electrophysiology

Tetrodes were made of 12 or 17 µm nichrome or 17 µm platinum-iridium wires and were gold-plated (nichrome) or cleaned (platinum-iridium) to reduce tetrode impedance to 150–400 kΩ. The tetrodes were loaded into a custom-made multielectrode drive (Kloosterman et al., 2009). Neural signals were recorded using the Cheetah data acquisition system and recording software (Neuralynx, Bozeman, MT). Signals were amplified 1000–5000 times and filtered between 600 Hz and 6 kHz (for single units) and between 1 and 475 Hz (for local field potentials). Units were sampled at 32 kHz, while local field potentials were sampled continuously at either 1 or 2 kHz. Tetrodes were lowered slowly, over 4–6 weeks. Tetrodes were initially lowered 100–300 µm each day until they were 300–500 µm past the CA1 layer and gamma activity and dentate spikes were detected in the LFP (Bragin et al., 1995). From that time, tetrodes were lowered 10–30 µm a day while recording long periods of sleep to check for the presence of units. When putative DG or CA3 units were detected, recordings were performed on the following day. Tetrodes with putative DG or CA3 units were not advanced further unless all units were lost.

Behavioral training

Before surgery, rats were handled daily for ~30 minutes to habituate them to human contact. Rats were also trained to sleep in a small, towel-lined dish on a pedestal. After surgery, rats recovered for 5–7 days before tetrode advancement began. Once tetrodes reached CA1 (2–3 days), rats were placed on a food restricted diet to reduce their body weight to 80–90% of their free feeding weight. Rats were then trained to forage for small food pellets or chocolate sprinkles in a cylinder (80 cm diameter, 50 cm height) with grey walls and brown paper covering the floor in a separate room from later behavior sessions. Rats were trained for 15–30 minutes a day for 5–10 days until they ran consistently for infrequent food rewards (~2–4 rewards per minute). If there was a long period between pretraining and the first day of recording, additional training sessions were added to maintain behavioral performance.

Once tetrodes reached the DG, recordings began in a series of environments. Each environment consisted of a raised platform (50 to 65 cm from the floor) in a different room, with different visual cues. The platforms differed in texture, color, and/or shape and had a similar area for exploration (rough black square 109 × 109 cm, smooth gray square 107 × 107 cm, textured green octagon 109 × 109 cm, and smooth black circle 117 cm diameter). All recording sessions were performed at the start of the day, before any tetrode turning, to maximize unit stability. The rat’s position during behavior was tracked by an overhead camera recording four LEDs mounted on the recording headstage (two red LEDs in the front and two green LEDs in the back). Each day of recording began with a baseline session as the rat slept or rested on a small pedestal (minimum 30 min). The animal next foraged for food reward in the four distinct environments (order chosen pseudorandomly each day). After the final foraging session, rats were returned to the pedestal for a second sleep session, which was continued until a minimum of 30 min of sleep had been recorded (sleep determined by visual assessment – rats were immobile, with their eyes closed, and were resting their head). The second sleep session typically resulted in more robust neural firing than the first session, as the rats were sated and more likely to sleep.

Perfusion and histology

On the final day of recording, rats were deeply anesthetized with Euthasol and perfused with saline followed by 4% paraformaldehyde (PFA) or formalin. To improve the quality of tetrode tracks, the brain was partially exposed and soaked in PFA or formalin for 4 hours with the drive attached before tetrodes were retracted. The brain was removed and soaked overnight in PFA or formalin before being transferred to a 30% sucrose solution for ≥ 3 d. The brain was sliced into 40 µm coronal sections. Slices were mounted, stained with cresyl violet, photographed, and a 3D reconstruction of the tetrode tracks was created using Free-D software (Andrey and Maurin, 2005). A top view of the tetrode track reconstruction was compared to a picture of the drive bundle to determine the identity of each tetrode track and high-magnification images of the deepest point of each tetrode track were acquired.

Cell activity and field detection

The firing of all cells during foraging sessions was velocity filtered with a threshold of 2 cm/sec. Cells were considered active during a foraging session if they 1) fired a minimum of 75 spikes in the 15–20 minute recording session, 2) had a spatial information score (Skaggs et al., 1996) of > 0.5 bits/spike and 3) had a statistically significant spatial information score (p < .01). Rate maps were generated by dividing the number of times a cell fired in each pixel of the rate map by the total time the rat occupied the pixel. Rate maps were smoothed using an adaptive binning algorithm described in Skaggs et al. (1996). The significance level of a cell’s spatial firing was calculated by shuffling the spike train of the cell and the position of the rat by a random amount (minimum 30 seconds), creating a new firing rate map, and computing the spatial information score from the shuffled data. This procedure was repeated 100 times and the cell’s spatial information score was considered significant if all spatial information scores from the shuffled data were less than the score for the unshuffled data. The number of place fields was calculated by finding all pixels (pixel size ~2.2 cm²) in the rate map in which the mean firing rate exceeded 20% of the cell’s peak firing rate. A field was defined as a region with ≥ 10 contiguous pixels that surpassed 20% of the peak firing rate.

Unit isolation

Single units were isolated manually using custom-written, cluster-cutting software. Peak amplitude and energy of waveforms were used to isolate cells, which were then assigned an isolation score based on the cluster’s separation from noise and other clusters. This score ranged from 1 (very good) to 5 (poor), and clusters that were rated as 4 or 5 (marginal and poor) were excluded from analysis. To confirm stability of recordings, cells were excluded from analysis if they did not fire in both baseline sleep sessions.

Cell selection

Previous recordings from the DG had found that plotting the spike width vs. mean firing rate of cells revealed three clusters (Neunuebel and Knierim 2014). Our results were consistent with these findings. Most cells recorded had low firing rates and higher spike widths; these putative excitatory DG cells were analyzed in this paper (Figure S3A). Another cluster, putative interneurons, had high mean firing rates (>10 Hz) and narrow spike widths and these cells were excluded from analysis (Figure S3B). Cells in the final cluster had intermediate firing rates (1–10 Hz) and spike widths. While the mean firing rates of some of these cells overlapped slightly with the highest rate putative excitatory cells, the cells’ low burstiness (portion of interspike intervals ≤ 6 ms) allowed this cluster to be more reliably separated (Figure S3A, right). These cells did not display spatially selective firing (Figure S3C), and were most often found in the hilus (3 in hilus, 1 each in GCL and CA3). The firing of these cells resembles the juxtacellularly labeled interneuron in the hilus (Data S1D). We believe these cells represent a class of hilar interneurons and these cells were also excluded from analysis. Although all interneuron types combined may equal or surpass the number of mossy cells in the hilus, the number of putative interneurons (both high rate and mid-rate) recorded in the hilus was lower than the number of putative mossy cells. This is due in part to the fact that we advanced tetrodes until we found lower rate, putative excitatory cells. In addition, on many tetrodes in the hilus, lower amplitude putative interneurons could be seen which did not meet our cluster isolation criteria and were thus excluded from analysis.

Cells were initially only analyzed if they were recorded on the final day of recording and on tetrodes where the tetrode track was located clearly in the GCL, hilus, or CA3. When extending analysis to previously recorded cells and tetrodes located near layer boundaries, in order to prevent repeated sampling of the same cells, only the recording day with the largest number of well-isolated, putative excitatory cells was used for each tetrode. Using these criteria, 242 cells were selected for analysis, including 108 cells from 27 tetrodes used in the initial (final day) analysis. Approximately 40% of these cells were from an earlier recording day (43 cells from 12 tetrodes) and 60% were from the final day and were a subset of the dataset initially analyzed (65 cells from 15 tetrodes). The remaining 134 cells came from 30 tetrodes that were not used in the initial analysis (either cells were not recorded on the final day of recording or the end of the tetrode track was located ambiguously between the hilus and the GCL or CA3). Of these cells, 62 were classified as GCL, 11 as hilus, and 61 as CA3.

Juxtacellular experiments

Surgical procedures

During surgery, rats were anesthetized initially with ketamine (80 mg/kg) and xylazine (10 mg/kg), with a surgical plane of anesthesia maintained with isoflurane. The skull was exposed and a recording chamber was glued to the skull above the DG. The center of the recording chamber was 3.1- 4.1 mm posterior to bregma and 1.8–2.8 mm lateral to the midline. A holder for a microdrive was placed and anchored to the skull. A dummy microdrive was used to position the microdrive holder such that the glass electrode tip was located in the recording chamber. Another holder for the miniature headstage was also anchored using dental acrylic.

Behavioral Training

Before surgery, rats were acclimated to human handling for 10 min daily for 3–4 days. After 4–5 days recovery from surgery, rats were trained to forage for food on a raised wooden platform (95cm × 95cm). Meanwhile the body weight of rats was reduced to 80–90% of their pre-surgery weight. Then rats were also trained for head-fixation for ~10 minutes, during which time they could sit or run on a treadmill, and were given pieces of Cheerios cereal or peanuts to eat.

Juxtacellular recordings

Juxtacellular recording and labeling in freely-moving rats were essentially performed as previously described (Tang et al., 2014). Prior to recording, rats were briefly anesthetized with isoflurane and a small craniotomy was made over the DG. A chlorinated silver wire, which was used as a reference, was placed in the chamber and secured with dental acrylic. The craniotomy was sealed with silicone elastomer (Kwik-Cast, World Precision Instruments). After 6–24 hours of recovery, the awake rat was head-fixed and the microdrive and miniature headstage were screwed onto their respective holders. A glass electrode filled with artificial cerebrospinal fluid (aCSF), with typical resistances ranging from 6–12 MΩ, was mounted on a micromanipulator and the tip was lowered to the pia, then the recording chamber was filled with agarose (3–5% in saline) to stabilize the recording pipette. aCSF contained in mM: 135 NaCl, 5.4 KCl, 5 HEPES, 1.8 CaCl2 and 1 MgCl2 plus Neurobiotin (1.5–2.5%; Vector Laboratories) and the pH and osmolarity of the aCSF were adjusted to ~7.2 and 290–320 mOsm, respectively.

The rat was then released onto the platform. The rat was allowed to sleep, groom, or run freely on a 95 × 95 cm square platform as the electrode was advanced to DG. As the electrode was lowered into the brain, the electrode tip resistance was monitored by small positive current pulses (200 ms duration) at a frequency of 1 Hz. An increase in electrode resistance was indicative of cell contact (Tang et al., 2014). The location of the GCL was indicated by the depth from pia, theta/gamma oscillation in the LFP when the rat was running, as well as frequent instances of high electrode resistance, indicating a densely packed cell layer (Diamantaki et al., 2016a).

For behavioral tracking, the headstage carried two battery powered green and red LED lights centered on the rat’s head. Behavior video was monitored and recorded at 60 Hz and 640 × 480 resolution with a Raspberry Pi computer and Pi camera module. Offline analyses were performed on the video with custom software in Python and Matlab.

The voltage signal was low-pass filtered with a cutoff of 50 kHz and amplified 20x using a BA-03X amplifier (NPI Electronic), and digitized at 25 kHz with the Micro3 1401 data acquisition unit in combination with Spike2 v8.03 data acquisition software (CED, UK). The glass electrode was advanced with a commercial micromanipulator (NM2104SE; Kleindiek Nanotechnik) or a customized microdrive with a miniature DC linear actuator (brushless DC micromotor; part#0515A006B+06A 125:1S2, Micromo, FL) (English et al., 2014; Long et al., 2010), which allowed us to estimate depth from pia. Juxtacellular recordings were targeted to the DG by taking advantage of characteristic signatures of the local field potential activity (as in Diamantaki et al., 2016a) and depth from pia.

On average, we made 3 penetrations per rat in a total of 94 rats. To avoid ambiguity, we attempted to label only one DG cell in each rat, and rats were perfused within 20–30 minutes of the labeling attempt. A cell was considered successfully labeled if it fired spikes during the entrainment stimulation protocol and histology revealed a single labeled cell (with one exception in which 3 cells expressed neurobiotin, but only one of the cells was located near the electrode tip; see Figure 6G legend)

Recording and labeling

Once a juxtacellular recording was established from a single active neuron, its activity was recorded while the rat explored the platform until sufficient coverage of the platform was achieved (average: 8.28 min, range: 3.3–15.5 min). After this foraging session, the cell was labelled with a standard protocol (Pinault 1996). Briefly, positive current pulses of 2.5 Hz (200 ms, 50% duty cycle) were injected. The amplitude of the current was increased rapidly from 0.1 nA to 1–10nA, until the cell’s spiking was entrained by the current injection. Typically, the spike waveforms were widened during current injection, a classical indicator of successful iontophoretic dye injection and cell labeling (Pinault et al., 1996).

Success rate

Labeling attempts were made on 46 out of 94 rats, and in 65% of the cases we could recover the structure of the labeled cell without ambiguity (30 cells in total, including cortical cells and hippocampal cells). In the remaining cases, we were either unable to find any labeled neurons, or multiple cells were labeled. The labeling of multiple cells by the same stimulation is often observed in the hippocampus (Claiborne et al., 1990; Pinault, 1996). Out of the 23 hippocampal neurons in which a single neuron was unambiguously labeled, 13 were located in dentate gyrus, 3 were in CA3, and 7 were in CA1.

Perfusion and histology

Within 20–30 minutes of a labeling attempt, rats were deeply anesthetized with Euthasol and perfused with PBS followed by PFA. The brain was removed, fixed overnight in PFA, and successively immersed in 15% and 30% sucrose solutions. The brain was sliced in 60 µm thick coronal sections which were then processed with the Streptavidin, Alexa Fluor 488 conjugate (1:1000, ThermoFisher Scientific) to reveal the morphology of the Neurobiotin-filled cells. If one hilar cell was labelled, the slices were further processed for GluR2/3 immunoreactivity (anti-GluR2/3 antibody, Cat. #AB1506, Millipore; Alexa Fluor® 546 Goat Anti-Rabbit IgG (H+L), Cat. #A-11010, ThermoFisher Scientific) to determine whether it was a mossy cell or an interneuron. Slices were mounted with VECTASHIELD Mounting Medium with DAPI (4’, 6-Diamidino-2-Phenylindole, Dihydrochloride) (Vector Laboratories). Cell images were acquired with confocal microscopy (Zeiss LSM 510 META or Zeiss LSM 700) and camera lucida drawings of morphology were manually traced with a drawing editor (http://ipe.otfried.org/).

Data analysis

Raw voltage traces were band-pass filtered with an 8^th order Butterworth filter between 400 and 8000 Hz. The signal was then thresholded interactively to remove background noise, and waveforms of putative spike events were extracted. Each event was then checked manually to remove potential movement or chewing artifacts. Data analysis was performed in the same way as the tetrode dataset.

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical tests

Unless otherwise stated, data are presented as mean ± s.e.m. and all p values are the output of post-hoc pairwise Dunn’s tests following rejection of the null hypothesis that all samples come from the same distribution using Kruskal-Wallis one-way ANOVA. For χ² tests, pairwise χ² tests were performed following rejection of the null hypothesis of a χ² test for all groups. All Dunn’s test and pairwise χ² p values have been adjusted for multiple comparisons using Šidák’s adjustment (Šidák, 1967) and results were considered significant if the adjusted p value was < .05. When comparing the observed mean firing rate overlap to shuffled distributions (Figure 7B), the p-value is defined as the number of shuffles that surpassed the observed value; if no shuffles surpassed that value, the result was considered significant with a significance of p < .01. Detailed statistical results can be found in Table S1.

Rate overlap and remapping analysis

For firing rate overlap and ratemap correlations, only cells active in at least one environment were considered for analysis. To calculate rate overlap, the mean firing rate of each cell was normalized to its mean firing rate in the most active room. For each of the 6 pairs of foraging sessions, if the cell was active in at least one of the two sessions, the rate overlap was defined as the product of the normalized mean firing rate in the two rooms. The average overlap value was then calculated for all cells in each area. For the same session pairs (with a field in at least one of the two sessions), the Pearson’s correlation coefficient was also calculated between the cell’s firing rate maps. It was possible that a cell would have the same spatial firing patterns in two environments, but the spatial patterns might be rotated relative to each other and to the fixed laboratory frame. Thus, we also calculated ratemap correlations following rotation of one map relative to the other in 10 degree steps. The rotation that resulted in the highest correlation was selected, and the distribution of correlation values was determined for the GCL, hilus, and CA3.

Separate shuffled distributions were generated for the GCL, hilus, and CA3. For each area, cell identity was randomly shuffled within the same foraging session (cell ID was separately shuffled within the 1^st, 2^nd, 3^rd, and 4^th sessions). Using the same procedures used for the observed data, we calculated an average rate overlap and ratemap correlation for the shuffled data. This procedure was repeated 100 times and the observed average overlap value and distribution of correlation values were compared to the shuffled values (Figure 7B, C).

Random forests classifier

Random forests models were generated using a Matlab implementation of the randomForest R package (Liaw and Wiener 2002). Random forests is an ensemble learning method that combines random subsampling of data (through bootstrap aggregating, also referred to as “bagging”) with random selection of features to generate a large number of decision trees (Breiman 2001). In decision tree learning, a hierarchy of splits is generated to separate all data into the appropriate class. At each node in the decision tree, the variable which is best able to partition data is selected. The data continue to split at each node until all points in each branch have the same classification. By using unique bootstrapped samples of the data and random subsets of features, random forests is capable of producing high accuracy classification models that are much less susceptible to overfitting than other supervised learning methods. To generate each tree, a bootstrapped sample of the training data is selected. At each node of the decision tree, only a random subset of features is considered and the best split based on this subset of features is determined. A large number of trees is trained in this way, and when presented with new data to classify, each tree is given a vote, with the most common classification among all trees considered to be the random forests classifier’s output.

The random forests technique does not require a separate cross-validation test, as the method is capable of generating a reliable estimate of prediction error, the “out of bag” (OOB) error. Due to the bootstrapping procedure used to train each tree, not all samples (in our case cells) are used in every tree. The samples not used in training a particular tree are the “out of bag” samples. Each sample in the training dataset is included in the bootstrapped data used to train ~2/3 of the trees. For each sample of training data, the classification generated based on the ~1/3 of trees trained without using that sample is compared to the actual classification. The proportion of misclassifications using this method generates the OOB error.

The random forests method also generates an estimate of variable importance for each variable by determining how much randomizing the values of that variable increases the OOB error rate. Our final model used the features: 1) mean firing rate during baseline session, 2) burstiness (number of ISIs ≤ 6 ms divided by total number of ISIs), 3) number of well-isolated (isolation scores 1–3) putative excitatory cells recorded on the same tetrode, 4) channel slope (best fit line through the peaks of the waveforms on all four tetrode wires, normalized to the highest peak and sorted; Figure S4A), and 5) whether the cell was closer to the GCL or CA3 (based on histology reconstruction). Without the final feature, misclassification errors between GCL and CA3 were prominent, because baseline firing properties of individual cells in the GCL and CA3 were very similar. Because a relatively large distance separates the GCL and CA3, the areas are distinguishable based on histology alone (as long as appropriate measures are in place to minimize significant electrode drift), with most ambiguity being between hilus and GCL or hilus and CA3 recordings. The model was made up of 75 trees and the number of features used at each node of each tree (mtry) was 2 (Figure S4B–C). Other features such as spike width, peak waveform amplitude, the number of putative interneurons recorded on the same tetrode, and difference between the peak amplitude of the largest and smallest waveform were included in our initial classification attempts, but these features were not included in the final classifier as they had very low variable importance and their inclusion did not improve the OOB error rate.

We also performed an unsupervised k-means clustering of data using the number of active rooms and total number of fields during behavior. This method had ~95% accuracy in classifying cells recorded on the final day into two clusters: 1) hilus and 2) combined GCL and CA3. (The latter two classes of cells are not discriminable based on these two parameters.) We used the random forests classification over the k-means clustering for a number of reasons. First, k-means clustering was not capable of accurately dividing between cells of the GCL and CA3. Second, k-means clustering was also unable to accurately classify cell types based on sleep firing properties (producing >30% error rates), instead relying on spatial firing and the number of active rooms to achieve high accuracy. This would not allow us to compare the spatial firing or remapping of all cells to the results from the final recording day. However, k-means clustering did reveal two separate clusters of cells based on the number of fields and active environments, and when classifying all 242 cells, the k-means and random forests classifications were in agreement > 90% of the time (Figure S4I).

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Streptavidin, Alexa Fluor 488 conjugate	ThermoFisher Scientific	Cat. # S11223; RRID AB_2336881
Rabbit polyclonal anti-GluR2/3	Millipore	Cat. # AB1506; RRID AB_90710
Alexa Fluor® 546 Goat Anti-Rabbit IgG (H+L)	ThermoFisher Scientific	Cat. #A-11010; RRID AB_2534077
Chemicals, Peptides, and Recombinant Proteins
Neurobiotin Tracer	Vector Laboratories	Cat. # SP-1120; RRID AB_2313575
Critical Commercial Assays
VECTASHIELD Mounting Medium with DAPI	Vector Laboratories	Cat. # H-1500; RRID AB_2336788
Software and Algorithms
Zen		http://www.zeiss.com/microscopy/us/downloads/zen.html
ImageJ		https://fiji.sc/
ipe		http://ipe.otfried.org/
Matlab	MathWorks	https://www.mathworks.com/products/matlab
R		https://www.r-project.org
Free-D	Andrey and Maurin, 2005	free-d.versailles.inra.fr
Other
Brushless DC micromotor	Micromo, FL	part#0515A006B+06 A 125:1S2
micromanipulator	Kleindiek Nanotechnik	NM2104SE

Highlights.

A decision tree classifier identified putative granule and mossy cells from tetrodes.

Granule cells are rarely active and typically have single firing fields.

Juxtacellularly identified mossy cells have multiple firing fields.

Granule cells and mossy cells differentially encode distinct environments.