Accelerated dynamic MRI Using Patch Regularization for Implicit motion CompEnsation (PRICE)

Abstract

Purpose

To introduce a fast algorithm for motion-compensated accelerated dynamic MRI.

Methods

An efficient patch smoothness regularization scheme, which implicitly compensates for inter-frame motion, is introduced to recover dynamic MRI data from highly undersampled measurements. The regularization prior is a sum of distances between each rectangular patch in the dataset with other patches in the dataset using a saturating distance metric. Unlike current motion estimation and motion compensation (ME-MC) methods, the proposed scheme does not require reference frames or complex motion models. The proposed algorithm, which alternates between inter-patch shrinkage step and conjugate gradient algorithm, is considerably more computationally efficient than ME-MC methods. The reconstructions obtained using the proposed algorithm is compared against state-of-the-art methods.

Results

The proposed method is observed to yield reconstructions with minimal spatiotemporal blurring and motion artifacts. In comparison to the existing state-of-the-art ME-MC methods, PRICE provides comparable or even better image quality with faster reconstruction times (approximately nine times faster).

Conclusion

The presented scheme enables computationally efficient and effective motion-compensated reconstruction in a variety of applications with large inter-frame motion and contrast changes. This algorithm could be seen as an alternative over the current state-of-the-art ME-MC schemes that are computationally expensive.

INTRODUCTION

Dynamic magnetic resonance imaging (DMRI) involves imaging physiological processes that are evolving in time. DMRI is challenged by the slow MRI encoding process, and hence often involves tradeoffs amongst the spatial resolution, temporal resolution, slice coverage and signal to noise. Accelerated imaging involving sparse k - t sampling and constrained reconstruction has demonstrated great potential to improve DMRI (1–8). Several regularization schemes including sparsity-based penalties (3, 5, 9–12), low-rank penalties (13–20) and combination of sparse and low-rank constraints (16, 20, 21) were introduced to accelerate imaging. These methods provide superior reconstructions when the inter-frame motion (e.g in breath-held and gated acquisitions) is relatively low. However, the parsimonious assumptions made by these schemes often break down in the presence of large inter-frame motion, which restricts the performance of these methods in free-breathing and/or ungated applications.

To address the above challenge, several motion estimation and compensation (ME-MC) schemes have been developed; these methods alternate between explicit estimation of inter-frame motion, followed by motion-compensated reconstruction (22–26). For example, the k-t FOCUSS scheme with ME-MC (22), which was introduced for cardiac cine MRI, alternates between motion estimation using block matching and sparsity based regularization of the residuals. Similarly, regional low-rank constraint, coupled with deformation estimation, was introduced in (23) to account for contrast variations in myocardial perfusion MRI. This approach is similar to the patch-based low-rank method introduced for breath-held cardiac cine MRI (24). A generalized deformation compensated compressed sensing (DC-CS) scheme capable to include a variety of penalties (e.g. sparse, low-rank) has also been proposed (27, 28). Other ME-MC schemes include motion-adaptive spatiotemporal regularization (MASTER) (29) and (25, 26) differ in the type of the motion model as well as the exact regularization penalties. The main challenge with all of these schemes is the complex motion estimation step, often involving a computationally expensive deformable image registration, block matching, or optical flow algorithms (29–31). In addition, the lack of a unifying cost function restricts the analysis of the convergence of the joint algorithm to undesirable fixed points. The above mentioned challenges limit the utility of these scheme in applications.

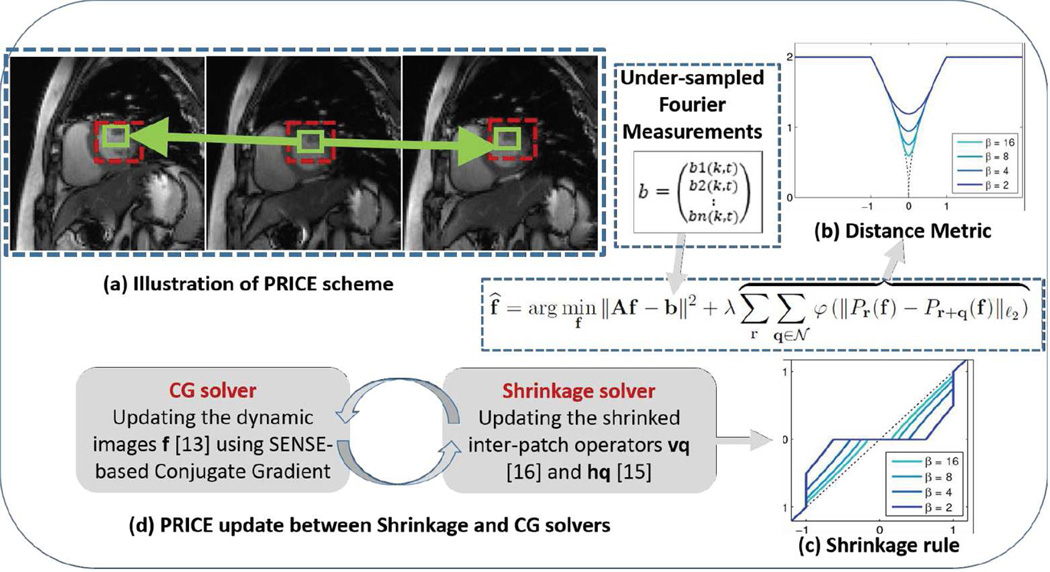
We propose a computationally efficient, patch smoothness regularization framework to overcome the above-mentioned drawbacks. The proposed scheme exploits the similarity of rectangular image sub-patches in a frame with other patches in its spatiotemporal neighborhood (see Fig 1). The regularization penalty, which involves the sum of robust inter-patch distances between patches in each others’ neighborhood, is similar to standard penalties in compressed sensing. The inter-patch distance metric is chosen to heavily penalize small differences, while the metric saturates for large differences (32). By comparing the neighboring patches in both spatial and temporal directions, the proposed framework implicitly compensates for the local motion of the pixels across time, therefore avoiding unnecessary explicit image registration or computation of the motion vectors (see Fig 1). We use the majorization of the regularization penalty to simplify the optimization scheme as an alternating minimization strategy; the algorithm alternates between an analytical inter-patch shrinkage step, and a quadratic update step that is efficiently solved by a conjugate gradient (CG) algorithm. The presence of a common cost function for these two steps enables us to derive efficient continuation strategies that encourage the convergence to the global minimum.

Fig 1.

(a) Illustration of the proposed PRICE scheme. The regularization term penalizes the differences between each patch and other patches in its cube shaped neighborhood. The green squares indicate the location of the patch in the current frame and the ones with the highest similarity in the neighboring frames. The dashed red box represents the neighborhood where the patches move within. The ability of the algorithm to exploit the similarity between corresponding patches enables it to provide implicit motion compensated recovery unlike the traditional ME-MC methods which explicitly do that. The distance metric used for the comparison is shown by the dotted black curve in (b). The metric heavily penalizes the distances between similar patches, while it saturates for large inter-patch distances. This saturating behavior enables the algorithm to minimize spatiotemporal blurring, resulting from averaging of dissimilar patches. The colored curves correspond to the different approximations of the distance metric, which enables fast algorithms. (c) The shrinkage rule for the inter-patch differences t · ν(|t|) using ℓ_p. We rely on continuation schemes as shown in (b) and (c) starting with low values of β and gradually increase it to high values, when the approximation is more accurate. (d) The algorithm alternates between a simple shrinkage step to denoise inter-patch differences and image update step, which involves a computationally efficient conjugate gradients algorithm.

The proposed scheme is based on our work on robust patch-based regularization algorithm (33, 34), which was developed for inverse problems involving static two-dimensional images. The main focus of this paper is to generalize this idea to dynamic MRI. This work has significant distinctions from our early conference work in (32), which relied on a slower iterative reweighed algorithm. While the algorithm in (32) was mainly validated using numerical phantoms and simulations, the proposed algorithm is validated using in-vivo prospective studies with multi-channel acquisitions. The PRICE scheme also has conceptual similarities to patch-based methods that rely on dictionary learning used in several applications including dynamic MRI (35, 36). In contrast to these schemes, we considerably reduce the search space by focusing on a smaller search neighborhood; this results in an algorithm whose computational complexity is comparable to classical total variation regularization. The PRICE scheme also has similarities to (37) that uses a combination of 2-D spatial and 1-D temporal non-local penalties. However, (37) does not compare a patch to shifted patches in the neighboring frames; our preliminary comparisons with this method (see (32)) demonstrated the benefit offered by our earlier framework in terms of free breathing myocardial perfusion.

The utility of the proposed PRICE scheme is demonstrated in the context of free-breathing cardiac cine and myocardial perfusion datasets, using retrospective and prospective experiments. We compare the algorithm against a classical compressed sensing scheme that exploits spatiotemporal finite difference sparsity, a combination of sparse and low-rank (16) as well as state-of-the-art ME-MC methods MASTER and DC-CS (27, 29).

THEORY

Dynamic MRI: model of the acquisition scheme

The multi-coil undersampled acquisition of the dynamic MRI dataset f (x, y, t) : ℤ³ → ℂ can be modeled as:

$${\mathbf{b}}_i(k_x,k_y,t)={\int }_{x,y}\mathbf{f}(x,y,t)s_i(x,y)e^{j(k_{x}x+k_{y}y)}dxdy+\mathbf{n}(k_x,k_y,t).$$ [1]

Here, b(k_x, k_y, t) represents the k-space measurements from all the coils, while f (x, y, t) is the dynamic dataset, and s_i(x, y) denotes the i^th coil sensitivity pattern. We assume n to be a complex zero mean Gaussian distributed white noise process of a specified standard deviation σ. The above relations can be compactly expressed in the vector form as

$$\mathbf{b}=\mathbf{A}\mathbf{f}+\mathbf{n},$$ [2]

where A is termed as the forward model. From now on, we will consider the dynamic dataset f as a 3-D volume indexed by the variable r = (x, y, t).

Implicit motion compensation using patch regularization

We propose to recover the dynamic dataset f from its undersampled measurements as the patch regularized optimization problem as:

$$\hat{\mathbf{f}}=\text{arg }\underset{\mathbf{f}}{\text{min}}\underset{𝒞(\mathbf{f})}{\underbrace{{\Vert \mathbf{A}\mathbf{f}-\mathbf{b}\Vert }^2+\lambda 𝒢(\mathbf{f})}},$$ [3]

The first term in the cost function ensures data fidelity with the k-space measurements, while λ is the regularization parameter. The regularization penalty 𝒢(f) is the sum of robust distances between patches:

$$𝒢(\mathbf{f})=\sum _{\mathbf{r}}\sum _{\mathbf{q}\in 𝒩}\phi ({\Vert P_{\mathbf{r}}(\mathbf{f})-P_{\mathbf{r}+\mathbf{q}}(\mathbf{f})\Vert }_{{\ell }_2}).$$ [4]

Here, P_r(f) is a patch extraction operator, which extracts a square shaped 2-D image patch of dimension (N + 1) × (N + 1) × 1, centered at the spatial location r from the dynamic dataset f (r):

$$P_{\mathbf{r}}(\mathbf{f})=\mathbf{f}(\mathbf{r}+\mathbf{p}),\mathbf{p}\in ℬ.$$ [5]

Here, β = [−N/2, ‥N/2] × [−N/2, ‥N/2] × 1 is the set of indices of the patch. Note from [3] that we compare each patch P_r(f) in the dataset with other patches P_r+q(f) in a cube-shaped neighborhood 𝒩 ∈ [−M/2, ‥M/2] × [−M/2, ‥M/2] × [−M/2, ‥M/2] around r (see Fig 1.a). Even though it is fixed in our study, the size of the neighborhood may be chosen depending on the severity of inter-frame motion. Specifically, the size of the search neighborhood (M) may need to be increased in high-resolution datasets or datasets with high inter-frame motion such as dynamic free breathing lung MRI where there is a considerably large amount of cardiorespiratory motion. While the formulation [3] has similarities to block matching used in k-t FOCUSS with ME-MC (22), the distinguishing aspect is a unifying cost function that captures both motion estimation and compensation.

The comparisons of each patch with its neighbors are performed using the distance metric φ. While convex ℓ₁ metrics could be chosen, our comparisons show that the thresholded ℓ_p, 0 < p < 1, metric

$$\phi (t)=\{\begin{array}{cc}|t{|}^p/p\hfill & \text{if }t<T\hfill \\ T^p/p\hfill & \text{if }t\ge T.\hfill \end{array}$$ [6]

provides the best reconstruction with 2–4 db gain over p = 1 without thresholding (33). Compared to convex penalties, the proposed saturating priors (see dotted curve in Fig 1.b) minimizes the averaging of dissimilar patches, thus resulting in less blurred reconstructions. For example, while a patch pair with difference greater than T will still contribute to a constant term of T^p/p in the cost, a small shrinkage of these inter-patch distances will not reduce the cost. This behavior translates to patch differences above T not being shrunk at each iteration as seen from [10] (see also Fig 1.c). By contrast, a non-saturating ℓ₁ penalty shrinks all patch differences, irrespective of the size of differences, resulting in blurring.

Iterative patch shrinkage algorithm

We use the majorization of the patch regularization penalty 𝒢(f) to develop an iterative patch shrinkage algorithm to solve [3]. Approximating the distance metric in [6] (dotted line in Fig 1.b) by its smoothed Huber-like versions, we rewrite the cost function with the approximated penalties as:

$${𝒞}_{\beta }(\mathbf{f})=\underset{\{{\mathbf{s}}_{\mathbf{r},\mathbf{q}}\}}{\text{min}}{\Vert \mathbf{A}\mathbf{f}-\mathbf{b}\Vert }^2+\lambda \sum _{\mathbf{r}}\sum _{\mathbf{q}\in 𝒩}{\psi }_{\beta }(\Vert {\mathbf{s}}_{\mathbf{r},\mathbf{q}}\Vert )+\frac{\lambda \beta }{2}\sum _{\mathbf{r},\mathbf{q}}{\Vert P_{\mathbf{r}}(\mathbf{f})-P_{\mathbf{r}+\mathbf{q}}(\mathbf{f})-{\mathbf{s}}_{\mathbf{r},\mathbf{q}}\Vert }^2.$$ [7]

Here, s_r,q is an auxiliary variable, which can be interpreted as a denoised version of the inter-patch difference (P_r(f) − P_r+q(f)). The above simplification is enabled by the half quadratic majorization of φ (38–41):

$$\phi (t)=\underset{s}{\text{min}}\{{\psi }_{\beta }(s)+\frac{\beta }{2}{(s-t)}^2\}.$$ [8]

The above majorization rule can be rewritten as:

$$\underset{r(t)}{\underbrace{\frac{t^2}{2}-\frac{1}{\beta }\phi (t)}}=\underset{s}{\text{max}}\{st-\underset{g(s)}{\underbrace{(\frac{1}{\beta }{\psi }_{\beta }(s)+\frac{s^2}{2})}}\}$$ [9]

From the theory in (42), the above relation is satisfied when g = r*, the Legendre-Fenchel dual of r, specified by r*(s) = max_t {s t − r(t)}. Thus, we obtain ψ_β(s) = β (r* (s) − s²/2). When r is not convex, we approximate it by the closest convex function of r; see (33) for details.

It is often difficult to determine an analytical expression for ψ_β. However, the associated shrinkage rule (see [11]) can be determined analytically as shown in (33), which is sufficient to implement an efficient algorithm. We use an alternating minimization algorithm to recover f as well as the denoised inter-patch differences s_r,q from multi-coil undersampled k - t measurements. We observe that the reformulation in [7] is remarkably similar to variable splitting; the only difference is that ψ_β = φ in the variable splitting formulation. If variable splitting strategy were used, one would be able to speed up the algorithm using alternating direction method of multipliers (ADMM). However, a challenge with ADMM schemes is the lack of monotonic convergence. While it is acceptable with convex cost functions, it may result in issues of convergence to local minima when non-convex distance metrics such as [6] are used. The monotonic convergence guaranteed by majorize-minimize framework is desirable in this setting. We also introduce continuation strategies to minimize the risk of local minima.

Step 1: Determination of denoised inter-patch differences s_r,q

When the variable f is a constant, the determination of the auxiliary variables s_r,q corresponding to different values of r and q can be decoupled. Specifically, the recovery of a specific patch ŝ_r,q simplifies to a shrinkage step similar to soft thresholding:

$${\mathbf{ŝ}}_{\mathbf{r},\mathbf{q}}=[P_{\mathbf{r}}(\mathbf{f})-P_{\mathbf{r}+\mathbf{q}}(\mathbf{f})]\nu (\Vert P_{\mathbf{r}}(\mathbf{f})-P_{\mathbf{r}+\mathbf{q}}(\mathbf{f})\Vert ).$$ [10]

The shrinkage rules for a variety of distance metrics are specified in (33). For example, when φ is the thresholded ℓ^p metric [6], we have

$$\nu (t)=\{\begin{array}{ccc}\hfill 0\hfill & \hfill \text{if}\hfill & \hfill |t|<{\beta }^{1/(p-2)}\hfill \\ \hfill 1-\frac{1}{\beta }|t{|}^{p-2}\hfill & \hfill \text{if}\hfill & \hfill {\beta }^{1/(p-2)}\le |t|<T\hfill \\ \hfill 1\hfill & \hfill \text{else}.\hfill \end{array}$$ [11]

Note from [10] and [11] that the smaller inter-patch differences are set to zero or shrunk, while the large inter-patch differences are preserved. The shrinkage rule is illustrated in Fig 1.c.

Step 2: Determination of the dataset f

If we assume the auxiliary variables s_r,q to be fixed, the minimization of [7] with respect to f simplifies to a quadratic subproblem. Combining the terms from adjacent patches for computational efficiency (see Appendix of (33) for details), we simplify this subproblem as

$$\hat{\mathbf{f}}=\text{arg }\underset{\mathbf{f}}{\text{min}}{\Vert \mathbf{A}\mathbf{f}-\mathbf{b}\Vert }^2+\lambda \frac{\beta }{2}\sum _{\mathbf{q}\in 𝒩}{\Vert {\mathbf{D}}_{\mathbf{q}}\mathbf{f}-{\mathbf{h}}_{\mathbf{q}}\Vert }^2.$$ [12]

Here, h_q(x) is specified by the sum of ŝ_r,q terms from the adjacent patches:

$$h_{\mathbf{q}}(\mathbf{x})=\sum _{\mathbf{p}\in ℬ}{\mathbf{ŝ}}_{\mathbf{x}-\mathbf{p},\mathbf{q}}(\mathbf{p}),$$ [13]

The operator D_q in [12] is the finite difference operator

$$({\mathbf{D}}_{\mathbf{q}}\mathbf{f})(\mathbf{x})=\mathbf{f}(\mathbf{x})-\mathbf{f}(\mathbf{x}+\mathbf{q}).$$ [14]

For example, (D_(1,0)f)(r) = f(r) − f(r + (1, 0, 0)) is the standard horizontal finite difference operator. Note that by using [10] in [12], the terms with inter-patch differences greater than T will still contribute to a constant term of T^p/p in the cost. This behavior translates to patch differences above T not being shrunk at each iteration as seen from [10] (see also Fig 1.c) while the terms with smaller inter-patch differences are penalized. We solve [12] efficiently using conjugate gradient (CG) algorithm.

METHODS

The breath-held CINE dataset considered in this study is distributed as part of the MASTeR software package (29), while the free breathing Cartesian dataset was acquired at New York University (43). The perfusion datasets were both acquired at the University of Utah. All the datasets used in this note were acquired under protocols approved by the Institutional Review Board (IRB) of the respective institutions.

Experiments involving cardiac CINE MRI

We first consider the retrospective undersampling of a fully sampled ECG-gated Cartesian breath-held dataset, acquired using a steady-state free precession (SSFP) sequence using a five channel cardiac array. The scan parameters were TE/TR= 2.0/4.1 ms, flip angle=45°, FOV=350 mm², slice thickness=12 mm, 8 views per segment, 224 phase-encoding lines, 256 read-out samples and 16 temporal frames. This dataset was undersampled by keeping a subset of the 224 phase-encoding lines consisting of a fully sampled low-frequency region (eight low-frequency lines) and a pseudo-randomly sampled high-frequency region chosen according to a Gaussian density; the specific pseudo random subsets varied from frame to frame.

In the second experiment, we consider the recovery of a prospectively undersampled free-breathing and prospectively ECG-gated cardiac CINE dataset. The data was acquired using a steady state free precession (SSFP) sequence on Siemens 3T scanner with 12 coil elements total (body and spine coil arrays). The acquisition parameters were FOV: 320 mm², matrix 128×128, TE/TR = 1.37/2.7 ms, BW: 1184 Hz/pixel, and flip angle = 40°. The acquisition lasted for two heart beats, while the subject was freely breathing, resulting in 16 lines/frame. The sampling pattern varies from frame to frame; some of the frames are sampled with dense low-frequency region, while the lines in other frames are sampled randomly in the low and high-frequency region. See (43) for more details about this dataset.

Experiments involving myocardial perfusion imaging

In the first experiment involving perfusion data, we retrospectively undersampled a fully-sampled Cartesian in-vivo myocardial perfusion dataset. The dataset was acquired without ECG-gating and the subject breathed heavily during the scan. The data was acquired using a saturation recovery FLASH sequence (with TR/TE =2.5/1 ms, saturation recovery time = 100 ms, 1 slices, 32 coil elements total, phase encodes × frequency encodes: 108 × 288, temporal resolution: ≈ 4frames/beat, spatial resolution: 2.5 × 2.5 × 8 mm³); the reader is referred to (6, 44) for more details about this dataset. The dataset was retrospectively undersampled using a Cartesian sampling pattern with a fully sampled low-frequency region and a randomly sampled high-frequency region. To make the computational complexity manageable, we have only considered 80 temporal frames out of 200. We only used the data corresponding to six of the 32 channels, which best cover the heart; we did not resort to any coil compression.

In the second perfusion experiment, we consider the retrospective undersampling of radially sampled free-breathing stress ECG-gated myocardial perfusion data, acquired with a saturation recovery FLASH sequence with TR/TE =2.6/1.2 ms, phase encodes × frequency encodes: 256 × 256, 3 slices/beat, flip angle=14°, voxel size =2.3 × 2.3 ×8 mm³, FOV: 280 mm², bandwidth 1002 Hz/pixel. This dataset has 67 temporal frames which are all considered for recovery. Seventy two radial spokes per frame, equally spaced over π radians with 256 samples per spoke were acquired. The radial pattern in successive frames were rotated by a uniform angle of π/288 radians across frames, which corresponds to a period of 4 across time. The details of this dataset are available at (45). We subsampled the dataset by retaining a subset of 24 spokes per frame. To obtain incoherent sampling, the spokes that are the closest in angles to a golden angle trajectory were retained; a similar subsampling strategy was used in (16). The 72 spoke data, acquired with a four coil cardiac array, was reconstructed using SENSE-based spatiotemporal TV regularization; simpler gridding based reconstructions exhibited considerable streaking artifacts and were found unacceptable for comparisons.

For all the radial acquisitions considered in this paper, we first gridded the radial data to a Cartesian grid to avoid the use of non-uniform Fourier transform computations within the reconstruction algorithms. Our previous experiments (16) show that the loss in image quality resulting from this approximation is minimal.

Implementation details

All the algorithms were implemented in MATLAB 2012 on a Linux Intel Xeon workstation machine with four cores, 3.2 GHz CPU, and 32 GB RAM.

Metrics used for quantitative comparison

The retrospective reconstructions were quantitatively compared to reference data using the following metrics. We evaluate these metrics in a square region of interest containing the heart.

• Signal to Error Ratio (SER): This metric gives a measure of overall accuracy in reproducing the spatiotemporal dynamics in the heart regions and defined as:

  $$\mathbf{S}\mathbf{E}\mathbf{R}=20{\text{log}}_{10}\left(\frac{{\Vert {\mathbf{\Gamma }}_{\mathbf{\text{orig}}}\Vert }_2}{{\Vert {\mathbf{\Gamma }}_{\mathbf{\text{orig}}}-{\mathbf{\Gamma }}_{\mathbf{\text{rec}}}\Vert }_2}\right),$$

  where ‖ · ‖₂ donates the ℓ₂ norm, and Γ_orig, Γ_rec denote the original and the reconstructed images respectively.
• Normalized High Frequency Error (HFEN): It measures the quality of fine features, edges, and spatial blurring in the images and defined as:

  $$\mathbf{H}\mathbf{F}\mathbf{E}\mathbf{N}=20{\text{log}}_{10}\left(\frac{{\Vert \text{LoG}({\mathbf{\Gamma }}_{\mathbf{\text{orig}}})\Vert }_2}{{\Vert \text{LoG}({\mathbf{\Gamma }}_{\mathbf{\text{orig}}})-\text{LoG}({\mathbf{\Gamma }}_{\mathbf{\text{rec}}})\Vert }_2}\right),$$

  where LoG is a Laplacian of Gaussian filter that capture edges. We use the same filter specifications as (35): kernel size of 15 × 15 pixels, with a standard deviation of 1.5.

• The Structural SIMilarity index (SSIM):We used the toolbox introduced by (46), with default contrast values [0.01 0.03], Gaussian kernel size of 11 × 11 pixels with a standard deviation of 1.5 pixels to compare the reconstructions.

Selection of parameters

To ensure fair comparisons in retrospective undersampling experiments, all algorithms were run with a range of parameter values, and the parameter set that resulted in the best SER was chosen. In the prospective experiment involving free breathing cardiac CINE data, the parameters of all the methods were tuned manually to get the best performance. Considering that we compare algorithms of very different flavors on datasets acquired at different conditions, we believe that this is a reasonable strategy to ensure fair comparisons. We used the reconstruction of the total variation regularization as an initial guess for the DC-CS scheme (27).

We set the neighborhood and patch sizes in PRICE to 5×5×5 and 3×3×1 (N=2; M=4), respectively for all the experiments. Our experiments (not shown here) shows that these settings were sufficient to capture the inter-frame motion in all the applications considered in this paper; larger neighborhood sizes did not significantly improve the performance, while they resulted in slower reconstructions. The continuation parameter β was initialized by 0.01 and was incremented by a factor of 1.5 in each outer iteration. Similarly, T was set to be about a half of the image maximum intensity value and divided by a small fraction in each outer iteration. Our experiments show that p = 0.5 in [6] gave the best tradeoff between computational complexity and quality of the reconstructions. We used 5 inner-iterations and 20 outer-iterations for all the experiments considered in this paper. These continuation strategies minimized the risk of convergence to local minimum and also provided fast convergence; see (33) for more details. The algorithm is terminated when the relative change in cost falls below small value ε; we have set ε as 1e-6 in our scheme.

RESULTS

Cardiac CINE datasets

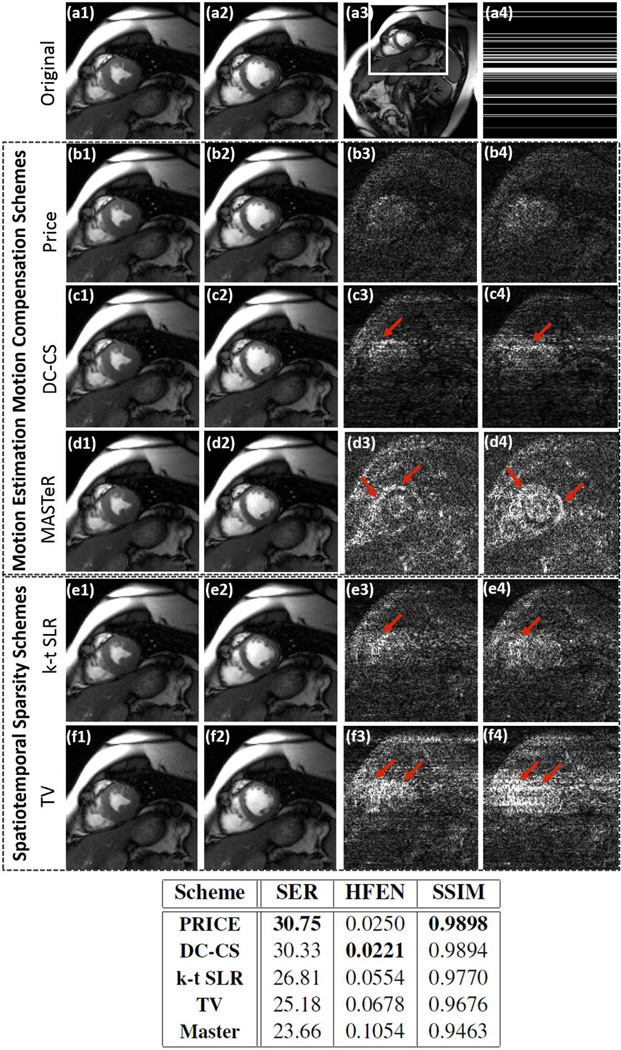
The reconstruction of the retrospectively undersampled cardiac CINE dataset using PRICE, spatiotemporal total variation based algorithm (TV), k-t SLR (16), and the state-of-the-art ME-MC methods (27, 29) are shown in Fig 2, along with their error images. The Cartesian sampling pattern corresponding to an undersampling factor of 6, was used to subsample the datasets. Two frames corresponding to peak diastole and systole cardiac phases are shown for each scheme; the error images are scaled by a factor of 7 for better visualization. We observe that the quality of the PRICE reconstructions is quite comparable to the DC-CS recovery, which explicitly compensates for the motion; the error images show that the errors associated with PRICE and DC-CS are more homogeneously distributed in the entire image, resulting in improved SER. By contrast, the errors associated with TV and MASTeR methods are more concentrated in the edge regions, indicating edge blurring. The table shows a quantitative comparison of the entire methods using SER, HFEN and SSIM metrics; all computed on the region of interest shown in first row. The run time of PRICE, DC-CS and MASTeR were 24.4 minutes, 3.8 hours, 3.3 hours respectively. The run time for k-t SLR was 25 minutes while TV took approximately 19 minutes.

Fig 2.

Recovery of a retrospectively undersampled CINE dataset using PRICE (second row; b1 &b2), explicit motion-compensated algorithms (third and fourth rows), k-t SLR and classical total variation regularization (fifth and sixth rows). The 256×224×16 dynamic dataset, which is acquired using ×5 coils, is retrospectively undersampled using Cartesian sampling pattern. The cropped cardiac images of the fully sampled data corresponding to peak diastole and systole cardiac phases are shown in (a1) and (a2). These images are cropped versions of the full frame shown in (a3). The sampling pattern for one frame is shown in (a4). The cropped reconstructed images are shown in the first two columns, while their error images scaled by a factor of 7 for better visualization are shown in the last two columns. The reconstructions using the PRICE algorithm is quite comparable to the DC-CS scheme, which explicitly compensates for the motion; the error images show that the errors associated with PRICE and DC-CS are more homogeneously distributed in the entire image, resulting in improved SER. By contrast, the errors with other methods (e.g. TV and MASTeR) are more concentrated in the edge regions, indicating edge blurring. The table shows a quantitative comparison of the entire methods using SER, HFEN and SSIM metrics; all computed on the region of interest as shown in (a3).

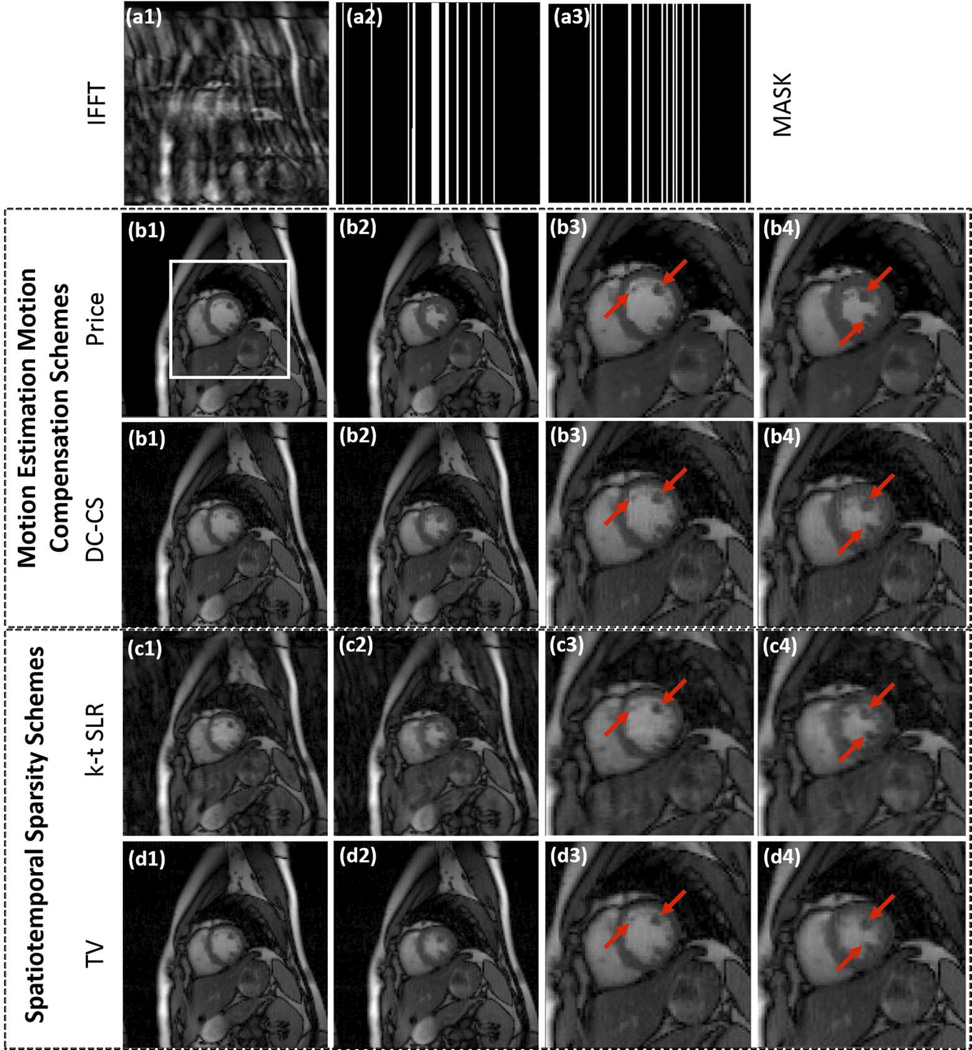
The experiments involving prospective Cartesian undersampled free breathing CINE data is shown in Fig 3. The comparisons show that the proposed scheme provides reconstructions with lower motion artifacts and less blurring compared to DC-CS, k - t SLR, and TV regularized reconstructions, especially near the myocardial borders and papillary muscles. The inter-frame motion in this dataset is relatively high, making it a challenging example. We found it difficult to optimize the parameters of MASTeR in the prospective experiments when the ground truth are not available and hence we have excluded them from the comparisons.

Fig 3.

Recovery of a prospectively undersampled Cartesian CINE dataset using PRICE, DC-CS, k-t SLR and TV algorithms. The 128×128×20 sized dataset is acquired using 12 coils and 16 Cartesian lines per phase. Two frames corresponding to peak diastole and systole cardiac phases are shown for each scheme along with their zoomed versions around the square box as shown in (b1). The sampling pattern varies from frame to frame; the sampling masks corresponding to two different frames are shown in (a2) and (a3). We observe that TV and k - t SLR reconstructions exhibit temporal blurring while DC-CS had some motion artifacts. PRICE is able to provide better reconstructions with less blurred myocardial borders and papillary muscles.

We observe that the spatial resolution of the second CINE dataset is slightly lower (voxel size of 2.5×2.5 mm²), resulting in a slightly higher signal to noise ratio. The higher SNR might have impacted our results; the achievable acceleration factors may be lower if higher spatial resolution was considered. The run time of PRICE and DC-CS were 7 minutes and 45 minutes respectively while k-t SLR took 10 minutes and TV approximately 7 minutes.

Myocardial perfusion MRI

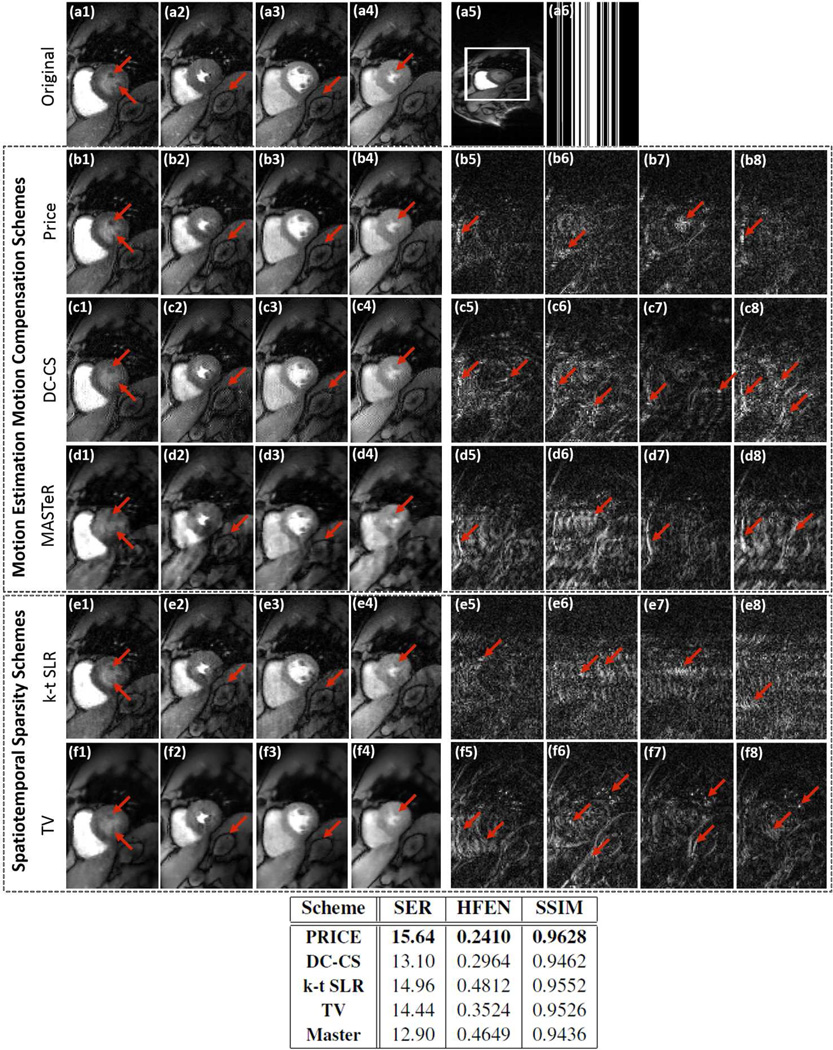
The results of the retrospectively undersampled ungated and free-breathing in-vivo myocardial perfusion experiment are shown in Fig 4. We consider the recovery from three fold undersampled Cartesian trajectory. The proposed algorithm is compared against DC-CS (27), k - t SLR, MASTeR (29), and spatiotemporal total variation regularization algorithm. Four frames corresponding to peak right ventricular blood enhancement, transition between right ventricle and left ventricle, peak left ventricular blood enhancement and the case when the enhanced blood leaves the heart are shown. The ungated acquisition enables us to acquire diastolic and systolic frames. This dataset is quite challenging due to quite significant cardiac and respiratory motion as well as contrast variations resulting from bolus passage. We observe that the PRICE scheme is able to provide reconstructions with lower spatial and temporal blurring compared to the other schemes. The quantitative metrics show about 1– 2.5 dB improvement compared to other reconstructions. Even though DC-CS results in crisp images, it exhibits pixelated interpolation artifacts in some frames due to inaccuracies during correction of the highly non-rigid cardiac motion between consecutive systole and diastole phases. Other authors have also reported similar artifacts when compensating for large motion with explicit motion compensation algorithms (26). The run time of MATLAB CPU versions of PRICE, DC-CS and MASTeR were 18.5 minutes, 1.4 hour, 1.2 hour respectively. The run time for k-t SLR was 38 minutes while TV took approximately 24 minutes.

Fig 4.

Evaluation of the ME-MC algorithms by retrospectively downsampling ungated & free-breathing myocardial perfusion MRI data. The images (a1)–(a4) correspond to frames in the time series with different cardiac/respiratory phases and different contrast due to bolus passage. These images are cropped from a 288×108×80 dataset acquired with 6 coils; one of these images are shown in (a5). We undersampled the Cartesian sampled data along the phase encoding direction to obtain a three-fold acceleration. One of the sampling masks are shown in (a6). The reconstructions and corresponding residuals using PRICE (b1–b4) & (b5–b8), DC-CS (c1–c4)& (c5–c8), MASTeR (d1–d4)& (d5–d8), k-t SLR (e1–e4)& (e5–e8) and TV (f1–f4)& (f5–f8) are shown. The error images are scaled by a factor of three for better visualization. The extensive inter-frame motion and contrast variations due to bolus passage makes this dataset very challenging. We observe that the PRICE scheme provides reconstructions with lower spatial and temporal blurring, compared to the other algorithms. The table above shows a quantitative comparison of the entire methods using SER, HFEN and SSIM metrics computed on the region of interest shown in (a5).

The experiments on the free-breathing ECG-gated radial stress perfusion MRI datasets, acquired from a normal subject and recovered from 24 rays are shown in Fig 5. The motion in this dataset is not as challenging as in the previous case since the acquisition was ECG-gated and the subject was instructed to breath shallowly. We observe that most of the motion compensated algorithms provide good reconstructions in this case. However, PRICE is considerably more computationally efficient than those explicit ME-MC methods. It is also seen from the error images that the motion compensated methods (PRICE and DC-CS) provide reduced edge blurring and better preservation of fine features, including papillary muscles and around the myocardium wall as shown in the red arrows. The run time of PRICE and DC-CS were 20.6 minutes and 1.6 hours respectively while k-t SLR took 50 minutes and TV approximately 33 minutes.

Fig 5.

Evaluation of the ME-MC algorithms by radially downsampling 256×256×67 adenosine free-breathing stress myocardial perfusion MRI data acquired from a normal subject. Three frames of the reference data acquired using 72 spokes/frame are shown in (a1)–(a3). This data is undersampled by retaining a subset of 24 spokes; the sampling trajectory for one of the frames is shown in (a4). The recovered images and their corresponding residual images using PRICE (b1–b3) & (b4–b6), DC-CS (c1–c3) & (c4–c6), k-t SLR (d1–d3) & (d4–d6), and TV (e1–e3) & (e4–e6) are shown. The three frames correspond to peak right ventricular blood enhancement, a transition between the right ventricle and the left ventricle and peak left ventricular blood enhancement respectively. It is seen from the error images that the motion compensated methods (PRICE and DC-CS) provide reduced edge blurring and better preservation of fine features, including papillary muscles and around the myocardium wall as shown by the red arrows.

DISCUSSION

We have introduced a patch regularization framework to recover DMRI from undersampled Fourier measurements. The proposed method utilizes the redundancy between patches in nearby frames to achieve implicit motion-compensated recovery. This makes it a computationally efficient alternative to ME-MC methods, which often require detailed motion models, reference frames, and careful initialization to minimize the convergence to local minimum. More importantly, the computational complexity of these methods are rather high. By contrast, the PRICE scheme formulates the motion-estimation and motion compensation steps into a simple cost-function, which is similar to classical total variation regularization.

Our experiments show that the performance of PRICE is comparable or slightly better than explicit motion compensation schemes. Note that the ME-MC schemes already provide superior reconstructions compared to non motion-compensated methods such as total variation regularization and k-t SLR; PRICE provides a computationally efficient alternative to the above explicit ME-MC methods. The experiments also show that PRICE can provide improved reconstruction of perfusion MRI data, which indicates that it is not very sensitive to the contrast changes between the frames. Specifically, the robust nature of the distance function minimizes the averaging of the patches that differ considerably in contrast/intenstity, thus reduces blurring in these regions. Note that the contrast changes are highly localized in space; the similarity of the patches in other regions can still be exploited effectively using the proposed PRICE algorithm. While the use of patch-based low-rank methods such as (23, 24) may further improve the results, it is not clear if these methods can be formulated as a simple and cost function as [3].

The choice of the parameters of PRICE is mainly motivated by the specific datasets we considered in this paper. These parameter values may have to be adjusted to obtain good performance on other datasets. Specifically, the size of the search neighborhood (M) may need to be increased in high-resolution datasets or datasets with high inter-frame motion. The computational complexity of the algorithm grows linearly with the number of patches that are compared. We observe that ME-MC algorithms involving block/patch matching will result in the same complexity tradeoffs. Likewise, the complexity of algorithms involving deformable models (e.g. DC-CS) also increases significantly with increased inter-frame motion. Our experiments show that the quality of the reconstructions are the best when the patch size is N = 2; the assumption of translational motion will be violated with larger patch sizes, restricting the performance. While ℓ_p; p < 1 penalties exhibit some saturation compared to ℓ₁ priors, we observe improved performance with perfect saturation. The reader is referred to Fig 2 of (34) for comparisons of different penalties. The convergence rate of the algorithms is dependent on p, with smaller p resulting in slower convergence.

The DC-CS algorithm derives a motion compensated dataset as the byproduct (27), which may be used for quantification. Since the motion compensation in PRICE algorithm is implicit, further post-processing steps for registration are required before quantification. However, the computational complexity of PRICE is considerably lower than DC-CS; the combined pipeline (recovery, followed by registration) is still expected to be smaller.

The acquisition window for the first fully sampled perfusion Cartesian dataset is approximately 225 ms. Since the heart may not be fully stationary during this window, the reference reconstructions may be corrupted by cardiac motion during this window. Since the acquisition window for the second perfusion dataset is shorter (187 ms), the effect of cardiac motion in the reference data may be less significant.

We observe from Fig. 3 that the DC-CS scheme provides higher errors in the Cartesian undersampling setting. This may be attributed to the assymetry of sampling; the original DC-CS implementation (27) uses radial patterns that allows symmetric undersampling of k-space. This problem may be mitigated by using a corresponding assymetric/direction dependent smoothness regularization of the deformation maps in DC-CS. However, this modification is beyond the scope of this note.

CONCLUSION

We introduced an iterative patch-based shrinkage algorithm to recover dynamic MRI from highly undersampled Fourier measurements. The proposed framework alternates between a patch shrinkage step and a quadratic subproblem that is solved efficiently using conjugate gradients algorithm. The comparison of PRICE against classical TV and k - t SLR schemes demonstrates the benefits of this framework in reducing motion-induced blurring and streaking artifacts. The algorithm is also seen to provide comparable or improved reconstructions over state-of-the-art ME-MC schemes, while being considerably more computationally efficient. The existence of a common cost function for both motion-estimation and motion compensation steps enable efficient continuation strategies that encourage the convergence to the global minimum. The proposed scheme may be thought of as an implicit motion-compensated compressed sensing scheme with computational complexity that is comparable to classical TV methods.