Evaluation of singlet oxygen explicit dosimetry for predicting treatment outcomes of benzoporphyrin derivative monoacid ring A-mediated photodynamic therapy

Abstract.

Existing dosimetric quantities do not fully account for the dynamic interactions between the key components of photodynamic therapy (PDT) or the varying PDT oxygen consumption rates for different fluence rates. Using a macroscopic model, reacted singlet oxygen (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) was calculated and evaluated for its effectiveness as a dosimetric metric for PDT outcome. Mice bearing radiation-induced fibrosarcoma tumors were treated with benzoporphyrin derivative monoacid ring A (BPD) at a drug-light interval of 3 h with various in-air fluences (30 to $350\mathrm{J}/{\mathrm{cm}}^2$) and in-air fluence rates (50 to $150\mathrm{mW}/{\mathrm{cm}}^2$). Explicit measurements of BPD concentration and tissue optical properties were performed and used to calculate ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, photobleaching ratio, and PDT dose. For four mice, in situ measurements of ${}^3{\mathrm{O}}_2$ and BPD concentration were monitored in real time and used to validate the in-vivo photochemical parameters. Changes in tumor volume following treatment were used to determine the cure index, $\mathrm{CI}=1-k/k_{\mathrm{ctr}}$, where $k$ and $k_{\mathrm{ctr}}$ are the tumor regrowth rates with PDT and without PDT, respectively. The correlation between CI and the dose metrics showed that the calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm is an effective dosimetric quantity for predicting treatment outcome and a clinically relevant tumor regrowth endpoint.

1. Introduction

As a nonionizing radiation treatment, photodynamic therapy (PDT) has been used effectively for the treatment of various easily accessible lesions, such as head and neck cancers, esophageal cancers, microinvasive lung cancer, and skin lesions such as premalignant actinic keratosis.^1–4 PDT requires the administration of a photosensitizer that localizes in tumor tissue and is excited by the appropriate treatment wavelength of light. With the absorption of light, the photosensizer transitions from its ground state to a short-lived excited singlet state. The singlet state photosensitizer transitions to a longer-lived electronically excited triplet state via intersystem crossing. In typical type II PDT, which is the focus of this study, the triplet state transfers energy to molecular ground state oxygen (${}^3{\mathrm{O}}_2$) that is present in the treatment environment to produce singlet-state oxygen (${}^1{\mathrm{O}}_2$). The production of ${}^1{\mathrm{O}}_2$ and reactions with the surrounding biological molecules are thought to be the major cause of cytotoxicity.⁵ Due to the high reactivity and short lifetime of ${}^1{\mathrm{O}}_2$, only cells that are proximal to the area of ${}^1{\mathrm{O}}_2$ production are directly affected by PDT.⁶ For that reason, PDT causes significantly less harm to healthy tissue than chemotherapy or radiation.^6,7 A well-defined dosimetric metric for PDT that is able to predict clinical outcomes that can also be implemented in a clinical setting would benefit the advance of the PDT field.

Benzoporphyrin derivative monoacid ring A (BPD, trademark Visudyne^®) is a commonly used photosensitizer that was approved by the US Food and Drug Administration in 2000 for the treatment of wet age-related macular degeneration.⁸ Utilizing a macroscopic model, reacted singlet oxygen (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) can be calculated to evaluate its effectiveness as a dosimetric predictor for BPD-mediated PDT outcome. In addition, several other dose metrics were evaluated in this study, including total light fluence, photobleaching ratio, and PDT dose, to predict the PDT outcome. Radiation-induced fibrosarcoma (RIF) tumors on mice were treated with BPD-PDT and a range of in-air fluences (30 to $350\mathrm{J}/{\mathrm{cm}}^2$) and in-air fluence rates (50 to $150\mathrm{mW}/{\mathrm{cm}}^2$). For each PDT treatment group, explicit measurements of BPD concentration in tumor and tissue optical properties were performed pre- and posttreatment. For a subset of mice, real-time in-vivo measurement of BPD concentration and tissue oxygenation level ($[{}^3{\mathrm{O}}_2]$) throughout PDT were taken to optimize the photosensitizer-specific PDT photochemical parameters ($\xi$, $\sigma$, and $g$), reduce their uncertainty from a previous study, and calculate ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$. These photochemical parameters were used to calculate ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ for each PDT treatment group. Other dose metrics, such as photobleaching ratio and PDT dose, were determined either directly using explicit measurements pre- and post-PDT or calculated using the time dependence of BPD concentration based on the macroscopic model and the definition of PDT dose. This study, to our knowledge, is the first to investigate the threshold value of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ and the relationship between various dose metrics (fluence, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) and the cure index (CI) at 14 days in an in-vivo mouse model for BPD-mediated PDT. The results of our study with additional real-time measurements of BPD concentration and $[{}^3{\mathrm{O}}_2]$ provide reduced uncertainties for the photochemical parameters determined for BPD-mediated PDT, as well as a validation that our macroscopic model can accurately predict the oxygen consumption for BPD-mediated PDT, making it feasible to determine ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ without oxygen measurements.

2. Theory and Methods

2.1. Tumor Model

RIF cells were cultured and $30\mu \mathrm{l}$ were injected at $1\times {10}^7\text{\hspace{0.17em}\hspace{0.17em}cells}/\mathrm{ml}$ in the right shoulders of 6 to 8 week old female C3H mice (NCI-Frederick, Frederick, Maryland), as described previously.^9–12 Animals were under the care of the University of Pennsylvania Laboratory Animal Resources. All studies were approved by the University of Pennsylvania Institutional Animal Care and Use Committee. Tumors were treated when they were $\sim 3$ to 5 mm in diameter. The fur of the tumor region was clipped prior to cell inoculation, and the treatment area was depilated with Nair (Church & Dwight Co., Inc., Ewing, New Jersey) at least 24 h before measurements. Mice were provided a chlorophyll-free (alfalfa-free) rodent diet (Harlan Laboratories Inc., Indianapolis, Indiana) starting at least 10 days prior to treatment to eliminate the fluorescence signal from chlorophyll-breakdown products, which have a similar emission range to the BPD fluorescence spectra used to determine the concentration of BPD in the tumor. During the whole treatment, mice were kept under anesthesia on a heat pad at 38°C [see Fig. 1(a)].

Fig. 1.

Experimental setup with the (a) multifiber contact spectroscopy probe and the (b) collimated beam treatment of RIF tumors on mouse shoulder.

2.2. Measurement of Interstitial Benzoporphyrin Derivative Monoacid Ring A Concentration

Fluorescence measurements were made by a custom-made multifiber spectroscopic contact probe [Fig. 1(b)] described previously^13,14 and analyzed using single value decomposition (SVD) fitting.¹⁵ Spectra were measured both before and after treatment to investigate the effects of and relationship between photobleaching and outcome. An empirical optical property correction factor (CF) is defined as the ratio of SVD between the tissue optical properties of interest (${\mu }_a$, ${\mu }_{\mathrm{s}}^{\prime }$) to the corresponding SVD for a reference tissue optical properties ${\mu }_{\mathrm{a}}=0.69$, ${\mu }_{\mathrm{s}}^{\prime }=11{\mathrm{cm}}^{-1}$,^13,16 with BPD as the photosensitizer and optical properties measured at 690 nm. A multiplicative CF of the following form was used to multiply by raw SVD to obtain ${\mathrm{SVD}}_{\mathrm{corr}}$:¹⁷

$$\mathrm{CF}=\frac{C_{01}(1+C_{02}{\mu }_{\mathrm{s}}^{\prime })}{{\mu }_{\mathrm{s}}^{\prime }}\times \exp [(b_1+b_s{\mu }_{\mathrm{s}}^{\prime }){\mu }_{\mathrm{eff}}].$$ (1)

The input optical properties are those measured at 690 nm. The factor was used on raw fluorescence SVD by multiplying it with CF to get ${\mathrm{SVD}}_{\mathrm{corr}}$. The values were optimized so that ${\mathrm{SVD}}_{\mathrm{corr}}$ for phantoms with the same concentration of BPD were matched [Fig. 2(a)]. Upon optimization, it was found that $C_{01}=0.41\pm 0.16$, $C_{02}=0.142\pm 0.013$, $b_1=0.85\pm 0.16$, and $b_2=-0.032\pm 0.014$. In previous publications,^13,16 the ${\mu }_{\mathrm{s}}^{\prime }$ dependence in Fig. 2(a) was reversed, and incorrect CF parameters were provided for the collimated beam geometry and their respective wavelengths. A separate tissue-simulating phantom with constant scattering and absorption and varying amounts of BPD were used as a calibration curve to correlate ${\mathrm{SVD}}_{\mathrm{corr}}$ to actual concentration in $\mu \mathrm{M}$ [Fig. 2(b)]. The line of best-fit [shown as a solid line in Fig. 2(b)] $[\mathrm{BPD}]=(0.0301\pm 0.0009)\times {\mathrm{SVD}}_{\mathrm{corr}}$ is used to convert ${\mathrm{SVD}}_{\mathrm{corr}}$ to [BPD] in units of $\mu \mathrm{M}$. Figure 2(c) shows the comparison of in-vivo and ex-vivo measurements using methods described previously,^13,16 with a solid line of best-fit of the form $y=0.9821x$ with $R^2=0.9772$ to indicate agreement to within 2%. The dashed line represents the line for $y=x$. Real-time in-vivo BPD concentration measurement over the course of treatment ($80\mathrm{mW}/{\mathrm{cm}}^2$, 2000 s exposure time) was also determined for a subset of four mice (not included in Table 3) using characteristic fluorescence spectra obtained at 30- to 300-s time intervals with excitation at the treatment light. SVD fitting was used to determine the BPD concentration. Measured data are shown in Fig. 3(a) with symbols.

Fig. 2.

Fluorescence optical property correction phantoms and verification with in-vivo and ex-vivo comparison. (a) Fluorescence SVD amplitude for phantom experiments with varying optical properties and the same BPD concentration ($0.25\mathrm{mg}/\mathrm{kg}$). The best-fit (shown as dashed lines) uses the form $a/\mathrm{CF}$, where CF is Eq. (2) and $a=7.645$. (Note, $\mathrm{CF}=1$ is normalized for ${\mu }_{\mathrm{a}}=0.69$, ${\mu }_{\mathrm{s}}^{\prime }=11{\mathrm{cm}}^{-1}$.) (b) BPD concentration (in $\mu \mathrm{M}$) versus the corrected SVD (${\mathrm{SVD}}_{\mathrm{corr}}$). The line of best-fit $[\mathrm{BPD}]=(0.0301\pm 0.0009)\times {\mathrm{SVD}}_{\mathrm{corr}}$ with $R^2=0.9986$ is used to convert ${\mathrm{SVD}}_{\mathrm{corr}}$ to [BPD] in $\mu \mathrm{M}$. (c) The measured in-vivo photosensitizer concentration using the multifiber contact probe obtained fluorescence spectra versus ex-vivo measured BPD concentration. The line of best-fit is of the form $y=0.9821x$ with $R^2=0.9772$. The dashed line in (c) represents the line for $y=x$.

Table 3.

In-air light fluence, in-air light fluence rate, ${\phi }_{\text{air}}$, photosensitizer concentrations pre- and post-PDT, [BPD]_pre and [BPD]_post, PDT dose at 3 mm depth, reacted singlet oxygen concentration, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, at 3 mm depth, tumor regrowth rate, $k$, and CI, for each PDT treatment group. Number of mice per group is shown in the second column. The same index for each PDT treatment group is used for Figs. 4 and 7.

Index	# mice	In-air fluence ($\mathrm{J}/{\mathrm{cm}}^2$)	${\phi }_{\text{air}}$ ($\mathrm{mW}/{\mathrm{cm}}^2$)	Time (s)a	${[\mathrm{BPD}]}_{\mathrm{pre}}$ ($\mu \mathrm{M}$)	${[\mathrm{BPD}]}_{\text{post}}$ ($\mu \mathrm{M}$)	PDT doseb ($\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$)	${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$c ($\mu \mathrm{M}$)	$k$ (1/days)	Cure index, $\mathrm{CI}=1-k/k_{\mathrm{ctr}}$
1	5	30	50	600	$0.53\pm 0.24$	$0.33\pm 0.14$	$14.1\pm 6.0$	$0.39\pm 0.15$	$0.40\pm 0.03$	$0.0337\pm 0.02$
2	5		75	400	$0.72\pm 0.22$	$0.32\pm 0.12$	$19.2\pm 6.0$	$0.45\pm 0.05$	$0.38\pm 0.03$	$0.0556\pm 0.03$
3	5		150	200	$0.56\pm 0.29$	$0.27\pm 0.09$	$15.2\pm 7.9$	$0.29\pm 0.05$	$0.40\pm 0.03$	$0.0237\pm 0.02$
4	3	70d	50	1400	$0.73\pm 0.21$	$0.07\pm 0.09$	$39.6\pm 8.1$	$0.90\pm 0.21$	$0.28\pm 0.02$	$0.3151\pm 0.08$
5	3	100d	75	1333	$0.41\pm 0.09$	$0.05\pm 0.03$	$28.7\pm 5.9$	$0.60\pm 0.20$	$0.37\pm 0.05$	$0.1037\pm 0.05$
6	3	135d	50	2700	$0.50\pm 0.18$	$0.04\pm 0.02$	$41.0\pm 8.4$	$0.78\pm 0.18$	$0.34\pm 0.08$	$0.1646\pm 0.04$
7	5		75	1800	$0.53\pm 0.21$	$0.05\pm 0.02$	$44.2\pm 10.9$	$0.82\pm 0.28$	$0.32\pm 0.02$	$0.2139\pm 0.07$
8	5		150	900	$0.58\pm 0.12$	$0.07\pm 0.02$	$50.2\pm 18.8$	$0.85\pm 0.31$	$0.28\pm 0.08$	$0.3240\pm 0.10$
9	3	150d	75	2000	$0.84\pm 0.27$	$0.10\pm 0.02$	$75.4\pm 17.9$	$1.30\pm 0.42$	0	$1\pm 0.08$
10	5		100	1500	$0.66\pm 0.24$	$0.07\pm 0.02$	$59.9\pm 12.2$	$1.03\pm 0.37$	$0.11\pm 0.02$	$0.7432\pm 0.08$
11	3	250d	75	3333	$0.58\pm 0.19$	$0.02\pm 0.02$	$64.0\pm 14.7$	$0.96\pm 0.26$	$0.25\pm 0.01$	$0.3878\pm 0.07$
12	5		150	1667	$0.77\pm 0.20$	$0.01\pm 0.02$	$93.0\pm 17.8$	$1.26\pm 0.29$	0	1
13	5	300	150	2000	$0.77\pm 0.26$	0	$97.9\pm 28.2$	$1.27\pm 0.24$	0	1
14	5	350	150	2333	$0.81\pm 0.34$	$0.04\pm 0.05$	$108.3\pm 20.8$	$1.35\pm 0.30$	0	1
15	5	Control	0	0	0	0	0	0	$0.41\pm 0.05$	0

^aTotal treatment time.

^bPDT dose is defined as the time integral of the product of the photosensitizer concentration and the light fluence rate ($\phi$), $[S_0](t)$ is calculated using the parameters in Table 1.

^c${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is calculated using Eqs. (4)–(6) using the parameters listed in Table 1.

^dOptical properties were measured in one mouse per group.

Fig. 3.

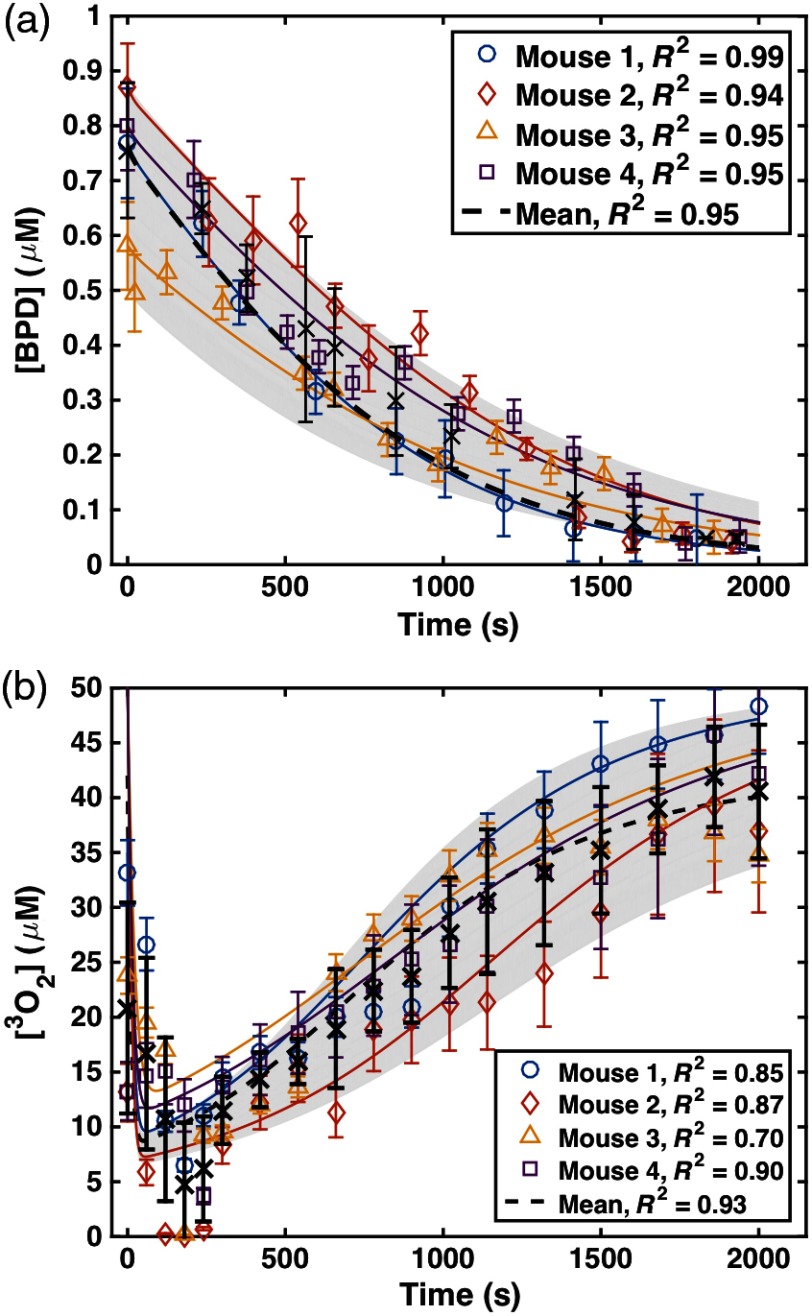
Real-time in-vivo measurement of (a) BPD concentration ([BPD]) at the tumor surface and (b) $[{}^3{\mathrm{O}}_2]$ concentration at 3 mm depth measured for four mice over the course of PDT light delivery ($80\mathrm{mW}/{\mathrm{cm}}^2$, $160\mathrm{J}/{\mathrm{cm}}^2$). The open symbols represent measured data and the solid curves represent the model-calculated [BPD] and $[{}^3{\mathrm{O}}_2]$ using Eqs. (4) and (5) and the photochemical parameters listed in Table 2. The black “x” symbols and dashed black line represent the mean data and fit to data, respectively. The PDT parameters used to model the mean data are summarized in Table 1.

2.3. Tissue Oxygen Concentration Measurements

For a subset of four mice (summarized in Table 2) administered with BPD ($1\mathrm{mg}/\mathrm{kg}$), the in-vivo tissue oxygen partial pressure ${\mathrm{pO}}_2$ was measured during PDT treatment using a phosphorescence-based bare fiber-type ${}^3{\mathrm{O}}_2$ probe (OxyLite Pro with NX-BF/O/E, Oxford Optronix, Oxford, United Kingdom) for an in-air light fluence rate of $80\mathrm{mW}/{\mathrm{cm}}^2$ for 2000 s. Measurements are presented for each 30 s interval during treatment. Then, ${}^3{\mathrm{O}}_2$ concentration was calculated by multiplying the measured ${\mathrm{pO}}_2$ with ${}^3{\mathrm{O}}_2$ solubility in tissue, which is $1.295\mu \mathrm{M}/\mathrm{mm}\mathrm{Hg}$.^18,19 Measured $[{}^3{\mathrm{O}}_2]$ was used to refine the photochemical parameters previously determined²⁰ for the singlet oxygen explicit dosimetry model used to calculate ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, and obtained values are summarized in Table 2. Individually measured $[{}^3{\mathrm{O}}_2](t)$ for each mouse were fit with the model-calculated values. Measured data are shown with symbols and calculated fits are shown with lines in Fig. 3(b).

Table 2.

PDT parameters ($\sigma$, $\xi$, and $g$) obtained for four mice treated with in-air fluence of $160\mathrm{J}/{\mathrm{cm}}^2$ and in-air fluence rate of ${\phi }_{\text{air}}=80\mathrm{mW}/{\mathrm{cm}}^2$ using individual fitting to $[{}^3{\mathrm{O}}_2](t)$ and $[S_0](t)$ simultaneously (see Fig. 3). The other photochemical parameters ($\delta =33\mu \mathrm{M}$ and $\beta =11.9\mu \mathrm{M}$) are kept the same as in Table 1.

Mouse	${[\mathrm{BPD}]}_0$ ($\mu \mathrm{M}$)	$\xi$ (${\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$)	$\sigma$ ($\mu {\mathrm{M}}^{-1}$)	$g$ ($\mu \mathrm{M}{\mathrm{s}}^{-1}$)	${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$a (mM)	${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$b (mM)
1	$0.76\pm 0.10$	$(60\pm 8)\times {10}^{-3}$	$(1.8\pm 0.3)\times {10}^{-3}$	$1.6\pm 0.4$	$1.23\pm 0.24$	$1.21\pm 0.40$
2	$0.87\pm 0.19$	$(60\pm 10)\times {10}^{-3}$	$(1.5\pm 0.4)\times {10}^{-3}$	$1.5\pm 0.4$	$1.64\pm 0.31$	$1.37\pm 0.17$
3	$0.58\pm 0.16$	$(50\pm 10)\times {10}^{-3}$	$(1.5\pm 0.4)\times {10}^{-3}$	$1.3\pm 0.3$	$1.05\pm 0.33$	$0.93\pm 0.13$
4	$0.80\pm 0.18$	$(50\pm 7)\times {10}^{-3}$	$(1.5\pm 0.3)\times {10}^{-3}$	$1.7\pm 0.3$	$1.44\pm 0.28$	$1.26\pm 0.21$

^aCalculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ using individually fit PDT photochemical parameters and ${[{}^3{\mathrm{O}}_2]}_0=50\mu \mathrm{M}$.

^bCalculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ using the mean PDT photochemical parameters from Table 1.

2.4. Photodynamic Therapy Treatment

An optical fiber with a microlens attachment was coupled with a 690-nm diode laser with a maximum output power of 8 W (B&W Tek Inc., Newark, Delaware) to produce a collimated beam with a diameter of 1 cm on the surface of the tumor [Fig. 1(a)]. Mice were treated with in-air fluence rates (${\phi }_{\text{air}}$) of 50 to $150\mathrm{mW}/{\mathrm{cm}}^2$ and total in-air fluences of 30 to $350\mathrm{J}/{\mathrm{cm}}^2$ at 690 nm to induce different PDT outcomes and assess the reciprocity between BPD concentration and light dose. The “in-air fluence rate” is defined as the calculated irradiance determined by laser power divided by the treatment area. The “in-air fluence” was calculated by multiplying the “in-air fluence rate” by the treatment time. All mice were injected with $1\mathrm{mg}/\mathrm{kg}$ BPD through tail injection at 3 h before the PDT treatment. RIF tumor-bearing mice with (i) no BPD and no light excitation and mice with (ii) no BPD but highest light excitation (${\phi }_{\text{air}}=150\mathrm{mW}/{\mathrm{cm}}^2$ and 2333 s exposure) were used as controls ($n=5$).

2.5. Tumor Regrowth Rate Analysis

Tumor volumes were tracked daily after PDT. Width ($a$) and length ($b$) were measured with slide calibers, and tumor volumes ($V$) were calculated using $V=\pi \times a^2\times b/6$.²¹ Tumor volumes were tracked for 14 days (Fig. 4), and the tumor regrowth factor ($k$) was calculated by the best exponential fit [with a form $f(d)=e^{kd}$] to the measured volumes over the days ($d$). CI was calculated for each treatment group as

$$\mathrm{CI}=1-\frac{k}{k_{\mathrm{ctr}}},$$ (2)

where $k$ is the tumor regrowth factor for each group and $k_{\mathrm{ctr}}$ is the regrowth factor for the control group, which has no injection of BPD or light illumination.

Fig. 4.

Tumor volumes over days after PDT treatment. Solid lines are the exponential fit to the data with a functional form of $e^{kd}$, where $d$ is days after PDT treatment. The resulting tumor regrowth rates, $k$, and its uncertainty, $\delta k$, are listed in Table 3.

2.6. Monte-Carlo Simulation of $\phi$ Distribution in Tumors

The diffusion theory is not valid for the simulation of $\phi$ in tissue when the lateral dimension of the beam geometry becomes comparable to the mean-free-path of the photons or when the region of interest is near the air–tissue interface.²² Based on a previous study,²³ an empirical six-parameter fitting equation was used to fit the Monte-Carlo (MC) calculated light fluence rate data²² for a 1-cm diameter field, with ${\mu }_{\mathrm{a}}=0.52$ to $0.80{\mathrm{cm}}^{-1}$ and ${\mu }_{\mathrm{s}}^{\prime }=7.9$ to $14.1{\mathrm{cm}}^{-1}$. The equation is of the following form:

$$\phi /{\phi }_{\text{air}}=\mathrm{INV}\times (1-b\times e^{-{\lambda }_{1}d})(C_2{e}^{-{\lambda }_{2}d}+C_3{e}^{-{\lambda }_{3}d}),$$ (3)

where the parameters ${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, $b$, $C_2$, and $C_3$ are functions of ${\mu }_{\mathrm{a}}$ and ${\mu }_{\mathrm{s}}^{\prime }$ and details of each can be found elsewhere.²³ $\mathrm{INV}={[\mathrm{SSD}/(\mathrm{SSD}+d)]}^2$, where the source-to-surface distance $\mathrm{SSD}=9.34\mathrm{cm}$ based on the measurement of light fluence rate in water for the same collimated beam as a function of depth and fit to the inverse–inverse square law formula. The inverse square law factor was added into the MC simulation results, which is suitable for parallel beams, to account for the divergence of the collimated beam from the microlens. The mean tissue optical properties are found to be ${\overline{\mu }}_{\mathrm{a}}=0.69\pm 0.12{\mathrm{cm}}^{-1}$ and ${\overline{\mu }}_{\mathrm{s}}^{\prime }=11\pm 3{\mathrm{cm}}^{-1}$ for RIF tumors at 690 nm, and the maximum error for using the mean optical properties is $\pm 15\%$ (data not shown).

2.7. Macroscopic Singlet Oxygen Modeling

The typical type II PDT process can be described by a set of kinetic equations, which can be simplified to describe the creation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$.^18,20 These equations are dependent on the temporal and spatial distribution of light fluence, photosensitizer concentration ($[S_0]$), ground state oxygen concentration ($[{}^3{\mathrm{O}}_2]$), and the photosensitizer-specific reaction-rate parameters. The relevant equations are

$$\frac{\mathrm{d}[S_0]}{\mathrm{d}t}=-\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\xi \sigma ([S_0]+\delta )\phi [S_0],$$ (4)

$$\frac{\mathrm{d}[{}^3{\mathrm{O}}_2]}{\mathrm{d}t}=-\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\xi \phi [S_0]+g(1-\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2](t=0)}),$$ (5)

$$\frac{\mathrm{d}{[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}}{\mathrm{d}t}=\frac{[{}^3{\mathrm{O}}_2]}{[{}^3{\mathrm{O}}_2]+\beta }\xi \phi [S_0],$$ (6)

where $g$ is the maximum oxygen supply rate to tissue, $\delta$ is the low-concentration correction, $\beta$ is the oxygen quenching threshold concentration, $\sigma$ is the specific photobleaching ratio, and $\xi$ is the macroscopic maximum oxygen supply rate. The value of each of these parameters was found by fitting the measured $[{}^3{\mathrm{O}}_2]$ to the calculated values; they are summarized in Table 1. If the parameters are 10% over- or underestimated, calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ will deviate up to 12%. An increased $\sigma$ estimates a smaller ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ while an increased $g$ or $\xi$ estimates larger ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$.

Table 1.

Photochemical parameters for BPD based on Ref. 20. The standard deviation for each parameter is based on the fitting of all mice [dashed line in Fig. 3(b)] and is smaller than those in Ref. 20.

Photochemical parameter	Definition	Value	References
$ϵ$ (${\mathrm{cm}}^{-1}\mu {\mathrm{M}}^{-1}$)	Photosensitizer extinction coefficient	0.0783	20
$\delta$ ($\mu \mathrm{M}$)	Low-concentration correction	33	20
$\beta$ ($\mu \mathrm{M}$)	Oxygen quenching threshold concentration	11.9	20
$\sigma$ ($\mu {\mathrm{M}}^{-1}$)	Specific photobleaching ratio	$(1.8\pm 0.3)\times {10}^{-5}$	20
$\xi$ (${\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$)	Specific oxygen consumption rate	$(55\pm 15)\times {10}^{-3}$	20
$g$ ($\mu \mathrm{M}{\mathrm{s}}^{-1}$)	Macroscopic maximum oxygen supply rate	$1.7\pm 0.4$	20
${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx},\mathrm{sh}}$ (mM)	Singlet oxygen threshold dose for tumor regrowth	$0.99\pm 0.12$	This study
${[{}^3{\mathrm{O}}_2]}_0$ ($\mu \mathrm{M}$)	Initial oxygen concentration	40	20

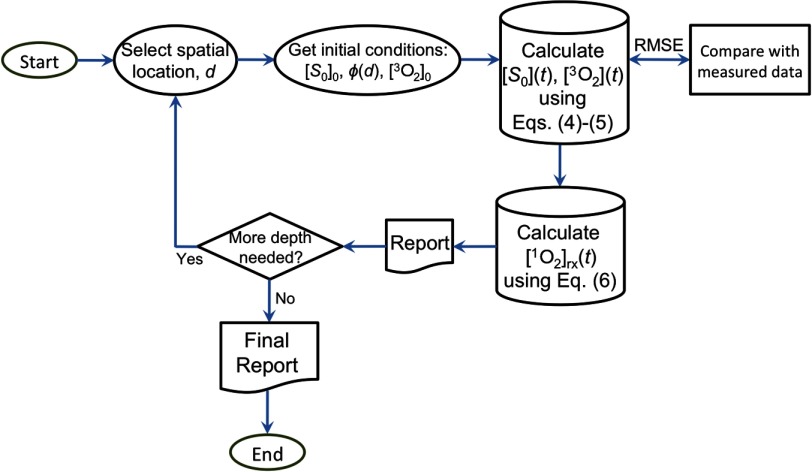
Figure 5 is a flowchart showing how ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is calculated. The depth dependence of $\phi$ is calculated using an analytical fit of MC simulation, Eq. (3), and published fitting parameters.²³ For each spatial location, $[S_0](t)$ and $[{}^3{\mathrm{O}}_2](t)$ can be calculated by solving the coupled differential equations [Eqs. (4) and (5)] using the initial conditions for ${[S_0]}_0$ based on fluorescence measurement before PDT and its assumed spatial homogeneous, the initial ${[{}^3{\mathrm{O}}_2]}_0$ value (e.g., $50\mu \mathrm{M}$ from Tables 1), and $\phi (d)$. The light fluence rate does not change with time. Finally, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is calculated using Eq. (6).

Fig. 5.

Flowchart for the calculation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ based on initial conditions of ${[S_0]}_0$ and $\phi (d)$. The initial oxygen concentration ${[{}^3{\mathrm{O}}_2]}_0$ is chosen to be $40\mu \mathrm{M}$ for most of the data analysis except for the individual fits for Fig. 3, where ${[{}^3{\mathrm{O}}_2]}_0=50\mu \mathrm{M}$.

For a subset of four mice, $[S_0]$ and $[{}^3{\mathrm{O}}_2]$ concentration over time during the course of PDT delivery were measured. $[S_0]$ was determined by collecting the characteristic fluorescence spectra of BPD due to excitation by the treatment light. To minimize the possible effect of optical properties change at 405 nm on fluorescence ${\mathrm{SVD}}_{\mathrm{corr}}$, which is not included in Eq. (1), we used ex-vivo measurement of $[S_0]$ to validate our in-vivo fluorescence method in the same mouse population [Fig. 2(c)]. $[{}^3{\mathrm{O}}_2]$ was measured using the phosophorescence-based oxygen probe mentioned in Sec. 2.3. These quantities over time were fit with Eqs. (4) and (5) to validate the parameters of $\xi$, $\sigma$, and $g$ obtained previously.²⁰ The objective function minimized during the fitting routine was the root-mean-square error (RMSE) between model-calculated $[{}^3{\mathrm{O}}_2]$ and measured $[{}^3{\mathrm{O}}_2]$ ($\mathrm{RMSE}={(|{[{{}^3\mathrm{O}}_2]}_{\text{measured}}-{{[{{}^3\mathrm{O}}_2]}_{\text{calculated}}}^2)}^{1/2}$). Minimization of the objective function was performed using the function “fminsearch” in MATLAB^®.

All fitting and simulation were performed using MATLAB^® R2014b (Natick, Massachusetts) on an iMac OSX version 10.10.5 (processor 2.9 GHz Intel Core i5, 16 GB memory). The calculation times were in seconds for the spatially coupled differential equations. A more detailed description of the macroscopic model has been published previously.^9,18,20,24

3. Results

BPD-mediated PDT with different in-air fluences, different ${\phi }_{\text{air}}$, and different exposure times was performed in mouse models bearing RIF tumors. Tissue optical properties, photosensitizer concentration, and tissue oxygenation were measured to calculate photobleaching percentage, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$. Table 3 summarizes all of the treatment conditions, as well as the measured and calculated quantities using the photochemical parameters summarized in Table 1.

Four mice, summarized in Table 2, were used to monitor the photosensitizer concentration and $[{}^3{\mathrm{O}}_2]$ throughout the treatment using ${\phi }_{\text{air}}=80\mathrm{mW}/{\mathrm{cm}}^2$ and total fluence of $160\mathrm{J}/{\mathrm{cm}}^2$. The measured results (open symbols) were compared to calculated values (solid lines) in Fig. 3 to validate the photochemical parameters used in the calculation of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$. $R^2$ values are provided to evaluate their fits. Calculations were performed using Eqs. (4)–(6) and the photochemical parameters found from individual fits of $[{}^3{\mathrm{O}}_2](t)$ summarized in Table 2, as well as the photochemical parameters for the mean data summarized in Table 1 and measured values of initial photosensitizer concentration.

Measured tumor volume over 14 days after treatment for each treatment group is shown in Fig. 4. Compared to control mice, all treatment conditions had significant control of the tumor regrowth after PDT. CI was calculated for each treatment group using Eq. (2). PDT using $150\mathrm{J}/{\mathrm{cm}}^2$ with $75\mathrm{mW}/{\mathrm{cm}}^2$ was a more effective treatment than with $100\mathrm{mW}/{\mathrm{cm}}^2$. Each tumor volume was normalized to the mean initial volume, so they are equal on day 0 (treatment date) before fitting for the tumor regrowth rate.

BPD concentration ([BPD]) was measured both before and after PDT treatment. Measured [BPD] was compared to model-calculated values for all of the treatment conditions and is shown in Fig. 6(a). The symbols represent the measured values, and the solid lines are model-calculated photosensitizer concentration during treatment. Figure 6(b) shows the spatial distribution of reacted singlet oxygen in the RIF tumor model. The symbols indicate ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm tumor depth for each treatment condition. The depth of 3 mm was chosen as it encompasses the initial tumor size of all treated tumors. Previous publications also calculated ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm, and results of this study can be compared to those directly.

Fig. 6.

(a) The temporal changes of BPD concentration versus fluence at 3 mm depth for the treatment conditions. The solid lines represent the calculated changes of photosensitizer concentration during treatment. The symbols show the measured BPD concentration pre- and post-PDT. Initial drug concentrations for the calculation were matched to measured values. (b) The spatial distribution of reactive singlet oxygen (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) in the RIF tumors calculated for different treatment conditions. ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm tumor depth is shown as symbols. $R^2$ values for each calculation are shown in the legend.

Several dose metrics were evaluated for predicting the treatment outcome. Figure 7 shows the correlation of CI (tumor control) versus in-air fluence, photobleaching ratio (%), PDT dose at 3 mm depth, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm depth. The mean of $k$ and $k_{\mathrm{ctr}}$ for all mice in each treatment group (number of mice per group is shown in Table 3) was used to determine CI using Eq. (1). Photobleaching was determined by the ratio of BPD ${\mathrm{SVD}}_{\mathrm{corr}}$ measured immediately following treatment (${[{\mathrm{SVD}}_{\mathrm{corr}}]}_{\text{post}}$) to the BPD concentration measured prior to treatment (${[{\mathrm{SVD}}_{\mathrm{corr}}]}_{\mathrm{pre}}$) and calculating $1-({[{\mathrm{SVD}}_{\mathrm{corr}}]}_{\text{post}})/({[{\mathrm{SVD}}_{\mathrm{corr}}]}_{\mathrm{pre}})$. PDT dose is defined by the time integral of the product of the $\phi$ at a 3-mm tumor depth and the local BPD concentration. Figures 7(a)–7(d) show the correlation of CI to fluence, photobleaching percentage, PDT dose, and mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ along with their line of best-fit. The lines of best-fit (shown with solid lines) are $\mathrm{CI}=(3.309\times {10}^{-3})x$, $\mathrm{CI}=(1.118\times {10}^{-3}){\mathrm{e}}^{0.06731x}$, $\mathrm{CI}=1.052/(1+1014.4{\mathrm{e}}^{-0.08172x})$, and $\mathrm{CI}=1.08/(1+3490{\mathrm{e}}^{-8.301x})$ with $R^2=0.6260$, 0.6274, 0.9360, and 0.9850 for fluence, photobleaching percentage, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm, respectively.

Fig. 7.

CI plotted against (a) fluence at a 3 mm tumor depth, (b) measured photosensitizer photobleaching (%), (c) calculated PDT dose at 3 mm depth, and (d) mean reacted singlet oxygen at 3 mm depth (${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$) calculated using Eqs. (4)–(6) and the parameters summarized in Table 1. The solid lines show the best-fit to the data with functional forms $\mathrm{CI}=(3.309\times {10}^{-3})x$, $\mathrm{CI}=(1.118\times {10}^{-3}){\mathrm{e}}^{0.06731x}$, $\mathrm{CI}=1.052/(1+1014.4{\mathrm{e}}^{-0.08172x})$, and $\mathrm{CI}=1.08/(1+3490{\mathrm{e}}^{-8.301x})$ with $R^2=0.6260$, 0.6274, 0.9360, and 0.9850 for (a), (b), (c), and (d), respectively. The gray region indicates the upper and lower bounds of the fit with 95% confidence level.

4. Discussions

As shown in Fig. 3, the photochemical parameters $\sigma$, $\xi$, and $g$ were validated by measuring [BPD] changes and $[{}^3{\mathrm{O}}_2]$ during the PDT treatment for individual mice and applying the parameters to the explicit dosimetry model. Based on a previous study, the parameters of $\sigma$, $\xi$, and $g$ were found to be $(1.8\pm 0.3)\times {10}^{-5}\mu {\mathrm{M}}^{-1}$, $(55\pm 15)\times {10}^{-3}{\mathrm{cm}}^2{\mathrm{mW}}^{-1}{\mathrm{s}}^{-1}$, and $1.7\pm 0.4\mu {\mathrm{M}}^{-1}$, respectively.²⁰ The standard deviation of each parameter is reduced based on the fitting of $[S_0]$ and $[{}^3{\mathrm{O}}_2]$ as shown in Fig. 3, which is a more robust data set for deriving the photochemical parameters. Each individually measured $[{}^3{\mathrm{O}}_2]$ in Fig. 3 was fitted to validate the photochemical parameters as shown in Table 2. RMSE between measured and calculated values of $[{}^3{\mathrm{O}}_2]$ was used as a measure of good fit.

To assess the effect of photochemical parameters, the values of calculated reacted singlet oxygen concentration, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, using the individually obtained photochemical parameters for each mouse (from Table 2) were compared to ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ calculated using the photochemical parameters from a previous study,²⁰ from Table 1. For the same mouse, ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ calculated using the two sets of photochemical parameters agree with each other to within a maximum uncertainty of 20% and a standard deviation of 8% (see Table 2). The good agreement between measurement and calculation of photosensitizer concentration and oxygen concentration (Fig. 3) provided a validation of the photochemical parameters determined previously and allowed for reduction in the uncertainty of each parameter. For BPD, the comparisons between the measured $[{}^3{\mathrm{O}}_2]$ and calculation for a subset of four mice (Fig. 3b) show that our macroscopic model can accurately predict $[{}^3{\mathrm{O}}_2]$ for the mice studied with $R^2$ values 0.70 to 0.90. The agreement between measured and calculated $[{}^3{\mathrm{O}}_2]$ makes it unnecessary to measure the oxygen concentration directly during PDT. One complication of the comparison between measurement and calculation for in-vivo oxygen concentration is the uncertainty of the depth at which oxygen concentration was measured, which lies at around 3 mm. To illustrate this effect, the spatial and temporal variations of $[{}^3{\mathrm{O}}_2]$ were shown for various ${\phi }_{\text{air}}$ (20, 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$): Figs. 8(a)–8(c) show the temporal changes of $[{}^3{\mathrm{O}}_2]$ at 1, 3, and 5 mm with $[\mathrm{BPD}]=0.57\mu \mathrm{M}$ (the mean value of BPD concentration for all mice studied); Figs. 8(d)–8(f) show the temporal changes of $[{}^3{\mathrm{O}}_2]$ at 1, 3, and 5 mm with $[\mathrm{BPD}]=0.87\mu \mathrm{M}$. Initial $[{}^3{\mathrm{O}}_2]$ of $40\mu \mathrm{M}$ and the photochemical parameters in Table 1 were used for the calculations. As the depth increases from 1 to 5 mm, the minimum value of ${[}^3{\mathrm{O}}_2]$ increases, while the rate of $[{}^3{\mathrm{O}}_2]$ recovery due to photobleaching (for 50 to 2000 s) decreases. Higher initial [BPD] will cause a larger drop of $[{}^3{\mathrm{O}}_2]$, depending on the light fluence rate. Lower light fluence rates will have less $[{}^3{\mathrm{O}}_2]$ consumption during PDT. The optimized depth for the best agreement between model and measurement is found to be 3 mm, corresponding to the placement of the oxygen probe during PDT.

Fig. 8.

Temporal dependence of $[{}^3{\mathrm{O}}_2](t)$ calculated for various in-air fluence rates (20, 50, 75, and $150\mathrm{mW}/{\mathrm{cm}}^2$) at depths of 1, 3, and 5 mm in the tumor for two initial BPD concentrations, [BPD]: (a)–(c) $0.57\mu \mathrm{M}$ and(d)–(f) $0.87\mu \mathrm{M}$. Photochemical parameters in Table 1 are used for $[{}^3{\mathrm{O}}_2]$ calculation using Eqs. (4) and (5).

Compared to control mice, all treated mice with total fluences larger than $30\mathrm{J}/{\mathrm{cm}}^2$ had significant control of the tumor regrowth after PDT (see Fig. 4). However, mice with tumors of about the same size, administered the same BPD dose, and treated with identical fluence exhibited different survival and tumor control as ${\phi }_{\text{air}}$ was changed. In the group of mice treated to $150\mathrm{J}/{\mathrm{cm}}^2$, CI increased as the source strength was lowered from 100 to $75\mathrm{mW}/{\mathrm{cm}}^2$. This is in agreement with prior reports of increased therapeutic response with a reduced ${\phi }_{\text{air}}$ by expanding the radius of ${}^1{\mathrm{O}}_2$ formation around a tumor capillary in a multicell tumor spheroid model.²⁵

Figure 6(a) compares the measured pre- and post-PDT BPD concentration, [BPD], versus calculated [BPD] during treatment for each treatment condition using the photochemical parameters summarized in Table 1. The good agreement [for mean $[S_0]$, $R^2=0.88$ in Fig. 6(a)] between the measured [BPD] pre- and post-PDT further validates the photochemical parameters (Table 1) used for the modeling. Figure 6(b) shows the spatial distribution of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ for each treatment condition. The value of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm is shown with symbols. While the comparison of CI versus ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ was done using ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm, the value of ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is almost a constant for depths between 1 and 4 mm for most of the PDT treatment groups, indicating that the correlation between ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ and CI in Fig. 7(c) should be equally valid for any depth between 1 and 4 mm.

Fluence, photosensitizer photobleaching ratio, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm were compared as dosimetric quantities to estimate the outcome of BPD-mediated PDT for RIF tumors on a mouse model. The outcome was evaluated by the calculation of CI. No tumor regrowth up to 14 days after treatment resulted in a CI of 1. The goodness of the fit and the corresponding upper and lower bounds of the fits (gray area) to the fluence, BPD photobleaching, PDT dose, and mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ are presented in Fig. 7. Figure 7(a) shows that, while fluence correlates linearly with the PDT outcome, it exhibits large uncertainties as defined by the large bounds of the gray area, as well as by the low value of $R^2=0.67$. As evident by the lower value of $R^2=0.63$ and a relatively large bound of gray area in Fig. 7(b), the BPD photobleaching ratio is not a better dosimetric quantity for predicting the PDT outcome as compared to fluence. The BPD concentration ($\sim 0.2$ to $0.8\mu \mathrm{M}$) as used clinically is much lower than the value of $\delta$ ($=33\mu \mathrm{M}$), and this may be a reason for the poor correlation of the photobleaching ratio and CI. In photobleaching-based implicit dosimetry, a much more sophisticated model than simple bleaching fraction is used, and the result of this study does not mean that other methodologies of photobleaching-based implicit dosimetry will not be applicable for PDT dosimetry. As shown in Fig. 7(c), PDT dose allows for reduced subject variation and improved predictive efficacy as compared to fluence and photobleaching. PDT dose showed a better correlation with CI with a higher value of $R^2=0.97$ and a narrower band of gray area as it accounts for both light dose and tissue [BPD] levels. However, PDT dose overestimates ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ in the presence of hypoxia as it does not account for the oxygen dependence of ${}^1{\mathrm{O}}_2$ quantum yield. The goodness of fit $R^2=0.99$ and the narrowest gray area in Fig. 7(d) shows that the mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ correlates the best with CI. ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ accounts for the key quantities of light fluence, photosensitizer concentration, and tissue oxygen level.

Based on the findings of this study, PDT dose and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ exhibit threshold dose behavior as they can be fitted by a sigmoid function $S(x)=1/\{1+e[-(x-x_0)/w_0]\}$, where $x_0=58\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$ with uncertainty $w_0=12\mu \mathrm{M}\mathrm{J}/{\mathrm{cm}}^2$ and $x_0=0.98\mathrm{mM}$ with uncertainty $w_0=0.12$ for PDT dose and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, respectively. For PDT dose, $x_0$ can be converted to the absorbed dose by BPD by multiplying by the extinction coefficient ($ϵ=0.0783{\mu \mathrm{M}}^{-1}{\mathrm{cm}}^{-1}$), resulting in $4.5\mathrm{J}/{\mathrm{cm}}^3$, which corresponds to $(16\pm 4)\times {10}^{18}\text{\hspace{0.17em}\hspace{0.17em}photons}/{\mathrm{cm}}^3$ (by dividing the energy per photon $hc/\lambda =2.88\times {10}^{-19}\mathrm{J}$ for $\lambda =690\mathrm{nm}$). The PDT dose threshold for BPD is in agreement with those reported for 2-(1-hexyloxyethyl)-2-devinyl pyropheophorbide-a (HPPH) ($19\times {10}^{18}\text{\hspace{0.17em}\hspace{0.17em}photons}/{\mathrm{cm}}^3$)¹⁶ and our preliminary results for BPD ($13.4\times {10}^{18}$).²⁶ The mean ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ threshold concentration of $x_0=0.98\pm 0.12\mathrm{mM}$ is similar to those published for HPPH (1.00 mM)¹⁶ and the published preliminary result for BPD (0.82 mM).²⁶ The increases for both PDT dose and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ threshold dose for BPD are due to an 11% increase of BPD drug concentration after a more comprehensive analysis of the fluorescence CF for mice revealed an 11% error in the original calibration curve for BPD concentration [Fig. 2(b)]. We want to point out that the definition of the value of the threshold doses for both PDT dose and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ is the value when $\mathrm{CI}=0.5$ rather than when $\mathrm{CI}=1$ (see Fig. 7). Both the current and previously published results²⁶ use the same photochemical parameters (Table 1).

5. Conclusion

The response of mouse RIF tumors to PDT depends on the tissue oxygenation, photosensitizer uptake, total energy delivered, and the $\phi$ at which the treatment is delivered. An accurate dosimetry quantity for the evaluation of the treatment outcome should account for all of these parameters. This study evaluated the efficacy and outcomes of different PDT treatments and how fluence, BPD photobleaching, PDT dose, and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ compare as dosimetric quantities. The correlation between CI and ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ suggests that ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ at 3 mm is the best quantity to predict the treatment outcome for a clinically relevant tumor regrowth endpoint. PDT dose is the second most effective dosimetry quantity when compared to fluence or photosensitizer photobleaching but is worse than ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$ as it does not account for the consumption of $[{}^3{\mathrm{O}}_2]$ for different $\phi$. For BPD in RIF tumors, our measurements show consistent temporal dependence of in-vivo oxygen concentration during PDT that can be well modeled by our macroscopic model (for mean $[{}^3{\mathrm{O}}_2]$, $R^2=0.70$), implying that it is not necessary to make $[{}^3{\mathrm{O}}_2]$ measurements during PDT to obtain ${[{}^1{\mathrm{O}}_2]}_{\mathrm{rx}}$, as well as by using our model. This study validated the model and photochemical parameters for BPD-mediated PDT for an endpoint that is clinically relevant.

Biographies

Michele M. Kim received her BA and MS degrees in physics from the University of Pennsylvania in 2012 and is currently a PhD candidate at the University of Pennsylvania in physics while pursuing a certificate in medical physics. Her research interests include preclinical and clinical photodynamic therapy dosimetry.

Rozhin Penjweini received her PhD in 2012 in physics from the University of Vienna. She is currently a postdoctoral researcher in the Department of Radiation Oncology at the University of Pennsylvania. Her current research interest is in vivo explicit photodynamic therapy (PDT) and singlet oxygen dosimetry. She also has practical experience in various fluorescence microscopy techniques for studying the structure, transport, and stability of nanomedicines for PDT treatment of cancer.

Timothy C. Zhu received his PhD in 1991 in physics from Brown University. He is currently a professor in the department of radiation oncology at the University of Pennsylvania. His current research interests include explicit PDT dosimetry, singlet oxygen explicit dosimetry (SOED), integrated system for interstitial and intracavitory PDT, diffuse optical tomography, in vivo dosimetry, and external beam radiation transport.

Disclosures

None of the authors have a financial conflict of interest in this work.