HOW SUBOPTIMAL IS SUBOPTIMAL CHOICE?

Abstract

In a frequently used suboptimal-choice procedure pigeons choose between an alternative that delivers three food pellets with p = 1.0 and an alternative that delivers ten pellets with p = 0.2. Because pigeons reliably choose the probabilistic (suboptimal) alternative, the procedure has been proposed as a nonhuman analog of human gambling. The present experiments were conducted to evaluate two potential threats to the validity of this procedure. Experiments 1 and 2 evaluated if pigeons obtained food at a lower unit price (i.e., pecks per pellet) on the suboptimal alternative than on the optimal alternative. When pigeons worked under this suboptimal procedure they all preferred the suboptimal alternative despite some pigeons paying a higher price for food on that alternative. In Experiment 2, when the unit price ratio more closely approximated the inverse of the expected value ratio, pigeons continued to prefer the suboptimal alternative despite its economic suboptimality. Experiment 3 evaluated if, in accord with the string-theory of gambling, the valuation of the suboptimal alternative was increased when pigeons misattributed a subset of the suboptimal no-food trials to the optimal alternative. When trial sequences were arranged to minimize these possible attribution errors, pigeons still preferred the suboptimal alternative. These data remove two threats to the validity of the suboptimal choice procedure; threats that would have suggested that suboptimal choice reflects economic maximization.

When choosing between two amounts of the same reinforcer, all else being equal, organisms prefer the larger amount (Catania, 1963; Neuringer, 1967). However, there are circumstances under which hungry organisms will choose a smaller over a larger amount of a food reward, and this has been studied in nonhuman research for over 40 years (Kendall, 1974). Choosing the smaller amount is perplexing from an economic perspective because it fails to maximize the overall rate of reinforcement (Spetch, Belke, Barnet, Dunn, & Pierce, 1990). Moreover, it is perplexing from an ecological perspective because it seemingly reduces the fitness of the organism (Stephens & Krebbs, 1986).

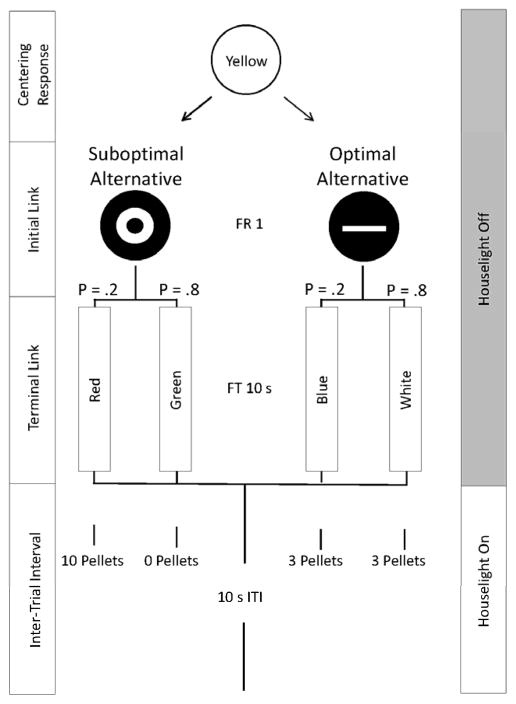
These suboptimal preferences in nonhumans bear a formal resemblance to human gambling. A variety of nonhuman laboratory preparations have been developed to further study suboptimal preferences that functionally resemble components of the human gambling milieu. One promising general preparation is the concurrent-chains procedure (Kendall, 1985; Roper & Zentall, 1999; Spetch et al., 1990); in particular, a variant in which pigeons choose between certain and probabilistic food rewards, each alternative offering a different amount of food (for review see Zentall & Laude, 2013). For example, and as illustrated in Figure 1, in the preparation used by Zentall and Stagner (2011) pigeons chose between a certain 3-pellet reward (the optimal alternative) and an alternative that delivered 10 pellets 20% of the time and no pellets 80% of the time (the suboptimal alternative). The expected payoff is 3 pellets for the certain-reward alternative, but only 2 pellets for the probabilistic alternative; hence the suboptimality of the latter choice. Despite these differences in expected payoffs, pigeons reliably develop and maintain a preference for the suboptimal alternative when terminal-link stimuli signal trial outcomes (Laude, Beckman, Daniels, & Zentall, 2014; Laude, Stagner, & Zentall, 2014; Zentall & Stagner, 2011; see Zentall, 2016 for review).

Fig. 1.

Suboptimal and optimal trial outcomes within the suboptimal-choice procedure. Initial-link and terminal-link stimulus assignments are shown in Table 1.

Zentall and Laude (2013) have argued that understanding why pigeons prefer the suboptimal alternative in such procedures may provide insights into the processes that contribute to problematic gambling in humans. Contributing to the validity of the procedure, Laude, Beckman et al. (2014) reported that pigeons that steeply discount delayed food rewards made more suboptimal choices. Among humans, problem and pathological gamblers tend to more steeply discount delayed rewards (MacKillop et al., 2014). Likewise, when human gamblers make choices under this procedure, they tend to make more suboptimal choices than do humans with no history of gambling (Molet et al., 2012). Thus, the validity of the procedure as a model of human gambling is reasonable, thus far.

The present experiments were conducted to evaluate two threats to the validity of the suboptimal choice procedure as a model of some important components of human gambling. The first validity threat is the possibility that the suboptimal choices are not as suboptimal as they appear. If one quantifies the price of food as responses-per-pellet (i.e., unit price; e.g., DeGrandpre, Bickel, Hughes, Layng, & Badger, 1993) rather than pellets per trial, then it is possible that the pigeons in these studies prefer the suboptimal alternative because, all else being equal, they prefer less work per food reward (e.g., Grossbard & Mazur, 1986); that is, to obtain food at a lower unit price on the suboptimal than on the optimal alternative. Specifically, within the Zentall and Stagner procedure, after making an initial-link choice, a fixed-time (FT) terminal-link is initiated (see Fig. 1). During the terminal link, discriminative stimuli are presented until food is delivered, or not. Pigeons presumably respond at different rates depending on the terminal-link stimuli that provide information about the upcoming reward amount (0, 3, or 10 pellets). If pigeons peck during the FT when a food-correlated stimulus is presented and withhold responses when, on 80% of the suboptimal trials, the no-food stimulus is presented, then the unit price of food may be lower on the suboptimal alternative than on the optimal alternative.¹ This unit-price hypothesis is consistent with the finding that when discriminative terminal-link stimuli are not presented, thereby increasing the probability that suboptimal terminal-link responding will be undifferentiated and that the unit price of food will be higher on that alternative, optimal choice is the rule (Zentall & Stagner, 2011). Evaluating this unit-price hypothesis from extant data is impossible because terminal-link responding has not been reported in published research using the Zentall and Stagner procedure (e.g., Zentall, 2016).

To evaluate the unit-price hypothesis, Experiment 1 replicated the Zentall and Stagner (2011) experiment while recording pigeons’ pecking during the presentation of the FT terminal-link stimuli. Experiment 2 repeated the experiment but presented terminal-link stimuli diffusely throughout the chamber, while darkening the response keys (to discourage pecking during the terminal links). By presenting all terminal-link stimuli diffusely and minimizing responding, we hoped to render the unit price ratio closer to the inverse of the expected value ratio. If suboptimal choice is influenced by obtained unit prices of food, this stimulus manipulation should shift preference toward the lower-priced optimal alternative.

Experiment 3 was conducted to evaluate an alternative account of suboptimal choice, one based on Rachlin’s string theory of gambling (e.g., Rachlin, Safin, Arfer, & Yen, 2015). According to this theory, the value of a gamble is assessed after a win, and is calculated as the value of the win summed with the discounted values of the string of losing wagers that precede the win. Because the win occurs temporally proximal to the calculation, its value is not discounted; whereas the negative values of the losses are discounted and, therefore, play less of a role in the decision to gamble. Applied to the procedure of Zentall and Stanger (2011), the value of the suboptimal alternative should be assessed after a “jackpot” win, calculated as the sum of the undiscounted 10-pellet reward and the discounted values of all preceding no-food suboptimal trials occurring since the prior jackpot. Because forced-choice optimal trials often intervene within the suboptimal string ending with a jackpot, it is possible that the string of no-food suboptimal trials prior to the optimal-trial “win” are included in the valuation of the optimal alternative. If so, this would decrease (increase) the value of the optimal (suboptimal) alternative, and could explain suboptimal choice. To evaluate this hypothesis, in Experiment 3 the Zentall and Stanger procedure was modified so forced trials occurred in nonoverlapping blocks of either optimal or suboptimal trials.

If suboptimal choice persists in these three experiments, then the validity of the suboptimal choice procedure as a model of nonhuman gambling-like behavior would be strengthened by removing two alternative accounts, both suggesting that suboptimal choice is not as suboptimal as it seems.

Experiment 1

Method

Subjects

Six unsexed pigeons, each with an extended history of participating in operant conditioning experiments, participated. Pigeons were housed individually in a colony room with a 12-hour light/dark schedule, maintained at 80 percent of their free-feeding weight, and given free access to water. The experimental protocol (#2307) was approved by the Institutional Animal Care and Use Committee at Utah State University.

Apparatus

Two Med Associates (St Albans, VT) ENV-007 modular operant chambers equipped with three response keys, a pellet feeder, and a house light were used. The two side response-keys were located 16.5 cm above the chamber floor and 2.5 cm from the sides of the chamber. The center key was centered equidistantly between the side keys and located 14.6 cm from the chamber floor. The side keys (Med, ENV 131M) could display shapes and colors. The center key (Colbourn, H21-17R) could display colors. Bioserv (Flemington, NJ) 45 mg grain-based pellets were dispensed into a receptacle located directly below the center key, 2.5 cm from the floor. Chambers were enclosed in a sound-attenuating cubicle and white noise was presented throughout the session. The house light was centered on the rear wall 26 cm from the floor. A PC computer controlled experimental events using MED-PC IV software.

Procedure

Pigeons received two pretraining sessions each composed of 78 trials. Trials began with the illumination of one of the three response keys with a shape or a color. A single peck to the key produced three food pellets. Six of these trials were completed on the center-yellow key. The remaining 72 trials were completed on the side keys, 36 trials on each key with the key illuminated with a shape (horizontal line or circle) or a color (red, green, blue, or white). The trial sequence was pseudorandomly determined with the constraint that 6 trials were completed on each location-stimulus combination. Trials were separated by a 10-s postreinforcer intertrial interval (ITI) during which the houselight was illuminated and the keys were darkened.

The suboptimal-choice procedure, illustrated in Figure 1, mirrored that used by Zentall and Stagner (2011). Each session was composed of 40 forced trials (20 optimal and 20 suboptimal trials) and 20 choice trials; within these constraints, trials were presented in random order. Trials started with the illumination of the yellow-center key. A single peck to that key turned it off and illuminated either one (forced trials) or both (choice trials) side keys with a shape correlated with the optimal or suboptimal alternatives. A single peck to one of these initial-link stimuli extinguished both keys. The chosen key was then illuminated with one of two terminal-link colors for 10 s (FT 10 s). The assignment of initial- and terminal-link stimuli is shown in Table 1.

Table 1.

Initial-link and terminal-link stimuli used in Experiments 1, 2, & 3

Pigeon	Suboptimal Initial Link	Optimal Initial Link	S100.2 Terminal Link	S00.8Terminal Link	O30.2 Terminal Link	O30.8 Terminal Link
Experiment 1
P1	Horizontal Line	Circle	White	Green	Blue	Red
P2	Horizontal Line	Circle	White	Green	Blue	Red
P3	Circle	Horizontal Line	Blue	Red	White	Green
P4	Circle	Horizontal Line	Blue	Red	White	Green
P5	Circle	Horizontal Line	Blue	Red	White	Green
P6	Horizontal Line	Circle	White	Green	Blue	Red
Experiment 2
P1	Triangle	Vertical Line	Yellow	Blue	Red	Green
P2	Triangle	Vertical Line	Yellow	Blue	Red	Green
P3	Vertical Line	Triangle	Red	Green	Blue	Yellow
P4	Vertical Line	Triangle	Red	Green	Blue	Yellow
P5	Vertical Line	Triangle	Red	Green	Blue	Yellow
P6	Triangle	Vertical Line	Yellow	Blue	Red	Green
Experiment 3
P1	Circle	Horizontal Line	Green	Red	Blue	White
P2	Circle	Horizontal Line	Green	Red	Blue	White
P3	Horizontal Line	Circle	White	Blue	Green	Red
P4	Horizontal Line	Circle	White	Blue	Green	Red
P5	Horizontal Line	Circle	White	Blue	Green	Red
P6	Circle	Horizontal Line	Green	Red	Blue	White

When the suboptimal alternative was chosen (or forced), there was a .2 probability of obtaining 10 pellets at the end of the FT 10 s; the remaining suboptimal trials ended without food. The terminal-link stimuli (presented on the response keys) were correlated with the number of pellets that would be delivered at the end of the terminal link. On the 20% of suboptimal trials ending with 10 pellets, the S10_0.2 terminal-link color was presented. On the remaining 80% of the suboptimal trials, the S0_0.8 terminal-link color was presented and no pellets were delivered at the end of the FT. When the optimal alternative was chosen, the S3_0.2 or S3_0.8 key-color was presented during the FT 10 with probability .2 and .8, respectively. Optimal terminal links ended with 3 food pellets delivered regardless of the terminal-link color. Trials were separated by a 10 s ITI during which the houselight was the only stimulus illuminated. The positions of the suboptimal and optimal initial-link stimuli were randomly determined between trials with the constraint that they appeared in both positions an equal number of times in each session.

Experiment 1 continued for a minimum of 30 sessions and until each pigeon’s percent suboptimal choice stabilized. Choice was judged stable when the mean proportion suboptimal choice over the final three sessions deviated from the mean of the preceding three sessions by 10% or less, with no monotonically increasing or decreasing trend.

Results and Discussion

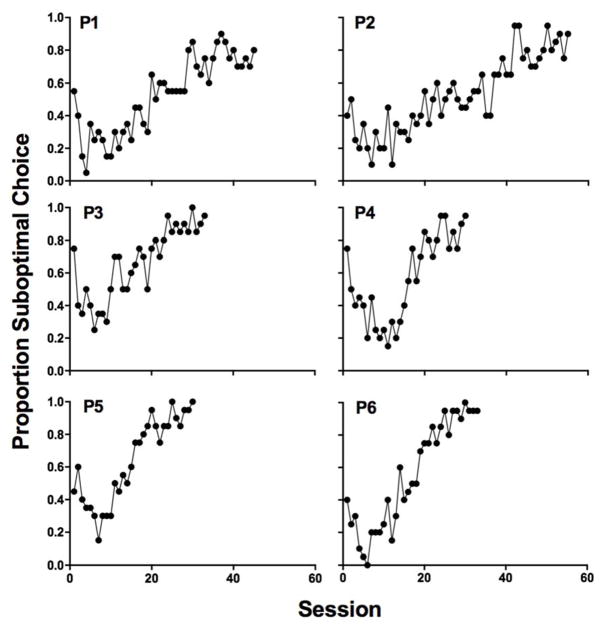
Figure 2 shows individual pigeons’ proportion suboptimal choice across successive sessions in Experiment 1. As with previous research using the suboptimal choice procedure (Laude, Beckman et al., 2014; Laude, Stagner et al., 2014; Zentall & Stagner, 2011), pigeons initially preferred the optimal alternative. However, with additional experience, initial-link choices gradually shifted to the suboptimal alternative. Pigeons’ preference met the stability criteria after a total of 30 (P4 & P5), 33 (P3 & P6), and 45 sessions (P1). Pigeon P2 met the stability criteria at session 32; however, additional sessions were conducted because of an initial-link response bias (discussed below). Using data from the final 6 sessions, a one-sample t-test revealed that pigeons’ preference for the suboptimal alternative was significantly greater than chance; t(5) = 12.2, p < .001.

Fig. 2.

Individual subjects’ proportion suboptimal choice presented against the sessions completed in Experiment 1.

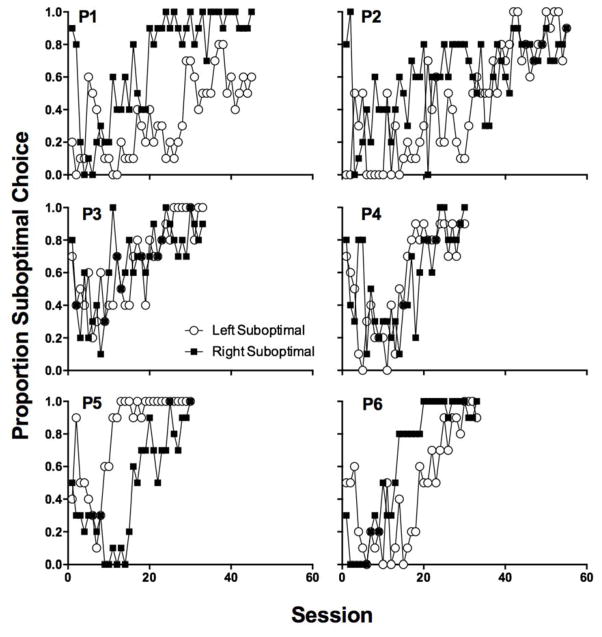
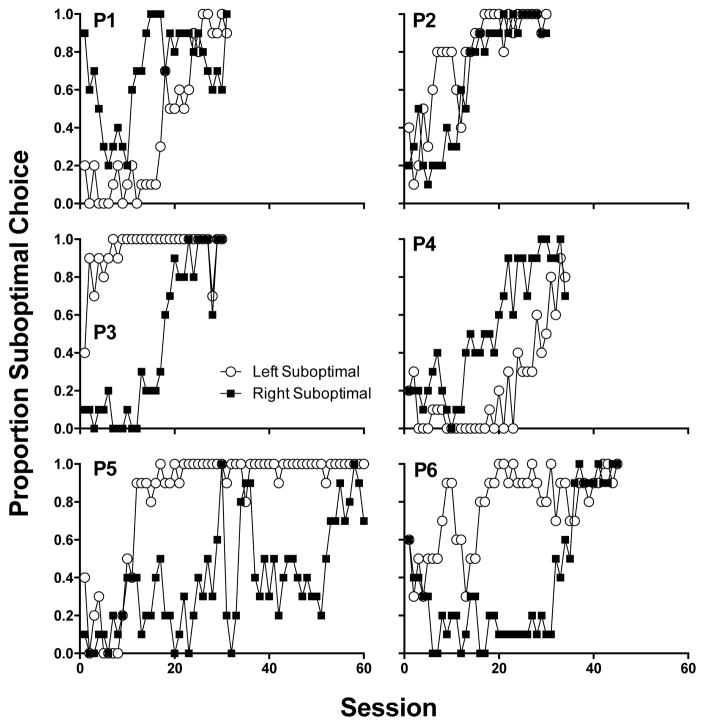
Figure 3 shows suboptimal choices separated by stimulus arrangement; the open symbols correspond to free-choice trials in which the suboptimal alternative was presented on the left key and the closed symbols show choice trials in which pecking the right key produced the suboptimal alternative. For four of the six pigeons a clear preference for the suboptimal alternative emerged on one key before it was observed (in most cases) on the other key. For example, in the terminal sessions P1 preferred the suboptimal alternative only when it was arranged on the right key; when the suboptimal alternative was arranged on the left key, the pigeon was indifferent between the optimal and suboptimal alternatives. For P2, from sessions 17 through 31, the suboptimal alternative was preferred when it appeared on the right key and avoided when arranged on the left key.

Fig. 3.

Individual subjects’ proportion suboptimal choices separated by the side on which they occurred in Experiment 1. Open (closed) symbols show the number of suboptimal choices made when the suboptimal initial-link stimulus was presented on the left (right) key.

These patterns might be due to a response bias favoring one side-key position over the other, though it is curious that the side bias was not observed in the initial sessions, when choice favored the optimal alternative regardless of its location. Another account of this “bias” is that the speed at which pigeons learned the functions of suboptimal stimuli varied by position. For example, if a pigeon first learned that the suboptimal initial-link stimulus, when it appeared on the right key occasionally led to 10 pellets, but the function of the same initial-link stimulus when it appeared on the left was unknown, then this could explain the side bias. This account is consistent with the finding that the same visual stimulus, when presented in two different locations, is not functionally identical for pigeons (e.g., Urcuioli, 2008). For P2, P5 and P6, preference was eventually consistent across these initial-link stimulus arrangements, but this consistency was not observed for P1.

Table 2 shows the median pecks per terminal link following suboptimal and optimal initial-link responses. Data come from the final six sessions and are separated by forced and choice trials. Pigeons tended to peck the S10_0.2 terminal-link stimulus (i.e., the “jackpot” stimulus on the suboptimal alternative) most frequently, whereas they infrequently pecked the S0_0.8 terminal-link stimulus (signaling a suboptimal loss). Pigeons responded at moderate rates to the S3_0.2 and S3_0.8 terminal-link stimuli.

Table 2.

Median responses emitted in terminal links and (in parentheses) the ratio of total responses emitted and total pellets obtained in the final six sessions of Experiments 1 and 2

Pigeon	Forced Trials				Choice Trials				Unit Price
	Suboptimal		Optimal		Suboptimal		Optimal
	S100.2	S00.8	O30.2	O30.8	S100.2	S00.8	O30.2	O30.8	Suboptimal	Optimal
Experiment 1
P1	4 (102/240)	0 (44/0)	0 (7/72)	1 (151/288)	4 (72/180)	0 (39/0)	0 (1/18)	2 (56/75)	0.61	0.47
P2	27 (645/240)	1 (62/0)	7 (182/72)	9 (936/288)	26 (557/210)	0 (53/0)	9 (18/6)	8 (87/27)	2.93	3.11
P3	5 (129/240)	0 (19/0)	2 (60/72)	4 (433/288)	4.5 (104/220)	0 (22/0)	3 (7/9)	3.5 (26/24)	0.60	1.34
P4	6 (151/240)	0 (38/0)	3.5 (113/72)	3 (336/288)	4.5 (90/200)	0 (48/0)	1 (8/9)	4.5 (68/42)	0.74	1.28
P5	9.5 (205/240)	.5 (64/0)	2.5 (73/72)	3 (379/288)	8 (201/240)	0 (68/0)	2.5 (5/6)	1 (5/15)	1.12	1.21
P6	30.5 (701/240)	0 (30/0)	6 (170/72)	4 (563/288)	28 (613/240)	0 (20/0)	11 (11/3)	7 (33/15)	2.84	2.06
Experiment 2
P1	0 (10/240)	0 (9/0)	0 (2/72)	0 (13/288)	1 (12/190)	0 (5/0)	0 (1/12)	0 (1/45)	0.08	0.04
P2	1 (43/240)	0 (5/0)	0 (1/72)	0 (26/288)	1 (33/240)	0 (1/0)	0 (0/0)	0 (0/9)	0.17	0.07
P3	1 (20/240)	0 (18/0)	0 (2/72)	0 (7/288)	1 (18/230)	0 (14/0)	0 (0/0)	0 (0/6)	0.15	0.03
P4	1 (29/240)	0 (14/0)	0 (1/72)	0 (8/288)	0 (13/200)	0 (17/0)	0 (0/12)	0 (0/48)	0.17	0.02
P5	0 (8/240)	0 (17/0)	0 (3/72)	0 (18/288)	0 (9/240)	0 (9/0)	0 (0/6)	0 (1/24)	0.09	0.06
P6	37 (888/240)	0 (21/0)	12.5 (247/72)	0 (195/288)	32.5 (791/240)	0 (30/0)	16 (51/12)	.5 (1/6)	3.6	1.31

Note. Data are separated by forced and choice trials, and by the terminal-link stimuli in each trial. The final columns provide obtained unit prices, calculated across forced and choice trials.

For the purpose of calculating unit prices, Table 2 also shows (in parentheses) the total pecks to each terminal-link stimulus and the total pellets earned over the final six sessions; these numbers are expressed as a response/pellet ratio (i.e., the unit price ratio). The final column of Table 2 provides the unit prices paid for food on the optimal and suboptimal alternatives, collapsed across forced and choice trials. Four pigeons paid a nominally lower price for food on the suboptimal alternative (P2, P3, P4, & P5), while the remaining two pigeons paid a lower price for food on the optimal alternative. These mixed data do not provide systematic evidence that preference for the suboptimal alternative, which developed in all pigeons, is due to the acquisition of food at a lower unit price on that alternative. At the same time, when considering the obtained unit prices of food on these alternatives, it would appear that suboptimal choice is not as economically suboptimal as one might surmise from the experimenter-arranged expected values.

To evaluate if pigeons would continue to prefer the suboptimal alternative if the ratio of suboptimal to optimal unit prices (i.e., suboptimal unit price/optimal unit price) were closer to the inverse ratio of the expected values of these alternatives (i.e., optimal/suboptimal), Experiment 2 was conducted using the same procedure, but the response keys were darkened during all terminal links (to discourage pecking) and terminal-link stimuli were presented diffusely throughout the chamber. If the only pecks made per trial in Experiment 2 were the center-key peck and the single side-key peck made in the initial link, then the ratio of suboptimal to optimal unit prices ([10 pecks/10 pellets]/[2 pecks/3 pellets] = 1.5) would equal the inverse of the expected-value ratio (3/2 pellets per trial = 1.5).

A similar experiment was conducted by Stagner, Laude, and Zentall (2011) but they diffusely presented only the S0_0.8 no-food stimulus. Their study was designed to evaluate if turning away from this bad-news stimulus could account for suboptimal choice (it did not). However, by presenting only the no-food stimulus diffusely and presenting all other stimuli on the response keys, Stagner et al. may have further reduced the unit price of food on the suboptimal alternative (on 80% of the trials no pecks were presumably emitted) relative to the price of food on the optimal alternative. In Experiment 2, all terminal-link key lights were off and terminal-link stimuli were presented diffusely on all trials.

Experiment 2

Methods

Subjects and apparatus

The same six pigeons participated in Experiment 2. All housing and feeding details were as in Experiment 1. The same operant chambers were used, but outside the chamber (and within the sound-attenuating cubicle) each was equipped with four strands of 120 v colored holiday lights. Each strand contained 35 bulbs and could be independently illuminated with a single color (red, blue, green, or yellow). When lit, the strands diffusely illuminated the chamber with their respective colored light.

Procedure

With the following exceptions, all procedures and stability criteria were as in Experiment 1: (a) no pretraining procedures were used; (b) following a peck to the initial-link stimulus (forced trials) or stimuli (choice trials) the chamber was diffusely illuminated with a terminal-link color throughout the FT 10-s terminal link; (c) the side keys were dark during the terminal link; and (d) the initial-link and terminal-link stimuli were changed from those used in Experiment 1 (see Table 1).

Results and Discussion

Pigeons’ proportion suboptimal choice across successive sessions of Experiment 2 are shown in Figure 4. Pigeons 5 and 6 continued the experiment after meeting the stability criteria because of an initial-link side bias similar to that observed in Experiment 1. In the final six sessions, all pigeons strongly preferred the suboptimal alternative; a one-sample t-test revealed that this preference was significantly greater than chance; t(5) = 12.8, p < .001.

Fig. 4.

Individual subjects’ proportion suboptimal choice presented against the sessions completed in Experiment 2.

Figure 5 shows the proportion of suboptimal choices in Experiment 2, separated by stimulus arrangement. All six pigeons’ preference for the suboptimal alternative emerged in one stimulus arrangement before it did in the other. This effect was most persistent in Pigeons 5 and 6. By the terminal sessions, however, preference for the suboptimal alternative was consistently observed regardless of initial-link stimulus arrangement.

Fig. 5.

Individual subjects’ proportion suboptimal choices separated by the side on which they occurred in Experiment 2. Open (closed) symbols show the number of suboptimal choices made when the suboptimal initial-link stimulus was presented on the left (right) key.

These transient patterns of position-biased initial-link choice are similar to those observed in Experiment 1. Because terminal-link stimuli were not displayed on the left and right key locations, presented instead diffusely throughout the chamber, there is no chance that the bias evident in Figure 5 was due to pigeons learning at different rates, depending on position, the functions of the suboptimal terminal-link stimuli. The bias must, therefore, be due either to an unaccounted-for position preference within the chamber, or to pigeons learning at different rates the function of the initial-link stimuli, depending on their left/right location (cf. Urcuioli, 2008).

The lower portion of Table 2 shows the median pecks, total pecks and food pellets earned (in parentheses), and unit prices obtained in suboptimal and optimal terminal links over the final six sessions. For 5 of 6 pigeons, dark keys were rarely pecked and, hence, the pigeons paid a very low unit price for food on both the suboptimal and optimal alternatives; the exception was Pigeon 6. This pigeon pecked the dark key reliably when the S10_0.2 and S3_0.2 stimuli appeared, suggesting that the latter stimulus acquired some excitatory properties due to its infrequency, the property shared with the jackpot S10_0.2 stimulus. Likewise, for this pigeon, the infrequency of pecking S3_0.8 during optimal terminal links suggests that this stimulus acquired inhibitory properties because its high probability of occurrence was shared with the S0_0.8 stimulus encountered in suboptimal terminal links.

In accord with the experimenter-arranged ratio of expected values on the optimal and suboptimal alternatives, all six pigeons paid a higher unit price for food on the suboptimal alternative. The median (across-pigeon) obtained suboptimal/optimal unit-price ratio was 2.59 (IQR=1.87 to 5.87), which exceeded the inverse of the ratio of expected values (1.5), rendering the suboptimal alternative even more suboptimal than programmed. A one-sample Wilcoxon Signed Rank test indicated that these unit price ratios significantly exceeded 1.5; p < .05. Despite the higher unit price, all six pigeons preferred the suboptimal alternative.

The results of Experiments 1 and 2 support previous research demonstrating that pigeons prefer an alternative that delivers 10 pellets with .2 probability over an alternative that delivers 3 pellets with certainty when trial outcomes are signaled by discriminative terminal-link stimuli (Laude, Beckman et al., 2014; Laude, Stagner et al., 2014; Zentall & Stagner, 2011). The results also demonstrate that pigeons’ preference for the suboptimal alternative does not result from lower unit prices on the suboptimal alternative. To the contrary, in Experiment 2 the suboptimal/optimal unit-price ratio exceeded the experimenter-arranged expected value ratio, such that if choice was based on unit prices alone, pigeons would strongly prefer the optimal alternative; they preferred the suboptimal alternative in all cases.

Experiment 3

Experiment 3 was conducted to evaluate a hypothesis derived from the string theory of gambling (Rachlin et al., 2015). Applied to the Zentall and Stagner (2011) procedure, string theory holds that the value of the suboptimal alternative is the sum of the values of the undiscounted “jackpot” food reward (10 pellets) and the discounted value of the string of nonreinforced suboptimal trials (losses) that separate the jackpot from the last food reward. The suboptimal-choice procedure, however, may make it difficult for the pigeon to correctly evaluate the value of the suboptimal string because forced trials on the suboptimal alternative (most of which end without food) are interspersed between optimal trials (each one ending with food). If losses on the suboptimal alternative intervene between food events on the optimal alternative, these discounted losses might be factored into and decrease the value of the optimal alternative, thereby promoting suboptimal choice. Likewise, if, upon a jackpot on the suboptimal alternative, the pigeon attributes only a portion of the string of suboptimal losses that preceded that win to the suboptimal alternative (the rest being misattributed to the optimal alternative when optimal “wins” interrupt the string of suboptimal losses), this misattribution would increase the value of the suboptimal string.

In Experiment 3 we sought to minimize the possibility of such misattribution of losses to the optimal alternative. To that end, all suboptimal and optimal forced trials were presented in nonoverlapping sequences at the beginning of each suboptimal-choice session. If pigeons mistakenly attribute suboptimal losses when calculating the value of the optimal alternative, then this procedural change should decrease pigeons’ preference for the suboptimal alternative.

Method

Subjects and apparatus

The same six pigeons were used in Experiment 3; their housing and feeding arrangements were unchanged. The operant chambers from Experiment 2 were used, but the strands of holiday lights were removed.

Procedure

The procedures were as arranged in Experiment 1, with three exceptions. First, forced and choice trials were no longer intermixed. Instead odd numbered sessions began with a block of 20 forced-optimal trials followed by a block of 20 forced-suboptimal trials (order reversed in even numbered sessions). To reduce the likelihood that a sequence of losses at the end of the forced trials would interfere with the calculation of the value of choice-trial outcomes, the sequence of suboptimal forced trials always ended with food delivery, while holding constant at .2 the overall probability of a forced-suboptimal win. The final 20 trials in each session were choice trials.

The second procedural difference from Experiment1 was that, throughout a condition, the optimal alternative was assigned to one side key (left or right) and the suboptimal alternative was assigned to the other side key. Finally, the stimulus assignments in the initial and terminal links were changed (see Table 1). After suboptimal choice met the previously used stability criteria, the assignment of the suboptimal and optimal alternatives to the left and right keys was reversed for three of the pigeons and choice was reassessed until stable.

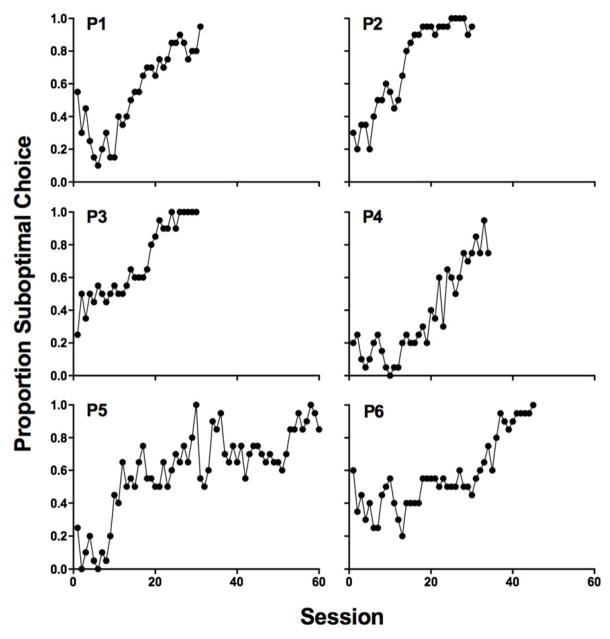
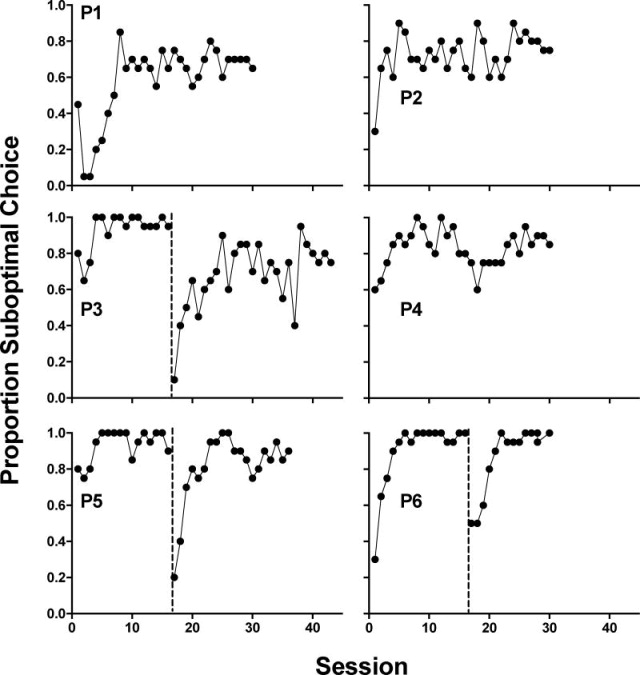
Results and Discussion

Figure 6 shows individual pigeons’ proportion suboptimal choice across successive sessions. When suboptimal and optimal initial-link stimuli were presented at unique and constant locations (i.e., left or right keys) and forced trials were not intermixed, all six pigeons reliably preferred the suboptimal alternative. For the three pigeons that underwent a reversal in the keys to which the stimuli were assigned, all of them quickly recovered their preference for the suboptimal alternative. Using the mean proportion suboptimal choices made over the last six sessions (i.e., not including data from the initial key assignments for pigeons P3, P5, and P6), a one-sample t-test revealed that preference for the suboptimal alternative was significantly greater than chance; t (5) = 5.94, p = .002.

Fig. 6.

Individual subjects’ proportion suboptimal choices presented against the sessions completed in Experiment 3.

Table 3 shows the median number of pecks made during terminal links during the final six sessions. The table also shows (in parentheses) the total pecks to each terminal-link stimulus and the total pellets earned in these sessions. Five of six pigeons emitted the highest rate of responding during the S10_0.2 terminal-links. The exception (P1) responded at a similar rate to all terminal-link stimuli that ended with the delivery of food and never responded during the S0_0.8 terminal-link stimulus.

Table 3.

Median responses emitted in terminal links and (in parentheses) the ratio of total responses emitted and total pellets obtained in the final six sessions of Experiment 3.

Pigeon	Forced Trials				Choice Trials				Unit Price
	Suboptimal		Optimal		Suboptimal		Optimal
	S100.2	S00.8	O30.2	O30.8	S100.2	S00.8	O30.2	O30.8	Suboptimal	Optimal
P1	5 (124/240)	0 (10/0)	5.5 (136/72)	3 (371/288)	3 (59/150)	0 (11/0)	3 (24/21)	3 (123/96)	0.52	1.37
P2	27.5 (693/240)	1 (61/0)	5.5 (152/72)	7 (762/288)	24 (451/180)	1 (51/0)	4 (17/15)	5 (113/57)	2.99	2.42
P3	9 (189/240)	0 (28/0)	1 (19/72)	0 (30/288)	7 (166/200)	0 (32/0)	0 (1/15)	0 (4/60)	0.94	0.12
P4	4.5 (118/240)	0 (10/0)	0 (9/72)	1 (192/288)	4 (87/210)	0 (23/0)	0 (2/9)	0 (9/36)	0.53	0.52
P5	32.5 (716/240)	0 (49/0)	3 (81/72)	19.5 (1895/288)	29 (442/170)	0 (20/0)	1 (23/27)	6 (397/93)	2.99	4.99
P6	31 (746/240)	0 (15/0)	14 (302/72)	3 (714/288)	29 (701/240)	0 (14/0)	0 (0/0)	0 (0/3)	3.08	2.8

Note. Data are separated by forced and choice trials, and by the terminal-link stimuli in each trial. The final columns provide obtained unit prices, calculated across forced and choice trials.

The unit prices paid for each food pellet on the optimal and suboptimal alternatives is presented in the right-most column of Table 2. Two pigeons obtained food at a lower unit price on the suboptimal alternative (P1 & P5), the remaining four pigeons obtained food at a lower price on the optimal alternative. Despite these between-subject differences, all pigeons developed a preference for the suboptimal alternative.

When suboptimal and optimal alternatives were presented in consistent locations and forced suboptimal trial blocks were separated from optimal trial blocks so that suboptimal losses would be less likely to be used in calculating the value of optimal-alternative reinforcers, pigeons consistently preferred the suboptimal alternative. Thus, it is unlikely that pigeons’ preference for the suboptimal alternative in Experiments 1 and 2 was the result of misattributing suboptimal losses (i.e., S0_0.8 signaled trials ending without food) to the value of the optimal alternative (and not using these losses in the accounting of the value of the suboptimal alternative), as might be hypothesized from the string theory of gambling (Rachlin et al., 2015).

General Discussion

The goal of the present experiments was to investigate two potential threats to the validty of the Zentall and Stagner (2011) and other suboptimal choice procedures. Both threats came in the form of alternative explanations of suboptimal choice; explanations that, if true, would recast suboptimal choice as economically adaptive. The first threat was the possibility that pigeons choose the suboptimal alternative because they obtain food at a lower unit price on that alternative. Across all three experiments there was no systematic evidence that suboptimal choice occurred because of relative obtained unit prices. Instead, pigeons developed a preference for the suboptimal alternative even when the unit price of suboptimal food was higher.

The second threat was derived from the string theory of gambling (Rachlin et al., 2015). We speculated that if pigeons misattribute some of the suboptimal losses to the optimal alternative, then when they evaluate the values of the optimal and suboptimal strings the value of the optimal string would be decreased relative to that programmed by the experimenter. When, in Experiment 3, optimal and suboptimal forced trials were presented in separate blocks so that opportunities for these misattributions were minimized, pigeons rapidly developed a preferrence for the suboptimal alternative. Thus, the string theory-inspired alternative account of suboptimal choice was not supported. Collectively, the results of these experiments support the valdity of the suboptimal choice procedure (Zentall & Stagner, 2011) as an animal model that captures some components of the human gambling millieu.

Having passed these validity tests, if the promise of this animal model of human gambling is to pay dividends, we must better understand the behavioral processes responsible for nonhuman “gambling.” At least two theories appear in the suboptimal choice literature, and they will be briefly discussed here. The first theory was forwarded by Laude, Stagner et al. (2014); they suggested suboptimal choice develops when conditioned inhibition toward the S0_0.8 stimulus declines with extended exposure to that stimulus. This conditioned inhibition to S0_0.8 is said to underlie initial preference for the optimal alternative (observed most clearly in our Experiments 1 and 2), but as this inhibition wanes (leaving only the excitatory properties of S10_0.2), suboptimal choice emerges. Our Experiment 3 was the only one in which pigeons did not prefer the optimal alternative for several sessions before suboptimal choice emerged. New terminal-link stimuli were arranged in Experiment 3 and, therefore, one would not a priori predict a failure of the new S0_0.8 stimulus to function as a conditioned inhibitor. Consistent with the hypothesis that pigeons must separately learn the function of the same stimulus when it appears in two locations, in Experiment 3 the S10_0.2 and S0_0.8 stimuli were presented in a single left/right location and this consistency may have facilitated learning the stimulus functions, hastening the decline in the conditioned inhibitory properties of S0_0.8.

The other prominent theory of suboptimal choice is the Signals for Good News (SiGN) hypothesis (McDevitt, Dunn, Spetch, & Ludvig (2016). According to this account, suboptimal choice occurs because of: (a) the uncertainty resolving properties of the suboptimal terminal-link stimuli and (b) discounting the value of food because of terminal-link duration. Considering the first of these factors, and extrapolating from their hypothesis, when the suboptimal alternative is selected there is uncertainty about when food will be delivered. The suboptimal amount (10 pellets) is predictable, but its time of delivery time is not. When S10_0.2 is the consequence of a suboptimal choice, this signals good news: a delay of 10 s, which is a delay reduction relative to the background average of 50-s of terminal link time until suboptimal food. This delay reduction renders the S10_0.2 stimulus a powerful conditioned reinforcer (Fantino, 1969). Meanwhile, the SiGN hypothesis holds that the signal for bad news, S0_0.8 in our experiments, does not punish suboptimal choice (see McDevitt et al., 2016 for a review of the supporting evidence). Finally, because there is no temporal uncertainty about the time until food following an optimal initial-link choice (10 s every time), there is no reduction in expected delay and, therefore, the optimal terminal-link stimuli acquire no conditioned reinforcing properties. The other suboptimal-choice determining factor in the SiGN hypothesis is that pigeons discount the value of food rewards because they are delayed after the initial-link choice. How these two factors are quantitatively combined to yield suboptimal choice has yet to be formalized in the SiGN hypothesis.

As the SiGN hypothesis qualitatively predicts a significant number of suboptimal choice findings (for review see McDevitt et al., 2016) this account holds promise for understanding human gambling in general, and the relation between steep delay discounting and human pathological gambling in particular (MacKillop et al., 2014). That is, if a pigeon steeply devalues delayed food reinforcers, then the relative value of conditioned reinforcers, obtained in a context of temporal uncertainty, may be more valuable than delayed food, and more likely to influence suboptimal choice (Laude, Beckman et al., 2014). By the same token, a human who steeply discounts certain but delayed outcomes may be particularly prone to conditioned reinforcers (like a very good poker hand) that signals a delay reduction to a “jackpot” reward.