Fatigue Damage of Collagenous Tissues: Experiment, Modeling and Simulation Studies

Abstract

Mechanical fatigue damage is a critical issue for soft tissues and tissue-derived materials, particularly for musculoskeletal and cardiovascular applications; yet, our understanding of the fatigue damage process is incomplete. Soft tissue fatigue experiments are often difficult and time-consuming to perform, which has hindered progress in this area. However, the recent development of soft-tissue fatigue-damage constitutive models has enabled simulation-based fatigue analyses of tissues under various conditions. Computational simulations facilitate highly controlled and quantitative analyses to study the distinct effects of various loading conditions and design features on tissue durability; thus, they are advantageous over complex fatigue experiments. Although significant work to calibrate the constitutive models from fatigue experiments and to validate predictability remains, further development in these areas will add to our knowledge of soft-tissue fatigue damage and will facilitate the design of durable treatments and devices. In this review, the experimental, modeling, and simulation efforts to study collagenous tissue fatigue damage are summarized and critically assessed.

I. Introduction

Soft collagenous tissues are comprised of networks of collagen fibers embedded in a ground substance and interspersed by fibroblasts. This unique structure provides pliability and strength important for normal physiological function. These attractive mechanical properties also make chemically treated, collagenous tissues suitable for a broad spectrum of medical applications such as cardiovascular grafting as well as ligament, tendon, cartilage, sclera and hernia repair and replacement. Yet, like artificial materials, the mechanical properties of soft tissues degrade with fatigue.¹ Soft tissues, including skin, brain, arteries,² venous and vaginal tissue,^3–5 and atherosclerotic plaque,⁶ exhibit softening and unrecoverable strains (permanent set) at the damaged state. These fatigue-induced changes are thought to play a role in the pathogenesis of native tissues and to limit the durability of nonviable tissue-derived implants and scaffolds. An in-depth understanding of the fatigue damage process in soft tissues would facilitate the development of methods to mitigate fatigue-induced property changes. Nonetheless, the fatigue damage process of soft tissues is not well understood.

Despite the need for soft-tissue fatigue analyses, there is relatively little experimental fatigue data in the literature. Fatigue experiments are often difficult and time-consuming to perform. Existing data are predominately limited to uniaxial fatigue tests, which may not represent physiological loading conditions. However, the incorporation of recently developed constitutive soft-tissue damage models in finite element solvers could potentially resolve this problem. Tissue fatigue damage models that can be calibrated from simple, isolated fatigue experiments, such as cyclic uniaxial loading, and then implemented in FE to simulate more complex and physiologically relevant loading conditions, will be extremely powerful tools for fatigue analysis. An advantage of using simulation-based fatigue analysis is that well-controlled parametric studies can better determine the precise effects of different loading, geometry, or design factors.

In this review, we discuss the experimental, modeling, and simulation work that has been done thus far to study soft collagenous tissue fatigue damage as well as some future directions in this field. We focus on the characterization and modeling of mechanical and structural changes of soft tissues for musculoskeletal and cardiovascular applications. The reader is referred to the reviews by Shepherd et al.,⁷ Rowland et al.,⁸ and Singhal et al.⁹ for more in depth discussion on tendon, extracellular matrix (ECM)-derived scaffold, and bioprosthetic heart valve fatigue respectively.

A. Musculoskeletal Applications

An estimated 16.4 million tendon and ligament injuries occur each year in the United States.⁷ These injuries are painful and difficult to repair. While many tendon and ligament injuries are often the result of rapid movements where stresses exceeding the ultimate tensile strength have been observed,^7,10,11 fatigue damage due to overuse and the poor healing response of these tissues likely precedes these events. Tendinopathies also occur in the absence of traumatic events¹² and may be the result of accumulated fatigue damage.¹³

Tendon and ligament injuries are often treated with biological tissue grafts.^14,15 For example, the gold standard treatment for anterior cruciate ligament injuries is repair via a patella tendon autograft¹⁶; however, this treatment requires the patient to undergo additional surgery to harvest the autograft and often results in donor site morbidity. Many researchers have attempted to develop synthetic ligament replacement materials to avoid the additional harvest surgery but without much success. These devices fail over time due to mechanical fatigue, creep, permanent elongation, and other factors.¹⁶ More recent efforts have been aimed toward the development of tissue-engineered constructs, and although there is great potential for using ECM-based grafts, creating durable constructs remains challenging.^8,16

The characterization of tendon and ligament fatigue properties is critical for understanding tissue pathogenesis and defining endpoints for tissue engineering endeavors. Fatigue analysis of potential replacement materials is equally important for assessing suitability and durability of new treatments. Many researchers have studied the fatigue properties of these tissues experimentally, but these experimental data are largely underutilized in modeling and simulation efforts. In the future, such efforts could assist in the evaluation of new tendon and ligament replacement materials and in the design of ECM-derived scaffolds.

B. Cardiovascular Applications

Tissue fatigue studies related to cardiovascular applications have been primarily focused on bioprosthetic heart valves (BHVs). Currently, the only proven effective, long-term treatment for valvular heart disease is open-chest cardiac valve repair or replacement surgery. BHVs have been used to treat valvular disease for more than four decades,¹⁷ and they continue to be one of the dominant replacement valve modalities, either as a conventional prosthetic valve design or more recently for minimally invasive transcatheter delivery.^18,19 There are two main types of BHVs: porcine BHVs, which are fabricated from whole glutaraldehye-treated porcine aortic valves, and pericardial BHVs, which consist of glutaraldehyde-treated bovine pericardium (GLBP) leaflets. Regardless of the specific design, long-term durability of the tissue leaflets is limited. BHVs often need to be replaced within 10 years after implantation and in as soon as 5 years in younger patients.²⁰ It has been hypothesized that clinical BHV failure due to structural deterioration is caused by localized leaflet damage at stressed regions.^20,21 Mechanical fatigue damage may also facilitate proteolytic degradation of the collagenous ECM, causing leaflet tears and perforations.²²

Fatigue of transcatheter aortic valve (TAV) leaflets will become an increasingly critical and prevalent problem in the coming 5 years. TAV intervention has been shown to be a viable treatment option for elderly high-risk patients with aortic stenosis.^23–25 However, TAV durability has been widely recognized by the valve industry and clinicians^26,27 as one of the critical issues limiting its use in low-risk patients, with longer life expectancies than the current high-risk TAV patients. Interestingly, 9 of the 10 TAV devices currently available are comprised of GLBP or porcine pericardium leaflets, similar to traditional BHVs in which leaflet durability is limited. Furthermore, because TAVs must be crimped into a small diameter catheter for delivery and deployment, they are subject to additional design constraints such as thinner leaflets and lack of valve stent-tip deflection, which may further impede long-term durability.

Few studies have been conducted on the fatigue properties of BHV leaflet materials and even less on the modeling and simulation of fatigue in these tissues. While the characterization and modeling of leaflet material fatigue properties will be an enabling step in the development of durable next-generation valve devices, simulation-based fatigue analyses will be essential for translating tissue-level fatigue to device-level fatigue. Recently, the feasibility of such simulation-based fatigue analysis of BHVs has been demonstrated.²⁸

II. Experimental Characterization of Fatigue Damage in Soft Collagenous Tissues

Few studies have investigated the experimental characterization of soft tissue fatigue effects, which is probably a result of the many associated challenges. The experimental methods are time-consuming and often involve complex testing instruments. Most groups rely on ex vivo experiments to study soft tissue fatigue, but in vivo methods are emerging. Ex vivo experiments are simpler to perform than in vivo studies; however, they do not always reflect the true in vivo mechanical environment.

A. Ex vivo Tissue Fatigue Testing

1. Isolated tissue material fatigue testing

In an attempt to characterize the specific effects of tensile, compressive, and flexural stresses on soft tissue material properties, several groups have taken an isolated material fatigue test approach. Uniaxial fatigue loading experiments are often adopted due to the relative simplicity of this approach. Uniaxial fatigue experiments can be categorized into two groups: load control experiments, in which specimens are cycled to a peak load and the progressive increase in tissue extension is monitored, and displacement control experiments, in which specimens are cycled to a peak displacement and the reduction in the peak load is monitored. Load control experiments are attractive because the specimens can be cycled to failure and thus be used to determine a typical stress vs. cycle (S–N) curve for the material; however, these experiments can be very difficult to control particularly for extensible soft tissues. Displacement control experiments typically do not result in specimen failure, but they are much easier to control. In these experiments, the progression of fatigue is determined through comparison of the tissue properties before and after fatigue.

Tendons and ligaments comprised mainly of axially aligned collagen fibers experience primarily tensile stresses in vivo; thus, fatigue studies of these tissues have been primarily limited to uniaxial tension. Through uniaxial fatigue testing, Schectman and Bader¹⁰ observed a decrease in ultimate tensile strength from approximately 100 MPa to 49.1 MPa for human extensor digitorum longus tendons post fatigue. Likewise, Wang et al.^29,30 showed a reduction in the failure strength of wallaby tail tendons after cyclic loading. In Provenzano et al.³¹ a uniaxial stretch of 5.14% was identified as the threshold to induce damage in the rat medial collateral ligament (MCL). This damage was realized by changes in the tissue stress-strain curve, namely, elongation of the toe region and reduction of the stiffness and ultimate stress.³¹ MCL cellular damage was observed at strains below the structural damage threshold, which they postulate may trigger the natural healing process in vivo.³¹ This hypothesis is supported by the finding of Ker et al.³² that high-stressed tendons in vivo have superior fatigue properties to low-stressed tendons, suggesting stress-mediated remodeling of the tissue. Fung et al.³³ also showed that at even low levels of fatigue, before mechanical property changes are evident, collagen fibers which are normally parallel and uniform in the rat patellar tendon become kinked. At increasing levels of fatigue, the tissue matrix became severely disrupted with poor fiber alignment and widening of the interfiber space.³³ Zec et al.³⁴ observed significant permanent sets induced in the fatigued rabbit ligament suggesting plastic deformation of the collagen fibers. Notably, these fatigue phenomena in tendons and ligaments are distinct from the creep rupture that occurs after prolonged application of a constant stress.^30,35,36 Furthermore, the tendon and ligament life cycles predicted from ex vivo test results are typically unreasonably low due to the absence of any healing mechanisms or possibly other experimental factors.⁷

Several groups have conducted ex vivo fatigue studies on viable tissue specimens in an effort to determine the relationships between mechanical and biological effects. Banes et al.^37,38 showed that fatigue loading stimulated deoxyribonucleic acid and collagen synthesis in the avian tendon. Contrarily, Devkota et al.³⁹ observed a significant increase in collagenase activity in addition to rising levels of inflammatory mediator prostaglandin E₂ (PGE₂) overcycling, and hypothesized that PGE₂ was a key factor in the degradation of the ECM.³⁹ There is evidence that collagenase⁴⁰ and inflammatory mediator⁴¹ activity in cyclically loaded tendons may be strain dependent. Increased apoptosis has also been observed in cyclically loaded tendons.^39,42 Experimental results between groups are not entirely consistent. Much work still remains to be done to correlate mechanical and biological fatigue effects.

Uniaxial fatigue testing has also been used to determine the fatigue properties of cardiovascular tissues mainly for heart valve applications. Early studies include those by Broom to characterize the effects of uniaxial fatigue in chemically fixed bovine and porcine mitral valve tissue^43,44 as well as porcine aortic valve tissue.⁴⁵ Continued cycling induced a reduction in tissue compliance and collagen crimp.^43–45 Broom concluded that preserving the natural collagen fiber crimp in fixed valve tissues will improve the fatigue properties of the tissue,⁴⁵ although this point is somewhat controversial.⁴⁶ Sun et al.⁴⁷ and Sellaro et al.⁴⁸ have since investigated the uniaxial tensile fatigue properties of GLBP. The results of Sellaro et al. demonstrated a strong dependency between the GLBP fatigue properties and the collagen fiber orientation with respect to the applied loading. In GLBP specimens cycled along the fiber direction, slight stiffening was observed in the fiber direction, as shown in Figure 1a from Sun et al.,⁴⁷ with little change to the cross-fiber direction, inducing slightly increased mechanical anisotropy.^47,48 These results can be explained physically by increased fiber alignment and un-crimping in the fiber direction^47,48 The specimens cycled in the cross-fiber direction again became stiffer along the loading direction, while the cross-loading direction or fiber direction became more compliant. This resulted in a complete reversal of the tissue mechanical anisotropy after fatigue, and can be explained by reorientation of the collagen fibers towards the direction of applied load.⁴⁸ Permanent set was observed in both groups presenting as elongation in the loading direction and contraction in the cross-loading direction,^47,48 as shown in Fig. 1b from Sun et al.⁴⁷ Collagen conformational changes were evident after only 20 million cycles of fatigue, which represents approximately 7 months in vivo.⁴⁸

Fig. 1.

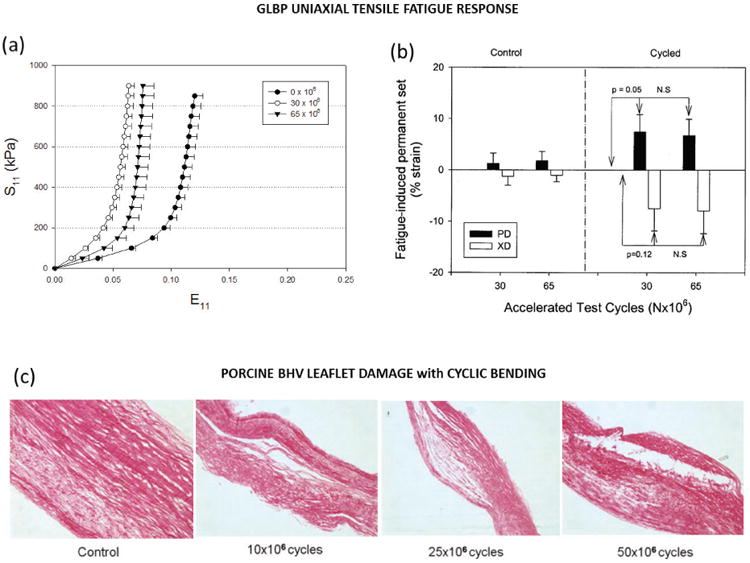
Fatigue induced (a) stiffening in the loading direction and (b) permanent set of GLBP specimens subjected to uniaxial stretch cycles adapted from Sun et al.⁴⁷ (c) Histological sections of porcine BHV leaflet specimens showing progressive delamination with increasing levels of bending fatigue adapted from Mirnajafi et al.⁵³

Uniaxial experiments are limited because they do not represent in vivo loading conditions. Ideally, biaxial fatigue testing experiments could be performed to determine the tissue fatigue properties under various loading protocols; however, these types of experiments would be extremely complex. In light of these points, García Páez et al.^49,50 have adopted a more physiologically relevant cyclic pressurization experimental set up for characterizing the fatigue properties of gluraladehyde-treated pericardium. They argue that the tissue durability can be estimated from the energy consumed during the initial loading cycles. The limitation of these studies is that they represent low fatigue states (≤4500 cycles) and the fatigue induced property changes were not rigorously determined.

Particularly for heart valve applications, tissue bending is also a primary loading modality. The leaflet experiences curvatures of up to 0.6 mm⁻¹ during diastole.⁵¹ Vesely et al.⁵² examined the opening characteristics of porcine BHVs and found correlation between areas of high bending curvature and tearing in the leaflets. Furthermore, in the uniaxial fatigue studies by Broom,^43–45 the tissues were subjected to compressive flexure upon unloading and this flexure was thought to be the cause of collagen fiber disruption apart from uncrimping. Yet, few studies have sought to characterize the fatigue effects of cyclic bending in heart valve tissues. Only Mirnajafi et al.⁵³ adopted an isolated cyclic bending test for valve tissue. Cyclic flexural fatigue of glutaraldehyde-treated porcine aortic valve leaflets induced a marked loss of flexural rigidity in just 10 million cycles.⁵³ Their results suggest that the primary mechanism of early to mid-level fatigue damage of porcine BHVs may be delamination induced by cyclic flexure damage as shown in the histological slides in Fig. 1c (from Mirnajafi et al.⁵³). This finding contrasts with pericardial BHVs in which tissue damage is thought to be a result of high tensile stress.⁵³ The discrepancy in fatigue mechanisms may be a result of the structural differences between leaflet and pericardial tissues. The aortic valve leaflet has a distinct tri-layer structure with the spongiosa layer, largely comprised of non-collagenous glycosaminoglycans (GAGs) and proteoglycans (PGs), between the mainly fibrous fibrosa and ventricularis layers composed of collagen and elastin. GLBP has a much more homogenous structure. Raghavan et al.⁵⁴ determined that glutaraldehyde only stabilizes the collagen component of the porcine BHV leaflets, and thus GAGs leach out under conditions of fatigue.²⁰ For this reason, the long-term fatigue response of glutaraldehyde-treated tissues is primarily based on the collagen fibers. This loss of GAGs may be responsible for the delamination of the ventricularis and fibrosa layers, the increased flexural rigidity of the leaflets, and has been suggested to be a pathway for leaflet calcification.²⁰ It has been suggested that chemical modifications such as the addition of neomycin to the typical glutaraldehyde tissue treatment⁵⁴ could help stabilize GAGs in addition to collagen to help mitigate this mechanism of porcine BHV fatigue. The loss of elastin supporting the collagen framework may also expedite fatigue and uncrimping of the collagen fibers.

These studies demonstrated that under cyclic tension, collagenous tissues exhibit stiffening and permanent set particularly along the loading direction. The permanent set phenomena has been hypothesized to occur as a result of the following mechanisms: (1) slippage of the collagen networks, (2) hydrolysis of the intermolecular cross-links, (3) or rupture of the glutaraldehyde cross-links in fixed tissues thus allowing for permanent deformation or uncrimping of the collagen networks.²² Cyclic bending fatigue may lead to collagen fiber distortion and increased flexural stiffness. There is also evidence that mechanical fatigue induces cellular changes in the tissue although the precise effects remain unclear. The main limitation of isolated material tests is that the in vivo mechanical environment may not be accurately reproduced, thus the soft-tissue fatigue-damage mechanisms identified in these experiments may not reflect the in vivo mechanisms.

2. Whole tissue implant fatigue testing

The in vivo mechanical environment is quite complex for heart valve applications. Different areas of the leaflets may experience drastically different loading conditions. Therefore, several groups have adopted whole-valve device-fatigue tests using accelerated wear testers (AWT), which can better replicate the in vivo hemodynamics, to gain a better understanding of the in vivo fatigue mechanisms of BHVs. AWT testing is also used frequently in commercial settings. In fact, the International Standards Organization⁵⁵ and the Food and Drug Administration⁵⁶ recommend that new BHV designs be tested up to 200 million cycles using AWTs to evaluate fatigue performance. Ultimately, similar fatigue effects in BHV materials were observed: softening, strength reduction, and collagen alteration. Billiar and Sacks⁵⁷ found a significant reduction in the ultimate tensile strength and alteration of the planar biaxial mechanical properties of porcine BHV leaflets after 200 million cycles of AWT tests. Hilbert et al.⁵⁸ used polarized light optics to characterize damage to the BHV collagen fiber architecture due to accelerated testing. For GLBP, they measured a 37% increase of collagen fiber crimp period after 360×10⁶ cycles.⁵⁸ Similarly, Liao et al.⁵⁹ observed loss of collagen crimp and leaflet thinning in decellurized aortic valves. Smith et al.⁶⁰ observed increased curvature and collagen fiber distortion in the central belly region of porcine BHV leaflets to 500×10⁶ AWT cycles.⁶⁰ Sacks and Smith⁶¹ showed that this fiber damage can occur in localized regions, likely those subjected to high stresses, long before any gross structural changes become evident. Wells et al.²² observed irreversible alteration of the glutaraldehyde crosslinks in porcine BHV leaflets after just 50×10⁶ cycles. Vyavahare et al.²⁰ and Raghavan et al.⁵⁴ also observed leaflet microstructural changes including damage to the type I collagen²⁰ and loss of GAG content.^20,54 These studies have been particularly useful in identifying concentrated damage regions within the leaflets and flawed designs. Still, the in vitro fatigue platform is void of biological factors that may accelerate leaflet fatigue in vivo.

B. In vivo tissue fatigue analysis

The ultimate goal of all tissue fatigue studies is to determine the in vivo fatigue response. In vivo studies have more clinical relevance. For instance, the results from in vivo experiments by Thornton and Bailey^62,63 demonstrated that the healing ligament is more susceptible to injury under cyclic loads than under static creep loads, which has important implications for the treatment and rehabilitation of ligament injuries. For this reason, many groups have adopted small animal in vivo models for studying tendon and ligament fatigue damage. Soslowsky et al.,⁶⁴ Scott et al.⁶⁵ and Millar et al.⁶⁶ have used in vivo running rat models to study supraspinatus tendon fatigue. Reductions in the tissue extensibility and tensile strength as well as increased cellularity and disruption of the collagen fiber structure were observed following cyclic loading.⁶⁴ Results suggested that insulin-like growth factor 1 (IGF-1)⁶⁵ and pro-inflammatory cytokines⁶⁶ may play a role in tendinopathy. Huang et al.⁶⁷ and Glazebrook et al.⁶⁸ used similar running rat models to study fatigue of the Achilles tendon. Achilles tendon gross structure was similar for exercised and control rats,^67,68 but collagen disorganization was observed histologically in exercised animals.⁶⁸ Fung et al.⁶⁹ developed an in vivo model which was adopted in several studies to characterize the mechanical and structural changes to the patellar tendon induced by cyclic loading in rats^69–72 and mice.⁷³ The tendon mechanical properties were measured through controlled uniaxial testing and the fibrous structure was assessed through noninvasive second harmonic generation. Figure 2 from Fung et al.⁶⁹ shows progressive damage and disruption to the collagen network with increasing levels of fatigue.^69,70,73 Analysis of mRNA expression showed modest changes in collagen I, III, and V at early and mid-stage fatigue life and greater changes for late fatigue life,⁶⁹ which are consistent with pathologic features of human tendon degeneration. Others have adopted the rabbit in vivo model.^74–76 Tendon microtears have been observed early in fatigue life,⁷⁶ but surprisingly, gene expression levels in exercised and control rabbits were similar.⁷⁵

Fig. 2.

In vivo second harmonic imaging of rat the patellar tendon over uniaxial fatigue cycling adapted from Fung et al.⁶⁹ Progressive damage and disruption to the collagen structure is shown from (a) the unfatigued to the (b) slightly, (c) moderately, and (d) highly fatigued states.

For BHV applications, in vivo studies are limited to the characterization of explanted BHVs. The effects of cyclic loading observed in isolated material tests and AWT cycling have also been observed in explanted valve tissues. For instance, Purinya et al.⁷⁷ found a ∼50% reduction in the strength of BHVs after only 48 months of in vivo implantation. However, the motivation for in vivo BHV studies was less about identifying fatigue effects in the tissue, but rather to identify critical valve design issues which may affect leaflet durability. Through extensive study it has become clear that BHV design features may have a significant impact on the long-term durability. For instance, consider two different pericardial BHVs: the Ionescu-Shiley (IS) valve and the Carpentier-Edwards Perimount (CEP) valve. The IS valve was taken off the market for its subpar durability of approximately 5 years,^78–84 whereas the CEP valve has an in vivo durability of up to 20 years. The limited durability of the IS valve was thought to be the result of the rigid stent and the suture hole in the leaflet near the top of the post.⁸⁰ IS valve failures were often associated with leaflet tearing initiating at the commisures and propagating down the suture attachments as shown in Figure 3 from Lawford et al.⁸⁵ For this reason, second generation pericardial BHVs, including the CEP, incorporated a flexible stent to act as a cushion and reduce stresses acting on the leaflets.⁹ After extensive comparison between these two valves, the rigid stent, thin leaflets, and poor leaflet coaptation of the IS valve were thought to be the cause of its early demise.⁸⁶ In rare cases, early CEP valve structural failures have also been observed.⁸⁷ These failures are thought to be largely due to heterogeneity in the structure and properties of the GLBP leaflets, which leads to leaflet tearing and/or prolapse due to elongation of one or more of the leaflets.^9,87,88 The main limitation of in vivo studies is that they are not well controlled due to patient variability, which makes it difficult to compare explanted valves and identify the mechanisms of fatigue.

Fig. 3.

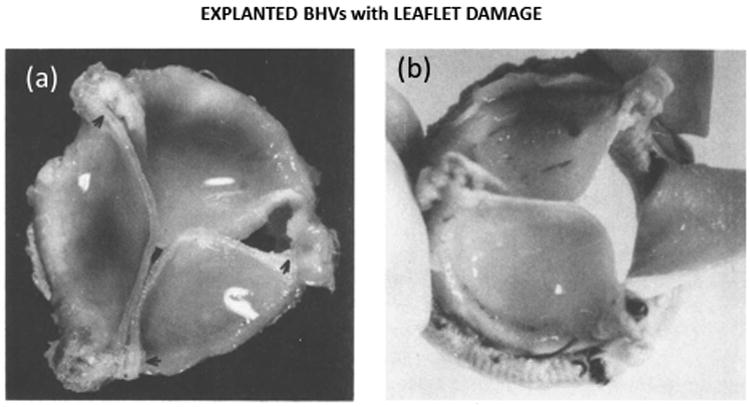
Explanted Ionescu-Shiley BHVs adapted from Lawford⁸⁵ displaying (a) leaflet sagging and damage near the commissure and (b) leaflet tearing along the suture attachments.

From the work that has been done to study fatigue damage in soft collagenous tissues, it is clear that there are significant and complex changes to the tissue mechanical properties and structure resulting from fatigue. However, the precise relationships between loading modalities, frequency and duration on these fatigue-induced changes have not been established. It is important to develop and calibrate soft tissue fatigue damage constitutive models in order to predict, and ultimately develop methods to mitigate these fatigue effects.

III. Constitutive Modeling of Soft Tissue Fatigue Damage

A computational platform to analyze fatigue will be a useful and inexpensive tool to quickly study the effects of soft tissue fatigue. Computational simulations provide for highly controlled and quantitative analyses to study the distinct effects of various loading conditions and design features on tissue durability, and are thus, advantageous over complex fatigue experiments. However, there are a limited number of the necessary constitutive models for describing the fatigue damage process in soft biological tissues.

A. Stress Softening

As a tissue becomes damaged, the stiffness will degrade and become “softer” much like rubber materials: this phenomenon is referred to as “stress softening.” Notably, the softening effect is the reduction of the peak stress required to produce a given stretch in the material with respect to the unfatigued state. Tissue stiffening in response to fatigue is often observed when referencing the post-fatigued state, when the permanent set stretches are not included in the overall deformation calculation. When permanent set is included in the analysis, tissues exhibit stress softening. Early soft tissue damage models only accounted for tissue stress softening, most of which were based on the pioneering work of Simo.⁸⁹ In 1987, Simo⁸⁹ introduced the concept of a fully three-dimensional finite-strain viscoelastic damage model, based on irreversible thermodynamics with internal variables. According to Simo's work,⁸⁹ a material is initially characterized by stored energy (strain energy), W. Damage initiates a departure of free energy; thus, for the purpose of soft-tissue-damage constitutive modeling, a strain energy reduction factor, also known as the stress softening or damage term, D, is incorporated into the strain energy function,

$$W=(1-D)W_0$$ (1)

where W₀ is the initial stored energy of the tissue. The softening term evolves from 0 at the undamaged state to 1 at complete tissue failure as a function of the maximum equivalent strain.⁸⁹ The equivalent strain, Ξ_t, is defined as a scalar measure of the stored energy at time, t, given by

$${\Xi }_t(\mathit{E}(t)):=\sqrt{2W^0(\mathbf{E}(t))}$$ (2)

where E(t) is the Green strain tensor at time t ∈ [0,T]. Tissue damage is evaluated when the equivalent strain at time t equals the maximum equivalent strain observed throughout the strain history. If the maximum equivalent strain exceeds the damage threshold for the particular material or tissue, damage is initiated. The degree of damage is a function of the maximum equivalent strain.

Many different damage evolution equations have been proposed. Early tissue damage models, including those by Arnoux et al.⁹⁰ and Hokanson and Yazdani,⁹¹ were typically restricted to isotropic damage. However, the damage response of soft tissue is highly dependent on the material orientations⁴⁸ and the direction of applied loads. Anisotropy in the stress softening response is particularly important for describing tissue damage under compression or bending, where the stress may be low and the fiber constituents are not bearing load, yet the matrix components are experiencing large deformations.

A common approach to implement anisotropy in the tissue softening consists of defining distinct damage criteria for the fibrous and matrix components.^2,92–97 Typically, for fiber reinforced composite materials, such as collagenous tissues, the strain energy function is split into fiber and matrix responses. The strain energy function is now given by

$$W=W_{\mathit{\text{vol}}}+(1-D_m)W_{\mathit{\text{iso}}}^m+(1-D_f)W_{\mathit{\text{iso}}}^f,$$ (3)

where W_vol, $W_{\mathit{\text{iso}}}^m$ and $W_{\mathit{\text{iso}}}^f$ are the volumetric, matrix, and fiber contributions to the strain energy respectively, and D_m and D_f are the softening terms corresponding to the matrix and fiber components respectively. Damage in soft tissue is assumed to be independent of hydrostatic pressure; hence, there is no softening term associated with the volumetric response.

The decomposition of the strain energy function, allows for independent definitions of the equivalent strain and thus damage, for the matrix and fiber constituents. Natali et al.^98,99 and Balzani et al.¹⁰⁰ used this approach but considered only damage to the fibrous components for tendon and arterial applications respectively. For added generality, Rodriguez et al.⁹⁴ introduced a damage model that incorporated both fiber and matrix damages of fibrous soft tissue. Isotropic matrix damage was defined using the standard continuum damage framework by Simo,⁸⁹ but fiber damage was considered to be a stochastic process related to the length and distribution of the collagen fibers.⁹⁴ Later, Calvo et al.,⁹² Peña et al.,² and Peña and Calvo⁹⁵ proposed similar damage models for fibrous tissue taking a continuum approach. Li and Robertson⁹⁷ took a multi-mechanism approach for modeling tissue damage by incorporating mechanical and enzymatic degradation of elastin, as well as the recruitment of collagen fibers. Peña and Doblare⁹⁶ have also adopted the pseudo-elastic approach of Dorfmann and Ogden¹⁰¹ to describe the softening of vena cava tissue because this approach is more appropriate for describing the unloading response of tissues compared to other continuum damage models.

B. Permanent Set

More recent tissue damage models have also included descriptions for the unrecoverable strains or tissue permanent set in addition to stress softening.^{3–6,102–105} Several different methodologies have been adopted to describe tissue permanent set. Gasser and Holzapfel¹⁰³ presented an elastoplastic constitutive model to capture permanent deformations in damaged biological fiber-reinforced composites. They postulate that the primary mechanism of permanent set in biological tissues is the rupture of proteoglycan bridges between adjacent collagen fibrils, which allows for relative sliding of the fibrils and plastic deformation of the matrix material in the direction of the fibers. Thus, they include a permanent set mechanism only in the fiber direction. The works by Ehret and Itskov³ and Peña 2011⁵ include tissue permanent set descriptions through the evolution of internal variables. While Francsechini et al.,⁴ Maher et al.^6,106 and Martin and Sun¹⁰⁴ used the pseudo-elasticity theory of Dorfmann and Ogden¹⁰¹ to describe the permanent set of brain, arterial, and GLBP tissue respectively. Maher et al.¹⁰⁶ presented a tissue damage constitutive model with distinct softening and permanent set definitions in the matrix and fibers, while many other tissue damage models only considered permanent set in the fibrous components.^5,103 Maher and Early¹⁰⁷ found that the artery undergoes more significant permanent deformations in the radial direction, thus supporting the inclusion of a non-collagenous matrix permanent set defnition. Briefly, damage effects by the pseudo-elasticity theory¹⁰¹ are enforced through an additive split of the isochoric stress tensor into the stress softened portion and the inelastic portion. The isochoric stress, S_isch, with softening and permanent set is then given by

$$S_{\mathit{\text{isch}}}=(1-D)S_0-S_{\mathit{\text{IN}}}$$ (4)

where S₀ is the undamaged stress tensor and S_IN is the inelastic stress. The magnitudes of the inelastic stresses are dependent on the maximum strain invariant values throughout loading, and thus the permanent sets evolve similar to the softening term, only when the maximum strain is exceeded.¹⁰⁶

C. Cycle Dependence

One major limitation of much of the existing modeling work on soft tissue fatigue is the lack of a cycle or time factor in the damage evolution equation. In the literature,^{2,5,89,90,92,94–96,100,106} the maximum value of Ξ_t(E(t)) over the past history up to the current time T was often used to evaluate damage evolution:

$${\Xi }_t^{\mathit{max}}:={max}_{0\le t\le T}\sqrt{2W^0(\mathit{E}(t))}$$ (5)

where Ξ_t and ${\Xi }_t^{\mathit{max}}$ define a damage surface, φ_d, in the strain space given by

$${\phi }_d(\mathit{E}(t),{\Xi }_t^{\mathit{max}}):={\Xi }_t(\mathit{E})-{\Xi }_t^{\mathit{max}}=0.$$ (6)

A non-increasing damage criterion in the strain space was defined by the condition φ_d < 0. However, it should be noted that such damage surface is not suitable for fatigue damage evolution because even if Ξ_t(E) is smaller than ${\Xi }_t^{\mathit{max}}$, fatigue damage could still occur over continued cycling. For instance, according to Eq. 6 a tissue specimen subjected to cyclic displacement-control loading cycles would only incur damage during the first cycle. However, uniaxial tension fatigue experiments⁴⁷ show that the structural and mechanical properties of GLBP tissue are altered at the low fatigue state (30×10⁶ loading cycles) and continue to change between low and moderate fatigue states (65×10⁶ cycles) under displacement control loading. The traditional tissue damage models can only be utilized to model damage induced by cyclic stretching with increasing magnitude. This limits the applicability of such models to study long-term fatigue damage when the loading conditions are relatively constant throughout fatigue life. The inclusion of a continuous damage mechanism is necessary.^97,108

Very few groups include a time or cycle dependent soft tissue damage mechanism. A continuous damage evolution parameter based on the accumulated equivalent strain has been presented in the literature,^97,108 where the accumulated equivalent strain, ${\Xi }_t^{\mathit{\text{acc}}}$, is given as

$${\Xi }_t^{\mathit{\text{acc}}}(t)={\int }_0^t|d\sqrt{2W^0(\mathit{E}(s))}/ds|ds.$$

The ${\Xi }_t^{\mathit{\text{acc}}}$ term allows for fatigue damage evolution; however, this approach is computationally expensive for long-term applications. We have recently presented an alternative approach with improved computational efficiency, by introducing a peak equivalent strain¹⁰⁴ which is evaluated for every loading cycle. The tissue damage is then updated only once per cycle given the magnitude of the peak equivalent strain:

$${\Xi }_n^{\mathit{\text{peak}}}={max}_{t\in [\frac{n}{f\prime }\frac{n+1}{f}]}\sqrt{2W^0(\mathit{E}(t))},n=0,1,2,3,\cdots ,n_{\mathit{\text{tot}}}$$ (7)

where f is the frequency and n is the number of loading cycles up to a maximum number, n_tot. We propose that the number of cycles until failure (n_tot) is given by the following equation:

$$n_{\mathit{\text{tot}}}({\Xi }_n^{\mathit{\text{peak}}})=\{\begin{array}{cc}\infty & \mathit{\text{if}}{\Xi }_n^{\mathit{\text{peak}}}<{\psi }_{\mathit{min}}\\ \frac{\beta (n_{\mathit{max}}-1)}{{\Xi }_n^{\mathit{\text{peak}}}-{\psi }_{\mathit{min}}+\beta }(\frac{1-{\mathit{exp}}^{\alpha (1-\frac{{\Xi }_n^{\mathit{\text{peak}}}}{{\psi }_{\mathit{max}}})}}{1-{\mathit{exp}}^{\alpha (1-\frac{{\psi }_{\mathit{min}}}{{\psi }_{\mathit{max}}})}})+1& \mathit{\text{if}}{\psi }_{\mathit{min}}\le {\Xi }_n^{\mathit{\text{peak}}}\le {\psi }_{\mathit{max}}\\ 1& \mathit{\text{if}}{\Xi }_n^{\mathit{\text{peak}}}>{\psi }_{\mathit{max}}\end{array}$$ (8)

Here, we introduced two parameters ψ_min and ψ_max, to define the boundaries of the fatigue damage evolution zone, where ψ_min represents the minimum equivalent strain to elicit the accumulation of fatigue damage and ψ_max represents the tissue maximum equivalent strain limit. The α and β terms are material constants governing the amount of damage incurred by a single cycle at ${\Xi }_n^{\mathit{\text{peak}}}$. Figure 4 demonstrates that by changing α, a large range of fatigue properties can be modeled. The distinguishing characteristic of our approach with respect to that of others, is that we considered an incremental accumulation of damage depending on ${\Xi }_n^{\mathit{\text{peak}}}$ which may not necessarily be ${\Xi }_t^{\mathit{max}}$. The incremental softening per cycle is then simply 1/n_tot.¹⁰⁴ The incremental permanent sets were also a function of 1/n_tot, but unlike the softening factor, the permanent set is anisotropic where the magnitude of the permanent set is proportional to the peak strain in each direction.²⁸

Fig. 4.

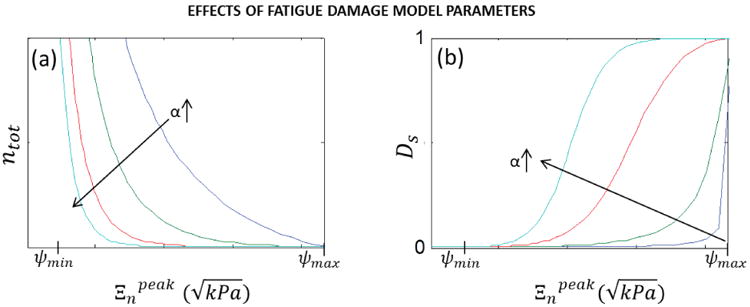
The effect of alpha on the (a) total cycles to failure and (b) stress-softening factor.¹⁰⁴

IV. Computational Simulation of Soft Tissue Fatigue Damage

Computational simulations utilizing tissue fatigue damage constitutive models calibrated from experimental tests could be extremely useful for studying tissue durability in a wide array of applications, yet little has been accomplished in this area. The advantage of numerical approaches is that complex conditions that may be difficult to replicate physically can be simulated. Several researchers have demonstrated the suitability of continuum damage models to capture the damage and failure responses of tissue through numerical and single-element FE simulations. Ehret and Itskov³ presented numerical simulations of the softening effect of mouse skin under cyclic uniaxial tension, while Li and Robertson⁹⁷ and Maher et al.¹⁰⁶ simulated arterial damage. Li and Robertson⁹⁷ also simulated elastin damage and failure in arterial strips subjected to cyclic loading, where a residual strain was observed upon elastin damage due to the collagen recruitment mechanism. Maher et al.¹⁰⁶ simulated softening and permanent set in arterial tissue in a single-element model.

Others have adopted more physiologically relevant multi-element simulations of whole tissues to investigate soft tissue damage. Balzani et al.¹⁰⁰ simulated damage to 2D arterial segments due to overstretching while incorporating the artery residual stresses at the unloaded state. Rodriguez et al.⁹⁴ simulated tissue damage under tensile torsion in a multi-element FE model; however, damage was only considered in the fibers. Both Calvo et al.⁹² and Peña et al.⁹⁵ simulated damage to the MCL under tension. The FE models of the human MCL were generated from magnetic resonance imaging (MRI) scans. The tissue mechanical and failure properties in Peña et al.⁹⁵ were adopted from experimental failure testing data for the rabbit MCL presented by Woo et al.¹⁰⁹ Calvo et al.⁹² also investigated arterial damage due to balloon angioplasty and clamping. Alastrué et al.¹¹⁰ implemented the continuum damage model by Calvo et al.⁹² and the stochastic damage model by Rodriguez et al.⁹⁴ to determine the effect of different methodologies on the predicted damage patterns. The damage patterns in both cases were similar, but the stochastic model predicted more evenly distributed damage compared to the highly localized damage surrounding areas of large stress gradients predicted by the continuum model.¹¹⁰ Gasser¹⁰² simulated the effects of supraphysiological pressures in AAA FE models reconstructed from computed tomography-angiography (CTA) images. Areas of localized damage and permanent deformations were identified,¹⁰² and demonstrated the promise for computational tissue damage modeling to be used for aneurysm rupture risk assessment.

Previous tissue damage simulations only considered a single loading cycle. Recently, we have investigated the fatigue response of soft tissue under cyclic loading in multi-element finite element simulations.^28,104,111 In Martin and Sun¹⁰⁴ uniaxial fatigue was simulated in a GLBP specimen using ABAQUS commercial FE software (Simulia, Providence, RI). The simulated fatigue behavior of GLBP is shown in Fig. 5a&b. Tissue permanent set in the simulated sample presented as elongation in the loading direction and narrowing in the perpendicular direction as expected (Fig. 5c). The simulated GLBP fatigue response in the loading direction agreed well with the experimental GLBP fatigue data presented by Sun et al.⁴⁷ The simulated responses in Fig. 5 a and b may appear inconsistent with the GLBP uniaxial fatigue response in Fig. 1a, because they each reference a different material configuration. The responses in Fig. 5 describe the GLBP tissue response with respect to the initial undamaged configuration, while the GLBP fatigue responses in Fig. 1a are referenced to the post-fatigued state. Thus, the tissue response in Fig. 1a does not include the tissue permanent set, and the tissue appears to become stiffer with fatigue. If the permanent set were ignored in the simulated responses in Fig. 5, the tissue would exhibit stiffening with fatigue as in the experiment. However, the confounding effects in the off-axis directions were not accurately modeled by this isotropic damage approach. An isotropic damage term may be appropriate under more homogenous loading conditions. The fatigue model has since been adapted to account for distinct fiber and matrix fatigue damage and permanent set descriptions.¹¹¹ Using the adapted model, the effects of the collagen fiber orientation on GLBP fatigue were investigated in uniaxial fatigue loading simulations.¹¹¹ The simulations demonstrated the model ability to describe GLBP fatigue effects observed experimentally, including increased anisotropy in GLBP specimens cycled along the fiber direction and the complete reversal of tissue anisoptropy in specimens cycled in the cross-fiber direction.⁴⁸

Fig. 5.

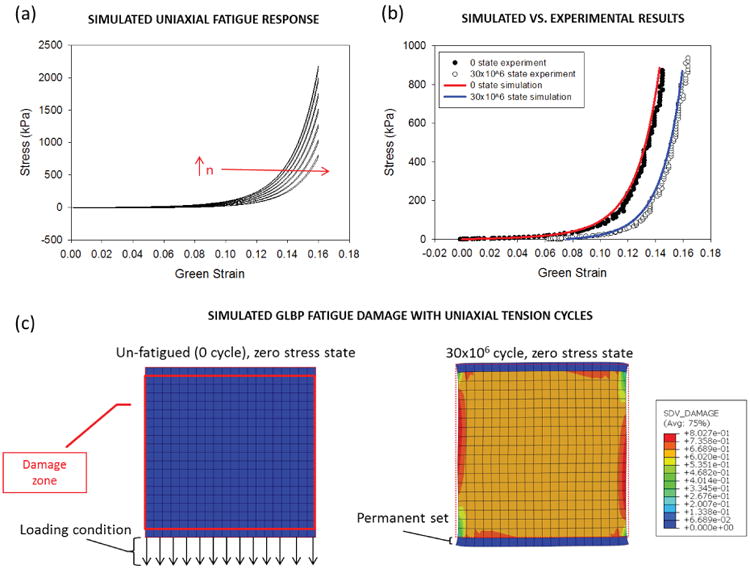
(a) The simulated GLBP stress-strain response during cyclic uniaxial displacement control loading (only cycles 1×10⁶, 5×10⁶, 10×10⁶, 15×10⁶, 20×10⁶, 25×10⁶ and 30×10⁶ are shown for clarity). (b) The uniaxial stress-strain response under load control of the simulated specimen compared to the actual specimen at the 0 state and the 30×10⁶ state. (c) Schematic of the initial model geometry and loading conditions on the left and specimen after simulated fatigue with a contour plot of the damage on the right. The red solid line represents the damage zone and the red dotted line represents the unfatigued geometry.

The tissue fatigue damage model in Martin and Sun¹⁰⁴ was then utilized to describe the overall fatigue damage of GLBP leaflets due to cyclic loading in BHV applications.²⁸ The effect of different leaflet and stent properties on the fatigue damage of the leaflets was investigated in a typical BHV model (Fig. 6a) subjected to cyclic pressurization.¹¹² This marked the first study where fatigue damage was simulated for BHV applications and the effect of BHV design parameters on the durability were quantitatively assessed. High fatigue damage was predicted near the leaflet commissures and along the suture attachments (Fig. 6b), which are common failure sites of explanted BHVs (Fig. 3). Figure 6c shows that decreasing the stent-tip deflection resulted in accelerated leaflet fatigue damage particularly in the commissural regions. The following factors were associated with accelerated fatigue of the GLBP leaflets: heterogeneity of leaflet elastic properties, poor leaflet coaptation, and little stent-tip deflection. Each of these factors has long since been known to accelerate fatigue of BHVs,^9.80.86–88 but this is the first study to show that this is analytically the case.

Fig. 6.

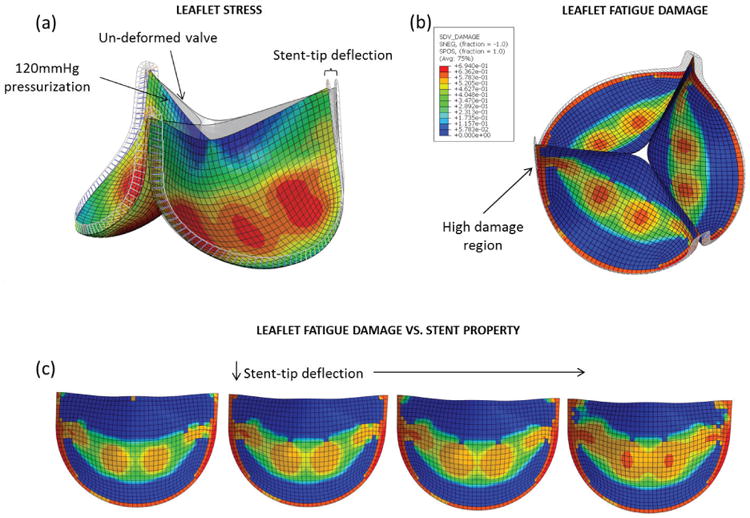
(a) BHV finite element model adopted from Sun et al.¹¹² in the pressurized state overlapped with the initial un-deformed geometry. (b) The BHV model at the fatigued state with contour plots of the leaflet damage, showing peak damage along the suture attachments. (c) Results from the stent-property parametric study showing increased leaflet fatigue damage, particularly in the commissural regions, with reduced stent-tip deflection.

These studies have demonstrated the exciting potential for simulation-based soft-tissue fatigue damage analysis. Such analyses can provide guidance for the design of durable tissue-derived devices and tissue engineering constructs, as well as surgical procedures and treatments to minimize soft tissue injury. Still, accurate modeling of the soft-tissue mechanical response is challenging. It is often difficult to achieve numerical convergence in large scale soft tissue FE simulations, and time-dependent mechanical property definitions only exacerbate this problem. In order to make simulation-based soft tissue damage analysis more realistic, computational convergence and efficiency should be further improved.

V. Future Directions

A. Calibration of Tissue Fatigue Constitutive Models

At this point, soft-tissue fatigue damage cannot be accurately predicted. Through parametric studies, we can investigate the relative durability of soft tissues and devices,^28,111 but the timing of fatigue events remains unknown. The limiting factor is the lack of the necessary experimental data to properly calibrate the soft tissue fatigue damage constitutive models. Calibration of these models requires extensive mechanical and structural analysis. Soft tissues must be fatigued under various loading magnitudes for various numbers of cycles to generate the needed data. Existing experimental fatigue datasets are not sufficiently comprehensive for modeling purposes. Hopefully, the recent development of fatigue damage constitutive models will guide the design of future soft tissue fatigue experiments.

B. Tissue Fatigue Simulation for Optimizing Tissue Implant Durability

Few groups have successfully implemented soft-tissue damage and fatigue models into commercial FE solvers. The challenges include complex and lengthy derivations of the constitutive relations and numerical instability. The efficient numerical approximation method for the tangent moduli, proposed by Sun et al.¹¹³ is an effective approach to simplifying the FE implementation of user-defined material models. Recent work²⁸ demonstrates the feasibility of computational platforms to analyze soft tissue fatigue in large-scale FE simulations. Such computational tools are critical for the design of new tissue implants or tissue-based constructs with enhanced durability.

One significant upcoming application will be the design of durable next-generation TAV devices. Simulation results indicate that TAV leaflets undergo higher strains than surgical BHV leaflets,^114,115 and asymmetric TAV deployments due to aortic root calcification result in higher leaflet stresses and strains than do nominal circular TAV deployments.¹¹⁵ These elevated leaflet stresses and strains will impact TAV device durability. New designs that reduce leaflet stresses and strains could improve durability. Computational TAV fatigue analyses could be used as a precursor to AWT testing to reduce design cycle time. Computational platforms also facilitate patient-specific analyses of valve durability. For instance, the suitability of different devices and configurations, such as the valve-in-valve configuration, could be assessed based on the patient's unique aortic characteristics.

C. Multi-scale Characterization of Tissue Fatigue Damage

Existing constitutive fatigue damage models can describe the mechanical effects of fatigue in soft tissue; however, to gain mechanistic insight into the progression of soft-tissue fatigue damage, further efforts to characterize and model the multi-scale tissue fatigue effects are necessary. Structural-based constitutive models with distinct descriptions of matrix and fiber damages could provide more mechanistic insight, but this would require extensive and complex experiments to determine the unique matrix and fiber fatigue parameters. Further work should also be done to determine the relationships between mechanical fatigue and the subsequent biological effects. While there is strong evidence that mechanical factors induce cellular changes in tissues, little has been done to mathematically model these effects. Tissue remodeling plays an important role in the durability of living tissues and tissue engineering constructs, while enzymatic degradation and calcification will limit the durability of tissue-derived implants and decellurized scaffolds.

VI. Conclusions

Mechanical fatigue damage is a critical issue for soft tissues and tissue-derived materials. The recent development of soft-tissue fatigue damage constitutive models has enabled simulation-based fatigue analyses of tissues under various conditions. Although significant work to calibrate the constitutive models from fatigue experiments and to validate predictability remains, further development in these areas will facilitate the design of durable treatments and devices.