Double propensity-score adjustment: A solution to design bias or bias due to incomplete matching

Abstract

Propensity-score matching is frequently used to reduce the effects of confounding when using observational data to estimate the effects of treatments. Matching allows one to estimate the average effect of treatment in the treated. Rosenbaum and Rubin coined the term “bias due to incomplete matching” to describe the bias that can occur when some treated subjects are excluded from the matched sample because no appropriate control subject was available. The presence of incomplete matching raises important questions around the generalizability of estimated treatment effects to the entire population of treated subjects. We describe an analytic solution to address the bias due to incomplete matching. Our method is based on using optimal or nearest neighbor matching, rather than caliper matching (which frequently results in the exclusion of some treated subjects). Within the sample matched on the propensity score, covariate adjustment using the propensity score is then employed to impute missing potential outcomes under lack of treatment for each treated subject. Using Monte Carlo simulations, we found that the proposed method resulted in estimates of treatment effect that were essentially unbiased. This method resulted in decreased bias compared to caliper matching alone and compared to either optimal matching or nearest neighbor matching alone. Caliper matching alone resulted in design bias or bias due to incomplete matching, while optimal matching or nearest neighbor matching alone resulted in bias due to residual confounding. The proposed method also tended to result in estimates with decreased mean squared error compared to when caliper matching was used.

1 Introduction

There is an increasing interest in estimating the causal effects of treatment using observational or nonrandomized data. Matching is an attractive analytic method to estimate the effect of treatments, interventions, and exposures. In matching, each treated or exposed subject is matched to one or more untreated or control subjects. Outcomes are then compared between treatment groups in the matched sample. When using conventional matching methods, one is estimating the average treatment effect in the treated (ATT): the effect of treatment in the sample or population of all subjects who were actually treated.¹

Dorn suggested that when designing an observational study, one should ask “how would the study be conducted if it were possible to do it by controlled experimentation?”, while Rubin believes that this question defines the objective of an observational study.² We motivate this paper by highlighting a consequence of the design of randomized controlled trials (RCTs) and a statistical method commonly used in the analysis of RCTs. First, randomization results in estimates of treatment effect that are internally consistent and unbiased. Because of the use of randomization there will, in expectation, be no systematic differences in baseline characteristics between treatment groups. Therefore, differences in outcomes between treatment groups represent an unbiased estimate of the effect of treatment in the population defined by the inclusion and exclusion criteria of the study. Furthermore, the inclusion and exclusion criteria of the study explicitly define the population to which the estimand applies. Thus, the estimate is expected to be unbiased and applies to a clearly defined population. Second, while a crude comparison of outcomes between treatment groups will, on average, result in unbiased estimation of the effect of treatment in RCTs, several authors have suggested that estimates of the effect of treatment derived from RCTs be adjusted for baseline covariates.^3,4 Covariate adjustment has two beneficial consequences: first, it permits for the elimination of residual confounding due to random imbalance in prognostically important covariates; second, it results in an analysis with increased statistical power.³ Furthermore, when outcomes are continuous and a linear model is used for covariate adjustment, the standard error of the estimated treatment effect will decrease compared to the crude or unadjusted estimator (while the converse will be observed when a generalized linear model is used for adjustment).³

We want to address these two design and analytic issues in the context of observational studies that use propensity-score matching to estimate the effect of treatment. The first issue relates to the internal consistency and generalizability of the estimated treatment effect. Rosenbaum and Rubin coined the term “bias due to incomplete matching” to refer to the bias that can occur when some treated subjects are excluded from the final matched sample because no appropriate control or untreated subject was found for those treated subjects.⁵ The occurrence of incomplete matching raises important issues around the generalizability of the estimated treatment effect. When incomplete matching occurs, frequently it is those treated subjects who are the most likely candidates for therapy that are excluded from the matched sample (due to an insufficient number of untreated subjects who resemble the most likely candidates for therapy). Thus, one is attempting to estimate the effect of treatment in all subjects who were treated, using a sample from which those subjects who most resemble ideal or typical candidates for therapy were excluded. Matching on the propensity score was intended as a solution to the bias due to incomplete matching that occurred when matching on sets of individual variables (e.g. matching directly on age, sex, blood pressure, heart rate, etc.).⁵ However, in practice, incomplete matching occurs frequently in studies that use propensity-score matching. Stürmer et al. conducted a systematic review of studies published prior to 2004 that used propensity-score methods.⁶ In this review, of 43 studies that used propensity-score matching and that reported the percentage of treated subjects included in the matched sample, the median matching rate was 91%, while the 25th and 75th percentiles were 66% and 97.5%, respectively, while the lowest reported matching rate was 26%. Thus, in 25% of published studies that used propensity-score matching, over one-third of treated subjects were excluded from the matched sample. Some readers, physicians, and decision-makers could question the generalizability of the conclusions about treatment efficacy in published studies in which a high proportion of treated subjects were excluded from the matched sample. Furthermore, while the inclusion and exclusion criteria of the study allow one to succinctly characterize the population about which one wishes to make inferences, the exclusion of some treated subjects makes it much more difficult to describe the population to which the estimand actually applies. The second issue is motivated by the use of covariate adjustment in RCTs. Matching on the propensity score balances, in expectation, the distribution of measured baseline covariates between treatment groups. However, as with RCTs, in any particular implementation of propensity-score matching, it is possible that residual imbalance of measured baseline covariates will be observed. In particular applications, there may remain the need to remove the effects of residual confounding that persists despite the use of propensity-score matching.

There are many algorithms for matching subjects on the propensity score. Optimal matching forms matched pairs of treated and untreated subjects so as to minimize the average within-pair difference in the propensity score.⁷ Nearest neighbor matching (NNM) matches each treated subject to the untreated subject with the nearest propensity score.^5,7 In the biomedical literature, matching is usually done without replacement, so that each control or untreated subject is included in at most one matched set. Nearest neighbor caliper matching is a refinement of the previous algorithm. A caliper distance is specified prior to the implementation of the algorithm. Only those matched pairs whose propensity scores differ by less than the specified caliper distance are included in the final matched sample. The use of caliper matching can result in the exclusion of some treated subjects because of a lack of untreated subjects with propensity scores close to those of some of the treated subjects. Rosenbaum and Rubin described the degree of bias reduction associated with different choices of caliper widths,⁵ while a more recent study determined optimal caliper widths in different scenarios.⁸

The choice between caliper matching and either optimal or NNM likely reflects a variance-bias trade-off.⁹ Caliper matching results in greater reduction in the bias due to confounding variables, because only matches that meet a certain quality criterion are included. However, caliper matching can result in a diminished sample size due to the possible exclusion of some treated subjects from the matched sample. Furthermore, the use of nearest neighbor or optimal matching may result in estimates with greater generalizability, since they do not suffer from incomplete matching. However, these two methods are also likely to result in estimates with greater bias due to confounding, due to the absence of a restriction on the quality of matches.

The objective of the current paper is to describe a method for reducing bias when using optimal or NNM. The motivation of the approach is twofold. First, to reduce bias due to incomplete matching (or generalizability bias) compared to when simple caliper matching is used; second, to reduce bias due to residual confounding compared to when simple NNM or simple optimal matching is used. The approach is based on using a regression model estimated in the untreated subjects in the matched sample to impute the missing potential outcomes for those subjects who were ultimately treated, had they not been treated. The paper is structured as follows: in Section 2, we describe the proposed method, which we refer to as double propensity-score adjustment. In Section 3, we describe an extensive series of Monte Carlo simulations to examine the performance of this method for estimating linear treatment effects. In particular, we examine bias, variance of the estimated treatment effect, and mean squared error (MSE). In Section 4, we present the results of these Monte Carlo simulations. In Section 5, we present a case study in which we illustrate the application of these methods when estimating the effect of drug prescribing on mortality in a cohort of patients discharged from hospital with a diagnosis of acute myocardial infarction (AMI). Finally, in Section 6, we summarize our findings and place them in the context of the existing literature.

2 Double propensity score adjustment

In this section we describe a method for reducing bias due to residual confounding when using optimal or NNM. The method is based on forming a matched sample using one of these two matching algorithms. Covariate adjustment using the propensity score is then used to minimize the effects of any residual confounding. We begin by providing basic background definitions and notation. Our proposed approach uses a similar framework to a biased-corrected matching estimator proposed by Abadie and Imbens.¹⁰

2.1 The potential outcomes framework

In a setting with two possible treatments, the potential outcomes framework assumes that the ith subject has a pair of potential outcomes: Y_i(0) and Y_i(1), the outcomes under the control and the active treatment, respectively.¹¹ However, each subject receives only one of the two treatments. Let Z denote the treatment received (Z = 0 for control treatment versus Z = 1 for active treatment). Thus, only one outcome, Y_i, is observed for the ith subject: the outcome under the treatment received.

2.2 Average treatment effects (ATEs)

For the ith subject, the effect of treatment is defined to be Y_i(1) – Y_i(0): the difference between the two potential outcomes. The ATE is defined as E[Y_i(1) – Y_i(0)], the average effect of treatment in an entire sample or population.¹ A related measure of effect is the average treatment effect for the treated (ATT), $\text{E}[Y(1)-Y(0)|\text{Z}=1]$, which is the average effect of treatment in those subjects who ultimately received the treatment.¹ It is the latter effect that is the focus of the current study.

2.3 The propensity score

In an observational study of the effect of treatment on outcomes, the propensity score is the probability of receiving the treatment of interest conditional on measured baseline covariates: $e=⪻(Z=1|X)$, where X denotes the measured baseline covariates.¹² Four different propensity score methods have been described for reducing the effects of confounding when estimating treatment effects using observational data: propensity-score matching, stratification on the propensity score, covariate adjustment using the propensity score, and inverse probability of treatment weighting (IPTW) using the propensity score.^12–14 As noted earlier, propensity-score matching allows one to estimate the ATT. The reader is referred elsewhere for a broader overview of propensity-score methods.^15,16 In conventional covariate adjustment using the propensity score, an appropriate regression model is used to regress the outcome on two variables: the propensity score and an indicator variable denoting treatment status. The regression coefficient for the treatment status indicator is used as the measure of treatment effect. Thus, if outcomes were continuous, a linear regression model would be used to regress the outcome on the propensity score and an indicator variable denoting treatment status. The regression coefficient for the treatment status indicator variable would denote the mean change in the continuous outcome due to treatment. If the outcomes were binary, a logistic regression model would be used, and the resultant odds ratio would be used as the measure of treatment effect. Difficulties with this approach when outcomes are binary have been described elsewhere.^17,18

2.4 Double propensity-score adjustment

Propensity score methods allow one to obtain estimates of the potential outcomes under the active treatment or exposure and under the control treatment or exposure. When using propensity-score matching, for the ith treated subject, one can estimate Y_i(1) by the observed outcome for the ith treated subject. Similarly, one can estimate Y_i(0) by the observed outcome for the control subject that was matched to the ith treated subject. Caliper matching imposes a bound on the quality of matches, so that matched treated and untreated subjects are required to have a propensity score that can differ by no more than a maximum quantity (the caliper distance). However, neither optimal matching nor NNM requires such a constraint. Thus, matched subjects may be more dissimilar when either of these two matching algorithms are used compared to when caliper matching is employed.

In our proposed method, propensity-score matching, using either optimal matching or nearest neighbor, is the first propensity-score method that is implemented. This will result in the matching of all treated subjects, thus avoiding generalizability bias or bias due to incomplete matching. Covariate adjustment using the propensity score is then used within the matched sample to reduce any residual confounding due to any remaining systematic differences between treated and untreated subjects in the matched sample. Our implementation of covariate adjustment using the propensity score is different than its typical implementation. Instead of implementing covariate adjustment using the propensity score and then using the estimated regression coefficient for an estimate of the effect of treatment, we use a univariate regression model with the propensity score to impute the missing potential outcomes for the treated subjects. Similar to Abadie and Imbens,¹⁰ we define two different regression models: $m_w(x)=E[Y(w)|X=x]$, for w = 0 and 1. These functions model the two potential outcomes as a function of the baseline covariate vector X. As noted by Imbens, given the assumption of no unmeasured confounders, we have that $m_w(x)=E[Y(w)|X=x]=E[Y(w)|W=w,X=x]=E[Y|W=w,X=x]$.¹ Thus, by restricting the sample to either the treated or untreated subjects, one can estimate the expected potential outcome by regressing the observed outcome on the observed baseline covariates. As suggested by the above notation, a regression model appropriate for estimating the expected response should be used. Thus, if outcomes were continuous, a linear model would be used, whereas if outcomes were binary, a logistic regression model would be an appropriate choice.

Using the untreated subjects in the matched sample, one can estimate the m₀(x) regression model, with the estimated propensity score as the single baseline covariate. One can then apply this estimated regression model to the set of treated subjects in the matched sample, to estimate ${\stackrel{\wedge }{Y}}_i(0)$ for the ith treated subject. The effect of treatment on the ith treated subject can then be estimated as: ${\stackrel{\wedge }{Y}}_i(1)-{\stackrel{\wedge }{Y}}_i(0)=Y_i-{\stackrel{\wedge }{Y}}_i(0)=Y_i-m_0(e_i)$, where we have replaced the potential outcome under treatment for the ith treated subject with the observed outcome. We have also replaced the observed outcome for the untreated subject to whom the ith treated subject was matched with the estimated potential outcome obtained using m₀ evaluated at the value of the propensity score value of the ith treated subject. The ATT can then be estimated as $\text{ATT}=\frac{1}{K}\sum _{i=1}^K(Y_i-m_0(e_i))=\frac{1}{K}\sum _{i=1}^K{Y}_i-\frac{1}{K}\sum _{i=1}^K{m}_0(e_i)$, where the matched sample consists of K matched pairs.

One could modify the proposed method by using the regression model m₁(x) to estimate the potential outcomes under treatment (Y(1)) for each treated subject. However, this modification is unnecessary. For conventional parametric regression models (such as linear or logistic regression), the mean predicted outcome will be equal to the mean observed outcome. Thus, using m₁(x) will result in the same estimator as using the observed outcomes for the treated subjects.

Thus, if outcomes are continuous, we fit two separate univariate linear regression models in the matched sample. First, using only the untreated subjects in the matched sample, a linear model is fit, in which the continuous outcome is regressed on the estimated propensity score. Second, using only the treated subjects in the matched sample, a linear model is fit, in which the continuous outcome is regressed on the estimated propensity score (these linear models are described earlier as m₀(x) and m₁(x), respectively). The first linear model (m₀(x)) is then applied to each treated subject in the matched sample to estimate their expected potential outcome, conditional on their estimated propensity score, had they not been treated (their counterfactual exposure). If outcomes are binary, we would fit two separate univariate logistic regression models in the matched sample. First, using only the untreated subjects in the matched sample, a logistic regression model is fit, in which the binary outcome is regressed on the estimated propensity score. Second, using only the treated subjects in the matched sample, a logistic regression model is fit, in which the binary outcome is regressed on the estimated propensity score (these logistic linear models are described earlier as m₀(x) and m₁(x), respectively). The first logistic regression model (m₀(x)) is then applied to each treated subject in the matched sample to estimate their expected potential outcome, conditional on their estimated propensity score, had they not been treated (their counterfactual exposure). Note that the imputed counterfactual potential outcome will be a proportion when outcomes are binary. It is important to note that we are not using including a treatment status indicator variable along with the propensity score in the logistic regression model and using the odds ratio as the measure of treatment effect. Instead, we are using the univariate logistic regression model to predict or estimate the missing potential outcome for treated subjects. If outcomes were integer counts, a Poisson regression model could replace the univariate logistic regression model and be used for imputing or estimating the missing counterfactual outcomes.

Note that we estimated the m₀(x) regression model using the untreated subjects in the matched sample, rather than using all untreated subjects in the original (unmatched) sample. While the latter choice could have been used, we think that fitting the model in a sample in which the propensity score had a similar distribution to that of the treated subjects would result in more accurate estimation of the potential outcomes under absence of treatment at values of the propensity score equal to those of the treated subjects.

3 Monte Carlo simulations—Methods

We conducted an extensive series of Monte Carlo simulations to examine the performance of double propensity-score adjustment. We compared its performance with four other methods: (i) conventional NNM, (ii) conventional optimal matching, (iii) conventional caliper matching, (iv) caliper matching with subsequent covariate adjustment using the propensity score. We assessed the performance of each method using three criteria: bias in estimating linear treatment effects (difference in means and risk differences), variability of the estimated treatment effect and MSE.

The design of our Monte Carlo simulations was based on a previous study that examined the performance of different caliper widths for use with greedy nearest neighbor caliper matching.⁸ As in the prior study, we assumed that there were 10 covariates (X₁–X₁₀) that affected either treatment selection or the outcome. The treatment-selection model was $\text{logit}(p_{i,\text{treat}})={\alpha }_{0,\text{treat}}+{\alpha }_L{x}_{1,i}+{\alpha }_L{x}_{2,i}+{\alpha }_M{x}_{4,i}+{\alpha }_M{x}_{5,i}+{\alpha }_H{x}_{7,i}+{\alpha }_H{x}_{8,i}+{\alpha }_{\mathrm{VH}}{x}_{10,i}$. For each subject, treatment status (denoted by z) was generated from a Bernoulli distribution with parameter p_i,treat.

For each subject we generated both a continuous and a dichotomous outcome. Outcomes were generated so that there was a heterogeneous treatment effect, so that bias would be induced due to incomplete matching. The continuous outcome was generated using the following linear model

$$y_i={\beta }_0+{\beta }_{\text{treat},\text{continuous}}{z}_i+{\alpha }_L{x}_{2,i}+{\alpha }_L{x}_{3,i}+{\alpha }_M{x}_{5,i}+{\alpha }_M{x}_{6,i}+{\alpha }_H{x}_{8,i}+{\alpha }_H{x}_{9,i}+{\alpha }_{\mathrm{VH}}{x}_{10,i}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+{\alpha }_L{z}_i{x}_{2,i}+{\alpha }_M{z}_i{x}_{5,i}+{\alpha }_H{z}_i{x}_{8,i}+{\alpha }_H{z}_i{x}_{9,i}+{\alpha }_{\mathrm{VH}}{x}_{10,i}+{\varepsilon }_i,$$

where ${\varepsilon }_i~N(0,\sigma =3)$. By including interactions between the four confounding variables (those variables that affect both treatment selection and the outcome), we introduced a heterogeneous treatment effect. This was done so that incomplete matching would result in biased estimation of the ATT. We selected the value of β_{treat,continuous} so that the ATT would be equal to 1. The required value of β_treat would depend on the treatment-selection model, the prevalence of treatment, and the distribution of the baseline covariates. In a given scenario, a bisection approach was used to determine the value of β_{treat,continuous} that resulted in an ATT of 1.

For each subject we also generated a dichotomous outcome using the following logistic model

$$\text{logit}(p_{i,\text{outcome}})={\beta }_{0,\text{outcome}}+{\beta }_{\text{treat},\text{binary}}{z}_i+{\alpha }_L{x}_{2,i}+{\alpha }_L{x}_{3,i}+{\alpha }_M{x}_{5,i}+{\alpha }_M{x}_{6,i}+{\alpha }_H{x}_{8,i}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}+{\alpha }_H{x}_{9,i}+{\alpha }_{\mathrm{VH}}{x}_{10,i}+{\alpha }_L{z}_i{x}_{2,i}+{\alpha }_M{z}_i{x}_{5,i}+{\alpha }_H{z}_i{x}_{8,i}+{\alpha }_H{z}_i{x}_{9,i}+{\alpha }_{\mathrm{VH}}{x}_{10,i}$$

A binary outcome was then generated for each subject from a Bernoulli distribution with parameter p_i,outcome. The intercept, β_0,outcome, in the logistic outcomes model was selected so that the marginal probability of the outcome if all subjects were untreated would be 0.10. The conditional log-odds ratio, β_treat,binary, was selected using methods described elsewhere so that absolute risk reduction in treated subjects due to treatment would be 0.02¹⁹ (i.e. the true ATT was −0.02). Briefly, for a given value of β_treat,binary, the marginal probability of the outcome in all treated subjects, if all these subjects were untreated, and the marginal probability of the outcome in all treated subjects if all these subjects were treated were computed. The risk difference is the difference between these two marginal probabilities. An iterative process was used to determine the value of β_treat,binary that would result in the desired risk difference (−0.02). Because we were simulating data with a desired ATT, the value of β_treat,binary would depend on the proportion of subjects that were treated.

The regression coefficients α_L, α_M, α_H, and α_VH, were set to log(1.25), log(1.5), log(1.75), and log(2), respectively. Thus, there were two covariates that had a weak effect on each of treatment selection and outcomes, there were two covariates that had a moderate effect on each of treatment selection and outcomes, two covariates that had a strong effect on each of treatment selection and outcomes, and one covariate that had a very strong effect on both treatment selection and outcomes.

Our Monte Carlo simulations had a complete factorial design in which the following two factors were allowed to vary: (i) the distribution of the 10 baseline covariates; (ii) the proportion of subjects who were treated. We considered five different distributions for the 10 baseline covariates: (a) the 10 covariates had independent standard normal distributions; (b) the 10 covariates were from a multivariable normal distribution. Each variable had mean zero and unit variance, and the pair-wise correlation between variables was 0.25; (c) the first five variables were independent Bernoulli random variables each with parameter 0.5, while the second five variable were independent standard normal random variables; (d) the 10 random variables were independent Bernoulli random variables, each with parameter 0.5; (e) the 10 random variables were correlated Bernoulli random variables. In this setting, 10 continuous variables were generated as in scenario (b). Each continuous variable was then dichotomized at the population mean (zero). For the second factor, we considered five different levels for the proportion of subjects that were treated: 0.05, 0.10, 0.20, 0.25, and 0.33. The value of ${\alpha }_{0,\text{treat}}$ in the treatment-selection model was modified to obtain the desired prevalence of treatment in the simulated datasets. We thus considered 25 different scenarios: five different distributions for the baseline covariates × five levels of the proportion of subjects who were treated (0.05, 0.10, 0.20, 0.25, and 0.33).

In each of the 25 scenarios, we simulated 1000 datasets, each consisting of 10,000 subjects. In each simulated dataset, we estimated the propensity score using a logistic regression model to regress treatment assignment on the seven variables that affect the outcome. This approach was selected as it has been shown to result in superior performance compared to including all measured covariates or those variables that affect treatment selection.²⁰ When using nearest neighbor matching and optimal matching, subjects were matched on the propensity score. When using caliper matching, subjects were matched on the logit of the propensity score using a caliper of width equal to 0.2 of the standard deviation of logit of the propensity score. This caliper width was selected as it has been shown to result in estimates with the lowest MSE compared to the use of other caliper widths.²¹

In each of the three matched sets (optimal matching, NNM, and caliper matching), the treatment effect was estimated as E[Y|Z = 1] – E[Y|Z = 0]. Thus, both a difference in means (continuous outcome) and a risk difference (binary outcome) were estimated in each propensity-score matched sample. We refer to these estimates as the crude matched estimators.

In each of the three matched sets, we then used the method described in Section 2 to minimize the effects of residual confounding. This was done in two different ways. First, the regression model m₀ was estimated using only the estimated propensity score (i.e. double propensity-score adjustment). Second, the regression model m₀ was estimated using the seven covariates that affected the outcome. We refer to these two approaches as PS adjust and covariate adjust, respectively.

Let θ denote the true treatment effect (1 and −0.02 for continuous and binary outcomes, respectively), and let θ_i denote the estimated treatment effect in the ith simulated sample (i = 1, … , 1000). Then, the mean estimated treatment effect was estimated as $\frac{1}{1,000}\sum _{i=1}^{1,000}{\theta }_i$ and MSE was estimated as $\frac{1}{1,000}\sum _{i=1}^{1,000}({\theta }_i-\theta )2$.

4 Monte Carlo simulations—Results

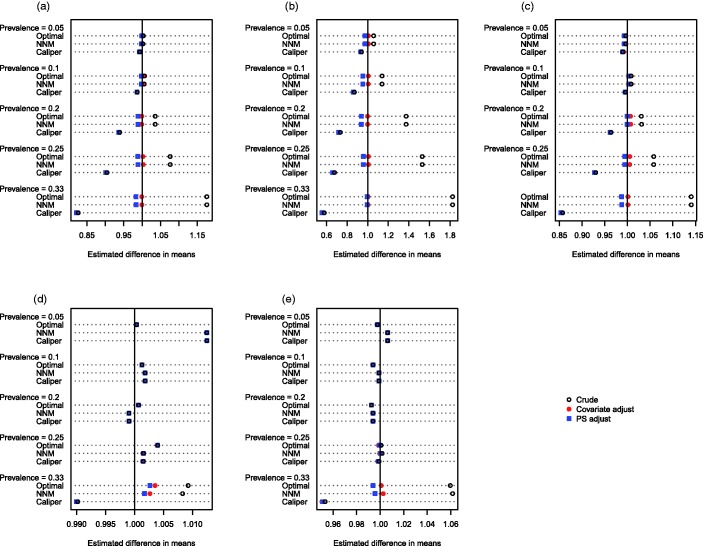
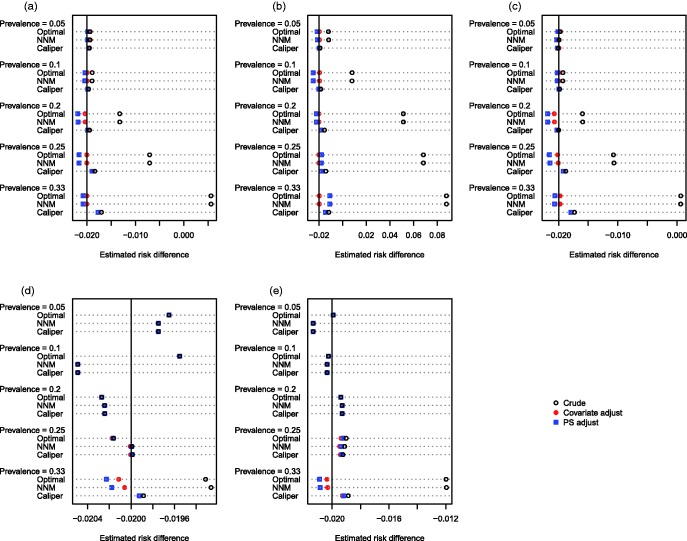
The mean estimated linear treatment effects are reported in Figures 1 (continuous outcome) and 2 (binary outcome). Each figure consists of five panels, one for each of the five distributions of the baseline covariates. Within each panel, there is one line for each combination of prevalence of treatment (0.05, 0.1, 0.2, 0.25, and 0.33) and matching method (optimal matching versus NNM versus caliper matching). On each line there are three different plotting symbols representing the three estimated treatment effects (the crude matched estimator, the matched and propensity-score adjusted estimator, and the matched and covariate adjusted estimator). The true treatment effects of 1 and −0.02 (for the continuous and binary outcomes, respectively) are denoted by a vertical line in each of the five panels.

Figure 1.

Estimated difference in means. (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

Figure 2.

Estimated risk difference. (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

We define two different types of bias to facilitate the discussion of the results of the simulations. First, confounding bias is bias in estimating the treatment effect due to residual differences in baseline characteristics between treatment groups. Second, target bias is bias in estimating the ATT due to the exclusion of some treated subjects from the matched sample. Thus, bias has been introduced due to the fact that the matched treated subjects are a nonrepresentative sample of the set of all treated subjects. Due to the presence of a heterogeneous treatment effect, the estimated treatment effect using the matched treated subjects differs systematically from the effect of treatment in the entire treated population.

When outcomes were continuous and at least some of the baseline covariates were continuous, several observations merit comment. First, when using crude NNM or optimal matching, bias increased as the prevalence of treatment increased. Since all treated subjects were included in the matched samples, the observed bias is entirely confounding bias due to residual differences between treated and untreated subjects in the matched sample. Second, when using crude caliper matching, bias increased as the prevalence of treatment increased. Third, when using caliper matching, subsequent covariate adjustment (using either the propensity score or the covariates individually) resulted in essentially unchanged estimates of treatment effect compared to when crude caliper matching was used. Taken together, these last two observations suggest that the bias observed when using crude caliper matching is almost entirely due to target bias, rather than confounding bias. Fourth, when using either NNM or optimal matching, subsequent covariate adjustment (using either the propensity score or the covariates individually) resulted in estimates of the ATT that had minimal bias. This reinforces our earlier conclusion that the observed bias when using either of these matching algorithms was confounding bias, rather than target bias. Subsequent adjustment using the covariates individually tended to eliminate slightly more bias than adjusting for the propensity score alone; however, differences were minor. Fifth, all methods resulted in essentially unbiased estimation when the prevalence of treatment was 5 or 10%. When all of the covariates were binary, the magnitudes of the observed biases were diminished compared to settings in which some of the covariates were continuous. When the covariates were independent Bernoulli random variables, then the bias in estimating the ATT was less than 1.5%, regardless of the method used. When the outcome was binary, the above patterns were still evident (Figure 2).

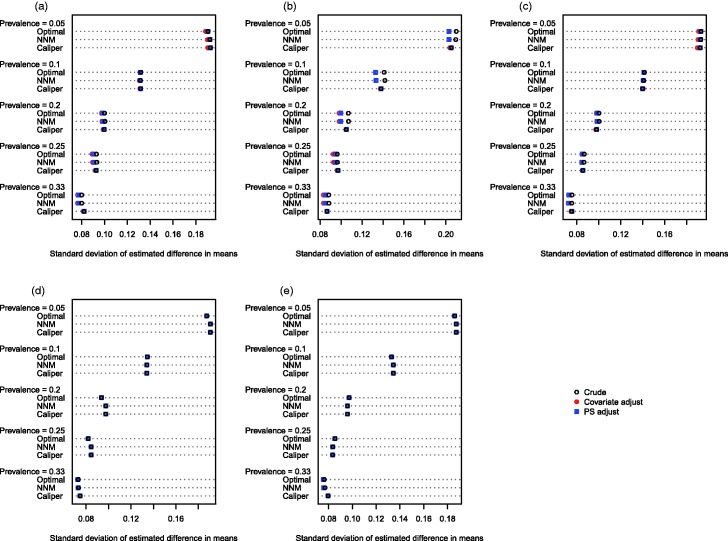
The empirical standard deviation of the estimated treatment effects across the 1000 stimulated datasets for each scenario is reported in Figures 3 (continuous outcome) and 4 (binary outcome). When outcomes were continuous (Figure 3), the empirical variance of the sampling distribution tended to be similar between the different analytic methods across the majority of scenarios. When the baseline covariates were correlated normal random variables and the prevalence of treatment did not exceed 20%, then the regression-adjusted estimates had modestly greater precision (decreased variability) compared to the crude estimates in the samples constructed using optimal matching or NNM. When caliper matching was used, regardless of the prevalence of treatment and of the distribution of baseline covariates, then the adjusted and unadjusted estimates had virtually identical variability. When outcomes were binary (Figure 4), and the baseline covariates were correlated normal random variables, the crude estimator in the matched samples constructed using optimal matching or NNM displayed greater variability compared to the adjusted estimates in these samples when the prevalence of treatment was less than or equal to 10%. However, when the prevalence of treatment exceeded 10%, the converse was observed. As above, when caliper matching was used, the crude estimates and the adjusted estimates displayed approximately equal variability, regardless of the prevalence of treatment and of the distribution of the baseline covariates.

Figure 3.

Standard deviation of estimated difference in means. (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

Figure 4.

Standard deviation of estimated risk difference. (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

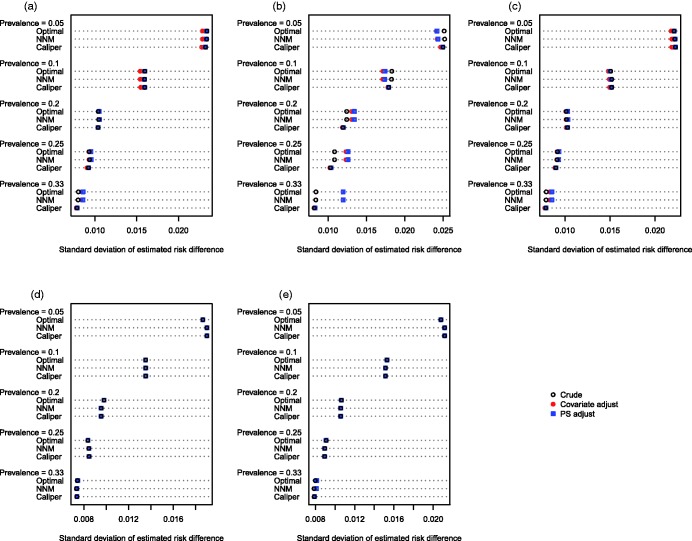
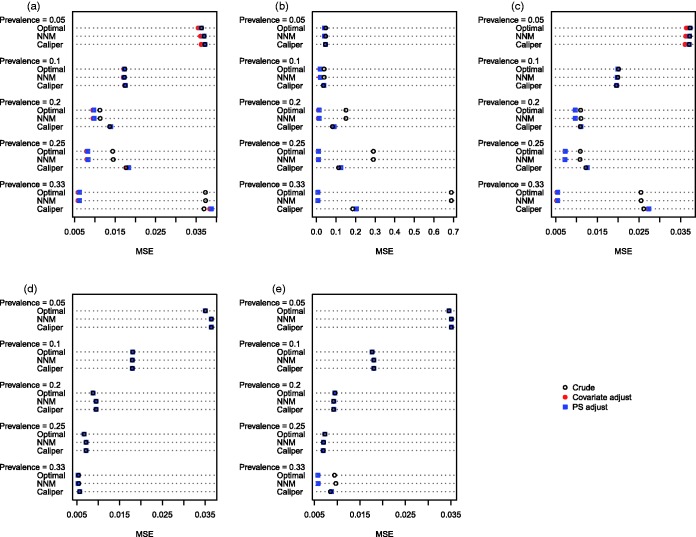
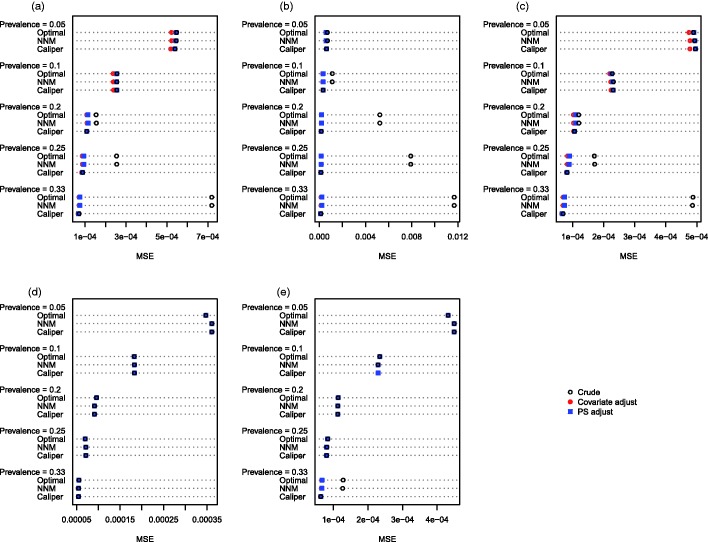
The MSE of the estimated treatment effects is reported in Figures 5 (continuous outcome) and 6 (binary outcome). Several findings warrant being highlighted. The first and most important observation involves the comparison, within each of the 25 different scenarios, of the MSE of the crude estimator in the caliper-matched sample with the adjusted estimator in either of the other two matched samples. When the outcome was continuous, then the double propensity score estimator had lower MSE in 20 of the 25 scenarios when optimal matching was used and in 18 of the 25 scenarios when NNM was used. When the outcome was binary, then in 19 of the 25 scenarios, the use of either optimal matching or NNM with subsequent propensity-score adjustment, resulted in estimates with lower MSE than the crude matched estimator in the sample obtained using caliper matching. Second, reduction in MSE due to subsequent covariate adjustment was negligible when all of the baseline covariates were binary, except when the prevalence of treatment was 33% and the covariates were correlated binary variables. Third, when using either optimal matching or NNM, subsequent regression adjustment tended to result in the greatest reduction in MSE when the prevalence of treatment was high.

Figure 5.

Mean squared error (difference in means). (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

Figure 6.

Mean squared error (risk difference). (a) Independent normal covariates, (b) correlated normal covariates, (c) mixture of normal and binary covariates, (d) independent binary covariates, (e) correlated binary covariates.

5 Case study

We used a sample of 9107 patients discharged from 103 acute care hospitals in Ontario, Canada, with a diagnosis of AMI or heart attack between 1 April 1999 and 31 March 2001. Data on these subjects were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, an initiative intended to improve the quality of care for patients with cardiovascular disease in Ontario.^22,23 The EFFECT study consisted of two phases. Data on patient demographics, vital signs and physical examination at presentation, medical history, and results of laboratory tests were collected for this sample.

For the current case study, the exposure of interest was whether the patient received a prescription for a statin lipid-lowering agent at hospital discharge. Three thousand and forty-nine (33.5%) patients received a prescription at hospital discharge. The outcome of interest for this case study was a binary variable denoting whether the patient died within 8 years of hospital discharge. Three thousand five hundred and ninety-three (39.5%) patients died within 8 years of hospital discharge.

A propensity score for statin treatment was estimated using logistic regression to regress an indicator variable denoting statin treatment on 30 baseline covariates. Restricted cubic smoothing splines were used to model the relationship between each of the 11 continuous covariates and the log-odds of statin prescribing. Each of the matching algorithms described earlier was used to form matched samples consisting of pairs of treated and untreated subjects. For regression adjustment in the matched sample, two different regression models were considered. The first used the propensity score as the sole covariate. The second adjusted for the 30 variables that were contained in the propensity score model. These variables denote demographic characteristics, vital signs on admission, classic cardiovascular risk factors, previous medical history and co-existing conditions, and results of initial laboratory tests.

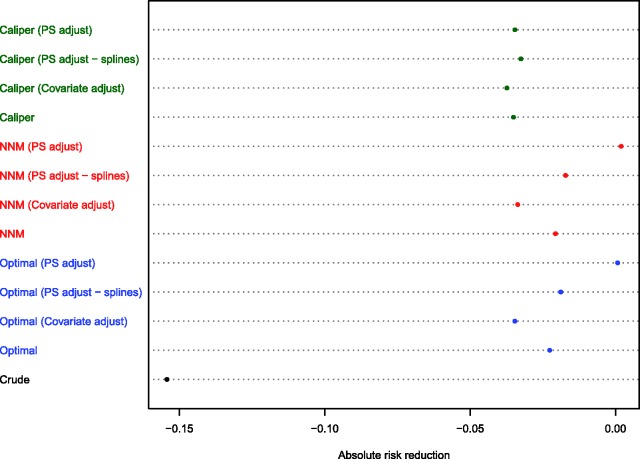
The different effect estimates are reported in Figure 7. As would be expected based on the results from the Monte Carlo simulations, the three estimates obtained in the caliper-matched sample (crude matched estimate and the two adjusted estimates) were all qualitatively similar (risk differences ranging from −0.037 to −0.035). The two estimates obtained using regression adjustment using the full multivariable model in the matched samples obtained using NNM and optimal matching were comparable to the three estimates obtained in the caliper-matched sample. Interestingly, the estimates obtained using propensity score covariate adjustment in the samples constructed using NNM and optimal matching were closer to the null treatment effect, whereas the crude or unadjusted estimates obtained in these two matched samples were between these estimates obtained using different adjustment methods.

Figure 7.

Estimated absolute reduction in the probability of 8-year mortality in AMI patients due to statin prescribing.

Due to the aberrant results obtained when using covariate adjustment using the propensity score in the different matched samples, we repeated this analysis using restricted cubic splines with four knots to model the relationship between the propensity score and the log-odds of the outcome.²⁴ Using this analytic strategy, the adjusted estimates were closer to the crude estimate obtained in the corresponding matched sample.

6 Discussion

We proposed a method based on double propensity-score adjustment to increase the degree of bias reduction when using optimal or NNM. An extensive series of Monte Carlo simulations was used to assess the performance of this method compared to that of conventional matching algorithms. In this section, we briefly summarize our findings and place them in the context of the prior literature. There were three primary findings from our Monte Carlo simulations. First, the use of optimal or nearest neighbor matching with subsequent regression adjustment resulted in estimates of treatment effect that had minimal bias compared to using either NNM or optimal matching alone or to the use of caliper matching with or without subsequent regression adjustment. Second, the use of optimal matching or NNM with subsequent regression adjustment using the propensity score resulted in estimates with lower MSE than the crude estimates obtained using caliper matching in over two-thirds of the scenarios. Third, double propensity score adjustment avoided bias due to incomplete matching, whereas this bias was not decreased when using subsequent regression adjustment in the samples formed using caliper matching.

These findings have important consequences for those using propensity-score matching to estimate the effects of treatments, interventions, and exposures. As noted earlier, caliper matching can be subject to “bias due to incomplete matching.” We found that, in the presence of a heterogeneous treatment effect, caliper matching tended to result in biased estimation of the ATT, and that the magnitude of the bias increased as the prevalence of treatment increased. This increase in bias was likely due to the exclusion of an increasing number of treated subjects due to an inadequate number of controls to which they could be matched. Matching methods such as optimal matching and NNM can result in biased estimation due to residual confounding since they do not impose a constraint on the quality of matches necessary for inclusion in the final matched sample. We found that double propensity score adjustment shares the advantages of both sets of methods. Propensity-score matching using nearest neighbor or optimal matching followed by subsequent regression adjustment resulted in estimates with minimal bias. Due to the inclusion of all treatment subjects, target bias or bias due to incomplete matching is avoided. Furthermore, the subsequent use of covariate adjustment eliminates the residual confounding due to the inclusion of some poor quality matches. Since this method uses the entire sample, concerns around generalizability have been mitigated.

Alternative methods of combining regression adjustment and propensity-score matching can be proposed. A simple approach would be to regress the outcome on a set of baseline covariates and on an indicator variable denoting treatment status in the matched sample. The regression coefficient for the treatment status variable could be used as the measure of treatment effect. We did not pursue this method because, when outcomes are binary, the resultant measure of effect would be an odds ratio. When outcomes are binary, our proposed method allows one to estimate risk differences (and the associated number needed to treat) and relative risks. Several clinical commentators have argued that these measures of effect have greater utility for clinical decision making than does the odds ratio.^25–28 Furthermore, propensity-score matching and covariate adjustment using the propensity score have been shown to result in biased estimation of both conditional and marginal odds ratios.^17,18

We examined the use of both optimal matching and NNM and found them to have comparable performance. Similar findings were reported in a recent study comparing the relative performance of 12 different matching algorithms.⁹ Consequently, we recommend that the latter be used in practice. From a computational perspective, NNM is substantially simpler than optimal matching. We examined the performance of two different methods for using subsequent covariate adjustment in the propensity-score matched sample: adjustment for the propensity score alone (double propensity score adjustment) and adjustment for all prognostically important covariates. While the performance of the latter was negligibly superior compared to that of the former, we advocate the use of the former for several reasons. First, in RCTs, there is debate about which covariates to include when estimating an adjusted effect, with some suggesting that the covariates should be specified prior to the analysis of the study data. This guideline would be simple to implement in the context of propensity-score matching by stipulating that the propensity score would be used for subsequent adjustment. Second, the propensity score can be thought of as a single covariate that encapsulates the distribution of the observed baseline covariates; thus, adjustment for the propensity score should approximate adjustment for all baseline covariates. Third, this approach may be preferable in settings with small sample sizes or when the outcome is rare.²⁹ Fitting a regression model that included all variables that affect the outcome may be problematic when the outcome is rare and the number of subjects is low.³⁰

Our proposed method of double propensity-score adjustment is similar to the practice of using regression adjustment in RCTs.^4,31 Regression adjustment in RCTs has been advocated for the following reasons: first, it allows for the removal of residual confounding due to minor differences in the distribution of measured baseline covariates between treatment groups. Second, it results in an analysis with increased statistical power compared to a crude or unadjusted analysis.³ Similarly, we found that regression adjustment in the matched sample formed using optimal or NNM resulted in increased bias reduction.

There is a paucity of methodological articles examining subsequent regression adjustment in propensity-score matched samples. In one of the most notable studies to date, Rubin and Thomas discussed methods for combining propensity-score matching with additional adjustment for prognostic covariates in settings with continuous outcome variables.³² They proposed two different analytic strategies. The first was to use regression adjustment within the propensity-score matched sample to further reduce bias due on residual confounding. The second was to match on the propensity score and on a limited set of prognostically important covariates. They note that the latter approach is the observational study analog of blocking in a randomized experiment (i.e. stratified randomization). Rubin suggested that the “combination of matching with regression adjustment is generally better than either alone” (page 234).² Rubin and Thomas suggest that model-based adjustment within the matched sample may perform better than in the original unmatched sample because of the reduced extrapolation involved within matched samples. Ho et al., in a similar spirit, describe matching as allowing nonparametric preprocessing that reduces model dependence in subsequent parametric analyses.³³ The underlying thought being that matching permits more efficient and robust subsequent regression adjustment than would be possible in the original, unmatched sample. Abadie and Imbens proposed a bias-corrected matched estimator for linear treatment effects when outcomes are continuous that is similar to ours, in that it uses regression models to impute missing potential outcomes in the matched sample.¹⁰ They demonstrated that the proposed approach resulted in greater bias reduction compared to matching alone. Our paper built upon their framework in two ways: first, by expanding the method to allow for examining binary outcomes; second, by focusing on the propensity score as the primary adjustment variable.

Lack of adequate overlap in the distribution of the propensity score is an issue that plagues many observational studies. There are no consistent approaches to dealing with insufficient overlap in the propensity score between treatment groups. Some analysts pursue an ad hoc approach, in which subjects with very low or very high propensity scores are excluded. In the context of IPTW using the propensity score, Crump et al. determined a strategy to optimize the precision of the estimated treatment effect (i.e. to minimize the standard error of the estimated treatment effect).³⁴ They found that an approximation to an optimal rule was to restrict the analysis to subjects whose propensity score lay within the interval [0.1, 0.9]. While this rule results in estimates with the greatest precision, it nonetheless can result in the exclusion of some subjects, thereby resulting in biased estimation of the ATE. Some argue that the exclusion of subjects with a very high or very low propensity score is justified, since the focus should be on those subjects for whom there exists clinical equipoise. However, under Rosenbaum and Rubin’s assumption of strongly ignorable treatment assignment, all that is required is that $0<⪻(Z=1|X)<1$.¹² In other words, one requires that each subject have a nonzero probability of receiving the treatment of interest. Since subjects with a high propensity score are often (by definition) treated, it is important to include these subjects in the sample in which the effect of treatment is estimated. Failure to do so may result in an estimate of treatment effect that is biased and that may not be applicable to those subjects in whom the treatment is frequently (but not always) used. The two effects of interest (the ATE and the ATT) are both well defined. The population to which the estimands apply can be explicitly described by the inclusion and exclusion criteria of the study. Once subjects are excluded on the basis of their propensity score, it is much more difficult to succinctly describe the populations to which the estimands apply. For these reasons, double propensity score adjustment is an attractive analytic approach since it results in excellent bias reduction and the population to which the estimand applies retains the ability to be easily characterized.

Assessing balance in baseline covariates induced by matching on the estimated propensity score is a critical component of a propensity-score matching analysis. Balance diagnostics for use with propensity-score matching have been described elsewhere.³⁵ A reasonable question would be how to conduct balance assessment when using double propensity score adjustment (or for that matter, any form of covariate adjustment in the propensity-score matched sample). As in Section 1, instructive lessons can be learnt from the analysis of RCTs. In RCTs, the ubiquitous “Table 1” describes the baseline characteristics of subjects in each of the different treatment groups. Readers often informally examine this table as a way of assessing whether randomization produced different treatment groups that were balanced with respective to prognostically important covariates. However, in RCTs, the primary analysis is often not a crude (unadjusted) analysis, but an adjusted analysis that adjusts for a set of baseline covariates.³⁶ Thus, in analyses that employ propensity-score matching, balance diagnostics conducted in the matched sample permit one to have a basic assessment of the comparability of treated and untreated subjects in the matched sample, with the understanding that additional differences have been removed through the use of covariate adjustment. While balance diagnostics have been described for use with propensity-score matching³⁵ and covariate adjustment using the propensity score,³⁷ subsequent research could develop methods for assessing balance when combining these two methods. However, that is beyond the scope of the current study.

There are several limitations of the current study that deserve mention. First, our study was based on Monte Carlo simulations. Thus, it is conceivable that different results would be observed under different data-generating processes. However, we examined 25 different scenarios characterized by different distributions for the baseline covariates and by the prevalence of treatment. The current study examined more scenarios than are typically examined in studies that use Monte Carlo simulations to examine the behavior of matching estimators. Second, our attention was focused on continuous and binary outcomes, and we did not consider the survival outcomes that occur frequently in the biomedical literature.³⁶ Prior studies examining combining matching and regression have restricted their focus to settings with continuous outcomes (e.g. Rubin and Thomas³²). The current study expands this focus to address settings with binary outcomes, thereby furthering the existing literature. Covariate adjustment using the propensity score has been shown to result in biased estimation of both conditional and marginal hazard ratios.^17,38 Consequently, simply regression adjustment in the propensity-score matched sample may lead to bias estimation of the underlying marginal hazard ratio. Further research is necessary for the optimal method to impute the unobserved potential outcomes (i.e. the unobserved event times or survival times under the treatment not received) and then to subsequently use regression adjustment to eliminate residual confounding. This needs to be addressed in future research. Third, further research is required into methods to estimate the standard error of the estimated treatment effect when double propensity score adjustment is used, particularly when outcomes are binary. However, the use of the bootstrap may hold promise.³⁹

In conclusion, regression adjustment using the propensity score in a matched sample constructed using either nearest neighbor or optimal matching allows the analyst to obtain unbiased estimates of the ATT when outcomes are continuous or binary. In contrast, the unadjusted estimate obtained in a sample formed by either of these matching methods resulted in biased estimation due to residual confounding. Furthermore, the naïve estimate obtained using caliper matching was biased due to incomplete matching (i.e. target bias or design bias). This bias was not reduced by subsequent regression adjustment. Double propensity score adjustment permits elimination of both bias due to design (incomplete matching or target bias) and bias due to confounding.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) received no financial support for the research, authorship, and/or publication of this article.