Influence of mixing conditions on the rheological properties and structure of capillary suspensions

Abstract

The rheological properties of a suspension can be dramatically altered by adding a small amount of a secondary fluid that is immiscible with the bulk liquid. These capillary suspensions exist either in the pendular state where the secondary fluid preferentially wets the particles or the capillary state where the bulk fluid is preferentially wetting. The yield stress, as well as storage and loss moduli, depends on the size and distribution of secondary phase droplets created during sample preparation. Enhanced droplet breakup leads to stronger sample structures. In capillary state systems, this can be achieved by increasing the mixing speed and time of turbulent mixing using a dissolver stirrer. In the pendular state, increased mixing speed also leads to better droplet breakup, but spherical agglomeration is favored at longer times decreasing the yield stress. Additional mixing with a ball mill is shown to be beneficial to sample strength. The influence of viscosity variance between the bulk and second fluid on the droplet breakup is excluded by performing experiments with viscosity-matched fluids. These experiments show that the capillary state competes with the formation of Pickering emulsion droplets and is often more difficult to achieve than the pendular state.

1. Introduction

Capillary suspensions are ternary solid-liquid-liquid systems. They consist of particle suspensions with a small amount of added secondary fluid that is immiscible with the bulk liquid.¹ The added fluid causes a sample-spanning particle network to form, which leads to dramatic alterations of the suspension rheology and stability.^{1, 2, 3, 4, 5, 6, 7, 8} This effect can be used as a simple method to tune the flow behavior of suspensions that would otherwise require the addition of binding agents, surfactants or other additives.⁹ Capillary suspensions can be used for various applications such as precursors for ceramic or glass filters with high porosity and simultaneously small pore size,^{10, 11, 12} improved polymer blends,^{5, 13, 14} slurries for printable electronics with accurately molded edge shape, good charge transfer properties and reduced resistivity.^{15, 16, 17}, thermal interface materials,¹⁸ slurries of renewable carbon sources used for generation of energy¹⁹ or the preparation of novel food products.²⁰

Capillary suspensions can be formed either with the secondary phase wetting more than the bulk phase, which is referred to as pendular state, or wetting less in the capillary state. In both cases, a percolating particle network arises leading to a transition in rheological properties due to network gelation.^{1, 8} In the pendular state, two adjacent particles are connected by a concave bridge, which induces a capillary force.⁴ In the capillary state, binary bridge between two particles are not formed. Instead, as was calculated numerically, small secondary phase droplets serve as a center for tetrahedral, octahedral, or small numbers of particles surrounding the second fluid drop due to energetic reasons.^{21, 22} The three phase contact angle θ, which the second fluid forms towards the particle surface in bulk environment, is smaller than 90° in the pendular state, where the secondary fluid wets better than the bulk fluid, while it is larger than 90° in the capillary state. The contact angle is derived directly from the Young equation.²³ The pro-rata composition of the solid and two liquid phases is described by the solid volume fraction ϕ, defined as the ratio of the solid volume to the total sample volume, and by the saturation S, which is defined as the ratio of the more wetting fluid volume to the sum of both fluid volumes.⁹ Thus, the saturation takes values in a range of 0 < S ≲ 0.1 for the pendular state where only a small amount of more wetting liquid is added, while the saturation is 0.9 ≲ S < 1 in the capillary state, where the less wetting liquid is the secondary fluid and the more wetting bulk represents the majority of the liquid volume.

The structure of capillary suspensions and their strength depends on the particle radius a, the interfacial tension Γ between the fluids and the wetting properties of both liquids, comprised by the three phase contact angle θ.⁹ Additionally, structure and strength are determined by the volume and number of the second fluid bridges in the pendular state or droplets in the capillary state. The capillary force F_c in a concave bridge of volume V_bridge between two equally sized spherical particles can be computed either by solving the Young-Laplace equation or by assuming a certain bridge shape. Typically, the attraction energy between such particles connected by the capillary force is many times higher than thermal energy kT.²⁴ Accordingly, the capillary force is then orders of magnitude higher than the van der Waals force,² as well as gravity.²⁵ This leads to an increased cohesion between particles in capillary suspensions compared to suspensions without added secondary fluid resulting in the observed marked changes in flow behavior and prevented particle sedimentation.²⁰ The capillary force of single bridges can be related to the macroscopic stress of a percolated capillary suspension network. The relationship between capillary force and yield stress σ_y for equally-sized particles in direct contact is given by^{8, 26, 27, 28}

$${\sigma }_y=f\left(\varphi ,N_{\text{bridge}}\right)\frac{F_c}{a^2}=f\left(\varphi ,N_{\text{bridge}}\right)f\left(V_{\text{bridge}}\right)\frac{2\pi \Gamma \cos \theta }{a}$$ (1)

with f(ϕ,N_bridge) being a function of particle volume fraction and the number of second fluid bridges per unit volume^{2, 29} and f(V_bridge) a function of the bridge volume. Both functions are, to our best knowledge, not yet described in a closed form as the number and volume of the second fluid droplets in a capillary suspension strongly depends on the saturation S and especially also on the mixing properties during sample preparation.⁵ In Fig. 1, a simple preliminary experiment where a capillary suspension was mixed using a vane geometry on a rheometer instead of a conventional stirrer is shown. In this experiment, different regions of the sample were exposed to different mixing intensities. As can be seen from the confocal images of Fig. 1b-d, a higher mixing intensity leads to a more homogeneous distribution of secondary fluid where many separate, small bridges between the solid particles are visible. Larger drop clusters are present in regions of lower mixing intensity where the second fluid was not well distributed. The general importance of different mixing procedures for capillary suspension preparation was also recently shown by Domenech and Velankar.⁵ The main aim of our study is to understand this influence of different mixing procedures in more detail.

Figure 1.

Influence of mixing intensity on the distribution of second fluid. (a) Vane geometry (top) and stirred suspension of spherical particles and second fluid in bulk liquid (bottom). Three confocal microscopy images were taken at different positions of the sample as denoted by the black circles. (b) Region of highest mixing intensity at vane edge, (c) intermediate mixing intensity and (d) lowest mixing intensity directly below the vane. The particles are shown in red, the second fluid in green and the bulk liquid in black.

The problem of mixing in capillary suspensions is very closely related to droplet breakup of the second fluid in the bulk liquid, which is a well-examined topic when particles are absent in emulsification theory and technology. Early droplet deformation and breakup theories were proposed by Taylor in the 1930s where droplet breakup in laminar flow was related to counteracting contributions of a droplet-deforming shear stress τ and the Laplace pressure 2Γ/R.^{30, 31} A droplet of size R breaks as soon as a critical stress is exceeded. This is captured by the critical Capillary number Ca_crit, which is defined as

$${\text{Ca}}_{\text{crit}}=\frac{{\tau }_{\text{crit}}R}{\Gamma }=\frac{{\dot{\gamma }}_{\text{crit}}{\eta }_{\text{b}}R}{\Gamma }$$ (2)

where the shear stress in laminar flow is just the product of shear rate $\dot{\gamma }$ and bulk liquid viscosity η_b. At a given stress and interfacial tension, Ca_crit determines the smallest possible droplet size R_crit that can be achieved. An extensive study on the critical capillary number was performed by Grace,³² who also showed that Ca_crit is strongly dependent on the viscosity ratio λ = η_d/η_b relating the droplet viscosity η_d to the bulk viscosity. The smallest droplets can be achieved for λ = 0.1-1 as Ca_crit steadily increases for smaller ratios. Ca_crit increases even faster for ratios larger than unity and droplet breakup becomes impossible for λ > 3.5 in laminar shear flow.³² However, deviations from Grace’s findings have to be considered when the flow field also contains elongational contributions,³³ the volume fraction of the droplet phase is high,^{34, 35} the flow is confined,³⁶ the flow field is not stationary,³⁷ or one or both liquids are non-Newtonian.³⁸ Droplet breakup becomes complicated further in the additional presence of particles.³⁹ Additionally, the viscosity of the droplet has to be considered independently of λ, an effect that is captured in the Ohnesorge number Oh. Oh becomes much larger than zero for a relatively high droplet viscosity, which indicates an additional impairment in droplet breakup.^{40, 41}

For droplet breakup under turbulent flow conditions, the concepts of Hinze are commonly used.⁴² Here, the minimum possible droplet size R_min is determined by a critical Weber number We_crit which is defined similarly to the Capillary number of laminar flow breakup theory, but with different droplet-deforming stress,

$${\text{We}}_{\text{crit}}=\frac{\tau R_{\text{crit}}}{\Gamma }=\frac{{\rho }_{\text{b}}{u}^2{R}_{\text{crit}}}{\Gamma }$$ (3)

with ρ_b being the density of the bulk liquid and u the velocity scale inside the droplet, which also is a function of R_crit.^{41, 42, 43} Hinze showed that R_crit is proportional to the power input per unit mass p = P/m for turbulent flow with Oh ≪ 1 with

$$R_{\text{crit}}\sim {\left(\frac{{\rho }_{\text{b}}}{\Gamma }\right)}^{-0.6}{p}^{-0.4}$$ (4)

Therefore, a higher specific power input leads to smaller droplets. When droplet breakup in turbulent flow is performed with a stirrer, the power input depends on the stirrer power P = Mω with the stirrer torque M and the angular speed ω. Using P = E/Δt, where E is the energy input and Δt is the stirring time, the energy input of the stirrer can be calculated as⁴⁴

$$E=M\omega \Delta t=M2\pi n\Delta t$$ (5)

where n is the rotational speed of the stirrer. Combining equations 4 and 5 predicts that an increased stirring speed n is expected to lead to smaller droplet sizes.

In many recent publications, capillary suspensions were prepared in a lab scale using a dissolver stirrer, where the secondary fluid was added to the suspension while stirring with a non-optimized stirring speed and mixing time. Thus, after giving details about our materials and experimental procedures in section 2, our study first evaluates the influence of different stirring speeds and times on the rheology and structure of capillary suspensions in both pendular and capillary states. This is described in section 3.1. We then examine different mixing approaches in section 3.2, where either an additional mixing step with a ball mill was applied after turbulent dissolver stirring or where the order of addition of the three sample components was changed. In section 3.3, a series of experiments where the viscosities of both liquids were matched to exclude any influence of the viscosity ratio λ on the droplet breakup during sample preparation were conducted. Finally, we summarize our findings in the conclusions of section 4.

2. Materials and methods

2.1. Materials

Experiments were performed using four different ternary solid-liquid-liquid material systems, each of them containing rigid micron-sized particles and two immiscible Newtonian fluids. An overview of these systems is given in Table 1, where the different sample compositions are termed C1 to C4. Scanning electron microscopy (SEM) images and particle size distributions of the different particle types are shown in Fig. 2. Solid densities have been measured by gas pycnometry (MultiVolume Pycnometer 1305, Micromeritics Instrument Corporation, Norcross, USA). Particle sizes were obtained by Fraunhofer diffraction (Helos H0309, Sympatec GmbH, Clausthal-Zellerfeld, Germany). Three-phase contact angles θ have been determined with the sessile drop method (OCA 15 EC, Dataphysics, Filderstadt, Germany) and evaluated via a numerical Young-Laplace fit to the imaged droplet contour.⁴⁵ Here, θ was measured as the angle that an equilibrated secondary fluid droplet forms towards a pellet of compressed solid particles surrounded by the bulk fluid. To avoid air entrapment in any open pellet pores, the pellet was completely soaked in the bulk fluid and degassed before the secondary fluid droplet was added.²⁰

Table 1.

Composition and properties of the material systems used in the present study.

Composition	Solid phase	Bulk fluid	Secondary	Solid volume fraction ϕ	Three-phase contact angle θ	Saturation S
C1	Glass beads (OMicron NP3)	Hexamoll DINCH +0.1% Tween20	Water	0.25	39 ±8°	0.010
C2	Hydrophobic CaCO3 (Socal U1S1)	Hexamoll DINCH	Water	0.15	156 ±5°	0.997
C3	α-Al2O3 (CT3000SG)	Paraffin oil	Sucrose solution	0.15	41 ±4°	0.018
C4	Glass beads (OMicron NP3)	Silicone oil AK100	Aqueous glycerol	0.30	49 ±7°	0.000-1.000

Figure 2.

SEM images of (a) SiO₂ glass beads (NP3), (b) hydrophobic CaCO₃ (Socal U1S1) and (c) α-Al₂O₃ (CT3000SG). (d) Particle size distribution of all three particle types.

Material composition C1 uses NP3 particles (OMicron NP3-P0, Sovitec, Fleurus, Belgium), hydrophilic solid glass beads with spherical shape, density ρ = 2.46 ±0.03 g/mL and mean particle diameter d_50,3 = 3.55 ±0.04 µm. 1,2-cyclohexane dicarboxylic acid diisononyl ester (Hexamoll DINCH, BASF, Ludwigshafen, Germany, η(20°C) = 46 mPas) is used as bulk fluid with 0.1 vol% of the nonionic surfactant Polysorbat 20 (Tween20, Carl Roth, Karlsruhe, Germany) added. The surfactant was necessary to avoid particle agglomeration that was otherwise too strong and would have made most C1 samples too inhomogeneous for an appropriate rheological characterization. The second fluid is ultrapure water (η(20°C) = 1 mPas). Composition C1 is in the pendular state as the glass beads are hydrophilic and the measured contact angle is θ = 39 ±8°. The surfactant (same amount of 0.1 vol% in the oil phase) had also been used in these contact angle measurements. Addition of surfactants to capillary suspensions has been shown to increase the contact angle.⁹ Due to relatively small droplet sizes in the capillary suspensions, the total liquid-liquid interface in the pendant drop experiment is probably much smaller than in the capillary suspension samples. Thus, the liquid-liquid interface in the contact angle measurement is likely more densely covered with surfactant leading to a higher contact angle. Thus, while the contact angle in the capillary suspensions is possibly lower than the measured 39°, the samples of system C1 certainly can be classified as pendular state. Capillary suspensions based on glass beads have already been used as model pendular state systems in previous studies.^{5, 8, 9}

Material composition C2 is based on non-spherical hydrophobic calcium carbonate (Socal U1S1, ρ = 2.32 g/mL, d_50,3 = 2.05 ±0.10 µm) manufactured by Solvay Advanced Functional Minerals (Salin-de-Giraud, France), which exhibit a structured rough surface. The hydrophobic surface modification was performed by the manufacturer. The bulk fluid is Hexamoll DINCH (without surfactant) and the second fluid is ultrapure water. Composition C2 is a capillary state model system (θ = 156 ±5°). These particles have been used several times previously and are already thoroughly investigated in capillary state model systems.^{1, 46}

Material composition C3 is a pendular state system (θ = 41 ±4°) that is utilized as precursor for ceramics production.^{10, 11} The solid phase is aluminum oxide powder (hydrophilic α-Al₂O₃, CT 3000 SG, ρ = 3.94 g/mL, d_50,3 = 0.65 ±0.03 µm), obtained from Almatis GmbH (Ludwigshafen, Germany). The bulk fluid is thin paraffin oil (“Paraffinöl dünnflüssig”, Carl Roth, Karlsruhe, Gemany, η(20°C) = 30 mPas), the second fluid a 50 vol% solution of sucrose (Carl Roth, Karlsruhe, Germany) in ultrapure water (solution viscosity η(20°C) = 80 mPas). For material compositions C1, C2 and C3, the solid volume fraction and saturation were kept constant during all experiments as shown in Table 1.

Material composition C4 is based on the same NP3 glass beads used for composition C1. Silicone oil (AK100, Wacker Chemie AG, Burghausen, Germany, η(20°C) = 104 mPas) and a mixture of glycerol (purity >99.5%, Carl Roth, Karlsruhe, Germany) with ultrapure water are used as the two immiscible liquids. The glycerol ratio was adjusted to 84.6 wt%, with a mixture viscosity of η(20°C) = 104 mPas to match the viscosity of the oil phase. Different sample compositions in the whole saturation range S = 0-1 are investigated. The contact angle (θ_pendular = 49 ±7°) was measured using the oil phase as bulk fluid. Therefore, composition C4 is in the pendular state when aqueous glycerol is used as the secondary fluid (0 < S ≲ 0.1). The contact angle of the silicone oil towards a pellet of compressed particles in aqueous glycerol also was measured using an inverted sessile drop method. In this case, the angle is θ_capillary = 119 ±13° and thus system C4 is expected to be in the capillary state when the aqueous glycerol is used as bulk (0.9 ≲ S < 1). As the viscosity ratio is λ = 1, the droplet breakup behavior in composition C4 and the resulting droplet size in particular is expected to be independent of which liquid is in the majority according to Grace theory.³²

2.2. Sample preparation

All particles were dried overnight at 105 °C before sample preparation to remove any trace water. The bulk and secondary fluids were used without any further treatment. All samples were prepared at room temperature.

If not explicitly stated, the pendular and capillary state model compositions C1 and C2 were prepared as follows. First, the particles and bulk fluid were placed in a glass beaker (inner diameter of 38 mm) and stirred with a dissolver stirrer (diameter of 25 mm) at constant stirring speed n₁ = 2000 rpm for a constant time interval Δt₁ = 20 min to fully disperse the particles in the bulk fluid. The second fluid was then added and the sample was again stirred.

The stirring speed n₂ and time Δt₂ were varied in this second step while the sample volumes as well as stirrer and beaker geometry were kept constant for all sample preparations. The total sample volume was always V = 30 mL.

For material composition C3, the samples were prepared in a similar way to samples C1 and C2, but with constant stirring parameters of n₁ = 1200 rpm, Δt₁ = 10 min, n₂ = 1000 rpm, Δt₂ = 2 min, V = 100 mL in a beaker with inner diameter of 65 mm and using a dissolver stirrer with 50 mm diameter. The resulting “preliminary” capillary suspension was then transferred into a custom-built ball mill.^{11, 12, 47} The samples were then homogenized on the ball mill with a rotation speed of 18 rpm in a 100 mm diameter vessel using 19-21 balls (mass m = 34.5 ± 1.3 g each) with 25 ± 2 mm diameter for different time intervals Δt₃ = 0-24 h.

For material composition C4, a dissolver stirrer with 36 mm diameter and a beaker with 46 mm diameter were used. Here, both fluids were first emulsified at 1250 rpm for 20 min. The particles were then added and stirred for another 2 min at 1250 rpm, followed by 1 min at 800 rpm. Stirring speeds and times were kept constant, as well as sample volume V = 55 mL, while the sample composition was varied.

2.3. Rheological measurements

Rheological properties were determined using rotational rheometry. For material compositions C1, C2 and C4, measurements were performed with a stress-controlled rheometer (Physica MCR 501, Anton Paar GmbH, Filderstadt, Germany) using a plate-plate geometry with 25 mm plate diameter and 1 mm gap width. For composition C4, silicon carbide sandpaper (P320C, Jean Wirtz, Düsseldorf, Germany) was glued to the plates before gap adjustment to avoid wall slip. For material composition C3, measurements were performed with the stress controlled rheometer Haake RS150 (Thermo Scientific, Karlsruhe, Germany) using a vane geometry (four vanes, each with a dimension of 22x5 mm, see Fig. 1a) with appropriate Searle cylinder (diameter of 20 mm).⁴⁸ All measurements were conducted at 20 °C.

Yield stress measurements were performed by increasing the shear stress from 0.1 Pa or 1 Pa to 1000 Pa or 5000 Pa stepwise with dwell time of 20 s per point. A plot of the measured strain vs applied shear stress shows a sharp transition from linear, elastic deformation at small stress to rapid deformation at large stress, see Fig. 3a. The yield stress σ_y was evaluated as the shear stress at the intersection of the two tangents.^{20, 49}

Figure 3.

Determination of (a) yield stress, σ_y, and (b) storage and loss moduli, G’ and G”. The yield stress is determined as the shear stress corresponding to the intersection point of two tangents fitted to the strain vs applied shear stress data. G’ and G” are evaluated at a frequency ω = 1 rad/s at a previously determined strain amplitude in the linear viscoelastic domain. The example data shown belongs to material composition C2 prepared with n₂ = 2000 rpm and Δt₂ = 5 min.

Oscillatory shear strain amplitude sweep measurements were performed at frequencies of ω = 1 rad/s as well as 100 rad/s while increasing the strain amplitude γ from 0.001% to 100%. In all cases, the upper limit of the linear viscoelastic (LVE) region was found to be independent of the frequency and, for most samples, have a value between 0.01% and 0.1%. Frequency sweep measurements with ω = 100-0.1 rad/s were performed using a strain amplitude inside the LVE region. Single values of the storage modulus G’ and loss modulus G” in the LVE region were evaluated at ω = 1 rad/s, as shown in Fig. 3b.

2.4. Microscopy

To gain a better insight into the microstructure, some samples of material composition C1 were imaged with an inverted bright field light microscope (Axio Observer D1, Carl Zeiss, Oberkochen, Germany) equipped with an objective having 10x magnification and a numerical aperture of 0.25 (A-PLAN 10x/0.25, Carl Zeiss). Some samples of material composition C4 were also imaged using an inverted confocal laser scanning microscope (TCS SP8, Leica Microsystems, Mannheim, Germany) equipped with a multi-immersion objective with numerical aperture of 0.7 and 20x magnification (HC PL APO, 20x/0.75 IMM CORR CS2, Leica Microsystems). The confocal microscope contains two solid-state lasers with excitation wavelengths of 488 nm and 552 nm to excite two different fluorescent dyes as shown in the example images of Fig. 1b-d. The materials in this image were prepared and imaged as described by Bossler and Koos.⁸ For the samples C4 imaged using confocal microscopy, small amounts of the fluorescent dye rhodamine B isothiocyanate (Sigma-Aldrich, Steinheim, Germany) were added to the aqueous glycerol before preparing the sample. The dye is excited by the 552 nm laser and the signal emitted in a wavelength interval of 560-660 nm was recorded.

3. Results and Discussion

3.1. Turbulent mixing with a dissolver stirrer

3.1.1. Influence of stirring speed

In the present study, the pendular state model system C1 and capillary state model system C2 were used to evaluate the influence of the stirring speed and time during sample preparation on the rheology of the resulting capillary suspension samples. The samples have been prepared with different stirring speeds n₂ upon the addition of the secondary fluid into the homogenized suspensions of particles in oil. The yield stress of these compositions is shown in Fig. 4.

Figure 4.

Dependence of the yield stress σ_y on the stirring speed n₂ for the (a) capillary state model system C2 and (b) pendular state model system C1. Both systems were prepared with a stirring time of Δt₂ = 1 min (filled squares) or 5 min (open circles).

The capillary state system (Fig. 4a) shows a strong increase in yield stress from 11 Pa to 420 Pa with increasing stirring speed from 400 rpm to 2000 rpm for stirring times of 1 min. The standard deviation between measurements also decreases, indicating a more homogeneous structure when faster stirring speeds are used. A similar trend can be seen for the pendular system (Fig. 4b) prepared with 1 min stirring time, where the yield stress increases from 165 Pa to 360 Pa when the stirring speed is increased from 400 rpm to 1200 rpm. The influence of the stirring speed here is weaker in the pendular state than in the capillary state and the yield stress reaches a constant value for stirring speeds larger than 1200 rpm.

The increase in stirring speed is directly proportional to an increase in stirring energy input and power input as described by equation 5. Therefore, higher speeds should lead to an enhanced droplet breakup under turbulent flow conditions and a decrease in secondary fluid droplet size (equation 4). The same should be true under laminar flow conditions, where Grace theory applies (equation 2) and increased stirring speed directly translates into larger shear rates and thus smaller droplet sizes when the system approaches Ca_crit. The overall number of droplets increases when the droplet size is decreased. Thus, there is a larger number of droplets available to serve as center of the basic building blocks for the capillary state network. Moreover, simulations have identified that smaller (e.g. tetrahedral) blocks show an increase in strength when compared to their larger (e.g. octahedral) cousins.²¹ This is manifested in the increased network strength as found in the yield stress data of Fig. 4. In the pendular state, the increased number of droplets also leads to a larger coordination number of bridges between particles raising the sample’s overall attractive capillary force and therefore also the yield stress (equation 1).

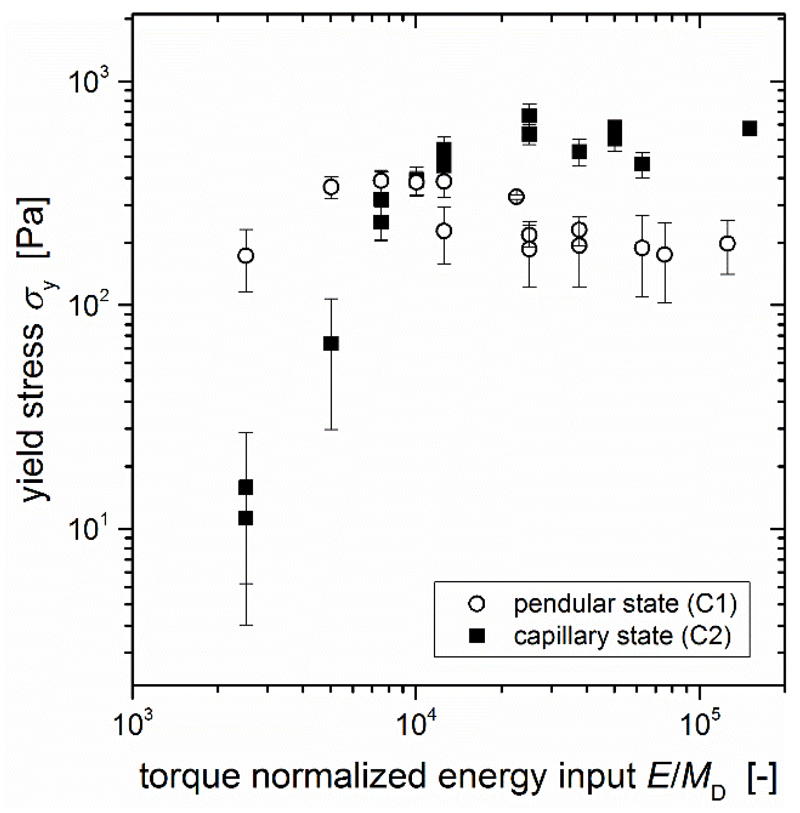
There appears to be a maximum energy input where the yield stress does not increase any further. This can be observed from the plateau value of the yield stress (σ_y ~ 360 Pa) for stirring speeds larger than 1200 rpm at 1 min stirring time in the pendular state sample (Fig. 4b). Such a plateau also occurs for the capillary state sample when a stirring time of 5 min is applied (Fig. 4a, σ_y ~ 500 Pa). Under the applied mixing conditions in the capillary state, this plateau is reached at E ≈ 400rpm·5min·2πM_D = 2000rpm·1min·2πM_D ≈ 12566·M_D as derived from a comparison of the yield stress values of the sample prepared at 400 rpm for 5 min and the sample prepared at 2000 rpm and 1 min. Both samples should have experienced this same energy input as the energy input is proportional to n₂·Δt₂ (see equation 5), and indeed show very similar yield stress values. This influence of the energy input can be seen even better in Fig. 5 where the yield stress of compositions C1 and C2 prepared at different Δt₂ and n₂ are plotted as function of the energy input E normalized by the dissolver torque M_D. The data presented in Fig. 5 includes all the data from Fig. 4 in a rescaled form, with some additional new points included. The abscissa E/M_D was calculated using equation 5 as E/M_D = 2π·n₂·Δt₂.

Figure 5.

Yield stress σ_y of different pendular state (C1, open circles) and capillary state (C2, filled squares) compositions as function of the dissolver torque normalized energy input E/M_D = 2πn₂Δt₂.

The yield stress also seems not to depend on the speed for the pendular state system (Fig. 4b) after 5 min of stirring, but the average value (σ_y ~ 200 Pa) is clearly smaller than for 1 min stirring time and these longer stirring times also show much larger errors between measurements. This behavior cannot be explained by the energy input alone as higher energy inputs should lead to smaller droplets contradicting this observed reduction in strength. To understand this effect, a closer look at the stirring time influence separately is necessary.

3.1.2. Influence of stirring time

For the capillary state sample system C2, the yield stress values discussed in section 3.1.1 increased with stirring speed until they reached a plateau. This effect was explained by an enhanced droplet breakup with increasing stirring energy input. The same findings can also be reproduced when the energy input is increased by varying the stirring time Δt₂ and keeping the speed constant as shown for n₂ = 400 rpm in Fig. 6a.

Figure 6.

Dependence of the (a) yield stress σ_y as well as (b) storage modulus G’, loss modulus G” and tanδ on the stirring time for the capillary state model system C2. The stirring speed of all samples was n₂ = 400 rpm.

As expected, the yield stress increases when Δt₂ is extended from 1 to 10 min and then enters a plateau region where no further increase is observed up to Δt₂ = 60 min. The storage and loss moduli, G’ and G” also increase with increasing stirring time and thus energy input (Fig. 6b). Interestingly, a plateau is not reached after 10 min, but both moduli continue to increase in the observed time range. This can additionally be seen in the decrease in tanδ = G”/G’, denoting a steadily increasing ratio of the elastic over the viscous properties of these capillary suspensions. Altogether, the capillary state strength always strengthens when the energy input during sample preparation is increased either by longer times or faster speed.

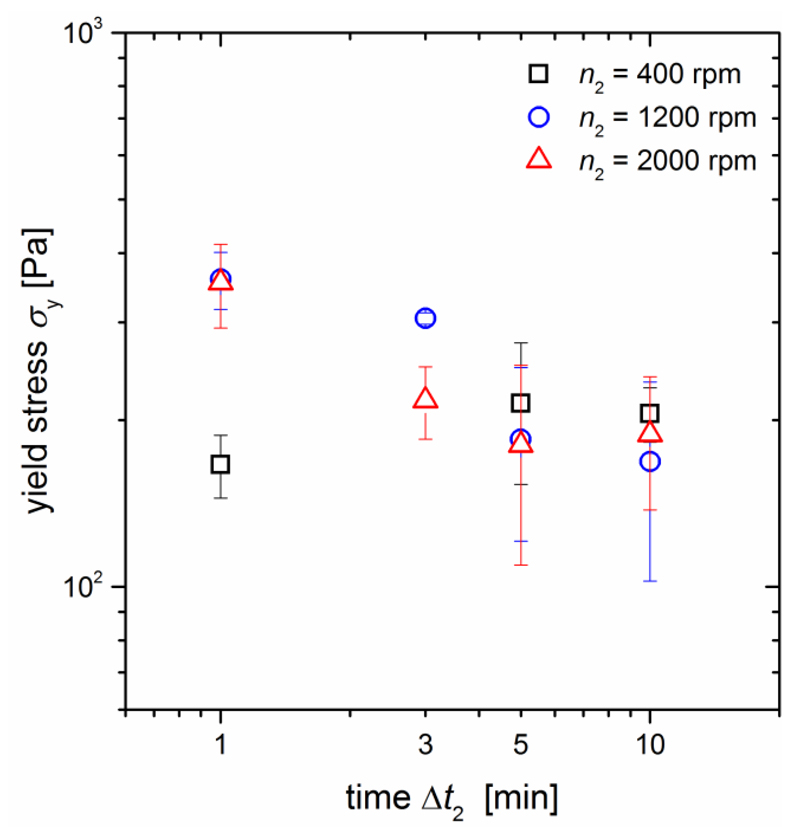
The same improvement in the network structure with increasing mixing time, as demonstrated for the capillary state sample, is not shown for the pendular state system C1 (Fig. 7). When the stirring time Δt₂ is increased from 1 to 10 min, the yield stress only increases very slightly at an applied speed of 400 rpm, while it decreases for speeds of 1200 rpm and 2000 rpm. High stirring speeds only lead to strong networks at relatively low stirring times. The standard deviation between consecutive measurements increases for all samples at longer stirring times and the yield stress tends to have similar values (200 Pa) independent of n₂. The decrease in yield stress values appears at shorter times for 2000 rpm than for 1200 rpm implying that this trend is related to the total energy input. The large error bars indicate severe inhomogeneities in the sample structure. Indeed, large agglomerates were visible by eye with increasing stirring time, whereas the samples were homogeneous in the beginning and lacked such large structures. Light microscopy images of samples stirred at 2000 rpm for 1 min and 10 min are shown in Fig. 8. The large agglomerates present after 10 min are clearly visible, while only small clusters are present for the 1 min stirring time.

Figure 7.

Dependence of the yield stress on the stirring time Δt₂ for the pendular state model system C1 for stirring speeds of n₂ = 400 rpm (black filled triangles), 1200 rpm (blue open triangles) and 2000 rpm (red half-filled triangles).

Figure 8.

Bright field microscopy images of the pendular state model system C1, prepared with stirring speed n₂ = 2000 rpm and stirring times (a) Δt₂ = 1min and (b) Δt₂ = 10min.

The droplet breakup enhancement due to increased energy input competes with the agglomeration kinetics, which increasingly dominates at longer mixing times. Such kinetics are well known from wet agglomeration processes where fluid is added to dry granular matter. The agglomeration occurs here at lower secondary liquid to solid fractions than is typical for wet granular materials^{7, 50} and may be due to the lower volume fraction allowing easier rearrangement of the particle network (through energy neutral rotations), causing dense agglomerates, which maximize the local coordination number, to form even without bridge coalescence. Spherical agglomerates grow with increasing mixing time and these agglomerates become increasingly compact and difficult to break since the fluid in the agglomerate is completely interconnected.⁵⁰ With a lab-scale dissolver stirrer, these agglomerates are effectively irreversible since their destruction would require very high shear rates that this type of stirrer cannot realize. It can be broken down much easier when the secondary fluid inside of an agglomerate is not completely interconnected, but merely is held together by many separate smaller fluid bridges.⁵⁰ To achieve such less densely packed agglomerates, the secondary fluid droplets must already be relatively small before agglomeration starts.⁵¹ This agglomeration type is favored when shear rates are high and the droplet fluid viscosity is rather small.⁵²

In a capillary suspension, large agglomerates destabilize the structure in a manifold way. An agglomerate immobilizes large amounts of secondary fluid, which is no longer well-distributed over the sample and thus the overall number of pendular bridges decreases. The large agglomerates also behave like large particles that are affected by gravitational forces (increasing with particle size cubed) or inertia (increasing with particle size squared) to a much greater degree compared to the capillary force, which has a linear dependence on particle size (see equation 1).²⁵

One necessary precondition to form compact agglomerates is that the added fluid must wet the particles. This is the case in the pendular state where the three-phase contact angle of the second fluid towards the particles is smaller 90°. In the capillary state, the second fluid wets the particles less well than the bulk fluid thereby preventing large-scale agglomeration due to the addition of the second fluid. This explains why these effects were not found for capillary state system C2 in Fig. 6. While the capillary state by itself is a clustered structure, these clusters are not directly stabilized by attractive capillary forces and negative Laplace pressure of the second fluid interspersing the cluster as is the case for the pendular state. Instead, stabilization is based on energetic favorability of small droplets being shielded by the solid particles.²¹ This kind of stabilization is not strong enough to build up large, densely-packed spherical agglomerates that are able to resist strong stirring for long times. In fact, these capillary clusters resemble the partially porous agglomerates of Knight et al., which have the tendency to break rather easily.⁵⁰

3.2. Alternative sample preparation methods

3.2.1. Mixing on a ball mill

In recent studies, pendular state systems based on aluminum oxide or silica have been prepared by first applying the dissolver stirrer method, discussed in section 3.1, followed by homogenization of the sample structure on a ball mill for Δt₃ = 24 h.^{11, 12, 47} Experiments with one of these aluminum oxide sample compositions, C3, have been reproduced while the homogenization time on the ball mill Δt₃ was varied, as shown in Fig. 9. These pendular state systems showed many agglomerates with sizes >100 µm (i.e. greater than 100 particle diameters) visible with the naked eye after the dissolver stirrer preparation (Δt₃ = 0 h, σ_y = 360 ±20 Pa). As discussed previously in section 3.1.2, these pendular state systems are prone to agglomeration.

Figure 9.

(a) Dependence of the yield stress on the ball mill processing time Δt₃ for the Al₂O₃-based pendular state model system C3. The line only serves as guide for the eyes. (b) SEM image of the sintered ceramic from material composition C3 prepared with Δt₃ = 24 h showing some of the residual aggregates. The mean size of single particles is d = 0.65 µm.

When the homogenization time is increased, the yield stress first decreases until a minimum value around σ_y = 230 Pa at Δt₃ = 1 h is reached. Then, the yield stress starts to increase until it reaches a plateau value around σ_y = 515 Pa after Δt₃ = 9.5 h. Further increases to the homogenization time, up to 24 h, do not have any impact on the yield stress. The yield stress decrease in the first hour on the ball mill can probably be attributed to a destabilization of the structure through increasing agglomeration. The increase in the yield stress for Δt₃ > 1 h can be ascribed to the mechanical load in the ball mill, which is completely different than the turbulent shear flow mixing from the dissolver stirrer preparation. Shear forces in the ball mill are comparably small, while the impact on the sample of balls colliding with each other or the bottom of the vessel is more important. The momentum at impact is very high due to the balls weight, and can easily smash any large agglomerates residing around impact position. Thus, in contrast to the turbulent shear flow from the dissolver stirrer, a reduction in agglomerate size and number is possible with sufficient mixing times. The quality of homogenization should depend on the mass of the balls and, to a lesser degree, on the rotational speed. With heavier balls, the momentum is higher and thus the probability to destroy any nearby agglomerate increases. It is, nevertheless, important to note that complete de-agglomeration does not occur. The yield plateau value does not indicate an absence of agglomerates, but more likely an equilibrium between agglomerate growth and disintegration. SEM images of a sintered aluminum oxide ceramic sample after 24 h of homogenization showed that flocs in a relatively narrow diameter range of 5-15 µm, each containing a small number of particles (d = 0.65 µm), are still present (Fig. 9b). There are, however, none of the very large agglomerates as found in the pendular state system C1 in Fig. 7b with sizes greater than 100 particle diameters. The ball mill homogenization cannot completely avoid particle agglomeration as this is inherent to pendular state systems since the preferred wetting of the second fluid towards the particles is less than 90°, and especially since there are droplets involved whose size is larger than single particle diameter, which is always the case when the second fluid is added to the suspension of pre-dispersed particles in the bulk fluid. The use of the ball mill, nevertheless, leads to much more homogeneous structures and higher yield stress values than the turbulent flow stirring alone. Finally it should be noted, that neither in this study nor in earlier experiments¹¹ any crushing of the aluminum oxide particles in the ball mill was observed. However, such crushing of particles can appear for other sample systems, e.g. the glass based system C1. Thus, while the ball mill can be a very helpful mixing instrument to prepare relatively homogeneous capillary suspensions, it is not applicable with all types of solid particles.

3.2.2. Secondary fluid emulsification before particle addition

One possible option to thwart the growth of agglomerates during mixing in pendular state systems is to change the mixing order so that the second fluid is first stirred into the pure bulk liquid to produce an unstabilized (or weakly stabilized) emulsion. Only afterwards are the particles added.⁵ The goal of this mixing order is to better control the second fluid droplet size. When the particles first come into contact with the second fluid, secondary fluid droplet size is ideally smaller than the particle size which is not the case for the conventional mixing order used in the preceding sections. This mixing order should avoid or at least reduce the buildup of compact agglomerates.

The pendular state model composition C1 is shown in Fig. 10 where this changed mixing order was applied. The second fluid was first emulsified with low energy input (3 min at 400 rpm) or high energy input (20 min at 2000 rpm). The particles were then added and stirring continued for a dispersing time Δt_d = 3 min with varied speeds n_d. Changes to the dispersing time after particle addition were avoided due to the complications described in section 3.1.2. The change in dispersing speed was expected to influence the yield stress as seen in section 3.1.1. However, no significant trend of the yield stress with the speed n_d can be seen. As composition C1 contains some small amounts of surfactant, the emulsion of second fluid in the bulk liquid is stable enough to show very little coalescence in the short rest time prior to particle addition. No further change in droplet size appears following the addition of particles, leading to the observed absence of dispersing speed influence. Nevertheless, the samples that have been pre-emulsified with relatively low energy input for all dispersing speeds show a weaker yield stress than the samples pre-emulsified with the higher energy input. Therefore, the energy input during pre-emulsification determines the resulting structure with higher energy input leading to stronger samples due to smaller droplets. This result agrees with droplet breakup theory as discussed thoroughly in section 3.1.1 and also with the findings of Domenech and Velankar.⁵

Figure 10.

Dependence of the yield stress on the stirring speed n_d for the pendular state model system C1 when the particles are added to a pre-emulsified mixture of secondary and bulk fluid. Dispersing time after particle addition was 3 min for all samples shown. Energy input for pre-emulsification was relatively low (t = 3 min, n = 400 rpm, filled squares) or high (t = 20 min, n = 2000 rpm, open circles).

Fig. 11 shows samples with the capillary state model composition C2 where the second fluid was first emulsified with relatively high energy input (20 min at 2000 rpm) before particle addition and further stirred with varied dispersing time or speed. Although a relatively high energy input (i.e. good droplet breakup) has been chosen for pre-emulsification, the yield stress depends strongly on the dispersing time as well as dispersing speed after particle addition, contrary to the behavior of composition C1 discussed before. Increased energy input after particle addition leads to stronger yield stress values, implying a further reduction in droplet size in this sample preparation step. The most probable explanation is not any difference between pendular and capillary state, but merely the fact that system C2 does not contain an emulsifier and thus the droplets of secondary fluid without stabilization tend to coalesce during and after the pre-emulsification step. The rate of coalescence directly competes with the droplet breakup and thus does not lead to comparatively small droplets of second fluid. The dependence of the yield stress on dispersing time and speed after particle addition then relies on identical breakup characteristics as already described in sections 3.1.1 and 3.1.2. Thus, a change in capillary suspension preparation order can be beneficial when the pre-emulsion is stabilized against droplet coalescence or the bulk fluid viscosity slows the kinetics adequately.

Figure 11.

Yield stress of the capillary state model system C2 when the particles are added to a pre-emulsified mixture of secondary and bulk fluid. Stirring time and speed for pre-emulsification always were t = 20 min and n = 2000 rpm. (a) Variation of dispersing time Δt_d after particle addition at constant speed n_d = 400 rpm. (b) Variation of dispersing speed n_d at constant time of Δt_d = 5 min.

3.3. Viscosity-matched model system

Theoretically, it should be possible to prepare both pendular and capillary state samples with a single sample composition by just modifying the ratio of the secondary and bulk fluid. However, there has never been a sample system reported that was able to exhibit both states. One possible explanation for this contradiction may be the dependence of the droplet breakup on the viscosity ratio of the two fluids. This is expected to be particularly critical when the viscosity ratio of dispersed to continuous liquid phase is larger than 3.5 since droplet breakup under shear flow conditions is practically impossible.³² For the pendular state sample system C1, the viscosity ratio of secondary to bulk fluid is λ = 0.019. The ratio would be λ = 1/0.019 ≈ 52 if the secondary fluid and bulk fluid were to be exchanged, a value much larger than the limit predicted by Grace.³² In reality, droplet breakup in this range is possible to some extent as the applied mixing does not obey the necessary preconditions described by Grace theory, e.g. the presence of solid particles changes the breakup behavior³⁹ and the dissolver stirrer also does not provide a laminar shear flow. Nevertheless, droplet breakup should be much more difficult for λ = 52 than for λ = 0.019. The influence of different λ ratios when exchanging the bulk and secondary fluid is avoided in material composition C4 as both fluids have the same viscosity. To also minimize any particle influence on the droplet breakup, both fluids were emulsified followed by particle addition as in section 3.2.2 for preparation of C4 samples. Despite the equal drop breakup behavior, this viscosity-matched system only leads to a stable pendular state suspension. A capillary state could not be prepared, as shown in Fig. 12. Thus, the viscosity ratio cannot be the only factor impeding the formation of a strong particle network in both states. Indeed, Hoffmann et al. also found that a change in viscosity ratio had effectively no direct influence on the strength of starch-based capillary suspensions.²⁰ However, direct comparisons to the current study is somewhat complicated since parts of the second fluid were absorbed by the starch granules in Hoffmann’s experiments.

Figure 12.

Variation in the (a) yield stress σ_y, and (b) storage G’ and loss moduli G” as a function of saturation S for the viscosity-matched composition C4. (c) Photographs illustrating different sample textures. The samples at S ≥ 0.5 did not have any measurable yield stress and clearly show a weakening of the structure in the photographs. Oscillatory measurements were made at a strain amplitude in the linear viscoelastic region with ω = 1 rad/s.

The absence of any capillary state structure can be seen directly from photographs of the sample texture (Fig. 12c) and is also obvious from the missing yield stress values (Fig. 12a) as well as in the oscillatory data (Fig. 12b) where the elastic storage modulus G’ is lower than the loss modulus G” at S ≥ 0.65. The sample with very little preferentially wetting liquid at S = 0.05 is clearly stronger than the sample at S = 0 indicating the buildup of a pendular state structure. No such strengthening appears when adding a small amount of non-preferentially wetting liquid (changing S from 1 to 0.95) where the formation of a capillary state network should be expected. No yield stress is measurable for any of the samples with S ≥ 0.5, which indicates that no particle percolation occurred. All of these higher saturation samples appear to be very viscous. This highly viscous behavior is substantiated by the high G” modulus, which dominates over G’ in the linear viscoelastic regime at ω = 1 rad/s for samples with S > 0.65. In the low and intermediate saturation range S < 0.5, all samples show a measurable yield stress and G’ dominates over G” indicating that these samples all demonstrate a gel-like behavior originating from particulate networks.

From the sample photographs (Fig. 12c), one can see that the sample with S = 0.05 is a pendular state network with a homogeneous structure. There is still a strong capillary attraction and a sample-spanning network for the S = 0.20 sample, but it is no longer homogeneous. This sample has agglomeration with the large flocs reaching sizes of 1 mm. At S = 0.35, all of the particles are incorporated into a single (or small number of) large agglomerate(s) and phase separation occurs such that the bulk (non-wetting) fluid is expelled from the tightly packed agglomerate. Due to these large structures, the rheological data measured at S = 0.20 and S = 0.35 should only be treated as rough estimations of the material strength since the continuum assumption may be violated even at the large gaps used. It is therefore unclear if the internal agglomerate strength, the interaction between agglomerates, or slip in a depletion region next to the plate is measured using the rotation rheometry experiments.

To understand the structural changes as the ratio of the two liquids is varied, certain key structures are imaged using a confocal microscope where the aqueous phase has been dyed, Fig. 13. The three different ternary structures appearing for S = 0.05, 0.20 and 0.35 can be directly compared to the three distinct open-pore morphologies recently discussed by Domenech et al., which were found in the same saturation ranges of particle-laden polymer blends (using polymer melts having viscosities of 8,000 and 13,000 mPas).⁵³ Domenech et al. found a pendular network (equivalent to the S = 0.05 sample here), a network of large agglomerates (akin to the S = 0.20 sample) and a bicontinuous structure in a saturation range in the order around S ≈ 0.5. They predicted this bicontinuous structure to be inaccessible when the fluid viscosities are lower, as is the case here (both liquids with η = 104 mPas), at which point they should collapse into a single, large agglomerate.⁵³ Their hypothesis seems to be borne out in the present system with S = 0.35, which could not be effectively imaged on the microscopic length scale.

Figure 13.

Confocal images of material composition C4 with (a) S = 0.05, (b) S = 0.20 and (c) S = 0.95. The red color denotes the aqueous glycerol, while particles and silicone oil are undyed. The particles are nevertheless visible by their distinct spherical shape with particle diameter around 3.5 µm. In (b), the dark regions inside of the agglomerates do not denote any lack of wetting liquid in the agglomerate but appear uncolored due to the refractive index mismatch between particles and fluids. In (c), the silica particles seem to extend into the bulk liquid because the image plane is not perpendicular to the oil droplet surface.

After several days at rest, the samples with S > 0.5 separated into three different layers, as shown in Fig. 14, further demonstrating the lack of a sample-spanning network. The bottom layer consists of unstabilized glass beads that are not in a capillary network and have settled due to gravity. A liquid layer of pure aqueous glycerol is in the middle. The top layer consists of distinct, particle coated Pickering droplets with a size of approximately 0.1 mm to 1 mm. For saturation values decreasing from 0.99 to 0.5, this layer consisting of droplets of the lower density silicone oil becomes thicker. These droplets are exceedingly stable, even after storage times longer than nine months. This stability is achieved through the Pickering effect,⁵⁴ where the interface between these droplets and the aqueous glycerol is covered by glass beads. One of these droplets is shown in the confocal image of Fig. 13c, where glass beads are visible surrounding the interface between the oil droplet (black) and the aqueous glycerol (red).

Figure 14.

Photographs of the samples containing material composition C4 with (from left to right) S = 0.65, S = 0.8, S = 0.9, S = 0.95 and S = 1. These photographs were taken more than nine months after sample preparation. Three distinct layers are visible for the samples with added secondary fluid. The top layer contains Pickering-stabilized emulsion droplets as shown in the magnified inset. The middle layer contains pure aqueous glycerol and the bottom layer is formed by the unstabilized, settled particles. The sample with S = 1 shows only two layers (aqueous glycerol over settled particles).

The appearance of Pickering emulsion droplets in the high saturation range can help to explain why a capillary state was not formed in this system. As the particles are added to the sample, they cover the interface between second fluid droplets and bulk liquid. Theoretically, the drops in a capillary state admixture should be smaller than the particles and form small clusters.²¹ Although the viscosities of both fluids were matched, the droplets did not have the requisite small size even with the high shear rate dissolver stirrer before particle addition. The rapid adsorption of the particles to the droplet surface prevented particle-assisted drop breakup and even made such drop deformation and breakup more difficult. The Pickering droplets are stabilized against coalescence when their surfaces become covered with particles, but there is no attraction between Pickering emulsion droplets and there will not be any network percolation as the particles do not have any notable attractive interactions. In material composition C4, no strong attractive particle interactions in aqueous glycerol arises as is evident by the lack of a measurable yield stress or high storage modulus G’ at S = 1. It is worth noting that this is in contrast to the capillary state system C2 based on hydrophobic CaCO₃, which already forms an attractive particle gel without any added secondary fluid. This attractive van der Waals network is then reinforced when the capillary state is formed with the addition of a secondary fluid. For this case, the attractive particles seem to enhance the droplet breakup until sufficiently small droplet sizes are reached for the formation of a capillary state network. Therefore, it appears that the capillary state can be much more difficult to form than the pendular state, especially when the particles do not have any other attractive interactions even when the viscosities of both fluids are matched and laminar drop breakup should be favorable. The formation of a capillary state network directly competes with the production of Pickering emulsion droplets, which do not increase the sample strength due to the low packing fraction of these drops.

4. Conclusions

The structure and strength of ternary liquid-liquid-solid systems strongly depends on the sample preparation method and the energy input during mixing of the sample. This is especially true for capillary suspensions where the secondary liquid only represents a small volume fraction of the whole sample. Different pendular state and capillary state model systems have been examined while varying the preparation conditions. Enhanced droplet breakup of the secondary fluid leads to stronger particle networks with more homogeneous network structures. Using a dissolver stirrer in capillary state systems, this can be achieved by increasing the energy input by either applying faster mixing speeds or a longer mixing times using turbulent mixing. In the pendular state, increased mixing speed also leads to better droplet breakup using the same stirrer, but spherical agglomeration is found to be favored at longer times. This agglomeration decreases the yield stress and leads to severe sample inhomogeneities. The additional use of a ball mill after turbulent stirring appears to be beneficial for the sample strength as it leads to a minimization of spherical agglomerates. This can be attributed to the different breakup mechanism dominated by impact forces of the balls instead of viscous shear forces. Emulsification of the second fluid before particle addition can also lead to stronger particle networks.

Experiments with viscosity matched fluids covering the entire saturation range from S = 0 to 1 have also been performed. These experiments show that the capillary state competes with the formation of large Pickering emulsion droplets and is often more difficult to achieve than the pendular state. This competition is independent of the viscosity ratio of secondary to bulk liquid, which seems to be only of minor importance. It can be hypothesized that the formation of a capillary state is enabled or enhanced if the capillary force is not the only attractive interaction present between particles. Further studies, however, have to be conducted to prove this hypothesis and to elucidate the nature of essential additional attractive forces. The contribution of, e.g., electrostatic, friction or van der Waals forces remains unclear up to now and a thorough investigation of such forces in the concurrent presence of capillary attraction is surely worth further examination.