Causal Discovery from Subsampled Time Series Data by Constraint Optimization

Abstract

This paper focuses on causal structure estimation from time series data in which measurements are obtained at a coarser timescale than the causal timescale of the underlying system. Previous work has shown that such subsampling can lead to significant errors about the system’s causal structure if not properly taken into account. In this paper, we first consider the search for the system timescale causal structures that correspond to a given measurement timescale structure. We provide a constraint satisfaction procedure whose computational performance is several orders of magnitude better than previous approaches. We then consider finite-sample data as input, and propose the first constraint optimization approach for recovering the system timescale causal structure. This algorithm optimally recovers from possible conflicts due to statistical errors. More generally, these advances allow for a robust and non-parametric estimation of system timescale causal structures from subsampled time series data.

1. Introduction

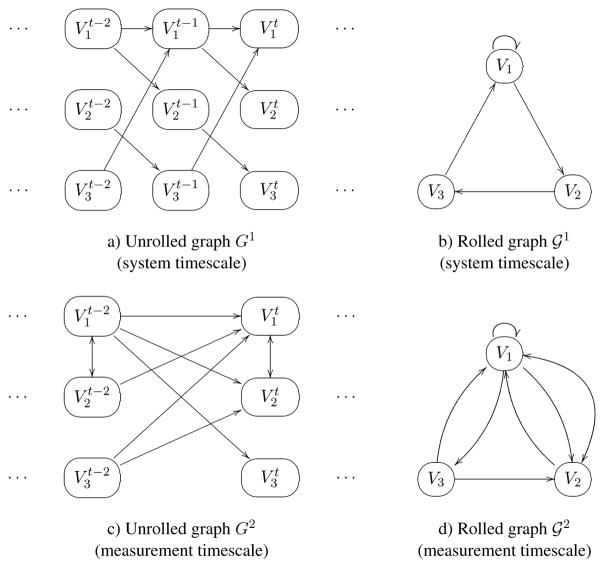
Time-series data has long constituted the basis for causal modeling in many fields of science (Granger, 1969; Hamilton, 1994; Lütkepohl, 2005). Despite the often very precise measurements at regular time points, the underlying causal interactions that give rise to the measurements often occur at a much faster timescale than the measurement frequency. While information about time order is generally seen as simplifying causal analysis, time series data that undersamples the generating process can be misleading about the true causal connections (Dash and Druzdzel, 2001; Iwasaki and Simon, 1994). For example, Figure 1a shows the causal structure of a process unrolled over discrete time steps, and Figure 1c shows the corresponding structure of the same process, obtained by marginalizing every second time step. If the subsampling rate is not taken into account, we might conclude that optimal control of V₂ requires interventions on both V₁ and V₃, when the influence of V₃ on V₂ is, in fact, completely mediated by V₁ (and so intervening only on V₁ suffices).

Figure 1.

Example graphs: a) G¹, b) 𝒢¹, c) G^u, d) 𝒢^u with subsampling rate u = 2.

Standard methods for estimating causal structure from time series either focus exclusively on estimating a transition model at the measurement timescale (e.g., Granger causality (Granger, 1969, 1980)) or combine a model of measurement timescale transitions with so-called “instantaneous” or “contemporaneous” causal relations that (are supposed to) capture any interactions that are faster than the measurement process (e.g., SVAR) (Lütkepohl, 2005; Hamilton, 1994; Hyvärinen et al., 2010). In contrast, we follow Plis et al. (2015a,b) and Gong et al. (2015), and explore the possibility of identifying (features of) the causal process at the true timescale from data that subsample this process.

In this paper, we provide an exact inference algorithm based on using a general-purpose Boolean constraint solver (Biere et al., 2009; Gebser et al., 2011), and demonstrate that it is orders of magnitudes faster than the current state-of-the-art method by Plis et al. (2015b). At the same time, our approach is much simpler and allows inference in more general settings. We then show how the approach naturally integrates possibly conflicting results obtained from the data. Moreover, unlike the approach by Gong et al. (2015), our method does not depend on a particular parameterization of the underlying model and scales to a more reasonable number of variables.

2. Representation

We assume that the system of interest relates a set of variables ${\mathbf{V}}^t=\{V_1^t,\dots ,V_n^t\}$ defined at discrete time points t ∈ ℤ with continuous (∈ ℝⁿ) or discrete (∈ ℤⁿ) values (Entner and Hoyer, 2010). We distinguish the representation of the true causal process at the system timescale from the time series data that are obtained at the measurement timescale. Following Plis et al. (2015b), we assume that the true between-variable causal interactions at the system timescale constitute a first-order Markov process; that is, that the independence V^t ⫫ V^t−k|V^t−1 holds for all k > 1. The parametric models for these causal structures are structural vector autoregressive (SVAR) processes or dynamic (discrete/continuous variable) Bayes nets. Since the system timescale can be arbitrarily fast (and causal influences take time), we assume that there is no “contemporaneous” causation of the form $V_i^t\to V_j^t$ (Granger, 1988). We also assume that V^t−1 contains all common causes of variables in V^t. These assumptions jointly express the widely used causal sufficiency assumption (see Spirtes et al. (1993)) in the time series setting.

The system timescale causal structure can thus be represented by a causal graph G¹ consisting (as in a dynamic Bayes net) only of arrows of the form $V_i^{t-1}\to V_j^t$, where i = j is permitted (see Figure 1a for an example). Since the causal process is time invariant, the edges repeat through t. In accordance with Plis et al. (2015b), for any G¹ we use a simpler, rolled graph representation, denoted by 𝒢¹, where V_i → V_j ∈ 𝒢¹ iff $V_i^{t-1}\to V_j^t\in G^1$. Figure 1b shows the rolled graph representation 𝒢¹ of G¹ in Figure 1a.

Time series data are obtained from the above process at the measurement timescale, given by some (possibly unknown) integral sampling rate u. The measured time series sample V^t is at times t, t − u, t − 2u, …; we are interested in the case of u > 1, i.e., the case of subsampled data. A different route to subsampling would use continuous-time models as the underlying system timescale structure. However, some series (e.g., transactions such as salary payments) are inherently discrete time processes (Gong et al., 2015), and many continuous-time systems can be approximated arbitrarily closely as discrete-time processes. Thus, we focus here on discrete-time causal structures as a justifiable, and yet simple, basis for our non-parametric inference procedure.

The structure of this subsampled time series can be obtained from G¹ by marginalizing the intermediate time steps. Figure 1c shows the measurement timescale structure G² corresponding to subsampling rate u = 2 for the system timescale causal structure in Figure 1a. Each directed edge in G² corresponds to a directed path of length 2 in G₁. For arbitrary u, the formal relationship between G^u and G¹ edges is

$$V_i^{t-u}\to V_j^t\in G^u\iff V_i^{t-u}⇝V_j^t\in G^1,\text{where}⇝\text{denotes}\mathrm{a}\text{directed}\text{path}.$$¹

Subsampling a time series additionally induces “direct” dependencies between variables in the same time step (Wei, 1994). The bi-directed arrow $V_1^t\leftrightarrow V_2^t$ in Figure 1c is an example: $V_1^{t-1}$ is an unobserved (in the data) common cause of $V_1^t$ and $V_2^t$ in G¹ (see Figure 1a). Formally, the system timescale structure G¹ induces bi-directed edges in the measurement timescale G^u for i ≠ j as follows:

$$V_i^t\leftrightarrow V_j^t\in G^u\iff \exists (V_i^t⇜V_c^{t-k}⇝V_j^t)\in G^1,k<u.$$

Just as 𝒢¹ represents the rolled version of G¹, 𝒢^u represents the rolled version of G^u: V_i → V_j ∈ 𝒢^u iff $V_i^{t-u}\to V_j^t\in G^u$ and V_i ↔ V_j ∈ 𝒢^u iff $V_i^t\leftrightarrow V_j^t\in G^u$.

The relationship between 𝒢¹ and 𝒢^u—that is, the impact of subsampling—can be concisely represented using only the rolled graphs:

$$V_i\to V_j\in {\mathcal{G}}^u\iff V_i\stackrel{u}{⇝}{V}_j\in {\mathcal{G}}^1$$ (1)

$$V_i\leftrightarrow V_j\in {\mathcal{G}}^u\iff \exists (V_i\stackrel{<u}{⇜}{V}_c\stackrel{<u}{⇝}{V}_j)\in {\mathcal{G}}^1,i\ne j$$ (2)

where $\stackrel{u}{⇝}$ denotes a path of length u and $\stackrel{<u}{⇝}$ denotes a path shorter than u (of the same length on each arm of a common cause). Using the rolled graph notation, the logical encodings in Section 3 are considerably simpler.

Danks and Plis (2013) demonstrated that, in the infinite sample limit, the causal structure 𝒢¹ at the system timescale is in general underdetermined, even when the subsampling rate u is known and small. Consequently, even when ignoring estimation errors, the most we can learn is an equivalence class of causal structures at the system timescale. We define ℋ to be the estimated version of 𝒢^u, a graph over V obtained or estimated at the measurement timescale (with possibly unknown u). Multiple 𝒢¹ can have the same structure as ℋ for distinct u, which poses a particular challenge when u is unknown. If ℋ is estimated from data, it is possible, due to statistical errors, that no 𝒢^u has the same structure as ℋ. With these observations, we are ready to define the computational problems focused on in this work.

Task 1

Given a measurement timescale structure ℋ (with possibly unknown u), infer the (equivalence class of) causal structures 𝒢¹ consistent with ℋ (i.e. 𝒢^u = ℋ by Eqs. 1 and 2).

We also consider the corresponding problem when the subsampled time series is directly provided as input, rather than 𝒢^u.

Task 2

Given a dataset of measurements of V obtained at the measurement timescale (with possibly unknown u), infer the (equivalence class of) causal structures 𝒢¹ (at the system timescale) that are (optimally) consistent with the data.

Section 3 provides a solution to Task 1, and Section 4 provides a solution to Task 2.

3. Finding Consistent 𝒢¹s

We first focus on Task 1. We discuss the computational complexity of the underlying decision problem, and present a practical Boolean constraint satisfaction approach that empirically scales up to significantly larger graphs than previous state-of-the-art algorithms.

3.1 On Computational Complexity

Considering the task of finding a single 𝒢¹ consistent with a given ℋ, a variant of the associated decision problem is related to the NP-complete problem of finding a matrix root.

Theorem 1

Deciding whether there is a 𝒢¹ that is consistent with the directed edges of a given ℋ is NP-complete for any fixed u ≥ 2.

Proof

Membership in NP follows from a guess and check: guess a candidate 𝒢¹, and deterministically check whether the length-u paths of 𝒢¹ correspond to the edges of ℋ (Plis et al., 2015b). For NP-hardness, for any fixed u ≥ 2, there is a straightforward reduction from the NP-complete problem of determining whether a Boolean B matrix has a uth root (Kutz, 2004)² for a given n×n Boolean matrix B, interpret B as the directed edge relation of ℋ, i.e., ℋ has the edge (i, j) iff A^u(i, j) = 1. It is then easy to see that there is a 𝒢¹ that is consistent with the obtained ℋ iff B = A^u for some binary matrix A (i.e., a uth root of B).

If u is unknown, then membership in NP can be established in the same way by guessing both a candidate 𝒢¹ and a value for u. Theorem 1 ignores the possible bi-directed edges in ℋ (whose presence/absence is also harder to determine reliably from practical sample sizes; see Section 4.3).

Knowledge of the presences and absences of such edges in ℋ can restrict the set of candidate 𝒢¹s. For example, in the special case where ℋ is known to not contain any bi-directed edges, the possible 𝒢¹s have a fairly simple structure: in any 𝒢¹ that is consistent with ℋ, every node has at most one successor.³ Whether this knowledge can be used to prove a more fine-grained complexity result for special cases is an open question.

3.2 A SAT-Based Approach

Recently, the first exact search algorithm for finding the 𝒢¹s that are consistent with a given ℋ for a known u was presented by Plis et al. (2015b); it represents the current state-of-the-art. Their approach implements a specialized depth-first search procedure for the problem, with domain-specific polynomial time search-space pruning techniques. As an alternative, we present here a Boolean satisfiability based approach. First, we represent the problem exactly using a rule-based constraint satisfaction formalism. Then, for a given input ℋ, we employ an off-the-shelf Boolean constraint satisfaction solver for finding a 𝒢¹ that is guaranteed to be consistent with ℋ (if such 𝒢¹ exists). Our approach is not only simpler than the approach of Plis et al. (2015b), but as we will show, it also significantly improves the current state-of-the-art in runtime efficiency and scalability.

We use here answer set programming (ASP) as the constraint satisfaction formalism (Niemelä, 1999; Simons et al., 2002; Gebser et al., 2011). It offers an expressive declarative modelling language, in terms of first-order logical rules, for various types of NP-hard search and optimization problems. To solve a problem via ASP, one first needs to develop an ASP program (in terms of ASP rules/constraints) that models the problem at hand; that is, the declarative rules implicitly represent the set of solutions to the problem in a precise fashion. Then one or multiple (optimal, in case of optimization problems) solutions to the original problem can be obtained by invoking an off-the-shelf ASP solver, such as the state-of-the-art Clingo system (Gebser et al., 2011) used in this work. The search algorithms implemented in the Clingo system are extensions of state-of-the-art Boolean satisfiability and optimization techniques which can today outperform even specialized domain-specific algorithms, as we show here.

We proceed by describing a simple ASP encoding of the problem of finding a 𝒢¹ that is consistent with a given ℋ. The input—the measurement timescale structure ℋ—is represented as follows. The input predicate node/1 represents the nodes of ℋ (and all graphs), indexed by 1 … n. The presence of a directed edge X → Y between nodes X and Y is represented using the predicate edgeh/2 as edgeh(X,Y). Similarly, the fact that an edge X → Y is not present is represented using the predicate no edgeh/2 as no edgeh(X,Y). The presence of a bidirected edge X ↔ Y between nodes X and Y is represented using the predicate confh/2 as confh(X,Y) (X < Y), and the fact that an edge X ↔ Y is not present is represented using the predicate no confh/2 as no confh(X,Y).

If u is known, then it can be passed as input using u(U); alternatively, it can be defined as a single value in a given range (here set to 1, …, 5 as an example):

urange(1..5). % Define a range of u:s
1 { u(U): urange(U) } 1. % u(U) is true for only one U in the range

Solution 𝒢¹s are represented via the predicate edge1/2, where edge1(X,Y) is true iff 𝒢¹ contains the edge X → Y. In ASP, the set of candidate solutions (i.e., the set of all directed graphs over n nodes) over which the search for solutions is performed, is declared via the so-called choice construct within the following rule, stating that candidate solutions may contain directed edges between any pair of nodes.

{ edge1(X,Y) } :- node(X), node(Y)

The measurement timescale structure 𝒢^u corresponding to the candidate solution 𝒢¹ is represented using the predicates edgeu(X,Y) and confu(X,Y), which are derived in the following way. First, we declare the mapping from a given 𝒢¹ to the corresponding 𝒢^u by declaring the exact length-L paths in a non-deterministically chosen candidate solution 𝒢¹. For this, we declare rules that compute the length-L paths inductively for all L ≤ U, using the predicate path(X,Y,L) to represent that there is a length-L path from X to Y.

% Derive all directed paths up to length U
path(X,Y,1) :- edge1(X,Y).
path(X,Y,L) :- path(X,Z,L-1), edge1(Z,Y), L <= U, u(U).

Second, to obtain 𝒢^u, we encode Equations 1 and 2 with the following rules that form predicates edgeu/2 and confu/2 describing the edges 𝒢¹ induces on the measurement timescale structure.

% Paths of length U, correspond to measurement timescale edges edgeu(X,Y) :- path(X,Y,L), u(L).
% Paths of equal length (<U) from a single node result in bi-directed edges confu(X,Y) :- path(Z,X,L), path(Z,Y,L), node(X;Y;Z), X < Y, L < U, u(U).

Finally, we declare constraints that require that the 𝒢^u represented by the edgeu/2 and confu/2 predicates is consistent with the input ℋ. This is achieved with the following rules, which enforce that the edge relations of 𝒢^u and ℋ are exactly the same for any solution 𝒢¹.

- edgeh(X,Y), not edgeu(X,Y).
- no_edgeh(X,Y), edgeu(X,Y).
- confh(X,Y), not confu(X,Y).
- no_confh(X,Y), confu(X,Y).

Our ASP encoding of Task 1 consists of the rules just described. The set of solutions of the encoding correspond exactly to the 𝒢¹s consistent with the input ℋ.

3.3 Runtime Comparison

Both our proposed SAT-based approach and the recent specialized search algorithm MSL (Plis et al., 2015b) are correct and complete, so we focus on differences in efficiency, using the implementation of MSL by the original authors. Our approach allows for searching simultaneously over a range of values of u, but Plis et al. (2015b) focused on the case u = 2; hence, we restrict the comparison to u = 2.

We simulated system timescale graphs with varying density and number of nodes (see Section 4.3 for exact details), and then generated the measurement timescale structures for subsampling rate u = 2. This structure was given as input to the inference procedures. Note that the input consisted here of graphs for which there always is a 𝒢¹, so all instances were satisfiable. The task of the algorithms was to output up to 1000 (system timescale) graphs in the equivalence class. The ASP encoding was solved by Clingo using the flag -n 1000 for the solver to enumerate 1000 solution graphs (or all, in cases where there were less than 1000 solutions).

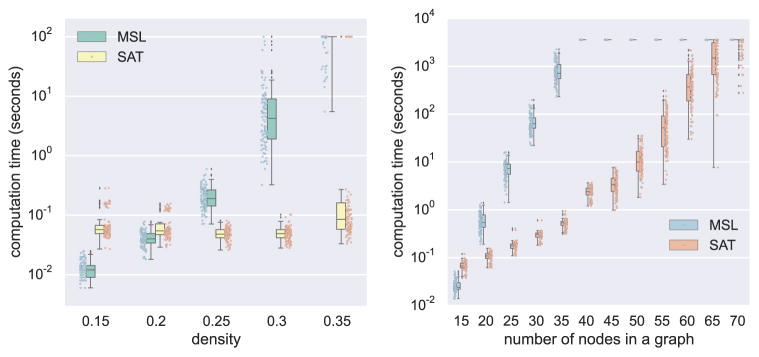
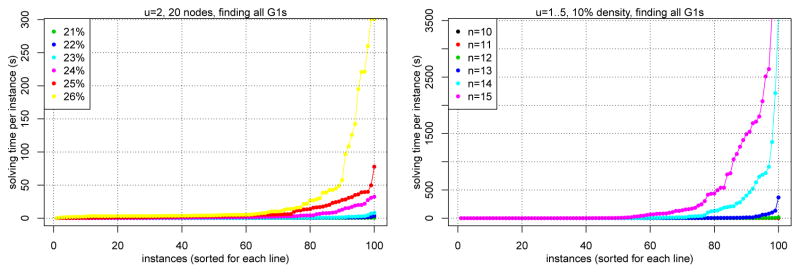
The running times of the MSL algorithm and our approach (SAT) on 10-node input graphs with different edge densities are shown in Figure 2. Figure 2 (right) shows the scalability of the two approaches in terms of increasing number of nodes in the input graphs and fixed 10% edge density. Our declarative approach clearly outperforms MSL. 10-node input graphs, regardless of edge density, are essentially trivial for our approach, while the performance of MSL deteriorates noticeably as the density increases. For varying numbers of nodes in 10% density input graphs, our approach scales up to 65 nodes with a one hour time limit; even for 70 nodes, 25 graphs finished in one hour. In contrast, MSL reaches only 35 nodes; our approach uses only a few seconds for those graphs. The scalability of our algorithm allows for investigating the influence of edge density for larger graphs. Figure 3 (left) plots the running times of our approach (when enumerating all solutions) for u = 2 on 20-node input graphs of varying densities. Finally, Figure 3 (right) shows the scalability of our approach in the more challenging task of enumerating all solutions over the range u = 1, …, 5 simultaneously. This also demonstrates the generality of our approach: it is not restricted to solving for individual values of u separately.

Figure 2.

Running times. Left: for 10-node graphs as a function of graph density (100 graphs per density and a timeout of 100 seconds); Right: for 10%-dense graphs as a function of graph size (100 graphs per density and a timeout of 1 hour).

Figure 3.

Left: Influence of input graph density on running times of our approach. Right: Scalability of our approach when enumerating all solutions over u = 1, …, 5.

4. Learning from Undersampled Data

Due to statistical errors in estimating ℋ and the sparse distribution of 𝒢^u in “graph space”, there will often be no 𝒢¹s that are consistent with ℋ. Given such an ℋ, neither the MSL algorithm nor our approach in the previous section can output a solution, and they simply conclude that no solution 𝒢¹ exists for the input ℋ. In terms of our constraint declarations, this is witnessed by conflicts among the constraints for any possible solution candidate. Given the inevitability of statistical errors, we should not simply conclude that no consistent 𝒢¹ exists for such an ℋ. Rather, we should aim to learn 𝒢¹s that, in light of the underlying conflicts, are “optimally close” (in some well-defined sense of “optimality”) to being consistent with ℋ. We now turn to this more general problem setting, and propose what (to the best of our knowledge) is the first approach to learning, by employing constraint optimization, from undersampled data under conflicts. In fact, we can use the ASP formulation already discussed—with minor modifications—to address this problem.

In this more general setting, the input consists of both the estimated graph ℋ, and also (i) weights w(e ∈ ℋ) indicating the reliability of edges present in ℋ; and (ii) weights w(e ∉ ℋ) indicating the reliability of edges absent in ℋ. Since 𝒢^u is 𝒢¹ subsampled by u, the task is to find a 𝒢¹ that minimizes the objective function:

$$f({\mathcal{G}}^1,u)=\sum _{e\in \mathcal{H}}I[e\notin {\mathcal{G}}^u]·w(e\in \mathcal{H})+\sum _{e\notin \mathcal{H}}I[e\in {\mathcal{G}}^u]·w(e\notin \mathcal{H}),$$

where the indicator function I(c) = 1 if the condition c holds, and I(c) = 0 otherwise. Thus, edges that differ between the estimated input ℋ and the 𝒢^u corresponding to the solution 𝒢¹ are penalized by the weights representing the reliability of the measurement timescale estimates. In the following, we first outline how the ASP encoding for the search problem without optimization is easily generalized to enable finding optimal 𝒢¹ with respect to this objective function. We then describe alternatives for determining the weights w, and present simulation results on the relative performance of the different weighting schemes.

4.1 Learning by Constraint Optimization

To model the objective function for handling conflicts, only simple modifications are needed to our ASP encoding: instead of declaring hard constraints that require that the paths induced by 𝒢¹ exactly correspond to the edges in ℋ, we soften these constraints by declaring that the violation of each individual constraint incurs the associated weight as penalty. In the ASP language, this can be expressed by augmenting the input predicates edgeh(X,Y) with weights: edgeh(X,Y,W) (and similarly for no edgeh, confh and no confh). Here the additional argument W represents the weight w((x → y) ∈ ℋ) given as input. The following expresses that each conflicting presence of an edge in ℋ and 𝒢^u is penalized with the associated weight W.

∼ edgeh(X,Y,W), not edgeu(X,Y). [W,X,Y,1]
∼ no_edgeh(X,Y,W), edgeu(X,Y). [W,X,Y,1]
∼ confh(X,Y,W), not confu(X,Y). [W,X,Y,2]
∼ no_confh(X,Y,W), confu(X,Y). [W,X,Y,2]

This modification provides an ASP encoding for Task 2; that is, the optimal solutions to this ASP encoding correspond exactly to the 𝒢¹s that minimize the objective function f(𝒢¹, u) for any u and input ℋ with weighted edges.

4.2 Weighting Schemes

We use two different schemes for weighting the presences and absences of edges in ℋ according to their reliability. To determine the presence/absence of an edge X → Y in ℋ we simply test the corresponding independence X^t−1 ⫫ Y ^t | V^t−1 \ X^t−1. To determine the presence/absence of an edge X ↔ Y in ℋ, we run the independence test: X^t ⫫ Y ^t | V^t−1.

The simplest approach is to use uniform weights on the estimation result of ℋ:

$$\begin{array}{llll}w(e\in \mathcal{H})\hfill & =\hfill & 1\hfill & \forall e\in \mathcal{H},\hfill \\ w(e\notin \mathcal{H})\hfill & =\hfill & 1\hfill & \forall e\notin \mathcal{H}.\hfill \end{array}$$

Uniform edge weights resemble the search on the Hamming cube of ℋ that Plis et al. (2015b) used to address the problem of finding 𝒢¹s when ℋ did not correspond to any 𝒢^u.

A more intricate approach is to use pseudo-Boolean weights following Hyttinen et al. (2014); Sonntag et al. (2015); Margaritis and Bromberg (2009). They used Bayesian model selection to obtain reliability weights for independence tests. Instead of a p-value and a binary decision, these types of tests give a measurement of reliability for an independence/dependence statement as a Bayesian probability. We can directly use their approach of attaching log-probabilities as the reliability weights for the edges. For details, see Section 4.3 of Hyttinen et al. (2014). Again, we only compute weights for the independence tests mentioned above in the estimation of ℋ.

4.3 Simulations

We use simulations to explore the impact of the choice of weighting schemes on the accuracy and runtime efficiency of our approach. For the simulations, system timescale structures 𝒢¹ and the associated data generating models were constructed in the following way. To guarantee connectedness of the graphs, we first formed a cycle of all nodes in a random order (following Plis et al. (2015b)). We then randomly sampled additional directed edges until the required density was obtained. Recall that there are no bidirected edges in 𝒢¹. We used Equations 1 and 2 to generate the measurement timescale structure 𝒢^u for a given u. When sample data were required, we used linear Gaussian structural autoregressive processes (order 1) with structure 𝒢¹ to generate data at the system timescale, where coefficients were sampled from the two intervals ±[0.2, 0.8]. We then discarded intermediate samples to get the particular subsampling rate.⁴

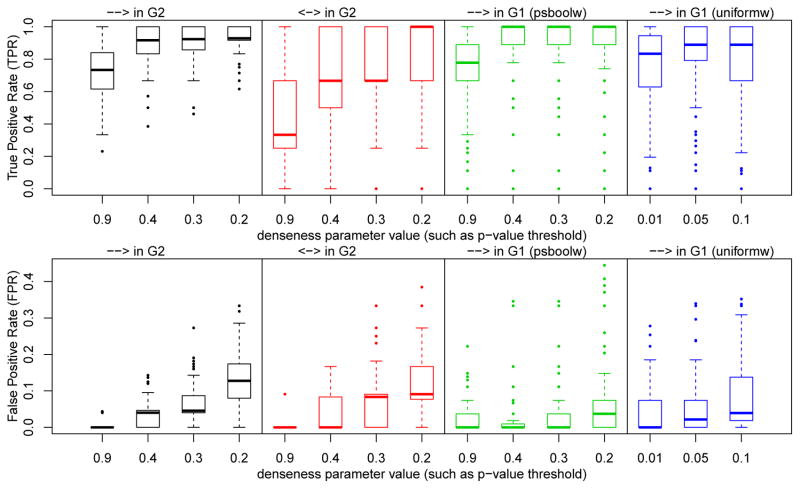
Figure 4 shows the accuracy of the different methods in one setting: subsampling rate u = 2, network size n = 6, average degree 3, sample size N = 200, and 100 data sets in total. The positive predictions correspond to presences of edges; when the method returned several members in the equivalence class, we used mean solution accuracy to measure the output accuracy. The x-axis numbers correspond to the adjustment parameters for the statistical independence tests (p-value threshold for uniform weights, prior probability of independence for all others). The two left columns (black and red) show the true positive rate and false positive rate of ℋ estimation (compared to the true 𝒢²), for the different types of edges, using different statistical tests. For estimation from 200 samples, we see that the structure of 𝒢² can be estimated with good tradeoff of TPR and FPR with the middle parameter values, but not perfectly. The presence of directed edges can be estimated more accurately. More importantly, the two rightmost columns in Figure 4 (green and blue) show the accuracy of 𝒢¹ estimation. Both weighting schemes produce good accuracy for the middle parameter values, although there are some outliers. The pseudo-Boolean weighting scheme still outperforms the uniform weighting scheme, as it produces high TPR with low FPR for a range of threshold parameter values (especially for 0.4).

Figure 4.

Accuracy of the optimal solutions with different weighting schemes and parameters (on x-axis). See text for further details.

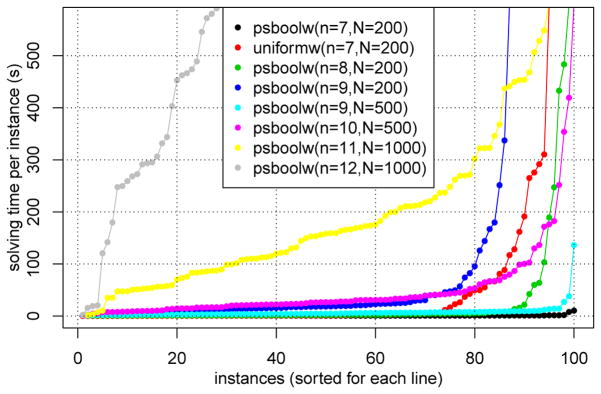
Finally, the running times of our approach are shown in Figure 5 with different weighting schemes, network sizes (n), and sample sizes (N). The subsampling rate was again fixed to u = 2, and average node degree was 3. The independence test threshold used here corresponds to the accuracy-optimal parameters in Figure 4. The pseudo-Boolean weighting scheme allows for much faster solving: for n = 7, it finishes all runs in a few seconds (black line), while the uniform weighting scheme (red line) takes tens of minutes. Thus, the pseudo-Boolean weighting scheme provides the best performance in terms of both computational efficiency and accuracy. Second, the sample size has a significant effect on the running times: larger sample sizes take less time. For n = 9 runs, N = 200 samples (blue line) take longer than N = 500 (cyan line). Intuitively, statistical tests should be more accurate with larger sample sizes, resulting in fewer conflicting constraints. For N = 1000, the global optimum is found here for up to 12-node graphs, though in a considerable amount of time.

Figure 5.

Scalability of our approach under different settings.

5. Conclusion

In this paper, we introduced a constraint optimization based solution for the problem of learning causal timescale structures from subsampled measurement timescale graphs and data. Our approach considerably improves the state-of-art; in the simplest case (subsampling rate u = 2), we extended the scalability by several orders of magnitude. Moreover, our method generalizes to handle different or unknown subsampling rates in a computationally efficient manner. Unlike previous methods, our method can operate directly on finite sample input, and we presented approaches that recover, in an optimal way, from conflicts arising from statistical errors. We expect that this considerably simpler approach will allow for the relaxation of additional model space assumptions in the future. In particular, we plan to use this framework to learn the system timescale causal structure from subsampled data when latent time series confound our observations.