Abstract
Background and Objective
When eye diseases are treated by topical administration, the success of treatment lies in the effective drug concentration in the target tissue. This is why the drug’s pharmacokinetic, in the different substructures of the eye, needs to be explored more accurately during drug development. The aim of the present analysis was to describe by rabbit model, the distribution of a drug after ocular instillation in the selected eye tissues and fluids.
Methods
By a top-down population approach, we developed and validated a population pharmacokinetics (PopPK) model, using tissue concentrations (tear, naso-lacrymal duct, cornea and aqueous humor) of a new src tyrosine kinase inhibitor (FV-60165) in each anterior segment’s tissue and fluid of the rabbit eye. Inter-individual variability was estimated and the impact of the formulation (solution or nanosuspension) was evaluated.
Results
The model structure selected for the eye is a 4-compartment model with the formulation as a significant covariate on the first-order rate constant between tears and the naso-lacrymal duct. The model showed a good predictive performance and may be used to estimate the concentration–time profiles after single or repeated administration, in each substructure of the eye for each animal included in the analysis.
Conclusions
This analysis allowed describing the distribution of a drug in the different selected tissues and fluids in the rabbit’s eyes after instillation of the prodrug as a solution or nanosuspension.
Key Points
| This study shows the benefit of the population approach to describe pharmacokinetics in non-clinical studies of ophthalmic drugs after topical administration. The pharmacokinetics modeling is a particularly added value to provide tailored answers with sparse data. |
| To improve the predictive performance of the models, sampling protocol must be optimized. When data are available, this approach could allow the prediction of drug concentrations in the target tissue (eye substructure) and the evaluation of drug efficacy. |
Introduction
The eye is a delicate organ extremely well protected by its anatomy, physiology and by systemic circulation (blood-aqueous and blood-retinal barriers). Owing to these features, a clinically relevant drug concentration is hardly reaching within the target ocular tissue following topical drug administration. Topical administration is the route of choice for the treatment of anterior segment diseases, most often with a local therapeutic effect. This route is non-invasive, painless and offers many advantages: fast effect, small dose required and not inducing systemic adverse effects. Topical bioavailability is, however, limited due to the precorneal loss factors increasing drug clearance and the cornea barrier limiting the distribution. All these factors contribute to the low bioavailability and low distribution of topically applied drugs and it is generally assumed that only 5 % or less of the instilled dose can effectively be distributed through the cornea [1, 2]. Describing pharmacokinetics in ocular target tissues is definitely a major challenge considering the eye complex anatomy and its dynamic physiological protection. During drug development, human pharmacokinetics is generally assessed after per os or intravenous administration by sampling plasma at different time points. But, for drugs administered by topical ocular route with a local therapeutic effect, the target tissues located in the eye can generally not be sampled. Exceptions are made in very rare cases of monitoring of drug levels in biopsies [3] or aqueous humor [4] collected from patients subjected to ophthalmic surgical procedures. That is why, for studying drugs distribution in ocular tissues, animal models are used. The ocular characteristics of these models permit to extrapolate to human pharmacokinetics. The rabbit remains the species of choice for the evaluation of ophthalmic compounds as this animal is easy to handle and provides a relatively reliable model for the evaluation of ocular kinetics [5]. We are developing a new src tyrosine kinase inhibitor (FV-60165, drug) investigated for the management of corneal neovascularization [6], which is a key step in stromal keratitis caused by Herpes Simplex Virus infection. To improve the therapeutic efficacy of drug candidates by improving its bioavailability, a prodrug strategy was retained and a lipophilic prodrug was designed. Due to its lipophilic nature, the prodrug (FV-80228, prodrug) can penetrate the corneal epithelium where enzymes hydrolyze it to the active hydrophilic compound (drug). The drug is then released into the stroma and, by diffusion, reaches the eye anterior chamber. Two formulations (solution or nanosuspension) were investigated during development process. The objective of this study was to describe a posteriori pharmacokinetics of our compound with a top-down population approach. Contrary to usual compartmental pharmacokinetic analyses [7, 8], population modeling allows estimating the individual drug penetration into different specific compartments of the eyes with only few samples. The present analysis aimed at developing and validating a population pharmacokinetic model able to predict the individual concentrations of the drug in selected ocular tissues and fluids. The inter-individual variability of all model parameters was planned to be assessed as well. It is worth emphasizing that this kind of methods would be helpful in preclinical drug development phase, in term of efficacy (predict the individual concentration available in the compartment of interest, here cornea) and safety (i.e., relationship between concentration in a compartment and side effect).
Materials and Methods
Animal studies and procedures of our laboratories comply with the Directive 2010/63/EU of the European parliament and the related French transposition texts. The experimental design was approved by the local “Comité d’Ethique pour la Protection des Animaux de Laboratoire” (Animal Care and Use Committee) and the study was performed in accordance with the internal Charter on the Humane Care and Use of Laboratory Animals.
Compounds
Drug (FV-60165) has following physico-chemical characteristics: MW = 450; Log P = 4.7 and Log D at pH 7.4 = 2.5. The prodrug (FV-80228) has following physico-chemical characteristics: MW = 554; Log P = 6.5 and Log D at pH 7.4 = 4.3. The prodrug is more lipophilic than the drug, thus penetrates the corneal epithelium where enzymes hydrolyze it to the active hydrophilic compound (drug).
Administration Protocol
Forty-two male HY79b pigmented rabbits (approximately 2–2.5 kg) were obtained from Hypharm-Roussay (France). All animals were housed individually in a temperature-controlled animal housing facility, with a 12 h light/night cycle and with free access to food and water. Prodrug was administered to animals. Two formulations were evaluated: a 0.6 % solution in 2-hydroxy-propyl-betacyclodextrine 7 % at pH 5, and a 0.6 % nanosuspension in 0.5 % carboxymethylcellulose 7 LFPH and 0.015 % tween 80 in phosphate buffered saline at pH 7.4. The rabbits were randomly assigned to two groups: those from “Group 1” (21 animals) received the solution and those from “Group 2” (21 animals) received the nanosuspension. Each rabbit received two 30 µL drops of either formulation into both eyes (with a 10-min interval between administrations of the first and of the second drop), corresponding to a total dose of prodrug of 720 μg per animal (2 × 180 μg/eye). The eye drops was instilled with a calibrated adjustable micropipette fitted with disposable tips into the lower conjunctival sac of the eye by pulling the lower lid away from the eyeball. After instillation, the upper and the lower lids were held together for a few seconds to avoid rapid removal of the eye drop from the ocular surface. Animals were observed for overall health and local tolerance to the formulations until the end of the study.
Sampling Protocol
At predetermined time-intervals after administration, animals (n = 3 per sampling time and per formulation) were anesthetized with an intramuscular injection of a mixture, ketamine/xylazine (25/5 mg/kg). Just before killing, tear fluid was collected from the left and the right eyes of each rabbit with Schirmer tear strips, and blood was collected by intracardiac puncture into tubes containing lithium heparin as anti-coagulant and processed to obtain plasma. Blood samples were obtained at 0.083, 0.25, 0.5, 1, 2, 4, and 8 h. The rabbits were killed immediately after blood sample extraction. Just after killing, the two eyes of each animal were removed and dissected to extract surgically the different eye substructures. Samples from cornea, aqueous humor, vitreous, choroid, retina and sclera were obtained from each eye. In parallel, the nasolacrimal duct was isolated from the skull. The ocular tissue and fluid samples were collected into pre-weighed, labeled cryotubes and then carefully weighed to determine the amount of each tissue (or fluid) collected. After collection, ocular samples were stored frozen until thawed for analysis. Concentration–time points of both prodrug and drug, were obtained from each matrix (tear fluid, naso-lacrymal duct, cornea and aqueous humor) after ocular instillation of the prodrug in rabbits. Standard pharmacokinetic parameters were calculated from the drug concentration in each matrix in each eye of each animal.
Analytical Methods
Each matrix is mixed with water and PMSF (Interchim) 30 mg/mL (10 % of the global weight) in Precellys 24 (Ozyme). An electrospray LC–MS/MS (LC system: Nexera X2, Shimadzu; MS/MS detector: API4000, AB Sciex) was used for prodrug and drug quantification in rabbit ocular tissue homogenates involving protein precipitation followed by chromatographic separation and tandem MS detection. The compounds were dissolved in DMSO and the working solutions for quality controls (QCs) and calibration curves were prepared separately in tubes acetonitrile, by successive dilutions. Stock and working solutions were stored at +5 ± 3 °C in their stability period (<24 days). 50 µL of ocular tissues homogenates for calibration standards and QCs was spiked with 5 µL of working solution. 150 µL of ACN was added. The tubes were capped, homogenized, centrifuged (10 min, 15,338 × g) and recovered in polypropylene 96 well-plates. The lower limit of quantification (LLOQ) of prodrug and drug was 0.5 ng/mL in plasma, 2 ng/mL in aqueous humor and 100 ng/mL in the tears with a range of quantification (RQ) of 0.5–100, 2–100, 100–10,000 ng/mL, respectively. For the cornea homogenate (dilution factor for homogenate = 1/6), the LLOQ was 1 ng/mL for the prodrug (RQ = [1–100 ng/mL]) and 10 ng/mL for the drug (RQ = [10–1000 ng/mL]). For the nasolacrimal duct homogenate (dilution factor for homogenate = 1/11) the LLOQ was 1 ng/mL for the prodrug (RQ = [1–100 ng/mL]) and 2.5 ng/mL for the drug (RQ = [2.5–1000 ng/mL]). Accuracy and precision fulfilled criteria used for drug determination in tissues using exploratory methods (<20 % except for LLOQ <25 %).
Population Pharmacokinetic Analysis
Analysis was performed using NONMEM (v 7.2.0, ICON Development Solutions, MD, USA). The different tissues (tear, naso-lacrymal duct, cornea, aqueous humor) were considered as different compartments. Because of its physiology, each eye was considered as an individual [8, 9]. So, a total of 84 individuals were considered in the dataset.
Pharmacostatistical Model (PSM)
In addition to the global multi-compartmental structure, many model configurations were tested, e.g., first-order rate constant or inter-compartmental clearance between the different compartments, a drug cleared or not from the naso-lacrymal duct, a drug cleared or not from the cornea, either fixed volumes of distribution at known physiological values to avoid an over-parameterization of the model or let free to be estimated by NONMEM. Regarding the nanosuspension formulation, two kinetics of administration situations were tested for nanosuspensions (1) administration with zero-order kinetic in the tear, in this case it would allow estimating the duration of the nanosuspension dissolution in the tear or (2) administration as a bolus as it was done for the solution. In the last case, the only way to take into account the formulation was to test it as a binary covariate on the relevant model parameters. The estimation of inter-individual variability (η) was evaluated using either a constant coefficient variation (CV) or proportional error model. The full non diagonal matrix (ω-block) and the different combinations of η correlations were evaluated as well as the possibility to fix some ω 2 to zero. The selection of a ω-block, if any, was made on the basis of the objective function value (OFV) decrease. Many algorithms were tested only one by one or by a combination. Given the complexity of the current model and the multi-compartmental structure, several differential equation solvers were evaluated. The model selection was performed on the basis of the knowledge of the eye structure, the minimization status (i.e., successful), the covariance phase (i.e., completed without any warning message), the absence of any correlation between parameter estimates larger than 0.95, the examination of standard error of the parameter estimates (i.e., ≤50 %), significant digit of the final parameter estimates (i.e., 3.0). The best pharmacostatistical model was selected based on the lowest OFV and the inspection of goodness of fits, i.e., population and individual weighted residuals (CWRES and IWRES), observed tissue concentrations (DV, for dependent variable) plots versus population and individual predicted concentrations (PRED and IPRED).
Handling of Topical Administration
In the current analysis, the distribution of the drug was analyzed after topical administration (2 × 30 µL of the prodrug). Given the fact that a maximum of only 10 µL could remain as administered in the tear (1/3rd of the administered dose was documented in the dataset) and based on the known huge inter-individual variability (linked to the naso-lacrymal and wink-mediated clearance), the fraction of drug that appears in the tears after prodrug administration (relative bioavailability in the tears: F 1) was also evaluated.
Covariate Screening
The only relevant covariate available in the current analysis is the formulation covariate. This covariate was tested on all the major parameters linked to the dissolution in the tears and to the distribution to the naso-lacrymal duct and to cornea. The significance of a parameter-covariate relationship was reflected by a decrease of OFV of at least 3.84 (p value <0.05 with one degree of freedom).
Final Model Validation
Depending on the method(s) retained in the selected final model, the standard error parameters’ estimates (SEE) were computed. SEEs were calculated as percentage of RSE (relative standard error, % RSE = 100 × SEE/parameter estimate). The individual predicted pharmacokinetic parameters were computed from the population parameters using all available sources of information (i.e., with individual covariates if any). Mean prediction error, and their associated 95 % CIs were also evaluated. The ηs were plotted against covariates to evidence a possible bias in covariate inclusion. Prediction-corrected visual predictive check (PcVPC) was used to evaluate the performance of the final model for each tissue compartment. The PcVPC method is based on 1000 simulations data from the model and the underlying design of the observed data [10]. As an improvement to the classical VPC, in the PcVPC, the variability coming from binning across independent variables was removed by normalizing the observed and simulated dependent variable based on the typical population prediction for the median independent variable in the bin [11].
Simulations were performed to predict for each rabbit eye, in each compartment, the full concentration–time profiles using the individual predicted model parameters, based on a single observed time point. To do this, additional virtual sampling was generated in the data set used to perform the simulations. In addition, to predict the tissue concentration–time profiles for a typical rabbit eye, simulations were performed using the estimated typical value for each model parameter, after topical administration of solution or nanosuspensions’ formulations.
Results
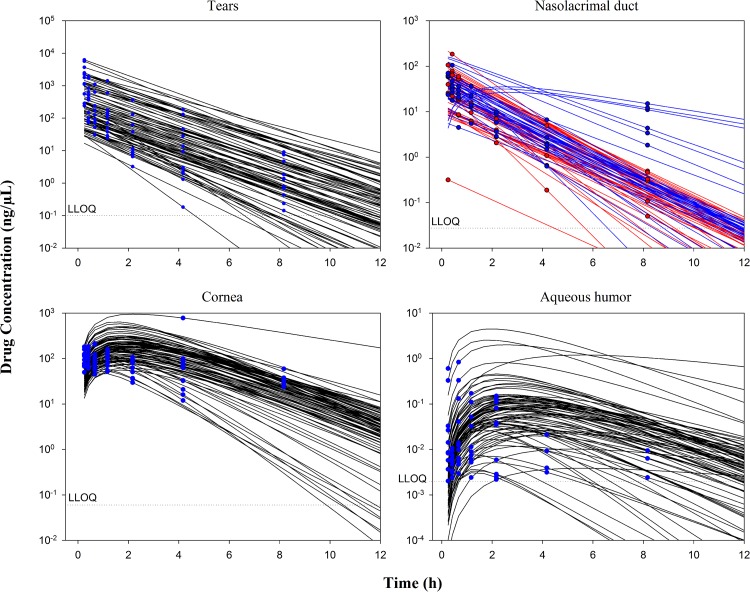
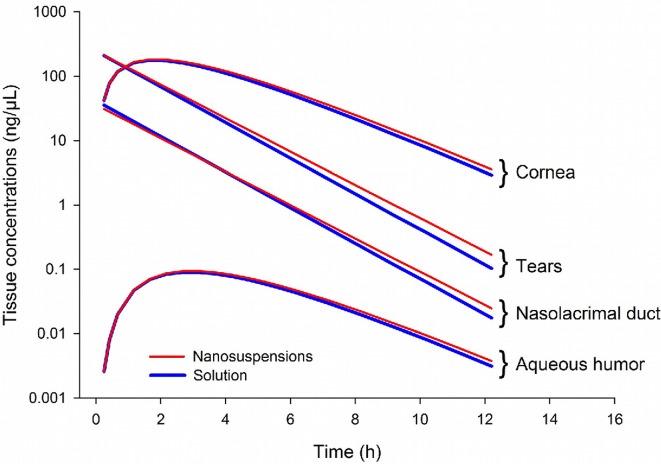
Most of the prodrug concentrations were below the LLOQ in plasma, ocular tissues and fluid samples, except in the tears (i.e., the site of drug administration) where the prodrug high concentrations was quantified. As expected, these results strongly suggested very quick hydrolysis of the prodrug into the drug in the tear fluid and cornea. Consequently, only the drug concentrations were documented in the data set and a total of 336 tissue drug concentrations values were collected. The multi-compartmental model structure of the eye finally selected in the current analysis is presented in Fig. 1. Describing the kinetic of administration of the nanosuspension as a zero-order administration in the tears, and the solution as a bolus administration was not successful. That is why the formulation was described as bolus administration in the tears for both formulations. Nevertheless, the quality of the results obtained with this model was not satisfactory: RSE % on volume of distribution of naso-lacrymal duct (V 2) was 52 % and on σ was 188 %. Consequently, the formulation was tested as a covariate on all the relevant model parameters and retained in the structural model on the first-order rate constant from the tears to naso-lacrymal duct (k 12) as follows: k 12 = θ i × FORMULATION + θ j × (1-FORMULATION). This choice improved the model quality criteria (RSE % on V 2 = 39.3 % and on σ = 107 %, with mean σ value of approximately 0.491 %). The proportional error model was selected to describe inter-individual variability. All the model parameters (F 1, k 12, k 13, V 1, V 2, V 3, Cl nl, Q, V 4, and Cl ah, see Table 1 for parameters definition) and the corresponding inter-individual variabilities, were fitted except the Cl c, fixed to 10 % of the Cl ah. This value was the result of an intensive sensitivity analysis (i.e., 25 runs launched with different fixed values of the Cl c as fraction of Cl ah from 0.1 to 2). This finding is consistent with the physiology (i.e., aqueous humor being a fluid with a higher turnover compared to the cornea tissue). None of the ω-block tested was selected, since they did not lead to any improvement of the model, and the diagonal matrix was therefore selected. Among the different models tested for residual variability, the model selected was the proportional error model for all compartments taken together leading to estimate only one σ. This was a logical outcome if we considered that the residual variability was linked to bioanalysis and that the analytical method was the same for all compartments. Among all the algorithms tested and previously mentioned, the classical FOCE-Interaction method followed by the MCMC Bayesian analysis method was selected and ADVAN13 subroutine was selected to solve the differential equations. The final model parameters were presented in Table 1. The final model was the PSM model, since the only covariate to be tested was the formulation as the latter was included straightaway in the structural model, to ensure higher model stability and better quality criteria. PRED and IPRED values were plotted versus DV in Fig. 2 to evaluate the global quality of the model fitting. This figure showed a good fit regarding both IPRED and PRED since all the weighted residuals were within the range [−4, +4] (Fig. 3), suggesting a good predictive performance of the model. The CWRES and IWRES were plotted versus PRED and IPRED, respectively, in Fig. 3. The model parameters’ estimates, their RSE % and 95 % CIs are presented in Table 1. All the percentage of RSE was lower than 20 %, except the RSE % of V 2 (population parameters of the volume of distribution of the naso-lacrymal duct) which was 39.3 % (lower than 50 %, so that the CI 95 % did not include zero) and of the proportional residual error which was 107 %. Nevertheless, the estimated proportional residual error was only about 0.491 %. The individual predicted pharmacokinetics parameters (P ind) were computed from the population parameters, using covariate included in the model (formulation on k 12). Mean prediction error of P ind toward the population predicted parameters (P pop) and their associated 95 % CIs are presented in Table 1. The results showed a slight, but significant mean prediction error for Cl ah, k 12, V 1, V 4, and for F 1. They showed no significant mean bias for Q, k 13, Cl nl, V 2, and V 3. PcVPC was used to evaluate the predictive performance of the final model at steady state. The results of the simulations performed are presented in Fig. 4 for each tissue compartment. Due to the huge range of concentration (0.0202–6260 ng/µL), Pc-VPC was represented in log scale. For each tissue compartment, all the observed concentration values were in the range of 5th to 95th percentile of predicted values from 1000 simulations using the final model. This PcVPC figure showed the good predictive performance of the model. In addition, the individual full concentration–time profiles predicted using the estimated individual model parameters, presented in Fig. 5, show the distribution behavior of the drug, in each compartment, for each rabbit eye used in the data set. Moreover, the predicted concentration–time profiles in each compartment, presented in Fig. 6, when considering a typical rabbit eye, after topical administration of solution or nanosuspensions’ formulations allow focusing on the predicted distribution of the drug in each compartment for each formulation, regardless of the inter-individual variability parameters.
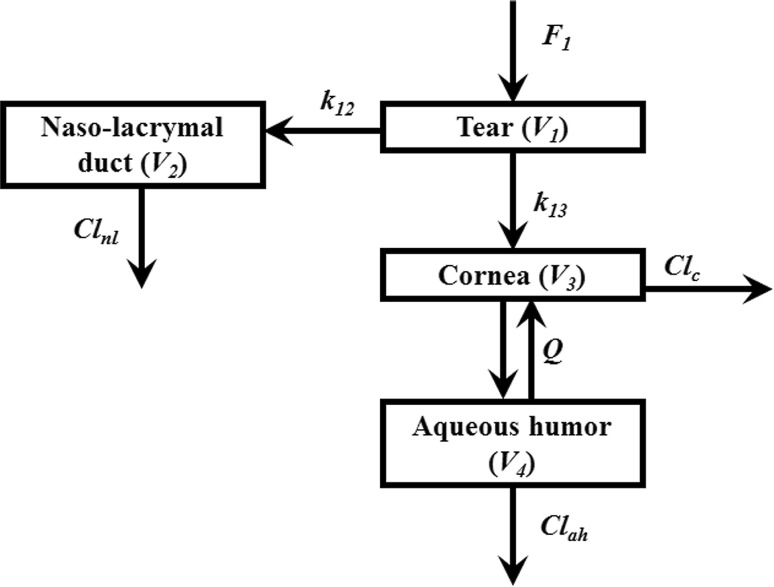
Fig. 1.
Multi-compartimental model of eye selected. F 1 relative bioavailability in the tears, k 12 (h−1) rate constant (tear to the naso-lacrymal duct) in nanosuspensions, k 12 (h−1) rate constant (tear to the naso-lacrymal duct) in solution, k 13 (h−1) rate constant (tear to cornea), Q (µL/h) inter-compartmental clearance (cornea/aqueous humor), Cl nl (µL/h) clearance from naso-lacrymal duct, Cl ah (µL/h) clearance from aqueous humor, Cl c clearance from cornea compartment = 0.1 × Cl ah, V 1 (µL) volume of distribution (tear), V 2 (µL) volume of distribution of naso-lacrymal duct, V 3 (µL) volume of distribution of cornea, V 4 (µL) volume of distribution of the aqueous humor
Table 1.
Final model: population parameters
| Parameter | Estimate | % RSE | [95 % CI] | Mean prediction error (%); [95 %CI] |
|---|---|---|---|---|
| F 1 | 0.300 | 6.65 | [0.260; 0.340] | 21.7 [10.4; 33.1] |
| k 12 (h−1) nanosuspensions | 0.259 | 12.1 | [0.197; 0.322] | −25.0 [−29.6; −20.4] |
| k 12 (h−1) solution | 0.299 | 12.6 | [0.224; 0.375] | −25.0 [−29.6; −20.4] |
| k 13 (h−1) | 0.340 | 5.28 | [0.304; 0.376] | 2.53 [−1.23; 6.29] |
| Q (µL/h)a | 0.136 | 19.8 | [0.0821; 0.190] | 32.2 [−2.45; 66.37] |
| Cl nl (µL/h)b | 275 | 9.87 | [220; 329] | 20.5 [−17.7; 58.7] |
| Cl ah (µL/h)c | 231 | 9.58 | [187; 274] | 13.8 [5.09; 22.5] |
| V 1 (µL) | 155 | 16.4 | [104; 206] | 39.7 [17.6; 61.9] |
| V 2 (µL) | 1.24 | 39.3 | [0.266; 2.22] | 93.1 [−11.0; 196] |
| V 3 (µL) | 42.8 | 5.54 | [38.1; 47.6] | 0.220 [−2.74; 3.18] |
| V 4 (µL) | 218 | 14.5 | [155; 282] | 29.4 [2.98; 55.7] |
| Estimate (%) | CV % | [95 % CI]—shrinkage % | ||
| Inter-individual variability | ||||
| F 1 | 60.5 | 17.6 | [48.7; 70.3]—1.97 | |
| k 12 | 80.0 | 18.3 | [63.8; 93.6]—91.5 | |
| k 13 | 45.3 | 16.7 | [37.0; 52.3]—59.7 | |
| Q | 172 | 17.3 | [139; 199]—17.8 | |
| Cl nl | 90.5 | 16.7 | [73.9; 104]—19.2 | |
| Cl ah | 92.0 | 16.9 | [74.9; 106]—74.4 | |
| V 1 | 153 | 17.0 | [124; 177]—47.4 | |
| V 2 | 437 | 18.4 | [347; 511]—60.6 | |
| V 3 | 51.1 | 18.2 | [40.8; 59.7]—98.5 | |
| V 4 | 265 | 18.6 | [210; 311]—81.8 | |
| Residual variability | ||||
| σ | 0.491 | 107 | [NA; 0.871]—99.8 | |
CI confidence interval, NA not applicable, F 1 relative bioavailability in the tears, k 12 (h−1) rate constant (tear to the naso-lacrymal duct) in nanosuspensions and in solution, k 13 (h−1) rate constant (tear to cornea), k 34 rate constant (cornea to aqueous humor, k 43 rate constant (from aqueous humor to cornea, k 20 elimination rate constant from naso-lacrimal duct, k 40 elimination rate constant from aqueous humor, Q (µL/h) inter-compartmental clearance (cornea/aqueous humor), Cl nl (µL/h) clearance from naso-lacrymal duct, Cl ah (µL/h) clearance from aqueous humor, V 1 (µL) volume of distribution (tear), V 2 (µL) volume of distribution of naso-lacrymal duct, V 3 (µL) volume of distribution of cornea, V 4 (µL) volume of distribution of the aqueous humor
a Q = k 34 × V 3 = k 43 × V 4
b Cl nl = k 20 × V 2
c Cl ah = k 40 × V 4
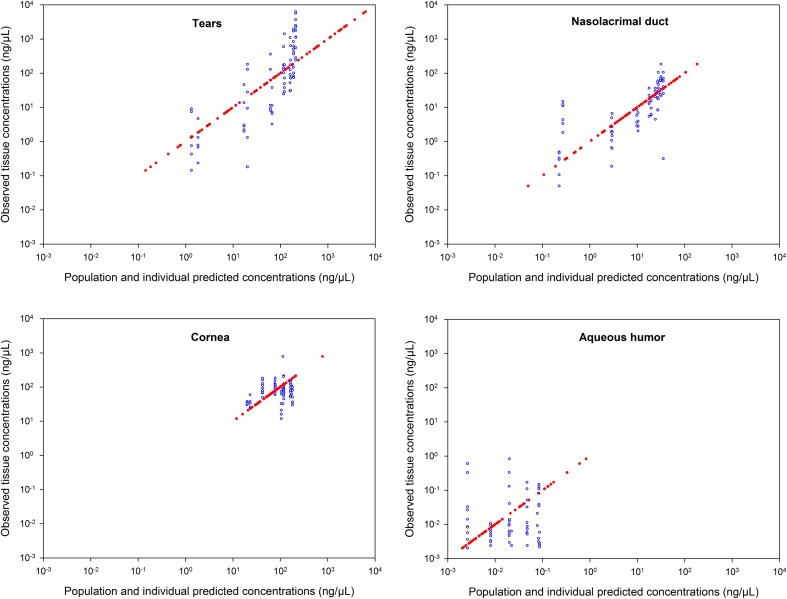
Fig. 2.
Relationship between individual predicted (IPRED, red solid dots) and population predicted (PRED, blue open circles) versus observed tissue concentrations in log–log scale in tears, nasolacrimal duct, cornea and aqueous humor
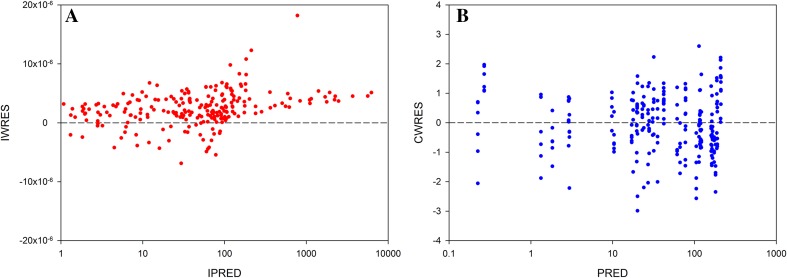
Fig. 3.
Relationship between individual weighted residuals (IWRES) and individual predicted concentrations in log scale (a); relationship between conditional weighted residuals (CWRES) and population predicted concentrations in log scale (b) from pooled data set (tears, nasolacrimal duct, cornea, and aqueous humor) of the 84 rabbit eyes
Fig. 4.
Prediction corrected visual predictive check of the final model (log scale) in the tears, in the nasolacrimal duct, in the cornea and in aqueous humor. Blue areas represent the 95 % CI of the 5th and 95th percentiles of the predictions; pink area represents the 95 % CI of the median of predictions; purple area represents the overlap between blue and pink areas; blue dots are observed tissue concentrations; solid red line represents the median of observations and dashed red lines represent the 5th and 95th percentiles of observations
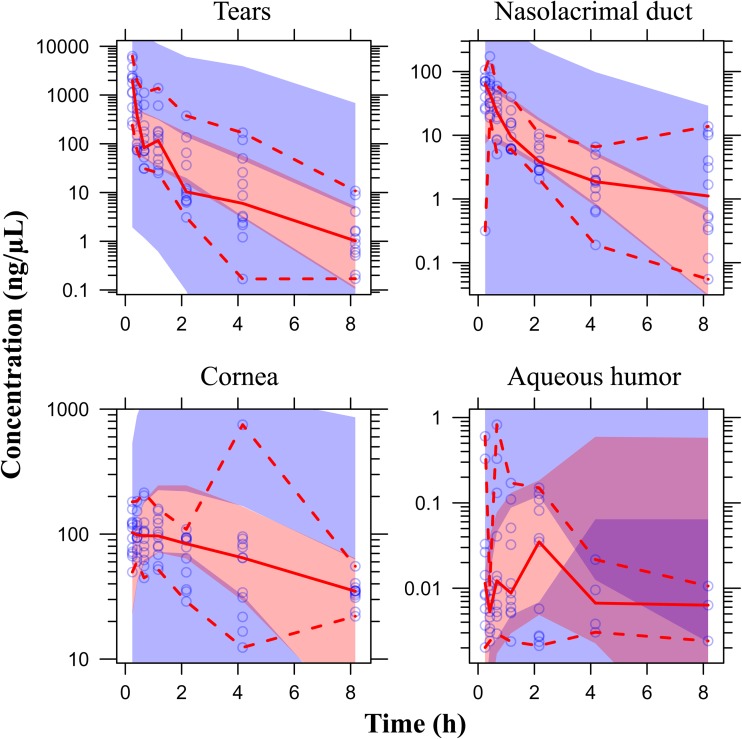
Fig. 5.
Predicted tissue concentration–time profiles (solid lines) and observed concentrations (dots) in the tears, nasolacrimal duct with solution formulation (red) and with nanosuspension formulation (blue), cornea and aqueous humor in each eye
Fig. 6.
Predicted tissue concentration–time profiles in the tears, nasolacrimal duct, cornea and aqueous humor for a typical rabbit eye with the solution or nanosuspensions
Discussion
The eyes are strongly protected against the environment and the systemic circulation by the blood-retinal barrier. Furthermore, after topical administration in the contralateral eye, each eye is considered as isolated [8, 9]. Therefore, each eye was considered as an individual and may be considered as a holistic multi-compartmental structure. The challenge of this work was (1) to develop and validate a population pharmacokinetic model able to predict the individual concentrations of a drug in each tissue of the anterior segment of the rabbit eye from the drug concentrations obtained in tears, cornea, naso-lacrymal duct and aqueous humor and (2) to determine the inter-individual variability of the model parameters. Furthermore, we needed to evaluate the impact of the formulation (solution or nanosuspension) on the drug pharmacokinetics. We developed and validated a PopPK model describing the pharmacokinetic of the drug in the different tissues of the anterior segment in the rabbit eye after topical administration of the prodrug. The model has good quality criteria for the prediction of ocular drug distribution over time. Overall, the estimated values for the PopPK model parameters were in the same magnitude as those published in the review of Worakol et al. [7] linked to the physiology of the rabbit eye: for instance, the published estimated clearance from the aqueous humor in the rabbit is approximately 3–4.7 µL/min (180–282 µL/h) while the PopPK model estimate we obtained was 231 µL/h for the Cl ah. Nevertheless, there is a probable perfect fit of the model to the data, illustrated by the very low IWRES of the drug together with the high η-shrinkage observed for some parameters (e.g., 74.4 % for Cl ah, 91.5 % for k 12, 98.5 % for V 3, and 81.8 % for V 4). These warnings regarding a probable perfect fit could suggest an over-parameterization of the model. However, the very low conditional number of 2.78, a numerical criterion that is usually higher than 1000 when the model is over-parameterized, mitigates this statement. The probable perfect fit and the high η-shrinkage observed are probably linked to the naive pooled nature of the data (only a single sampling time point per compartment was reported per eye) and to the intrinsic physiology of the eye requiring a structural model with numerous flow rates and volumes of distribution (i.e., estimation of many first-order rate constants k 12, k 13, k30, k34, k43, and k40 and volumes V 1, V 2, V 3, and V 4). A simplification of the structural model would have been an option to avoid the high η-shrinkage. However, given that the target tissue is the cornea and that it was important to estimate the individual concentrations in the target tissue, it would not have been possible to further simplify the structural model. Formulation’s inclusion led to an estimated mean population value for k 12 of 0.299 h−1 for the solution, and of 0.259 h−1 for the nanosuspension suggesting a low impact of the formulation on the drug tissue distribution. Cl nl was found to be the highest clearance for the drug which is a result consistent with physiological considerations. Because of the inherent difficulty in measuring concentrations in eye tissues and fluids (small size of the samples making difficult dissection and collection, and relatively low drug concentrations in these samples), pharmacokinetics/pharmacodynamics modeling may be used to anticipate on the results obtained in non-clinical studies of ophthalmic drugs. It is particularly of added value to provide fit-for-purpose pharmacokinetics/pharmacodynamics models when enough data is available. The warnings reported in the present analysis, could be addressed if the study has been designed according to the specifications of a population analysis. Nevertheless, the present modeling work has been performed retrospectively once pharmacokinetic data were provided. When the appropriate pharmacokinetics or pharmacodynamics data are available, this approach could allow the prediction of drug concentrations in the target tissue, the evaluation of efficacy and/or safety (e.g., change of the pharmacokinetics variable in the target tissue) and the identification of the impact of covariates on tissue distribution in specific populations (e.g., albino or pigmented rabbits and genetic polymorphisms). This is all the more interesting if there are more covariates to evaluate (in the present analysis, only the impact of the formulation was investigated). Based on simulations, this population pharmacokinetic model may be used to optimize sampling schemes in future experiments, and improve the predictive performance of subsequent population pharmacokinetic models. As shown in Fig. 5, concentration–time profiles were simulated in tears, naso-lacrymal duct, cornea and aqueous humor for each rabbit eye, using only a single sampling time point for each simulated profile. In addition, Fig. 6 shows the predicted tissue concentration–time profiles for a typical rabbit eye after solution and nanosuspensions’ formulations. Despite the statistically significant relationship between the formulation covariate and k 12, there was only a 13.4 % difference between the estimated typical value of k 12 between the two formulations (0.299 h−1 for the solution and 0.259 h−1 for nanosuspensions). In literature, only three cases of pharmacokinetic/pharmacodynamic models [12–14] were reported concerning drug pharmacokinetics in the eye after topical administration and none with PopPK model describing pharmacokinetics in ocular tissue samples. Pamulapati et al. [12] described pharmacokinetics with a three physiologically based compartmental model (cornea, aqueous humor and iris-ciliary body) with zero-order rate constant on cornea, but without including tears or the nasolacrimal compartment. In fact, Pamulapati choice of structural model may have a huge impact on pharmacokinetics after topical administration. For Sakanaka et al. [13, 14] pharmacokinetic parameters were estimated by a nonlinear least-squares computer program with six (for timolol) or seven (for bunazosin) compartmental model. The authors [12–14] used a naive pool data approach by considering the samples as collected from only one “mean” individual (no population approach assessed) closing the door to any estimation of inter-individual variability. We found only one published top-down analysis after topical administration of fluorescein in the human eye [15], based on in vivo fluorimetric measurements. Nevertheless, this measurement technique is not applicable to compounds during preclinical drug development stage. This model is in agreement with the pharmacokinetics principle of parsimony and, at the same time, allows adequate fitting of the data.
The challenge in ophthalmic pharmaceutical research is to optimize the pharmacokinetic parameters of drugs particularly in terms of bioavailability and distribution. Further simulations, based on the developed and qualified model for a particular compound, can be performed using specific dosing regimen or subpopulations of interest to answer specific questions linked to drug distribution. Rare cases concerning pharmacokinetic/pharmacodynamic modeling were reported in the literature. Even if the strategy of drug delivery is mainly based on pharmacokinetics [16, 17], little is known about drug distribution in the eye after topical application because only few analyses have been performed.
Conclusion
We developed and validated a PopPK model describing the pharmacokinetics of the drug in the different tissues of the anterior segment in the rabbit eye after topical administration of the prodrug. If optimized pharmacokinetic sampling schemes and relevant safety and efficacy data available, this approach could allow the prediction of drug concentrations in the target tissue, the evaluation of efficacy and/or safety (e.g., change of the pharmacodynamics variable in the target tissue) and the identification of the impact of covariates on tissue distribution in specific populations (e.g., albino or pigmented rabbits and genetic polymorphisms). This is all the more interesting if there are more covariates to evaluate (in the present analysis, only the impact of the formulation was investigated). Based on simulations, this population pharmacokinetic model may be used to optimize sampling schemes in future experiments, and improve the predictive performance of subsequent population pharmacokinetic models.
Acknowledgments
Many thanks to Serge Burgell, Christelle Carbonnier, Julien Fanelli, and Franck Pineau (Animal Study Conduct Team 1, Animal Research and Welfare) for their part in eye tissue collection, to Marilyn Calderone (Chemical Development, Lead Generation and Candidate Release) for her involvement in the formulations area and to Catherine Bougette (Shared Services, Disposition Safety and Animal Research) for her assistance in drafting.
Compliance with Ethical Standards
Funding
No sources of funding were received for the conduct of this study.
Conflicts of interest
ND, SK, FG, A-LC, AT, GF, CL and DF have no potential conflicts of interests to declare.
Ethical approval
The experimental design was approved by the local “Comité d’Ethique pour la Protection des Animaux de Laboratoire” (Animal Care and Use Committee) and the study was performed in accordance with the internal Charter on the Humane Care and Use of Laboratory Animals.
References
- 1.Shirasaki Y. Molecular design for enhancement of ocular penetration. J Pharm Sci. 2008;97(7):2462–2496. doi: 10.1002/jps.21200. [DOI] [PubMed] [Google Scholar]
- 2.Kaur IP, Kanwar M. Ocular preparations: the formulation approach. Drug Dev Ind Pharm. 2002;28(5):473–493. doi: 10.1081/DDC-120003445. [DOI] [PubMed] [Google Scholar]
- 3.Torkildsen G, O’Brien TP. Conjunctival tissue pharmacokinetic properties of topical azithromycin 1 % and moxifloxacin 0.5 % ophthalmic solutions: a single-dose, randomized, open-label, active-controlled trial in healthy adult volunteers. Clin Ther. 2008;30:2005–2014. doi: 10.1016/j.clinthera.2008.10.020. [DOI] [PubMed] [Google Scholar]
- 4.Schmitz K, Banditt P, Motschmann M, et al. Population pharmacokinetics of 2 % topical dorzolamide in the aqueous humor of humans. Invest Ophthalmol Vis Sci. 1999;40:1621–1624. [PubMed] [Google Scholar]
- 5.Del Amo EM, Urtti A. Rabbit as an animal model for intravitreal pharmacokinetics: clinical predictability and quality of the published data. Exp Eye Res. 2015;137:111–124. doi: 10.1016/j.exer.2015.05.003. [DOI] [PubMed] [Google Scholar]
- 6.Sharma S, Mulik S, Kumar N, et al. An anti-inflammatory role of VEGFR2/Src kinase inhibitor in HSV-1 induced immunopathology. J Virol. 2011;85(12):5995–6007. doi: 10.1128/JVI.00034-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Worakul N, Robinson JR. Ocular pharmacokinetics/pharmacodynamics. Eur J Pharm Biopharm. 1997;44:71–83. doi: 10.1016/S0939-6411(97)00064-7. [DOI] [Google Scholar]
- 8.Ranta VP, Urtti A. Transscleral drug delivery to the posterior eye: prospects of pharmacokinetic modeling. Adv Drug Deliv Rev. 2006;58:1164–1181. doi: 10.1016/j.addr.2006.07.025. [DOI] [PubMed] [Google Scholar]
- 9.Hughes PM, Olejnik O, Chang-Lin JE, et al. Topical and systemic drug delivery to the posterior segments. Adv Drug Deliv Rev. 2005;57:2010–2032. doi: 10.1016/j.addr.2005.09.004. [DOI] [PubMed] [Google Scholar]
- 10.Karlsson MO, Savic RM. Diagnosing model diagnostics. Clin Pharmacol Ther. 2007;82(1):17–20. doi: 10.1038/sj.clpt.6100241. [DOI] [PubMed] [Google Scholar]
- 11.Bergstrand M, Hooker AC, Wallin JE, et al. Prediction-corrected visual predictive checks for diagnosing nonlinear mixed-effects models. AAPS J. 2011;13(2):143–151. doi: 10.1208/s12248-011-9255-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pamulapati CR, Schoenwald RD. Ocular pharmacokinetics of a novel tetrahydroquinoline analog in rabbit: compartmental analysis and PK-PD evaluation. J Pharm Sci. 2012;101(1):414–423. doi: 10.1002/jps.22764. [DOI] [PubMed] [Google Scholar]
- 13.Sakanaka K, Kawazu K, Tomonari M, et al. Ocular pharmacokinetic/pharmacodynamic modeling for bunazosin after instillation into rabbits. Pharm Res. 2004;21(5):770–776. doi: 10.1023/B:PHAM.0000026426.20012.36. [DOI] [PubMed] [Google Scholar]
- 14.Sakanaka K, Kawazu K, Tomonari M, et al. Ocular pharmacokinetic/pharmacodynamic modeling for multiple anti-glaucoma drugs. Biol Pharm Bull. 2008;31(8):1590–1595. doi: 10.1248/bpb.31.1590. [DOI] [PubMed] [Google Scholar]
- 15.Abduljalil K, Diestelhorst M, Doroshyenko O, et al. Modelling ocular pharmacokinetics of fluorescein administered as lyophilisate or conventional eye drops. Eur J Clin Pharmacol. 2008;64(5):521–529. doi: 10.1007/s00228-007-0457-3. [DOI] [PubMed] [Google Scholar]
- 16.Gaudana R, Ananthula HK, Parenky A, et al. Ocular drug delivery. AAPS J. 2010;12(3):348–360. doi: 10.1208/s12248-010-9183-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kompella UB, Kadam RS, Lee VH. Recent advances in ophthalmic drug delivery. Ther Deliv. 2010;1(3):435–456. doi: 10.4155/tde.10.40. [DOI] [PMC free article] [PubMed] [Google Scholar]