The variability in beta‐cell function in placebo‐treated subjects with type 2 diabetes: application of the weight‐HbA1c‐insulin‐glucose (WHIG) model

Abstract

Aim

The weight‐glycosylated haemoglobin (HbA1C)‐insulin‐glucose (WHIG) model describes the effects of changes in weight on insulin sensitivity (IS) in newly diagnosed, obese subjects receiving placebo treatment. This model was applied to a wider population of placebo‐treated subjects, to investigate factors influencing the variability in IS and β‐cell function.

Methods

The WHIG model was applied to the WHIG dataset (Study 1) and two other placebo datasets (Studies 2 and 3). Studies 2 and 3 consisted of nonobese subjects and subjects with advanced type 2 diabetes mellitus (T2DM). Body weight, fasting serum insulin (FSI), fasting plasma glucose (FPG) and HbA1c were used for nonlinear mixed‐effects modelling (using NONMEM v7.2 software). Sources of interstudy variability (ISV) and potential covariates (age, gender, diabetes duration, ethnicity, compliance) were investigated.

Results

An ISV for baseline parameters (body weight and β‐cell function) was required. The baseline β‐cell function was significantly lower in subjects with advanced T2DM (median difference: Study 2: 15.6%, P < 0.001; Study 3: 22.7%, P < 0.001) than in subjects with newly diagnosed T2DM (Study 1). A reduction in the estimated insulin secretory response in subjects with advanced T2DM was observed but diabetes duration was not a significant covariate.

Conclusion

The WHIG model can be used to describe the changes in weight, IS and β‐cell function in the diabetic population. IS remained relatively stable between subjects but a large ISV in β‐cell function was observed. There was a trend towards decreasing β‐cell responsiveness with diabetes duration, and further studies, incorporating subjects with a longer history of diabetes, are required.

What is Already Known about this Subject

• Type 2 diabetes mellitus (T2DM) has a slow disease progression, which is associated with a gradual decline in β‐cell function.

• The weight‐glycosylated haemoglobin‐insulin‐glucose (WHIG) model describes the effects of placebo treatment on β‐cell function and insulin sensitivity in newly diagnosed, obese subjects with T2DM.

• It is not known whether the WHIG model can be applied to a wider population of people with T2DM.

What this Study Adds

• The WHIG model described the disease progression of T2DM in a wider population of subjects with T2DM, including subjects with advanced T2DM.

• The variability in insulin sensitivity was small but there was large interindividual variability in β‐cell function.

• Diabetes duration was not a significant covariate for the β‐cell parameters but a trend towards lower β‐cell function with diabetes duration was observed.

Table of Links

LIGANDS
Insulin

This Table lists key ligands in this article that are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY 1.

Introduction

Type 2 diabetes mellitus (T2DM) is characterized by hyperglycaemia due to insulin resistance and pancreatic β‐cell dysfunction. If T2DM is left untreated, people with T2DM are at risk of developing many microvascular and macrovascular complications 2. However, it is the continued deterioration in β‐cell function that undermines the long‐term effectiveness of many antidiabetic drugs to maintain euglycaemia 3. Therefore, it is not surprising that the goal in the treatment of T2DM has shifted from maintaining euglycaemia to delaying the progression of the disease by restoring or slowing the decline in β‐cell function 4, 5.

The function of pancreatic β‐cells cannot be measured directly, and methods to assess the changes in β‐cell function are required. Pancreatic β‐cells respond to high glucose concentrations by increasing the release of insulin from the pancreas. Therefore, the concentrations of fasting serum insulin (FSI) and fasting plasma glucose (FPG) can be used to reflect the balance between hepatic glucose output and insulin secretion, maintained by a feedback loop between the liver and the β‐cells 6. This relationship can be described mathematically using the homeostatic model assessment (HOMA) to estimate β‐cell function and insulin sensitivity (IS) in people with T2DM 6, 7.

There are two semi‐mechanistic models that have utilized the homeostatic relationship between FSI and FPG. The de Winter model 8 was first developed to describe the progression of T2DM in subjects treated with metformin, gliclazide or pioglitazone. Glycosylated haemoglobin (HbA1c), a marker of glucose exposure over 3 months, was also described in the model, and is influenced by the concentrations of FPG. This model was recently updated to the weight‐HbA1c‐insulin‐glucose (WHIG) model, to include the effect of weight on IS in placebo‐treated subjects 9, 10. In this study 9, a change in body weight was found to be a driver of IS, whereby a median weight loss of 4.1 kg was associated with a 30% increase in IS. Furthermore, the HbA1c model was expanded to include three transit compartments, to reflect the lifespan of the glycosylated red blood cells 9.

The WHIG model has only been evaluated in newly diagnosed, obese subjects who entered a weight loss program. These subjects represent a subset of the entire diabetic population and it is not known whether this model can be used to describe the changes in weight, IS and β‐cell function in the wider diabetic population. Therefore, the aim of the present study was to investigate the use of the WHIG model in a wider population of placebo‐treated subjects with T2DM and to examine factors that may influence the variability in the parameter estimates.

Methods

Datasets

Data from the placebo arms of three randomized, double blind, multicentre, placebo‐controlled phase II/III clinical trials in patients with T2DM were used, including the dataset used to build the WHIG model (Study 1 8). The study design for the placebo arms are described in Table 1. Study 1 included a weight loss component, while subjects from Studies 2 and 3 were maintained on a stable diet and exercise regimen. The study was conducted according to International Conference on Harmonization Good Clinical Practice guidelines, and applicable laws and regulations. Ethics approval was obtained from the institutional review board and informed written consent was obtained from each subject. The ClinicalTrials.gov identifiers for these studies are NCT0023660 (Study 1), NCT01071850 (Study 2) and NCT01117584 (Study 3).

Table 1.

The inclusion criteria and study design of the trials

	Study 1	Study 2		Study 3
N	181	59		64
ClinicalTrials.gov No.	NCT0023660	NCT01071850		NCT01117584
Disease status	Treatment naïve	Treatment naïve (n = 28) and prior treatment (n = 31)		Inadequately controlled on a daily dose of 1.5 g metformin (>6 weeks)
BMI ( kg m −2 )	27–50	20–45
HbA1c (%) a	<10.5	6.8–9.5		7.0–9.5
Diet and exercise regimen	600 kcal deficient diet and physical activity at all visits	Reported at stable diet and exercise regimen throughout the study
Study design
Trial duration	66 weeks	14 weeks
Washout phase	–	–	6 weeks	–
Placebo run‐in	6 weeks	2 weeks
Placebo treatment phase	60 weeks	12 weeks
Follow‐up phase	–	4 weeks

BMI, body mass index; HbA1c, glycosylated haemoglobin

^aAs measured at the first clinic visit

Study 1 included newly diagnosed, treatment naïve, obese subjects (n = 181) [body mass index (BMI) >27 kg m⁻² and <50 kg m⁻²], and investigated the effects of diet and exercise on weight loss and glucose control. Subjects first entered a 6‐week placebo run‐in before the placebo treatment phase. These subjects were followed for up to a total of 66 weeks.

Study 2 consisted of treatment‐naïve subjects (n = 29) and subjects who had previously been treated with an antidiabetic drug (n = 37). Subjects who had been previously treated entered a 6‐week washout phase, followed by a placebo run‐in phase (2 weeks) and placebo treatment phase (12 weeks). Treatment‐naïve subjects only entered the placebo run‐in phase and placebo treatment phase.

Study 3 included subjects (n = 65) who had been inadequately controlled on metformin (1500 mg daily, HbA1c >7%) for at least 6 weeks prior to the start of the study. In contrast to Study 2, these subjects did not enter a washout phase prior to the start of the study. This study also consisted of a 2‐week placebo run‐in, followed by a 12‐week placebo treatment phase.

Measurements of weight, FSI, FPG and HbA1c

The timing and frequency of weight measurements and the collection of FSI, FPG and HbA1c samples are shown in Table S1 and S2. In all studies, weight was measured at every clinic visit. For Study 1, up to 22 weight measurements were recorded, while for Studies 2 and 3 seven measurements were taken from each subject.

FSI was measured less frequently than the other glycaemic markers. In Study 1, there were up to four, and in Studies 2 and 3 five, observations of FSI for each subject. In Study 1, there were 18 measurements of FPG and 19 measurements of HbA1c from each subject, compared with seven and six measurements, respectively, in Studies 2 and 3. Subjects who had received prior treatment in Study 2, had an additional measurement of weight, FSI, FPG and HbA1c during the 6‐week washout phase.

The WHIG model

The WHIG model 9 is shown in Figure S1. This model consists of a turnover model for body weight, a closed‐form solution for FSI and FPG with steady‐state assumptions, and three transit compartments for HbA1c 9. The equations relevant to the present study (treatment effects, IS and β‐cell function) are outlined below. Glucose–insulin homeostasis was modelled as a feedback mechanism between FSI and FPG, and these equations are shown in Supplementary Results (NONMEM control stream).

Dynamics of body weight

A turnover model was used to describe the dynamics of body weight (Figure S1). The effects of diet and exercise counselling, and placebo treatment on body weight were modelled as two step‐functions: a treatment effect of diet and exercise counselling at screening (EF_DE , t > 0) and a placebo treatment effect at the start of the placebo treatment phase (EF_PL, t > placebo run‐in phase). EF_DE and EF_PL were expressed as a relative change from baseline. The treatment effects of placebo, diet and exercise, however, can wear off with time. A linear function describing the rate of treatment loss (EF_LOSS) was added, to describe the wearing off of treatment effects with time (Eq. (1)). The net treatment effect on body weight (EF_W, Eq. (1)) was modelled on the input side of the turnover model of body weight (Eq. (2)).

$${\mathit{EF}}_W=\frac{\left(100-\left({\mathit{EF}}_{\mathit{DE}}+{\mathit{EF}}_{\mathit{PL}}\right)\right)}{100}\times \frac{\left(100+\left({\mathit{EF}}_{\mathit{\text{LOSS}}}\times \raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$365$}\right.\right)\right)}{100}$$ (1)

$$\raisebox{1ex}{$\mathit{\text{dWGT}}$}\!\left/ \!\raisebox{-1ex}{$\mathit{dt}$}\right.={\mathit{WGT}}_{\mathit{kin}}\times {\mathit{EF}}_W-{\mathit{WGT}}_{\mathit{\text{kout}}}\times \mathit{WGT}$$ (2)

where t is time in days.

IS

The dynamics of IS are driven proportionally by the change in body weight (∆WGT). The effect of weight change on IS (EF_S, Eq. (3)) was scaled with a scaling factor (Scale _EFS):

$${\mathit{EF}}_S=1+{\mathit{\text{Scale}}}_{\mathit{EFs}}\times ∆\mathit{WGT}$$ (3)

∆WGT was calculated as the difference between the baseline weight and the current weight. At baseline (t = 0), the value of EF_S is 1. A reduction in weight from baseline will increase IS (EF_S >0), while an increase in weight will result in a decrease in IS (EF_S <0).

The IS was then calculated using the estimated baseline IS as a logit function (s₀):

$$\mathit{\text{IS}}=\frac{1}{1+{\mathit{exp}}^{\left(s_0\right)}}\times {\mathit{EF}}_S$$ (4)

Dynamics of β‐cell function

The dynamics of β‐cell function was modelled as the result of two components: a disease progression component (BF) and a treatment effect (EF_B). BF is a logistic decay function to describe the natural deterioration in β‐cell function from baseline (Eq. (5)). It consists of parameters to estimate the baseline β‐cell function (b₀) and the rate of β‐cell decline per year from baseline (r_B):

$$\mathit{BF}=\frac{1}{\left(1+{\mathit{exp}}^{\left(b_0+r_B\times t/365\right)}\right)}$$ (5)

where t is time in days. b₀, like s_0, provides an indicator of the disease status of subjects at study entry. The parameter r_B can have either a positive or negative value to indicate either a decline in β‐cell function with time, or an improvement in β‐cell function over time.

In the WHIG model, the treatment effect, EF_B, was estimated empirically and was modelled with a logistic increase and decline to describe the initial improvement and subsequent decline in β‐cell function due to the effect of weight loss 9. As Studies 2 and 3 were short trials, this treatment effect was simplified to a step function (Eq. (6)):

$${\mathit{EF}}_B=1+{\mathit{EF}}_{\mathit{BT}}\times {\mathit{OC}}_1$$ (6)

where EF_BT is the estimated treatment effect and OC₁ is a parameter to switch on the treatment effect. At baseline (t = 0), OC₁ = 0 to indicate no treatment effect (EF_B = 1). At t > 0, OC₁ takes the value of 1 to switch on the effect of placebo treatment on β‐cell function.

A limitation of using the step function is that the treatment effect remains constant throughout the duration of the study, and changes in the treatment effect with time cannot be described. The overall effect of β‐cell function on FSI production is a function of BF and EF_B (Eq. (7)):

$$B=\mathit{BF}\times {\mathit{EF}}_B$$ (7)

Dynamics of HbA1c

There are three transit compartments for HbA1c. The first transit compartment is shown in Eq. (8) and the remaining transit compartments can be seen in the NONMEM control stream (see Supporting information). Postprandial glucose (PPG) was not measured; however, it may contribute to the production of HbA1c in addition to FPG. The potential contribution of PPG, therefore, was estimated. At t > 0, the effect of PPG was scaled by a scaling parameter (Scale_PPG, Eq. (8)).

$$\raisebox{1ex}{$\mathit{\text{dHbA}}1c\left(1\right)$}\!\left/ \!\raisebox{-1ex}{$\mathit{dt}$}\right.={\mathit{HbA}1c}_{\mathit{kin}}\times \mathit{PPG}\times {\mathit{\text{Scale}}}_{\mathit{PPG}}\times \mathit{FPG}–{\mathit{HbA}1c}_{\mathit{\text{kout}}}$$ (8)

The mean transit time (MTT) of HbA1c is estimated and the rate constant of HbA1c elimination (HbA1c_kout) was calculated as $\frac{3}{\mathit{MTT}}$.

Population analyses

Population pharmacodynamic analyses were conducted using the population modelling package NONMEM® 7.2.0 (ICON Development Solutions, Hanover, MD, USA) 11, using the first‐order conditional estimation method with interaction (FOCE‐I). Model development was managed using Perl‐Speaks‐NONMEM 3.5.3 (Uppsala, Sweden) 12, Pirana 2.8.1 (Amsterdam, The Netherlands) 13 and R (Version 3.2.5, Vienna, Austria) 14. All observations were log‐transformed prior to the analysis and residual variability was described with proportional error models for weight, FSI, FPG and HbA1c. The interindividual variation (IIV) for PPG, Scale_EFs, baseline weight and residual error models were log‐normally distributed, while all other parameters were assumed to be normally distributed. As the structure of the model was already developed, the model‐building procedure included: (i) exploratory data analysis and data exclusion; (ii) sensitivity analyses; (iii) covariate modelling; and (iv) model evaluation.

• i Exploratory data analysis and data exclusion. For Studies 2 and 3, some observations and subjects were excluded from the analyses, to avoid bias. The reference range for FSI is below 25 mI U l⁻¹ 15. There was one outlying FSI observation, of 343 mI U l⁻¹, indicating noncompliance with the fasting protocol. This FSI observation and the corresponding FPG were excluded from the analyses.

There were two subjects who terminated the trial on the second visit (18 days) and three subjects with only one FSI observation. These individuals were excluded from the analyses. In total, only 1% of the original dataset was excluded, to avoid bias in parameter estimates. After removing these observations, the median FSI of the dataset was 14.8 mI U l⁻¹ (range 2.7–99.8 mI U l⁻¹).

In one arm of Study 2, subjects entered a 6‐week washout phase; however, there was only one observation collected during this phase. Therefore, observations during this phase were not used for model development.

• Sensitivity analyses. Sensitivity analyses were conducted on various system‐specific parameters that were considered difficult to estimate in Studies 2 and 3. β‐cell function (B, Eq. (7)) involves both estimating the natural decline in β‐cell function from baseline (BF, Eq. (5)), and the positive treatment effect on β‐cell function (EF_B, Eq. (6)). One of the main parameters that is difficult to estimate is r_B, the rate of β‐cell function decline from baseline. The effect of fixing the population estimate of r_B to a published value of 0.209 9 and estimating r_B was tested.

Additionally, a sensitivity analysis was conducted on EF_B, the treatment effect on β‐cell function, as it can confound the estimate of r_B. Subjects from Studies 2 and 3 did not enter a weight loss program, so estimates of EF_B are likely to be too small or insignificant to counteract the rate of disease progression (r_B). The effect of removing EF_B to improve the estimate of r_Bwas tested.

Lastly, MTT was considered difficult to estimate owing to the short trial duration of Studies 2 and 3. Therefore, the effect of fixing MTT to a previously published value of 38.9 days 9 and estimating this parameter was tested.

• Covariate modelling. Potential covariate effects were identified by visual inspection of covariate plots against the empirical Bayes estimates (EBEs). Statistical significance was determined by stepwise inclusion into the model, and was guided by the objective function value (OFV, −2log likelihood), whereby a significance level of P < 0.01 was considered statistically significant (corresponding to drop in OFV by 6.63 points with d.f. = 1) 16. The covariates investigated included age, gender, ethnicity, diabetes duration and compliance with placebo treatment (by pill count), for parameters describing the treatment effect (EF_DE, EF_PL, EF_B) and parameters describing the disease status (b₀, s₀, r_B). The duration of diabetes was not known for subjects enrolled in Study 1, and therefore was assumed to be 1 year to enable diabetes duration to be tested as a covariate in the model.

The potential covariate effect of diabetes duration was investigated visually using EBE plots vs. diabetes duration for Studies 2 and 3. The disposition index was used to explore potential relationships between model‐derived estimates of b₀ and s₀ and diabetes duration. The disposition index is the hyperbolic relationship between IS and β‐cell function (or insulin secretion), whereby a decrease in IS (high FPG) is compensated by an increase in β‐cell function, to stimulate insulin release 17.

The baseline values of body weight, FPG, FSI and HbA1c were tested as potential covariates on the parameters describing the treatment effect. The transformation of random effect parameters 18 were investigated for the random effect variables that were non‐normally distributed.

Sources of interstudy variability (ISV) were investigated by inspecting plots of EBEs vs Study. As Study 3 did not include a washout phase, it is possible that residual treatment effects of metformin continued in this placebo study. This was further investigated by testing ISV as a fixed effect on baseline parameters (weight, FPG, FSI and HbA1c), i.e. on parameters describing the treatment effect (EF_DE, EF_PL, EF_B) and the disease status (b₀, s₀, r_B).

• Model evaluation and statistical methods. Model selection was guided by a significant drop in OFV (P < 0.01), goodness‐of‐fit plots and visual predictive checks (VPCs). Model stability was assessed by the ability of the model to achieve a successful covariance step and a low condition number (<1000 19). The condition number is calculated as the square root of the ratio of the largest eigenvalue to the smallest eigenvalue of the correlation matrix to evaluate collinearity of the parameters 19. The VPC of the final model was evaluated by comparing the 10th, 50th and 90th percentiles of the observations with the corresponding 10th, 50th and 90th percentiles of the simulations (n = 1000) 20.

Significant differences between baseline measurements were evaluated using the unpaired t‐test in R. A P value of <0.001 was considered statistically significant.

Results

Characteristics of the subjects

The demographics of the subjects from each study are shown in Table 2. There were significant differences in the body weight distribution for all three studies (Figure 1). Subjects from Study 1 had a higher baseline body weight compared with Study 2 (median difference 24.1 kg) and Study 3 (median difference 14.8 kg). The distribution of height and BMI, however, was comparable between studies. At baseline, the insulin‐to‐glucose ratio was lower in Studies 2 and 3 compared with Study 1 (Table 2, Figure 1), indicating that subjects from Studies 2 and 3 had a poorer β‐cell function. Furthermore, subjects enrolled in Study 3 had a longer duration of diabetes than those in Study 2 (median difference 3.1 years).

Table 2.

Baseline characteristics and estimates of subjects from each study. Data are medians (interquartile ranges)

	Study 1	Study 2	Study 3
N	181	66	65
Age (years)	54 (48–60)	55 (48–60)	57 (51–63)
% Female	63	56	45
Height (m)	1.68 (1.62–1.77)	1.61 (1.56–1.68)	1.68 (1.60–1.73)
BMI ( kg m −2 )	31.8 (29.1–35.6)	29.6 (26.6–33.8)	31.0 (28.9–34.2)
Baseline measurements
Weight (kg)	104.2 (94.3–115.4)	79.3 (68.6–87.9)	89.0 (81.2–97.6)
FSI (μU ml −1 )	17.8 (12.3–27.4)	12.1 (8.2–18.2)	13.4 (9.1–21.6)
FPG (mmol l −1 )	7.6 (7.0–8.5)	7.2 (6.3–8.6)	8.5 (7.4–10.1)
HbA1c (%)	6.7 (6.3–7.2)	7.4 (7.1–7.9)	7.7 (7.2–8.2)
Insulin/glucose ratio	2.27 (1.69–3.01)	1.51 (1.04–2.18)	1.47 (1.10–2.44)
Diabetes duration (years) a	–	2.7 (1.3–4.6)	5.8 (2.9–8.8)

BMI, body mass index; FPG, fasting plasma glucose; FSI, fasting serum insulin; HbA1c, glycosylated haemoglobin

^aDiabetes duration is not known for Study 1

Figure 1.

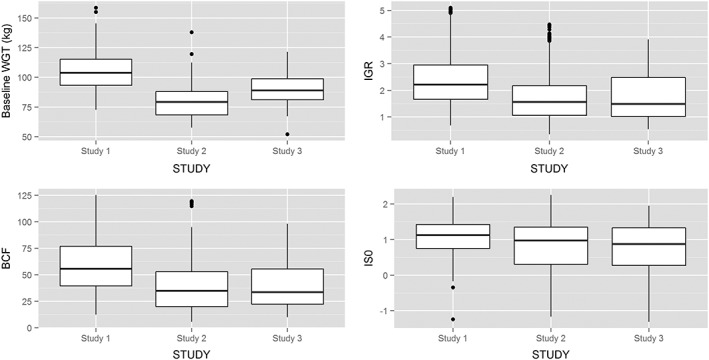
Interstudy variability in placebo arms (Study 1, Study 2 and Study 3). IGR, insulin/glucose ratio; B, β‐cell function; IS, insulin sensitivity

Population model

A total of 8587 observations from Study 1, 1526 observations from Study 2 and 1554 observations from Study 3 were used for population pharmacodynamic modelling. As with the WHIG model, a full omega block (n = 10) was used to account for all correlations between parameters (Table S3). The covariance between the residual error of FSI and FPG was also estimated.

An ISV on weight was modelled to show a shift in the population mean for each study. From the base model, this was found significantly to improve the model (ΔOFV −88.03 points). An ISV was also added for b₀ (Study 1 vs. Studies 2 and 3), which was also significant (ΔOFV −88.9 points). The IIV for s₀ was non‐normally distributed and was transformed using the Box–Cox transformation 18 to improve the model (ΔOFV −44.2 points, P < 0.001):

$${\eta }_{\mathit{st}}=\frac{\left[{\left({\mathit{exp}}^{{\eta }_{s_0}}\right)}^{{\theta }_{sh\mathit{ape}}}-1\right]}{{\theta }_{sh\mathit{ape}}}$$ (9)

where η_st is the Box–Cox transformed random effect for s₀, η _so is the normally distributed random effect and θ_shape is a parameter determining the shape of the distribution. Age, diabetes duration, gender and ethnicity were not significant covariates for these baseline parameters.

In the WHIG model, there were two treatment effects on weight, in the placebo run‐in phase and the treatment phase. These treatment effects were maintained for Study 1. However, the additional placebo effect during the treatment phase for Studies 2 and 3 was not significant and was removed from the model. The lack of a washout phase in Study 3 did not influence the parameter estimates of treatment effects and disease status. An ISV was added for baseline weight but this was also added for Study 2.

Compliance with placebo pills was explored as a potential covariate on the treatment effects for weight (EF_DE). For Studies 2 and 3, the median compliance was 99.8% (range 61.3–100%) and 100% (range 87.1–100%), respectively. However, overall compliance with placebo treatment was not a significant covariate for the treatment effects on weight. The effect of prior treatment in Studies 2 and 3 was also investigated as a covariate on the treatment effects (EF_DE, EF_B) but it did not result in an improvement in the model.

Parameter estimates

When estimated, the MTT parameter increased from 38.9 days to 53 days, corresponding to a 26% lower estimate of HbA1c_kout (from 0.0771 to 0.0566) and OFV decreased by 32.9 points (P < 0.001). This resulted in approximately 20–30% lower estimates of the effect of postprandial glucose (PPG) and an increase of 23% on the estimate of EF_B (treatment effect on β‐cell function). Therefore, estimating MTT not only indicates a slower glycosylation rate of the red blood cells, but this estimate also shifted the contribution to the production of HbA1c from PPG to FPG (Eq. (7), by increasing the estimate of EF_B, insulin and consequently FPG). Although this resulted in a significant improvement in the OFV (−24.6 points, P < 0.001), the model was ill‐conditioned (eigenvalue number > 5000), most likely due to the short trial duration of Studies 2 and 3. This parameter was therefore fixed to the previously published value of 38.9 days, and the shift in the relative contribution of FPG and PPG on the HbA1c was thus not considered.

The effect of estimating r_B was also tested. When estimated, the population estimate for r_B was 0.502 (ΔOFV −26.4 points), which is twofold higher than the previous estimate of 0.209 9. This corresponds to a reduction in β‐cell function by 12%, compared with the previous estimate of 5% per year 9. The effect of removing the treatment effect on β‐cell function (EF_B) on the estimate of r_B was tested but the estimate of r_B remained high (0.562). Factors that may have confounded the estimate of r_B include the short trial duration and the relatively sparse number of FSI observations (4–5 per subject). As the previous estimate of r_B was based on a long clinical trial with detailed collection of observations (n = 8587), the population estimate of r_B was fixed to 0.209 because it is a more plausible estimate of disease progression.

Model‐derived estimates of s₀ and b₀ are shown in Table 3. In contrast to s₀, there were substantial differences in b₀ between studies. When grouped by diabetes duration, the disposition index revealed a decrease in the insulin secretory response in subjects with a longer diabetes duration, although there was large scatter between the groups (Figure 2).

Table 3.

Comparison of the baseline insulin sensitivity and baseline beta‐cell function parameter estimates of each study

	Study 1	Study 2	Study 3
s0 (%)	24.5 (19.3–31.9)	27.4 (20.8–43.1)	29.5 (20.1–43.1)
b0 (%)	57.0 (40.0–76.5)	39.1 (25.3–59.5)	30.2 (19.0–49.2)
rB (logistic function)	0.368 (0.149–0.645)	0.369 (0.043–0.770)	0.148 (−0.325–0.558)

b_0, baseline β‐cell function; s₀, baseline insulin sensitivity; r_B, the rate of beta‐cell function decline. Values are median (interquartile range)

Figure 2.

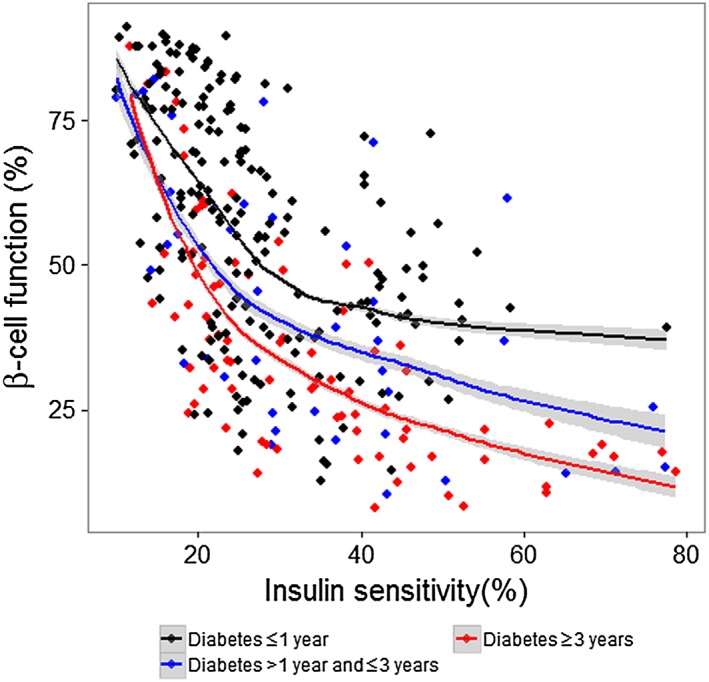
The disposition index of subjects grouped by their diabetes duration. A robust loess smooth curve was plotted, with a 95% confidence interval around the mean

Final model evaluation

The VPCs of the final model showed good agreement between the observations and the simulated concentrations between the studies and for each pharmacodynamic measure (Figure 3). The final parameter estimates are shown in Table 4. With the exception of r_B and MTT, all parameters were estimated with acceptable precision (residual standard error <30%), without any significant shrinkage (<30%).

Figure 3.

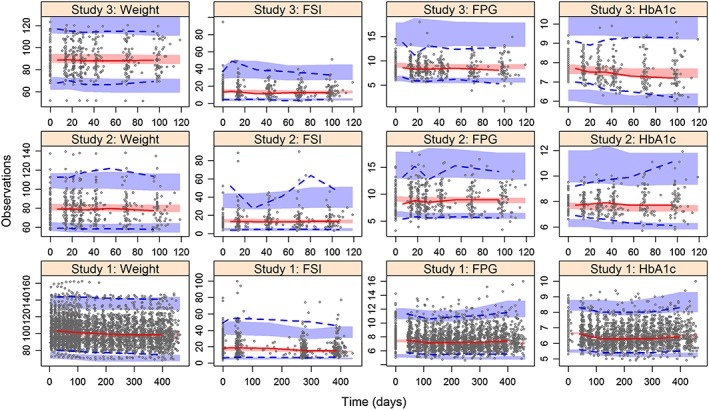
Visual predictive checks of the observations of weight, fasting serum insulin (FSI), fasting plasma glucose (FPG) and glycosylated haemoglobin (HbA1c) stratified by study. The shaded areas are the 95% confidence intervals of the 10th, 50th and 90th percentiles of the simulated concentrations. The dotted lines are the 10th and 90th percentiles from the observations and the solid line is the 50th percentile of the observations. The dots are the observations

Table 4.

Final population parameter estimates from the final model

	Parameter estimate (RSE%)	IIV a (RSE%) [Shrinkage%]
Weight
WGT t 1/2 (days)	73.9 (5)	–
Baseline WGT (kg)	102 (1)	16.1 (4) [0]
β‐cell function
Baseline β‐cell function, logistic function ( b0 ):
Study 1	–0.298 (31)	1.13 (13) [9.5]
Studies 2 and 3	0.677 (17)
rB , rate of β‐cell function loss per year, logistic function	0.209 (fixed)	0.408 (16) [19]
EFBT , treatment effect on β‐cell function (%)	0.0781 (31)	0.053 (12) [15.8]
Insulin sensitivity
s0 , baseline insulin sensitivity, logistic function	0.963 (5)	0.485 (13) [6.4]
θshape , shape parameter for IIV distribution of s 0	–0.476 (15)	–
Scale EFS , scaling factor for effect of weight change on insulin sensitivity	0.0458 (9)	75.7 (10) [19.9]
HbA1c
HbA1c kin , HbA1c production rate % per day	0.0152 (3)	–
MTT, mean transit time (days)	38.9 (fixed)	–
PPG	0.057 (7)	25.6 (10) [6]
Scale PPG	0.967 (1)
Treatment effects
EFDE , placebo, diet and exercise effect at placebo run‐in	3.0 (16)	21.3 (16) [12.3]
EFPL , placebo effect at treatment phase (Study 1 only)	3.46 (16)	28.9 (18) [24.9]
EFLOSS , rate of loss of placebo treatment effect (% /year)	3.76 (24)	70.4 (16) [24.1]
Residual errors
Weight	0.0096 (1)	–
FSI	0.265 (4)	41.5 (6) [22.2]
FPG	0.0841 (4)	29 (11.3) [7.2]
HbA1c	0.0254 (3)	22 (10) [19.8]

FPG, fasting plasma glucose; FSI, fasting serum insulin; HbA1c, glycosylated haemoglobin; IIV, inter‐individual variability (%); PPG, postprandial glucose; RSE, residual standard error; WGT, weight; WGT t_1/2, half‐life of weight compartment

^aNormally distributed IIV (b ₀ , r_B , EF_B , s₀ , EF_DE , EF_PL ,DPR) were reported as absolute values

Discussion

The most critical factor in the emergence of T2DM is obesity, which reduces IS 21. Diet and exercise are commonly recommended for newly diagnosed subjects with T2DM and can reduce HbA1c by 1.0% 22. Using the WHIG model, the relationship between weight change, IS and, ultimately, HbA1c can now be described mechanistically 9. Although there are many published disease models for T2DM 23, 24, the WHIG model only requires measurements of body weight, FSI, FPG and HbA1c, all of which are collected routinely in clinical practice. This is particularly valuable for people with a longer history of T2DM, who require complex treatment regimens to maintain euglycaemia.

In the present study, we investigated the effect of applying the WHIG model to a wider population of people with T2DM. Although the change in body weight is proportional to the change in IS, an ISV parameter for baseline weight was required to account for the differences in the median body weight in each study. Subjects from Study 1 had experienced the most weight loss [−3.4 (−24.3 to 5.9) kg, median (range)] from baseline, and therefore had much larger increases in IS (median increase in IS = 23.2%). By contrast, weight loss from baseline was not significant in Study 2 [−0.53 (−9.2 to 4.5) kg] or Study 3 [−1.0 (−7.6 to 9.4) kg]. In spite of this, implementing the change in weight as a predictor of IS for Studies 2 and 3 improved the model predictions, as judged by the OFV (ΔOFV −34.4) and the agreement between the observed and simulated concentrations of FPG (Figure 2).

Subjects enrolled in Study 3 had previously been treated with metformin but did not have a washout phase prior to starting the placebo trial. Although we accounted for potential residual treatment effects of metformin continuing into the present study, this did not significantly improve the model. Furthermore, the estimated treatment effects (EF_{DE ,} EF_B) and disease status (b₀, s₀) were not significantly different between studies. The lack of a washout phase for Study 3, therefore, was not accounted for in this model because the baseline treatment effects were comparable to the estimates from Study 2. It is possible that these subjects were no longer responding to the effects of metformin because of the study inclusion criteria (inadequately controlled on metformin for over 6 weeks).

There was little variability in IS between subjects with T2DM but there were substantial differences in β‐cell function (Table 4). This is in agreement with previous studies, which showed few changes in IS in subjects diagnosed with T2DM, but the deterioration in β‐cell function continued well after the diagnosis of T2DM 25, 26. Subjects in Study 1 had a higher median baseline β‐cell function (57%) compared with those in Study 2 (39.1%) and Study 3 (30.2%). As the progression of the decline in β‐cell function was described using a logistic decay function, subjects with a lower baseline β‐cell function had lower rates of disease progression as it is not possible for subjects to have a complete loss of β‐cell function. Therefore, subjects from Study 3 had the slowest rate of β‐cell function loss (r_B), which may be associated with their longer history of T2DM. An ISV parameter was required to account for the differences in the baseline β‐cell function. However, other covariates were not significant in explaining the differences in β‐cell function.

Diabetes duration was expected to be a significant covariate for the β‐cell parameters because β‐cell function typically deteriorates with diabetes duration. However, the variability in the diagnosis of T2DM may have confounded diabetes duration as a potential covariate for disease progression parameters – i.e. while some subjects were diagnosed early, others may have been diagnosed when their diabetes was already fairly advanced. The mean time lapse between the onset of T2DM to the diagnosis of T2DM can vary by up to 6 years 27.

In the UK Prospective Diabetes Study, the rate of decline of β‐cell function was approximately 25% over 6 years (about 4% per year) 3, 28. A model developed using the Belfast Study proposed two phases (Phase A, 1.7%; Phase B, 18.2%) associated with the decline in β‐cell function 25. This is consistent with the use of the original sigmoid treatment function for EF_B (see the Supporting information) and logistic disease progression function (BF, Eq. (5)). However, when r_B was estimated, the median rate of loss in baseline β‐cell function was about 12%, which is much higher than the rate of β‐cell function found in previous studies 3, 8, 9, 28.

We fixed the estimate of r_B to previously published values because the estimates of r_B and b₀ are influenced by FSI observations. In our dataset, FSI observations were sparse (4–5 observations per subject) compared with the other pharmacodynamic measurements, and were also influenced by subjects who were not compliant with the fasting protocol. Potential outliers can be seen in Figure 3, whereby some subjects had an FSI over 60 mI U l⁻¹ (reference range: <30 mI U l⁻¹). These outlying FSI observations (and paired FPG concentrations) were not excluded owing to the significant loss in data (>10%). Furthermore, the shrinkage was low when estimating the IIV for r_B (19%, Table 3). Studies 2 and 3 were also short trials, so the relationship between diabetes duration and β‐cell function may become more apparent with the inclusion of people with a longer history of T2DM (>5 years).

One of the major drawbacks in describing the natural progression of T2DM is the need to investigate the untreated population owing to the increased risk of diabetic complications. The Belfast Study is the only longitudinal study to have been conducted in untreated people with T2DM 26. Long placebo trials are uncommon, particularly in people with advanced T2DM. Therefore, future studies, providing longitudinal data on the treated population, may provide more insight on the relationship between disease progression and diabetes duration.

Conclusion

In the present study, we showed that the WHIG model can be applied to a wider population of people with T2DM. The change in body weight as a predictor of IS was a significant improvement in the model and can also be applied to people who are not obese. When the WHIG model was applied to people at varying stages of disease severity, large IIV in β‐cell function was observed but there were no statistically significant covariates to explain this variability. As it is not possible to obtain longitudinal data for the untreated population, the application of this model to the treated population with a longer history of T2DM is necessary further to investigate the relationship between β‐cell function and diabetes duration. In the future, the disease‐modifying properties of drugs can be investigated by comparing the treatment effects of antidiabetic drugs with the effects of placebo.

Competing Interests

Top Institute Pharma (TI Pharma) received funding from partners to support the collaboration between academic and industry partners. J.K.D. received financial support from TI Pharma for the submitted work, W.D. is employed by Janssen Research and Development; N.P. and H.N. are employees of Takeda Pharmaceuticals; W.K. is employed by Astellas Pharma Europe and S.V. is employed by Merck & Co. Katia Verhamme works for a group which has previously received unconditional research grants from Pfizer/Boehringer Ingelheim, Yamanouchi, GSK and Novartis, none of which are related to the topic of this research.

This work was supported by Top Institute Pharma (TIPharma), PKPD Platform 2.0.

Contributors

J.K.D. conducted the study, analysed the data and wrote the manuscript. W.D. and M.D. contributed to the study concept and study design. W.D. and W.K. contributed data to the study; W.D. and S.C. contributed to the analysis of the WHIG model and approved the use of the WHIG diagram for this manuscript. W.D., N.P., H.N. and S.V. contributed to the interpretation of the results. All authors reviewed and approved the final version of the manuscript.

Supporting information

Table S1 The collection of weight, fasting serum insulin (FSI), fasting plasma glucose (FPG) and glycosylated haemoglobin (HbA1c) data for Study 1

Table S2 The collection of weight, fasting serum insulin (FSI), fasting plasma glucose (FPG) and glycosylated haemoglobin (HbA1c) data for Studies 2 and 3

Table S3 The parameter estimates for the full omega block (covariance–variance matrix). The residual standard errors are shown in brackets. Baseline β‐cell function (b₀), baseline insulin sensitivity (s₀), the rate of beta‐cell function decline (r_B), treatment effect of diet and exercise (EF_DE), loss of treatment effect with time (EF_LOSS) and effect of placebo treatment (EF_PL) were normally distributed, while the scaling factor for weight change Scale_EFS, baseline weight (WGT) and postprandial glucose (PPG) were log‐normally distributed

Figure S1 The weight (WGT)‐glycosylated haemoglobin (HbA1c)‐insulin‐glucose model [10]. The model includes the change in WGT as a driver for insulin sensitivity (IS). There is a feedback mechanism between fasting serum insulin (FSI) and fasting plasma glucose (FPG). FSI is also influenced by the overall β‐cell function (B). EFB is the estimated treatment effect on β‐cell function, which consisted of a logistic increase function (EFB_I) and a logistic decline function (EFB_D). The HbA1c compartment consists of three transit compartments. The estimated effect of postprandial glucose concentration (PPG) on the production of HbA1c is shown

Figure S2 Empirical Bayes estimate (EBE) plots of baseline β‐cell function (b₀), baseline insulin sensitivity (s₀) and the rate of beta‐cell function decline (r_B) against diabetes duration for Studies 2 and 3

Supporting info item

Duong, J. K. , de Winter, W. , Choy, S. , Plock, N. , Naik, H. , Krauwinkel, W. , Visser, S. A. G. , Verhamme, K. M. , Sturkenboom, M. C. , Stricker, B. H. , and Danhof, M. (2017) The variability in beta‐cell function in placebo‐treated subjects with type 2 diabetes: application of the weight‐HbA1c‐insulin‐glucose (WHIG) model. Br J Clin Pharmacol, 83: 487–497. doi: 10.1111/bcp.13144.