Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Jan 12;2(2):397–407. doi: 10.1021/acsenergylett.6b00626

Insights into Photosystem II from Isomorphous Difference Fourier Maps of Femtosecond X-ray Diffraction Data and Quantum Mechanics/Molecular Mechanics Structural Models

Jimin Wang ‡, Mikhail Askerka †, Gary W Brudvig †, Victor S Batista †,*
PMCID: PMC5307371  PMID: 28217747

Abstract

graphic file with name nz-2016-00626d_0008.jpg

Understanding structure–function relations in photosystem II (PSII) is important for the development of biomimetic photocatalytic systems. X-ray crystallography, computational modeling, and spectroscopy have played central roles in elucidating the structure and function of PSII. Recent breakthroughs in femtosecond X-ray crystallography offer the possibility of collecting diffraction data from the X-ray free electron laser (XFEL) before radiation damage of the sample, thereby overcoming the main challenge of conventional X-ray diffraction methods. However, the interpretation of XFEL data from PSII intermediates is challenging because of the issues regarding data-processing, uncertainty on the precise positions of light oxygen atoms next to heavy metal centers, and different kinetics of the S-state transition in microcrystals compared to solution. Here, we summarize recent advances and outstanding challenges in PSII structure–function determination with emphasis on the implementation of quantum mechanics/molecular mechanics techniques combined with isomorphous difference Fourier maps, direct methods, and high-resolution spectroscopy.

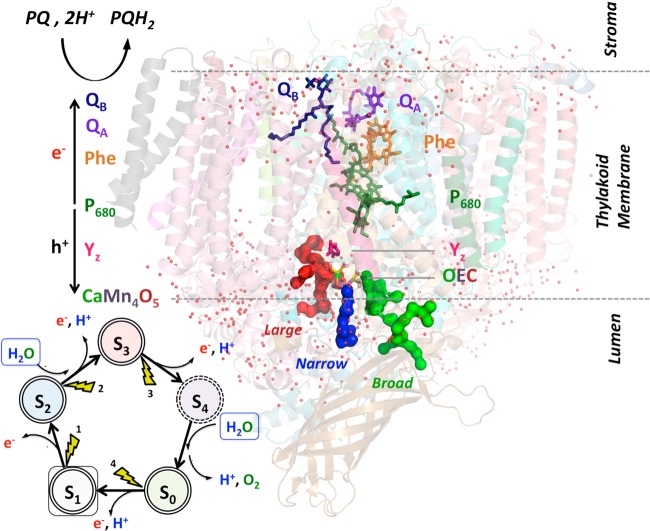
Photosystem II (PSII) is the only known protein complex capable of catalyzing direct solar water-splitting into O2, protons, and electrons.1−4 Understanding its structure–function relations can provide fundamental insights, essential for the design of artificial photosynthetic systems. The oxygen-evolving complex (OEC) of PSII is a CaMn4O5 oxo-manganese cofactor that binds substrate water and splits it into O2, protons, and electrons through a stepwise catalytic cycle (Figure 1). During each turn of the cycle, the OEC evolves through five “storage” states, Sn (n = 0–4), where S1 is the dark stable state while S0 and S4 are the most reduced and oxidized forms, respectively.5,6

Figure 1.

Figure 1

Open in a new tab

Catalytic cycle of water oxidation, driven by solar light absorption. Each cycle is initiated by light absorption by the chlorophylls P680, followed by a charge separation. On the donor side, the electron sequentially reduces the special pheophytin and the pair of quinones QA and QB. After accepting two electrons, QBH2 is replaced by an oxidized quinone from a plastoquinone (PQ) pool. On the donor side, the hole oxidizes tyrosine Yz, which in turn oxidizes the oxygen-evolving complex. In each turn of the cycle, the OEC of PSII evolves through “storage” states, Sn (n = 0–4), catalyzing water splitting, as follows: 2H2O → O2 + 4H+ + 4e–. The water supply and proton release are likely happening through the water channels (labeled Large, Narrow and Broad) surrounding the OEC on the luminal side.

The detailed analysis of the catalytic reaction has been challenging and benefited from an interdisciplinary approach, including computational modeling, crystallography, and spectroscopy,7 combined with mutagenesis and kinetic studies. Major breakthroughs in protein X-ray crystallography have resolved the PSII crystal structure from 3.8 Å, to the highest 1.9 Å resolution (PDB accession number 3ARC/3WU2),8,9 establishing the architecture of the OEC and its ligation scheme. A challenge has been that even at the highest resolution, the X-ray dose used for X-ray data collection caused reduction of the OEC,8b consistent with previous studies based on extended X-ray absorption fine structure (EXAFS) spectrometry.10−12

In recent years, X-ray free electron laser (XFEL) pulses with different approaches applied to serial femtosecond crystallography (SFX)13−17 have enabled collection of PSII diffraction data on the femtosecond scale before the onset of significant radiation damage. Several developments emerged from the analysis of XFEL data, and direct comparisons were made to computational structural models. Here, we focus on insights into the PSII machinery obtained from isomorphous difference Fourier methods in crystallography combined with direct methods and quantum mechanics/molecular mechanics (QM/MM) calculations.18−22

Isomorphous Difference Fourier Methods: The S1 to S2 Transition. A fundamental limitation of X-ray crystallography is that only the intensity of the scattered radiation is measured, I(h) = |F(h)|2, with the structure factor

graphic file with name nz-2016-00626d_m001.jpg 1

describing the total radiation diffracted by the plane of atoms specified by the Miller indices h = (h, k, l). The phases αj = 2πh·rj must be modeled or inferred from the intensity data. The radiation scattered from each atom j is described by a complex number, fj exp(2πih·rj), defined by the atomic fractional coordinates rj (coordinates expressed as fractions of the unit cell vectors), scattering indices h, and tabulated atomic scattering factors fj.23 The overall pattern of intensities is evaluated to obtain the crystal structure (unit cell) and symmetry (space group), and the atomic coordinates rj of a proposed structural model are refined to match the calculated intensities to the experimental values at a given resolution.

Tracking subtle changes due to chemical transformations, such as those induced by the S-state transitions of PSII, requires the analysis of electron density differences. Here, we consider the electron density difference due to the S1 [model (I)] to S2 state [model (II)] transition:

graphic file with name nz-2016-00626d_m002.jpg 2

Equation 2 requires calculation of phases αII and αI for both models and gives the difference of electronic densities as obtained from the refined models. The difficulty with such an approach when applied to very similar structures is that real features in the observed intensity data are not sufficiently distinct from those due to the model bias inherent in the calculation of the phases.

Isomorphous difference Fourier methods24,25 have important advantages relative to calculations of electronic density differences obtained from refined structural models, allowing for analysis of small changes between an isomorphous pair of structures, i.e., structures with the same cell parameters, orientation, and overall conformation of the system in the unit cell, except for small differences deliberately introduced such as the light-induced S1 to S2 transition. Contrary to eq 2, isomorphous difference methods compute electron density difference maps (as the Fourier transform of the difference of observed amplitudes) with calculated phases for only one of the models:

graphic file with name nz-2016-00626d_m003.jpg 3

Remarkably, such an approximation over the phases gives a very accurate description of the exact map of electron density differences, even when the phases dominate the Fourier transform.

The isomorphous difference Fourier method was initially developed to analyze small ligand binding (comparable in size to a water ligand) such as azide or cyanide binding to heme proteins even when direct Fourier maps were unable to identify the underlying subtle structural changes at relatively low resolution.25−30 In its original application, experimental phases were available.25−28 In the absence of experimental phases, model phases are used (eq 3) as in the study of Kern et al. where structural changes in the OEC during the S1 to S2 transition were explored for XFEL data obtained at 5.9 Å resolution.14,15 We used high-resolution model phases followed by 3-crystal 6-fold noncrystallographic symmetry (NCS) averaging,18 as described in the Supporting Information of ref (18), using model phases from two high-resolution structures of the same protein (3ARC and 3BZ1).8a,31 NCS averaging utilizes a more accurate bulk solvent density from high-resolution models where the bulk solvent correction is more reliable than low-resolution models and allows for accurate modeling of the side chains of surface residues that would otherwise influence the bulk solvent correction and thus the model phases. This approach has recently allowed us to enhance the intensity of weak signals and raise them to a statistically significant level for direct observation of structural changes associated with the S1 to S2 transition18 not visible in calculations of electronic density differences obtained from refined structural models.14 The density differences are fully consistent with those observed in QM/MM structural models (Figure 2).18

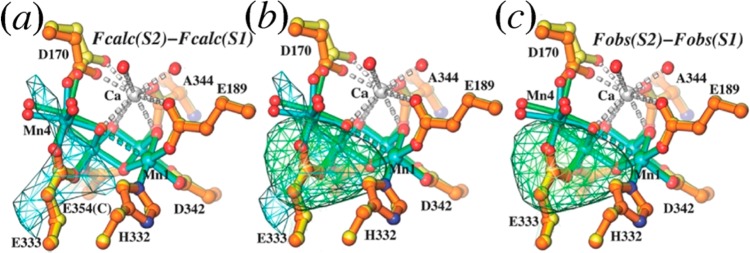
Figure 2.

Figure 2

Open in a new tab

Comparison of the difference Fourier maps calculated using QM/MM S1 and S2 models and using corresponding SFX data sets. (a) Simulated S2-minus-S1 difference Fourier maps calculated using the QM/MM S1 and S2 models. The highest peak near the OEC results from the displacement of Mn4. (b) Comparison of the simulated S2-minus-S1 (from panel a) and the observed S2-minus-S1 (from panel c) difference Fourier maps using SFX data sets with color codes according to panels a and c. (c) Observed S2-minus-S1 difference Fourier maps contoured at +3σ (green mesh). Adapted from ref (18). Copyright 2014 American Chemical Society.

The isomorphous difference analysis provided valuable physical insights on changes in the coordination sphere of the dangling Mn center (Mn4, Figure 2), induced by the S1 to S2 state transition of the OEC. According to control calculations based on QM/MM models, the S1 to S2 state transition involves oxidation of the dangling Mn (Mn4) in the OEC,18 from Mn(III) to Mn(IV), inducing a contraction of the octahedral coordination sphere of Mn(IV) that results from loss of the Jahn–Teller distortions present for Mn(III). Such a contraction and the decrease of the Mn1–Mn4 distance produce a distinct positive peak in the simulated FModel(S2) – FModel(S1) difference Fourier map next to the dangling Mn. This peak is detectable at the resolution corresponding to the experimental data, in good agreement with the results of the experimental isomorphous difference map obtained from the SFX data sets reported for 4IXR and 4IXQ(14) (Figure 2). We note that the contraction due to the Jahn–Teller distortion is in fact fairly small (i.e., the Mn(III) coordination distance is typically 2.1 Å instead of 1.9 Å). Nevertheless, they can be detected even at 5.9 Å resolution because they involve movement of the Mn center, with the negative component of the density change compensated by displacement of the D170 (Figure 2) ligand.

The structure of PSII in the dark stable S1 state solved at 1.95 Å resolution using femtosecond XFEL pulses represents a significant development.17 These SFX experiments enabled collection of PSII diffraction data at the highest resolution before the onset of significant radiation damage. However, simulations of EXAFS spectra based on the coordinates of the model show that they are not fully consistent with EXAFS data for the S1 state because of lack of accuracy in the position of the O atoms of μ-oxo bridges next to the strongly scattering Mn and Ca ions.20 Historically, accurate detection of light O atoms next to metal centers has been challenging. The absence of the O4 μ-oxo bridge in the 3.3 Å resolution structure of PSII32 is an example analogous to the missing carbon atom in the MoFe center of nitrogenase at 1.55 Å resolution prior to the 1.16 Å resolution structure. The difficulty is partly due to ripple effects induced by premature Fourier series termination for data with insufficient (nominal and spatial) resolution. In hindsight, once the presence of the ligand is established, the Fo–Fc maps can be used to confirm the location of light ligands, although the accuracy of this method is still limited by the tailing effect of heavier metal ion centers.

Isomorphous Difference Fourier Maps Modified for a Varying Unit Cell: S3 State. The S3 state of PSII has been studied by some of the most recent XFEL experiments16 because it is one of the most important intermediates in the catalytic cycle, detectable right before O–O bond formation and reduction of the OEC. The comparative analysis of the S1 and S3 electron density maps has been challenging, with the two states obtained at different nominal resolution of 5.0 and 5.5 Å, respectively. The challenges are due to (i) the different kinetics between aqueous solution and individual microcrystals, which may have prevented PSII in crystals from fully achieving the S3 state, and (ii) changes in the crystallographic unit cell that may have increased the extent of nonisomorphism.

It has been necessary to modify the isomorphous difference Fourier method and apply it by computing two sets of electron density maps, because the original method was not applicable to analyze structures with different unit cells. Only paired and intensity-scaled reflections were used in reciprocal space for each unit cell, with only one set of model phases.33,34 The resulting maps were realigned using least-squares procedures (LSQ), as implemented in the Rave package, and back Fourier-transformed to generate new sets of observed amplitudes (FobsLSQ) for calculation of difference Fourier map as follows:19

graphic file with name nz-2016-00626d_m004.jpg 4

To minimize the Fourier series termination effect, only the reflections present in both data sets with 5.0 and 5.5 Å resolution were included in the analysis. The resulting spatial resolution was limited by the lowest resolution of the compared structures.

The analysis based on realigned difference Fourier maps provided valuable insights on the expansion of the CaMn4O5 cluster (Figure 3), during the S1 to S3 transition, likely induced upon binding of substrate water molecule to the dangling Mn as shown by QM/MM calculations.19Figure 3 shows the difference Fourier maps, obtained according to eq 4, based on the rescaling to SFX data sets from the S1 and S3 states of PSII.19 It reveals significant changes in the Fourier maps localized at the OEC. The electron density differences at the OEC are consistent with the QM/MM models, as corresponding to an expansion of the CaMn4O5 cluster during the S1 to S3 transition.19,22

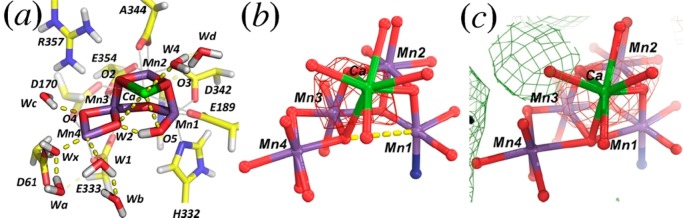
Figure 3.

Figure 3

Open in a new tab

Comparison of QM/MM-derived S3 model and SFX data sets. (a) QM/MM-optimized structure of the OEC in the S3 state (Mn oxidation states: IV, IV, IV, IV), including coordination of water ligands as well as D1-D61, D1-His337, and CP43-R357. (b) Simulated S3-minus-S1 difference Fourier maps based on the QM/MM-derived S3 and S1 models. (c) Observed S3-minus-S1 modified difference Fourier maps contoured at +3σ (green) and −3σ (red) after map least-squares superposition. Adapted from ref (19). Copyright 2016 American Chemical Society.

The QM/MM rearragement is consistent with binding of a water molecule through a “carousel” mechanism,16,19 suggesting that some fraction of the PSII in microcrystals must have advanced beyond the S2 state.35 Considering that the S1 to S2 conversion resulted in a positive peak inside the OEC near Mn4 (Figure 2), the net negative peak observed during the S1 to S3 transition suggestes that the S3 fraction must have overcompensated whatever fraction of the S2 was formed. Interestingly, because the metal cluster expands upon S2 to S3 oxidation and the cluster contracts during the S1 to S2 conversion, it is conceivable that the S2 to S3 oxidation might indicate binding of a water molecule, as suggested by various computational models.19,22,36−39

Computational Noise in XFEL Data Sets. Approximations and statistical inferences of the algorithms used for data reduction often introduce nonrandom noise to the experimental data. The analysis of how the resulting computational noise affects the distribution of X-ray scattering intensities is important because noise can scramble weak structural signals of crystallographic data sets (Figures 4 and 5).

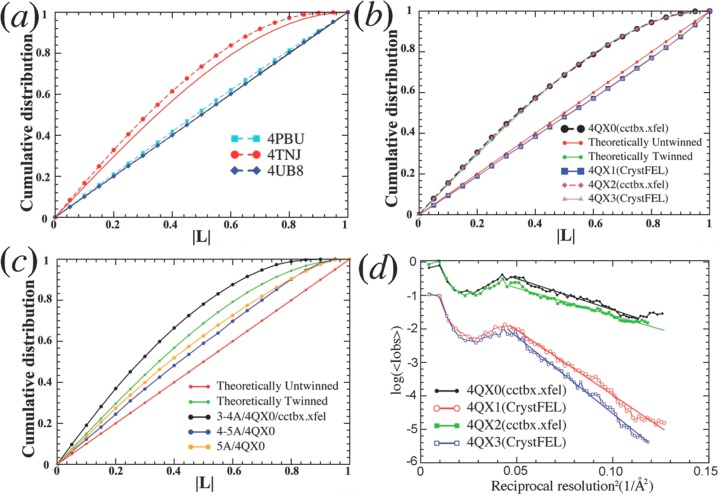
Figure 4.

Figure 4

Open in a new tab

L-test plots for selected SFX data sets. (a) L-test results for data sets of PSII XFEL data are compared for 4PBU (processed with CrystFEL), 4TNJ (cctbx.xfel), and 4UB8 (mosflm/scala). (b) L-test results for data sets obtained for proteins other than PSII. Data processed using cctbx.xfel (4QX0 and 4QX2) appear to be maximally twinned, whereas data processed from the same crystals using CrystFEL (4QX1 and 4QX3) do not. (c) The cctbx.xfel-processed 4QX0 data set is divided into three resolution ranges for L-test: (i) below 5 Å (orange), (ii) between 5 and 4 Å (blue), and (iii) between 4 and 3 Å (black). (d) Comparison of the Wilson plots (logarithm mean intensity versus inverse resolution squared) obtained from two cctbx.xfel processed data sets (black/4QX0 and green/4QX2) and two otherwise similar data sets processed using CrystFEL (red/4QX1 and blue/4QX3) from similar crystals.

Figure 5.

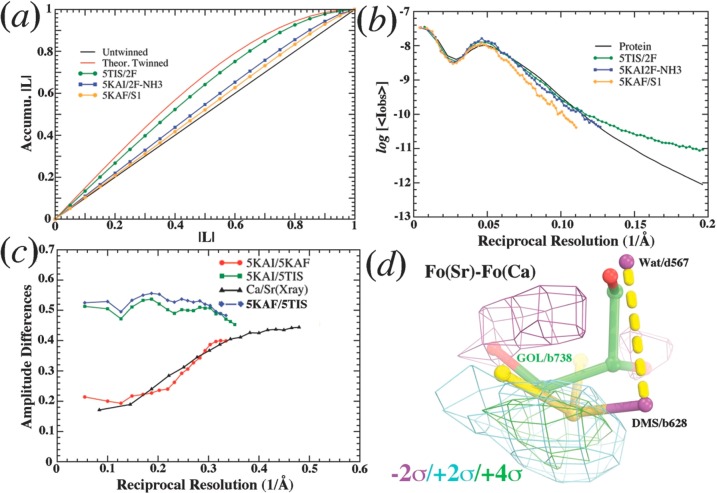
Figure 5

Open in a new tab

An analysis of Young et al. (2016) data sets.52 (a) L-test for 5TIS (green), 5KAF (gold), and 5KAI (blue) data sets. Untwinned line is shown in black, and theoretically twinned curve is in red. (b) Wilson plot for 5TIS (green), 5KAF (gold), and 5KAI (gold) data sets after all data sets were scaled to 5KAF and placed on the same absolute scale, i.e., logarithms of mean intensity as a function of reciprocal resolution squared. For comparison, the corresponding plot for all protein data sets in the PDB is shown in black. (c) Amplitude differences as a function of reciprocal resolution between 5KAI and 5KAF (red), between 3ARC and 4IL6 (black), between 5KAI and 5TIS (green), and between 5KAF and 5TIS (blue). (d) Isomorphous difference Fourier maps between Sr and Ca data set contoured at +2σ (cyan), + 4σ (green), and −2σ (magenta) show the largest features for the replacement of a glycerol (b738) by DMSO (DMS/b628) and a water molecule (d567).

A classic example of computational noise concerned the treatment of negative and weak intensity measurements that concluded with a Bayesian statistical solution formulated by French and Wilson (1978).40 The probability of measuring the intensity of any reflection as negative is known,41 although sometimes disregarded.42 Proper processing of negative intensities, however, is critical for the quality of the data and XFEL maps produced from microcrystals. Discussions on negative intensities can be found elsewhere.43 Here, we limit the presentation to the simplest example showing why it is important to include negative intensity measurements during an intensity merging process. If one measures a systematically absent Bragg reflection (with null average intensity) several times, it is likely that after background subtraction half of the measurements will be positive and half negative. If the five negative measurements are disregarded, arguing that the intensity (i.e., amplitude square) must be positive, the mean value of the reflection would be positive instead of null. Thus, this reflection would be no longer absent.

Improper treatment of negative and weak intensity measurements could lead to various skewed intensity distributions, detectable by statistical tests. With properly processed data sets, the probability density of any given acentric Bragg reflection with intensity between I and I + dI follows the single exponential function, exp[−I/⟨I⟩], known as the Wilson intensity distribution, where ⟨I⟩ is the mean intensity of all noncentric Bragg reflections.44 The probability density of fractional intensity differences between pairs of Bragg reflections selected locally in reciprocal space, L ≡ (I1 – I2)/[(I1 + I2)/2], provides the L-test because the first and second moments ⟨|L|⟩ and ⟨L2⟩ are 1/2 and 1/3 for untwinned acentric data, respectively. If twinning occurs, as observed in crystal lattices where the unit cell can adopt more than one orientation, the L moments are lowered and reach a value of 3/8 and 1/5 for fully twinned data.45

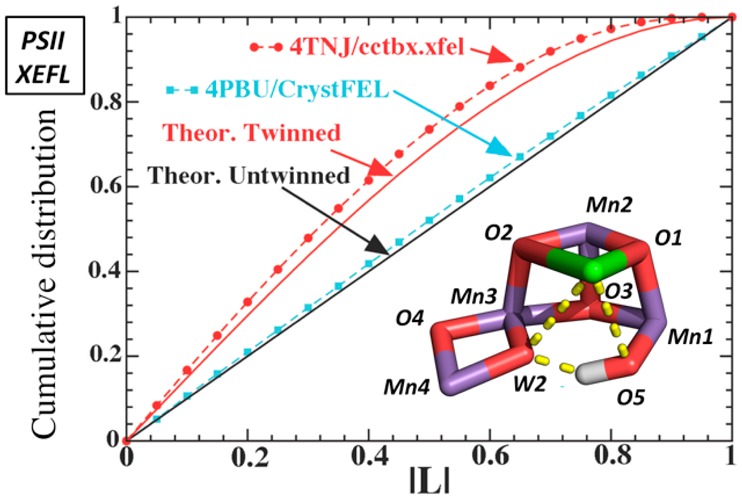
When twinning is physically impossible, as for the PSII crystals with P212121 symmetry, the skewed intensity distribution identified by the L-test quantifies the level of computational noise introduced in the data sets. Figures 4 and 5 shows that an outstanding challenge in the field is the reduction of computational noise in the XFEL data sets of PSII structures.45 In particular, Figure 4 analyzes data sets processed with the CrystFEL, cctbx.xfel, and mosflm XFEL-specific programs, which have been used to process the XFEL PSII data deposited in the PDB.42,46−49Figure 4a shows that the 4TNJ PSII data set has a much higher level of computational noise than the 4PBU (or other PSII) data sets, processed using the CrystFEL program (or other programs).13−17 When the same L-tests are extended to XFEL data sets from other proteins, it is clear that the problem is not related to the PSII crystals but rather to a data-processing artifact specific to cctbx.xfel (Figure 4b).42,50

Figure 4 analyzes the cctbx.xfel-processed data as divided into three resolution ranges: (i) below 5 Å, (ii) 5–4 Å, and (iii) 4–3 Å. The L-tests were performed on each of the three blocks of data, independently. The 4–3 Å range exhibits the highest level of computational noise because the average intensities are the lowest (Figure 4c). Consistently, Wilson plots (i.e., logarithm of mean intensity in a given resolution shell versus the reciprocal resolution squared for this shell) for data sets processed with cctbx.xfel are displaced upward, at higher resolutions, relative to those obtained with CrystFEL from the same crystals (Figure 4d). It is thus concluded that cctbx.xfel has systematically overestimated the intensities of weak reflections, as also acknowledged by the authors of cctbx.xfel.51 In fact, recent inclusion of negative intensities after background subtraction by reprocessing XFEL data sets of the synaptotagmin-1/SNARE complex has partly alleviated the unusual behavior of the L-test and made the XFEL data set comparable to that of the synchrotron data set.51

Analysis of the Most Recent XFEL Structures. Shortly after submission of this manuscript, a new XFEL experiment was reported with the analysis of PSII in the dark stable S1 state (5KAF, 3.0 Å resolution), the S3 state (5TIS, 2F or two-flashes state, at 2.25 Å), and ammonia-bound S3 (5KAI, 2F-NH3 state at 2.8 Å),52 because NH3 is analyzed as an analog of water. The corresponding 5KAF and 5KAI data sets were collected using the same wavelength and experimental setup, having practically the same unit cell parameters (i.e., the maximal cell parameter difference between them is 0.5 Å or 0.25%, smaller than the variations of cell parameters of about 3 Å reported for the two structures).52 Thus, the 5KAF and 5KAI isomorphous pair is suitable for analysis based on the classic isomorphous difference Fourier method. As a control, we calculated isomorphous difference Fourier maps at 2.1 and 3.0 Å resolution between the 4IL6 and 3ARC/3WU2 data sets, using the model-derived phases of 3ARC/3WU2,8a,53 where 4IL6 represents the data set of the Sr-substituted OEC in the presence of dimethyl sulfoxide (DMSO or DMS) and 3ARC/3WU2 represents the structure of wild-type Ca-containing enzyme in the presence of glycerol. The 3ARC/4IL6 pair is ideally suited for a control experiment because it has amplitude differences as a function of reciprocal resolution that are similar to those of the 5KAF/5KAI pair (Figure 5c). The 3ARC/4IL6 has an overall amplitude difference of 31.3% at 3.0 Å resolution (and 35.9% at 2.1 Å resolution), while that for the 5KAF/5KAI pair is 28.7% at 3.0 Å resolution (Figure 5c). The maximal change in fractional unit cell parameters for the 3ARC/4IL6 is 0.33%, which is only slightly larger than the 5KAF/5KAI pair (0.25%).

In the 3ARC/4IL6 difference-Fourier maps, the largest positive peak observed at +7.4σ pinpoints the replacement of a glycerol molecule (GOL/b738) with a DMSO (DMS/b628) molecule plus an ordered water molecule (d567) (Figure 5d). Corresponding 2Fo(Sr/DMSO)-Fo(Ca/GOL) maps and 2Fo(Ca/GOL)-Fo(Sr/DMSO) have also unambiguously confirmed this replacement.

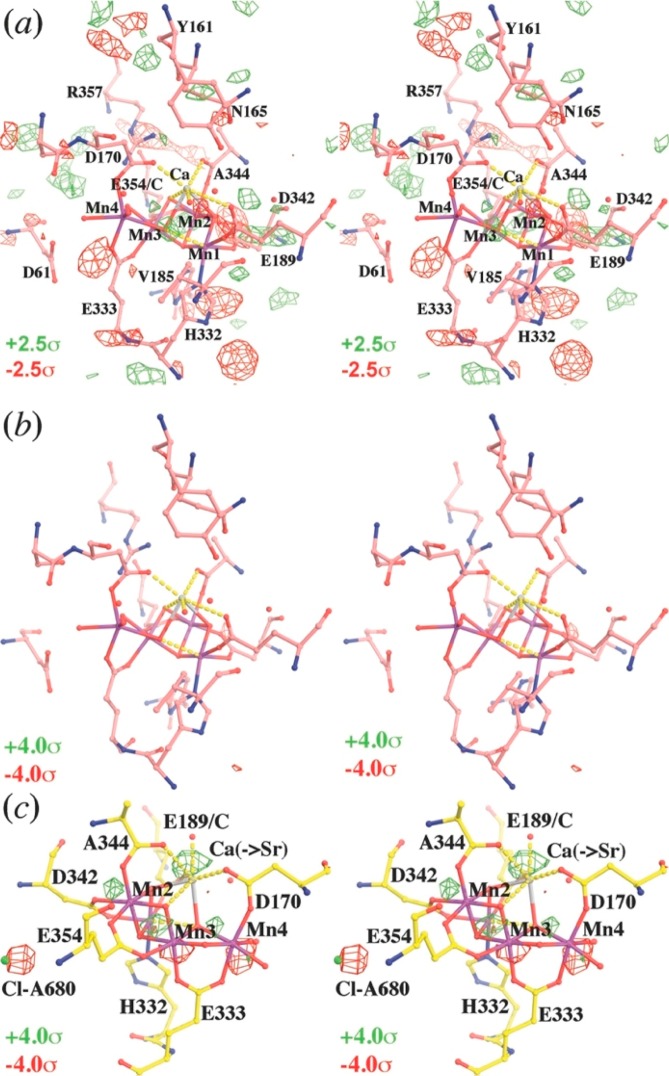
The second largest peak is associated with the substitution of Ca by Sr at the OEC (Figure 6c) because Sr is larger and denser than Ca. Upon Sr substitution, the OEC slightly expands, and three of the four Mn centers exhibit significant peaks above ±4σ due to subtle displacements. Noticeably, Cl-A680 also has a significant negative peak on it, implying a possible loss of occupancy for this Cl– anion (Figure 6c).

Figure 6.

Figure 6

Open in a new tab

Isomorphous difference Fourier maps in stereodiagram. (a) Between 5KAI and 5KAF contoured at ±2.5σ (green and red). (b) At ± 4.0σ (green and red). (c) Between 4IL6 and 3ARC contoured at ±4.0σ (green and red).

In contrast to the analysis of the Sr substituted PSII, the isomorphous difference Fourier maps between 5KAI and 5KAF calculated at various resolutions (using model phases retrieved from the PDB), exhibit no significant detectable difference at the ±2.5σ contour level at the OEC site, nor at ±4σ in its vicinity (Figure 6ab), suggesting no detectable NH3 binding.

5TIS is the first PSII XFEL data set collected at room temperature with sufficiently high resolution for reliable Wilson-plot analysis (Figure 5). However, even for this data set, the L-test (Figure 5a) shows significant deviations from the expected straight line, similarly to the L-test of all of the PSII X-ray data sets deposited in the PDB that have been analyzed by using cctbx.xfel. Furthermore, the mean intensity (Figure 5b) does not exhibit the proper decay and is higher than expected. Therefore, it remains a major challenge to determine whether there is sufficient signal to be extracted in individual XFEL images at high resolution, particularly when detectable X-ray photons might be less than 1 per pixel. In that case, the proper way to obtain accurate estimates of intensities would be to use tens of thousands of individual images to enhance very weak signals with statistically sound treatments of negative and weak intensity signals. Otherwise, as the resolution increases, the mean intensity at high resolution would approach the asymptotic value of the lowest detectable photon numbers per pixel.54

Direct Methods. Direct methods infer information about phases from measured intensities,55−58 exploiting constraints between the phases of different Fourier components due to the atomicity of the molecules and the fact that the electron density should be zero or positive at any point of the unit cell. For example, phases for small molecules and medium-sized molecular structures can be directly retrieved from accurately measured amplitudes, using the Hauptman–Karle algorithm.57,58 However, that method is often not particularly useful when applied to large proteins because the probability of phase relationship is often too broad, and the overall B-factor for protein data sets can be as much as 10 times larger than for small molecules, making the electron density function for atoms very broad and phase retrieval very challenging. To overcome the broadening of the electron density distribution around atoms, one can use normalized structure factors, resulting in point-atoms in maps. To alleviate the ripple effects of premature Fourier series termination, Wilson-expected values are used to fill in missing high-resolution terms.59

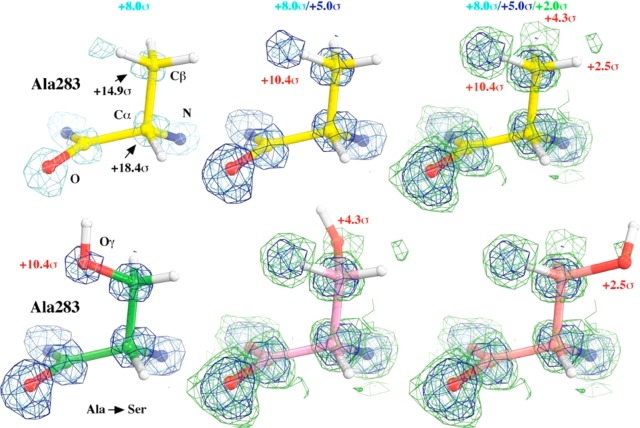
Direct methods have suggested that conventional X-ray diffraction data sets, based on an analysis of the 3ARC data,8a exhibit extensive oxidative modifications (Figure 7).59Figure 7 shows, for example, an Ala residue that has been converted into Ser (A283S).59 Analogous changes are observed in about 10% of the residues (i.e., at least 538 residues out of the total of 5351 have been modified). The radiation-induced oxygen insertion in amino acids and proteins has been studied for over a century using a variety of biophysical methods (see ref (59) for a brief historical review, including two recent specific studies on oxidation of PSII protein residues60,61). Radiation splits an H2O molecule into a highly reactive hydroxyl radical and a highly reductive hydrated electron. The hydroxyl radical is thought to be responsible for the observed oxygen insertion chemistry, while the hydrated electron is responsible for reduction of metal centers such as Mn at the OEC.8a We note that Fe is not significantly reduced in the 5EJX crystal structure because the Fe–O bond distance is 1.75 Å, only slightly elongated relative to the corresponding bond length of 1.73 Å in a low-dose synchrotron structure (code 3M23).16 However, while an elongated Fe–O bond distance would confirm reduction by free electrons, the lack of elongation cannot rule out radiation damage.

Figure 7.

Figure 7

Open in a new tab

Direct-methods generated E-map showing conversion of Ala to Ser in the PSII 3ARC data set. The E-map was contoured at +8.0σ (cyan), + 5.0σ (blue), and +2.0σ (green) followed by an interpretation of Ser residue in three different rotameric positions (green, pink, and light red). Adapted with permission from ref (59). Copyright 2016 Wiley.

We note that the peaks interpreted as additional oxygen atoms were relatively small because only the second half of the data set exhibits protein modifications. These specific fingerprints, in only part of the diffraction data, are nevertheless quite distinct relative to nonspecific damage that usually reduces the diffraction intensity of the entire data set.

Ongoing Challenges

Other outstanding challenges include an ongoing debate about the possibility of radiation damage during XFEL experiments. In addition to room-temperature SFX, the two highest-resolution SFX data sets for PSII have been recorded by using multiple shots per frozen crystal at liquid N2 temperatures.17 While the use of cryogenic temperatures has been a common methodology for conventional crystallographic data sets (e.g., for the highest-resolution data set of PSII reported8a), there is evidence that the diffusion rate of hydroxyl radicals generated by radiation might be faster than the rate of sample translation for bringing unexposed parts of the sample to the exposing position. As a consequence, oxygen atoms might be added to many of the protein residues, as observed in cytochrome c peroxidase.59,62

The self-amplified self-emission process represents another XFEL challenge because the process is highly stochastic with large fluctuations.63 Femtosecond pulses of XFEL are thus quite different from one another, in terms of their intensity profiles. Usually, the effect of such variation is not included in SFX modeling theories.64−67 Therefore, it is conceivable that the SFX data might have recorded a destruction process of molecules in the crystal lattice and that such a destructive process may differ from one XFEL pulse to another, partially explain why merging statistics of XFEL data sets does not always provide significant statistical improvements.68,69

Conclusions

We have reviewed recent advancements in the field of PSII structural characterization, with emphasis on outstanding challenges and insights from isomorphous difference Fourier maps of femtosecond X-ray diffraction data as well as direct methods in conjunction with QM/MM structural models. The crystal structure of PSII obtained at 1.9 Å resolution using conventional X-ray crystallography8a represents a milestone achievement that has confirmed and established many structural features of PSII. However, it is now clear that the reported data reflect X-ray radiation-induced modifications.8a Similarly, the SFX structure at 1.95 Å resolution is a significant breakthrough, although several challenges remain to be addressed with respect to the analysis of data collected for SFX structures. In particular, the quality of the overall data statistics and the methods for data processing remain challenging. We have reviewed some historical literature on statistically sound approaches that might provide valuable solutions to improve both accuracy and consistency of XFEL data sets.62,69 The crystallographic community has decades of experience on how to properly process still diffraction images, for example, in Laue diffraction.70 Like SFX diffraction experiments, one-shot-per-crystal determination using Laue diffraction has also been developed.71 In the next few years, achieving atomic resolution of the OEC for the various S-state intermediates would also require overcoming the variable initial S-state composition due to extensive dark adaptation prior to data collection as well as the intrinsic uncertainty in the positions of oxygen atoms due to weak diffraction of oxygen atoms next to the heavier manganese centers. The resulting structural information should be particularly valuable for understanding structure–function relations of PSII that could inform the development of biomimetic photocatalytic systems.

Acknowledgments

The authors acknowledge support by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, Photosynthetic Systems. Experimental work was funded by Grant DE-FG02-05ER15646 (G.W.B.), computation work by Grant DESC0001423 (V.S.B), and crystallographic study by National Institutes of Health Grant P01 GM022778.

Biographies

Jimin Wang (1982, B.Sc. Chemistry, Peking University, China; 1988, Ph.D. Chemistry under advisor Professor Joseph Kraut, UC San Diego, United States; 1988–1996, Post-Doctoral Associate and Associate Research Scientist under advisor Professor Thomas A. Steitz, Molecular Biophysics and Biochemistry or MBB, Yale University) is currently a Research Scientist, MBB, Yale University.

Mikhail Askerka (1990, Moscow, Russia; M.S. (2011) in Chemistry from Moscow State University) is a Ph.D. student in Physical Chemistry working with Victor Batista and John Tully. His research focuses on the computational studies of photosystem II and development of new methodologies for electronic friction of molecules on metal surfaces.

Gary W. Brudvig (1954, Grand Forks, ND, United States; B.S. (1976) University of Minnesota, Ph.D. (1981) Caltech) has been a Professor at Yale since 1982, where he currently is the Benjamin Silliman Professor and Chair of Chemistry, Professor of Molecular Biophysics and Biochemistry, and Director of the Yale Energy Sciences Institute.

Victor S. Batista (1966, Buenos Aires, Argentina; Lic. Ciencias Quimicas (1989) from Universidad de Buenos Aires) received his Ph.D. in Theoretical Chemistry (1996) from Boston University. Having completed postdoctoral programs at UC Berkeley (1997–1999) and the University of Toronto (2000), he is now a Professor at Yale University.

The authors declare no competing financial interest.

References

  1. Vinyard D. J.; Ananyev G. M.; Dismukes G. C. Photosystem II: The reaction center of oxygenic photosynthesis. Annu. Rev. Biochem. 2013, 82, 577–606. 10.1146/annurev-biochem-070511-100425. [DOI] [PubMed] [Google Scholar]
  2. McEvoy J. P.; Brudvig G. W. Water-splitting chemistry of photosystem II. Chem. Rev. 2006, 106, 4455–4483. 10.1021/cr0204294. [DOI] [PubMed] [Google Scholar]
  3. Blankenship R. E.Molecular Mechanisms of Photosynthesis, 2nd ed; John Wiley & Sons: Chichester, 2014. [Google Scholar]
  4. Barber J.Photosystem II: The water splitting enzyme of photosynthesis and the origin of oxygen in our atmosphere. Q. Rev. Biophys. 2016, 49, DOI: 10.1017/S0033583516000093. [DOI] [PubMed] [Google Scholar]
  5. Joliot P.; Kok B.. Oxygen evolution in photosynthesis. In Bioenergetics of Photosynthesis; Govindjee, Ed.; Academic Press: New York, 1975; pp 387–412. [Google Scholar]
  6. Kok B.; Forbush B.; McGloin M. Cooperation of charges in photosynthetic O2 evolution-I. A linear four step mechanism. Photochem. Photobiol. 1970, 11, 457–475. 10.1111/j.1751-1097.1970.tb06017.x. [DOI] [PubMed] [Google Scholar]
  7. Debus R. J. FTIR studies of metal ligands, networks of hydrogen bonds, and water molecules near the active site Mn4CaO5 cluster in Photosystem II. Biochim. Biophys. Acta, Bioenerg. 2015, 1847, 19–34. 10.1016/j.bbabio.2014.07.007. [DOI] [PubMed] [Google Scholar]
  8. a Umena Y.; Kawakami K.; Shen J.-R.; Kamiya N. Crystal structure of oxygen-evolving photosystem II at a resolution of 1.9 Å. Nature 2011, 473, 55–60. 10.1038/nature09913. [DOI] [PubMed] [Google Scholar]; b Luber S.; Rivalta I.; Umena Y.; Kawakami K.; Shen J. R.; Kamiya N.; Brudvig G. W.; Batista V. S. S1-state model of the O2-evolving complex of photosystem II. Biochemistry 2011, 50, 6308–6311. 10.1021/bi200681q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Zouni A.; Witt H. T.; Kern J.; Fromme P.; Krauss N.; Saenger W.; Orth P. Crystal structure of photosystem II from Synechococcus elongatus at 3.8 Å resolution. Nature 2001, 409, 739–743. 10.1038/35055589. [DOI] [PubMed] [Google Scholar]
  10. Yano J.; Kern J.; Irrgang K. D.; Latimer M. J.; Bergmann U.; Glatzel P.; Pushkar Y.; Biesiadka J.; Loll B.; Sauer K.; et al. X-ray damage to the Mn4Ca complex in single crystals of photosystem II: a case study for metalloprotein crystallography. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 12047–12052. 10.1073/pnas.0505207102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Grundmeier A.; Dau H. Structural models of the manganese complex of photosystem II and mechanistic implications. Biochim. Biophys. Acta, Bioenerg. 2012, 1817, 88–105. 10.1016/j.bbabio.2011.07.004. [DOI] [PubMed] [Google Scholar]
  12. Vogt L.; Ertem M. Z.; Pal R.; Brudvig G. W.; Batista V. S. Computational insights on crystal structures of the oxygen-evolving complex of photosystem II with either Ca2+ or Ca2+ substituted by Sr2+. Biochemistry 2015, 54, 820–825. 10.1021/bi5011706. [DOI] [PubMed] [Google Scholar]
  13. Kern J.; Alonso-Mori R.; Hellmich J.; Tran R.; Hattne J.; Laksmono H.; Glockner C.; Echols N.; Sierra R. G.; Sellberg J.; et al. Room temperature femtosecond X-ray diffraction of photosystem II microcrystals. Proc. Natl. Acad. Sci. U. S. A. 2012, 109, 9721–9726. 10.1073/pnas.1204598109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kern J.; Alonso-Mori R.; Tran R.; Hattne J.; Gildea R. J.; Echols N.; Glockner C.; Hellmich J.; Laksmono H.; Sierra R. G.; et al. Simultaneous femtosecond X-ray spectroscopy and diffraction of photosystem II at room temperature. Science 2013, 340, 491–495. 10.1126/science.1234273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kern J.; Tran R.; Alonso-Mori R.; Koroidov S.; Echols N.; Hattne J.; Ibrahim M.; Gul S.; Laksmono H.; Sierra R. G.; et al. Taking snapshots of photosynthetic water oxidation using femtosecond X-ray diffraction and spectroscopy. Nat. Commun. 2014, 5, 4371. 10.1038/ncomms5371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kupitz C.; Basu S.; Grotjohann I.; Fromme R.; Zatsepin N. A.; Rendek K. N.; Hunter M. S.; Shoeman R. L.; White T. A.; Wang D.; et al. Serial time-resolved crystallography of photosystem II using a femtosecond X-ray laser. Nature 2014, 513, 261–265. 10.1038/nature13453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Suga M.; Akita F.; Hirata K.; Ueno G.; Murakami H.; Nakajima Y.; Shimizu T.; Yamashita K.; Yamamoto M.; Ago H.; et al. Native structure of photosystem II at 1.95 Å resolution viewed by femtosecond X-ray pulses. Nature 2015, 517, 99–103. 10.1038/nature13991. [DOI] [PubMed] [Google Scholar]
  18. Askerka M.; Wang J.; Brudvig G. W.; Batista V. S. Structural changes in the oxygen-evolving complex of photosystem II induced by the S1 to S2 transition: A combined XRD and QM/MM study. Biochemistry 2014, 53, 6860–6862. 10.1021/bi5011915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Askerka M.; Wang J.; Vinyard D. J.; Brudvig G. W.; Batista V. S. S3 state of the O2-evolving complex of photosystem II: Insights from QM/MM, EXAFS, and femtosecond X-ray diffraction. Biochemistry 2016, 55, 981–4. 10.1021/acs.biochem.6b00041. [DOI] [PubMed] [Google Scholar]
  20. Askerka M.; Vinyard D. J.; Wang J.; Brudvig G. W.; Batista V. S. Analysis of the Radiation-Damage-Free X-ray Structure of Photosystem II in Light of EXAFS and QM/MM Data. Biochemistry 2015, 54, 1713–1716. 10.1021/acs.biochem.5b00089. [DOI] [PubMed] [Google Scholar]
  21. Pal R.; Negre C. F. A.; Vogt L.; Pokhrel R.; Ertem M. Z.; Brudvig G. W.; Batista V. S. S0-state model of the oxygen-evolving complex of photosystem II. Biochemistry 2013, 52, 7703–7706. 10.1021/bi401214v. [DOI] [PubMed] [Google Scholar]
  22. Askerka M.; Vinyard D. J.; Brudvig G. W.; Batista V. S. NH3 binding to the S2 state of the O2-evolving complex of photosystem II: Analog of H2O binding during the S2 → S3 transition. Biochemistry 2015, 54, 5783–5786. 10.1021/acs.biochem.5b00974. [DOI] [PubMed] [Google Scholar]
  23. Henry N. F. M., Lonsdale K.. International Tables for X-ray Crystallography; Kynoch Press: Birmingham, U.K., 1969; Vol. I–IV. [Google Scholar]
  24. Rould M. A.; Carter C. W. Jr. Isomorphous difference methods. Methods Enzymol. 2003, 374, 145–163. 10.1016/S0076-6879(03)74007-5. [DOI] [PubMed] [Google Scholar]
  25. Kraut J. Structural Studies with X-Rays. Annu. Rev. Biochem. 1965, 34, 247–268. 10.1146/annurev.bi.34.070165.001335. [DOI] [PubMed] [Google Scholar]
  26. Stryer L.; Kendrew J. C.; Watson H. C. The Mode of Attachment of the Azide Ion to Sperm Whale Metmyoglobin. J. Mol. Biol. 1964, 8, 96–104. 10.1016/S0022-2836(64)80152-2. [DOI] [PubMed] [Google Scholar]
  27. Kraut J.; Wright H. T.; Kellerman M.; Freer S. T. Pi-, delta-, and gamma-chymotrypsin: three-dimensional electron-density and difference maps at 5 Å resolution, and comparison with chymotrypsinogen. Proc. Natl. Acad. Sci. U. S. A. 1967, 58, 304–311. 10.1073/pnas.58.1.304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Poulos T. L.; Freer S. T.; Alden R. A.; Xuong N. H.; Edwards S. L.; Hamlin R. C.; Kraut J. Crystallographic determination of the heme orientation and location of the cyanide binding site in yeast cytochrome c peroxidase. J. Biol. Chem. 1978, 253, 3730–3735. [PubMed] [Google Scholar]
  29. Wang J. M.; Mauro M.; Edwards S. L.; Oatley S. J.; Fishel L. A.; Ashford V. A.; Xuong N. H.; Kraut J. X-ray structures of recombinant yeast cytochrome c peroxidase and three heme-cleft mutants prepared by site-directed mutagenesis. Biochemistry 1990, 29, 7160–7173. 10.1021/bi00483a003. [DOI] [PubMed] [Google Scholar]
  30. Edwards S. L.; Mauro J. M.; Fishel L. A.; Wang J. M.; Miller M. A.; Xuong N. H.; Kraut J. Where is the radical in compound I of cytochrome c peroxidase? Clues from crystallography and mutagenesis. Prog. Clin Biol. Res. 1988, 274, 463–475. [PubMed] [Google Scholar]
  31. Guskov A.; Kern J.; Gabdulkhakov A.; Broser M.; Zouni A.; Saenger W. Cyanobacterial photosystem II at 2.9-Å resolution and the role of quinones, lipids, channels and chloride. Nat. Struct. Mol. Biol. 2009, 16, 334–342. 10.1038/nsmb.1559. [DOI] [PubMed] [Google Scholar]
  32. Ferreira K. N.; Iverson T. M.; Maghlaoui K.; Barber J.; Iwata S. Architecture of the photosynthetic oxygen-evolving center. Science 2004, 303, 1831–1838. 10.1126/science.1093087. [DOI] [PubMed] [Google Scholar]
  33. Kleywegt G. J.; Jones T. A.. Halloween...Masks and Bones. In From First Map to Final Model; Bailey S., Hubbard R., Waller D., Eds.; SERC Daresbury Laboratory: Warrington, U.K., 1994.
  34. Winn M. D.; Ballard C. C.; Cowtan K. D.; Dodson E. J.; Emsley P.; Evans P. R.; Keegan R. M.; Krissinel E. B.; Leslie A. G. W.; McCoy A.; et al. Overview of the CCP4 suite and current developments. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2011, 67, 235–242. 10.1107/S0907444910045749. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sauter N. K.; Echols N.; Adams P. D.; Zwart P. H.; Kern J.; Brewster A. S.; Koroidov S.; Alonso-Mori R.; Zouni A.; Messinger J.; et al. No observable conformational changes in PSII. Nature 2016, 533, E1–2. 10.1038/nature17983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ugur I.; Rutherford A. W.; Kaila V. R. Redox-coupled substrate water reorganization in the active site of Photosystem II-The role of calcium in substrate water delivery. Biochim. Biophys. Acta, Bioenerg. 2016, 1857, 740–748. 10.1016/j.bbabio.2016.01.015. [DOI] [PubMed] [Google Scholar]
  37. Retegan M.; Krewald V.; Mamedov F.; Neese F.; Lubitz W.; Cox N.; Pantazis D. A. A five-coordinate Mn(IV) intermediate in biological water oxidation: spectroscopic signature and a pivot mechanism for water binding. Chem. Sci. 2016, 7, 72. 10.1039/C5SC03124A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Capone M.; Narzi D.; Bovi D.; Guidoni L. Mechanism of water delivery to the active site of photosystem II along the the S2 to S3 transition. J. Phys. Chem. Lett. 2016, 7, 592–596. 10.1021/acs.jpclett.5b02851. [DOI] [PubMed] [Google Scholar]
  39. Li X. C.; Siegbahn P. E. M. Alternative mechanisms for O2 release and O-O bond formation in the oxygen evolving complex of photosystem II. Phys. Chem. Chem. Phys. 2015, 17, 12168–12174. 10.1039/C5CP00138B. [DOI] [PubMed] [Google Scholar]
  40. French S.; Wilson K. Treatment of Negative Intensity Observations. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1978, 34, 517–525. 10.1107/S0567739478001114. [DOI] [Google Scholar]
  41. Wilson A. J. C. Probability of Measuring Intensity of a Reflection as Negative. Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr. 1978, 34, 474–475. 10.1107/S0567739478000923. [DOI] [Google Scholar]
  42. Hattne J.; Echols N.; Tran R.; Kern J.; Gildea R. J.; Brewster A. S.; Alonso-Mori R.; Glockner C.; Hellmich J.; Laksmono H.; et al. Accurate macromolecular structures using minimal measurements from X-ray free-electron lasers. Nat. Methods 2014, 11, 545–548. 10.1038/nmeth.2887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wang J. Estimation of the quality of refined protein crystal structures. Protein Sci. 2015, 24, 661–669. 10.1002/pro.2639. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wilson A. J. C. The Probability Distribution of X-Ray Intensities. Acta Crystallogr. 1949, 2, 318–321. 10.1107/S0365110X49000813. [DOI] [Google Scholar]
  45. Padilla J. E.; Yeates T. O. A statistic for local intensity differences: robustness to anisotropy and pseudo-centering and utility for detecting twinning. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2003, 59, 1124–1130. 10.1107/S0907444903007947. [DOI] [PubMed] [Google Scholar]
  46. White T. A.; Kirian R. A.; Martin A. V.; Aquila A.; Nass K.; Barty A.; Chapman H. N. CrystFEL: a software suite for snapshot serial crystallography. J. Appl. Crystallogr. 2012, 45, 335–341. 10.1107/S0021889812002312. [DOI] [Google Scholar]
  47. Kabsch W. Processing of X-ray snapshots from crystals in random orientations. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2014, 70, 2204–2216. 10.1107/S1399004714013534. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Powell H. R.; Johnson O.; Leslie A. G. Autoindexing diffraction images with iMosflm. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2013, 69, 1195–1203. 10.1107/S0907444912048524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Evans P. Scaling and assessment of data quality. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2006, 62, 72–82. 10.1107/S0907444905036693. [DOI] [PubMed] [Google Scholar]
  50. Sawaya M. R.; Cascio D.; Gingery M.; Rodriguez J.; Goldschmidt L.; Colletier J. P.; Messerschmidt M. M.; Boutet S.; Koglin J. E.; Williams G. J.; et al. Protein crystal structure obtained at 2.9 Å resolution from injecting bacterial cells into an X-ray free-electron laser beam. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 12769–12774. 10.1073/pnas.1413456111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Lyubimov A. Y.; Uervirojnangkoorn M.; Zeldin O. B.; Zhou Q.; Zhao M.; Brewster A. S.; Michels-Clark T.; Holton J. M.; Sauter N. K.; Weis W. I.; et al. Advances in X-ray free electron laser (XFEL) diffraction data processing applied to the crystal structure of the synaptotagmibn-1/SNARE complex. eLife 2016, 5, e18740. 10.7554/eLife.18740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Young I. D.; Ibrahim M.; Chatterjee R.; Gul S.; Fuller F. D.; Koroidov S.; Brewster A. S.; Tran R.; Alonso-Mori R.; Kroll T.; et al. Structure of photosystem II and substrate binding at room temperature. Nature 2016, 540, 453. 10.1038/nature20161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Saito K.; Umena T.; Kawakami K.; Shen J. R.; Kamiya N.; Ishikita H. Deformation of chlorin rings in the Photosystem II crystal structure. Biochemistry 2012, 51, 4290–4299. 10.1021/bi300428s. [DOI] [PubMed] [Google Scholar]
  54. Wang J.; Wing R. A. Diamonds in the rough: a strong case for the inclusion of weak-intensity X-ray diffraction data. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2014, 70, 1491–1497. 10.1107/S1399004714005318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Cochran W.; Woolfson M. M. The Theory of Sign Relations between Structure Factors. Acta Crystallogr. 1955, 8, 1–12. 10.1107/S0365110X55000017. [DOI] [Google Scholar]
  56. Klug A. Joint Probability Distributions of Structure Factors and the Phase Problem. Acta Crystallogr. 1958, 11, 515–543. 10.1107/S0365110X58001456. [DOI] [Google Scholar]
  57. Karle J.; Hauptman H. The Probability Distribution of the Magnitude of a Structure Factor 0.1. The Centrosymmetric Crystal. Acta Crystallogr. 1953, 6, 131–135. 10.1107/S0365110X5300048X. [DOI] [Google Scholar]
  58. Hauptman H.; Karle J. The Probability Distribution of the Magnitude of a Structure Factor 0.2. The Non-Centrosymmetric Crystal. Acta Crystallogr. 1953, 6, 136–141. 10.1107/S0365110X53000491. [DOI] [Google Scholar]
  59. Wang J. X-ray radiation-induced addition of oxygen atoms to protein residues. Protein Sci. 2016, 25, 1407–1419. 10.1002/pro.2934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Frankel L. K.; Sallans L.; Limbach P. A.; Bricker T. M. Identification of oxidized amino acid residues in the vicinity of the Mn4CaO5 cluster of Photosystem II: implications for the identification of oxygen channels within the Photosystem. Biochemistry 2012, 51, 6371–6377. 10.1021/bi300650n. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Frankel L. K.; Sallans L.; Bellamy H.; Goettert J. S.; Limbach P. A.; Bricker T. M. Radiolytic mapping of solvent-contact surfaces in Photosystem II of higher plants: experimental identification of putative water channels within the photosystem. J. Biol. Chem. 2013, 288, 23565–23572. 10.1074/jbc.M113.487033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wang J. Oxygen additions in serial femtosecond crystallographic protein structures. Protein Sci. 2016, 25, 1797–1802. 10.1002/pro.2987. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Sauter N. K. XFEL diffraction: developing processing methods to optimize data quality. J. Synchrotron Radiat. 2015, 22, 239–248. 10.1107/S1600577514028203. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Neutze R.; Wouts R.; van der Spoel D.; Weckert E.; Hajdu J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 2000, 406, 752–757. 10.1038/35021099. [DOI] [PubMed] [Google Scholar]
  65. Leonov A.; Ksenzov D.; Benediktovitch A.; Feranchuk I.; Pietsch U. Time dependence of X-ray polarizability of a crystal induced by an intense femtosecond X-ray pulse. IUCrJ 2014, 1, 402–417. 10.1107/S2052252514018156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Stumpf V.; Gokhberg K.; Cederbaum L. S. The role of metal ions in X-ray-induced photochemistry. Nat. Chem. 2016, 8, 237–241. 10.1038/nchem.2429. [DOI] [PubMed] [Google Scholar]
  67. Lunin V. Y.; Grum-Grzhimailo A. N.; Gryzlova E. V.; Sinitsyn D. O.; Petrova T. E.; Lunina N. L.; Balabaev N. K.; Tereshkina K. B.; Stepanov A. S.; Krupyanskii Y. K. Efficient calculation of diffracted intensities in the case of nonstationary scattering by biological macromolecules under XFEL pulses. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2015, 71, 293–303. 10.1107/S1399004714025450. [DOI] [PubMed] [Google Scholar]
  68. Gati C.; Bourenkov G.; Klinge M.; Rehders D.; Stellato F.; Oberthur D.; Yefanov O.; Sommer B. P.; Mogk S.; Duszenko M.; et al. Serial crystallography on in vivo grown microcrystals using synchrotron radiation. IUCrJ 2014, 1, 87–94. 10.1107/S2052252513033939. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Rossmann M. G. Serial crystallography using synchrotron radiation. IUCrJ 2014, 1, 84–86. 10.1107/S2052252514000499. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Moffat K. Laue diffraction. Methods Enzymol. 1997, 277, 433–447. 10.1016/S0076-6879(97)77024-1. [DOI] [PubMed] [Google Scholar]
  71. Cornaby S.; Szebenyi D. M.; Smilgies D. M.; Schuller D. J.; Gillilan R.; Hao Q.; Bilderback D. H. Feasibility of one-shot-per-crystal structure determination using Laue diffraction. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2010, 66, 2–11. 10.1107/S0907444909037731. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from ACS Energy Letters are provided here courtesy of American Chemical Society

RESOURCES