Significance
Rotating spiral waves have been observed in a wide variety of nonlinear spatially distributed systems in physics, chemistry, and biology, called excitable media. In medicine, they are associated with cardiac arrhythmias. Nevertheless, how exactly these waves are initiated in excitable tissue remains largely unknown. Several candidate mechanisms have been proposed over the last century, largely based on the assumption of wave breaking due to unexcitable obstacles or the medium’s refractoriness. Here, we have identified a generic mechanism for self-sustained spiral wave generation in inhomogeneous excitable media by localized regions with the fast propagation velocity. We believe our theory creates constructive options to fight these deadly phenomena.
Keywords: excitable media, spirals, reentry, cardiology, ablation
Abstract
Self-sustained waves of electrophysiological activity can cause arrhythmia in the heart. These reentrant excitations have been associated with spiral waves circulating around either an anatomically defined weakly conducting region or a functionally determined core. Recently, an ablation procedure has been clinically introduced that stops atrial fibrillation of the heart by destroying the electrical activity at the spiral core. This is puzzling because the tissue at the anatomically defined spiral core would already be weakly conducting, and a further decrease should not improve the situation. In the case of a functionally determined core, an ablation procedure should even further stabilize the rotating wave. The efficacy of the procedure thus needs explanation. Here, we show theoretically that fundamentally in any excitable medium a region with a propagation velocity faster than its surrounding can act as a nucleation center for reentry and can anchor an induced spiral wave. Our findings demonstrate a mechanistic underpinning for the recently developed ablation procedure. Our theoretical results are based on a very general and widely used two-component model of an excitable medium. Moreover, the important control parameters used to realize conditions for the discovered phenomena are applicable to quite different multicomponent models.
In their seminal theoretical work, Norbert Wiener and Arturo Rosenblueth (1) showed in 1946 that the self-sustained activity in the cardiac muscle can be associated with an excitation wave rotating around an obstacle. This mechanism has since been very successfully applied to the understanding of the generation and control of malignant electrical activity in the heart (2). It is also well known that self-sustained excitation waves, called spirals, can exist in homogeneous excitable media. It has been demonstrated that spirals rotating within a homogeneous medium or anchored at an obstacle are generically expected for any excitable medium. Examples are known in myocardial tissues and the mammalian brain (3, 4), in the aggregation of amoeba colonies (5), in autocatalytic chemical reactions (6, 7), and in the spreading depression in chicken retina (8), as well as in the catalytic reactions of carbon monoxide gas on a platinum surface (9) and also in intracellular calcium dynamics (10). Spirals have important consequences for medicine, where they are known to cause sudden cardiac death (11, 12). Recently, an atrial defibrillation procedure was clinically introduced that locates the spiral core region by detecting the phase-change point trajectories of the electrophysiological wave field and then, by ablating that region, restores sinus rhythm (13, 14). This is clearly at odds with the Wiener–Rosenblueth mechanism because a further destruction of the tissue near the spiral core should not improve the situation.
Here, we show theoretical results that help to resolve this issue. We found that spirals can be anchored not only at an obstacle, but also at a region where the propagation velocity is higher than in the surrounding medium. Moreover, in the presence of such a fast propagation region (FPR), spirals can be nucleated after application of one stimulus only. Thus, FPRs can be more disruptive to plane wave propagation than the obstacle, where spiral generation needs at least two stimuli (15–17). In general, our findings have important consequences for excitable media dynamics and, in particular, provide understanding of the medical ablation procedure that can stop atrial fibrillation (13, 14) by destruction of a FPR at the spiral core.
Mathematical Model
Because the phenomenon of spiral generation is universal, it is best investigated from a general point of view. Let us consider a medium that consists of active elements locally connected to each other by a diffusion-like coupling (characterized by a coupling strength ). The medium’s resting state can be excited by the application of a suprathreshold external stimulus that initiates a propagating excitation wave. Such a wave consists of a rapid transition (wavefront) from a stable resting state to an excited state, followed by a plateau, and finally by a recovery transition (waveback) toward the resting state.
This type of dynamics is usually modeled by a system of nonlinear reaction–diffusion equations. For instance, such systems are commonly used to simulate electrophysiological waves in cardiac or nervous tissue (18), chemical waves in Dictyostelium discoideum (19), and in the chemical Belousov–Zhabotinsky reaction (20).
Our study is based on the general two-component reaction–diffusion system of the form
| [1] |
| [2] |
Here, the local kinetics of an activator and an inhibitor is specified by the nonlinear functions and . Our numerical simulations are based on a slightly modified Barkley model (21) that is a very common example of a two-component reaction–diffusion system (Eqs. 1 and 2), where the nonlinear functions and are:
| [3] |
| [4] |
The parameter predetermines a large time-scale difference between the fast activator and the slow inhibitor . This excitable medium model assumes the existence of a stable resting state at and .
Unidirectional Propagation Block in a One-Dimensional Medium
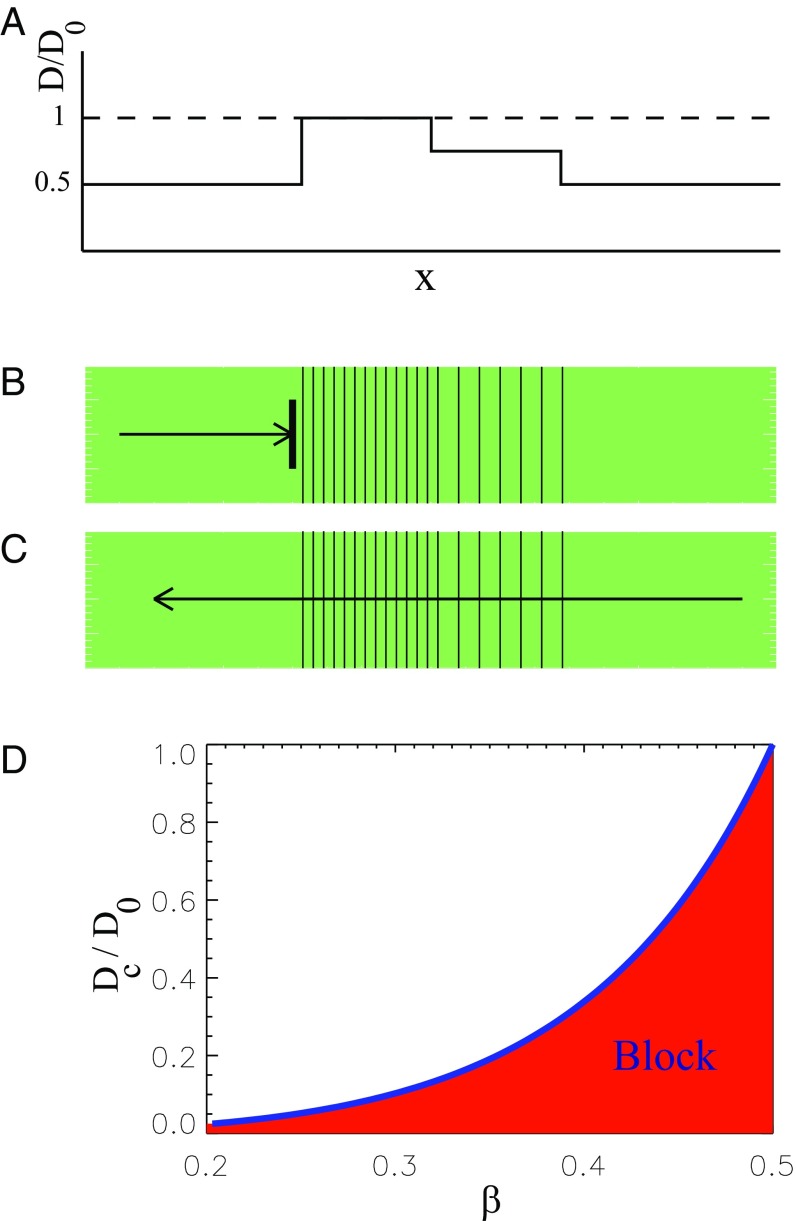
For a general excitable medium, unidirectional propagation block can be realized based on a phenomenon termed source–sink mismatch in the cardiology literature (22). This we demonstrate exemplarily in Fig. 1, where we assume that an initially homogeneous one-dimensional (1D) medium with the coupling strength is remodeled so that the coupling strength is decreased everywhere except in a central region (Fig. 1A). In the central region, we assume a stepped variation so that the coupling strength steps from left to right from , over , to , and then back to . A wave traveling to the right is blocked (Fig. 1B), whereas a wave traveling to the left passes through. The conduction block for the right-traveling wave can be explained by the source–sink mismatch induced by a sharp increase of the coupling strength above a critical value (23–25). In other words, the flux generated by the poorly coupled cells (source) with is insufficient to raise the activity of the well-coupled cells (sink) with above the excitation threshold. Because of the two-step increase, the left-traveling wave propagation continues because the individual changes in at each step do not exceed the critical value (Fig. 1C). Finally, the left-traveling wave is leaving the central region because well-coupled elements (source) very easily excite poorly-coupled cells (sink). Although this step sequence might seem artificial at first sight, let us point out that the phenomenon is general. All it requires is a sufficiently steep increase of the coupling strength on one side and a smoother one on the other.
Fig. 1.
Conditions for a unidirectional propagation block due to a sharp increase of the coupling strength . (A) The stepwise spatial variation of the parameter , with . (B) A right-traveling wave is blocked because it cannot overcome a large step in , where is greater than the critical value. (C) A left-traveling wave propagates over the two steps in , both of which are less than the critical value. (D) The critical value of the coupling strength at the inhomogeneity boundary as a function of the excitation threshold .
To clarify the conditions for a possible propagation block induced by a fast parameter increase in a 1D medium, we consider a limiting case and set . In this limit, Eq. 1 describes a bistable distributed system, where, in addition to the resting state, there exists an excited state and an unstable steady state , which represents the excitation threshold. Under certain conditions, it is possible to induce a wavefront (e.g., propagating from left to right) and corresponding to a transition from to (26). The propagation velocity of this front reads
| [5] |
where the function is determined by the specific form of . Thus, in a homogeneous medium, the propagation velocity is an increasing function of both parameters and .
To analyze the conditions for a conduction block, we are taking into account that the time derivative in Eq. 1 vanishes in the case of a motionless front. Hence, the profile of the front in the general case of the synchronous jumps of the parameters and at is a solution of the ordinary differential equation
| [6] |
where , for and , for . The boundary conditions and the continuity condition at read as
| [7] |
| [8] |
Multiplying Eq. 6 by , integrating over from to , and using Eqs. 7 and 8, we obtain the following equation:
| [9] |
that determines the value at the point of the parameter jump as a function of the ratio . Note that the front can be stopped only if . Thus, Eq. 9 for gives the critical ratio , above which the propagating block can be observed for general form of the kinetic function .
Fig. 1D summarizes the analytical results for the critical value of the relative increase of the coupling strength that leads to propagation block as a function of excitation threshold . Note that a region with a stronger coupling strength can be recognized as a FPR because the propagation velocity is proportional to , according to Eq. 5. For the function , given by Eq. 3, the critical ratio can be expressed analytically as
| [10] |
For used in our simulations, it gives .
This analytic prediction agrees with direct numerical computations as illustrated by Fig. 2. In Fig. 2A, the propagation block is due to a jump of the coupling strength . Here and , while everywhere. A wave initiated in the left part of this 1D medium is blocked and approaches a stationary profile shown in Fig. 2A. Note that the spatial derivatives of the variable has a jump at the point that, however, corresponds to the continuity condition (Eq. 8). Moreover, the front can be stopped, if the parameter is nonuniformly distributed (27) (e.g., and ), whereas everywhere, as shown in Fig. 2B. Here, the profile of the variable is perfectly smooth. In both cases, the ratio slightly exceeds the critical value determined by Eq. 10. Because of this, the approached value is slightly smaller than the excitation threshold .
Fig. 2.
Stationary profile of a front initially propagating from left to right and stopped due to a jump in the medium’s parameters at . Numerical simulations of a slightly modified Barkley model (Eqs. 1–4) with . (A) for , for and everywhere. (B) for , for , and everywhere.
The Effect of FPRs in Two Dimensions
To extend our results on a 2D case, numerical simulations of Eqs. 1–4 with no-flux boundary conditions have been performed for , , , and in a rectangular region of size . Spatial step , time step . The variable and are varied within the well-determined range and . This spatiotemporal dynamics of the variables and is represented in Figs. 3–7 by color-coded distribution of the excitation phase , where . The phase is defined as , where an angle determines the direction of the vector with components and on the phase plane. According to this definition, corresponds to the resting state of the medium (green areas in Figs. 3–7), yellow (dark blue) narrow regions represent the wavefront (waveback), and red areas correspond to a wave plateau, whereas blue ones represent the refractory regions.
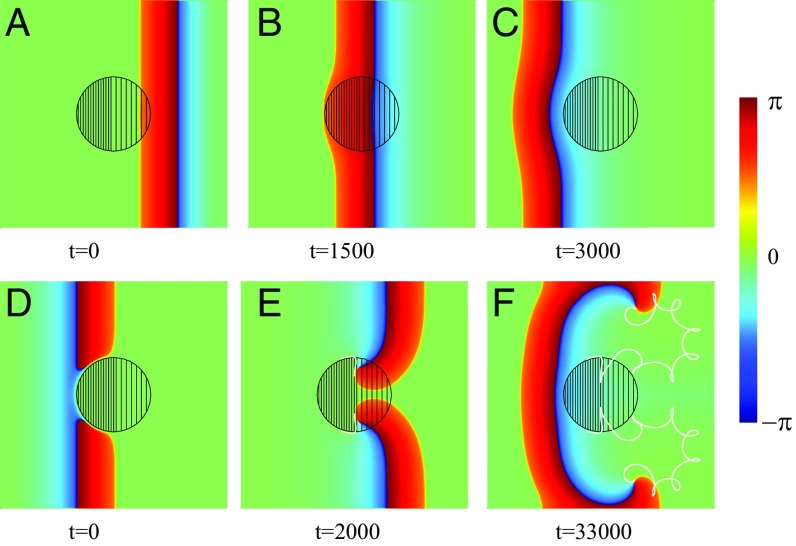
Fig. 3.
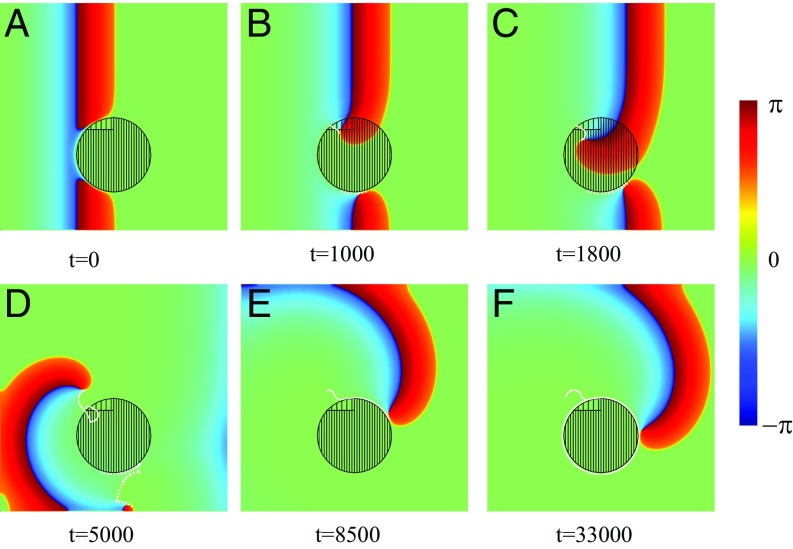
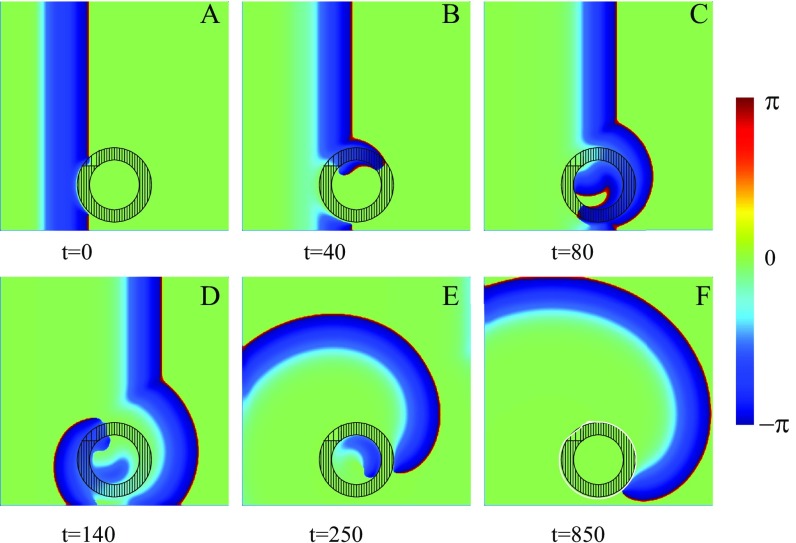
Spiral wave initiation due to a FPR in a 2D inhomogeneous medium. Within the left-hand part of the central circular FPR (dense filling). Within the right-hand part, (rare filling). Within the rest of the medium, . Snapshots of a left-traveling wave (A–C) and a wave propagating in the opposite direction (D–F) are shown. The trajectories of the created phase-change points are shown by white lines (E and F).
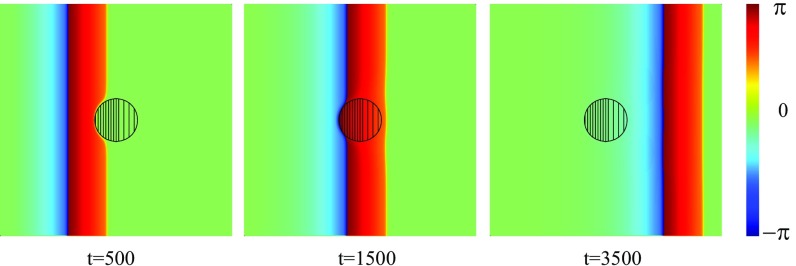
Fig. 7.
Dynamics of an initially planar wave propagating from left to right in a medium with a small-size FPR. The coupling strength is fixed to everywhere except the central circular region of the radius , where within the left part (dense filling) and in the right part (rare filling). everywhere.
Let us now consider a 2D excitable medium with a FPR. Although this example may seem again rather simple, it captures the generic and essential mechanism. Fig. 3 shows numerical results of the wave propagation simulated for the excitable media model described by Eqs. 1–4. Everywhere, except the circular FPR of radius , (with ) and within the left half of the FPR and in the right half . A planar left-traveling excitation wave initiated at the right propagates unbroken (i.e., the wave travels through the region with a continuous wavefront that speeds up slightly within the FPR) (Fig. 3B). Finally, the wave approaches the left medium’s boundary and disappears due to the no-flux boundary conditions.
This is in stark contrast to a right-traveling wave. There, a plane wave created near the left side of the medium is blocked at the FPR due to the sharp increase of the parameter exceeding the critical value. This results in a wave break and the creation of two phase-change points (spiral tips), where the wavefront coincides with the waveback, as shown in Fig. 3D. Because of the propagation block, the spiral tips move along the boundary of the FPR until they reach its vertical symmetry axis. There, the increase of the parameter is not sufficient to block the wave anymore, and the spiral tips penetrate into the FPR (solid white lines in Fig. 3E). Moreover, the waves are able to penetrate into the left-hand part of the FPR like a 1D wave does in Fig. 1C. They start to rotate around the phase-change points, and two counterrotating spirals separate from the FPR, as shown in Fig. 3F. The further dynamics of these counterrotating spirals is determined by the parameters of the medium and the boundary conditions. They represent a source of a self-sustained activity. It is remarkable that they were created immediately with the first incoming wave.
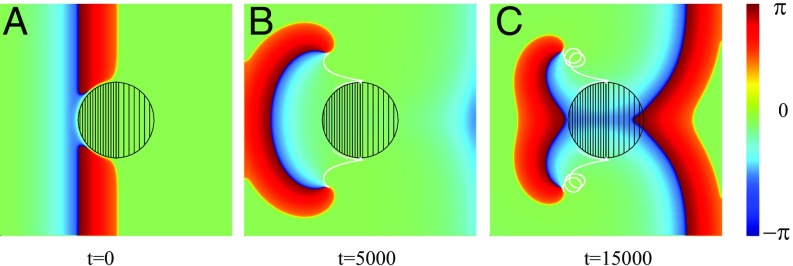
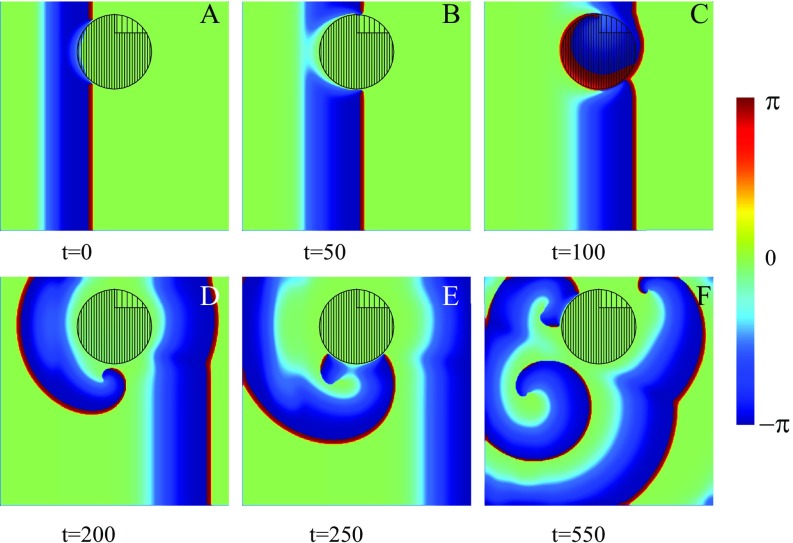
In the above example, we demonstrated a generic mechanism for the generation of two spirals. Of course, the perfect symmetry observed is a direct consequence of the chosen geometry, and this will not be the case in general. Let us therefore demonstrate an example where the symmetry is broken. As we shall show below, the asymmetry of the inhomogeneity within the FPR allows one of the spirals to travel away, while the other pins to the region. This we show exemplarily in Fig. 4, where an asymmetric inhomogeneity of the region was simulated. As in the previous case, a right-traveling wave is blocked at the FPR (Fig. 4A), and two spiral tips are created. A clockwise-rotating spiral penetrates into the central region, while the other, counterclockwise-rotating spiral moves around the FPR (Fig. 4B). As a result, the clockwise spiral rotates faster and pushes the counterclockwise spiral toward the medium’s boundary (Fig. 4C), where it eventually disappears (Fig. 4D). The clockwise-rotating spiral continues to move around the FPR (Fig. 4E). In other words, the single remaining spiral is pinned and circulates around the FPR.
Fig. 4.
Spiral wave initiation due to an asymmetric FPR slightly shifted of center. Within the FPR (dense filling), except a small region where (rare filling). Within the rest of the medium, . (A) A wave initially propagating from the left is blocked and broken. (B–D) The trajectories of the spiral tips are shown by white solid and dotted lines. (E and F) One spiral tip disappears due to the collision with the medium’s boundary (dotted line). The trajectory of the remaining tip is shown (solid line).
Spatial Inhomogeneity of the Parameter A
Note that in the two examples illustrated by Figs. 3 and 4, the medium inhomogeneity is solely due to the variations of the coupling strength , while the parameter is spatially uniform. This parameter characterizes, for example, cardiac ion channel density, which can be effected by heart disease (28). According to Eq. 10, the inhomogeneity of the parameter is equally important for the wave block. To check these predictions, the corresponding numerical computations have been performed for the 2D inhomogeneous medium, where the coupling strength is fixed as , while in the left part of the central circular-shaped FPR of radius and in the right part, as shown in Fig. 5. Within the rest of the medium, .
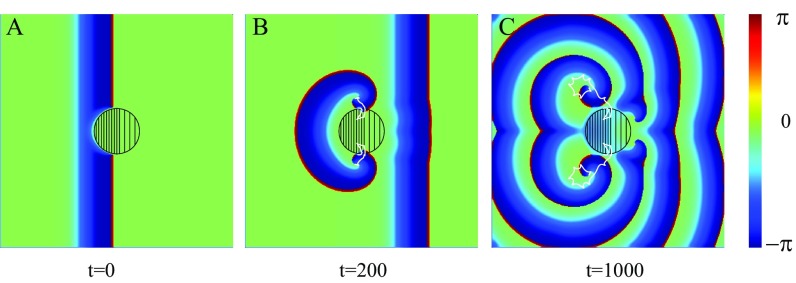
Fig. 5.
Spiral wave initiation due to a FPR breaking up of a plane wave induced near the left edge of the medium and propagating to the right. (A–C) The parameter is fixed to within the left part of the central circular region (dense filling) and in the right part (rare filling). Within the rest of the medium, . The trajectories of two created spiral tips are shown by white solid lines in B and C.
Initially, a plane wave is originated near the left edge of the medium, and the motion of this wave to the right is blocked by the FPR. Again, because of a nonzero value of , the propagating wave is broken, and two spiral tips are created, as shown in Fig. 5A. These spiral tips are moving along the FPR boundary. They can penetrate into this region only near the right part of the FPR boundary, where . After this penetration, they also can cross the boundary between the right and left parts of the inhomogeneity, because here the ratio is below the critical one determined by Eq. 10 (Fig. 5B). The wavefronts start to rotate around the spiral tips, and then two spiral waves leave the central region, as shown in Fig. 5C.
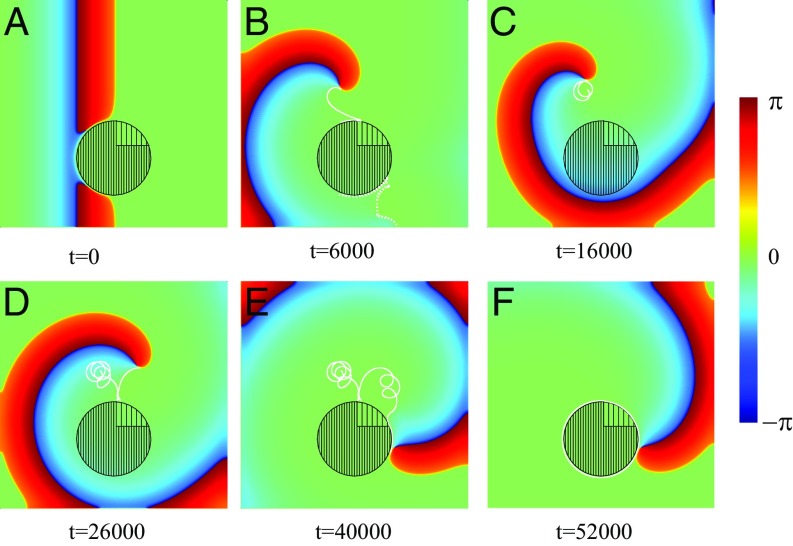
As before, pure mirror symmetric dynamics of two simultaneously created spiral waves can be destroyed by the use of an asymmetric shape of the FPR, as shown in Fig. 6. A planar wave propagating from the left medium’s boundary is stopped and broken. As a result, two spiral tips are created (Fig. 6A). These two spiral tips first move along the FPR boundary. Then, the clockwise-rotating wave reaches the right part of the FPR, where the ratio is less than a critical value for a wave block. Here, the front can penetrate into the FPR and starts to rotate. This rotation pushes the counterrotating wave toward the bottom boundary of the medium and forces it to disappear (Fig. 6B). The remaining spiral wave first makes several rotations near the FPR and then starts to rotate around it, as shown in Fig. 6C.
Fig. 6.
Spiral wave initiation due to an asymmetric FPR. The parameter is fixed to everywhere except the circular region, where (dense filling) and (rare filling). Snapshots of a wave propagating from left to right are shown. (A–F) The trajectories of two created spiral tips are shown by white solid and dotted lines in B–F. One spiral tip disappears due to the collision with the medium’s boundary (dotted line). The trajectory of the remaining spiral tip is shown in C–F (white solid line).
This scenario is very similar to the one illustrated in Fig. 4. Thus, the numerical results obtained for the FPR created by spatial variation of the parameter are very similar to ones for spatial variations of the coupling strength .
Discussion
General Properties.
Our results demonstrate a generic mechanism for spiral wave creation in an excitable media with FPRs. The mechanism requires a sufficiently steep increase of the propagation velocity, due to spatial variations of the parameter and/or . Please note that spatial variations of the excitation threshold will not result in a wave break and thus the creation of spiral waves. Moreover, our numerical results clearly demonstrate that the existence of a propagation block strongly depends on the local curvature of the inhomogeneity boundary. In the special case of a straight boundary, the critical ratio is given by Eq. 10. With decreasing radius of the FPR, the critical ratio increases. This can be seen from the following numerical result: Let us assume that the parameter is spatially homogeneous (), but within the left part of the central circular shaped FPR , while in the right one . Everywhere else, . If the radius of the inhomogeneity region is given as , an initially planar wave is stopped at its boundary, as shown in Fig. 3D. Nevertheless, for smaller , a planar wave penetrates into the FPR, and no spiral tips are created, as shown in Fig. 7.
In addition, as is well known for the case of obstacles, our findings carry over to three dimensions, where the FPRs can nucleate scroll waves (or rotors), which are a 3D version of spirals. In this situation, of course, geometry and inhomogeneity structure will also be very important, just as they are in two dimensions.
Let us stress again that the exemplary shown phenomena are truly generic. In the simulations, the shape and size of the chosen FPR can easily be extended to other geometry and other structured inhomogeneity. The fundamental and generic properties reported remain the same.
The FPR mechanism also represents an important generic correction to the commonly accepted notion that at least two stimuli are needed to create spiral waves in an excitable medium (15–17). Our analysis emphasizes the important role of the FPR as the nucleation center for reentry in contrast to the common expectation that a wave break occurs at the boundary between an excitable and unexcitable region. Please note that a possibility to initiate a permanent reentry activity after a single stimulation was also demonstrated in a much less generic reaction–diffusion system (29, 30) and in a strongly anisotropic 2D tissue (31, 32). In a medium with a nonlocalized inhomogeneity, a creation of a drifting spiral wave, which disappears after several rotations, has been reported (25).
The proposed mechanism for an initiation of a well-developed and permanently rotating spiral wave represents an alternative to the scenarios mentioned above. Because of its simplicity and generality, it can be realized in quite different excitable media.
Relevance to Ablation Procedures in Medicine.
The spiral wave dynamics illustrated by Fig. 4 resembles many features of the electrophysiological excitation dynamics observed during atrial fibrillation (13, 14). Indeed, it is well known that atrial fibrosis in the aging heart can lead to spatial variations in the electrical conductivity of the functional syncytium, comprising interconnected cardiomyocytes embedded in a variably sized nonconducting extracellular matrix (33). This can decrease the conductivity of a part of the cardiac muscle, and it is reasonable to assume that some regions within this part remain unchanged. These high-conductivity regions resemble the FPRs in our model. These FPRs can cause malignant electric activity. As shown in our theoretical examples, the single spiral pinned at the FPR can determine the dynamics, because it would have a faster period than the wave trains produced by the pacemaker. This then would lead to the destruction of the cardiac rhythm and would be identified by a cardiologist as cardiac tachycardia or fibrillation.
Of course, the structure of a real atrial tissue is much more complicated than the very general model description considered above. In the modern literature, the Fenton–Karma (FK) model (34, 35) is widely used to simulate electrical activity in atrial tissue in more detail (35, 36). To validate the applicability of our findings, the simulations with the FK model have been performed and are shown in SI Text. These data not only reproduce all scenarios obtained above with the Barkley model, but also open new possibilities for self-sustained reentry creation (see Figs. S1–S3). It is shown that for the chosen parameter set of the FK model, the propagation block is achievable at the relatively strong inhomogeneity, which is, however, not unusual for cardiac tissue (36–38).
Fig. S1.
Spiral wave initiation due to a FPR in a 2D medium. Within the left-hand part of the central circular FPR, cm2/ms (dense filling). Within the right-hand part, (rare filling). Within the rest of the medium, . Snapshots of a right-traveling wave are shown. (A–C) The trajectories of the created phase-change points are shown by white lines. The domain has a size cm2, The FPR radius is cm, and the parameter .
Fig. S3.
Spiral wave initiation due to a FPR in a 2D medium. Within the domain with a dense filling, cm2/ms. Within the domain with rare filling, . Within the rest of the medium, . Snapshots of an initially right-traveling wave are shown. (A–F) The trajectory of the created phase-change point is shown by a white line. The domain has a size cm2, The FPR radius is cm, and the parameter .
Note that a variety of cardiac disease processes can cause ion-channel remodeling, in particular, resulting in a variation of the ion current density (28). This remodeling can be simulated in the framework of our model as a variation of the parameter . It is natural to assume that, in a living organism, this remodeling can occur not uniformly in space, and one can expect the existence of some spots with relatively small remodeling or even remodeling-free regions. Thus, the ion-channel remodeling is also able to create FPRs and can cause spiral wave creation.
In the context of the proposed mechanism, one can assume that the self-sustained electric activation pattern is due to a spiral wave pinned to a FPR. Hence, a FPR would be identified as the spiral wave core region in this measurement (13, 14). This could be clinically validated by the measurement of the coupling strength within the spiral core and in the surrounding tissue. By destroying the spiral core region (i.e., by completely suppressing propagation in this area), the FPR would be transferred to a real obstacle, where the Wiener–Rosenblueth mechanism would act. This mechanism, however, is less likely to produce reentry, and thus the probability for spiral wave initiation should be significantly reduced. What we described above provides a mechanistic underpinning of the recently clinically introduced local ablation procedure terminating atrial fibrillation (13, 14).
We believe that the FPR mechanism also has important consequences for the understanding of the effects of surgical treatment on epilepsy in the human brain (39). There are already direct experimental measurements indicating the existence of true spiral waves of cortical neuronal activities, which may provide a spatial framework to organize cortical oscillations (4). The discovered mechanism can be one possible reason for a spontaneous spiral wave creation. Like in the case of the cardiac tissue, the necessary conditions for spiral wave initiation can be created by variations of the coupling strength or ion-channel density due to different disease processes.
In conclusion, this study may have important consequences for the treatment of malignant electrical activities in the heart and brain. The generic mechanism presented here remains, of course, to be investigated in more detail.
SI Text
Although the main topic of the paper is to illustrate a scenario of self-sustained reentry generation in quite different kinds of excitable media, it is important to validate the relevance of the findings to atrial arrhythmias. To this aim, we are using the well-known FK model (34, 35), which is widely applied to simulate electrical activity in atrial tissue (35, 36). Parameter values for the FK model were chosen as set 1 from ref. 35, and the propagation block has been induced due to a sharp variation of the coupling strength .
It is important to stress that, for this parameter set, the excitation threshold is rather small in comparison with used above in the Barkley model. This results in a very small critical ratio , which leads to a wave propagation block (Fig. 1D). In the corresponding 1D simulations, the critical value has been determined.
In our simulations, we use the well-established value of the coupling strength cm2/ms (35) as a “normal” value corresponding to the FPR (dense filling), while within the surrounding medium . The intermediate value of the coupling strength (rare filling) is . This very strong variation of the coupling strength is not unusual for cardiac tissue (36–38). For instance, similar values have been used to simulate figure-of-eight reentry pattern (36) and reentry initiation during bradycardia (24).
The three-component FK model was simulated on a square grid by using a standard finite difference scheme with spatial discretization cm and time step ms. The variables and vary within the range and . The spatiotemporal dynamics of these variables is represented by color-coded distribution of the excitation phase , where . The phase is defined as , where an angle determines the direction of the vector with components and on the phase plane. According to this definition, corresponds to the resting state of the medium (green areas in Figs. S1–S3). Red narrow regions represent the wavefront.
Let us first reproduce the general idea of the self-sustained rotor initiation realized with the Barkley model and represented in Fig. 3 D–F. The simulation results obtained for the FK model are shown in Fig. S1. The simulated domain includes a circular-shaped FPR of radius cm. A wave initiated at the left domain boundary is blocked at the FPR due to the sharp increase of the coupling strength (Fig. S1A). Two separated wave segments continue to move along the FPR boundary and reach the right part of the FPR, where the value of the coupling strength is smaller than the critical one. Here, both wave segments are able to penetrate inside the FPR. Moreover, they are able to penetrate inside the left part of the FPR, because the wave propagation from the left to the right is not blocked (Fig. 1C). They collide in the middle of the FPR, and this collision pushes both waves into the surrounding region. The trajectories of the both phase-change points are shown by white lines (Fig. S1B). They describe hypocycloidal trajectories as determined by the medium parameters (Fig. S1C) (35).
In the second example of our simulations, the internal structure of the FPR and its location are asymmetric, as shown in Fig. S2. A wave propagating from the left side is broken, and both wave segments continue to move along the FPR boundary (Fig. S2A). A clockwise-rotating wave segment penetrates into the central region, while the other, counterclockwise-rotating segment continues to move around the FPR (Fig. S2B). The wave, which has penetrated into the FPR, is propagating much faster than the wave within the surrounding media due to the large difference in the coupling strength. The ratio between the conduction velocities should be estimated as . As a result, this wave quickly occupies the FPR (Fig. S2C). After this, it propagates to the left. However, due to collision with the right propagating wave, it is broken and starts to curve around the newly created phase-change point (Fig. S2D). Then, it collides with the FPR and additional two phase-change points are created (Fig. S2E). This process of new phase-change point creation is continued further and further. The corresponding spatiotemporal activity resembles that of atrial fibrillation (Fig. S2F).
Fig. S2.
Spiral wave initiation due to an asymmetric FPR in a 2D medium. Within the part of the circular FPR with a dense filling, cm2/ms. Within the part with a rare filling, . Within the rest of the medium, . Snapshots of an initially right-traveling wave are shown. (A–F) The domain has a size cm2, The FPR radius is 0.5 cm, and the parameter .
This is different from the wave dynamics shown in Fig. 3, because the central region of the FPR is occupied quickly. To prevent this fast occupation of the FPR, we decreased the coupling strength in the middle of the FPR, as shown in Fig. S3. Again, the right propagating wave is broken, and the initial situation shown in Fig. S3A is very similar to one in Fig. 2B. However, the wave that penetrated inside the FPR is not able to cross the central area as fast as in the previous case. It starts to move around the core with the normal coupling strength (Fig. S3 C and D). However, this fast rotation within a narrow channel with the large coupling strength is impossible, because the wavefront dies due to collision with its own refractory tail. The wave slowly propagating around the FPR survives (Fig. S3E). Thus, the spiral wave created after application of a single stimulus is anchored at the FPR (Fig. S3F).
The computational results described above reproduce typical properties of the atrial tissue and the general scenario of self-sustained reentry initiation shown in the main text.
Acknowledgments
We thank Gerd Hasenfuß, Alain Pumir, Marco Tarantola, Markus Zabel, and Wolfram Zimmermann for critically commenting on the drafts of this manuscript. This work was supported by the Max Planck Society and the German Center for Cardiovascular Research and Grant DFG-SFB937 Collective Behavior of Soft and Biological Matter.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1611475114/-/DCSupplemental.
References
- 1.Wiener N, Rosenblueth A. The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Arch Inst Cardiol Mex. 1946;16:205–265. [PubMed] [Google Scholar]
- 2.Luther S, et al. Low-energy control of electrical turbulence in the heart. Nature. 2011;475:235–239. doi: 10.1038/nature10216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Allesie MA, Bonke FIM, Schopman FJG. Circus movement in rabbit atrial muscle as a mechanism of tachycardia. Circ Res. 1973;33:54–62. [PubMed] [Google Scholar]
- 4.Huang X, et al. Spiral waves in disinhibited mammalian neocortex. J Neurosci. 2004;24:9897–9902. doi: 10.1523/JNEUROSCI.2705-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gerisch G. Periodische Signale steuern die Musterbildung in Zellverbänden. Naturwissenschaften. 1971;58:430–438. doi: 10.1007/BF00624616. [DOI] [PubMed] [Google Scholar]
- 6.Zaikin AN, Zhabotinsky AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating systems. Nature. 1970;225:535–537. doi: 10.1038/225535b0. [DOI] [PubMed] [Google Scholar]
- 7.Winfree AT. Spiral waves of chemical activity. Science. 1972;175:634–636. doi: 10.1126/science.175.4022.634. [DOI] [PubMed] [Google Scholar]
- 8.Gorelova NA, Bures J. Spiral waves of spreading depression in the isolated chicken retina. J Neurobiol. 1983;14:353–363. doi: 10.1002/neu.480140503. [DOI] [PubMed] [Google Scholar]
- 9.Jakubith S, Rotermund HH, Engel W, von Oertzen A, Ertl G. Spatiotemporal concentration patterns in a surface reaction: Propagating and standing waves, rotating spirals, and turbulence. Phys Rev Lett. 1990;65:3013–3016. doi: 10.1103/PhysRevLett.65.3013. [DOI] [PubMed] [Google Scholar]
- 10.Lechleiter J, Girard S, Peralta E, Clapham D. Spiral calcium wave propagation and annihilation in Xenopus laevis oocytes. Science. 1991;252:123–126. doi: 10.1126/science.2011747. [DOI] [PubMed] [Google Scholar]
- 11.Carmiliet E, Vereecke J. Cardiac Cellular Electrophysiology. Kluwer; Dordrecht, The Netherlands: 2002. [Google Scholar]
- 12.Davidenko JM, Pertsov AV, Salomonsz R, Baxter W, Jalife J. Stationary and drifting spiral waves of excitation in isolated cardiac muscle. Nature. 1992;355:349–351. doi: 10.1038/355349a0. [DOI] [PubMed] [Google Scholar]
- 13.Narayan SM, et al. Treatment of atrial fibrillation by the ablation of localized sources. J Am Coll Cardiol. 2012;60:628–636. doi: 10.1016/j.jacc.2012.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shivkumar K, Ellenbogen KA, Hummel JD, Miller JM, Steinberg JS. Acute termination of human atrial fibrillation by identification and catheter ablation of localized rotors and sources: First multicenter experience of focal impulse and rotor modulation (FIRM) ablation. J Cardiovasc Electrophysiol. 2012;23:1277–1285. doi: 10.1111/jce.12000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zykov VS. Simulation of Wave Processes in Excitable Media. Manchester Univ Press; Manchester, UK: 1987. [Google Scholar]
- 16.Fox JJ, Gilmour RF, Jr, Bodenschatz E. Conduction block in one-dimensional heart fibers. Phys Rev Lett. 2002;89:198101. doi: 10.1103/PhysRevLett.89.198101. [DOI] [PubMed] [Google Scholar]
- 17.Quail T, Shrier A, Glass L. Spatial symmetry breaking determines spiral wave chirality. Phys Rev Lett. 2014;113:158101. doi: 10.1103/PhysRevLett.113.158101. [DOI] [PubMed] [Google Scholar]
- 18.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Martiel JL, Goldbeter A. A model based on receptor desensitization for cyclic AMP signaling in Dictyostelium cells. Biophys J. 1987;52:807–828. doi: 10.1016/S0006-3495(87)83275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tyson JJ. Oscillations, bistability, and echo waves in models of the Belousov-Zhabotinskii reaction. Ann N Y Acad Sci. 1979;316:279–295. [Google Scholar]
- 21.Barkley D. A model for fast computer simulation of waves in excitable media. Physica D. 1991;49:61–70. [Google Scholar]
- 22.Rudy Y. Reentry: Insights from theoretical simulations in a fixed pathway. J Cardiovasc Electrophysiol. 1995;6:294–312. doi: 10.1111/j.1540-8167.1995.tb00402.x. [DOI] [PubMed] [Google Scholar]
- 23.Mornev OA. Elements of “Optics” of autowaves. In: Krinsky VI, editor. Self-Organization Autowaves and Structures Far from Equilibrium. Vol 28. Springer; Berlin: 1984. pp. 111–118. [Google Scholar]
- 24.Zemlin CW, Pertsov AM. Bradycardic onset of spiral wave re-entry: Structural substrates. Europace. 2007;9:vi59–vi63. doi: 10.1093/europace/eum205. [DOI] [PubMed] [Google Scholar]
- 25.Zemlin CW, Mitera BG, Pertsov AM. Spontaneous onset of atrial fibrillation. Physica D. 2009;238:969–975. doi: 10.1016/j.physd.2008.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fisher RA. The wave of advance of advantageous genes. Ann Eugen. 1937;7:355–369. [Google Scholar]
- 27.Gao X, Zhang H, Zykov V, Bodenschatz E. Stationary propagation of a wave segment along an inhomogeneous excitable stripe. New J Phys. 2014;16:033012. [Google Scholar]
- 28.Nattel S. Effects of heart disease on cardiac ion current density versus current amplitude: Important conceptual subtleties in the language of arrhythmogenic ion channel remodeling. Circ Res. 2008;102:1298–1300. doi: 10.1161/CIRCRESAHA.108.178087. [DOI] [PubMed] [Google Scholar]
- 29.Kohl P, Hunter P, Noble D. Stretch-induced changes in heart rate and rhythm: Clinical observations, experiments and mathematical models. Prog Biophys Mol Biol. 1999;71:91–138. doi: 10.1016/s0079-6107(98)00038-8. [DOI] [PubMed] [Google Scholar]
- 30.Weise LD, Panfilov AV. Emergence of spiral wave activity in a mechanically heterogeneous reaction-diffusion-mechanics system. Phys Rev Lett. 2012;108:228104. doi: 10.1103/PhysRevLett.108.228104. [DOI] [PubMed] [Google Scholar]
- 31.Christensen K, Manani KA, Peters NS. Simple model for identifying critical regions in atrial fibrillation. Phys Rev Lett. 2015;114:028104. doi: 10.1103/PhysRevLett.114.028104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kudryashova NN, Teplenin AS, Orlova YV, Selina LV, Agladze K. Arrhythmogenic role of the border between two areas of cardiac cell alignment. J Mol Cell Cardiol. 2014;76:227–234. doi: 10.1016/j.yjmcc.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 33.Rother J, et al. Crosstalk of cardiomyocytes and fibroblasts in co-cultures. Open Biol. 2015;5:150038. doi: 10.1098/rsob.150038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fenton F, Karma A. Vortex dynamics in three-dimensional continuous myocardium with fiber rotation: Filament instability and fibrillation. Chaos. 1998;8:20–47. doi: 10.1063/1.166311. [DOI] [PubMed] [Google Scholar]
- 35.Fenton FH, Cherry EM, Hastings HM, Evans SJ. Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos. 2002;12:852–892. doi: 10.1063/1.1504242. [DOI] [PubMed] [Google Scholar]
- 36.Rappel WJ, Zaman JAB, Narayan SM. Mechanisms for the termination of atrial fibrillation by localized ablation: Computational and clinical studies. Circ Arrhythm Electrophysiol. 2015;8:1325–1333. doi: 10.1161/CIRCEP.115.002956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Arora R, et al. Arrhythmogenic substrate of the pulmonary veins assessed by high-resolution optical mapping. Circulation. 2003;107:1816–1821. doi: 10.1161/01.CIR.0000058461.86339.7E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hocini M, et al. Electrical conduction in canine pulmonary veins: Electrophysiological and anatomic correlation. Circulation. 2002;105:2442–2448. doi: 10.1161/01.cir.0000016062.80020.11. [DOI] [PubMed] [Google Scholar]
- 39.Engel J. A greater role for surgical treatment of epilepsy: Why and when? Epilepsy Curr. 2003;3:37–40. doi: 10.1046/j.1535-7597.2003.03201.x. [DOI] [PMC free article] [PubMed] [Google Scholar]