Dynamical theory of shear bands in structural glasses

Significance

When glasses are under imposed stresses or strains, they are subject to plastic deformation. Unlike their crystal counterparts, shear within the glasses localizes in thin bands, known as shear bands. Forming the shear bands can lead to structural failure of the whole sample and prevent using glasses as structural materials. In this work, we show how shear bands arise dynamically by the coupling of activated dynamics of configurationally rearranging regions with elastic strain transport. This result also explains the non-Newtonian flow of glasses.

Abstract

The heterogeneous elastoplastic deformation of structural glasses is explored using the framework of the random first-order transition theory of the glass transition along with an extended mode-coupling theory that includes activated events. The theory involves coupling the continuum elastic theory of strain transport with mobility generation and transport as described in the theory of glass aging and rejuvenation. Fluctuations that arise from the generation and transport of mobility, fictive temperature, and stress are treated explicitly. We examine the nonlinear flow of a glass under deformation at finite strain rate. The interplay among the fluctuating fields leads to the spatially heterogeneous dislocation of the particles in the glass, i.e., the appearance of shear bands of the type observed in metallic glasses deforming under mechanical stress.

Whether and how glasses flow have been fascinating questions for a long time. In the absence of stress, a glass seems to be static on human timescales, the molecules being arranged like a frozen snapshot of the liquid state. In fact, molecules in the glass are constantly moving and the glass itself is not in a state of equilibrium. Even without applied stress, molecules do change their locations through rare, activated events. These events occur at a rate that is both spatially and temporally heterogeneous. Glasses therefore continue to evolve, albeit slowly, as they approach equilibrium and age (1). These activated events are accelerated by applied stresses and typically will act to reduce the stress so that under sufficient stress the glass will not just deform elastically but visibly flow and possibly break. The deformations caused by stress are not uniform in the glass, but appear to concentrate in shear bands (2–4). In this work, we show how shear bands arise dynamically by the coupling of the activated dynamics of configurationally rearranging regions with elastic strain transport. The heterogeneous activated dynamics of glasses under mechanical deformation are described using a first-principle framework based on the random first-order transition (RFOT) theory along with an extended mode-coupling theory that describes how activated events are coupled in space and time (5–10).

The random first-order transition theory of glasses is a microscopic theory that has already provided a unified quantitative description of large number of aspects of the behavior of supercooled liquids and structural glasses (11). The theory brings together two seemingly disparate aspects of glass formation: the breaking of replica symmetry that occurs in mean-field models and a theory of the activated events that tend to locally restore replica symmetry in systems with short-range interactions (7, 8, 12–14). In mean-field models, there is a special temperature $T_d$ at which a dynamical transition to immobility occurs discontinuously. Above this temperature the system is well described by ordinary mode-coupling theory. Below this temperature, however, an exponentially large number of frozen states suddenly emerge. In the mean-field theory these states individually live forever. For systems of finite dimensions with finite range forces, this transition at the dynamical temperature $T_d$ is wiped out by locally activated events. A theory of these ergodicity-restoring activated events resembling the nucleation theory of ordinary first-order transition allows one to estimate relaxation timescales. These thermally activated motions cease only at a lower thermodynamic transition temperature $T_K$ where the configurational entropy would vanish, as happens in the mean-field approximation. When these features are combined, one finds that cooperatively rearranging regions (CRRs) emerge that reach the nanometer length scale at the usual laboratory glass transition temperature. These regions continue to evolve as the glass ages. The rate at which rearrangement occurs locally may be called the “mobility.” Mode-coupling effects then allow the mobility once it has been generated by activated events below $T_d$ to be transported out from its source—giving a microscopic basis for the notion of facilitation (15, 16). Mobility transport is an essential feature determining the detailed distribution of relaxation times in glasses and supercooled liquids (17).

Within RFOT theory the heterogeneous dynamics of the glass can be understood in terms of a mobility field $\mu (x,t)$ that has space and time dependences. Previously we detailed how a continuum description of the mobility-field dynamics can be derived by explicitly expanding the mode-coupling memory kernels of a spatially inhomogeneous system, using a Taylor series in terms of the gradients of the mobility that is basically the local memory kernel (10, 18). To account for the random nature of molecular motion in the glasses, the equations for the mobility field are then completed by introducing stochastic terms for mobility generation and transport effects to describe a state of constrained local equilibrium. We have shown this framework quantitatively describes a broad range of experimental measurements on dynamics both in glasses and in equilibrated supercooled liquids. One of the theory’s most dramatic predictions is the existence and speed of the front-like transformation of stable glasses that occurs when they are heated (10, 16). The theory also predicts the hysteretic character of calorimetric experiments and the temperature dependence of the stretching exponent in the supercooled liquids and explicitly quantifies the appearance of two seemingly distinct equilibration mechanisms in aging glasses found recently in experiment (19) but predicted earlier by Lubchenko and Wolynes (1).

To describe shear bands we must first understand how stress affects glass mobility (19). RFOT theory describes this effect by first noting that when a sample of glass is put under a uniform shear stress $\sigma$, the energy per unit volume is immediately raised by an amount ${\sigma }^2/2G$, where $G$ is the elastic shear modulus. This additional energy can be released by accessing a state of zero local shear through a reconfiguration event. Stress then can rejuvenate glasses much as they rejuvenate when they are heated because stress increases the rate at which local reconfiguration events occur. For sufficient applied stress, the additional stress energy becomes so large that reconfiguration can occur without any free energy barrier. By determining the critical value of stress that makes the free energy barrier vanish, RFOT theory has predicted the mechanical strength of the glass, explaining why glasses are among the strongest known materials (20). In this work, we describe the dynamical behavior of the glass when external forces are applied by coupling the RFOT theory of mobility generation and transport under stress with elastic theory.

Several phenomenological models have been developed to explain how amorphous solids deform (3, 4, 21, 22). The free-volume model proposed by Spaepen and colleagues (23–25) nearly three decades ago inspired the notion of a shear transformation zone (STZ). That model postulates that plastic flows are caused by a series of driven creation events of free volume via individual jumps of particles. The shear transformation zone theory argues that the plastic deformation involves irreversible rearrangements of small clusters of particles whose detailed nature is, however, left unspecified (26). It was later realized that particle rearrangements in a shear transformation zone might be triggered by neighboring particle jumps that again are described by the free-volume model (27–30). Impressionistically this model has many points in common with the present framework but the STZ theory introduces many phenomenological parameters. In contrast, the RFOT theory allows first-principle calculation of all of the elements of elastoplastic deformation, using only input thermodynamic and elastic data.

Theoretical Framework

To account for the dynamics of a deformed glass, we first recount the continuum mechanics for a glass, emphasizing the role of spatiotemporal fluctuations. Initially the fluctuations of the local properties of the glass are inherited from the liquid state from which it is formed. When the liquid is cooled at a rate faster than the basic relaxation time, persistent disordered structures of the liquid state are to a first approximation frozen in at the glass transition temperature. The structure, however, actually continues to evolve, proceeding to lower-energy states. This protocol gives rise to frozen internal stresses within the sample of a glass. At the continuum level the equation of motion for these stresses can be found by equating the internal stress force $\partial {\sigma }_{ik}/\partial x_k$ to the product of the acceleration ${\ddot{u}}_i$ and its mass density $\rho$,

$$\rho {\ddot{u}}_i=\frac{\partial {\sigma }_{ik}}{\partial x_k},$$ [1]

where $u_i$ is the $i\text{th}$ component of the displacement vector, and ${\sigma }_{ik}$ is the element of the internal stress tensor (31). This stress is a key to understanding the nontrivial behavior of the glass under applied forces.

Glass dynamics occur on a range of length scales and timescales and strongly depend on the glass’s history. When a stress is applied for times short compared with the structural relaxation time $({\tau }_{\alpha })$, a glass elastically deforms much like a familiar crystalline solid. During this time interval, the internal stresses give rise to material deformations following the theory of elasticity; i.e., ${\sigma }_{ik}=\mathrm{\hspace{0.17em}2}G{u}_{ik}$, where $G$ is the elastic shear modulus, and $u_{ik}$ is the strain relative to the initial glassy configuration. On the other hand, when stresses are applied sufficiently slowly compared with the relaxation time, the glass behaves like an ordinary fluid. On these longer timescales the stress tensor depends on the local velocity of material deformation following the usual expression for viscous stresses in fluids; i.e., ${\sigma }_{ik}=\mathrm{\hspace{0.17em}2}\eta {\dot{u}}_{ik}$, where $\eta$ is the viscosity that depends linearly on the relaxation time, i.e., $\eta \sim G\tau$. At intermediate times, the local dynamics are reasonably well described by a local Maxwell model for viscoelasticity (31),

$$\frac{\partial {\sigma }_{ik}}{\partial t}=2G{\dot{u}}_{ik}-\mu {\sigma }_{ik},$$ [2]

where $u_{ik}$ is the strain tensor, $u_{ik}\equiv \frac{1}{2}\left(\frac{\partial u_i}{\partial x_k}+\frac{\partial u_k}{\partial x_i}\right)$, and $\mu$ a space and time varying quantity itself is the local mobility that is the inverse of the structural relaxation time, $\mu \approx \mathrm{\hspace{0.17em}1}/{\tau }_{\alpha }$ of a small region. In RFOT theory the well-known global nonexponential dynamics of glasses arise through the fluctuations of local mobility that dynamically depend on space and time.

Owing to the aperiodic structure of glasses, we must complete the description of the stress evolution by introducing stochastic sources for the stress fluctuations as is familiar in the continuum theory due to Landau (32):

$$\frac{\partial {\sigma }_{ik}}{\partial t}=2G{\dot{u}}_{ik}-\mu {\sigma }_{ik}+\delta h_{ik}.$$ [3]

The generation noise term $\delta h_{ik}$ satisfies the local fluctuation–dissipation relation $⟨\delta h_{ik}(x,t)\delta h_{ik}(x\prime ,t\prime )⟩=\mathrm{\hspace{0.17em}2}\mu ⟨{\sigma }_{ik}(x,t){\sigma }_{ik}(x\prime ,t\prime )⟩$, where the correlations between the components of the random stress tensor depend on $\zeta$ and $\eta$, which are the second viscosity and the dynamic viscosity, respectively, and can be written as $⟨{\sigma }_{ik}(r_1,t_1){\sigma }_{lm}(r_2,t_2)⟩=\mathrm{\hspace{0.17em}2}T\left[\eta \left({\delta }_{il}{\delta }_{km}+{\delta }_{im}{\delta }_{kl}\right)+\left(\zeta -\frac{2}{3}\eta \right){\delta }_{ik}{\delta }_{lm}\right]\delta (r_1-r_2)\delta (t_1-t_2)$. Here we treat the glass as incompressible, so the fluctuations of the shear stress generation noise term can be reduced to being described by $⟨\delta h_{ik}(x,t)\delta h_{ik}(x\prime ,t\prime )⟩=\mathrm{\hspace{0.17em}4}\eta \mu T\left(1+{\delta }_{ik}\right)\delta (x-x\prime )\delta (t-t\prime ).$ In general both normal and shear stresses must be considered, depending on the Poisson ratio. We neglect also direct heating by shear, assuming a relatively high thermal conduction. Furthermore, in heating and cooling protocols we presently ignore the thermal expansion of the glass, which can introduce additional strains.

The local mobility field is defined as the longtime rate at which particles in a glass reconfigure. This field is formulated in real space through the low-frequency Fourier transform of the memory kernel of the mode-coupling theory (MCT). As discussed earlier by Bhattacharyya, Bagchi, and Wolynes (BBW) (15, 33), activated processes provide an extra decay channel for structural correlations beyond conventional mode-coupling theory, which ultimately restores the ergodicity of the glass. In the BBW treatment the total mobility field has two distinct contributions, one coming directly from the activated dynamics and another part coming from idealized mode coupling (18):

$$\mu (r,t)={\mu }_{hop}(r,t)+{\mu }_{mct}(r,t).$$ [4]

The completely microscopic theory of the mode-coupling memory kernel leads to a rather complicated mathematical form involving coupling to density fluctuation modes with other wave vectors. For inhomogeneous systems the relevant correlations must be rewritten in terms of multipoint spectral quantities. Expanding the resulting extended MCT with activated processes in a Taylor series in spatial and temporal derivatives of the mobility field leads to continuum equations that again must be supplemented with local random forces to restore the local fluctuation–dissipation theorem, giving the equation

$$\frac{\partial {\mu }_{mct}}{\partial t}=\frac{\partial }{\partial x_i}\left(\frac{2{\mu }^2{\xi }^2}{{\overline{\mu }}_{mct}}\frac{\partial {\mu }_{mct}}{\partial x_i}\right)-\frac{2{\mu }^2}{{\overline{\mu }}_{mct}}\left({\mu }_{mct}-{\overline{\mu }}_{mct}\right)+\delta g+\frac{\partial \delta j}{\partial x_i},$$ [5]

where $\xi$ is a length scale corresponding to the range of the four-point correlation function (34). In this equation ${\overline{\mu }}_{mct}=\overline{\mu }-{\mu }_{hop}$, where $\overline{\mu }$ is the uniform solution of the BBW equations for a uniform system. Here we approximate ${\mu }_{hop}$ by using the ultralocal theoretical analysis of aging glasses by Lubchenko and Wolynes. This theory contains a local fictive temperature $T_f$, which, when combined with the ambient temperature $T$, determines the local energy density (1). In the absence of stress, well below $T_d$ the rates of the reconfiguration events depend both on the local fictive temperature $T_f$ and on the ambient temperature $T$ assumed uniform,

$$\overline{\mu }={\mu }_0\exp \left\{-\frac{{\gamma }^2}{4k_{B}T\mathrm{\Delta }{c}_p{T}_g\left(\frac{T-T_K}{T_K}-\ln \frac{T}{T_f}\right)}\right\},$$ [6]

where $\gamma (T)=\frac{3\sqrt{3\pi }}{2}{k}_{B}T\ln \left[\frac{{(a/d_L)}^2}{\pi e}\right]$, $d_L$ is the Lindemann length, and $a$ is the interparticle spacing. Adding stress changes this relation because under a uniform stress $\sigma$, the energy per unit volume of a rearranging region is immediately raised by an amount of ${\sigma }^2/2G$, where $G$ is the elastic shear modulus. An additional factor $\kappa$ is needed to account for additional strain energy relieved by harmonically distorting the surrounding region of a region once that region becomes stress-free (35). As discussed by Wisitsorasak and Wolynes (20), this factor is analogous to the energy cost of distorting an inclusion in a solid body as calculated by Mackenzie (35). The $\kappa$ is given in terms of Poisson’s ratio $\nu$ as $\kappa =3-6/(7-5\nu )$. For a typical Poisson’s ratio for metallic glasses $\kappa$ is approximately equal to 1.8. This relief of strain energy lowers the activation free-energy barrier. If the applied stress is large enough, the free-energy barrier will vanish, leading to the limiting strength of the glass typically near half the Frenkel limit (20).

Simply adding the relieved strain energy to the reconfigurational driving force allows one to write the barrier for the flow of a glass under stress in terms of the same function that gives the activation free energy for an equilibrium liquid in terms of its configurational entropy $\mathrm{\Delta }{F}^{‡}=\mathrm{\Delta }{F}^{‡}(T{s}_c+\mathrm{\Delta }\mathrm{\Phi }+\kappa {\sigma }^2{V}_{\text{bead}}/2G)$, where $\mathrm{\Delta }\mathrm{\Phi }$ is the excess energy of the glassy states frozen in at the fictive temperature, $\mathrm{\Delta }\mathrm{\Phi }=\mathrm{\Delta }{c}_p(T_g)T_g\ln (T_f/T)$. The crossover to barrierless reconfiguration finally occurs once the stress is large enough so that condition $s_c(T_c)=s_c^{\text{perc}}-\frac{\mathrm{\Delta }\mathrm{\Phi }}{T}-\kappa \frac{{\sigma }^2}{2GT}{V}_{\text{bead}}$ is satisfied. In this relation $s_c^{\text{perc}}$ is the critical configurational entropy where percolation-like clusters can form spontaneously. This condition from RFOT theory looks much like the J-point scenario where barrierless reconfiguration can be approached by tuning either the temperature $T$ or the stress $\sigma$ (36). As this critical value is approached from below, the RFOT predicts that the shapes of cooperatively rearranging regions in glassy liquids change from being relatively compact regions to fractal ones (37). Following Stevenson et al.’s (37) theory for the beta relaxation without stress, the weight for such rearrangements is exponentially suppressed when $\delta s_c\equiv s_c-\left(s_c^{\text{perc}}-\frac{\mathrm{\Delta }\mathrm{\Phi }}{T}-\kappa \frac{{\sigma }^2}{2G}{V}_{\text{bead}}N\right)$ is positive, but barrierless reconfiguration dominates at higher stress. Thus, to capture the transition to barrierless reconfiguration, we can then write the local mobility as in ref. 18,

$$\overline{\mu }={\mu }_0\exp \left\{\frac{-\mathrm{\Theta }(\delta s_c)\cdot {\gamma }^2}{\left[4k_{B}T\mathrm{\Delta }{c}_p{T}_g\left(\frac{T-T_K}{T_K}-\ln \frac{T}{T_f}\right)+\kappa \frac{{\sigma }^2}{2G}\right]}\right\},$$ [7]

where $\mathrm{\Theta }(\delta s_c)$ is the Heaviside step function that is defined as a piecewise constant function: $\mathrm{\Theta }(\delta s_c)=\mathrm{\hspace{0.17em}1}$ for $\delta s_c>\mathrm{\hspace{0.17em}0}$, $\mathrm{\Theta }(\delta s_c)=\mathrm{\hspace{0.17em}1}/2$ for $\delta s_c=\mathrm{\hspace{0.17em}0}$, and $\mathrm{\Theta }(\delta s_c)=\mathrm{\hspace{0.17em}0}$ for $\delta s_c<\mathrm{\hspace{0.17em}0}$. We see that in RFOT theory all of the quantities determining the local mobility are given explicitly in terms of quantities available from independent experiments and are not treated as ad hoc adjustable parameters.

The fictive temperature determines the local energy density of a region (1). Following the arguments of Lubchenko and Wolynes, the fictive temperature relaxes following an ultralocal relation with the local decay rate also given by the mobility $\mu (r,t)$:

$$\frac{\partial T_f}{\partial t}=-\mu \left(T_f-T\right)+\delta \eta .$$ [8]

Again a random term is needed to ensure the fluctuation–dissipation relations are locally obeyed. These fluctuations in the local fictive temperature arise from the happenstance nature of the activated events that generate and transport the mobility field. The fluctuating barriers ultimately cause the nonexponential time correlations found in glasses. We treat the random force terms in the equation as coarse-grained white noises with strengths and correlation lengths that also reflect the length scales of the activated events. The noise intensities are found by requiring the linearized equations to satisfy locally fluctuation–dissipation relations. The local fictive temperature fluctuation $\delta \eta$ is thus $⟨\delta \eta (x,t)\delta \eta (x\prime ,t\prime )⟩=\mathrm{\hspace{0.17em}2}\mu T^2\frac{k_B}{\mathrm{\Delta }{c}_p{N}^{‡}}\delta (x-x\prime )\delta (t-t\prime )$, where $N^{‡}$ is the number of molecular units in a cooperatively rearranging region. The fluctuations in mobility generation $\delta g$ and in the transport of mobility $\delta j$ lead to fluctuations in free-energy barrier heights that cause the stretched exponential relaxation with a bare stretching parameter ${\beta }_0=\mathrm{\hspace{0.17em}1}/\sqrt{1+{(\delta F^{‡}/k_{B}T)}^2}$. Linearizing the mobility equation while treating $\overline{\mu }$ as constant, the local fluctuation–dissipation relation yields a mobility-generating noise with correlations $⟨\delta g(x,t)\delta g(x\prime ,t\prime )⟩=\mathrm{\hspace{0.17em}2}\overline{\mu }{\mu }^2\left(1/{\beta }_0^2-1\right){\left(T_g/T\right)}^2\delta (x-x\prime )\delta (t-t\prime )$ and a random mobility flux with correlations $⟨\delta j(x,t)\delta j(x\prime ,t\prime )⟩=\mathrm{\hspace{0.17em}2}\overline{\mu }{\xi }^2{\mu }^2\left(1/{\beta }_0^2-1\right){\left(T_g/T\right)}^2\delta (x-x\prime )\delta (t-t\prime )$ (10).

Results and Discussion

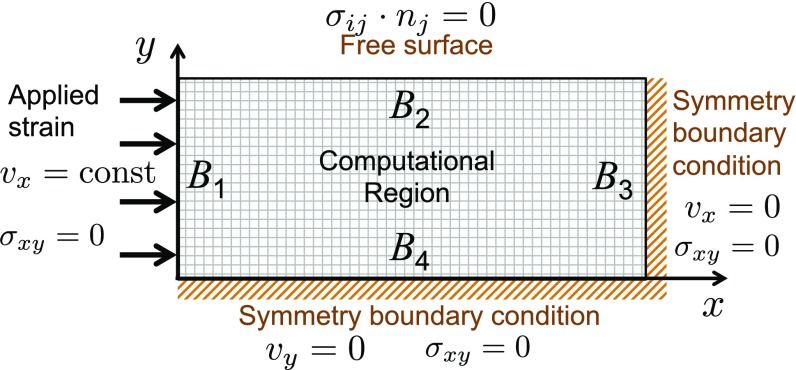
In this work, we carried out for illustration numerical calculations of the mechanical responses of a sample mimicking the bulk metallic glass ${\mathrm{Zr}}_{41.2}{\mathrm{Ti}}_{13.8}{\mathrm{Cu}}_{12.5}{\mathrm{Ni}}_{10}{\mathrm{Be}}_{22.5}$ (Vitreloy 1) under uniaxial compression with controlled strain rates (Fig. 1). These calculations are analogous to experiments carried out by Lu et al. (38). Full 3D calculation would be very computer-time demanding. Due to the symmetry of the macroscopic problem, we study instead a model in two dimensions of such a sample with uniaxial compression along the x direction. This essentially describes a thin-layer slab, but where surface mobility changes are neglected (39). We solve the system of Eqs. 1, 3–5, and 8 numerically by a finite-difference method that takes account of the stiffness of the equations, thereby neglecting sound waves (40, 41). To treat the stochastic terms in the numerical calculations, we used the Euler–Maruyama method in which random numbers are normally distributed (41). Consequently the mobility may rarely become negative locally. To avoid such unrealistic situations, the negative values of the mobility when they occur are set to zero. The computational domain used in this study is an 80 $\times$ 30 rectangular grid with a grid size of 1 nm. To mimic the uniaxial compression experiment the left boundary $B_1$ and the top surface are taken to undergo uniaxial compression along the x direction and to be free, respectively. At the same time the boundary conditions on the bottom $B_4$ and the right surface $B_3$ correspond to the symmetry conditions.

Fig. 1.

Schematic diagram represents the boundary conditions of a 2D system of a deformed glass. A sample is compressed on the left boundary with constant rate, whereas the boundary on the top is the free surface boundary.

To account for the fluctuations we note that we are essentially studying a thin slab roughly of width $\xi$ in the third dimension. Vitreloy 1 is a bulk glass-forming metallic alloy that exhibits high resistance to deformation in comparison with its crystalline counterpart (42). We chose to investigate this system because all of its relevant material properties are well documented in the literature (42–46). The Kauzmann ($T_K$), glass transition ($T_g$), and crystallization temperatures ($T_x$) are 553 K, 623 K, and 710 K, respectively, and the elastic modulus is 34.10 GPa (38, 42). In the laboratory the samples of the glass were tested at various temperatures ($T$) above and below the nominal glass transition: 603 K, 613 K, 623 K (the glass transition temperature of Vitreloy 1), 633 K, and 643 K. In the laboratory the samples also were compressed at various strain rates ($\dot{ϵ}$) ranging from $1\times {10}^{-4}$ s⁻¹ to $1\times {10}^{-2}$ s⁻¹ and the stress and strain were measured. The preparation procedure used by us follows the experimental setups as described in ref. 38.

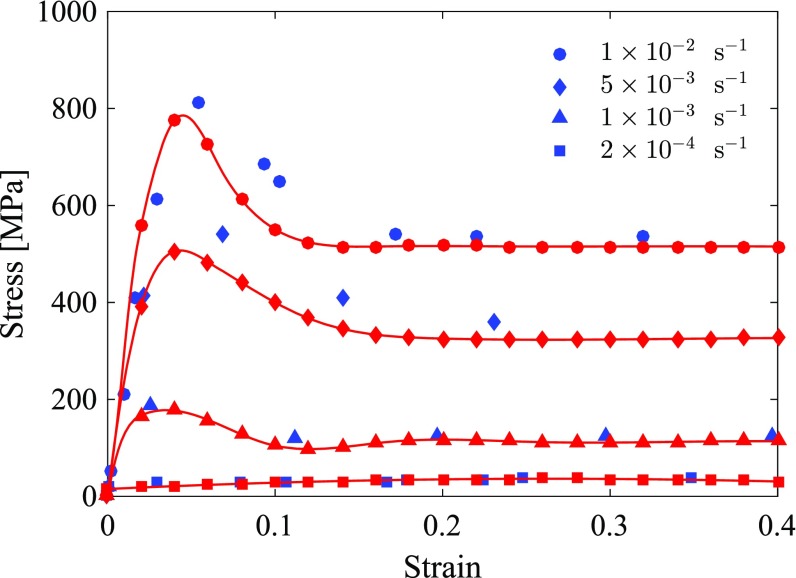
Fig. 2 shows the predicted stress and strain histories for the 2D Vitreloy 1 glass slab at different applied strain rates. The experimental results from ref. 38 for the same system in 3D are shown as blue symbols for comparison. As seen from the graph, both in our numerical calculations and in the laboratory the stress initially linearly increases as the strain increases. The linear behavior of the glass in this regime indicates the glass acts simply as an elastic solid. Increasing stress allows the glass to relax at a faster rate, leading to the apparently non-Newtonian fluid behavior in the late regime of the stress–strain curve where the stresses reach a plateau regime. Before transiting to the plateau regime an overshoot of the stress occurs at a high strain rate whose magnitude strongly depends on the strain rate. For strain rates below $1\times {10}^{-3}$ s⁻¹, no stress overshoot is observed.

Fig. 2.

The predicted stress–strain curves for a 2D sample of a Vitreloy 1 metallic glass at different strain rates. The ambient temperature of the glass is set to $T=643$ K, while the sample is being compressed. The stress initially linearly increases as the strain increases. The curves then transit to the steady-state regime. Once the applied strain rate is higher than a threshold, a stress overshoot appears. The blue symbols are experimental data taken from ref. 38 for a 3D sample of Vitreloy 1. The red symbols show the simulation results.

It is worth mentioning that, in studies of some metallic glasses such as ${\mathrm{Zr}}_{58.5}{\mathrm{Cu}}_{15.6}{\mathrm{Ni}}_{12.8}$ ${\mathrm{Al}}_{10.3}{\mathrm{Nb}}_{2.8}$ metallic glass compressed at a high strain rate of 0.2 s⁻¹, the stress–strain curve exhibits a more intricate nonlinear oscillation in which the stress overshoot is followed by undershoot (22, 46). In our 2D calculation we have never seen this behavior. This issue may require full 3D simulation of a larger system.

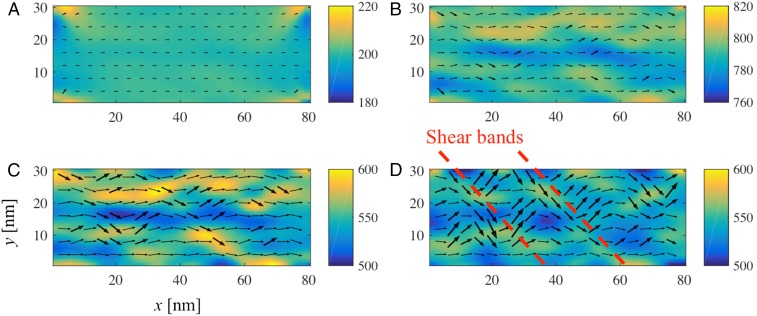
Apart from these global measurements the numerical calculations resolve how the flows develop in space and time. Fig. 3 shows various stages of the Vitreloy 1 flow after the sample was compressed with a strain rate of 0.01 s⁻¹. The colored contour plots show the level of the equivalent stress (47), which is defined as ${\sigma }_{eq}\equiv \frac{1}{\sqrt{2}}\sqrt{{({\sigma }_{xx}-{\sigma }_{yy})}^2+{\sigma }_{yy}^2+{\sigma }_{xx}+6{\sigma }_{xy}^2}$. Each subplot is also superimposed with a vector field showing the normal strain axes. Fig. 3 A–D is shown when the strains ($ϵ$) equal 0.01, 0.03, 0.1, and 0.2, respectively. The initial stage of the compression is shown in Fig. 3A. The stress increases quickly and reaches a maximum value when the strain is approximately equal to 0.03. Shear bands start developing at this stage.

Fig. 3.

Predictions of the various deformation fields in the Vitreloy 1 model under the applied strain rate of 0.01 s⁻¹ at various stages of deformation. The ambient temperature $T=643$ K. Each plot shows the equivalent stress overlaid with the strain field. The color bar on the right of each plot shows the magnitude of the stress in units of MPa. (A) The strain $ϵ=0.01$, (B) $ϵ$ = 0.03, (C) $ϵ$ = 0.1, and (D) $ϵ=0.2$.

Snapshots of the mobility field and the fictive temperature pattern are presented in Fig. 4 A and B for the case when the strain is equal to 0.2. Both plots also show the strain fields. The corresponding stress pattern at the same time is shown in Fig. 3D. The regions that develop shear bands also have higher mobility and higher fictive temperature than their neighboring regions. Experimental observations of similar results have been found in many other metallic glasses (3, 48).

Fig. 4.

A 2D simulation snapshot of the Vitreloy 1 specimen under a strain rate of 0.01 s⁻¹. The ambient temperature is equal to $T=643$ K. The data are shown when the strain is equal to 0.2. The color contour in A shows the logarithm of the mobility field and that in B represents the fictive temperature field. Both plots are superimposed with the strain field.

The plots in Figs. 3 and 4 emphasize the interplay among the stress, strain, mobility, and fictive temperature fields in which these fluctuations lead to a very heterogeneous flow of the sample. The heterogeneity of the glass reflects the fact that the rates of reconfiguration events vary throughout the sample. These fluctuation are not completely independent from their neighbors, but become correlated over short length scales that then grow as the flow proceeds much like a rejuvenation front (16). This correlation allows the glass to differentially deform different regions to develop shear banding patterns like those in the laboratory (3, 4, 49, 50). We have marked the shear bands observed in our simulation in Fig. 3D with dashed lines. Note that neither band is perpendicular to the sides of the domain. The tilted angle of the band is 45° with respect to the horizontal axis and the width of the bands is ∼10 nm.

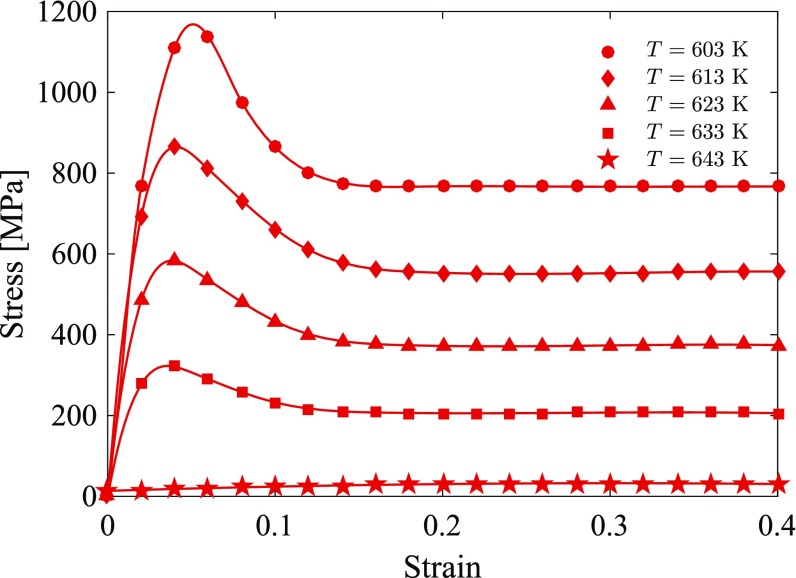
We also studied the temperature dependence of shear deformation and show the results for this in Effect of Temperature on Stress-Strain Behavior, Effect of Strain Rate and Temperature on Apparent Viscosity, and Figs. S1–S3. At fixed strain rates, the ambient temperature strongly influences the magnitude of the overshoot stress and the steady-state stress values.

Fig. S1.

The simulation results showing the effect of temperature on the stress–strain behavior of Vitreloy 1. The graph plots the simulation results of the steady-state stress vs. the strain at five different temperatures, $T=603$ K, 613 K, 623 K, 633 K, and 643 K, when the Vitreloy 1 specimens were compressed with the strain rate of $2\times {10}^{-4}$ s⁻¹. Solid lines are interpolating curves to guide the eye.

Fig. S3.

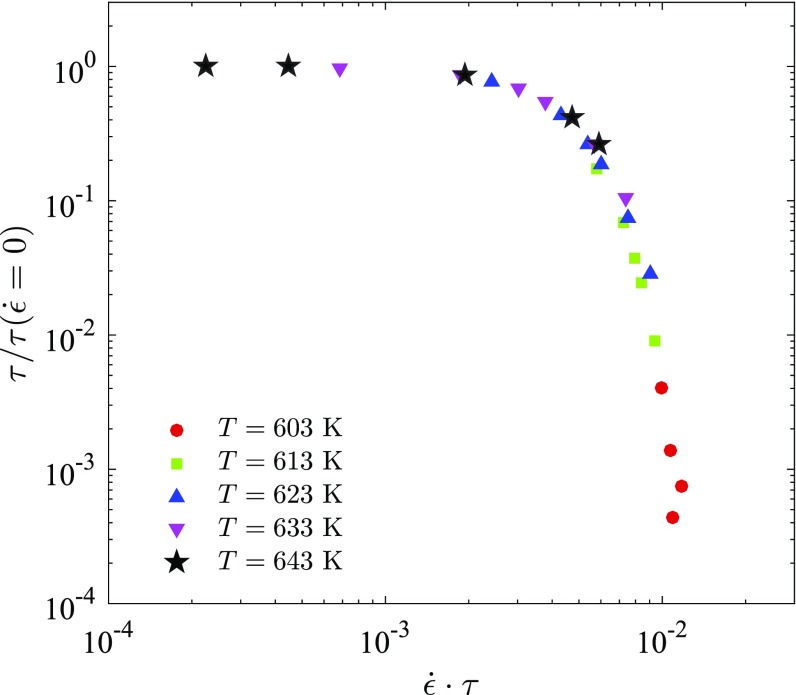
Normalized relaxation time, $\tau /\tau (\dot{ϵ}=0)$, vs. normalized strain rate, $\dot{ϵ}$, of Vitreloy 1 glass at temperature $T$ = 603 K, 613 K, 623 K, 633 K, and 643 K.

Effect of Temperature on Stress–Strain Behavior

The influence of temperature on the flow behavior is shown in Fig. S1. In this plot, all specimens were compressed at the strain rate of $2\times {10}^{-4}$ s⁻¹, using the numerical scheme described in the main text. The graph clearly shows that the temperature strongly influences the magnitude of the overshoot stress and the steady-state stress values. When the temperature is high (643 K) and the strain rate is low ($\dot{ϵ}=2\times {10}^{-4}$ s⁻¹), the stress monotonically increases as the strain. All of the stresses finally reach their steady-state values and subsequently level off after the strain increases beyond 0.2.

Effect of Strain Rate and Temperature on Apparent Viscosity

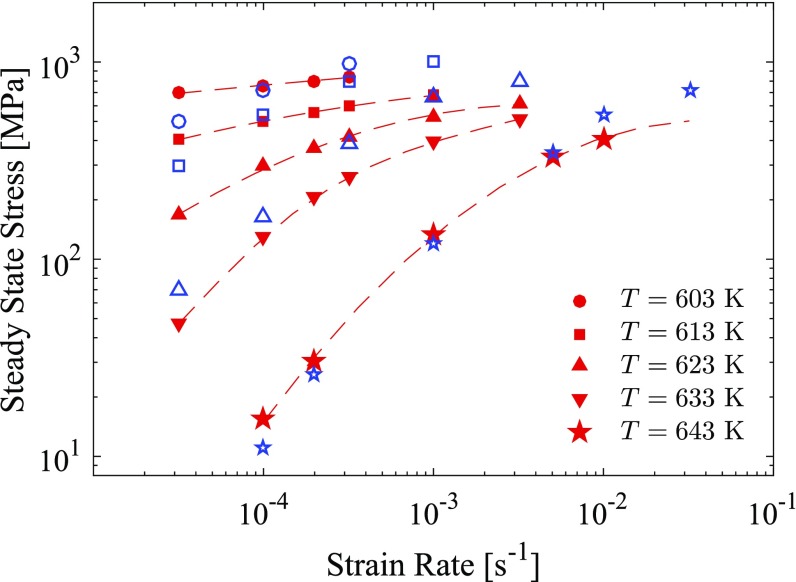
The values of the steady-state stress with respect to the strain rate are plotted in Fig. S2 at various temperatures: 603 K, 613 K, 623 K (the glass transition temperature), 633 K, and 643 K. The steady-state stress for each temperature linearly increases with the strain rate at low strain rates. At higher strain rates, a nonlinear relation between the stress and the strain rate appears, and the curves tend to bend.

Fig. S2.

The steady-state stress vs. the strain rate of Vitreloy 1 glass at various temperatures. Dashed lines are interpolating curves to guide the eye. The blue symbols refer to experimental data taken from ref. 38. The red symbols are the simulation results.

Fig. S3 shows that a master curve can be constructed in terms of the normalized structural relaxation time, $\tau /\tau (\dot{ϵ}=0)$, for the steady-state stress of Vitreloy 1 with respect to normalized strain rate $\dot{ϵ}$. The structural relaxation is the inverse of the mobility. Fig. S3 also illustrates the shear thinning behavior of the deeply supercooled liquid at high shear rates. The relaxation time decreases at growing shear rates. The crossover marks the transition between activated and collision transport (51). We note that in the latter regime, which is dominated by mode-coupling effects, the shear thinning is a general trend for which similar results are reported by others (52, 53).

Summary

In the present work we have shown how RFOT theory naturally leads to shear bands in a 2D flow situation mimicking experiments on real metallic glasses. Extensions of the calculations to 3D are conceptually straightforward but computationally demanding. The shear bands correspond to regions of transiently high mobility that will also allow local crystallization and cavitation to occur in them, ultimately leading to material failure.