Interactive Data Exploration with Smart Drill-Down

Abstract

We present smart drill-down, an operator for interactively exploring a relational table to discover and summarize “interesting” groups of tuples. Each group of tuples is described by a rule. For instance, the rule (a, b, ⋆, 1000) tells us that there are a thousand tuples with value a in the first column and b in the second column (and any value in the third column). Smart drill-down presents an analyst with a list of rules that together describe interesting aspects of the table. The analyst can tailor the definition of interesting, and can interactively apply smart drill-down on an existing rule to explore that part of the table. We demonstrate that the underlying optimization problems are NP-Hard, and describe an algorithm for finding the approximately optimal list of rules to display when the user uses a smart drill-down, and a dynamic sampling scheme for efficiently interacting with large tables. Finally, we perform experiments on real datasets on our experimental prototype to demonstrate the usefulness of smart drill-down and study the performance of our algorithms.

I. Introduction

Analysts often use OLAP (Online Analytical Processing) operations such as drill down (and roll up) [7] to explore relational databases. These operations are very useful for analytics and data exploration and have stood the test of time; all commercial OLAP systems in existence support these operations. (Recent reports estimate the size of the OLAP market to be $10+ Billion [21].)

However, there are cases where drill down is ineffective; for example, when the number of distinct values in a column is large, vanilla drill down could easily overwhelm analysts by presenting them with too many results (i.e., aggregates). Further, drill down only allows us to instantiate values one column at a time, instead of allowing simultaneous drill downs on multiple columns—this simultaneous drill down on multiple columns could once again suffer from the problem of having too many results, stemming from many distinct combinations of column values.

In this paper, we present a new interaction operator that is an extension to the traditional drill down operator, aimed at providing complementary functionality to drill down in cases where drill down is ineffective. We call our operator smart drill down. At a high level, smart drill down lets analysts zoom into the more “interesting” parts of a table or a database, with fewer operations, and without having to examine as much data as traditional drill down. Note that our goal is not to replace traditional drill down functionality, which we believe is fundamental; instead, our goal is to provide auxiliary functionality which analysts are free to use whenever they find traditional drill downs ineffective.

In addition to presenting the new smart drill down operator, we present novel sampling techniques to compute the results for this operator in an interactive fashion on increasingly larger databases. Unlike the traditional OLAP setting, these computations require no pre-materialization, and can be implemented within or on top of any relational database system.

We now explain smart drill-down via a simple example.

Example 1

Consider a table with columns ‘Department Store’, ‘Product’, ‘Region’ and ‘Sales’. Suppose an analyst queries for tuples where Sales were higher than some threshold, in order to find the best selling products. If the resulting table has many tuples, the analyst can use traditional drill down to explore it. For instance, the system may initially tell the analyst there are 6000 tuples in the answer, represented by the tuple (⋆, ⋆, ⋆, 6000, 0), as shown in Table I. The ⋆ character is a wildcard that matches any value in the database. The Count attribute can be replaced by a Sum aggregate over some measure column, e.g., the total sales. The right-most Weight attribute is the number of non-⋆ attributes; its significance will be discussed shortly. If the analyst drills down on the Store attribute (first ⋆), then the operator displays all tuples of the form (X, ⋆, ⋆, C, 1), where X is a Store in the answer table, and C is the number of tuples for X (or the aggregate sales for X).

TABLE I.

Initial Summary

Store	Product	Region	Count	Weight
⋆	⋆	⋆	6000	0

Instead, when the analyst uses smart drill down on Table I, she obtains Table II. The (⋆, ⋆, ⋆, 6000) tuple is expanded into 3 tuples that display noteworthy or interesting drill downs. The number 3 is a user specified parameter, which we call k.

TABLE II.

Result After First Smart Drill Down

Store	Product	Region	Count	Weight
⋆	⋆	⋆	6000	0
⊲ Target	bicycles	⋆	200	2
⊲ ⋆	comforters	MA-3	600	2
⊲ Walmart	⋆	⋆	1000	1

For example, the tuple (Target, bicycles, ⋆, 200, 2) says that there are 200 tuples (out of the 6000) with Target as the first column value and bicycle as the second. This fact tells the analyst that Target is selling a lot of bicycles. The next tuple tells the analyst that comforters are selling well in the MA-3 region, across multiple stores. The last tuple states that Walmart is doing well in general over multiple products and regions. We call each tuple in Table II a rule to distinguish it from the tuples in the original table that is being explored. Each rule summarizes the set of tuples that are described by it. Again, instead of Count, the operator can display a Sum aggregate, such as the total Sales.

Say that after seeing the results of Table II, the analyst wishes to dig deeper into the Walmart tuples represented by the last rule. For instance, the analyst may want to know which states Walmart has more sales in, or which products they sell the most. In this case, the analyst clicks on the Walmart rule, obtaining the expanded summary in Table III. The three new rules in this table provide additional information about the 1000 Walmart tuples. In particular, one of the new rules shows that Walmart sells a lot of cookies; the others show it sells a lot of products in the regions CA-1 and WA-5.

TABLE III.

Result After Second Smart Drill Down

Store	Product	Region	Count	Weight
⋆	⋆	⋆	6000	0
⊲ Target	bicycles	⋆	200	2
⊲ ⋆	comforters	MA-3	600	2
⊲ Walmart ⊲⊲ Walmart ⊲⊲ Walmart ⊲⊲ Walmart	⋆	⋆	1000	1
	cookies	⋆	200	2
	⋆	CA-1	150	2
	⋆	WA-5	130	2

When the analyst clicks on a rule r, smart drill down expands r into k sub-rules that as a set are deemed to be “interesting.” (We discuss other smart drill down operations in Section II-C.) There are three factors that make a rule set interesting. One is if it contains rules with high Count (or total sales) fields, since the larger the count, the more tuples are summarized. A second factor is if the rules have high weight (number of non-⋆ attributes). For instance, the rule (Walmart, cookies, AK-1, 200, 3) seems more interesting than (Walmart, cookies, *, 200, 2) since the former tells us the high sales are concentrated in a single region. A third desirability factor is diversity: For example, if we already have the rule (Walmart, ⋆, ⋆, 1000, 1) in our set, we would rather have the rule (Target, bicycles, ⋆, 200, 2) than (Walmart, bicycles, ⋆, 200, 2) since the former rule describes tuples that are not described by the first rule.

In this paper we describe how to combine or blend these three factors in order to obtain a single desirability score for a set of rules. Our score function can actually be tuned by the analyst (by specifying how weights are computed), providing significant flexibility in what is considered a good set of rules. We also present an efficient optimization procedure to maximize score, invoked by smart drill down to select the set of k rules to display.

Relationship to Other Work

Compared to traditional drill down, our smart drill down has two important advantages:

• Smart drill down limits the information displayed to the most interesting k facts (rules). With traditional drill down, a column is expanded and all attribute values are displayed in arbitrary order. In our example, if we drill down on say the store attribute, we would see all stores listed, which may be a very large number.

• Smart drill down explores several attributes to open up together, and automatically selects combinations that are interesting. For example, in Table II, the rule (Target, bicycles, ⋆, 200, 2) is obtained after a single drill down; with a traditional approach, the analyst would first have to drill down on Store, examine the results, drill down on Product, look through all the displayed rules and then find the interesting rule (Target, bicycles, ⋆, 200, 2).

Incidentally, note that in the example we only described one type of smart drill down, where the analyst selects a rule to drill down on (e.g., the Walmart rule going from Table II to Table III). In Section II-C we describe another option where the analyst clicks on a ⋆ in a column to obtain rules that have non-⋆ values in that column.

Our work on smart drill down is related to table summarization and anomaly detection [29], [28], [30], [13]. These papers mostly focus on giving the most “surprising” information to the user, i.e., information that would minimize the Kullback-Liebler(KL) divergence between the resulting maximum entropy distribution and the actual value distribution. For instance, if a certain set of values occur together in an unexpectedly small number of tuples, that set of values may be displayed to the user. In contrast, our algorithm focuses on rules with high counts, covering as much of the table as possible. Thus our work can be thought of as complementary to anomaly detection. Furthermore, our summarization is couched in an interactive environment, where the analyst directs the drill down and can tailor the optimization criteria.

Our work is also related to pattern mining. Several pattern mining papers [36], [8], [39] focus on providing one shot summaries of data, but do not propose interactive mechanisms. Moreover, to the best of our knowledge, other pattern mining work is either not flexible enough [15], [34], [12], restricting the amount of tuning the user can perform, or so general [24] as to preclude efficient optimization. Our work also merges ‘interesting pattern mining’ into the OLAP framework. We discuss related work in detail in Section V.

Contributions

Our chief contribution in this paper is the smart drill down interaction operator, an extension of traditional drill down, aimed at allowing analysts to zoom into the more “interesting” parts of a dataset. In addition to this operator, we develop techniques to support this operator on increasingly larger datasets:

• Basic Interaction: We demonstrate that finding the optimal list of rules is NP-Hard, and we develop an algorithm to find the approximately optimal list of rules to display when the user performs a smart drill down operation.

• Dynamic Sample Maintenance: To improve response time on large tables, we formalize the problem of dynamically maintaining samples in memory to support smart drill down. We show that optimal identification of samples is once again NP-Hard, and we develop an approximate scheme for dynamically maintaining and using multiple samples of the table in memory.

We have developed a fully functional and usable prototype tool that supports the smart drill-down operator that was demonstrated at VLDB 2015 [20]. From this point on, when we provide result snippets, these will be screenshots from our prototype tool. Our prototype tool also supports traditional drill-down: smart drill-down can be viewed as a generalization of traditional drill-down (with the weighting function set appropriately). In Section IV-A, we compare smart drill-down with traditional drill-down and show that smart drill-down returns considerably better results.

Our tool and techniques are also part of a larger effort for building DataSpread [6], a data analytics system with a spreadsheet-based front-end, and a database-based back-end, combining the benefits of spreadsheets and databases.

Overview of paper

• In Section II, we formally define smart drill down. After that, we describe different schemes for weighting rules, and our interactive user interface.

• In Section III, we present our algorithms for finding optimal sets of rules, as well as our dynamic sampling schemes for dealing with large tables.

• Based on our implemented smart drill down, in Section IV we experimentally evaluate performance on real datasets, and show additional examples of smart drill down in action.

• We describe related work in Section V, and conclude in Section VI.

II. Formal Description

We describe our formal problem in Section II-A, describe different scoring functions in Section II-B, and describe our operator interfaces in Section II-C.

A. Preliminaries and Definitions

Tables and Rules

As in a traditional OLAP setting, we assume we are given a star or snowflake schema; for simplicity, we represent this schema using a single denormalized relational table, which we call 𝒟. For the purpose of the rest of the discussion, we will operate on this table 𝒟. We let T denote the set of tuples in 𝒟, and C denote the set of columns in 𝒟.

Our objective (formally defined later) is to enable smart drill downs on this table or on portions of it: the result of our drill downs are lists of rules. A rule is a tuple with a value for each column of the table. In addition, a rule has other attributes, such as count and weight (which we define later) associated with it. The value in each column of the rule can either be one of the values in the corresponding column of the table, or ⋆, representing a wildcard character representing all values in the column. For a column with numerical values in the table, we allow the corresponding rule-value to be a range instead of a single value. The trivial rule is one that has a ⋆ value in all columns. The Size of a rule is defined as the number of non-starred values in that rule.

Coverage

A rule r is said to cover a tuple t from the table if all non-⋆ values for all columns of the rule match the corresponding values in the tuple. We abuse notation to write this as t ∈ r. At a high level, we are interested in identifying rules that cover many tuples. We next define the concept of subsumption that allow us to relate the coverage of different rules to each other.

We say that rule r₁ is a sub-rule rule r₂ if and only if r₁ has no more stars than r₂ and their values match wherever they both have non-starred values. For example, rule (a, ⋆) is a sub-rule of (a, b). If r₁ is a sub-rule of r₂, then we also say that r₂ is a super-rule of r₁. If r₁ is a sub-rule of r₂, then for all tuples t, t ∈ r₂ ⇒ t ∈ r₁.

Rule Lists

A rule-list is an ordered list of rules returned by our system in response to a smart drill down operation. When a user drills down on a rule r to know more about the part of the table covered by r, we display a new rule-list below r. For instance, the second, third and fourth rule from Table II form a rule-list, which is displayed when the user clicks on the first (trivial) rule. Similarly, the second, third and fourth rules in Table III form a rule-list, as do the fifth, sixth and seventh rules.

Scoring

We now define some additional properties of rules; these properties help us score individual rules in a rule-list.

There are two portions that constitute our scores for a rule as part of a rule list. The first portion dictates how much the rule r “covers” the tuples in 𝒟; the second portion dictates how “good” the rule r is (independent of how many tuples it covers). The reason why we separate the scoring into these two portions is that they allow us to separate the inherent goodness of a rule from how much it captures the data in 𝒟.

We now describe the first portion: we define Count(r) as the total number of tuples t ∈ T that are covered by r. Further, we define MCount(r, R) (which stands for ‘Marginal Count’) as the number of tuples covered by r but not by any rule before r in the rule-list R. A high value of MCount indicates that the rule not only covers a lot of tuples, but also covers parts of the table not covered by previous rules. We want to pick rules with a high value of MCount to display to the user as part of the smart drill down result, to increase the coverage of the rule-list.

Now, onto the second portion: we let W denote a function that assigns a non-negative weight to a rule based on how good the rule is, with higher weights assigned to better rules. As we will see, the weighting function does not depend on the specific tuples in 𝒟, but could depend on the number of ⋆s in r, the schema of 𝒟, as well as the number of distinct values in each column of 𝒟. A weighting function is said to be monotonic if for all rules r₁, r₂ such that r₁ is a sub-rule of r₂, we have W(r₁) ≤ W(r₂); we focus on monotonic weighting functions because we prefer rules that are more “specific” rather than those that are more “general” (thereby conveying less information). We further describe our weighting functions in Section II-B.

Thus, the total score for our list of rules is given by

$$\text{Score}(R)=\sum _{r\in R}\underset{\text{coverage of }r\text{ in }𝒟}{\underbrace{\mathit{\text{MCount}}(r,R)}}\times \underset{\text{weight of }r}{\underbrace{W(r)}}$$

Our goal is to choose the rule-list of a given length that maximizes total score.

We use MCount rather than Count in the above equation to ensure that we do not redundantly cover the same tuples multiple times using multiple rules, and thereby increase coverage of the table. If we had defined total score as ∑_r∈R Count(r)W(r), then our optimal rule-list could contain rules that repeatedly refer to the most ‘summarizable’ part of the table. For instance, if a and b were the most common values in columns A and B, then for some weighting functions W, the summary may potentially consist of rules (a, b, ⋆), (a, ⋆, ⋆), and (⋆, b, ⋆), which tells us nothing about the part of the table with values other than a and b.

Our smart drill downs still display the Count of each rule rather than the MCount. This is because while MCount is useful in the rule selection process, Count is easier for a user to interpret. In any case, it would be a simple extension to display MCount in another column.

Formal Problem

We now formally define our problem:

Problem 1

Given a table T, a monotonic weighting function W, and a number k, find the list R of k rules that maximizes

$$\sum _{r\in R}W(r)\times \mathit{\text{MCount}}(r,R)$$

for one of the following smart drill down operations:

• [Rule drill down] If the user clicked on a rule r′, then all r ∈ R must be super-rules of r′

• [Star drill down] If the user clicked on a ⋆ on column c of rule r′, then all r ∈ R must be super-rules of r′ and have a non-⋆ value in column c

Throughout this paper, we use the Count aggregate of a rule to display to the user. We can also use a Sum of values over a given ‘measure column’ c_m instead. We discuss how to modify our algorithms to use Sum instead of Count in our technical report [19].

B. Weighting Rules

We now describe our weighting function W that is used to score individual rules. At a high level, we want our rules to be as descriptive of the table as possible, i.e. given the rules, it should be as easy as possible to reproduce the table. We consider a general family of weighting functions, that assigns for each rule r, a weight W(r) depending on how expressive the rule is (i.e., how much information it conveys). We mention some canonical forms for function W(r) (their detailed interpretations are described in the technical report); later, we specify the full family of weighting functions our techniques can handle:

Size Weighting Function

W(r) = | {c ∈ C | r(c) ≠ ⋆} | : Here we set weight equal to the number of non-starred values in the rule r i.e. the size of the rule. For example, in Table II, the rule (Target, bicycles, ⋆) has weight 2.

Bits Weighting Function

W(r) = ∑_{c∈C:r(c)≠⋆} ⌈log₂(|c|)⌉ where |c| refers to the number of distinct possible values in column c. This function weighs each column based on its inherent complexity, instead of equally like the Size function.

Other Weighting Functions

Even though we have given two example weighting functions here, our algorithms allow the user to leverage any weighting function W, subject to two conditions:

• Non-negativity: For all rules r, W(r) ≥ 0.

• Monotonicity: If r₁ ≥ r₂, then W(r₁) ≤ W(r₂). Monotonicity means that a rule that is less descriptive than another must be assigned a lower weight.

A weight function can be used in several ways, including expressing a higher preference for a column (by assigning higher weight to rules having a non-⋆ value in that column), or expressing indifference towards a column (by adding zero weight for having non-⋆ value in that column).

C. Smart drill down Operations

When the user starts using a system equipped with the smart drill down operator, they first see a table with a single trivial rule as shown in Table I. At any point, the user can click on either a rule, or a star within a rule, to perform a ‘smart drill down’ on the rule. Clicking on a rule r causes r to expand into the highest-scoring rule-list consisting of super-rules of r. By default, the rule r expands into a list of 3 rules, but this number can be changed by the user. The rules obtained from the expansion are listed directly below r, ordered in decreasing order by weight (the reasoning behind the ordering is explained in Section III).

Instead of clicking on a rule, the user can click on a ⋆, say in column c of rule r. This will also cause rule r to expand into a rule-list, but this time the new displayed rules are guaranteed to have non-⋆ values for in column c. Finally, when the user clicks on a rule that has already been expanded, it reverses the expansion operation, i.e. collapses it.

III. Smart drill down Algorithms

We now describe online algorithms for implementing the smart drill down operator. We assume that all columns are categorical (so numerical columns have been bucketized beforehand). We further discuss bucketization of numerical attributes in the Extensions section in the technical report [19].

A. Problem Reduction and Important Property

When the user drills down on a rule r′, we want to find the highest scoring list of rules to expand rule r′ into. If the user had clicked on a ⋆ in a column c, then we have the additional restriction that all resulting rules must have a non-⋆ value in column c. We can reduce Problem 1 to the following simpler problem by removing the user-interaction based constraints:

Problem 2

Given a table T, a monotonic weight function W, and a number k, to find the list R of k rules that maximizes the total score given by :

$$\mathit{\text{Score}}(R)=\sum _{r\in R}W(r)\mathit{\text{MCount}}(r,R)$$

Problem 1 with parameters (T, W, k) can be reduced to Problem 2 as follows:

1. [Rule drill down] If the user clicked on rule r in Problem 1, then we can conceptually make one pass through the table T to filter for tuples covered by rule r, and store them in a temporary table T_r. Then, we solve Problem 2 for parameters (T_r, W, k).

2. [Star drill down] If the user clicked on a ⋆ in column c of rule r, then we first filter table T to get a smaller table T_r consisting of tuples from T that are covered by r. In addition, we change the weight function W from Problem 1 to a weight function W′ such that : For any rule r′, W′(r′) = 0 if r′ has a ⋆ in column c, and W′(r′) = W(r′) otherwise. Then, we solve Problem 2 for parameters (T_r, W′, k).

   Algorithm 1.

   Greedy Algorithm for Problem 3

   Input: k (Number of rules required), T (database table), mw (max weight), W     (weight function)
   Output: S (Solution set of rules)
   S = ϕ
   for i from 1 to k do
   	Rm = Find_best_marginal_rule(S, T, mw, W)
   	S = S ∪ {Rm}
   return S

As a first step towards solving Problem 2, we show that the rules in the optimal list must effectively be ordered in decreasing order by weight. Note that the weight of a rule is independent of its MCount. The MCount of a rule is the number of tuples that have been ‘assigned’ to it, and each tuple assigned to rule r contributes W(r) to the total score. Thus, if the rules are not in decreasing order by weight in a rule list R, then switching the order of rules in R transfers some tuples from a lower weight rule to a higher weight rule, which can increase total score.

Lemma 1

Let R be a rule-list. Let R′ be the rule-list having the same rules as R, but ordered in descending order by weight. Then Score(R′) ≥ Score(R).

The proof of this lemma, as well as other proofs, can be found in the technical report [19]. Thus, it is sufficient to restrict our attention to rule-lists that have rules sorted in decreasing order by weight. Or equivalently, we can define Score for a set of rules as follows:

Definition 2

Let R be a set of rules. Then the Score of R is Score(R) = Score(R′) where R′ is the list of rules obtained by ordering the rules in the set R in decreasing order by weight.

This gives us a reduced version of Problem 2:

Problem 3

Given a table T, a monotonic weight function W, and a number k, find the set (not list) R of k rules which maximizes Score(R) as defined in Definition 2.

The reduction from Problem 2 to Problem 3 is clear. We now first show that Problem 3, and consequently Problem 1 and Problem 2 are NP-Hard, and then present an approximation algorithm for solving Problem 3.

B. NP-Hardness for Problem 3

We reduce the well known NP-Hard Maximum Coverage Problem to a special case of Problem 3; thus demonstrating the NP-Hardness of Problem 3. The Maximum Coverage Problem is as follows:

Problem 4

Given a universe set U, an integer k, and a set S = {S₁, S₂, …S_m} of subsets of U (so each S_i ⊂ U), find S′ ⊂ S such that |S′| = k, which maximizes Coverage(S′) = | ∪_s∈S′ s|.

Thus, the goal of the maximum coverage problem is to find a set of k of the given subsets of U whose union ‘covers’ as much of U as possible. We can reduce an instance of the Maximum Coverage Problem (with parameters U, k, S) to an instance of Problem 3, which gives us the following lemma:

Lemma 2

Problem 3 is NP-Hard.

C. Algorithm Overview

Given that the problem is NP-Hard, we now present our algorithms for approximating the solution to Problem 3. The problem consists of finding a set of rules, given size k, that maximizes Score.

The next few sections fully develop the details of our solution:

• We show that the Score function is submodular, and hence an approximately optimal set can be obtained using a greedy algorithm. At a high level, this greedy algorithm is simple to state. The algorithm runs for k steps; we start with an empty rule set R, and then at each step, we add the next best rule that maximizes Score

• In order to find the rule r to add in each step, we need to measure the impact on Score for each r. This is done in several passes over the table, using ideas from the a-priori algorithm [4] for frequent item-set mining.

In some cases, the dataset may still be too large for us to return a good rule set in a reasonable time; in such cases, we run our algorithm on a sample of the table rather than the entire table. In Section III-E, we describe a scheme for maintaining multiple samples in memory and using them to improve response time for different drill down operations performed by the user. Our sampling scheme dynamically adapts to the current interaction scenario that the user is in; drawing from ideas in approximation algorithms and optimization theory.

D. Greedy Approximation Algorithm

Submodularity

We will now show that the Score function over sets of rules has a property called submodularity, giving us a greedy approximation algorithm for optimizing it.

Definition 3

A function f : 2^S → ℝ for any set S is said to be submodular if and only if, for every s ∈ S, and A ⊂ B ⊂ S with s ∉ A: f(A ∪ {s}) − f(A) ≥ f(B ∪ {s}) − f(B)

Intuitively, this means that the marginal value of adding an element to a set S cannot increase if we add it to a superset of S instead. For monotonic non-negative submodular functions, it is well known that the solution to the problem of finding the set of a given size with maximum value for the function can be found approximately in a greedy fashion.

Lemma 3

For a given table T, the Score function over sets S of rules, defined by the following is submodular:

$$\mathit{\text{Score}}(S)=\sum _{r\in S}\mathit{\text{MCount}}(r,S)W(r)$$

High-Level Procedure

Based on the submodularity property, the greedy procedure, shown in Algorithm 1, has desirable approximation guarantees. Since Score is a submodular function of the set S, this greedy procedure is guaranteed to give us a score within a $1-\frac{1}{e}$ factor of the optimum (actually, it is $1-{\left(\frac{k-1}{k}\right)}^k$ for k rules, which is much better for small k).

The expensive step in the above procedure is when Score is computed for every single rule. Since the number of rules can be as large as the table itself, this is very time-consuming.

Instead of using the procedure described above directly, we instead develop a “parameterized” version that will admit further approximation (depending on the parameter) in order to reduce computation further. We describe this algorithm next.

Parametrized Algorithm

Our algorithm pseudo-code is given in the box labeled Algorithm 1. We call our algorithm BRS (for Best Rule Set). BRS takes four parameters as input: the table T, the number k of rules required in the final solution list, a parameter m_w (which we describe in the next paragraph), and the weight function W.

The parameter m_w stands for Max Weight. m_w tells the algorithm to assume that all rules in the optimal solution have weight ≤ m_w. Thus, if S_o denotes set of rules with maximum score, then as long as m_w ≥ max_r∈SoW(r), BRS is guaranteed to return S_o. On the other hand if m_w < W(r) for some r ∈ S_o, then there is a chance that the set returned by BRS does not contain r. BRS runs faster for smaller values of m_w, and may only return a suboptimal result if m_w < max_r∈SoW(r). In practice, max_r∈SoW(r) is usually small. This is because as the size (and weight) of a rule increases, its Count falls rapidly. The Count tends to decrease exponentially with rule size, while Weight increases linearly for common weight functions (such as W(r) = Size(r)). Thus, rules with high weight and size have very low count, and are unlikely to occur in the optimal solution set S_o. Our experiments in Section IV also show that the weights of rules in the optimal set tend to be small. In the technical report [20], we describe strategies for setting k, m_w and other parameters.

BRS initializes the solution set S to be empty, and then iterates for k steps, adding the best marginal rule at each step. To find the best marginal rule, it calls a function to find the best marginal rule given the existing set of rules S.

Finding the Best Marginal Rule

To find the best marginal rule, we need to find the marginal values of several rules and choose the best one. A brute-force way to do this would be to enumerate all possible rules, and to find the marginal value for each rule in a single pass over the data. But the number of possible rules may be as large as the size of the table, making this step very expensive in terms of computation and memory.

To avoid counting too many rules, we leverage a technique inspired by the a-priori algorithm for frequent itemset mining [4]. Recall that the a-priori algorithm is used to find all itemsets that have a support greater than a threshold. Unlike the a-priori algorithm, our goal is to find the single best marginal rule. Since we only aim to find one rule, our pruning power is significantly higher than a vanilla a-priori algorithm, and we terminate in much fewer passes over the dataset.

We compute the best marginal rule over multiple passes on the dataset, with the maximum number of passes equal to the maximum size of a rule. In the j^th pass, we compute counts and marginal values for rules of size j. To give an example, suppose we had three columns c₁, c₂, and c₃. In the first pass, we would compute the counts and marginal values of all rules of size 1. In the second pass, instead of finding marginal values for all size 2 rules, we can use our knowledge of counts from the first pass to upper bound the potential counts and marginal values of size 2 rules, and be more selective about which rules to count in the second pass. For instance, suppose we know that the rule (a, ⋆, ⋆) has a count of 1000, while (⋆, b, ⋆) has a count of 100. Then for any value c in column c₃ we would know that the count of (⋆, b, c) is at most 100 because it cannot exceed that of (⋆, b, ⋆). This implies that the maximum marginal value of any super-rule of (⋆, b, c) having weight ≤ m_w is at most 100m_w. If the rule (a, ⋆, ⋆) has a marginal value of 800, then the marginal value of any super-rule of (⋆, b, ⋆) cannot possibly exceed that of (a, ⋆, ⋆). Since our aim is to only find the highest marginal value rule, we can skip counting for all super-rules of (⋆, b, ⋆) for future passes.

We now describe the function to find the best marginal rule. The pesudo-code for the function is in the technical report. The function maintains a threshold H, which is the highest marginal value that has been found for any rule so far. The function makes several iterations (Step 3), counting marginal values for size j rules in the j^th iteration. We maintain three sets of rules. C is the set of all rules whose marginal values have been counted in all previous iterations. C_n is the set of rules whose marginal values are going to be counted in the current pass. And C_o is the set of rules whose marginal values were counted in the previous iteration. For the first pass, we set C_n to be all rules of size 1. Then we compute marginal values for those rules, and set C = C_o = C_n.

For the second pass onwards, we are more selective about which rules to consider for marginal value evaluation. We first set C_n to be the set of rules of size j which are super-rules of rules from C_o. Then for each rule r from C_n, we consider the known marginal values of its sub-rules from C, and use them to upper-bound the marginal value of all super-rules of r, as shown in Step 3.3.2. Then we delete from C_n the rules whose marginal value upper bound is less than the currently known best marginal value, since they have no chance of being returned as the best marginal rule. Then we make as actual pass through the table to compute the marginal value of the rules in C_n, as shown in Step 3.5. If in any round, the C_n obtained after deleting rules is empty, then we terminate the algorithm and return the highest value rule.

The reader may be wondering why we did not simply count the score of each rule using a variant of the a-priori algorithm in one pass, and then pick the set of rules that maximizes score subsequently. This is because doing so will lead to a sub-optimal set of rules: by not accounting for the rules that have already been selected, we will not be able to ascertain the marginal benefit of adding an additional rule correctly.

E. Dynamic Sampling for Large Tables

BRS makes multiple passes over the table in order to determine the best set of rules to display. This can be slow when the table is too large to fit in main memory. We can reduce the response time of smart drill down by running BRS on a sample of the table instead, trading off accuracy of our rules for performance. If we had obtained a sample s by selecting each table tuple with probability p, and run BRS on s, then we multiply the count of each rule found by BRS, by $\frac{1}{p}$ to estimate its count over the full table.

In Section III-E1, we describe the problem of optimally allocating memory to different samples. We show that the problem is NP-Hard, and describe an approximate solution. In Section III-E2, we describe a component of the system called the SampleHandler, which is responsible for creating and maintaining multiple samples of different parts of the table in memory, and creating temporary samples for BRS to process. Detailed descriptions of the sampling problem and the SampleHandler are in the technical report. The technical report also contains some additional optimizations, and ways to set the minimum sample size.

1) Deciding what to sample

We are given a memory capacity M, and a minimum sample size minSS, both specified by the user. minSS is the minimum number of tuples on which we are allowed to run BRS, without accessing the hard disk. A higher value of minSS increases both accuracy and computation cost of our system.

At any point, we have a tree U of rules displayed to the user. Initially, the tree consists of a single node corresponding to the empty rule. When the user drills down on a rule r, the sub-rules of r obtained by running BRS are added as children of node r. Our system maintains multiple samples in memory, with one sample per rule in U. Specifically, for each rule r ∈ U, we choose an integer n_r, and create a sample s_r consisting of n_r uniformly randomly chosen tuples covered by r from the table. Because of the memory constraint, we must have ∑_r∈U n_r ≤ M.

When a user attempts to drill down on r, the SampleHandler takes all n_r tuples from s_r, and also tuples covered by r from samples s_r′ for all r′ ∈ U that are sub-rules of r. If the total number of such tuples is ≥ minSS, then we run BRS on that set of tuples to perform the drill down. Note that this set of tuples forms a uniformly random sample of tuples covered by r. If not, then we need to access the hard disk to obtain more tuples covered by r.

Leaves of tree U correspond to rules that may be drilled down on next. We assume there is a probability distribution over leaves, which assigns a probability that each leaf may be drilled down on next. This can be a uniform distribution, or a machine learned distribution using past user data. We aim to set sample sizes n_r so as to maximize the probability that the next drill down can be performed without accessing disk.

If r′ is a sub-rule of r, and covers x times as many rules as r, then it means that when drilling down on r, s_r′ can contribute around $\frac{n_{r\prime }}{x}$ tuples to the sample for r. We denote the ratio of selectivities x by S(r′, r). S(r′, r) is defined to be 0 if r′ is not a sub-rule of r. If r is to be drilled down on next, the total number of sample tuples we will have for r from all existing samples is given by ess(r) = ∑_r′∈U S(r′, r)n_r′. We can drill down on r without accessing hard disk, if ess(r) ≥ minSS. We now formally define our problem:

Problem 5

Given a tree of rules U with leaves L, a probability distribution p over L, an integer M, and selectivity ratio S(r₁, r₂) for each r₁, r₂ ∈ U, choose an integer n_r ≥ 0 for each r ∈ U so as to maximize :

$$\sum _{r\prime \in L}{p}_{r\prime }{I}_{[\mathit{\text{ess}}(r\prime )\ge \mathit{\text{min}}SS]}$$

where the I’s are indicator variables, with : ∑_r∈U n_r ≤ M

Problem 5 is non-linear and non-convex because of the indicator variables. We can show that Problem 5 is NP-Hard using a reduction from the knapsack problem.

Lemma 4

Problem 5 is NP-Hard.

Proof

(Sketch; details in [20]) Suppose we are given an instance of the knapsack problem with m objects, with the i^th object having weight w_i and value υ_i. We are also given a weight limit W, and our objective is to choose a set of objects that maximizes value and has total weight < W. We will reduce this instance to an instance of Problem 5.

We first scale the w_is and W such that all w_is are < 1. For Problem 5, we set M to (m + W) × minSS. Tree U has m special nodes r₁, r₂, …r_m, and each r_i has two leaf children r_i,1, r_i,2. All other leaves have expansion probability 0. The S values are such that ∀i ∈ {1, 2, ‥m}, j ∈ {1, 2} : (S(x, r_i,j) ≠ 0 ⇒ x = r_i,j ‖x = r_i). In reality, the S values cannot be exactly zero, but can be made small enough for all practical purposes. Thus, ∀1 ≤ i ≤ m, j ∈ {1, 2} : ess(r_i,j) = n_ri,j + n_riS(r_i, r_i,j). In addition, S(r_i, r_i,1) = 1, and S(r_i, r_i,2) = 1 − w_i. Finally, $\forall i:p_{r_{i,1}}=\frac{2}{2m+1}$ and $p_{r_{i,2}}=\frac{{\upsilon }_i}{(2m+1){\sum }_{j=1}^m{\upsilon }_i}$. So in any optimal solution, ∀i : ess(r_i,1) = minSS, and we’ve to decide which i’s also have ess(r_i,2) = minSS. Having ess(r_i,2) = minSS requires consuming w_i × minSS extra memory and gives an extra $\frac{{\upsilon }_i}{(2m+1)({\sum }_{j=1}^m{\upsilon }_j)}$ probability value. Thus, having ess(r_i,2) = minSS is equivalent to picking object i from the knapsack problem. Solving Problem 5 with the above U, S, p and picking the set of i’s for which ess(r_i,2) = minSS gives a solution to the instance of the knapsack problem.

Approximate DP Solution

Even though the problem as stated is NP-Hard, with an additional simplifying assumption, we can make the problem approximately solvable using a Dynamic Programming algorithm. The assumption is: for each r ∈ L, we assume that its ess can get sample tuples only from samples obtained for itself and its immediate parent. That is, we set S(r₁, r₂) to be zero if r₁ ≠ r₂ and r₂ is not a child of r₁. This is similar to what we had for tree U in our proof of Lemma 4. ess(r) now becomes ess(r′) = n_r′ + n_rS(r, r′) where r is the parent of r′.

We present the idea behind the approximate solution below. A more detailed description can be found in the technical report. The solution consists of two main steps:

• Locally Optimal Solutions : For each rule r₀ ∈ U \ L, let M_r0 be the set consisting of r₀ and its leaf children. We consider the number of tuples assigned to members of M_r0. Each such assignment of numbers has a ‘cost’ equal to total number of tuples assigned, and ‘value’ equal to sum of probabilities of M_r0 members with ess > minSS. We consider all ‘locally optimal’ assignments, where probability value cannot be increased without increasing the cost.

• Combining Solutions : Then, we use dynamic programming to pick one optimal solution per r₀ so as to get maximum probability value with the given cost constraint. We discretize costs, say to have granularity 100. Let M₀, M₁, …M_D be the sets for which we have found locally optimal solutions. We make D iterations in all, where in the i^th iteration, we try different locally optimal solutions for M_i and use it to update the maximum attainable value for each cost.

2) Design of the SampleHandler

We now briefly describe the design of the SampleHandler, which given a certain memory capacity M, and a minimum sample size minSS, creates, maintains, retrieves, and removes samples, all in response to user interactions on the table. A detailed description, with some potential optimizations, can be found in [20].

At all points, the SampleHandler maintains a set of samples in memory. Each sample s is represented as a triple: (a) A ‘filter’ rule f_s, (b) a scaling factor N_s (c) a set T_s of tuples from the table. The set T_s consists of a $\frac{1}{N_s}$ uniformly sampled fraction of tuples covered by f_s. The scaling factor N_s is used to translate the count of a rule on the sample into an estimate of the count over the entire table. The sum of |T_s| over all samples s is not allowed to exceed capacity M at any time.

Whenever the user drills down on a rule r, our system calls the SampleHandler with argument r, which returns a sample s whose filter value is given by f_s = r and has |T_s| ≥ minSS. The T_s of the returned sample consists of a uniformly random set of tuples covered by r. The SampleHandler also computes N_s when a sample is created. Then we run BRS on sample s to obtain the list of rules to display. The SampleHandler uses one of the mechanisms below to obtain such a sample s:

• Find: If the SampleHandler finds an existing sample s in memory, which has r as its filter rule (i.e. f_s = r) and at least minSS tuples (|T_s| ≥ minSS, then it simply returns sample s.

• Combine: If Find doesn’t work i.e., if the Sample-Handler cannot find an existing sample with filter r and ≥ minSS tuples, then it looks at all existing samples s′ such that f_s′ is a sub-rule of r. If the set of all tuples that are covered by r, from all such T_s′ ’s combined, exceeds minSS in size, then we can simply treat that set as our sample for rule r.

• Create: If Combine doesn’t work either, then the SampleHandler needs to create a new sample s with f_s = r by making a pass through the table. Since accessing the hard disk is expensive, it also creates samples for rules other than r and augments existing samples in the same pass. It first deletes all existing samples, then uses the algorithm from Section III-E1 to determine how many tuples to sample for each rule, and uses reservoir sampling [26], [35] to create a uniformly random sample of a given size for each rule.

IV. Experiments

We have implemented a fully-functional interactive tool instrumented with the smart drill down operator, having a web interface. We now describe our experiments on this tool with real datasets.

Datasets

The first dataset, denoted ‘Marketing’, contains demographic information about potential customers [1]. A total of N = 9409 questionnaires containing 502 questions were filled out by shopping mall customers in the San Francisco Bay area. This dataset is the summarized result of this survey. Each tuple in the table describes a single person. There are 14 columns, each of which is a demographic attribute, such as annual income, gender, marital status, age, education, and so on. Continuous values, such as income, have been bucketized in the dataset, and each column has up to 10 distinct values.

The columns (in order) are as follows: annual household income, gender, marital status, age, education, occupation, time lived in the Bay Area, dual incomes?, persons in household, persons in household under 18, householder status, type of home, ethnic classification, language most spoken in home.

The second dataset, denoted ‘Census’, is a US 1990 Census dataset from the UCI Machine Learning repository [5], consisting of about 2.5 million tuples, with each tuple corresponding to a person. It has 68 columns, including ancestry, age, and citizenship. Numerical columns, such as age, have been bucketized beforehand in the dataset. We use this dataset in Section IV-B in order to study the accuracy and performance of sampling on a large dataset.

Unless otherwise specified, in all our experiments, we restrict the tables to the first 7 columns in order to make the result tables fit in the page. We use the current implementation of our the smart drill down operator, and insert cropped screenshots of its output in this paper. We set the k (number of rules) parameter to 4, and m_w to 5 for the Size weighting and 20 for the Bits weighting function (see Section II-B). Memory capacity M for the SampleHandler is set to 50000 tuples, and minSS to 5000.

A. Qualitative Study

We first perform a qualitative study of smart drill down. We observe the effects of various user interface operations on the Marketing Dataset (the results are similar on the Census dataset), and then try out different weight functions to study their effects.

1) Testing the User Interface

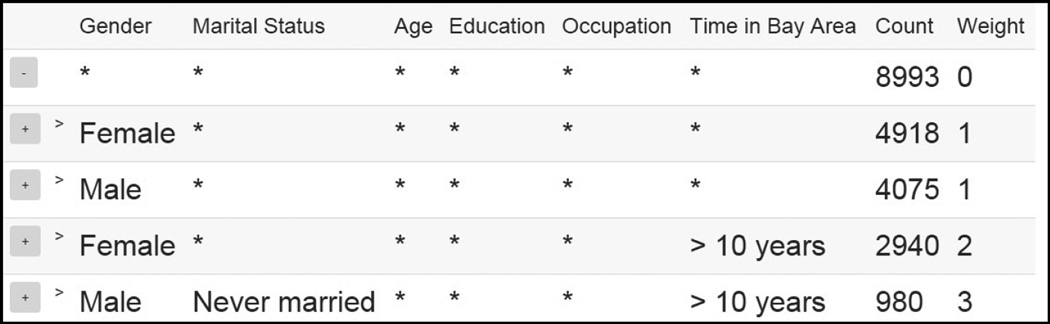
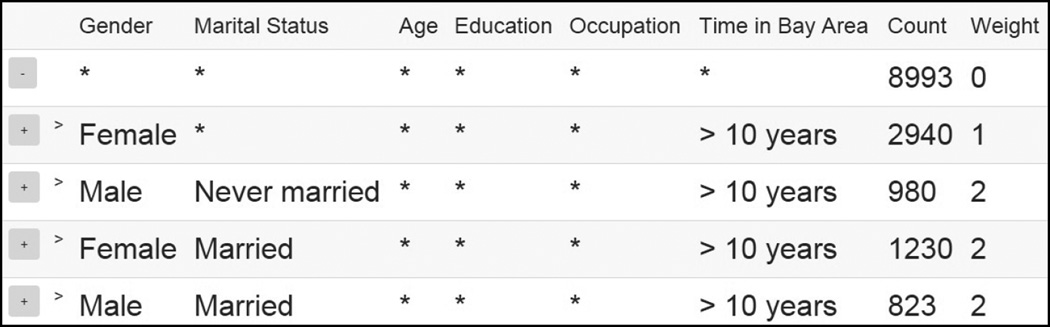
We now present the rule-based summaries displayed as a result of a few different user actions. To begin with, the user sees an empty rule with the total number of tuples as the count. Suppose the user expands the rule. Then the user will see Figure 1. The first two new rules simply tell us that the table has 4918 female and 4075 male tuples. The next two rules also slightly more detailed, saying that there are 2940 females who have been in the Bay Area for > 10 years, and 980 males who have never been married and been in the Bay Area for > 10 years. Note that the latter two rules give very specific information which would require up to 3 user clicks to find using traditional drill down, whereas smart drill down displays that information to the user with a single click.

Fig. 1.

Summary after clicking on the empty rule

Now suppose the user decides to further explore the table, by looking at education related information of females in the dataset. Say the user clicks on the ⋆ in the ‘Education’ column of the second rule. This opens up Figure 2 that shows the number of females with different levels of education, for the 4 most frequent levels of education among females. Instead of expanding the ‘Education’ column, if the user had simply expanded the third rule, it would have displayed Figure 3.

Fig. 2.

Star expansion on ‘Education’ Column

Fig. 3.

A rule expansion

2) Weighting functions

Our system can display optimal rule lists for any monotonic weighting function. By default, we assign a rule weight equal to its size. In this section, we consider other weighting functions.

We first try the weighting function given by:

$$W(r)=\sum _{c\in C:r(c)\ne \star }\lceil {\text{log}}_2(|c|)\rceil$$

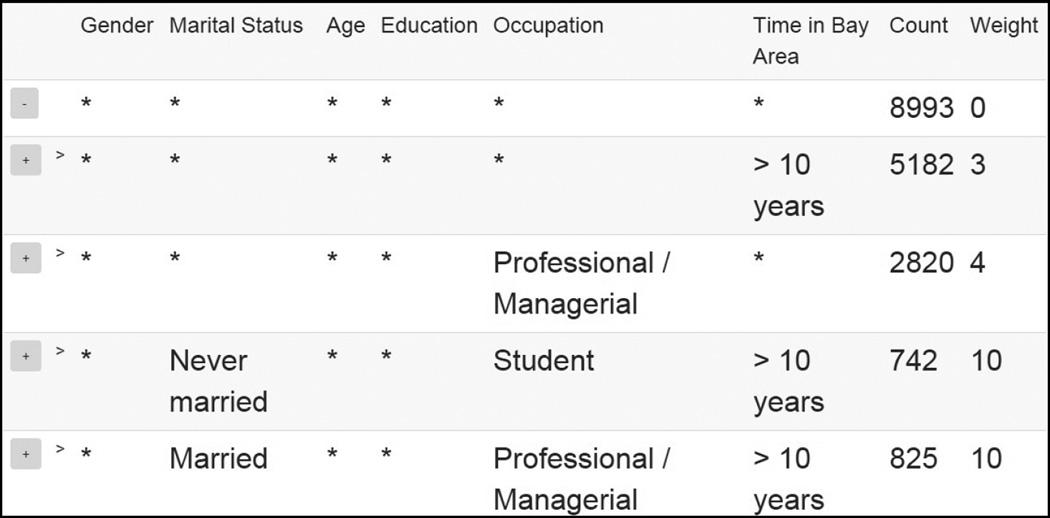
where |c| refers to the number of distinct possible values in column c. This function gives higher weight to rules that have non-⋆ values in columns that have many possible values. The rule summary for this weighting is in Figure 6 (contrast with Figure 1). The weighting scheme gives low weight for non-⋆ values in binary columns, like the gender column. Thus, this summary instead gives us information about the Marital Status/Time in Bay Area/Occupation columns instead of the Gender column like in Figure 1.

Fig. 6.

Bits scoring

The other weighting function we try is given by:

$$W(r)=\text{Min}(0,\text{Size}(r)-1)$$

This gives us Figure 7. This weighting gives a 0 weight to rules with a single non-⋆ value, and thus forces the algorithm to finds good rules having at least 2 non-⋆ values. As a result, we can see that our system only displays rules having 2 or 3 non-⋆ values, unlike Figure 1 which has two rules displaying the total number of males and females, that have size 1.

Fig. 7.

Size minus one weighting

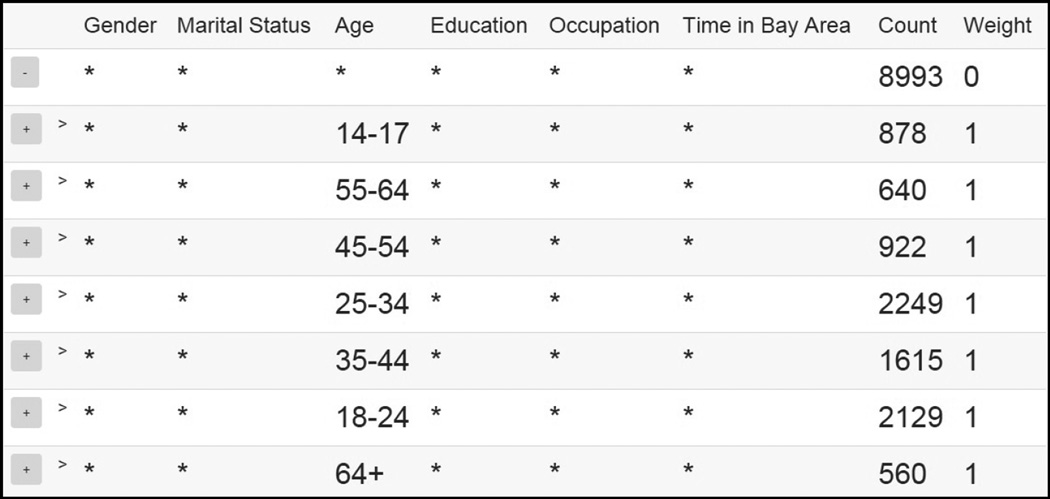
A regular drill down can be thought of as a special case of smart drill-down with the right weighting function and number of rules (see technical report for details). We use this to perform a drill down on the ‘Age’ column using our experimental prototype. The result is shown in Figure 4. We can contrast it with Figure 1; the latter gives information about multiple columns at once and only displays high count values. Regular drill down on the other hand, serves a complementary purpose by focusing on detailed evaluation of a single column.

Fig. 4.

A regular drill down on Age

B. Quantitative Study

The performance of our algorithm depends on various parameters, such as m_w (the max weight) and minSS (minimum required sample size). We now study the effects of these parameters on the computation time and accuracy of our algorithm. We use the Marketing and Census datasets. The Marketing dataset is relatively small with around 9000 tuples, whereas the Census dataset is quite large, with 2.5 million tuples. The accuracy of our algorithm depends on m_w and minSS, rather than the underlying database size. The worst case running time for large datasets is close to the time taken for making one pass on the dataset. When we expand a rule using an existing sample in memory, the running time is small and only depends on minSS rather than on the dataset size.

1) Effects of m_w

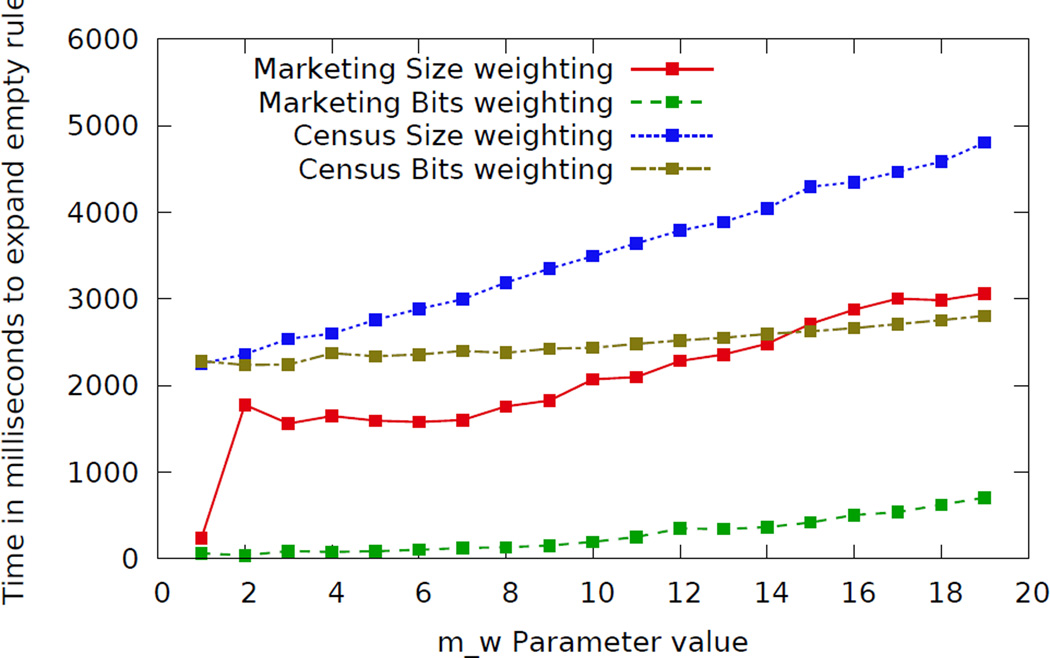
Our algorithm for finding the best marginal rule takes an input parameter called m_w. The algorithm is guaranteed to find the best marginal rule as long as its weight is ≤ m_w, but runs faster for smaller values of m_w. We now study the effect of varying m_w on the speed of our algorithm running on a Dell XPS L702X laptop with 6GB RAM and an Intel i5 2.30GHz processor.

We fix a weighting function W, and a value of m_w. For that value of the W and m_w parameters, we find the time taken for expanding the empty rule. We repeat this procedure 10 times and take the average value of the running times across the 10 iterations. This time is plotted against m_w, for W(r) = Size(r) and W(r) = ∑_{c∈C:r(c)≠⋆}⌈log₂(|c|)⌉ in Figure 5. The figure shows that running time seems to be approximately linear in m_w.

Fig. 5.

Running time for different values of parameter m_w

For the Census dataset, the running time is dominated by time spent in making a pass through the 2.5 million tuples to create the first sample. The response time for the next user click should be quite small, as the sample created for the first expansion can usually be re-used for the next rule expansion.

The value of m_w required to ensure a correct answer is equal to the maximum weight of a selected rule. Thus, for size scoring on the Marketing dataset, according to Figure 1, we require m_w ≥ 3. For the second weighting function, according to Figure 6, the minimum required value of m_w is 10. At these values of m_w, we see that the expansion takes 1.5 seconds and about 0.25 seconds respectively. Of course, the minimum value of m_w we can use is not known to us beforehand. But even if we use more conservative values of m_w, say 6 and 20 respectively, the running times are about 1.5 and 0.5 seconds respectively.

2) Effects of minSS

We now study the effects of the sampling parameter minSS. This parameter tells the SampleHandler the minimum sample size on which we run BRS. Higher values of minSS cause our system to use bigger samples, which increases the accuracy of count estimates for displayed rules, but also correspondingly increases computation time.

We consider one value of minSS and one weight function W at a time. For those values of minSS and W, we drill down on the empty rule and measure the time taken. We also measure the percent error in the estimated counts of the displayed rules. That is, for each displayed rule r, if the displayed (estimated) count if c₁ and the actual count (computed separately on the entire table) is c₂, then the percent error for rule r is $\frac{100\times |c_1-c_2|}{c_2}$. We consider the average of percent errors over all displayed rules. For each value of minSS and W, we drill down on the empty rule and find the computation time and percent error 50 times, and take the average value for time and error over those 50 iterations. This average time is plotted against minSS, for W(r) = Size(r) and W(r) = ∑_{c∈C:r(c)≠⋆}⌈log₂(|c|)⌉ in Figure 8(a). The average percent error is plotted against minSS, for W(r) = Size(r) and W(r) = ∑_{c∈C:r(c)≠⋆}⌈log₂(|c|)⌉ in Figure 8(b).

Fig. 8.

(a) Running time for different values of parameter minSS (b) Error in Count for different values of parameter minSS (c) Average number of incorrect rules for different values of parameter minSS

Figure 8(a) shows that sampling gives us noticeable time savings. The percent error decreases approximately as $\frac{1}{\sqrt{\mathit{\text{min}}SS}}$, which is again expected because the standard deviation of estimated Count is approximately inversely proportional to the square root of sample size.

In addition, we measure the number of incorrect rules per iteration. If the correct set of rules to display is r₁, r₂, r₃ and the displayed set is r₁, r₃, r₄ then that means there is one incorrect rule. We find the number of incorrect displayed rules across 50 iterations, and display the average value in Figure 8(c). This number for the Marketing dataset is almost always 0 for the Size weighting function, and between 1 and 2 for the Bits weighting function. For the Census dataset, it is around 1 for minSS ≤ 1000 and falls to about 0.3 for larger values of minSS. Note that even when we display an ‘incorrect’ rule, it is usually the 5^th or 6^th best rule instead of one of the top 4 rules, which still results in a reasonably good summary of the table.

3) Scaling properties of our algorithms

The computation time for a smart drill-down is linear in both the table size |T| and in parameter minSS. That is, the runtime can be written as a × |T| + b × minSS where a and b are constants. In the worst-case where we cannot form a sample from main memory and need to re-create a sample, a stands for the time taken to read data from hard disk. That is, a × |T| is the time taken to make a single sequential scan over the table on disk. The constant b is bigger than a, because BRS makes multiple passes over the sample, while creating a sample only requires a single pass over the table.

When the |T| is small, the runtme is dominated by the b × minSS term, as seen for the Marketing Dataset in Figure 8(a). When |T| is large relative to minSS, like for the Census Dataset, the runtime is dominated by the a × |T| term (this is when we need to create a fresh sample from hard disk). When we have a few million tuples, our total runtime is only a few seconds. But if the dataset consisted of billions of tuples, the process of reading the table to create a sample could itself take a very long time. To counteract this, we could preprocess the dataset by down-sampling it to only a million tuples, and perform the summarization on the million tuple sample (which also effectively summarizes the billion tuple table).

V. Related Work

There has been work on finding cubes to browse in OLAP systems [29], [28], [30]. This work, along with other existing work [25] focuses on finding values that occur more often or less often that expected from a max-entropy distribution. The work does not guarantee good coverage of the table, since it rates infrequently occurring sets of values as highly as frequently occurring ones. Some other data exploration work [31] focuses on finding attribute values that divide the database in equal sized parts, while we focus on values that occur as frequently as possible.

There is work on constructing ‘explanation tables’, sets of rules that co-occur with a given binary attribute of the table [13]. This work again focuses on displaying rules that will cause the resulting max entropy distribution to best approximate the actual distribution of values. A few vision papers [22], [11] suggest frameworks for building interactive data exploration systems. Some of these ideas, like maintaining user profiles, could be integrated into smart drill down. Reference [10] proposes an extension to OLAP drill-down that takes visualization real estate into account, by clustering attribute values. But it focuses on expanding a single column at a time, and relies on a given value hierarchy for clustering.

Some related work [17], [16] focuses on finding minimum sized Tableaux that provide improved support and confidence for conditional functional dependencies. There has also been work [9], [23], [38], [14] on finding hyper-rectangle based covers for tables. In both these cases, the emphasis is on completely covering or summarizing the table, suffering from the same problems as traditional drill down in that the user may be presented with too many results. The techniques in the former case may end up picking rare “patterns” if they have high confidence, and in the latter case do not scale well to a large number of attributes (in their case, ≥ 4).

Several existing papers also deal with the problem of frequent itemset mining [4], [37], [18]. Vanilla frequent itemset mining is not directly applicable to our problem because the flexible user-specified objective function emphasizes coverage of the table rather than simply frequent itemsets. However, we do leverage ideas from the a-priori algorithm [4] as applicable. Several extensions have been proposed to the a-priori algorithm, including those for dealing with numerical attributes [33], [27]. We can potentially use these ideas to improve handing of numerical attributes in our work. Unlike our paper, there has been no work on dynamically maintaining samples for interaction in the frequent itemset literature, since frequent itemset mining is a one-shot problem.

There has also been plenty of work on pattern mining. Several papers [36], [8], [39] propose non-interactive schemes that attempt to find a one shot summary of the table. These schemes usually consume a large amount of time processing the whole table, rather than allowing the user to slowly steer into portions of interest. In contrast, our work is interactive, and includes a smart memory manager that can use limited memory effectively while preparing for future requests.

Our Smart Drill-Down operator is tunable because of the flexible weighting function, but the monotonicity of the weighting function and the use of MCount, still make it possible for us to get an approximate optimality guarantee for the rules we display. In contrast, much of the existing pattern mining work [15], [34], [12] is not not tunable enough, providing only a fixed set of interestingess parameters. On the other hand, reference [24] allows a fully general scoring function, necessitating the use of heuristics with no optimality guarantees, and very time consuming algorithms. A lot of pattern mining work [15], [39], [36] also focuses on itemsets rather than Relational Data, which does not allow the user to express interest in certain ‘columns’ over others.

We use sampling to find approximate estimates of rule counts. Various other database systems [2], [3] use samples to find approximate results to SQL aggregation queries. These systems create samples in advance and only update them when the database changes. In contrast, we keep updating our samples on the fly, as the user interacts with our system. There is work on using weighted sampling [32] to create samples favouring data that is of interest to a user, based on the user’s history. In contrast, we create samples at run time in response to the user’s commands.

VI. Conclusion

We have presented a new data exploration operator called smart drill down. Like traditional drill down, it allows an analyst to quickly discover interesting value patterns (rules) that occur frequently (or that represent high values of some metric attribute) across diverse parts of a table.

We presented an algorithm for optimally selecting rules to display, as well as a scheme for performing such selections based on data samples. Working with samples makes smart drill down relatively insensitive to the size of the table.

Our experimental results on our experimental prototype show that smart drill down is fast enough to be interactive under various realistic scenarios. We also showed that the accuracy is high when sampling is used, and when the maximum weight (m_w) approximation is used. Moreover, we have a tunable parameter minSS that the user can tweak to tradeoff performance of smart drill down for the accuracy of the rules.