Point process models for localization and interdependence of punctate cellular structures

Abstract

Background

Accurate representations of cellular organization for multiple eukaryotic cell types are required for creating predictive models of dynamic cellular function. To this end, we have previously developed the CellOrganizer platform, an open source system for generative modeling of cellular components from microscopy images. CellOrganizer models capture the inherent heterogeneity in the spatial distribution, size, and quantity of different components among a cell population. Furthermore, CellOrganizer can generate quantitatively realistic synthetic images that reflect the underlying cell population. A current focus of the project is to model the complex, interdependent nature of organelle localization.

Results

We built upon previous work on developing multiple non-parametric models of organelles or structures that show punctate patterns. The previous models described the relationships between the subcellular localization of puncta and the positions of cell and nuclear membranes and microtubules. We extend these models to consider the relationship to the endoplasmic reticulum, and to consider the relationship between the positions of different puncta of the same type. Our results do not suggest that the punctate patterns we examined are dependent on ER position or inter- and intra-class proximity. With these results, we built classifiers to update previous assignments of proteins to one of 11 patterns in three distinct cell lines.

Conclusion

Our generative models demonstrate the ability to construct statistically accurate representations of puncta localization from simple cellular markers in distinct cell types, capturing the complex phenomena of cellular structure interaction with little human input. This protocol represents a novel approach to vesicular protein annotation, a field that is often neglected in high-throughput microscopy. These results suggest that spatial point process models provide useful insight with respect to the spatial dependence between cellular structures.

Introduction

A major challenge in systems biology is to create accurate predictive models of intracellular processes and their relation to cellular behavior (1–3). While many such models have been created for both prokaryotic and eukaryotic cells, often little or no consideration is given to the spatial organization of subcellular structures. However, systems such as MCell (4), VirtualCell (5), Simmune (6) and SmolDyn (7) can perform spatially-realistic cell simulations if information about spatial organization is available. Providing such information in a structured manner is one of the main goals of the open source CellOrganizer system (http://CellOrganizer.org), which can currently learn models of cell shape, nuclear shape, chromatin texture, vesicular size, shape and location, and microtubule distribution (8–13). CellOrganizer provides a generative framework for modeling aspects of cell organization that goes beyond descriptive approaches described previously (14). It enables the capture of spatial information about organelles including localization, associations and interactions.

Inter-model dependence is an important aspect of these generative models. For example, cell shape can be modeled as statistically dependent on a nuclear shape model, and object-based vesicular models can subsequently depend on both nuclear and cell shape. An initial approach for modeling vesicular distributions (9,13) considered spatial location to be dependent only on cell and nuclear shape. However, it is well known that vesicle localization in the cell can be actively maintained, implying a relationship between vesicle position and cytoskeletal components, microtubules in particular (15); vesicular-cytoskeletal interactions have been previously simulated (16). Recently, out initial organelle model was improved by introducing a dependency of the position of the organelle on the distance to the nearest microtubule in the cell. Using immunofluorescence images from the Human Protein Atlas (17), the ability to distinguish eleven punctate patterns using these models was demonstrated (18). During the course of that study, it was observed that many of the proteins annotated as ‘vesicular’ in the HPA were not in vesicles at all but rather part of cytoplasmic complexes with similar appearance. We therefore use the more general term ‘puncta’ to refer to both vesicles and apparent punctate structures. Here we investigate whether the location pattern of puncta also depends significantly on the position of the endoplasmic reticulum, and, most importantly, explore whether positions of puncta of the same type are dependent upon each other. With this question in mind; we model puncta position as a spatial point process within the cytoplasm. A relative coordinate system, based on the nuclear and cell boundaries, the microtubule structure, and the endoplasmic reticulum, is introduced to allow for comparison across multiple cell types.

Spatial point processes (19–21) are useful and powerful mathematical models for analyzing the spatial structure of both regular and irregular point patterns. A spatial point pattern is a group of observed locations of events in a multidimensional space. Such patterns have found use in a wide variety of scientific fields: ecology, geography, spatial epidemiology, and, to a limited extent, biology. There is a hierarchy of models for how points, or objects, are spatially distributed. These range from models of complete independence between points, Poisson point processes, to models of pairwise and higher order interdependence, including clustering and repulsive phenomena, such as Markov and Cox processes.

Materials and Methods

Dataset

The dataset consisted of confocal images of A-431, U-2OS and U-251MG cell lines from the HPA that were previously selected (18). The Human Protein Atlas (HPA, http://proteinatlas.org) is a project to explore the human proteome and contains high-resolution images of subcellular location patterns for numerous proteins in the above cell lines. These images were collected as 8-bit TIFF images and acquired using standard stains for nucleus, endoplasmic reticulum, microtubule cytoskeleton and one other specific protein. The size of the images was 1728×1728 pixels; each pixel corresponds to 0.08 microns in the sample plane. Eleven proteins tagged in all cell lines were chosen as ‘founder proteins’, representative of eleven specific types of punctate patterns.

Homogeneous Poisson processes

Assume that for a random variable X⁽ⁿ⁾ = (X₁, ⋯, X_n) with a realization of punctate pattern x⁽ⁿ⁾ = (x₁, ⋯, x_n) over a cell cytoplasm w, x_i is the coordinates of the i^th punctum location and n is the number of puncta.

The simplest case for the positions of puncta is that they are completely random. This hypothesis follows a homogeneous Poisson process (20),

$$f(X^{(n)}\mid n)=\frac{1}{Z}{b}^n,$$ (1)

where Z is a normalizing constant and b is a constant that represents the unnormalized density of each punctum. Assume that the number of puncta is known in each cell and that the normalizing constant is

$$Z={\int }_w{b}^{n}d{X}_1\cdots d{X}_n=b^n{\mid w\mid }^n.$$ (2)

where w is the cytoplasm of a cell.

Correspondingly, the homogeneous Poisson becomes

$$f(X^{(n)}\mid n)=\frac{1}{{\mid w\mid }^n}.$$ (3)

In this simple case, it is not necessary to estimate b since it cancels out.

To test this hypothesis, a Monte Carlo test (22) was performed with test statistic

$$T_K={\int }_0^{r_{max}}{\left(\widehat{K}(r)-K_{\mathit{Poi}}(r)\right)}^2,$$ (4)

where K(r) is a Ripley’s K-function. The expected number of puncta within radius r of an observed puncta is K_Poi(r) = πr² under the hypothesis of complete spatial randomness.

We calculated $t_K^1,\cdots ,t_K^{m-1}$ as values of the test statistic T_K for m−1 random samples from the Poisson distribution and $t_K^{\ast }$ as the value of the test statistic T_K for an observed protein pattern, where m was set to the number of cells in the images of that protein multiplied by 100. A consistent Monte Carlo p-value was then calculated as

$$\frac{1+{\sum }_{i=1}^{m-1}I(t_K^{\ast }\ge t_K^i)}{m}.$$ (5)

Inhomogeneous Poisson processes

For spatially-dependent processes, we constructed six factors (f₁ through f₆) that our founder patterns might depend upon, as described in Results. We use the definition of the density of an inhomogeneous Poisson point process (20)

$$f(X^{(n)}\mid n)=\frac{1}{Z_{\theta }}{\prod }_{i=1}^n{b}_{\theta }(X_i),$$ (6)

where b_θ is a trend term that introduces dependence of the positions of puncta on other components in a cell and θ is a parameter vector of coefficients (that capture the dependence on each component) that can be estimated by maximizing log pseudolikelihood; Z_θ is a normalizing constant. The b_θ terms are log-linear combinations of some number of factors, such as log(b_θ) = θ₁f₁ + θ₂f₂. Different combinations of factors correspond to different models and therefore have different predictions of puncta distribution. We therefore sought to use five-fold cross-validated likelihood to choose the model that most accurately captures the relationships between puncta and other organelles. However, there is a normalizing constant in equation 6 that we can ignore when comparing models of the same structure but is required for comparing models with different factors.

Given the number of puncta in a single cell, the normalizing constant is a high-dimensional integral,

$$Z_{\theta }={\int }_w{\prod }_{i=1}^n{b}_{\theta }(X_i)d{X}_1\cdots d{X}_n.$$ (7)

We performed Monte Carlo integration to estimate this constant. Under the assumption that puncta locations are independent of each other, the high-dimensional integration above was simplified as

$$Z_{\theta }={\left({\int }_w{b}_{\theta }(X_u)d{X}_u\right)}^n.$$ (8)

Furthermore, ∫_wb_θ(X_u)dX_u was approximated by Monte Carlo integration,

$${\int }_w{b}_{\theta }(X_u)d{X}_u=\mid w\mid {\int }_w{b}_{\theta }(X_u)\frac{1}{\mid w\mid }d{X}_u=\mid w\mid {\int }_w{b}_{\theta }(X_u)p(X_u)d{X}_u=\mid w\mid E_{p(X_u)}[b_{\theta }(X_u)],$$ (9)

where $p(X_u)=\frac{1}{\mid w\mid }$ distributed uniformly over cytoplasm w.

The above integral is equal to the expected value of b_θ(X_u) with respect to random variable X_u distributed according to p(X_u). We estimate the expected value by sampling according to p and calculating the average of b_θ. To guarantee the accuracy of the approximation, the number of samples was chosen to be 5000 under the condition that it is nearly equal to the effective size,

$$n_e=\frac{M}{1+2{\sum }_{k=1}^{\infty }{\rho }_k},$$ (10)

where ρ_k is an autocorrelation function of lag k.

Then the likelihood of x⁽ⁿ⁾ was calculated as

$$\begin{array}{c}{L}_{\theta }\left(x^{(n)}\right)={\int }_{x_1}^{x_1+\mathrm{\Delta }{x}_1}\cdots {\int }_{x_n}^{x_n+\mathrm{\Delta }{x}_n}f\left(X^{(n)}\mid n\right)d{X}_1\cdots d{X}_n\approx f(x^{(n)}\mid n)\mathrm{\Delta }{x}_1\cdots \mathrm{\Delta }{x}_n\\ \mathrm{\Delta }{x}_1=\cdots =\mathrm{\Delta }{x}_n=0.01\end{array}$$

We then estimated the performance of different models by five-fold cross-validated likelihood. Assume proteins are indexed by i with segmented c⁽ⁱ⁾ cells, randomly split into 5 roughly equal-sized groups. Let ${\tau }_l^i:\{1,\cdots ,n_i\}\mapsto \{1,2,3,4,5\}$ be an index that indicates the partition to which cell is allocated by the randomization (e.g., ${\tau }_1^i=2$ means that the 1^st cell of protein i is assigned to the second fold. The cross-validation estimate of prediction error is

$$R^{CV}(\alpha )=\frac{1}{c^{(i)}}{\sum }_{l=1}^{c^{(i)}}{\mathit{logL}}_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}[X^{(n_l)}\mid \alpha ],$$ (11)

where α indexes models of combinations of factors and n_l is the number of puncta in l^th cell; ${\mathit{logL}}_{\widehat{\theta }}^{-{\tau }_l^i}[·\mid \alpha ]$ is the log likelihood fit of model α in l^th cell with ${({\tau }_l^i)}^{th}$ group of cells removed; θ̂⁽ⁱ⁾are the parameters trained by other four groups of the data. By maximizing R^CV(α) on α, we chose the model indexed by α̂.

Markov spatial point processes

Assume that there are dependences between the positions of puncta of the same type. Markov (Gibbs) processes (20) exhibit aggregation (or inhibition) due to interaction between points, explicating the spatial distribution of puncta by

$$f(X^{(n)}\mid n)=\frac{1}{Z_{\theta }}{\mathrm{\Pi }}_{i=1}^n{b}_{\theta }(X_i){\mathrm{\Pi }}_{i<j}{h}_{\theta }(X_i,X_j).$$ (12)

The interaction terms h_θ introduce pairwise interaction between puncta.

We tried different models to characterize interactions between puncta, Strauss hard processes (23,24) and Fiksel processes (25), as defined in equations 13 and 14. In these models, free parameters δ, r, κ are required to define the allowed interaction range of each punctum.

The Strauss hard point process is

$$\begin{array}{c}f(X^{(n)}\mid n)=\{\begin{array}{cc}0& \forall \Vert X_i-X_j\Vert <\delta ,i\ne j\\ \frac{1}{Z_{\theta }}{\mathrm{\Pi }}_{i=1}^n{b}_{\theta }(X_i){\gamma }^{S(X^{(n)})}& \mathit{otherwise}\end{array}.\\ S(X^{(n)})=\#\{(i,j):i<j,\Vert X_i-X_j\Vert <r\}.\end{array}$$ (13)

S(X⁽ⁿ⁾) is the number of unordered pairs of point than lie closer than radius r. Each pair of puncta closer than r units contributes γ to the density.

The Fiksel point process is

$$f(X^{(n)}\mid n)=\{\begin{array}{cc}0& \forall \Vert X_i-X_j\Vert <\delta ,i\ne j\\ \frac{1}{Z_{\theta }}{\mathrm{\Pi }}_{i=1}^n{b}_{\theta }(X_i){\mathrm{\Pi }}_{i<j}exp\left(a\ast exp(-\kappa \ast d(X_i,X_j))\right)& \delta \le \Vert X_i-X_j\Vert <r\end{array}.$$ (14)

This interaction model states that no pair of points is permitted to come closer than the hard core distance δ and that they do not interact (that is, influence each other) if the distance between them is more than radius r.

Similarly to Poisson models, the normalizing constant in equation 13 and 14 is first estimated in the following steps. The conditional density in these cases can be written as

$$f(X^{(n)}\mid n)=\frac{1}{Z_{\theta }}{B}_{\theta }(X^{(n)})H_{\theta }(X^{(n)}),$$ (15)

Where Z_θ is a normalizing constant, B_θ(X⁽ⁿ⁾) denotes the trend terms and H_θ(X⁽ⁿ⁾) represents the interaction terms. Given the number of puncta n, the constant is expressed as

$$Z_{\theta }={\int }_w{B}_{\theta }(X^{(n)})H_{\theta }(X^{(n)})d{X}^{(n)}.$$ (16)

A Monte Carlo integration was used to estimate it. A short derivation gives

$$\begin{array}{l}{Z}_{\theta }={\int }_w{B}_{\theta }(X^{(n)})H_{\theta }(X^{(n)})d{X}^{(n)}\\ ={\left({\int }_w{b}_{\theta }(X_u)d{X}_u\right)}^n\times {\int }_w{H}_{\theta }(X^{(n)})\frac{B_{\theta }(X^{(n)})}{{\left({\int }_w{b}_{\theta }(X_u)d{X}_u\right)}^n}d{X}^{(n)}\\ ={\left({\int }_w{b}_{\theta }(X_u)d{X}_u\right)}^n{E}_{p(X^{(n)})}\left(H_{\theta }(X^{(n)})\right),\end{array}$$ (17)

Where the puncta generating distribution is,

$$X^{(n)}~p(X^{(n)}),p(X^{(n)})=\frac{B_{\theta }(X^{(n)})}{{\left({\int }_w{b}_{\theta }(X_u)d{X}_u\right)}^n}.$$ (18)

According to equation 17, the normalizing constant can be estimated by calculating the expected value of E_{p(X⁽ⁿ⁾)}(H_θ(X⁽ⁿ⁾)) and the simpler integration of ∫_wb_θ(X_u)dX_u, respectively. We estimated the expected value by generating a number of random samples according to p(X⁽ⁿ⁾) in equation 18, calculating H_θ for each sample and averaging these values. The number of generated samples was chosen (see equation 10) in order to guarantee that the average converges to the expected value. The simpler integration was estimated by Monte Carlo integration (see equation 9).

Software availability

The source code will be available in the next release of CellOrganizer (http://CellOrganizer.org). In addition, a Reproducible Research Archive containing all source code and processed results is available at http://murphylab.web.cmu.edu/software.

Results

Preprocessing

As in our prior work (18), we analyzed images of proteins from HPA that were annotated as “vesicles”. Each image includes four fluorescence channels: a particular punctate protein along with nuclear, microtubule and endoplasmic reticulum (ER) markers (see Figure 1a). We then processed these images to identify the positions of the components for each channel. The nucleus was segmented using CellOrganizer as described previously (13). To estimate the position of the plasma membrane, we blurred the microtubule channel and applied a threshold (under the assumption that regions within the cell would have at least some staining or autofluorescence in this channel). For microtubule locations, we chose pixels with locally maximal intensity to represent locations on filaments. A discretization of the ER was obtained through the same procedure. To locate puncta for each protein, we used Gaussian object unmixing to resolve the image into separate Gaussian objects and took their centers as the positions of puncta, as described previously (13,18). After these steps, maps of the nuclear boundary, cell boundary, discretized microtubules, ER landmarks, and detected puncta locations were available for each cell in the dataset (see Figure 1b). Pixel positions were normalized to the range [0,1] using the minimum and maximum pixel number in X and Y.

Figure 1.

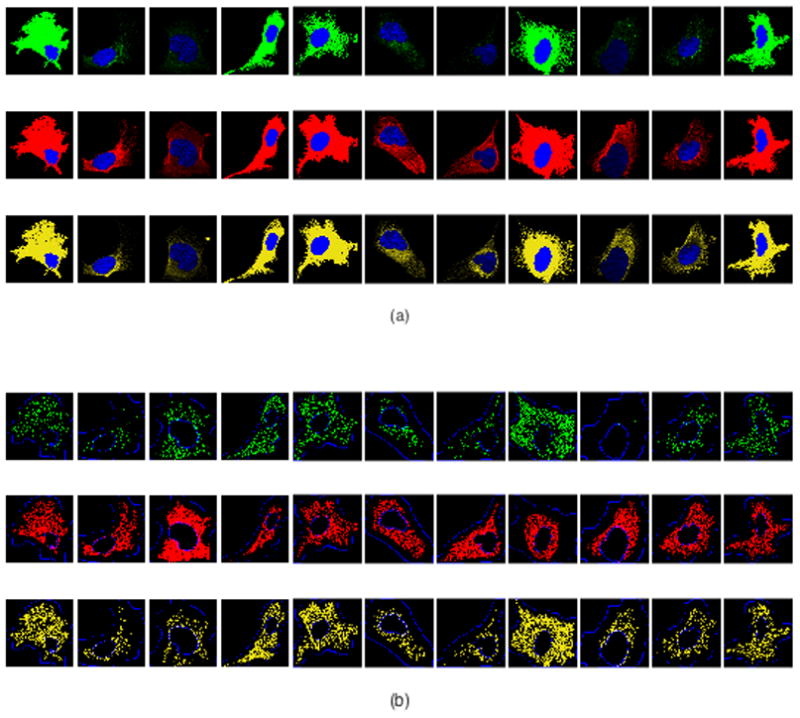
Illustration of initial image processing. Founders in cell type U-2OS (from left to right): COPE, SEC23B, FLOT1, CLTA, EEA1, RAB7A, TMEM192, CAT, APC, TFRC, and VPS35. (a) Representative original images depicting stains for nucleus (blue), microtubules (red), ER (yellow) and the specific protein (green). (b) Processed images showing nuclear and cell boundaries (blue), discretized microtubules (red), discretized ER landmarks (yellow) and detected puncta locations (green).

Assessing the non-randomness of puncta distributions

We first asked whether the puncta distribution in each cell was completely uniform over the cytoplasm (denoted w). In this case, the positions of puncta would be realizations of a homogeneous Poisson process (see Methods), which satisfies the property that the density is constant across every sub region of w.

To test this hypothesis for each of the founder proteins (Table 1) we used a Monte Carlo-based location test (22) as described in the Methods. The observed protein patterns for each cell and each founder were compared against samples generated from the homogenous Poisson model, retaining observed cell boundaries. Estimate of the p-value was computed. We adjusted each p-value using family-wise Bonferroni correction by multiplying p-values by the number of tests (the number of cells in this case), considering that the statistical tests were performed simultaneously and independently across all cells. As shown in Table 2, the hypothesis that the puncta are uniformly distributed in the cytoplasm was rejected at level α=0.01 for essentially all cells for all patterns. Thus, the patterns must depend upon one or more aspects of cell structure.

Table 1.

Proteins and antibodies used to model eleven distinguishable punctate subpatterns. These are the founder proteins used previously (18).

Gene name	Gene Description	Proposed annotation
COPE	Coatomer protein complex, subunit epsilon	COPI
SEC23B	Sec23 homolog B (S. cerevisiae)	COPII
FLOT1	Flotillin 1	Caveolae
CLTA	Clathrin, light chain A	Coated Pits
EEA1	Early endosome antigen 1	Early Endosome
RAB7A	RAB7A, member RAS oncogene family	Late Endosome
TMEM192	Transmembrane protein 192	Lysosomes
CAT	Catalase	Peroxisome
APC	Adenomatous polyposis coli	RNP bodies
TFRC	Transferrin receptor	Recycling Endosome
VPS35	Vacuolar protein sorting 35 homolog (S. cerevisiae)	Retromer

Table 2.

Test for non-uniform distribution of puncta in the cytoplasm.

Gene name	Number of cells	Number of cells with p<0.01	Largest p-value
COPE	25	25	0.0004
SEC23B	19	19	0.00052
FLOT1	17	17	0.00058
CLTA	51	51	0.00019
EEA1	44	44	0.00022
RAB7A	15	15	0.00066
TMEM192	19	19	0.00052
CAT	74	74	0.00013
APC	10	10	0.001
TFRC	44	44	0.00022
VPS35	18	18	0.00055

Modeling puncta dependences on other structures

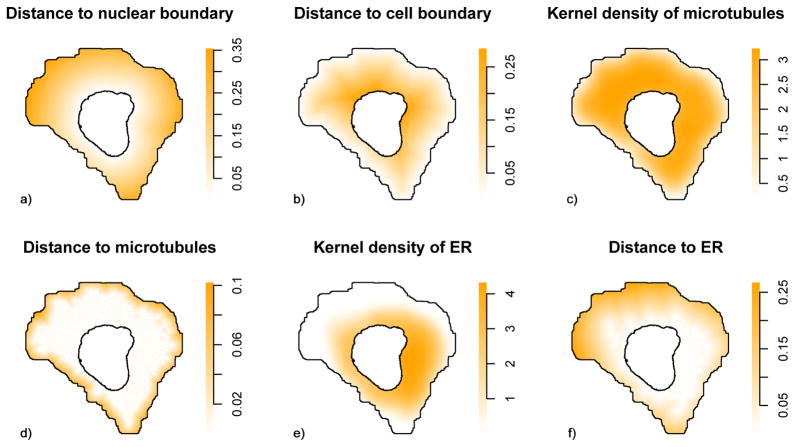
We next considered factors on which puncta localization might depend, cellular landmarks that could potentially contribute to the observed heterogeneity. To this end, six intuitive factors (Figure 2) were constructed, reflecting potential dependence of patterns upon cellular membranes, microtubule networks, and the ER. Given that the puncta are expected to be located in the cytoplasm, our most basic factors were grounded in the positions of the nuclear and cell boundary. Factors 1 and 2 consisted of the distance from puncta to the nuclear and cell boundary. To capture the relationship between vesicles (and other puncta) and the microtubule network, we designed a third and fourth factor. The third factor was the kernel probability density of microtubules, for which we used Scott’s rule of thumb for estimating the smoothing bandwidth (26). As the fourth factor, we calculated the distance from each point to the nearest discretized microtubule. These four factors are the same as considered in our previous work (18). To extend the model, we defined fifth and sixth factors to quantify the spatial arrangement of puncta relative to ER. These were done using the same approach as the third and fourth factors but using the ER distribution instead of microtubules (Figure 2).

Figure 2.

Illustrations of extracted factors. Examples of maps of factors used to model puncta distributions. The factors are calculated from images of probes for DNA, microtubules and endoplasmic reticulum after processing as describes in the Methods. The values of each factor at each position in a typical cell are shown.

We then projected the coordinates of each punctum into a space spanned by the factors described above, a coordinate system that we believed was comparable across widely varying cell morphologies and interior organelle arrangements. Ideally, puncta localization would exhibit some simple structure in this new coordinate system. Since puncta do not localize in exactly the same position in every cell, the simplest nontrivial structure is that of a line. In this case, overall puncta localization could be explained in terms of a log linear weighted sum over some or all of the factors (referred to as trend terms). We used generalized linear models to capture these relationships; these models have interpretations as inhomogeneous spatial point processes (20) (see Methods). Different combinations of factors in trend terms produced models with qualitatively different predictions of the spatial distribution of puncta localization; examples are shown in Figure 3. From a visual perspective, the example pattern produced from a model including microtubule distribution was more similar to the measured pattern than that produced by either a random model or a model depending only on nuclear pattern.

Figure 3.

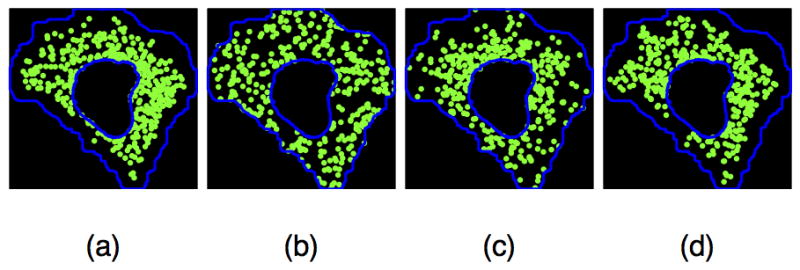
Comparison of observed puncta localization and synthetic puncta patterns from different models. (a) An observed pattern for FLOT1. (b) Example of randomly placed puncta within the same cell and nuclear boundaries (null distribution). (c) Example synthesized pattern of puncta from a model depending on nuclear and cell shapes only (an inhomogeneous model with a combination of factors 1 and 2. (d) Example synthesized pattern of puncta from a model depending on microtubule distribution (an inhomogeneous model with a combination of factors 3 and 4).

To identify the best model quantitatively over all cells, we used five-fold cross-validation to estimate the likelihood (27) of models using different combinations of the factors (Supplementary Table 1). We found that the best models were composed of factors 1, 3, 4 or factors 1–4, since both have very similar likelihoods. Analysis of the effect over all eleven patterns of leaving out factors of each organelle compared to the model with all factors reveals that the microtubule factors are the most important followed by the nuclear factor and the cell factor (Supplementary Table 2). Leaving out the cell factor causes the smallest decrease in likelihood, suggesting that it duplicates information in the other factors (this is verified by observing that adding the cell factor to a model with only the nuclear factor improves it slightly while adding it to a model with only the microtubule factors actually worsens it). Given that cell membrane location is estimated from the microtubule distribution, this result seems reasonable. Leaving out the ER factors (from the full model) causes a substantial positive effect, presumably because relying on those factors causes overfitting (i.e., failure to generalize to the held out images). Interestingly, adding the ER factors improves a model with only the nuclear factor or both the nuclear and cell factors, suggesting that the ER pattern does provide useful information when microtubule information is not available (however, again, the ER actors lead to overfitting when added to a model with just the microtubule factors). In summary, we found strong dependence of the patterns of all eleven puncta on nuclear and microtubule position (which includes their dependence on cell shape).

Analysis of dependence between puncta positions

We further considered the possibility that the positions of puncta are also dependent upon each other, that is, that the position of a punctum of one class is affected by the positions of other puncta of that same class. Markov spatial point processes allow inhomogeneous process models to be extended to capture interactions between puncta (see Methods). These models are typically composed of two parts, trend terms and interaction terms. The trend terms, b_θ(·), are same as those of the Poisson model, log-linear combinations of our factors. So, the total contributions from trend terms are ${\mathrm{\Pi }}_{i=1}^n{b}_{\theta }(x_i)$, where n is the number of puncta in a cell. Interaction terms, h_θ(·), are added in attempt to model between-punctum relationships. An interaction term h_θ(x_i, x_j) is defined to be the interaction between puncta x_i and x_j in the cell; the total contributions of interactions terms to puncta distribution are thus Π_i<jh_θ(x_i, x_j). If h_θ(x_i, x_j) = 1, Markov process models reduce to inhomogeneous Poisson models.

Although so far we have concerned ourselves with modeling the position of the center of each punctum, puncta are not points and occupy volume. Strauss hard-core process models (23,24) represent a modification of point processes that allow them to consider both the volume of objects and a maximum possible radius for interaction between them. To incorporate this, we assume that puncta have a typical size such that their centers are always farther away from each other than a certain distance δ, and therefore, for any pair of puncta x_i and x_j in a single cell, we modify the interaction terms so that is satisfies h_θ(x_i, x_j) = 0 if ||x_i − x_j|| < δ. To estimate δ we calculated the minimum distance between pairwise puncta across all cells. We also consider a further modification that pairwise puncta closer than a radius r interact with a constant strength, that is, h_θ(x_i, x_j) = γ if ||x_i − x_j|| ≤ r. It is not obvious how to estimate a meaningful fixed value for the interaction radius r in a data-driven manner. Instead, we first ascertained a reasonable interval [r_min, r_max],

$$r_{\mathit{min}}=\frac{1}{m}{\mathrm{\sum }}_{l=1}^m{d}_l^{\mathit{min}},r_{\mathit{max}}=\frac{1}{m}{\mathrm{\sum }}_{l=1}^m{d}_l^{\mathit{max}},$$

where $d_l^{\mathit{min}}=\underset{i<j}{min}\Vert x_i-x_j\Vert$ and $d_l^{\mathit{max}}=\underset{i<j}{max}\Vert x_i-x_j\Vert$, x_i, x_j are adjacent puncta in the l^th cell; m is the number of training cells. Different r values in this interval were sampled and the best value chosen by optimizing pseudolikelihood as described below. We summarize the Strauss hard process model as

$$\begin{array}{l}{h}_{\theta }(x_i,x_j)=0\text{if}\Vert x_i-x_j\Vert <\delta ,\\ h_{\theta }(x_i,x_j)=\gamma \text{if}\delta \le \Vert x_i-x_j\Vert \le r,\\ h_{\theta }(x_i,x_j)=1\text{if}\Vert x_i-x_j\Vert >r.\end{array}$$

A further modification, referred to as a Fiksel process (25), involves assuming a more complicated interaction structure such that the strength of interaction is not fixed but varies with between-punctum distance. We thus have

$$\begin{array}{c}{h}_{\theta }(x_i,x_j)=0\text{if}\Vert x_i-x_j\Vert <\delta ,\\ h_{\theta }(x_i,x_j)=\mathit{exp}\left(a\ast \mathit{exp}(-\kappa \Vert x_i-x_j\Vert )\right)\text{if}\delta \le \Vert x_i-x_j\Vert \le r,\\ h_{\theta }(x_i,x_j)=1\text{if}\Vert x_i-x_j\Vert >r.\end{array}$$

where a is a parameter indicating the strength of interaction and κ is rate parameter controlling the decaying of the interaction with increasing distance. We picked κ = 1 here since there was no marked distinction when trying different values of κ.

In these models, parameters are of two kinds: free parameters and regular parameters. Given values of free parameters including δ, r and κ, the regular parameters, θ,γ,a, were optimized by maximizing log pseudolikelihood (27); doing this for different values of r allowed the choice of the best r. Different groups of values of free parameters in Strauss hard and Fiksel Markov processes are indicative of different interactions between puncta. However, the free parameters can only be determined by heuristic methods, and we picked realistic values for them in a data-driven manner as described above. We then maximized log pseudolikelihood to optimize the regular parameters. As seen in Table 3, for each pattern the likelihoods for the different Markov models were similar to those of the Poisson model. We therefore did not find support for the idea that the localization of a punctum is dependent upon the positions of other puncta for any of the eleven patterns.

Table 3.

Comparison of the cross-validated average log-likelihood of different models. The radius for models Fiksel3 and Strauss3 was 0.0031291 and for Fiksel9 and Strauss9 was 0.0097915. All models used factors 1 through 4, except the models for peroxisomes and RNP bodies did not use factor 2. The small differences between the models suggests minimal dependence of puncta positions upon each other.

Location	Fiksel3	Fiksel9	Strauss3	Strauss9	Poisson
COPI	−0.749	−0.751	−0.750	−0.748	−0.749
COPII	−0.587	−0.596	−0.587	−0.593	−0.587
Caveolae	−0.610	−0.619	−0.607	−0.614	−0.610
Coated pits	−0.719	−0.700	−0.717	−0.699	−0.700
Early Endosomes	−0.718	−0.709	−0.718	−0.709	−0.709
Late Endosomes	−0.607	−0.613	−0.606	−0.611	−0.607
Lysosomes	−0.577	−0.581	−0.577	−0.576	−0.577
Peroxisomes	−0.714	−0.698	−0.713	−0.697	−0.698
RNP bodies	−0.593	−0.594	−0.593	−0.591	−0.593
Recycling Endosomes	−0.665	−0.676	−0.664	−0.674	−0.665
Retromer	−0.743	−0.712	−0.741	−0.715	−0.712

Measure of localization dissimilarity between patterns

Having demonstrated that the inhomogeneous Poisson model yields an appropriate description of the spatial distribution of these punctate proteins, we compared the spatial distributions of different proteins using the Poisson models for the set of factors that gave the best pseudolikelihood. For this, we used the total variation of protein distribution across all cells. The estimate of total variation was implemented by five-fold cross validation.

For each cell line, segmented c⁽ⁱ⁾ cells of protein i were randomly split into 5 roughly equal-sized groups. ${\tau }_l^i:\{1,\cdots ,n_i\}\mapsto \{1,2,3,4,5\}$ is an index that indicates the partition to which cell is allocated by the randomization. For the l^th cell, punctate objects were sampled as $f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}$ within cytoplasm $w_l^{(i)}$, where θ̂⁽ⁱ⁾ was trained by the cells with the ${({\tau }_l^i)}^{th}$ fold cells removed. Given proteins i and j, we measured the total variation between them as

$$\begin{array}{l}{v}_{ij}=\frac{1}{c^{(i)}+c^{(j)}}\left({\mathrm{\sum }}_{l=1}^{c^{(i)}}{\int }_{w_l^{(i)}}\left|f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}(u)-f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}(u)\right|du+{\mathrm{\sum }}_{l=1}^{c^{(j)}}{\int }_{w_l^{(j)}}\left|f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}(u)-f_{{\widehat{\theta }}^{(j)}}^{-{\tau }_l^j}(u)\right|du\right)\\ \approx \frac{1}{c^{(i)}+c^{(j)}}\left({\mathrm{\sum }}_{l=1}^{c^{(i)}}\frac{\left|w_l^{(i)}\right|}{M}{\mathrm{\sum }}_{m=1}^M\left|f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}(u_m)-f_{{\widehat{\theta }}^{(j)}}^{-{\tau }_l^j}(u_m)\right|+{\mathrm{\sum }}_{k=1}^{c^{(j)}}\frac{\left|w_l^{(j)}\right|}{M}{\mathrm{\sum }}_{m=1}^M\left|f_{{\widehat{\theta }}^{(i)}}^{-{\tau }_l^i}(u_m)-f_{{\widehat{\theta }}^{(j)}}^{-{\tau }_l^j}(u_m)\right|\right)\end{array}$$ (20)

where M is the number of samples of Monte Carlo simulation.

We did this calculation for all pairs of the eleven founders for each cell line to determine which protein models were distinguishable (results for U-2OS are shown in Table 4). The results showed that founders FLOT1 and TMEM192 in cell line U-2OS are somewhat similar but that other pairs of founders are quite dissimilar. The results for cell lines A-431 and U-251MG (See Supplementary Tables 3 and 4) were similar.

Table 4.

Dissimilarity between subpatterns in cell line U-2OS with values ~1 meaning absolutely distinguishable, while values ~0 are indistinguishable. We calculated the total variation of founders to discover dependency difference between subpatterns. Minimum values and founders involved shown in bold.

	COPE	SEC23B	FLOT1	CLTA	EEA1	RAB7A	TMEM192	CAT	APC	TFRC	VPS35
COPE	0	0.6753	0.5896	0.2954	0.1125	0.6205	0.5722	0.2874	0.4494	0.1758	0.5376
SEC23B	0.6753	0	0.1366	0.7954	0.6555	0.2017	0.1885	0.7402	0.2871	0.4811	0.9991
FLOT1	0.5896	0.1366	0	0.7447	0.5725	0.1630	0.0910	0.6878	0.1964	0.4040	0.9482
CLTA	0.2954	0.7954	0.7447	0	0.2024	0.7635	0.7552	0.0916	0.6386	0.4237	0.2514
EEA1	0.1125	0.6555	0.5725	0.2024	0	0.5955	0.5723	0.1890	0.4500	0.2089	0.4519
RAB7A	0.6205	0.2017	0.1630	0.7635	0.5955	0	0.1741	0.7250	0.2262	0.4237	0.9811
TMEM192	0.5722	0.1885	0.0910	0.7552	0.5723	0.1741	0	0.7129	0.1687	0.3897	0.9833
CAT	0.2874	0.7402	0.6878	0.0916	0.1890	0.7250	0.7129	0	0.6217	0.3872	0.3175
APC	0.4494	0.2871	0.1964	0.6386	0.4500	0.2262	0.1687	0.6217	0	0.2563	0.8960
TFRC	0.1758	0.4811	0.4040	0.4237	0.2089	0.4237	0.3897	0.3872	0.2563	0	0.6912
VPS35	0.5376	0.9991	0.9482	0.2514	0.4519	0.9811	0.9833	0.3175	0.8960	0.6912	0

Classifying proteins into eleven patterns

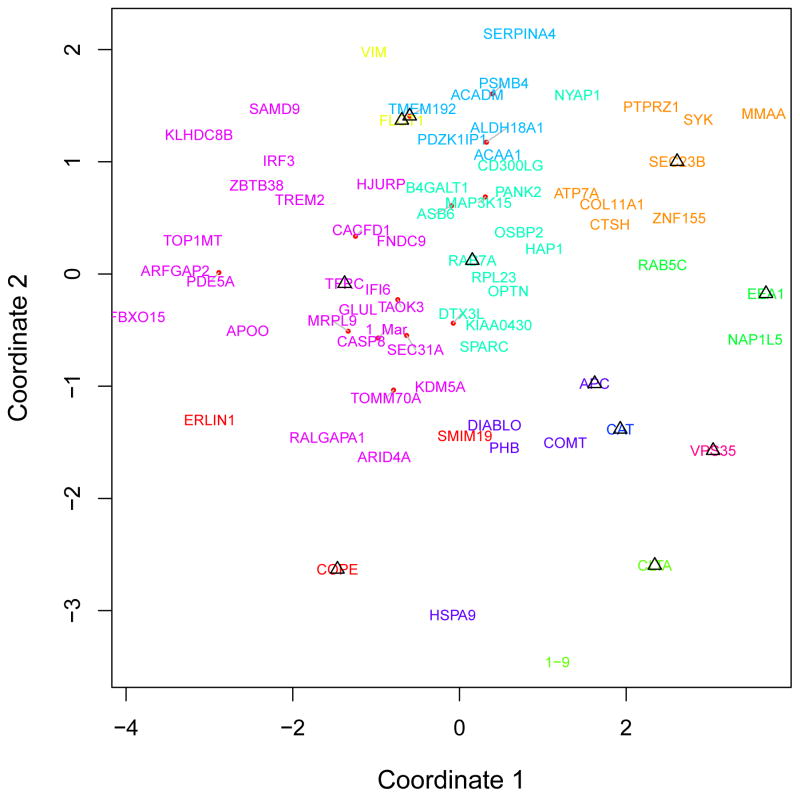
These results suggest it would be possible to form a basis for assigning detailed subcellular locations to punctate proteins for which limited information is available. We created discriminative features for each protein by combining numerical descriptors of punctate protein patterns (puncta size, distribution, number of puncta and average intensity of puncta) with a measure of the degree of dissimilarity between the given protein and each of the eleven founder proteins. Thus, the subcellular localization of each non-founder protein was represented by a numerical feature vector with fifteen elements (four for puncta properties and eleven for similarities to founders). Using the feature vectors of the founder proteins, we then applied the nearest neighbor algorithm to classify non-founder protein patterns into eleven classes. To visualize the classification results, each protein was placed in 2-dimensional space by nonmetric multidimensional scaling (see Figure 4 and Supplementary Figure 1, 2).

Figure 4.

Classification of proteins in U-2OS into eleven punctate subpatterns. Different colors correspond to COPI, COPII, Caveolae, Coated Pits, Early Endosome, Late Endosome, Lysosomes, Peroxisome, RNP bodies, Recycling Endosome and Retromer, respectively. A dissimilarity matrix among 59 proteins was calculated by metric multidimensional scaling.

We then compared these results to previous classification results (18). Such comparison enabled us to identify proteins that were assigned to the same pattern by both classifiers. This provided more convincing evidence that the assigned subcellular location of these proteins is correct (See Table 5 and Supplementary Tables 5 and 6).

Table 5.

Proteins in U-2OS assigned to eleven subpatterns. For each protein, we calculated the distance from it to founders of subpatterns and classified it to the subpattern that has the shortest distance.

	Structure	Proteins classified with this approach	Previously classified
1	COPI	SMIM19, ERLIN1
2	COPII	ZNF155, SYK, PTPRZ1, ATP7A, CTSH, COL11A1, MMAA	ZNF155, SYK, PTPRZ1, ATP7A
3	Caveolae	VIM	IFI6, ACAA1, SERPINA4, ASB6
4	Coated pits		NAP1L5
5	Early Endosomes	RAB5C, NAP1L5	RAB5C, COL11A1, MMAA
6	Late Endosomes	KIAA0430, PANK2, MAP3K15, B4GALT1, OSBP2, SPARC, HAP1, OPTN, RPL23, DTX3L, CD300LG, NYAP1, ASB6	KIAA0430, PANK2, MAP3K15, B4GALT1, OSBP2, SPARC, HAP1, OPTN, RPL23, PHB, DIABLO, CASP8, 1_Mar, CTSH, FNDC9, SEC31A, GLUL, MRPL9, ARFGAP2, HSPA9, KDM5A, ALDH18A1, RALGAPA1, COMT, TAOK3, HJURP, TREM2, VIM, PSMB4, ERLIN1, TOMM70A
7	Lysosomes	PDZK1IP1, ACAA1, SERPINA4, ACADM, ALDH18A1, PSMB4	PDZK1IP1, ZBTB38, CACFD1, NYAP1
8	Peroxisomes
9	RNP bodies	PHB, DIABLO, HSPA9, COMT	FBXO15, PDE5A, CD300LG, ACADM, KLHDC8B, APOO, TOP1MT, SAMD9, IRF3
10	Recycling Endosomes	CASP8, 1_Mar, ZBTB38, FNDC9, IFI6, SEC31A, GLUL, MRPL9, FBXO15, ARFGAP2, PDE5A, KDM5A, KLHDC8B, APOO, TOP1MT, SAMD9, RALGAPA1, CACFD1, IRF3, TAOK3, HJURP, ARID4A, TREM2, TOMM70A	DTX3L, SMIM19
11	Retromer		1–9, ARID4A

Discussion

CellOrganizer provides a systematic framework for modeling dependent localization of cellular proteins, a critical relationship in understanding dynamic, functional relationships. Here, we extend CellOrganizer to capture and non-parametrically model potential relationships among individual constituents in a cell using available cellular markers. We use spatial point processes to characterizing the subcellular localization of a punctate object relative to the positions of the nucleus, cell membrane, microtubule network, ER and other puncta in an individual cell.

We found evidence that punctum distributions are dependent on the nuclear and cell membranes and microtubules. While our models did not suggest inter-puncta dependence, we lacked the statistical power to reject this possibility given our sample size. However, a similar lack of spatial dependence was observed for constitutive exocytosis events (28).

Another goal was to recognize punctate protein patterns among previously uncharacterized proteins. To this end, we started by ensuring that the founder proteins could be distinguished by measuring the dissimilarity between them. The results indicated that the founder protein patterns are almost completely distinguishable in each cell line such that it is feasible for us to make use of dependence dissimilarity as discriminative features for classification of uncharacterized proteins. We compared our predictions with those previously made and identified proteins highly likely to be localized in one of the eleven founder patterns.

The methods described here are complementary to image analysis methods for dissecting subcellular compartmentalization and trafficking, such as tracking and morphological analysis of endocytic pathways (29). The fusion of various organelle detection methods with frameworks for constructing generative models of inter-organelle dependence such as those described here is expected to be highly useful for learning the relationships among different cellular components in a wide range of applications.

Supplementary Material

SupFigure1

Supplementary Figure 1. Classification of proteins in A-431 into eleven punctate subpatterns. Different colors correspond to COPI, COPII, Caveolae, Coated Pits, Early Endosome, Late Endosome, Lysosomes, Peroxisome, RNP bodies, Recycling Endosome and Retromer, respectively. A dissimilarity matrix among 25 proteins was calculated by metric multidimensional scaling.

SupFigure2

Supplementary Figure 2. Classification of proteins in U-251MG into eleven punctate subpatterns. Different colors correspond to COPI, COPII, Caveolae, Coated Pits, Early Endosome, Late Endosome, Lysosomes, Peroxisome, RNP bodies, Recycling Endosome and Retromer, respectively. A dissimilarity matrix among 365 proteins was calculated by metric multidimensional scaling.

Table 6.

Proteins in U-2OS assigned to the same patterns. We picked the proteins assigned into the same classes based on the classification results displayed in Table 5.

	Structure	Number of proteins of same class	Specific proteins in the same patterns
1	COPI	0
2	COPII	4	ZNF155, SYK, PTPRZ1, ATP7A
3	Caveolae	0
4	Coated pits	0
5	Early Endosomes	1	RAB5C
6	Late Endosomes	9	KIAA0430, PANK2, MAP3K15, B4GALT1, OSBP2, SPARC, HAP1, OPTN, RPL23
7	Lysosomes	1	PDZK1IP1
8	Peroxisomes	0
9	RNP bodies	0
10	Recycling Endosomes	0