Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Feb 8.
Published in final edited form as: J Biomech. 2016 Nov 29;52:24–30. doi: 10.1016/j.jbiomech.2016.11.053

Quantifying the competing relationship between adduction range of motion and baseplate micromotion with lateralization of reverse total shoulder arthroplasty

Josie Elwell 1, Joseph Choi 2, Ryan Willing 1,*
PMCID: PMC5309173  NIHMSID: NIHMS839333  PMID: 28024662

Abstract

Lateralizing the center of rotation (COR) of reverse total shoulder arthroplasty (rTSA) could improve functional outcomes and mitigate scapular notching, a commonly occurring complication of the procedure. However, resulting increases in torque at the bone-implant interface may negatively affect initial fixation of the glenoid-side component, especially if only two fixation screws can be placed. Shoulder-specific finite element (FE) models of four fresh-frozen cadaveric shoulders were constructed. Scapular geometry and material property distributions were derived from CT data. Generic baseplates with two and four fixation screws were virtually implanted, after which superiorly-oriented shear loads, accompanied by a compressive load, were applied incrementally further from the glenoid surface to simulate lateralization of the COR. Relationships between lateralization, adduction range of motion (ROM), the number of fixation screws and micromotion of the baseplate (initial implant fixation) were characterized. Lateralization significantly increases micromotion (p = 0.015) and adduction ROM (p = 0.001). Using two, versus four, baseplate fixation screws significantly increases micromotion (p = 0.008). The effect of lateralization and the number of screws on adduction ROM and baseplate fixation is variable on a shoulder-specific basis. Trade-offs exist between functional outcomes, namely adduction ROM, and initial implant fixation and the negative effect of lateralization on implant fixation is amplified when only two fixation screws are used. The possibility of lateralizing the COR in order to improve functional outcomes of the procedure should be considered on a patient-specific basis accounting for factors such as availability and quality of bone stock.

Keywords: Reverse total shoulder arthroplasty, Finite element modelling, Fixation, Lateralization, Adduction range of motion

1. Introduction

Reverse total shoulder arthroplasty (rTSA) has gained popularity in treating conditions involving a rotator cuff deficiency, namely cuff tear arthropathy (CTA), massive irreparable rotator cuff tears, and revision of previously failed hemi- or conventional total shoulder arthroplasty (TSA). The goals of rTSA are to restore range of motion (ROM) and provide pain relief; however, post-operative ROM may be limited by impingement, in some cases leaving the patient with an adduction deficit. Additionally, repeated impingement of the polyethylene humeral cup on the scapular neck may be the primary cause of scapular notching, which has been reported to occur in as many as 96% of rTSAs. Scapular notching may contribute to loosening of the glenoid component (Nicholson et al., 2011).

Lateralizing the COR of rTSA away from the glenoid increases ROM in both adduction and abduction, and could therefore decrease the incidence of adduction deficit and scapular notching (Gutiérrez et al., 2008a; Gutiérrez et al., 2008b, Hettrich et al., 2015). However, this may come at the cost of compromising primary implant stability and long-term survival of rTSA, because lateralization of the COR increases joint contact forces and bending moments at the bone-implant interface of the glenoid (Costantini et al., 2015). The effect of lateralizing the COR on primary mechanical stability (micromotion) of the glenoid-side implant component (the baseplate) has previously been investigated using bone substitute (Harman et al.,2005; Virani et al.,2008). However, it is unknown whether or not lateralizing the COR would amplify differences in initial fixation due to subject- and surgery-specific factors such as patient-specific bone density distributions or modified fixation strategies. For example, the results of a recent in-vitro biomechanical study with cadaveric shoulders has suggested that the use of two peripheral fixation screws (versus the typical usage of four screws) does not compromise primary stability of the baseplate in the context of baseplate micromotion (James et al., 2013). However, whether or not the same is true when the COR is lateralized has not been reported.

We hypothesize that there is a trade-off between rTSA ROM and baseplate fixation; COR lateralization will increase impingement-free adduction ROM, but baseplate micromotion will also increase significantly. Furthermore, we hypothesize that using fewer fixation screws (two versus four) will significantly increase baseplate micromotion, especially when the COR is lateralized. Therefore, the aims of this study were to (1) develop shoulder-specific rTSA finite element (FE) models capable of predicting impingement-free adduction ROM and baseplate micromotion under standardized loads, (2) measure the effect of COR lateralization on impingement-free adduction ROM and baseplate micromotion, and (3) measure the effect of using only two (superior and inferior) versus four fixation screws on baseplate micromotion at various COR lateralization distances.

2. Methods

2.1 Geometry

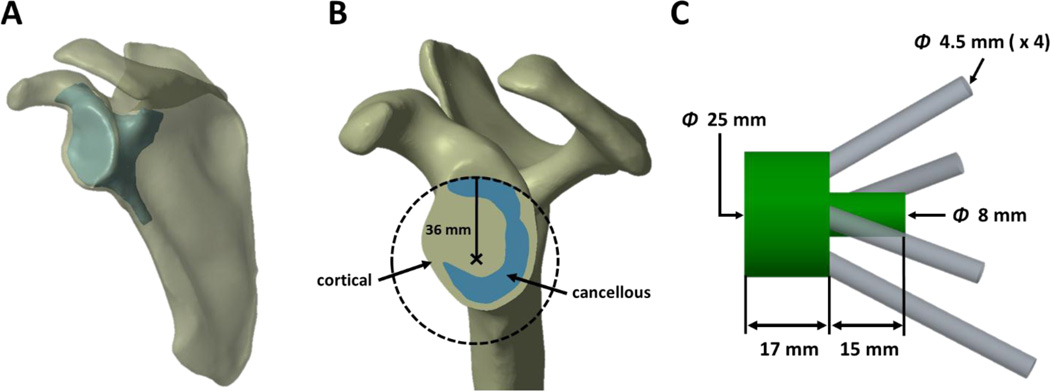
Four (4) fresh-frozen shoulders from three (3) cadaveric specimens (age 71–78, 2 male, 1 female, 2 left, 2 right) underwent computed tomography (CT) scanning using an Ingenuity CT (Philips Healthcare, Amsterdam, Netherlands) scanner at 120 kVa and 200 mA at a resolution of 0.68 × 0.68 × 0.33 mm. Three-dimensional (3D) models of each shoulder were created by first segmenting the scapula from the CT image data using a minimum threshold segmentation technique (HU > 250) in the open-source software 3D Slicer (Fedorov et al., 2012 – http://www.slicer.org), from which 3D surface models representing the exterior cortical boundary were created using a marching cubes algorithm. This model reconstruction technique is well established and provides models with sufficient accuracy for FE modelling (Willing et al., 2013; Lalone et al., 2015). The cortical-cancellous boundary in the region of the glenoid was identified manually in a slice-by-slice manner, and was also reconstructed as a 3D model (Fig. 1A). These surface models were assembled and imported into SolidWorks (Dassault Systèmes SolidWorks Corp., Waltham, MA, USA), and converted to solid CAD models. In Creo Parametric 2.0 (PTC Inc., Needham, MA, USA), a virtual reaming procedure was performed in order to create a 36 mm diameter circular glenoid ream parallel to a plane containing points on the superior, inferior, and posterior rims of the glenoid, centered slightly posteriorly and inferiorly to the anatomic center of the glenoid (Aequalis®-Reversed II Surgical Technique, Tornier, Inc.) (Fig. 1B).

Figure 1.

Figure 1

Open in a new tab

Representative models showing A) the external cortical boundary and cortical-cancellous boundary in the region of the glenoid, cropped to reduce computational costs of mapped material properties, B) the glenoid ream, and C) glenoid component geometry.

A generic glenoid component, representing a baseplate, metallic spacer, a central post, and four locking fixation screws (anterior, posterior, inferior and superior), was modelled as a monoblock. The assembled baseplate and metallic spacer were represented as a 25 mm diameter, 17 mm thick cylinder, allowing up to 16 mm of COR lateralization. The method of simulating lateralization, related to load application, will be discussed in a subsequent section. The central post was represented as a 15 mm long, 8 mm diameter cylinder positioned on the center of the back surface of the metallic spacer (Aequalis®-Reversed II Surgical Technique, Tornier, Inc.). The fixation screws were modelled as 4.5 mm diameter cylinders, representing the major diameter of commonly used bone screws (Chae et al., 2015) (Fig. 1C). Placement of the glenoid component, as well as screw trajectories, were determined on a shoulder-specific basis according to manufacturers’ suggestions for an existing rTSA system (Aequalis®-Reversed II Surgical Technique, Tornier, Inc.) and peer-reviewed literature for achieving the best possible initial fixation (Humphrey et al., 2008). All screw configurations were reviewed for clinical relevance by a board certified, shoulder fellowship trained orthopaedic surgeon experienced in rTSA (J.C.). Additional models for each shoulder were created where the glenoid component contained only 2 fixation screws; the anterior and posterior screws and corresponding holes in the scapula were removed while all other portions of the glenoid component remained unchanged. Therefore, the total number of geometric models was 8: 2 different screw configurations for each of the 4 shoulders.

2.2 Meshing

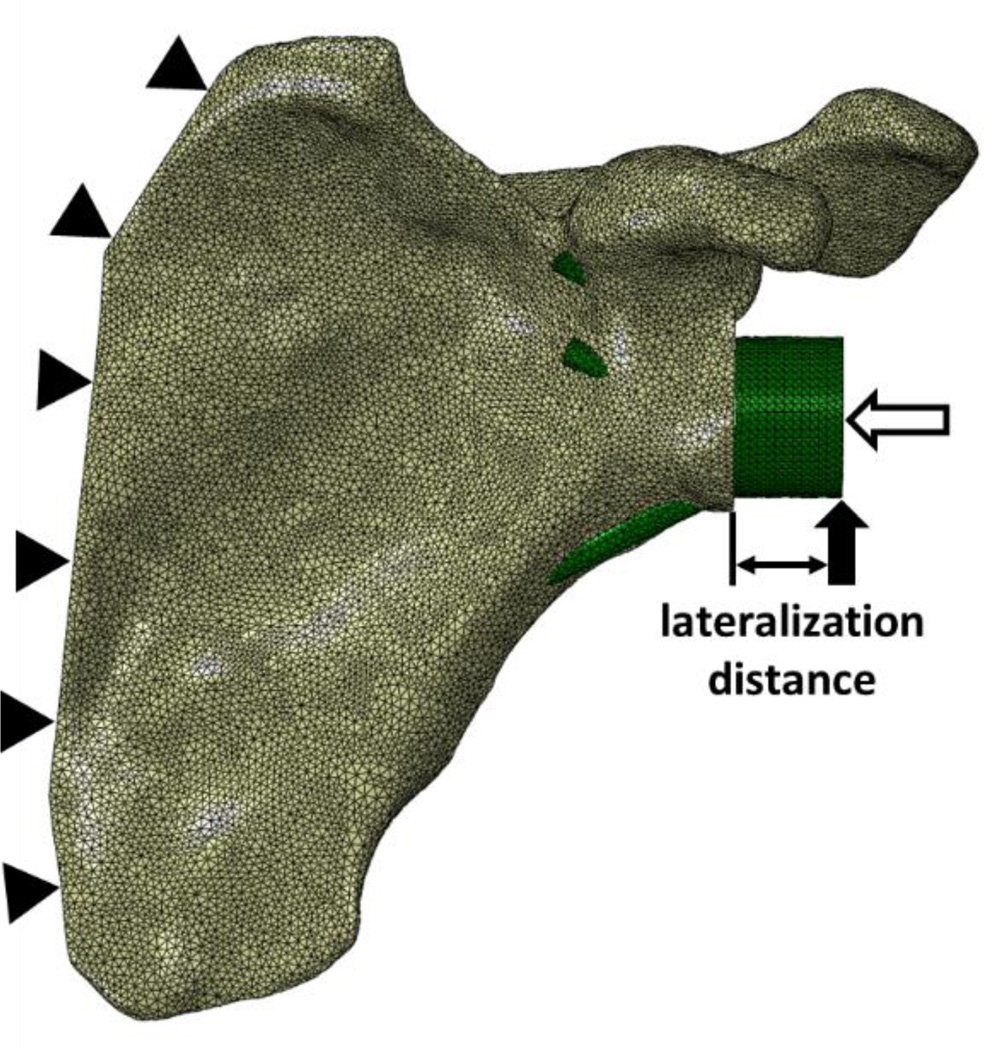
Finite element meshes of each model were created using Abaqus 6.14-2 (Dassault Systèmes Simulia Corp., Providence, RI, USA) comprising quadratic, tetrahedral elements (Fig. 2). A typical element edge length of 1.3 mm was chosen following a mesh convergence study on a single specimen. A carefully planned meshing technique ensured that screw and screw-hole boundaries initially shared identical node locations.

Figure 2.

Figure 2

Open in a new tab

A representative meshed FE model where the solid and unfilled arrows represent shear and compressive load applications, respectively, and the distance between the glenoid and the shear load is the degree of lateralization of the COR. Solid triangles represent fixed-displacement boundary conditions at the medial border of the scapula.

2.3 Material Properties

The baseplate, metallic spacer, and central post were assigned titanium material properties with an elastic modulus of 113.8 GPa and a Poisson’s ratio of 0.34 (Allegheny Technologies Inc., 2012). Similarly, the screws were also modelled as titanium, however the elastic modulus was reduced to 50.6 GPa to account for the increased stiffness of the oversized cylindrical screw geometries which were employed. Linear, isotropic, elastic material properties were used to model bone. Cortical bone was assigned an elastic modulus of 17,500 MPa and a Poisson’s ratio of 0.3. Cancellous bone material properties were assigned on an element-by-element basis as calculated from corresponding CT data (Taddei et al., 2008 – http://bonemat.org); a linear relationship between Hounsfield Unit (HU) and density with a slope of 0.002 and an intercept of 0.001 was defined. Subsequently, previously established equations to convert Hounsfield Units (HU) to elastic modulus were employed (Pomwenger et al., 2014), resulting in cancellous bone element elastic moduli ranging from 0 (empty space) to 17,500 MPa.

2.4 Loads, Boundary Conditions, and Contact

The FE models were constrained by fixed-displacement boundary conditions along the medial border of each scapula. A simulated joint reaction force was applied directly to the baseplate/spacer component, including a 1 × BW (686 N, assuming a 70 kg individual) compressive load oriented normal to the glenoid surface, and a superiorly oriented shear load of the same magnitude (Anglin et al., 2000; Harman et al., 2005; Virani et al., 2008; Bergmann et al., 2011) applied on the inferior portion of the baseplate/spacer (Fig. 2). Compressive and shear loads were applied as pressures over the lateral surface and 1 mm2 areas on the inferior portion of the baseplate/spacer, respectively. Lateralization of the COR was simulated by applying the shear loads incrementally further from the surface of the glenoid while the geometry of the baseplate/spacer remained unchanged. Lateralization of 0–16 mm in 4 mm increments was investigated. Therefore, results were based on a total of 40 simulations (4 shoulders × 5 levels of lateralization × 2 screw configurations).

A sensitivity analysis for friction properties was performed prior to determining friction coefficients used in the final models. Three different friction scenarios were applied to 2 shoulders at 2 levels of lateralization, 0 and 8 mm. The friction scenarios were as follows: friction coefficients of 0.8 or 1.7 at all bone-implant interfaces or a combination of frictionless sliding contact at the spacer/central post-bone interfaces and frictional contact at screw-bone interfaces with a friction coefficient of 0.8 (Zhang et al., 1999). The friction application chosen for use in final models was an isotropic friction model with a combination of frictionless sliding contact and frictional contact with a coefficient of 0.8.

2.5 Measuring Results

Micromotion of the baseplate/spacer in each model was measured on a node-by-node basis at the implant-glenoid interface. In-plane translations (displacement in the plane of the reamed glenoid face) and normal translations (displacement perpendicular to the reamed glenoid face) were calculated. Absolute micromotion was then calculated for each node, after which the average was taken. Average absolute micromotion of the baseplate/spacer will herein be referred to as absolute micromotion to avoid confusion in discussing averages taken across the specimen pool. Absolute micromotion for each configuration (combination of lateralization level and number of fixation screws) was normalized with respect to the baseline configuration, defined as 0 mm lateralization with four fixation screws for each shoulder.

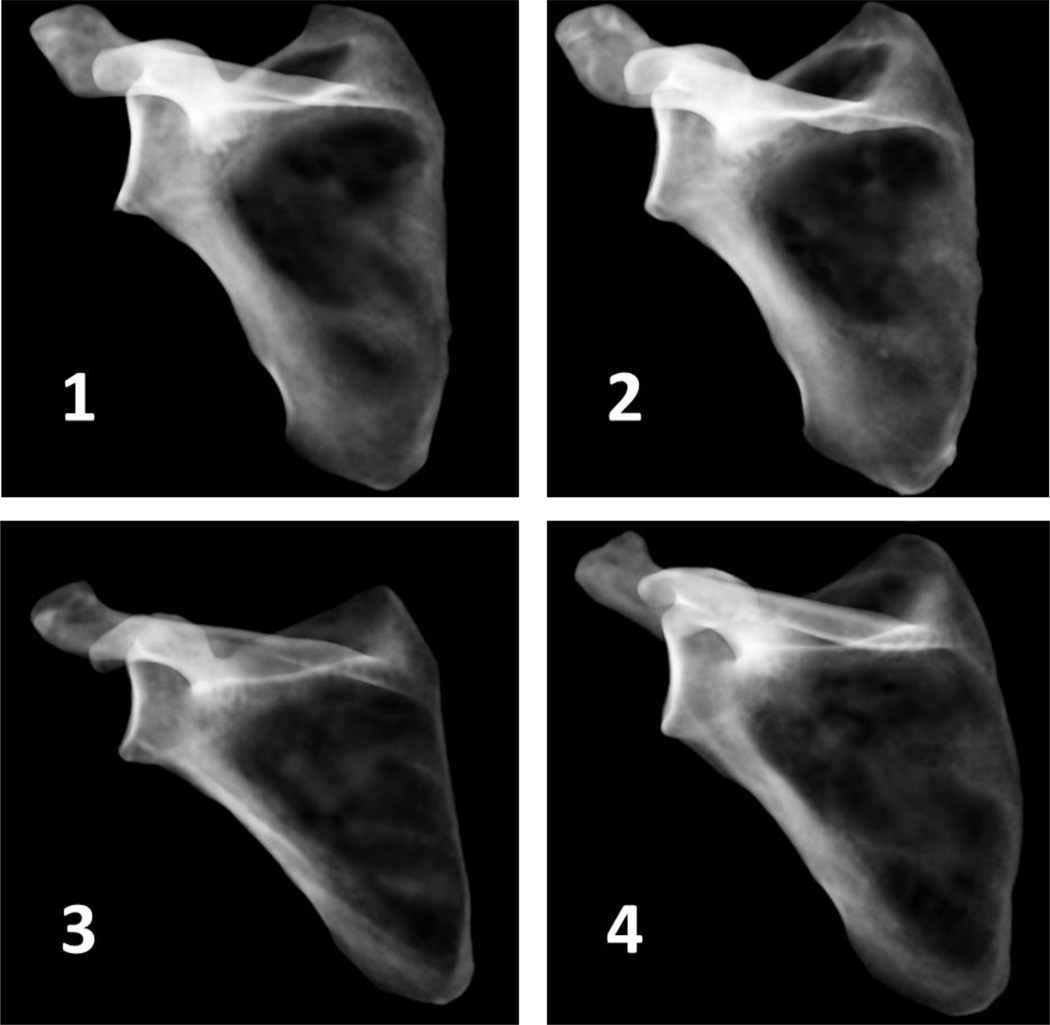
Specimen bone quality was quantified by calculating the average density of cancellous bone in the glenoid region, and visualized using simulated x-rays based on mapped material property data in ParaView 4.3.1 (Ahrens et al., 2005 – http://www.paraview.org).

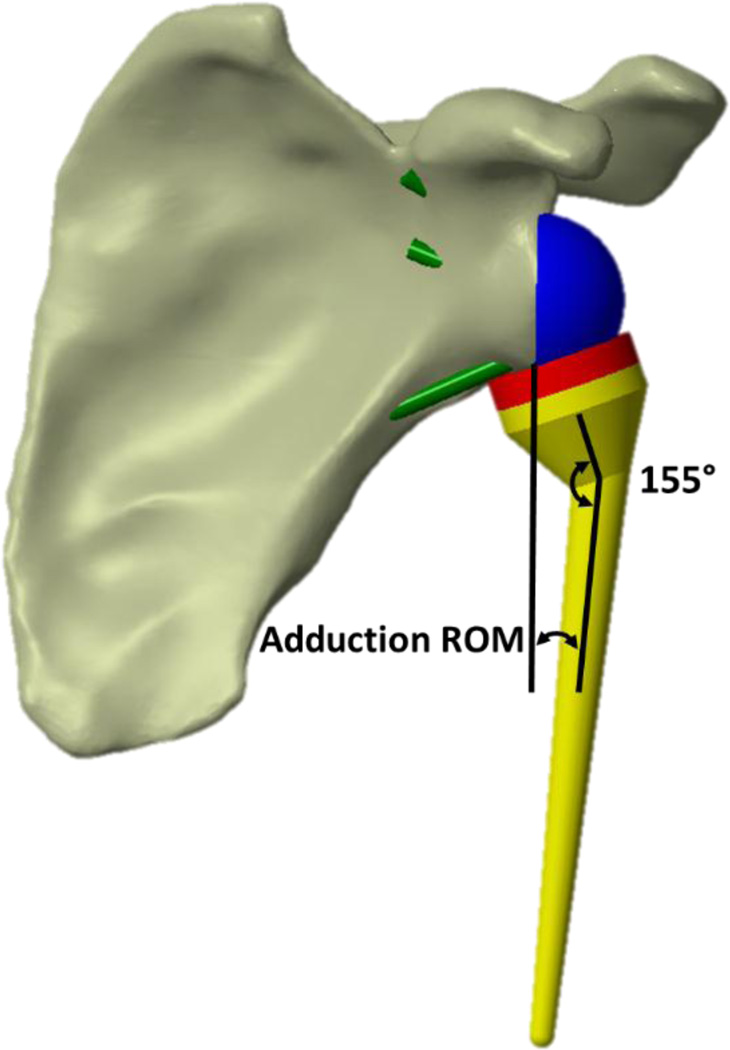
Adduction ROM at each lateralization level was measured as the angle between the central axis of a humeral stem with a 155° head-neck-shaft angle and a plane parallel to the reamed glenoid face at the point when the humeral cup was just impinging with any glenoid-side entity; bone or implant (Fig. 3). The only glenoid-side implant component affecting impingement after lateralization was the geometry of the spacer, which was the same diameter as the baseplate (25 mm).

Figure 3.

Figure 3

Open in a new tab

Representative implanted rTSA, with 0 mm of lateralization, showing the entities between which the angle was measured in order to characterize adduction ROM.

A two-way repeated-measures ANOVA with a Greenhouse-Geisser correction was performed with micromotion as the dependent variable to determine the effects of lateralization and the number of screws. A one-way repeated-measures ANOVA with a Greenhouse-Geisser correction and Post Hoc pairwise comparisons with a Bonferroni correction were performed to determine the effect of lateralization on adduction ROM. A p-value less than 0.05 was considered statistically significant.

3. Results

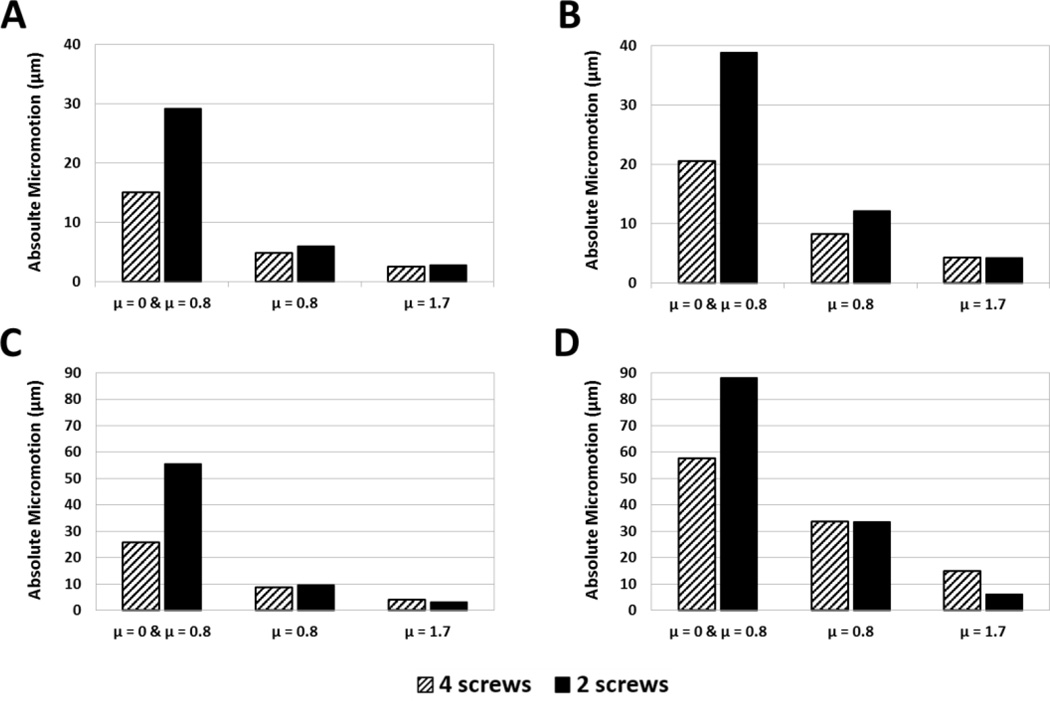
Results of the friction sensitivity analysis for a subset of specimens, used to determine friction application in final models, are shown (Fig. 4). Friction properties had a large influence on resulting micromotions, and frictional contact included at all interfaces appeared to over-constrain the model and yielded very small micromotions. The combination of frictionless contact (µ = 0) on the spacer/central post and frictional contact (µ = 0.8) for the screws provided micromotion values closer in magnitude (although still roughly 70% lower for 0 mm of lateralization) to previous in-vitro studies than the other configurations (Harman et al., 2005; Virani et al., 2008). Thus, this combination was chosen for all subsequent models.

Figure 4.

Figure 4

Open in a new tab

Results of the friction sensitivity analysis for specimens 1 (A & B) and 3 (C &D) at 0 mm (A &C) and 8 mm (B & D) of lateralization. Three friction applications were examined: frictionless sliding contact at the baseplate/central post-bone interfaces in combination with frictional contact at screw-bone interfaces with a friction coefficient of 0.8 and frictional contact at all implant-bone interfaces with friction coefficients of 0.8 and 1.7.

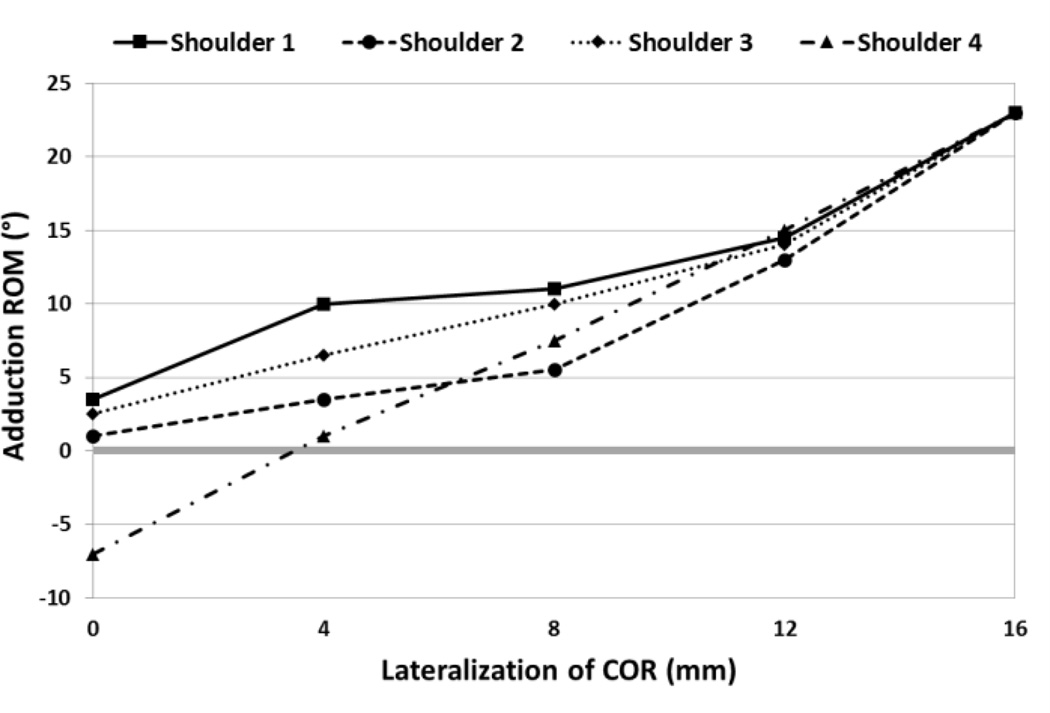
Lateralization had a significant effect on adduction ROM (p = 0.001). Shoulder-specific relationships between lateralization and adduction ROM are shown in Fig. 5. A negative value for adduction ROM was calculated for one shoulder at one level of lateralization (0 mm), indicating an adduction deficit. Post Hoc pairwise comparisons showed a statistically significant difference in adduction ROM at 16 mm compared with all other levels of lateralization.

Figure 5.

Figure 5

Open in a new tab

Specimen-specific relationships between lateralization of COR and adduction ROM, where a negative value for adduction ROM represents an adduction deficit.

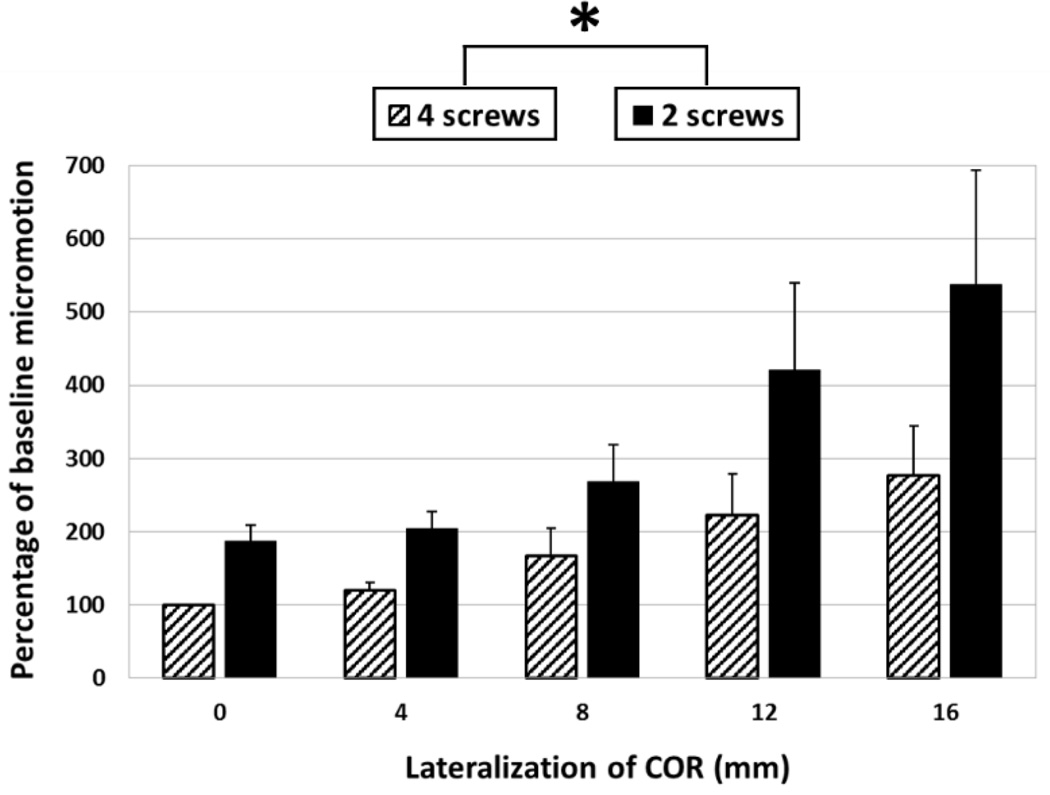
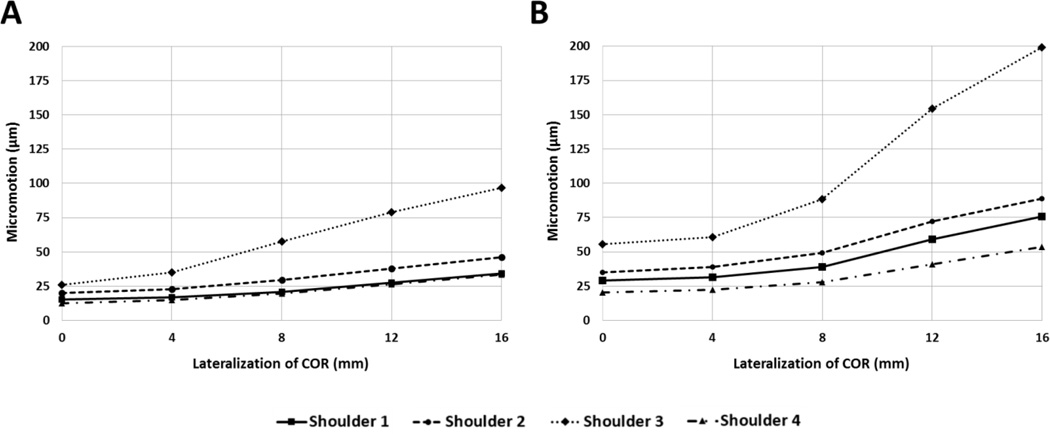
Absolute micromotion of the baseline configuration (0 mm of lateralization and 4 fixation screws) averaged across all shoulders was 18.3 ± 5.9 µm. Absolute micromotion, expressed as a percentage of baseline micromotion for each shoulder, are shown in Fig. 6. Absolute micromotion was significantly affected by both lateralization (p = 0.015) and the number of screws (p = 0.008). The interaction between lateralization and the number of screws was also significant (p = 0.024). Shoulder-specific results comparing degree of COR lateralization and absolute micromotion for 4 and 2 fixation screw configurations demonstrate that both lateralization and the number of screws affect micromotion, but the magnitude varies between shoulders (Fig. 7A and 7B, respectively). Average cancellous bone densities are shown in Table 1, and simulated x-rays in Figure 8.

Figure 6.

Figure 6

Open in a new tab

The effect of lateralization and the number of screws on the average percent change in micromotion from the baseline. Note: baseline micromotion of each specimen was taken to be 100% and therefore standard deviation was 0. An asterisk indicates statistical significance (p < 0.05).

Figure 7.

Figure 7

Open in a new tab

Shoulder-specific relationships between lateralization of COR and average absolute micromotion of the baseplate for (A) 4 fixation screw configurations and (B) 2 fixation screw configurations.

Table 1.

Average density of the cancellous bone in the region of the glenoid for each shoulder.

Shoulder Average cancellous
bone density (g/cm3)
1 0.59
2 0.61
3 0.45
4 0.59
Open in a new tab

Figure 8.

Figure 8

Open in a new tab

Simulated x-rays of each shoulder generated by mapping density values to opacity and projecting onto a black background, where darker areas represent less dense bone.

4. Discussion

We hypothesized that lateralizing the COR and reducing the number of fixation screws would both affect micromotion of the baseplate; and our results have supported this hypothesis. Minimizing micromotion is key factor in bony in-growth and long term fixation of the implant. Furthermore, our results confirmed that adduction ROM is also significantly increased by lateralization, but there is a trade-off; lateralization increases adduction ROM of rTSA at the cost of compromising primary implant stability. This trade-off, however, is variable even within our small shoulder population. Although three of the four shoulders exhibit very similar trends in the relationships between lateralization, the number of screws, and micromotion, one shoulder follows a different trend, which may be attributed to bone quality and specimen size differences. This supports the notion that, although we can generally quantify trade-offs that exist between lateralization and primary implant stability, the actual trade-off may vary on a patient-specific basis. Therefore, simulation-aided pre-operative planning of rTSA performed on a patient-specific basis may be required to provide truly optimal outcomes.

The method of simulating lateralization in the present study was very similar to the experimental setup used by Harman et al. (2005), who also reported lateralization having a significant effect on micromotion, whereas Virani et al. (2008) reported that lateralization did not have a significant effect on baseplate micromotion and supported their experimental results with FE models. However, their study achieved lateralization by using glenospheres of varying geometry, while the present study opted to use a consistent spacer design to avoid confounding results due to implant design variations. The results of the present study showed lower average micromotions than those measured in both of these experimental studies, possibly due to differences in experimental/modelling setups and the exact locations where displacements were measured. Another notable difference is that this study uses specimen-specific geometries and material property variations from real scapulae, whereas the previous experimental studies utilized foam blocks of artificial bone substitute with homogeneous material properties.

Some patients do not have adequate bone stock available to place four fixation screws. An experimental study performed by James et al. (2013) concluded that there were no statistical differences in central displacement of the glenosphere when two (superior and inferior) versus four fixation screws were used, whereas our results indicate that the number of screws does have a significant effect on micromotion (p=0.008); however, the trends are similar. At 0 mm of lateralization in the present study, two screw configurations increased absolute micromotion from 18.3 ± 5.9 µm to 35.0 ± 14.9 µm (87%) with respect to four screws, indicating that two screw configurations provide less rigid primary fixation. The clinical implications of these differences, however, are unknown. The differences in the conclusions of James et al. and the current study may be due, in part, to differing study designs. We employed a computational technique, benefiting from smaller variability and an enhanced ability to detect small differences in metrics that may not be detectable using in-vitro studies with small sample sizes.

The difference between two and four screw configurations appears to increase with lateralization (Fig. 6). However, this trend may be affected by one shoulder (shoulder 3), which showed larger increases in micromotion with lateralization in both screw configurations (Fig. 7). The relatively larger micromotions and increases in shoulder 3 can be attributed to a lower average cancellous bone density (see Table 1 and Fig. 8), likely due to a diagnosis of osteopenia, and the fact that it was a smaller specimen. Loading was not adjusted for specimen size or bone quality, however in-vivo loading magnitudes would vary depending on both weight and activity level of a patient. Quality and availability of bone stock, as well as patient activity level, could be key factors in determining whether or not to lateralize, as shoulder 3 also only received the second-lowest increase in adduction ROM compared with other specimens (Fig. 5).

Several studies have investigated the effect of a laterally offset COR on adduction ROM. Henninger et al. (2012) concluded that resting abduction angle was not significantly affected by lateralization in a cadaveric experimental study. Conversely, and supported by the results of this study, Gutiérrez et al. (2008a, 2008b) reported that adduction deficit was significantly affected by lateralization in two separate studies; one experimental using sawbones and the other computational. Differences could be accounted for by the role of deltoid tension in the cadaveric study by Henninger et al., whereas the present study, as well as the studies by Gutiérrez et al., do not account for soft tissue contribution to adduction angle. Only one shoulder exhibited an adduction deficit in our study, which was alleviated by lateralizing the COR by only 4 mm (Fig.5). It is possible that adduction deficits would be prevalent in other shoulders with varying implant parameters (head-neck angle of the humeral stem, humeral cup depth, glenosphere placement, etc.) and inclusion of the contribution of factors such deltoid tension, scapular orientation, and scapulothoracic motions.

It should be noted that all shoulders converged to a 23° adduction ROM at 16 mm lateralization, at which point impingement always occurred between the humeral cup and the metallic spacer. The metallic spacer was the same diameter as the baseplate (25 mm) and the glenosphere would be placed on the lateral portion of the baseplate/spacer combination. This is analogous to the lateralization technique called bony increased-offset (BIO). Two clinical studies, performed by Boileau et al. (2011) and Athwal et al. (2015), utilized BIO with autologous grafts harvested from the humeral head that were the same diameter as the baseplate and reported scapular notching rates of 40% and 19% respectively, both of which are lower than reported in other studies using the Grammont style prosthesis. Another clinical study performed by Valenti et al. (2011) reported no scapular notching in 76 patients with a minimum of 24 month follow-up when lateralizing with a metallic spacer. This suggests lateralizing the COR with the technique simulated in this study may contribute to reducing scapular notching rates.

A secondary finding of the current study is the strong sensitivity of simulation results to frictional properties. In varying only friction coefficients, three different definitions yielded disparate relationships between the variables studied (Fig. 4). In several configurations, when relatively large friction coefficients were used, micromotion of the baseplate was inexplicably greater when using four screws versus only two. Experimental validation would be required to confirm quantitative reliability of predicted micromotions in relation to several model parameters (e.g. friction). Future work should focus on identifying more accurate frictional properties for simulating rTSA micromotion, including eventual optimization of frictional coating distributions based on simulation models.

Some limitations of this study relate to simplifications required to produce consistency across all FE models as well as lower computational costs. Mapped cancellous bone material properties were not applied to the scapula in its entirety, but instead only to the glenoid region, the area in which the fixation screws are placed. This simplification was made to lower computational costs of simulations, but may have artificially increased the stiffness of the scapula. Additionally, the elimination of screw thread geometry simplified meshing and reduced computational costs of the models, however, modelling actual thread geometry may provide more accurate results and should be considered in future work. Our results are based on a relatively small sample size (4 shoulders) due to the development time associated with each model. Consequently, a potential limitation of our study is that our results don't necessarily capture the true variability in shoulder shape and material property distribution present in a population. However, each model received the same treatment, and we were able to calculate statistically significant, and similarly trending effects due to changes in the independent variables. Finally, arthritic shoulders may have altered bone morphology (lower strength and geometric deformities). For this reason, future work should consider arthritic shoulders to determine if similar trends to those in this study are observed.

The modelling technique employed in this study, incorporating shoulder-specific scapular geometry and bone material property distributions, demonstrated that it is necessary to consider the trade-offs between adduction ROM and primary implant fixation during lateralization on a shoulder-specific basis. In general, lateralization significantly increases both micromotion and adduction ROM, however the decision to lateralize or not should still be considered on a shoulder-specific basis; and this decision can be better informed through the use of patient-specific computer models.

Acknowledgments

Research reported in this publication was supported, in part, by the National Institute Of Arthritis And Musculoskeletal And Skin Diseases of the National Institutes of Health under Award Number R03AR066841. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of Interest

Dr. Joseph Choi receives consulting payments from Lima Corporate; however, none of the material presented is based on any of their products. None of the other authors have any conflict of interest, including any financial or personal relationships with other people or organizations that could inappropriately influence their work.

References

  1. Allegheny Technologies Incorporated. ATI Ti-6Al-4V, Grade 5 Technical Data Sheet. 2012 Available: www.atimetals.com.
  2. Ahrens J, Geveci B, Law C. ParaView: An End-User Tool for Large Data Visualization. Visualization Handbook: Elsevier; 2005. (ISBN-13:978:0123875822) [Google Scholar]
  3. Anglin C, Wyss UP, Pichora DR. Glenohumeral contact forces. Journal of Engineering in Medicine. 2000;214(6):637–644. doi: 10.1243/0954411001535660. [DOI] [PubMed] [Google Scholar]
  4. Athwal GS, MacDermid JC, Reddy KM, Marsh JP, Faber KJ, Drosdowech D. Does bony increased-offset reverse shoulder arthroplasty decrease scapular notching? Journal of Shoulder and Elbow Surgery. 2015;24(3):468–473. doi: 10.1016/j.jse.2014.08.015. [DOI] [PubMed] [Google Scholar]
  5. Bergmann G, Graichen F, Bender A, Rohlmann A, Halder A, Beier A, Westerhoff P. In vivo gleno-humeral joint loads during forward flexion and abduction. Journal of Biomechanics. 2011;44(8):1543–1552. doi: 10.1016/j.jbiomech.2011.02.142. [DOI] [PubMed] [Google Scholar]
  6. Boileau P, Moineau G, Roussanne Y, O’Shea K. Bony increased-offset reversed shoulder arthroplasty: minimizing scapular impingement while maximizing glenoid fixation. Clinical Orthopaedics and Related Research. 2011;469(9):2558–2567. doi: 10.1007/s11999-011-1775-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chae S, Lee H, Kim SM, Lee J, Han S, Kim S. Primary Stability of Inferior Tilt Fixation of the Glenoid Component in Reverse Total Shoulder Arthroplasty: A Finite Element Study. Journal of Orthopaedic Research. 2015 doi: 10.1002/jor.23115. [DOI] [PubMed] [Google Scholar]
  8. Costantini O, Choi DS, Kontaxis A, Gulotta LV. The effects of progressive lateralization of the joint center of rotation of reverse total shoulder implants. Journal of Shoulder and Elbow Surgery. 2015;24(7):1120–1128. doi: 10.1016/j.jse.2014.11.040. [DOI] [PubMed] [Google Scholar]
  9. Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin J-C, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward SR, Miller JV, Pieper S, Kikinis R. 3D Slicer as an Image Computing Platform for the Quantitative Imaging Network. Magnetic Resonance Imaging. 2012;30(9):1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gutiérrez S, Levy JC, Frankle MA, Cuff D, Keller TS, Pupello DR, Lee WE., 3rd Evaluation of abduction range of motion and avoidance of inferior scapular impingement in a reverse shoulder model. Journal of Shoulder and Elbow Surgery. 2008a;17(4):608–615. doi: 10.1016/j.jse.2007.11.010. [DOI] [PubMed] [Google Scholar]
  11. Gutiérrez S, Comiskey CA, 4th, Luo ZP, Pupello DR, Frankle MA. Range of Impingement- Free Abduction and Adduction Deficit After Reverse Shoulder Arthroplasty. The Journal of Bone and Joint Surgery. 2008b;90-A(12):2606–2615. doi: 10.2106/JBJS.H.00012. [DOI] [PubMed] [Google Scholar]
  12. Harman M, Frankle M, Vasey M, Banks S. Initial glenoid component fixation in “reverse” total shoulder arthroplasty: A biomechanical evaluation. Journal of Shoulder and Elbow Surgery. 2005;14(1S):162S–167S. doi: 10.1016/j.jse.2004.09.030. [DOI] [PubMed] [Google Scholar]
  13. Henninger HB, Barg A, Anderson AE, BachusK N, Burks RT, Tashjian RZ. Effect of lateral offset center of rotation in reverse total shoulder arthroplasty: a biomechanical study. Journal of Shoulder and Elbow Surgery. 2012;21(9):1128–1135. doi: 10.1016/j.jse.2011.07.034. [DOI] [PubMed] [Google Scholar]
  14. Hettrich CM, Permeswaran VN, Goetz JE, Anderson DD. Mechanical tradeoffs associated with glenosphere lateralization in reverse shoulder arthroplasty. Journal of Shoulder and Elbow Surgery. 2015;24(11):1774–1781. doi: 10.1016/j.jse.2015.06.011. [DOI] [PubMed] [Google Scholar]
  15. Hsu SH, Greiwe RM, Saifi C, Ahmad CS. Reverse Total Shoulder Arthroplasty-Biomechanics and Rationale. Operative Techniques in Orthopaedics. 2011;21(1):52–59. [Google Scholar]
  16. Humphrey CS, Kelly JD, 2nd, Norris TR. Optimizing glenosphere position and fixation in reverse total shoulder arthroplasty, Part Two: The three-column concept. Journal of Shoulder and Elbow Surgery. 2008;17(4):595–601. doi: 10.1016/j.jse.2008.05.038. [DOI] [PubMed] [Google Scholar]
  17. James J, Allison MA, Werner FW, McBride DE, Basu NN, Nanavati VN. Reverse shoulder arthroplasty glenoid fixation: is there a benefit in using four instead of two screws? Journal of Shoulder and Elbow Surgery. 2013;22(8):1030–1036. doi: 10.1016/j.jse.2012.11.006. [DOI] [PubMed] [Google Scholar]
  18. Lalone EA, Willing RT, Shannon HL, King GJ, Johnson JA. Accuracy assessment of 3D bone reconstructions using CT: an intro comparison. Medical Engineering & Physics. 2015;37(8):729–738. doi: 10.1016/j.medengphy.2015.04.010. [DOI] [PubMed] [Google Scholar]
  19. Nicholson GP, Strauss EJ, Sherman SL. Scapular Notching: Recognition and Strategies to Minimize Clinical Impact. Clinical Orthopaedics and Related Research. 2011;469(9):2521–2530. doi: 10.1007/s11999-010-1720-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Pomwenger W, Entacher K, Resch H, Schuller-Götzburg P. Need for CT-based bone density modelling in finite element analysis of shoulder arthroplasty revealed through a novel method for result analysis. Biomedical Engineering. 2014;59(5):421–430. doi: 10.1515/bmt-2013-0125. [DOI] [PubMed] [Google Scholar]
  21. Taddei F, Schileo E, Helgason B, Cristofolini L, Viceconti M. The material mapping strategy influences the accuracy of CT-based finite element models of bones: an evaluation against experimental measurements. Medical Engineering & Physics. 2007;29(9):973–979. doi: 10.1016/j.medengphy.2006.10.014. [DOI] [PubMed] [Google Scholar]
  22. Tornier Incorporated. Aequalis®-Reversed II Surgical Technique. Available: www.tornier.com.
  23. Valenti P, Sauzieres P, Katz D, Kalouche I, Kilinc A. Do Less Medialized Reverse Shoulder Prostheses Increase Motion and Reduce Notching? Clinical Orthopaedics and Related Research. 2011;469(9):2550–2557. doi: 10.1007/s11999-011-1844-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Virani NA, Harman M, Levy J, Pupello DR, Frankle MA. In vitro and finite element analysis of glenoid bone/baseplate interactive the reverse shoulder design. Journal of Shoulder and Elbow Surgery. 2008;17(3):509–521. doi: 10.1016/j.jse.2007.11.003. [DOI] [PubMed] [Google Scholar]
  25. Willing RT, Lalone EA, Shannon HL, Johnson JA, King GJ. Validation of a finite element model of the human elbow for determining cartilage contact mechanics. Journal of Biomechics. 2015;46(10):1767–1771. doi: 10.1016/j.jbiomech.2013.04.001. [DOI] [PubMed] [Google Scholar]
  26. Zhang Y, Ahn PB, Fitzpatrick DC, Heiner AD, Poggie RA, Brown TD. Interfacial Frictional Behavior: Cancellous Bone, Cortical Bone, and a Novel Porous Tantalum Material. Journal of Musculoskeletal Research. 1999;3(4):245–251. [Google Scholar]

RESOURCES