Minimum number of myosin motors accounting for shortening velocity under zero load in skeletal muscle

Abstract

Key points

• Myosin filament mechanosensing determines the efficiency of the contraction by adapting the number of switched ON motors to the load.

• Accordingly, the unloaded shortening velocity (V ₀) is already set at the end of latency relaxation (LR), ∼10 ms after the start of stimulation, when the myosin filament is still in the OFF state.

• Here the number of actin‐attached motors per half‐myosin filament (n) during V ₀ shortening imposed either at the end of LR or at the plateau of the isometric contraction is estimated from the relation between half‐sarcomere compliance and force during the force redevelopment after shortening.

• The value of n decreases progressively with shortening and, during V ₀ shortening starting at the end of LR, is 1–4.

• Reduction of n is accounted for by a constant duty ratio of 0.05 and a parallel switching OFF of motors, explaining the very low rate of ATP utilization found during unloaded shortening.

Abstract

The maximum velocity at which a skeletal muscle can shorten (i.e. the velocity of sliding between the myosin filament and the actin filament under zero load, V ₀) is already set at the end of the latency relaxation (LR) preceding isometric force generation, ∼10 ms after the start of electrical stimulation in frog muscle fibres at 4°C. At this time, Ca²⁺‐induced activation of the actin filament is maximal, while the myosin filament is in the OFF state characterized by most of the myosin motors lying on helical tracks on the filament surface, making them unavailable for actin binding and ATP hydrolysis. Here, the number of actin‐attached motors per half‐thick filament during V ₀ shortening (n) is estimated by imposing, on tetanized single fibres from Rana esculenta (at 4°C and sarcomere length 2.15 μm), small 4 kHz oscillations and determining the relation between half‐sarcomere (hs) compliance and force during the force development following V ₀ shortening. When V ₀ shortening is superimposed on the maximum isometric force T ₀, n decreases progressively with the increase of shortening (range 30–80 nm per hs) and, when V ₀ shortening is imposed at the end of LR, n can be as low as 1–4. Reduction of n is accounted for by a constant duty ratio of the myosin motor of ∼0.05 and a parallel switching OFF of the thick filament, providing an explanation for the very low rate of ATP utilization during extended V ₀ shortening.

Key points

• Myosin filament mechanosensing determines the efficiency of the contraction by adapting the number of switched ON motors to the load.

• Accordingly, the unloaded shortening velocity (V ₀) is already set at the end of latency relaxation (LR), ∼10 ms after the start of stimulation, when the myosin filament is still in the OFF state.

• Here the number of actin‐attached motors per half‐myosin filament (n) during V ₀ shortening imposed either at the end of LR or at the plateau of the isometric contraction is estimated from the relation between half‐sarcomere compliance and force during the force redevelopment after shortening.

• The value of n decreases progressively with shortening and, during V ₀ shortening starting at the end of LR, is 1–4.

• Reduction of n is accounted for by a constant duty ratio of 0.05 and a parallel switching OFF of motors, explaining the very low rate of ATP utilization found during unloaded shortening.

Abbreviations

C_f

filament compliance

C_hs

half‐sarcomere compliance

C_p

constant compliance of the elastic element in parallel with motors

C_p0

compliance of motors just at the end of unloaded shortening

C_v

variable compliance in parallel with motors

hs

half‐sarcomere

l₀

fibre length at 2.1 μm

L

half‐sarcomere length change

LR

latency relaxation

n

number of actin‐attached motors per half‐thick filament

N

number of motors per half‐thick filament available for interaction with actin

r

duty ratio

s

strain in the array of myosin motors

S_M6

spacing of the sixth‐order myosin meridional reflection

T

force

T₀

plateau force reached during an isometric tetanus

τ

force constant during isometric force development of detachment of motors attached at the end of the preceding unloaded shortening

V₀

unloaded shortening velocity

Introduction

During muscle contraction force and shortening are generated by the relative sliding of two sets of filaments – the thick filaments, mainly composed of the motor protein myosin II, and the thin, actin‐containing filaments. In each sarcomere, the structural unit of the muscle, the myosin motors, arranged in two bipolar arrays emerging from the thick filament, undergo transient cyclical interactions with the overlapping thin filaments originating from the ends of the sarcomere. During each interaction, an ATP‐driven working stroke in the myosin motor pulls the thin filament towards the centre of the sarcomere. From the array arrangement of the motors in each half‐sarcomere (hs) unique properties emerge such as the possibility to adapt the number of motors engaged in the isotonic contraction to the external load, while the motor force and working stroke remain practically constant (Piazzesi et al. 2007; Caremani et al. 2013, 2015).

The textbook model of striated muscle regulation provides that, following the sudden increase in intracellular [Ca²⁺] induced by cell membrane depolarization, Ca²⁺ binding to troponin in the thin filament leads to a structural change in tropomyosin that switches the thin filament ON, making the actin available for the interaction with the myosin motors. Structural and biochemical experiments have recently substantiated a second regulatory mechanism in the thick filament (Woodhead et al. 2005; Zoghbi et al. 2008; Cooke, 2011; Linari et al. 2015). The thin filament‐based mechanism is responsible for the ability of muscle to shorten under low load and implies a fast signalling pathway between the Ca²⁺‐activated thin filament and the thick filament, before a significant number of myosin motors have attached to actin. The second mechanism controls the recruitment of myosin motors for contraction against high loads and is based on mechanosensing in the thick filament. In agreement with the first mechanism, the maximum velocity at which a skeletal muscle can shorten, that is the velocity of filament sliding under zero load (unloaded shortening velocity, V ₀), is set at the end of the latent period for isometric force generation (latency relaxation, LR), about 10 ms after the start of electrical stimulation in Rana esculenta at 4°C (Lombardi & Menchetti, 1984; Brunello et al. 2006), when Ca²⁺‐induced activation of the actin filament is already maximal (Caputo et al. 1994; Yagi, 2003) and resting viscosity has dropped to zero (Lombardi & Menchetti, 1984). At this time, the thick filament is in the OFF state, characterized by the myosin motors lying on the surface of the filament on a quasi‐helical arrangement with a 14.34 nm axial periodicity (Woodhead et al. 2005; Zoghbi et al. 2008; Reconditi et al. 2011). The OFF state is preserved during unloaded shortening imposed immediately after LR, suggesting that V ₀ sliding is promoted by very few constitutively ON myosin motors (Linari et al. 2015). Moreover, if V ₀ shortening is imposed at the plateau of the isometric contraction, when the thick filament is fully ON, the OFF state is progressively recovered (Linari et al. 2015). These findings show the role of thick filament mechanosensing in determining the efficiency of the contraction by adapting the number of motors to the mechanical task, and have an important energetic counterpart in the original observation that the rate of ATP splitting is unexpectedly low during rapid shortening of frog skeletal muscle (Kushmerick et al. 1969; Rall et al. 1976; Homsher et al. 1981). According to Homsher et al. (1981), the ATP splitting rate during prolonged unloaded shortening could be accounted for by the rate of motor detachment if the fraction of myosin motors attached to actin became as low as 0.02.

The existing estimates of the number of actin‐attached motors per half‐thick filament during V ₀ shortening rely on stiffness measurements from the force response to step stretches. With this method, it has been recently concluded (extended data in fig. 2 in Linari et al. 2015) that the number of motors attached to actin during unloaded shortening decreases to an almost constant fraction of ∼0.1 of those attached at T ₀ with a time constant of ∼3 ms, much shorter than the time constant (∼20 ms) of the recovery of the OFF state by the thick filament (Linari et al. 2015). However, as shown in Fig. 5 of Appendix A, at the low levels of sarcomere stiffness attained during V ₀ shortening, stiffness measurements are influenced by inertial effects and this limits the power of the method to give direct quantitative information on the stiffness changes. Regardless, from the changes in the initial delay of the force response to the stretch a strong qualitative indication emerges that the stiffness, and thus the number of attached motors, is smaller during V ₀ shortening imposed at the end of LR than during V ₀ shortening imposed at T ₀.

Figure 2. Half‐sarcomere compliance during delayed force development.

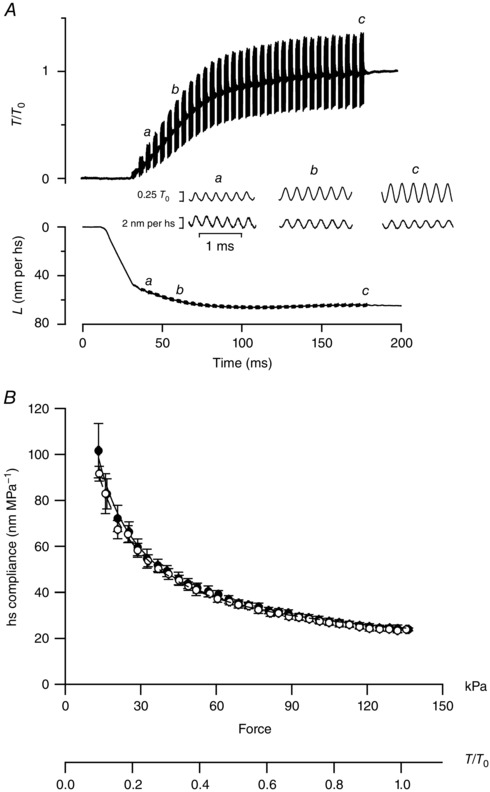
A, force (T/T ₀) and hs length change (L) in response to 4 kHz length oscillations imposed during the isometric force development delayed by unloaded shortening starting at the end of the latent period (delay dev). Time 0 is the start of stimulation. The inset between force and hs traces shows the responses on an expanded time scale to oscillations at three different times (a–c); upper traces: force, lower traces: hs length change. B, hs compliance–force relations during dev (filled circles, same data as in Fig. 1 C) and delay dev (open circles). Continuous line: same as Fig.  1 C, dashed line: fit of delay dev data with model 2. See text for details. Parameters of the fit are reported in Table 1.

Figure 5. Force and hs sarcomere length responses to a step stretch imposed on a contracting fibre.

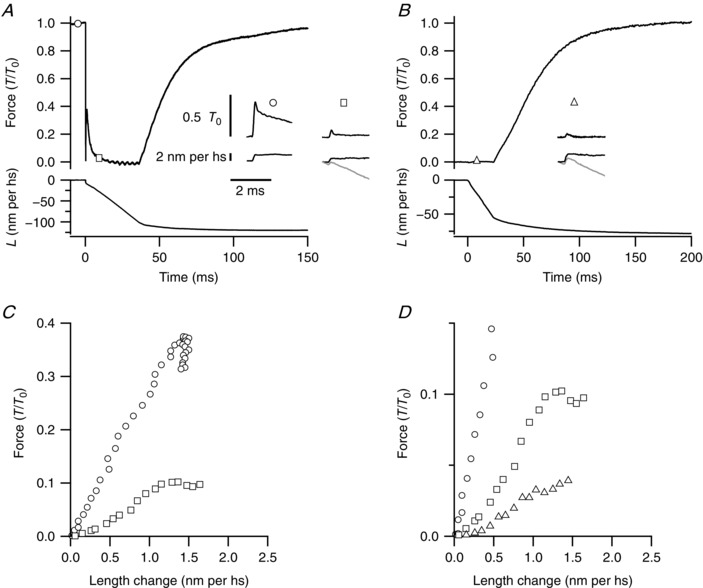
A, time course of force (T/T ₀, upper trace) and hs length change (L, lower trace) in response to a ramp‐faced shortening at V ₀ (amplitude ∼10% of the initial fibre length, plus a 0.8% step release) applied at T ₀. Time 0 corresponds to the start of shortening. The circle and the square on the force trace mark the time (T ₀ and 8 ms of V ₀ shortening, respectively) at which the step stretches, shown in the inset, are imposed in subsequent contractions. In the inset, L for the step stretch superimposed on V ₀ shortening (black) was obtained from the original trace (grey) by subtracting the L trace from a contraction without step stretch. B, time course of force (upper trace) and L (lower trace) in response to a ramp‐faced shortening at V ₀ (amplitude ∼5% of the initial fibre length), imposed at the end of the LR, taken as time zero. The triangle on the force trace marks the time (8 ms after the start of shortening) at which the step stretch, shown in the inset, is imposed in a subsequent contraction. C, superimposed force–L plots during the step stretches in A, as defined by the symbols. Time resolution 5 μs per point. D, superimposed force–L plots during the step stretches in A and B, as defined by the symbols. Note that the vertical scale is amplified about three times relative to C.

In this work the number of motors during V ₀ shortening is measured by exploiting the recently refined method that allows the measurement of hs stiffness during force development to be extended to a very low level of isometric force (0.05 T ₀), yet without significant inertial effects (Fusi et al. 2014). The rationale for the use of this protocol is as follows: immediately after V ₀ shortening stops and isometric contraction resumes, the motors that were interacting during shortening should transiently add their contribution to hs stiffness as an elastic element in parallel with that represented by the nascent force‐generating motors.

Comparing the hs compliance – force relationships during initial force development with those during force development following unloaded shortening starting either at the end of LR or at T ₀, we find that: (1) during V ₀ shortening starting at T ₀, the first rapid phase of reduction of the fraction of attached motors (from the T ₀ value to ∼17% of the T ₀ value within 10 ms) is followed by a slow phase of further progressive reduction, which is accounted for by the progressive switch of the thick filament to the OFF state during V ₀ shortening (Linari et al. 2015), combined with a constant duty ratio of ∼0.05; and (2) the fraction of motors attached during V ₀ shortening at the end of LR is as low as 0.01. These results account for the minimization of ATP consumption and provide a clue for identifying the exothermic reaction that is responsible for the transient unexplained energy production during unloaded shortening (Homsher et al. 1981; Woledge et al. 1985).

Methods

Ethical approval

Frogs (R. esculenta) were killed by decapitation and destruction of the brain and the spinal cord, in agreement with the Italian regulation on animal experimentation (Authorization 956/2015‐PR in compliance with Decreto Legislativo 26/2014 and with EU directive 2010/63).

Fibre preparation and mechanical setup

Single fibres were dissected from the lateral head of the tibialis anterior muscle. Fibres were mounted between the levers of a capacitance force transducer and a loudspeaker motor in a thermo‐regulated trough. The hs length change (L) in a fibre segment 700–1000 μm long, selected near the force transducer end, was measured by a striation follower (Lombardi & Piazzesi, 1990, and references therein). The physiological solution bathing the fibre had the following composition: 115 mm NaCl, 2.5 mm KCl, 1.8 mm CaCl₂, 3 mm phosphate buffer, pH 7.1. The experiments were performed at a temperature of 4°C on a total of six fibres with cross‐sectional area 8100 ± 2600 μm² (mean ± SD) and isometric force 134 ± 14 kPa (mean ± SEM).

Experimental protocols and data analysis

The fibre length at rest (l ₀) was set at a sarcomere length of 2.15 μm. In the protocols in which stiffness was measured during force redevelopment at the end of various amounts of unloaded shortening the length of the fibre was increased by the same amount as that of the unloaded shortening, so that in all cases stiffness measurements during the rise of force always started at the same sarcomere length. Fibres were electrically stimulated to develop fused tetani at 4 min intervals, using stimuli of alternating polarity with frequency 18–25 Hz. The hs‐compliance during the rise of force was measured by applying cycles of 4 kHz length oscillations (2 nm per hs peak‐to‐peak at maximum) in four different conditions: during the isometric force development following the start of stimulation (dev, six fibres), during force redevelopment (five of the six fibres) after 10 ± 2 and 35 ± 7 ms of unloaded shortening superimposed on the plateau of the isometric tetanus (early redev and late redev, respectively) and after 37 ± 7 ms of unloaded shortening applied at the end of the latency relaxation (delay dev, five of the six fibres, four of which were also used for the redev protocol). When V ₀ shortening was imposed at T ₀, attainment of the steady velocity of hs shortening was preceded by the Huxley and Simmons transient (Huxley & Simmons, 1971), which was accelerated by superimposing, on the ramp‐faced shortening, an initial stepwise shortening. The unloaded shortening velocity (2.03 ± 0.09 μm s⁻¹ per hs in the six fibres used in this work) was directly measured on the L trace just before the shortening end, when the sarcomere length of the population under inspection was the same as that during the subsequent stiffness measurement and corresponded to the value pre‐set on the striation follower.

The response to 4 kHz oscillations imposed on an isometrically contracting fibre in the force range between 0.05 T ₀ and T ₀ is almost purely elastic, with only a small phase advance (≤10 deg) of the force (T) relative to the L trace (see fig. 2D in Fusi et al. 2014). The hs‐compliance was estimated in the range 0.05 T ₀ to T ₀ from T over L changes as already described (Fusi et al. 2014). Compliance data were grouped into force classes of amplitude 0.03 T ₀ and averaged; error bars in Figs 1 C, 2 B and 3 and the error of the means reported in the text are SEM (unless otherwise specified). Details of the fitting procedure of the hs compliance – force relationships in Figs 1 C and 2 B are provided in the text.

Figure 1. Half‐sarcomere compliance during isometric force development and redevelopment following V ₀ shortening.

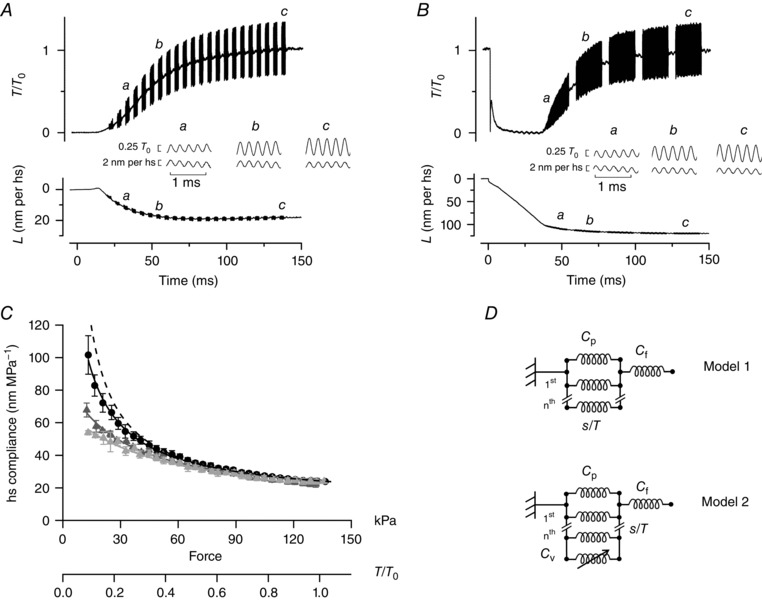
A, force (T/T ₀) and hs length change (L) in response to 4 kHz length oscillations imposed during the isometric force development (dev). Time 0 is the start of stimulation. The inset between force and hs traces shows the responses on an expanded time scale at three different times as indicated by the figures (a–c); upper traces: force, lower traces: hs length change. B, force and hs length change in response to 4 kHz oscillations imposed during force redevelopment following 35 ms of unloaded shortening (late redev) starting at the tetanus plateau. Time 0 is the start of V ₀ shortening, on which a stepwise shortening of about 6 nm is superimposed. The inset between force and hs length traces shows the responses on an expanded time scale at three different times (a–c). C, relations between hs compliance and force determined during dev (black filled circles), early redev (light grey triangles) and late redev (dark grey triangles) in six fibres. Black continuous line: fit of dev data with model 1. Light grey and dark grey lines: fit of early redev and late redev, respectively, with model 2. See text for details. Dashed line: expected relation in the absence of any elastic elements in parallel with the motors. The parameters of the fit are reported in Table 1. D, simplified mechanical models of the half‐sarcomere. In model 1 the filament compliance C _f is in series with the parallel of motor array (s/T) and an elastic element with constant compliance C _p (Fusi et al. 2014). In model 2 one more elastic element with variable compliance C _v is added in parallel with motors.

Figure 3. Recovery of the OFF state of thick filament and duty ratio during unloaded shortening.

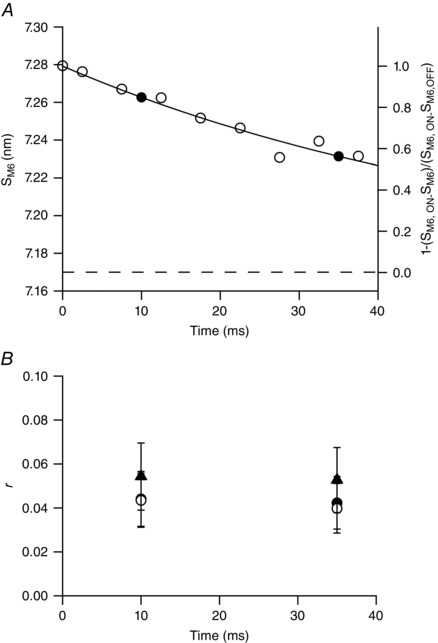
A, open circles and left ordinate: S _M6 as a function of time following the imposition of unloaded shortening on the tetanus plateau after subtracting the effect on spacing of the instantaneous compliance of the thick filament (from fig. 2 of Linari et al. 2015). Continuous line: exponential fit on open circles assuming as asymptote S _M6 at rest (7.17 nm, dashed line). Filled symbols: fraction of the thick filament in the ON state at 10 and 35 ms following the start of unloaded shortening, estimated as [1 – ((S _M6,ON – S _M6)/(S _M6,ON – S _M6,OFF))] (right ordinate). B, values of duty ratio (r) after 10 and 35 ms of unloaded shortening under different assumptions as detailed in the text: open circles, all motors are in the OFF state at the end of LR; filled circles and filled triangles, respectively 24 and 56 motors are constitutively ON.

Results

Parallel elasticity during force redevelopment following different extents of V ₀ shortening

Fig. 1 shows the results of the experiments in which the relations between hs compliance (C _hs) and force have been determined by imposing 4 kHz length oscillations during initial force development (dev, Fig. 1 A), and during force redevelopment following either 10 ms (30 nm per hs) of unloaded shortening (early redev, record not shown) or 35 ms (80 nm per hs) of unloaded shortening (late redev, Fig. 1 B) imposed at T ₀.

The corresponding hs compliance – force relations are shown in Fig. 1 C (dev, black circles; early redev, light grey triangles; late redev, dark grey triangles). Under all conditions, the hs compliance reduces with the increase of force due to the increase in the number of actin‐attached motors. However, while for forces larger than 60–70 kPa (∼0.5 T ₀) the three relations are roughly indistinguishable, for forces smaller than 60–70 kPa the relations during early and late redevelopment lie well below that during initial force development. In particular, the early redev relation lies below the late redev relation.

These results indicate that, in the range of forces smaller than 60–70 kPa, the value of hs compliance during force rise depends on the preceding history: if force rises following a period of unloaded shortening imposed at T ₀, during which motor attachment/detachment promotes V ₀ filament sliding, hs compliance is lower than that at the same force during the initial force development. This is because the motors interacting just before the end of V ₀ shortening transiently add their stiffness to that of motors that attach afresh during force development after the end of shortening. To fit the C _hs–force relations during force redevelopment from V ₀, we implemented the mechanical model given by Fusi et al. (2014) according to this explanation. In the original model (model 1 in Fig 1 D), myofilaments are represented by a spring in series with the parallel array of many springs, representing myosin motors, plus another spring corresponding to the parallel elastic component responsible for the deviation of the C _hs–force relation from a linear behaviour. The equation describing C _hs as a function of force is

$$C_{\mathrm{hs}}=C_{\mathrm{f}}+\frac{s\times C_{\mathrm{p}}}{s+T\times C_{\mathrm{p}}}$$ (1)

where C _f is the filament compliance, s is the strain of the motors exerting the isometric force, C _p is the compliance of the parallel component and T is the force.

The fit of the dev relation with eqn (1) is shown by the continuous black line in Fig. 1 C and the resulting estimates of the parameters are reported in Table 1. C _f (12.8 ± 1.5 nm MPa⁻¹), s (1.66 ± 0.08 nm) and C _p (269 ± 38 nm MPa⁻¹) are in very good agreement with what was found previously in single frog fibres with both mechanical and X‐ray diffraction experiments (Brunello et al. 2014; Fusi et al. 2014; Piazzesi et al. 2014). T ₀ in these experiments is 134 ± 14 kPa, and thus the compliance of the array of motors at T ₀, s/T ₀, is (1.66/0.134 =) 12.4 ± 1.4 nm MPa⁻¹, which is 20 times smaller than that of the parallel element. This explains why in the region of high and moderate forces the dev relation (black circles) is practically indistinguishable from the hs compliance – force relation expected in the absence of the parallel element [dashed line in Fig. 1 C, C _p = ∞, so that eqn (1) reduces to $C_{\mathrm{hs}}=C_{\mathrm{f}}+s/T$; see also Fusi et al. (2014)]. Only in the region of low forces, in which the number of attached motors is reduced, does the contribution of the parallel elasticity become evident with a downward deviation of the dev relation from the dashed line.

Table 1.

Mechanical parameters of the half‐sarcomere estimated from the hs compliance–force relations

	C f (nm MPa−1)	s (nm)	C p (nm MPa−1)	Cp0 (nm MPa−1)	τ (kPa)
dev	12.8 ± 1.5	1.66 ± 0.08	269 ± 38
early redev	12.8	1.66	269	72 ± 9	76 ± 15
late redev	12.8	1.66	269	111 ± 13	76 ± 15
delay dev	12.8	1.66	269	818 ± 124	76

Abbreviations: C _f, filament compliance; C _p, constant compliance in parallel with motors; C _p0, compliance of motors responsible for V ₀ shortening preceding force rise; τ, force constant of detachment of these motors; s, strain in the array of motors

In the implemented version of the model used to fit the early redev and late redev data (model 2, Fig. 1 D), we introduce, in parallel with force‐generating motors and C _p, a variable compliance, C _v, with an exponential dependence on force defined as C _v = C _p0 × exp(T/τ), where C _p0 is the value of C _v at zero force (i.e. just before the force rise) and represents the compliance of motors cycling at V ₀, and τ is the force constant of their detachment.

C _hs as a function of force becomes:

$$\begin{array}{ccc}& & C_{\mathrm{hs}}=C_{\mathrm{f}}\hfill \\ & & +\frac{s\times C_{\mathrm{p}}\times C_{\mathrm{p}0}\times \exp \left(\frac{T}{\tau }\right)}{s\times (C_{\mathrm{p}}+C_{\mathrm{p}0}\times \exp \left(\frac{T}{\tau }\right))+T\times C_{\mathrm{p}}\times C_{\mathrm{p}0}\times \exp \left(\frac{T}{\tau }\right)}\hfill \end{array}$$ (2)

The light and dark grey lines in Fig. 1 C are the result of the global fit of eqn (2) to the early redev (light grey triangles) and late redev data (dark grey triangles), respectively. The number of free parameters to be estimated by the fit is reduced to C _p0 and τ by assuming that, like C _f and s, C _p is also not affected by the preceding unloaded shortening from T ₀. In addition, τ is constrained to be a shared parameter between early and late redevelopment. The results of the fit are reported in Table 1. The comparison between C _p0 of early redev (72 ± 9 nm MPa⁻¹) and C _p0 of late redev (111 ± 13 nm MPa⁻¹) indicates that this parameter increases by ∼50% with the progression of V ₀ shortening from 10 to 35 ms after the start of shortening. This indicates a corresponding reduction in the number of motors interacting during V ₀ shortening. With a motor compliance at T ₀ of 12.4 nm MPa⁻¹, the fraction of motors cycling at V ₀ relative to those attached at T ₀ is (12.4/72 =) 0.17 ± 0.01 after 10 ms of unloaded shortening and (12.4/111 =) 0.11 ± 0.01 after 35 ms of unloaded shortening.

Parallel elasticity during force development following V ₀ shortening imposed at the end of LR

Fig. 2 shows the results of the experiments in which the relation between hs compliance and force has been determined by imposing 4 kHz oscillations during initial force development delayed by shortening at V ₀ (for 20 ms in Fig. 2 A) imposed at the end of LR (delay dev). The delay dev hs compliance – force relation (Fig. 2 B, open circles) from five fibres in which the period of unloaded shortening ranged from 19 to 54 ms (37 ± 17 ms, mean ± SD) is only slightly shifted below the dev relation (black circles) at low forces. No significant changes were detectable between relations with different duration of the unloaded shortening. Fitting the open circles with eqn (2) (dashed line) under the same constraints used for the data depicted in Fig. 1, and fixing τ to the value (76 kPa) estimated for the data shown in grey, gives C _p0 = 818 ± 124 nm MPa⁻¹ (Table 1).

This value is very large, so that the contribution of C _p0 to the total parallel elasticity is quite small. However, the estimate of C _p0 is of crucial importance as it allows the calculation of the fraction of motors interacting during V ₀ shortening imposed at the end of LR, relative to those at T ₀, using the same argument as for the early and late redev. In this case, the fraction of motors is as low as (12.4/818 =) 0.015 ± 0.002.

Discussion

Number of motors attached during V ₀ shortening depends on the duration and phase of shortening

By comparing the hs compliance – force relation during the initial force development with that during force redevelopment following V ₀ shortening imposed at T ₀, we find that during force redevelopment there is an initial, smaller value of the compliance of the elasticity in parallel with force‐generating motors, due to the transient contribution of the fraction of motors responsible for V ₀ shortening just before the shortening end. Assuming that the elastic properties of the actin‐attached motors are the same independently of their force and state, the ratio between the compliance of the motor array at T ₀ (s/T ₀) and that of this transient elasticity (C _p0) gives an estimate of the fraction of motors responsible for filament sliding in the period just preceding the end of V ₀ shortening.

At an early phase of V ₀ shortening imposed at T ₀, that is after 10 ms, or 30 nm per hs of shortening, the fraction of attached motors reduces to 0.17 of the isometric value. This value is in accordance with that previously found at a similar time by measuring stiffness with stretches (Extended Data fig. 2c in Linari et al. 2015), confirming that the stiffness, and thus the fraction of attached motors, drops quickly (time constant ∼3 ms) following the start of V ₀ shortening. Later during V ₀ shortening (35 ms, or 80 nm per hs) the fraction of attached motors reduces further to 0.11 of the isometric value. This result indicates that, beyond the rapid (3 ms) adaptation of the number of attached motors to the unloaded shortening condition, a slower process takes place while unloaded shortening continues, during which the population of detached myosin motors undergoes a slow secondary transition.

The actual number of motors per half‐thick filament attached at any time during unloaded shortening can be calculated if one knows what fraction of the 294 myosin heads per half‐thick filament is attached at T ₀. In R. esculenta this fraction is 0.22 ± 0.06 (Brunello et al. 2014), giving a number of motors per half‐thick filament responsible for the isometric force (n ₀) of (294 × 0.22 =) 65 ± 18. Consequently, the number of motors attached during V ₀ shortening (n) is (65 × 0.17 =) 11 ± 3 motors at 10 ms from the start of shortening and (65 × 0.11 =) 7 ± 2 motors at 35 ms.

The same calculation applied to the fraction of motors estimated for V ₀ shortening imposed at the end of LR indicates that in this case, n is as low as (65 × 0.015 =) 1. However, this analysis is correct only if the parallel elasticity identified during the initial force development by the compliance C _p (= 269 nm MPa⁻¹) is due to a non‐motor elastic element such as titin or MyBP‐C. In this respect it must be noted that a contribution from MyBP‐C to parallel elasticity would be present only transiently (see discussion in Fusi et al. 2014). Alternatively, C _p could be due to a fraction of motors generating stiffness but no force and should be considered in the calculus of the fraction of motors already present at the end of LR. This fraction, relative to the number of motors at T ₀, can be calculated from the compliance ratio and would be (12.4/269 =) 0.046, which corresponds to (65 × 0.046 =) 3 motors per half‐thick filament. These non‐force‐generating motors could be those responsible for V ₀ shortening imposed at the end of LR and add to give a total of 4 motors after V ₀ shortening.

Relation between the number of motors during V ₀ shortening and the structural state of the thick filament

The mechanism that can explain the slow decrease in the number of attached motors during V ₀ shortening imposed at T ₀ is suggested by the recent evidence of the progressive recovery of the OFF state of the myosin motors during V ₀ shortening, as measured by the recovery of various X‐ray signals characterizing the resting structure of the thick filament (Linari et al. 2015). Specifically, (1) the high intensity of both the first myosin layer line reflection (ML1, which marks the three‐stranded helical arrangement of the myosin motors lying on the surface of the thick filament folded toward the centre of the sarcomere in their OFF state) and of the so‐called forbidden axial reflections [M2, M4 and M5, associated with the perturbations of the helical arrangement of myosin motors in the C‐zone of the thick filament (Malinchik & Lednev, 1992; Reconditi et al. 2014)]; and (2) the short spacing (7.17 nm) of the sixth‐order axial reflection [S _M6, determined by the mass periodicity in the thick filament backbone (Huxley et al. 2006)]. At T ₀ the thick filament is fully ON, as shown by the loss of the intensities of ML1 and forbidden reflections and by the increase of S _M6 to 7.29 nm (S _M6,ON). Following the imposition of V ₀ shortening, the OFF structure progressively recovers, as shown by the recovery of the intensity of both ML1 and forbidden reflections and by the reduction of S _M6 (fig. 2 in Linari et al. 2015). Within the period of shortening explored by X‐rays (40 ms) the OFF state has recovered halfway. In Fig. 3 the open circles are S _M6 data from fig. 2 of Linari et al. (2015) and, assuming that the recovery is an exponential process that brings S _M6 back to the resting value (S _M6,OFF = 7.17 nm, horizontal dashed line), the fit of the data (continuous line) gives τ = 61 ± 3 ms. The same data can be replotted as [1 – ((S _M6,ON – S _M6)/(S _M6,ON – S _M6,OFF))] (right ordinate in Fig. 3 A), which gives a more general representation of the time course of extinction of the ON state of the thick filament and thus of the reduction of the number of motors available for the interaction with the actin filament (N). If thick filament switching concerned all the motors, then following the start of V ₀ shortening N would have decreased from 294 (N ₀) to the fraction of N ₀ indicated by the filled circles in Fig. 3 A, that is (294 × 0.847 =) 249 motors at 10 ms and (294 × 0.562 =) 165 at 35 ms.

The ratio of the number of attached motors n, estimated by C _p0, over the number of available motors N, calculated from the filled circles in Fig. 3 A, gives the duty ratio r at the corresponding times during V ₀ shortening (filled circles in Fig. 3 B). The value of r is 0.044 ± 0.012 at 10 ms and 0.042 ± 0.012 at 35 ms, that is r remains constant independently of the time of shortening and therefore of the degree of the ON state of the thick filament. The result of this analysis is striking but expected if one considers that the mechano‐kinetic properties of the myosin motors responsible for r are unequivocally defined by the load and by the motor isoform, both conditions being constant in the experiments of Fig. 3 B.

The above calculation, however, relies on the oversimplification that the population of actin‐interacting motors depends entirely on the switch of the thick filament, while, to account for V ₀ shortening at the end of LR, a minimum number of motors must be ON even in the fully OFF filament. An estimate of the number (N _c) of these ‘constitutively’ ON motors is provided by the conclusion that during V ₀ shortening r is 0.043 and is constant. If during V ₀ shortening at the end of LR n = 1 (as in the case in which C _p is due to a non‐motor element in the hs), N _c is (n/r =) 23. However, under the hypothesis that C _p is due to non‐force‐generating motors with the same stiffness as the force‐generating motors, n responsible for V ₀ shortening at the end of LR would be 3 (that add to n during V ₀ shortening) and N _c would become 70. With an average of only 1–3 motors interacting with actin during initial shortening at V ₀, there could be some probability that at a given time one half‐thick filament has no actin‐attached motors. This condition, however, has no effect on the progression of shortening as the cyclical attachment–detachment of motors is ensured by the fraction of constitutively ON motors. In fact: (1) from L recording there is no evidence of the rise of any sarcomere inhomogeneity during the whole period of unloaded shortening (up to 80 nm per hs) and thus all the half‐sarcomeres in the population under examimation are shortening at V ₀; and (2) in the SL range used in these experiments (2.15–2.05 μm) steady shortening at V ₀ cannot be sustained by any elastic or viscoelastic passive structure and can only be driven by motors.

The presence of a minimum number of constitutively ON motors even with the thick filament fully OFF imposes a revision of the analysis relative to the time course of the switching OFF of the motors in Fig. 3 A. In fact, in this case, the exponential process concerns only the fraction of motors not constitutively ON, that is (N ₀ − N _c). This correction implies an iterative procedure to calculate the changes of r and N _c that follow from the change of the number of available motors, taking into account the different values of n during V ₀ shortening. The iterative process converges to values of r and N _c of 0.042 and 24, respectively, with one attached motor (Fig. 3 B, open circles), and 0.053 and 56, respectively, with three attached motors (Fig. 3 B, filled triangles).

A consequence of the hypothesis that C _p is due to a fraction of motors that at the end of LR generate stiffness but no force is that we need a revision of models 1 and 2. In fact, in this case, the elastic element in parallel with force‐generating motors is also due to motors that are attached at the end of LR, and add their contribution only transiently at the beginning of force rise, since later they will detach and a unique population of force‐generating motors will emerge. This situation is described by a model (Model 3) in which there is a unique parallel elasticity responsible for an initial stiffness that becomes zero during force development. In terms of a compliance, this parallel element can be represented by an initial compliance C′_p0 that exponentially rises to infinite during force development, according to eqn (3):

$$C_{\mathrm{hs}}=C_{\mathrm{f}}+\frac{s\times C{}_{\mathrm{p}0}^{\prime }\times \exp \left(\frac{T}{\tau }\right)}{s+T\times C{}_{\mathrm{p}0}^{\prime }\times \exp \left(\frac{T}{\tau }\right)}$$ (3)

The parameters C _f, s and τ estimated using eqn (3) for a global fit of the four C _hs–T relations of Figs 1 and 2 are 11.7 ± 1.3 nm MPa⁻¹, 1.64 ± 0.04 nm and 61 ± 10 kPa, respectively, not significantly different from the corresponding estimates obtained using eqn (2) (Table 1). It must be noted that dev data by themselves could not have been fit with eqn (3), because for the dev relation the effect of the parallel elasticity at high force is too small to represent a constraint for fit to an exponential (see Fusi et al. 2014). The value of C′_p0 in each V ₀ shortening phase is given in Table 2. In all cases C′_p0 is not significantly different from the equivalent compliance calculated from the parallel (C _p//C _p0) of the two contributions estimated with eqn (2). This demonstrates the robustness of either analysis, but, at the same time, does not allow the underlying question about the nature of the parallel elasticity defined with the dev relation to be solved. Consequently, depending on the nature of C _p, the minimum value of n during V ₀ shortening at the end of LR can be either 1 or 4. It is worth noting that, if C _p is contributed by both motor and non‐motor elasticities, n for each phase assumes any intermediate value within the range given in Table 3. In particular, during V ₀ imposed at T ₀, n is between 11 and 15 at 10 ms and between 7 and 11 at 35 ms.

Table 2.

Parallel elastic elements estimated with Models 2 and 3

		dev	delay dev	early redev	late redev
Model 2	C p//C p0 (nm MPa−1)	269 ± 38	202 ± 23	57 ± 6	79 ± 7
Model 3	C′p0 (nm MPa−1)	229 ± 26	177 ± 20	54 ± 6	74 ± 8

Model 2: values of the parallel of C _p and C _p0 in the four experimental conditions explored under the assumption that C _p is also due to motors. Model 3: initial values of the unique compliance C′_p0 representing motors transiently present during the early phases of contraction.

Table 3.

Estimates of the number of attached motors during unloaded shortening and duty ratio

	n
	delay dev	early redev	late redev	Duty ratio
From C p0 (Model 2)	1	11 ± 3	7 ± 2	0.043 ± 0.012
From C′p0 (Model 3)	4 ± 1	15 ± 4	11 ± 3	0.053 ± 0.015

Given a constant duty ratio of 0.053, this difference in n reflects a corresponding difference in N. In particular, at the end of LR, in the case that C _p were totally due to motor elasticity (n = 3), N _c would be 56. This possibility appears contradicted by considering the X‐ray diffraction evidence (Reconditi et al. 2011) that the fraction of motors constitutively ON cannot be higher than 0.1, that is N _c ≤ 30 and n ≤ 2. This suggests that, at least in part, C _p is due to non‐motor elasticity.

Energetics of V ₀ shortening

The findings that V ₀ shortening can be sustained by a minimum number of motors per half‐thick filament of 1–4, and that this is achieved by switching OFF the great majority of motors on the thick filament have the potential to explain longstanding unresolved questions on the energetics of rapid shortening of skeletal muscle. The original observation that the rate of ATP utilization is unexpectedly low during rapid shortening of frog skeletal muscle (Kushmerick et al. 1969; Rall et al. 1976) evolved to an even more dramatic contradiction following the experiments of Homsher et al. (1981), in which large unloaded shortenings were used (from sarcomere length of 2.6 to 1.8 μm, lasting 300 ms, frog sartorius muscle at 0°C). The ATP splitting rate during these prolonged rapid shortenings became as low as that during isometric contraction (1.7 s⁻¹ per myosin head). Actually one would expect an increase in the rate of ATP utilization with the increase in shortening velocity, since the rate of motor detachment (which can be estimated from the velocity of sliding between actin and myosin filaments divided by the maximum distance over which a motor remains attached) increases with shortening velocity. Under these conditions, the reduced ATPase rate could be explained only by assuming that the fraction of attached motors should have reduced to 0.02, which could not be predicted by any current mechano‐kinetic model (Huxley, 1957; Eisenberg et al. 1980). A further problem raised by the Homsher et al. experiments (and before by Rall et al. 1976) was the excess of energy liberated as heat during rapid shortening (the so‐called unexplained energy), which was followed by a deficit of heat production during the following isometric contraction, when the ATP splitting was temporarily increased. To explain the reduction of the rate of ATP utilization during rapid shortening, Huxley implemented his model assuming that motors attach in two stages, both necessary for ATP splitting, the first of which is rapidly reversible and is the one favoured during rapid shortening (Huxley, 1973). This hypothesis, however, could not explain either the basis of the extra heat produced during shortening or the increase of ATP hydrolysis following the end of shortening.

The progressive switching OFF of motors during prolonged V ₀ shortening defined in this work (see also Linari et al. 2015) gives a striking explanation of the associated reduction of the ATPase rate (Homsher et al. 1981) without any special assumption on the chemomechanical cycle and thus any change in duty ratio: the number of attached motors per half‐thick filament hypothesized in that work to explain the results, (294 × 0.02 =) 6, is within the range of values expected with a constant duty ratio of 0.05, once the progressive switching OFF of the thick filament (Fig. 3 A) is taken into account.

The rate of ATP splitting during shortening at different velocities has been measured also in mammalian skinned fibres at 10–15°C using NADH‐linked assays (Potma & Stienen, 1996; Sun et al. 2001). In contrast to frog muscle results, in this case the ATP splitting rate increased monotonically with shortening velocity attaining, at V ₀, values 6–9 times larger than at T ₀. The discrepancy was attributed to different species, but it is more probably related to the suppression of the OFF state of the thick filament due to both the non‐physiological temperature and the expanded lattice at which those experiments were done (Fusi et al. 2015). In fact, these same conditions are responsible for the finding that in skinned relaxed mammalian fibres the ATPase rate is one order of magnitude larger than in intact resting muscle (Cooke, 2011, and references therein).

Finally it is worth noting that a switching OFF mechanism such as that described here cannot operate for myosin in solution. This provides a clear explanation of the apparent contradiction between the low ATPase rate determined during unloaded shortening in situ (Homsher et al. 1981) and the relatively fast rate of the hydrolysis step found for frog myosin at the same temperature in solution (5 s⁻¹; Ferenczi et al. 1978).

Implications for the chemo‐mechanical cycle

In fibres from R. esculenta the duty ratio decreases from 0.22 in isometric contraction to 0.05 during V ₀ shortening, due to both the strain‐dependent increase of the rate constant of the forward transition between attached states and the conformation‐dependent increase in the rate of detachment (Huxley, 1957; Huxley & Simmons, 1971; Piazzesi & Lombardi, 1995; Caremani et al. 2013, 2015). The ATP hydrolysis step and the attachment step become the rate‐limiting steps in the cycle and, in the absence of the mechanism that switches OFF the motors on the thick filament, during prolonged rapid shortening the motors would accumulate in both the M.ADP.Pi state (which is already populated with 50% of the motors in isometric contraction) and the M.ATP state (Kodama & Yamada, 1978; see also Extended Data fig. 2b of Linari et al. 2015). However, this hypothesis cannot explain either the excess of heat liberation during rapid shortening or the transient rise in free creatine immediately after the shortening ends (Homsher et al. 1981), which is a clear indication of an abrupt rise of ADP release that is readily rephosphorylated by creatine phosphokinase.

Both phenomena provide useful hints for the mechanism hypothesized here for the switching OFF and ON of the myosin motors during and after unloaded shortening. The mechanism is based on the crucial assumption in Caremani et al. (2013, 2015) chemo‐mechanical model that the structural/mechanical transitions in the attached myosin motors are orthogonal to the biochemical transitions. Under these conditions, during unloaded shortening the release of ADP occurs mainly from the motor conformation at the end of the working stroke (the AM₄.ADP state) (see fig. 4E and F in Caremani et al. 2015). We suggest that during V ₀ shortening the AM₄.ADP motors undergo a compressive force and detach before ADP release [wasting the mechanical energy accumulated in their spring as heat, in agreement with the postulated exothermic reaction (Homsher et al. 1981; Woledge et al. 1985)] to form a M₄ ^‡.ADP state. In concert with the structural change occurring in the thick filament under zero force, the M₄ ^‡.ADP state is captured in a state similar to the resting OFF state (M₄ ^‡.ADP_OFF), lying along the thick filament surface folded toward the centre of the sarcomere. In this state, biochemically and energetically different from the M.ADP.Pi state constituting the OFF state at rest or before the motor has undergone the working stroke, the release of ADP and binding of ATP is prevented. When the shortening ends and force redevelops, switching ON of the motors accumulated in the M₄ ^‡.ADP_OFF state increases the population of M₄ ^‡.ADP motors that rapidly release ADP, explaining the abrupt increase in the ADP rephosphorylation rate responsible for the transient increase in free creatine.

Figure 4. Chemo‐mechanical cycle relevant for the ON–OFF transition of myosin motors during unloaded shortening.

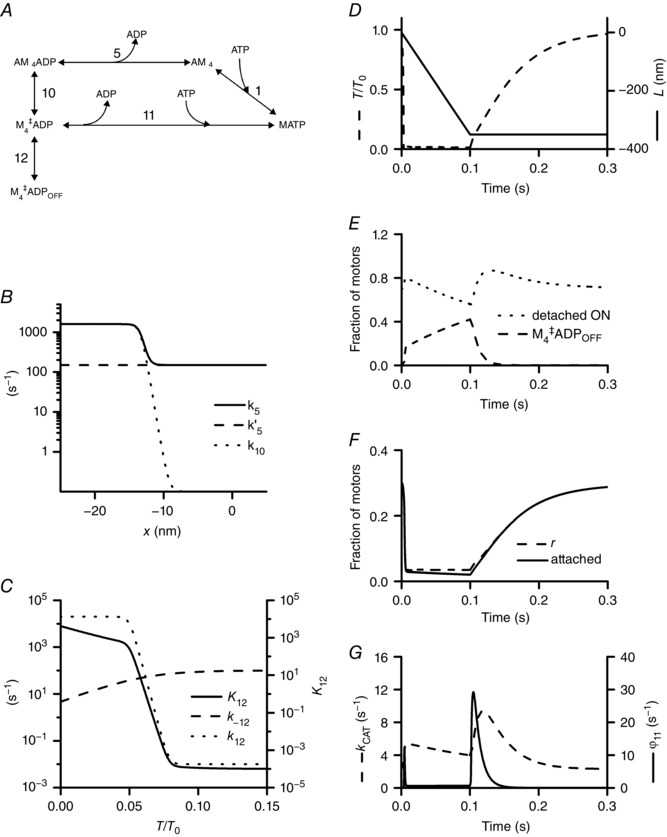
A, scheme of the transitions that implement the original scheme shown in fig. 1 of Caremani et al. (2015). The various states are defined in the text. B, x‐dependence of the rate constants of the forward transitions for step 5 [k ₅, continuous line, from fig. 5D of Caremani et al. (2015); k ₅′, dashed line, as assumed in the present model] and step 10 (k ₁₀, dotted line). C, force dependence of the equilibrium constant (K ₁₂, continuous line) and of the rate constants (k ₁₂, dotted line; k _–12, dashed line) of the ON–OFF transition. D–F, time course of the relevant parameters of the simulation, calculated during 0.1 s unloaded shortening (V = 3.5 μm s^–1 per hs) starting at time zero and the following 0.2 s in isometric condition. D, force (upper) and hs length change (lower). E, fraction of motors in the detached ON state (dotted line) and in the OFF state (dashed line). F, fraction of attached motors (continuous line) and of the duty ratio r (dashed line). G, rate of ATP hydrolysis (k _CAT, dashed line, left ordinate) and flux through step 11 (φ₁₁, continuous line, right ordinate, compressed 2.5 times).

The idea is tested by introducing a minimal modification in the reaction scheme shown in fig. 1 of Caremani et al. (2015), consisting of the introduction of a transition in parallel with step 5, which allows the motors under negative strain to detach before ADP release to form the unconventional detached M^‡ ₄.ADP state (see Fig. 4 A, step 10 and further explanations in Appendix B). The rate of this transition (k ₁₀, dotted line in Fig. 4 B) increases from zero to ∼1500 s⁻¹ within a few nanometres of negative strain. In the scheme of Caremani et al. (2015), a strain‐dependent increase in the rate of ADP release (k ₅, continuous line in Fig. 4 B from fig. 5D in Caremani et al. 2015) was assumed to increase the overall rate of detachment of negatively strained motors and fit the force–velocity relation at low load. Note that assuming strain‐sensitivity for a chemical reaction was a somewhat simplistic solution necessary under the conditions that detachment occurs at the end of the working stroke only after ADP release. The new scenario suggested by this work provides that, during V ₀ shortening, there is a progressive accumulation of motors in an unconventional detached M^‡ ₄.ADP state, allowing a more orthodox solution for the strain‐dependent detachment, which does not imply a chemical step and leaves the rate of ADP release only conformation‐dependent (k ₅′, dashed line in Fig. 4 B).

The transition of the M^‡ ₄.ADP state to the OFF motors (step 12) is assumed to occur via a rapid reaction, the equilibrium constant of which (K ₁₂) increases sharply at very low forces (Fig. 4 C, continuous line). During 100 ms unloaded shortening (Fig. 4 D) the calculated changes in the fractional occupancies of the various motor states (Fig. 4 E and F) show the ability of the model to predict the observed slow conversion of the thick filament to the OFF state at the expense of the population of the detached motors available for attachment to actin (compare the dotted line in Fig. 4 E with the plot in Fig. 3 A), as well as the reduction in the number of attached motors (continuous line in Fig. 4 F) at constant duty ratio (dashed line in Fig. 4 F). In particular it can be noted that the slow rise in the fraction of the motors in the OFF state does not imply a rate‐limiting step for the ON–OFF transition (k ₁₂ at zero force is > 10⁴ s⁻¹, Fig. 4 C, dotted line), but it is rather the consequence of the kinetics of the overall reaction scheme at low load. After the initial increase related to the drop of the load, the rate of ATP hydrolysis (dashed line in Fig. 4 G) reduces during V ₀ shortening in parallel with the switching OFF of the motors and the reduction of the detached population. Following the end of shortening, the rise of force (Fig. 4 D) reduces K ₁₂, inducing a rapid transient increase in M₄ ^‡.ADP motors that release ADP and bind a new ATP (step 11) with the same fast kinetics that characterizes the product release from the unconventional detached state M^*.ADP.Pi in fig. 1 of Caremani et al. 2015 (step 7). The transient high flux through step 11 just after the end of shortening (continuous line in Fig. 4 G) implies the abrupt rise of ADP that accounts for the transient ADP rephosphorylation‐dependent increase of free creatine and thus a slower transient increase in the ATPase rate (dashed line in Fig. 4 G), as reported by Homsher et al. (1981).

Finally, it is worth noting that there is an astonishing agreement, also in quantitative terms, between many of the observed and calculated mechano‐kinetic parameters (maximum velocity of shortening, time course of switching OFF of motors, ATP hydrolysis rate, duty ratio), notwithstanding that the simulation is derived from a kinetic scheme optimized for the performances of rabbit psoas fibres at 12°C, while the experiments are done on frog tibialis anterior at 4°C. This can be explained taking into account that the kinetic properties of the two fast skeletal muscles become similar at the two temperatures considered.

Additional information

Competing interests

None declared.

Author contributions

The experiments were performed by LF, VP, EB, MC, PB, JDP, MR, VL and GP. All the authors contributed to the conception and design of the experiments, the collection, analysis and interpretation of data, and drafting the article or revising it critically for important intellectual content. All authors approved the final version of the manuscript, all persons designated as authors qualify for authorship and all those who qualify for authorship are listed.

Funding

This study was supported by Ente Cassa di Risparmio di Firenze 2012.0611, FIRB‐Futuro in Ricerca project RBFR08JAMZ, MIUR‐PRIN project 2010R8JK2X.

Appendix A. Stiffness measurements during unloaded shortening

In previous work (see supplementary information in Linari et al. 2015) the number of motors attached during V ₀ shortening superimposed on the otherwise isometric contraction (T ₀) has been estimated by determining the hs stiffness with small step stretches (1–2 nm per hs, complete in 100 μs) imposed at different times following the start of shortening. In Fig. 5 A the force response to a step stretch of ∼2 nm per hs imposed 8 ms following the start of shortening (square) is compared to that to the same step imposed at T ₀ (circle). A step release is superimposed at the start of the ramp shortening to accelerate the exhaustion of Huxley and Simmons quick recovery, so that at 8 ms the force is already close to zero.

When the step is imposed at T ₀, the plot of force versus hs length change during the 100 μs taken by the step to be completed exhibits the characteristics of pure elasticity (Fig. 5 C, circles), with the shape of a straight line starting from the origin (Ford et al. 1977). Instead the plot of force versus hs length change during the step imposed 8 ms following the start of shortening (Fig. 5 C, squares) exhibits an initial downward deviation from the straight line marking a substantial delay between the start of the length change and the start of the force response. The non‐linearity of the force–length plot originates from the very small value that the hs stiffness assumes going from T ₀ to V ₀, which, combined with the density of the fibre, causes an increase in the propagation time of the mechanical perturbation from the point along the fibre selected for the striation follower signal to the force transducer attachment. A detailed analysis of the phase difference between the striation follower signal and the force has shown that in the range of isometric forces above 0.05 T ₀ the stiffness is large enough for these inertial effects to be absent (Fusi et al. 2014). The contamination of the force response by the inertial effect is even larger when the stretch is imposed during V ₀ shortening starting at the end of LR (Fig. 5 B, triangle): as shown by the plot superposition (Fig. 5 D), the force–length plot for the step imposed during V ₀ shortening after LR (triangles) exhibits a much larger downward deviation from a straight line, as the force starts rising only after the first ∼0.3 nm of lengthening. Everything else being constant (density of the fibre, acceleration of the imposed length perturbation), this finding per se is a qualitative indication that in this case the stiffness is lower than that during V ₀ shortening from T ₀.

Appendix B. Model simulation

The simulation described in Fig. 4 is obtained by introducing minimal modifications in the reaction scheme used by Caremani et al. (2015) to simulate the mechano‐kinetic parameters underlying the force–velocity relation of the fast mammalian skeletal muscle (rabbit psoas) at 12°C. The unique modification of the scheme of fig. 1 of Caremani et al. (2015) consists of the introduction of a transition in parallel with step 5 (the ADP release step), which allows the motors undergoing a negative strain under V ₀ shortening to detach before the ADP release and form the unconventional detached M^‡ ₄.ADP state (Fig. 4 A, step 10). This implementation provides a straightforward explanation for the transient excess of shortening heat (Homsher et al., 1981; Woledge et al., 1985). Depending on the force on the filament, M^‡ ₄.ADP motors can be converted to motors in the OFF state (step 12) or rapidly release the ADP and bind another ATP (step 11). For reasons of clarity, in Fig. 4 A only the part of the reaction scheme relevant to this aspect is reported, everything else being unchanged with respect to the model described in Caremani et al. (2015). M₄ is the last of the four structural states of the attached motor (M₁–M₄) generated by three consecutive transitions (M₁→M₂, M₂→M₃, M₃→M₄) each implying a forward ∼3 nm step in the working stroke, the kinetics of which is controlled by the load (Reconditi et al. 2004). In Fig. 4 B the plots versus x (where x is the relative axial position between the motor and the actin site and is zero for the position of the centre of distribution of the attached M₁ motors in isometric contraction) of the forward rate functions for both steps 5 (k ₅′, dashed line) and 10 (k ₁₀, dotted line) of the present model are compared to the plot of the forward rate of step 5 of the original model (k ₅, continuous line from fig. 4D in Caremani et al. 2015). The strain dependence of step 5 assumed in the original model is substituted with the strain‐dependence of step 10. As shown by the superposition of the rate constants in Fig. 4 B, the kinetic requirements of the low load shortening are equally satisfied by either k ₅ or the parallel of k ₅′ and k ₁₀. From the time course of the occupancies of the relevant states during and after 100 ms V ₀ shortening (Fig. 4 D–F) it can be seen that the M₄ ^‡.ADP_OFF motors (Fig. 4 E, dashed line) continue to rise through the whole shortening period and, after the shortening ends, return to zero (in other words the thick filament recovers its 100% ON state) within 50 ms, when the number of attached motors (Fig. 4 F, continuous line) and thus the force (Fig. 4 D, dashed line) have attained their half‐maximum value, as observed (Linari et al. 2015). Since the equilibrium constant of the ON–OFF transition (K ₁₂, Fig. 4 C, continuous line) must switch in favour of the ON state as soon as the force starts to rise, the observed time and force dependence of the recovery of the ON state is obtained by selecting a relatively low value of the rate constant k _–12 (100 s⁻¹ at maximum, Fig. 4 C, dashed line). In Fig. 4 F the superimposition of the time courses of the duty ratio r (dashed line) and the number of attached motors (continuous line) allows a better appreciation of the different behaviour during unloaded shortening. The superimposition of time courses in Fig. 4 G makes evident the sequence of the transient increase of the flux through step 11 (continuous line, right ordinate) with respect to the ATP hydrolysis rate (dashed line, left ordinate).