Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2016 Dec 29;121(3):1507–1514. doi: 10.1021/acs.jpcc.6b11235

Investigating State Restriction in Fluorescent Protein FRET Using Time-Resolved Fluorescence and Anisotropy

Thomas S Blacker †,‡,§, WeiYue Chen ∥, Edward Avezov ⊥, Richard J Marsh †, Michael R Duchen §, Clemens F Kaminski ∥, Angus J Bain †,‡,*
PMCID: PMC5309863  PMID: 28217242

Abstract

graphic file with name jp-2016-11235g_0007.jpg

Most fluorescent proteins exhibit multiexponential fluorescence decays, indicating a heterogeneous excited state population. FRET between fluorescent proteins should therefore involve multiple energy transfer pathways. We recently demonstrated the FRET pathways between EGFP and mCherry (mC), upon the dimerization of 3-phosphoinositide dependent protein kinase 1 (PDK1), to be highly restricted. A mechanism for FRET restriction based on a highly unfavorable κ2 orientation factor arising from differences in donor–acceptor transition dipole moment angles in a far from coplanar and near static interaction geometry was proposed. Here this is tested via FRET to mC arising from the association of glutathione (GSH) and glutathione S-transferase (GST) with an intrinsically homogeneous and more mobile donor Oregon Green 488 (OG). A new analysis of the acceptor window intensity, based on the turnover point of the sensitized fluorescence, is combined with donor window intensity and anisotropy measurements which show that unrestricted FRET to mC takes place. However, a long-lived anisotropy decay component in the donor window reveals a GST-GSH population in which FRET does not occur, explaining previous discrepancies between quantitative FRET measurements of GST-GSH association and their accepted values. This reinforces the importance of the local donor–acceptor environment in mediating energy transfer and the need to perform spectrally resolved intensity and anisotropy decay measurements in the accurate quantification of fluorescent protein FRET.

Introduction

Förster Resonance Energy Transfer (FRET) describes the nonradiative transmission of electronic energy from a donor molecule to a nearby acceptor due to dipole–dipole coupling.1,2 FRET measurements have found widespread application in the study of nanoscale processes in the biosciences, such as changes in conformation and intermolecular interactions.3,4 FRET is well understood for homogeneous populations of donors and acceptors,2,5 but in recent years, the use of genetically encodable fluorescent protein FRET pairs has become widespread.6 Many fluorescent proteins exhibit multiexponential fluorescence decay kinetics,7−9 indicating the existence of multiple emitting states, molecular conformations, or local environments. Noninteracting populations in fluorescent protein FRET have previously been recognized.10−12 However, it remains an open question as to whether these arise as an intrinsic property of the dipole–dipole interaction, environmental heterogeneity such as variations in the FRET interaction geometry, or misfolding leading to the production of subpopulations of chromophores incapable of participating in FRET.10,13

Accurate quantitative application of fluorescent protein FRET is crucially dependent on the correct understanding of the underlying photophysics. This point is strongly evidenced by our recent work on the homodimerization of 3-phosphoinositide dependent kinase-1 (PDK1) using the standard FRET pair of enhanced green fluorescent protein (EGFP) and mCherry (mC).14 Both proteins exhibit intrinsic biexponential fluorescence decays.15 Combining time-resolved fluorescence intensity and anisotropy measurements of the donor and acceptor, we found that FRET was highly restricted, involving transfer from only one emitting state of EGFP to the minority decay component of mC. In contrast, when emulating unrestricted FRET by the optical excitation of mC across the donor–acceptor spectral overlap, no such constraint was observed.15 It was calculated that conventional intensity based FRET techniques,16−21 which would not report this restriction, would lead to an underestimation of the true PDK1 interacting fraction by over an order of magnitude.14

We proposed two mechanisms for the FRET restrictions between EGFP and mC.15 First, that the intrinsic energy transfer rates for the two donor (EGFP) populations were widely dissimilar. Given close fluorescence lifetimes for the two populations (2.4 ns and 3.1 ns15) this hypothesis would imply a low radiative rate coupled with a “compensating” fast nonradiative decay channel for the FRET inactive donors. However, precision measurements of the stimulated emission depletion (STED) dynamics in recombinant EGFP in our group indicate that both emitting populations have strong transition dipole moments.22 This mitigates against a significant difference in the radiative decay rates of the two populations. The second mechanism recognized that, in a far from coplanar FRET interaction geometry, small differences in the relative donor–acceptor transition dipole moment angles for the two populations would give rise to a large disparity in the κ2 orientation parameters23 and the corresponding FRET rates.

Here we test the second hypothesis by probing FRET to mC in a system where EGFP is replaced by the synthetic fluorophore Oregon Green 48824 (OG). OG is spectrally similar to EGFP but is characterized by a monoexponential fluorescence lifetime of ∼4 ns.25 Moreover, given its considerably smaller hydrodynamic volume and molecular weight compared to EGFP (880 Å3 and 0.5 kDa vs 58000 Å3 and 29 kDa25−27), OG displays a significantly higher degree of orientational mobility. FRET with OG as opposed to EGFP should therefore, in principle, be characterized by less complex population dynamics and should sample a greater range of donor–acceptor orientations.

Fluorescence Dynamics in FRET between Oregon Green and mCherry

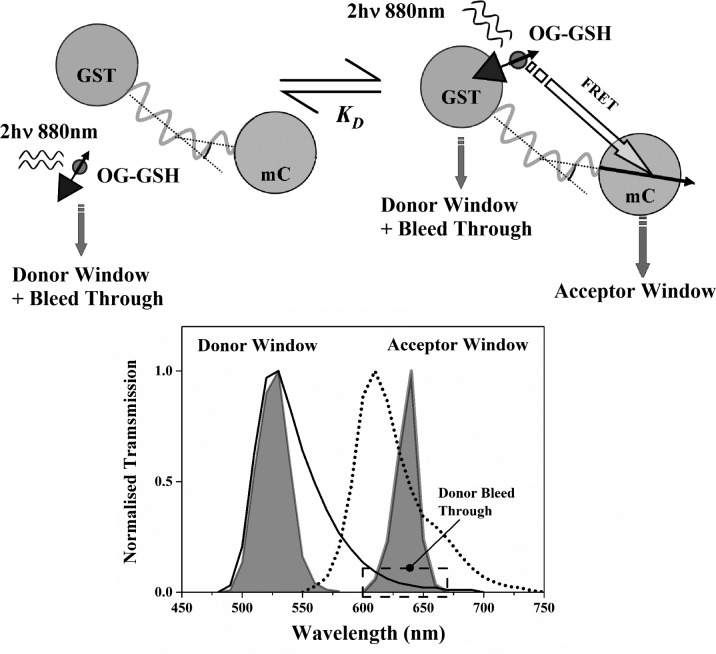
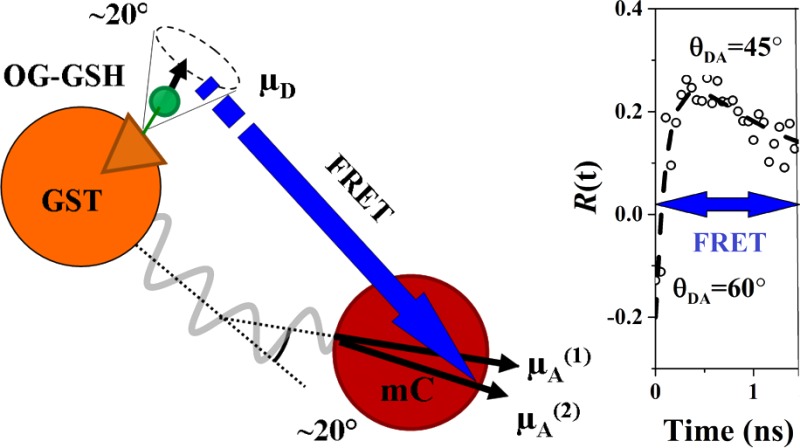
The FRET system studied here consists of mC fused to the enzyme glutathione S-transferase (GST) and its substrate, glutathione (GSH), attached to OG. FRET between OG and mC can occur when GSH attaches to its binding site on GST. The affinity of GSH for GST is sufficiently high (KD ≈ 20 μM28) that their binding is routinely exploited in the purification of recombinant proteins,29,30 ensuring a significant population of donor–acceptor complexes for FRET measurements. An overview of the fluorescence and FRET dynamics in the OG-GSH/GST-mC system is illustrated in Figure 1. Fluorescence following two-photon excitation of OG at 880 nm is detected in two spectral windows: 515–540 nm (the donor window ΔλD) and 630–650 nm (the acceptor window ΔλA). The contribution of mC fluorescence in the donor window is negligible (see Supporting Information Appendix S1); however, there is unavoidable “bleed through” of OG emission superimposed on the sensitized mC emission arising from FRET (see Figure 1). Characterization of the intrinsic fluorescence and anisotropy properties of OG-GSH (donor) and GST-mC (acceptor) is thus an essential first step in the analysis of the energy transfer dynamics of these molecules.

Figure 1.

Figure 1

Open in a new tab

Illustration of the fluorescence dynamics between OG and mC arising from the association of GSH and GST. Free and bound OG-GSH is excited by two-photon excitation at 880 nm. This causes intrinsic OG and sensitized (FRET excited) mC fluorescence which collectively span 490–750 nm. Time-resolved fluorescence intensity and anisotropy measurements are made in two spectral windows illustrated by the gray areas (filter transmission curves) superimposed on the OG (solid line) and mC (dotted line) emission spectra. Donor window measurements report solely OG fluorescence dynamics (spontaneous emission from free OG-GSH and spontaneous emission plus nonradiative FRET transfer from OG-GSH-GST-mC). The contribution from OG (donor) bleed through in the acceptor window leads to more complex intensity and anisotropy dynamics, necessitating the new approaches applied in this work.

Materials and Methods

Fluorescent Probes

Production of OG-GSH and recombinant GST-mC has been detailed elsewhere.24 In this work, FRET was studied in mixtures of approximately 60 μM OG-GSH and 30 μM GST-mC in phosphate buffered saline at pH 7.4. Given a KD of 20 μM for the GSH-GST interaction, this implied that approximately a quarter of the total OG-GSH would be part of a complex with GST-mC.28 Photophysical characterization of the isolated donor and acceptor molecules was performed on solutions of approximately 10 μM OG-GSH and 4 μM GST-mC, respectively. For two-photon characterization (see Supporting Information Appendix S2), unconjugated OG was obtained from Life Technologies (Paisley, UK).

Fluorescence Intensity and Anisotropy Measurements

Time-resolved fluorescence measurements were performed using time-correlated single photon counting (TCSPC)31 using an apparatus described previously.15,32 Experimental procedures are detailed in Supporting Information Appendix S3. Fluorescence intensity and anisotropy analysis followed established protocols15,32 (see Supporting Information Appendix S4).

Results and Discussion

OG-GST and GST-mC: Intrinsic Fluorescence and Anisotropy Dynamics

Measurements of the fundamental population and rotational dynamics of the isolated donor and acceptor molecules are detailed in Supporting Information Appendix S5. Akin to OG in solution,25 OG-GSH fluorescence decayed with a single lifetime of 4.26(±0.06) ns and yielded rotational correlation times of 0.251(±0.008) ns and 0.279(±0.003) ns with single-photon and two-photon excitation, respectively. Measurements emulating unrestricted FRET to GST-mC used single photon excitation at wavelengths spanning the donor–acceptor spectral overlap with fluorescence detection in the acceptor window (Figure 1). Across this range, GST-mC exhibited a biexponential fluorescence decay with a constant mean lifetime of 1.564(±0.002) ns, in line with previous measurements of recombinant mC.15 Attachment to GST leads to a less marked disparity in the short and long lifetimes, referred hereafter as states 1 and 2, respectively, with overlap-weighted average values of 1.315(±0.002) ns and 1.897(±0.003) ns, with 57.2(±0.2)% of GST-mC in the short lifetime state, lower than for mC alone.15 Weighted by the spectral overlap, the fluorescence anisotropy of GST-mC decayed with a minority amplitude fast decay component of 1.1(±0.1) ns and a majority component with a longer rotational correlation time of 28(±1) ns. Rigid body rotational diffusion, where each of these components corresponds to the motion of a distinct species, was ruled out by poor fits of this composite anisotropy model32 (Supporting Information Equation S6, χR2 = 4.8 ± 0.5) to the data. Models of restricted rotational diffusion of mC relative to GST were found to be more appropriate, with the fitting parameters indicating constrained mC motion within an angular range of between 15° and 20° (see Supporting Information Appendix S5).

Donor Window Intensity and Anisotropy Decays in the Presence of FRET

The differential equations describing OG-mC FRET and their solutions are similar in form to our previous work15 and are set out in Supporting Information Appendix S6. Following two-photon excitation of the OG-GSH/GST-mC mixture at 880 nm, at which direct acceptor excitation can be neglected (Supporting Information Appendix S2), detection of fluorescence in the donor window should in principle yield decay dynamics described by

graphic file with name jp-2016-11235g_m001.jpg 1

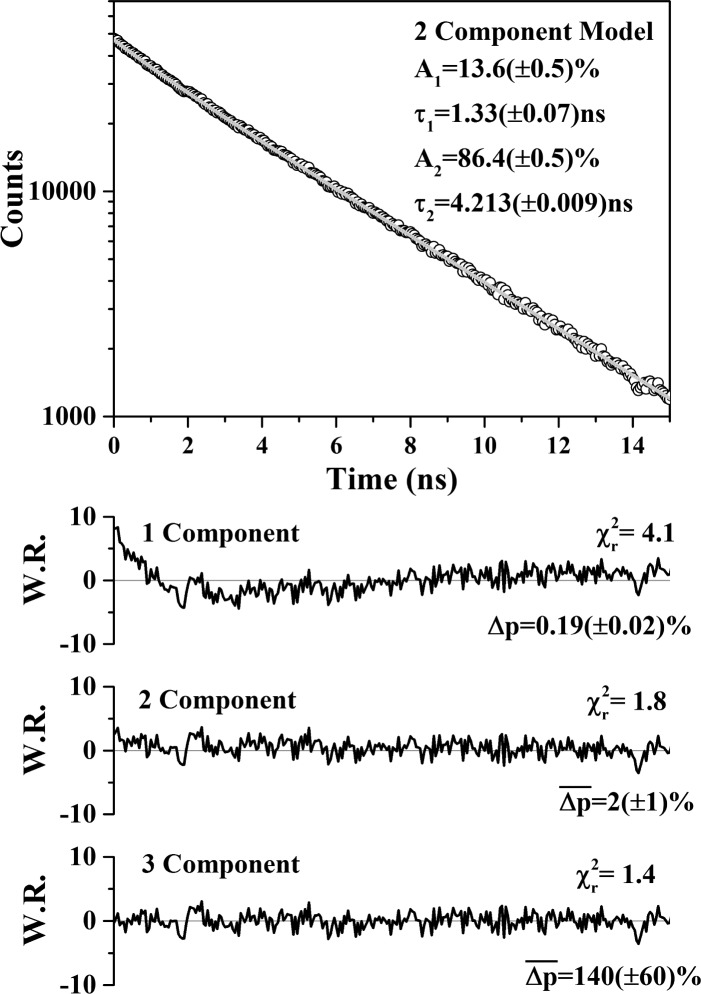
Here F1I and F2I are the fraction of donors participating in FRET to the two emitting states of mC with corresponding FRET rates kFRET1 and kFRET2. Single-, two-, and three-component fits to the data (Figure 2) were performed. From the weighted residuals it was clear that a single exponential decay was a poor description of the fluorescence dynamics. The three-component fit gave a slightly lower χR2 value than that for the two-component model (1.4 vs 1.8). However, the uncertainties in the fitted values were unacceptably large, suggesting overparametrization.33 The two-component fit extracted lifetimes of 4.213(±0.009) ns and 1.33(±0.07) ns. By comparison with the fluorescence lifetime measurements on pure OG-GSH, it was clear the former corresponded to noninteracting OG-GSH, τDNI = 1/kFD with the latter corresponding to the OG-GSH population undergoing FRET. This suggested a total interacting fraction F1I + F2I = 0.136(±0.005), based on the relative amplitudes of the decay components. From eq 1, two interacting donor lifetimes are expected, arising from FRET to each of the two states in GST-mC, corresponding to τD1 = 1/(kFD+kFRET1) and τD2 = 1/(kFD+kFRET2). The recovery of only one interacting lifetime corresponds to one of two possible scenarios. First, that FRET to mC had taken place exclusively to one state, either the short lifetime state (kFRET2 = 0 and F2I = 0) or the longer lived state (kFRET1 = 0 and F1I = 0) or, second, that the rates of energy transfer to both states were sufficiently close as to be indistinguishable in the overall fluorescence decay.

Figure 2.

Figure 2

Open in a new tab

Donor window fluorescence intensity decay of a mixture of 60 μM OG-GSH and 30 μM GST-mC with 880 nm excitation. The decay departs from the single exponential found for OG-GSH and is best fit to a biexponential decay with the 1.33 ns lifetime corresponding to the OG population undergoing FRET with an interacting fraction FI = (F1I+F2I) = 0.136(±0.005). The lifetimes yield a FRET rate of 0.51(±0.04) ns–1.

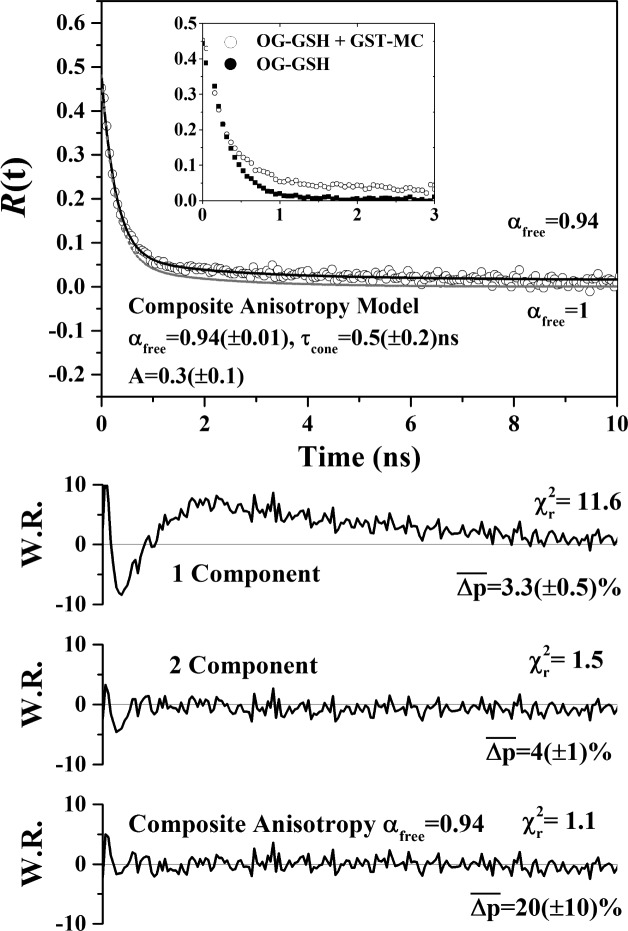
The donor window fluorescence anisotropy should, in principle, contain population weighted contributions from noninteracting freely rotating OG-GSH and a fast lifetime but more slowly rotating component arising from energy transfer within the OG-GSH-GST-mC complex. Due to the fast transfer dynamics (kFRET = 0.5 ns–1), the contribution of the latter to the total fluorescence signal by 2 ns after excitation was calculated to be less than 6% (see Supporting Information Appendix S7). Emission in the donor window should therefore be dominated by noninteracting OG. The measured anisotropy decay is shown in Figure 3, where it can be seen in the inset that FRET does not alter the early time dynamics as would be expected for rapid large angle acceptor motion.34,35 The longer lived anisotropy decay component observed in the OG-GSH GST-mC solution implies the presence of a subpopulation of associating but FRET inactive GSH and GST. An inhomogeneous OG-GSH population is indicated by the poor fit of homogeneous single and double exponential decays to R(t) seen from the weighted residuals. The fluorescence anisotropy of a heterogeneous (composite) system is given by a time dependent weighted sum of the individual anisotropies (Supporting Information Equation S6)15,36

graphic file with name jp-2016-11235g_m002.jpg 2

where the WI(t) and WNI(t) are the time dependent weighting factors of the interacting and noninteracting OG-GSH populations, respectively (Supporting Information Equation S7), and ηfree denotes the fraction of noninteracting OG-GSH that is not bound to GST-mC. The anisotropy is best fit by this model when ROGbound(t) corresponds to the restricted rotational diffusion of OG with a cone angle of 25(±6)°, a local diffusion coefficient D = 0.10(±0.05) ns–1, and ηfree = 0.94(±0.01). A full description of the analysis is set out in the Supporting Information Appendix S7.

Figure 3.

Figure 3

Open in a new tab

Donor window fluorescence anisotropy of OG-GSH. The inset is a comparison of the early time anisotropy for a pure solution of OG-GSH and the OG-GSH GST-mC mixture. R(t) is best described by a composite anisotropy model (black line) in which 6(±1)% of the noninteracting OG-GSH is bound to GST-mC. A fully nonbound noninteracting fraction (ηfree = 1) is unable to reproduce the observed anisotropy (gray line).

The environment of OG-GSH and its local motion when attached to GST is less constrained and more rapid than for EGFP in the PDK1 FRET system (25° vs 15° and 0.1 ns–1 vs 0.01 ns–1).15 Given an interacting fraction of 13.6(±0.5)% (Figure 2), 86.4(±0.5)% of the total OG-GSH population is FRET inactive. From the composite anisotropy analysis, 6(±1)% of this population corresponded to FRET inactive OG-GSH bound to GSH. This is a significant result, as while this corresponds to just 5.2(±0.9)% of the total OG-GSH population, it represents 28(±3)% of the total bound OG-GSH population. Thus, despite the increase in conformational freedom, FRET does not occur in these complexes. It should be noted that conventional intensity decay measurements are insensitive to this phenomenon, which contribute to overestimates of the dissociation constant of GSH and GST previously made using this FRET pair24 (see Supporting Information Appendix S8).

Noninteracting fluorescent protein populations have been observed in previous studies and have been ascribed to the presence of unmatured mC or photoconversion of its chromophore.10,37,38 From our recent work, we know that restricted FRET to only one of the two emitting mC populations is possible.15 To fully investigate the nature of the incomplete FRET between OG and mC, fluorescence intensity and anisotropy measurements in the acceptor window are crucial.

Acceptor Window Intensity and Anisotropy Measurements

As depicted in Figure 1, the composite fluorescence in the acceptor window arises from both sensitized acceptor fluorescence and the bleed through from interacting and noninteracting donor populations.15 The population dynamics that contribute to the acceptor window fluorescence are set out in detail in Supporting Information Appendix S6. With the possibility of FRET to two states in mC, the acceptor window intensity decay I(t,ΔλA) has the form

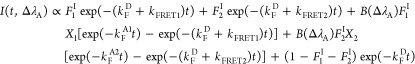graphic file with name jp-2016-11235g_m003.jpg 3

B(ΔλA) quantifies the proportion of acceptor fluorescence detected relative to the donor,15 and Xi is the FRET amplitude to state i with fluorescence decay rate kFAi.

graphic file with name jp-2016-11235g_m004.jpg 4

For states with fluorescence lifetimes that vary over the donor–acceptor spectral overlap, X1 and X2 can be modeled as possessing a single lifetime calculated from the overlap-weighted averages15 (see Supporting Information Appendix S9). The first two terms in eq 3 correspond to the bleed through of interacting donor fluorescence, the third and fourth describe the growth and decay the acceptor emission as a result of FRET transfer, and the final term corresponds to the bleed through of the noninteracting donor fluorescence. In practice the interacting donor bleed through terms have a lower weighting relative to the noninteracting donor bleed through (F1I+F2I = 0.136 vs 1-F1I-F2I = 0.864) and only contribute to the fluorescence at early times. However, even with prior knowledge of some parameters (e.g., kFD, F1I+F2I, kFA1, kFA2), the number of independent decay components involved cannot be resolved reliably, even with good quality time-resolved fluorescence data.33 To obtain a fuller picture of the FRET dynamics, the measurement of additional fluorescence observables is necessary.15 In our study of FRET between EGFP and mC arising from PDK1 homodimerization this was provided by the acceptor window fluorescence anisotropy.15 The large value of the donor–acceptor angle θDA (65°) and the slow rotational diffusion times of both interacting and noninteracting species relative to the energy transfer and excited state lifetimes (krot ≈ 0.05 ns–1 vs kFRET ≈ 0.2 ns–1 and kF ≈ 0.4 ns–1) gave rise to an acceptor window anisotropy that principally depended on the time dependent weighting of a positive anisotropy from the noninteracting donor population with that of the negative anisotropy created by FRET to the acceptor.15 Had FRET to mC been unrestricted, the anisotropy, while exhibiting a rapid drop due to FRET (observed) as the intensity weightings of EGFP and mC became comparable, would have been followed by a subsequent rise as the donor weighting became dominant due to the significantly longer average lifetime of EGFP compared to mC (2.75 ns vs 1.57 ns).15 The absence of this rise in the anisotropy could only occur if FRET had exclusively populated the minority (longer lived) mC species. With OG-GSH/GST-mC, however, the rotational depolarization of the noninteracting donor emission, FRET, and the local motion of OG in the GSH-GST complex all occur on comparable time scales. Consequently the acceptor window anisotropy could not on its own be used as an unequivocal measure of the population dynamics of FRET transfer.

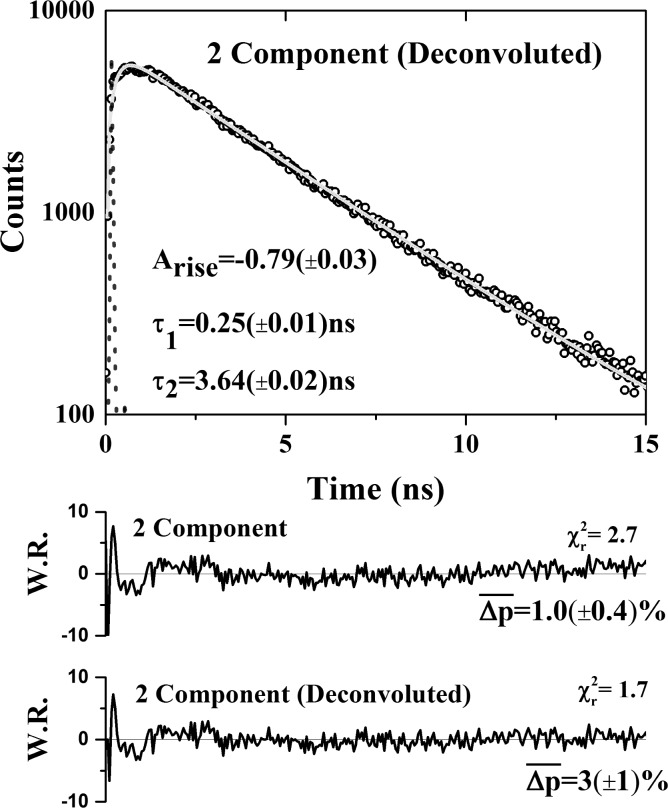
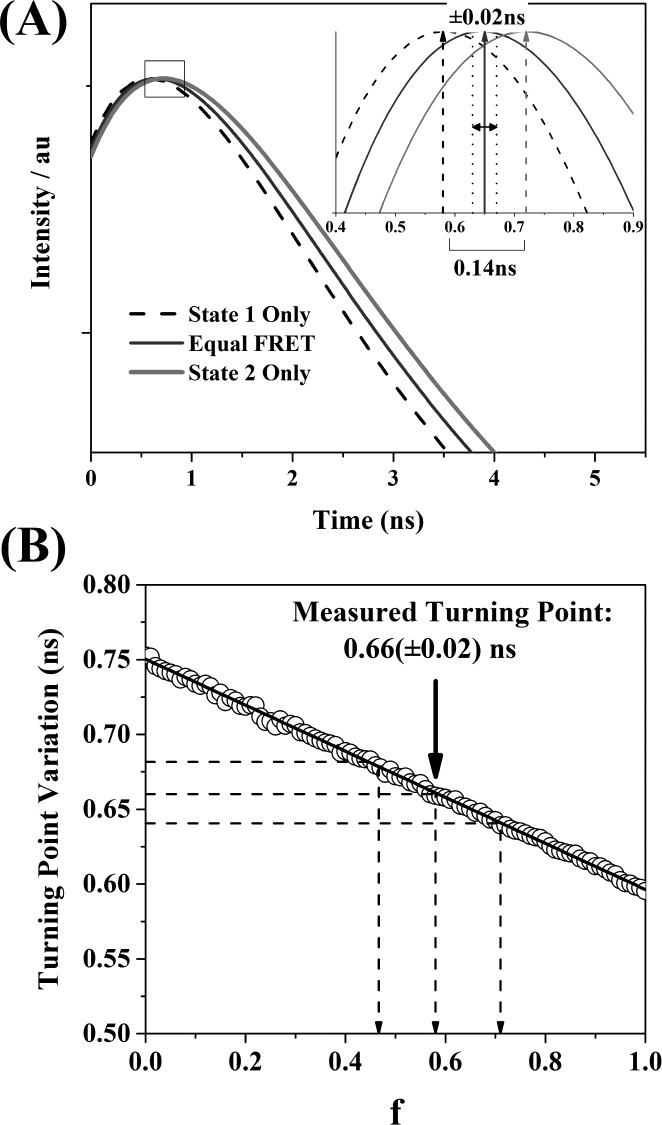
Despite the underlying complexity of the acceptor window intensity signal (eq 3), we have found that a biexponential rise (negative amplitude component) and decay (positive amplitude component) model provides the most accurate description of the measured data possible, even with high signal-to-noise levels.15,39 In the current system, as shown in Figure 4, we observe a rise lifetime of τrise = 0.25(±0.01) ns, a decay lifetime of τdecay = 3.64(±0.02) ns, and ratio of rise to decay amplitudes of |Arise| = 0.79(±0.03). Despite this fit accurately describing the shape of the decay, with χR2 = 1.7 and mean parameter uncertainties of 3(±1)%, previous work in our group has shown that it is not possible to relate these quantities to the underlying parameters describing the FRET interaction, with the degree of noninteracting bleed through (here around 70% of the measured signal, see Supporting Information Appendix S10) playing a significant role in distorting the rise and decay times in the biexponential fits and their corresponding amplitudes (see Supporting Information Appendix S11).39 However, the time at which the sensitized fluorescence plus donor bleed through reached its maximum value, or turnover point, could be directly related to the FRET parameters. This physically significant feature corresponds to the point at which the rate of increase in the fluorescence intensity due to FRET equals the rate of decrease of fluorescence due to emission by both sensitized acceptors and donor bleed through. This position is therefore a function of all the parameters describing the FRET interaction, allowing the determination of unknown parameter values from the output of a simple biexponential fit.39

Figure 4.

Figure 4

Open in a new tab

Fluorescence intensity decay of a mixture of 60 μM OG-GSH and 30 μM GST-mC with 880 nm excitation and detection in the acceptor window. Biexponential fitting yields rise and decay times of 0.25(±0.01) ns and 3.64(±0.02) ns, respectively. The fit parameters imply a turning point of the data set of 0.66(±0.02) ns.

Plots of eq 3 for FRET to only state 1 or state 2, or in equal proportion to both states, are shown in Figure 5A. The turning points of the curves were seen to be sensitive to the proportion of FRET to each state. FRET to only the short lifetime mC state resulted in a turnover point at 0.58 ns, whereas FRET to only the long lifetime state caused a turnover at 0.72 ns. Equal FRET to both states resulted in a turnover point halfway between the two. As such, it appeared that there was a linear dependence of the turnover point on the fraction of FRET to each state. This relationship was theoretically verified by using MATLAB (The Mathworks, USA) to numerically solve eq 3 for its turning point as the proportion of FRET to states 1 and 2 was varied. The turning point was linearly correlated with the fraction of total donors interacting with acceptor state 1, f, with a gradient of −0.1373(±0.005) ns and a y-intercept (all FRET to state 2, f = 0) of 0.7157(±0.0003) ns. However, this solution neglects the impact of any potential artifacts introduced by the presence of an IRF in real acceptor window fluorescence decay data. We therefore performed numerical simulations of the iterative reconvolution fitting process on simulated data sets (Supporting Information Appendix S11). It was confirmed that the turning point of the data decreased linearly with f, as shown in Figure 5B. We observed that the influence of the IRF (fwhm ∼60 ps) was to shift the turning point to later times by, on average, 0.026(±0.005) ns. Nonetheless, a linear relationship was maintained, with gradient of −0.1540 (±0.0005) ns and intercept of 0.7504 (±0.0003) ns. Therefore, based on these simulations, the turning point of 0.66 (±0.02) ns extracted from the real acceptor window data would imply that 60(±10)% of the interacting acceptors are in the short lifetime state. This mirrors the 57.2(±0.2)% of short lifetime GST-mC present with optical excitation weighted by the donor–acceptor spectral overlap, suggesting that acceptor state selection is completely relaxed in the OG-GSH-GST-mC system.

Figure 5.

Figure 5

Open in a new tab

(A) The turning point of the theoretical acceptor window fluorescence decay based on eq 3 is sensitive to changes in the proportion of FRET to the two states available in GST-mC. (B) In numerical simulations, the turning point position decreased linearly as the fraction of interacting acceptors in the short lifetime state, f, was varied from 0 to 1. The experimentally observed turning point of 0.66(±0.02) ns therefore implied that 60(±10)% of the acceptors were in the short lifetime state, reflecting that observed with optical excitation.

The anisotropy decay of the FRET mixture in the acceptor window will be an associated combination of the anisotropy decays of the sensitized acceptor and the donor bleed through. As shown in Figure 6A, a model in which the donor–acceptor angle θDA remains static over the time scales at which FRET occurs (Supporting Information Appendix S12) could not be fit to the measured data set. For example, the model giving the lowest χR2 (θDA = 40°) fitted well to the tail of the decay, but the anisotropy was greatly underestimated at delay times below 1.5 ns. Thus, it is likely that the functional form of the sensitized acceptor fluorescence anisotropy decay was made more complex due to the orientational freedom of the donor.

Figure 6.

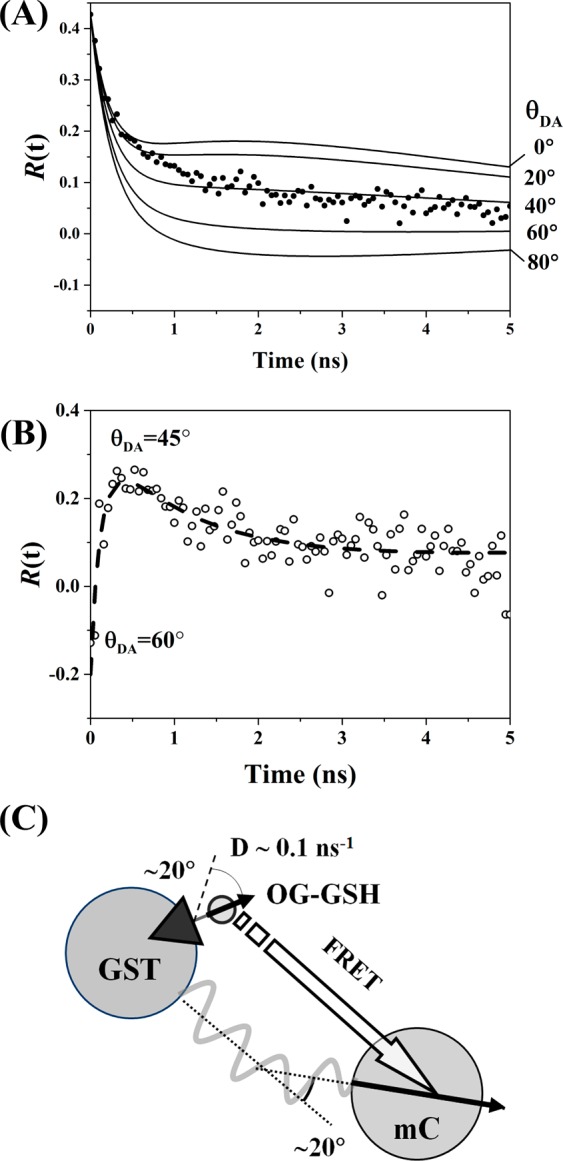
Figure 6

Open in a new tab

(A) Fluorescence anisotropy decay of a mixture of 60 μM OG-GSH and 30 μM GST-mC with 880 nm excitation and detection in the acceptor window (630–650 nm). The fixed dipole angle model cannot be fit to the data with χR2 minimized at an unacceptable value of 3.05 with θDA ∼ 40°. (B) Predicted form of the intrinsic acceptor anisotropy by subtraction of the calculated donor bleed through from the composite anisotropy measured in (A). The initial rise, plateau, and decay imply a time-varying θDA consistent with the measured orientational freedom of both the donor and acceptor. (C) Schematic structure of the OG-GSH-GST-mC complex, the negative initial anisotropy recovered in (B) implies a close to 60° value for θDA.

The form of RAI(t) was estimated by performing an intensity-weighted subtraction of the theoretical donor window anisotropy contribution predicted from the experimental data (Figure 6B) and also from the best (arbitrary) mathematical representation of the data provided by a three exponential fit (χR2 = 1.1), yielding the dashed line in Figure 6B, as detailed in Supporting Information Appendix S12. RAI(t) is characterized by a negative anisotropy (−0.13) at early time followed by a rise peaking around 0.4 ns later at approximately 0.24, followed by a slower decay. Based on the approach of Lipari and Szabo,40 the diffusion coefficient of the donor motion in OG-GSH-GST-mC was calculated to be the same order of magnitude as kFRET (0.1 ns–1 compared to 0.5 ns–1). In this regime, an analytical model for RAI(t) developed by Tanaka et al.35 is seen to be sensitive to the relative orientations of the donor and acceptor rotation axes and their diffusion coefficients41,42 yielding rise and decay characteristics similar to Figure 6B. At early times RAI(t) will largely correspond to the orientational dynamics of FRET transfer (i.e., a time evolving θDA), and at later times the intrinsic rotational dynamics of mC will play a larger role. The early time value of RAI(t) (via Supporting Information Equation S49) thus corresponds to an initial value for θDA of around 60° decreasing to 45° as shown in Figure 6B. These observations, while largely qualitative, indicate that the FRET interaction is far from static, reflecting the orientational freedom of both donor and acceptor in the GSH-GST complex (Figure 6C). Approaches such as molecular dynamics simulations of RAI(t) as recently demonstrated by Nunthaboot et al.43 may allow a more quantitative investigation of this system.

Conclusions

By combining time-resolved fluorescence intensity and anisotropy measurements of the OG-GSH-GST-mC complex, we have shown that the state restriction observed in fluorescent protein to fluorescent protein FRET is relaxed when the donor is replaced by a more mobile synthetic fluorophore. This demonstrates that the restricted geometry of a fluorescent protein tandem construct, which will remain effectively static on the time scales over which FRET occurs, is a significant cause of the differential energy transfer dynamics between the heterogeneous excited state populations.15 As such, the precise configuration of a fluorescent protein FRET pair will not only govern the fluorescence decay rate of the interacting donor but also cause the fluorescence lifetime and quantum yield of the sensitized acceptor to differ from that observed with direct optical excitation. Failure to account for these phenomena in both intensity-based and time-resolved fluorescence studies could therefore result in greatly inaccurate quantitative measurements of interacting fractions and FRET efficiencies.

In the OG-GSH-GST-mC system, the rapid depolarization of the donor fluorescence ruled out use of the (composite) acceptor window anisotropy as a means of probing the acceptor population dynamics. A new approach to the analysis of the acceptor window fluorescence intensity showed that the measured turnover point of the data was sensitive to the proportion of FRET to each state to within ±10%, a degree of precision largely determined by the ∼0.6 ns separation of the two acceptor lifetimes. As the turning point is sensitive to each parameter describing the FRET interaction (Supporting Information Equation S45), and only relies on a simple biexponential fit, this method of analysis could be applicable in situations where FRET dynamics require extraction from lower signal-to-noise data, as for example in live cell fluorescence lifetime imaging microscopy (FLIM).

Despite the apparent relaxation of state restriction in FRET to mC, donor window anisotropy measurements revealed the presence of a bound but FRET-inactive OG-GSH population pointing to the presence of FRET inactive mC. FRET inactive acceptor states have previously been ascribed to “nonmatured” protein populations with altered spectral characteristics, protonated forms of the fluorophore, photoconversion during the FRET process, or excited-state blinking.10−12 Vogel et al. considered the existence of unfavorable, static donor–acceptor geometries as the most likely cause of incomplete FRET between fluorescent proteins.12 Our work points to this as the major cause of FRET restriction between EGFP and mC in the PDK1 homodimer.15 However, the discovery of a noninteracting population of OG-GSH-GST-mC complexes points to a continuing role for both photophysical and protein structural heterogeneity as factors for consideration in the interpretation of incomplete FRET with fluorescent proteins.

In conclusion, we have shown that energy transfer restrictions are relaxed by increased angular freedom in the molecular frame, emphasizing the importance of the local donor–acceptor geometry in controlling fluorescent protein FRET. Nevertheless, incomplete energy transfer in OG-GSH-GST-mC remained, the detection of which was made possible through donor window anisotropy measurements, a nonstandard FRET technique. Our work demonstrates both the advantage and necessity of a full understanding of the photophysics and the local environment of each donor–acceptor pair and also the critical importance of performing spectrally resolved intensity and anisotropy decay measurements in the accurate quantification of fluorescent protein FRET.

Acknowledgments

Work at UCL was supported through BBSRC grant BB/L020874/1. W.Y.C. was funded by the China Scholarship Council (CSC) and Cambridge Trust (CCEIT). C.F.K. acknowledges Wellcome Trust, MRC, and EPSRC funding. This project was initiated during the inaugural Professor Anne Warner postdoctoral fellowship awarded to T.S.B. through the CoMPLEX Doctoral Training Centre at UCL. We dedicate this paper to the memory of Anne Warner in recognition of her unique and pioneering role in supporting interdisciplinary research and developing postgraduate training at the physical/life sciences interface.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.6b11235.

  • Extended methods and discussion, absorption and emission spectra, fluorescence and anisotropy decay fits and data tables, turning point modeling and supporting references (Appendices S1–S12, Figures S1–S19, and Tables S1–S4) (PDF)

Author Present Address

# Cancer Cell Biology & Imaging, King’s College London, New Hunt’s House, Newcomen Street, London SE1 1UL, United Kingdom.

The authors declare no competing financial interest.

Supplementary Material

jp6b11235_si_001.pdf (1.2MB, pdf)

References

  1. Scholes G. D. Long-Range Resonance Energy Transfer in Molecular Systems. Annu. Rev. Phys. Chem. 2003, 54, 57–87. 10.1146/annurev.physchem.54.011002.103746. [DOI] [PubMed] [Google Scholar]
  2. Akrap N.; Seidel T.; Barisas B. G. Förster Distances for Fluorescence Resonant Energy Transfer between mCherry and Other Visible Fluorescent Proteins. Anal. Biochem. 2010, 402 (1), 105–106. 10.1016/j.ab.2010.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Vafabakhsh R.; Levitz J.; Isacoff E. Y. Conformational Dynamics of a Class C G-Protein-Coupled Receptor. Nature 2015, 524 (7566), 497–501. 10.1038/nature14679. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Yang P. S.; Johny M. B.; Yue D. T. Allostery in Ca2+ Channel Modulation by Calcium-Binding Proteins. Nat. Chem. Biol. 2014, 10 (3), 231–238. 10.1038/nchembio.1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Patterson G. H.; Piston D. W.; Barisas B. G. Förster Distances between Green Fluorescent Protein Pairs. Anal. Biochem. 2000, 284 (2), 438–440. 10.1006/abio.2000.4708. [DOI] [PubMed] [Google Scholar]
  6. Piston D. W.; Kremers G.-J. Fluorescent Protein FRET: The Good, the Bad and the Ugly. Trends Biochem. Sci. 2007, 32 (9), 407–414. 10.1016/j.tibs.2007.08.003. [DOI] [PubMed] [Google Scholar]
  7. Rizzo M. A.; Springer G. H.; Granada B.; Piston D. W. An Improved Cyan Fluorescent Protein Variant Useful for FRET. Nat. Biotechnol. 2004, 22 (4), 445–449. 10.1038/nbt945. [DOI] [PubMed] [Google Scholar]
  8. Borst J. W.; Hink M. A.; van Hoek A.; Visser A. J. W. G. Effects of Refractive Index and Viscosity on Fluorescence and Anisotropy Decays of Enhanced Cyan and Yellow Fluorescent Proteins. J. Fluoresc. 2005, 15 (2), 153–160. 10.1007/s10895-005-2523-5. [DOI] [PubMed] [Google Scholar]
  9. Hess S. T.; Sheets E. D.; Wagenknecht-Wiesner A.; Heikal A. A. Quantitative Analysis of the Fluorescence Properties of Intrinsically Fluorescent Proteins in Living Cells. Biophys. J. 2003, 85 (4), 2566–2580. 10.1016/S0006-3495(03)74679-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Visser A. J. W. G.; Laptenok S. P.; Visser N. V.; van Hoek A.; Birch D. J. S.; Brochon J.-C.; Borst J. W. Time-Resolved FRET Fluorescence Spectroscopy of Visible Fluorescent Protein Pairs. Eur. Biophys. J. 2010, 39 (2), 241–253. 10.1007/s00249-009-0528-8. [DOI] [PubMed] [Google Scholar]
  11. Millington M.; Grindlay G. J.; Altenbach K.; Neely R. K.; Kolch W.; Bencina M.; Read N. D.; Jones A. C.; Dryden D. T. F.; Magennis S. W. High-Precision FLIM-FRET in Fixed and Living Cells Reveals Heterogeneity in a Simple CFP-YFP Fusion Protein. Biophys. Chem. 2007, 127 (3), 155–164. 10.1016/j.bpc.2007.01.008. [DOI] [PubMed] [Google Scholar]
  12. Vogel S. S.; Nguyen T. A.; van der Meer B. W.; Blank P. S. The Impact of Heterogeneity and Dark Acceptor States on FRET: Implications for Using Fluorescent Protein Donors and Acceptors. PLoS One 2012, 7 (11), e49593. 10.1371/journal.pone.0049593. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Laptenok S. P.; Borst J. W.; Mullen K. M.; van Stokkum I. H. M.; Visser A. J. W. G.; van Amerongen H. Global Analysis of Förster Resonance Energy Transfer in Live Cells Measured by Fluorescence Lifetime Imaging Microscopy Exploiting the Rise Time of Acceptor Fluorescence. Phys. Chem. Chem. Phys. 2010, 12 (27), 7593–7602. 10.1039/b919700a. [DOI] [PubMed] [Google Scholar]
  14. Masters T. A.; Calleja V.; Armoogum D. A.; Marsh R. J.; Applebee C. J.; Laguerre M.; Bain A. J.; Larijani B. Regulation of 3-Phosphoinositide-Dependent Protein Kinase 1 Activity by Homodimerization in Live Cells. Sci. Signaling 2010, 3 (145), ra78. 10.1126/scisignal.2000738. [DOI] [PubMed] [Google Scholar]
  15. Masters T. A.; Marsh R. J.; Armoogum D. A.; Nicolaou N.; Larijani B. B.; Bain A. J. Restricted State Selection in Fluorescent Protein Forster Resonance Energy Transfer. J. Am. Chem. Soc. 2013, 135 (21), 7883–7890. 10.1021/ja312230b. [DOI] [PubMed] [Google Scholar]
  16. Erickson M. G.; Alseikhan B. A.; Peterson B. Z.; Yue D. T. Preassociation of Calmodulin with Voltage-Gated Ca2+ Channels Revealed by FRET in Single Living Cells. Neuron 2001, 31 (6), 973–985. 10.1016/S0896-6273(01)00438-X. [DOI] [PubMed] [Google Scholar]
  17. Gordon G. W.; Berry G.; Liang X. H.; Levine B.; Herman B. Quantitative Fluorescence Resonance Energy Transfer Measurements Using Fluorescence Microscopy. Biophys. J. 1998, 74 (5), 2702–2713. 10.1016/S0006-3495(98)77976-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Chen H.; Puhl H. L.; Koushik S. V.; Vogel S. S.; Ikeda S. R. Measurement of FRET Efficiency and Ratio of Donor to Acceptor Concentration in Living Cells. Biophys. J. 2006, 91 (5), L39–L41. 10.1529/biophysj.106.088773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hoppe A.; Christensen K.; Swanson J. A. Fluorescence Resonance Energy Transfer-Based Stoichiometry in Living Cells. Biophys. J. 2002, 83 (6), 3652–3664. 10.1016/S0006-3495(02)75365-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Nagy P.; Bene L.; Hyun W. C.; Vereb G.; Braun M.; Antz C.; Paysan J.; Damjanovich S.; Park J. W.; Szöllsi J. Novel Calibration Method for Flow Cytometric Fluorescence Resonance Energy Transfer Measurements between Visible Fluorescent Proteins. Cytometry, Part A 2005, 67A (2), 86–96. 10.1002/cyto.a.20164. [DOI] [PubMed] [Google Scholar]
  21. Elder A.; Domin A.; Kaminski Schierle G.; Lindon C.; Pines J.; Esposito A.; Kaminski C. A Quantitative Protocol for Dynamic Measurements of Protein Interactions by Forster Resonance Energy Transfer-Sensitized Fluorescence Emission. J. R. Soc., Interface 2009, 6 (Suppl_1), S59–S81. 10.1098/rsif.2008.0381.focus. [DOI] [Google Scholar]
  22. Masters T. A.Time-Resolved Fluorescence Studies of Enhanced Green Fluorescent Protein and the Molecular Dynamics of 3-Phosphoinositide Dependent Protein Kinase 1, Dr. Thesis, UCL (University Coll. London), 2009. [Google Scholar]
  23. Dale R. E.; Eisinger J.; Blumberg W. E. The Orientational Freedom of Molecular Probes. The Orientation Factor in Intramolecular Energy Transfer. Biophys. J. 1979, 26 (2), 161–193. 10.1016/S0006-3495(79)85243-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Chen W.; Avezov E.; Schlachter S. C.; Gielen F.; Laine R. F.; Harding H. P.; Hollfelder F.; Ron D.; Kaminski C. F. A Method to Quantify FRET Stoichiometry with Phasor Plot Analysis and Acceptor Lifetime Ingrowth. Biophys. J. 2015, 108 (5), 999–1002. 10.1016/j.bpj.2015.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rusinova E.; Tretyachenko-Ladokhina V.; Vele O. E.; Senear D. F.; Alexander Ross J. B. Alexa and Oregon Green Dyes as Fluorescence Anisotropy Probes for Measuring Protein–protein and Protein–nucleic Acid Interactions. Anal. Biochem. 2002, 308 (1), 18–25. 10.1016/S0003-2697(02)00325-1. [DOI] [PubMed] [Google Scholar]
  26. Bhunia D.; Chowdhury R.; Bhattacharyya K.; Ghosh S. Fluorescence Fluctuation of an Antigen-Antibody Complex: Circular Dichroism, FCS and smFRET of Enhanced GFP and Its Antibody. Phys. Chem. Chem. Phys. 2015, 17 (38), 25250–25259. 10.1039/C5CP04908C. [DOI] [PubMed] [Google Scholar]
  27. Müller C. B.; Loman A.; Pacheco V.; Koberling F.; Willbold D.; Richtering W.; Enderlein J. Precise Measurement of Diffusion by Multi-Color Dual-Focus Fluorescence Correlation Spectroscopy. EPL (Europhysics Lett. 2008, 83 (4), 46001. 10.1209/0295-5075/83/46001. [DOI] [Google Scholar]
  28. Armstrong R. N. Glutathione S-Transferases: Reaction Mechanism, Structure, and Function. Chem. Res. Toxicol. 1991, 4 (2), 131–140. 10.1021/tx00020a001. [DOI] [PubMed] [Google Scholar]
  29. Smith D. B.; Johnson K. S. Single-Step Purification of Polypeptides Expressed in Escherichia Coli as Fusions with Glutathione S-Transferase. Gene 1988, 67 (1), 31–40. 10.1016/0378-1119(88)90005-4. [DOI] [PubMed] [Google Scholar]
  30. Harper S.; Speicher D. W. Purification of Proteins Fused to Glutathione S-Transferase. Methods Mol. Biol. 2011, 681, 259–280. 10.1007/978-1-60761-913-0_14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Becker W.Advanced Time-Correlated Single Photon Counting Applications; 2015. [Google Scholar]
  32. Blacker T. S.; Marsh R. J.; Duchen M. R.; Bain A. J. Activated Barrier Crossing Dynamics in the Non-Radiative Decay of NADH and NADPH. Chem. Phys. 2013, 422, 184–194. 10.1016/j.chemphys.2013.02.019. [DOI] [Google Scholar]
  33. Köllner M.; Wolfrum J. How Many Photons Are Necessary for Fluorescence-Lifetime Measurements?. Chem. Phys. Lett. 1992, 200 (1–2), 199–204. 10.1016/0009-2614(92)87068-Z. [DOI] [Google Scholar]
  34. White S. S.; Li H.; Marsh R. J.; Piper J. D.; Leonczek N. D.; Nicolaou N.; Bain A. J.; Ying L.; Klenerman D. Characterization of a Single Molecule DNA Switch in Free Solution. J. Am. Chem. Soc. 2006, 128 (35), 11423–11432. 10.1021/ja0614870. [DOI] [PubMed] [Google Scholar]
  35. Tanaka F.; Mataga N. Dynamic Depolarization of Interacting Fluorophores. Effect of Internal Rotation and Energy Transfer. Biophys. J. 1982, 39 (2), 129–140. 10.1016/S0006-3495(82)84500-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ludescher R. D.; Peting L.; Hudson S.; Hudson B. Time-Resolved Fluorescence Anisotropy for Systems with Lifetime and Dynamic Heterogeneity. Biophys. Chem. 1987, 28 (1), 59–75. 10.1016/0301-4622(87)80075-3. [DOI] [PubMed] [Google Scholar]
  37. Kremers G.-J.; Hazelwood K. L.; Murphy C. S.; Davidson M. W.; Piston D. W. Photoconversion in Orange and Red Fluorescent Proteins. Nat. Methods 2009, 6 (5), 355–358. 10.1038/nmeth.1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Macdonald P. J.; Chen Y.; Mueller J. D. Chromophore Maturation and Fluorescence Fluctuation Spectroscopy of Fluorescent Proteins in a Cell-Free Expression System. Anal. Biochem. 2012, 421 (1), 291–298. 10.1016/j.ab.2011.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Blacker T. S.; Duchen M. R.; Bain A. J.. Heterogeneity and Restricted State Selection in FRET with Fluorescent Proteins; International Society for Optics and Photonics: 2016; p 971401. [Google Scholar]
  40. Lipari G.; Szabo A. Effect of Librational Motion on Fluorescence Depolarization and Nuclear Magnetic Resonance Relaxation in Macromolecules and Membranes. Biophys. J. 1980, 30 (3), 489–506. 10.1016/S0006-3495(80)85109-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tanaka F. Theory of Time-Resolved Fluorescence under the Interaction of Energy Transfer in a Bichromophoric System: Effect of Internal Rotations of Energy Donor and Acceptor. J. Chem. Phys. 1998, 109 (3), 1084. 10.1063/1.476651. [DOI] [Google Scholar]
  42. Tanaka F. Effects of Internal Rotations on the Time-Resolved Fluorescence in a Bichromophoric Protein System Under the Energy Transfer Interaction. J. Fluoresc. 2000, 10 (1), 13–20. 10.1023/A:1009427327771. [DOI] [Google Scholar]
  43. Nunthaboot N.; Tanaka F.; Kokpol S.; Visser N. V.; van Amerongen H.; Visser A. J. W. G. Molecular Dynamics Simulation of Energy Migration between Tryptophan Residues in Apoflavodoxin. RSC Adv. 2014, 4 (59), 31443. 10.1039/C4RA03779K. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp6b11235_si_001.pdf (1.2MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES